1 Introduction

Computer-aided engineering (CAE) has become a norm in the past decades for accelerating product development. Now, we are equipped to run complex simulations, but are usually limited while formulating the most effective design of the geometry during the design development phase. This is one of the most time-consuming and creatively demanding phases in product development as aesthetics, functionality, manufacturability and feasibility have to be taken into consideration.

Most structural optimization methods evaluate the most optimal design from the strain/stress graph (Madsen et al. 2000; Papadrakakis et al. 1998), but it neglects the possibility of having an entirely new design unrelated to the existing one as shown in (Linden 2002). When stress/strain graph is taken as the base for design, only modifications to the existing design at the selected parameters can be achieved. With this approach, degrees of freedom for the optimization engine is constrained, resulting in restricted solutions. Use of large set of points without fitting techniques allows the optimization engine to search the unrestricted solution space. This lack of constraints allows formation of the most unconceivable of designs as demonstrated by (Linden 2002) when he obtained a 5 point bent antenna as the optimal compared to the regular cylindrical and helical antennas. However, modelling the geometry during optimisation routine has been a time-consuming and computationally expensive problem with the traditional NURBS method because it requires a set of grid arranged data points, functions, knot vectors and weights of each of the data points (Xie et al. 2012), and this lays the foundation for the problem that is addressed in this paper. The proposed ADT method is able to provide a non-self-intersecting surface in lesser time as compared to NURBS method.

This paper critically reviews the previous approaches for formulating geometry for CFD methods and design optimization in section 2, Delaunay Triangulation-based algorithm is detailed in section 3, adapted Delaunay triangulation (ADT) Methodology is evaluated and compared with NURBS method in section 4 while its capabilities are discussed in section 5. A case study utilizing proposed method is provided in section 6. The conclusion and extended areas of applications are discussed in section 7.

2 A review on geometry generation for simulation and optimization

2.1 Optimization methods and CFD

There are various computational methods and tools available for optimization problems with various constraints and interrelationships (Simpson et al. 2008). Such optimisation problems may have an unexpected solution that completely differs from the existing design (Linden 2002). The goal of these optimization methods is to find the global optimal solutions for satisfying given objective functions. These methods can be widely classified as traditional interpolation methods and artificial intelligence methods (Sobieszczanski-Sobieski and Haftka 1997).

Traditional methods such as metamodeling (Wang and Shan 2006), Kriging (Simpson et al. 2001), conjugate gradient methods (Kannan and Kramer 1994) and the neural network as described by Papadrakakis et al. (Papadrakakis et al. 1998) and Madsen et al. (Madsen et al. 2000) utilise the gradient function that relates the objective function to the design variables and finds the best solution by interpolating the values in the gradient function. It does not have to carry out the entire simulation for each change in the design parameter, and hence provides a faster solution. The gradient function is generated from earlier experiments and previous data are used to train the learning engine of these systems. It is unable to extrapolate from the given set of data for results with the same accuracy.

Although SOA requires more computing effort than gradient projection methods or other local search methods, it does not require gradients of the objective function. In addition, it is not restricted to modify only given design parameters as it can use randomly generated parameter values for evaluation. Various modifications to the population size, mutation probability and selection of individuals can be made to further improve the efficiency (Guo et al. 2010). Plenty of other mechanical design experiments have been conducted for antenna design (Linden 2002; Robinson et al. 2002, vehicle suspension design (Baumal et al. 1998, structural optimisation (Papadrakakis et al. 1998; Robinson et al. 2002) etc. using SOA. The downside to this method is the numerous simulations that need to be run for each set of a design conceived. Such approach has not been evaluated in turbulent and transient CFD studies. All points of contact between the fluid and the geometry in CFD application may not be feasible to define numerically; hence, a rendering of geometry and its transient simulation is necessary. This gives rise to a problem of a great number of geometry designs needing to be rendered and simulated.

2.2 Surface representation methods

Generating surfaces based on unorganized scattered points have been an interesting area of study as it is difficult to incorporate all these points and generate a single continuous 3D surface without holes or intersections (Attali 1998). One of the existing methods tries to fit these points into Bezier or B-Spline surface generating a free-form surface (Leal Narvaez et al. 2011; Pizo and Motta 2009), usually leaving out a number of outlier points for achieving C1 continuity. Research has been made in configuring surfaces from scattered points and is broadly classified (J.-D. Boissonnat and Cazals 2002) as (a) local projections, (b) sculpting methods, (c) implicit methods and (d) deformable models.

Local projections methods described by Boissonnat (Boissonnat 1984) and Levin (Levin 2004) construct the surface as a function defined in a local reference domain. These methods are fast but perform poorly with non-uniform and very sparse datasets. The sculpting methods described in (Boissonnat 1984) and (Amenta et al. 1998) are based on the removal of triangles from a spatial arrangement, such as the Delaunay triangulation. But, reconstructed surface may not pass through all the sample points and may have additional holes. The implicit methods studied as basis function in Ohtake et al. 2003; and NURBS in Leal et al. 2010 and Hoppe et al. 1992 estimate a tangent plane from the sample data and use distance to the plane as a distance function. The zero-set of this function is then sampled at grid points and the surface is generated from these points. The deformable models presented in Hong-Kai et al. 2001 and Wang 2003 from an initial shell to which deformations are applied to minimize a function of energy and reduce deviation. These methods converge to local minima, and hence could be significantly different from the true surface if the initial shell is not appropriately placed.

Sculpting and deformable models based methods require the surface to be smooth and not contain any noise (Boissonnat and Cazals 2002). These methods fail to be robust with noisy-randomly spread points and may require prohibitively large amounts of time to generate the output. Hence, local projections and implicit NURBS-based methods are the most robust and widely used methods for generation of free-form surfaces.

While critically reviewing above approaches, it can be inferred that DT method has distinct advantages over other approaches (Ebeida et al. 2011). Hence, this method has been adopted for configuring free-form surfaces in the research work reported in this paper. This novel approach can generate surface from random points without discounting any point as an outlier as a part of optimisation routine.

3 Surface preparation

3.1 Generating NURBS surface

NURBS are resolution independent and provide smooth curves and excellent continuity with fewer control points. But, there are other parameters that greatly affect the performance of NURBS such as weights, knots and the degree of the curve (Ravi Kumar et al. 2002; Xie et al. 2012). All these values must be perfectly controlled to achieve the desired output as NURBS surface. NURBS requires a rectangular grid of control points that form the individual curves that can be used as guides to form a surface. This topology cannot be extended to incorporate different feature but, can be patched with another such surface to generate complex shapes (Michálková and Bastl 2015).

For this study, in order to generate a NURBS surface from a set of random points, point cloud data was fitted into linearly interpolated rectangular grid. Then, a required number of points are taken from this grid to form the NURBS grid. The NURBS surface is generated using these points as the control points. For simplicity, the weights of each grid point are taken as one and the degree of the curve is taken as three. The knot vectors are defined as zero for the first three and one for the last three with uniform spacing in the remaining knots at the centre to ensure the curves pass through the start and end points.

3.2 The proposed adapted Delaunay triangulation (ADT) methodology

The Delaunay triangulation is a well-known method used for surface reconstruction, modelling of terrain and building meshes for space-discretised solvers such as the finite element method or finite volume method. This method maximizes all the angles in the triangle to avoid long, narrow triangles. The method has been very successful in regenerating of surfaces applications as it provides the smallest polygon (only 3 sides) that can be used to define the surface with higher detailing. Polygons with higher number of sides are an added constraint as fitting four or more random points in one plane is tough and generating a non-overlapping surface by patching these planes might not always be possible. The ADT method discussed in our previous work (Bhattarai et al. 2017; Bhattarai et al. 2018) can be adopted to generate non-overlapping detailed surfaces from a set of predefined points. As highlighted in the literature, this method is much faster and can accommodate all the points in the cloud to form the surface by patching flat triangular surfaces with C0 continuity, i.e. continuous with sharp edges. This current paper adds to our previous work by enabling random points cloud sets and providing performance comparison with NURBS surface and optimizing the random sets of points to generate most force on the surface. ADT in this work refers to adapted Delaunay triangulation which is dissimilar to adaptive Delaunay tessellation (Constantiniu et al. 2008). Adaptive Delaunay tessellation is a meshing technique used to provide triangular mesh to the surface of a solid geometry.

The proposed ADT method was specifically developed for CFD applications coupled with mechanical design optimization problems as these problems demand highly computationally expensive and time-consuming operations. Although most response surface optimization problems are for open free-form surfaces, closed surfaces could also be generated from this algorithm with the help of user inputs regarding the presence of closed surface and the plane for split boundary. This will allow the algorithm to separate the random points cloud into two sets and generate two different non-overlapping surfaces which can be patched together to form the final closed surface. The detailed algorithm for the Delaunay triangulation-based method can be presented as follows:

  1. (1)

    Define space limits for the 3D points cloud suitable for the problem at hand

$$ {x}_{\mathrm{min}}\le x\le {x}_{\mathrm{max}};{y}_{\mathrm{min}}\le y\le {y}_{\mathrm{max}};{z}_{\mathrm{min}}\le z\le {z}_{\mathrm{max}} $$
(1)
  1. (2)

    Define the number of points desired to define the surface

$$ \left[n\right]=\left\{1,\dots \dots \dots, \kern0.5em n\right\} $$
(2)
  1. (3)

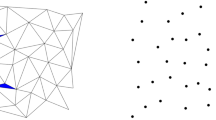
    Plot the 3D points cloud with aforementioned n points. (Refer Fig. 1.)

Fig. 1
figure 1

Generated points (step 3)

Full size image
$$ f(x)=\mathrm{random}\left(\left\{x:{x}_{\mathrm{min}}\le x\le {x}_{\mathrm{max}}\right\}\right) $$
(3)
$$ S=\left\{f\left({x}_i,{y}_i,{z}_i\right),\forall i\in n\right\} $$
(4)
  1. (4)

    Evaluate the spread of the coordinates by calculating their standard deviation

$$ v(x)= stdev\left(\left\{f\left({x}_i\right),\forall i\in n\right\}\right) $$
(5)
$$ V=\left\{v(x),v(y),v(z)\right\} $$
(6)
  1. (5)

    Use standard deviation to determine the depth axis of the surface. Higher standard deviation can be chosen to generate widely spread surface and lower standard deviation to generate narrow surface. Lower deviation can be used to design aerodynamic surfaces while higher deviation can be used to design turbomachinery. The chosen axis is the axis perpendicular to the generated surface

$$ \mathrm{depth}.\mathrm{axix}:= \mathrm{axis}\ \mathrm{with}\ \min\ \mathrm{or}\ \max\ \left\{V\right\} $$
(7)
  1. (6)

    If min or max standard deviation is the same, follow the priority order of Z-axis first and Y-axis second. (take min for example)

$$ {\displaystyle \begin{array}{c} depth. axis:= z\ axis, if\ v(x)=v(y)=v(z)\\ {}:= y- axis, if\ \mathit{\min}\left\{V\right\}=v(x)=v(y)\end{array}} $$
(8)
  1. (7)

    Create a set of 2D points with the remaining two coordinate axis values. Marked by ‘x’ in Fig. 2.

Fig. 2
figure 2

2D projection (step 7)

Full size image
$$ {\displaystyle \begin{array}{l}P=\left\{f\left( xi, yi, zi\right),\forall i\in n\right\}-\left\{f(ui)\right\}\\ {}\mathrm{where},\kern0.5em u:= z,\mathrm{if}\ \mathrm{depth}.\mathrm{axis}\ \mathrm{is}\ \mathrm{z}\ \mathrm{axis}\\ {}\kern2.5em := y,\mathrm{if}\ \mathrm{depth}.\mathrm{axis}\ \mathrm{is}\ \mathrm{y}\ \mathrm{axis}\\ {}\kern2.5em := x,\mathrm{if}\ \mathrm{depth}.\mathrm{axis}\ \mathrm{is}\ \mathrm{x}\ \mathrm{axis}\end{array}} $$
(9)
  1. (8)

    Apply 2D Delaunay algorithm to the generated set P to form triangles with the highest area to perimeter ratio without any intersections as shown in Fig. 3.

  2. (9)

    Obtain the triangulation information (set of points that form a triangle) from 2D Delaunay output.

  3. (10)

    Form a surface with the same triangulations in 3D space with respective x, y and z coordinates. (Refer Fig. 4.)

Fig. 3
figure 3

2D triangulation (step 9)

Full size image
Fig. 4
figure 4

Surface generation (step 10)

Full size image

This simple yet effective algorithm is the basis of the method suggested in this paper. This triangulation approach ensures inclusion of all the points in the random points cloud without self-intersection of the surface. It also preserves the sharp features of the randomly spread points which would otherwise be lost with NURBS based approaches. A flowchart for the entire optimization cycle is presented in Fig. 5.

Fig. 5
figure 5

Flowchart for ADT algorithm integrated with an optimisation process

Full size image

4 Model evaluation and comparison

The outputs generated from the different input values with the proposed ADT method and the NURBS-based method are compared in this section. A discretised domain of Euclidean space was defined where a surface could be configured. A set of random points from 3-dimensional space was generated as the input for the surface configuration using both ADT and NURBS methods. The outputs generated are listed in Table 1 along with their specifications.

Table 1 Comparison of ADT and NURBS method
Full size table

The first column in Table 1 shows the surfaces configured from ADT method and the second column shows the same from NURBS method. The third column overlaps both these surfaces to provide a visual comparison of deviation. The first row comparison was made with 9 data points which shows that ADT method has a file size of 306 bytes while NURBS has 1376 bytes. Similarly, the computation time taken is 0.0038 s for ADT and 0.018 s for NURBS. The overlap shows a wide deviation but the deviation is still under 5% statistically as seen from the Student’s paired t test and Wilcoxon signed-rank test. The same trend follows for iterations with 45, 100, 169 and 200 points. Although the difference in the file size and computation time for the two methods does not seem much at the first iteration, the difference grows with the increase in the number of points. However, the deviation on the overlapping column has visually reduced with the increase in number of points.

The similarity of the surfaces generated from the said methods can be evaluated by using various statistical tools. The comparison was made on the deviation of the coordinate points on z-axis between ADT surface and the NURBS surface. This problem can be classified as a paired sample test because it consists of pair of z-axis coordinate for the same x-axis and y-axis coordinates. Hence, Student’s paired t test or/and Wilcoxon signed-rank test can be used to determine if the two sets of data being compared have major differences or if they are fairly similar. Student’s paired t test is a parametric test that takes into account the values of each measurement while Wilcoxon paired test is a non-parametric test which makes comparison by ranking the differences between the values. Both the tests were done on the given sets of coordinates with the hypotheses that both the sets do not have significant difference. It can be concluded with 95% confidence that surfaces generated from ADT and NURBS are similar.

It can be seen from the statistical methods that the surfaces are similar, but we can visually see in Table 1 that the surfaces are different when superimposed because of the sharp edges in the ADT model and smooth curves in the NURBS model. Close approximation of the NURBS model can be obtained from the ADT model with sufficient carefully placed control points but the sharp edges of the ADT model are not possible to be achieved from a single NURBS surface.

The comparison of file size and configuring time in Fig. 6 shows that there is the distinct advantage of using the ADT surface generation over the NURBS method for optimization applications with minimal processing of the random data fed as input.

Fig. 6
figure 6

Storage and computation time required comparison

Full size image

5 Discussion and evaluation of ADT

The advantages and differences of the two methods employed in this paper can be listed as follows:

  1. (1)

    Storage: The ADT method requires lesser storage space as compared to the NURBS method as can be seen in the Fig. 6. The memory requirement for ADT is almost half that required for NURBS. Although the difference in the storage requirement appears to be 5912 bytes for 200 points, this difference can grow up by a multiple of thousands in stochastic optimization applications. If a population of 50 individuals is optimized for 1000 generations, 50,000 geometries need to be configured and that requires 296-megabyte extra space owing to the difference of 5912 bytes in ADT and NURBS file size.

  2. (2)

    Speed of generation: The ADT method is almost 3 times faster than the NURBS-based method for the generation of the surface. This is mostly because ADT does not require pre-processing of the data and aligning them into a grid to form curves that define the surface. As seen in Table 1, with a time difference of 0.0129 s for each geometry with 200 points, 645 s can be reduced from the total optimization cycle.

  3. (3)

    Surface quality: The geometric continuity of the ADT surface is C0 while that for NURBS surface is C1 or higher depending on the order of the curve chosen. This is why ADT surface has sharp edges and corners but NURBS has smooth surface without any sharp edges. Hence, NURBS is desirable where smooth surfaces are necessary, but for other applications, ADT surfaces which are comprised of flat triangles, sharp edges and corners may be sufficient. The ADT surfaces can very closely resemble the NURBS surface if the control points are placed accordingly, but a single NURBS cannot recreate the sharp edges and corners of the ADT surface.

  4. (4)

    Outliers: ADT method provides same weight to all the control points and ensures that all the points lie on the surface, but NURBS requires the random data set to be fitted into polynomial equations to form grids for generation of the desired surface. This consumes much time and discounts the value of individual point which are away from the mean. A single change in the control point has a drastic effect in the final ADT surface while the same may not be true for the NURBS surface. For stochastic optimization operations, this property is of great interest because each operation done on each set yields a different result for ADT while it might not yield a different result for NURBS surface.

  5. (5)

    Robustness: Delaunay methods are very robust and can handle large number of random points that are fairly scattered. Similarly, ADT is capable of generating surfaces from any set of random points that are fairly scattered in space, but for NURBS, the points must be uniformly laid and arranged in grids. NURBS requires parameters such as knot vectors, weights and polynomial functions adding to its complexity. A generic approach might not be able to provide the surface for all sets of random points. Also, ADT method generates surfaces in VTK format compatible with open source rendering and simulation packages.

These advantages and differences clearly highlight the benefits of using the ADT method for configuring surfaces from random points for application in computationally expensive stochastic optimization problems for CFD applications. This method helps reduce the amount of data produced and also aids handling of data by simplifying the operations, reducing memory requirement and decreasing the amount of time required for processing.

6 Case study: optimizing a surface

A case study on faceted 3D surface generated from the ADT method made with random points was conducted to test the surface generation approach. The problem was defined as maximizing the force on the surface from a water jet striking on it. The initial population of surfaces consist of some flat surfaces along with the randomly generated surfaces. The volumetric space domain for surface generation was limited to a maximum of 36 mm × 30 mm × 13 mm with 1 mm discretization in each direction. The diameter of the jet was taken as 18 mm and its velocity as 4.34 m/s to resemble Pelton turbine design parameters. The CFD simulation was conducted on DualSPHysics solver engine by modelling only a half of the domain to save computational expenses as the flow is symmetric along the longitudinal cross-section. The following figure shows the SPH solution environment (Fig. 7).

Fig. 7
figure 7

DualSPHysics solution environment (original in colour)

Full size image

Genetic algorithm was chosen as the stochastic optimizaiton tool and the chromosomes were defined as the coordinates of points that form the surface. Random selection, 2 point crossover reproduction and random mutation of 0.01% were the operators used for optimization. Initial population of 48 individuals made of 101 coordinate points were generated. This initial population consisted of a flat surface, an approximation of existing Pelton turbine bucket and randomly generated surfaces. The 4 elite individuals from each generation were carried forward to the next generation to preserve the best solutions from being lost during the cycle. The evolution of the force readings for the 3 optimization runs carried out for 50 generations is shown in Fig. 8.

Fig. 8
figure 8

The optimal design readings for each generation

Full size image

The results show an improvement in performance for bucket shaped surfaces. Although the existing bucket shape (19.08 N) or the flat surface (21.96 N) did not come out as the optimal shape, the best-performing surfaces did have similar valley like features. These shapes, which appeared rough and irregular, had the existing bucket like valley exactly where the jet hits the surface as decipted with the red circles in the figure below. The contours on the figure are a gradient where blue is deep and yellow is high in the z-axis. Since this optimization attempt was made for a stationery plate, smaller cup shape might be ideal for generating the maximum force on the surface. Figure 9 shows the optimal shapes that resulted from the optimization process.

Fig. 9
figure 9

Optimization results geometry (original in colour)

Full size image

These optimized shapes resulted went through 50 generations of crossover and mutation operations with 48 individuals in each generation. That sums up to 2400 simulations run in total for the entire operation. Each simulation was run for 0.07 s runtime with 0.01 s timesteps which allowed enough time for flow to settle on the surface. The time taken on average for each of the simulation was 107.53 s and for each optimization run was 0.05 s on average on a 3.4-GHz Intel Xeon E1245 processor with 16GB RAM and 2 GB NVIDIA Quadro 4000 GPU unit with 256 CUDA enabled cores. (Two different computers were used for the two experiments as the SPH simulations required computers with CUDA enabled GPU processors while the Fluent simulation required computers with licensed software.) The storage requirement for each simulation was an average of 9.60 MB. These time and storage requirements were inclusive of the geometry generation, simulation and the optimization cycle for each individual without any user intervention.

The results were then verified with Ansys Fluent which reinforced the results. The error between the fluent readings and DualSPHysics readings were minimal for the flat surface and 10–15% for the random surfaces. A 3.3-GHz Intel Core i5-4590 processor workstation with 8GB RAM was used for Ansys Fluent simulations. An average of 25GB was required for each of the simulations. The simulation was run for a total of 0.0225 s with time steps of 0.00005 s owing to Cournat number limitations. Each simulation took 1.5 h to complete not accounting for geometry creation and meshing. This highlights the advantage in running the optimization with the proposed method as compared to running a single simulation on the commercial CFD package.

The simulation conducted in this study was a simplified study, but the study has proven the capability of the proposed method. The suggested design has the features of the established designs and further investigations by limiting the search domain and increasing the number of iterations could provide more realistic results after refinement.

Another case study was conducted on Pelton turbine bucket in rotating condition. Although simulation results showed 7.5% improvement in the performance, actual performance optimization of 1.5% was achieved over the existing design. The performance was validated experimentally in the testing rig present in the University of the West of Scotland Chemical Engineering Laboratory.

The same method can be applied on other turbomachinery with higher number of variables and more iterations to generate more optimal designs. Nevertheless, time and computational power requirements will be significantly less than compared to NURBS-based geometry computation. Thus, this method can be used as preliminary design optimization stage to test numerous designs in less time. The final optimized design can then be tested with the more accurate Eulerian methods for further validation.

7 Conclusion

The geometric design conception and optimization phase is still considered as a bottleneck in the product development cycle. The reasons for this being limited computational power and processing time and the desire to generate effective design. An alternative for NURBS-based design optimization process has been presented in this paper. The proposed approach reduces the amount of data produced in the entire optimization process. For example, this method requires only 3 coordinate points values for each point and no additional parameters such as knots and weights. The proposed approach is hence robust and allows exploring radical changes in conventional bucket designs, which may not be perceived during conceptualisation stage.

The method provides faster and simpler construction of surfaces compatible with proposed methodology and can be used together with stochastic optimization algorithms. The proposed method has fewer variables and hence provides consistent outputs for the same data. Sudden changes in the gradient and sharp corners that other random points surface generation methods cannot render are accommodated in this method. In general, the computational data storage requirement for the proposed ADT method is half that required for similar NURBS surface and the time required is 1/3 of that required for generating NURBS surface. These attributes are most desirable for stochastic design optimization applications of free-form surfaces where the performance of the surface is interdependent on its geometry, such as fluid flow over the surface.

The applications of this method include but are not limited to optimization of turbomachinery, aerodynamic surfaces, landscape, breakwater design and city planning to ensure healthy flow of fresh air. Any response surface optimization problem involving fluid flow can be modelled and optimized with this method. There is very limited exploration with sharp edged, ribbed or contoured features in CFD applications. But, Formula 1 aerodynamic study has shown that there might be scope for additional features to the conventional smooth surface (Diasinos et al. 2017). This method was suggested to be used together with computational fluid dynamics simulation software and stochastic optimization algorithms to produce an optimal surface for geometric design problems that can aid develop smarter products.

8 Replication of results

The codes formulated to compare the ADT method and the NURBS method are provided in the supplementary material as a MATLAB file. It requires installation of a few packages for successful compilation.

The codes formulated for the case study are provided as R file. DualSPH has to be installed for the CFD operations. Few other R packages are necessary to run this code successfully. It should be noted that the results might not be identical because of the stochastic nature of the work.