Abstract
Reliability-based design is concerned with ensuring that constraints are enforced with acceptable probability under inherent variability in properties. In aircraft design, such a constraint may be that aeroelastic instability does not occur at velocities encountered by the aircraft. This approach can be complicated, as the aeroelastic instability speed is a discontinuous function of material properties, on account of particular modes only becoming unstable for some parameter values. In reliability analysis, it is common to use surrogate models due to the computational expense associated with Monte Carlo Simulation, however, such methods can be inaccurate when emulating discontinuous functions such as the aeroelastic instability speed. In this paper, an alternative approach is proposed in which Gaussian process surrogate models are fitted directly to each of the modal eigenvalues at the design air-speed, and used to emulate a stability margin based upon the most critical eigenvalue. Using this approach, it is shown that the reliability may be estimated for the aeroelastic stability using smooth emulators, thereby overcoming the problems associated with discontinuities. The method is demonstrated for layup optimisation of composite plate wings with uncertain ply angles, in which the probability of aeroelastic instability occurring is minimised for a prescribed air-speed. In uncertainty quantification, a good agreement is found with Monte Carlo Simulation with an order of two magnitudes reduction in model runs. Through reliability-based design, reductions in the probability of failure of up to 99.8% are achieved by increasing the stability margin at the design speed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Composite materials are being used to an increasing degree in aerospace structures due to a number of useful attributes including high specific strength and stiffness, and anisotropic behaviour which may be exploited to tailor the properties of the structure. A large amount of work has been undertaken since the 1970s in the field of aeroelastic tailoring, which has sought to exploit the anisotropic properties of composite materials for the efficient design of aircraft structures subject to aeroelastic load cases. Aeroelastic tailoring has been used to eliminate divergence in forward-swept wings (Weisshaar 1981), improve aileron effectiveness (Pettit and Grandhi 2003), alleviate gust loads (Pettit and Grandhi 2003; Kim and Hwang 2005), and prevent flutter occurring at design air speeds (Weisshaar and Ryan 1986; Eastep et al. 1999; Kameyama and Fukunaga 2007).
Mathematical models can represent behaviour to a high degree of accuracy, however, in reality all materials and processes are subject to variability, and it is impossible to guarantee exact values for the parameters used in design. Composite materials require complex manufacturing processes which can introduce uncertainty from a number of sources (Sriramula and Chryssanthopoulos 2009), such as fibre misalignment and waviness (Potter et al. 2008), or variability in the fibre and matrix volume fractions and elastic moduli (Chamis 2004). Uncertainty is typically accounted for using safety factors or worst-case scenarios which can be overly conservative and result in inefficient designs, as well as inhibiting the adoption of new technologies and techniques (Pettit 2004). There is therefore a need for methods which may be used to incorporate uncertainty into design.
Numerous techniques have been used to model uncertainty in aeroelasticity of composite structures. Monte Carlo Simulation (MCS) is a commonly used technique, and was used by Murugan et al. (2008) to model the aeroelastic response of a composite rotor blade with uncertain elastic moduli and Poisson’s ratio. Monte Carlo Simulation can be computationally expensive due to the large number of model runs required, and as such, it is common to use surrogate models in order to reduce the computation time. A perturbation method, based upon a linear Taylor series approximation, was used by Liaw and Yang (1991) to estimate the mean and variance of the flutter speed of a composite plate with uncertainty in the ply orientations, thickness, elastic moduli, and material and air densities. Polynomial Chaos Expansion (PCE), in which orthogonal polynomials are used as a surrogate model, was used by Pettit and Beran (2004) to model limit cycle oscillations of a two degree of freedom aerofoil with uncertain pitching stiffness and angle of attack. Manan and Cooper (2009) used a non-intrusive Polynomial Chaos Expansion to model flutter of composite plate wings with uncertain ply orientations, thickness, and longitudinal and shear moduli. A similar analysis was undertaken by Scarth et al. (2014), in which lamination parameters were used to represent the ply orientation uncertainty in order to reduce the number of random variables. High Dimensional Model Representations was used by Murugan et al. (2012) to model the aeroelastic response of a composite rotor blade with spatially varying uncertainty in the stiffness.
The above work details the calculation of metrics in order to quantify the effects of uncertainty on model outputs. Such metrics may be used as an optimisation objective or constraint in line with various design strategies. Reliability-Based Design Optimisation (RBDO) is one such approach, the aim of which is to ensure that constraints are enforced such that the probability of failure does not exceed an acceptable threshold (Choi et al. 2007). Calculating failure probabilities can be highly computationally expensive, and as such, it is common to use approximate methods such as the First Order Reliability Method (FORM) (Hasofer and Lind 1974), in which the failure surface defined by constraints is approximated using Taylor series expansions about the most probable point. Numerous authors have used FORM in the aeroelastic design of simple models. Pettit and Grandhi (2003) used FORM in the minimum-weight design of a wing with uncertain thickness, subject to constraints upon the root bending moment and shear force under gust loading, as well as the aileron effectiveness. Stanford and Beran (2012) used FORM in the minimum-thickness design of a plate model subject to constraints based upon the amplitude of limit cycle oscillations, with uncertainty in the Mach number and elastic modulus. Other surrogate modelling techniques have been used in the reliability-based design of composite wings, for example, Manan and Cooper (2009) minimised the probability of aeroelastic instability occurring in composite plate wings at a specified air-speed using a Polynomial Chaos Expansion surrogate model. Additionally, polynomial response surfaces were used by Borello et al. (2010) for estimating the reliability with respect to the flutter speed of both metallic and composite wings with uncertain material properties.
Optimisation using objectives or constraints based upon aeroelastic stability can be complicated by the fact that the aeroelastic instability speed can be a discontinuous function of model parameters. Such discontinuities arise as individual modes stabilise or destabilise with variations in model parameters, resulting in mode-switching behaviour. This behaviour was noted by Haftka (1973) in an early investigation, in which the flutter speed of a metallic delta wing was found to be a discontinuous function of the thickness of different wing segments. Housner and Stein (1974) noted that the flutter speed of composite wings is a discontinuous function of the ply orientations in a number of parametric studies. Georghiades and Banerjee (1998) used a modal elimination technique to show the discontinuities to be characterised by a marked change in the contribution of each mode to the flutter mode shape. Kameyama and Fukunaga (2007) used contour plots to visualise the instability speed as a discontinuous function of lamination parameters, which are themselves functions of the ply orientations, and noted distinct regimes of behaviour attributable to each type of instability.
The discontinuous behaviour described above cannot be accurately emulated using many surrogate modelling techniques, which are built upon an assumption of smoothness. As such, there has been some interest in developing surrogate modelling approaches for emulating discontinuous functions in aeroelastic stability and dynamics. Beran et al. (2006) used multi-resolution Polynomial Chaos Expansions, which utilised Haar wavelets to model local effects due to bifurcating aerofoils undergoing limit cycle oscillations. A multi-element PCE was used by Chassaing et al. (2012) to model discontinuous behaviour in bifurcating two degree of freedom aerofoils with uncertain structural damping, however, discretising the input space into multiple elements was found to significantly increase the required computational effort. Convex hulls were used by Scarth et al. (2014) to partition the space of random variables in accordance with the feasible types of aeroelastic instability, in order to fit multiple Polynomial Chaos Expansion surrogate models. Support Vector Machines, a type of surrogate model used to emulate discrete-valued functions, were used by Missoum et al. (2010) to estimate the reliability of two degree of freedom aerofoils undergoing limit cycle oscillations, in the minimisation of an uncertain, nonlinear stiffness term. Additionally, Becker et al. (2013) developed an approach in which classification and regression trees were used in conjunction with Gaussian Process Emulators to emulate bifurcating systems.
Computationally efficient methods are required in order to account for material uncertainty in the design of composite aircraft wings, subject to objectives or constraints based upon aeroelastic stability. It has been highlighted that application of such approaches may be impeded by the fact that the aeroelastic instability speed is a discontinuous function of model parameters, on account of mode-switching behaviour. The use of surrogate models to emulate the instability speed can therefore be inaccurate, as such models are typically built upon an assumption of smoothness. Whereas some specialist algorithms have been developed to emulate this behaviour, these methods can often result in increased computational expense due to the need to partition the input parameter space.
In this paper, an alternative approach is presented in which the need to emulate the discontinuous behaviour is circumvented by fitting a surrogate model to each of the modal eigenvalues, rather than directly emulating the instability speed. The expression for the reliability is rewritten as a function of a stability margin based upon the real part of each of these eigenvalues. This approach enables the problem to be reformulated from that of approximating a discontinuous function, to that of approximating multiple continuous functions, and exploits the fact that each model evaluation presents an opportunity for surrogate models to ‘learn’ about multiple eigenvalues. Using this approach, the reliability may therefore be estimated without the need to partition the input parameter space. The proposed approach is demonstrated in the reliability-based design of a simple composite plate wing model, with uncertainty in the ply orientations. It should, however, be noted that the surrogate modelling techniques used are entirely non-intrusive, and can be applied to any black-box model. Despite the simple analytical model used in this demonstration, the advantages of the proposed approach should be preserved when applied to more detailed wing models. It will always be the case that each of the eigenvalues is defined for the entire input parameter space regardless of the wing stability, whereas the instability speed may be discontinuous due to elimination of particular types of instability for some parameter values. As such, it will in general be simpler to emulate the eigenvalues instead of the instability speed.
2 Model definition
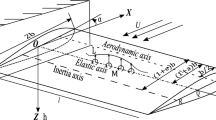
In this paper, a simplified wing model is used to demonstrate the application of the developed approaches. In this model, a composite wing with semi-span s and chord length c, is idealised as a flat, rectangular, cantilever plate. Relevant dimensions of the plate as well as the direction of applied airflow relative to the global coordinate system are shown in Fig. 1. The plate is composed of n plies, each of which is stacked with fibres at angle 𝜃 i from the global coordinate system. The aim of the design process is to optimise the orientation of each of these plies. In Fig. 1 the material coordinate directions 1 and 2 refer to the direction of the fibres, and that perpendicular to the fibres respectively.
The dimensions and material properties used throughout this paper are shown in Table 1, wherein subscripts indicate the material direction to which the property refers. For simplicity, in each of the case studies, laminates are fixed to a thickness of 2mm and a total of 16 plies.
3 Deterministic modelling
3.1 Composite material properties
In classical lamination theory (Tsai and Hahn 1980), the constitutive equation relating applied bending moments to the curvature of a symmetrically laminated plate may be written as
where the respective components of the moments and curvatures are: M = {M x , M y , M x y }T and κ = {κ x , κ y , κ x y }, and the components of laminate out-of-plane stiffness matrix D are D i j (i, j = 1,2,6).
The stiffness components from (1), may be expressed as a linear combination of material invariants U 1 − 5, laminate thickness t, and lamination parameters ξ 9 − 12 in accordance with (Tsai and Hahn 1980; Miki and Sugiyama 1993)
The material invariants, U 1 − 5, are are defined as
where Q i j are the reduced stiffness components of an individual ply with respect to material coordinate axes, which are in turn defined as
where E 11, E 22, G 12 and ν 12 are the lamina longitudinal, transverse and shear moduli, and Poisson’s ratio respectively.
By defining a non-dimensional through-thickness coordinate, u = 2z/t, the out-of-plane lamination parameters are defined as
where 𝜃(u) denotes the distribution of the ply orientations throughout the laminate thickness. In practice, the laminate has a discrete set of plies with orientations \([\theta _{1},\dots ,\theta _{n}]\), as shown in Fig. 1, and (8) reduces to a through-thickness summation. The lamination parameters are defined solely as functions of the ply orientations and, as such, give the directional component of the laminate stiffness. Use of lamination parameters is beneficial as they may be uniquely defined for a sequence of ply orientations using (8), and used to represent this stacking sequence using a maximum of four parameters regardless of the total number of plies. It should, however, be noted that the restriction to out-of-plane stiffnesses relies upon an assumption that the stacking sequence is symmetric about the laminate mid-plane.
3.2 Aeroelastic model
The aeroelastic stability of the simple composite plate shown in Fig. 1 is modelled using the Rayleigh Ritz method combined with a modified strip theory (Wright and Cooper 2008). In this approach, the out-of-plane displacement at any point on the plate is approximated using simple polynomial shape functions which satisfy the boundary conditions, given as
where w is the out-of-plane displacement, and q i (t)is the generalised displacement of the ith mode represented by shape function γ i (x, y). Neglecting structural damping, and utilising the approach undertaken by Stodieck et al. (2013) and Scarth et al. (2014), the equation of motion of the plate can be expressed in the classical aeroelastic form as
where A is the mass matrix, B and C are the aerodynamic damping and stiffness matrices respectively, E is the structural stiffness matrix, q is a vector of the generalised displacements \(\{q_{1}\dots ,q_{n}\}\) and ρ and V are the air density and velocity. In first-order form, (10) may be re-expressed as
Noting that system matrix Q in (11) is a function of air-speed, the eigenvalues of this matrix may be found to assess the stability of the wing at a given air-speed, as well as give the frequency and damping ratio of each mode. Instability occurs when the real part of one of the eigenvalues is positive; this instability is flutter if the imaginary part is non-zero and is divergence otherwise. The aeroelastic instability speed may be found by solving (11) at multiple air-speed increments until one of the eigenvalues becomes positive. Previous work by Stodieck et al. (2013) has validated the application of this approach to the geometry shown in Fig. 1 through comparison with a finite element model coupled with Doublet Lattice aerodynamics.
In order to illustrate the described process, example plots of the eigenvalues against air-speed are shown in Fig. 2, in which λ j denotes an eigenvalue corresponding to the j thmode. Plots are shown for three example sets of lamination parameters, which are used to calculate laminate stiffness in line with (2). In each plot, the instability speed is given by the lowest velocity at which an eigenvalue crosses zero on the real axis. For example, in Fig. 2a mode 2 becomes unstable at around 120m/s. This instability is flutter as the eigenvalues are complex conjugate. In Fig. 2b, mode 2 remains stable and instability instead occurs in mode 3. Figure 2c shows divergence occurring in mode 1, as the corresponding eigenvalues are wholly real.
3.3 Deterministic stability trends
The optimisation and uncertainty quantification work in this paper is concerned with how variations in the composite ply orientations affect the aeroelastic stability. Such trends may be visualised in the space of lamination parameters, which are themselves functions of the ply orientations, as given by (8). Example surface plots of the instability speed are shown in Fig. 3, with respect to two lamination parameter planes; Fig. 3a shows variations in instability speed with ξ 9 and ξ 10 with ξ 11 = ξ 12 = 0, and Fig. 3b shows variations with respect to ξ 11 and ξ 12, with ξ 9 = ξ 10 = 0. Such plots are obtained by determining the instability speed using the process illustrated Fig. 2, for a large range of values of ξ 9 − 12. It should be noted that the lamination parameters are constrained to feasible regions (Bloomfield et al. 2009), and as such, trends are only plotted for feasible parameter values.
From Fig. 3, it can be seen that the surface defined by the instability speed is a discontinuous function of the lamination parameters, and therefore of the ply orientations. Such discontinuities have been reported upon in the literature (e.g. Haftka 1973, Housner and Stein 1974, Georghiades and Banerjee 1998, Kameyama and Fukunaga 2007), and found to be caused by a modal interchange phenomenon, in which changes in model parameters give rise to different types of aeroelastic instability, characterised by a marked change in mode-shape. In order to more clearly investigate this behaviour, an example plot of instability speed against ξ 11 is shown in Fig. 4, assuming constant values for ξ 9, ξ 10 and ξ 12. Such a plot is essentially a means of visualising trends with varying bend-twist coupling behaviour. Instability speeds are shown in this plot for three different types of aeroelastic instability; divergence and two types of flutter which are referred to as ‘flutter 1’ and ‘flutter 2’. The critical instability speed, given by the minimum air-speed at which instability occurs, is highlighted in this plot as a solid line.
From Fig. 4 it can be seen that multiple types of instability may be possible for a given value of ξ 11; there is a region of Fig. 4 in which both flutter 1 and flutter 2 occur at different speeds, and similarly, a region in which both flutter 2 and divergence are possible. It should be emphasised that in practice the wing would be destroyed by the instability which occurs at a lower speed, however, model output may be obtained for both speeds. It may also be noted that each instability speed is only defined for distinct ranges of ξ 11, as the corresponding type of instability only occurs in these regions. This phenomenon is notable in Fig. 2, in which mode 2 becomes unstable in Fig. 2a, but not in Fig. 2b.
The discontinuities highlighted in Figs. 3 and 4 can complicate reliability analysis, as commonly used techniques such as FORM, as well as surrogate modelling techniques such as Polynomial Chaos Expansion and Kriging, are based upon an assumption of smoothness. It can be difficult to apply such techniques separately to the individual instability speeds highlighted in Fig. 4, as each type of instability is limited to a region of the parameter space which is not known a priori.
In this paper, an alternative approach is presented in which surrogate models are instead fitted to the real part of each of the eigenvalues. The benefits of such an approach are demonstrated in Fig. 5, in which the real part of the eigenvalues of the first three modes are plotted against ξ 11 for the same lamination parameter range used in Fig. 4, assuming an air-speed of 120m/s. The distance from instability of the eigenvalue with maximum real part, highlighted as a solid line in Fig. 5, can be thought of as a stability margin for a given air-speed. Such a margin is essentially a measure of the damping of the most critical mode. Although this margin is itself a non-smooth function of ξ 11, it may be approximated by fitting multiple surrogate models to the real parts of each of the eigenvalues which, unlike the instability speeds, are defined across the full range of ξ 11. A reliability-based optimisation, and surrogate modelling strategy based upon this principal is outlined in subsequent sections.
4 Reliability-based design overview
Reliability-based design is concerned with ensuring that failure, defined using a limit state function g(x), does not occur above some acceptable probability. The limit state is comparable to the constraints used in deterministic optimisation problems, with the distinction that imposed constraints may be violated with some acceptable probability (Choi et al. 2007). A general reliability-based design optimisation problem may be expressed as
where f(x, p) is the objective, g(x, p) the limit state function, x is the design variable whose lower and upper bounds are denoted x L and x U respectively, p are parameters which the designer does not control, P f is the acceptable probability of failure, and an overbar denotes a deterministic value. For the sake of simplicity, an unconstrained approach is undertaken in this paper, in which the probability of failure is minimised as an objective, rather than used as a constraint. For aeroelastic stability, such an objective is concerned with minimising the probability that the aeroelastic instability speed does not exceed a prescribed air-speed, which may be expressed as
where V crit denotes the instability speed, determined using the approach illustrated in Fig. 2, and V des is the design air-speed, which is prescribed by the designer. The design variables, \(\boldsymbol {\theta } = \{\theta _{1},\dots ,\theta _{n}\}\), are the orientations of each ply as shown in Fig. 1, which take values from set Θ.
Determining the failure probabilities used in reliability-based design can be computationally expensive, and as such, it is common to use surrogate models. It would, however, be difficult to use such surrogate models to estimate the objective of (13), as the critical instability speed is discontinuous as discussed previously. Such an approach is also wasteful, as calculating the instability speed requires that the eigenvalue problem in (11) is solved across a range of velocity increments, when it is only the stability at design velocity V des which is of concern. Noting the latter observation, (13) may be re-written as
where,
where λ i (𝜃, V des) denotes the i th eigenvalue of (11), evaluated at air-speed V des, for a laminate with ply orientations specified by 𝜃, and M is the number of modes considered in the analysis. Λis used to denote the concept of a stability margin, whose sign convention is chosen such that a positive margin indicates a stable wing, and a negative margin indicates instability. The use of this stability margin in the objective only requires that the stability of the wing is assessed at the design air-speed, thereby reducing the required computation time. This margin can be approximated by fitting surrogate models to the real part of each eigenvalue, which unlike the instability speeds, are defined across the entire input parameter space, as illustrated in Fig. 5. This surrogate modelling approach is described in detail in the next section.
5 Surrogate modelling
5.1 Overview
Due to the high computation time associated with reliability-based design, it can be desirable to estimate the probability of failure using surrogate models which may be evaluated in a fraction of the time required by the model itself. Fitting surrogate models to the aeroelastic instability speed can be complicated by the fact that the critical instability speed is a discontinuous function of model parameters, as discussed previously and shown in Fig. 4. In the previous section, an optimisation strategy was presented in which failure probabilities are instead calculated using a stability margin evaluated at the design air-speed. The motivation behind this method is that the stability margin may be estimated using surrogate models fitted to the individual eigenvalues, which are defined for the entire input parameter space and therefore doe not require that model inputs are partitioned. This surrogate modelling approach is discussed in detail in this section, and demonstrated in an uncertainty quantification case study.
A regression-based surrogate modelling approach for approximating scalar-valued quantities may be described as follows. The surrogate model is first trained using a small set of n samples \(\{\mathbf {x}^{(1)},\dots ,\mathbf {x}^{(n)}\}\). The bracketed superscripts are a sample index, with each x (i) being a d-dimensional vector of model parameters. A surrogate model, \(\hat {f}({\mathbf {x}})\), is fitted to in some way minimise the approximation error based upon model outputs at these data points. Model outputs may subsequently be approximated at ‘test’ point x as \(\hat {f}(\mathbf {x})\). This approach is common to many surrogate modelling techniques, with differences arising in the mathematical description of the surrogate model and the means by which it is fitted. In this paper, Gaussian process emulators (Rasmussen and Williams 2006; Oakley and O’Hagan 2002) are used. This section is concerned with how this approach may be modified in order to emulate multiple eigenvalues, and subsequently predict the stability margin based upon the maximum emulated value. An overview of the approach is provided in Algorithm 1, with detailed description of the various components provided in the following subsections.
5.2 Use of lamination parameters in surrogate models
In Algorithm 1, the out-of-plane lamination parameters are used as inputs to the surrogate model. Each of the x (i) terms described above is therefore a four-dimensional lamination parameter sample. This use of lamination parameters has been shown to be advantageous (Scarth et al. 2014), as a small number random variables may be used to represent ply orientation uncertainty, regardless of the number of plies. Lamination parameter samples are obtained in steps 2 and 7 of the algorithm through simulation of (8).

5.3 Eigenvalue sorting using modal assurance criterion
In step 5 of Algorithm 1, multiple Gaussian process emulators are fitted to the real part of each of the eigenvalues of (11). The aeroelastic model output gives rise to n samples of eigenvalues corresponding to m modes, however, there is no guarantee that modal eigenvalues will be outputted in the same order from one sample to another. Before fitting the emulators, it is therefore necessary to sort the eigenvalues such that results corresponding to the same mode are grouped together across all samples. This sorting is achieved by comparing the mode-shapes of each sample with those of a reference sample using the Modal Assurance Criterion (MAC), and grouping together results with the most similar mode-shape. In this investigation, the reference sample is arbitrarily chosen as the first sample in the data set. It should, however, be noted that in order to ensure that this sample captures all of the potential modes across the spread of behaviour, it may be necessary retain a larger number of modes than is necessary for a deterministic analysis. For two mode-shape vectors, ϕ i and ϕ j , the MAC is defined as (Wright and Cooper 2008)
5.4 Gaussian process emulators
Gaussian process emulators are a form of surrogate model which may be used to approximate continuous-valued functions. In the proposed approach, multiple Gaussian processes are used to emulate the real part of each of the eigenvalues for a given air-speed. A Gaussian process is a distribution over functions, which represents model output at fixed input parameter values as a Gaussian distribution rather than a deterministic value (Rasmussen and Williams 2006). Suppose the model output is scalar-valued and may be represented as a function, y = f(x). Suppose also that the value of this function is known for a set of n training samples \(\{\mathbf {x}^{(1)},\dots , \mathbf {x}^{(n)}\}\), with each \(\mathbf {x}^{(i)}\in \mathbb {R}^{d}\) being a sample of a d-dimensional parameter vector x. The Gaussian process is described by its mean and covariance functions, which may be parameterised as
where β is a vector of regression weights, h(x)is taken as {1, x T}, σ 2 is a scaling factor, and B is a diagonal matrix of length-scales which govern how much output f(x)varies with changes to input x. The emulator is fitted by determining the conditional distribution with respect to the training data, and finding values for the unknown hyperparameters, β, σ, and B. Maximum likelihood estimation is used to find optimal values for parameter B. The remaining hyperparameter dependencies are inferred following the Bayesian approach of Oakley and O’Hagan (2002). The resulting emulator may be simulated as a Student-t process with mean m ∗(x), and covariance \(\hat {\sigma }^{2}c^{*}(\mathbf {x},\mathbf {x^{\prime }})\), given by
where t is a covariance vector such that t i = c(x, x (i)), A is defined as A i j = c(x (i), x (j)), and H is defined as \(\boldsymbol {H}^{\mathrm {T}} = \{\mathbf {h}^{\mathrm {T}}(\mathbf {x}^{(i)}),\dots ,\mathbf {h}^{\mathrm {T}}(\mathbf {x}^{(n)})\}\). A distinction is also made between x, which denotes a test point for which the value of f(x) is to be predicted, and x (i) which is a training data point for which f(x (i)) = y i is known. In this paper, a simplified approach is taken in which the model output is approximated using the emulator mean function, given by (20).
5.5 Uncertainty quantification case study
In this section, the surrogate modelling approach described above is demonstrated in an uncertainty quantification case study. Uncertainty is modelled as an independent and identically distributed, additive Gaussian error applied to the orientation of each ply, with zero mean and standard deviation of five degrees. Sixteen example layups have been chosen, in which all combinations of a stacking sequence parameterised as [𝜃 1, 𝜃 2, 𝜃 3, 𝜃 4,02,902] S are modelled, with 𝜃 1 − 4 restricted to − 45° or 45° . In these examples, the stability margin is calculated at an air-speed of 120m/s.
The approach is validated by comparing results obtained using the surrogate model, against direct Monte Carlo Simulation using 10,000 model runs. Convergence studies have been undertaken in which the number of samples used to train the surrogate model is increased until a sufficiently good agreement is found with Monte Carlo estimates of the Probability Density Function (PDFs). Accuracy of the model is assessed using the Root Mean Square Error (RMSE) of predictions of the Monte Carlo data set, defined as
where N is the total number of Monte Carlo samples, \(\hat {y_{i}}\) is the i th sample predicted by the surrogate model, and y is the i th sample of outputted by the actual model.
In practice it may not be possible to validate surrogate models using such a large data set. A more efficient alternative is to use cross-validation, whereby the training samples are partitioned into two sets, one of which is used to train the surrogate model, and a second which is used to assess the accuracy of the model (Efron and Gong 1983; Stone 1974). For example, in leave-one-out cross-validation, a single sample is omitted when fitting the surrogate model, and the difference between the model output and surrogate prediction is measured for this sample. The process is repeated for each of the training samples, and error determined using measures such as the Mean Square Error (Rasmussen and Williams 2006).
An example convergence plot of the RMSE of the surrogate model for a [452,− 452,02,902] S laminate is shown in Fig. 6. From this plot it has been identified that 30 training samples is sufficient to achieve convergence. This procedure has been repeated for each example layup, and the resulting number of required training samples is listed in Table 2. Estimates of the mean and standard deviation obtained using both the Gaussian process emulator and direct Monte Carlo Simulation are also shown, in order to demonstrate that a good agreement is achieved. Example PDFs determined using both the surrogate model and direct Monte Carlo Simulation are shown in Figs. 7, 8 and 9. Results are shown for Gaussian processes trained with an increasing number of samples, in order to further demonstrate the convergence.
The PDF for the [45,− 453,02,902] S laminate, shown in Fig. 7a, is unimodal. The equivalent PDF for the aeroelastic instability speed of this laminate is shown in Fig. 7b. It can be seen that this PDF is bimodal, which may be attributed to a mode-switch, in which the uncertainty causes the inputs to cross a discontinuity. In this case, each peak corresponds to a different type of flutter. In this case, using the stability margin therefore considerably simplifies the PDF.
It is not always possible to simplify behaviour such that the PDF is unimodal. For example, the PDF shown in Fig. 8 is bimodal due to a switch in the eigenvalue which is closest to instability, from the first to the second mode. As such, the two peaks of the stability margin PDF in Fig. 8c may be attributed the first and second modes respectively. The PDFs of the individual eigenvalue real parts, shown in Fig. 8a and b, are unimodal as the underlying function is smooth. As such, by fitting separate Gaussian Process Emulators to each of the eigenvalue real parts as described above, the stability margin may be emulated as two separate, smooth functions. From each of the plots in Fig. 8, it can be seen that using this approach a good agreement is achieved with Monte Carlo results using 30 training data points.
Figure 9 is an example of the most complicated possible behaviour, as the first mode becomes non-oscillatory, and as such, the real part of the eigenvalue for this mode is a non-smooth function of model inputs. Such behaviour may be noted in the eigenvalue plot of Mode 1 shown in Fig. 5. The PDF for this mode, shown in Fig. 9a, is therefore bimodal, with the lower peak attributable to the real part of the complex conjugate oscillatory root, and the upper peak the most-critical branch of the real-valued non-oscillatory root. The Gaussian Process Emulator does not accurately predict behaviour in the vicinity of this non-smooth point. It is, however, the upper peak of this PDF which is critical, at which point the eigenvalues are locally smooth and the emulator gives accurate predictions. The PDF of the stability margin, shown in Fig. 9c, may therefore be emulated using 30 training data points despite the inaccurate prediction of the non-smooth behaviour.
In the above examples, a good agreement with Monte Carlo Simulation is typically achieved using between 20 and 40 training data points. This observation corresponds to an order of two magnitudes reduction in the required number of model runs, compared to direct simulation.
6 Reliability-based design optimisation case study
In this section, the surrogate modelling approach described in Section 5, is used to estimate the objective of the reliability-based design optimisation outlined in (14–15). In this case study, the ply orientations are optimised in order to minimise the probability of aeroelastic instability occurring at air-speeds of 145m/s and 150m/s, as indicated by a negative stability margin at these flight conditions.
The design space of composite ply orientations typically gives rise to objective functions which are highly multi-modal, with numerous local optima, as the laminate stiffnesses are nonlinear expressions of periodic functions in the design variables (Ghiasi et al. 2009; Callahan and Weeks 1992). As such, the design space is non-convex, and gradient based optimisers are likely to converge to local optima, depending upon the choice of initial design. An extensive body of research (e.g. Nagendra et al. 1992, Callahan and Weeks 1992, Le Riche and Haftka 1993) has instead used genetic algorithms for stacking sequence optimisation of composite laminates. These global search methods are capable of searching the complex design space without becoming trapped by local optima (Ghiasi et al. 2009). Additionally, the use of genetic algorithms enables the ply orientations may be restricted to a discrete set of angles, as is common practice in industry, and facilitates the implementation of other commonly used composite design rules.
Genetic algorithms have therefore been used in the present work. In each case, the algorithm is run for a population size of 20, over 75 generations. A ply contiguity constraint is enforced to prevent more than four plies of the same orientation being stacked consecutively, in order to avoid matrix cracking. A mid-plane symmetry constraint is enforced by parameterising only half of the plies, and as such, the total number of design parameters is eight. Three strategies are undertaken in which permissible orientations are taken from one of three sets of discrete values: i) 0°, ± 45°, and 90°, ii) 0°, ± 30°, ± 45°, ± 60° and 90°, and iii) all angles between − 85° and 90° at 5° increments.
The obtained reliability-based designs are compared with ‘deterministic’ designs, in which the aeroelastic instability speed is maximised. The nominal value, mean, and standard deviation of the stability margin, as well as the probability of failure are shown for each design in Table 3. In each case these designs constitute the ‘best’ layup achieved after 75 generations. The failure probabilities are determined in Monte Carlo Simulation of the aeroelastic model, using 10,000 samples. Probabilities smaller than 0.01 are not shown, as it is not possible to calculate such probabilities with less than 10 percent coefficient of variation with this sample size. Stability margin PDFs for optimised designs are illustrated in Figs. 10 and 11 for 145m/s and 150m/s design speeds. Plots of eigenvalue real parts against air-speed are shown in Fig. 12 for deterministic and reliability-based designs achieved using layup strategy i) and a design speed of 145m/s, in order to give physical insight into results. Additionally, the instability speed PDFs which correspond to each of the optimised designs are shown in Figs. 13 and 14 for the sake of comparison.
The failure probabilities for the deterministic designs are notably high. The deterministic trends in Figs. 3 and 4 show that the highest instability speed is on the boundary between two flutter modes, and is therefore at the edge of a discontinuity. It can be seen in Figs. 13 and 14, that the proximity of the deterministic designs to a discontinuity gives rise to a high probability of a switch from flutter 1 to flutter 2, and as such the PDF is bimodal, with a peak attributable to each type of flutter. The high area of the lower peak below the design instability speed results in a high probability of failure.
This high probability of failure may also be observed in Figs. 10 and 11 as a high probability of a negative stability margin at the design air-speed, indicated by the area of the PDFs below zero. In Table 3, each of the deterministic designs has a relatively low nominal stability margin. From Fig. 12 it can be seen that this low margin is due to the fact that mode 3 approaches instability at sub-critical air speeds, despite the fact that mode 2 ultimately becomes unstable as mode 3 re-stabilises. For the deterministic design, the nominal stability margin is less than one standard deviation, and as such it is very probable that uncertainty will cause mode 3 to become unstable, as there is insufficient margin at the design speed.
Reliability-based design can be seen to result in substantial reductions in the probability of failure. Across the various optimisation strategies employed, reductions in the probability of failure of between 82% and 97% are achieved. Smaller reductions are typically made for the 150m/s design speed, with the largest reductions achieved using layup strategy iii), due to the larger design space. These improvements are achieved by increasing the stability margin at the design air-speed, in order to provide greater capacity to accommodate uncertainty in material properties. For example, in Table 3, the reliability-based designs for a 145m/s design air-speed have a nominal stability margin of approximately three standard deviations, which can be seen in Fig. 12 to be result of the eigenvalue corresponding to mode 3 moving further from instability at 145m/s. Such a result is achieved by choosing a design with lamination parameters further from the discontinuity, which can be seen from Figs. 13 and 14 to significantly reduce the probability of a mode-switch.
7 Conclusions
In this paper, a surrogate modelling approach has been presented for use in the reliability-based aeroelastic design of composite wings. The major focus of the work was to overcome the problem of estimating the reliability using surrogate models such as Gaussian process emulators, which cannot accurately emulate discontinuities in the aeroelastic instability speed. This problem was overcome by rewriting the expression for the reliability as a function of a stability margin, which is based upon the modal eigenvalues as determined at the design air-speed. The main contribution of the work is the development of a surrogate modelling approach, in which multiple Gaussian process emulators are fitted to the real part of each of these eigenvalues. It has been shown that through such an approach, the stability margin can be emulated using entirely smooth functions, without the need to partition the input parameter space. The proposed approach has the added benefit of reducing the computation time as equations need only be solved at a single air-speed, rather than across a range of velocity increments.
The approach has been demonstrated in application to both the uncertainty quantification, and reliability-based design of composite plate wings with uncertain ply orientations. In the uncertainty quantification case study, the surrogate model achieved a good agreement with Monte Carlo Simulation using between 20 and 50 training samples, corresponding to an order of two magnitudes reduction in the model runs. In the optimisation case study, reductions in the probability of failure of between 82% and 97% were achieved relative to equivalent deterministic designs. These improvements were attained by providing additional stability margin at the design air-speed in order to accommodate the uncertainty, thereby considerably reducing the probability of a mode-switch substantially lowering the flutter speed.
References
Becker W, Worden K, Rowson J (2013) Bayesian sensitivity analysis of bifurcating nonlinear models. Mech Syst Signal Process 34(1–2):57–75
Beran PS, Pettit CL, Millman DR (2006) Uncertainty quantification of limit-cycle oscillations. J Comput Phys 217(1):217–247
Bloomfield MW, Diaconu CG, Weaver PM (2009) On feasible regions of lamination parameters for lay-up optimization of laminated composites. Proc R Soc Math Phys Eng Sci 465:1123–1143
Borello F, Cestino E, Frulla G (2010) Structural uncertainty effect on classical wing flutter characteristics. J Aerosp Eng 23(4):327–338
Callahan KJ, Weeks GE (1992) Optimum design of composite laminates using genetic algorithms. Compos Eng 2(3):149–160
Chamis CC (2004) Probabilistic simulation of multi-scale composite behavior. Theor Appl Fract Mech 41 (1–3):51–61
Chassaing JC, Lucor D, Trėgon J (2012) Stochastic nonlinear aeroelastic analysis of a supersonic lifting surface using an adaptive spectral method. J Sound Vib 331(2):394–411
Choi SK, Canfield RA, Grandhi RV (2007) Reliability-based structural design. Springer
Eastep FE, Tischler VA, Venkayya VB, Khot NS (1999) Aeroelastic tailoring of composite structures
Efron B, Gong G (1983) A leisurely look at the bootstrap, the jackknife, and cross-validation. Am Stat 37 (1):36–48
Georghiades GA, Banerjee JR (1998) Role of modal interchange on the flutter of laminated composite wings. J Aircr 35(1):157–161
Ghiasi H, Pasini D, Lessard L (2009) Optimum stacking sequence design of composite materials part i: constant stiffness design. J Compos Struct 90:1–11
Haftka RT (1973) Automated procedure for design of wing structures to satisfy strength and flutter requirements. Tech. rep., NASA
Hasofer AM, Lind NC (1974) Exact and invariant second-moment code format. J Eng Mech Div 100 (1):111–121
Housner JM, Stein M (1974) Flutter analysis of swept wing subsonic aircraft with parameter studies of composite wings. Technical Note TN D-7539
Kameyama M, Fukunaga H (2007) Optimum design of composite plate wings for aeroelastic characteristics using lamination parameters. Comput Struct 85(3-4):213–224
Kim TU, Hwang IH (2005) Optimal design of composite wing subjected to gust loads. Comput Struct 83 (19–20):1546–1554
Le Riche R, Haftka RT (1993) Optimization of laminate stacking sequence for buckling load maximization by genetic algorithm. AIAA J 31(5):951–956
Liaw DG, Yang HTY (1991) Reliability of initially compressed uncertain laminated plates in supersonic flow. AIAA J 29(6):952–960
Manan A, Cooper J (2009) Design of composite wings including uncertainties: a probabilistic approach. J Aircr 46(2):601–607
Miki M, Sugiyama Y (1993) Optimum design of laminated composite plates using lamination parameters. AIAA J 31(5):921–922
Missoum S, Dribusch C, Beran P (2010) Reliability-based design optimization of nonlinear aeroelasticity problems. J Aircr 47(3):992–998
Murugan S, Ganguli R, Harursampath D (2008) Aeroelastic response of composite helicopter rotor with random material properties. J Aircr 45(1):306–322
Murugan S, Chowdhury R, Adhikari S, Friswell MI (2012) Helicopter aeroelastic analysis with spatially uncertain rotor blade properties. Aerosp Sci Technol 16(1):29–39
Nagendra S, Haftka RT, Gurdal Z (1992) Stacking sequence optimization of simply supported laminates with stability and strain constraints. AIAA J 30(8):2132–2137
Oakley JE, O’Hagan A (2002) Bayesian inference for the uncertainty distribution of computer model outputs. Biometrika 89(4):769–784
Pettit CL (2004) Uncertainty quantification in aeroelasticity: recent results and research challenges. J Aircr 41(5):1217–1229
Pettit C, Beran P (2004) Polynomial Chaos expansion applied to airfoil limit cycle oscillations. In: 45th AIAA/ASME/ASCE/AHS/ASC Structures, structural dynamics & materials conference structures, structural dynamics, and materials and co-located Conferences/ American Institute of Aeronautics and Astronautics
Pettit CL, Grandhi RV (2003) Optimization of a wing structure for gust response and aileron effectiveness. J Aircr 40(6):1185–1191
Potter K, Khan B, Wisnom M, Bell T, Stevens J (2008) Variability, fibre waviness and misalignment in the determination of the properties of composite materials and structures. Compos Appl Sci Manuf 39(9):1343–1354
Rasmussen CE, Williams C (2006) Gaussian processes for machine learning. The MIT Press
Scarth C, Cooper JE, Weaver PM, Silva GHC (2014) Uncertainty quantification of aeroelastic stability of composite plate wings using lamination parameters. Compos Struct 116(1):84–93
Sriramula S, Chryssanthopoulos MK (2009) Quantification of uncertainty modelling in stochastic analysis of FRP composites. Compos Appl Sci Manuf 40(11):1673–1684
Stanford B, Beran P (2012) Computational strategies for reliability-based structural optimization of aeroelastic limit cycle oscillations. Struct Multidiscip Optim 45(1):83–99
Stodieck O, Cooper JE, Weaver PM, Kealy P (2013) Improved aeroelastic tailoring using tow-steered composites. Compos Struct 106:703–715
Stone M (1974) Cross-validatory choice and assessment of statistical predictions. J R Stat Soc Ser B (Methodol) 36(2):111–147
Tsai SW, Hahn HT (1980) Introduction to composite materials CT. Technomic Publishing Co. Inc, Lancaster
Weisshaar TA (1981) Aeroelastic tailoring of forward swept composite wings. J Aircr 18(8):669–676
Weisshaar TA, Ryan RJ (1986) Control of aeroelastic instabilities through stiffness cross-coupling. J Aircr 23(2):148–155
Wright JR, Cooper JE (2008) Introduction to aircraft aeroelasticity and loads. Wiley, New York
Acknowledgements
The authors would like to recognise the support of the EPSRC who fund the ACCIS Centre for Doctoral Training, (EP/G036772/1), and Embraer S.A who provided additional funding.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Scarth, C., Cooper, J.E. Reliability-based aeroelastic design of composite plate wings using a stability margin. Struct Multidisc Optim 57, 1695–1709 (2018). https://doi.org/10.1007/s00158-017-1838-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00158-017-1838-6