Download PDF

Structural and Multidisciplinary Optimization

, Volume 57, Issue 3, pp 947–963 | Cite as

Concurrent wing and high-lift system aerostructural optimization

Open Access
RESEARCH PAPER
First Online:
Received:
Revised:
Accepted:
  • 479 Downloads

Abstract

A method is presented for concurrent aerostructural optimization of wing planform, airfoil and high lift devices. The optimization is defined to minimize the aircraft fuel consumption for cruise, while satisfying the field performance requirements. A coupled adjoint aerostructural tool, that couples a quasi-three-dimensional aerodynamic analysis method with a finite beam element structural analysis is used for this optimization. The Pressure Difference Rule is implemented in the quasi-three-dimensional analysis and is coupled to the aerostructural analysis tool in order to compute the maximum lift coefficient of an elastic wing. The proposed method is able to compute the maximum wing lift coefficient with reasonable accuracy compared to high-fidelity CFD tools that require much higher computational cost. The coupled aerostructural system is solved using the Newton method. The sensitivities of the outputs of the developed tool with respect to the input variables are computed through combined use of the chain rule of differentiation, automatic differentiation and coupled-adjoint method. The results of a sequential optimization, where the wing shape and high lift device shape are optimized sequentially, is compared to the results of simultaneous wing and high lift device optimization.

Keywords

Aerostructural optimization High lift devices Coupled adjoint sensitivity analysis 
Download article PDF

1 Introduction

Although knowledge of the physics of high-lift devices (HLD) has come a long way since the fundamental paper of A.M.O Smith on high-lift aerodynamics in 1975 (Smith 1975), analysis and optimization of high-lift devices still proves to be a difficult subject. Through the use of Computational Fluid Dynamics (CFD) and increased computing capabilities, extensive research on the subject has become possible. In early days, this research mainly focused on achieving high-lift requirements to satisfy take-off and landing performance requirements. However, over the past years the focus has switched to reducing weight and complexity (van Dam 2002) as aircraft manufacturers tend to use less complex high-lift devices (Reckzeh 2003). The importance of weight and aerodynamic performance of high-lift devices in aircraft design is illustrated by Meredith (1993). According to Meredith, an increase of 0.1 in lift coefficient at constant angle of attack results in a reduction of approach attitude by about one degree, reducing landing gear length and thereby saving up to 1400 lb. Moreover, an increase of 1.5% in maximum lift coefficient (\(C_{L_{\max }}\)) may result in an extra 6600 lb payload at fixed approach speed while an 1% increase in take-off lift over drag ratio (L/D) is equal to a 2800 lb increase in payload or a 150 nm range increase.

Even though numerous semi-empirical methods exist to predict the wing weight, drag and lift of multi-element wings (Raymer 2012; Torenbeek 1982; Roskam 2000; Pepper et al. 1996), the accuracy of these methods does not yield the level of accuracy required by the industry, requiring e.g. a drag prediction accuracy of one drag count (van Dam 2003). To achieve the required accuracy, more physics based methods are required such as Computational Fluid Dynamics (CFD) and Finite Element Methods (FEM) tools. Example of application of such high-fidelity analysis for wing optimization can be found in the work of Martins et al. (2004), Kennedy and Martins (2014) and Barcelos and Maute (2008). The downside of these tools is that they require the use of high performance computational resources, making optimization problems in some cases too costly to solve. An alternative to the high-fidelity 3D aerodynamic solvers is the quasi-three-dimensional (Q3D) analysis methodology, which combines two-dimensional viscous airfoil data with inviscid three-dimensional wing aerodynamic data. This methodology requires only a portion of the computational power required for high-fidelity tools while generating sufficiently accurate results. Examples of using the Q3D method for aerodynamic analysis was presented by van Dam (2002), Elham (2015) and Mariens et al. (2014). Elham and Van Tooren developed a coupled-adjoint aerostructural analysis and optimization tool by coupling a Q3D method to a FEM (Elham and van Tooren 2016a). This tool has been validated for drag prediction and twist deformation. Using the coupled adjoint method, the tool is able to compute the derivatives of the outputs with respect to the inputs analytically enabling gradient based optimization.

In the traditional design methodology, the design of wing shape and HLD is done sequentially. The wing planform and airfoil shapes are designed (or optimized) first and then the HLD shape is determined (Flaig and Hilbig 1993; Nield 1995). It is known that sequential design and optimization may result in a sub-optimal design. In this paper a method for concurrent aerostructural optimization of wing and HLD is presented. In such a method the shape of the wing planform, airfoil, HLD as well as the wingbox structure is optimized simultaneously to minimize the aircraft mission fuel weight and satisfy the aircraft field performance requirements, that are the main drivers for HLD design.

The structure of this paper is as follows: First, the basic framework of the aerostructural analysis and optimization is described. Then the modifications applied to the aerostructural tool are explained, followed by a description of the method for predicting maximum lift. Then the method of coupling the modified methods is explained, followed by a validation of the extended model. Finally, a test case optimization is presented for a Fokker 100 class wing.

2 Aerostructural analysis and optimization framework

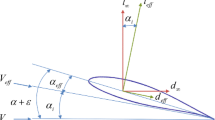
The present research expands the methodtool developed by Elham and van Tooren (2016a) for coupled-adjoint aerostructural analysis and optimization of lifting surfaces to include the analysis and optimization of HLD. This tool employs a Q3D method to compute the aerodynamic characteristics of a wing. Using the Q3D method reduces the computational effort to perform aerodynamic analysis but attains a high level of accuracy. In the Q3D methodology proposed by Elham and van Tooren, the total wing drag is then decomposed into three components: profile drag, induced drag and wave drag. The induced drag is calculated from a Vortex Lattice Method (VLM) analysis using Trefftz plane analysis based on the method of Katz and Plotkin (1991). The VLM analysis is also used to compute the lift distribution over the wing. Profile drag and wave drag are then computed using the viscous 2D solver MSES (Drela and Giles 1987; Drela 2013) following the strip theory. In this approach, the wing is divided into a number of spanwise sections (or strips), for which the aerodynamic forces and moments are computed using the effective flow properties, which are determined from the free stream flow properties taking into account the effects of sweep (Λ) and downwash (α i ). The Q3D method is coupled to the structural analysis tool FEMWET (Elham and van Tooren 2016b), which simulates the wingbox structure using equivalent panels and computes the wing deformation using a FEM. The coupled aerostructural system is formulated using 4 governing equations R 1 to R 4 as follows:
$$ \left[ \begin{array}{ll} R1({\Gamma},U,\alpha,\alpha_{\text{i}})\\ R2({\Gamma},U,\alpha,\alpha_{\text{i}})\\ R3({\Gamma},U,\alpha,\alpha_{\text{i}})\\ R4({\Gamma},U,\alpha,\alpha_{\text{i}})\\ \end{array} \right] = \left[ \begin{array}{ll} AIC\ {\Gamma} - RHS\\ KU-F\\ L - nW_{des}\\ C_{{l_{2d}}} - C_{{l_{v}lm}} \end{array} \right] = \mathbf{0} $$
(1)
R 1 and R 2 are the governing equations of respectively the VLM and FEM. R 3 relates to the condition where the total lift is equal to the weight times the design load factor. R 4 states that the sectional viscous lift coefficient should be the same as the lift distribution from the VLM analysis, corrected for sweep. The system is solved using the Newton method for iteration where the updates on the state variables are determined using (2).
$$ \underbrace{\left[ \begin{array}{llll} \frac{\partial R1}{\partial {\Gamma}} & \frac{\partial R1}{\partial U} & \frac{\partial R1}{\partial \alpha} & \frac{\partial R1}{\partial \alpha_{i}} \\ \frac{\partial R2}{\partial {\Gamma}} & \frac{\partial R2}{\partial U} & \frac{\partial R2}{\partial \alpha} & \frac{\partial R2}{\partial \alpha_{i}} \\ \frac{\partial R3}{\partial {\Gamma}} &\frac{\partial R3}{\partial U} & \frac{\partial R3}{\partial \alpha} & \frac{\partial R3}{\partial \alpha_{i}}\\ \frac{\partial R4}{\partial {\Gamma}} & \frac{\partial R4}{\partial U} & \frac{\partial R4}{\partial \alpha} & \frac{\partial R4}{\partial \alpha_{i}}\\ \end{array} \right]}_{J} \left[ \begin{array}{ll} {\Delta} {\Gamma} \\ {\Delta} U \\ {\Delta} \alpha \\ {\Delta}\alpha_{i} \end{array} \right] = - \left[ \begin{array}{lll} R1({\Gamma},U,\alpha,\alpha_{i})\\ R2({\Gamma},U,\alpha,\alpha_{i})\\ R3({\Gamma},U,\alpha,\alpha_{i})\\ R4({\Gamma},U,\alpha,\alpha_{i})\\ \end{array} \right] $$
(2)
In order to facilitate gradient based optimization, the coupled-adjoint method is used Kenway et al. (2014). The sensitivity of any function of interest I with respect to any design variable x is computed by:
$$ \frac{dI}{dx} \,=\, \frac{\partial I}{\partial x} - {\lambda_{1}^{T}} \left( \frac{\!\partial R_{1}}{\partial x} \!\right) - {\lambda_{2}^{T}} \left( \frac{\!\partial R_{2}}{\partial x} \!\right) - {\lambda_{3}^{T}} \left( \frac{\!\partial R_{3}}{\partial x} \!\right) - {\lambda_{4}^{T}} \left( \frac{\!\partial R_{4}}{\partial x} \!\right) $$
(3)
where λ is the adjoint vector computed using the following equation:
$$ \left[\begin{array}{llll} \frac{\partial R_{1}}{\partial {\Gamma}} & \frac{\partial R_{1}}{\partial U} & \frac{\partial R_{1}}{\partial \alpha} & \frac{\partial R_{1}}{\partial \alpha}\\ \frac{\partial R_{2}}{\partial {\Gamma}} & \frac{\partial R_{2}}{\partial U} & \frac{\partial R_{2}}{\partial \alpha} & \frac{\partial R_{2}}{\partial \alpha}\\ \frac{\partial R_{3}}{\partial {\Gamma}} & \frac{\partial R_{3}}{\partial U} & \frac{\partial R_{3}}{\partial \alpha} & \frac{\partial R_{3}}{\partial \alpha}\\ \frac{\partial R_{4}}{\partial {\Gamma}} & \frac{\partial R_{4}}{\partial U} & \frac{\partial R_{4}}{\partial \alpha} & \frac{\partial R_{4}}{\partial \alpha}\\ \end{array}\right]^{T} \left[\begin{array}{ll} \lambda_{1}\\ \lambda_{2}\\ \lambda_{3}\\ \lambda_{4}\\ \end{array}\right] =\left[\begin{array}{ll} \frac{\partial I}{\partial {\Gamma}}\\ \frac{\partial I}{\partial u}\\ \frac{\partial I}{\partial \alpha}\\ \frac{\partial I}{\partial \alpha_{i}}\\ \end{array}\right] $$
(4)

For a complete description of this coupled-adjoint aerostructural analysis and optimization method and derivation of the coupled-adjoint method, the reader is referred to Elham and van Tooren (2016a).

3 Maximum lift prediction

Since MSES more often than not fails to converge at high angles of attack, the Pressure Difference Rule (PDR), developed by Valarezo and Chin (1994) is used for the estimation of \(C_{L_{\max }}\). The PDR states that for a given chord Reynolds number and free stream Mach number, there exist a relation between the wing stall and the pressure difference between the suction peak and trailing edge pressure. While Valarezo and Chin made use of a higher-order panel method to obtain the pressure difference at several spanwise section, any other reliable method may be used such as the Q3D method described in this paper, due to the fact that empirical data is used in the analysis which takes viscous effects into account. Furthermore it was identified that this rule can be used for 3D wing analysis even though it relies on 2D sectional data. This is due to the fact that at the critical stall section, the suction peak of the 3D wing will be equal to that of the 2D flow for the respective airfoil section.

The PDR is implemented as follows: First, the effective Reynolds number is computed at several wing stations based on the local clean chord, taking into account sweep and downwash. Then, using the free stream Mach number, the critical pressure difference (\({\Delta } C_{p_{\text {crit}}}\)) for a number of spanwise sections is computed from Fig. 1.
Fig. 1

Airfoil critical pressure difference for stall. Valarezo and Chin (1994)

The effective pressure distribution over each specified spanwise section is then computed from a 2D linear strength vortex panel method, based on the method of Katz and Plotkin (1991), using the effective flow properties as described in Section 2. To analyze the airfoil using the panel method code the effective angle of attack and the effective Mach number are required. These values are obtained from the global angle of attack and free stream Mach number by adjusting for sweep effects and downwash (see Elham and van Tooren (2016a) for more details).

Besides producing the given outputs, the panel method is able to produce the derivatives of the outputs with respect to the inputs using a combination of the chain rule of differentiation and Automatic Differentiation (AD) in reverse mode using the Matlab AD toolbox Intlab (Rump 1999).

In order to account for the decambering effect of the boundary layer and wakes on aft segments of a multi-element wing, Valarezo and Chin incorporated a reduction in effective flap deflection in their research (Valarezo and Chin 1994). The same flap reduction method has been applied to the Fokker 100 wing aerodynamic analysis (Obert 1986). The flap reduction angles used in both researches are shown in Fig. 2. Since the flap reduction angles of both researches are matching up to moderate flap angles of 20∘, it is assumed that the same reduction angles can be used for any flap configuration in this research.
Fig. 2

Flap angle reduction. Valarezo and Chin (1994) and Obert (1986)

Based on the PDR method the wing stall occurs when at one of the spanwise stations \({\Delta } C_{p_{\text {2d}}} = {\Delta } C_{p_{\text {crit}}}\). Here \({\Delta } C_{p_{\text {2d}}}\) is the 2D pressure difference computed using the Q3D method, see Fig. 3.
Fig. 3

Computing \({\Delta } C_{p_{\text {2d}}}\) using a panel code

4 Aerostructural coupling

In order to enable wing aerostructural analysis and optimization at high-lift conditions, the PDR described in the previous section is coupled with FEMWET. This further enhances the accuracy of predicting \(C_{L_{\max }}\) as it takes into account aeroelastic effects in the analysis. The coupled system is defined following set of equations:
$$ {\text{Sys}}_{\text{PDR}} = \left[ \begin{array}{lll} R1({\Gamma},U,\alpha,\alpha_{i})\\ R2({\Gamma},U,\alpha,\alpha_{i})\\ R3({\Gamma},U,\alpha,\alpha_{i})\\ R4({\Gamma},U,\alpha,\alpha_{i})\\ \end{array} \right] =\left[\begin{array}{ll} AIC\ {\Gamma} - RHS\\ KU-F\\ KS\\ C_{l_{{2d}_{\text{inv}}}} - C_{l_{\perp}} \end{array} \right] = \mathbf{0} $$
(5)
Here the third governing equation is the Kreisselmeier-Steinhauser (KS) aggregation function (Wrenn 1989). The KS function is essential in establishing a single governing equation for the PDR condition, which allows for coupling this condition with the FEMWET analysis, effectively achieving an aerostructural prediction of \(C_{L_{\max }}\):
$$ \text{KS} = f_{\max} + \frac{1}{\rho_{_{\text{KS}}}}\log_{e} \sum\limits_{k=1}^{K} e^{\rho_{_{\text{KS}}} (f_{k} (X) -f_{\max})} $$
(6)
where f k = \({\Delta } C_{p_{\text {crit}_{k}}} - {\Delta } C_{p_{\text {2d}_{k}}}\). In this equation a value of 80 is used for \({\rho _{_{\text {KS}}}}\).

The fourth equation in (5) states that the inviscid 2D lift computed by the panel method is equal to the VLM lift distribution, corrected for sweep. The system is solved using the same Newton method for iteration described in Section 2.

As mentioned before, the coupling of the PDR with FEMWET allows for taking aeroelastic effects into account in determining \(C_{L_{\max }}\). A representation of the coupling is presented in Fig. 4.
Fig. 4

Wing deformation in \(C_{L_{\max }}\) prediction

5 Sensitivity analysis

In order to use the Newton method for iteration, the partial derivatives of the governing equations with respect to the state variables (matrix J in (2)) are required. Additionally, to perform gradient based optimization, the sensitivities of any function of interest with respect to the design variables such as the wing planform or airfoil shape are required. The present tool computes all of the required derivatives through a combination of AD, chain rule of differentiation and the aforementioned coupled-adjoint method.

In Table 1, the partial derivatives of the governing equations of the coupled system (5) are presented. The first row is computed with relative ease where the partial derivative of R 1 with respect to Γ is the Aerodynamic Influence Matrix (AIC) matrix and the partial derivatives of R 1 with respect to U, α and α i are computed through AD. Moving to the second row, the derivative of R 2 with respect to Γ is computed using AD and the derivative of R 2 with respect to U is the stiffness matrix K.
Table 1

Partial derivatives of aerostructural PDR system

 

Γ

U

α

α i

R 1

AIC

\(\frac {\partial AIC}{\partial U}{\Gamma } - \frac {\partial RHS}{\partial U} \)

\( - \frac {\partial RHS}{\partial \alpha } \)

0

R 2

\( -\frac {\partial F}{\partial {\Gamma }}\)

K

0

0

R 3

0

0

\(\frac {\partial KS}{\partial \alpha }\)

\(\frac {\partial KS}{\partial \alpha _{i}}\)

R 4

\(-\frac {\partial C_{l_{\perp }}}{\partial {\Gamma }}\)

\(\frac {\partial C_{l_{{2d}_{\text {inv}}}}}{\partial U}\)

\(\frac {\partial C_{l_{{2d}_{\text {inv}}}}}{\partial \alpha }\)

\(\frac {\partial C_{l_{{2d}_{\text {inv}}}}}{\partial \alpha _{i}}\)

Computing the third and fourth row requires more attention. Starting with row 3, the partial derivative of f k in (6) with respect to α and α i are computed analytically through:
$$ \frac{\partial f_{k}}{\partial \alpha} = - \frac{\partial {\Delta} C_{p_{{2d}_{k}}}}{\partial {\Delta} C_{p_{\text{eff}_{k}}}} \left[ \frac{d {\Delta} C_{p_{\text{eff}_{k}}}}{d \alpha_{\text{eff}}} \frac{d \alpha_{\text{eff}}}{d \alpha} \right] $$
(7)
$$\begin{array}{@{}rcl@{}} \frac{\partial f_{k}}{\partial \alpha_{i}} &=& \frac{\partial {\Delta} C_{p_{\text{crit}_{k}}}}{\partial {\text{Re}}_{\text{eff}}}\frac{\partial {\text{Re}}_{\text{eff}}}{\partial \alpha_{i}} - \frac{\partial {\Delta} C_{p_{{2d}_{k}}}}{\partial \alpha_{i}}\\ &&- \frac{\partial {\Delta} C_{p_{{2d}_{k}}}}{\partial {\Delta} C_{p_{{\text{eff}}_{k}}}} \left[ \frac{d {\Delta} C_{p_{{\text{eff}}_{k}}}}{d \alpha_{\text{eff}}} \frac{d \alpha_{\text{eff}}}{d \alpha_{i}} + \frac{d {\Delta} C_{p_{{\text{eff}}_{k}}}}{d M_{\text{eff}}} \frac{d M_{\text{eff}}}{d \alpha_{i}} \right]\\ \end{array} $$
(8)
Moving on to the fourth row in Table 1, the partial derivative of R 4 with respect to Γ may be computed using AD. The remaining terms in the fourth rows are a bit more challenging however. These terms are computed using the combined use of AD, chain rule of differentiation and the adjoint method within MSES.

6 Verification and validation

While the aerostructural tool developed by Elham and Van Tooren has been validated for wing drag and wing deformation (Elham and van Tooren 2016a), the enhanced method needs to be validated for maximum wing lift coefficient prediction and computation of wing lift over drag ratios in high-lift conditions. Finally, the sensitivities are verified through Finite Differencing (FD).

6.1 Maximum lift coefficient

For validating the accuracy of the \(C_{L_{\max }}\) computation using the PDR, the 3D Royal Aircraft Establishment (RAE) experimental database (Lovell 1977) is used. For the current research, the basic body-off model was used without wing extension and with trailing edge Fowler flaps extending from 0.142 of the half span to the wing tip, see Figs. 5 and 6.
Fig. 5

RAE Wing planform

Fig. 6

RAE airfoil design

The analysis was conducted in the RAE 11.5- by 8.5-ft low-speed wind tunnel at a nominal Mach number of 0.223, corresponding to a Reynolds number of 1.35e6 based on the mean wing chord. Furthermore, in the PDR analysis it was assumed that the wing was rigid and thus no wing deflection occurs. Below, in Fig. 7a the computed results are shown together with experimental values for \(C_{L_{\max }}\)(Lovell 1977).
Fig. 7

Validation of \(C_{L_{\max }}\) computation

The maximum error between the computed and experimental results is 4.38% at a flap deflection of 10∘. A second test case has been performed to validate \(C_{L_{\max }}\) of the Fokker 100 class wing, for which the geometry and flow parameters are described in Section 7. Using the PDR, the clean \(C_{L_{\max }}\) was predicted to be 1.71 (See Fig. 7b). Compared to the actual value of 1.72 (Obert 2009), this is an error of 0.58%. The largest error is 9.17% at a flap deflection of 24∘. Considering the fact that in Valarezo and Chin (1994) the PDR has been validated against experimental data for numerous multi-element wing combinations up to flap angles of 40 degrees, the inaccuracy of the Fokker 100 \(C_{L_{\max }}\) at high flap deflections may well be attributed to the fact that the exact flap geometry of the Fokker 100 wing was unavailable for this research.

6.2 Wing weight

The total wing weight is then computed using the following equation:
$$ W_{\text{wing}} = 2 W_{\text{wingbox}}^{\text{FEM}} + W_{\sec} $$
(9)
where W wingboxFEM is the optimum wingbox weight computed using FEM. The factor 2 counts for non-optimum weight components. Elham and van Tooren (2016a) used a factor of 1.5 for the non-optimum weights. As reported in Elham and van Tooren (2016a) using the factor of 1.5 for non-optimum weights for A320 class wings produced remarkably accurate results. Initial investigation in the wing weight prediction of the Fokker 100 wing showed that this method underestimates the actual wing weight by 12%, which is likely due to the fact that the Fokker 100 design is a relatively old design and therefore far from optimal. After increasing the non-optimal weight factor from 1.5 to 2, results agreed much better with actual wing weight data of the Fokker 100 wing (Paul 1993). The method developed by Torenbeek (1992) is used to compute the wing secondary weights. This method includes an empirical method for flap weight estimation. The primary and secondary wing weight of Fokker 100 is estimated to be 2853 kg and 1543 kg respectively using the mentioned method. It makes the total wing structural weight equal to 4369 kg. Comparing to the actual wing weight of Fokker 100 equal to 4343 kg, the weight estimation methods seems to be accurate enough for this research.

6.3 Airfield performance

Airfield performance is governed by the take-off and landing distances. Regulations for take-off and landing performance are presented in FAR 25, which defines the take-off distance as the ground covered from standstill to the point where the aircraft is at 35 ft above the ground. The landing distance is defined as the ground covered from a point where the aircraft is at 50 ft above the ground to standstill. Take-off distance is the sum of the ground roll, rotation, transition and climbing distances. Airfield performance is approximated following the method from Raymer (2012) which has been adjusted for current regulations. This method takes the wing design parameters, stall speed and design weight, together with the computed drag and lift coefficient from the Q3D analysis at the characteristic take-off and landing velocities and calculates the respective take-off and landing distances:
$$ [s_{\text{TO}}, s_{\text{LNG}}] \,=\, {\text{Airfield\_Performance}}(X,V_{s_{1-g}},W_{\text{des}},C_{D_{\text{des}}},C_{L_{\text{des}}}) $$
(10)
The ground run distance is computed from:
$$ s_{GR} = \frac{1}{2gK_{A}} \ln\left( \frac{K_{T} + K_{A} {V_{f}^{2}}}{K_{T} + K_{A} {V_{i}^{2}}}\right) $$
(11)
Here V i is the initial velocity taken as 0 for the ground run, and V f is the velocity at the start of rotation which may be no less than 1.1 V s-1g according to Raymer. Coefficients K A and K T are defined as:
$$ K_{T} = \frac{\bar{T}}{W} - \mu_{r} $$
(12)
$$ K_{A} = \frac{\rho}{2\left( W/S\right)}(\mu_{r} C_{L} - D_{\text{aero}}) $$
(13)
Here \(\bar {T}\) is the average thrust taken to be equal to the thrust at V = \(1/\sqrt {2} V_{f}\). The rolling friction coefficient μ r is taken to be 0.03. Weight is equal to MTOW and the density is taken to be 1.225k g/m 3. For large aircraft, the rotation time to lift-off attitude may be assumed to be three seconds. Therefore s R can be approximated to be 3.3 V s-1g. During transition, the aircraft accelerates from 1.1 V s-1g to 1.13 V s-1g. The average speed during transition is therefore 1.12 V s-1g. The average lift coefficient during transition may be assumed to be 90% of \(C_{L_{\max }}|_{_{\text {TO}}}\). The average load factor during transition is equal to 1.2, which gives a rotation arc radius of R = 0.205V s-1g. The climb angle at the end of transition is determined from:
$$ \gamma = \frac{T}{W}-\frac{D}{L}\mid_{{1.13V}_{\text{s-1g}}} $$
(14)
The distance traveled and altitude gained during transition is computed by:
$$ s_{\text{TR}} = R \sin{\gamma} $$
(15)
$$ h_{\text{TR}} = R(1-\cos{\gamma}) $$
(16)
The value of h TR needs to be checked against the 35 ft obstacle height. If the obstacle height is cleared before the end of the transition segment, the following equation is to be used to compute the transition distance:
$$ s_{TR} = \sqrt{R^{2} - (R-h_{\text{TR}})^{2}} $$
(17)
Finally, unless the obstacle height is cleared during transition, the horizontal distance traveled during climb to clear the 35 ft obstacle height is found from:
$$ s_{C} = \frac{35{\text{ft}} - h_{TR}}{\tan{\gamma}} $$
(18)

Landing distance is computed analogously to take-off distance, taking into account that approach speed V A must be at least 1.23 times higher than V s-1g, the approach angle should not be steeper than 3 deg and the touch down velocity V T D is assumed to be 1.15 times V s-1g according to Raymer. This results in an average flaring velocity V F L of 1.19 times \(V_{S_{0}}\). The load factor during landing can be taken as 1.2 and the rolling friction coefficient due to deployed brakes during the ground run can be taken to be 10 times higher than during take-off. It should be noted that typically, the aircraft rolls free for 1 to 3 seconds before the pilot applies the brakes.

Validation of this method is performed for the Fokker 100 aircraft of which details are described in Section 7. The computed take-off and landing distance are compared to Fokker 100 performance data in Table 2.
Table 2

Fokker 100 Airfield performance

 

Actual

Computed

𝜖

s TO[m]

1760

1827

3.6%

s LNG[m]

1345

1436

6.3%

6.4 Sensitivities Verification

Finally, the sensitivities computed by the presented analysis tool are verified through Finite Differencing (FD). In their paper, Elham and van Tooren (2016a) have already verified the sensitivities of several outputs of FEMWET. For this reason, only the sensitivities of landing distance with respect to a number of input variables are verified for a Fokker 100 class wing. From the research by Elham and van Tooren, it has been observed that while MSES computes sensitivities with a large number of digits, it only reports them up to 4 digits. The reported sensitivity of drag is therefore limited to an order of 10−3, which is not sufficient to perform verification through finite differencing. In order to still be able to verify the computed sensitivities, an empirical aerodynamic analysis tool has been developed, which does not rely on sensitivities computed by MSES but instead computes them using AD. The results of the sensitivity verification is shown below in Table 3.
Table 3

Sensitivity verification

Function

Variable

FD

Coupled-adjoint

Relative difference (%)

FD step size

s LNG [m]

Thickness of wing upper panel at root section [m]

−58.5482

−58.6677

2.03 × 10−1

1e-9

...

Thickness of wing lower panel at root section [m]

−38.5779

−38.8700

7.57 × 10−1

1e-9

...

First Chebyshev mode amplitude at root section [-]

−299.5294

−298.8453

2.28 × 10−1

1e-6

...

Inboard leading edge sweep [rad]

942.4716

944.4626

2.11 × 10−1

1e-9

...

Span up to wing kink [m]

−168.8636

−168.8063

3.39 × 10−2

1e-9

...

Flap span [m]

−1304.3331

−1300.6584

2.81 × 10−1

1e-9

...

Flap overlap [%c]

17567.2443

17567.8219

3.28 × 10−3

1e-9

...

Flap gap [%c]

13016.4608

13017.0928

4.85 × 10−3

1e-9

...

Flap deflection [rad]

−2984.6424

−2984.3981

1.87 × 10−3

1e-9

7 Test case application

As a test case, the aerostructural optimization of a Fokker 100 class aircraft wing is considered. The aerostructural optimization is performed using SNOPT (Gill et al. 2005) and is formulated as follows:
$$\begin{array}{@{}rcl@{}} && min W^{*}_{\text{fuel}} (X)\\ && ~~~~~~~X = [T,P,P_{f},G_{j},G_{t_{k}},W^{*}_{\text{fuel}},MTOW^{*}] \\ &&s.t. \text{Failure}_{k} \le 0 \\ && ~~~~~~~~1 - \frac{L_{\delta}}{L_{\delta_{\min}}}\leq 0 \\ && ~~~~~~~\frac{s_{\text{TO}}}{s_{\text{TO}_{0}}} -1 \leq 0 \\ && ~~~~~~~\frac{s_{\text{LNG}}}{s_{\text{LNG}_{0}}} -1 \leq 0 \\ && ~~~~~~~\frac{W_{\text{fuel}}}{W_{\text{fuel}}^{*}} -1 = 0 \\ && ~~~~~~~\frac{\text{MTOW}}{\text{MTOW}^{*}} -1 = 0 \\ && ~~~~~~~X_{\text{lower}} \le X \le X_{\text{upper}} \end{array} $$
In the design vector X, the variables T, P and P f represent respectively the equivalent panel thickness of the wingbox, the planform geometry variables and the high-lift device planform geometry variables. The last two group of design variables are shown in Fig. 8.
Fig. 8

Planform design variables

The fourth group of design variables, G j , is used to define the wing airfoils’ shapes. At 8 spanwise positions, the airfoil geometry is perturbed normal to its surface by a value (Δn) which is determined based on basis functions g j , the Chebyshev polynomials, and the mode amplitudes G j as follows:
$$ {\Delta} n(s) = \sum\limits_{j=1}^{J} G_{j}\ g_{j}(s) $$
(19)
Here s is the fractional arc length of the segment that the perturbation is applied to. In order to send a single set of shape design variables to the optimizer which applies to all analysis cases, the airfoil surface is split in sections as shown in Fig. 9. Through this method, the effect of perturbations on the cruise wing with respect to e.g. cruise drag can be combined with the effect of the same perturbation on \(C_{L_{\max }}\) in landing configuration. A total of 9 shape variables are used to perturb respectively sections A-C and A-B and 1 shape variable is used for respectively sections C-G and B-G in order to prevent extreme discontinuities at intersections B and C. A total of 20 shape variables are thus defined per airfoil section and are active in both clean and high-lift wing configuration analysis. It should be noted that as a result of splitting the airfoil sections, points B and C remain stationary during the optimization. Although it is possible to accommodate for horizontal and vertical perturbation of these points through the use of finite differencing, this is beyond the scope of the present research.
Fig. 9

2D Airfoil shape design space

The fifth group of design variables is used to perturb the flap’s position using the mode amplitudes \(G_{t_{k}}\) (see Fig. 9). The mode amplitudes consist of two translational modes. \(G_{t_{1}}\) controls the horizontal translation of the flap and \(G_{t_{2}}\) the vertical translation. The third mode amplitude \(G_{t_{3}}\) controls the flap deflection.

The final group of variables are used to avoid unnecessary iterations for aeroelastic analysis. The optimization problem is subject to a number of constraints including constraints on structural failure and aileron effectiveness as described in Elham and van Tooren (2016a). In the same research, Elham and Van Tooren included a constraint on wing loading to take airfield performance into account. In the present research, the wing loading constraint is replaced by constraints on take-off and landing distance.

In total, a number of 835 inequality and 2 equality constraints are defined, and a total of 214 design variables are used for optimization (Table 4).
Table 4

Optimization variables and constraints

Variable group

Symbol

#

Equivalent panel thickness

T

40

Wing planform

P

8

Flap planform

P f

1

Airfoil shape

G j

160

Flap position

\(\text {G}_{t_{k}}\)

3

Surrogate variables

X ∗

2

Constraint

Equation

 

Compression upper panel

F compression ≤ 0

104

Compression lower panel

F compression ≤ 0

52

Tension upper panel

F tension ≤ 0

52

Tension lower panel

F tension ≤ 0

104

Buckling upper panel

F buckling ≤ 0

104

Buckling lower panel

F buckling ≤ 0

52

Shear front spar

F shear ≤ 0

78

Buckling front spar

F buckling ≤ 0

78

Shear rear spar

F shear ≤ 0

78

Buckling rear spar

F buckling ≤ 0

78

Fatigue

F fatigue ≤ 0

52

Aileron Effectiveness

\(1 - \frac {M_{a}}{M_{a_{\min }}}\leq 0\)

1

Take-off distance

\( \frac {s_{\text {TO}}}{s_{\text {TO}_{0}}} -1\leq 0\)

1

Landing distance

\(\frac {s_{\text {LNG}}}{s_{\text {LNG}_{0}}} - 1\leq 0\)

1

Fuel weight

\(\frac {W_{\text {fuel}}}{W_{\text {fuel}}^{*}} - 1 = 0\)

1

Maximum Take Off Weight

\(\frac {\text {MTOW}}{\text {MTOW}^{*}} - 1 = 0\)

1

For aerodynamic analysis, it is assumed that the high-lift system consists of one continuous single slotted flap with a maximum deflection of 20∘. It is assumed that the take-off is performed with flaps retracted as the Fokker 100 has been certified to take-off without flaps (Obert 2009). So the flap is optimized only for landing requirement. However the take-off performance was still taken into account since modifying the wing planform geometry affects the take-off performance. The wingbox internal structure is initiated by performing an aeroelastic optimization, aimed to minimize structural weight while satisfying failure constraints such as material failure and fatigue under the load cases listed in Table 5 and a constraint on aileron effectiveness.
Table 5

Load cases for wing aeroelastic optimization (Dillinger et al. 2013; Saunders et al. 1995)

Load case

type

H [m]

M

n [g]

1

pull up, M D

7500

0.84

2.5

2

pull up, V D

0

0.57

2.5

3

push down, M D

7500

0.84

-1

4

gust, M D

7500

0.84

1.3

5

roll, 1.15V D

4000

0.81

1

6

cruise, M cruise

10670

0.77

1

7

take-off, V 2

0

-

1

8

landing, V A

0

-

1

The structural analysis is performed for the load cases listed in Table 5. Fatigue is simulated by limiting the stress in the wing box lower panel to 42% of the maximum allowable stress of the material in a 1.3g gust load case (Hürlimann et al. 2011). The aircraft rolling moment due to aileron deflection (L δ ) in the critical roll case is limited to be higher or equal to L δ of the initial aircraft.

The mission fuel weight (W fuel) is computed based on the method of Roskam (2003). The required fuel use for cruise is computed using the Bréguet range equation, while statistical factors are used to determine the fuel weight of the remaining segments of the mission. The total aircraft drag is assumed to be the sum of the wing drag and the drag of the rest of the aircraft based on Fokker 100 aircraft data (Obert 2009). The drag of the aircraft minus wing is kept constant during the optimization. The aircraft range, cruise Mach number, altitude and engine parameters are determined based on aircraft data. The aircraft Maximum take-off Weight (MTOW) is assumed to be equal to the payload weight, the aircraft fuel weight, the wing structural weight and a weight components that is called the rest weight. which is the operational empty weight minus the wing structural weight. The rest weight of the aircraft is computed from the Fokker 100 weight data and is kept constant during optimization.

The extended design structure matrix of this optimization is shown in Fig. 10.
Fig. 10

Extended Design Structure Matrix (Lambe and Martins 2012)

In order to compare the proposed optimization procedure to conventional optimization schemes, two optimizations were performed for the Fokker 100 wing:

  • Wing A (Concurrent optimization): The wing planform and airfoil shape and the high lift device geometry are optimized simultaneously for minimizing the aircraft mission fuel weight and satisfying the field performance constraints, (7).

  • Wing B (Sequential optimization): Wing planform and airfoils are first optimized for minimum fuel weight (based on the cruise condition) without any airfield performance constraint. Then the high-lift devices are optimized for satisfying the field performance requirements.

The optimization histories of both wings A and B are shown in Fig. 11. Both optimizations have been performed using 8 parallel 3.50 GHz processors and 63 GB of RAM. The optimization of wing A finished in 12 hours after 18 iterations with a total number of 109 objective function evaluations. The initial optimization of Wing B finished in 7 hours after 15 iterations with a total number of 73 function evaluations. The subsequent high-lift device optimization finished in 12.5 hours after 4 iterations and 86 function evaluations. The computational cost breakdown of the tool is as follows: Wing aerostructural analysis is performed in 159.6 seconds, of which 133.5 seconds may be attributed to the coupled adjoint sensitivity analysis. The high-lift wing analysis, which includes the computation of \(C_{L_{\max }}\), takes 349.1 seconds to complete of which 268.7 seconds can be attributed to the coupled-adjoint analysis.
Fig. 11

History of wing aerostructural optimizations

In Fig. 12 the contours of the wingbox and fuel tank (both shown in blue) of wing A is shown. The front and rear spar position as function of local chord length were kept constant during the optimization. In Fig. 13 the optimized planforms of cases A and B are overlaid with the initial planform design. It can be seen that both optimized wings have a higher aspect ratio of respectively 10.65 and 9.74 compared to 8.26 of the initial wing. Quarter chord sweep angles of cases A and B were reduced to respectively 14.9∘ and 16.9∘ compared to the initial sweep angle of 18.5∘ (Table 6). The difference in the planforms originate from the different optimization schemes as a pure cruise wing design tends to have an increased sweep angle and larger wing loading to reduce pressure drag than a wing design which takes into account airfield performance. The fuel weight reduction of wing A is 9.65% and 9.20% for wing B while the wing weight is only marginally reduced by respectively 3.6% and 3.3% for wings A and B respectively.
Fig. 12

Optimized wingbox layout

Fig. 13

Inititial and optimized wing planforms

Table 6

Initial and optimized wing geometry variables

Parameter

Initial

Wing A

Wing B

c r [m]

5.97

5.52

5.49

λ [-]

0.18

0.10

0.12

b 1 [m]

4.70

3.97

4.39

b 2 [m]

9.34

11.73

10.42

Λ1 [∘]

25.5

21.26

21.46

Λ2 [∘]

21.5

18.23

20.91

𝜖 1 [∘]

−0.65

−0.80

−0.76

𝜖 2 [∘]

−5.40

−4.32

−4.34

b f [m]

6.50

5.06

5.50

From Table 7 it can be deducted that the reduced fuel weight is primarily achieved through reducing the total drag by respectively 28.7% and 25.0% for wings A and B. The induced drag of respectively wings A and B is reduced by 24.4% and 14.1% by increasing the aspect ratio. The largest reduction has been in pressure drag which has seen a reduction of respectively 57.1% and 60.3%. This reduction in pressure drag is a result of the optimized airfoil shapes which can be seen in Fig. 14. Despite the increased normal Mach number due to the reduced sweep angle, the optimizer was able to reduce the strength of the shock wave and even at several spanwise positions completely remove the shock wave on the airfoils at cruise speed, see Fig. 15. The lift distribution on the initial as well as the optimized wings are plotted in Fig. 16.
Table 7

Characteristics of the initial and the optimized aircraft

 

MTOW [kg]

W fuel [kg]

W wing [kg]

S wing [m 2]

\(C_{L_{\text {cruise}}}\)

\(C_{D_{\text {cruise}}}\)

\(C_{D_{i}}\)

\(C_{D_{p}}\)

\(C_{D_{f}}\)

Initial

43090

7260

4369

95.4

0.41

0.0188

0.0078

0.0063

0.0047

Concurrent

42487

6559

4468

92.6

0.42

0.0132

0.0059

0.0027

0.0046

Sequential

42492

6592

4446

90.1

0.43

0.0141

0.0067

0.0025

0.0049

Fig. 14

Initial and optimized airfoil shape on sections perpendicular to the sweep line

Fig. 15

Initial and optimized pressure distribution on sections perpendicular to the sweep line

Fig. 16

Lift distribution of the initial wing and optimized wings in cruise condition

Notably, the structural weight of both wings A and B has increased to a small degree. While a higher aspect ratio typically results in a larger structural weight near the root in order to withstand the increased bending moment, the weight penalty has been partially countered by reducing wing sweep and increasing wing flexibility. This increase in flexibility has been achieved by reducing the equivalent panel thickness of the outboard wing sections, which becomes visible in Fig. 17. The wing tip vertical and twist deformation under 1g load of the initial wing are respectively 0.39m and −0.84∘. For a 2.5g pull up these values are 1.12m and −2.24∘. The vertical and twist deformation of the tip of the wing A under 1g load are 0.94m and −1.29∘ and for wing B 0.75m and −1.25∘. For a 2.5g pull up these deformations are 2.37m and −3.02∘ for wing A and 1.93m and −2.99∘ for wing B. The wing deformation under 2.5g pull up is shown graphically in (Fig. 18).
Fig. 17

Wingbox Von Mises stress distribution in roll maneuver

Fig. 18

Initial and optimized wing deformed shapes under 2.5g pull up

In Table 8 the flap designs for the initial and optimized designs are listed. Because wing B has a smaller wing span and wing area than wing A, it is expected to require a larger flap span to maintain airfield performance. Indeed, from Table 8 it follows that the flap span for the wing A is reduced by 11.8% and for wing B only by 7.23%. The flap weight of the wings A and B is also reduced by respectively 22.9% and 17.9%. Flap overlap (h f ), gap (g f ) and deflection angle (δ f ) have all increased in landing configuration in order to increase flap efficiency to counter the reduced flap span and increased wing loading as can be seen in Fig. 19. It is also notable that both optimization schemes result in similar flap settings, despite changes to wing geometry.
Table 8

Characteristics of the initial and the optimized high-lift system

 

W flap [kg]

S flap [m 2]

b f [m]

h f [%c]

g f [%c]

δ f [∘]

Initial

576

17.1

6.50

5.00

2.40

20.00

Concurrent

443

13.0

5.06

5.69

2.75

28.24

Sequential

473

14.0

5.50

5.78

2.42

27.76

Fig. 19

Initial and optimized flap landing configuration on sections perpendicular to the sweep line

The high-lift performance characteristics of the optimized wings are listed in Table 9. It can be seen that both wings A and B have increased \(C_{L_{\max }}\) in take-off and landing configuration as a result of both a reduced sweep angle and increased flap deflection. While both wings have a reduced wing area, the stall speed \(V_{s_{1}g}\) at MTOW and MLW remain similar to the initial design as a result of the increased \(C_{L_{\max }}\) values.
Table 9

High-Lift characteristics of the initial and the optimized aircraft

 

\(C_{{L_{\max }}|_{_{TO}}}\)

\(C_{{L_{\max }}|_{_{LNG}}}\)

\(V_{s_{\text {1-g}}}|_{_{\text {MTOW}}}\) [m/s]

\(V_{s_{\text {1-g}}}|_{_{\text {MLW}}}\) [m/s]

\(\frac {L}{D}|_{_{V_{2}}}\)

\(\frac {L}{D}|_{_{V_{A}}}\)

s TO [m]

s LNG [m]

Initital

1.71

1.91

65.03

51.91

19.99

12.84

1827

1436

Concurrent

1.75

2.12

64.69

50.81

23.39

11.15

1767

1432

Sequential

1.76

2.03

65.68

52.36

22.00

11.24

1835

1431

While wing A meets both airfield performance requirements, wing B is not able to achieve take-off performance with flaps retracted. Although this seems to be an infeasible solution, it is a result of the optimization formulation, in which take-off is always performed with flaps retracted. So the wing planform was not design to satisfy the field performance and the flap optimization was not performed for take-off condition. When considering the design of wing B, it can be seen that its wing loading has increased due to the small wing area. While this is beneficial for cruise flight, it is undesirable for maintaining airfield performance.

8 Conclusion

An enhanced coupled-adjoint aerostructural analysis and optimization tool has been presented which enables the optimization of high-lift devices from the start of the design process. The semi-empirical Pressure Difference Rule has been implemented in an existing quasi-three-dimensional aerodynamic analysis and coupled to the structural solver FEMWET to compute the wing \(C_{L_{\max }}\) taking into account aeroelastic effects. The coupled system is solved using the Newton method.

The modified aerostructural tool is able to compute the derivatives of the outputs with respect to the inputs using a combination of the chain rule of differentiation, automatic differentiation and coupled-adjoint method. Wing weight is computed using the empirical method of Torenbeek which enables optimization taking into account the specific weight of high-lift devices. Airfield performance is determined using the method of Raymer which includes lift and drag terms at take-off and landing. Validation of the modifications showed good levels of accuracy for L/D, \(C_{L_{\max }}\), wing weight and airfield performance.

The tool was then used for gradient based aerostructural wing and high-lift system optimization for a Fokker 100 class wing. Design variables include flap span and settings, wing planform, airfoil geometry and wingbox structure. The optimization was performed for minimizing the fuel weight, while satisfying constraints on structural failure, \(C_{L_{\max }}\) in take-off and landing configuration and the roll requirement. The flaps were retracted in the take-off configuration as the Fokker 100 is certified to perform take-off with flaps retracted. Two types of optimizations were performed. The proposed concurrent optimization scheme where the high-lift system was optimized from the start of the process and a more conventional sequential optimization, in which the planform was first optimized for cruise performance after which the high-lift system was sized to minimize fuel weight for the fixed optimized planform taking into account airfield performance.

The concurrent optimization resulted in a fuel weight reduction of 9.65%, while sequential optimization reduced fuel weight by 9.20%. The reduced fuel weight was attributed to a reduction in pressure drag resulting from modified airfoil shapes, reducing shock waves over the wing. The optimized wings both have an increased aspect ratio and reduced sweep angle, which resulted in a reduction of induced drag. To counter the weight penalty due to these modifications, the structural stiffness was reduced near the wing tip. The optimizer reduced flap weight of both optimized wings by respectively 22.9% and 17.9% by reducing flap span. It can be concluded that the proposed method of combining the optimization of high-lift and cruise wing design is promising and provides ample opportunities for more research.

Notes

References

  1. Barcelos M, Maute K (2008) Aeroelastic design optimization for laminar and turbulent flows. Comput Methods Appl Mech Eng 197(19-20):1813–1832.  https://doi.org/10.1016/j.cma.2007.03.009 CrossRefMATHGoogle Scholar
  2. Dillinger JKS, Klimmek T, Abdalla MM, Gurdal Z (2013) Stiffness optimization of composite wings with aeroelastic constraints. J Aircr 50(4):1159–1168.  https://doi.org/10.2514/1.C032084 CrossRefGoogle Scholar
  3. Drela M (2013) MSES: Multi-Element Airfoil Design/Analysis Software, Ver. 3.11. Massachusetts Institute of Technology, CambridgeGoogle Scholar
  4. Drela M, Giles MB (1987) Viscous-inviscid analysis of transonic and low reynolds number airfoils. AIAA J 25(10):1347–1355.  https://doi.org/10.2514/3.9789 CrossRefMATHGoogle Scholar
  5. Elham A (2015) Adjoint quasi-three-dimensional aerodynamic solver for multi-fidelity wing aerodynamic shape optimization. Aerosp Sci Technol 41(1270-9638):241–249.  https://doi.org/10.1016/j.ast.2014.12.024 CrossRefGoogle Scholar
  6. Elham A, van Tooren MJL (2016a) Coupled adjoint aerostructural wing optimization using quasi-three-dimensional aerodynamic analysis. Struct Multidisc Optim 54:889–906.  https://doi.org/10.1007/s00158-016-1447-9 MathSciNetCrossRefGoogle Scholar
  7. Elham A, van Tooren MJL (2016b) Tool for preliminary structural sizing, weight estimation, and aeroelastic optimization of lifting surfaces. Proc Inst Mech Eng Part G: J Aerospace Eng 230(2):280–295.  https://doi.org/10.1177/0954410015591045 CrossRefGoogle Scholar
  8. Flaig A, Hilbig R (1993) High-lift design for large civil aircraft. In: AGARD-CP-515: High-lift system aerodynamicsGoogle Scholar
  9. Gill P, Murray W, Saunders M (2005) Snopt: An sqp algorithm for large-scale constrained optimization. SIAM Rev 47(1):99–131.  https://doi.org/10.1137/S0036144504446096 MathSciNetCrossRefMATHGoogle Scholar
  10. Hürlimann F, Kelm R, Dugas MO, Kress G (2011) Mass estimation of transport aircraft wingbox structures with a CAD/CAE-based multidisciplinary process. Aerosp Sci Technol 15(4):323–333.  https://doi.org/10.1016/j.ast.2010.08.005 CrossRefGoogle Scholar
  11. Katz J, Plotkin A (1991) Low-speed aerodynamics, 2nd edn. McGraw-Hill, Inc., New YorkMATHGoogle Scholar
  12. Kennedy GJ, Martins JRRA (2014) A parallel aerostructural optimization framework for aircraft design studies. Struct Multidiscip Optim 60(6):1079–1101.  https://doi.org/10.1007/s00158-014-1108-9 CrossRefGoogle Scholar
  13. Kenway GKW, Kennedy GJ, Martins JRRA (2014) Scalable parallel approach for high-fidelity steady-state aeroelastic analysis and adjoint derivative computations. AIAA J 52(5):935–951.  https://doi.org/10.2514/1.J052255 CrossRefGoogle Scholar
  14. Lambe AB, Martins JRRA (2012) Extensions to the design structure matrix for the description of multidisciplinary design, analysis, and optimization processes. Struct Multidiscip Optim 46(2):273–284.  https://doi.org/10.1007/s00158-012-0763-y CrossRefMATHGoogle Scholar
  15. Lovell DA (1977) A wind-tunnel investigation of the effects of flap span and deflection angle, wing planform and a body on the high-lift performance of a 28∘ swept wing. Aeronautical Research Council, C.P. 1372, London, United KingdomGoogle Scholar
  16. Mariens J, Elham A, van Tooren MJL (2014) Quasi-three-dimensional aerodynamic solver for multidisciplinary design optimization of lifting surfaces. J Aircr 51(2):547–558.  https://doi.org/10.2514/1.C032261 CrossRefGoogle Scholar
  17. Martins JRRA, Alonso JJ, Reuther JJ (2004) High-fidelity aerostructural design optimization of a supersonic business jet. J Aircr 41(3):523–530.  https://doi.org/10.2514/1.11478 CrossRefGoogle Scholar
  18. Meredith PT (1993) Viscous phenomena affecting high-lift systems and suggestions for future CFD development. High-Lift System Aerodynamics, AGARD-CP-515Google Scholar
  19. Nield BN (1995) An overview of the Boeing 777 high-lift aerodynamic design. Aeronautical JournalGoogle Scholar
  20. Obert E (1986) A procedure for the determination of trimmed drag polars for transport aircraft with flap deflected. Fokker B.V., A-173, AmsterdamGoogle Scholar
  21. Obert E (2009) Aerodynamic design of transport aircraft, 1st edn. IOS Press, AmsterdamGoogle Scholar
  22. Paul (1993) Flügel, transporter, masserelevante daten. LTH Masseanalyse - Deutche Aerospace Airbus, 501 52-01, Hamburg, GermanyGoogle Scholar
  23. Pepper RS, van Dam CP, Gelhausen PA (1996) Design methodology for high-lift systems on subsonic transport aircraft. In: 6th AIAA, NASA, and ISSMO symposium on multidisciplinary analysis and optimization. AIAA, Reston, VA.  https://doi.org/10.2514/6.1996-4056, pp 707–723
  24. Raymer DP (2012) Aircraft design: a conceptual approach, 5th edn. AIAA, Washington.  https://doi.org/10.2514/4.869112 CrossRefGoogle Scholar
  25. Reckzeh D (2003) Aerodynamic design of the high-lift-wing for a megaliner aircraft. Aerosp Sci Technol 7 (2):107–119.  https://doi.org/10.1016/S1270-9638(02)00002-0 CrossRefGoogle Scholar
  26. Roskam J (2000) Airplane design part, VI: preliminary calculation of aerodynamic, thrust and power characteristics. DARcorporation, Lawrence, KSGoogle Scholar
  27. Roskam J (2003) Airplane design part, V: component weight estimation. DARcorporation, LawrenceGoogle Scholar
  28. Rump SM (1999) Intlab - interval laboratory, development in reliable computing. Springer, Dordrecht, pp 77–104.  https://doi.org/10.1007/978-94-017-1247-7_7 MATHGoogle Scholar
  29. Saunders CR, Hertof RJD, vd Sluis JC (1995) Fokker 100 type specification. Fokker B.V., AmsterdamGoogle Scholar
  30. Smith AMO (1975) High-lift aerodynamics. J Aircr 12(6):501–529.  https://doi.org/10.1899/15-9834.6 CrossRefGoogle Scholar
  31. Torenbeek E (1982) Synthesis of subsonic airplane design, 1st edn. Delft University Press, Delft.  https://doi.org/10.1007/978-94-017-3202-4 CrossRefGoogle Scholar
  32. Torenbeek E (1992) Development and application of a comprehensive, design-sensitive weight prediction method for wing structures of transport category aircraft. Delft University of Technology, Delft. LR-693Google Scholar
  33. Valarezo WO, Chin VD (1994) Method for the prediction of wing maximum lift. J Aircr 31(1):103–109.  https://doi.org/10.2514/3.46461 CrossRefGoogle Scholar
  34. van Dam CP (2002) The aerodynamic design of multi-element high-lift systems for transport airplanes. Prog Aerosp Sci 38(2):101–144.  https://doi.org/10.1016/S0376-0421(02)00002-7 MathSciNetCrossRefGoogle Scholar
  35. van Dam CP (2003) Aircraft design and the importance of drag prediction. In: C.D-based aircraft drag prediction and reduction, vol. 2. von Karman Institute for Fluid Dynamics, Rhode-St-Gense, Belgium, pp 1–37Google Scholar
  36. Wrenn GA (1989) An indirect method for numerical optimization using the Kreisselmeier-Steinhauser function. NASA 4220Google Scholar

Copyright information

© The Author(s) 2017

Open AccessThis article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Authors and Affiliations

  1. 1.Faculty of Aerospace EngineeringDelft University of TechnologyDelftNetherlands
  2. 2.Institute of Aircraft Design and Lightweight StructuresTechnische Universität BraunschweigBraunschweigGermany

Personalised recommendations