Topological derivative-based topology optimization of structures subject to design-dependent hydrostatic pressure loading

Abstract

In this paper the topological derivative concept is applied in the context of compliance topology optimization of structures subject to design-dependent hydrostatic pressure loading under volume constraint. The topological derivative represents the first term of the asymptotic expansion of a given shape functional with respect to the small parameter which measures the size of singular domain perturbations, such as holes, inclusions, source-terms and cracks. In particular, the topological asymptotic expansion of the total potential energy associated with plane stress or plane strain linear elasticity, taking into account the nucleation of a circular inclusion with non-homogeneous transmission condition on its boundary, is rigorously developed. Physically, there is a hydrostatic pressure acting on the interface of the topological perturbation, allowing to naturally deal with loading-dependent structural topology optimization. The obtained result is used in a topology optimization algorithm based on the associated topological derivative together with a level-set domain representation method. Finally, some numerical examples are presented, showing the influence of the hydrostatic pressure on the topology of the structure.

Appendix: Topological Derivative Evaluation

In order to evaluate the difference between the functionals $\mathcal {J}_{\chi }(u)$ and $\mathcal {J}_{\chi _{\varepsilon }}(u_{\varepsilon })$, respectively defined in (2.7) and (2.18), we start by taking η = u _ε −u as test function in the variational problem (2.8). Then we have the following equality

$$\begin{array}{@{}rcl@{}} {\int}_{\mathcal{D}} \sigma(u) \cdot \nabla u^{s} &=& {\int}_{\mathcal{D}} \sigma(u) \cdot \nabla u_{\varepsilon}^{s} \\ &&- {\int}_{{\Gamma}_{N}} \overline{q} \cdot (u_{\varepsilon} - u) \\ &&- {\int}_{\omega}p \, \text{div} (u_{\varepsilon} - u). \end{array} $$

(A.1)

After replacing (A.1) into (2.7) we obtain

$$\begin{array}{@{}rcl@{}} \mathcal{J}_{\chi}(u) &=& \frac{1}{2} {\int}_{\mathcal{D}} \sigma(u) \cdot \nabla u_{\varepsilon}^{s} \\ &&- \frac{1}{2} {\int}_{{\Gamma}_{N}} \overline{q} \cdot (u_{\varepsilon}+u) \\ &&- \frac{1}{2} {\int}_{\omega} p \, \text{div}(u_{\varepsilon}+u). \end{array} $$

(A.2)

In the same way, let us set η = u _ε −u as test function in the variational problem (2.19). Thus

$$\begin{array}{@{}rcl@{}} {\int}_{\mathcal{D}} \sigma_{\varepsilon}(u_{\varepsilon}) \cdot \nabla u_{\varepsilon}^{s} &=& {\int}_{\mathcal{D}} \sigma_{\varepsilon}(u_{\varepsilon}) \cdot \nabla u^{s} \\ &&+ {\int}_{{\Gamma}_{N}} \overline{q} \cdot (u_{\varepsilon} - u) \\ &&+ {\int}_{\omega}p \, \text{div}(u_{\varepsilon} - u) \\ &&+ \kappa {\int}_{B_{\varepsilon}}p \, \text{div}(u_{\varepsilon} - u). \end{array} $$

(A.3)

After replacing (A.3) into (2.18), it follows

$$\begin{array}{@{}rcl@{}} \mathcal{J}_{\chi_{\varepsilon}}(u_{\varepsilon}) &=& \frac{1}{2} \displaystyle{\int}_{\mathcal{D}} \sigma_{\varepsilon}(u_{\varepsilon}) \cdot \nabla u^{s} \\ &&-\frac{1}{2} \displaystyle{\int}_{{\Gamma}_{N}} \overline{q} \cdot (u_{\varepsilon}+u) \\ &&- \frac{1}{2} \displaystyle{\int}_{\omega}p \, \text{div}(u_{\varepsilon}+u) \\ &&- \frac{1}{2} \kappa \displaystyle{\int}_{B_{\varepsilon}} p \, \text{div}(u_{\varepsilon}+u). \end{array} $$

(A.4)

From (A.2) and (A.4), the variation of the energy shape functionals can be written as

$$\begin{array}{@{}rcl@{}} \mathcal{J}_{\chi_{\varepsilon}}(u_{\varepsilon}) - \mathcal{J}_{\chi}(u) &=& \frac{1}{2} {\int}_{\mathcal{D}} \sigma_{\varepsilon}(u_{\varepsilon}) \cdot \nabla u^{s} \\ &&- \frac{1}{2} {\int}_{\mathcal{D}} \sigma(u_{\varepsilon}) \cdot \nabla u^{s} \\ &&- \frac{1}{2} \kappa {\int}_{B_{\varepsilon}} p \, \text{div}(u_{\varepsilon}+u). \end{array} $$

(A.5)

Now, by taking into account the definition for the contrast γ _ε given by (2.17), we have

$$\begin{array}{@{}rcl@{}} \mathcal{J}_{\chi_{\varepsilon}}(u_{\varepsilon}) - \mathcal{J}_{\chi}(u) &=& \frac{1}{2} {\int}_{\mathcal{D} \setminus B_{\varepsilon}} \sigma(u_{\varepsilon}) \cdot \nabla u^{s} \\ &&+ \frac{1}{2} {\int}_{B_{\varepsilon}} \gamma \sigma (u_{\varepsilon}) \cdot \nabla u^{s} \\ &&- \frac{1}{2} {\int}_{\mathcal{D} \setminus B_{\varepsilon}} \sigma(u_{\varepsilon}) \cdot \nabla u^{s} \\ &&- \frac{1}{2} {\int}_{B_{\varepsilon}} \sigma(u_{\varepsilon}) \cdot \nabla u^{s} \\ &&- \frac{1}{2} \kappa {\int}_{B_{\varepsilon}} p \, \text{div}(u_{\varepsilon}+u). \end{array} $$

(A.6)

Let us add and subtract the term

$$\begin{array}{@{}rcl@{}} \frac{1}{2}\kappa {\int}_{B_{\varepsilon}} p \, \text{div}(u). \end{array} $$

(A.7)

Thus, the following expression is obtained after canceling the identical terms

$$\begin{array}{@{}rcl@{}} \mathcal{J}_{\chi_{\varepsilon}}(u_{\varepsilon}) - \mathcal{J}_{\chi}(u) &=& \displaystyle{\int}_{B_{\varepsilon}} \frac{\gamma - 1}{2\gamma}\sigma_{\varepsilon}(u_{\varepsilon}) \cdot \nabla u^{s} \\ &&- \kappa \displaystyle{\int}_{B_{\varepsilon}} p \, \text{div}(u) \\ &&- \frac{1}{2}\kappa {\int}_{B_{\varepsilon}} p \, \text{div}(u_{\varepsilon} - u). \end{array} $$

(A.8)

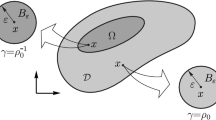
Note that the variation of the energy shape functional results in an integral concentrated into the inclusion B _ε . Therefore, in order to apply the definition for the topological derivative given by (2.2), we need to know the asymptotic behavior of the function u _ε with respect the small parameter ε. Thus, let us introduce the following ansätz:

$$\begin{array}{@{}rcl@{}} u_{\varepsilon} = u + w_{\varepsilon} + \tilde{u}_{\varepsilon}, \end{array} $$

(A.9)

where u is solution of the unperturbed problem (2.7), w _ε is solution to an auxiliary exterior problem and $\tilde {u}_{\varepsilon }$ is the remainder.

After applying the operator σ _ε in the ansätz (A.9) we have

$$\begin{array}{@{}rcl@{}} \sigma_{\varepsilon}(u_{\varepsilon}) = \sigma_{\varepsilon}(u) + \sigma_{\varepsilon}(w_{\varepsilon}) + \sigma_{\varepsilon}(\tilde{u}_{\varepsilon}). \end{array} $$

(A.10)

By expanding σ(u) in Taylor’s series around the point $\hat {x}$ we obtain

$$\begin{array}{@{}rcl@{}} \sigma_{\varepsilon}(u_{\varepsilon}) &=& \sigma_{\varepsilon}(u)(\hat{x}) \\ &&+\gamma_{\varepsilon} \nabla \sigma(u(\xi))(x - \hat{x}) \\ &&+\sigma_{\varepsilon}(w_{\varepsilon})+\sigma_{\varepsilon}(\tilde{u}_{\varepsilon}), \end{array} $$

(A.11)

where ξ is an intermediate point between x and $\hat {x}$. On the boundary of the inclusion B _ε we have

$$\begin{array}{@{}rcl@{}} [\![ \sigma_{\varepsilon}(u_{\varepsilon}) ]\!]n = -\kappa pn. \end{array} $$

(A.12)

After evaluating (A.12) we obtain

$$\begin{array}{@{}rcl@{}} (\sigma(u_{\varepsilon})_{|_{\mathcal{D} \setminus \overline{B_{\varepsilon}}}} - \gamma \sigma(u_{\varepsilon})_{|_{B_{\varepsilon}}})n = -\kappa pn \quad \text{on} \quad \partial B_{\varepsilon}. \end{array} $$

(A.13)

Then, let us evaluate (A.11) on ∂ B _ε to have

$$\begin{array}{@{}rcl@{}} -\kappa pn &=& (1 - \gamma) \sigma(u)(\hat{x})n \\ &&- \varepsilon(1 - \gamma) (\nabla \sigma(u(\xi))n)n \\ &&+ [\![ \sigma_{\varepsilon}(w_{\varepsilon})]\!]n + [\![ \sigma_{\varepsilon}(\tilde{u}_{\varepsilon}) ]\!]n, \end{array} $$

(A.14)

since $(x - \hat {x}) = -\varepsilon n$ on ∂ B _ε . By choosing σ _ε (w _ε ) such as

$$\begin{array}{@{}rcl@{}} [\![ \sigma_{\varepsilon}(w_{\varepsilon}) ]\!]n = ((\gamma - 1) \sigma(u)(\hat{x}) - \kappa p \mathrm{I})n \quad \text{on} \quad \partial B_{\varepsilon}, \end{array} $$

(A.15)

the following auxiliary boundary value problem is considered and formally obtained when $\varepsilon \rightarrow 0$: Find σ _ε (w _ε ) such that:

$$\begin{array}{@{}rcl@{}} \left\{ \begin{array}{l} \begin{array}{rclccccc} \text{div} \sigma_{\varepsilon}(w_{\varepsilon}) & = & 0 & & \text{in} & \mathbb{R}^{2},\\ \sigma_{\varepsilon}(w_{\varepsilon}) &\rightarrow& 0 & & \text{in} & \infty, \\ \left[\!\left[\sigma_{\varepsilon}(w_{\varepsilon})\right]\!\right]n &= &\hat{u} & & \text{on} & \partial B_{\varepsilon}, \end{array} \end{array} \right. \end{array} $$

(A.16)

with $\hat {u} = ((\gamma - 1) \sigma (u)(\hat {x}) - \kappa p \mathrm {I})n$. The boundary value problem (A.16) admits an explicit solution. For p = 0, its solution can be found in (Novotny and Sokołowski 2013, Ch. 5, pp. 156), for instance. Since the stress σ _ε (w _ε ) is uniform inside the inclusion, the solution of (A.16) for p ≠ 0 can be written in a following compact form

$$\begin{array}{@{}rcl@{}} \sigma_{\varepsilon}(w_{\varepsilon})_{|_{B_{\varepsilon}}} = \mathbb{T}_{\gamma}\sigma(u)(\hat{x}) + \mathrm{T}_{\gamma}, \end{array} $$

(A.17)

where $\mathbb {T}_{\gamma }$ is a fourth order isotropic tensor given by

$$\begin{array}{@{}rcl@{}} \mathbb{T}_{\gamma} = \frac{\gamma (1-\gamma)}{2(1 + \beta\gamma)}\left( 2\beta \mathbb{I} + \frac{\alpha - \beta}{1 + \alpha \gamma}\mathrm{I}\otimes\mathrm{I}\right) \end{array} $$

(A.18)

and T _γ is a second order isotropic tensor written as

$$\begin{array}{@{}rcl@{}} \mathrm{T}_{\gamma} = \kappa p \frac{\alpha \gamma}{1 + \alpha \gamma} \mathrm{I}. \end{array} $$

(A.19)

The result shown in (A.17) fits the famous Eshelby’s problem. This problem, formulated by Eshelby (1957) and Eshelby (1959), represents one of the major advances in the continuum mechanics theory of the 20^th century (Kachanov et al. 2003).

Now we can construct $\sigma _{\varepsilon }(\tilde {u}_{\varepsilon })$ in such a way that it compensates for the discrepancies introduced by the higher-order terms in ε as well as by the boundary-layer w _ε on the exterior boundary $\partial \mathcal {D}$. It means that the remainder $\tilde {u}_{\varepsilon }$ must be solution to the following boundary value problem: Find $\tilde {u}_{\varepsilon }$ such that:

$$ \left\{ \begin{array}{rclccc} \text{div}\sigma_{\varepsilon}(\tilde{u}_{\varepsilon}) &=& 0 & &\text{in}& \mathcal{D},\\ \sigma_{\varepsilon}(\tilde{u}_{\varepsilon}) &=& \gamma_{\varepsilon}\sigma(\tilde{u}_{\varepsilon}),\\ \tilde{u}_{\varepsilon} &=& -w_{\varepsilon} & &\text{on}& {\Gamma}_{D},\\ \sigma(\tilde{u}_{\varepsilon})n &=& -\sigma(w_{\varepsilon})n & &\text{on}& {\Gamma}_{N},\\ \left[\!\left[\sigma_{\varepsilon}(\tilde{u}_{\varepsilon})\right]\!\right]n &=& 0 & &\text{on}& \partial\omega,\\ \begin{array}{r} \left[\!\left[ \tilde{u}_{\varepsilon} \right]\!\right] \\ \left[\!\left[ \sigma_{\varepsilon}(\tilde{u}_{\varepsilon}) \right]\!\right]n \end{array} \!\!\!\! & \begin{array}{c} = \\ = \end{array} & \!\!\!\!\left. \begin{array}{c} 0 \\ \varepsilon h \end{array} \right\} & &\text{on}&\partial B_{\varepsilon} \end{array} \right. $$

(A.20)

with h = (1−γ)(∇σ(u(ξ))n)n. The estimate $\|\tilde {u}_{\varepsilon }\|_{H^{1}(\mathcal {D})} = O(\varepsilon ^{2})$ for the remainder $\tilde {u}_{\varepsilon }$ holds true. See, for instance, the book by Novotny and Sokołowski (2013, Ch. 5, pp 155).

From the above results, we can evaluate the integrals in (A.8) explicitly. In fact, after replacing the ansätz for u _ε given by (A.9) in the first integral of (A.8) we have

$$\begin{array}{@{}rcl@{}} {\int}_{B_{\varepsilon}} \sigma_{\varepsilon}(u_{\varepsilon}) \cdot \nabla u^{s} &=& \underbrace{{\int}_{B_{\varepsilon}} \sigma_{\varepsilon}(u) \cdot \nabla u^{s}}_{(a)} \\ &&+ \underbrace{{\int}_{B_{\varepsilon}} \sigma_{\varepsilon}(w_{\varepsilon}) \cdot \nabla u^{s}}_{(b)} \\ &&+ \mathcal{E}_{1}(\varepsilon). \end{array} $$

(A.21)

The remainder $\mathcal {E}_{1}(\varepsilon )$ is given by

$$\begin{array}{@{}rcl@{}} \mathcal{E}_{1}(\varepsilon) &=&{\int}_{B_{\varepsilon}} \sigma_{\varepsilon}(\tilde{u}_{\varepsilon}) \cdot \nabla u^{s} \\ &\leq& \|\sigma_{\varepsilon}(\tilde{u}_{\varepsilon})\|_{L^{2}(B_{\varepsilon})} \|\nabla u \|_{L^{2}(B_{\varepsilon})} \\ &\leq& c_{1}\|\tilde{u}_{\varepsilon}\|_{H^{1}(\mathcal{D})} \| \nabla u \|_{L^{2}(B_{\varepsilon})} \\ &\leq& c_{2} \varepsilon^{3} = O(\varepsilon^{3}), \end{array} $$

(A.22)

where we have used the Cauchy-Schwarz inequality together with the estimation for the remainder $\tilde {u}_{\varepsilon }$. The term (a) in (A.21) can be developed in power of ε as follows

$$\begin{array}{@{}rcl@{}} {\int}_{B_{\varepsilon}} \sigma_{\varepsilon}(u) \cdot \nabla u^{s} &=& {\int}_{B_{\varepsilon}} \gamma \sigma(u) \cdot \nabla u^{s} \\ &=& \pi \varepsilon^{2} \gamma \sigma(u)(\hat{x}) \cdot \nabla u^{s}(\hat{x}) \\ &&+ \mathcal{E}_{2}(\varepsilon), \end{array} $$

(A.23)

with the remainder $\mathcal {E}_{2}(\varepsilon )$ defined as

$$\begin{array}{@{}rcl@{}} \mathcal{E}_{2}(\varepsilon) &=& {\int}_{B_{\varepsilon}} (h(x)-h(\hat{x})) \\ &\leq& \| h(x)-h(\hat{x}) \|_{L^{2}(B_{\varepsilon})} \|1\|_{L^{2}(B_{\varepsilon})} \\ &\leq& c_{1} \varepsilon \|x - \hat{x}\|_{L^{2}(B_{\varepsilon})} \leq c_{2} \varepsilon^{3} = O(\varepsilon^{3} ), \end{array} $$

(A.24)

where we have introduced the notation

$$\begin{array}{@{}rcl@{}} h(x)-h(\hat{x}) =\sigma(u)(x)\cdot\nabla u^{s}(x) - \sigma(u)(\hat{x})\cdot\nabla u^{s}(\hat{x}). \end{array} $$

(A.25)

Note that, we have used again the Cauchy-Schwarz inequality and the interior elliptic regularity of function u. Since the exact solution of the auxiliary problem (A.16) is known, the term (b) in (A.21) can be written as

$$\begin{array}{@{}rcl@{}} {\int}_{B_{\varepsilon}} \!\!\sigma_{\varepsilon}(w_{\varepsilon}) \cdot \nabla u^{s} \,=\, \pi \varepsilon^{2} \nabla u^{s}(\hat{x}) \cdot (\mathbb{T}_{\gamma}\sigma(u)(\hat{x}) \,+\, \mathrm{T}_{\gamma}) \,+\, \mathcal{E}_{3}(\varepsilon). \end{array} $$

(A.26)

The remainder $\mathcal {E}_{3}(\varepsilon )$ is given by

$$\begin{array}{@{}rcl@{}} \mathcal{E}_{3}(\varepsilon) &=& {\int}_{B_{\varepsilon}} \sigma_{\varepsilon}(w_{\varepsilon}) \cdot (\nabla u^{s} - \nabla u^{s}(\hat{x})) \\ &\leq& \| \sigma_{\varepsilon}(w_{\varepsilon})\|_{L^{2}(B_{\varepsilon})} \| \nabla u-\nabla u(\hat{x})\|_{L^{2}(B_{\varepsilon})} \\ &\leq& c_{1} \varepsilon \|x - \hat{x}\|_{L^{2}(B_{\varepsilon})} \leq c_{2}\varepsilon^{3} = O (\varepsilon^{3}), \end{array} $$

(A.27)

where we have used again the Cauchy-Schwarz inequality and the interior elliptic regularity of function u.

The second term in (A.8) can be developed as follows

$$ \kappa {\int}_{B_{\varepsilon}}p \, \text{div}(u) = \pi \varepsilon^{2} \kappa p \, \text{div}(u)(\hat{x}) + \mathcal{E}_{4}(\varepsilon), $$

(A.28)

where the remainder $\mathcal {E}_{4}(\varepsilon )$ is defined as

$$\begin{array}{@{}rcl@{}} \mathcal{E}_{4}(\varepsilon) &=& \kappa {\int}_{B_{\varepsilon}} p(\text{div}(u) - \text{div}(u)(\hat{x})) \\ &\leq& c_{1} \| x-\hat{x} \|_{L^{2}(B_{\varepsilon})} \| 1 \|_{L^{2}(B_{\varepsilon})} \\ &\leq& c_{2} \varepsilon^{3} = O(\varepsilon^{3}). \end{array} $$

(A.29)

Once again, we have used the Cauchy-Schwarz inequality together with the interior elliptic regularity of function u.

After replacing the ansätz for u _ε given by (A.9) into the last term of (A.8) we have

$$\begin{array}{@{}rcl@{}} \frac{1}{2} \kappa {\int}_{B_{\varepsilon}}p \, \text{div}(u_{\varepsilon} - u) &=& \frac{1}{2} \kappa {\int}_{B_{\varepsilon}}p \, \text{div}(w_{\varepsilon} + \tilde{u}_{\varepsilon}) \\ &=& \frac{1}{2} \kappa {\int}_{B_{\varepsilon}}p \, \text{div}(w_{\varepsilon}) \\ &&+\mathcal{E}_{5}(\varepsilon). \end{array} $$

(A.30)

where the remainder $\mathcal {E}_{5}(\varepsilon )$ has the following bound thanks to the estimate for $\tilde {u}_{\varepsilon }$

$$\begin{array}{@{}rcl@{}} \mathcal{E}_{5}(\varepsilon) &=& \frac{1}{2} \kappa {\int}_{B_{\varepsilon}}p \, \text{div}(\tilde{u}_{\varepsilon}) \\ &\leq& c_{1} \| \nabla \tilde{u}_{\varepsilon} \|_{L^{2}(B_{\varepsilon})} \| 1 \|_{L^{2}(B_{\varepsilon})} \\ &\leq& c_{2} \varepsilon \| \tilde{u}_{\varepsilon} \|_{H^{1}(\mathcal{D})} \leq c_{2} \varepsilon^{3} = O(\varepsilon^{3}). \end{array} $$

(A.31)

By using the constitutive relation and after algebraic manipulations, we have

$$\begin{array}{@{}rcl@{}} \frac{1}{2} \kappa {\int}_{B_{\varepsilon}}p \, \text{div}(w_{\varepsilon}) = \frac{1}{2} \kappa {\int}_{B_{\varepsilon}} \frac{p}{2 \gamma \rho (\mu + \lambda)} \text{tr}\sigma_{\varepsilon}(w_{\varepsilon}), \end{array} $$

(A.32)

where trσ _ε (w _ε ), evaluated inside the inclusion, is given by

$$\begin{array}{@{}rcl@{}} \text{tr} \sigma_{\varepsilon}(w_{\varepsilon})_{|_{B_{\varepsilon}(\hat{x})}} = \frac{\alpha \gamma}{1 + \alpha \gamma}((1-\gamma)\text{tr}\sigma(u)(\hat{x}) + 2\kappa p). \end{array} $$

(A.33)

From the above results, the variation of the energy shape functionals, given by (A.8), can be developed in power of ε as follows

$$\begin{array}{@{}rcl@{}} &&\mathcal{J}_{\chi_{\varepsilon}}(u_{\varepsilon}) - \mathcal{J}_{\chi}(u) = \\ &&-\pi \varepsilon^{2} \frac{1 - \gamma}{2\gamma} \left[\gamma \sigma(u)(\hat{x}) + (\mathbb{T}_{\gamma}\sigma(u)(\hat{x}) + \mathrm{T}_{\gamma})\right] \cdot \nabla u^{s}(\hat{x}) \\ &&-\pi \varepsilon^{2} \kappa p \, \text{div}(u)(\hat{x}) -\pi \varepsilon^{2} \frac{\alpha}{2}\frac{1-\gamma}{1+\alpha \gamma} \kappa p \, \text{div}(u)(\hat{x}) \\ &&-\pi \varepsilon^{2} \frac{p^{2}}{2\mu \rho (1+\alpha \gamma)} +\sum\limits_{i=1}^{5} \mathcal{E}_{i}(\varepsilon), \end{array} $$

(A.34)

where the remainders $\mathcal {E}_{i}(\varepsilon ) = o(\varepsilon ^{2})$, for i = 1,...,5, as previously shown. By defining the function f(ε) = π ε ² and after applying the topological derivative concept in (A.34), we obtain

$$\begin{array}{@{}rcl@{}} D_{T} \mathcal{J}_{\chi}(\hat{x}) &=& -\mathbb{P}_{\gamma}\sigma(u)(\hat{x}) \cdot \nabla u^{s}(\hat{x}) \\ &&- \frac{1+\alpha}{1+\alpha \gamma}\kappa p \, \text{div}(u)(\hat{x}) \\ &&- \frac{1}{2 \rho \mu} \frac{p^{2}}{(1+\alpha \gamma)}, \end{array} $$

(A.35)

where $\mathbb {P}_{\gamma }$ is a fourth order isotropic tensor given by Ammari and Kang (2007)

$$ \mathbb{P}_{\gamma} = \frac{1}{2}\frac{1-\gamma}{1+\beta \gamma}\left( (1+\beta)\mathbb{I} + \frac{1}{2}(\alpha - \beta)\frac{1-\gamma}{1+\alpha \gamma}\mathrm{I} \otimes \mathrm{I}\right), $$

(A.36)

with the coefficients α and β defined as

$$\begin{array}{@{}rcl@{}} \alpha = \frac{\lambda + \mu}{\mu} \quad \text{and} \quad \beta = \frac{\lambda + 3\mu}{\lambda + \mu}. \end{array} $$

(A.37)