1 Introduction

Stiffened composite panel construction is characterised by a thin skin that is stabilised in compression by longitudinal stringers, running across the panel width at regular intervals. A stiffened panel loaded by compression undergoes shortening, at a certain value of shortening or load level, transverse deflections occur all in a sudden, this is called buckling. The skin between the stiffeners acts like a supported plate and this may assume a number of different buckled configurations distinguished by their differing wave number. The behaviour of the panel, if loaded beyond buckling is called post-buckling. It is well known that the buckling load does not represent the maximum load that the structure can carry. As a matter of fact, failure may not occur until the applied load is several times the buckling load (Stevens et al. 1995). This post buckling strength capacity has significant potential for weight saving.

The extensive use of stiffened panels as structural elements leads to the need for highly complex optimization of components where several objectives have to be performed at the same time. Venkataraman and Haftka (2004) used the model complexity, analysis complexity and optimization method complexity to classify the difficulty of the optimization process in structural analysis. Model complexity can be understood as the level of realism with which the problem is being analysed, e.g. use of analytic or numerical models. At any of these model levels the type of analysis can vary from linear elastic to geometrically and materially nonlinear. The optimization complexity takes into account the number of design variables, number of objectives, type of optimization (global vs. local) and uncertainty. Venkataraman (1999) presents a detailed review of analysis methods used for stiffened panels.

An efficient method for analysing stiffened panels in buckling is the Finite Strip Method (FSM), pioneered by Wittrick (1968) and Cheung (1968), in which the panel is divided into strips and the displacement field in these strips is described by trigonometric functions. Programs such as VICONOPT (Butler and Williams 1993)and COSTADE (Mabson et al. 1996) make use of FSM for the structural analysis. Another program for the design of buckled stiffened panels is PANDA2 (Bushnell 1987) that can analyse panels using FSM, finite difference energy method or smeared representation of the stiffeners. VICONOPT and PANDA2 use the method of feasible directions for carrying out the optimization while COSTADE uses the Improving Hit-and-Run algorithm (Zabinsky 1998).

With increasing computational power, recently, more FE analysis and Genetic Algorithms have been employed in the optimization of post-buckled stiffened panels (Bisagni and Lanzi 2002; Kang and Kim 2005; Lanzi and Giavotto 2006; Rikards et al. 2006). Most of these papers make use of meta-models to approximate the response of the stiffened panels in order to reduce the computational resources needed for the task. Artificial Neural Networks (ANNs) and Genetic Algorithms (GAs) have been used not only for structural optimization. Worden and Staszewski (2000) used ANNs and GAs to find the optimal position of sensors for impact detection in composite panels while Mallardo et al. (2013) performed this task on more complex composite stiffened panels.

With increasing optimization complexity, the computational resources required for the solution, especially if a multiobjective optimization problem is faced, typically increase with dimensionality of the problem at a rate that is more than linear. Then, massive computer resources are required for the design of realistic structures carrying a large number of load cases and having many components with several parameters describing the detailed geometry. One obvious solution is to break up large optimization problems into smaller subproblems and coordination problems to preserve the couplings among these subproblems as proposed by Sobieszczanski-Sobieski et al. (1987) where different levels of substructuring are used to represent the structure. Liu et al. (2000) developed a two-level optimization procedure for analysing a composite wing where the response at the lower (panel) level was used to build a Response Surface for the optimal buckling load that is used later for the global (wing) problem optimization. Wind et al. (2008) developed a multilevel approach to optimize an structure consisting of several components. It was optimized as a whole (global) as well as on the component (local) level. The approach used a global model to calculate the interactions for each of the components. These components were then optimized using the prescribed interactions, followed by a new global calculation to update the interactions. Hansen and Horst (2008) presented another approach to solve the structural optimization task by dividing the complete task into two separate optimization problems: a sizing task and a topology task although this approach can be better referred as a hybrid strategy where both tasks are performed simultaneously.

In recent years, several approaches to integrate industrial processes have been proposed. Structural simulations based on robust and reliability based designs are well established techniques for structural sizing. Reliability Based Design Optimization (RBDO) is a method to achieve the confidence in product reliability at a given probabilistic level, while Robust Design Optimization (RDO) is a method to improve the product quality by minimizing variability of the output performance function.

In order to simulate the structural behaviour of a stiffened panel, a procedure is presented for design in a unified platform, reproducing the flow of information among the different structural departments in industry. The set of design variables can be divided into a group of variables describing the main conceptual layout that affect the dimensions of the model and a second group of variables influencing the material behaviour. In the presented method, the panel robustness is described using the second statistical moment (the variance) of the performance function. This concept can be used at any stage, but in order to improve the maximum efficiency in the optimization strategy, robustness evaluation is limited to the preliminary design only.

The developed multilevel approach can be associated to the family of the multilevel parametrisation models Kampolis et al. (2007). The optimization problem is decomposed into two levels of design modifications, corresponding to different sets of design variables. Geometrically nonlinear elastic finite element analysis is used at the Preliminary Design stage to find the set of optimum panel architectures, that are later used to build a metamodel based on Radial Basis Function Networks where a robust design is found. Once the robust design is available the next stage optimization, Detailed Design, takes place using geometrically and materially nonlinear finite element analysis to find the optimum layup in order to maximise the load that the panel can bear.

While previous optimization approaches only consider elastic analysis of stiffened composite panels the present approach includes progressive failure analysis based on continuum damage mechanics for the analysis of post-buckled panels at the Detailed Design stage, keeping the geometry obtained at the Preliminary Design constant, i.e the size of the component to be optimized does not change, but the model complexity does. The inclusion of progressive failure analysis makes it possible to better utilize the load bearing capacity of composite stiffened panels, ultimately leading to weight savings.

2 Robust multiobjective optimization at multiple stages

Multiobjective optimization or vector optimization is the process of optimizing systematically and simultaneously a collection of objective functions. The multiobjective optimization problem may contain a number of constraints which any feasible solution (including all optimal solutions) must satisfy. The optimal solutions can be defined from a mathematical concept of partial ordering or domination. An extensive review of multiobjective optimization methods can be found in Marler and Arora (2004) and Coello (2000, Zitzler et al. (2000) for methods based on evolutionary algorithms.

Kassapoglou and Dobyns (2001) used a gradient based method to optimized cost and weight of a composite panel under combined compression and shear by varying the cross section of the stiffeners and their spacing. The Pareto front was constructed by varying the spacing of the stiffeners. Lanzi and Giavotto (2006) performed a similar task using Genetic Algorithms and Neural Networks. A Design of Experiments (DoE), using Finite Elements, was conducted in order to train the neural networks, and the optimization was performed on these networks. Similarly, the number and cross section of stiffeners and the stacking sequence of the skin and the stiffeners were used as the design space. Irisarri et al. (2009) performed stacking optimization where the number of plies in a laminate was minimized while the buckling margins were maximized. This was performed by running several models for different number of plies starting at N layers and reducing the number until no buckling margin was found. The orientation of each laminae was optimized for every laminate and Pareto fronts were constructed showing the trade-offs between the buckling margin and the number of plies with different number of orientations.

When both multilevel and multiobjective algorithms are present, the multilevel iteration scheme can be integrated into a Pareto front search algorithm, which can use either genetic/evolutionary algorithms or gradient methods to explore the design space at different levels. The proposed Multilevel/Multiobjective Approach can be defined as

$$\begin{array}{@{}rcl@{}} \begin{array}{ccc} &\text{Preliminary Design}\\ \text{Min./Max.} & f_{m}\left(\mathbf{x}\right) & m=1,2,\ldots,M;\\ \text{Subject to} & g_{j}\left(\mathbf{x}\right)\leqslant0 & j=1,2,\ldots,J;\\ & h_{k}\left(\mathbf{x}\right)=0 & k=1,2,\ldots,K;\\ & x_{i}^{\left(L\right)}\leqslant x_{i}\leqslant x_{i}^{\left(U\right)} & i=1,2,\ldots,n; \end{array} \end{array} $$
$$\begin{array}{@{}rcl@{}} \begin{array}{ccc} &\textrm{Detailed Design}\\ \text{Min./Max.} & o_{u}\left(\mathbf{y}\right) & u=1,2,\ldots,U;\\ \text{Subject to} & p_{s}\left(\mathbf{y}\right)\leqslant0 & s=1,2,\ldots,S;\\ & q_{t}\left(\mathbf{y}\right)=0 & t=1,2,\ldots,T;\\ & y_{r}^{\left(L\right)}\leqslant y_{r}\leqslant y_{r}^{\left(U\right)} & r=1,2,\ldots,v; \end{array} \end{array} $$
(1)

where x are the design variables, f m is the m−t h objective function, \(f_{m}\left (\mathbf {x}\right )=\mathbf {z}\) is the objective space in Level 1, g j is the j−t h inequality constraint, h k is the k−t h equality constraint and \(\mathbf {x}^{\left (L\right )}\leq \mathbf {x}\leq \mathbf {x}^{\left (U\right )}\) is the design space in Level 1, while y are the design variables, o u is the u−t h objective function, \(o_{u}\left (\mathbf {y}\right )=\mathbf {w}\) is the objective space in Level 2, p s is the s−t h inequality constraint, q t is the t−t h equality constraint and \(\mathbf {y}^{\left (L\right )}\leq \mathbf {y}\leq \mathbf {y}^{\left (U\right )}\) is the design space in Level 2. Notice that some of the objectives from one level can be used at the other level (\(f\bigcap o\ne \varnothing \wedge f\bigcap o=\varnothing \)).

2.1 Multiobjective evolutionary algorithms (MOEAs)

Evolutionary algorithms is the general term used to define a population based stochastic and heuristic search algorithm inspired by biological evolution and genetic operators such as reproduction, mutation, crossover and natural selection. Individuals in a population represent a candidate solution to the optimization problem. The solution with higher fitness has higher chances of survival and reproduction. The population then evolves according to the genetic operators, and through this process better solutions are generated, this process is repeated until the termination condition is met.

One type of Evolutionary algorithm that is well suited for optimizing combinatorial and continuous optimization problems through mutation and crossover is Genetic algorithms (GAs) popularized by Holland (1975).

Being a population-based approach, GAs are well suited to solve multiobjective optimization problems. A generic single objective GA can be modified to find a set of multiple non dominated solutions in a single run. The ability of GAs to simultaneously search different regions of a solution space makes it possible to find a diverse set of solutions for difficult problems with nonconvex, discontinuous, and multimodal solutions spaces. The crossover operator of GA may exploit structures of good solutions with respect to different objectives to create new non dominated solutions in unexplored parts of the Pareto front. In addition, most multiobjective GAs do not require the user to prioritise, scale, or weigh objectives. Therefore, GAs have been the most popular heuristic approach to multiobjective design and optimization problems. Schaffer (1985) presents one of the first treatments of multiobjective genetic algorithms.

In contrast to single objective optimization, where the fitness function is the same as the objective function, in multiobjective optimization, fitness assignment and selection must support multiple objectives. Consequently the main difference between MOEAs and simple GAs is the way on which fitness assignment and selection works. There are several versions of MOEAs that use different fitness assignment and selection strategies. They can be categorised as aggregation based approaches, population based approaches and Pareto based approaches that are the most popular techniques.

2.2 Approximation models

For large scale designs, surrogate models may be needed to efficiently face the optimization problem. Approximation Models are models that imitate the behaviour of the simulated model as closely as possible while being computationally cheaper to evaluate. The exact, inner working of the simulation code is not assumed to be known (or even understood), solely the input-output behaviour is important.

An artificial neural network (ANN) is an emulation of biological neural system. An artificial neural network is composed of many artificial neurons that are linked together according to a specific network architecture (Hassoun 1995). In most cases an artificial neural network is an adaptive system that changes its structure based on external or internal information that flows through the network during the learning phase.

One type of ANN is the Radial Basis Function (RBF) Networks, which uses radial basis functions as activation functions. One of the advantages of using RBFs is the fact that the interpolation problem becomes insensitive to dimension of the space in which the data sites lie (Buhmann 20001), by approximating multivariable functions by linear combination of single variable functions.. The unique existence of the interpolants can be guaranteed adding low order polynomials and some extra mild conditions (Hardy 1990):

$$\begin{array}{@{}rcl@{}} \varphi\left(\mathbf{x}\right)&=&\sum\limits_{i=1}^{N}a_{i}\rho\left(\left\Vert \mathbf{x}-\mathbf{x}_{i}\right\Vert \right)+b\\ \sum\limits_{i=1}^{N}a_{i}&=&0 \end{array} $$
(2)

and the special case of the method of cross validation called leave-one-out cross validation (LOOCV) can be used for choosing an optimal value of the shape parameter (Rippa 1999).

2.3 Random simulation

When the stochastic properties of one or more random variables are available, random simulations can take place in order to characterise the statistical nature of the model’s response to the given variation in the input properties. Monte Carlo methods are considered to be the most accurate resource for estimating the probabilistic properties of uncertain system response from known random inputs. Sampling values of random variables following a probabilistic distribution generate system simulations to be analysed by Monte Carlo simulations.

Random sampling is used with the aim of generating the possible inputs. There are several sampling techniques such as simple random sampling, systematic sampling, stratified sampling, descriptive sampling, etc. Simple random sampling is used to characterise the statistic properties of a function when a large enough number of samples are used. A more efficient approach which needs a smaller number of function evaluations is the stratified sampling approach (Cochran 2007). A special case of this sampling approach is the Latin Hypercube sampling technique (McKay et al. 1979). When a single normally distributed variable is sampled using the Simple Random Sampling technique, the sample points are generated without taking into account the previously generated sample points and the sampled points can be clustered. Latin Hypercube Sampling first decides how many points will be used and then distributes them evenly in order to have a sampled point in each probability interval.

2.4 Robust design optimization

Robust design, in which the structural performance is required to be less sensitive to the random variations induced in different stages of the structural service life cycle, has gained an ever increasing importance in recent years (Messac and Ismail-Yahaya 2002; Jin et al. 2005). It is an engineering methodology for optimal design of products and process conditions that are less sensitive to system variations. It has been recognised as an effective design method to improve the quality of the product/process. Several stages of engineering design are identified in the literature, including conceptual design, preliminary design and detailed design (Keane and Nair 2005; Wang et al. 2002).

Robust design may be involved in the stages of parameter design and tolerance design. Traditional optimization techniques tend to ”over-optimize”, producing solutions that perform well at the design point but may have poor off-design characteristics. It is important that the designer ensures robustness of the solution, defined as the system’s insensitivity to any variation of the input parameters. It is quite possible that the optimal solution will not be the most stable solution.

For design optimization problems, the structural performance defined by design objectives or constraints may be subject to large scatter at different stages of the service life-cycle. It can be expected that this might be more crucial for structures with nonlinearities. Such scatters may not only significantly worsen the structural quality and cause deviations from the desired performance, but may also add to the structural costs, including inspection, repair and other maintenance costs.

From an engineering perspective, well-designed structures minimise these costs by performing consistently in presence of uncontrollable variations during the whole life. This raises the need of structural robust design to decrease the scatter of the structural performance. One possible way is to reduce or even to eliminate the scatter of the input parameters, which may either be practically impossible or add much to the total costs of the structure; another way is to find a design in which the structural performance is less sensitive to the variation of parameters without eliminating the cause of parameter variations, as in robust design.

The principle behind the structural robust design is that, the quality of a design is justified not only by the mean value but also by the variability of the structural performance. For the optimal design of structures with uncertainty variables, a straightforward way is to define the optimality conditions of the problems on the basis of expected function values response mean performance. However, the design which minimises the expected value of the objective function as a measure of structural performance may be still sensitive to the variation of the stochastic parameters and this raises the task of robustness of the design.

From the mathematical point of view, the Robust Design Optimization can be stated as:

$$\begin{array}{@{}rcl@{}} \begin{array}{ccc} \text{Min./Max.} & f\left\{ E\left(H\left(\mathbf{x}\right)\right),\sigma\left(H\left(\mathbf{x}\right)\right)\right\} \\ \text{Subject to} & g_{j}\left(\mathbf{x}\right)\le0 & j=1,2,\ldots,J;\\ & h_{k}\left(\mathbf{x}\right)=0 & k=1,2,\ldots,K;\\ & \sigma\left(H\left(\mathbf{x}\right)\right)\le\sigma_{M}\\ & x_{i}^{\left(L\right)}\le x_{i}\le x_{i}^{\left(U\right)} & i=1,2,\ldots,n; \end{array} \end{array} $$
(3)

where \(E\left (H\left (\mathbf {x}\right )\right )\) and \(\sigma \left (H\left (\mathbf {x}\right )\right )\) are the first and the second statistical moments of optimization function \(H\left (\mathbf {x}\right )\), \(g_{j}\left (\mathbf {x}\right )\) is the j−t h constraint function, σ M denotes the upper limit for the standard deviation of the structural performance and, \(x_{i}^{\left (L\right )}\) and \(x_{i}^{\left (U\right )}\) are the lower and upper bounds for the i−t h design variable.

In formulation 3 the robust structural design optimization problem is shown to be an optimum vector problem in which two criteria namely the statistical mean \(E\left (H\left (\mathbf {x}\right )\right )\) and the standard deviation \(\sigma \left (H\left (\mathbf {x}\right )\right )\) of the objective are to be optimized.

3 Methodology description

The solutions at Preliminary Design stage are found using elastic analysis and trying to define the optimum geometry of the stiffened panel for the given boundary conditions. At Detailed Design stage, material nonlinearities are included, keeping the geometry obtained in the previous level constant. The separation of design variables for different stages makes this approach very efficient, since a lower number of solutions have to be tried because there are less design variables to mix. Another point is that the more complex geometry optimization is done elastically, taking lower time to calculate than a full material nonlinear analysis, so that more runs can be done in a reasonable amount of time. The material properties, including stacking sequence of the composite layup, are then optimized in the next stage. The use of this strategy does not guarantee that the obtained solution will be the global optimum.

The iteration between levels can be finished at any point where the decision maker believes to have obtained a reasonable or the optimum solution. There is no need for the iteration to always finish after both stages have been optimized. The only requirement is that all stages are optimized at least once. The optimization methodology is presented in Table 1.

Table 1 Formulation of the optimization methodology
Full size table

4 Example problem

During post-buckling, the buckled shape of the skin, i.e., the wave number, does not remain constant under increasing compressive loading. At certain load values sudden changes in buckling patterns are observed. These secondary instabilities are characterised by a sudden change from the initial post-buckled mode-shape to a higher one. This phenomenon is referred to as a mode-switch, mode-jump or mode-change. Such abrupt changes are dynamic in nature and cause considerable numerical difficulties when using quasi-static arc-length-related procedures in finite element analysis. A better way forward is to use explicit dynamic analysis (Bisagni 2000). The prediction of the collapse load is difficult because of the susceptibility of composites to the effect of through-thickness stresses. It follows that there are a number of locations in the panel and a variety of damage mechanisms which could lead to final collapse. Another difficultly associated with research into compression of composite stiffened panels is that the post-buckling collapse is so destructive that usually the evidence of the failure mechanism cannot be retrieved from the debris of a laboratory test (Stevens et al. 1995; Orifici et al. 2009).

Several damage mechanisms can be present when a composite stiffened panel is loaded under compression, which under increasing load combine and lead to the failure of the panel. The main damage mechanisms experienced by composites can be divided into intralaminar (fiber failure, matrix cracking or crushing and fiber-matrix shear), and interlaminar (skin-stiffener debonding)(Tsai and Wu 1971; Orifici et al. 2009).

Tsai and Wu (1971) proposed a phenomenological strength criterion that can be applied to composite materials for estimating the load-carrying capacity of a structure. This criterion can give a good approximation of the beginning of the failure process. Another way to analyse composite structures is to use progressive failure based on Continuum Damage Mechanics, where Hashin (1980) criteria can be used for the damage onset and the amount of dissipated energy drives the damage propagation.

In order to model interlaminar failure or debonding, two main approaches are commonly used. The virtual crack closure technique (VCCT) and the use of cohesive zone models (CZM). VCCT is a method based on LEFM, appropriate for problems in which brittle crack propagation occurs along predefined surfaces. The VCCT technique is based on Irwin’s assumption that when a crack extends by a small amount, the energy released in the process is equal to the work required to close the crack to its original length (Krueger 2002). The CZM are based on continuum damage mechanics and relate traction to displacement jumps at an interface where a crack may occur. Damage initiation is related to the interfacial strength and new crack surfaces are formed when the dissipated energy is equal to the fracture toughness (Turon et al. 2007).

The optimization in this validation is decomposed into two stages, i.e. Preliminary Design and Detailed Design. This kind of approach can be effective if it is possible to separate the constraints and design variables that are strongly dependent on the Preliminary Design from the constraints and design variables that are primarily dependent on Detailed Design variables. Then, high and low stages analyses and optimizations are carried out separately and tied together by an iterative scheme going from one stage of design modification to the other and vice-versa seeking an overall optimum design. This is possible if the interaction between the levels is sufficient to allow effective refinements of the objective functions and is insufficient to drastically change the Design Variable’s domain.

Both stages are modelled using nonlinear explicit dynamics finite elements analysis using Abaqus (Version 2011). The mesh size and use of nonlinear material behaviour increase the complexity of the models from Preliminary to Detailed design stage.

4.1 Optimization of a composite stiffened panel

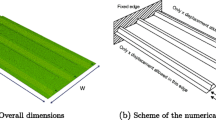
A composite stiffened panel is to be optimized; the only fixed dimensions are the overall dimensions of the panel W = 618.4 mm and L = 1196.0 mm, as shown in Fig. 1. The panel is fixed at one of the transversal edges and loaded by increasing uniform displacement at the opposite end (The panel is loaded in pure compression). The panel is allowed to move only in the direction of the loading on the longitudinal edges. The goal is to obtain a panel with minimum mass while being able to carry as much load as possible in post-buckling. The response of the panel has to be insensitive to manufacturing tolerances.

Fig. 1
figure 1

Stiffened panel geometry

Full size image

For each stage of design, a set of Design Variables and a set of constraint equations are defined, corresponding to the respective design requirements. Finally, the objective functions at different stages must be defined depending, in general, on all the design variables. The boundary conditions are kept constant at every level.

The density of the stringers and skin is 1550 \(\mathrm {\left [Kg/m^{3}\right ]}\) and the density of the interface is 1600 \(\mathrm {\left [Kg/m^{3}\right ]}\). Other material properties for the stringers and skin as well as for the interface between them are reported in Table 2.

Table 2 Material properties
Full size table

4.2 Preliminary design optimization

In order to find the best solution according to the decision-maker, an a posteriori preference articulation will be performed (first search then decide approach), i.e. the Pareto front will be obtained and later the optimum solution will be chosen by the decision-maker. At the Preliminary Design stage the material is considered as linear elastic and the failure is tracked by the Tsai-Wu index. Geometric nonlinearities are included and no debonding between skin and stringer is allowed.

4.2.1 Problem definition

The design space is defined in Table 3a. It takes into account all the parameters that define the geometry of the panel, including thickness of the skin (by taking into account the number of layers) and the thickness, cross section and number of the stringers. For sake of simplicity only symmetrical layups with 8,10 and 12 layers with predefined orientations are used. The cross section geometry of the stringer is defined by the parameters shown in Fig. 2.

Fig. 2
figure 2

Stringer Geometry Parameters

Full size image
Table 3 Preliminary design - problem definition
Full size table

The constraints are defined in Table 3b. These are the result of previous knowledge and needs from the decision-maker and impose bounds on the results of the optimization. Table 3c shows the defined objectives for this problem. Tsai-Wu index criterion is used in order to have a better understanding of the solution, where a solution with higher reaction force at a given shortening obtained by elastic design does not necessarily have to carry more load than when damage is included.

4.2.2 Optimization

The optimization is done using the Archive based Micro Genetic Algorithm (AMGA) (Tiwari et al. 2008), which is an evolutionary optimization algorithm and relies on genetic variation operators for creating new solutions. It uses a generational scheme, however, it generates a small number of new solutions at every iteration, therefore it can also be classified as an almost steady-state genetic algorithm. The algorithm works with a small population size and maintains an external archive of good solutions obtained.

The parent population is created from the archive using a strategy similar to environmental selection. The creation of the mating pool is based on binary tournament selection. Any genetic variation operator can be used to create the offspring population. The update of the elite population (archive) is based on the domination level of the solutions, diversity of the solutions, and the current size of the archive. In order to reduce the number of function evaluations per generation, AMGA uses a small size for the parent population and the mating pool. The parent population is created from the archive using only the diversity information of variables. Using an external archive that stores a large number of solutions provides useful information about the search space as well as tends to generate a large number of non-dominated points at the end of the simulation

4.2.3 Results

Presenting the results to the decision-maker can be a daunting problem when there are more than 3 objectives due to the fact that is impossible to represent graphically a space with more than 3 dimensions. Another way to present the results can be in a tabular form. The part of the objective space that was explored is shown in Fig. 3. When the feasible objective space is available, the Pareto front can be constructed using non-dominating sorting.

Fig. 3
figure 3

Explored objective space

Full size image

The next step is to choose a solution from the Pareto front. The decision-maker can rely on his experience and knowledge about the problem to do so. For illustration, let us suppose that the designer wants to use a panel with a mass of around 4.53 kilograms, in this case there are two possible solutions illustrated in Fig. 4, both solutions have comparable mass, but solution “1” has higher reaction force and Tsai-Wu index than solution “2”.

Fig. 4
figure 4

Choosing a solution from the Pareto front

Full size image

These solutions are completely different in the design space, one has less stringers, but bigger stringer cross section, while the other has more stringers and smaller cross sections, the number of layers and therefore the thicknesses of the skin and stringers are the same.

It seems that solution “1” is a better solution when only the reaction force is considered, however, the lower Tsai-Wu index value of solution “2” indicates that, when damage is considered, this panel will possibly fail at a higher load than solution “1”, but a design with a lower value of the Tsai-Wu index does not necessarily fail at a higher load as pointed out by Groenwold and Haftka (2006). To be completely sure which panel carries more load, it is recommended to analyse both solutions including progressive failure. Once progressive failure analysis of both architectures is carried out, solution “2” is found to be a better choice giving a higher reaction force.

The optimum design variables for this solution are (Table 4):

Table 4 Optimum inputs for preliminary design
Full size table

4.3 Optimizing for robustness

Once the decision is taken, the next step is first to check for the solution robustness, and if it is not robust enough optimize for Robustness. A meta-model from this data, shown in Fig 5, is obtained from the solutions in the Pareto front previously found. The approximation is based on a neural network employing a hidden layer of radial units and an output layer of linear units.

Fig. 5
figure 5

Pareto Front Meta-model

Full size image

Monte Carlo simulation using descriptive sampling is then used to describe the statistical moments (mean and standard deviation) of the outputs or objectives (mass, reaction force and Tsai-Wu index) due to the random variability of the inputs. It is assumed that the discrete input (design variables) do not have any unpredictability, so that only the continuous variables (cross section parameters) are used for this purpose. Table 5b presents the statistical characteristics of the input variables. It is assumed that the inputs are described by a truncated normal distribution with the mean, standard deviation and bounds shown in it. The mean values are the ones obtained form the optimization at the first stage. The manufacturing tolerances can be included by setting the correct lower and upper bound, .i.e. ±0.1 mm in this example.

Table 5 Robust design - problem definition
Full size table

4.3.1 Problem definition

In order to optimize for robustness the problem defined in Table 5 has to be solved.

The Design space is defined in the neighbourhood of the chosen deterministic solution at the first stage, only the continuous design variables are considered to have random variations.

The constraints are set such that only improvements to the deterministic solution can be obtained, i.e. the constraints are the values of the objectives obtained in the deterministic solution.

4.3.2 Optimization

Once the meta-model is available, the optimization can be done by exploring the solution’s neighbourhood with a gradient based algorithm that encapsulates the Monte Carlo simulations. The optimizer is in charge of finding a more robust solution, while the Monte Carlo simulation is giving the statistics of the problem being solved.

4.3.3 Results

In order to get a robust design the standard deviations of the objectives have to be optimized as well. A new Pareto front in a 6 dimensional space is generated and the decision-maker has to choose a solution from all the points obtained in the front. She can choose the design with the lowest standard deviation of the reaction force, the smallest mass, or any combination that she deems the best. For this problem the standard deviation of the Tsai-Wu index was judged to be the main factor affecting the overall robustness of the design.

The optimum input variable values are summarised in Table 6. The optimum response values are recapitulated in Table 7 and their distributions shown in Fig. 6. Comparing the results in Table 7, it can be seen that a small increase in the mass and standard deviation of the mass gives a higher reaction force, lower Tsai-Wu index, and lower standard deviations for the reaction force and Tsai-Wu index, leading in general to a better more robust solution.

Fig. 6
figure 6

Comparison between deterministic and robust solutions

Full size image
Table 6 Optimum inputs for robust design
Full size table
Table 7 Comparison of outputs for robust design
Full size table

Figure 6 illustrates these differences, showing graphically the lower variability of the response due to random inputs. Notice that the objective in this step was not to improve the solution drastically, but rather to find a solution with lower variability when dealing with random inputs that is desirable in industry, where the designer should consider manufacturing tolerances.

4.4 Detailed design optimization

At the Detailed Design stage, progressive damage and failure in the material is considered to predict correctly the postbuckling load regime. Nonlinear explicit dynamic finite element analysis is performed. The intralaminar failure is analysed using continuum damage mechanics, taking into account all the possible failure modes including fibre failure in tension or compression, matrix cracking or crushing and shear failure of the matrix. The interlaminar failure is model using cohesive elements based on cohesive zone models. The layup of the composite parts (skin and stringers) are optimized. At this stage, the design variables at Preliminary Design stage are frozen (kept constant), i.e. the geometry does not change.

4.4.1 Problem definition

During the Preliminary Design Level optimization, the geometry of the panel was established, leading to the use of 8 layers in the skin and 10 in the stringers. For sake of simplicity, only four orientations (-45°, 0°, 45°, 90°) and symmetric layups are considered. The design space is defined in Table 8a.

Table 8 Detailed design-problem definition
Full size table

The design space contains only discrete variables. The objective space is constrained by the constraints defined in Table 8b. Only one constraint is used in this level, since the geometry and therefore the mass of the panel is not changing. The Reaction Force constraint is used in order to obtain better results than the previous stage. The value of the constraint around the reaction force from the robust design including damage propagation and failure. Table 8c shows the defined objectives. The main objective chosen at this stage is to find the panel that carries the biggest amount of load for the architecture obtained at the previous stage. The internal energy is also optimized and it used as an indicator of the panel stiffness.

4.4.2 Optimization

The optimization is done using the Non-dominated Sorting Genetic Algorithm (NSGA-II) (Deb et al. 2002) which is a multiobjective technique that deals with the high computational complexity of non-dominated sorting, lack of elitism and need of a sharing parameter specification by using a fast non-dominated sorting, an elitist Pareto dominance selection and a crowding distance method. In NSGA-II, the solutions are first sorted according to restriction fulfilment.

Feasible solutions come first, and then infeasible solutions are sorted by increasing degree of constraint violation. Feasible solutions and every set of solutions with the same violation degree are then respectively sorted according to Pareto dominance. This sorting is performed by successively extracting form the chosen subpopulation the current set of non-dominated solutions (fronts). All the solutions in a front are given the same rank value, beginning at 0 for the first front extracted, 1 for the second and so on. This way, solutions can be sorted according to rank. Finally, within every group of solutions having the same rank, solutions are sorted according to the crowding distance. This criterion places first those solutions whose closest neighbours are farther, thus enhancing diversity.

4.4.3 Results

There are only two objectives present, so that they can be presented in a simple way to the decision maker on a table or on a scatter plot of the solutions. Figure 7 shows all the solutions that were obtained using the NSGA-II algorithm for this level, it can be seen that there are several solutions violating the constraints, and an overall optimum solution maximizing both of the objectives, the reaction force and the internal energy. In this case, it can be said that the Pareto front converges to a single point. The result of the optimization in the design variable space is shown in Table 9 and 10.

Fig. 7
figure 7

Solutions for Detailed Design stage

Full size image
Table 9 Skin layup optimization
Full size table
Table 10 Stringers layup optimization
Full size table

Notice that the fibres tend to orient themselves in the direction of the load as it would be expected. A comparison of the solutions obtained in Level 1 and Level 2 is shown in Fig. 8, it can be seen that the reaction force was dramatically improved from 0.658 MN to 0.829 MN, the solution is also stiffer, but it fails at a lower shortening.

Fig. 8
figure 8

Response of the optimum solutions at different stages

Full size image

In this validation, this result is satisfactory, so that no further iterations are needed, i.e. that the solution obtained is the final one.

The final panel is characterised by the stringer cross section defined in Table 6 with the layup found in Table 10 and skin layup in Table 9.

5 Conclusions

The main aim of this manuscript was to develop a methodology that can be used efficiently for multilevel/multiscale analysis of aerospace composite components. It presented the main concepts and methodologies necessary to implement a Robust Multilevel-Multiobjective Design Optimization method. It was shown that a combination of optimization methods is the best solution when dealing with a multilevel optimization, and the use of a multilevel iteration scheme can be integrated into a Pareto front search algorithm, which can use either genetic/evolutionary algorithms or gradient methods to explore the design space at different levels and for different purposes. The architecture was also presented showing the way in which it can be implemented to optimize the performance of a composite stiffened panel. A Multilevel optimization strategy that includes progressive failure analysis and robust design optimization for composite stiffened panels was presented. The design was made at two stages, in the first stage the geometry and the robustness of the design were optimized and in the second stage, the load bearing capacity of the panel was maximized. In order to find the optimum design of a real component, subjected to different types of load combinations, a more realistic design should include more load cases generating more objectives and constraints and increasing complexity to the problem.