A globally convergent sequential convex programming using an enhanced two-point diagonal quadratic approximation for structural optimization

Abstract

In this study, we propose a sequential convex programming (SCP) method that uses an enhanced two-point diagonal quadratic approximation (eTDQA) to generate diagonal Hessian terms of approximate functions. In addition, we use nonlinear programming (NLP) filtering, conservatism, and trust region reduction to enforce global convergence. By using the diagonal Hessian terms of a highly accurate two-point approximation, eTDQA, the efficiency of SCP can be improved. Moreover, by using an appropriate procedure using NLP filtering, conservatism, and trust region reduction, the convergence can be improved without worsening the efficiency. To investigate the performance of the proposed algorithm, several benchmark numerical examples and a structural topology optimization problem are solved. Numerical tests show that the proposed algorithm is generally more efficient than competing algorithms. In particular, in the case of the topology optimization problem of minimizing compliance subject to a volume constraint with a penalization parameter of three, the proposed algorithm is found to converge well to the optimum solution while the other algorithms tested do not converge in the maximum number of iterations specified.

Appendix: The test problems

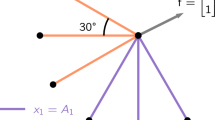
1.1 A.1 Shape and size design of a two-bar truss

This problem was proposed by Svanberg (1987). The problem can be mathematically stated as

$${\begin{array}{*{20}lllll} {\text{minimize}\quad f_{0} \left(\boldsymbol{ x} \right)=c_{1} x_{1} \sqrt{1+x_{2}^{2}} } \\ {\quad x} \\ {\mathrm{subject{\kern4pt} to}\quad f_{_{1}} \left(\boldsymbol{ x} \right)=c_{2} \sqrt{1+x_{2}^{2}} \left({\frac{8}{x_{1}} +\frac{1}{x_{1} x_{2}} } \right)-1\le 0} \\ \\ {\quad \quad \quad \quad f_{2} \left(\boldsymbol{ x} \right)=c_{2} \sqrt{1+x_{2}^{2}} \left({\frac{8}{x_{1}} -\frac{1}{x_{1} x_{2}} } \right)-1\le 0} \\ \\ {\quad \quad \quad \quad 0.2\le x_{1} \le 4.0,} \\ {\quad \quad \quad \quad 0.1\le x_{2} \le 1.6,} \\ \\ {\text{where}{\kern4pt} c_{1} =1.0{\kern4pt} and{\kern4pt} c_{2} =0.124.} \\ \end{array}} $$

The initial point is x ⁰=(1.0,1.0)^T.

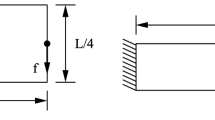
1.2 A.2 Vanderplaats’ cantilever beam

This problem was proposed by Vanderplaats (1984). The optimization problem is to minimize the volume of a p-segmented cantilever beam with constraints on the maximum stress of each segment and the tip deflection. A cantilever beam with five segments is depicted below. The cantilever beam has a rectangular cross-section, and the width and height of each segment are selected as design variables. The optimization problem is formulated as

$${\begin{aligned}{} \mathrm{{\kern9pt} minimize}\quad\quad\, f_{0} \left(\textbf{{b,h}} \right)&=\sum\limits_{i=1}^p {b_{i} h_{i} l_{i}} \\ \mathrm{{}subject{\kern4pt} to}\quad f_{j} \left(\textbf{b,h} \right)&=\frac{\sigma_{i}} {\overline{\sigma} }-1\le 0\quad \quad j=1,\ldots ,p, \\ \quad \quad \quad \quad f_{p+j} \left(\textbf{b,h} \right)&=h_{i} -20b_{i} \le 0\quad j=1,\ldots ,p, \\ \quad \quad \quad f_{2p+1} \left(\textbf{b,h} \right)&=\frac{y_{p}} {\overline{y}}-1\le 0, \\ \quad \quad \quad 1.0&\le b_{i} \le 100, \\ \quad \quad \quad 5.0&\le h_{i} \le 100. \\ \end{aligned}} $$

1.3 A.3 Svanberg’s five-variate cantilever beam

This optimization problem was proposed by Svanberg (1987). The sizing design variables are considered to minimize weight subject to a single displacement constraint. The optimization problem is formulated as

$${\begin{array}{*{20}lllll} {\text{minimize}\quad f_{0} \left(\mathbf{\boldsymbol{ x}} \right)=c_{1} \left({x_{1} +x_{2} +x_{3} +x_{4} +x_{5}} \right)} \\ {\quad x} \\ {\mathrm{subject{\kern4pt}to}} {\kern5pt} f_1 (\mathbf{\boldsymbol{ x}})=61/{x_{1}^{3}}+37/{x_{2}^{3}}+19/{x_{3}^{3}}\\ \\ {\kern79pt} +7/{x_{4}^{3}}+1/{x_{5}^{3}}-c_2\leq0,\\ \\ {\kern48pt} 0,001\leq x_i \leq 10,\quad i=1,2,3,4,5 \end{array}} $$

The initial point is x ⁰=(5.0,5.0,5.0,5.0,5.0)^T.

1.4 A.4 Fleury’s weight-minimization-like problem

This problem was proposed by Fleury (1979). The optimization problem is formulated as

$${\begin{array}{*{20}llll} {\text{minimize} \quad f_{o} \left(\mathbf{\boldsymbol{ x}} \right)=\sum\limits_{i=1}^{1,000} {x_{i} ,}} \\ {\quad x} \\ {\text{subject} \ \ \text{to}\quad f_{1} \left(\mathbf{\boldsymbol{ x}} \right)=\sum\limits_{i=1}^{950} {\frac{1}{x_{i}} +10^{-6}\sum\limits_{i=951}^{1,000} {\frac{1}{x_{i}} -1,000\le 0,}} } \\ \\ {\kern15pt} {\quad \quad \quad \quad f_{2} \left(\mathbf{\boldsymbol{ x}} \right)=\sum\limits_{i=1}^{950} {\frac{1}{x_{i}} -10^{-6}\sum\limits_{i=951}^{1,000} {\frac{1}{x_{i}} -900\le} } 0,} \\ \\ {\quad \quad \quad {\kern24pt} 10^{-6}\le x_{i} \le 10^{6},\quad \quad i=1,\cdots ,1000.} \\ \end{array}} $$

The initial point is $x_{i}^{0} =10^{-5}$. The optimum point is known to be $x_{i}^{\ast } =1$ for i=1,2,⋯ ,950 and $x_{i}^{\ast } =10^{-6}$for i=951,952,⋯ ,1000 with f ₀(x ^∗)=950.0005. We set the move limit of the first outer iteration to 0.01 as Groenwold and Etman (2010a) did.

1.5 A.5 MBB beam topology optimization

The classical topology optimization problem for the Messerschmitt-Bolkow-Blöhm (MBB) beam to minimize compliance with a volume constraint is shown below. The design domain is discretized by the plane stress element, and the popular solid isotropic material with penalization (SIMP) scheme is used for this problem. A detailed description of the MBB problem is given by Bendsøe and Sigmund (2003).

The optimization problem can be stated as

$${\begin{array}{*{20}c} {\text{minimize}\quad f_{0} \left({\mathit{\boldsymbol{ x}}} \right)=\mathbf{u}^{T}\mathbf{Ku}=\sum\limits_{e=1}^n {x_{e}^{p} \mathbf{u}_{e}^{T} \mathbf{k}_{e} \mathbf{u}_{e}} } \\ {\text{subject}{\kern4pt} \text{to}\quad f_{1} \left(\mathbf{\boldsymbol{ x}} \right)=\sum\limits_{e=1}^n {x_{e} -fV_{0} \le 0,}} \\ \\ {\quad \quad \quad \quad \mathbf{Ku}=\mathbf{f},} \\ {\quad \quad \quad \quad 0.001\le x_{e} \le 1,} \\ \end{array}} $$

where x _e , u, K, and f represent the eth design variable representing density, the displacement vector, the global stiffness matrix assembled by an interpolated element stiffness matrix $x_{e}^{p} k_{e}$, and the external force applied, respectively. The eth element displacement vector and desired volume fraction are denoted as u _e and f, respectively. The sensitivity of the objective function with respect to the eth design variable can be represented as

$$\frac{df_{0}} {dx_{e}} =-\frac{p}{\rho_{e}} \textbf{u}_{e}^{\textbf{T}} k_{e} \textbf{u}_{e} $$

For finite element analysis, the standard element known as ‘Q4’ is used, a four-node membrane based on isoparametric displacement. Furthermore, to avoid the checkerboard problem, the sensitivity filter proposed by Sigmund (1997) is used with the filter radius set to 8 % of the beam height.