New analytical benchmarks for topology optimization and their implications. Part I: bi-symmetric trusses with two point loads between supports

Abstract

Extending some results by Sokół and Lewiński (Struct Multidisc Optim 42:835–853, 2010), the optimal topology of bi-symmetric trusses with two symmetrically placed pointloads is determined analytically, and verified by highly accurate numerical calculations. It is rather remarkable that Michell’s best-known classical solution had to wait over hundred years for its generalization from one to two point loads. Some implications of these solutions, including properties of so-called O-regions, are also discussed.

Introduction

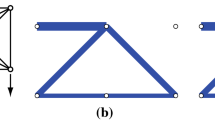
The aim of this paper is to find the truss of least volume with possibly an infinite number of bars which may be stressed to a given limit. The truss is to transmit two symmetrically placed forces of the same magnitude, acting along a line connecting two supports of given location (Fig. 1a). The feasible domains will be chosen as rectangles of various heights h; the limiting case of h being infinite. As can be seen from Fig. 1b, h ₁ denotes the vertical distance of the highest point of the optimal truss from the horizontal axis of symmetry, if the structural domain is the full plane (or if the optimal height of the truss is smaller than the height of the feasible domain (h ₁ < h in Fig. 1b)). Only one quarter of the structural domain, together with symmetry conditions, is shown in Fig. 1b. By recently introduced symmetry principles (Rozvany 2011), the optimal topologies to be discussed are equally valid for two pin supports, or for a pin and a roller support.

Fig. 1

Class of problems considered and notation (ξ = d/L)

The present paper differs from those by Sokół and Lewiński (2010, 2011a), because in the latter the feasible domain was a half-plane (above or below the line of supports) and there was only a vertical axis of symmetry. In the present paper (i) the feasible domain is a rectangle or the full plane, and we have two axes of symmetry, (ii) the adjoint strain field is also given for the memberless central region of some of the optimal layouts.

Various cases of truss topology problems with two symmetrical loads between two supports (pin or roller) and for different domains (full or half-plane) were recently reviewed briefly by Sokół and Lewiński (2011b).

The line notation in this text is as follows. Thick and thin continuous lines denote concentrated and ‘distributed’ truss members, broken lines domain boundaries, dotted lines region boundaries and dash-dot lines axes of symmetry or skew-symmetry.

For trusses with a size- and sign-independent stress constraint and a single load condition, the specific cost function is

$$ A=\,k\,\left| F \right|, \quad k\,=\,1/\sigma_p , $$

(1)

where A is the member cross-sectional area, F is the member force, k is a constant, and σ _p is the constant permissible stress.

The known optimality conditions (Michell 1904; Prager and Rozvany 1977) for the above problem are

$$ \bar{{\varepsilon }}=k{\rm sgn} F \quad \left( {{\rm for}\,\,\,F\ne 0} \right),\quad \left| {\bar{{\varepsilon }}} \right|\le k\quad \left( {{\rm for}\,\,\,F=0} \right), $$

(2)

where $\bar{{\varepsilon }}$ provides the ‘adjoint strain field’, which must be kinematically admissible (satisfying kinematic support and continuity conditions). The optimal structural volume can also be calculated from the ‘dual formula’:

$$ V={\rm {\bf P}}^T\overline{{\bf u}}, $$

(3)

where the vector P denotes the external forces and $\overline{{\bf u}}$ the adjoint displacements at these forces.

The optimal adjoint strain fields for plane Michell trusses may consist of the following types of regions (e.g. Prager and Rozvany 1977; similar regions were defined and used for grillages, see (Rozvany 1972)):

• T-region  with a tensile and a compression member at right angles: $\bar{{\varepsilon }}_1 \,=-\,\bar{{\varepsilon }}_2 =k$,

• S-region  with members having forces of the same sign in any direction: ${\bar{{\varepsilon }}_1 \,=\,\,\bar{{\varepsilon }}_2 ,} \; {\left| {\varepsilon_i } \right|=k} \; {\left( {i=1,\;2} \right)}$,

• R-regions  with only one member at any point: ${\left| {\bar{{\varepsilon }}_1 } \right|\,=\,\,k,}$ ${\left| {\bar{{\varepsilon }}_2 } \right|\le k}$, or

• O-region  with no members: ${\left| {\bar{{\varepsilon }}_1 } \right|\,\le \,\,k,} \; {\left| {\bar{{\varepsilon }}_2 } \right|\le k} ,$

where subscripts 1 and 2 indicate principal strains. The concept of O-regions was introduced already in the 1970s (e.g. Rozvany and Hill 1976). A special case of O-regions, in which both principal strains are zero (rigid region with $\bar{{\varepsilon }}_1 =\bar{{\varepsilon }}_2 =0)$, will be termed a Z-region. Another special case of O-regions, so-called V-regions (with ${\begin{array}{*{20}c} {\left| {\bar{{\varepsilon }}_1 } \right|\le k,} \quad {\bar{{\varepsilon }}_2 =0} \\ \end{array} })$ is introduced in this paper (see Section  2.1).

Referring to Fig. 1, the following types of optimal topologies exist:

Topology 1::

h ≥ h ₁,

Topology 2::

$h_1 \ge h\ge d/\sqrt 2$,

Topology 3::

$h\le d/\sqrt 2$.

Exact analytical solutions with numerical confirmation will be presented for Topologies 1 and 2, but only high resolution numerical solutions for Topology 3, for which the analytical solution is not yet available.

Details of optimal topologies

Topology 2/3 (limiting case between topologies 2 and 3)

This topology with $h=d/\sqrt 2$ is discussed first, because for this case we have a complete adjoint strain fields for all analytical solutions, some of which are shown in Fig. 2. The optimal solution for Topology 2/3 depends on the relative magnitude of (L − d) and h.

Fig. 2

Type 2/3 topology

If (L − d) = 0, then we have the solution in Fig. 2a, which is the classical solution by Michell (1904). The strain fields for the quarter domain consist of two T-regions: one has constant principal directions, the other one consists of a circular fan. This solution is in fact valid even when h > h ₁, because the T-regions shown in Fig. 2a can be extended even to the entire plane, satisfying the optimality condition of Michell in (2).

The layout in Fig. 2a will become part of all other topologies in Fig. 2b–d (shown partially on the left hand side of these diagrams). The right hand side of these layouts consists of concentrated horizontal bars along the domain boundaries. It is important to note that these optimal topologies are only valid if the domain has a limited height, i.e. $h=d/\sqrt 2$.

This is because in Fig. 2b, for example, kinematic continuity would not be satisfied if we moved upwards the present domain boundary (the strains in the two T-regions would cause an overlapping of the horizontal displacements). However, since the adjoint strain field in O-regions may be non-unique (see Section 4.2), there should be some other adjoint displacement field for the present problem of restricted height, which can be extended for greater height values.

In Fig. 2b and d the central part of the adjoint strain field consists of T-regions and Z-regions, see the definitions above. In Fig. 2c, however, there is also an R-region, with a horizontal principal strain of $\bar{{\varepsilon }}_1 =-k$. The value of $\bar{{\varepsilon }}_2$ can be calculated from the condition that the strains must be zero in the direction of the region boundary with the Z-region. Then elementary calculations give $\bar{{\varepsilon }}_2 =k\tan^2\alpha$. This implies $\bar{{\varepsilon }}_2 =0$ and $\bar{{\varepsilon }}_2 =k$, respectively, for Fig. 2b (with α = 0) and Fig. 2d (with α = π/4).

The solution in Fig. 2b was actually presented by the second author previously (Rozvany 2011).

Extending the region pattern in Fig. 2b to d, we can also construct optimal strain fields for any value of L − d > 2h.

For 0 < L − d < h the optimal topology is discussed in greater detail subsequently. For this case the optimal adjoint strain field is shown in Fig. 3a. Each quarter of the central, memberless O-region consists of a T-region and a V-region (see Section 1). The state of adjoint strains in these two regions, respectively, is represented by the Mohr-circles in Fig. 3b and c. It can be seen from Fig. 3b that the strain along the boundary of the T- and V-regions is

$$ \bar{{\varepsilon }}_{\rm B} =k\,\cos\left( {2\alpha } \right). $$

(4)

Moreover, one can infer from Fig. 3c that for the V-region, we have

$$ k\,\cos\left( {2\alpha } \right)=\left( {\bar{{\varepsilon }}_{1} /2} \right)\left( {1+\cos\left( {2\alpha } \right)} \right)\Rightarrow \bar{{\varepsilon }}_{1} =k\big({1-\tan^{2}\alpha }\big). $$

(5)

It can be seen that for α = 0 and α = 45° (5) gives the correct $\bar{{\varepsilon }}_{1}$ values for the limiting cases in Fig. 2a and b. The above adjoint strain field satisfies all optimality criteria of Michell (1904) (see also (2) in this paper). With this addition, we have complete analytical solution for all aspect ratios of Type 2/3 topologies, and also for the O-region of all Type 3 topologies.

Fig. 3

Optimal adjoint strain fields for Topology 2/3 with 0 < L − d < h

Topology 1

The topology of the optimal truss for h = ∞ (or h ≥ h ₁, see Fig. 1b) can be constructed as follows. We can infer from numerical results that the optimal layout is that of a ‘Michell cantilever’¹ and a horizontal bar. The geometry of this structure is fully determined by three angles: θ ₁, θ ₂ and γ ₂, shown in Fig. 4.

Fig. 4

Layout of the upper left quarter of Topologies 1 and 2

To make the paper self-consistent, it is useful to outline the so-called Lommel functions U _n (·,·) that play the fundamental role in deriving coordinates and the displacement field in the Hencky net of mutually orthogonal members in region ABDC (see Fig. 4). Following the notation by Lewiński et al. (1994) we will use in the present paper two functions: G _n (·,·) and F _n (·,·), defined as

$$ G_n \left( {\alpha ,\beta } \right)=\left( {\frac{\alpha }{\beta }} \right)^{n/2}I_n \left( {2\sqrt {\alpha \beta } } \right) $$

(6)

and

$$ F_n \left( {\alpha ,\beta } \right)=\sum\limits_{m=0}^\infty {\left( {-1} \right)^mG_{2m+n} \left( {\alpha ,\beta } \right)} , $$

(7)

where I _n (·) denotes the modified Bessel function of the first kind. Many important properties of functions G _n and F _n can be found in the paper mentioned before (Lewinski et al. 1994).

Now, the coordinates of the point D, connecting the horizontal bar with the Michell continuum, can be written as:

$$ \begin{array}{rll} x_{\rm D} &=&d\left[ \cos \left( \gamma_2 \right)\cos \left( \gamma_2 +\theta_2 -\theta_1 \right)\,F_0 \left( \theta_1 ,\theta_2 \right) \right. \\ &&{\kern8pt} +\,\sin \left( \theta_2 -\theta_1 \right)\;F_1 \left( \theta_1 ,\theta_2 \right) \\ &&{\kern8pt} -\left.\sin \left( \gamma_2 \right)\sin \left( \gamma_2 +\theta_2 -\theta_1 \right)\;F_2 \left( \theta_1 ,\theta_2 \right) \right], \\ y_{\rm D} &=&d\left[ \cos \left( \gamma_2 \right)\sin \left( \gamma_2 +\theta_2 -\theta_1 \right)\,F_0 \left( \theta_1 ,\theta_2 \right) \right. \\ &&{\kern8pt} +\,\cos \left( \theta_2 -\theta_1 \right)\;F_1 \left( \theta_1 ,\theta_2 \right) \\ &&{\kern8pt} +\left.\sin \left( \gamma_2 \right)\cos \left( \gamma_2 +\theta_2 -\theta_1 \right)\;F_2 \left( \theta_1 ,\theta_2 \right) \right]. \end{array} $$

(8)

Equations (8) are obtained by rearranging (2.9–11) of the paper by Sokół and Lewiński (2010). In the latter paper the displacement field of the domain RBDCNR (divided by appropriate sub-regions) was derived in detail. In particular, the adjoint displacements of points N and D (normalized with k = 1) are defined by:

$$ \begin{array}{rll} \emph{w}_x^{\rm N} &=&d\,\cos \left( {2\gamma_2 } \right), \\ \emph{w}_y^{\rm N} &=&d\,\left[ {-1+\sin \left( {2\gamma_2 } \right)} \right] \end{array} $$

(9)

and

$$ \begin{array}{rll} \emph{w}_x^{\rm D} &=&u^{\rm D}\cos \left( {\gamma_2 +\theta_2 -\theta _1 } \right)-\emph{v}^{\rm D}\sin \left( {\gamma_2 +\theta_2 -\theta_1 } \right), \\ \emph{w}_y^{\rm D} &=&u^{\rm D}\sin \left( {\gamma_2 +\theta_2 -\theta _1 } \right)+\emph{v}^{\rm D}\cos \left( {\gamma_2 +\theta_2 -\theta_1 } \right), \end{array} $$

(10)

where

$$ \begin{array}{rll} u^{\rm D}\!/d&=&2\theta_1 \sin \left( {\gamma_2 } \right)G_0 \left( {\theta _1 ,\theta_2 } \right) \\ &&+\,\cos \left( {\gamma_2 } \right)\left[ {G_0 \left( {\theta_1 ,\theta_2 } \right)+2\theta_2 G_1 \left( {\theta_1 ,\theta_2 } \right)} \right] \\ &&+\left[ {\cos \left( {\gamma_2 } \right)-\sin \left( {\gamma_2 } \right)} \right]\left[ {F_1 \left( {\theta_1 ,\theta_2 } \right)-F_2 \left( {\theta_1 ,\theta_2 } \right)} \right], \\ \emph{v}^{\rm D}/d&=&-2\theta_2 \sin \left( {\gamma_2 } \right)G_1 \left( {\theta _1 ,\theta_2 } \right) \\ &&\!-\left( {1+2\theta_2 } \right)\cos \left( {\gamma_2 } \right)G_0 \left( {\theta_1 ,\theta_2 } \right) \\ &&\!+\!\left[ {\cos \left( {\gamma_2 } \right)-\sin \left( {\gamma_2 } \right)} \right]\!\left[ {F_1 \left( {\theta_1 ,\theta_2 } \right)+F_2 \left( {\theta_1 ,\theta_2 } \right)} \right]. \end{array} $$

(11)

The (8)–(11) are general and valid for any angles: θ ₁, θ ₂ and γ ₂. They can be simplified considerably for a specific problem. For the problem under consideration, one can show that the angles θ ₁, θ ₂ and γ ₂ must satisfy

$$ \gamma_2 =\pi /4\quad{\rm and}\quad\theta_1 =\theta_2 +\gamma_2 . $$

(12)

The first relation under (12) comes directly from the zero value of the horizontal displacement at point N: $\emph{w}_x^{\rm N} =0$ and (9)₁. The second constraint can be derived from the fact that the upper chord BD should connect smoothly to horizontal bar DS at the point D, see (5.1) by Sokół and Lewiński (2010) and the detailed explanation given there. Now, by (12) the coordinates of point D can be expressed as

$$ \begin{array}{rll} x_{\rm D} &=&\frac{d}{\sqrt 2 }\left[ {F_0 \left( {\pi /4+\theta_2 ,\theta _2 } \right)+F_1 \left( {\pi /4+\theta_2 ,\theta_2 } \right)} \right]\,, \\ y_{\rm D} &=&\frac{d}{\sqrt 2 }\,\left[ {F_1 \left( {\pi /4+\theta_2 ,\theta_2 } \right)+F_2 \left( {\pi /4+\theta_2 ,\theta_2 } \right)} \right]\,, \end{array} $$

(13)

while the displacements of the point D can be written as

$$ \begin{array}{rll} \emph{w}_x^{\rm D} &=&\frac{d}{\sqrt 2 }\left[ {\frac{\pi }{2}\;G_0 \left( {\pi /4+\theta_2 ,\theta_2 } \right)+g\left( {\theta_2 } \right)} \right], \\ \emph{w}_y^{\rm D} &=&\frac{-d}{\sqrt 2 }g\left( {\theta_2 } \right), \end{array} $$

(14)

where the auxiliary function

$$ g\left( \alpha \right)=\left( {1+2\alpha } \right)G_0 \left( {\pi /4+\alpha ,\alpha } \right)+2\alpha \,G_1 \left( {\pi /4+\alpha ,\alpha } \right) $$

(15)

is introduced to shorten the notation.

Note that both the horizontal and vertical displacements of the point N defined in (9) are equal to zero for γ ₂ = π/4. The reason for this strange result comes from the fact that the displacements (9) and (10) are derived by means of a rigid rotation around point R. The magnitude of this rotation is not known in advance but can be determined from the boundary conditions. This procedure was described in detail by Sokół and Lewiński (2011a, see (23) and (24) there). The displacements of points N and D adjusted in this way (without normalization) can be written as

$$ \begin{array}{rll} \overline{{\emph{w}}}_x^{\rm N} &=&k\emph{w}_x^{\rm N} \\ \overline{{\emph{w}}}_y^{\rm N} &=&k\left( {\emph{w}_y^{\rm N} +\psi \,d} \right) \end{array} $$

(16)

and

$$ \begin{array}{rll} \overline{{\emph{w}}}_x^{\rm D} &=&k\left( {\emph{w}_x^{\rm D} -\psi y_{\rm D} } \right) \\ \hfill \overline{{\emph{w}}}_y^{\rm D} &=&k\left( {\emph{w}_y^{\rm D} +\psi \,x_{\rm D} } \right) \end{array} $$

(17)

where ψ denotes the angle of the rigid rotation. It can be determined from the zero value of the horizontal displacement of point S, lying at the vertical axis of symmetry (see Fig. 4). We know that for fully stressed truss the virtual elongation of the bar DS is equal to its length (L − x _D), thus

$$ \overline{{\emph{w}}}_x^{\rm S} =\overline{{\emph{w}}}_x^{\rm D} +k\left( {L-x_{\rm D} } \right)=0. $$

(18)

From (18) and (17)₁ one can easily deduce that

$$ \psi =\frac{L-x_{\rm D} +\emph{w}_x^{\rm D} }{y_{\rm D} }. $$

(19)

Now, the adjusted (properly rotated) displacement $\overline{{\emph{w}}}_y^{\rm N}$ can be written as

$$ \overline{{\emph{w}}}_y^{\rm N} =\frac{k\,d}{y_{\rm D} }\left( {L-x_{\rm D} +\emph{w}_x^{\rm D} } \right) $$

(20)

where x _D, y _D and $\emph{w}_x^{\rm D}$ are given in (13) and (14).

The forces for the layout in Fig. 4 are given by: Q _y  = P/2, F _x  = Q _y d/y _D and F _y  = 0. The horizontal reaction Q _x at point N can be obtained from Chan’s formula (see (2.47) in the paper by Sokół and Lewiński (2010)), while the reactions at point R can easily be obtained from the equilibrium equations. These reaction forces, however, do not generate any virtual work in (3), because the corresponding virtual displacements are zero (points R and N in Fig. 4).

The volume of one quarter of the full structure can be calculated by adding the volume of the Michell’s continuum and the volume of the horizontal bar DS (see Sokół and Lewiński 2010). However, it is more elegant and convenient to use the dual method (see (3))

$$ V=Q_y \overline{{\emph{w}}}_y^N =\frac{Pd}{2y_{\rm D} \sigma_p }\left( {L-x_{\rm D} +\emph{w}_x^{\rm D} } \right). $$

(21)

The volume in (21) is a function of one variable V = V(θ ₂) and its minimum can be determined from the necessary condition V′(θ ₂) = 0. This leads to the transcendental equation

$$ \xi \,q\left( {\theta_2 } \right)=\sqrt 2 , $$

(22)

where ξ = d/L and function q(θ ₂) is defined by

$$ \begin{array}{rll} q\left( {\theta_2 } \right)&=&\left( {\pi /2+4\theta_2 } \right)\left[ {F_1 \left( {\pi /4+\theta_2 ,\theta_2 } \right)} \right. \\ &&-\left. F_0 \left( {\pi /4+\theta_2 ,\theta_2 } \right) \right]+2F_1 \left( {\pi /4+\theta_2 ,\theta_2 } \right) \\ &&+\,2\theta_2 \left[ {G_0 \left( {\pi /4+\theta_2 ,\theta_2 } \right)-G_1 \left( {\pi /4+\theta_2 ,\theta_2 } \right)} \right].\\ \end{array} $$

(23)

Equation (22) uniquely defines the optimal angle θ ₂ because the function q(θ ₂) is monotonic (it is a decreasing function for θ ₂ ≥ 0 which starts from $q\left( 0 \right)=\sqrt 2$ and then asymptotically approaches 0 for θ ₂ → ∞). The lower limit of ξ for which the solution of (22) is valid for the rectangular domain shown in Fig. 1a is equal to ξ = 0.182027. This corresponds to θ ₂ = π/4 which means that the upper chord RBDS starts vertically from the support. For lower values of ξ the external fans extend beyond vertical lines drawn above the supports and the solution is formally infeasible. However, if we allow the horizontal expansion of our rectangle domain outside the supports, we can obtain the feasible solution for ξ < 0.182027. In this case the lowest limit of ξ for which the solution of (22) makes physical sense is equal to ξ = 0.0477491. This corresponds to θ ₂ = π/2 and θ ₁ = 3π/4. For lower values of ξ the internal circular fan goes outside the symmetry line connecting two supports, and that is obviously infeasible. Thus we can conclude that for ξ < 0.0477491 the optimal solution is not known.

Examples of optimal layouts of Topology type 1 are shown in Fig. 5. For increasing ξ the angle θ ₂ decreases and at the same time the height and the volume of the structure increase. Obviously, the final solution for ξ = 1 is identical with the well known Michell’s solution (1904) (with θ ₂ = 0, θ ₁ = π/4, and 4V = PL/σ _p (2 + π)). All solutions have been confirmed by numerical calculations. The exact layouts are given on the left side and their numerical equivalents on the right.

Fig. 5

The optimal layouts of Topology 1 for selected positions of loads a ξ = 0.25, c ξ = 0.5, e ξ = 0.75, g ξ = 1, and their numerical confirmations b, d, f, h

The exact and numerically calculated volumes are compared in Section 3.

Topology 2

In this case y _D  = h and then by (13)₂ we have

$$ h=\frac{d}{\sqrt 2 }\left[ {F_1 \left( {\pi /4+\theta_2 ,\theta_2 } \right)+F_2 \left( {\pi /4+\theta_2 ,\theta_2 } \right)} \right]. $$

(24)

Obviously this case is simpler than the previous one (compare (22), (23) and (24)). For the limiting case $h=d/\sqrt 2$ one can easily obtain θ ₂ = 0 and then the total volume of the optimal truss becomes

$$ 4V=\frac{P{\kern 1pt}L}{\sigma_p }\left[ {2\sqrt 2 \left( {1-\xi } \right)+\left( {2+\pi } \right)\xi } \right]. $$

(25)

The above formula gives the correct volume for special cases. For ξ = 1 we obtain 4V = PL/σ _p (2 + π), which is the solution by Michell (1904). For $\xi =\sqrt 2 /\big( {1+\sqrt 2}{\kern1pt}\big)$ we obtain $4V=PL/\sigma_p \left( {4+\pi } \right)\big( {2-\sqrt 2}{\kern1pt}\big)$, which can also be readily derived from the second author’s solution (Rozvany 2011, here Fig. 2b).

Three examples of Topology 2 with $\xi =\sqrt 2 /( {1+\sqrt 2 } )$ and three different permissible heights are shown in Fig. 6. The topologies in Fig. 6e and f are actually of type 2/3 (see Section 2.1, Fig. 2).

Fig. 6

The optimal layouts of Topology 2 constrained by the allowable height a h = h ₁, c $h=(h_1 +d/\sqrt 2 )/2$, e $h=d/\sqrt 2$, and their numerical equivalents b, d, f

Topology 3

The exact solutions for Topology 3 are not known at present, but the optimal layouts can be predicted on the basis of numerical solutions (e.g. those in Fig. 7). Here the value ξ = d/L = 0.5 was assigned to the length ratio. The layout in Fig. 7a was calculated for $h=d/\sqrt 2 =L\,\sqrt 2 /4\approx 0.353553L$. It is the limiting case between topology types 2 and 3, hence this layout is similar to the one presented in Fig. 6e and f (see also Fig. 2 in Section 2.1). By progressively decreasing the height h of the structural domain for the numerical solutions, we find that additional T-regions develop in the optimal topology, similarly to a long cantilever (Lewiński et al. 1994), but following a different geometry (see Fig. 8).

Fig. 7

Some numerical layouts of upper-left quarter of Topology 3, constrained by allowable heights: a $h=d/\sqrt 2$, b h = 0.5d, c h = 0.3d, d h = 0.26d, e h = 0.2d

Fig. 8

Some optimal layouts for Topology 3

In Fig. 8 the upper horizontal bar is connected to the chord of a circular fan having an angular width of 45° and a curved three-sided region, which is similar to that derived by Chan (for details see the paper by Lewiński et al. (1994)). The upper border of this region can be a straight line if the height is sufficiently small (Fig. 8b) or it starts with a straight section and smoothly passes into a curved section (Fig. 8a). It is to be noted that contrary to Topologies type 1 and 2 the external (upper) chord has not a constant cross section in the straight segment. The three-sided domain above the circular fan is connected with a region with straight members in one direction. This is the reason why the rest of the regions with Hencky nets are different from those derived for the long cantilever problem by Lewiński et al. (1994). Nevertheless, there are also some similarities in forming subsequent new regions if the permissible height is decreased. On the basis of many additional numerical tests we have established that switching from the first sub-type (Fig. 8a) to the second one (Fig. 8b) occurs at a height value in the range of h ∈ (0.24d, 0.25d).

The adjoint strain field in empty regions of Topology 3 can be filled the same way as described in Section 2.1 (Fig. 2).

Confirmation of the analytical results by numerical calculations

All exact solutions presented in this paper have been confirmed by numerical calculations. They were performed using an improved version of the program developed by Sokół (2011a). This newer version of the program makes use of the ‘adaptive ground structure’ approach, similar to that proposed by Gilbert and Tyas (2003), however, it applies a different strategy of adding-removing of the active bars from a huge number of potential members of the full ground structure. In the present version the program is capable of solving large-scale problems with the number of potential members exceeding one billion (10⁹). This program was announced in 2011 (see Sokół 2011b) and will be presented in detail in a separate paper in a near future. It should be noted that this program uses a linear programming formulation, and therefore the solution obtained guaranteed to be the absolute minimum volume for the given discretization of nodes.

As was shown in Figs. 5 and 6, the numerical layouts are very close to the analytical ones. A comparison of the volumes obtained by numerical and analytical calculations is given in Table 1. Even in the worst cases (Fig. 5a and b) the numerically optimized volume differs from the exact one by no more than 0.1%.

Table 1 Comparison of numerical and analytical solutions

Important implication of the results for basic properties of exact optimal Michell topologies

R, S, O and Z regions in optimal Michell topologies

Various types of optimal regions were defined—in the context of grillages—already in the early 1970s (e.g. Rozvany 1972), and the present notation (including O-regions) was used a few years later (e.g. Rozvany and Hill 1976, p. 208).

In a highly creative recent research paper, Melchers (2005) used the notation N and B for our O- and Z-regions. He pointed out that for Michell trusses relatively few known solutions contain regions other than T-type. This is possibly so, because much of the theory of T-regions is based on the mathematically similar theory of slip lines in plasticity, which was developed earlier. However, for Michell structures with line supports, there are in general R-regions in the solution, and T-regions are rather an exception (see Rozvany et al. 1997, e.g. Figs. 5 and 6). In the same paper Z-regions (which are special cases of O-regions) were used in several solutions.

Since, in the definition of O-regions (see above), we have non-strict inequalities, and the essential point is that we have no members in these regions, the central memberless parts of the topologies in Fig. 2b to d can be regarded as O-regions, although they contain T-, Z- and R-regions.

Non-uniqueness of the optimal adjoint displacement fields in O-regions

The optimal O-regions containing T-, Z- and R-regions are not necessarily unique for a given optimal Michell truss topology, as was demonstrated earlier (Rozvany et al. 1997). For the simple problem in Fig. 9, the domain has a restricted height of a and two hinge supports, and is loaded by a horizontal couple. The fairly obvious optimal topology consists of two parallel bars. A simple optimal adjoint strain field is shown in Fig. 9, but an alternative strain field consists of cycloids which was given by Hemp (1973, p. 95). Hemp’s corresponding displacement field is

$$ \begin{array}{rll} \overline{{u}}&=&-\pi k y/2+k a\;\Big[ {\arccos \left( {1-2y/a} \right)/2} \\ &&+\left( {x/a-\sqrt {\left( {y/a} \right)\left( {1-y/a} \right)} } \right)\left( {1-2y/a} \right) \Big], \\ \overline{{\emph{v}}}&=&\pi k x/2+k a\;\left[ \left( {x/a} \right)^2-\left( {y/a} \right)\left( {1-y/a} \right) \right], \end{array} $$

(26)

which gives $\overline{{u}}=\overline{{v}}=0$ at the two hinges, and the displacements $\overline{{u}}=\pm kL$ at the forces, which implies the correct structural volume by (3).

Fig. 9

A simple example of a non-unique optimal adjoint strain field containing Z-regions

The above example demonstrates that the adjoint strain field may be non-unique in a memberless part (i.e. O-region) of an optimal Michell topology.

An even much simpler example of non-uniqueness of the adjoint strain field is shown in Fig. 10. In this problem we have two vertical line supports at a distance of 3L from each other, and a horizontal point load at a distance L from the right hand support. The optimal layout obviously consists of a single horizontal bar between the load and the nearer support. The principal adjoint strain in the vertical direction is everywhere zero: $\bar{{\varepsilon }}_y =0$. In Fig. 10a we have an R-region on the right hand side and an O-region on the left hand side, where the inequality in (2) admits a horizontal strain of − k/2. An alternative, discontinuous adjoint strain field is given in Fig. 10b, in which we have a Z-region and an R-region on the left, both admissible by (2).

Fig. 10

A trivially simple new example showing the non-uniqueness of adjoint strains in O-regions

In Figs. 2, 9 and 10 the optimal truss layout is unique, only the adjoint strain field is non-unique. The above non-uniqueness is, therefore, not to be confused with the finding (Rozvany 2011) that a Michell truss problem may have either one or an infinite number of optimal solutions (of the same weight).

In a recent paper (Rozvany and Sokół 2012, Fig. 6) another example of an O-region is given, which covers a half plane and has principal adjoint strains that have a constant absolute value which is greater than zero and smaller than k. Both Fig. 10a, and this latter example disprove the notion that in O-regions the adjoint principal strains are either zero or k.

Relaxation of optimality criteria

The authors believe that, if there exists at least one feasible solution for a Michell problem, then there exists also an optimal solution satisfying Michell’s optimality criteria in (2) exactly. Nevertheless temporary relaxation of optimality criteria (as suggested by Melchers 2005), followed by an optimization within the set of solutions obtained by the relaxed conditions, can be very useful in finding optimal topologies.

An important example for this was Morley’s (1966) contention that no optimal solution satisfying known optimality criteria exists for a square clamped domain in flexure (either reinforced plate or grillage). It was the greatest breakthrough in the optimal grillage theory when Melchers (Lowe and Melchers 1972) found the exact solution of the above problem (by temporarily relaxing and then enforcing the relevant optimality criteria). As indicated above, we do have the optimal adjoint strain fields for Type 2/3 and Type 3 topologies for the memberless central parts of these problems, but it will be a highly challenging task to find these for Type 1 and Type 2 topologies, because of their partially curved boundaries.

Concluding remarks

In this paper we have presented exact analytical solutions for a new class of Michell truss problems: two symmetrically placed point loads in between supports, the feasible domain being symmetric to the line of supports. The exact solutions have been confirmed by very close numerical results. A rather remarkable historical aspect of this development is the fact that it has taken over hundred years to find the exact (analytical) extension of Michell’s best-known classical (1904) solution to two point loads. Some important general implications of these solutions have also been pointed out.