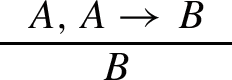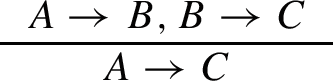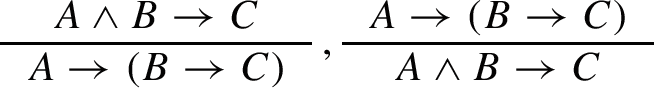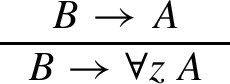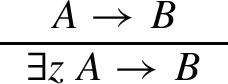Herbrandized modified realizability

Abstract

Realizability notions in mathematical logic have a long history, which can be traced back to the work of Stephen Kleene in the 1940s, aimed at exploring the foundations of intuitionistic logic. Kleene’s initial realizability laid the ground for more sophisticated notions such as Kreisel’s modified realizability and various modern approaches. In this context, our work aligns with the lineage of realizability strategies that emphasize the accumulation, rather than the propagation of precise witnesses. In this paper, we introduce a new notion of realizability, namely herbrandized modified realizability. This novel form of (cumulative) realizability, presented within the framework of semi-intuitionistic logic is based on a recently developed star combinatory calculus, which enables the gathering of witnesses into nonempty finite sets. We also show that the previous analysis can be extended from logic to (Heyting) arithmetic.

1 Introduction

Notions of realizability have a rich history, with the first generation dating back to the 40s, with the pioneering Kleene’s realizability [10] and Kreisel’s modified realizability [12]. These realizability strategies, closely connected with the Brouwer–Heyting–Kolmogorov foundational interpretation of intuitionistic logic developed in the early 1900s, aim to explicitly reveal the constructive content of proofs, decide disjunctions, and offer precise witnesses for existential statements. Later, a second generation of realizability strategies emerged, shifting the focus from precise witnesses to bounds for those witnesses. Examples of such realizability strategies include the bounded modified realizability (BMR) [7] and the confined modified realizability (CMR) [9], which draw inspiration from earlier works of Ulrich Kohlenbach, Fernando Ferreira, and Paulo Oliva. In 1996, Kohlenbach introduced the monotone functional interpretation [11], and in 2005, Ferreira and Oliva introduced the bounded functional interpretation [8]. [Although with different approaches] Both strategies differ from the well-known Gödel’s functional (Dialectica) interpretation since they do not rely on precise witnesses but instead on majorizing functionals. BMR and CMR apply the concept of majorizability in all finite types to the realizability method, also delivering bounds instead of precise realizers.

In 2017, a new type of combinatory calculus was introduced, incorporating star types [6] that enable the formation of sets of potential witnesses. The focus can now shift from bounds for witnesses to finite sets of possible witnesses. Based on this calculus, a cumulative/herbrandized functional interpretation was developed within the framework of classical first-order predicate logic, drawing on the corresponding Shoenfield version of the Dialectica interpretation. This cumulative interpretation followed in the footsteps of a previous work of Benno van den Berg, Eyvind Briseid and Pavol Safarik [18] in the context of nonstandard arithmetic. For a comparison between this later approach and the one pursued in [6], see [2]. Another cumulative interpretation based on (this time denumerable) sets can be found in [1].

Based on the above prior research, this paper shows how the star combinatory calculus can serve as the basis for a novel modified realizability approach, namely the herbrandized modified realizability, within the domains of semi-intuitionistic logic and Heyting arithmetic.

Overview: The paper is structured as follows. In the next section we recall the star combinatory calculus and its nice proof-theoretic properties. In Sect. 3 we introduce the herbrandized modified realizability in the semi-intuitionistic context and establish the corresponding soundness and characterization theorems. We finish the paper with some final notes, including the possibility of extending the previous analysis to the Heyting arithmetic context.

2 Background: star combinatory calculus

As the star combinatory calculus serves as the base of the realizability notion introduced in this paper, we start this session by revisiting this calculus and its main properties. For further details on the star combinatory calculus, please consult [6].

Let us fix a language $\mathcal {L}$ of pure first-order logic containing at least one constant symbol. We are going to define the language $\mathcal {L}^{\omega }_*$, a language in all finite types (based on a given ground type G).

Definition 1

The types are inductively generated as follows:

• (i) The ground type (G) is a type;

• (ii) If $\sigma$ and $\tau$ are types, $\sigma \rightarrow \tau$ is a type;

• (iii) If $\sigma$ is a type, $\sigma ^*$ is a type (a star type).

Each type represents a class of objects. As usual, informally the type $\sigma \rightarrow \tau$ represents the functionals from objects of type $\sigma$ to objects of type $\tau$. The intended meaning of $\sigma ^*$ is the type of all finite non-empty subsets of objects of type $\sigma$.

Remark 1

Any type is of the form $\sigma _1 \rightarrow (\sigma _2 \rightarrow (\cdots \rightarrow (\sigma _n \rightarrow \rho )\cdots ))$ with $\rho$ the type G or a star type. We follow the convention of associating $\rightarrow$ to the right, abbreviating the above type by $\sigma _1 \rightarrow \cdots \rightarrow \sigma _n \rightarrow \rho$.

For each functional symbol f of $\mathcal {L}$, with arity n ($n\ge 0$), f denotes a constant of $\mathcal {L}^{\omega }_*$, of type $G \rightarrow \cdots \rightarrow G \rightarrow G$ with n arrows.

Additionally, we have the logical constants or combinators:

• $\Pi _{\sigma ,\tau }$ of type $\sigma \rightarrow \tau \rightarrow \sigma$, for each pair of types $\sigma$, $\tau$;

• $\Sigma _{\rho ,\sigma ,\tau }$ of type $(\rho \rightarrow \sigma \rightarrow \tau ) \rightarrow (\rho \rightarrow \sigma ) \rightarrow \rho \rightarrow \tau$, for each triple of types $\rho$, $\sigma$, $\tau$;

and the star constants:

• $\mathfrak {s}_{\sigma }$ of type $\sigma \rightarrow \sigma ^*$, for each type $\sigma$;

• $\cup _{\sigma }$ of type $\sigma ^* \rightarrow \sigma ^* \rightarrow \sigma ^*$, for each type $\sigma$;

• $\bigcup _{\sigma ,\tau }$ of type $\sigma ^* \rightarrow (\sigma \rightarrow \tau ^*) \rightarrow \tau ^*$, for each pair of types $\sigma$, $\tau$.

Definition 2

The terms of $\mathcal {L}^{\omega }_*$ are inductively generated as follows:

• (i) Constants are terms;

• (ii) For each type $\sigma$, there exists a countable infinite number of variables of type $\sigma$ (usually denoted by $x, y, z \ldots$). Variables are terms;

• (iii) If t is a term of type $\sigma \rightarrow \tau$ and q is a term of type $\sigma$, then tq is a term of type $\tau$.

The fact that the term t has type $\sigma$ is sometimes denoted by $t^{\sigma }$ or $t:\sigma$.

Concerning the intended meaning of the star constants above: $\mathfrak {s}_{\sigma }t$ represents a set with a unique element t; $\cup _{\sigma }tq$ represents the union of the sets t and q and $\bigcup _{\sigma ,\tau }tq$ for $t: \sigma ^*$ and $q: \sigma \rightarrow \tau ^*$ represents the union $\bigcup _{w\in t} qw$.

The star combinatory calculus has the following conversions:

• $\Sigma _{\rho ,\sigma ,\tau } tqr \rightsquigarrow tr(qr)$ ($t: \rho \rightarrow \sigma \rightarrow \tau ,\,q: \rho \rightarrow \sigma ,\,r: \rho$)

• $\Pi _{\sigma ,\tau }tq \rightsquigarrow t$ ($t: \sigma ,\,q: \tau$)

• $\bigcup _{\sigma ,\tau }(\mathfrak {s}_\sigma t)q \rightsquigarrow qt$ ($t: \sigma , \,q: \sigma \rightarrow \tau ^*$)

• $\bigcup _{\sigma ,\tau }(\cup _\sigma tq)r \rightsquigarrow \cup _\tau (\bigcup _{\sigma ,\tau } tr)(\bigcup _{\sigma ,\tau } qr)$ ($t: \sigma ^*, \,q: \sigma ^*,\, r: \sigma \rightarrow \tau ^*$)

Given two terms t and q of the same type, we say that we have a one-step reduction, which we denote by $t \succ _1 q$, if q is obtained from t applying one of the above conversions to a subterm of t. We write $t \succeq q$, and say that t reduces to q (or we have a reduction from t to q) if q is obtained from t by an arbitrary number (possibly zero) of one-step reductions.

A term is said to be normal if it is not possible to apply any one-step reduction on the term. A term t is said to be strongly normalizable if there is no infinite chain of one-step reductions starting from t.

The star combinatory calculus has the following three key properties, whose proofs can be found on [6].

Theorem 1

The star combinatory calculus has the strong normalization property.

Theorem 2

The star combinatory calculus has the Church–Rosser property, that is, each term has a unique normal form.

Definition 3

A term t of star type is said to be set-like if it is constructed from terms of the form $\mathfrak {s}q$ and the constant $\cup$.

Theorem 3

If t is a normal closed term of star type, then t is set-like.

For each type $\rho$, we have an equality symbol $=_\rho$ and a membership symbol $\in _\rho$.

An atomic formula is a formula of the form $\bot$, $t^\rho =_\rho q^\rho$, $t^\rho \in _\rho q^{\rho ^*}$ or $R(t_1^G,\ldots ,t_n^G)$ where R is a relational symbol of $\mathcal {L}$.

Definition 4

The formulas of $\mathcal {L}^{\omega }_*$ are inductively generated as follows:

• (i) Atomic formulas are formulas;

• (ii) If A and B are formulas and x is a variable, then $A \vee B, A \wedge B, A \rightarrow B,\forall x \, A$ and $\exists x \, A$ are formulas.

• (iii) If A and B are formulas, x is a variable of type $\rho$ and t is a term of type $\rho ^*$ where $x^{\rho }$ does not occur, then $\forall x \in t\, A, \exists x \in t\, A$ are formulas. [$\forall x \in t$ and $\exists x \in t$ are called bounded quantifications.]

A formula is said to be $\exists$-free if it does not contain any unbounded existential quantifiers $\exists x$.

We use the following abbreviations:

• $\lnot A:\equiv A \rightarrow \bot$

• $A \leftrightarrow B:\equiv (A \rightarrow B) \wedge (B \rightarrow A)$

The theory $\textrm{IL}^{\omega }_*$ that we are about to introduce is intuitionistic logic in all finite types. First we start by listing what we call the $\textrm{IL}$ axioms and rules.

Axioms of $\textrm{IL}$:

• $A \vee A \rightarrow A$, $A \rightarrow A \wedge A$

• $A \rightarrow A \vee B$, $A \wedge B \rightarrow A$

• $A \wedge B \rightarrow B \wedge A, A \vee B \rightarrow B \vee A$

• $\bot \rightarrow A$

• $\forall x\, A \rightarrow A[t/x]$, $A[t/x] \rightarrow \exists x\, A$, where t is a term free for x in A and A[t/x] denotes the formula obtained from A after replacing each instance of x by t.

Rules of $\textrm{IL}$:

In the following rules, x does not occur free in B.

The theory $\textrm{IL}^{\omega }_*$ is an extension of $\textrm{IL}$ (in the language of all finite types) with the following axioms and axiom schemes:

• (i) Axioms for $=_\rho$:

  • $x =_\rho x$

  • $x =_\rho y \wedge A \rightarrow A'$, where A is an atomic formula and $A'$ is obtained from A replacing some instances of x by y.

• (ii) $\forall x \in t\, A(x) \leftrightarrow \forall x (x \in t \rightarrow A(x))$, $\exists x \in t\, A(x) \leftrightarrow \exists x (x \in t \wedge A(x))$

• (iii) $\Sigma xyz= xz(yz)$, $\Pi xy = x$

• (iv) Axioms for star types:

  • $w \in \mathfrak {s}x \leftrightarrow w=x$

  • $w \in \cup xy \leftrightarrow w \in x \vee w \in y$

  • $z \in x \wedge w \in yz \rightarrow w \in \bigcup xy$

  • $\bigcup (\mathfrak {s}x)y = yx$

  • $\bigcup (\cup xy)z = \cup (\bigcup xz)(\bigcup yz)$

Remark 2

From the equalities of the conversions and the axioms for equality, we conclude that reduction implies equality.

Lemma 1

Let t be a closed term of type $\rho ^*$. Then there are closed terms $q_1,\ldots ,q_n$ of type $\rho$ such that

$$\begin{aligned} \textrm{IL}^{\omega }_*\vdash w\in t \leftrightarrow w=q_1 \vee \ldots \vee w=q_n \end{aligned}$$

Proof

Since reduction implies equality and due to the axioms of equality, we only need to show the case when t is in normal form, that is, when t is set-like. The proof follows by induction on the complexity of t. If t is $\mathfrak {s}q$, by the axiom for $\mathfrak {s}$, we can take the term q. If t is $\cup rs$, we apply the induction hypothesis. Let $r_1,\ldots ,r_m$ be the terms associated to r and $s_1,\ldots ,s_l$ be the terms associated to s. Then, by the axiom for $\cup$:

$$\begin{aligned} \textrm{IL}^{\omega }_*\vdash w\in \cup rs \leftrightarrow w=r_1 \vee \ldots \vee w=r_m \vee w=s_1\vee \ldots \vee w=s_l \end{aligned}$$

$\square$

Given that terms are derived solely from constants and variables through the operation of application, we naturally achieve what is commonly referred to as combinatorial completeness.

Theorem 4

(Combinatorial completeness) For each term $t^\sigma$ and variable $x^\rho$ there exists a term of type $\rho \rightarrow \sigma$, denoted by $\lambda x.t$, whose variables are those of t except x, such that for all term s of type $\rho$:

$$\begin{aligned} \textrm{IL}^{\omega }_*\vdash (\lambda x.t)s =_\sigma t[s/x] \end{aligned}$$

where t[s/x] is the term obtained replacing in t every occurrence of x by s.

Remark 3

In fact, we get $(\lambda x.t)s \succeq t[s/x]$.

Definition 5

A type is said to be end-star if it is of the form $\rho _1 \rightarrow \ldots \rightarrow \rho _n \rightarrow \tau ^*$.

For ease of reading, we denote $\mathfrak {s}x$ by $\{x\}$, $\cup xy$ by $x \cup y$ and $\bigcup xy$ by $\bigcup _{w \in x} yw$.

Let $\sigma$ be the type $\rho _1 \rightarrow \ldots \rightarrow \rho _n \rightarrow \tau ^*$ (with $n\ge 0$) and a, b be terms of type $\sigma$. The following abbreviations will also be useful:

$$\begin{aligned} a \sqsubseteq _{\sigma } b:\equiv \forall x_1^{\rho _1},\ldots ,x_n^{\rho _n} (ax_1\cdots x_n \subseteq _{\tau ^*} bx_1\cdots x_n) \end{aligned}$$

where $a' \subseteq _{\tau ^*} b':\equiv \forall x (x \in a' \rightarrow x \in b')$ for $a',b'$ of type $\tau ^*$.

$$\begin{aligned} a \sqcup _{\sigma } b:\equiv & {} \lambda x_1^{\rho _1},\ldots ,x_n^{\rho _n}.ax_1\cdots x_n \cup bx_1\cdots x_n\\ \bigsqcup _{w \in F} fw:\equiv & {} \lambda x_1^{\rho _1},\ldots ,x_n^{\rho _n}.\bigcup _{w \in F} fwx_1\cdots x_n \end{aligned}$$

$\underline{x}\sqsubseteq \underline{x}'$ denotes $\bigwedge _i x_i \sqsubseteq x'_i$, where $\underline{x}$ (respectively $\underline{x}'$) denotes the tuple of $x_i$ (respectively $x'_i$).

Remark 4

We have $a \sqsubseteq _{\sigma } a \sqcup _{\sigma } b, b \sqsubseteq _{\sigma } a \sqcup _{\sigma } b$ and $\forall z \in F (fz \sqsubseteq _{\sigma } \bigsqcup _{w \in F} fw)$.

Remark 5

The relation $\sqsubseteq _{\tau ^*}$ is simply $\subseteq _{\tau ^*}$.

3 The herbrandized modified realizability

In this section, we define the new realizability notion (the herbrandized modified realizability) within $\textrm{IL}^{\omega }_*$ and prove the corresponding soundness and characterization theorems.

Definition 6

Given a formula A, we define $A^{HR}$ as a formula, with the free variables of A, of the form:

$$\begin{aligned} A^{HR} \equiv \exists \underline{x}\,A_{HR}(\underline{x}) \end{aligned}$$

where $A_{HR}$ is a $\exists$-free formula. The definition is by induction on the complexity of A:

If A is atomic, $A^{HR}:\equiv A_{HR}:\equiv A$.

If $A^{HR} \equiv \exists \underline{x}\,A_{HR}(\underline{x})$ and $B^{HR} \equiv \exists \underline{u}\,B_{HR}(\underline{u})$:

• $(A \vee B)^{HR}:\equiv \exists \underline{x},\underline{u}(A_{HR}(\underline{x}) \vee B_{HR}(\underline{u}))$

• $(A \wedge B)^{HR}:\equiv \exists \underline{x},\underline{u}(A_{HR}(\underline{x}) \wedge B_{HR}(\underline{u}))$

• $(A \rightarrow B)^{HR}:\equiv \exists \underline{U}\forall \underline{x}(A_{HR}(\underline{x}) \rightarrow B_{HR}(\underline{U}\underline{x}))$

• $(\exists z \,A(z))^{HR}:\equiv \exists Z,\underline{x}\exists z \in Z \,A_{HR}(z,\underline{x})$

• $(\forall z \,A(z))^{HR}:\equiv \exists \underline{X}\forall z \,A_{HR}(z,\underline{X}z)$

• $(\exists z \in t\,A(z))^{HR}:\equiv \exists \underline{x}\exists z \in t\,A_{HR}(z,\underline{x})$

• $(\forall z \in t\,A(z))^{HR}:\equiv \exists \underline{x}\forall z \in t\,A_{HR}(z,\underline{x})$

Remark 6

If A is an $\exists$-free formula, then $A^{HR} \equiv A_{HR} \equiv A$.

Remark 7

By induction on the logical structure of the formulas, it can be shown that, for any formula A, the variables $\underline{x}$ in $A^{HR} \equiv \exists \underline{x}\,A_{HR}(\underline{x})$ are of end-star type.

Theorem 5

(Monotonicity) For any formula A with $A^{HR} \equiv \exists \underline{x}\,A_{HR}(\underline{x})$:

$$\begin{aligned} \underline{x}\sqsubseteq \underline{x}' \wedge A_{HR}(\underline{x}) \rightarrow A_{HR}(\underline{x}') \end{aligned}$$

Proof

The proof is by induction on the logical structure of the formula. For atomic formulas the result is trivial. The induction step in the cases $A \wedge B$, $A \vee B$, $\exists z \in t\,A(z)$ and $\forall z \in t\,A(z)$ follows from the induction hypothesis.

• Case $A \rightarrow B$

  We assume $\underline{U}\sqsubseteq \underline{U}'$ and $\forall \underline{x}(A_{HR}(\underline{x}) \rightarrow B_{HR}(\underline{U}\underline{x}))$. We need to show that $\forall \underline{x}(A_{HR}(\underline{x}) \rightarrow B_{HR}(\underline{U}'\underline{x}))$. Take $\underline{x}$ such that $A_{HR}(\underline{x})$. By hypothesis, we get $B_{HR}(\underline{U}\underline{x})$. We note that from $\underline{U}\sqsubseteq \underline{U}'$ we get $\underline{U}\underline{x}\sqsubseteq \underline{U}'\underline{x}$. By induction hypothesis, we have that $B_{HR}(\underline{U}'\underline{x})$. Thus $\forall \underline{x}(A_{HR}(\underline{x}) \rightarrow B_{HR}(\underline{U}'\underline{x}))$.

• Case $\forall z\, A(z)$

  We assume $\underline{X}\sqsubseteq \underline{X}'$ and $\forall z \,A_{HR}(z,\underline{X}z)$. We need to show $\forall z \,A_{HR}(z,\underline{X}' z)$. This follows from the induction hypothesis, noting that $\underline{X}\sqsubseteq \underline{X}'$ implies $\underline{X}z \sqsubseteq \underline{X}'z$.

• Case $\exists z\, A(z)$

  We assume $Z \sqsubseteq Z', \underline{x}\sqsubseteq \underline{x}'$ and $\exists z \in Z \,A_{HR}(z,\underline{x})$. We need to show $\exists z \in Z' \,A_{HR}(z,\underline{x}')$. Take z such that $z\in Z$ and $A_{HR}(z,\underline{x})$. Since $Z \sqsubseteq Z'$, we have that $z\in Z'$. From the induction hypothesis we get $A_{HR}(z,\underline{x}')$. Thus $\exists z \in Z' \,A_{HR}(z,\underline{x}')$.

$\square$

Consider the following Choice and Independence of Premises Principles:

$$\begin{aligned} \textrm{AC}^{\omega }_*\text {: } \forall x^\rho \exists y^\sigma \,A(x,y) \rightarrow \exists f^{\rho \rightarrow \sigma ^*} \forall x \exists y \in fx \,A(x,y) \end{aligned}$$

and

$$\begin{aligned} \textrm{IP}^*_{\not \exists } \text {: } (B(x) \rightarrow \exists y \,A(y)) \rightarrow \exists w (B(x) \rightarrow \exists y \in w \,A(y)) \end{aligned}$$

where B is an $\exists$-free formula.

The theory $\textrm{IL}^{\omega }_*+ \textrm{AC}^{\omega }_*+ \textrm{IP}^*_{\not \exists }$ proves the following Collection Principle:

Lemma 2

(Collection)

$$\begin{aligned} \textrm{IL}^{\omega }_*+ \textrm{AC}^{\omega }_*+ \textrm{IP}^*_{\not \exists } \vdash \forall \underline{x}\in \underline{y}\exists \underline{z}\, A(\underline{x},\underline{z}) \rightarrow \exists \underline{w}\forall \underline{x}\in \underline{y}\exists \underline{z}\in \underline{w}\, A(\underline{x},\underline{z}) \end{aligned}$$

Theorem 6

(Soundness) Let A be a formula with free variables $\underline{a}$. Let $T_{\not \exists }$ be a set of $\exists$-free formulas. If

$$\begin{aligned} \textrm{IL}^{\omega }_*+ \textrm{AC}^{\omega }_*+ \textrm{IP}^*_{\not \exists } + T_{\not \exists } \vdash A(\underline{a}) \end{aligned}$$

then there exist closed terms $\underline{t}$ such that

$$\begin{aligned} \textrm{IL}^{\omega }_*+T_{\not \exists } \vdash A_{HR}(\underline{a},\underline{t}\underline{a}) \end{aligned}$$

Proof

Fix $A^{HR} \equiv \exists \underline{x}\,A_{HR}(\underline{x})$, $B^{HR} \equiv \exists \underline{u}\,B_{HR}(\underline{u})$ and $C^{HR} \equiv \exists \underline{p}\,C_{HR}(\underline{p})$.

We use the tuple notation combined with the lambda notation as per the following example: if $\underline{x}$ denotes the tuple of $x_i$, then $\lambda \underline{x},\underline{y}.\underline{x}$ denotes the tuple of $\lambda \underline{x},\underline{y}.x_i$.

The proof is by induction on the deduction of the formula.

• Case $A \rightarrow A \wedge A$

  We need terms $\underline{t}_{\underline{X}'},\underline{t}_{\underline{X}''}$ such that:

  $$\begin{aligned} \forall \underline{x}(A_{HR}(\underline{x}) \rightarrow A_{HR}(\underline{t}_{\underline{X}'}\underline{x}) \wedge A_{HR}(\underline{t}_{\underline{X}''}\underline{x})) \end{aligned}$$

  We take $\underline{t}_{\underline{X}'}:=\underline{t}_{\underline{X}''}:=\lambda \underline{x}.\underline{x}$.

• Case $A \vee A \rightarrow A$

  We need terms $\underline{t}_{\underline{X}''}$ such that:

  $$\begin{aligned} \forall \underline{x},\underline{x}' (A_{HR}(\underline{x}) \vee A_{HR}(\underline{x}') \rightarrow A_{HR}(\underline{t}_{\underline{X}''}\underline{x}\underline{x}')) \end{aligned}$$

  We take $\underline{t}_{\underline{X}''}:=\lambda \underline{x},\underline{x}'.\underline{x}\sqcup \underline{x}'$.

• Case $A \wedge B \rightarrow A$

  We need terms $\underline{t}_{\underline{X}'}$ such that:

  $$\begin{aligned} \forall \underline{x},\underline{u}(A_{HR}(\underline{x}) \wedge B_{HR}(\underline{u}) \rightarrow A_{HR}(\underline{t}_{\underline{X}'}\underline{x}\underline{u})) \end{aligned}$$

  We take $\underline{t}_{\underline{X}'}:=\lambda \underline{x},\underline{u}.\underline{x}$.

• Case $A \rightarrow A \vee B$

  We need terms $\underline{t}_{\underline{X}'},\underline{t}_{\underline{U}}$ such that:

  $$\begin{aligned} \forall \underline{x}(A_{HR}(\underline{x}) \rightarrow A_{HR}(\underline{t}_{\underline{X}'}\underline{x}) \vee B_{HR}(\underline{t}_{\underline{U}}\underline{x})) \end{aligned}$$

  We take $\underline{t}_{\underline{X}'}:= \lambda \underline{x}.\underline{x}$. For $\underline{t}_{\underline{U}}$ we take an arbitrary closed term of adequate type, which exists due to combinatorial completeness and the existence of a constant of type G.

• Case $A \wedge B \rightarrow B \wedge A$

  We need terms $\underline{t}_{\underline{X}'},\underline{t}_{\underline{U}'}$ such that:

  $$\begin{aligned} \forall \underline{x},\underline{u}(A_{HR}(\underline{x}) \wedge B_{HR}(\underline{u}) \rightarrow B_{HR}(\underline{t}_{\underline{U}'}\underline{x}\underline{u}) \wedge A_{HR}(\underline{t}_{\underline{X}'}\underline{x}\underline{u})) \end{aligned}$$

  We take $\underline{t}_{\underline{X}'}:= \lambda \underline{x},\underline{u}.\underline{x}, \quad \underline{t}_{\underline{U}'}:= \lambda \underline{x},\underline{u}.\underline{u}$.

• The case $A \vee B \rightarrow B \vee A$ is analogous to the above.

• Case $\bot \rightarrow A$

  We need terms $\underline{t}_{\underline{x}}$ such that:

  $$\begin{aligned} \bot \rightarrow A_{HR}(\underline{t}_{\underline{x}}) \end{aligned}$$

  We take arbitrary closed $\underline{t}_{\underline{x}}$.

• Case $\forall z\, A \rightarrow A(t)$

  We need terms $\underline{t}_{\underline{X}''}$ such that:

  $$\begin{aligned} \forall \underline{X}' (\forall z\, A_{HR}(z,\underline{X}' z) \rightarrow A_{HR}(t,\underline{t}_{\underline{X}''}\underline{X}')) \end{aligned}$$

  We take $\underline{t}_{\underline{X}''}:=\lambda \underline{X}'.\underline{X}'t$.

• Case $A(t) \rightarrow \exists z\, A$

  We need terms $t_{Z'},\underline{t}_{\underline{X}'}$ such that:

  $$\begin{aligned} \forall \underline{x}(A_{HR}(t,\underline{x}) \rightarrow \exists z\in t_{Z'}\underline{x}\, A_{HR}(z,\underline{t}_{\underline{X}'}\underline{x})) \end{aligned}$$

  We take $t_{Z'}:=\lambda \underline{x}.\{t\}, \quad \underline{t}_{\underline{X}'}:= \lambda \underline{x}.\underline{x}$.

• Case

  

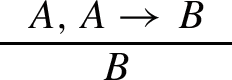
  By induction hypothesis, we obtain closed terms $\underline{t}_{\underline{x}},\underline{t}_{\underline{U}}$ such that:

  $$\begin{aligned} A_{HR}(\underline{t}_{\underline{x}}) \end{aligned}$$
  $$\begin{aligned} \forall \underline{x}(A_{HR}(\underline{x}) \rightarrow B_{HR}(\underline{t}_{\underline{U}}\underline{x})) \end{aligned}$$

  We need terms $\underline{t}_{\underline{u}}$ such that

  $$\begin{aligned} B_{HR}(\underline{t}_{\underline{u}}) \end{aligned}$$

  We take $\underline{t}_{\underline{u}}:= \underline{t}_{\underline{U}}\underline{t}_{\underline{x}}$.

• Case

  

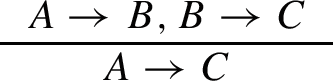
  By induction, we have closed terms $\underline{t}_{\underline{U}},\underline{t}_{\underline{P}}$ such that:

  $$\begin{aligned}{} & {} \forall \underline{x}(A_{HR}(\underline{x}) \rightarrow B_{HR}(\underline{t}_{\underline{U}}\underline{x}))\\{} & {} \forall \underline{u}(B_{HR}(\underline{u}) \rightarrow C_{HR}(\underline{t}_{\underline{P}}\underline{u})) \end{aligned}$$

  We need terms $\underline{s}_{\underline{P}}$ such that:

  $$\begin{aligned} \forall \underline{x}(A_{HR}(\underline{x}) \rightarrow C_{HR}(\underline{s}_{\underline{P}}\underline{x})) \end{aligned}$$

  We take $\underline{s}_{\underline{P}}:= \lambda \underline{x}.\underline{t}_{\underline{P}}(\underline{t}_{\underline{U}}\underline{x})$.

• Cases

  

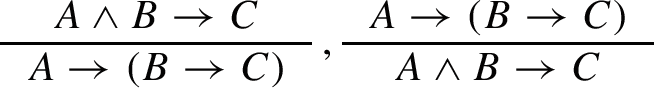
  To realize $A \wedge B \rightarrow C$ we need closed terms $\underline{t}_{\underline{P}}$ such that:

  $$\begin{aligned} \forall \underline{x},\underline{u}(A_{HR}(\underline{x}) \wedge B_{HR}(\underline{u}) \rightarrow C_{HR}(\underline{t}_{\underline{P}}\underline{x}\underline{u})) \end{aligned}$$

  To realize $A \rightarrow (B \rightarrow C)$ we need closed terms $\underline{t}_{\underline{P}}$ such that:

  $$\begin{aligned} \forall \underline{x}(A_{HR}(\underline{x}) \rightarrow \forall \underline{u}(B_{HR}(\underline{u}) \rightarrow C_{HR}(\underline{t}_{\underline{P}}\underline{x}\underline{u}))) \end{aligned}$$

  These two formulas are equivalent in $\textrm{IL}^{\omega }_*$, therefore the terms which realize $A \wedge B \rightarrow C$ are exactly those which realize $A \rightarrow (B \rightarrow C)$.

• Case

  

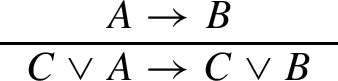
  By induction we have terms $\underline{t}_{\underline{U}}$ such that

  $$\begin{aligned} \forall \underline{x}(A_{HR}(\underline{x}) \rightarrow B_{HR}(\underline{t}_{\underline{U}}\underline{x})) \end{aligned}$$

  We need terms $\underline{t}_{\underline{P}'},\underline{t}_{\underline{U}'}$ such that

  $$\begin{aligned} \forall \underline{p},\underline{x}(C_{HR}(\underline{p}) \vee A_{HR}(\underline{x}) \rightarrow C_{HR}(\underline{t}_{\underline{P}'}\underline{p}\underline{x}) \vee B_{HR}(\underline{t}_{\underline{U}'}\underline{p}\underline{x}) \end{aligned}$$

  We take $\underline{t}_{\underline{P}'}:=\lambda \underline{p},\underline{x}.\underline{p},\quad \underline{t}_{\underline{U}'}:= \lambda \underline{p},\underline{x}.\underline{t}_{\underline{U}}\underline{x}$.

• Case

  

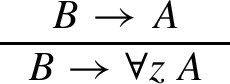
  where z is not free in B By induction, we have terms $\underline{t}_{\underline{X}}$ such that

  $$\begin{aligned} \forall \underline{u}(B_{HR}(\underline{u}) \rightarrow A_{HR}(z,\underline{t}_{\underline{X}}z\underline{u})) \end{aligned}$$

  We need $\underline{s}_{\underline{X}}$ such that

  $$\begin{aligned} \forall \underline{u}(B_{HR}(\underline{u}) \rightarrow \forall z\, A_{HR}(z,\underline{s}_{\underline{X}}\underline{u}z)) \end{aligned}$$

  We take $\underline{s}_{\underline{X}}:= \lambda \underline{u}, z.\underline{t}_{\underline{X}}z\underline{u}$.

• Case

  

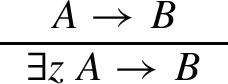
  where z is not free in B

  By induction we have terms $\underline{t}_{\underline{U}}$ such that

  $$\begin{aligned} \forall \underline{x}(A_{HR}(z,\underline{x}) \rightarrow B_{HR}(\underline{t}_{\underline{U}}z\underline{x})) \end{aligned}$$

  We need terms $\underline{s}_{\underline{U}}$ such that

  $$\begin{aligned} \forall z',\underline{x}(\exists z \in z'\, A_{HR}(z,\underline{x}) \rightarrow B_{HR}(\underline{s}_{\underline{U}}z'\underline{x})) \end{aligned}$$

  We take $\underline{s}_{\underline{U}}:= \lambda z',\underline{u}.\bigsqcup _{z\in z'}\underline{t}_{\underline{U}}z\underline{x}$.

• The axioms for $=$, $\Pi$ and $\Sigma$, as well as the axioms for the star types, are $\exists$-free formulas and therefore don’t need terms.

• Case $\forall z\in t\, A (z) \rightarrow \forall z (z \in t \rightarrow A(z))$

  We need terms $\underline{t}_{\underline{X}'}$ such that

  $$\begin{aligned} \forall \underline{x}(\forall z\in t\, A_{HR}(z,\underline{x}) \rightarrow \forall z(z\in t \rightarrow A_{HR}(z,\underline{t}_{\underline{X}'}\underline{x}z))) \end{aligned}$$

  We take $\underline{t}_{\underline{X}'}:= \lambda \underline{x},z.\underline{x}$.

• Case $\forall z\in t\, A (z) \leftarrow \forall z (z \in t \rightarrow A(z))$

  We need terms $\underline{t}_{\underline{X}}$ such that

  $$\begin{aligned} \forall \underline{X}' (\forall z (z\in t \rightarrow A_{HR}(z,\underline{X}'z)) \rightarrow \forall z\in t\, A_{HR}(z,\underline{t}_{\underline{X}}\underline{X}')) \end{aligned}$$

  We take $\underline{t}_{\underline{X}}:= \lambda \underline{X}'.\bigsqcup _{z\in t} \underline{X}'z$.

• Case $\exists z \in t\, A(z) \rightarrow \exists z (z \in t \wedge A(z))$

  We need terms $\underline{t}_{\underline{X}}$ and $t_{Z}$ such that

  $$\begin{aligned} \forall \underline{x}(\exists z \in t \, A_{HR}(z,\underline{x}) \rightarrow \exists z \in t_{Z}\underline{x}(z\in t \wedge A_{HR}(z,\underline{X}\underline{x}))) \end{aligned}$$

  We take $t_{Z}:= \lambda \underline{x}.t,\quad \underline{t}_{\underline{X}}:= \lambda \underline{x}.\underline{x}$.

• Case $\exists z \in t\, A(z) \leftarrow \exists z (z \in t \wedge A(z))$

  We need terms $\underline{t}_{\underline{X}}$ such that

  $$\begin{aligned} \forall z',\underline{x}(\exists z \in z' (z\in t \wedge A_{HR}(z,\underline{x})) \rightarrow \exists z \in t\, A_{HR}(z,\underline{t}_{\underline{X}} z'\underline{x})) \end{aligned}$$

  We take $\underline{t}_{\underline{X}}:= \lambda z',\underline{x}.\underline{x}$.

• Case $\textrm{AC}^{\omega }_*\text {: } \forall z \exists w \,A(z,w) \rightarrow \exists W \forall z \exists w \in Wz \,A(z,w)$

  We need terms $t_{W''}, \underline{t}_{\underline{X}''}$ such that:

  $$\begin{aligned}&\forall W',\underline{X}' (\forall z \exists w \in W'z\, A_{HR}(z,w,\underline{X}'z) \rightarrow \\&\qquad \qquad \qquad \qquad \exists W \in t_{W''}W'\underline{X}' \forall z' \exists w' \in Wz'\, A_{HR}(z',w',\underline{t}_{\underline{X}''}W'\underline{X}'z')) \end{aligned}$$

  We take $t_{W''}:= \lambda W',\underline{X}'.\{W'\}, \quad \underline{t}_{\underline{X}''}:= \lambda W',\underline{X}'.\underline{X}'$.

• Case $\textrm{IP}^*_{\not \exists } \text {: } (A \rightarrow \exists w \,B(w)) \rightarrow \exists z (A \rightarrow \exists w \in z \,B(w))$ where A is an $\exists$-free formula.

  We need terms $t_{Z'},\underline{t}_{\underline{U}}$ such that

  $$\begin{aligned} \forall w',\underline{u}((A \rightarrow \exists w \in w' \, B_{HR}(w,\underline{u})) \rightarrow \exists z \in t_{Z'} w' \underline{u}(A \rightarrow \exists w \in z\, B_{HR}(w,\underline{t}_{\underline{U}} w' \underline{u}))) \end{aligned}$$

  We take $t_{Z'}:= \lambda w',\underline{u}.\{ w' \},\quad \underline{t}_{\underline{U}}:= \lambda w',\underline{u}.\underline{u}$.

• The formulas in $T_{\not \exists }$ verify themselves.

$\square$

Theorem 7

(Characterisation theorem) For any formula A:

$$\begin{aligned} \textrm{IL}^{\omega }_*+ \textrm{AC}^{\omega }_*+ \textrm{IP}^*_{\not \exists } \vdash A \leftrightarrow A^{HR} \end{aligned}$$

Proof

The proof is by induction on the logical structure of the formula. The result is immediate for $\exists$-free formulas. For the induction step, we use the induction hypothesis immediately, for instance, in order to show $A \wedge B \leftrightarrow (A \wedge B)^{HR}$ we show that $A^{HR} \wedge B^{HR} \leftrightarrow (A \wedge B)^{HR}$.

The equivalence for the cases $A \wedge B$, $A \vee B$, $\exists z\, A(z)$ and $\exists z \in t\, A(z)$ is evidently a consequence of the logical rules; for instance, for $A \wedge B$, we just drag the quantifiers inside and outside.

For the remaining cases, the right to left implication is also consequence of the logical rules.

We focus on the reciprocal.

• Case $A \rightarrow B$

  We are going to show that $(\exists \underline{x}\, A_{HR}(\underline{x}) \rightarrow \exists \underline{u}\, B_{HR}(\underline{u}))\rightarrow (\exists \underline{U}'''\forall \underline{x}(A_{HR}(\underline{x}) \rightarrow B_{HR}(\underline{U}'''\underline{x})))$.

  From $\exists \underline{x}\, A_{HR}(\underline{x}) \rightarrow \exists \underline{u}\, B_{HR}(\underline{u})$ we have $\forall \underline{x}(A_{HR}(\underline{x}) \rightarrow \exists \underline{u}\, B_{HR}(\underline{u}))$. Using $\textrm{IP}^*_{\not \exists }$ we obtain $\forall \underline{x}\exists \underline{u}' (A_{HR}(\underline{x}) \rightarrow \exists \underline{u}\in \underline{u}'\, B_{HR}(\underline{u}))$. By monotonicity, we get $\forall \underline{x}\exists \underline{u}' ( A_{HR}(\underline{x}) \rightarrow B_{HR}(\bigsqcup _{\underline{u}\in \underline{u}'}\underline{u}))$, i.e., $\forall \underline{x}\exists \underline{u}'' ( A_{HR}(\underline{x}) \rightarrow B_{HR}(\underline{u}''))$. Applying $\textrm{AC}^{\omega }_*$, we get $\exists \underline{U}'' \forall \underline{x}\exists \underline{u}'' \in \underline{U}''\underline{x}(A_{HR}(\underline{x}) \rightarrow B_{HR}(\underline{u}''))$. By monotonicity, we obtain $\exists \underline{U}'' \forall \underline{x}(A_{HR}(\underline{x}) \rightarrow B_{HR}(\bigsqcup _{\underline{u}'' \in \underline{U}''\underline{x}}\underline{u}''))$, and therefore $\exists \underline{U}'''\forall \underline{x}(A_{HR}(\underline{x}) \rightarrow B_{HR}(\underline{U}'''\underline{x}))$.

• Case $\forall z\, A(z)$

  We are going to show that $\forall z \exists \underline{x}\, A_{HR}(z,\underline{x}) \rightarrow \exists \underline{X}' \forall z\, A_{HR}(z,\underline{X}' z)$.

  From $\forall z \exists \underline{x}\, A_{HR}(z,\underline{x})$, applying $\textrm{AC}^{\omega }_*$ we obtain $\exists \underline{X}\forall z\exists \underline{x}\in \underline{X}z\, A_{HR}(z,\underline{x})$. By monotonicity we have $\exists \underline{X}\forall z\, A_{HR}(z,\bigsqcup _{\underline{x}\in \underline{X}z}\underline{x})$. Thus $\exists \underline{X}' \forall z\, A_{HR}(z,\underline{X}' z)$.

• Case $\forall z\in t\, A(z)$

  We are going to show that $\forall z\in t\exists \underline{x}\, A_{HR}(z,\underline{x}) \rightarrow \exists \underline{x}\forall z\in t\, A_{HR}(z,\underline{x})$.

  Using collection (Lemma 2, involving $\textrm{AC}^{\omega }_*$ and $\textrm{IP}^*_{\not \exists }$), we get $\exists \underline{w}\forall z\in t \exists \underline{x}\in \underline{w}\, A_{HR}(z,\underline{x})$. Take $\underline{x}':=\bigsqcup _{\underline{x}\in \underline{w}}\underline{x}$. Then, by monotonicity, we get $A_{HR}(z,\underline{x}')$ for all $z\in t$.

$\square$

Corollary 1

If

$$\begin{aligned} \textrm{IL}^{\omega }_*+ \textrm{AC}^{\omega }_*+ \textrm{IP}^*_{\not \exists } + T_{\not \exists } \vdash \forall \underline{z}\exists \underline{w}\, A(\underline{z},\underline{w}) \end{aligned}$$

where $\underline{z},\underline{w}$ are the only free variables of A, then there exist closed terms $\underline{r}$ such that

$$\begin{aligned} \textrm{IL}^{\omega }_*+ \textrm{AC}^{\omega }_*+ \textrm{IP}^*_{\not \exists } + T_{\not \exists } \vdash \forall \underline{z}\exists \underline{w}\in \underline{r}\underline{z}\, A(\underline{z},\underline{w}) \end{aligned}$$

Proof

We have:

$$\begin{aligned} (\forall \underline{z}\exists \underline{w}\, A(\underline{z},\underline{w}))^{HR} \equiv \exists \underline{W}', \underline{X}' \forall \underline{z}\exists \underline{w}\in \underline{W}'\underline{z}\, A_{HR}(\underline{z},\underline{w},\underline{X}'\underline{z}) \end{aligned}$$

Using Soundness, we get terms $\underline{t},\underline{r}$ such that, for arbitrary $\underline{z}$

$$\begin{aligned} \exists \underline{w}\in \underline{r}\underline{z}\, A_{HR}(\underline{z},\underline{w},\underline{t}\underline{z}) \end{aligned}$$

thus

$$\begin{aligned} \exists \underline{x}\exists \underline{w}\in \underline{r}\underline{z}\, A_{HR}(\underline{z},\underline{w},\underline{x}) \end{aligned}$$

which is just $(\exists \underline{w}\in \underline{r}\underline{z}\, A(\underline{z},\underline{w}))^{HR}$. By the Characterization Theorem, we obtain $\exists \underline{w}\in \underline{r}\underline{z}\, A(\underline{z},\underline{w})$ for arbitrary $\underline{z}$. $\square$

Corollary 2

If

$$\begin{aligned} \textrm{IL}^{\omega }_*+ \textrm{AC}^{\omega }_*+ \textrm{IP}^*_{\not \exists } + T_{\not \exists } \vdash \forall \underline{z}\exists \underline{w}\, A(\underline{z},\underline{w}) \end{aligned}$$

where A is an $\exists$-free formula whose only free variables are $\underline{z},\underline{w}$, then there exist closed terms $\underline{r}$ such that

$$\begin{aligned} \textrm{IL}^{\omega }_*+ T_{\not \exists } \vdash \forall \underline{z}\exists \underline{w}\in \underline{r}\underline{z}\, A(\underline{z},\underline{w}) \end{aligned}$$

Proof

We have:

$$\begin{aligned} (\forall \underline{z}\exists \underline{w}\, A(\underline{z},\underline{w}))^{HR} \equiv \exists \underline{W}' \forall \underline{z}\exists \underline{w}\in \underline{W}'\underline{z}\, A(\underline{z},\underline{w}) \end{aligned}$$

Using Soundness, we get terms $\underline{r}$ such that

$$\begin{aligned} \textrm{IL}^{\omega }_*+ T_{\not \exists } \vdash \forall \underline{z}\exists \underline{w}\in \underline{r}\underline{z}\, A(\underline{z},\underline{w}) \end{aligned}$$

$\square$

Remark 8

We also have the previous results in the absence of the variables $\underline{z}$. Due to Lemma 1, we conclude the following:

Corollary 3

If

$$\begin{aligned} \textrm{IL}^{\omega }_*+ \textrm{AC}^{\omega }_*+ \textrm{IP}^*_{\not \exists } + T_{\not \exists } \vdash \exists x \, A(x) \end{aligned}$$

where x is the only free variable of A, then there exist closed terms $t_1,\ldots ,t_n$ such that

$$\begin{aligned} \textrm{IL}^{\omega }_*+ \textrm{AC}^{\omega }_*+ \textrm{IP}^*_{\not \exists } + T_{\not \exists } \vdash A(t_1) \vee \ldots \vee A(t_n) \end{aligned}$$

Corollary 4

If

$$\begin{aligned} \textrm{IL}^{\omega }_*+ \textrm{AC}^{\omega }_*+ \textrm{IP}^*_{\not \exists } + T_{\not \exists } \vdash \exists x \, A(x) \end{aligned}$$

where A is an $\exists$-free formula whose only free variable is x, then there exist closed terms $t_1,\ldots ,t_n$ such that

$$\begin{aligned} \textrm{IL}^{\omega }_*+ T_{\not \exists } \vdash A(t_1) \vee \ldots \vee A(t_n) \end{aligned}$$

4 Final notes

4.1 Atomic versus $\exists$-free

The axiom scheme for equality, on page 5, was formulated with A an atomic formula. As is well known, this atomic formulation is enough to ensure we have the result for any formula A within the system. Instead of using atomic formulas, we could have presented the scheme with A an $\exists$-free formula. From our interpretation perspective, the $\exists$-free formulas are still computationally empty.

4.2 The translation of the universal quantification

Note that, in the case of the bounded modified realizability $(\cdot )^{br}$ [7], the translation of the universal quantification needs to be more evolved, namely

$$\begin{aligned} (\forall z A(z))^{br}:\equiv \widetilde{\exists } \underline{X}\widetilde{\forall } a \forall z\le ^* a A_{br}(z,\underline{X}a) \end{aligned}$$

Monotonicity explains this need, because one has to ensure that

$$\begin{aligned} X\le ^* Y \rightarrow Xz\le ^* Yz \end{aligned}$$

which is the case if z is monotone, i.e., if $z\le ^* z$, thus the need to consider monotone majorants a such that $z\le ^* a$. In the case of the herbrand modified realizability we can deal with z itself since

$$\begin{aligned} X \sqsubseteq Y \rightarrow Xz \sqsubseteq Yz \end{aligned}$$

4.3 Herbrand realizability for nonstandard arithmetic

The paper [18] of Benno van den Berg, Eyvind Briseid and Pavol Safarik significantly influenced the work in [6] where the star combinatory calculus (as formulated here) was introduced, alongside a Herbrandized functional interpretation of classical first-order logic. In [18], two functional interpretations for nonstandard arithmetic (intuitionistic and classical) were presented, based on the idea that realizing an external existential quantifier involves exhibiting a finite list of candidates, being the realizer among the elements of such list. Technically, the setting of higher type was extended with types for finite sequences, carrying a structure of preorder (with $x\preceq y$ if every element in the list coded by x also occurs in the list coded by y). The novelty of [6] was that such functional interpretations still work in theories of standard arithmetic and even, for pure logic. Identical parallelism is done in the current work concerning realizability. In [18], a Herbrand realizability was introduced, in the context of nonstandard arithmetic with types for finite lists. Despite the nonstandard setting of [18], the Herbrand realizability makes perfect sense for theories of standard arithmetic and can be developed even in the context of pure logic. Note the challenge that emerges with herbrandized realizability notions or herbrandized functional interpretations in the context of pure logic (as opposed to arithmetic). How to address finite sets when the concept of finiteness itself is not a logical notion? The way out of this situation is the star combinatory calculus. Note also that the way the existential witnesses are accumulated in the present paper differs slightly from the manner they are treated in [18]. For instance, [18] identifies elements of $(\sigma \rightarrow \rho ^\star )^\star$ with elements of $\sigma \rightarrow \rho ^\star$, which we do not. Another difference between the Herbrand realizability in [18] and the present herbrandized modified realizability is that the existentially quantified variables in our context are of end-star type while in [18] are of star type. Further elaboration on the distinction between the formulation in [18] and the treatment based on the star combinatory calculus can be found in [2].

4.4 The star calculus on arithmetic

The possibility of extending the star calculus to the arithmetic setting keeping the strong normalization and the Church–Rosser properties was already discussed in [4] but without proofs of such results. We present here such proofs.

We denote the ground type as N, intending it to represent natural numbers; and we consider the following constants from the language of arithmetic: 0 of type N, S of type $N \rightarrow N$ and $R_{\sigma }$ of type $N \rightarrow \sigma \rightarrow (\sigma \rightarrow N \rightarrow \sigma ) \rightarrow \sigma$. Note that $\sigma$ can be of star type.

We assign the following conversions to the new constants above:

• $R_{\sigma }0qr \rightsquigarrow q$ ($q: \sigma ,\ r: \sigma \rightarrow N \rightarrow \sigma$)

• $R_{\sigma }(St)qr \rightsquigarrow r(Rtqr,t)$ ($t: N,\ q: \sigma ,\ r: \sigma \rightarrow N \rightarrow \sigma$)

We are going to show, adapting the proof in [6] based on Tait’s reducibility technique [14, 15], that the star calculus in the extended (arithmetical) context remains strongly normalizable. First some definitions.

Definition 7

Given a term t of type $\sigma ^*$, we define a finite set of terms of type $\sigma$, the surface elements of t, which we denote by $\textrm{SM}(t)$, by induction on the complexity of t as follows:

• (i) If t is of the form $\mathfrak {s}(q)$ then $\textrm{SM}(t)$ is $\{q\}$;

• (ii) If t is of the form $\cup qr$, then $\textrm{SM}(t)$ is $\textrm{SM}(q) \cup \textrm{SM}(r)$;

• (iii) In any other case, $\textrm{SM}(t)$ is $\emptyset$.

Definition 8

The set ${\textrm{Red}}_{\sigma }$ of the reducible terms of type $\sigma$ is defined recursively in the complexity of the type $\sigma$ as follows:

• (i) $t \in {\textrm{Red}}_N:\equiv$ t is strongly normalizable;

• (ii) $t \in {\textrm{Red}}_{\sigma \rightarrow \tau }:\equiv$ for all q, if $q \in {\textrm{Red}}_{\sigma }$ then $tq \in {\textrm{Red}}_{\tau }$;

• (iii) $t \in {\textrm{Red}}_{\sigma ^*}:\equiv$ t is strongly normalizable and if, for any term obtained by reduction of t, its surface elements are reducible.

The proofs of lemmas 1, 2, 3 and 4 presented in [6] on pages 526–527, are already applicable in the new context. We just recall here the statement of two of those results:

Lemma 3

If $t \in {\textrm{Red}}_{\sigma }$, then t is strongly normalizable;

Lemma 4

If t is a reducible term and $t \succeq q$, then q is reducible.

Theorem 8

All terms in the star combinatory calculus for arithmetic are reducible.

Proof

Following the proof in [6], we only need to show that the arithmetical constants are reducible. It is clear that $0 \in {\textrm{Red}}_N$. We have that if t is a reducible term of type N (i.e., strongly normalizable), then $St \in {\textrm{Red}}_N$. Thus $S \in {\textrm{Red}}_{N \rightarrow N}$.

Following Remark 1, we assume that $\sigma$ is $\sigma _1 \rightarrow \cdots \rightarrow \sigma _n \rightarrow \rho$, with $\rho$ star type or N. We just need to prove that $R_{\sigma }$ is reducible.

Let $t \in {\textrm{Red}}_N, q \in {\textrm{Red}}_\sigma , r \in {\textrm{Red}}_{\sigma \rightarrow N \rightarrow \sigma }$ and $t_1,\ldots , t_n$ with $t_i \in {\textrm{Red}}_{\sigma _i}$. We show that $R tqrt_1\cdots t_n \in {\textrm{Red}}_{\rho }$. Since t is strongly normalizable, there exist finite normal forms of t, which we here denote $t^{(1)},\ldots ,t^{(k)}$. Each $t^{(i)}$ is of the form $S\cdots St^*$ with $\mu _i(t)$ instances of S at the beginning of the term, where $t^*$ is not of the form $St'^*$. We define $\mu (t):=\max _i \mu _i(t)$. The proof is by induction on $\mu (t)$.

For $R tqrt_1\cdots t_n$ with $\mu (t)=0$, we have that any $t'$ obtained by reduction of t is not of the form $St'^*$, therefore we can only apply the conversion of $R_\sigma$ if $t'$ is 0. Thus, in a sequence of one-step reductions of $R tqrt_1\cdots t_n$ we have two cases:

• We do not apply a conversion on R, therefore, as the terms involved are strongly normalizable, $R tqrt_1\cdots t_n$ also is;

• we reach the form $R 0q'r't'_1\cdots t'_n$ with $q \succeq q', r \succeq r', t_i \succeq t'_i$. We have $R 0q'r't'_1\cdots t'_n \succ _1 q't'_1\cdots t'_n \in {\textrm{Red}}_\rho$ (using Lemma 4).

Thus $R tqrt_1\cdots t_n$ with $\mu (t)=0$ is strongly normalizable.

We have $\textrm{SM}(R t'q'r't'_1\cdots t'_n)=\emptyset$. As $q't'_1\cdots t'_n \in {\textrm{Red}}_\rho$, the surface elements of terms obtained by reduction of $q't'_1\cdots t'_n$ are reducible. Thus the surface elements of terms obtained by reduction of $R tqrt_1\cdots t_n$ with $\mu (t)=0$ are reducible.

We assume that $R tqr \in {\textrm{Red}}_\sigma$ for all $t \in {\textrm{Red}}_N$ with $\mu (t) \le m$ and for all $q \in {\textrm{Red}}_\sigma , r \in {\textrm{Red}}_{\sigma \rightarrow N \rightarrow \sigma }$. In a sequence of one-step reductions of $R tqrt_1\cdots t_n$ with $\mu (t)=m+1$ we have 3 cases (here, $q \succeq q', r \succeq r', t_i \succeq t'_i$):

• We do not apply a conversion on R, therefore, as the terms involved are strongly normalizable, $R tqrt_1\cdots t_n$ also is;

• we reach the form $R 0q'r't'_1\cdots t'_n$, case analogous to $\mu (t)=0$

• we reach the form $R (St')q'r't'_1\cdots t'_n$. We have $R (St')q'r't'_1\cdots t'_n \succ _1 r'(R t'q'r',t')t'_1\cdots t'_n \in {\textrm{Red}}_\rho$ since $\mu (t') \le m$ (using lemma 4).

Thus $R tqrt_1\cdots t_n$ with $\mu (t)=m+1$ is strongly normalizable. We have $\textrm{SM}(R t'q'r't'_1\cdots t'_n)=\emptyset$. As $r'(R t'q'r',t')t'_1\cdots t'_n \in {\textrm{Red}}_\rho$, the surface elements of terms obtained by reduction of $r'(R t'q'r',t')t'_1\cdots t'_n$ are reducible. Thus the surface elements of terms obtained by reduction of $R tqrt_1\cdots t_n$ with $\mu (t)=m+1$ are reducible. Therefore $R tqrt_1\cdots t_n \in {\textrm{Red}}_\rho$. We conclude that $R_{\sigma }$ is reducible. $\square$

Corollary 5

The star combinatory calculus on arithmetic has the property of strong normalization.

Theorem 9

The star combinatory calculus on arithmetic has the Church–Rosser property, that is, each term has a unique normal form.

Proof

Since we have the strong normalization property, by Newman’s lemma [16], it is enough to show that if $t_0 \succ _1 t_1$ and $t_0 \succ _1 t_2$, there exists a term $t_3$ such that $t_1 \succeq t_3$ and $t_2 \succeq t_3$ (that is, the calculus is weakly confluent). If the reductions from $t_0$ to $t_1$ and from $t_0$ to $t_2$ involve subterms which do not intersect, we obtain $t_3$ from $t_0$ by applying both conversions.

We focus then on the case where one of the subterms to reduce is included in the other. We note that, for any of the conversions (including the new conversions for the recursor), the resulting terms depend on subterms of the original term, which are not altered. Thus, if $t_1$ is obtained from $t_0$ by the conversion, any other reduction $t_2$ is obtained from $t_0$ by reduction of one of the subterms q. We obtain $t_3$ taking $t_1$ and applying the same reductions for every instances of q in the subterm resulting from the conversion. Then $t_3$ is obtained from $t_2$ applying the same conversion as from $t_0$ to $t_1$.

We illustrate with the following two cases involving R:

• If $t_0 \equiv R(St)qr$, $t_1 \equiv r(Rtqr,t)$, $t_2 \equiv R(St)qr'$ then we take $t_3 \equiv r'(Rtqr',t)$

• If $t_0 \equiv R0qr$, $t_1 \equiv q$, $t_2 \equiv R0q'r$ then we take $t_3 \equiv q'$.

$\square$

Theorem 10

If t is a closed normal term of type N then t is a numeral $\overline{n}$, i.e., it is of the form $S\cdots S0$.

Proof

Closed terms are of the form $at_1\cdots t_m$ where $t_i$ are closed terms and a is a constant. After the proof in [6], we only need to verify if $R_\sigma t_1\cdots t_m$ can be a closed normal term of type N. The only possibility would be $R_\sigma tqrt_1\cdots t_n$ (where $\sigma$ is $\sigma _1 \rightarrow \cdots \rightarrow \sigma _n \rightarrow N$).

By an inductive argument we may suppose that t is a numeral. Therefore $R_\sigma tqrt_1\cdots t_n$ is not normal.

Thus, the recursor does not contribute for the closed normal terms of type N, being those the terms $S\cdots S0$ with a finite (possible zero) number of S’s. $\square$

Theorem 11

If t is a closed normal term of star type $\rho ^*$, then t is set-like and $\textrm{SM}(t)$ is a finite non-empty set of closed normal terms of type $\rho$.

Proof

The proof, by induction on the term t, that t is set-like, i.e., t is of the form $\mathfrak {s}r$ or $\cup t_1t_2$, can be found in [4]. The last assertion of the theorem follows immediately, noticing that: i) $\textrm{SM}(\mathfrak {s}r)=\{r\}$, and being $\mathfrak {s}r$ a closed normal term of type $\rho ^*$, then r has to be a closed normal term of type $\rho$, ii) $\textrm{SM}(\cup t_1t_2)=\textrm{SM}(t_1) \cup \textrm{SM}(t_2)$, following the result by induction hypothesis.

$\square$

The star combinatory calculus within the arithmetic framework was also used in [3, 5] in the context of herbrandized functional interpretations for (respectively classical and semi-intuitionistic) second-order arithmetic.

4.5 Heyting arithmetic $\textrm{HA}^{\omega }_*$

Although the herbrandized modified realizability was introduced in Sect. 3 within the realm of logic, specifically semi-intuitionistic logic, it can also be applied within the Heyting arithmetic context.

With that in view, consider the star combinatory calculus in the language of arithmetic described in Sect. 4.4. Consider also the universal axioms for the successor S and the recursor R (as in [17] or [13]) and the (unrestricted) induction axiom scheme:

• $A(0) \wedge \forall n (A(n)\rightarrow A(Sn)) \rightarrow \forall n\,A(n).$

We denote by $\textrm{HA}^{\omega }_*$ the theory consisting of $\textrm{IL}^{\omega }_*$ (in the language of arithmetic) with the above arithmetical axioms.

The soundness theorem has an arithmetical extension.

Theorem 12

(Soundness, arithmetical extension) Let A be a formula with free variables $\underline{a}$. Let $T_{\not \exists }$ be a set of $\exists$-free formulas. If

$$\begin{aligned} \textrm{HA}^{\omega }_*+ \textrm{AC}^{\omega }_*+ \textrm{IP}^*_{\not \exists } + T_{\not \exists } \vdash A(\underline{a}) \end{aligned}$$

then there exist closed terms $\underline{t}$ such that

$$\begin{aligned} \textrm{HA}^{\omega }_*+T_{\not \exists } \vdash A_{HR}(\underline{a},\underline{t}\underline{a}) \end{aligned}$$

Proof

The axioms for S and R are $\exists$-free formulas and do not require terms.

Consider the axiom scheme $A(0) \wedge \forall n (A(n)\rightarrow A(Sn)) \rightarrow \forall n\,A(n)$.

We need terms $\underline{r}_{\underline{X}'}$ such that:

$$\begin{aligned} \forall \underline{x},\underline{X}(A_{HR}(0,\underline{x}) \wedge \forall n,\underline{x}' (A_{HR}(n,\underline{x}') \rightarrow A_{HR}(Sn,\underline{X}n\underline{x}')) \rightarrow \forall n\, A_{HR}(n,\underline{r}_{\underline{X}'}\underline{x}\underline{X}n)) \end{aligned}$$

Take $\underline{r}_{\underline{X}'}:= \lambda \underline{x},\underline{X},n. Rn\underline{x}\tilde{\underline{X}}$ where $\tilde{\underline{X}}:= \lambda \underline{x},n.\underline{X}n\underline{x}$. Take $\underline{x},\underline{X}$ such that

$$\begin{aligned} A_{HR}(0,\underline{x}) \wedge \forall n,\underline{x}' (A_{HR}(n,\underline{x}') \rightarrow A_{HR}(Sn,\underline{X}n\underline{x}')) \end{aligned}$$

We show that $\forall n\, A_{HR}(n,\underline{r}_{\underline{X}'}\underline{x}\underline{X}n)$ using the induction axiom. First note that $\underline{r}_{\underline{X}'}\underline{x}\underline{X}0 = \underline{x}$. Now assume $A_{HR}(n,\underline{r}_{\underline{X}'}\underline{x}\underline{X}n)$. By the assumption we have $A_{HR}(Sn,\underline{X}n(\underline{r}_{\underline{X}'}\underline{x}\underline{X}n))$. Furthermore, we have:

$$\begin{aligned} \underline{r}_{\underline{X}'}\underline{x}\underline{X}(Sn) = R(Sn)\underline{x}\tilde{\underline{X}} = \tilde{\underline{X}}(Rn\underline{x}\tilde{\underline{X}},n)=\tilde{\underline{X}}(\underline{r}_{\underline{X}'}\underline{x}\underline{X}n,n)=\underline{X}n(\underline{r}_{\underline{X}'}\underline{x}\underline{X}n) \end{aligned}$$

which gives us the result. $\square$