Vector spaces with a union of independent subspaces

Abstract

We study the theory of K-vector spaces with a predicate for the union X of an infinite family of independent subspaces. We show that if K is infinite then the theory is complete and admits quantifier elimination in the language of K-vector spaces with predicates for the n-fold sums of X with itself. If K is finite this is no longer true, but we still have that a natural completion is near-model-complete.

1 Introduction

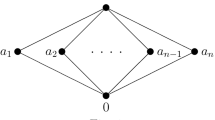
We study the theory $T_K$ of vector spaces over a field K with a predicate X for the union of an infinite family of independent subspaces.

We show (Theorem 3.12) that, if K is infinite, then $T_K$ is complete and admits quantifier elimination in the expansion of the language of vector spaces by predicates for the n-fold sums $X^n$ of X with itself. From this, we deduce its total transcendence (Corollary 3.13). We also investigate (Sect. 4) the case of finite K, where completeness fails and there are completions which do not eliminate quantifiers in the language described above, although they are still near-model-complete in the language of vector spaces together with a predicate for X (Remark 4.2).

We were led to the study of this theory while considering the following question from [4, 5]. Let G be a locally definable connected abelian group in an o-minimal structure, and assume that G is generated by a definable subset. Is G a cover of a definable group? Recall that a group is locally definable iff both its domain and the graph of its multiplication are countable unions of definable sets. A subset A of a locally definable set Z is discrete iff, for every definable $Y\subseteq Z$, the intersection $A\cap Y$ is finite. In the cited papers it is shown that the answer is positive if and only if the following two conditions hold.

• 1. There is a maximal $k\in \omega$ such that G has a discrete subgroup isomorphic to ${\mathbb Z}^k$.

• 2. If G is not already definable, then $k\ne 0$.

By [1] condition 1 is always satisfied, but it remains open whether 2 holds. In fact, outside the o-minimal context, condition 2 might fail: in every model of $T_K$, the locally definable group $(\bigcup _{n\in \omega } X^n, +)$ is definably generated, but it contains no discrete copy of $\mathbb Z$. The case of $\mathbb R^\omega$, made into a model of $T_K$ as in Example 2.3 below, appears as Example 1.11 in [2]. It follows from our results that its theory is totally transcendental.

2 The theory

Definition 2.1

Let K be an infinite field. Let $L_K$ be the union of the language $L_\text {K-vs}:=\{+,0,\lambda \cdot \mid \lambda \in K\}$ of K-vector spaces with the family of unary predicates $\{X^n\mid n\in \omega \}$. Let $T_K$ be the theory axiomatised as follows.

• 1. The reduct to $L_\text {K-vs}$ is a K-vector space.

• 2. The predicate $X:=X^1$ is closed under multiplication by every $\lambda \in K$. In other words, it is a union of subspaces.

• 3. The predicates $X^n$ are interpreted as the n-fold sums $\{{x}_{0}+\ldots +{x}_{n-1}\mid x_j\in X\}$ of X with itself, with the convention that $X^0=\{0\}$.

• 4. The parallelism relation $x\parallel y:=x+y\in X$ is an equivalence relation on $X\setminus \{0\}$; we call the union of an equivalence class with $\{0\}$ an axis.

• 5. There are infinitely many axes.

• 6. The axes are linearly independent: if ${Y}_{0},\ldots ,{Y}_{n}$ are pairwise distinct axes and $a_i\in Y_i\setminus \{0\}$, then ${a}_{0},\ldots ,{a}_{n}$ are linearly independent.

Observe that, by axioms 2 and 4, each axis is a subspace.

Remark 2.2

If V is a K-vector space and $\{V_i\mid i\in I\}$ is an infinite family of independent subspaces, then $(V, \bigcup _{i\in I} V_i)$ is a model of $T_K$, where X is interpreted as $\bigcup _{i\in I} V_i$. Conversely, every model of $T_K$ is of this form, by setting $\{V_i\mid i\in I\}$ to be the family of the axes.

Proof

Left to right: independence ensures that if $x,y,x+y\in \bigcup _{i\in I} V_i$, then there must be $i\in I$ such that $x,y,x+y\in V_i$. From this, it is easily inferred that $\parallel$ is an equivalence relation on $X\setminus \{0\}$, and that the set of axes is precisely $\{V_i\mid i\in I\}$; the remaining axioms are easily checked to hold. Right to left is immediate. $\square$

Example 2.3

The K-vector space $K^\omega$ may be turned into a model of $T_K$ by interpreting X as the set of elements with support of size at most 1; in other words, $f\in X$ iff there is at most one $n\in \omega$ such that $f(n)\ne 0$. The axes are precisely the sets $V_i=\{f\in K^\omega \mid \forall j\in \omega \; f(j)\ne 0\rightarrow j=i\}$. Observe that the subspace $\bigcup _{n\in \omega } X^n$ of finite support elements is the direct sum of the $V_i$, while $K^\omega$ is their direct product.

Notation 2.4

We denote by M a model of $T_K$. For $A\subseteq M$, we will write $\mathcal {F}(A)$ for the intersection of A with the $\bigvee$-definable subspace $\bigcup _{n\in \omega } X^n(M)$. The subspace generated by a subset B of a vector space will be denoted by $\langle B\rangle$. If a is a tuple, for instance $a\in M^{n}$, we denote its coordinates by using subscripts, starting at 0, so $a=({a}_{0},\ldots ,{a}_{n-1})$, and its length (in this example, n) by $\left|a\right|$. In order to avoid confusion, we write indices of a sequence of tuples as superscripts, as in ${a}^{0},\ldots ,{a}^{\ell }\in M^n$. If a is a tuple, by $\langle a\rangle$ we mean $\langle \{a_i\mid i<\left|a\right|\}\rangle$. All tuples we consider have finite length.

Observe that X(M) is the union of the axes of M, and that each axis is definable with parameters. We sometimes write X, $X^n$ in place of X(M), $X^n(M)$ if M is clear from context. While theories of pure vector spaces are known to be strongly minimal, and in particular stable, expanding them by an arbitrary unary predicate may destroy stability, and in fact even result in a theory with the independence property, see [3]. Nevertheless, this is not the case for $T_K$, whose models are in fact easily classified.

Theorem 2.5

For every ordinal $\alpha$ such that $\left|K\right|\le \aleph _\alpha$, there are at most $2^{\aleph _0+\left|\alpha \right|}$ models of $T_K$ of size $\aleph _\alpha$. In particular, (every completion of) $T_K$ is superstable.

Proof

Each $M\vDash T_K$ of size $\aleph _\alpha$ is determined up to isomorphism by ${\text {codim}}(\mathcal {F}(M))$ and, for each positive cardinal $\kappa \le \aleph _\alpha$, the number of $\kappa$-dimensional axes of M. This information can be coded by a function from $\omega +\alpha$ to itself, and superstability follows by [6, Theorem VIII.2.1]. $\square$

3 Infinite fields

In this section, K is an infinite field. We prove quantifier elimination for $T_K$, from which completeness and total transcendence will readily follow.

Remark 3.1

If $a\in X^n\setminus X^{n-1}$, there is a unique n-element set ${\text {supp}}(a):=\{{m}_{0},\ldots ,{m}_{n-1}\}$ of pairwise nonparallel elements of $X\setminus \{0\}$ with $a={m}_{0}+\ldots +{m}_{n-1}$. Call it the support of a.

Definition 3.2

Fix $M\vDash T_K$.

• 1. The collection of axes of M is denoted by ${{\,\textrm{axes}\,}}(M)$.

• 2. If $a\in \mathcal {F}(M)$ and $Y\in {{\,\textrm{axes}\,}}(M)$, we define the projection $\pi _Y(a)$ to be the unique element of ${{\,\textrm{supp}\,}}(a)$ in Y if one exists, and 0 otherwise.

• 3. If $a\in \mathcal {F}(M)$, we define ${{\,\textrm{axes}\,}}(a)$ to be $\{Y\in {{\,\textrm{axes}\,}}(M)\mid \pi _Y(a)\ne 0\}$.

• 4. If $a\in \mathcal {F}(M)$, we define the weight w(a) of a to be the cardinality $\left|{{\,\textrm{axes}\,}}(a)\right|=\left|{{\,\textrm{supp}\,}}(a)\right|$.

• 5. Similarly, for $A\subseteq \mathcal {F}(M)$, we define ${{\,\textrm{axes}\,}}(A)$ to be the set $\bigcup _{a\in A} {{\,\textrm{axes}\,}}(a) = \{Y\in {{\,\textrm{axes}\,}}(M)\mid \pi _Y(A)\ne \{0\}\}$ and define the weight $w(A)$ of A as the cardinality $\left|{{\,\textrm{axes}\,}}(A)\right|$.

• 6. If $A\subseteq \mathcal {F}(M)$ we define $\hat{A}:=\langle \{\pi _Y(A)\mid Y\in {{\,\textrm{axes}\,}}(A)\}\rangle$.

Remark 3.3

The following facts will be used without explicit mention.

• 1. If $a\in X^n$ there are at most n axes Y with $\pi _Y(a)\ne 0$. In other words, $w(a)\le n$.

• 2. For $a\in M$ and $\lambda \in K\setminus \{0\}$, we have ${{\,\textrm{axes}\,}}(a) = {{\,\textrm{axes}\,}}(\lambda a)$.

• 3. We have ${{\,\textrm{axes}\,}}(\lambda _0 a_0 + \cdots + \lambda _{n} a_{n}) \subseteq \bigcup _{i \le n} {{\,\textrm{axes}\,}}(a_i)$, and the equality holds if the supports of $\lambda _0 a_0, \ldots , \lambda _n a_{n}$ are disjoint.

• 4. For every $a,b\in \mathcal F(M)\setminus \{0\}$, there can be at most w(b) many $\lambda \in K$ such that ${{\,\textrm{supp}\,}}(a)\cap {{\,\textrm{supp}\,}}(\lambda b)\ne \emptyset$. It follows that, if K is infinite, $a\in \mathcal {F} (M)$, and $S\subseteq X$ is a finite set, then there is $\lambda \in K$ such that the support of $\lambda a$ is disjoint from S.

• 5. If $A_0, A_1$ are subspaces of $\mathcal {F} (M)$, then ${{\,\textrm{axes}\,}}(A_0+A_1) = {{\,\textrm{axes}\,}}(A_0) \cup {{\,\textrm{axes}\,}}(A_1)$.

• 6. Clearly, $A\subseteq \hat{A}$ always holds.

• 7. If $A\subseteq \mathcal {F}(M)$ is a subspace, then $\hat{A}=\bigoplus _{Y\in {{\,\textrm{axes}\,}}(A)}\pi _Y(A)$.

Lemma 3.4

Let K be an infinite field. For every finite-dimensional subspace $A\subseteq \mathcal {F}(M)$ there is $a_\dagger \in A$ such that ${{\,\textrm{axes}\,}}(A)={{\,\textrm{axes}\,}}(a_\dagger )$. In particular, $w(A)=\max _{a\in A} w(a)$, and $w(A)=n\in \omega$ if and only if $A\subseteq X^n$ and .

Proof

Since K is infinite, point 4 of Remark 3.3 above tells us that for every $a,b\in A$ there is $\lambda \ne 0$ such that ${{\,\textrm{supp}\,}}(a)\cap {{\,\textrm{supp}\,}}(\lambda b)=\emptyset$, from which we deduce that ${{\,\textrm{axes}\,}}(a-\lambda b)={{\,\textrm{axes}\,}}(a)\cup {{\,\textrm{axes}\,}}(b)={{\,\textrm{axes}\,}}({\langle \{a,b\}\rangle })$. The conclusion then follows by induction on $\dim A$. $\square$

The assumption that K is infinite cannot be removed, see Proposition 4.1.

Lemma 3.5

The following statements hold.

• 1. Every finite-dimensional subspace of $\mathcal {F}(M)$ is contained in some $X^n(M)$.

• 2. If A is a finite-dimensional subspace of $\mathcal F(M)$, then so is $\hat{A}$, and ${{\,\textrm{axes}\,}}(A) = {{\,\textrm{axes}\,}}(\hat{A})$. Moreover, for all axes Y, we have $\pi _Y(A) = \pi _Y(\hat{A})$.

Proof

If $A\subseteq M$ is a finite dimensional subspace, then A has nonzero projection only on finitely many axes $Y_0, \ldots , Y_{n-1}$, and $\pi _{Y_i}(A)$ has finite dimension for each $i< n$, so also $\hat{A} = \bigoplus _{i< n} \pi _{Y_i}(A)$ has finite dimension. Moreover, $\pi _{Y_i}(A) \subseteq X$, so $A \subseteq \hat{A} \subseteq X^n$. The rest is clear.$\square$

Below, we consider the bilinear map $\cdot :K^n\times M^n\rightarrow M$ defined as $\lambda \cdot a:=\sum _{i< \left|a\right|} \lambda _i a_i$.

Definition 3.6

Let $a=({a}_{0},\ldots ,{a}_{\left|a\right|-1})$ be a tuple from M.

• 1. We set ${a}^*:K^{\left|a\right|}\rightarrow M$ to be the linear function $\lambda \mapsto \lambda \cdot a$.

• 2. If $W\subseteq K^{\left|a\right|}$, let $W\cdot a :=\{\lambda \cdot a \mid \lambda \in W \} = a^*(W)$.

• 3. If $\langle a\rangle \subseteq \mathcal {F}(M)$, let $g_a$ be the function from the family of subspaces of $K^{\left|a\right|}$ to $\omega$ with

  $$\begin{aligned} g_a(W)=\left|\{Y\in {{\,\textrm{axes}\,}}(\langle a\rangle )\mid W=\ker \pi _Y\circ {a}^*\}\right| \end{aligned}$$

Observe that, by definition, $g_a(W)$ is at most $w(\langle a\rangle )$.

Remark 3.7

We have $W \subseteq \ker \pi _Y\circ {a}^*$ if and only if $Y\not \in {{\,\textrm{axes}\,}}(W \cdot a)$. If we also have, for all $\lambda \in K^{\left|a\right|} \setminus W$, that $Y \in {{\,\textrm{axes}\,}}(\lambda \cdot a)$, then $W = \ker \pi _Y\circ {a}^*$. Finally, note that if $Y \not \in {{\,\textrm{axes}\,}}(\langle a\rangle )$, then $\ker \pi _Y\circ {a}^* = K^{\left|a\right|}$, so $\ker \pi _Y \circ {a}^*$ is interesting only when $Y\in {{\,\textrm{axes}\,}}(\langle a\rangle )$.

Lemma 3.8

Suppose that a is a tuple with $\langle a\rangle \subseteq \mathcal F(M)$, and let W be a subspace of $K^{\left|a\right|}$. Then $g_a(W)\ge r$ if and only, if for every finite set $\{{\lambda }^{0},\ldots ,{\lambda }^{\ell }\}\subseteq K^{\left|a\right|}\setminus W$,

$$\begin{aligned} \left|\left( \bigcap _{i\le \ell } {{\,\textrm{axes}\,}}(\lambda ^i\cdot a)\right) \setminus {{\,\textrm{axes}\,}}(W \cdot a)\right|\ge r \end{aligned}$$

(*)

In other words, (*) says there are at least r axes ${Y}_{0},\ldots ,{Y}_{r-1}$ such that for each $j<r$ we have $W\subseteq \ker (\pi _{Y_j}\circ {a}^*)$ and for every $i\le \ell$ we have $\lambda ^i\notin \ker (\pi _{Y_j}\circ {a}^*)$.

Proof

If $W=\ker \pi _Y\circ {a}^*$ and $\lambda \in K^{\left|a\right|}\setminus W$, then Y is an axis of $\lambda \cdot a$ but not of $W \cdot a$. It follows that $g_a(W)\ge r\Longrightarrow$ (*). For the opposite implication we observe that, since $\left|{{\,\textrm{axes}\,}}(\langle a\rangle )\right|$ is finite, there are $\lambda ^0, \ldots , \lambda ^{\ell } \in K^{\left|a\right|} \setminus W$ such that $\bigcap _{i \le \ell } {{\,\textrm{axes}\,}}(\lambda ^i \cdot a) = \bigcap _{\lambda \in K^{\left|a\right|} \setminus W} {{\,\textrm{axes}\,}}(\lambda \cdot a)$. It follows that (*) implies the existence of pairwise distinct axes ${Y}_{0},\ldots ,{Y}_{r-1}\notin {{\,\textrm{axes}\,}}(W \cdot a)$ such that $Y_i\in \bigcap _{\lambda \in K^{\left|a\right|}\setminus W} {{\,\textrm{axes}\,}}(\lambda \cdot a)$, hence such that $W= \ker \pi _{Y_i}\circ {a}^*$.$\square$

Lemma 3.9

If $\langle a\rangle \subseteq \mathcal {F}(M)$, then the quantifier-free type ${{\,\textrm{qftp}\,}}(a)$ of a determines $g_a$.

Proof

An inspection of the language $L_K$ shows that knowing ${{\,\textrm{qftp}\,}}(a)$ amounts precisely to knowing which linear combinations $\lambda \cdot a$ lie in which $X^n$. Because we are assuming $\langle a\rangle \subseteq \mathcal {F}(M)$, this is the same as knowing all weights $w(\lambda \cdot a)$. Now let $W\subseteq K^{\left|a\right|}$ be a subspace. Since K is infinite, by Lemma 3.4 there is $\lambda \in W$ such that $w(W\cdot a)=w(\lambda \cdot a)$. If $a \equiv ^{\textrm{qf}}b$, then $w(\lambda \cdot a) = w(\lambda \cdot b) \le w(W \cdot b)$, so $w(W\cdot a) \le w(W\cdot b)$ and by symmetry $w(W \cdot a) = w(W \cdot b)$. We have thus proved that ${{\,\textrm{qftp}\,}}(a)$ determines the function sending a subspace $W\subseteq K^{\left|a\right|}$ to $w(W \cdot a)$.

If $W_0, W_1$ are subspaces of $K^{\left|a\right|}$, then ${{\,\textrm{axes}\,}}((W_0+W_1)\cdot a)={{\,\textrm{axes}\,}}(W_0 \cdot a)\cup {{\,\textrm{axes}\,}}(W_1 \cdot a)$. Therefore, for every $W\subseteq K^{\left|a\right|}$ and every $\lambda ^0,\ldots ,\lambda ^\ell \in K^{\left|a\right|}\setminus W$, we have

$$\begin{aligned} \left| \left( \bigcup _{i\le \ell } {{\,\textrm{axes}\,}}(\lambda ^i\cdot a)\right) \setminus {{\,\textrm{axes}\,}}(W \cdot a) \right|= w(\langle W\cup \{\lambda ^0,\ldots ,\lambda ^\ell \}\rangle \cdot a)-w(W \cdot a) \end{aligned}$$

By using induction and the inclusion–exclusion principle, it follows that ${{\,\textrm{qftp}\,}}(a)$ also determines, for every subspace $W\subseteq K^{\left|a\right|}$, every finite $\{\lambda ^0,\ldots ,\lambda ^\ell \}\subseteq K^{\left|a\right|}\setminus W$, and every $r\in \omega$, whether condition (*) in Lemma 3.8 holds or not. By the aforementioned lemma, this information in turn determines $g_a$. $\square$

Proposition 3.10

Let $a = (a_0, \ldots , a_{n-1})$ and $b = (b_0, \ldots , b_{n-1})$ be tuples of the same length from $M,N\vDash T_K$ respectively, and denote by A and B the respective generated subspaces. Assume $a\equiv ^{\textrm{qf}}b$, $A\subseteq \mathcal {F}(M)$, and $B\subseteq \mathcal F(N)$. Then the map $a_i\mapsto b_i$ extends to an isomorphism $\hat{A}\rightarrow \hat{B}$.

Proof

Since $a\equiv ^{\textrm{qf}}b$, by Lemma 3.4 we have $w(A)=w(B)$. Observe that

$$\begin{aligned} \hat{A}:=\langle \{\pi _{Y}(\lambda \cdot a)\mid Y\in {{\,\textrm{axes}\,}}(A), \lambda \in K^{\left|a\right|}\}\rangle \end{aligned}$$

and similarly for $\hat{B}$. By Lemma 3.9 we have $g_a=g_b$, hence for each subspace W of $K^{\left|a\right|}$ there is a bijection between the set of axes Y of A with $\ker \pi _Y \circ {a}^* = W$ and the set of axes Z of B with $\ker \pi _Z \circ {b}^* = W$. Putting together these bijections as W varies, we obtain a bijection $\sigma :{{\,\textrm{axes}\,}}(A)\rightarrow {{\,\textrm{axes}\,}}(B)$ with $\ker \pi _Y \circ {a}^* = \ker \pi _{\sigma (Y)} \circ {b}^*$. This implies that the map $\pi _{Y}(\lambda \cdot a)\mapsto \pi _{\sigma (Y)}(\lambda \cdot b)$ is well-defined; let $h:\hat{A}\rightarrow \hat{B}$ be its linear extension. By construction, each restriction $h\upharpoonright \pi _Y(\hat{A})$ is an isomorphism onto $\pi _{\sigma (Y)}(\hat{B})$, and since $\hat{A}=\bigoplus _{Y\in {{\,\textrm{axes}\,}}(A)} \pi _Y(\hat{A})$ and $\hat{B}=\bigoplus _{Y\in {{\,\textrm{axes}\,}}(A)}\pi _{\sigma (Y)}(\hat{B})$, the map h is an isomorphism. Moreover, each coordinate $a_i$ of a is the sum of its projections on the axes of A, and analogously for B. Let us also observe that if $\lambda \in K^{\left|a\right|}$ is the i-th vector of the standard base, then $a_i = \lambda \cdot a$ and $b_i = \lambda \cdot b$. Hence h extends $a_i\mapsto b_i$ and we are done. $\square$

Lemma 3.11

In every $\omega$-saturated $N\vDash T_K$, every axis is infinite-dimensional, and the codimension of $\mathcal {F}(N)$ is infinite.

Proof

Both statements are proven by easy compactness arguments, the first one using that every axis is infinite, and the second one using that there are infinitely many axes. $\square$

Theorem 3.12

For every infinite K, the theory $T_K$ eliminates quantifiers in $L_K$ and is complete.

Proof

The vector space $\{0\}$, with 0 in every $X^n$, is a substructure embedding in every $M\vDash T_K$, hence completeness is a consequence of quantifier elimination and it suffices to prove the latter. To this end, we show that if $M, N\vDash T_K$ are $\omega$-saturated, then the family of partial isomorphisms between finitely generated substructures A of M and B of N has the back-and-forth property.

Let $f:A\rightarrow B$ be a partial isomorphism as above, and let $a\in M\setminus A$. We need to extend f to an isomorphism of finitely generated substructures which includes a in its domain.

To this aim fix a complement $\mathcal {I}(A)$ of $\mathcal {F}(A)$ in A, observe that $\mathcal {I}(A)\cap \mathcal {F}(M)=\{0\}$, and let $\mathcal {I} (M)$ be a complement of $\mathcal {F} (M)$ which includes $\mathcal {I} (A)$. Then let $\mathcal {I}(B):=f(\mathcal {I}(A))$ and let $\mathcal {I} (N)$ be a complement of $\mathcal {F} (N)$ which includes $\mathcal {I} (B)$.

It suffices to deal with the cases $a \in \mathcal {I} (M)$ and $a \in \mathcal {F} (M)$.

Suppose first that $a\in \mathcal {I} (M)$. By Lemma 3.11 the codimension of $\mathcal {F} (N)$ in N is infinite, so we can choose $b\in \mathcal {I} (N) \setminus \mathcal {I}(B)$ and extend $f:A\rightarrow B$ to a linear map which sends a to b. This yields the required isomorphism since $\mathcal {F} (\langle A \cup \{a\}\rangle ) = \mathcal {F} (A)$ and $\mathcal {F} (\langle B \cup \{b\}\rangle ) = \mathcal {F} (B)$.

Now suppose that $a\in \mathcal {F} (M)$. By Proposition 3.10, we may extend f to an isomorphism

$$\begin{aligned} \hat{f}:\widehat{\mathcal {F}(A)}\oplus \mathcal {I}(A)\rightarrow \widehat{\mathcal {F}(B)}\oplus \mathcal {I}(B) \end{aligned}$$

so we can assume that $a\in \mathcal {F} (M) \setminus \widehat{\mathcal {F} (A)}$. Write a as the sum of the elements of its support, that is $a=\sum _{i<w(a)} m_i$, with each $m_i\in X(M)$ and if $i\ne j$. It is enough to extend the isomorphism $\hat{f}$ to the elements $m_i$, so we may assume that $a \in X(M)$ and $a\not \in \widehat{\mathcal {F} (A)}$. Since $a\in X(M)\setminus \{0\}$, the set ${{\,\textrm{axes}\,}}(a)$ has a unique element; call it Y. We distinguish two cases.

Suppose $Y \in {{\,\textrm{axes}\,}}(\mathcal {F} (A))$. Then there is $c\in X(M) \cap \widehat{\mathcal {F} (A)}$ such that $a\parallel c$. By Lemma 3.11 each axis of N has infinite dimension, so we may find $b \in X(N)\setminus \widehat{\mathcal {F}(B)}$ such that $b \parallel \hat{f}(c)$ and we extend the isomorphism by sending a to b.

Suppose now that $Y\not \in {{\,\textrm{axes}\,}}(\mathcal {F} (A))$. The axioms of $T_K$ ensure that N has infinitely many axes, hence we may find $b \in X(N)$ such that $b\not \in {{\,\textrm{axes}\,}}(\mathcal {F} (B))$ and we extend the isomorphism by sending a to b. $\square$

Corollary 3.13

For every infinite field K, the theory $T_K$ is totally transcendental.

Proof

It is well-known that a theory is totally transcendental if and only if each of its reducts to a countable sublanguage is $\omega$-stable. Therefore, it suffices to prove that, if K is countably infinite and $M\vDash T_K$ is countable, then so is $S_1(M)$. By quantifier elimination and the axioms of $T_K$, every $p(x)\in S_1(M)$ is determined by boolean combinations of formulas of the form $x-m\in X^n$, for $m\in M$ and $n\in \omega$ (when $n=0$, this is the same as $x-m=0$).

Clearly, there is a unique 1-type extending $\{x-m\notin X^n\mid n\in \omega , m\in M\}$. It is therefore enough to count those p(x) containing, for some $n\in \omega$ and $m\in M$, the formula $x-m\in X^n$. Since each $h_m:=y\mapsto y-m$ is a definable bijection, and because there are only countably many $h_m$, up to translating we may assume that $p(x)\vdash x\in X^n$ and that n is minimal such, that is, for all $m\in M$ and $n_0<n$ we have $p(x)\vdash x-m\notin X^{n_0}$. In other words, it suffices to show that, for each $n\in \omega$, there are only countably many types p(x) such that $p(x)\vdash \{x\in X^n\}\cup \{x-m\notin X^{n_0}\mid n_0<n\}$.

Let p, n be as above. If $n=0$, then $p(x)\vdash x=0$. For $n=1$, we argue as follows. Let $m\in X(M)\setminus \{0\}$, and let Y be the corresponding axis; view it as a definable set, defined by $(x\in X)\wedge (x+m\in X)$. Again by quantifier elimination, the structure induced on Y is that of a pure K-vector space, and Y is stably embedded because $T_K$ is stable by Theorem 2.5. Hence, Y is a strongly minimal set, and there is a unique nonrealised type concentrating on Y, call it $p_Y$. Since M is countable, there are only countably many axes in M, hence only countably many such $p_Y$. Now, for a type p(x) satisfying the assumptions above with $n=1$, there are only two possibilities: either there is $Y\in {{\,\textrm{axes}\,}}(M)$ such that $p=p_Y$, or p is the uniquely determined type of an element of X in a new axis; more precisely, this is the unique type as above which furthermore satisfies $p(x)\vdash \{x+m\notin X\mid m\in X(M)\}$; call it $p_{\textrm{na}}$.

For $n\ge 2$, in some monster model $\mathfrak U\vDash T_K$, fix $a\vDash p$, and write $a={a}_{0}+\ldots +{a}_{n-1}$ as the sum of the elements in its support. Minimality of n implies that, for each $i<n$, either there is $Y_i\in {{\,\textrm{axes}\,}}(M)$ such that $a_i\vDash p_{Y_i}$, or $a_i\vDash p_{\textrm{na}}$. Up to a permutation of the coordinates we may assume that, for a suitable $k<n$, the first case happens for $i<k$, and the second one for $k\le i <n$. Again by quantifier elimination, there is a unique n-type q(y) such that . Because there are only countably many axes in M, there are only countably many choices for such a q(y). Since p(x) is the pushforward of q(y) along the definable function $y\mapsto \sum _{i<n}y_i$, it is uniquely determined by q. $\square$

4 The finite field case

If K is finite, then the number of axes of a given dimension becomes first-order expressible, hence $T_K$ is incomplete. Since there is a structure that embeds in every model of $T_K$, namely the vector space $\{0\}$ with 0 belonging to every $X^n$, it follows that $T_K$ cannot eliminate quantifiers in $L_K$. A natural completion to consider is $T_{K,\infty }$, obtained by requiring that every axis is infinite-dimensional. Even $T_{K,\infty }$ does not eliminate quantifiers in $L_K$, since the conclusion of Lemma 3.4 fails, as shown below.

Proposition 4.1

If K is finite and $M\vDash T_{K,\infty }$, there are $a,b\in M^2$ with $a\equiv ^{\textrm{qf}}b$, with both subspaces $\langle a\rangle$ and $\langle b\rangle$ included in $X^{\left|K\right|}(M)$, but with $w(\langle a\rangle )=\left|K\right|<\left|K\right|+1= w(\langle b\rangle )$.

Proof

For every $i<\left|K\right|$, choose linearly independent $m_i\parallel m_i'$ in X in such a way that if $i\ne j$ then . Choose $m\in X$ with , fix an enumeration $(\lambda _i)_{1\le i\le \left|K\right|-1}$ of $K\setminus \{0\}$, and set

$$\begin{aligned} a_0:=\sum _{i< \left|K\right|}m_i \qquad a_1:=\sum _{i< \left|K\right|}m_i'\qquad b_0:=a_0 \qquad b_1:=m+\sum _{1\le i< \left|K\right|-1}\lambda _i m_i \end{aligned}$$

Let $a=(a_0, a_1)$ and $b=(b_0, b_1)$. By definition, for $x\in \{a,b\}$, we have $w(x_0)=w(x_1)=\left|K\right|$. Moreover, an easy computation shows that, for every $\lambda ,\mu \in K\setminus \{0\}$, we have $w(\lambda x_0+\mu x_1)=\left|K\right|$, and it follows that $\langle a\rangle , \langle b\rangle \subseteq X^{\left|K\right|}$, hence that $a\equiv ^{\textrm{qf}}b$. Nevertheless, by construction ${{\,\textrm{axes}\,}}(\langle a\rangle )=\{{{\,\textrm{axes}\,}}(m_i)\mid i<\left|K\right|\}$, while ${{\,\textrm{axes}\,}}(\langle b\rangle )={{\,\textrm{axes}\,}}(\langle a\rangle )\cup {{\,\textrm{axes}\,}}(m)$, and since m and the $m_i$ are all in X we have $w(\langle a\rangle )=\left|K\right|<\left|K\right|+1=w(\langle b\rangle )$. $\square$

Remark 4.2

For finite K, the proof of Theorem 3.12 may be adapted to prove quantifier elimination for $T_{K, \infty }$ in the expansion of $L_K$ by predicates $P_{k,n,i}({a}_{0},\ldots ,{a}_{k})$ such that, if $A:=\langle {a}_{0},\ldots ,{a}_{k}\rangle \subseteq X^n$, then $P_{k,n,i}$ codes the isomorphism type of $\hat{A}$ (with i ranging over the possible isomorphism types). These predicates are $\exists$-definable in $L_K$, and in fact already in $L_\text {K-vs}\cup \{X\}$ hence, in this language, $T_{K, \infty }$ is near-model-complete, that is, every formula is equivalent to a boolean combination of existential ones.