1 Introduction

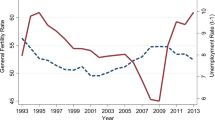
During the last four decades, researchers have observed an increase of the mean age at birth in developed economies (e.g. Frejka and Sardon 2006; see also Fig. 1).Footnote 1 Despite the plethora of studies that incorporate endogenous fertility in models of economic growth (e.g. Galor and Weil 2000; Blackburn and Cipriani 2002; de la Croix and Doepke 2009; Vogl 2016; Strulik 2017; Futagami and Konishi 2019), only a limited number of studies have explicitly considered issues pertaining to the timing of childbearing (Iyigun, 2000; Momota and Horii 2013; d’Albis et al. 2018). In this study, we take explicit account of the timing of childbearing in order to enrich our understanding of the factors that cause its delay. We show that, by accounting for factors that have so far eluded the attention of the aforementioned literature, we can uncover empirically observed patterns in the dynamics of cohort fertility rates, both analytically and quantitatively. In this respect, our framework can facilitate a more accurate design of policies aimed at the economic impact of demographic change (e.g. population ageing).

Fig. 1
figure 1

Increasing mean age at birth in recent decades

Full size image

Since the latter parts of the twentieth century, some developed countries witnessed a moderate, but also persistent, increase in their total fertility rate (TFR) known as the ‘fertility rebound’ (Luci-Greulich and Thévenon 2014).Footnote 2 For some researchers, this marked the end of low fertility rates (e.g. Goldstein et al. 2009)—an outcome with significant socio-economic implications, since it occurred in countries with below-replacement fertility rates. Although the TFR increase has been modest, the cumulative impact could have significant repercussions by alleviating the strain that population ageing imposes, and will continue to impose, on social security systems and on national healthcare services. Nevertheless, in light of the delay in childbearing, and given the methodology used to measure the TFR, one could argue that the observed reversal in fertility trends may, at the outset, reflect a mere tempo adjustment: the initial stages of childbearing postponement cause a notable drop in the TFR measurement, but as higher birth rates eventually materialise at older reproductive ages, the TFR adjusts upwards.

Obviously, if the fertility rebound is just a figment of the TFR measurement in an environment of postponed childbearing, then any attempt to delve deeper into its underlying characteristics and its potential implications seems of rather limited interest. Is it a mere statistical correction though? A look at Fig. 2, which depicts data on completed cohort fertility (CCF)—a measure which, compared to TFR, reflects the intertemporal elements of fertility choice more accurately—reveals that this is not always the case.Footnote 3 While Japan and South European countries have seen successive generations of birth cohorts bearing fewer children on average, other developed nations, e.g. USA, Canada, Nordic countries, and Northwestern European countries, have either already experienced increased fertility from several successive generations of birth cohorts, or seem to be entering a similar phase of demographic change. For these countries, the tempo effect of delayed childbearing seems to have coincided with an actual quantum effect of increased overall childbearing. Put differently, for some countries, and for a significant number of successive cohorts, the increase in the number of births at older reproductive ages was more pronounced than the decrease in the number of births at younger reproductive ages, thus leading to an actual increase in cohort fertility. This outcome has also been pointed out by Andersson et al. (2009) whose empirical analysis led them to the conclusion that ‘fertility postponement does not always imply fewer children’ (Andersson et al. 2009; p.325).

Fig. 2
figure 2

The evolution of completed cohort fertility (CCF)

Full size image

Motivated by these facts, our study aims to present a model that is consistent with the aforementioned trends in the timing of childbearing and the dynamics of cohort fertility. It emphasises and formalises the idea that, for a reversal towards higher cohort fertility to emerge, factors that have a direct impact on childbearing preferences (e.g. cultural change, medical advances, family-related policies) must complement economic factors (e.g. the return to education)— and be sufficiently strong as well— in contributing to the postponement of parenthood as the economy grows. When these conditions do apply, then a rebound of cohort fertility is a genuine change in demographic trends, rather than a mere statistical correction.

To motivate our approach even further, consider the 2020 Inglehart-Welzel world cultural map, which distinguishes groups of countries whose populations’ cultural profiles are open to more progressive changes, from groups of countries whose populations’ cultural profiles are more rigidly attached to traditional values.Footnote 4 Based on this, the 2020 Inglehart-Welzel index of secular-rational vs traditional values gives a numerical score, with higher values indicating a greater degree of cultural openness (as opposed to cultural rigidity). In Table 1, we report these scores for the groups of countries whose data we use in Fig. 2a–c. Computing the average across each group, we observe that Nordic countries display a greater degree of cultural openness than the groups of countries whose demographic data are displayed in Fig. 2b and c. What is particularly interesting from the combined reading of Fig. 2a–c and Table 1 is that the CCF rebound is more pronounced in countries with a high degree of cultural openness, whereas countries that are culturally rigid are the ones that see motononically declining CCF rates.

Table 1 Secular-rational vs traditional values (WVS)
Full size table

So far, existing models have focused solely on the return to human capital investment as the factor that generates a postponement of childbearing (e.g. Iyigun 2000; d’Albis et al. 2018). This is an outcome that emerges in this study as well: we construct an overlapping generations model in which parents have two reproductive periods. In the first period, they face a trade-off between childrearing and human capital investment; in the second period, the trade-off is between childrearing and labour supply. We verify that the rise of the return to education motivates individuals to postpone parenthood for the latter stage of their reproductive age—an outcome that finds strong empirical support in the existing literature (e.g. Bloemen and Kalwij 2001; McCrary and Royer 2011).

Nonetheless, the existing evidence suggests that the return to education is not the only factor promoting the postponement of childbearing. On the contrary, there are several other factors that can have a more direct impact on the timing of childbearing. For example, cultural changes towards gender equality, female emancipation, the gradual decline of the importance of traditional family values, and the corresponding gradual increase of the desire for individual autonomy have been shown to be major determinants of the postponement of parenthood (e.g. van de Kaa 1987; Liefbroer 2005; Bernhardt and Goldscheider 2006; Mills et al. 2011). This is aptly reflected in Beaujouan’s (2020) argument that the ‘rise in late childbearing across the low-fertility countries […] certainly reflects the diversity of childbearing norms and constraints across different countries’ (Beaujouan 2020; p. 225). These changes in cultural values and social norms, which have raised the desirability and the acceptability of late childbearing, have been supported by medical advances that gave individuals more freedom and ability to choose this aspect of family planning—advances such as improved contraception methods (e.g. Goldin and Katz 2002) and in vitro fertilisation (e.g. Tan et al. 1992). It is also worth emphasising the example of Nordic countries, where the institutional and policy environments are considered models on how to sustain relatively high fertility rates in developed nations (Bernhardt 1992). Some researchers have argued that these policies merely reflect and, at the same time, accommodate the progressive cultural environment of Nordic countries. Andersson (2008) could not be more explicit when he argues that ‘family policy has never specifically targeted childbearing but has rather aimed at strengthening women’s participation in the labour market and promoting gender and social equality […] Policies are explicitly focusing on individuals […] the goal is to enable women and men to raise the number of children they want to have’ (Andersson 2008; p. 90).

Our model’s novelty is to capture the aforementioned ideas by incorporating a direct, preference-related factor that reinforces agents’ desire to delay some of their childbearing in the process of economic growth. We show that an intermediate stage of demographic change in a developed economy, where cohort fertility actually recuperates, emerges if and only if this preference-related factor contributes to the postponement of parenthood. This outcome is consistent with existing views and evidence that link the recuperation of fertility rates to culturally induced changes that directly affect people’s preferences (e.g. Arpino et al. 2015; Esping‐Andersen and Billari 2015; Feichtinger et al. 2017; Beaujouan 2020). Nonetheless, the model also shows that the trend reversal from declining to increasing cohort fertility is followed by yet another reversal towards once more decreasing fertility rates. This latest phase of demographic change will eventually lead to a cohort fertility that is even lower compared to the one that marked the onset of the fertility rate’s recuperation. This outcome has major policy implications: It implies that, even when the rebound the fertility is a true change in demographic trends, it is still a temporary one. The likelihood that cohort fertility will eventually drop below the one that marks the onset of the CCF rebound means that governments should be less reluctant and more proactive in the design and implementation of policies that will address the adverse future socioeconomic implications of population ageing.

We also undertake a series of numerical examples to test our analytical results quantitatively, using data from countries whose cohort fertility dynamics display the different phases of demographic change that emerge in our model. This quantitative analysis shows that our model is a reasonably good fit for the actual data of completed cohort fertility in these countries.

In light of the fact that there are countries which, despite experiencing a shift in the timing of childbearing, have not undergone a rebound in cohort fertility rates, we should emphasise that our model is consistent with such outcomes. As we indicated previously, the preference-related factors that reinforce the delay in childbearing must be sufficiently strong to generate a rebound of cohort fertility; if the impact of these factors is not strong enough, cohort fertility declines monotonically. If anything, the fact that the rebound in completed cohort fertility is observed in countries that are widely considered as the most progressive ones, in terms of their cultural norms and in terms of their family-oriented policies, offers even more credence to the ideas and mechanisms that we advance through our model. This is perhaps a testament to the fact that the explicit consideration of the direct, preference-related factors relevant to the timing of childbearing, opens an avenue for further research. This research can uncover several relevant, but yet unexplored mechanisms, in the joint dynamics of demographic change and economic growth. Indeed, the reduced-form manner through which we incorporate the preference characteristics that underlie the timing of childbearing opens up a wide array of possibilities for future research and policy implications.

Given that the results of our model are inexorably linked to the so-called fertility rebound in developed economies, this study is also related to research work that has uncovered this phase of demographic change in models of economic growth. In Futagami and Konishi (2019), a fertility rebound emerges because of the rising longevity induced by R&D-driven technological progress, whereas Ohinata and Varvarigos (2020) attribute the fertility rebound to differences in the human capital elasticities of childrearing costs and output. However, none of these studies considers issues pertaining to the timing of childbearing, which is actually the key underlying mechanism of this study.Footnote 5 Furthermore, the fertility rebound in these models is the final phase of a three-stage process of demographic change; i.e. they do not uncover a reversal back to declining fertility rates. However, a look at the completed cohort fertility of Nordic countries (see Fig. 2a) is indicative of yet another reversal towards declining fertility rates—a reversal that it is likely to occur gradually in other developed nations.

The remaining analysis is organised as follows. In Sect. 2, we present the model’s set-up and derive the optimal choices regarding fertility and human capital investment. Section 3 is devoted to the dynamics of cohort fertility. Section 4 presents the quantitative investigation and implications of our analytical results. In Sect. 5, we conclude.

2 The economy

Time is discrete and indexed by \(t\). The economy is populated by a mass of overlapping generations of agents who have a lifespan of four periods. The first period of an agent’s lifetime is childhood—a period during which each agent is largely inactive. The remaining three periods represent collectively an agent’s adulthood and are divided into early youth (indexed by EY), late youth (indexed by LY), and maturity (indexed by M). The biological disposition of the population renders early youth and late youth as the only reproductive periods. The cost structure of childrearing is simple. In particular, we assume that each child requires a rearing cost that accounts for a fraction \(\theta \in (\mathrm{0,1})\) of her parent’s available time.

Although there is heterogeneity across the total population of agents who are alive in any given period—emanating from the overlapping generations structure—the agents who belong in a specific age group, and in a given period, are identical. Consequently, we can focus on an agent as being the representative one. With this in mind, consider an agent who is born in period \(t-1\). Next period, she is endowed with a unit of time and decides how to allocate it between childrearing and a learning activity that supports the accumulation of human capital—an activity for which she dedicates \({i}_{t}\) units of time.Footnote 6 Therefore, an agent who decides to raise \({n}_{t,EY}\) children in her early youth, must abide by

$$1=\theta {n}_{t,EY}+{i}_{t}$$
(1)

Let us use \({\overline{h} }_{t}\) to denote the average stock of human capital. Learning activities can contribute to further improvements in knowledge and skills, i.e. the elements that constitute the human capital that will be available during an agent’s late youth. Specifically, we assume that each agent’s human capital evolves according to.

$${h}_{t+1}=\eta \left[X\left({\overline{h} }_{t}\right)+{i}_{t}{\overline{h} }_{t}\right], \eta >0$$
(2)

where \(X({\overline{h} }_{t})\in [\mathrm{0,1})\) is a continuous function that satisfies \({X}^{^{\prime}}({\overline{h} }_{t})>0\) and \({X}^{^{\prime\prime} }({\overline{h} }_{t})<0\). Defining

$$x({\overline{h} }_{t})=\frac{X({\overline{h} }_{t})}{{\overline{h} }_{t}}$$
(3)

it is also assumed that \({x}^{^{\prime}}({\overline{h} }_{t})<0\). According to the second term in (2), the existing average stock of human capital complements an agent’s effort towards improvements in her knowledge and skills (e.g. through formal education; see Glomm and Ravikumar 1992). At the same time, however, the first term in (2) points out an externality that also allows individuals to pick up some of the existing knowledge effortlessly (e.g. through direct observation or interactions with others).Footnote 7

During their late youth, agents are also endowed with a unit of time. They decide how much to consume and how to allocate their available time between childrearing and labour. The latter is supplied to perfectly competitive firms which produce units of the economy’s consumption good by utilising effective labour under a linear production technology. By ‘effective’ labour, it is meant that, in order to determine labour services, each worker’s time is augmented by her stock of human capital. The linear production technology implies that the wage per unit of effective labour is constant over time. Therefore, we save on notation by normalising the constant wage rate to 1.

Upon reaching their maturity, agents will not receive any time endowment. Nevertheless, they will still have consumption needs to satisfy. For this reason, they have access to a storage technology through which units of output stored during an agent’s late youth will deliver, on a one-to-one basis, units of output during an agent’s maturity. Given the above, the budget constraints faced by each agent during late youth and maturity are given by

$${c}_{t+1,LY}=(1-\theta {n}_{t+1,LY}){h}_{t+1}-{s}_{t+1}$$
(4)

and

$${c}_{t+2,M}={s}_{t+1}$$
(5)

where \({c}_{t+1,LY}\) denotes consumption during late youth, \({c}_{t+2,M}\) denotes consumption during maturity, \({s}_{t+1}\) is the amount of income stored during late youth, and \({n}_{t+1,LY}\) is the total number of children reared by an agent in late youth.

It should be noted that, given the age and demographic structures of the model, the completed cohort fertility of agents who are born in \(t-1\) and, therefore, enter adulthood in t, is

$${N}_{t}={n}_{t,EY}+{n}_{t+1,LY}$$
(6)

Indeed, the expression in (6) captures closely the definition of cohort fertility as it measures the number of all children reared by agents, who were born in the same period, during their reproductive lives. This is somehow different to the total fertility rate, for which the corresponding formula would be \({n}_{t,EY}+{n}_{t,LY}\), thus measuring fertility as if the period-t age-specific fertility rates apply to those who begin their reproductive lives in period t. As we shall see shortly, this is not the case in an environment of childbearing postponement; that is why the focus of our analysis is the cohort fertility rate that is presented in (6).

The lifetime utility of an agent who begins adulthood in period t is given by

$${V}_{t}=\mathrm{ln}({c}_{t+1,LY})+\beta \mathrm{ln}({c}_{t+2,M})+\delta \mathrm{ln}({\nu }_{t})$$
(7)

where \(\beta \in (\mathrm{0,1})\) and \(\delta >0\). The term \(\mathrm{ln}({\nu }_{t})\) captures the utility that agents enjoy by the children they rear over their lifetime. In this context, however, the felicity that agents enjoy from parenthood depends on other factors as well, in addition to the number of children they bear. Formally, we assume that \({\nu }_{t}\) is determined by

$${\nu }_{t}={A}_{t}{n}_{t,EY}+{A}_{t+1}{n}_{t+1,LY}$$
(8)

where \({A}_{\tau }\) (\(\tau =t,t+1,...\)) is the variable that measures other factors that affect the utility that parents enjoy from bearing and rearing children, thus measuring it in effective terms. In the absence of these factors (i.e. when \({A}_{t+1}={A}_{t}=1\)) the utility enjoyed from childrearing would be captured by the term \(\mathrm{ln}({n}_{t,EY}+{n}_{t+1,LY})\) which is exactly the formulation most commonly used in the literature (see Iyigun 2000). In this respect, our study enriches existing studies through the adoption of the additional preference-related factors that weigh the utility enjoyed from childbearing in different periods of an agent’s reproductive age. Later, when we present the agents’ optimal choices, we will delve into a more detailed discussion on the interpretation of the variables \({A}_{t}\) and \({A}_{t+1}\), the ideas that justify their presence, as well as their role in agents’ decision-making.

2.1 Equilibrium analysis

Individuals make their choices so as to maximise their lifetime utility in (7), subject to the constraints in Eqs. (1), (2), (4), (5), and (8). We follow several other studies of growth and demographic change (e.g. Galor and Weil 2000; de la Croix and Doepke 2009; Strulik 2017; Iyigun 2000; d’Albis et al. 2018) in treating fertility as continuous variable. Put differently, agents in these types of models choose their fertility rates. In order to solve this problem, we can substitute these constraints in (7) and maximise with respect to \({n}_{t,EY}\), \({n}_{t+1,LY}\) and \({s}_{t+1}\). When maximising their lifetime utility, agents take \({\overline{h} }_{t}\), \({A}_{t}\), and \({A}_{t+1}\) as given. The respective first order conditions are given by

$$\frac{(1-\theta {n}_{t+1,LY})\theta \eta {\overline{h} }_{t}}{(1-\theta {n}_{t+1,LY})\eta [X({\overline{h} }_{t})+(1-\theta {n}_{t,EY}){\overline{h} }_{t}]-{s}_{t+1}}\ge \frac{\delta {A}_{t}}{{A}_{t}{n}_{t,EY}+{A}_{t+1}{n}_{t+1,LY}},{n}_{t,EY}\ge 0$$
(9)
$$\frac{\theta \eta [X({\overline{h} }_{t})+(1-\theta {n}_{t,EY}){\overline{h} }_{t}]}{(1-\theta {n}_{t+1,LY})\eta [X({\overline{h} }_{t})+(1-\theta {n}_{t,EY}){\overline{h} }_{t}]-{s}_{t+1}}\ge \frac{\delta {A}_{t+1}}{{A}_{t}{n}_{t,EY}+{A}_{t+1}{n}_{t+1,LY}},{n}_{t+1,LY}\ge 0$$
(10)

and

$$\frac{1}{(1-\theta {n}_{t+1,LY})\eta [X({\overline{h} }_{t})+(1-\theta {n}_{t,EY}){\overline{h} }_{t}]-{s}_{t+1}}\ge \frac{\beta }{{s}_{t+1}},{s}_{t+1}\ge 0$$
(11)

The expressions in (9)–(11) offer familiar conditions, according to which the marginal benefit from each activity must be equal to the corresponding marginal cost—both expressed in terms of utility. Given that agents within an age cohort are identical, the condition \({\overline{h} }_{t}={h}_{t}\) holds in equilibrium. Henceforth, this condition is going to be applied to all the subsequent derivations and results.

We can express (11) as an equality in order to derive the optimal amount of storage that ultimately determines consumption in the final period of an agent’s lifetime. That is,

$${s}_{t+1}=\frac{\beta }{1+\beta }(1-\theta {n}_{t+1,LY})\eta [X({h}_{t})+(1-\theta {n}_{t,EY}){h}_{t}]=\frac{\beta }{1+\beta }(1-\theta {n}_{t+1,LY}){h}_{t+1}$$
(12)

According to Eq. (12), agents will store a fixed fraction of disposable labour income in order to finance consumption in the final period of their lifetime. Intuitively, this fraction is increasing in the utility weight of consumption during maturity. We can substitute this result in (9) and solve for \({n}_{t,EY}\). Eventually, we get

$$\theta {n}_{t,EY}\ge \frac{\delta [1+x({h}_{t})]}{1+\beta +\delta }-\frac{1+\beta }{1+\beta +\delta }\frac{{A}_{t+1}}{{A}_{t}}\theta {n}_{t+1,LY}$$
(13)

The next step is to substitute (12) in (10) and solve for \({n}_{t+1,LY}\) to derive

$$\theta {n}_{t+1,LY}\ge \frac{\delta }{1+\beta +\delta }-\frac{1+\beta }{1+\beta +\delta }\frac{{A}_{t}}{{A}_{t+1}}\theta {n}_{t,EY}$$
(14)

As we can see, the agent’s fertility choices depend, among other factors, on the ratio \(\frac{{A}_{t+1}}{{A}_{t}}\), which is the relative utility weighting of childrearing in the two reproductive periods. Specifically, the results in (13)–(14) reveal that an increase of this ratio shifts childrearing from early to late youth. This is an intuitive outcome of course: when preferences shift in this manner, the agent find optimal to rebalance her choices in favour of the reproductive period in which childrearing becomes more desirable, in relative terms. Naturally, an important issue involves the underlying reasons for the shift in \(\frac{{A}_{t+1}}{{A}_{t}}\). Our study considers a scenario whereby the shift of the agents’ preferences, in a manner that increases the appeal of childbearing during the latter stages of their reproductive age, occurs as a consequence of changes that follow the process of economic development.

There is a broad set of empirically relevant arguments to interpret and justify this scenario. Some of them are cultural in nature: they involve a shift away from traditional values and norms, which prioritise family and children as key aspirations, and towards an environment that fosters gender equality and attitudes of individual autonomy, personal development, and self-fulfilment among younger generations, together with the understanding that parenthood requires a certain level of emotional maturity (Liefbroer, 2005; Mills et al. 2011). The impact of these cultural factors in shifting the desired age of childbearing is reinforced by medical advances such as improved means of contraception and fertility treatments that have gradually improved the likelihood of successful conception by women who are at a later stage of their reproductive age (Tan et al. 1992), also by a shift in the policy agenda that is meant to accommodate the change in the prevailing cultural environment (Andersson, 2008). Since all these factors gradually materialise as economies reach higher stages of economic development, henceforth we will assume that the relative utility weighting of childrearing in late vs early youth is increasing in \({h}_{t}\). Formally,

$$\frac{{A}_{t+1}}{{A}_{t}}=\gamma ({h}_{t})$$
(15)

such that \({\gamma }^{^{\prime}}({h}_{t})>0\).

For presentation purposes, in what follows, we define the composite parameter term

$$\psi \equiv 1+\frac{\delta }{1+\beta }$$
(16)

By virtue of (16), we have \(\frac{\delta }{1+\beta +\delta }=\frac{\psi -1}{\psi }\) and \(\frac{1+\beta }{1+\beta +\delta }=\frac{1}{\psi }\). Substituting these, together with (15), in (13)–(14), we can rewrite them as follows:

$$\theta {n}_{t,EY}\ge \frac{(\psi -1)[1+x({h}_{t})]}{\psi }-\frac{\gamma ({h}_{t})}{\psi }\theta {n}_{t+1,LY}$$
(17)
$$\theta {n}_{t+1,LY}\ge \frac{\psi -1}{\psi }-\frac{1}{\gamma ({h}_{t})\psi }\theta {n}_{t,EY}$$
(18)

We also impose the following restrictionsFootnote 8:

Assumption 1. \(x(0)<\frac{1}{\psi -1}\).

Assumption 2. \(\psi \gamma (0)<1+x(0)\).

Assumption 3. \(\frac{1}{\psi }\underset{{h}_{t}\to \infty }{\mathrm{lim}}\gamma ({h}_{t})>1+\underset{{h}_{t}\to \infty }{\mathrm{lim}}x({h}_{t})\).

Together with (17) and (18), these allow us to derive.

Lemma 1

Under Assumptions 1–3, there exist \({h}^{*}\) and \({h}^{**}\) such that \({h}^{**}>{h}^{*}\) and.

$${n}_{t,EY}={n}_{EY}({h}_{t})=\{\begin{array}{ccc}\frac{(\psi -1)[1+x({h}_{t})]}{\theta \psi }& if& {h}_{t}\le {h}^{*}\\ \frac{\psi [1+x({h}_{t})]-\gamma ({h}_{t})}{\theta (\psi +1)}& if& {h}^{*}<{h}_{t}<{h}^{**}\\ & & \\ 0& if& {h}_{t}\ge {h}^{**}\end{array}$$
(19)
$${n}_{t+1,LY}={n}_{LY}({h}_{t})=\{\begin{array}{ccc}0& if& {h}_{t}\le {h}^{*}\\ \frac{\psi -\frac{1+x({h}_{t})}{\gamma ({h}_{t})}}{\theta (\psi +1)}& if& {h}^{*}<{h}_{t}<{h}^{**}\\ & & \\ \frac{\psi -1}{\theta \psi }& if& {h}_{t}\ge {h}^{**}\end{array}$$
(20)
$${i}_{t}=i({h}_{t})=\{\begin{array}{ccc}\frac{1-(\psi -1)x({h}_{t})}{\psi }& if& {h}_{t}\le {h}^{*}\\ \frac{1+\gamma ({h}_{t})-\psi x({h}_{t})}{\psi +1}& if& {h}^{*}<{h}_{t}<{h}^{**}\\ & & \\ 1& if& {h}_{t}\ge {h}^{**}\end{array}$$
(21)

These solutions satisfy \({{n}^{^{\prime}}}_{EY}({h}_{t})\le 0\), \({{n}^{^{\prime}}}_{LY}({h}_{t})\ge 0\), and \({i}^{^{\prime}}({h}_{t})\ge 0\).

Proof

See Appendix A.1. □

Lemma 1 shows an agent’s optimal decisions regarding education investment and fertility at different stages of her reproductive life. It reveals the outcome in.

Proposition 1

When the economy transitions to higher stages of economic development, agents increase their investments in education and shift some of their childbearing towards the latter phase of their reproductive age.

Proof

It follows from Lemma 1. □

Consider an economy where human capital is below \({h}^{*}\). At this point, the non-economic factors that directly affect the utility from parenthood have not evolved sufficiently enough to motivate agents to postpone parenthood. This is because the marginal gain in utility from doing so falls short of the marginal utility loss of foregone labour income and, therefore, reduced consumption expenditures. Under such circumstances, agents in their early youth effectively face a trade-off between childrearing and investing in education. In order to understand how economic growth affects this trade-off, recall that the stock of human capital has two conflicting effects on the incentive to invest in education. On the one hand, it is a substitute for such investment through the impact of the direct externality (i.e. the term \(X({h}_{t})\) in Eq. 2); on the other hand, it increases the marginal return of this investment. The latter effect is in fact dominant; therefore, agents increase their education investment at the expense of fertility (a key mechanism behind the so-called demographic transition).

Now, consider an economy that has exceeded the threshold level \({h}^{*}\). In this phase, the factors that are captured by the evolution of \({A}_{t}\) become relevant, in the sense that the effective benefit of postponing childbearing is high enough to induce agents to have children in their late youth. This supresses the utility gain of having children in the earlier reproductive period; hence, agents smooth their overall childbearing profile by reducing even further the number of children they rear in their early youth. Consequently, they have more time available to invest in their education—an outcome that supports human capital accumulation and growth. As long as the economy grows even further, the process whereby agents postpone parenthood continues.

Finally, consider an economy that is positioned above the threshold level \({h}^{**}\). Under these circumstances, the combined effects of the return to education investment and of the preference factors determining the desirability of childrearing at different phases of the reproductive age, motivate agents to commit fully to education during their early youth and to rear children during their late youth. Since there is no trade-off involved in this choice, the fertility rate settles down and remains constant as the economy continues to grow.

The preceding analysis and discussion explain the mechanisms that transpire at each stage of economic development. Our main focus, however, is to illustrate and analyse the dynamics of completed cohort fertility in an economy that gradually transitions through all these distinct phases. As it stands, the general functional forms for \(x({h}_{t})\) and \(\gamma ({h}_{t})\) are not particularly conducive to clear-cut—rather than convoluted—results with regard to the dynamics of human capital accumulation and cohort fertility. For this reason, the remainder of our study will adopt specific functions for \(x({h}_{t})\) and \(\gamma ({h}_{t})\).

2.2 Human capital dynamics and the transition to higher stages of economic development

In what follows, we adopt.

$$\gamma\left(h_t\right)=\frac{\underline g+\overline gh_t}{1+h_t},\overline g\geq1\geq\underline g\geq0.$$
(22)

Notice that the case where \(\underline{g}=\overline{g }=1\) reduces the model to a baseline scenario where the preference-related factors that affect the timing of childbearing, i.e. the term \(\frac{{A}_{t+1}}{{A}_{t}}\), do not change with the stock of human capital as \({\gamma }^{^{\prime}}({h}_{t})=0\). Instead, the formulation in (20) is one whereby, in relative terms, childbearing preferences shift towards agents’ latter reproductive periods, i.e. \({\gamma }^{^{\prime}}({h}_{t})>0\). Furthermore, we adopt \(X({h}_{t})=\frac{\xi {h}_{t}}{1+{h}_{t}}\) (\(0<\xi <1\)) which, by virtue of (3), implies that

$$x({h}_{t})=\frac{\xi }{1+{h}_{t}}$$
(23)

Given (22) and (23), the threshold levels \({h}^{*}\) and \({h}^{**}\) can be defined explicitly throughFootnote 9

$${h}^{*}=\frac{1+\xi -\underline{g}\psi }{\overline{g }\psi -1}$$
(24)
$${h}^{**}=\frac{(1+\xi )\psi -\underline{g}}{\overline{g }-\psi }$$
(25)

while education investment in Eq. (21) can be rewritten as

$${i}_{t}=i({h}_{t})=\{\begin{array}{ccc}\frac{1}{\psi }[1-\frac{\xi (\psi -1)}{1+{h}_{t}}]& {\text{if}}& {h}_{t}\le {h}^{*}\\ \frac{1}{\psi +1}(1+\frac{\underline{g}+\overline{g}{h }_{t}-\psi \xi }{1+{h}_{t}})& {\text{if}}& {h}^{*}<{h}_{t}<{h}^{**}\\ & & \\ 1& {\text{if}}& {h}_{t}\ge {h}^{**}\end{array}$$
(26)

We illustrate (26) diagrammatically in Fig. 3a. In terms of human capital accumulation (which dictates the process of output growth in this model), we can combine (2), (3), (23), and (26) to derive

Fig. 3
figure 3

Investment, ecucation and human capital dynamics

Full size image
$${h}_{t+1}=f({h}_{t})=\{\begin{array}{ccc}\frac{\eta {h}_{t}}{\psi }(1+\frac{\xi }{1+{h}_{t}})& {\text{if}}& {h}_{t}\le {h}^{*}\\ \frac{\eta {h}_{t}}{\psi +1}(1+\frac{\xi +\underline{g}+\overline{g}{h }_{t}}{1+{h}_{t}})& {\text{if}}& {h}^{*}<{h}_{t}<{h}^{**}\\ \eta {h}_{t}(1+\frac{\xi }{1+{h}_{t}})& {\text{if}}& {h}_{t}\ge {h}^{**}\end{array}$$
(27)

The expression in (27) is the one that governs the evolution of human capital. Before we delve into its analysis, we will also consider the following parametric restrictionsFootnote 10:

Assumption 4. \(\psi >1+\xi\).

Assumption 5. \(\eta >\frac{\psi (\overline{g }-\underline{g})+\xi }{\overline{g }(1+\xi )-\underline{g}}\).

Given these, we can show that human capital and, therefore, the economy’s output evolve according to the result in.

Lemma 2

Under Assumptions 4–5, the economy sustains positive growth along all the stages of the transition and in the long run. That is, \({h}_{t+1}>{h}_{t}\forall t\) .

Proof

See Appendix A.2. □

The expression in (27) also reveals that \(\underset{{h}_{t}\to +\infty }{\mathrm{lim}}f({h}_{t})=+\infty\) applies to each distinct branch of human capital formation. Together with Lemma 2, these imply that, as long as \({h}_{0}<{h}^{*}\)—a condition that is assumed to hold thereafter—the economy will experience a transition through all the phases that are associated with the threshold levels in \({h}^{*}\) and \({h}^{**}\) (see Fig. 3b). Although our main objective is to examine the dynamics of completed cohort fertility during this transition, this is an analysis that we will undertake in the following section. Before we do this, we should briefly mention the outcomes that transpire when Assumption 5 is violated.

If \(\eta\) is not as high as Assumption 5 requires, then the complementarity between the stock of human capital and education investment can generate path-dependent outcomes. Specifically, whether the economy will achieve a high income/long-run growth equilibrium, or it will converge to a poverty trap of permanently low income, will depend on whether the initial condition \({h}_{0}\) is above or below an unstable steady state, acting as an endogenous threshold.Footnote 11 Under such circumstances, the results and implications of this study will apply only to economies for which \({h}_{0}\) is above the threshold, as long as they can sustain positive growth in the long-run. The reason we rule out this scenario in our model is mainly because our focus and objective are quite different. We do not aim at presenting a framework of ‘club’ convergence through which one can investigate persistent differences in per capita income among countries and how these may explain observed cross-country differences in demographic characteristics. Although these issues are indubitably important, they go beyond our objective. Instead, our focus is to analyse and get a better understanding of the gradual transition between different phases of demographic change, experienced by currently developed countries. These are countries whose growth rates have been, on average, positive over a quite protracted period of time; therefore, frameworks of multiple, path-dependent equilibria are not necessarily the most relevant ones for our analysis.

2.3 The dynamics of cohort fertility

The previous section analysed the factors that explain the shift of the timing of childbearing in a growing economy. In this part, we will examine the dynamics of the cohort’s fertility rate, i.e. of the total number of children that an agent gives birth to during her lifetime, as expressed in (6). To facilitate the tractability of the analysis, and to ensure closed-form solutions, in what follows, we will also make use of the parametric version adopted in Sect. 2.2.

Combining (6), (19), (20), (22), and (23), it follows that the cohort fertility, for those who begin their reproductive age in \(t\), is

$${N}_{t}=N({h}_{t})=\{\begin{array}{ccc}\frac{\psi -1}{\theta \psi }(1+\frac{\xi }{1+{h}_{t}})& {\text{if}}& {h}_{t}\le {h}^{*}\\ \frac{1}{\theta (1+\psi )}(2\psi +\frac{\psi \xi -\underline{g}-\overline{g}{h }_{t}}{1+{h}_{t}}-\frac{1+\xi +{h}_{t}}{\underline{g}+\overline{g}{h }_{t}})& {\text{if}}& {h}^{*}<{h}_{t}<{h}^{**}\\ \frac{\psi -1}{\theta \psi }& {\text{if}}& {h}_{t}\ge {h}^{**}\end{array}$$
(28)

Now, let us define the composite term

$$\widehat{h}\equiv \frac{\sqrt{\overline{g }\xi +\overline{g }-\underline{g}}-\underline{g}\sqrt{\psi \xi +\overline{g }-\underline{g}}}{\overline{g }\sqrt{\psi \xi +\overline{g }-\underline{g}}-\sqrt{\overline{g }\xi +\overline{g }-\underline{g}}}$$
(29)

It follows that the impact of human capital on the cohort fertility \(N({h}_{t})\) can be summarised in.

Lemma 3

It is \({h}^{*}<\widehat{h}<{h}^{**}\) and, therefore,

$${N}^{^{\prime}}({h}_{t})\{\begin{array}{ccc}<0& if& {h}_{t}<{h}^{*}\\ >0& if& {h}^{*}<{h}_{t}<\widehat{h}\\ <0& if& \widehat{h}<{h}_{t}<{h}^{**}\\ =0& if& {h}_{t}>{h}^{**}\end{array}$$

Proof

See Appendix A.3. □

Recall that the initial condition satisfies \({h}_{0}<{h}^{*}\). With this in mind, we can now characterise the dynamics of cohort fertility. This is done through.

Proposition 2

As the economy grows, cohort fertility initially declines. Then, the economy enters a phase of fertility rebound in which cohort fertility increases. Subsequently, cohort fertility declines again until it eventually settles down in the long run.

Proof

It follows from Lemma 1 and Lemma 3. □

As we can see from Proposition 2, the dynamics of cohort fertility are traced along four distinct phases (see also Fig. 4).Footnote 12 During the first phase, agents rear children only during their early youth. Consequently, the only mechanisms at work are the change in the return to human capital investment and its impact on the trade-off between education and fertility—a trade-off which, as we have already established, works in favour of the former. As the economy enters the second phase, however, economic growth leads to a postponement of parenthood. When this happens, childbearing in late youth is initially more responsive to those preference factors that foster the postponement of childbearing. As a result, there is a recuperation stage during which cohort fertility increases. Nevertheless, the economy eventually enters a later stage where the decline in early youth’s childbearing becomes more pronounced, as agents reap the benefits of accumulating human capital by deciding to postpone parenthood even further. Consequently, cohort fertility declines until the fourth phase in which the shift in the timing of childbearing is complete. During this phase, cohort fertility settles down to a stationary level as the economy grows even further.

Fig. 4
figure 4

The dynamics of cohort fertility

Full size image

Taking account of the above, another implication for the dynamics of fertility comes in the form of.

Corollary 1

The fertility rebound is a temporary phenomenon. It is followed by another change in trend where cohort fertility will once again decline as the economy grows.

Proof

It follows from Lemma 3 and the preceding analysis. □

2.4 What contributes to the recuperation of cohort fertility?

The previous analysis and discussion have revealed that, broadly speaking, the phase of fertility rebound is attributed to the shift in the timing of childbearing from the early to the late reproductive age. However, the same shift can occur purely as a result of the impact of human capital on the return to education. In other words, the presence of other factors that directly affect the utility from rearing children—such as the ones captured by the evolution of the variable \({A}_{t}\) in this model—seem redundant. We will use this section to show that this conjecture is actually a false one.

Let us reconsider the problem after eliminating the impact of the factors associated with the evolution of the variable \({A}_{t}\). We can do this by simply setting \(\underline{g}=\overline{g }=1\) in (22), meaning that \({A}_{t+1}={A}_{t}\)\(\forall t\) throughout. Given this, we can combine (17) and (18) to obtain the solutions for fertility as follows:

$${n}_{t,EY}={n}_{EY}({h}_{t})=\frac{1}{\theta (1+\psi )}[\psi (1+\frac{\xi }{1+{h}_{t}})-1]$$
(30)
$${n}_{t+1,LY}={n}_{LY}({h}_{t})=\frac{1}{\theta (1+\psi )}(\psi -1-\frac{\xi }{1+{h}_{t}})$$
(31)

From these expressions, it is straightforward to verify that \({{n}^{^{\prime}}}_{EY}({h}_{t})<0\) and \({{n}^{^{\prime}}}_{LY}({h}_{t})>0\). In other words, a shift in the timing of childbearing still occurs as the economy grows, even in the absence of the preference factors that affect an agent’s utility from bearing children during the different phases of her reproductive age. In terms of intuition, the increase in the return to education motivates agents to postpone parenthood, thus devoting more resources in the accumulation of human capital during their early youth.

Now, let us consider the evolution of cohort fertility. Combining (6), (30), and (31), it follows that

$${N}_{t}=N({h}_{t})=\frac{(\psi -1)}{\theta (1+\psi )}(2+\frac{\xi }{1+{h}_{t}})$$
(32)

from which it can be easily verified that \({N}^{^{\prime}}({h}_{t})<0\): despite the change in the age-pattern of childbearing, a fertility rebound never occurs.

Note that ‘shutting down’ the direct, preference-related factors for the delay in childbearing is not necessary for the rebound in cohort fertility to disappear as a distinct demographic change. This is possible, even in the presence of these factors, as long as their impact is not sufficiently strong. To see this, suppose that we relax Assumption 3. In this case, Lemma 3 does not apply because \(\widehat{h}<{h}^{*}\), meaning that \({N}^{^{\prime}}({h}_{t})\le 0\) \(\forall {h}_{t}\). In other words, even though the shift in childbearing preferences contributes to the delay in the timing of childbirth, this impact is not pronounced enough to reverse the decline in cohort fertility rates.

To visualise these differences, Fig. 5 presents the dynamics of cohort fertility under two different scenarios regarding the preference parameter \(\overline{g }\), higher values of which capture a greater responsiveness to the factors—among them, several cultural ones—that promote the postponement of childbearing. Given the values of all other parameters, these two scenarios differ in that \(\overline{g }=1.176\) violates Assumption 3, whereas \(\overline{g }=1.307\) is consistent with it.Footnote 13 In other words, the former scenario captures a culturally rigid environment, whereas the latter scenario captures a culturally open one. The dynamics in Fig. 5 clearly indicate that the rebound of cohort fertility emerges in the economy where agents’ preferences are more responsive to changes that induce a delay in childbearing, in contrast to the economy where agents’ preferences are not as responsive and in which cohort fertility declines monotonically. These outcomes are consistent with the descriptive data presented in the ‘Introduction’: we observed that a rebound of cohort fertility is evident in the group of countries where cultural openness scores are, on average, higher (see Fig. 2a–b, and the left and middle columns of Table 1), whereas a monotonic decline of fertility rates is present in countries whose cultural openness scores are, on average, lower (see Fig. 2c and the right column of Table 1). These implications are formalised in.Footnote 14

Fig. 5
figure 5

Cultural openness and cohort fertility dynamics

Full size image

Corollary 2

A rebound of cohort fertility does not emerge when the shift in the timing of childbearing is solely attributed to economic factors, such as the return to education. A fertility rebound can only occur if the process of economic growth prompts a pronounced change in preferences which, in turn, intensifies the postponement of parenthood.

Proof

It follows from Lemma 3, Proposition 2 and the preceding analysis.

The shift in the timing of childbearing that stems solely from the change in the return to education does not generate a sufficiently strong response to alter the dynamics of cohort fertility, even after accounting for the postponement of parenthood. However, the evolution of \({A}_{t}\) along the process of economic growth intensifies the shift in the age profile of childbearing; therefore, it may generate dynamic patterns consistent with a (temporary) recuperation of cohort fertility. This outcome may explain why the recuperation of cohort fertility is an outcome that has, so far, been observed in a subset of developed countries, and at different levels of intensity and duration among them.

2.5 Fertility rebound and the ‘lowest-low’ fertility

Among the various points of discussion that surround the recent demographic trends in several developed economies, some researchers have pointed out the possibility that the fertility rebound has marked the end of what is termed as the ‘lowest-low’ fertility (Kohler et al. 2002). This is the view according to which, prior to the fertility rebound, some developed economies witnessed what are most likely to be their lowest observed rates of fertility (Goldstein et al. 2009).

What is the current model’s implication and prediction on the issue? We formalise this through.

Proposition 3

The lowest cohort fertility of the economy is not the one that materialises prior to the fertility rebound. It is the one to which the economy will converge in the long run, i.e., after the phase of fertility rebound.

Proof

Consider the expression in (28) and Lemma 3. Given these, the lowest total fertility rate prior to the fertility rebound is \(\frac{\psi -1}{\theta \psi }(1+\frac{\xi }{1+{h}^{*}})\). This is in fact higher compared to \(\frac{\psi -1}{\theta \psi }\) which is the total fertility rate to which the economy will converge after \({h}_{t}\) exceeds \({h}^{**}\). □

Evidently, the model’s results do not concur with the idea that developed economies have already witnessed what will prove to be their lowest rates of fertility. To understand why this happens, recall that, prior to the phase of fertility rebound, agent’s decisions entail a trade-off between education investment and childrearing during the same period, i.e., in early youth. The direct externality in the human capital technology (quantified by the parameter \(\xi\)) fosters fertility in that period because it acts as a substitute to investment in education—an effect that does not appear after the fertility rebound and the shift in the timing of childbearing, simply because there is no trade-off between education investment in early youth and childbearing in late youth. It is exactly for this reason that cohort fertility will eventually fall below the one that marked the onset of the fertility rebound in this model.

3 Calibration and numerical examples

In this section, we undertake a quantitative analysis of our model’s results. Specifically, we replicate data from countries whose cohort fertility dynamics are consistent the patterns generated by our model, i.e., the Nordic countries in Fig. 2a.Footnote 15

It should be noted that this section mainly serves as the platform to offer a visualisation of our analytical results, in light of the empirically observed, non-monotone evolution of cohort fertility rates. Still, however, the parametric version of our theoretical model has the ability to generate series with a reasonable fit to the actual data. Naturally, the set-up of our model is flexible enough to admit more structure and more general functional forms, thus potentially allowing a more comprehensive quantitative analysis.

We investigate the quantitative performance of our model aiming at (i) helping the reader visualise our analytical results and (ii) showing that a parametric version of our theoretical model can reasonably replicate the empirical data. To this end, we provide numerical examples by calibrating our model to Finland and Sweden where the non-monotone dynamics are more pronounced as we can see in Fig. 2a. For our calibration strategy, we set parameter values to produce an initial level of completed cohort fertility (CCF) which is close to the average CCF of the first phase of fertility decline in the empirical datasets for each country. We also produce a steady-state level of CCF close to what we observe in the data. Finally, we try to generate a speed of converge—from the initial to the steady state cohort fertility—such that the time series we produce from our model is comparable to what we observe in the data. All parameter values satisfy our model’s assumptions and conditions.

3.1 Example 1: the evolution of CCF in Finland

Our first numerical example is provided by calibrating our model to Finland. Following what is now standard in the literature, we set \(\beta =0.5\) (e.g. de la Croix and Doepke 2003). Given the methodological approach we described above, we set \(\xi =0.0273\), \(\delta =0.46\) and the initial stock of human capital equal to \({h}_{0}=0.1\) for our model to match the average CCF of Finland’s 1945–1950 birth cohorts, i.e. 1.86. We also set \(\eta =1.813\), \(\underline{g}=0.007\), and \(\overline{g }=1.3068\) so that the model’s speed of convergence towards the steady state closely follows the fertility dynamics we observe in the data. Finally, we set \(\theta =0.129\) to calibrate the model’s steady state as close as possible to Finland’s CCF for the 1975 birth cohort.

Figure 6 illustrates the cohort fertility dynamics of our model relative to the real data from Finland. As we can see, our model’s analytical results (see Proposition 2) can qualitatively replicate the empirical data. In the initial phase, there is a drop of CCF. Subsequently, we observe a phase of fertility rebound as the CCF increases. In the next phase, we observe yet another trend reversal towards declining CCF—again, consistent with our analytical results. Quantitatively, it works well in the first phase and slightly overestimates the maximum cohort fertility rate in the second phase (by roughly 0.1 units). It converges to a steady-state value which is slightly lower compared to Finland’s CCF of the 1975 birth cohort. It should be noted, however, that this outcome could imply that Finland has not yet converged to its CCF steady state. This is a reasonable assumption to make, given the latest phase of CCF decline we observe in Nordic countries (see Fig. 2a).

Fig. 6
figure 6

Cohort fertility dynamics in Finland and in the model

Full size image

3.2 Example 2: the evolution of CCF in Sweden

The second example calibrates our model to Sweden. We retain the value for \(\beta\) and set \(\xi =0.014\), \(\delta =0.305\), and the initial stock of human capital \({h}_{0}=0.07\) for our model to match Sweden’s average CCF in the first phase of fertility decline (i.e. for the 1941–1948 birth cohorts; that is, 1.998). We also set \(\theta =0.0856\), \(\eta =1.5316\), \(\underline{g}=0.007\), and \(\overline{g }=1.2035\), for the same reasons as explained above.

Figure 7 reveals that our model’s analytical results can account qualitatively for the three phases in the evolution of CCF in Sweden. The cohort fertility rate initially falls, then it rebounds for some periods and, subsequently, it falls again towards its steady-state level. In the case of Sweden, the quantitative performance of the model is, on average, close to the data during the first phase, while it once more slightly overestimates the CCF peak during the fertility rebound—by roughly 0.1 units. The model performs quite well in the third phase, in the sense that it replicates Sweden’s decline of the CCF below the level that marked the onset of the fertility rebound.

Fig. 7
figure 7

Cohort fertility dynamics in Sweden and in the model

Full size image

4 Conclusions

The purpose of this study was to offer a theoretical backdrop behind the changes in demographic trends that several developed countries have witnessed in recent years. We constructed a growth model where both economic-related and preference-related factors contribute to the postponement of parenthood. The model was able to reproduce, both analytically and quantitatively, the cohort fertility dynamics of these countries. A phase of fertility rebound emerges because the preference-related factors cause a significant boost to a cohort’s ‘late’ fertility, increasing it at a rate which is higher compared to the decrease of the same cohort’s ‘early’ fertility. This situation is only temporary though. Eventually, the decrease of ‘early’ fertility will dominate; hence, cohort fertility will once more decline over time, gradually settling to a fertility rate which is even lower compared to the one that marked the onset of the fertility rebound.

This study’s prediction concerning the prospects of fertility rates, for countries that have gone through the process of fertility rebound, has major policy implications. After all, the fertility rebound was seen as a process with the potential to converge towards replacement levels, thus facilitating countries in alleviating the adverse socioeconomic consequences of population ageing. Given the likelihood that this is not going to happen solely through the working of forces such as economic, cultural, and medical ones, and the equally likely outcome that cohort fertility will fall at levels below the ones observed at the beginning of the fertility rebound, there is major scope for governments to design and adopt policies that will aim at addressing the future socioeconomic repercussions of ever lower rates of fertility.

In addition to the previously mentioned results, our study offers wider implications of a methodological nature. It showed that a model can account for empirically relevant, yet previously unexplored, patterns in the evolution of fertility rates, once we consider explicitly the preference related factors behind the delay in childbearing. In this respect, our model opens up a wide avenue for future research that will attempt a more explicit structure of these factors, thus uncovering further unexplored issues on the relation between growth and demographic change.

We constructed our model with the objective of delivering analytically tractable results, thus being able to precisely identify the conditions that are important for generating the empirically observed rebound of cohort fertility. As always, analytical tractability necessitates the adoption of some simplifying assumptions. For example, our model focused on human capital–based arguments, thus missing the potential role of physical capital and of the interest rate on parental saving. In the context of endogenous timing of childbirth, these issues have been addressed by Momota and Horii (2013) who found the possibility of endogenous cycles in the economy’s dynamics. What their explicit consideration of physical capital, and its impact on saving rates, did not generate was the rebound in fertility rates. This is perhaps an indication that, although indubitably important in general, the roles of physical capital and of interest rates on saving are not critical for the demographic aspects that our study sought to explain. Another example of a simplifying assumption is the presence of scale effects in the time cost of childrearing, i.e. the idea that the time cost per child is decreasing in the number of children raised. Although this assumption will have most likely caused a higher equilibrium fertility rate throughout an agent’s reproductive age (i.e. in both early and late youth), there is nothing inherent in this assumption to suggest that it would have altered the main message of our study, which is the rebound of cohort fertility in an environment of delay in the timing of childbearing. If it did, then it would have led to results that are at odds with the actual data; after all, the delay in childbearing and the fertility rebound are outcomes that we observe empirically. In any case, our model provides a flexible enough platform for future research to investigate and uncover the implications of these extensions.