Cryptography in the Multi-string Model

Abstract

The common random string model introduced by Blum, Feldman, and Micali permits the construction of cryptographic protocols that are provably impossible to realize in the standard model. We can think of this model as a trusted party generating a random string and giving it to all parties in the protocol. However, the introduction of such a third party should set alarm bells going off: Who is this trusted party? Why should we trust that the string is random? Even if the string is uniformly random, how do we know it does not leak private information to the trusted party? The very point of doing cryptography in the first place is to prevent us from trusting the wrong people with our secrets.

In this paper, we propose the more realistic multi-string model. Instead of having one trusted authority, we have several authorities that generate random strings. We do not trust any single authority; we only assume a majority of them generate random strings honestly. Our results also hold even if different subsets of these strings are used in different instances, as long as a majority of the strings used at any particular invocation is honestly generated. This security model is reasonable and at the same time very easy to implement. We could for instance imagine random strings being provided on the Internet, and any set of parties that want to execute a protocol just need to agree on which authorities’ strings they want to use.

We demonstrate the use of the multi-string model in several fundamental cryptographic tasks. We define multi-string non-interactive zero-knowledge proofs and prove that they exist under general cryptographic assumptions. Our multi-string NIZK proofs have very strong security properties such as simulation-extractability and extraction zero-knowledge, which makes it possible to compose them with arbitrary other protocols and to reuse the random strings. We also build efficient simulation-sound multi-string NIZK proofs for circuit satisfiability based on groups with a bilinear map. The sizes of these proofs match the best constructions in the single common random string model.

We also suggest a universally composable commitment scheme in the multi-string model. It has been proven that UC commitment does not exist in the plain model without setup assumptions. Prior to this work, constructions were only known in the common reference string model and the registered public key model. The UC commitment scheme can be used in a simple coin-flipping protocol to create a uniform random string, which in turn enables the secure realization of any multi-party computation protocol.

1 Introduction

The Problem

In the common random string model, the parties executing a protocol have access to a uniformly random bit-string. A generalization of this model is the common reference string (CRS) model, where the string may have a non-uniform distribution. Blum, Feldman and Micali [7] introduced the CRS model (with a uniform random string) to construct non-interactive zero-knowledge (NIZK) proofs. Some setup assumption was needed, since only languages in BPP can have non-interactive or two-round zero-knowledge proofs in the plain model [30]. There are other examples of protocols that cannot be realized in the standard model but are possible in the CRS model, for instance universally composable (UC) commitment [12]. The CRS-model has therefore found widespread use in the field of cryptology.

Using the CRS-model creates a problem: where should the CRS come from? One option is to have a trusted third party that generates the CRS, but this raises a trust issue. It is possible that the parties cannot find a party that they all trust. Would Apple trust a CRS generated by Microsoft? Would US government agencies be willing to use a CRS generated by their Russian counterparts?

Alternatively, the parties could generate the CRS themselves at the beginning of the protocol. If a majority are honest, they could for instance use multi-party computation to generate a CRS. However, this makes the whole protocol more complicated and requires them to have some initial rounds of interaction. They could also trust a group of parties to jointly generate a CRS; however, this leaves them with the task of finding a volunteer group of authorities to run a multi-party computation protocol whenever a CRS is needed. There is also no guarantee that different sets of parties can agree on trusting the same group of authorities, so potentially this method will require authorities to participate in many generations of CRS’s.

The Multi-string Model

We propose the multi-string model as a solution to the above mentioned problem. In the multi-string model a number of authorities assist the protocol execution by providing random strings. If a majority of the authorities are honest the protocol will be secure.

There are two reasons that the multi-string model is attractive. First, the authorities play a minimal role in the protocol. They simply publish random strings, they do not need to perform any computation, be aware of each other or any other parties, or have any knowledge about the specifics of the protocol to be executed. This permits easy implementation; the parties wishing to execute a protocol can for instance simply download a set of random strings from agreed upon authorities on the Internet. Second, the security of the protocol only needs to rely on a majority of the authorities being honest at the time they created the strings. Even if they are later corrupted, the random strings can still be used. This is in contrast with multi-party computation protocols such as [6, 16, 32] where the actual players must be aware of each other at all times with a majority of players remaining uncorrupted at all times. Also, no matter how untrustworthy the other parties in your protocol are, the protocol is secure if a majority of the authorities is honest. In other words, the honesty of a small group of parties can be magnified and used by any set of parties.

A natural generalization of the uniform random multi-string model described above is the common reference multi-string model where the strings are sampled with a non-uniform distribution. Since it is easier to generate uniform random strings and they can be sampled without learning any secret trapdoor information about them we are most interested in the uniform random multi-string model. However, for some of our results the common reference multi-string model permits a relaxation of the underlying cryptographic assumptions.

Related Work

In the context of non-interactive proofs witness-indistinguishablity can be obtained without a CRS [3, 39] or zero-knowledge may be obtained using superpolynomial simulation techniques [1]. But it is impossible to construct non-interactive zero-knowledge proofs under standard assumptions without some sort of setup [30]. To the best of our knowledge the multi-string model is the simplest trustworthy setup.

Multi-party computation is possible under computational assumptions when an honest majority is available [32] and information theoretically when more than 2/3 of the parties are honest [6, 16]. However, if more parties are corrupt general multi-party computation is impossible without some setup. Canetti, Lindell, Ostrovsky, and Sahai [14] used the CRS-model as a setup to overcome this problem. As an alternative, Barak, Canetti, Nielsen, and Pass [2] suggested the registered public key model as a relaxed setup that makes multi-party computation possible. In the registered public key model, parties can only register correctly generated keys. While there is no longer a common reference string in the registered public key model, the underlying problem still persists: who is the trusted party that will check that the parties only register correctly generated public keys?

In the information-theoretic setting Beaver suggested commodity-based [4] and server-assisted [5] cryptography where multi-party computation is made possible with the assistance of third parties that are oblivious to the actual protocol executed as a way to reduce the involvement of multiple parties. In his protocols the servers give distinct correlated values to the parties in the protocol. We on the other hand rely on computational assumptions, but get a simpler setup model. In the multi-string model each server provides the same input to all parties and in the uniform random multi-string model this input is just a random bit-string.

Results

As argued above, the multi-string model is a reasonable and simple setup assumption. The next question is whether there are interesting protocols that can be securely realized in the multi-string model. We will answer this question affirmatively in two separate directions: Our first set of results give constructions of NIZK proofs in the multi-string model. Our second set of results give UC commitment and general UC-secure multi-party computation in the multi-string model in the presence of adaptive adversaries. We stress that different parties may have different beliefs about which common strings were generated by honest parties and which were generated maliciously and that our results hold despite these different beliefs (even if only a subset of strings are used) as long as the number of honestly generated strings used in any application satisfies the threshold.

1.1 Non-interactive Zero-Knowledge

A zero-knowledge proof [32, 34] is a two-party protocol, where a prover tries to convince a verifier of the truth of some statement, typically membership of an NP-language. The proof should have the following three properties: completeness, soundness, and zero-knowledge. Completeness means that a prover who has an NP-witness for the truth of the statement can convince the verifier. Soundness means that if the statement is false, then it is impossible to convince the verifier. Zero-knowledge means that the verifier does not learn anything else from the proof than the fact that the statement is true. Interactive zero-knowledge proofs are known to exist in the plain model without a CRS, however, non-interactive and 2-round zero-knowledge proofs only exist for trivial languages [30]. Instead, much research has gone into constructing non-interactive zero-knowledge proofs in the CRS-model [7, 8, 18, 21–24, 26, 39, 41].

Multi-string NIZK

We define the notion of multi-string NIZK proofs in Sect. 2. In the definitions, the adversary sees honestly generated strings and pick the ones she likes. The adversary may also generate some of the strings itself, possibly in a malicious and adaptive manner. Our definition of multi-string NIZK proofs calls for completeness, soundness and zero-knowledge to hold in a threshold manner. If t _c out of n common reference strings are honest, then the prover holding an NP-witness for the truth of the statement should be able to create a convincing proof. If t _s out of n common reference strings are honest, then it should be infeasible to convince the verifier of a false statement. If t _z out of n common reference strings are honestly generated, then it should be possible to simulate the proof without knowing the witness.

It is desirable to minimize t _c , t _s , t _z . As we shall see, t _c =0 is achievable, however, multi-string soundness and multi-string zero-knowledge are complementary in the sense that there is a lower bound t _s +t _z >n for non-trivial languages, see Sect. 2.

A natural question is under which assumptions we can obtain multi-string NIZK proofs. We prove that if one-way functions exist then the existence of single-string NIZK proofs imply the existence of multi-string NIZK proofs.

Beyond Vanilla Multi-string NIZK

It is undesirable to require a group of authorities to produce random strings for each proof we want to make. We prefer it to be possible to use the same strings over and over again, so each authority has to produce only one single random string. We must therefore consider a setting, where multiple protocols may be running concurrently and where the adversary simultaneously acts as prover in some multi-string NIZK proofs and as verifier in other multi-string NIZK proofs. When the protocol designer has to prove security in such a setting, some of the proofs are simulated while we still need other proofs to be sound. Moreover, in some cases we may want to extract the witness from a proof. To enable security proofs, where we have both simulations of some proofs and witness extraction of other proofs going on at the same time, we introduce the notions of simulation-extractable multi-string NIZK and extraction zero-knowledge multi-string NIZK.

In simulation-extractable multi-string NIZK, we require that it be possible to extract a witness from the proof if t _s strings are honestly generated, even if the adversary sees simulated proofs for other statements. In extraction zero-knowledge, we require that if there are t _z honest strings, then even if the adversary sees extractions of witnesses in some proofs, the other proofs remain zero-knowledge and reveal nothing. We offer a multi-string NIZK proof based on general assumptions, which is both simulation-extractable and extraction zero-knowledge.

Multi-string NIZK Proofs from Bilinear Groups

Groth, Ostrovsky, and Sahai [39] constructed NIZK proofs from groups with a bilinear map. Their CRS contains a description of a bilinear group and a set of group elements. The group elements can be chosen such that the CRS gives either perfect soundness or perfect zero-knowledge. Soundness strings and simulation strings are computationally indistinguishable, so this gives an NIZK proof in the CRS model.

There is a technical hurdle to overcome when trying to apply their techniques in the multi-string model: single-string NIZK proofs rely on the common reference string to contain a description of a bilinear group. In the multi-string model, authorities generate their random strings obliviously of other authorities. There is therefore no agreement on which bilinear group to use. One might try to let the prover pick the bilinear group, however, this too causes problems since now we need to set up the random strings such that they will work for many choices of bilinear groups.

We resolve these problems by inventing a novel technique to “translate” common reference strings in one group to common reference strings in another group. Each authority picks its own bilinear group and the prover also picks a bilinear group. Using our translation technique, we can translate simulation reference strings chosen by the authorities to simulation reference strings in the prover’s bilinear group. Similarly, we can translate soundness reference strings chosen by the authorities to soundness reference strings in the prover’s bilinear group.

The resulting multi-string NIZK proofs for circuit satisfiability have size $\mathcal{O}((n+|C|)k)$, where n is the number of random strings, |C| is the size of the circuit, and k is a security parameter specifying the size of a group element. Typically n will be much smaller than |C|, so this matches the best single-string NIZK proofs of [39] that have complexity $\mathcal{O}(|C|k)$.

1.2 Multi-party Computation

Canetti’s UC framework [11] defines secure execution of a protocol under concurrent execution of arbitrary protocols. Informally a protocol is UC secure if its execution is equivalent to the parties handing their protocol inputs to an honest trusted third party that computes everything securely and returns the resulting outputs to the involved parties. We refer the reader to Sect. 6 for a sketch of the UC framework.

UC Commitment

It is known that in the plain model any (well-formed) ideal functionality can be securely realized if a majority of the parties are honest. On the other hand, there are certain functionalities that are provably impossible to realize in the plain model if half or more of the parties may be corrupted. An example of an unrealizable two-party functionality in the plain model is UC commitment [12].

We demonstrate that in the multi-string model UC commitment can be securely realized. The key idea in this construction is to treat each common random string as the key for a commitment scheme. By applying threshold secret sharing techniques, we can spread the message over several commitments and tolerate a minority of fake common reference strings.

General Multi-party Computation

Canetti, Lindell, Ostrovsky, and Sahai [14] showed that any (well-formed) ideal functionality can be securely realized in the CRS-model, even against adversaries that can adaptively corrupt arbitrary parties and where parties are not assumed to be able to securely erase any of their data. However, it was an open question where the CRS should come from, since the parties provably could not compute it themselves.

Armed with our multi-string UC commitment it is straightforward to solve the problem. We run a coin-flipping protocol using the UC commitment given above to create a CRS. We can then use the CRS to securely realize any ideal functionality. This result points out a nice feature of the multi-string model; it scales extremely well. We just require a majority of the authorities to be honest. Then no matter which group of parties, even if it is a large group of mostly untrustworthy parties, we can magnify the authorities’ honesty to enable this entire group to do secure computation.

UC Multi-string Model

We formalize the multi-string model in the UC framework as an ideal functionality that provides random strings and allows the adversary to inject a minority of malicious strings before a protocol execution. This functionality is easy to implement with a set of authorities that provide random strings on request.

We note that each string should only be used in one protocol; we do not guarantee security if many protocols use the same strings. Canetti, Dodis, Pass, and Walfish [15] have demonstrated that it is not possible to have one fixed global common random string that is used for multiple arbitrary protocol executions and this result extends to the multi-string model. Orthogonally to our work, they instead suggest the augmented common reference string model where general UC secure multi-party computation is possible.

Follow-up Works

The conference version of this article [38] initiated the study of constructing UC secure protocols without relying on a single trusted external entity. In other words, one of the important contributions of our work is to initiate research where the beliefs in which cryptographic objects (e.g., reference strings) have the correct properties need not be agreed upon by all players, and different players may have different beliefs. There were a number of follow-up works (that consider not just random strings but also other cryptographic gadgets) where different participants may have different beliefs [28, 35].

2 Definitions

We model algorithms and adversaries as Turing machines. They get a security parameter k as input written in unary, which we will often omit writing explicitly. The adversary may be an interactive Turing machine that keeps state between different invocations and may or may not have bounded running time.

We say a function $\nu:\mathbb{N}\to[0;1]$ is negligible if for all constants c>0 there exists a K _c so for all k>K _c we have ν(k)<k ^−c. For two functions f,g we write f(k)≈g(k) if |f(k)−g(k)| is negligible. We say f is overwhelming if f(k)≈1.

Let R be a polynomial time computable binary relation. For pairs (x,w)∈R we call x the statement and w the witness. Let L be the NP-language consisting of statements in R.

A multi-string proof system for a relation R consists of probabilistic polynomial time algorithms K,P,V, which we will refer to as, respectively, the key generator, the prover and the verifier. The key generation algorithm can be used to produce common reference strings Σ. We are most interested in the case where the key generator outputs a uniformly random string of polynomial length ℓ(k) but for the sake of generality we permit other types of key generators in our definitions as well.

The prover takes as input $(\vec{\varSigma},x,w)$, where $\vec{\varSigma}$ is a tuple of n common reference strings and (x,w)∈R, and produces a proof π. The verifier takes as input $(\vec{\varSigma},x,\pi)$ and outputs 1 if the proof is acceptable and 0 if rejecting the proof. We call (K,P,V) a (t _c ,t _s ,t _z ,n)-NIZK proof system for R if it has the (t _c ,n)-completeness, (t _s ,n)-soundness and (t _z ,n)-zero-knowledge properties defined below. We remark that (1,1,1,1)-NIZK proofs correspond to standard NIZK proofs in the common reference string model (with composable zero-knowledge [37], which is stronger than the standard definition of zero-knowledge).

(t _c ,n)-Completeness

Completeness means that the prover can create acceptable proofs for true statements when at least t _c out of n common reference strings have been generated honestly.

Definition 1

(K,P,V) is (perfectly) (t _c ,n)-complete if for all non-uniform polynomial time adversaries $\mathcal{A}$ we have

$$\Pr \bigl[(\vec{\varSigma},x,w)\gets\mathcal{A}^{K} \bigl(1^k\bigr);\pi\gets P(\vec {\varSigma},x,w): V(\vec{\varSigma},x, \pi)=1 \textnormal{ or } (x,w)\notin R \bigr]=1, $$

where K is an oracle that on the ith query outputs Σ _i ←K(1^k) and the tuple $\vec{\varSigma}=(\varSigma_{1},\ldots,\varSigma_{n})$ output by $\mathcal {A}$ includes at least t _c common reference strings (possibly with repetition) generated by K.

The protocols we construct in this paper are (t _c ,n)-complete for all 0≤t _c ≤n. This means that the prover always outputs an acceptable proof whenever (x,w)∈R; even if all the common reference strings are chosen adversarially. We remark that with t _c =0 the adversary could in principle choose all Σ _i =⊥. Typically we handle this by using a default common reference string such as Σ=K(1^k;0) in place of bad common reference strings.

The definition could be generalized slightly to computational (t _c ,n)-completeness where the equality only needs to hold approximately. If the verifier is deterministic the multi-string NIZK proof can easily be made perfectly complete though by letting the prover use the witness itself as a replacement proof in the negligibly few occasions where the normal NIZK proof is not accepting. The same holds for single-string NIZK proofs and indeed all known constructions of single-string NIZK proofs can easily be made perfectly complete, so we will with little loss of generality assume throughout the paper that both multi-string and single-string NIZK proofs are perfectly complete.

(t _s ,n)-Soundness

Soundness says that an adversary cannot forge a proof when at least t _s out of n common reference strings have been honestly generated.

Definition 2

(K,P,V) is (statistically) (t _s ,n)-sound if for all adversaries $\mathcal{A}$ we have

$$\Pr \bigl[(\vec{\varSigma},x,\pi)\gets\mathcal{A}^{K} \bigl(1^k\bigr):V(\vec{\varSigma },x,\pi)=1 \textnormal{ and } x\notin L \bigr]\approx0, $$

where K on the ith query outputs Σ _i ←K(1^k) and the tuple $\vec{\varSigma}=(\varSigma_{1},\ldots,\varSigma_{n})$ output by $\mathcal {A}$ includes at least t _s common reference strings generated by K.

The definition above refers to statistical (t _s ,n)-soundness, where the adversary has unbounded time. We call it perfect (t _s ,n)-soundness, when the probability is exactly 0.

(t _s ,n)-Proof of Knowledge

Soundness prohibits giving valid proofs for false statements, but does not imply the ability to compute a witness for the statement. Strengthening the notion of soundness, we define a proof of knowledge as a proof system where it is possible to extract a witness from a valid proof.

Definition 3

We say (K,P,V) is a (statistical) (t _s ,n)-proof of knowledge for R with extractor (E ₁,E ₂) if E ₁,E ₂ are probabilistic polynomial time algorithms such that for all adversaries $\mathcal{A}$ we have

$$\Pr \bigl[\varSigma\gets K\bigl(1^k\bigr):\mathcal{A}(\varSigma)=1 \bigr] \approx \Pr \bigl[(\varSigma,\xi)\gets E_1 \bigl(1^k\bigr):\mathcal{A}(\varSigma)=1 \bigr], $$

and for all adversaries $\mathcal{A}$ we have

$$\begin{aligned}[t] \Pr \bigl[ & (\vec{\varSigma},\vec{\xi},x,\pi)\gets \mathcal{A}^{E_1} \bigl(1^k\bigr);w\gets E_2(\vec{\varSigma},\vec{\xi},x, \pi): \\ & V(\vec {\varSigma},x,\pi)=1 \textnormal{ and } (x,w)\notin R \bigr] \approx0,\end{aligned} $$

where the oracle E ₁ on query i returns (Σ _i ,ξ _i )←E ₁(1^k) and is queried at most a polynomial number of times by the adversary, and the adversary outputs $\vec{\varSigma},\vec{\xi}$ with t _s pairs (Σ _i ,ξ _i ) having been generated by E ₁ and the remaining n−t _s pairs being of the form (Σ _i ,⊥).

As in the definition of soundness, we can define a perfect (t _s ,n)-proof of knowledge by requiring the equalities to be exact instead of allowing a negligible difference. A statistical (t _s ,n)-proof of knowledge is statistically (t _s ,n)-sound and a perfect (t _s ,n)-proof of knowledge is perfectly (t _s ,n)-sound.

(t _z ,n)-Zero-Knowledge

Zero-knowledge means that the adversary learns nothing from the proof (besides the truth of the statement) if at least t _z out n common reference strings have been honestly generated. We capture zero-knowledge by requiring that the proof can be simulated without knowing the witness. A simulator for (K,P,V) consists of two probabilistic polynomial time algorithms (S ₁,S ₂). S ₁ takes 1^k as input and outputs (Σ,τ), respectively a simulation reference string and a simulation trapdoor. S ₂ takes as input $(\vec{\varSigma},\vec{\tau},x,w)$ and simulates a proof π when $\vec{\tau}=(\tau_{1},\ldots,\tau_{n})$ is an n-tuple with exactly t _z values τ _i ≠⊥.

We will strengthen the standard definition of zero-knowledge by splitting the definition into two parts. The first part says that the adversary cannot distinguish real common reference strings from simulation reference strings. The second part, says that even with access to the simulation trapdoors the adversary cannot distinguish real proofs from simulated proofs on a set of simulation reference strings.

Definition 4

We say (K,P,V) is (computationally) (t _z ,n)-zero-knowledge if there is a simulator (S ₁,S ₂) with reference string indistinguishability and simulation indistinguishability as described below.

Reference string indistinguishability :

For all non-uniform polynomial time adversaries $\mathcal{A}$ we have

$$\Pr \bigl[\varSigma\gets K\bigl(1^k\bigr):\mathcal{A}(\varSigma)=1 \bigr]\approx\Pr \bigl[(\varSigma,\tau)\gets S_1 \bigl(1^k\bigr):\mathcal{A}(\varSigma)=1 \bigr]. $$

(t _z ,n)-simulation indistinguishability :

For all non-uniform interactive polynomial time adversaries $\mathcal{A}$ we have

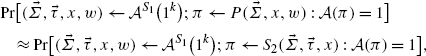
where S ₁ on the ith query outputs (Σ _i ,τ _i )←S ₁(1^k), and the adversary outputs (x,w)∈R and $\vec{\varSigma},\vec{\tau}$ with t _z pairs (Σ _i ,τ _i ) generated by S ₁ and n−t _z pairs of the form (Σ _i ,⊥).

Lower Bounds for Multi-string NIZK Proofs

Soundness and zero-knowledge are complementary. Intuitively, an adversary that controls enough strings to simulate a proof can prove anything and we no longer have soundness. We capture this formally in the following theorem.

Theorem 5

If L is an NP-language with a (t _c ,t _s ,t _z ,n)-NIZK proof system (K,P,V) (for any t _c ≥0) then L∈BPP or t _s +t _z >n.

Proof

Assume without loss of generality t _c =n and that we have an (n,t _s ,t _z ,n)-NIZK proof system for the relation R defining L with simulator (S ₁,S ₂) and t _s +t _z ≤n. We will build a probabilistic polynomial time algorithm that has more than 2/3 chance of deciding whether x∈L or x∉L.

We first construct a decision algorithm that works well for large statements. Our algorithm gets x as input and sets k=|x|. It simulates t _z common reference strings (Σ _i ,τ _i )←S ₁(1^k) and generates n−t _z common reference strings Σ _j ←K(1^k) setting τ _j =⊥. It then simulates the proof $\pi\gets S_{2}(\vec{\varSigma},\vec{\tau},x)$ and outputs $V(\vec{\varSigma},x,\pi)$. It is clear that this is a probabilistic polynomial time algorithm.

Let us analyze the probability of the algorithm deciding membership correctly on a family of worst-case choices of statements $\{x_{k}\}_{k=1}^{\infty}$ with |x _k |=k. For x _k ∉L the (t _s ,n)-soundness gives us overwhelming (in k) probability of outputting 0 since n−t _z ≥t _s common reference strings have been generated correctly.

For x _k ∈L the (n,n)-completeness means that a prover with access to a witness w _k with overwhelming probability outputs an acceptable proof if all common reference strings are generated correctly. The reference string indistinguishability property gives overwhelming probability of accepting the proof even when some of the common reference strings are simulated. The (t _c ,n)-simulation indistinguishability, where we give (x _k ,w _k ) as non-uniform advice to $\mathcal{A}$, shows that a simulated proof also has overwhelming probability of being accepted. We therefore have overwhelming probability of the algorithm outputting 1 on x _k ∈L.

We now have an algorithm that decides membership of L correctly with overwhelming probability as the size of the statements grows. This implies that there is at most a constant number of statements for which the algorithm has less than 2/3 probability of giving the right decision. We get a BPP decision algorithm for L by hardcoding these statements and the corresponding membership decision into our algorithm. □

It is in the verifier’s interest to minimize t _s to make it more probable that the protocol is sound and it is in the prover’s interest to minimize t _z to make it more probable that the protocol is zero-knowledge. In many cases, choosing n odd and setting $t_{s}=t_{z}=\frac{n+1}{2}$ will be a reasonable compromise. However, there are also cases where it is appropriate to have an imbalance between t _s and t _z . Consider for instance the case, where Alice wants to e-mail an NIZK proof to Bob, but does not know Bob’s preferences with respect to common reference strings. She may pick a set of common reference strings and make a multi-string proof. Bob did not participate in deciding which common reference strings to use, however, if they belong to trustworthy authorities he may be willing to believe that one of them is honest. On the other hand, Alice gets to choose the authorities, so she may be willing to believe that all of them are honest. The appropriate choice in this situation, is a multi-string NIZK proof with t _s =1,t _z =n.

Simulation-Soundness

In security proofs it is often useful to simulate a proof for a false statement. However, seeing a simulated proof for a false statement might enable an adversary to generate more proofs for false statements. We say a multi-string NIZK proof is simulation-sound if an adversary cannot prove any false statement even after seeing simulated proofs of arbitrary statements.

Definition 6

A (t _c ,t _s ,t _z ,n)-NIZK proof system (K,P,V) with simulator (S ₁,S ₂) is simulation-sound if for all non-uniform polynomial time adversaries $\mathcal {A}$ we have

$$\Pr \bigl[(\vec{\varSigma},x,\pi)\gets\mathcal{A}^{S_1',S_2'(\cdot,\cdot,\cdot)} \bigl(1^k\bigr): (\vec{\varSigma},x,\pi)\notin Q \textnormal{ and } x \notin L \textnormal{ and } V(\vec{\varSigma},x,\pi)=1 \bigl]\approx0, $$

where $S_{1}'$ on query i runs (Σ _i ,τ _i )←S ₁(1^k) and returns Σ _i , and $S_{2}'$ on input $(\vec{\varSigma}_{j},I_{j},x_{j})$ where I _j contain t _z indices corresponding to common reference strings in $\vec{\varSigma}_{j}$ that have been generated by S ₁, returns $\pi\gets S_{2}(\vec{\varSigma}_{j},\vec{\tau}_{j},x_{j})$ where τ _j containing the t _z simulation trapdoors generated by S ₁ corresponding to the indices in I _j in the same positions and the remaining entries are ⊥, and Q is a list of statements and corresponding proofs $(\vec{\varSigma}_{j},x_{j},\pi_{j})$ in the queries to $S_{2}'$.

Simulation-Extractability

Since we are working in the multi-string model, we assume strings can be used by anybody who comes along. Knowledge extraction and zero-knowledge may both be very desirable properties, however, we may also imagine security proofs where we at the same time need to extract witnesses from some proofs and simulate other proofs. This joint simulation/extraction is for instance often seen in security proofs in the UC framework [11].

Combining simulation-soundness and knowledge extraction, we may therefore require that even after seeing many simulated proofs, whenever the adversary makes a new proof we are able to extract a witness. We call this property simulation-extractability. Simulation-extractability implies simulation-soundness, because if we can extract a witness from the adversary’s proof, then obviously the statement must belong to the language in question.

Definition 7

We say the (t _c ,t _s ,t _z ,n)-NIZK proof of knowledge (K,P,V) with simulator (S ₁,S ₂) and extractor (E ₁,E ₂) is simulation-extractable if there is a probabilistic polynomial time algorithm SE ₁ that outputs (Σ,τ,ξ) where (Σ,τ) is distributed identically to the output of S ₁, and for all non-uniform polynomial time adversaries $\mathcal {A}$ we have

where $SE_{1}'$ on query i outputs (Σ _i ,ξ _i ) from (Σ _i ,τ _i ,ξ _i )←SE ₁(1^k), and $S_{2}'$ on input $(\vec{\varSigma}_{j},I_{j},x_{j})$ outputs $\pi_{j}\gets S_{2}(\vec{\varSigma}_{j},\vec{\tau}_{j},x_{j})$ where $\vec{\tau}_{j}$ as in the definition of simulation-soundness is such that the t _z pairs (Σ _i ,τ _i ) in $(\vec{\varSigma}_{j},\vec{\tau}_{j})$ corresponding to the indices in I _j have been generated by $SE_{1}'$ and the remaining pairs are of the form (Σ _i ,⊥), and Q is a list of statements and corresponding proofs $(\vec{\varSigma}_{j},x_{j},\pi_{j})$ made by $S_{2}'$, and $\vec{\varSigma},\vec{\xi}$ contains exactly t _s pairs (Σ _i ,ξ _i ) generated by $SE_{1}'$ and the remaining pairs are of the form (Σ _i ,⊥).

Extraction Zero-Knowledge

Combining simulation soundness and knowledge extraction, we may also require that even after seeing many extractions it should still be hard to distinguish real proofs and simulated proofs from one another. This definition resembles the definition of public-key encryption secure against chosen ciphertext attack.

Definition 8

We say the (t _c ,t _s ,t _z ,n)-NIZK proof of knowledge (K,P,V) with simulator (S ₁,S ₂) and extractor (E ₁,E ₂) is extraction zero-knowledge if there is a probabilistic polynomial time algorithm SE ₁ that outputs (Σ,τ,ξ) with an identical distribution to S ₁ when restricted to (Σ,τ) and for all non-uniform polynomial time adversaries $\mathcal {A}$ we have

where $SE_{1}''$ on query i outputs (Σ _i ,τ _i ) from (Σ _i ,τ _i ,ξ _i )←SE ₁(1^k), and $E_{2}'$ on input $(\vec{\varSigma}_{j},I_{j},x_{j},\pi_{j})$ outputs $w\gets E_{2}(\vec{\varSigma}_{j},\vec{\xi}_{j},x_{j},\pi_{j})$ where I _j contains exactly t _s indices corresponding to strings Σ _i in $\vec{\varSigma}_{j}$ generated by $SE_{1}''$ and $\vec{\xi}_{j}$ in the same positions has the corresponding ξ _i extraction keys and ⊥ in all other positions, and after seeing π the adversary does not make a query of the form $(\vec{\varSigma},*,x,\pi)$.

3 Multi-string NIZK Proofs Based on General Assumptions

As a warm-up, we will start out with a simple construction of a multi-string NIZK proof that works for t _c =0 and all choices of t _s ,t _z ,n where t _s +t _z >n. We use two tools in the construction, a length-doubling pseudorandom generator PRG and a zap (ℓ _zap,P _zap,V _zap).

Zaps

Zaps, introduced by Dwork and Naor [20], are two-round public coin witness-indistinguishable proofs, where the verifier’s first message is a random string that can be fixed once and for all and be reused in subsequent zaps. It follows from Dwork and Naor’s construction that zaps exist if NIZK proofs exist in the common random string model.

A zap for the NP-relation R is a triple (ℓ _zap,P _zap,V _zap), consisting of an input-increasing polynomial ℓ _zap, a probabilistic polynomial time prover P _zap and a probabilistic polynomial time verifier V _zap. Given an ℓ _zap(k)-bit random string σ, a statement x and a witness w such that (x,w)∈R, the prover outputs a proof π. The verifier given σ,x,π outputs 1 if accepting and 0 if rejecting the proof. The zap is complete, sound, and witness-indistinguishable as defined below.

Definition 9

(Completeness of zap)

We say (ℓ _zap,P _zap,V _zap) is (perfectly) complete if for all (x,w)∈R we have

$$\Pr \bigl[\sigma\gets\{0,1\}^{\ell_{\mathrm{zap}}(k)}; \pi\gets P_{\mathrm{zap}}( \sigma,x,w): V_{\mathrm{zap}}(\sigma,x,\pi)=1 \bigl] = 1. $$

Definition 10

(Soundness of zap)

We say (ℓ _zap,P _zap,V _zap) is (statistically) sound if for all adversaries $\mathcal {A}$ we have

$$\Pr \bigl[\sigma\gets\{0,1\}^{\ell_{\mathrm{zap}}(k)}; (x,\pi)\gets \mathcal {A} (\sigma): x\notin L \ \land\ V_{\mathrm{zap}}(\sigma,x,\pi)=1 \bigl] \approx0. $$

Definition 11

(Witness-indistinguishability of zap)

We say (ℓ _zap,P _zap,V _zap) is (computationally) witness-indistinguishable if for all non-uniform polynomial time interactive adversaries $\mathcal {A}$ we have

$$\begin{aligned}[t] \Pr \bigl[ & \sigma\gets\{0,1\}^{\ell_{\mathrm{zap}}(k)}; (x,w_0,w_1) \gets \mathcal {A} (\sigma); b\gets\{0,1\}; \pi\gets P_{\mathrm {zap}}(\sigma,x,w_b):\\ & \mathcal {A} (\pi)=b \bigl]\approx\frac{1}{2},\end{aligned} $$

where we require $\mathcal {A}$ outputs (x,w ₀,w ₁) such that (x,w ₀)∈R and (x,w ₁)∈R.

We will use zaps for circuit satisfiability. The verifier may not know the size of the circuit when generating the common reference string so we need zaps that work for arbitrarily large circuits. Following Dwork and Naor’s construction such zaps exist if we have NIZK proofs that work for arbitrarily large circuits. Using the non-interactive version of Naor’s statistically binding commitment scheme with security based on the existence of one-way functions [25, 43] such an NIZK proof can be constructed by committing to each wire-value in the circuit and making NIZK proofs for each wire commitment that it contains 0 or 1 and making NIZK proofs for each gate that the committed values respect the gate. We conclude that one-way functions can be used to stretch NIZK proofs to work for arbitrary circuit sizes and hence to get zaps for arbitrary circuit sizes.

Multi-string NIZK Proofs

A common reference string in our multi-string NIZK proof will consist of a random value r and an initial message σ for the zap. Given a statement x∈L, the prover makes n zaps using initial messages σ ₁,…,σ _n for the statement

$$x\in L \quad\textnormal{or}\quad \mbox{there are }t_z \textnormal{ common random strings where } r_i \textnormal{ is a pseudorandom value}. $$

In the simulation, we create simulation reference strings as r:=PRG(τ) enabling the simulator to make zaps without knowing a witness w for x∈L if instead the simulator knows the seeds of t _z pseudorandom values r _i .

Common reference string: :

Generate $r\gets\{0,1\}^{2k}; \sigma\gets\{0,1\}^{\ell_{\mathrm{zap}}(k)}$. Output Σ:=(r,σ).

Proof: :

Given input (Σ ₁,…,Σ _n ), a statement x and a witness w such that (x,w)∈R, replace any malformed Σ _i with the default CRS $\varSigma_{i}=(0^{2k},0^{\ell_{\mathrm{zap}}(k)})$ and construct a polynomial size circuit C that is satisfiable if and only if

$$x\in L\quad\textnormal{ or } \quad \bigl|\bigl\{r_i\ | \ \exists \tau_i : r_i=\mathrm{PRG}(\tau_i)\bigr\}\bigr|\geq t_z. $$

The prover does this using a witness-preserving NP-reduction so it can use w to compute a witness W for C being satisfiable. For all n common reference strings generate π _i ←P _zap(σ _i ,C,W). Return the proof Π:=(π ₁,…,π _n ).

Verification: :

Given n common reference strings (Σ ₁,…,Σ _n ) (again replacing any malformed Σ _i with the default CRS $(0^{2k},0^{\ell_{\mathrm{zap}}(k)})$), a statement x and a proof Π=(π ₁,…,π _n ) return 1 if and only if all of them satisfy V _zap(σ _i ,C,π _i )=1, where C is generated as in the proof.

Simulated reference string: :

Select τ←{0,1}^k;r:=PRG(τ) and $\sigma\gets \{0,1\}^{\ell_{\mathrm{zap}}(k)}$. Output ((r,σ),τ).

Simulated proof: :

Given input (Σ ₁,…,Σ _n ),(τ ₁,…,τ _n ),x such that there are exactly t _z non-trivial τ _i where r _i =PRG(τ _i ) we wish to simulate a proof Π. As in a proof, use the witness-preserving NP-reduction to get a circuit C that is satisfiable if and only if x∈L or |{r _i | ∃τ _i :r _i =PRG(τ _i )}|≥t _z . Use the t _z values τ _i ≠⊥ to get r _i =PRG(τ _i ) and compute a witness W for the satisfiability of C. For all n common reference strings, generate π _i ←P _zap(σ _i ,C,W). Return the simulated proof Π:=(π ₁,…,π _n ).

Lemma 12

The construction given above is a (0,t _s ,t _z ,n)-NIZK proof with uniformly random common reference strings for Circuit Satisfiability assuming PRG is a length-doubling pseudorandom number generator and (ℓ,P _zap,V _zap) is a zap.

Proof

Direct verification of our construction reveals that we have perfect completeness even for t _c =0.

Let us now prove that we have statistical (0,t _s ,t _z ,n)-soundness. Any honestly generated common reference string has negligible probability of containing a pseudorandom value r. With t _s honestly generated strings and t _z >n−t _s , there is negligible probability that Σ ₁,…,Σ _n have t _z or more pseudorandom values. If x∉L, the resulting circuit C is unsatisfiable. Also, at least one of the common reference strings has a correctly generated initial message for the zap. By the statistical soundness of the zap there is negligible probability that there exists a valid zap on this initial message for C being satisfiable.

We now turn to the question of computational (0,t _s ,t _z ,n)-zero-knowledge. Computational reference string indistinguishability follows from the pseudorandomness of PRG. With at least t _z simulated reference strings the only difference between proofs using the witness of x∈L and simulated proofs using the simulation trapdoors is the witnesses we are using in the zaps. Computational simulation indistinguishability therefore follows from a standard hybrid argument using the witness indistinguishability of the zaps. □

Theorem 13

Assuming one-way functions exist,¹ the existence of NIZK proofs for all NP-languages in the common random string model is equivalent to the existence of multi-string NIZK proofs for all NP-languages in the uniformly random multi-string model.

Proof

If one-way functions exist then pseudorandom generators exist [40]. If NIZK proofs exist in the common random string model then zaps exist in the common random string model [20]. Lemma 12 now shows that if one-way functions and NIZK proofs with common random strings exist then multi-string NIZK proofs exist with uniformly random strings.

Next, we will show that the existence of (n,t _s ,t _z ,n)-NIZK proofs implies the existence of standard NIZK proofs. The key generator picks n common reference strings for the NIZK proof and concatenates them to get a single common reference string. The prover interprets the common reference string as n common reference strings and runs the multi-string prover. The verifier interprets the common reference string as n common reference strings and runs the multi-string verifier. Completeness, soundness, and zero-knowledge follow directly from the multi-string completeness, soundness, and zero-knowledge. If the multi-string NIZK proof uses random strings then we get a random string NIZK proof. □

4 Multi-string Simulation-Extractable NIZK Proofs

We will now construct advanced multi-string NIZK proofs of knowledge that are both simulation-extractable and extraction zero-knowledge.

To permit the extraction of witnesses, we include a public key for an encryption scheme secure against adaptive chosen ciphertext attacks (K _CCA2,E,D) in each common reference string. The encryption scheme should have perfect decryption. To deal with bad public keys injected by the adversary we require without loss of generality that the encryption algorithm on an invalid public key outputs some ciphertext although with no guarantees of security or decryptability. In a proof, the prover will make a (t _s ,n)-threshold secret sharing of the witness and encrypt the shares under the n public keys. To extract the witness, the extractor decrypts t _s of these ciphertexts and combines the shares to get the witness.

We will use a strong one-time signature scheme (K _sots,Sign,Vfy) to prevent modifications of valid proofs. The prover generates a key (vk _sots,sk _sots)←K _sots(1^k) that she will use to sign the proof. The implication is that the adversary who sees simulated proofs must use a different vk _sots in her forged proof because she cannot forge the strong one-time signature.

Each common reference string will contain a random 2k-bit value, which in a simulation string will instead be a pseudorandom 2k-bit value. The prover will prove that she encrypted a (t _s ,n)-threshold secret sharing of the witness, or that she knows how to evaluate t _z pseudorandom functions PRF on vk _sots using the seeds of the respective common reference strings. On a real common reference string, this seed is not known and therefore she cannot make such a proof. On the other hand, in the simulation the simulator does know these seeds and can therefore simulate without knowing the witness.

Simulation soundness follows from the adversary’s inability to guess the pseudorandom functions’ evaluations on vk _sots, even if she knew the evaluations on many other verification keys.

Zero-knowledge under extraction attack follows from the adaptive chosen ciphertext attack security of the encryption scheme. Even after many extractions the ciphertexts still reveal nothing about the witness or whether the seed for a pseudorandom function has been used to simulate a proof.

Common reference string/simulation string: :

Generate $(pk_{1},dk_{1}),(pk_{2},dk_{2})\gets K_{\mathrm{CCA2}}(1^{k}); r\gets \{0,1\}^{2k}; \sigma\gets\{0,1\}^{\ell_{\mathrm{zap}}(k)}$. Return Σ:=(pk ₁,pk ₂,r,σ).

The simulators and extractors S ₁,E ₁,SE ₁ will generate the simulated reference strings in the same way, except for choosing τ←{0,1}^k and r:=PRF _τ (0). We use the simulation trapdoor τ and the extraction key ξ:=dk ₁.

In case the adversary supplies us with malformed common reference strings, we replace them with the default common reference string Σ:=K(1^k;0), so in the following we will without loss of generality assume that all common reference strings have the form (pk ₁,pk ₂,r,σ).

Proof: :

P((Σ ₁,…,Σ _n ),x,w) where (x,w)∈R runs as follows: Generate a key pair for the strong one-time signature scheme (vk _sots,sk _sots)←K _sots(1^k). Use (t _s ,n)-threshold secret sharing to get shares w ₁,…,w _n of w. Encrypt the shares as $c_{1i}:=E_{pk_{1i}}(w_{i},vk_{\mathrm{sots}};r_{1i})$ for i=1,…,n and encrypt dummy values $c_{2i}\gets E_{pk_{2i}}(0^{2k})$. Consider the statement:

“All c _1i encrypt (w _i ,vk _sots), where w ₁,…,w _n is a (t _s ,n)-secret sharing of a witness w such that (x,w)∈R or there exist at least t _z seeds τ _i such that $r_{i}=\mathrm{PRF}_{\tau_{i}}(0)$ and c _2i encrypts $\mathrm{PRF}_{\tau_{i}}(vk_{\mathrm{sots}})$.”

Reduce this statement to a polynomial size circuit C and a satisfiability witness W. For all i create a zap π _i ←P _zap(σ _i ,C,W) for C being satisfiable. Finally, sign everything using the strong one-time signature $\mathit{sig}\gets \mathrm{Sign}_{sk_{\mathrm{sots}}}(vk_{\mathrm{sots}},x,\varSigma _{1},c_{11},c_{21},\pi_{1},\allowbreak \ldots,\varSigma_{n},c_{1n},c_{2n},\pi_{n})$.

The proof is Π:=(vk _sots,c ₁₁,c ₂₁,π ₁,…,c _1n ,c _2n ,π _n ,sig).

Verification: :

To verify Π of the form described above, verify the strong one-time signature and verify the n zaps π ₁,…,π _n .

Extraction: :

To extract a witness check that the proof is valid. Next, use the t _s extraction keys in $\vec{\xi}$ to decrypt the corresponding t _s ciphertexts. Check that the plaintexts are of the form (w _i ,vk _sots) and combine the t _s secret shares to recover the witness w. If any of the checks fail return ⊥.

Simulated proof: :

To simulate a proof use the t _z simulation trapdoors in $\vec{\tau}$. These are τ _i such that $r_{i}=\mathrm{PRF}_{\tau_{i}}(0)$. As in the proof generate (vk _sots,sk _sots)←K _sots(1^k). Create t _z pseudorandom values $v_{i}:=\mathrm{PRF}_{\tau_{i}}(vk_{\mathrm{sots}})$. Encrypt the values as $c_{2i}\gets E_{pk_{2i}}(v_{i})$. For the other reference strings, just let $c_{2i}\gets E_{pk_{2i}}(0^{2k})$. Let w ₁,…,w _n be a (t _s ,n)-threshold secret sharing of 0 and encrypt these values as $c_{1i}\gets E_{pk_{1i}}(w_{i},vk_{\mathrm{sots}})$. Let again C be the circuit corresponding to the statement

“All c _1i encrypt (w _i ,vk _sots), where w ₁,…,w _n is a (t _s ,n)-secret sharing of a witness w or there exist at least t _z seeds τ _i such that $r_{i}=\mathrm{PRF}_{\tau_{i}}(0)$ and c _2i encrypts $\mathrm{PRF}_{\tau_{i}}(vk_{\mathrm{sots}})$.”

From the creation of the ciphertexts c _2i we have a witness W for C being satisfiable. Create zaps π _i ←P _zap(σ _i ,C,W) for C being satisfiable. Finally, make a strong one-time signature on everything $\mathit{sig}\gets \mathrm{Sign}_{sk_{\mathrm{sots}}}(vk_{\mathrm{sots}},x,\varSigma _{1},c_{11},c_{21},\pi_{1},\ldots,\varSigma_{n},c_{1n},\allowbreak c_{2n},\pi_{n})$. The simulated proof is Π:=(vk _sots,c ₁₁,c ₂₁,π ₁,…,c _1n ,c _2n ,π _n ,sig).

Lemma 14

The construction given above is a (0,t _s ,t _z ,n)-NIZK proof of knowledge for Circuit Satisfiability for all choices of t _s +t _z >n with simulation-extractability and extraction zero-knowledge. If the public-key encryption scheme has random public keys then the construction has uniform random strings.²

Proof

Perfect completeness follows by direct verification. Common reference strings and simulated reference strings are indistinguishable by the pseudorandomness of the pseudorandom function PRF. The (t _z ,n)-zero knowledge property follows from the extraction zero-knowledge property that we will now prove.

The adversary knows the simulation trapdoors τ _i , and has access to an extraction oracle. She selects a statement x and a witness w and has to distinguish a proof on a simulated reference string created either by the prover using a real witness or the simulator using the simulation trapdoors. We consider a series of hybrid experiments.

Hybrid 1: :

This is the experiment where we run the adversary on a simulated reference string and make the challenge proof using the witness w as a real prover would do.

Hybrid 2: :

We modify hybrid 1 by encrypting t _z pseudorandom values in c ₂₁,…,c _2n when making the challenge proof. We know t _z seeds τ _i such that $r_{i}=\mathrm{PRF}_{\tau_{i}}(0)$. Instead of setting $c_{2i}\gets E_{pk_{2}}(0^{2k})$, we encrypt $c_{2i}\gets E_{pk_{2}}(\mathrm{PRF}_{\tau_{i}}(vk_{\mathrm{sots}}))$.

By the semantic security of the encryption scheme, hybrid 1 and hybrid 2 are computationally indistinguishable.

Hybrid 3: :

We modify hybrid 2 by reducing the pseudorandom values and the randomness used in forming the ciphertexts c ₂₁,…,c _2n to form a witness W for C being satisfiable. We use this witness in the zaps when creating the challenge proof instead of using the witness w.

By the witness-indistinguishability of the zaps, hybrid experiments 2 and 3 are indistinguishable.

Hybrid 4: :

We modify hybrid 3 such that if the adversary’s extraction query is of the form $(\vec{\varSigma},I,x,\varPi)$, where the index contains some i where Σ _i has been generated by $SE_{1}'$ and c _1i is recycled from the challenge proof then the extraction oracle returns ⊥.

To make a valid proof, the adversary has to give a strong one-time signature using her chosen verification key. By the existential unforgeability of the strong one-time signature scheme, this verification key has to differ from the verification key vk _sots used in the challenge. This means c _1i contains the wrong verification key. The regular behavior of the extraction oracle in hybrid 3 would therefore also be to return ⊥, so there is negligible difference between hybrid 3 and hybrid 4.

Hybrid 5: :

We modify hybrid 4 by making a (t _s ,n)-threshold secret sharing w ₁,…,w _n of 0 instead of secret sharing w and encrypting these shares as $c_{1i}\gets E_{pk_{1i}}(w_{i},vk_{\mathrm{sots}})$ in the challenge proof.

Hybrid 4 and hybrid 5 are indistinguishable. We have ruled out that the adversary ever makes an extraction query requiring decryption of a ciphertext c _1i that has been recycled from the challenge proof. A hybrid argument using the chosen ciphertext attack security of the encryption scheme can now be used to see that the adversary cannot distinguish encryptions of shares of a threshold secret sharing of w from shares of a threshold secret sharing of 0. The remaining n−t _z <t _s shares do not reveal whether w or 0 has been secret shared.

Hybrid 6: :

We modify hybrid 5 by switching back to the original extraction oracle. Hybrid 6 is identical to the case where we give the adversary a simulated challenge proof.

Since there is negligible probability of forging a strong one-time signature, we can give a similar argument as we did when going from hybrid 3 to hybrid 4 that either type of extraction oracle with overwhelming probability outputs ⊥ when facing a query $(\vec{\varSigma},I,x,\varPi)$ where the index indicates some i where c _1i has been recycled from the challenge proof.

Next, let us consider simulation-sound extractability. Here the adversary sees the extraction keys but not the simulation trapdoors of the common reference strings generated by $SE_{1}'$. She has access to a simulation oracle and in the end she outputs a statement and a proof. By the unforgeability of the strong one-time signature scheme, she cannot reuse a strong verification key vk _sots used in a simulated proof. Let us look at a simulated reference string generated by $SE_{1}'$. Since the adversary does not know the seed for the pseudorandom function, she cannot encrypt a pseudorandom function evaluation of vk _sots. The zaps, of which at least one uses a correctly generated initial message, then tell us that c ₁₁,…,c _1n contain a (t _s ,n)-threshold secret sharing of w. Decrypting t _s of these ciphertexts, permits us to reconstruct the witness w.

A similar proof, shows that the construction gives a statistical (0,t _s ,t _z ,n)-proof of knowledge. With overwhelming probability a random 2k-bit value r is not pseudorandom, so by the statistical soundness of the zaps c ₁₁,…,c _1n must encrypt a (t _s ,n)-threshold secret sharing of a witness for x∈L. □

Theorem 15

If NIZK proofs with uniform random strings and CCA2-secure public key encryption with uniformly random public keys exist, then multi-string NIZK proof of knowledge with simulation-extractability and extraction zero-knowledge exist in the uniform random strings model for all languages in NP.

Proof

CCA2-secure public key encryption implies the existence of one-way functions, from which it is possible to construct both pseudorandom functions [31] and strong one-way functions. NIZK proofs with uniform random strings imply the existence of zaps. Lemma 14 now gives us the existence of multi-string NIZK proofs of knowledge with simulation-extractability and extraction zero-knowledge in the uniform random strings model. □

5 Multi-string NIZK Proofs from Bilinear Groups

We will use bilinear groups to construct a (0,t _s ,t _z ,n)-simulation-sound NIZK proof for circuit satisfiability consisting of $\mathcal{O}((n+|C|)k)$ bits, where |C| is the number of gates in the circuit and k is a security parameter specifying the size of the bilinear group elements. Typically, n will be much smaller than |C|, so the complexity matches the best known NIZK proofs for circuit satisfiability in the single common reference string model [39] that have proofs of size $\mathcal{O}(|C|k)$.

Setup

We will use bilinear groups generated by $(p,\mathbb{G},\mathbb{G}_{T},e,g)\gets\mathcal{G}(1^{k})$ such that:

• p is a k-bit prime.

• $\mathbb{G},\mathbb{G}_{T}$ are cyclic groups of order p.

• g is a generator of $\mathbb{G}$.

• $e:\mathbb{G}\times\mathbb{G}\rightarrow\mathbb{G}_{T}$ is a bilinear map such that e(g,g) generates $\mathbb{G}_{T}$ and for all $a,b\in\mathbb{Z}_{p}$ we have e(g ^a,g ^b)=e(g,g)^ab.

• Group operations, group membership, and the bilinear map are efficiently computable.

• Given a description $(p,\mathbb{G},\mathbb{G}_{T},e,g)$ it is efficiently verifiable that indeed it is a bilinear group and that g generates $\mathbb{G}$.

• There is an efficient sampling algorithm that given a random string of 61k bits interprets it as 60 statistically close to uniformly random group elements. The sampling algorithm is efficiently reversible, such that given 60 group elements we can pick at random one of the 61k-bit strings that would lead to sampling them.

• The length of the description of $(p,\mathbb{G},\mathbb{G}_{T},e,g)$ is at most 4k bits.³

• If uniformly random reference strings are desired we will additionally assume $\mathcal{G}$ simply outputs a uniformly random 4k-bit string from which $(p,\mathbb{G},\mathbb{G}_{T},e,g)$ can be sampled.

The security of our multi-string NIZK proof will rely on the decisional linear (DLIN) assumption introduced by Boneh, Boyen, and Shacham [10], which says that given group elements (f,g,h,f ^r,g ^s,h ^t) it is hard to tell whether t=r+s or t is random. Throughout the paper, we use bilinear groups $(p,\mathbb{G},\mathbb{G}_{T},e,g)\gets\mathcal{G}(1^{k})$ generated such that the DLIN assumption holds for $\mathcal{G}$, which we formally define below.

Definition 16

(DLIN group generator)

A bilinear group generator $\mathcal{G}$ as described above is a DLIN group generator if for all non-uniform polynomial time adversaries $\mathcal{A}$

Example

We will offer a class of candidates for DLIN groups as described above. Consider the elliptic curve y ²≡x ³+1modq, where q≡2mod3 is a prime. It is straightforward to check whether a point (x,y) is on the curve. Furthermore, picking $y\in\mathbb{Z}_{q}$ and computing x≡(y ²−1)^{(1+2(q−1))/3}modq gives us a point on the curve. The curve has a total of q+1 points after including also the point at infinity.

When generating bilinear groups, we will pick p as a k-bit prime. We then let q≡2mod3 be the smallest prime⁴ such that p|q+1 and define $\mathbb{G}$ to be the order p subgroup of the curve. The target group is the order p subgroup of $\mathbb{F}_{q^{2}}^{*}$ and the bilinear map is the modified Weyl-pairing [9]. Verification of $(p,\mathbb{G},\mathbb{G}_{T},e,g)$ being a bilinear group is straightforward, since it corresponds to checking that p,q are primes such that p|q+1 and q≡2mod3 and g is an order p element on the curve. A random point on the curve can be sampled by picking $y\gets\mathbb{Z}_{q}\cup\{\infty\}$ and solving for the unique x such that y≡x ³+1modq or letting it be the point of infinity in case y=∞. A random element of the group $\mathbb{G}$ can be sampled by picking a random point (x,y) on the curve and raising it to $\frac{1+2(q-1)}{p}$. These sampling processes are reversible since multiplying a group element with a random point on the curve of order $\frac{1+2(q-1)}{p}$, i.e., a random point raised to p, gives a random (x,y) on the curve that would generate the group element.

Pseudorandom Generators in DLIN Groups

Before proceeding, let us demonstrate that the DLIN assumption permits the construction of a pseudorandom number generator. Consider a DLIN group $(p,\mathbb{G},\mathbb{G}_{T},e,g)$. Choose $x,y\gets\mathbb{Z}_{p}^{*}$ at random and set f=g ^x, h=g ^y. Given random elements $u,v\gets \mathbb{G}$, we can compute w=u ^1/x v ^1/y. The DLIN assumption says that (f,h,u,v,w) is indistinguishable from (f,h,u,v,r), where r is a random group element from $\mathbb{G}$. In other words, we can create a pseudorandom generator (x,y,u,v)↦(g ^x,g ^y,u,v,u ^1/x v ^1/y) that stretches our randomness with an extra group element.

We will need a bigger stretch, so let us generalize the construction above using the idea of synthesizers from Naor and Reingold [44]. We pick M pairs $(x_{i},y_{i})\gets\mathbb{Z}_{p}^{*}\times\mathbb{Z}_{p}^{*}$ and create corresponding $f_{i}=g^{x_{i}}$, $h_{i}=g^{y_{i}}$. We can now stretch 2N group elements u ₁,v ₁,…,u _N ,v _N with MN extra group elements by computing $w_{ij}:=u_{j}^{1/x_{i}}v_{j}^{1/y_{i}}$.

If the N pairs of group elements (u _j ,v _j ) are chosen at random, then (f ₁,h ₁,…,f _M ,h _M ,u ₁,v ₁,…,u _N ,v _N ,w ₁₁,…,w _MN ) looks like a random 2M+2N+MN-tuple of group elements. To see this, consider the following hybrid experiment E _I,J , where we pick w _ij at random for pairs (i,j) where i<I∨(i=I∧j<J) and compute the rest of the w _ij ’s according to the method described above. We need to prove that the w _ij ’s generated in, respectively, E _1,1 and E _M,N+1 are indistinguishable.

Consider first experiments E _I,J ,E _I,J+1 for 1≤I≤M,1≤J≤N. In case there is a non-uniform polynomial time adversary $\mathcal{A}$ that can distinguish these two experiments, then we can break the DLIN assumption as follows. We have a challenge (f,h,u,v,w) and wish to know whether w=u ^1/x v ^1/y or w is random. We let f _I :=f,h _I :=h and generate all the other f _i ,h _i ’s according to the protocol. We set u _J :=u, v _J :=v and w _IJ :=w. For i<I we pick w _ij at random. Also, for i=I, j<J we pick w _ij at random. For i=I,j>J we pick r _j ,s _j at random and set $(u_{j},v_{j},w_{Ij})=(f^{r_{j}},h^{s_{j}},g^{r_{j}+s_{j}})$. For j<J we select (u _j ,v _j ) at random. Finally, for i>I we compute all w _ij according to the protocol. If (u,v,w) is a linear tuple, we have the distribution from experiment E _I,J , whereas if (u,v,w) is a random tuple we have the distribution from experiment E _I,J+1. An adversary distinguishing these two experiments, therefore permits us to distinguish linear tuples from random tuples. We conclude the proof by observing E _I+1,1=E _I,N+1.

Observe, it is straightforward to provide a witness for (u,v,w) being a linear tuple. The witness consists of π=u ^y/x and (u,v,w) is a linear tuple if and only if there is a π such that e(u,h)=e(f,π) and e(g,πv)=e(w,h). In other words, we can provide MN proofs π _ij for w _ij being correct. Furthermore, all these proofs consist of group elements and can be verified by checking a set of pairing product equations. It follows from Groth [37] that there exists a simulation-sound NIZK proof of size $\mathcal{O}(MN)$ group elements for the w _ij ’s having been computed correctly.

Multi-string NIZK Proofs from DLIN Groups

One could hope that the construction from Sect. 3 could be implemented efficiently using groups with a bilinear map. However, this strategy does not work because each common reference string is generated at random and independently of the others. This means that even if the common reference strings contain descriptions of groups with bilinear maps, most likely they are different and incompatible groups.

In our construction, we instead let all the common reference strings describe different groups and we also let the prover pick a group with a bilinear map. Our solution to the problem described above, is to translate simulation reference strings created by the authorities into simulation reference strings in the prover’s group. This translation will require the use of a pseudorandom generator that we constructed earlier. As mentioned earlier this pseudorandom generator is constructed in such a way that there exist linear size simulation-sound NIZK proofs for a value being pseudorandom [37].

Consider a common reference string with group $\mathbb{G}_{i}$ and the prover’s group $\mathbb{G}$. We will let the common reference string contain a random string r _i . The prover will choose a string s _i . Consider the pair of strings (r _i ⊕s _i ,s _i ). Since strings can be interpreted as group elements, we have corresponding sets of group elements in respectively $\mathbb{G}_{i}$ and $\mathbb{G}$. However, since r _i is chosen at random it is unlikely that r _i ⊕s _i corresponds to a pseudorandom value in $\mathbb{G}_{i}$ and at the same time s _i corresponds to a pseudorandom value in $\mathbb{G}$. Of course, the prover has some degree of freedom in choosing the group $\mathbb{G}$, but if we are careful and chooses a pseudorandom generator that stretches the input sufficiently then we can use an entropy argument for it being unlikely that both strings are pseudorandom values.

Now we use non-interactive zaps and NIZK proofs to bridge the two groups. The prover will select s _i such that r _i ⊕s _i is a pseudorandom value in $\mathbb{G}_{i}$ specified by the common reference string and give an NIZK proof for this using that common reference string. In her own group, she gets n values s ₁,…,s _n and proves that t _z of those are pseudorandom or C is satisfiable. In the simulation, she knows the simulation trapdoors for t _z reference strings and she can therefore simulate NIZK proofs of r _i ⊕s _i being pseudorandom. This means, she can select the corresponding s _i ’s as pseudorandom values and use this to prove that there are at least t _z pseudorandom values in her own group, so she does not need to know the satisfiability witness w for C being satisfiable to carry out the proof in her own bilinear group.

There is another technical detail to consider. We want the construction to be efficient in n. Therefore, instead of proving directly that there are t _z pseudorandom values or C is satisfiable, we use a homomorphically encrypted counter. In the simulation, we set the counter to 1 for each pseudorandom value and to 0 for the rest of the values in the prover’s group. The homomorphic property enables us to multiply these ciphertexts and get an encrypted count of t _z . It is straightforward to prove that the count is t _z or C is satisfiable.

These ideas describe how to get soundness. We can set up the common reference strings such that they enable us to make simulation-sound NIZK proofs in their bilinear groups. With a few extra ideas, we then get a (0,t _s ,t _z ,n)-simulation-sound NIZK proof for circuit satisfiability when t _s +t _z >n.

Common reference string/simulation reference string: :

Generate a DLIN group $(p,\mathbb{G},\mathbb{G}_{T},e,g)\gets \mathcal{G}(1^{k})$. Generate a common reference string for a simulation-sound NIZK proof on basis of this group $\sigma\gets K_{\text{sim-sound}}(p,\mathbb{G},\mathbb{G}_{T},e,g)$ as in [37]. Also, pick a random string r←{0,1}^61k. Output $\varSigma:=(p,\mathbb{G},\mathbb{G}_{T},e,g,\sigma,r)$.

If one can sample DLIN groups from uniformly random strings the common reference strings can be uniformly random bit-strings.

When generating a simulation reference string, use the simulator for the simulation-sound NIZK proof to generate $(\sigma,\tau)\gets S_{\text{sim-sound}}(p,\mathbb{G},\mathbb{G}_{T},e,g)$. Output Σ as described above and simulation trapdoor τ.

It is possible to efficiently verify the validity of the bilinear group, the correct length of r and that σ gives perfect completeness. If either check fails we will assume the prover and verifier replace it with a default common reference string.

Proof: :

Given (Σ ₁,…,Σ _n ),C,w such that C(w)=1 do the following. Pick a group $(p,\mathbb{G},\mathbb{G}_{T},e,g)\gets\mathcal{G}(1^{k})$. Pick also keys for a strong one-time signature scheme (vk _sots,sk _sots)←K _sots(1^k). Encode vk _sots as a tuple of $\mathcal{O}(1)$ group elements from $\mathbb{G}$.

For each common reference string Σ _i do the following. Pick a pseudorandom value with 6 key pairs, 6 input pairs and 36 structured elements. This gives us a total of 60 group elements from $\mathbb{G}_{i}$. Concatenate the tuple of 60 group elements with vk _sots to get $\mathcal{O}(1)$ group elements from $\mathbb{G}_{i}$. Make a simulation-sound NIZK proof, using σ _i , for these $\mathcal{O}(1)$ group elements being of a form such that the first 60 of them constitute a pseudorandom value. From [37] we know that the size of this proof is $\mathcal{O}(1)$ group elements from $\mathbb{G}_{i}$. Define s _i ∈{0,1}^61k to be a random string such that r _i ⊕s _i parses to the 60 group element pseudorandom value.

From now on we will work in the group $(p,\mathbb{G},\mathbb{G}_{T},e,g)$ chosen by the prover. Pick pk:=(f,h) as two random group elements. This gives us a CPA-secure encryption scheme [10], encrypting a message $m\in\mathbb{G}$ with randomness $r,s\in\mathbb{Z}_{p}$ as E _pk (m;r,s):=(f ^r,h ^s,g ^r+s m). For each i=1,…,n we encrypt 1=g ⁰ as c _i ←E _pk (1). Also, we take s _i and parse it as a tuple z _i of 60 group elements.

Make a non-interactive zap π using the group $(p,\mathbb{G},\mathbb{G}_{T},e,g)$ and combining techniques of [39] and [37] for the following statement:

$$ \begin{aligned}[t] &C \textnormal{ satisfiable } \lor {\Biggl(} \prod _{i=1}^nc_i \textnormal{ encrypts } g^{t_z} \land \forall i: \\ & \quad{} c_i \textnormal{ encrypts } g^0 \textnormal { or } g^1 \ \land\ \bigl( z_i \textnormal{ is a pseudorandom value } \lor c_i \textnormal{ encrypts }g^0 \bigr) {\Biggr)}. \end{aligned} $$

(1)

The zap consists of $\mathcal{O}(n+|C|)$ group elements and has perfect soundness.

Sign everything $\mathit{sig}\gets \mathrm{Sign}_{sk_{\mathrm{sots}}}(vk_{\mathrm{sots}},C,\varSigma_{1},s_{1},\pi _{1},c_{1},\ldots,\varSigma_{n},s_{n},\pi_{n},c_{n},p,\mathbb{G},\allowbreak \mathbb {G}_{T},e,g,f,h,\pi)$.

The proof is $\varPi:=(vk_{\mathrm{sots}},s_{1},\pi_{1},c_{1},\ldots,s_{n},\pi_{n},c_{n},p,\mathbb {G},\mathbb{G}_{T},e,g,f,h,\pi,\mathit{sig})$.

Verification: :

Given common reference strings Σ ₁,…,Σ _n , a circuit C and a proof as described above, do the following. For all i check the simulation-sound NIZK proofs π _i for r _i ⊕s _i encoding a pseudorandom value in $\mathbb{G}_{i}$ using common reference string σ _i . Verify $(p,\mathbb{G},\mathbb{G}_{T},e,g)$ is a group with a bilinear map. Verify the zap π. Verify the strong one-time signature on everything. Output 1 if all checks are ok.

Simulated proof: :

We are given reference strings Σ ₁,…,Σ _n , of which t _z are simulation strings where we know the simulation trapdoors τ _i for the simulation-sound NIZK proofs. We wish to simulate a proof for a circuit C being satisfiable.

We start by choosing a group $(p,\mathbb{G},\mathbb{G}_{T},e,g)\gets \mathcal{G}(1^{k})$ and public key $f,h\gets\mathbb{G}$. We create ciphertexts c _i ←E _pk (g ¹) for the t _z simulation reference strings, where we know the trapdoor τ _i , and set c _i ←E _pk (g ⁰) for the rest. We also choose a strong one-time signature key pair (vk _sots,sk _sots)←K _sots(1^k).

For t _z of the common reference strings, we know the simulation key τ _i . This permits us to choose an arbitrary string s _i and simulate a proof π _i that r _i ⊕s _i encodes a 60 element pseudorandom value. This means, we are free to choose s _i such that it encodes a pseudorandom value z _i in $\mathbb{G}^{60}$. For the remaining n−t _z <t _s reference strings, we select s _i such that r _i ⊕s _i does encode a pseudorandom value in $\mathbb{G}_{i}$ and carry out a real simulation-sound NIZK proof π _i for it being a pseudorandom value concatenated with vk _sots.

For all i we have c _i encrypting g ^b, where b∈{0,1}. We have $\prod_{i=1}^{n}c_{i}$ encrypting $g^{t_{z}}$. We also have for the t _z simulation strings, where we know τ _i that s _i encodes a pseudorandom value, whereas for the other common reference strings we have c _i encrypts g ⁰. This means we can create the non-interactive zap π for (1) without knowing C’s satisfiability witness.

Sign everything $\mathit{sig}\gets \mathrm{Sign}_{sk_{\mathrm{sots}}}(vk_{\mathrm{sots}},C,\varSigma_{1},s_{1},\pi _{1},c_{1},\ldots,\varSigma_{n},s_{n},\pi_{n},c_{n},p,\mathbb{G},\allowbreak \mathbb {G}_{T},e,g,f,h,\pi)$.

The simulated proof is $\varPi:=(vk_{\mathrm{sots}},s_{1},\pi_{1},c_{1},\ldots,s_{n},\pi_{n},c_{n},p,\mathbb {G},\mathbb{G}_{T},e,g,f,h,\pi,\allowbreak \mathit{sig})$.

Theorem 17

If $\mathcal{G}$ is a DLIN group generator as defined in the beginning of this section, then the construction above gives us a (0,t _s ,t _z ,n)-simulation-sound NIZK proof for circuit satisfiability, where the proofs have size $\mathcal{O}((n+|C|)k)$ bits. The scheme can be set up with uniformly random reference strings if we can sample groups with bilinear maps from uniformly random strings.

Proof

We have already argued in the construction that if we can sample groups and group elements from random strings and vice versa given groups and group elements sample random strings that yield these group elements then we can use uniformly random strings. Perfect completeness follows by straightforward verification.

Let us prove that we have statistical (0,t _s ,t _z ,n)-soundness. Consider first an arbitrary group $(p,\mathbb{G},\mathbb{G}_{T},e,g)$ chosen by the prover. By assumption, it can be verified that this describes a group with a bilinear map.

We will now bound the probability of both r _i ⊕s _i and s _i sampling pseudorandom 60-tuples of group elements in their respective groups for a random choice of r _i . Consider first the probability that a random string s _i specifies a pseudorandom value in $\mathbb{G}^{60}$. There are at most 2^24k pseudorandom strings, since the 12 pairs (f _i ,h _i ) and the 12 pairs (u _j ,v _j ) fully define the pseudorandom value. 60 random group elements have at least 59k bits of entropy, so we get a probability of at most 2^24k−59k=2^−35k of s _i specifying a pseudorandom value in $\mathbb{G}^{60}$. Similarly, for a random choice of r _i we have at most probability 2^−35k that r _i ⊕s _i is a pseudorandom value in the group specified by the common reference string. With r _i ,s _i both chosen at random, we have a combined maximal probability of 2^−70k of both r _i ⊕s _i and s _i specifying pseudorandom values. The prover can choose the group freely, giving her at most 2^4k different choices for describing the group $\mathbb{G}$ and g. She can also choose s _i freely, giving her 2^61k possibilities. Since r _i is chosen at random, there is at most probability 2^4k+61k−70k=2^−5k of it being possible to choose s _i and the group $\mathbb{G}$ such that both r _i ⊕s _i and s _i specify pseudorandom values. With overwhelming probability, we can therefore assume that no honestly generated common reference string exists such that both r _i ⊕s _i and s _i specify pseudorandom values in $\mathbb{G}_{i}$ and $\mathbb{G,}$ respectively.

Any common reference string Σ _i that is honestly generated has overwhelming probability of having a common reference string σ _i for the simulation-sound NIZK with perfect soundness. Whenever the prover makes a proof using this string, she must therefore pick s _i such that r _i ⊕s _i is pseudorandom. Consequently, s _i does not specify a pseudorandom value in the group $\mathbb{G}$. The zap has perfect soundness, so it shows that C is satisfiable or c _i contains g ⁰. Similarly, for any string Σ _i that is not honestly generated, the zap demonstrates that C is satisfiable or c _i contains g ⁰ or g ¹. Since at least t _s >n−t _z strings are honestly generated, we see that if C is unsatisfiable, then $\prod_{i=1}^{n}c_{i}$ contains one of the values $g^{0},\ldots,g^{t_{z}-1}$. The zap therefore shows us that C must be satisfiable.

To argue computational (0,t _s ,t _z ,n)-simulation-soundness, observe that simulated proofs are signed with a strong one-time signature. Since the signature scheme has existential unforgeability, the adversary must choose a different vk _sots that it has not seen in a simulation. Recall, whenever we make a simulation-sound NIZK using a particular common reference string Σ _i , we concatenate vk _sots to r _i ⊕s _i to get the statement we wish to prove. By the simulation-soundness of the NIZK proofs on honestly generated strings, we cannot forge such a proof even though we have already seen simulated proofs. Therefore, r _i ⊕s _i must be a pseudorandom string. We can now argue (0,t _s ,t _z ,n)-simulation-soundness just as we argued (0,t _s ,t _z ,n)-soundness.

It remains to prove computational (0,t _s ,t _z ,n)-zero-knowledge. Reference string indistinguishability follows from the reference string indistinguishability of the simulation-sound NIZK proofs. We will now consider simulation indistinguishability, so consider a case where the adversary sees simulated reference strings and gets the simulation trapdoors that allow the simulation of proofs for the reference strings. The adversary, chooses a set of common reference strings and receives a proof generated with the satisfiability witness for C or alternatively a simulated proof and wants to distinguish between the two possibilities.

Let us start with a simulated proof and compare it with a hybrid experiment, where we use the satisfiability witness for C in the non-interactive zap. By the computational witness-indistinguishability of the zap, the adversary cannot tell these two experiments apart. Next, let us choose all c _i ’s as encryptions of g ⁰. By the semantic security of the encryption scheme, the adversary cannot detect this change. We already select s _i such that r _i ⊕s _i specifies a pseudorandom value for the reference strings not generated by S ₁. Let us switch to also selecting s _i such that r _i ⊕s _i specify a pseudorandom value in the common reference strings where we do know the simulation trapdoor. By the pseudorandomness of the strings, the adversary cannot detect this change either. Finally, instead of simulating the proofs for r _i ⊕s _i specifying a pseudorandom value in $\mathbb{G}_{i}$, let us make a real proof. By the zero-knowledge property of the simulated reference strings for the simulation-sound NIZK proofs, the adversary cannot distinguish here either. With this last modification, we have actually ended up constructing proofs exactly as a real prover with access to a satisfiability witness does, so we have (0,t _s ,t _z ,n)-zero-knowledge. □

6 Multi-party Computation in the UC Framework

In the rest of the paper, we will work in Canetti’s UC framework. The universal composability (UC) framework, see [11] for a detailed description, is a strong security model capturing security of a protocol under concurrent execution of arbitrary protocols. We model everything happening concurrently with the protocol but not directly related to it through an environment $\mathcal{Z}$. The environment can at its own choosing give inputs to the parties running the protocol and according to the protocol specification the parties may give outputs to the environment. In addition, there is an adversary $\mathcal{A}$ that attacks the protocol. $\mathcal{A}$ can communicate freely with the environment. She can adaptively corrupt parties, in which case she learns the entire history of the party and gains complete control over the actions of the party. The environment learns whenever a party is corrupted.

To model security we use a simulation paradigm. We specify the functionality $\mathcal{F}$ that the protocol should realize. The functionality $\mathcal{F}$ can be seen as a trusted party that handles the entire protocol execution and tells the parties what they would output if they executed the protocol correctly. In the ideal process, the parties simply pass on inputs from the environment to $\mathcal{F}$ and whenever receiving a message from $\mathcal{F}$ they output it to the environment. In the ideal process, we have an ideal process adversary $\mathcal{S}$. $\mathcal{S}$ does not learn the content of messages sent from $\mathcal{F}$ to the parties, but is in control of when, if ever, a message from $\mathcal{F}$ is delivered to the designated party. $\mathcal{S}$ can corrupt parties and when doing so it learns the history of the party. As the real world adversary, $\mathcal{S}$ can freely communicate with the environment.

Comparing these two models we say that the protocol securely realizes $\mathcal{F}$ if no environment can distinguish between the two worlds. This means, the protocol is secure, if for any polynomial time $\mathcal{A}$ running in the real world, there exists a polynomial time $\mathcal{S}$ running in the ideal process with $\mathcal{F}$, so no non-uniform polynomial time environment can distinguish between the two worlds.

One of our goals is to show that any well-formed functionality can be securely realized in the multi-string model. By well-formed functionality, we mean a functionality that is oblivious of corruptions of parties, runs in polynomial time, and in case all parties are corrupted it reveals the internal randomness used by the functionality to the ideal process adversary. This class contains all functionalities that we can reasonably expect to implement with multi-party computation, because an adversary can always corrupt a party and just have it follow the protocol, in which case the other parties in the protocol would never learn that it was corrupted.

Ideal Functionalities

Let us formalize the multi-string model in the UC framework. Figure 1 gives an ideal multi-string functionality $\mathcal{F}_{\mathrm{MCRS}}$.

Fig. 1.

The ideal multi-string generator.

We will assume parties can broadcast their messages and we make this assumption explicit by giving them access to the ideal broadcast functionality in Fig. 2. Ideal broadcast permits each party to broadcast messages to other parties. We remark that broadcast can be securely realized in a constant number of rounds if authenticated communication is available [33]. Furthermore, authenticated communication can be securely realized using digital signatures, so one possible setup is that the parties somehow have exchanged verification keys for a digital signature scheme.

Fig. 2.

The ideal authenticated broadcast functionality.

6.1 Tools

We will now present a few tools that we will need in our constructions.

Encryption Scheme with Pseudorandom Public Keys and Pseudorandom Ciphertexts

An encryption scheme (K _pseudo,E,D) has pseudorandom ciphertexts of length ℓ _E (k) if for all non-uniform polynomial time adversaries $\mathcal{A}$ we have

where R _pk (m) runs $c\gets\{0,1\}^{\ell_{E}(k)}$ and returns c. Moreover, an encryption scheme has pseudorandom public keys of length ℓ _K (k) if correctly generated public keys are computationally indistinguishable from random strings of length ℓ _K (k) bits.

We will use an encryption scheme with pseudorandom public keys and pseudorandom ciphertexts with errorless decryption. Damgård and Nielsen [19] show that such encryption schemes, which they call simulatable encryption schemes, exist under standard assumptions such as RSA or DDH.

Tag-Based Simulation-Sound Trapdoor Commitment

A tag-based simulation sound trapdoor commitment scheme [42] has four probabilistic polynomial time algorithms (K _tag-com,Com,TCom,Topen). The key generation algorithm K _tag-com produces a commitment key ck as well as a trapdoor key tk. The commitment key specifies amongst other things the message space, which we will assume is of the form {0,1}^ℓ for some suitable ℓ polynomially bounded by k. There is a commitment algorithm that takes as input the commitment key ck, a message m∈{0,1}^ℓ and any tag tag∈{0,1}^∗ and outputs a commitment c:=Com _ck (tag;m;r). To open a commitment c with tag tag we reveal m and the randomness r. Anybody can now verify c=Com _ck (tag;m;r). As usual, the commitment scheme must be both hiding and binding.

The algorithms Tcom,Topen allow us to create an equivocal commitment and later open this commitment to any value we prefer. We create an equivocal commitment and an equivocation key as (c,ek)←Tcom _tk (tag). Later we can open it to any message m as r←Topen _ek (tag;m), such that c=Com _ck (tag;m;r).

We require that equivocal commitments and openings are indistinguishable from real openings. For all non-uniform polynomial time adversaries $\mathcal{A}$ we have the following trapdoor property:

where $\mathcal{R}(m,\mathit{tag})$ returns uniformly random coins r and $\mathcal{O}(m,\mathit{tag})$ computes (c,ek)←Tcom _tk (tag);r←Topen _ek (tag,m) and returns r. Both oracles ignore queries with tags that have already been queried.

The tag-based simulation-soundness property means that a commitment using tag remains binding even if we have made equivocations for commitments using different tags. For all non-uniform polynomial time adversaries $\mathcal{A}$ we have the following simulation-soundness property:

where $\mathcal{O}(\mathrm{Com},\mathit{tag})$ computes (c,ek)←Tcom _tk (tag), returns c and stores (c,tag,ek), and $\mathcal{O}(\mathrm{Open},c,m,\mathit{tag})$ returns r←Topen _ek (tag,m) if (c,tag,ek) has been stored, and where Q is the list of tags for which equivocal commitments have been made by $\mathcal{O}$.

Tag-based simulation-sound trapdoor commitments were implicitly used in Di Crescenzo, Ishai and Ostrovsky [25]. The explicit term was coined by Garay, MacKenzie, and Yang [27], while the definition presented here is from MacKenzie and Yang [42]. The latter paper offers a construction based on one-way functions as well as more efficient constructions based on the DSA or the strong RSA assumptions.

Since we are working over random strings, we want K _tag-com to output public keys that are random or pseudorandom. We say the commitment scheme has pseudorandom keys if there is a polynomial ℓ _tag-com such that $ck\gets \{0,1\}^{\ell_{\text{tag-com}}(k)}$ is computationally indistinguishable from correctly generated commitment keys. This property can also be achieved based on the existence of one-way functions.

Tag-Based Simulation-Extractable Commitment Scheme

We will need something stronger than tag-based simulation-sound trapdoor commitments, namely tag-based simulation-extractable commitments. A tag-based simulation-extractable commitment is a tag-based simulation-sound trapdoor commitment scheme (K _se-com,SCom,STcom,STopen) with an additional algorithm Extract that given an extraction key ξ is able to extract the committed message. More precisely, with the trapdoor key we can make equivocal commitments, however, for all other tags the adversary will with overwhelming probability make commitments from which a unique possible message can be extracted. For all non-uniform polynomial time adversaries $\mathcal{A}$ we have the following simulation-extractability property:

where $\mathcal{O}(\mathrm{Com},\mathit{tag})$ computes (c,ek)←STcom _τ (tag), returns c and stores (c,tag,ek), and $\mathcal{O}(\mathrm{Open},c,m,\mathit{tag})$ returns r←STopen _ek (tag,m) if some (c,tag,ek) has been stored, and where Q is the list of tags for which equivocal commitments have been made by $\mathcal{O}$.

We will construct a tag-based simulation-extractable commitment scheme from tag-based simulation-sound trapdoor commitments and encryption schemes with pseudorandom public keys and pseudorandom ciphertexts. We use a tag-based simulation-sound trapdoor commitment scheme to commit to each bit of m. If m has length ℓ this gives us commitments c ₁,…,c _ℓ . When making equivocal commitments, we can use the trapdoor key to create equivocal commitments c ₁,…,c _ℓ that can be opened to any bit we like.

We need to make this commitment scheme extractable. We therefore encrypt the openings of the commitments. Now we can extract messages but we have reintroduced the problem of equivocation. An equivocal commitment may have two different openings of a commitment c _i to, respectively, 0 and 1, however, if we encrypt the opening then we are stuck with one possible opening. This is where the pseudorandomness property of the encryption scheme comes in handy. We can simply make two encryptions, one of an opening to 0 and one of an opening to 1. Since the ciphertexts are pseudorandom, we can open the ciphertext containing the opening we want and claim that the other ciphertext was chosen as a random string [14].

To recap, the idea so far is to commit to a bit b by making a tag-based simulation-sound trapdoor commitment c _i to this bit and create a ciphertext C _i,b containing an opening of c _i to b, while choosing C _i,1−b as a random string. We now present the full commitment scheme in Fig. 3.

Fig. 3.

Tag based simulation-extractable commitment.

Theorem 18

Tag-based simulation-extractable commitment schemes exist if encryption schemes with pseudorandom ciphertexts exist. If encryption schemes with pseudorandom public keys and pseudorandom ciphertexts exist then tag-based simulation-extractable commitments with pseudorandom public keys exist.

Proof

Tag-based simulation-sound trapdoor commitments with pseudorandom keys can be built from one-way functions [42] so the assumptions give us the tools needed in the construction in Fig. 3. This also shows that we have pseudorandom keys for the tag-based simulation-extractable commitment scheme if the encryption scheme has pseudorandom public keys.

We now need to prove that even after seeing equivocal commitments and equivocations it is hard to come up with a commitment with a different tag and open this commitment to a message that differs from the extracted message. Consider first the case where the adversary for some index i creates c _i ,C _i0,C _i1 such that both C _i0 and C _i1 decrypt to valid openings of c _i to, respectively, 0 and 1. Since tag has not been used before, we have not used (tag,i) in any commitment we have equivocated before so this breaks the simulation-sound binding property of the tag-based simulation-sound trapdoor commitment. The errorless decryption property of the pseudorandom encryption scheme now tells us that if the adversary opens all triples c _i ,C _i0,C _i1 successfully to either 0 or 1, then we get the opening when decrypting.

We also need to prove that we have the trapdoor property. We will modify the oracle in several steps and show that $\mathcal{A}$ cannot tell the difference. Let us start with the oracle R(⋅,⋅) that on input (tag,m) returns a randomly chosen randomizer $r_{1},R_{1,m_{1}},C_{1,1-m_{1}},\ldots,r_{\ell},R_{\ell,m_{\ell }},C_{1,1-m_{\ell}}$. Instead of making commitments c _i :=Com _ck ((tag,i);m _i ;r _i ), we may instead run $(c_{i},ek_{i})\gets\mathrm{Tcom}_{tk}(\mathit{tag},i); r_{i}\gets \mathrm{Topen}_{ek_{i}}(m_{i})$ and use r _i as the randomizer. By the trapdoor property of the tag-based simulation-sound commitment the two oracles are indistinguishable to $\mathcal{A}$.

Next, consider the oracle O(⋅,⋅) where we make equivocations to both r _i0 and r _i1 such that c _i =Com _ck ((tag,i);b;r _i,b ) for both b=0 and b=1. We encrypt r _i,b with randomness R _i,b . We then return $r_{i},R_{i,m_{i}},c_{i,1-m_{i}}$. By the pseudorandomness of the ciphertexts this is indistinguishable from the previously modified R(⋅,⋅) oracle. □

6.2 UC Commitment in the Multi-string Model

We will now show how to securely realize the ideal UC commitment functionality $\mathcal{F}_{\mathrm{COM}}^{1:N}$ described in Fig. 4 in the multi-string model. Let us start by giving some intuition behind our construction. To prove that our UC commitment is secure, we will describe an ideal process adversary $\mathcal{S}$ that interacts with $\mathcal{F}_{\mathrm{COM}}^{1:N}$ and makes a black-box simulation of $\mathcal{A}$ running with $\mathcal{F}_{\mathrm{BC}},\mathcal{F}_{\mathrm{MCRS}}$ and P ₁,…,P _N . There are two general types of issues that can come up in the ideal process simulation. First, when $\mathcal{F}_{\mathrm{COM}}^{1:N}$ tells $\mathcal{S}$ that a party has committed to some message, $\mathcal{S}$ does not know which message it is but has to simulate to $\mathcal{A}$ that this party makes a UC commitment. Therefore, we want to be able to make equivocal commitments and later open them to any value. Second, if a corrupt party controlled by $\mathcal{A}$ sends a UC commitment then $\mathcal{S}$ needs to input some message to $\mathcal{F}_{\mathrm{COM}}^{1:N}$. In this case, we need to extract the message from the UC commitment.

Fig. 4.

The ideal commitment functionality.

As a tool to get both the equivocation/simulation property and at the same time the extractability property, we will use a tag-based simulation-extractable commitment. Our idea in constructing a UC commitment is to use each of the n common random strings output by $\mathcal{F}_{\mathrm{MCRS}}$ as a public key for a tag-based simulation-extractable commitment scheme. This gives us a set of n commitment schemes of which at least $t=\lceil\frac{n+1}{2} \rceil$ are secure. Without loss of generality, we will from now on assume we have exactly t secure commitment schemes. In the ideal process, $\mathcal{S}$ simulates $\mathcal{F}_{\mathrm{MCRS}}$ and can therefore pick the honest strings as simulation-extractable public keys where it knows both the simulation trapdoors and the extraction keys.

To commit to a message m, a party makes a (t,n)-threshold secret sharing of it and commits to the n secret share using the n public keys specified by the random strings. When making an equivocal commitment, $\mathcal{S}$ makes honest commitments to n−t random shares for the adversarial keys and equivocal commitments with the t simulation-extractable keys. Since the adversary knows at most n−t<t shares, $\mathcal{S}$ can later open the commitment to any message by making suitable trapdoor openings of the latter t shares. To extract a message m from a UC commitment made by the adversary, $\mathcal{S}$ extracts t shares from the simulation-extractable commitments and combines the shares to get the only possible adversarial message m.

One remaining issue is when the adversary recycles a commitment or parts of it. We may risk that it uses an equivocal commitment made by an honest party, in which case $\mathcal{S}$ is unable to extract a message. To guard against this problem, we let the tag for the simulation-extractable commitment scheme contain the identity of the sender P _i forcing the adversary to use a different tag and enabling $\mathcal{S}$ to extract.

Another problem arises when $\mathcal{A}$ corrupts a party, which enables it to send messages on behalf of this party. At this point, however, $\mathcal{S}$ learns the message so we just need to force $\mathcal{A}$ to reuse the same message if it reuses parts of the equivocal commitment. We therefore introduce a second commitment scheme, which will be a standard trapdoor commitment scheme, and use this trapdoor commitment scheme to commit to the shares of the message. The tag for the simulation-extractable commitment will include this trapdoor commitment. Therefore, if reusing a tag the adversary must also reuse the same trapdoor commitment in the tag, which in turn binds her to use the same share as the one the party committed to before being corrupted. We now describe the full UC commitment scheme, which has the additional benefit of being non-interactive.

Commitment: :

On input (multi,sid,(ck ₁,σ ₁),…,(ck _n ,σ _n )) from $\mathcal{F}_{\mathrm{MCRS}}$ and (commit,sid,m) from $\mathcal{Z}$, the party P _i does the following. She makes a (t,n)-threshold secret sharing s ₁,…,s _n of m. She picks randomizers r _j and makes commitments $c_{j}:=\mathrm{Com}_{ck_{j}}(s_{j};r_{j})$. She also picks randomizers R _j and makes tag-based commitments $C_{j}:=\mathrm{SCom}_{\sigma_{j}}((P_{i},c_{j});s_{j};R_{j})$. The commitment is c:=(c ₁,C ₁,…,c _n ,C _n ). She broadcasts (broadcast,sid,commit,c) (using ssid=commit).

Receiving commitment: :

A party on input (multi,sid,(ck ₁,σ ₁),…,(ck _n ,σ _n )) from $\mathcal{F}_{\mathrm{MCRS}}$ and (broadcast,sid,commit,P _i ,c) from $\mathcal{F}_{\mathrm{BC}}$ outputs (commit,sid,P _i ) to the environment.

Opening commitment: :

Party P _i wishing to open her commitment broadcasts (broadcast,sid,open,s ₁,r ₁,R ₁,…,s _n ,r _n ,R _n ) (using ssid=open).

Receiving opening: :

A party receiving an opening (broadcast,sid,open,P _i ,s ₁,r ₁,R ₁,…,s _n ,r _n ,R _n ) from $\mathcal{F}_{\mathrm{BC}}$ to a commitment she received earlier checks that all commitments are correctly formed $c_{j}=\mathrm{Com}_{ck_{j}}(s_{j};r_{j})$ and $C_{j}=\mathrm{SCom}_{\sigma_{j}}((P_{i},c_{j});\allowbreak s_{j};R_{j})$. She also checks that s ₁,…,s _n are valid shares of a (t,n)-threshold secret sharing of some message m∈{0,1}^ℓ(k). In that case she outputs (open,sid,P _i ,m) to the environment.

Theorem 19

$\mathcal{F}_{\mathrm{COM}}^{1:N}$ can be securely realized in the $(\mathcal{F}_{\mathrm{BC}},\mathcal{F}_{\mathrm{MCRS}})$-hybrid model assuming tag-based simulation-extractable commitment schemes with pseudorandom public commitment keys exist.

Proof

We claim that the protocol described above is a secure realization of $\mathcal{F}_{\mathrm{COM}}^{1:N}$. Let us describe the ideal-process adversary $\mathcal{S}$, which runs a black-box simulation of $\mathcal{A}$. In particular, $\mathcal{S}$ simulates the parties P ₁,…,P _N and the ideal functionalities $\mathcal{F}_{\mathrm{MCRS}}$ and $\mathcal{F}_{\mathrm{BC}}$. The dummy parties that are actually involved in the protocol and communicate with $\mathcal{Z}$ are written as $\tilde{P}_{1},\ldots,\tilde{P}_{N}$.

Communication: :

$\mathcal{S}$ forwards all communication between the simulated adversary $\mathcal{A}$ and the environment $\mathcal{Z}$. Also, whenever $\mathcal{A}$ delivers a message to a party P _i she simulates this message delivery.

Common random strings: :

Whenever $\mathcal{A}$ asks $\mathcal{F}_{\mathrm{MCRS}}$ for a common random string select (ck,tk)←K _trapdoor(1^k) and (σ,τ,ξ)←K _se-com(1^k) and return (crs,sid,(ck,σ)), while storing the corresponding keys (ck,tk,σ,τ,ξ).

When $\mathcal{A}$ inputs (multi,sid,(ck ₁,σ ₁),…,(ck _n ,σ _n )) to $\mathcal{F}_{\mathrm{MCRS}}$ $\mathcal{S}$ checks that more than half the pairs (ck ₁,σ ₁),…,(ck _n ,σ _n ) match the stored public keys. In that case, $\mathcal{S}$ sends (multi,sid,(ck ₁,σ ₁),…,(ck _n ,σ _n )) to all parties and halts the simulation of $\mathcal{F}_{\mathrm{MCRS}}$. Note, we only need t stored keys so if there are more than t honest public key pairs $\mathcal{S}$ just uses t of the secret key tuples.

Commitment by honest party: :

On receiving (commit,sid,P _i ) from $\mathcal{F}_{\mathrm{COM}}^{1:N}$ we learn that P _i has made a commitment, albeit we do not know the message. If the multi-string has not yet been delivered, $\mathcal{S}$ waits until $\mathcal{A}$ has submitted reference strings to $\mathcal{F}_{\mathrm{MCRS}}$ and delivers them to P _i .

$\mathcal{S}$ makes a (t,n)-threshold secret sharing s ₁,…,s _n of 0. For the n−t reference strings where she does not know the trapdoors she commits to s _j as c _j :=Com _tk (s _j ;r _j ) and $C_{j}:=\mathrm{SCom}_{\sigma_{j}}(P_{i},c_{j};s_{j};R_{j})$. For the t reference strings where she does know the trapdoors, she makes trapdoor commitments (c _j ,ek _j )←Tcom(tk) and equivocal commitments $(C_{j},EK_{j})\gets \mathrm{STcom}_{\tau_{j}}(P_{i},c_{j})$. She simulates broadcasting (broadcast,sid,commit,c ₁,C ₁,…,c _n ,C _n ).

Opening by honest party: :

When $\mathcal{S}$ receives (open,sid,P _i ,m) from $\mathcal{F}_{\mathrm{COM}}^{1:N}$ it means that $\tilde{P}_{i}$ has been instructed to open the commitment and it was a commitment to m. $\mathcal{S}$ recalls the n−t shares for adversarial reference strings and fit them into a (t,n)-threshold secret sharing s ₁,…,s _n of m. She opens the n−t commitment pairs c _j ,C _j correctly and equivocates the t commitment pairs c _j ,C _j where she knows the corresponding equivocation keys as $r_{j}\gets \mathrm{Topen}_{ek_{j}}(s_{j})$ and $R_{j}\gets \mathrm{STopen}_{EK_{j}}((P_{i},c_{j}),s_{j})$. She simulates P _i broadcasting (broadcast,sid,open,s ₁,r ₁,R ₁,…,s _n ,r _n ,R _n ).

Honest party receiving commitment: :

On $\mathcal{A}$ delivering (broadcast,sid,commit,P _i ,c ₁,C ₁,…,c _n ,C _n ) from $\mathcal{F}_{\mathrm{BC}}$ to a party P _j deliver the corresponding (commit,sid,P _i ) message from $\mathcal{F}_{\mathrm{COM}}^{1:N}$ to the dummy party $\tilde{P}_{j}$.

Honest party receiving opening: :

On $\mathcal{A}$ delivering (broadcast,sid,open,P _i ,s ₁,r ₁,R ₁,…,s _n ,r _n ,R _n ) from $\mathcal{F}_{\mathrm{BC}}$ to a party P _j check that she has received a commitment from P _i and continue if she already has received a commitment or after she receives a commitment.

Check that the commitments contain a consistent (t,n)-threshold secret sharing of s ₁,…,s _n of a message m and for all j we have $c_{j}=\mathrm{Com}_{ck_{j}}(s_{j};r_{j})$ and $C_{j}=\mathrm{SCom}_{\sigma_{j}}(P_{i},c_{j};s_{j};R_{j})$. If the checks pass deliver (open,sid,P _i ,m) from $\mathcal{F}_{\mathrm{COM}}^{1:N}$ to the dummy party $\tilde{P}_{j}$ that outputs the opening to $\mathcal{Z}$.

Corruption: :

If $\mathcal{A}$ corrupts a party P _i , $\mathcal{S}$ corrupts the corresponding dummy party $\tilde{P}_{i}$. $\mathcal{S}$ needs to simulate the history of this party. Receipt of commitments and openings is already known to $\mathcal{A}$. If the party has not yet made a commitment there is therefore no history to simulate. If the party has made a commitment and already opened it $\mathcal{A}$ already has a simulated history. If the party has made a commitment but not yet opened it, $\mathcal{S}$ must simulate an opening of the commitment. On corrupting $\tilde{P}_{i}$ she learns the message and she can now use the opening simulation for honest parties described earlier.

Once a party is corrupted it is controlled by $\mathcal{A}$. $\mathcal{S}$ will forward communication between $\tilde{P}_{i}$ and the environment $\mathcal{Z}$ as prescribed by the simulated $\mathcal{A}$.

Commitment by corrupt party: :

When a corrupt party P _i makes a commitment (broadcast,sid,commit,P _i ,c ₁,C ₁,…,c _n ,C _n ), $\mathcal{S}$ must input some message to $\mathcal{F}_{\mathrm{COM}}^{1:N}$.

After simulating the receipt by $\mathcal{F}_{\mathrm{BC}}$ $\mathcal{S}$ uses the extraction keys to extract t committed values $s_{j}\gets\mathrm{Extract}_{\xi_{j}}((P_{i},c_{j}),C_{j})$. The only case, where she cannot extract a value s _j from C _j may be when the tag (P _i ,c _j ) has been used before by $\mathcal{S}$ in making an equivocal commitment. However, this can only happen if P _i used (P _i ,c _j ) as a tag when it was honest and then upon corruption $\mathcal{S}$ made an equivocation of c _j to some s _j . But then $\mathcal{S}$ does not need to extract from C _j since it already knows the purported value s _j contained in the commitment.

After having obtained t shares $\mathcal{S}$ reconstructs m and inputs (commit,sid,m) to $\mathcal{F}_{\mathrm{COM}}^{1:N}$ on behalf of the dummy party $\tilde{P}_{i}$. In case she did not manage to extract a message, she inputs m:=0 to $\mathcal{F}_{\mathrm{COM}}^{1:N}$. Note that inputting a dummy value 0 is fine since as we will show in the proof we will not end up in a situation where $\mathcal{S}$ needs to ask $\mathcal{F}_{\mathrm{COM}}^{1:N}$ to open the dummy commitment.

Opening by corrupt party: :

When a corrupt party wants to open a commitment by broadcasting (broadcast,sid,open,s ₁,r ₁,R ₁,…,s _n ,r _n ,R _n ), $\mathcal{S}$ simulates the receipt by $\mathcal{F}_{\mathrm{BC}}$, checks the opening and if acceptable inputs (open,sid,m) to $\mathcal{F}_{\mathrm{COM}}^{1:N}$.

To see that this gives us a good simulation, consider the following hybrid experiments.

Hybrid 1: :

This is the protocol executed with $\mathcal{A}$ and environment $\mathcal{Z}$ and parties P ₁,…,P _n in the $(\mathcal{F}_{\mathrm{BC}},\mathcal{F}_{\mathrm{MCRS}})$-hybrid model.

Hybrid 2: :

This is the protocol, where we generate and store (ck,tk,σ,τ,ξ) and return (ck,σ) whenever $\mathcal{A}$ queries $\mathcal{F}_{\mathrm{MCRS}}$ for a common random string.

Since both commitment schemes have pseudorandom keys, hybrid 1 and hybrid 2 cannot be distinguished.

Hybrid 3: :

This is hybrid 2 modified such that honest party P _i uses the t known trapdoors to make equivocal commitments corresponding to these keys to the secret shares instead of making real commitments. When opening the commitments P _i uses the equivocation keys to generate randomizers so the commitments open to the (t,n) secret sharing of the message.

Hybrid 2 and hybrid 3 are indistinguishable due to the trapdoor properties of the commitment schemes.

Hybrid 4: :

We modify hybrid 3 such that when an honest party P _i uses a (t,n)-threshold secret sharing of 0 instead of a threshold secret sharing of m when making a commitment. In the opening phase it opens the n−t pairs (c _j ,C _j ) where it does not know the trapdoors to the s _j ’s it committed to. It reconstructs shares s _j for the t equivocal commitments so s ₁,…,s _n is a (t,n)-threshold secret sharing of m. It then opens the equivocal commitments to these values.

Hybrid 3 and hybrid 4 are perfectly indistinguishable since n−t<t shares in a (t,n)-threshold secret sharing scheme do not reveal anything about m.

Hybrid 5: :

We now turn to modify the way we handle corrupt parties. Whenever a corrupt party P _i submits a commitment (broadcast,sid,commit,c ₁,C ₁,…,c _n ,C _n ) to $\mathcal{F}_{\mathrm{BC}}$ we want to extract a message.

For any of the t C _j ’s where we know the extraction key there are two cases to consider. One case is where (P _i ,c _j ) has been used as a tag when P _i was still honest. In this case, we learned an opening s _j ,r _j of c _j upon corruption and will therefore consider s _j the share. The second case is when (P _i ,c _j ) has not been used as a tag in a simulation-extractable commitment. In that case, we can extract a share s _j .

We now have t secret shares that we combine to get a possible message m. We abort the simulation if the commitment is ever successfully opened to a different message.

Hybrid 4 and hybrid 5 are indistinguishable since there is negligible probability of aborting. An abort happens if the extracted m does not match the opening. There are two ways this could happen. One possibility is that c _j created by an honest party that is later corrupted is opened to a different share than in the simulation. However, this would imply a breach of the binding property of the trapdoor commitment scheme. Another possibility is that the extraction fails. However, this would imply breaking the simulation-extractability of the commitment scheme.

We conclude the proof by observing that hybrid 5 is identical to the simulation. □

6.3 Multi-party Computation

We will now show how to generate a common random string on the fly using UC commitments. More precisely, we will securely realize the ideal functionality $\mathcal{F}_{\mathrm{CRS}}$ in Fig. 5 that produces a random bit-string.

Fig. 5.

The ideal common random string generator.

Coin-flipping

The parties will use the natural coin-flipping protocol where all parties commit to random strings and subsequently open all the commitments and use the exclusive-or of the random strings as the output.

Commitment: :

P _i chooses at random r _i ←{0,1}^ℓ(k). It submits (commit,sid,r _i ) to $\mathcal{F}_{\mathrm{COM}}^{1:N}$. $\mathcal{F}_{\mathrm{COM}}^{1:N}$ on this input sends (commit,sid,P _i ) to all parties.

Opening: :

Once P _i sees (commit,sid,P _j ) for all j, it sends (open,sid) to $\mathcal{F}_{\mathrm{COM}}^{1:N}$. $\mathcal{F}_{\mathrm{COM}}^{1:N}$ on this input sends (open,sid,P _i ,r _i ) to all parties.

Output: :

Once P _i sees (open,sid,P _j ,r _j ) for all j, it outputs $(\mathbf{crs},\mathit{sid},\bigoplus_{j=1}^{N}r_{j})$ and halts.

Theorem 20

The ideal common reference string generator $\mathcal{F}_{\mathrm{CRS}}$ can be (perfectly) securely realized in the $\mathcal{F}_{\mathrm{COM}}^{1:N}$-hybrid model.

Proof

We claim the protocol above securely realizes $\mathcal{F}_{\mathrm{CRS}}$. Consider the following ideal process adversary $\mathcal{S}$ working in the $\mathcal{F}_{\mathrm{CRS}}$-hybrid model, giving her a common reference string Σ. She runs a black-box simulation of $\mathcal{A}$, a simulated copy of $\mathcal{F}_{\mathrm{COM}}^{1:N}$ and simulated parties P ₁,…,P _N , not to be confused with the dummy parties $\tilde{P}_{1},\ldots,\tilde{P}_{N}$ that interact with $\mathcal{Z}$ and $\mathcal{F}_{\mathrm{CRS}}$. Whenever the simulated $\mathcal{A}$ communicates with the environment $\mathcal{Z}$, $\mathcal{S}$ simply forwards those messages. We now list the events that can happen in the protocol.

On activation of P _i , $\mathcal{S}$ simulates $\mathcal{F}_{\mathrm{COM}}^{1:N}$ receiving a commitment from P _i by outputting (commit,sid,P _i ) to all parties and $\mathcal{A}$.

On delivery of commitments from all parties to an honest party P _i , she selects r _i at random, subject to the continued satisfiability of condition $\varSigma=\bigoplus_{j=1}^{N}r_{j}$ and stores it. She then simulates $\mathcal{F}_{\mathrm{COM}}^{1:N}$ receiving an opening of P _i ’s commitment to r _i .

In case $\mathcal{A}$ corrupts a party P _i , the simulator corrupts the corresponding dummy party $\tilde{P}_{i}$. If P _i has made a commitment but it has not yet been opened, $\mathcal{S}$ selects r _i at random, subject to the continued satisfiability of the condition $\varSigma=\bigoplus_{j=1}^{N}r_{j}$, and simulates that this was the commitment P _i made. In all other cases of corruption, either r _i has not yet been selected, or the commitment has already been opened and $\mathcal{A}$ already knows r _i .

The two experiments, $\mathcal{A}$ running with parties P ₁,…,P _N in the $\mathcal{F}_{\mathrm{COM}}^{1:N}$-hybrid model, and $\mathcal{S}$ running with dummy parties $\tilde{P}_{1},\ldots,\tilde{P}_{N}$ in the $\mathcal{F}_{\mathrm{CRS}}$-hybrid model are perfectly indistinguishable to $\mathcal{Z}$. To see this, consider a hybrid experiment, where we run the simulation and choose all r _i ’s at random and then set $\varSigma:=\bigoplus_{i=1}^{N}r_{i}$. Inspection shows that this gives a perfect simulation of $\mathcal{Z}$’s view of the protocol in the $\mathcal{F}_{\mathrm{COM}}^{1:N}$-hybrid model. At the same time, also here we get a uniform random distribution on Σ and the r _j ’s subject to the condition $\varSigma=\bigoplus_{j=1}^{N}r_{j}$. □

Multi-party Computation

Armed with a coin-flipping protocol we can generate random strings. Canetti, Lindell, Ostrovsky, and Sahai [14] demonstrated that with access to a common random string it is possible to do any kind of multi-party computation in the presence of a malicious adaptive adversary that can corrupt any number of parties. The multi-party computation protocol of Canetti, Lindell, Ostrovsky, and Sahai [14] assumes the existence of encryption schemes with pseudorandom public keys and pseudorandom ciphertexts and enhanced trapdoor permutation, and when using a uniformly random string it also assumes the existence of encryption schemes with dense public keys and dense ciphertexts [21].

The requirement for encryption schemes with pseudorandom public keys and pseudorandom ciphertexts is not explicitly stated in [14], however, a careful reading reveals that such encryption schemes are used. Encryption Schemes with pseudorandom public keys and pseudorandom ciphertexts imply the existence of augmented non-committing encryption [19], which is also used in their construction.

Enhanced trapdoor permutation are trapdoor permutations that remain hard to invert even given the random coins of the domain sampler. Enhanced trapdoor permutations can for instance be built from the RSA assumption [13]. The construction in [13] has the additional feature that the public keys are dense so via a standard hardcore-bit transformation [29] this also gives an example of an encryption scheme with dense public keys and dense ciphertexts.

We now have the following corollary to Theorems 18, 19, and 20.

Theorem 21

For any well-formed functionality $\mathcal{F}$ there is a non-trivial protocol that securely realizes it in the $(\mathcal{F}_{\mathrm{BC}},\mathcal{F}_{\mathrm{MCRS}})$-hybrid model assuming the existence of encryption schemes with pseudorandom public keys and pseudorandom ciphertexts and assuming the existence of enhanced trapdoor permutations with dense public keys.

Proof

From [14] we find that any well-formed functionality $\mathcal{F}$ has a non-trivial protocol that securely realizes it in the $(\mathcal{F}_{\mathrm{BC}},\mathcal{F}_{\mathrm{CRS}})$-hybrid model assuming the existence of encryption schemes with pseudorandom public keys and pseudorandom ciphertexts and enhanced trapdoor permutations with dense public keys.

Theorem 20 shows that we can securely realize $\mathcal{F}_{\mathrm{CRS}}$ in the $\mathcal{F}_{\mathrm{COM}}^{1:N}$-hybrid model. Therefore, by the universal composability theorem [11], we can securely realize $\mathcal{F}$ in the $(\mathcal{F}_{\mathrm{BC}},\mathcal{F}_{\mathrm{COM}}^{1:N})$-hybrid model.

Theorem 19 shows that we can securely realize $\mathcal{F}_{\mathrm{COM}}^{1:N}$ in the $(\mathcal{F}_{\mathrm{BC}},\mathcal{F}_{\mathrm{MCRS}})$-hybrid model assuming the existence of simulation-extractable commitments, which Theorem 18 shows can be built from encryption schemes with pseudorandom public keys and pseudorandom ciphertexts. By the universal composability theorem [11] we see that $\mathcal{F}$ can be securely realized in the $(\mathcal{F}_{\mathrm{BC}},\mathcal{F}_{\mathrm{MCRS}})$-hybrid model under the stated cryptographic assumptions. □