Variable exponent diffusion for image detexturing

Abstract

We consider a variational approach to the problem of structure + texture decomposition (also known as cartoon + texture decomposition). As usual for many variational problems in image analysis and processing, the energy we minimize consists of two terms: a data-fitting term and a regularization term. The main feature of our approach consists of choosing parameters in the regularization term adaptively. Namely, the regularization term is given by a weighted $p(\cdot )$-Dirichlet-based energy $\int \!a({\varvec{x}}){\,\!|\,\!}\nabla u {\,\!|\,\!}^{p({\varvec{x}})}$, where the weight and exponent functions are determined from an analysis of the spectral content of the image curvature. Our numerical experiments, both qualitative and quantitative, suggest that the proposed approach delivers better results than state-of-the-art methods for extracting the structure from textured and mosaic images, as well as competitive results on image enhancement problems.

1 Introduction

Given an image, the structure + texture (cartoon + texture) image decomposition refers to the problem of a decomposition of the image intensity function into the sum of two components: the structure component representing homogeneous image regions separated by salient edges and the texture component containing repeating patterns and noise.

Structure + texture image decomposition remains a topic of intensive research due to various applications including low-light image enhancement [1], defect detection [2], image compression [3], image super-resolution [4], and image composition and content-aware image resizing [5]. In applied mathematics, the problem of structure + texture image decomposition led to developing a number of novel variational approaches and numerical algorithms [6, Chapter 1], [7, Section 5.2], [8, Section 15.2], [9, Chapter 5].

In this paper, we attack the structure + texture decomposition problem using a variational approach based on a generalization of the total variation energy. Total variation (TV) regularization was introduced to image processing thirty years ago [10], and since then, it has remained one of the most popular variational regularization technique, and was successively used in a vast majority of image processing tasks. We generalize the TV approach by considering a weighted $p(\cdot )$-Dirichlet-based energy, where the weight and exponent are spatially varying.

1.1 Related work

Several approaches to the problem of structure + texture extraction are based on variational methods and their rigorous mathematical analysis was initiated in [6, Chapter 1]. The image total variation, introduced in [10], was used for texture suppression purposes in [11, 7, Section 5.2], and [9, Chapter 5]. The reader is also referred to [11] for a survey of TV-based structure + texture image decomposition methods. TV-based approaches lead to several variants involving higher order schemes in [12, 13], adaptive TV energies in [5], non-convex regularizations in [14, 15], and low-rank approximations in [16, 17]. Variational approaches with different norms were considered in [6, 18]. A possible issue with TV-based approaches is that they tend to oversmooth the recovered image and blur the main edges.

The variational deep priors approach [19] is an hybrid variational method, where the regularizer (or prior) is learned from data. More precisely, a family of denoisers parameterized over the noise variance are trained on images corrupted by Gaussian noise with given variance, and used as the regularizer in the variational formulation. The difficulty with this approach is that the family of denoisers may fail to remove the details at a given frequency, since it is not specifically trained for this task.

Several methods based on morphological component analysis (MCA) [8, 20,21,22,23,24,25] were proposed for extracting the structure of an image. Filter-based methods include the fast nonlinear filter proposed in [26] and a variant using banks of filters [27]. Another filter-based method is the popular guided filter approach introduced in [28]. It may suffer from halo artifacts, an issue that was addressed by considering a gradient domain guided filter in [29]. Variants include [14, 15, 30, 31] or the very recent work [32]. The problem with edge preserving image smoothing approaches is that they are not initially designed to deal with image textures, rely on local properties and may fail to suppress certain high contrast textures.

Other methods include machine learning-based approaches [33,34,35], approaches based on patch recurrence [36, 37] or the very recent generalized smoothing framework [38, 39]. Finally, it is also possible to extract the texture first. Textures can be characterized by their power spectrum [40]. A power-spectrum-based two-pass approach was very recently introduced in [41]. The difficulty is that in general there is no rigorous or definitive mathematical description of textures [42], and thus, statistical tests on the power spectrum may not be always sufficient for extracting the texture or high-frequency details components.

1.2 Motivation, contribution, and organization

In our treatment of the structure + texture image decomposition problem, we follow the general variational approach and minimize an energy functional consisting of data-fitting and regularization terms (variants of this approach can be found in [7, Section 5.2] and [9, Chapter 5], for example). However, the choice of the regularization term we use in this study has several important differences with the regularization terms commonly used in the structure + texture image decomposition studies. First of all, the conventional variational decomposition approaches mainly focus on selecting texture-insensitive data-fitting terms and the total variation energy constitutes a very popular choice for the regularization term. In contrast to these conventional approaches, our regularization term is data-dependent and imposes strong smoothing in texture-rich image regions. Namely, we consider in this work weighted $p(\cdot )$-Dirichlet energies

$$\begin{aligned} \int \!a({\varvec{x}}){\,\!|\,\!}\nabla u {\,\!|\,\!}^{p({\varvec{x}})} \end{aligned}$$

with spatially varying weight $a({\varvec{x}})$ and exponent $p({\varvec{x}})$, where the weight and exponent are defined to preserve salient image edges while suppressing the image texture. We propose two schemes for automatically selecting the exponent $p({\varvec{x}})$ and the weight $a({\varvec{x}})$, one for the problem of structure extraction, where we enforce $0<p({\varvec{x}})\le 1$, and one for the problem of detail enhancement, where we enforce $1\le p({\varvec{x}})\le 2$. For both cases, the weight $a({\varvec{x}})$ and exponent $p({\varvec{x}})$ are determined from an analysis of the spectral content of the level-set and mean curvatures of the image intensity function. Our choice of the level-set curvature spectral content is motivated by its sensitivity to both the low-contrast and high-contrast textures. On the other hand, the mean curvature is much more numerically stable than the level-set curvature and, therefore, the use of image mean curvature is preferable when dealing with detail enhancement tasks. Similarly, setting $0<p({\varvec{x}})\le 1$ leads to aggressive image texture smoothing, while choosing $1\le p({\varvec{x}})\le 2$ yields more gentle smoothing which is appropriate for image sharpening purposes through the standard unsharp-masking procedure.

Unlike the methods from [43] and [44], we use a single pass of an ADMM-based optimization procedure, making the proposed approach more efficient.

Our numerical experiments suggest that the proposed approach delivers better results than state-of-the-art methods for extracting the structure from textured images and mosaic images, as well as competitive results on image enhancement problems.

The rest of this work is organized as follows: We describe our approach in Sect. 2. The results of our numerical experiments are provided in Sect. 3, as well as additional possible applications of the proposed approach. Finally, we conclude in Sect. 4.

2 Proposed approach

2.1 A visual illustration of the approach

We start with summarizing the whole approach. It is illustrated visually in Fig. 1. Given an input image, in Fig. 1a, we want to remove the texture and extract the main structure of the image, as in Fig. 1d. First, we compute the level-set curvature (3) of the image as shown in Fig. 1b, or the surface mean curvature (4), which is then used to define a disparity measure (6). Next, we use this disparity measure to define a weight function (shown in the top row of Fig. 1c), and an exponent function (shown in the bottom row of Fig. 1c). Finally, the image structure, in Fig. 1d, is obtained by minimizing the weighted $p(\cdot )$-Dirichlet energy (1), or (2), defined in terms of these weight and exponent functions.

Fig. 1

A visual illustration of the approach: a the input image; b the level-set curvature (3); c top image: the weight function $a(\cdot )$; Bottom image: the exponent function $p(\cdot )$; d the extracted structure

2.2 Weighted p-Dirichlet energy

Given a bounded domain $\Omega \subset \mathbb {R}^2$, and a function f defined on $\Omega$,¹ we consider the following weighted $p(\cdot )$-Dirichlet energy

$$\begin{aligned} \int _\Omega \left( a({\varvec{x}}){\,\!|\,\!}\nabla u {\,\!|\,\!}^{p({\varvec{x}})}\right) +\frac{\lambda }{2}\int _\Omega \left( H\!\left[ u-f\right] \right) ^2\longrightarrow \min , \end{aligned}$$

(1)

with variable exponent $p({\varvec{x}})$ and weight function $a({\varvec{x}})$. H is a smoothing operator, and we use the convolution with a Gaussian

$$\begin{aligned} H[u-f]=G_{\sigma }*(u-f),\quad G_{\sigma }({\varvec{x}})=G({\varvec{x}}/\sigma )/\sigma ^2, \end{aligned}$$

where, unless explicitly mentioned, $\sigma =1$. An alternative to (1) consists in using the $L_1$ norm for the fitting term, leading to

$$\begin{aligned} \int _{\Omega } \left( a({\varvec{x}}) {\,\!|\,\!}\nabla u{\,\!|\,\!}^{p({\varvec{x}})} \right) + \lambda \int _{\Omega } {\,\!|\,\!}H \!\left[ u-f\right] {\,\!|\,\!}\rightarrow \min . \end{aligned}$$

(2)

The solution u to the problem (1), respectively (2), extracts the main structure of the original image f. Natural and structure images are usually sparse in the gradient domain, thus the consideration of the $L_p$-based gradient regularization term $\int _{\Omega } {\,\!|\,\!}\nabla u{\,\!|\,\!}^{p({\varvec{x}})}$ with an exponent $0<p({\varvec{x}})\le 1$, which promotes sparsity.

In (1), respectively (2), the first term enforces sparseness of the resulting image, while the second term corresponds to a fitting term that enforces similarities with the input image. The weight $\lambda$ controls the trade-off between these two terms. In practice, for the structure extraction problem, we would like to assign more weight to the first term in the textured regions, and a low weight in the non-textured regions, thus the introduction of a spatially varying weight $a({\varvec{x}})$ for the first term. Similarly, using a spatially varying exponent $p({\varvec{x}})$ allows us to control the gradient sparsity of the structure image $u({\varvec{x}})$, by using low values for $p({\varvec{x}})$ in textured regions. We discuss further the expressions used for $a({\varvec{x}})$ and $p({\varvec{x}})$ in Sect. 2.4.

The $p(\cdot )$-Dirichlet energy term (1) with variable exponent $p({\varvec{x}})$ was previously considered in [43,44,45,46,47]. The case $p({\varvec{x}})\ge 1$ was considered in [45,46,47]. It leads to a convex energy for which more results and tools are available. Similarly to [43, 44], we consider for structure extraction the case with $0<p({\varvec{x}})\le 1$, for which fewer results exist. The case $p\equiv \textrm{const}, \; p \in [0,\infty )$ was studied in [48, 49], where the weighted graph p-Laplacian is applied to problems in image and mesh processing. Indeed, for $p\in [2,\infty )$

$$\begin{aligned} \Delta _p u = \mathop {\textrm{div}}({\,\!|\,\!}\nabla u{\,\!|\,\!}^{p-2} \nabla u) = 0 \end{aligned}$$

is the Euler–Lagrange equation to $\int _\Omega {\,\!|\,\!}\nabla u{\,\!|\,\!}^{p}$.

One problem with the case $p<1$ is that the energy (1) is non-convex, and thus, the uniqueness of the minimizer is not guaranteed. In practice, we minimize (1) with the alternating direction method of multipliers (ADMM) [50], see also [51], and found experimentally that the obtained minimizer delivered very good results. The energy (2) is non-convex as well, when $p < 1$, and similarly dealt with by ADMM.

2.3 Minimization of the weighted $p(\cdot )$-Dirichlet energy

We use a variant of ADMM to solve numerically (1). The problem (1) can be rewritten as

$$\begin{aligned} \int _{\Omega } a({\varvec{x}}){\,\!|\,\!}{\varvec{\xi }}{\,\!|\,\!}^{p({\varvec{x}})} + \frac{\lambda }{2}\int _\Omega \left( H\!\left[ u-f\right] \right) ^2 \rightarrow \min \end{aligned}$$

with the constraint

$$\begin{aligned} {\varvec{\xi }}= \nabla u. \end{aligned}$$

The minimization is performed by the repetition of the following steps

$$\begin{aligned} {\varvec{\xi }}_{k+1}&\leftarrow \max \left\{ {\,\!|\,\!}{\varvec{s}}_k{\,\!|\,\!}-\frac{a({\varvec{x}})}{r{\,\!|\,\!}\nabla u_k{\,\!|\,\!}^{1-p({\varvec{x}})}}, 0\right\} \frac{{\varvec{s}}_k}{{\,\!|\,\!}{\varvec{s}}_k{\,\!|\,\!}}, \\ {\varvec{s}}_k&= \nabla u_k-\frac{\varvec{\mu }_k}{r}, \\ u_{k+1}&\leftarrow \mathrm {Solution \; of} -r (\Delta u - \mathop {\textrm{div}}({\varvec{\xi }}_{k+1})) \\&\quad + \mathop {\textrm{div}}(\varvec{\mu }_k) + \lambda H^{*} H\!\left[ u-f\right] = 0, \\ \varvec{\mu }_{k+1}&\leftarrow \varvec{\mu }_{k}+\rho \left( {\varvec{\xi }}_{k+1}-\nabla u_{k+1}\right) . \end{aligned}$$

See “Appendix A” for a derivation of these steps. A similar approach is used for solving numerically (2). See “Appendix B” for details.

One of the remaining issues to be resolved is the definition of the functions for the exponent $p({\varvec{x}})$ and the weight function $a({\varvec{x}})$. We propose to learn them from information gathered from the input image. In particular, we use the curvature information.

2.4 Computation of $p({\varvec{x}})$ and $a({\varvec{x}})$

For the image structure extraction problem, it seems reasonable to force the weight $a({\varvec{x}})$ in (1), or (2), to be large for the small-scale image details and texture regions of the image that we want to suppress, and low, otherwise. It corresponds to assigning more weight in the textured regions to the first term of (1), whose task is to enforce gradient sparsity of $u({\varvec{x}})$. Similarly, the exponent $p({\varvec{x}})$ controls the gradient sparsity of the structure image $u({\varvec{x}})$, thus it makes sense to force low values in textured regions. Perfect expressions for $a({\varvec{x}})$ and $p({\varvec{x}})$ are not known in general, and we need to estimate them from the input image using, for example, the curvature information.

We can assume that small-scale image details and texture contribute to the high-frequency part of the level-set curvature

$$\begin{aligned} k({\varvec{x}})=\mathop {\textrm{div}}\left( \frac{\nabla f({\varvec{x}})}{{\,\!|\,\!}\nabla f({\varvec{x}}){\,\!|\,\!}}\right) . \end{aligned}$$

(3)

Fig. 2

An example of natural image is shown with the computed level-set curvature (3) and the mean curvature (4), scaled by a factor 50. Notice the noise in the region where the level-set curvature is close to 0 (the blue sky)

Fig. 3

Structure extraction from a test image (left). The extracted image structure obtained by our approach is shown in the middle ($L_2$ fitting term is used (A1)) and right images ($L_1$ fitting term is used (B3))

One possible issue with the level-set curvature $k(\cdot )$ is that it is difficult to estimate it robustly in some cases. Indeed, for natural images with less texture (consider for example a perfectly blue sky), ${\,\!|\,\!}\nabla f({\varvec{x}}){\,\!|\,\!}$ is close to 0, making (3) ill-defined. An illustration of this fact is shown in Fig. 2. An alternative is to view the image as the height field $z=f({\varvec{x}})$ and to consider instead the surface mean curvature²

$$\begin{aligned} K_m = \frac{1}{2} \mathop {\textrm{div}}\left( \frac{\nabla f}{\sqrt{1 + {\,\!|\,\!}\nabla f{\,\!|\,\!}^2}} \right) . \end{aligned}$$

(4)

For images with lots of structure such as, for example, mosaics, using the level-set curvature (3) is preferable. However, for images containing less texture, it is better to use the mean curvature (4) to avoid visual artifacts.

Let ${{\tilde{k}}}({\varvec{x}})$ be obtained from $k({\varvec{x}})$ (or similarly from $K_m({\varvec{x}})$ when the mean curvature is used instead) by suppressing high frequencies of $k({\varvec{x}})$ (respectively, $K_m({\varvec{x}})$). In practice, we use the Butterworth low-pass filter

$$\begin{aligned} \left[ 1+\left( \frac{{\,\!|\,\!}\omega {\,\!|\,\!}}{b}\right) ^m\right] ^{-1} \end{aligned}$$

(5)

with cutoff frequency b. We estimate the difference between k and ${{\tilde{k}}}$ by ${\,\!|\,\!}k - {{\tilde{k}}}{\,\!|\,\!}$, smooth it by convolution with the Gaussian kernel $G_\sigma$ ($\sigma =3$ was used in our experiments) and normalize it to obtain the disparity

$$\begin{aligned} d({\varvec{x}})=\frac{G_\sigma * {\,\!|\,\!}k - {{\tilde{k}}}{\,\!|\,\!}}{\max \left( G_\sigma * {\,\!|\,\!}k - {{\tilde{k}}}{\,\!|\,\!}\right) }, \end{aligned}$$

(6)

where, by construction, $0\le d({\varvec{x}})\le 1$.

Under the assumption that the small-scale details and texture contribute to the high-frequency content of the curvature, the disparity function $d({\varvec{x}})$ is a normalized function, which is close to 0 in non-textured regions (where the curvature k and the filtered curvature ${{\tilde{k}}}$ agree), and close to 1 in textured regions (where the curvature k is high, and the filtered curvature ${{\tilde{k}}}$ low). This disparity function can be used for providing expressions for the spatially varying weight $a({\varvec{x}})$ and exponent $p({\varvec{x}})$.

2.4.1 Structure extraction

For the problem of structure extraction, we define the weight $a({\varvec{x}})$ and the variable exponent $p({\varvec{x}})$ from the disparity $d({\varvec{x}})$ as follows

$$\begin{aligned} a({\varvec{x}}) = d({\varvec{x}})^2 \quad \text{ and }\quad p({\varvec{x}}) = 1 - \frac{d({\varvec{x}})}{2}. \end{aligned}$$

(7)

As stated earlier, our goal is to set $a({\varvec{x}})$ to be large in textured regions (i.e., to give more weight to the regularization term and enforce gradient sparsity) and low in non-textured regions. Removing the high frequency curvature content affects corners and some other salient image features. So if $d({\varvec{x}})$ is small, it is better to reduce the smoothing effect of the $p(\cdot )$-Dirichlet term. A simple choice for such a reduction is $a({\varvec{x}})=d({\varvec{x}})^2$. For the expression of the exponent $p({\varvec{x}})$, a constant equal to 1 would correspond to the TV model [10], which preserves image edges. Using $p({\varvec{x}})<1$ further enforces (gradient) sparsity. Lower values of $p({\varvec{x}})$ should be obtained in textured regions, where the normalized disparity $d({\varvec{x}})$ is close to 1.

2.4.2 Image sharpening

For the problem of image sharpening, we use the following variant

$$\begin{aligned} a({\varvec{x}}) = d({\varvec{x}})^2 \quad \text{ and }\quad p({\varvec{x}}) = 2 - d({\varvec{x}}). \end{aligned}$$

(8)

In the case of image detail sharpening, we use the same expression for $a({\varvec{x}})$ with a similar justification. When we deal with the image sharpening problem, we need an accurate smoothing method preserving salient edges. The choice $p({\varvec{x}})<1$ is too aggressive for this purpose, so we choose $p({\varvec{x}})$ such that $1<p({\varvec{x}})<2$, justifying our choice for (8).

3 Numerical experiments and applications

We compare the approach described in this work to recent approaches for the problem of structure + texture extraction. A direct application is the extraction of the structure image from a mosaic image. We also consider another possible application of image structure extraction: sharpening details in images. For each of these problems, we compare the proposed approach to recent and state-of-the-art methods.

3.1 Structure + texture decomposition

When considering the problem of structure + texture decomposition, the goal is to extract the structure u from an input image f, the texture component is then given by $f-u$. We compute u as a minimizer of the $p(\cdot )-$Dirichlet energy with an $L_2$ (1) or $L_1$ fitting term (2) using the numerical method described in Sect. 2. We use the left image in Fig. 3 as a first test image. The middle and right images in Fig. 3 illustrate the results obtained by our approach when using the $L_2$ fitting term or the $L_1$ fitting term, respectively.

Fig. 4

Structure extracted from Fig. 3, left image, for different approaches

Fig. 5

The zoomed regions from Fig. 4

Fig. 6

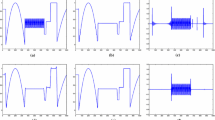
Cross section along the blue line (left image) for some of the structure images shown in Fig. 4

Fig. 7

A zoom on selected regions shown in Fig. 4 when the $L_2$ (1), respectively, $L_1$ (2) are used

A visual comparison between our approach, [19, 32, 39, 41] is provided in Fig. 4, where zooms on two selected regions are also shown. These selected regions are further magnified in Fig. 5. We can see that the methods from [32] and [19] tend to over-smooth the structure, while the method from [39] fails to remove the texture from the napkin properly, see the zoomed regions and Fig. 5, as well. Visually, the best results are obtained by our approach and the method from [41]. The zoomed regions in Figs. 4 and 5 demonstrate that both approaches retain the main structure of the face, while removing the texture from the napkin.

To better appreciate the results obtained with the method from [41] and our approach, we show in Fig. 6 the one dimensional signals corresponding to a cross section of Fig. 6. The cross section is done along the line in blue color in Fig. 6, left image. The top-most graphs correspond to the initial signal, while the graphs shown in the middle correspond to a slice of the structure obtained from our approach (the middle image) and the method from [41] (the right image). Ultimately, we want to preserve the low frequency components of the signal, without over-smoothing the sharp features or shrinking the signal too much, and while removing the high frequency components. The difference between the two signals is shown in the bottom-most graphs. It corresponds to the texture information of the image (the high-frequency components).

3.1.1 $L_2$ against $L_1$ fitting term

One could expect the $L_1$ fitting term to lead to a better fit than the $L_2$ fitting term in the regions of low disparity and thus a better preservation of the main edges of the image structure. In practice, however, we did not find a large difference between the results obtained when a $L_2$ fitting term (1) or a $L_1$ fitting term (2) are used. Figure 3 illustrates the results obtained in each case. A zoom on the selected regions shown in Fig. 4 is shown in Fig. 7.

3.1.2 Parameters sensitivity

The proposed approach depends on two main parameters: b, the cutoff frequency of the Butterworth filter (5), and $\lambda$, the weight controlling the trade-off between the fitting term and the regularization term in (1), respectively (2). Intuitively, lower values of b suppress more terms in the spectrum of the filtered curvature ${{\tilde{k}}}$; thus, it forces the suppression of the image edges. Consequently, b should be set low enough to suppress texture, but not too low; otherwise, it tends to smooth the main image edges as well. The parameter $\lambda$ controls the weight of the fitting term against the regularization term. Higher values for $\lambda$ force the image structure u to stay closer to the input image f. The sensitivity of the proposed approach to these two parameters is illustrated in Fig. 8 when the $L_2$ fitting term is used, and in Fig. 9 when the $L_1$ fitting term is used.

Fig. 8

Influence of the two main parameters b and $\lambda$ when minimizing (1)

Fig. 9

Influence of the two main parameters b and $\lambda$ when minimizing (2)

3.1.3 Ablation study

Fig. 10

Influence of the spatially varying weight $a({\varvec{x}})$ and exponent $p({\varvec{x}})$ functions on the result. a (1) is minimized with the parameters $b=80$ and $\lambda =15$. In b, c and d either the weight function $a({\varvec{x}})$ or the exponent function $p({\varvec{x}})$ is set to a constant

In Fig. 10, we study the impact of the spatially varying weight function $a({\varvec{x}})$ and the spatially exponent function $p({\varvec{x}})$, by individually setting them to a constant value. In (a), the proposed approach (1) with the parameter values $b=80, \lambda =15$ is used. In (b), the weight function is set to a constant $a({\varvec{x}})=1$, while the exponent function $p({\varvec{x}})$ is kept varying. The result appears to be oversmoothed and the main features of the structure image are not preserved. In (c) and (d), the weight function $a({\varvec{x}})$ is spatially varying, while the exponent function $p({\varvec{x}})$ is kept constant to the values 1/2 and 1, respectively. When $p({\varvec{x}})=1/2$, the result is too smooth overall, though it appears to be sharper than (b). The case $p({\varvec{x}})=1$ allows to preserve sharper edges for the face (top row), but cannot filter the texture on the napkin (bottom row). Overall, (a) delivers the best result.

3.2 Extracting a structure image from a mosaic image

Fig. 11

Extracting the structure from mosaic images via different approaches

Fig. 12

Extracting the structure from mosaic images via different approaches

Fig. 13

Image structure extraction from a mosaic image via different approaches

A direct application of structure extraction methods is used for dealing with the problem of extracting the main structure image from a mosaic image. Several examples of mosaic images are shown in Figs. 11, 12 and 13. These mosaic images are processed by our approach, and the methods from [19, 32, 39, 41]. While the method from [41] performed very well for extracting the image structure from a textured image (see Figs. 4, 5, 6), it is surprisingly having difficulties with mosaic images. In most cases, it fails at removing the tile patterns. The method from [19] performs very well on several of these mosaic images, but is also significantly slower, and can over-smooth parts of the images sometimes. Our approach performs similarly well: On some images, it delivers slightly worse results than [19], while on others, it does a better job at preserving some of the main image details.

3.3 Quantitative analysis

In general, there are no widely used metrics or quantitative methods for comparing the output of structure + texture decomposition methods and we have to rely essentially on visual and qualitative comparisons, as done in the previous sections.

One possible approach for a quantitative analysis of image structure extraction methods could be as follows: generate a synthetic structure image s (for example, a piecewise constant function), load a texture image t from a data-set, such as, for example, [52] and form the image $s+t$ (with appropriate weighting, if necessary). Then, one can compute a structure image $s_1$ with a given structure extraction method and compare it with the known structure s using the peak signal-to-noise ratio (PSNR) or the structural similarity index measure (SSIM). We will use the simple example from Fig. 14 to show that this approach cannot work in general.

Figure 14 shows a synthetic textured image (st) and two possible decompositions into structure and texture: $st = s_1 + t_1 = s_2 + t_2$. The structure (respectively, texture) images differ only by a constant shift (i.e., $s_1 = s_2 + c$, where c is a constant). In this example, the synthetic image is obtained from the sum of the first structure and texture ($s_1$ and $t_1$). The corresponding scores are: $\textrm{PSNR}(s_1,s_2)=16.5$, $\textrm{SSIM}(s_1,s_2)=0.71$, and are relatively low. Additionally, we have: $\textrm{PSNR}(st,s_1)=16.31$, $\textrm{SSIM}(st,s_1)=0.68$, and $\textrm{PSNR}(st,s_2)=41.6$, $\textrm{SSIM}(st,s_2)=0.96$. This synthetic example illustrates that the problem is ill-posed and that a quantitative analysis on a synthetic data-set is difficult to perform in general.

Fig. 14

An example illustrating the difficulty of performing a quantitative analysis. A synthetic image is obtained from the sum of the first structure and texture. The second structure and texture (obtained by a constant shift) yield the same synthetic image. Note that the textures are scaled by 5 for visibility purposes

In spite of these difficulties, a recent work [53] proposed a method for trying to quantify the performance of structure extraction methods. The approach is interactive and relies on the user to select points on an extracted structure image. These points are classified in two separate categories: The structure category and the texture category. Scores are computed with different methods for the neighborhoods of points in each category and combined by cross-entropy. Intuitively, neighborhoods of points in the structure category should be similar to the input image, and neighborhoods of points in the texture category should have the texture smoothed (they should not preserve edges). This method does not seem to be widely used so far, outside of the work [32], possibly because it relies on a user to select key points. Nevertheless, we provide in Table 1 the scores obtained with this approach on the images used in Figs. 4, 11, 12, and 13.

Table 1 T3SI scores [53] (Higher value, shown in bold font, is better)

3.4 Running time

The proposed approach was implemented in MATLAB.³ The running times for the structure extraction from the textured image (Fig. 4), and from the mosaic images in Figs. 11, 12 and 13 are provided in Table 2. These running times were obtained on an Intel CORE i3 at 3.3GHz using a single thread and are averaged over multiple runs. All the other methods used in the comparison [32, 39, 41] are similarly implemented in MATLAB and run in the same conditions. The computational timings for [19] are omitted from this table, because they are not directly comparable to the other methods. The approach relies on a denoiser implemented by a deep neural network and is not competitive when run on a CPU. One can observe that our schemes show competitive computational times, while providing high quality results.

Table 2 Running times (in sec.) for the structure extraction from textured and mosaic images

The most time-consuming part (approximately $25\%$ of the total time) in our approach is the solution at each iteration of a simple linear PDE in the second step of the minimization procedure described in Sect. 2.3. This PDE is solved in frequency space using the fast Fourier transform.

All these approaches, with the exception of [41], are iterative, and run for a sufficient number of iterations to compute the image structure. For energy-based methods, such as ours, the energy can also be monitored and used as a stopping criterion.

The time-consuming part in the method described in [32] is the computation at each iteration of the edge aware filters and their application, while the method [39] needs to solve a linear system at each iteration by the pre-conditioned conjugate gradient method. The method described in [41] spent most of its time is in computing statistics on image patches.

3.5 Image details sharpening and enhancement

Fig. 15

Applications to image sharpening. An input image is sharpened by proper re-scaling of the texture information. Different methods for computing the image structure (and thus the texture) are compared

Fig. 16

Zooms on selected regions of the sharpened images in Fig. 15

Another domain of application is image sharpening. Given an input image f, we extract the structure u using the approach described in Sect. 2 and then compute the texture $t = f - u$. We use a simple method to sharpen the details: We simply multiply the texture by a constant. The sharpened image ($f_S$) is finally obtained by $f_S = u + \alpha (f - u)$. In the results shown in Fig. 15, we set $\alpha =5$. For comparison, we show also the results obtained by combining the approach previously described for image sharpening with different state-of-the-art approaches [32, 39, 41] for the structure extraction. A zoom on the regions highlighted in red and green color in the top-left image of Fig. 15 is shown in Fig. 16. Both methods from [39] and [32] generate artifacts, which are highlighted by the white color boxes in Fig. 16. The method from [41] and our approach do not generate such artifacts while sharpening the image details.

Fig. 17

An example of enhancing an image with mist. Left: The original image; middle: Enhanced image with the level-set curvature (3) used for the structure extraction; right: enhanced image with the surface mean curvature (4) used for the structure extraction. In both cases, $b=50,\lambda =1$ are used

Fig. 18

Zooms on selected regions of the dehazed images in Fig. 17

Enhancing images with haze or mist is another example of possible application. An example of an image and its processed versions is shown in Fig. 17, with zooms on selected regions shown in Fig. 18. The process is relatively similar to image sharpening: given an observed image, its structure is extracted and the recovered details are amplified. When dealing with natural images, we saw in Sect. 2.4 that the surface mean curvature (4) was more stable than the level-set curvature (3). This is illustrated in the middle and right images in Fig. 17, where the level-set curvature, respectively, the surface mean curvature, is used for the computation of the disparity term (6). We can observe in the middle image visual artifacts coming from the use of the level-set curvature, and amplified by the image enhancement process. The image on the right does not have these artifacts. The zoomed regions in Fig. 18 indicate that both methods are able to enhance image details despite the haze.

4 Discussion and conclusion

We have presented in this work an approach for extracting the structure and texture of an image. The approach is based on minimizing a weighted version of a $p(\cdot )$-Dirichlet energy with spatially variable weight and exponent functions. Our choices of the weight and exponent functions are adapted for the tasks considered in the paper: structure extraction and image details sharpening. In both cases, we construct the functions based on an analysis of the spectral contents of the level-set or mean curvature of the image intensity.

For the structure extraction problem, we demonstrated experimentally the advantages of the proposed approach over recent state-of-the-art structure + texture decomposition methods on textured images and mosaic images. In particular, we have demonstrated that our approach does a good job at preserving the main edges and appearance of the input image, while removing high frequency details.

Using a recent method [53], we have tried to quantify the result of these different methods on the structure extraction task. However, we have also shown with a simple synthetic example that the problem of structure extraction is ill-posed, and that a quantitative analysis is difficult to do in general, and that the results are difficult to interpret.

Finally, we have demonstrated a few possible applications, such as sharpening image details, and enhancing an image with mist or haze. The former illustrated the advantages of our approach against other recent methods, while the latter was used to demonstrate the advantage of using the surface mean curvature for determining the weight and exponent functions of the $p(\cdot )$-Dirichlet energy.

Appendices

Appendix A Minimization by ADMM

We use a variant of ADMM to solve numerically (1) and (2). The problem (1) can be rewritten as

$$\begin{aligned} \int _{\Omega } a({\varvec{x}}){\,\!|\,\!}{\varvec{\xi }}{\,\!|\,\!}^{p({\varvec{x}})} + \frac{\lambda }{2}\int _\Omega \left( H\!\left[ u-f\right] \right) ^2 \rightarrow \min \end{aligned}$$

with the constraint

$$\begin{aligned} {\varvec{\xi }}= \nabla u. \end{aligned}$$

The corresponding augmented Lagrangian is

$$\begin{aligned} L_{a,p}(u,{\varvec{\xi }},\varvec{\mu })&= \int _\Omega \Bigl \{a({\varvec{x}}){\,\!|\,\!}{\varvec{\xi }}\,{\,\!|\,\!}^{p({\varvec{x}})} +\frac{\lambda }{2}H\!\left[ u-f\right] ^2 \nonumber \\&\quad {}+ \varvec{\mu }\cdot ({\varvec{\xi }}-\nabla u) +\frac{\rho }{2}{\,\!|\,\!}{\varvec{\xi }}-\nabla u{\,\!|\,\!}^2 \Bigr \}, \end{aligned}$$

(A1)

where $\varvec{\mu }({\varvec{x}})$ is the vector of Lagrange multipliers and $\rho >0$ is a constant. The Lagrangian (A1) is minimized by block descent and updating in turns ${\varvec{\xi }}, u$ and $\varvec{\mu }$

$$\begin{aligned} {\varvec{\xi }}_{k+1}&= \mathop {\mathrm {arg\,min}}\limits L_{a,p}(u_k, {\varvec{\xi }}, \varvec{\mu }_k), \\ u_{k+1}&= \mathop {\mathrm {arg\,min}}\limits L_{a,p}(u, {\varvec{\xi }}_{k+1}, \varvec{\mu }_k), \\ \varvec{\mu }_{k+1}&= \mathop {\mathrm {arg\,min}}\limits L_{a,p}(u_{k+1}, {\varvec{\xi }}_{k+1}, \varvec{\mu }). \end{aligned}$$

There is no closed-form solution for the first step. Instead, we resort to an approximation for the $p^{\textrm{th}}$ power of the $L_p$ norm of ${\varvec{\xi }}$

$$\begin{aligned} {\varvec{\xi }}_{k+1}= & {} \max \left\{ {\,\!|\,\!}{\varvec{s}}_k{\,\!|\,\!}-\frac{a({\varvec{x}})}{r{\,\!|\,\!}\nabla u_k{\,\!|\,\!}^{1-p({\varvec{x}})}}, 0\right\} \frac{{\varvec{s}}_k}{{\,\!|\,\!}{\varvec{s}}_k {\,\!|\,\!}},\nonumber \\ {\varvec{s}}_k= & {} \nabla u_k-\frac{\varvec{\mu }_k}{r}. \end{aligned}$$

(A2)

For fixed ${\varvec{\xi }}$ and $\varvec{\mu }$, computing the optimal u leads to solving the linear PDE

$$\begin{aligned} -r (\Delta u - \mathop {\textrm{div}}({\varvec{\xi }}_{k+1})) + \mathop {\textrm{div}}(\varvec{\mu }_k) + \lambda H^{*} H\!\left[ u-f\right] = 0, \end{aligned}$$

where $H^{*}$ is the adjoint of the operator H. This can be done with the fast Fourier transform (FFT). Finally, the Lagrange multipliers are updated with

$$\begin{aligned} \varvec{\mu }_{k+1}=\varvec{\mu }_{k}+\rho \left( {\varvec{\xi }}_{k+1}-\nabla u_{k+1}\right) . \end{aligned}$$

Appendix B $L_1$ fitting term

Similarly, we rewrite (2) as

$$\begin{aligned} \int _{\Omega } a({\varvec{x}}){\,\!|\,\!}{\varvec{\xi }}{\,\!|\,\!}^{p({\varvec{x}})} + \lambda \int _{\Omega }{\,\!|\,\!}r {\,\!|\,\!}\rightarrow \min \end{aligned}$$

with the constraints

$$\begin{aligned} {\varvec{\xi }}= \nabla u, \end{aligned}$$

and

$$\begin{aligned} r = H[u-f]. \end{aligned}$$

The corresponding augmented Lagrangian is

$$\begin{aligned} L_{a,p}(u, r, {\varvec{\xi }}, \varvec{\mu }, z)&= \lambda \int _{\Omega }{\,\!|\,\!}r {\,\!|\,\!}+ \int _{\Omega } a({\varvec{x}}){\,\!|\,\!}{\varvec{\xi }}{\,\!|\,\!}^{p({\varvec{x}})} \nonumber \\&\quad + \int _{\Omega } z (r-H[u-f]) \nonumber \\&\quad + \frac{\rho _1}{2}\int _{\Omega }{\,\!|\,\!}r - H[u-f]{\,\!|\,\!}^2 \nonumber \\&\quad + \int _{\Omega } \varvec{\mu }\cdot ({\varvec{\xi }}- \nabla u) + \frac{\rho _2}{2}\int _{\Omega }{\,\!|\,\!}{\varvec{\xi }}- \nabla u{\,\!|\,\!}^2, \end{aligned}$$

(B3)

where $\varvec{\mu }({\varvec{x}})$ is vector of Lagrange multipliers associated with the constraint ${\varvec{\xi }}=\nabla u$, $z({\varvec{x}})$ is the Lagrange multiplier associated with the constraint $r=H[u-f]$, and $\rho _1>0, \rho _2>0$ are constants. Similarly to above, we use the approximation

$$\begin{aligned} {\varvec{\xi }}_{k+1} = \max \left\{ {\,\!|\,\!}{\varvec{s}}_k{\,\!|\,\!}- \frac{a(x)}{\rho _2 {\,\!|\,\!}\nabla u_k{\,\!|\,\!}^{1-p(x)}}, 0 \right\} \frac{{\varvec{s}}_k}{{\,\!|\,\!}{\varvec{s}}_k{\,\!|\,\!}}, \end{aligned}$$

where ${\varvec{s}}_k = \nabla u_k - \frac{1}{\rho _2} \varvec{\mu }_k$ for solving the sub-problem in ${\varvec{\xi }}$. The $L_1$ fitting term gives a sub-problem in r which is solved by shrinkage

$$\begin{aligned} r_{k+1}= & {} \max \left\{ {\,\!|\,\!}H[u_k-f]-\frac{1}{\rho _1}z_k{\,\!|\,\!}-\frac{\lambda }{\rho _1},0\right\} \\{} & {} \mathop {\textrm{sign}}(H[u_k-f]-\frac{1}{\rho _1}z_k). \end{aligned}$$

The updated u is obtained by solving the linear PDE

$$\begin{aligned}{} & {} -\left( \rho _1 H^* H + \rho _2 \Delta \right) u + \rho _1 H^* H f - H^*(\rho _1 r - z)\\{} & {} \quad - \mathop {\textrm{div}}(\rho _2 {\varvec{\xi }}- \varvec{\mu }) = 0. \end{aligned}$$

Finally, the Lagrange multipliers are updated with

$$\begin{aligned} \varvec{\mu }_{k+1}&= \varvec{\mu }_k - \rho _2 ({\varvec{\xi }}_{k+1} - \nabla u_{k+1}) \\ z_{k+1}&= z_k - \rho _1 (r_{k+1} - H[u_{k+1}-f]). \end{aligned}$$