Abstract
The size of wood is reduced by splitting or chipless cutting whilst logging trees, limbing, or preparing wood to be a fuel, for example, or in order to improve the efficiency of wood drying processes. Low costs of wood processing are desirable in each of these processes. The article presents experimental and simulation tests run in ABAQUS software, which allow for an analysis of the geometry of cutting tools used during the splitting or chipless cutting of wood in order to determine the cutting force and driving force of the machine executing such a process. The tests involved wood of Pinus sylvestris L. (moisture content: 8.74% ± 0.1%) in four configurations (chipless cutting transverse to the fibres (90°–90°), splitting along the fibres (0°–90°), splitting radially to the grain (90°–0°) and splitting tangentially to the grain (90°–0°)). Analysis of the force and strength of the blade proved that an effective tip angle of the knife blade falls between 30° and 45°. The presented results also suggested that splitting wood along the fibres (0°–90°) is preferable in a machine process, while splitting tangentially and radially to the wood grain (90°–0°) is preferable when splitting wood using manual tools.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
As indicated by archaeological discoveries, tools for splitting wood have been known to mankind since the Stone Age (Kriiska et al. 2013). Even back then, their shape already displayed an acute angle of the cutting edge (Fig. 1a). Various shapes of tools for the splitting and chipless cutting of wood have been developed over the years (Fig. 1). Generally, all of the presented geometries allow for the splitting and cutting of wood. However, the design of modern tools and machines for wood processing should be aimed at reducing the energy consumption of the process (Spinelli et al. 2015; Orłowski et al. 2020; Warguła and Kukla 2020) as well as the impact on the environment (Manzone 2015; Prada et al. 2015; Spinelli et al. 2018) and machine operators (Magagnotti et al. 2014; Gulci et al. 2018; Licow et al. 2020). These requirements can be achieved when designing machines by changing the construction of cutting mechanisms (Spinelli et al. 2015; Reczulski 2018; Flizikowski et al. 2021) or by changing the method and type of fuel used to power the drive units of the machines (Prinz et al. 2018; Warguła et al. 2020a, b), for example. Amateur manual tools or industrial wood splitting machines prevail among splitting machines (Tajboš and Lukáč 2015). One characteristic part of such machines is the splitting wedge. A similar cutting mechanism is used when chiplessly cutting wood, which is becoming increasingly popular in silviculture due to the use of harvesters equipped with specialised heads enabling the process of such cutting (Harvánek et al. 2021). The design of machines which process wood by dividing it into parts, for example chopping, shredding, cutting or splitting, requires a trade-off between two parameters related to the blade of the cutting mechanism. The first one is the durability of the blade, while the second one is the cutting or splitting force. A blade shape, which reduces the cutting force, is typically not very durable, and vice versa, the tools with a shape that increases durability also increase the cutting force.
Shape of wood splitting tools—a Stone Age tools (based on Kriiska et al. 2013) and modern tools—b a simple splitting wedge; c, d a refracted splitting wedge; e a concave splitting wedge; f a convex splitting wedge
Research is underway on the geometry of blades that would be durable and consume less energy during the processes of wood splitting and chipless cutting. Kováč et al. (2014) investigated the impact of the shape of the splitting wedge of a horizontal wood splitter on the driving force. This research indicated that the shape of the blade has a major impact on the energy consumed when splitting wood. Changing the shape can limit the energy consumption by 50%, with a simultaneous increase in the tendency for the blade to blunt and bend. This research was based on experiments, a fact which contributes to the limited number of the studied cases. Tajboš and Lukáč (2015) studied wood splitting mechanisms that were adapted for vehicles with hydraulic propulsion, analysing how the cross-section of a log affects the wood splitting duration while it is split. They reported that the average wood splitting duration increased along with the cross-section of the wood; however, this measurement displayed a wide range of values, which may suggest that this is not the primary factor affecting this parameter. Erber and Stampfer (2020) investigated factors, which affect the efficiency of splitting large wooden logs. They found that wood defects lowered the efficiency of the splitting process by approximately 32%. The use of splitters will primarily split wood parallel to the growth of its fibres. On the other hand, the method of chipless wood cutting is also being developed; it is characterised by the blade moving perpendicular to the growth of wood fibres. Harvánek et al. (2021) analysed the cutting force for chipless cutting using various tools. They indicated that the most preferable blade thickness is 10 mm, with a cutting edge angle of 30°. Such a blade demonstrated the least wear, but at the same time, it required the highest driving force. The research took an experimental approach, and the most preferable thickness of the blade (10 mm) was the thickest among those tested. This suggests that a broader examination of this type of tool may provide new conclusions. Studies on the influence of the material or tool on woodworking processes—also processes of reducing the size of wood—can be found in the research by Hatton et al. (2015), who described the cutting force when cutting branches of various diameters, or Melicherčík et al. (2021), who investigated the cutting force during the limbing processes.
The analyses of the geometric properties of wood splitting and cutting tools available in the literature are based on experimental tests with a limited scope. This indicates that it would be preferable to develop a research methodology for these tools based on numerical tests (FEM), which would allow for an analysis of a wide spectrum of geometrical properties of the tools. Such research is being developed in order to test the material properties of wood and its resistance to wood splitting (Ostapska and Malo 2021a, b); however, such methods cannot assess the influence of working tools on the processes of splitting wood. The procedure during the creation of such a research methodology is based on the results of the experiment (Ostapska and Malo 2021a), followed by recreating it under the conditions of numerical methods, for example the finite element method (FEM) (Ostapska and Malo 2021b), to support streamlined engineering methods for testing wood. Prediction of the cutting force is a basis for machine design and still a valid trend in science, especially in terms of designing innovative tools (Gochev et al. 2018; Chuchala et al. 2020; Wellenreiter et al. 2021).
The article presents the results of experimental tests where pine wood (Pinus sylvestris L.) was split and chiplessly cut using three blade shapes (with tip angles α of 30°, 60° and 120°). Based on the experiments and a material model of wood (Warguła et al. 2021) created in the software program ABAQUS Standard 2020 in an elastic–plastic range, a simulation model was developed to analyse the influence of the geometrical parameters of a blade on its cutting force. When multiplying the cutting force by the blade speed, it is possible to determine the power necessary to cut wood. Such information can be useful when designing energy-efficient machines for reducing the size of wood. The purpose of the article is to determine an effective shape of the tip angle of the blade and to establish wood splitting directions preferable for machine splitting and for using manual tools.
2 Material and methods
2.1 Materials and methods—the experiment
The measurements in this study were done on pine wood (Pinus sylvestris L. Sp. Pl. 1000, 1753—Scots pine) available for commercial sale in Poland. Research by Chuchala et al. (2014) shows that the place where the tree grows is of great importance for the properties of the wood; the examined wood came from the Polish State Forests, Złotkowo Forest District, Suchy Las. It consisted of samples acclimatised for six months at 20 °C and relative humidity (RH) of about 46%, so that they reached a moisture content (MC) of 8.74% ± 0.1%. A climatic chamber was used for this purpose. The MC was checked with a Mettler Toledo moisture analyser during conditioning, until the desired value was obtained. The measurement consisted of precisely weighing the sample (± 0.001 g) and simultaneous drying (change of MC from the measured value to oven-dry). The average density of the tested samples was 450 kg m−3 ± 5%. The samples were cut mechanically from timber free of defects such as knots, rot, etc. They were made from selected logs in order to obtain representative and reproducible test results. Due to the anisotropic properties of pine wood, which can be approximated by orthotropic properties (in lengthwise, tangential and radial directions), the tests were performed with four different wood splitting or chipless cutting directions (A–D), which are presented in Fig. 2.
Types of specimens subjected to splitting or chipless cutting, with the line of contact between the blade and the wood: a chipless cutting transverse to the fibres (90°–90°); b splitting along the fibres (0°–90°); c splitting radially to the grain (90°–0°); d splitting tangentially to the grain (90°–0°), in brackets the directions of cutting are indicated in accordance with the directions of wood fiber according to Kivimaa (1950)
The tests of splitting and chipless cutting of wood were performed with cutting tools presented in Fig. 3. The tests were performed for: steel blades with tip angles α of 30°, 60°, 120° and cutting edge radius (0.1 µm). The blades were made with a positive deviation from the nominal size (20 k6), while the samples were made with a negative deviation from the nominal size (20 h6). This made it possible to analyze the cutting process, without taking into account the secondary effects that could arise at the tip of the blade only in the case of samples that were subject to significant deformation before splitting or cutting. The blade was new and made of HARDOX steel, type 500, with the edges not rounded. The roughness of the blade surface for the arithmetic average of profile height deviations from the mean line (Ra) was equal to 1.472 ± 0.277 µm, and the highest roughness according to maximum peak to valley height of the profile for 10 highest profiles (Rz) was equal to 8.14 ± 1.1 µm.
The test involved pushing a knife with a given shape into wood samples with a specific speed until they were destroyed (Fig. 4). During such an experiment, changes in the values of force and displacement were recorded over time. Seven repetitions were performed with a single blade, and the five most similar results were selected for the analysis. The tests were carried out on an MTS Insight testing machine with a 50 kN load cell, at a temperature of 25 °C and with a relative humidity of 40%. The strain rate for each of the cases was 0.02 mm/s.
2.2 Materials and methods—simulation
The simulation was done with a material model developed by the authors, which is presented in detail in another scientific publication (Warguła et al. 2021), which also compared the results of modelling and experimental studies, indicating that the average accuracy of the model in determining the maximum breaking force of the material is 8% (14% for the tensile test, 2.5% for compression and 6.5% for shearing). The analysis was performed in ABAQUS Standard 2020, in an elastic–plastic range. This software also performed a simulation that allowed the impact of geometrical parameters of the blade on the value of the cutting force to be analysed. The construction of the simulation model is presented in Fig. 5.
The model consists of two elements: a blade with a variable tip angle α and a wooden cube measuring 20 × 20 × 20 mm that takes into account approximated orthotropic properties (in lengthwise, tangential and radial directions). In the model, the wooden cube was mounted on the bottom surface, while kinematic excitation in the form of a constant speed (vy = 0.5 mm/s) was applied to the blade, considered as a rigid body. The tests were performed for a very low speed, maintaining a quasi-static nature, so as to minimise the impact of speed on the test and to focus on the impact of blade geometry. Despite that for such a low speed the above mentioned impact of speed should be neglected, not like for a high cutting speed, where the impact of speed is crucial (Dvoracek et al. 2021), it may slightly affect the material deformation and the influence of the blade geometry, which is why the velocity was drastically minimized. The value of the splitting force FS (force of reaction at the reference point RP1) was derived from the analysis as a function of the displacement x.
The properties of the material were defined using the model presented in an article by Warguła et al. (2021). The density of the material was defined as 450 kg/m3. The elastic properties were modelled using 9 engineering constants presented in Table 1 in order to gain orthotropic properties of the wooden cube. The modelling for the breakage of the material used the ‘Fail stress’ sub-option, where data for each of the directions were entered in accordance with Table 2. The experimental curves and their approximations, presented in Fig. 6, were used to model plastic properties with isotropic reinforcement. This property was defined in the ‘Potential’ sub-option as a unit tensor. To reflect the cooperation of the blade with the material being split, the contact between the cutting edge of the blade and the wood was modelled by setting the coefficient of friction µ at 0.25 in a tangential direction and selecting the ‘Hard contact’ property, preventing penetration in a normal direction (Kretschmann 2010; Aira et al. 2014). The C3D8R finite elements were also used in this study and the size of each element was 1 mm. The nodes on the cutting edge of the tool were adjusted with the nodes of the elements on the wooden cube at the beginning stage of cutting. By default, for the element deletion, the upper bound to all damage variables at a material point was set as 1.
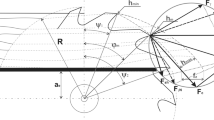
To determine the state of stress in the blade, the relationship between the geometrical parameters of the blade and the load and cross-sections, or surfaces subjected to load was analysed (Fig. 7).
The following relationships were established based on this analysis:
where \({F}_{s}\) is the splitting force, \({F}_{N}\) is the normal force, \({\sigma }_{c}\) is the compressive stress, \({p}_{con}\) is the contact stress, \(\alpha\) is the tip angle of the blade and \(x\) is the depth of blade penetration.
3 Results and discussion
Figures 8, 9, and 10 present the results of simulation and experimental tests for blades with tip angles α of 30°, 60° and 120° in all four directions. When analysing the results, it can be seen that the resulting characteristics varied greatly, though the value of maximum splitting force was similar. Considering the purpose of this analysis, such a model serves in the assessment of the maximum splitting force, and as a result it can be used for establishing demand for the cutting or splitting power. In the case of directions C (90°–0°) and D (90°–0°), the values for all three angles were almost identical.
In the case of direction A (90°–90°), considerable discrepancy can be observed for lower angles. In the case of direction B (0°–90°), the situation was opposite—there was high discrepancy for higher angles. Direction A (90°–90°) corresponded to cutting rather than splitting—it requires a large deformation to break the sample, and thus the most force; therefore, it is not as important during the splitting process. Due to the growing discrepancy at high angles, the applicability of the model has been limited to a range of α ≤ 15° ÷ 120° > , which is sufficient, since the use of higher tip angles leads to crushing wood (as in the production of hog fuel, in which wood is crushed with blunt tools (Alakangas et al. 2006; European Standard EN ISO 17225–1:2014; Nati et al. 2015)) instead of cutting or splitting it.
The percentage difference in the values of the results of the experimental and simulation tests is presented in Fig. 11. It can be observed that the arithmetic mean difference in the results is at the level of 15%. The divergence between the force characteristics obtained from simulations and experiments is caused by the simplification of using an orthotropic approach to wood material modelling, which is in reality the anisotropic material. Additionally, the wooden cube is modelled as a homogenous material without taking into consideration the grains and the damage model does not take into account the fracture on the division surface between grains. Nevertheless, if we consider that the peak value of the cutting force is a crucial information in tool optimization, we can consider the presented model as useful enough. Although, above mentioned aspects could be improved to make the model more precise and accurate.
Figure 12 presents the simulation results for a blade with a tip angle of 60° splitting in all four directions, taking into account the breaking deformations that result from experimental tests (7 mm, 3.5 mm, 1.5 mm and 1.8 mm for directions A (90°–90°), B (0°–90°), C (90°–0°) and D (90°–0°), respectively). Based on these results, it can be concluded that machine splitting of wood along the fibres (direction B (0°–90°)) is the most preferable, since it requires the least force despite requiring more deformation than splitting tangentially or radially to the wood grain (directions C (90°–0°) and D (90°–0°)). Although the force in these directions increased the fastest, quick breakage causes demand for considerably less force to break down wood than doing so transversely to the fibres (90°–90°) (chipless cutting requires the most deformation). This is why wood is usually split in this direction using the manual method, since it requires the least work (the product of force and displacement). The relationships described in the literature are based on the research methodology for machines and tools, or in patent descriptions. Manually operated tools used to split wood are mainly proposed or tested for work with wood tangentially or radially to the wood grain (90°–0°) (Mutin 1994; Päivinen and Heinimaa 2009; Gregg 2015). Most commercial machine splitters with a splitting wedge were also proposed and tested in that regard (Albright 2006; Biberger 2012; Kováč et al. 2014), but there are some that process wood along the fibres (0°–90°). Machines for splitting wood along the fibres (0°–90°) typically have a conical auger for splitting wood (Ober 1978; York 1983; Wentzell 1987; Bolton 2006; Erber and Stampfer 2020). Tests for breaking down wood transversely to the fibres (90°–90°) are mainly conducted on the heads of harvesters used for chipless cutting (Bergström and Di Fulvio 2014; Harvánek et al. 2020; Gao et al. 2021) or for limbing heads (Gerasimov et al. 2012; Mederski et al. 2018; Melicherčík et al. 2021). Figure 13 presents a simulation of the process of splitting wood in direction B (0°–90°), while Fig. 14 presents a simulation of splitting and chiplessly cutting wood in each of the four directions, where a difference can be observed in the moment that the sample breaks, in accordance with the characteristics presented in Fig. 12.
Figures 15 and 16 present the results for splitting along the fibres (0°–90°) for all the blades under study with varying tip t angles. Based on these results, it is apparent that in the initial phase the increase in force is identical, and that not until a certain blade penetration value is exceeded (the higher the angle, the earlier) that it deviates from the reference characteristics, which means a higher value of the maximum splitting force. It should be noted that for an angle of 15°, the force drops near the end. This indicates that it is not reasonable to use blades below 15°, since they are less durable without changing the maximum force.
A maximum splitting force resulting from simulation tests in all splitting directions and all the analysed tip angles of the blade is presented in Fig. 17, in the form of experimental and approximated functions FS(α). In the case of directions A (90°–90°) and B (0°–90°), there were quite unambiguous relationships described by a quadratic and linear function, respectively. In the case of directions C (90°–0°) and D (90°–0°), these relationships were more ambiguous; however, they can still be quite precisely approximated by a second-order curve. When analysing the results, it can be observed that for tip angles lower than 45° there is a slight force increase (except direction A (90°–90°)) with an almost constant force when splitting the wood radially or tangentially to the rings (directions C (90°–0°) and D (90°–0°)).
To be able to perform a full functional analysis of the tested blades, compressive stresses (Fig. 18) and contact stresses (Fig. 19) were also listed as a function of the variable tip angle α. The highest values of the compressive stress were obtained for splitting directions C (90°–0°) and D (90°–0°), which can be explained by the high force for little blade penetration. The lowest value of the compressive stress was recorded in the range of 45°–60°, amounting to approx. 30 MPa. In the case of a dynamic zero-pulse load, this seems to be a reasonable value when using carbon steel, due to the fatigue limit. In directions A (90°–90°) and B (0°–90°), only a slight force increase was noted for the lower angles, which once again proves the advantage of splitting along the fibres during a machine process.
When analysing the contact stresses, one can notice an increase along with an increasing tip angle. A considerable increase occurred at angles higher than 45°, even up to a value of 18 MPa for direction C (90°–0°) (at lower angles, the contact stresses did not exceed 4 MPa).
When comparing an analysis of the force and stresses in devices for splitting wood mechanically, it is recommended to use blades with a tip angle between 30° and 45°. It should also be noted that buckling of the blade can additionally occur at lower tip angles of the blade. A similar angle of wedge (35°), which lies in the specified range, was used by Kováč et al. (2014) during the simple wood splitting tests.
4 Conclusion
Based on the analysis, the model used in this study can be deemed useful for determining the wood splitting and cutting force, and thus for determining the power requirements of machines which split and chiplessly cut wood. Based on an analysis of the force and durability of the blade, a blade with a tip angle of 30°–45° was found to be an efficient solution. The results also indicate that splitting wood along its fibres (0°–90°) is the most preferable in a machine process, while splitting wood tangentially or radially to the grain (90°–0°) is more preferable in a manual process. The splitting force for two different directions of splitting can be greater than 300%, which shows the importance of positioning the wood in the splitting machine and how it can affect its exploitation.
Based on the obtained results, by using such simplified model to perform an analysis, which will result in designing the tool for wood splitting an increased safety factor should be taken into consideration due to the estimated mean error of 15%. The advantages of such model are low computational time of analysis and ease of implementation. However, one has to be aware that for a selected direction the divergence between experimental and simulation results may exceed 50% due to the anisotropy of wood and complex damage mechanics on the wood grains. It shows the direction for the future research in this area. Additionally, in the future, this research will be extended to more complex geometries of splitting wedges- or multi-blade splitting wedges in order to establish which splitting wedges are most efficient.
References
Aira JR, Arriaga F, Íñiguez-González G, Crespo J (2014) Static and kinetic friction coefficients of Scots pine (Pinus sylvestris L.), parallel and perpendicular to grain direction. Mater Constr 64(315):e030–e030
Alakangas E, Valtanen J, Levlin J-E (2006) CEN technical specification for solid biofuels—fuel specification and classes. Biomass Bioenerg 30(11):908–914
Albright BD (2006) Wood splitter with multiple wood splitting wedges on a rotating member. US7108029B2, filed Jun 16, 2004. https://worldwide.espacenet.com/patent/search/family/035479348/publication/US7108029B2?q=US7108029B2. Accessed 1 Sept 2022
Bergström D, Di Fulvio F (2014) Evaluation of a novel prototype harvester head in early fuel-wood thinnings. Int J for Eng 25(2):156–170
Biberger K (2012) Wood splitter. EP2279838B1, filed September 19, 2012. https://worldwide.espacenet.com/patent/search/family/042779181/publication/EP2279838B1?q=EP2279838B1. Accessed 1 Sept 2022
Bolton SD (2006) Hands free wood splitter. US7934525B2, filed May 29, 2009. https://worldwide.espacenet.com/patent/search/family/041087713/publication/US7934525B2?q=US7934525B2. Accessed 1 Sept 2022
Chuchala D, Orlowski KA, Sandak A, Sandak J, Pauliny D, Barański J (2014) The effect of wood provenance and density on cutting forces while sawing Scots pine (Pinus sylvestris L.). BioResources 9(3):5349–5361
Chuchala D, Ochrymiuk T, Orlowski KA, Lackowski M, Taube P (2020) Predicting cutting power for band sawing process of pine and beech wood dried with the use of four different methods. BioResources 15(1):1844–1860
Dvoracek O, Lechowicz D, Krenke T, Moseler B, Tippner J, Haas F, Emsenhuber G, Frybort S (2021) Development of a novel device for analysis of high-speed cutting processes considering the influence of dynamic factors. Int J Adv Manuf Technol 113:1685–1697. https://doi.org/10.1007/s00170-021-06769-1
EN ISO 17225-1 (2014) Solid biofuels–fuel specifications and classes: general requirements. ISO, Geneva
Erber G, Stampfer K (2020) Splitting of large logs with an excavator-based cone splitter. Int J for Eng 31(2):146–155
Flizikowski J, Kruszelnicka W, Macko M (2021) The development of efficient contaminated polymer materials shredding in recycling processes. Polymers 13(5):713. https://doi.org/10.3390/polym13050713
Gao Y, Kang F, Kan J, Wang Y, Tong S (2021) Analysis and experiment of cutting mechanical parameters for Caragana korshinskii (C.k.) branches. Forests 12:1359. https://doi.org/10.3390/f12101359
Gerasimov Y, Seliverstov A, Syunev V (2012) Industrial round-wood damage and operational efficiency losses associated with the maintenance of a single-grip harvester head model: a case study in Russia. Forests 3(4):864–880
Gochev Z, Vukov G, Atanasov V, Vitchev P, Kovachev G (2018) Factors influencing the cutting power in longitudinal milling of solid wood. Ann Warsaw Univ Life Sci-SGGW, for Wood Technol 102:103–111
Gregg JC (2015) Cross axe, US20150352738A1, filed June 9, 2014. https://worldwide.espacenet.com/patent/search/family/054768843/publication/US2015352738A1?q=US20150352738A1. Accessed 1 Sept 2022
Gulci S, Akay AE, Spinelli R, Magagnotti N (2018) Assessing the exposure of chipper operators to wood dust in a roadside landing area. Fresenius Environ Bull 27(6):4132–4138
Harvánek P, Kováč J, Krilek J, Ťavoda J (2020) Analýza Reznej Sily V Procese Priečneho Delenia Dreva. In: TECHNOFORUM 2020 new trends in machinery and technologies for biosystems, pp 59–66. https://doi.org/10.15414/2020.9788055221663
Harvánek P, Kováč J, Melicherčík J (2021) Analysis of cutting force in the process of chipless felling wood. Wood Research 66(1):153–160
Hatton B, Pot G, Bouzgarrou BC, Gagnol V, Gogu G (2015) Experimental determination of delimbing forces and deformations in hardwood harvesting. Croatian J for Eng J Theory Appl for Eng 36(1):43–53
Kivimaa E (1950) Cutting force in wood working. Helsinki, Finland
Kováč J, Krilek J, Kučera M, Barcík Š (2014) The impact of design parameters of a horizontal wood splitter on splitting force. Drvna Industrija: Znanstveni Časopis Za Pitanja Drvne Tehnologije 65(4):263–271
Kretschmann D (2010) Mechanical Properties of Wood. Wood Handbook: Wood as an Engineering Material: Chapter 5; General Technical Report FPL.; GTR-190; Centennial, Ed.; Department of Agriculture, Forest Service, Forest Products Laboratory, Madison, pp 5.1–5.46
Kriiska A, Tarasow A, Kirs J (2013) Wood-chopping tools of the Russian-Karelian type from Estonia. In: Johanson K, Tõrv M (eds) Man, his time, artefacts, and paces: collection of articles dedicated to Richard Indreko. University of Tartu, Tartu, pp 317–345
Licow R, Chuchala D, Deja M, Orłowski KA, Taube P (2020) Effect of pine impregnation and feed speed on sound level and cutting power in wood sawing. J Clean Prod 272:122833
Magagnotti N, Picchi G, Sciarra G, Spinelli R (2014) Exposure of mobile chipper operators to diesel exhaust. Ann Occup Hyg 58(2):217–226
Manzone M (2015) Energy consumption and CO2 analysis of different types of chippers used in wood biomass plantations. Appl Energy 156:686–692
Mederski PS, Bembenek M, Karaszewski Z, Pilarek Z, Łacka A (2018) Investigation of log length accuracy and harvester efficiency in processing of oak trees. Croatian J for Eng J Theory Appl for Eng 39(2):173–181
Melicherčík J, Krilek J, Kováč J, Harvánek P (2021) Influence of knife geometry on selected factors pertaining to the delimbing process. BioResources 16(1):1757
Mutin SI (1994) Heavy-duty axe, RU2024389C1, filed April 30, 1991. https://worldwide.espacenet.com/patent/search/family/021572303/publication/RU2024389C1?q=RU2024389C1. Accessed 1 Sept 2022
Nati C, Magagnotti N, Spinelli R (2015) The improvement of hog fuel by removing fines, using a trommel screen. Biomass Bioenerg 75:155–160
Ober HR (1978) Log splitting apparatus. US4091851A, filed April 15, 1977. https://worldwide.espacenet.com/patent/search/family/025143005/publication/US4091851A?q=US4091851A. Accessed 1 Sept 2022
Orłowski KA, Ochrymiuk T, Hlaskova L, Chuchala D, Kopecky Z (2020) Revisiting the estimation of cutting power with different energetic methods while sawing soft and hard woods on the circular sawing machine: a Central European case. Wood Sci Technol 54(2):457–477
Ostapska K, Malo KA (2021a) Crack path tracking using DIC and XFEM modelling of mixed-mode fracture in wood. Theoret Appl Fract Mech 112:102896
Ostapska K, Malo KA (2021b) Calibration of a combined XFEM and mode I cohesive zone model based on DIC measurements of cracks in structural scale wood composites. Compos Sci Technol 201:108503
Päivinen M, Heinimaa T (2009) The usability and ergonomics of axes. Appl Ergon 40(4):790–796
Prada M, Martínez-Alonso C, Sánchez-García S, Canga E (2015) Analysis of three forest chippers: productivity, costs and GHG emissions in Northern Spain. J Clean Prod 101:238–244
Prinz R, Laitila J, Eliasson L, Routa J, Järviö N, Asikainen A (2018) Hybrid solutions as a measure to increase energy efficiency–study of a prototype of a hybrid technology chipper. Int J for Eng 29(3):151–161
Reczulski M (2018) Optimization of the clearance angle in industrial disc chipper. Wood Res 63(2):295–304
Spinelli R, Cavallo E, Eliasson L, Facello A, Magagnotti N (2015) The effect of drum design on chipper performance. Renew Energy 81:57–61
Spinelli R, de Arruda Moura AC, da Silva PM (2018) Decreasing the diesel fuel consumption and CO2 emissions of industrial in-field chipping operations. J Clean Prod 172:2174–2181
Tajboš J, Lukáč T (2015) New technique and technology of industrial splitting of stacked wood–log-splitter WS 800. Res Agric Eng 51(1):20–27
Warguła Ł, Kukla M (2020) Determination of maximum torque during carpentry waste comminution. Wood Res 65:771–784
Warguła Ł, Kukla M, Lijewski P, Dobrzyński M, Markiewicz F (2020a) Impact of compressed natural gas (CNG) fuel systems in small engine wood chippers on exhaust emissions and fuel consumption. Energies 13(24):6709. https://doi.org/10.3390/en13246709
Warguła Ł, Kukla M, Lijewski P, Dobrzyński M, Markiewicz F (2020b) Influence of the use of liquefied petroleum gas (LPG) systems in woodchippers powered by small engines on exhaust emissions and operating costs. Energies 13(21):5773. https://doi.org/10.3390/en13215773
Warguła Ł, Wojtkowiak D, Kukla M, Talaśka K (2021) Symmetric nature of stress distribution in the elastic-plastic range of pinus L. Pine wood samples determined experimentally and using the finite element method (FEM). Symmetry 13:39. https://doi.org/10.3390/sym13010039
Wellenreiter P, Hernandez RE, Cáceres C, Blais C (2021) Effects of helix angle and feed per knife on cutting forces, noise, and power consumption produced during helical planing of sugar maple wood. Can J for Res 52(1):109–116
Wentzell TH (1987) Automated log splitter, US4646800A, July 26, 1985. https://worldwide.espacenet.com/patent/search/family/025055158/publication/US4646800A?q=US4646800A. Accessed 1 Sept 2022
York FL (1983) Powered wood splitter with multiple work heads, US4403635A., May 19, 1980. https://worldwide.espacenet.com/patent/search/family/022538165/publication/US4403635A?q=US4403635A. Accessed 1 Sept 2022
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Warguła, Ł., Wojtkowiak, D., Kukla, M. et al. Modelling the process of splitting wood and chipless cutting Pinus sylvestris L. wood in terms of designing the geometry of the tools and the driving force of the machine. Eur. J. Wood Prod. 81, 223–237 (2023). https://doi.org/10.1007/s00107-022-01878-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00107-022-01878-4