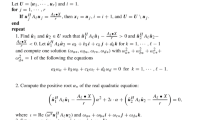Matrix Representation of Magnetic Pseudo-Differential Operators via Tight Gabor Frames

Abstract

In this paper we use some ideas from [12, 13] and consider the description of Hörmander type pseudo-differential operators on $\mathbb {R}^d$ ($d\ge 1$), including the case of the magnetic pseudo-differential operators introduced in [15, 16], with respect to a tight Gabor frame. We show that all these operators can be identified with some infinitely dimensional matrices whose elements are strongly localized near the diagonal. Using this matrix representation, one can give short and elegant proofs to classical results like the Calderón-Vaillancourt theorem and Beals’ commutator criterion, and also establish local trace-class criteria.

1 Introduction

1.1 Main goals

In this work we continue the study of Gabor frame decomposition of Pseudo-Differential Operators (in short $\Psi$DO’s) on $\mathbb {R}^d$ ($d\ge 1$), as proposed in [12, 13], in order to characterize Hörmander type $\Psi$DO’s with symbols in class $S^p_0(\mathbb {R}^{2d})$, with $p\in \mathbb {R}$, [14], including the “magnetic twisted case” introduced in [15, 16, 20]. We recall that these are symbols $a(\xi ,x)$ such that $(1+\xi ^2)^{{ -p/2}}\, a(\xi ,x)$ is uniformly bounded, but no decay is gained by differentiation, see Definition 3.1. Our main result (Theorem 3.1) shows that their infinitely dimensional matrices in the tight “magnetic” Gabor frame (2.5) that we consider, are strongly localized around their diagonal, with some precise growth condition.

This matrix representation leads almost immediately to a short proof for the “magnetic” version of the Calderón-Vaillancourt Theorem in [15] (Theorem 3.7 in this paper) which completes our previous result in [7] regarding the Beals commutator criterion (Theorem 3.8 in this paper).

At the same time, we shed new light on some previous results obtained in [7, 9,10,11] and we include some developments of the ideas which were introduced there. For example, in Corollary 3.6 we obtain in a straightforward way that the magnetic Moyal product (see (3.15)) of a symbol of class $S_0^p$ with a symbol of class $S_0^q$ produces a symbol of class $S_0^{p+q}$. Moreover, in Theorem 3.9 we give a short and straightforward proof of the fact that if $p<-d$, then the corresponding pseudo-differential operators are locally trace class. We also hope that our approach could be relevant for the further development of the magnetic super-operator calculus [17].

Let us emphasize that the type of arguments we develop in this paper are related in spirit with the “partition of unity” techniques developed in [3,4,5, 18].

1.2 General Notation

For $N\in \mathbb {N}\setminus \{0\}$, let $\mathscr {S}(\mathbb {R}^N)$ be the space of Schwartz test functions on $\mathbb {R}^N$ with the canonical Fréchet topology and $\mathscr {S}^\prime (\mathbb {R}^N)$ its topological dual with its strong dual topology and let us denote by $\langle \cdot \,,\,\cdot \rangle _{{\mathscr {S}', \mathscr {S}}}:\mathscr {S}^\prime (\mathbb {R}^N)\times \mathscr {S}(\mathbb {R}^N)\rightarrow \mathbb {C}$ the canonical duality map. We denote by $\mathcal {L}(\mathcal {V}_1;\mathcal {V}_2)$ the space of linear continuous operators between the topological vector spaces $\mathcal {V}_1$ and $\mathcal {V}_2$ with its strong topology (of uniform convergence on bounded sets).

For some $d\ge 2$ we consider the d-dimensional real affine space $\mathcal {X}$ that we shall freely identify with $\mathbb {R}^d$ considering fixed a “base point”. Let $\Xi :=\mathcal {X}\times \mathcal {X}^*$ where $\mathcal {X}^*$ is the dual space of $\mathbb {R}^d$. We shall always distinguish between position variables and momentum variables. We recall the notation $<x>:=\sqrt{1+|x|^2}$ and similarly for $\xi \in \mathcal {X}^*$. We use the notation $\Xi :=\mathcal {X}\times \mathcal {X}^*$.

We shall work with the usual Lebesgue measure on $\mathcal {X}$ and the associated Hilbert space $L^2(\mathcal {X})$ with the scalar product considered anti-linear in the first factor and denoted by $\big (\cdot ,\cdot \big )_{L^2(\mathcal {X})}$. We notice that:

$$\begin{aligned} \langle \overline{f},\phi \rangle _{{\mathscr {S}', \mathscr {S}}}\,=\,\big (f,\phi \big )_{L^2(\mathbb {R}^d)},\quad \forall (f,\phi )\in L^2(\mathbb {R}^d)\times \mathscr {S}(\mathbb {R}^d). \end{aligned}$$

(1.1)

We will use the Hörmander multi-index notation $\partial ^a_x:=\partial _{x_1}^{a_1}\cdot \ldots \cdot \partial _{x_d}^{a_d}$ for $x\in \mathcal {X}$ and $\partial ^a_{\xi }:=\partial _{\xi _1}^{a_1}\cdot \ldots \cdot \partial _{\xi _d}^{a_d}$ for $\xi \in \mathcal {X}^*$ and $|a|:=a_1+\ldots +a_d$ for any $a\in \mathbb {N}^d$.

Given any measurable function $F:\mathcal {X}\rightarrow \mathbb {C}$ we denote by F(Q) the operator of multiplication with the function F. Let $\mathcal L (\mathcal {H})$ be the $C^*$-algebra of bounded linear operators and $\mathbb {U}(\mathcal {H})$ the group of unitary operators on the complex Hilbert space $\mathcal {H}$.

Let us fix our notations and normalization for the Fourier transform:

$$\begin{aligned} \begin{aligned}&\mathcal {F}_\mathcal {X}:L^1(\mathcal {X})\rightarrow C(\mathcal {X}^*),\quad \big (\mathcal {F}_{\mathcal {X}}f\big )(\xi ):=(2\pi )^{-d/2}\int _{\mathcal {X}}dx\,e^{-i<\xi ,x>}\,f(x),\\&\mathcal {F}_{\mathcal {X}^*}:L^1(\mathcal {X}^*)\rightarrow C(\mathcal {X}),\quad \big (\mathcal {F}_{\mathcal {X}^*}\hat{f}\big )(x):=(2\pi )^{-d/2}\int _{\mathcal {X}^*}d\xi \,e^{i<\xi ,x>}\,\hat{f}(\xi ). \end{aligned} \end{aligned}$$

(1.2)

They have unitary extensions to $L^2$ which are inverse to each other.

1.3 The Magnetic Field

We shall consider “regular” magnetic fields B, described by smooth closed 2-forms on $\mathcal {X}\cong \mathbb {R}^d$ which have components of class $BC^\infty (\mathcal {X})$, i.e.:

$$\begin{aligned} B:=\sum _{1\le j,k\le d} B_{jk}(x) dx_j\wedge dx_k\,, \quad |||B|||_N:=\max _{1\le j,k\le d}\Vert B_{jk}\Vert _{BC^N(\mathcal {X})}<\infty ,\, \forall \; N\ge 0. \end{aligned}$$

(1.3)

The topological triviality of the affine space $\mathcal {X}$ implies that these 2-forms are also exact, hence we can always find a 1-form

$$\begin{aligned} A=\sum _j A_j(x) dx_j \end{aligned}$$

(1.4a)

on $\mathcal {X}$ such that

$$\begin{aligned} B=dA, \text{ i.e. } B_{jk}(x)=(\partial _jA_k)(x)-(\partial _kA_j)(x). \end{aligned}$$

This choice is far from being unique and we may consider gauge transformations $A\mapsto A^\prime =A+dF$ with $F\in C^\infty (\mathcal {X})$ so that $B=dA=dA^\prime$. The following explicit choice:

$$\begin{aligned} A_k(x)\,=\,\underset{1\le j\le d}{\sum }\int _0^1\,s\, x_j\, B_{jk}(sx)\,ds , \end{aligned}$$

(1.4b)

proves that for any regular B we can always choose its vector potential to have smooth components which grow at most polynomially at infinity.

2 The Gabor Frame

2.1 Definition

We shall consider the lattice $\Gamma =\underset{1\le j\le d}{\sum }\mathbb {Z}\mathfrak {e}_j\cong \mathbb {Z}^d$ defined by the canonical orthonormal basis $\{\mathfrak {e}_j\}_{1\le j\le d}$ of $\mathcal {X}\cong \mathbb {R}^d$ and let $\Gamma _*$ be the dual lattice:

$$\begin{aligned} \Gamma _*:=\big \{\gamma ^*\in \mathcal {X}^*\, \text{ s.t. }\,<\gamma ^*,\gamma >\in 2\pi \mathbb {Z},\forall \gamma \in \Gamma \big \}. \end{aligned}$$

Once fixed the lattice $\Gamma \subset \mathcal {X}$ as above, let us choose a quadratic partition of unity associated with the lattice $\Gamma$, i.e. a function $\mathcal {g}\in C^\infty _0(\mathcal {X})$ such that

$$\begin{aligned} \mathop \textrm{supp} \nolimits \mathcal {g}\subset (-1,1)^d,\quad \underset{\gamma \in \Gamma }{\sum }\,\mathcal {g}(x-\gamma )^2\,=\,1,\quad \forall x\in \mathcal {X}. \end{aligned}$$

(2.1)

With any $f\in L^2(\mathcal {X})$ we associate the $\Gamma$-indexed sequence:

$$\begin{aligned} f_\gamma =\mathcal {g}\,\tau _{\gamma }(f),\quad (\tau _\gamma f)(x)=f(x+\gamma ), \quad \gamma \in \Gamma . \end{aligned}$$

Each $f_\gamma$ has compact support in $(-1,1)^d\subset (-\pi ,\pi )^d$. On this support it coincides with its own $2\pi \mathbb {Z}^d$ periodization that we denote by $\mathring{f}_\gamma$. We can then define its Fourier sequence:

$$\begin{aligned} \widehat{[f_\gamma ]}_{\gamma ^*}:= & {} \,\big (\vartheta _{\gamma ^*}\,,\, f_\gamma \big )_{L^2((-\pi ,\pi )^d)},\quad \gamma ^*\in \Gamma _*,\nonumber \\ \vartheta _{\gamma ^*}(x):= & {} (2\pi )^{-d/2}e^{i(2\pi )^{-1}<\gamma ^*,x>} \end{aligned}$$

(2.2)

for which we can write

$$\begin{aligned} \mathring{f}_\gamma =\underset{\gamma ^*\in \Gamma _*}{\sum }\,\widehat{[f_\gamma ]}_{\gamma ^*}\,{\vartheta _{\gamma ^*}}, \end{aligned}$$

(2.3)

with convergence of the series in $L^2$.

We are now ready to introduce our “magnetic” Gabor frame (for a general introduction to Gabor frames, see [6]). We use an extra uni-modular factor containing a ’local gauge’, which reminds on the choice proposed by Luttinger [19]. Given A as in (1.4), we shall consider the following family of unitary operators on $L^2(\mathcal {X})$, indexed by $\gamma \in \Gamma$:

$$\begin{aligned} \big (\mathbf {\Lambda }^A_{\gamma }f\big )(x):= \Lambda ^A(x,\gamma )f(x),\quad \forall f\in L^2(\mathcal {X}). \end{aligned}$$

where we use the shortcut notation:

$$\begin{aligned} \Lambda ^A(x,\gamma ):=\,e^{-i\int _{[x,\gamma ]}A}. \end{aligned}$$

(2.4)

We warn the reader that in [7] we used the notation $e^{i\varphi (x,\gamma )}$ instead, with $\varphi (x,\gamma )=\int _{[\gamma ,x]}A$; see [7, Eq. (1.4)].

Definition 2.1

Given $\Gamma \subset \mathcal {X}$ and $\mathcal {g}\in C^\infty _0(\mathcal {X};[0,1])$ as in (2.1), the family of functions:

$$\begin{aligned} \mathcal {G}^A_{\gamma ,\gamma ^*}:=\,\mathbf {\Lambda }^A_\gamma \, \tau _{-\gamma }(\vartheta _{\gamma ^*}\,\mathcal {g})\in \mathscr {S}(\mathcal {X}) \end{aligned}$$

(2.5)

is called the magnetic Gabor frame on $L^2(\mathcal {X})$ associated with $(\Gamma , \mathcal {g})$.

We shall use the notation $\widetilde{\Gamma }:=\Gamma \times \Gamma _*$, with elements of the form $\tilde{\alpha }:=(\alpha ,\alpha ^*),\tilde{\beta }:=(\beta ,\beta ^*),\ldots$. We again warn the reader about two other changes of notation compared to [7]. There, we directly identified an element of the form $(2\pi )^{-1}\gamma ^*$ with some $m\in \mathbb {Z}^d$, thus the Gabor frame elements introduced in [7] are indexed by two copies of $\mathbb {Z}^d$ instead of $\Gamma$ and $\Gamma _*$. Also, in that paper, the translation $\tau _\gamma$ acts like $(\tau _\gamma f)(x)=f(x-\gamma )$.

2.2 Properties of the Magnetic Gabor Frame

In this subsection we extend a technical result of [7] in order to cover the $L^2$ case.

Proposition 2.2

We have the following properties:

• (i) The Gabor frame $\Big \{\mathcal {G}^A_{\tilde{\gamma }} \Big \}$ indexed by $\tilde{\gamma }:=(\gamma ,\gamma ^*)\in \widetilde{\Gamma }$ is a Parseval frame in $L^2(\mathcal {X})$, i.e. the map:

  $$\begin{aligned} \mathfrak {U}^A_{\mathcal {g},\Gamma }:L^2(\mathcal {X})\ni f\mapsto \big \{\big (\mathcal {G}^A_{\tilde{\alpha }},\,f\big )_{L^2(\mathcal {X})}\big \}\in \ell ^2\big (\widetilde{\Gamma }\big ) \end{aligned}$$

  is an isometry.

• (ii) Given the magnetic Gabor frame $\Big \{\mathcal {G}^A_{\tilde{\gamma }} \Big \}$, we have for any $f\in L^2(\mathcal {X})$ the identity:

  $$\begin{aligned} f\,=\,\underset{\tilde{\alpha }\in \widetilde{\Gamma }}{\sum }\,\big ( \mathcal {G}^A_{\tilde{\alpha }},\,f\big )_{L^2(\mathcal {X})}\,\mathcal {G}^A_{\tilde{\alpha }} \end{aligned}$$

  with the above series converging in the $L^2(\mathcal {X})$ norm.

Proof

Instead of (i), we shall prove the following apparently stronger result:

$$\begin{aligned} \forall v,f\in L^2(\mathcal {X}),\quad \big (v,f\big )_{L^2(\mathcal {X})}=\underset{\tilde{\alpha }\in \widetilde{\Gamma }}{\sum }\,\big (v,\,\mathcal {G}^A_{\tilde{\alpha }}\big )_{L^2(\mathcal {X})}\, \big (\mathcal {G}^A_{\tilde{\alpha }},\,f\big )_{L^2(\mathcal {X})} \end{aligned}$$

(2.6)

with the series converging for the $\ell ^2(\widetilde{\Gamma })$ norm. Let us compute the finite sums:

$$\begin{aligned}&\underset{|\alpha |\le N}{\sum }\,\underset{|\alpha ^*|\le M}{\sum }\,\big (v\,,\,\mathcal {G}^A_{\alpha ,\alpha ^*}\big )_{L^2(\mathcal {X})}\, \big (\mathcal {G}^A_{\alpha ,\alpha ^*}\,,\,f\big )_{L^2(\mathcal {X})}=\\&\quad (2\pi )^{-d}\int _{\mathcal {X}}dx\int _{\mathcal {X}}dy\,\overline{v(x)}\,\, f(y)\underset{|\alpha |\le N}{\sum }\,\Big (\Lambda ^A(x,\alpha )\overline{\Lambda ^A(y,\alpha )}\Big ) \mathcal {g}(x-\alpha )\mathcal {g}(y-\alpha )\\&\qquad \times \underset{|\alpha ^*|\le M}{\sum }\,e^{(i/(2\pi ))<\alpha ^*,x-y>}. \end{aligned}$$

Define

$$\begin{aligned} F_\alpha := \mathcal {g}\, \tau _\alpha \Big (\overline{\Lambda ^A(\cdot ,\alpha )} f\Big ),\quad V_\alpha := \mathcal {g}\, \tau _\alpha \Big (\overline{\Lambda ^A(\cdot ,\alpha )} v\Big ). \end{aligned}$$

Then the above double series reads as

$$\begin{aligned}&\underset{|\alpha |\le N}{\sum }\,\underset{|\alpha ^*|\le M}{\sum }\, \overline{\widehat{[V_\alpha ]}_{\alpha ^*}}\, \widehat{[F_\alpha ]}_{\alpha ^*}. \end{aligned}$$

The hypothesis concerning the functions $v,f,\mathcal {g},{\Lambda }^A(\cdot ,\alpha )$ and the Parseval identity related to (2.3) imply that the limit of the integral for $M\nearrow \infty$ exists and is equal to:

$$\begin{aligned}&\underset{M\nearrow \infty }{\lim }\,\underset{|\alpha |\le N}{\sum }\,\underset{|\alpha ^*|\le M}{\sum }\,\big (v\,,\,\mathcal {G}^A_{\alpha ,\alpha ^*}\big )_{L^2(\mathcal {X})}\, \big (\mathcal {G}^A_{\alpha ,\alpha ^*}\,,\,f\big )_{L^2(\mathcal {X})}=\\&\quad \underset{|\alpha |\le N}{\sum }\,\int _{\mathcal {X}}dx\,\overline{v(x+\alpha )}\,f(x+\alpha )\,\mathcal {g}(x)^2=\int _{\mathcal {X}}dx\,\overline{v(x)}\,f(x)\,\underset{|\alpha |\le N}{\sum }\,\mathcal {g}(x-\alpha )^2. \end{aligned}$$

The quadratic $\Gamma$-partition of unity property (2.1) of $\mathcal {g}$ together with the Dominated Convergence Theorem imply (2.6) and thus (i).

Now let us prove (ii). From (2.6) we know that the sequence

$$\begin{aligned} f_{N,M}:=\,\underset{|\alpha |\le N}{\sum }\,\underset{|\alpha ^*|\le M}{\sum }\,\big (\mathcal {G}^A_{\alpha ,\alpha ^*},\,f\big )_{L^2(\mathcal {X})}\, \mathcal {G}^A_{\alpha ,\alpha ^*}\,\in \,L^2(\mathcal {X}) \end{aligned}$$

converges to $f\in L^2(\mathcal {X})$ in the weak topology on $L^2(\mathcal {X})$. To prove its convergence for the norm topology on $L^2(\mathcal {X})$ we show that it is a Cauchy sequence. Let us choose $N<N'$ and $M<M'$ and compute:

$$\begin{aligned}&\big \Vert f_{N',M'}-f_{N,M}\big \Vert _{L^2(\mathcal {X})}\\&\quad =\underset{\Vert v\Vert _{L^2(\mathcal {X})}=1}{\sup }\,\big |\big (v\,,\, f_{N',M'}-f_{N,M}\big )_{L^2(\mathcal {X})}\big |\\&\quad =\underset{\Vert v\Vert _{L^2(\mathcal {X})}=1}{\sup }\,\Big |\underset{|\alpha |\le N'}{\sum }\,\underset{|\alpha ^*|\le M'}{\sum }\,\big (v\,,\,\mathcal {G}^A_{\alpha ,\alpha ^*}\big )_{L^2(\mathcal {X})}\, \big (\mathcal {G}^A_{\alpha ,\alpha ^*}\,,\,f\big )_{L^2(\mathcal {X})}\\&\qquad - \underset{|\alpha |\le N}{\sum }\,\underset{|\alpha ^*|\le M}{\sum }\,\big (v\,,\,\mathcal {G}^A_{\alpha ,\alpha ^*}\big )_{L^2(\mathcal {X})}\, \big (\mathcal {G}^A_{\alpha ,\alpha ^*}\,,\,f\big )_{L^2(\mathcal {X})}\Big |\\&\quad =\underset{\Vert v\Vert _{L^2(\mathcal {X})}=1}{\sup }\,\Big |\Big (\underset{N<|\alpha | \le N'}{\sum }\,\underset{|\alpha ^*|\le M'}{\sum }\, +\underset{|\alpha |\le N}{\sum }\,\underset{M<|\alpha ^*|\le M'}{\sum } \Big )\\&\qquad \big (v\,,\,\mathcal {G}^A_{\alpha ,\alpha ^*}\big )_{L^2(\mathcal {X})}\, \big (\mathcal {G}^A_{\alpha ,\alpha ^*}\,,\,f\big )_{L^2(\mathcal {X})}\Big |\\&\quad \le \left( \Big (\underset{N<|\alpha |}{\sum }\,\underset{\alpha ^*\in \Gamma _*}{\sum }\ +\underset{\alpha \in \Gamma }{\sum }\,\underset{M<|\alpha ^*|}{\sum }\,\Big )\,\big |\big (\mathcal {G}^A_{\alpha ,\alpha ^*}\,,\, f\big )_{L^2(\mathcal {X})}\big |^2\right) ^{1/2}, \end{aligned}$$

where in the last inequality we used the Cauchy-Schwarz inequality and (i) in order to get rid of v. Using once again (i) we may conclude that the above remainder converges to 0 for N and M going to $\infty$, thus $f_{N,M}$ converges in norm, and its strong limit must equal f.

2.3 Infinite Matrices Associated With Operators in a Magnetic Gabor Frame

Suppose that we have a continuous operator $T:\mathscr {S}(\mathcal {X})\rightarrow \mathscr {S}^\prime (\mathcal {X})$. Notice that any $T\in \mathcal L \big (L^2(\mathcal {X})\big )$ and the closure of any symmetric operator on $\mathscr {S}(\mathcal {X})$ are examples of such operators. Given the magnetic Gabor frame (2.5) we can associate with it the following “infinite matrix”:

$$\begin{aligned} \mathbb {M}^A[T]_{\tilde{\alpha },\tilde{\beta }}:=\,\big \langle T\mathcal {G}^A_{\tilde{\beta }},\,\overline{\mathcal {G}^A_{\tilde{\alpha }}}\big \rangle _{{\mathscr {S}', \mathscr {S}}}. \end{aligned}$$

(2.7)

Frequently we shall write the above matrix elements using Formula (1.1).

Notation 2.3

We shall denote by $\mathscr {M}_\Lambda$ the complex linear space of infinite matrices with complex entries indexed by a regular lattice $\Lambda$. We shall work with the lattices $\Gamma , \Gamma _*$ and $\widetilde{\Gamma }=\Gamma \times \Gamma _*$.

Given any linear operator $T:\mathscr {S}(\mathcal {X})\rightarrow L^2(\mathcal {X})$, one may consider it as an operator in the Hilbert space $L^2(\mathcal {X})$ with domain $\mathscr {S}(\mathcal {X})$ and define its adjoint $T^*:\mathcal {D}(T^*)\rightarrow L^2(\mathcal {X})$ putting:

$$\begin{aligned} \mathcal {D}(T^*):=\big \{v\in L^2(\mathcal {X}),\,\big |\big (v,T\varphi \big )_{L^2(\mathcal {X})}\big |\le C(T,v)\Vert \varphi \Vert _{L^2(\mathcal {X})},\, \forall \varphi \in \mathscr {S}(\mathcal {X})\big \} \end{aligned}$$

and $\big (T^*v,\varphi \big )_{L^2(\mathcal {X})}:=\big (v,T\varphi \big )_{L^2(\mathcal {X})}$ for any $\varphi \in \mathscr {S}(\mathcal {X})$.

Proposition 2.4

Let $T:\mathscr {S}(\mathcal {X})\rightarrow L^2(\mathcal {X})$ be as above and assume that $\mathscr {S}(\mathcal {X})\subset \mathcal {D}(T^*)$. Then for any $\varphi \in \mathscr {S}(\mathcal {X})$, we have the identity in $L^2(\mathcal {X})$:

$$\begin{aligned} T\varphi \,=\,\underset{\tilde{\alpha }\in \widetilde{\Gamma }}{\sum }\,\left( \underset{\tilde{\beta }\in \widetilde{\Gamma }}{\sum }\,\mathbb {M}^A[T]_{\tilde{\alpha },\tilde{\beta }}\Big (\mathcal {G}^A_{\tilde{\beta }},\,\varphi \Big )_{L^2(\mathcal {X})}\right) \,\mathcal {G}^A_{\tilde{\alpha }}, \end{aligned}$$

(2.8)

where the series indexed by $\widetilde{\Gamma }$ converge in the norms of $\ell ^2(\widetilde{\Gamma })$ and $L^2(\mathcal {X})$ resp. . Also, if $\psi , \varphi \in \mathscr {S}(\mathcal {X})$ then

$$\begin{aligned} \big (\psi ,T\varphi \big )_{L^2(\mathcal {X})}\,=\,\underset{\tilde{\alpha }\in \widetilde{\Gamma }}{\sum }\,\Big (\psi \,,\, \mathcal {G}^A_{\tilde{\alpha }}\Big )_{L^2(\mathcal {X})}\left( \underset{\tilde{\beta }\in \widetilde{\Gamma }}{\sum }\,\mathbb {M}^A[T]_{\tilde{\alpha },\tilde{\beta }}\Big (\mathcal {G}^A_{\tilde{\beta }},\,\varphi \Big )_{L^2(\mathcal {X})}\right) . \end{aligned}$$

(2.9)

Proof

We use Proposition 2.2 for $T\varphi \in L^2(\mathcal {X})$ and write:

$$\begin{aligned} T\varphi \,&=\,\underset{\tilde{\alpha }\in \widetilde{\Gamma }}{\sum }\,\Big (\mathcal {G}^A_{\tilde{\alpha }}\,,\,T\varphi \Big )_{L^2(\mathcal {X})}\,\mathcal {G}^A_{\tilde{\alpha }}=\,\underset{\tilde{\alpha }\in \widetilde{\Gamma }}{\sum }\,\Big (T^*\mathcal {G}^A_{\tilde{\alpha }}\,,\,\varphi \Big )_{L^2(\mathcal {X})}\,\mathcal {G}^A_{\tilde{\alpha }} \end{aligned}$$

with the series converging in $L^2(\mathcal {X})$. Using once again Proposition 2.2 for $\varphi \in \mathscr {S}(\mathcal {X})$ we obtain that

$$\begin{aligned} \Big (T^*\mathcal {G}^A_{\tilde{\alpha }},\varphi \Big )_{L^2(\mathcal {X})}&=\underset{\tilde{\beta }\in \widetilde{\Gamma }}{\sum }\,\big (T^*\mathcal {G}^A_{\tilde{\alpha }},\big (\mathcal {G}^A_{\tilde{\beta }},\varphi \big )_{L^2(\mathcal {X})}\mathcal {G}^A_{\tilde{\beta }}\big )_{L^2(\mathcal {X})}\\&=\underset{\tilde{\beta }\in \widetilde{\Gamma }}{\sum }\,\big (\mathcal {G}^A_{\tilde{\alpha }},T\mathcal {G}^A_{\tilde{\beta }}\big )_{L^2(\mathcal {X})}\,\big (\mathcal {G}^A_{\tilde{\beta }},\varphi \big )_{L^2(\mathcal {X})} \end{aligned}$$

with the series converging in the norm of $\ell ^2(\widetilde{\Gamma })$. This proves (2.8). Concerning (2.9), we use again Proposition 2.2 and write

$$\begin{aligned} \big ( \psi ,T\varphi \big )_{L^2(\mathcal {X})}\,&=\, \,\underset{\tilde{\alpha }\in \widetilde{\Gamma }}{\sum }\,\Big (\psi \, ,\, \mathcal {G}^A_{\tilde{\alpha }}\Big )_{L^2(\mathcal {X})}\big (T^*\mathcal {G}^A_{\tilde{\alpha }}\, ,\,\varphi \big )_{L^2(\mathcal {X})}\\&=\, \underset{\tilde{\alpha }\in \widetilde{\Gamma }}{\sum }\,\Big (\psi \, ,\, \mathcal {G}^A_{\tilde{\alpha }}\Big )_{L^2(\mathcal {X})}\, \underset{\tilde{\beta }\in \widetilde{\Gamma }}{\sum }\,\mathbb {M}^A[T]_{\tilde{\alpha },\tilde{\beta }}\Big (\mathcal {G}^A_{\tilde{\beta }}\,,\,\varphi \Big )_{L^2(\mathcal {X})}\,. \end{aligned}$$

3 The Matrix Form of the Magnetic Weyl Calculus in a Magnetic Gabor Frame

3.1 Brief Reminder of the Magnetic Weyl Calculus

Let us recall the magnetic Weyl quantization [15, 16, 20]. Given $\Phi \in \mathscr {S}(\Xi )$, we define its quantization $\mathfrak {Op}^A(\Phi )\in \mathcal {L}\big (\mathscr {S}(\mathcal {X});\mathscr {S}(\mathcal {X})\big ),$ by

$$\begin{aligned} \big (\mathfrak {Op}^A(\Phi )\varphi \big )(x):= & {} { (2\pi )^{-d}}\int _{\mathcal {X}^*}d\xi \int _{\mathcal {X}}dy\,\Lambda ^A(x,y)\,\,e^{i<\xi ,x-y>}\\{} & {} \times \Phi \big ((x+y)/2,\xi \big )\,\varphi (y), \forall \varphi \in \mathscr {S}(\mathcal {X}) \end{aligned}$$

where we used the notation introduced in (2.4). It has been proven in [20] (Proposition 3.5) that this “quantization” $\Phi \mapsto \mathfrak {Op}^A(\Phi )$ may be extended to the following isomorphism of topological linear spaces $\mathfrak {Op}^A$ from $\mathscr {S}^\prime (\Xi )$ onto $\mathcal {L}\big (\mathscr {S}(\mathcal {X});\mathscr {S}^\prime (\mathcal {X})\big )$ defined by

$$\begin{aligned} \langle \mathfrak {Op}^A(\Phi )\phi ,\psi \rangle _{\mathscr {S}',\mathscr {S}}&={ (2\pi )^{-d}}{ \int _{\mathcal {X}^*}d\xi \int _{\mathcal {X}}dx}\int _{\mathcal {X}}dy\,\Lambda ^A(x,y)\\&\quad \times e^{i<\xi ,x-y>}\Phi \left( \frac{x+y}{2},\xi \right) \phi (y)\psi (x),\\&\quad \forall (\phi ,\psi )\in \mathscr {S}(\mathcal {X})\times \mathscr {S}(\mathcal {X}). \end{aligned}$$

We shall call $F\in \mathscr {S}^\prime (\Xi )$ the distribution symbol of $\mathfrak {Op}^A(F)\in \mathcal {L}\big (\mathscr {S}(\mathcal {X});\mathscr {S}^\prime (\mathcal {X})\big )$.

Later on we shall work more particularly with the Hörmander classes of symbols indexed by $p\in \mathbb {R}$:

$$\begin{aligned} \begin{aligned}&S_0^p(\mathcal {X}\times \mathcal {X}^*):=\,\big \{F\in C^\infty (\Xi ) \text{ s.t. } \nu ^{p,\rho }_{n,m}(F)<\infty ,\,\forall (n,m)\in \mathbb {N}\times \mathbb {N}\big \},\\&\quad \text {where:} \ \nu ^{p}_{n,m}(F):=\underset{|\alpha |\le n}{\max }\,\underset{|\beta |\le m}{\max }\,\underset{(x,\xi )\in \Xi }{\sup }<\xi >^{-p}\big |\big (\partial _x^\alpha \partial _\xi ^\beta F\big )(x,\xi )\big |. \end{aligned} \end{aligned}$$

(3.1)

3.2 The Main Results

Let us come back to our Gabor frame $\big \{\mathcal {G}^{A}_{\gamma ,\gamma ^*}\big \}_{(\gamma ,\gamma ^*)\in \Gamma \times \Gamma _*}$ and compute the associated matrix for an operator of the form $\mathfrak {Op}^A(\Phi )$ for some $\Phi \in \mathscr {S}^\prime (\Xi )$ (using (1.1)):

$$\begin{aligned} \mathbb {M}^A[\mathfrak {Op}^A(\Phi )]_{\tilde{\alpha },\tilde{\beta }}&:=\Big (\mathcal {G}^A_{\tilde{\alpha }}\,,\,\mathfrak {Op}^A(\Phi )\mathcal {G}^A_{\tilde{\beta }}\Big )_{L^2(\mathcal {X})}\nonumber \\&={(2\pi )^{-2d}}\int _{\mathcal {X}}dx\int _{\mathcal {X}}dy\int _{\mathcal {X}^*}d\eta \, \Lambda ^A(\alpha ,x)\,e^{-\frac{i}{2\pi }<\alpha ^*,x-\alpha>}\mathcal {g}(x-\alpha )\nonumber \\&\quad \Lambda ^A(x,y)\,e^{i<\eta ,x-y>}\,\Phi \big ((x+y)/2,\eta \big )\,\Lambda ^A(y,\beta )\nonumber \\&\quad e^{\frac{i}{2\pi }<\beta ^*,y-\beta >}\mathcal {g}(y-\beta ). \end{aligned}$$

(3.2)

Let us denote by $<x,y,z>:=\big \{u:=x+t(y-x)+st(z-y)\in \mathcal {X},\,(t,s)\in [0,1]\times [0,1]\big \}$ the triangle with vertices $\{x,y,z\}$ and by

$$\begin{aligned} \Omega ^B(x,y,z):=\,e^{-i\int _{<x,y,z>}B}. \end{aligned}$$

Then we notice that Stokes’ formula implies the identity:

$$\begin{aligned} \Lambda ^A(\alpha ,x)\Lambda ^A(x,y)\Lambda ^A(y,\beta )=\Lambda ^A(\alpha ,\beta )\Omega ^B(\alpha ,x,y)\Omega ^B(\alpha ,y,\beta ) \end{aligned}$$

(3.3)

and for our class of magnetic fields introduced in Subsection 1.3 we also have the following estimates:

$$\begin{aligned}&\big |\partial _x^a\partial _y^b\partial _z^c\Omega ^B(x,y,z)\big |\nonumber \\&\quad \le \,C_{ab}(B)\, \big (1+\text {diameter}(<x,y,z>)+\text {area}(<x,y,z>)\big )^{|a+b+c|}. \end{aligned}$$

(3.4)

Here is the main result of the paper.

Theorem 3.1

Given some $p\in \mathbb R$ and some $\Phi \in \mathscr {S}^\prime (\Xi )$, the following two statements are equivalent:

• (i) $\Phi$ belongs to $S^p_0(\mathcal {X}\times \mathcal {X}^*)$.

• (ii) For any $(n_1,n_2)\in \mathbb {N}^2$ there exists some constant $C_{n_1,n_2}(\Phi ,B)>0$ such that the $\widetilde{\Gamma }$-indexed matrix of $\mathfrak {Op}^A(\Phi )$ in the magnetic Gabor frame $\big \{\mathcal {G}^A_{\tilde{\gamma }}\big \}_{\tilde{\gamma }\in \widetilde{\Gamma }}$ has the following behavior:

  $$\begin{aligned}{} & {} \underset{(\tilde{\alpha },\tilde{\beta })\in \widetilde{\Gamma }^2}{\sup }<\alpha -\beta>^{n_1}<\alpha ^*-\beta ^*>^{n_2}<\alpha ^*+\beta ^*>^{-p}\,\big |\mathbb {M}^A[\mathfrak {Op}^A(\Phi )]_{\tilde{\alpha },\tilde{\beta }}\big |\nonumber \\{} & {} \quad \le \,C_{n_1,n_2}(\Phi ,B). \end{aligned}$$

  (3.5)

Proof that (i) implies (ii).

Let us assume that (i) holds. Let us start from (3.2) and make the following change of variables:

$$\begin{aligned} \mathcal {X}\times \mathcal {X}\ni (x,y)\mapsto (z,v):=\big ((x+y-\alpha -\beta )/2,x-y-\alpha +\beta \big )\in \mathcal {X}\times \mathcal {X}\end{aligned}$$

and also the following similar bijective change of indices for the $\widetilde{\Gamma }\times \widetilde{\Gamma }$-indexed series:

$$\begin{aligned} \begin{array}{lcl} \Gamma \times \Gamma \ni (\alpha ,\beta )&{}\mapsto &{}(\mu ,\nu ):=\big (\alpha +\beta ,\alpha -\beta \big )\in [\Gamma ]^2_\circ ,\\ \Gamma _*\times \Gamma _*\ni (\alpha ^*,\beta ^*)&{}\mapsto &{}(\mu ^*,\nu ^*):=\big (\alpha ^*+\beta ^*,\beta ^*-\alpha ^*\big )\in [\Gamma ^*]^2_\circ , \end{array} \end{aligned}$$

(3.6)

where

$$\begin{aligned}{}[\Gamma ]^2_\circ:= & {} \{(\mu ,\nu )\in \Gamma \times \Gamma ,\,\text { where }\mu _j\hbox { and }\nu _j\hbox { for }1\\\le & {} j\le d\hbox { are simultaneously even or odd}\} \end{aligned}$$

and similarly for $\Gamma _*$. With these new indices we consider the corresponding matrix

$$\begin{aligned} \widetilde{\mathbb {M}}[\mathfrak {Op}^A(\Phi )]_{\tilde{\mu }(\tilde{\alpha },\tilde{\beta }),\tilde{\nu }(\tilde{\alpha },\tilde{\beta })}:=\mathbb {M}[\mathfrak {Op}^A(\Phi )]_{\tilde{\alpha },\tilde{\beta }}. \end{aligned}$$

Using (3.3) and making the change $\zeta =\eta -\mu ^*/(4\pi )$ we obtain that:

$$\begin{aligned}&\widetilde{\mathbb {M}}[\mathfrak {Op}^A(\Phi )]_{\tilde{\mu },\tilde{\nu }}={ (2\pi )^{-2d}}\Lambda ^A\big ((\mu +\nu )/2,(\mu -\nu )/2\big )\,e^{\frac{i}{4\pi }<\mu ^*,\nu>}\,\times \\ {}&\hspace{0.5cm}\times \, e^{\frac{i}{2\pi }<\nu ^*,z>}\,\int _{\mathcal {X}}dz\,\int _{\mathcal {X}^*}d\zeta \,e^{i<\zeta ,\nu>}\,\int _{\mathcal {X}}dv\,e^{i<\zeta ,v>}\,\times \nonumber \\ {}&\quad \times \,\mathcal {g}(z+v/2)\mathcal {g}(z-v/2)\,\Theta ^B_{\mu ,\nu }(z,v)\, \Phi \big (z+{ \mu /2},\zeta +\mu ^*/(4\pi )\big ),\nonumber \end{aligned}$$

(3.7)

where

$$\begin{aligned} \Theta ^B_{\mu ,\nu }(z,v):=\Omega ^B(\alpha (\mu ,\nu ),x(z,v),y(z,v))\,\Omega ^B(\alpha (\mu ,\nu ),y(z,v),\beta (\mu ,\nu )). \end{aligned}$$

Let us fix some arbitrary $(n_1,n_2)\in \mathbb {N}^2$ and rewrite (3.7) (for any $(m_1,m_2,m_3)\in \mathbb {N}^3$):

$$\begin{aligned}&\Big |\widetilde{\mathbb {M}}^A[\mathfrak {Op}^A(\Phi )]_{\tilde{\mu },\tilde{\nu }}\Big |\le (2\pi )^{-2d}\nonumber \\&\times \quad \Big |\int _{\mathcal {X}^*}d\zeta \,\int _{\mathcal {X}\times \mathcal {X}}dz\,dv\,\left[ \left( \frac{1-\Delta _z}{<\nu ^*>^2}\right) ^{m_1} \hspace{-8pt}e^{\frac{i}{2\pi }<\nu ^*,z>}\right] \nonumber \\&\quad \left[ \left( \frac{1-\Delta _\zeta }{<\nu>^2} \right) ^{m_2}e^{i<\zeta ,\nu>}\right] \,\left[ \left( \frac{1-\Delta _v}{<\zeta>^2}\right) ^{m_3} e^{i<\zeta ,v>}\right] \nonumber \\&\qquad \times \,\mathcal {g}(z+v/2)\mathcal {g}(z-v/2) \,\Theta ^B_{\mu ,\nu }(z,v)\,\Phi \big (z+{ \mu /2},\zeta +{ \mu ^*/(4\pi )}\big )\Big |. \end{aligned}$$

(3.8)

Since the support of $\mathcal {g}$ is included in $(-1,1)^d$, we may assume $|z_j\pm v_j/2|\le 1$ for all $1\le j\le d$. Thus

$$\begin{aligned} 2|z_j|= |z_j-v_j/2+z_j+v_j/2|\le 2,\quad |v_j|= |z_j+v_j/2-(z_j-v_j/2)|\le 2, \end{aligned}$$

and the integral with respect to z and v in (3.8) is restricted to $|z_j|\le 1$ and $|v_j|\le 2$ for all $1\le j\le d$. Using the bounds in (3.4) and restricting to $|z_j|\le 1,|v_j|\le 2$ implies:

$$\begin{aligned} \begin{aligned} \big |\partial _z^a\partial _v^b\Theta ^B_{\mu ,\nu }(z,v)\big |\,&\le \,C_{ab}(B)<z+v/2>^{|a+b|}<v>^{|a+b|}<\nu>^{|a+b|}<z-v/2>^{|a+b|}\\&\le \,C'_{a,b}(B)<\nu >^{|a+b|}. \end{aligned} \end{aligned}$$

(3.9)

Integrating by parts with respect to z we obtain a decay in $\nu ^*$ of the type $<\nu ^*>^{-2m_1}$, at the price of up to $2m_1$ derivatives acting on $\Theta ^B_{\mu ,\nu }(z,v)$, which produce a growth like $<\nu >^{2m_1}$. Then integrating by parts with respect to v we produce a decaying factor $<\zeta >^{-2m_3}$ at a price of up to $2m_3$ derivatives acting on $\Theta ^B_{\mu ,\nu }(z,v)$, which produce another growth like $<\nu >^{2m_3}$. Finally, integrating by parts with respect to $\zeta$ will produce a decay $<\nu >^{-2m_2}$ together with some powers of v (they are bounded on the domain of integration), while the decay $<\zeta >^{-2m_3}$ is not affected (it can only be improved). Hence (3.8) reads as:

$$\begin{aligned}&\Big |\tilde{\mathbb {M}}^A[\mathfrak {Op}^A(\Phi )]_{\tilde{\mu },\tilde{\nu }}\Big |\le C<\nu ^*>^{-2m_1}<\nu>^{2m_1+2m_3-2m_2} \nonumber \\&\quad \int _{\mathcal {X}^*} d\zeta<\zeta>^{-2m_3}\, { <\zeta +\mu ^*/(4\pi )>^p}. \end{aligned}$$

Now we choose $2m_1\ge n_1$, $2m_3>|p|+d+1$ and $2m_2>2m_1+2m_3+n_2$. The decay in $\nu ^*$ and $\nu$ holds, the function $<\zeta >^{-d-1}$ is integrable, hence we only need to check that the quantity

$$\begin{aligned}<\mu ^*/(4\pi )>^{-p}\,<\zeta>^{-|p|}\, { <\zeta +\mu ^*/(4\pi )>^p} \end{aligned}$$

(3.10)

is uniformly bounded in $\zeta$ and $\mu ^*$ for any $p\in \mathbb {R}$.

Let us show that for every $s\in \mathbb {R}$ we have

$$\begin{aligned} \begin{aligned}&<x+y>^s\, \le \, {2^{|s|/2}}<x>^s\;<y>^{|s|}, \quad \text {or equivalently}\\&<x+y>^s\,<x>^{-s}\; <y>^{-|s|}\le {2^{|s|/2}}. \end{aligned} \end{aligned}$$

(3.11)

When $s>0$ we can reduce it to $1+|x+y|^2\le 2(1+|x|^2)(1+|y|^2)$, while when $s<0$ we use that $s=-|s|$ and

$$\begin{aligned}<x>^{|s|}=<(x+y)+(-y)>^{|s|}\le 2^{|s|/2}<x+y>^{|s|}\, <y>^{|s|}. \end{aligned}$$

Now use $s=p$, $x=-\mu ^*/(4\pi )$ and $y=\zeta +\mu ^*/(4\pi )$ in (3.11) and we get that the quantity in (3.10) is bounded by $2^{|p|/2}$. This ends the proof of (ii).

Proof that (ii) implies (i).

Suppose that $\Phi \in \mathscr {S}^\prime (\Xi )$ is such that (3.5) is valid. Then $\mathfrak {Op}^A(\Phi )\in \mathcal {L}\big (\mathscr {S}(\mathcal {X});\mathscr {S}^\prime (\mathcal {X})\big )$ and has a distribution kernel given by:

$$\begin{aligned} \mathfrak {K}^A[\Phi ]\,=\,(2\pi )^{-d/2}\Lambda ^A\,\big [\big (\Upsilon ^*\circ (\mathrm{{1}\hspace{-3pt}\textbf{l}}_{\mathcal {X}}\otimes \mathcal {F}_{\mathcal {X}^*}^*)\big )\Phi \big ] \end{aligned}$$

where $\Upsilon ^*:\mathscr {S}^\prime (\mathcal {X}\times \mathcal {X})\rightarrow \mathscr {S}^\prime (\mathcal {X}\times \mathcal {X})$ is the extension to tempered distributions of the change of variables map $\mathcal {X}\times \mathcal {X}\ni (x,y)\mapsto \big ((x+y)/2,(x-y)\big )\in \mathcal {X}\times \mathcal {X}$. Using the magnetic Gabor frame and Proposition 2.4 we can write:

$$\begin{aligned} \mathfrak {K}^A[\Phi ]\,=\,\underset{(\tilde{\alpha },\tilde{\beta })\in \widetilde{\Gamma }\times \widetilde{\Gamma }}{\sum }\mathbb {M}^A[\mathfrak {Op}^A(\Phi )]_{\tilde{\alpha },\tilde{\beta }}\Big (\mathcal {G}^A_{\tilde{\alpha }}\otimes \overline{\mathcal {G}^A_{\tilde{\beta }}}\Big ) \end{aligned}$$

where each term belongs to $\mathscr {S}(\mathcal {X}\times \mathcal {X})$ and the series converges in the weak distributional sense. Thus, we shall approximate the distribution kernel $\mathfrak {K}^A[\Phi ]$, in the weak tempered distribution topology, by a family $\mathfrak {K}^A_N[\Phi ]$ indexed by $N\in \mathbb N$ of integral kernels of class $\mathscr {S}(\mathcal {X}\times \mathcal {X})$ defined by:

$$\begin{aligned} \mathfrak {K}^A_N[\Phi ]:=\,\underset{|\tilde{\alpha }|\le N,|\tilde{\beta }|\le N}{\sum }\mathbb {M}^A[\mathfrak {Op}^A(\Phi )]_{\tilde{\alpha },\tilde{\beta }}\Big (\mathcal {G}^A_{\tilde{\alpha }}\otimes \overline{\mathcal {G}^A_{\tilde{\beta }}}\Big ). \end{aligned}$$

The symbols associated to the distribution kernels $\mathfrak {K}^A_N[\Phi ]$, denoted by $\Phi _N\in \mathscr {S}(\Xi )$, are defined by:

$$\begin{aligned} \Phi _N(z,\zeta ):&=\int _{\mathcal {X}}dv\,e^{-i<\zeta ,v>}\,{ \Lambda ^A\big (z-v/2,z+v/2\big ) }\,\mathfrak {K}^A_N[\Phi ]\big (z+v/2,z-v/2\big )\\ \nonumber&=\,\underset{|\tilde{\alpha }|\le N,|\tilde{\beta }|\le N}{\sum }\mathbb {M}^A[\mathfrak {Op}^A(\Phi )]_{\tilde{\alpha },\tilde{\beta }}\,\times \\ \nonumber&\quad \times \,\int _{\mathcal {X}}dv\,e^{-i<\zeta ,v>}\,\Lambda ^A\big (z-v/2,z+v/2\big )\,\mathcal {G}^A_{\tilde{\alpha }}\big (z+v/2\big )\, \overline{\mathcal {G}^A_{\tilde{\beta }}\big (z-v/2\big )}\,. \end{aligned}$$

Let us compute:

$$\begin{aligned}&\int _{\mathcal {X}}dv\,e^{-i<\zeta ,v>}\,\Lambda ^A\big (z-v/2,z+v/2\big )\,\mathcal {G}^A_{\tilde{\alpha }}\big (z+v/2\big )\,\overline{\mathcal {G}^A_{\tilde{\beta }}\big (z-v/2\big )}\\&\quad =(2\pi )^{-d}\int _{\mathcal {X}}dv\,e^{-i<\zeta ,v>}\,\Lambda ^A\big (z-v/2,z+{ v/2}\big )\Lambda ^A\big (z+v/2,\alpha \big )\Lambda ^A\big (\beta ,z-v/2\big )\,\times \nonumber \\&\qquad \qquad \times \,e^{\frac{i}{2\pi }<\alpha ^*,z+v/2-\alpha>}\,e^{-\frac{i}{2\pi }<\beta ^*,z-v/2-\beta >}\,\mathcal {g}\big (z+v/2-\alpha \big )\,\mathcal {g}\big (z-v/2-\beta \big ).\nonumber \end{aligned}$$

(3.12)

We make the change of variables:

$$\begin{aligned} \left\{ \begin{array}{l} \mathcal {X}\ni z\mapsto z':=z-(\alpha +\beta )/2\in \mathcal {X},\\ \mathcal {X}\ni v\mapsto v':=v-(\alpha -\beta )\in \mathcal {X}, \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} \left\{ \begin{array}{l} \Gamma \times \Gamma \ni (\alpha ,\beta )\mapsto (\mu ,\nu ):=\big (\alpha +\beta ,\alpha -\beta \big )\in \Gamma \times \Gamma ,\\ \Gamma _*\times \Gamma _*\ni (\alpha ^*,\beta ^*)\mapsto (\mu ^*,\nu ^*):=\big (\alpha ^*+\beta ^*,\alpha ^*-\beta ^*\big )\in \Gamma _*\times \Gamma _*, \end{array}\right. \end{aligned}$$

and introduce

$$\begin{aligned} \Theta ^B(z',v',\mu ,\nu )&:=\Lambda ^A(\beta ,\alpha )\Lambda ^A\big (z-v/2,z+v/2\big )\Lambda ^A\big (z+v/2,\alpha \big )\Lambda ^A\big (\beta ,z-v/2\big )\\&=\Omega ^B\big (z'-v'/2+\beta ,z'+v'/2+\alpha ,\alpha \big )\,\Omega ^B\big (z'-v'/2+\beta ,\alpha ,\beta \big ). \end{aligned}$$

Then the integral in (3.12) reads as:

$$\begin{aligned}&(2\pi )^{-d}\Lambda ^A(\alpha ,\beta )\int _{\mathcal {X}}dv'\,e^{-i<\zeta ,v'+\nu>}\,e^{\frac{i}{2\pi }<\nu ^*,z'>}\,e^{\frac{i}{4\pi }<\mu ^*,v'>}\times \nonumber \\&\hspace{4cm}\times \,\Theta ^B(z',v',\mu ,\nu )\, \mathcal {g}(z'+v'/2)\, \mathcal {g}(z'-v'/2). \end{aligned}$$

(3.13)

On the support of $\mathcal {g}\in C^\infty _0(\mathcal {X})$ we have $z'\pm v'/2\in (-1,1)^d$. Thus we must have $|v'_j|<2$ and $|z'_j|<1$, where the second inequality implies

$$\begin{aligned} 2z_j-2<\mu _j<2z_j+2,\quad \forall \, 1\le j\le d. \end{aligned}$$

This last condition implies that there exists some finite set $\Sigma (z)\subset \Gamma$ with $\#\Sigma (z)\le 5^d$ such that for $\mu \notin \Sigma (z)$ the above integral vanishes.

From the definition of $\Phi _N$ we see that we need to control multiple series involving $\mu$, $\nu$, $\nu ^*$ and $\mu ^*$. We have just seen that there are only finitely many $\mu$’s which contribute, uniformly in z and $\zeta$. The series in $\nu$ and $\nu ^*$ will be controlled by using the strong decay of the matrix elements, so we only need to worry about the sum over $\mu ^*$. In order to get some decay in $\mu ^*$ we have to perform some partial integration.

Let us consider the “image” lattices

$$\begin{aligned} \begin{aligned}&\hat{\Gamma }^2:=\big \{(\mu ,\nu )\in \Gamma \times \Gamma ,\,\big ((\mu +\nu )/2,(\mu -\nu )/2\big )\in \Gamma \times \Gamma \big \}\\&\hat{\Gamma }^2_N:=\big \{(\mu ,\nu )\in \hat{\Gamma }^2,\,|(\mu +\nu )/2|\le N,\,|(\mu -\nu )/2|\le N\big \}, \end{aligned} \end{aligned}$$

and similarly $[\widehat{\Gamma _*}]^2$ and $[\widehat{\Gamma _*}]^2_N$. Then we can write:

$$\begin{aligned} \Phi _N(z,\zeta )&=(2\pi )^{-d} \underset{\mu \in \Sigma (z),(\mu ,\nu )\in \hat{\Gamma }^2_N}{\sum }\hspace{-24pt}\Lambda ^A\big ((\mu +\nu )/2,(\mu -\nu )/2\big )\hspace{-18pt} \underset{(\mu ^*,\nu ^*)\in [\widehat{\Gamma _*}]^2_N}{\sum }\hspace{-12pt}\mathbb {M}^A[\mathfrak {Op}^A(\Phi )]_{\tilde{\mu }(\tilde{\alpha },\tilde{\beta }),\tilde{\nu }(\tilde{\alpha },\tilde{\beta })}\\&\quad \times \, \hspace{-12pt}\int \limits _{\underset{1\le j\le d}{\prod }\{|v'_j|\le 2\}}\hspace{-12pt}dv' e^{-i<\zeta -\mu ^*/(4\pi ),v'>}\, e^{-i<\zeta ,\nu>}\,e^{\frac{i}{2\pi }<\nu ^*,z'>}\,\mathcal {g}\big (z'+v'/2\big )\,\mathcal {g}\big (z'-v'/2\big )\,\Theta ^B(z',v',\mu ,\nu ). \end{aligned}$$

A crucial observation is that, for any multi-indices $(a,b)\in \mathbb {N}^d\times \mathbb {N}^d$, if we consider $\big (\partial _z^a\partial _\zeta ^b\Phi _N\big )(z,\zeta )$, we can generate powers of $v'$, of $\nu$ and $\nu ^*$. On the support of $\mathcal {g}$, the variables $v_j'$ are bounded. Integrating by parts $M\ge d+1+|p|$ times with respect to $v'$ we can make appear a factor of the type $<\zeta -\mu ^*/(4\pi )>^{-d-1-|p|},$ at the price of some extra powers of $\nu$. Due to (3.5) we see that the summation over the indices $\nu$ and $\nu ^*$ are under control, and we only need to bound the series

$$\begin{aligned} \sum _{\mu ^*\in \Gamma _*}\,<\zeta -\mu ^*/(4\pi )>^{-d-1}\,<\mu ^*/(4\pi )>^p<\zeta -\mu ^*/(4\pi )>^{-|p|}. \end{aligned}$$

Using (3.11) with $x=-\zeta$ and $y=\zeta -\mu ^*/(4\pi )$ we have

$$\begin{aligned}<\mu ^*/(4\pi )>^p<\zeta -\mu ^*/(4\pi )>^{-|p|}\le 2^{|p|/2}\, <\zeta >^p, \end{aligned}$$

thus the series with respect to $\mu ^*$ can also be bounded by a constant times $<\zeta >^p$, hence we have just proved that for any pair of multi-indices a, b there exists a constant $C_{a,b}$ such that for any $N\ge 1$ we have

$$\begin{aligned} \big |\big (\partial _z^a\partial _\zeta ^b\Phi _N\big )(z,\zeta )\big |\,\le \,C_{a,b}\, <\zeta >^p,\quad \forall (z,\zeta )\in \Xi . \end{aligned}$$

Notice, that the above estimate is uniform for z and $\zeta$ restricted to compact sets, and the symbol $\Phi$ will be the uniform limit of $\Phi _N$ on compact sets when $N\rightarrow +\infty$.

Notation 3.2

For $p\in \mathbb R$, we denote by $\mathscr {M}^p_{\widetilde{\Gamma },\infty }$ the complex linear space of infinite matrices indexed by the lattice $\widetilde{\Gamma }$ and verifying the estimate (3.5). We say that they have rapid off-diagonal decay.

Proposition 3.3

Let $p,q\in \mathbb R$, and let $(\mathbb {M},\mathbb {M}^\prime )\in \mathscr {M}^p_{\widetilde{\Gamma },\infty }\times \mathscr {M}^q_{\widetilde{\Gamma },\infty }$. Then their matrix product is an element of $\mathscr {M}^{p+q}_{\widetilde{\Gamma },\infty }$.

Proof

We apply the inequality (3.11) twice, first with $s=p$, $x=\alpha ^*+\gamma ^*$ and $y=-\gamma ^*+\beta ^*$, and second with $s=q$, $x=\beta ^*+\gamma ^*$ and $y=-\gamma ^*+\alpha ^*$, and obtain

$$\begin{aligned}<\alpha ^* +\beta ^*>^{p+q}\le & {} { 2^{(|p|+|q|)/2}}<\alpha ^*+\gamma ^*>^p<\beta ^*-\gamma ^*>^{|p|}\\< & {} \beta ^*+\gamma ^*>^q <\alpha ^*-\gamma ^*>^{|q|}. \end{aligned}$$

Then for any $(m_1,m_2)\in \mathbb {N}\times \mathbb {N}$ we have the bound:

$$\begin{aligned}&<\alpha -\beta>^{m_1}\,<\alpha ^*-\beta ^*>^{m_2} \,<\alpha ^*+\beta ^*>^{p+q}\big |(\mathbb {M}\cdot \mathbb {M}^\prime )_{\tilde{\alpha },\tilde{\beta }}\big |\\&\qquad \le {2^{(|p|+|q|+m_1+m_2)/2}}\underset{\tilde{\gamma }\in \widetilde{\Gamma }}{\sum }\Big (<\alpha -\gamma>^{m_1}\,<\alpha ^*-\gamma ^*>^{m_2+|q|} \,<\alpha ^*+\gamma ^*>^{p}|\mathbb {M}_{\tilde{\alpha },\tilde{\gamma }}| \Big ) \\&\qquad \qquad \times \Big (\,<\gamma -\beta>^{m_1}\,<\gamma ^*-\beta ^*>^{m_2+|p|} \, <\gamma ^*+\beta ^*>^{q}|\mathbb {M}^\prime _{\tilde{\gamma },\tilde{\beta }}|\Big ). \end{aligned}$$

Using (3.5) with $n_1>m_1+d$ and $n_2>m_2+|p|+|q| +d$, we see that the series on the right hand side converges and is uniform in $\alpha ,\alpha ^*,\beta ,\beta ^*$.

Proposition 3.4

Let $p,q\in \mathbb {R}$, let $(\Phi ,\Psi )\in S^p_0(\mathcal {X}\times \mathcal {X}^*)\times S^q_0(\mathcal {X}\times \mathcal {X}^*)$, and consider their infinite matrices with respect to a magnetic Gabor frame $\big \{\mathcal {G}^A_{\alpha ,\alpha ^*}\big \}_{(\alpha ,\alpha ^*)\in \Gamma \times \Gamma _*}$. Then:

$$\begin{aligned} \mathbb {M}^A\big (\mathfrak {Op}^A(\Phi )\mathfrak {Op}^A(\Psi )\big )\,=\,\mathbb {M}^A\big (\mathfrak {Op}^A(\Phi )\big )\cdot \mathbb {M}^A\big (\mathfrak {Op}^A(\Psi )\big ) \end{aligned}$$

(3.14a)

where

$$\begin{aligned} \big (\mathbb {M}_1\cdot \mathbb {M}_2\big )_{\alpha ,\alpha ^*;\beta ,\beta ^*}:=\,\underset{(\gamma ,\gamma ^*)\in \Gamma \times \Gamma _*}{\sum }\big (\mathbb {M}_1\big )_{\alpha ,\alpha ^*;\gamma ,\gamma ^*}\big (\mathbb {M}_2\big )_{\gamma ,\gamma ^*;\beta ,\beta ^*}. \end{aligned}$$

(3.14b)

Proof

Let us start with the definition of the left hand side in (3.14a) and write:

$$\begin{aligned}&\big (\mathbb {M}^A\big (\mathfrak {Op}^A(\Phi )\mathfrak {Op}^A(\Psi )\big )\big )_{\alpha ,\alpha ^*; \beta ,\beta ^*}\\&\quad =\big (\mathcal {G}^A_{\alpha ,\alpha ^*}\,,\,\mathfrak {Op}^A(\Phi )\mathfrak {Op}^A(\Psi )\mathcal {G}^A_{\beta ,\beta ^*}\big )_{L^2(\mathcal {X})}\\&\quad =\big (\mathfrak {Op}^A(\overline{\Phi })\mathcal {G}^A_{\alpha ,\alpha ^*}\,,\,\mathfrak {Op}^A(\Psi )\mathcal {G}^A_{\beta ,\beta ^*}\big )_{L^2(\mathcal {X})}\\&\quad =\underset{(\gamma ,\gamma ^*)\in \Gamma \times \Gamma _*}{\sum }\overline{\big (\mathcal {G}^A_{\gamma ,\gamma ^*}\,,\,\mathfrak {Op}^A(\overline{\Phi })\mathcal {G}^A_{\alpha ,\alpha ^*}\big )}_{L^2(\mathcal {X})}\big (\mathcal {G}^A_{\gamma ,\gamma ^*}\,,\,\mathfrak {Op}^A(\Psi )\mathcal {G}^A_{\alpha ,\alpha ^*}\big )_{L^2(\mathcal {X})}\\&\quad =\underset{(\gamma ,\gamma ^*)\in \Gamma \times \Gamma _*}{\sum }\big (\mathbb {M}^A\big (\mathfrak {Op}^A(\Phi )\big )\big )_{\alpha ,\alpha ^*;\gamma ,\gamma ^*}\big (\mathbb {M}^A\big (\mathfrak {Op}^A(\Psi )\big )\big )_{\gamma ,\gamma ^*;\beta ,\beta ^*}. \end{aligned}$$

Remark 3.5

We notice that for any $\Phi \in S^0_0(\mathcal {X}^*,\mathcal {X})$ we have the equalities:

$$\begin{aligned}&\big (\mathbb {M}^A\big (\mathfrak {Op}^A(\overline{\Phi })\big )\big )_{\alpha ,\alpha ^*;\gamma ,\gamma ^*}=\,\big (\mathbb {M}^A\big (\mathfrak {Op}^A(\Phi )^*\big )\big )_{\alpha ,\alpha ^*;\gamma ,\gamma ^*} =\,\overline{\big (\mathbb {M}^A\big (\mathfrak {Op}^A(\Phi )\big )\big )}_{\gamma ,\gamma ^*;\alpha ,\alpha ^*}. \end{aligned}$$

Let us recall from [15, 20] that the “magnetic” Moyal product $\sharp ^B$ is defined by the equality:

$$\begin{aligned} \mathfrak {Op}^A\big (\phi \sharp ^B\psi \big ):=\, \mathfrak {Op}^A(\phi )\,\mathfrak {Op}^A(\psi ),\quad \forall (\phi ,\psi )\in \mathscr {S}(\Xi )\times \mathscr {S}(\Xi ). \end{aligned}$$

It is given explicitly by the following integral:

$$\begin{aligned} \Big (\phi \sharp ^B\psi \big )(X)=&{} \pi ^{-2d}\int _{\Xi \times \Xi }dY\,dY'\,e^{-2i(<\xi -\eta ,x-y'>-<\xi -\eta ',x-z>)}\,\times \nonumber \\ {}&\hspace{4cm}\times \,\omega ^B_x(y,y')\,\phi (Y)\,\psi (Y') \end{aligned}$$

(3.15)

where $\omega ^B_x(y,y')$ is the exponential of $(-i)$ multiplied with the flux of B through the triangle with vertices $x-y-y',x-y+y',x+y-y'$.

As shown in [15, 20], this “magnetic” Moyal product may be extended as a composition law on a large class of tempered distributions on $\mathcal {X}\times \mathcal {X}^*$ that contains the Hörmander classes for all $p\in \mathbb {R}$.

By using a direct combination of Propositions 3.4 and 3.3 with Theorem 3.1, we get:

Corollary 3.6

Given $(p,q)\in \mathbb {R}\times \mathbb {R}$ and $(\Phi ,\Psi )\in S^p_0(\mathcal {X}\times \mathcal {X}^*)\times S^q_0(\mathcal {X}\times \mathcal {X}^*)$ we have that $\Phi \sharp ^B\Psi \in S^{p+q}_0(\mathcal {X}\times \mathcal {X}^*)$.

3.3 A Magnetic Version of the Calderón-Vaillancourt Theorem

Let us consider a symbol $F\in S^0_0(\mathcal {X}^*,\mathcal {X})$ and a regular magnetic field B obeying (1.3). In [15] the following result is proven, using pseudo-differential calculus techniques:

Theorem 3.7

Under the above assumptions, we have that $\mathfrak {Op}^A(F)$ is bounded in $L^2(\mathcal {X})$. Moreover, there exist $c(d)>0$, $p(d)\in \mathbb {N}$, and $N\ge 0$, such that for all $F\in S^0_0(\mathcal {X}^*,\mathcal {X})$ and any regular B obeying (1.3) we have

$$\begin{aligned} \big \Vert \mathfrak {Op}^A(F)\big \Vert _\mathcal {L (L^2(\mathcal {X}))}\,\le \,c(d)\big (1+|||B|||_N\big )\,\underset{|\alpha |\le p(d)}{\max }\,\underset{|\beta |\le p(d)}{\max }\,\underset{X\in \Xi }{\sup }\,\big |\big (\partial _x^\alpha \partial _\xi ^\beta \,F\big )(X)\big |. \end{aligned}$$

Proof

Let us present here a simple proof of the boundedness of the operator $\mathfrak {Op}^A(F)$ in $L^2(\mathcal {X})$, based on the use of magnetic Gabor matrices. Given any $f\in \mathscr {S}(\mathcal {X})$ we have $\mathfrak {Op}^A(F)f\in L^2(\mathcal {X})$ and

$$\begin{aligned} \big \Vert \mathfrak {Op}^A(F)f\big \Vert _{L^2(\mathcal {X})}= & {} \sup _{g\in \mathscr {S}(\mathcal {X}),\, \Vert g\Vert _{L^2(\mathcal {X})}=1} \big \vert \big (g,\mathfrak {Op}^A(F)f\big )_{L^2(\mathcal {X})}\big \vert . \end{aligned}$$

From (2.9) we have:

$$\begin{aligned} \big \vert \big (g,\mathfrak {Op}^A(F)f\big )_{L^2(\mathcal {X})}\big \vert&\le \underset{(\gamma ,\gamma ^*),\, (\alpha ,\alpha ^*)\in \Gamma \times \Gamma _*}{\sum }\ \big |\big (\mathcal {G}^A_{\gamma ,\gamma ^*},g\big )_{L^2(\mathcal {X})}\big |\,\big |\mathbb {M}^A[F]_{\gamma ,\gamma ^*;\alpha ,\alpha ^*}\big |\\&\big |\big (\mathcal {G}^A_{\alpha ,\alpha ^*},\,f\big )_{L^2(\mathcal {X})}\big |. \end{aligned}$$

The estimate (3.5) applied with $p=0$ implies that there exists a constant $C_d(F,B)$ depending on a finite number of seminorms of F and B such that

$$\begin{aligned}\big |\mathbb {M}^A[F]_{\gamma ,\gamma ^*;\alpha ,\alpha ^*}\big | \le C_d(F,B) \,<\gamma -\alpha>^{-d-1} \, <\gamma ^*-\alpha ^*>^{-d-1}.\end{aligned}$$

Applying the Schur test in $\ell ^2(\Gamma \times \Gamma ^*)$ and using the isometric property from Proposition 2.2(i) we obtain that

$$\begin{aligned} \big \vert \big (g,\mathfrak {Op}^A(F)f\big )_{L^2(\mathcal {X})}\big \vert \le C_d(F,B) \Vert g\Vert _{L^2(\mathcal {X})}\, \Vert f\Vert _{L^2(\mathcal {X})} \end{aligned}$$

and we are done, up to a density argument.

3.4 On the Beals Commutator Criterion

Finally let us now complete the result in [7] and also prove the reciprocal statement for the Beals criterion.

In order to state this criterion let us recall the “basic symbols”:

• The position coordinates $Q_j:=\mathfrak {Op}^A(q_j)=\mathfrak {Op}^0(q_j)$ with $q_j(x,\xi ):=x_j$ for $1\le j\le d$

• The “magnetic” momenta $P^A_j:=\mathfrak {Op}^A(p_j)=\mathfrak {Op}^0(p_j)-A_j$ with $p_j(x,\xi ):=\xi _j$ for $1\le j\le d$.

Let us notice that the symbols $q_j$ for $1\le j\le d$ are not Hörmander type symbols and that the above operators are continuous as operators in $\mathscr {S}(\mathcal {X})$ and respectively in $\mathscr {S}^\prime (\mathcal {X})$.

Theorem 3.8

If $\Phi \in S^0_0(\mathcal {X}\times \mathcal {X}^*)$, then $\mathfrak {Op}^A(\Phi )$ defines a bounded linear operator on $L^2(\mathcal {X})$ having bounded repeated commutators of the form $[L_1,[L_2,\ldots [L_N,T]\ldots ]]$ for any $N\in \mathbb {N}$ and any family $\{L_1,\ldots ,L_N\big \}$ (void if $N=0$) with $L_m$ any of the basic observables $\big \{Q_1,\ldots ,Q_d,P^A_1,\ldots ,P^A_d\big \}$.

Conversely, assume that a linear map $T:\mathscr {S}(\mathcal {X})\mapsto \mathscr {S}'(\mathcal {X})$ can be extended to a bounded operator on $L^2(\mathcal {X})$, and all its possible commutators as above have the same property; then T is a magnetic pseudo-differential operator with a symbol of class $S^0_0(\mathcal {X}\times \mathcal {X}^*)$.

Proof

Let us prove the direct implication. Using (3.15) we have:

$$\begin{aligned} \big [Q_j,\mathfrak {Op}^A(\Phi )\big ]=\mathfrak {Op}^A\big (q_j\sharp ^B\Phi -\Phi \sharp ^Bq_j\big ), \end{aligned}$$

with

$$\begin{aligned}&\big (q_j\sharp ^B\Phi -\Phi \sharp ^Bq_j\big )(X)\\&\quad =\pi ^{-2d} \int _{\Xi \times \Xi }dY\,dY'\, e^{-2i(<\xi -\eta ,x-y'>-<\xi -\eta ',x-y>)}\,\omega ^B_x(y,y')\, \big (y_j\Phi (y',\eta ')-y_j'\Phi (y,\eta )\big )\\&\quad =i(\partial _{\xi _j}\Phi )(x,\xi )\,, \end{aligned}$$

and

$$\begin{aligned} \big [P^A_j,\mathfrak {Op}^A(\Phi )\big ]=\mathfrak {Op}^A\big (p_j\sharp ^B\Phi -\Phi \sharp ^Bp_j\big ), \end{aligned}$$

with

$$\begin{aligned}&\big (p_j\sharp ^B\Phi -\Phi \sharp ^Bp_j\big )(x,\xi )=\\ {}&\quad =\pi ^{-2d}\int _{\Xi \times \Xi }dY\,dY'\,e^{-2i(<\xi -\eta ,x-y'>-<\xi -\eta ',x-y>)}\,\omega ^B_x(y,y')\,\times \\ {}&\hspace{3cm}\times \, \big (\eta _j\Phi (y',\eta ')-\eta _j'\Phi (y,\eta )\big )\\ {}&\quad =-i\big (\partial _{x_j}\Phi \big )(x,\xi )\,+\,(2\pi )^{-d}\int _{\mathcal {X}}dv\int _{\mathcal {X}^*}d\eta \,e^{-i<\xi -\eta ,v>}\Phi (x,\eta )\,\times \\ {}&\hspace{6cm}\times \, \underset{1\le k\le d}{\sum }v_k\int _{-1/2}^{1/2}dr\,B_{kj}(x+rv)\\ {}&\quad =-i\big (\partial _{x_j}\Phi \big )(x,\xi )\,+\,i(2\pi )^{-d}\int _{\mathcal {X}}dv\int _{\mathcal {X}^*}d\eta \,e^{-i<\xi -\eta ,v>}\,\times \\ {}&\hspace{4cm}\times \, \underset{1\le k\le d}{\sum }\big (\partial _{\eta _k}\Phi \big )(x,\eta )\int _{-1/2}^{1/2}dr\,B_{kj}(x+rv). \end{aligned}$$

We see that both above commutators have symbols in $S^0_0(\mathcal {X}\times \mathcal {X}^*)$, which remains true regardless how many commutators we perform afterwards. Then the Calderón-Vaillancourt theorem implies that these commutators can be extended to bounded operators on $L^2(\mathcal {X})$.

The converse statement has been proved in [7], but now we can give a more transparent explanation of the strategy used there. The main idea was to first show that the matrix elements of $\mathbb {M}^A(T)$ obey an estimate like in (3.5), and secondly, to construct a symbol “by hand”, similarly with what we do here in Theorem 3.1(ii).

The main idea behind the proof of (3.5) is the following: knowing that operators like $[Q_{j_1},[Q_{j_2},[\ldots ,[Q_{j_n},T]\ldots ]$ extend to bounded operators on $L^2(\mathcal {X})$, the matrix element of T must decay faster than any power of $<\alpha -\alpha '>$. Also, the boundedness of $[P^A_{j_1},[P^A_{j_2},[\ldots ,[P^A_{j_n},T]\ldots ]$ plus integration by parts, leads to fast decay in $<\alpha ^*-\beta ^*>$. All details may be found in [7].

3.5 Local Schatten-Class Properties

For the non-magnetic case, a lot of results of this type are available in the literature [1, 21]. They not only give optimal decay conditions on the symbol, but also on its minimal regularity. Within our class of magnetic operators, we give a result which is close to be optimal even for the non-magnetic case:

Theorem 3.9

Let $\Phi \in S^p_0(\mathcal {X}\times \mathcal {X}^*)$ with $p<-d$. Then for every $q>d$, the operators $<\cdot >^{-q}\, \mathfrak {Op}^A(\Phi )$ and $<\cdot>^{-q/2}\, \mathfrak {Op}^A(\Phi )\, <\cdot >^{-q/2}$ are trace class. Moreover, if $p<-d/2$ and $r>d/2$, then $\mathfrak {Op}^A(\Phi )\, <\cdot >^{-r}$ is Hilbert-Schmidt.

Proof

The integral kernel of $<\cdot >^{-q}\, \mathfrak {Op}^A(\Phi )$ is

$$\begin{aligned} \underset{(\tilde{\alpha },\tilde{\beta })\in \widetilde{\Gamma }\times \widetilde{\Gamma }}{\sum }\mathbb {M}^A[\mathfrak {Op}^A(\Phi )]_{\tilde{\alpha },\tilde{\beta }}\, <x>^{-q}\mathcal {G}^A_{\tilde{\alpha }}(x)\, \overline{\mathcal {G}^A_{\tilde{\beta }}}(y), \end{aligned}$$

hence this operator can be seen as a series of rank-one operators. There exists a constant C such that the trace norm of these rank-one operators is bounded by $C <\alpha >^{-q}$ uniformly in $\alpha ^*$ and $\tilde{\beta }=(\beta ,\beta ^*)$. Hence $<\cdot >^{-q}\, \mathfrak {Op}^A(\Phi )$ is trace class if we can prove that

$$\begin{aligned} \underset{\alpha ^*, \beta ^*\in \Gamma ^*}{\sum }\,\, \underset{\alpha ,\beta \in \Gamma }{\sum }\,<\alpha >^{-q}\, \big | \mathbb {M}^A[\mathfrak {Op}^A(\Phi )]_{\tilde{\alpha },\tilde{\beta }}\big | \, <\infty . \end{aligned}$$

Let us choose $n_1=n_2=d+1$ in (3.5). Then we have

$$\begin{aligned}&<\alpha>^{-q}\, \big | \mathbb {M}^A[\mathfrak {Op}^A(\Phi )]_{\tilde{\alpha },\tilde{\beta }}\big |\\&\qquad \le C_{n_1n_2}(\Phi ,B)\,<\beta -\alpha>^{-d-1}<\alpha>^{-q}<\alpha ^*-\beta ^*>^{-d-1} <\alpha ^*+\beta ^*>^{p}. \end{aligned}$$

Since $p<-d$ and $q>d$, the series is convergent.

The proof for $<\cdot>^{-q/2} \mathfrak {Op}^A(\Phi ) <\cdot >^{-q/2}$ is similar; here we need to show

$$\begin{aligned} \sum _{\alpha ,\beta \in \Gamma }<\beta>^{-q/2}<\beta -\alpha>^{-d-1}<\alpha >^{-q/2}<\infty , \end{aligned}$$

which again is a consequence of the Young inequality for convolutions. Finally, denoting by T the operator $\mathfrak {Op}^A(\Phi )\, <\cdot >^{-r}$, we have $T^*T=<\cdot>^{-r}\, \mathfrak {Op}^A(\overline{\Phi })\,\mathfrak {Op}^A(\Phi )\,<\cdot >^{-r}$. The symbol of the product in the middle belongs to $S_0^{2p}$ with $2p<-d$ while $r>d/2$, hence $T^*T$ is trace-class.

$\square$