Nuclear Fourier Transforms

Abstract

The paper deals with the problem under which conditions for the parameters $s_1,s_2\in \mathbb R$, $1\le p,q_1,q_2\le \infty$ the Fourier transform $\mathcal {F}$ is a nuclear mapping from $A^{s_1}_{p,q_1}({\mathbb R}^n)$ into $A^{s_2}_{p,q_2}({\mathbb R}^n)$, where $A\in \{B,F\}$ stands for a space of Besov or Triebel–Lizorkin type, and $n\in \mathbb N$. It extends the recent paper ‘Mapping properties of Fourier transforms’ (Triebel in Z Anal Anwend 41(1/2):133–152, https://doi.org/10.4171/ZAA/1697, 2022) by the third-named author, where the compactness of $\mathcal {F}$ acting in the same type of spaces was studied.

1 Introduction

Let $\mathcal {F}$ be the classical Fourier transform, extended in the usual way to $\mathcal {S}'({\mathbb R}^n)$, $n\in \mathbb N$. The mapping properties

$$\begin{aligned} \mathcal {F}\mathcal {S}({\mathbb R}^n)= \mathcal {S}({\mathbb R}^n), \qquad \mathcal {F}\mathcal {S}'({\mathbb R}^n)= \mathcal {S}'({\mathbb R}^n), \end{aligned}$$

(1.1)

and

$$\begin{aligned} \mathcal {F}: \ L_p ({\mathbb R}^n) \hookrightarrow L_{p'} ({\mathbb R}^n), \quad 1\le p \le 2, \quad \frac{1}{p} + \frac{1}{p'} =1, \quad \mathcal {F}L_2 ({\mathbb R}^n) = L_2 ({\mathbb R}^n), \end{aligned}$$

(1.2)

are cornerstones of Fourier analysis. These basic assertions have been complemented in [25] covering in particular the following observation. Let $A^s_{p,q}({\mathbb R}^n)$ with

$$\begin{aligned} A \in \{B,F \}, \quad 1<p,q_1,q_2 < \infty \quad \text {and} \quad s_1 \in \mathbb R, \quad s_2 \in \mathbb R, \end{aligned}$$

(1.3)

be the usual function spaces of Besov and Triebel–Lizorkin type. We denote

$$\begin{aligned} d^n_p = 2n \left( \frac{1}{p} - \frac{1}{2} \right) , \quad 1<p<\infty , \quad n\in \mathbb N, \end{aligned}$$

(1.4)

and introduce

$$\begin{aligned} \tau ^{n+}_p = \max (0, d^n_p) \quad \text {and} \quad \tau ^{n-}_p = \min (0, d^n_p). \end{aligned}$$

(1.5)

Then

$$\begin{aligned} \mathcal {F}: \quad A^{s_1}_{p,q_1} ({\mathbb R}^n) \hookrightarrow A^{s_2}_{p,q_2} ({\mathbb R}^n) \end{aligned}$$

(1.6)

is compact if

$$\begin{aligned} \text {both} \quad s_1 > \tau ^{n+}_p \quad \text {and} \quad s_2 < \tau ^{n-}_p\ . \end{aligned}$$

(1.7)

If (independently)

$$\begin{aligned} \text {either} \quad s_1 < \tau ^{n+}_p \qquad \text {or} \quad s_2 > \tau ^{n-}_p, \end{aligned}$$

(1.8)

then there is no continuous embedding of type (1.6). We refer to Fig. 1 below for some diagram. It was one of the main aims of [25] to deal with the degree of compactness of $\mathcal {F}$ in (1.6) in case of (1.7), expressed in terms of entropy numbers. In the present paper we look for conditions ensuring that the mapping $\mathcal {F}$ in (1.6) is nuclear. Recall that a linear continuous mapping $T: \ A\hookrightarrow B$ from the Banach space A into the Banach space B is called nuclear if it can be represented as

$$\begin{aligned} Tf = \sum ^\infty _{k=1} \langle f, a_k'\rangle \, b_k, \qquad \{a'_k \} \subset A', \quad \{b_k \} \subset B, \end{aligned}$$

(1.9)

such that $\sum ^\infty _{k=1} \Vert a'_k\vert A'\Vert \cdot \Vert b_k \vert B \Vert$ is finite, where $A'$ is the dual of A. In particular, any nuclear mapping is compact. We refer to Sect. 3.1 for further details and some history of the topic.

Our main result is Theorem 3.4 characterising in particular under which conditions the compact mapping (1.6) under the assumptions (1.7) is nuclear. We refer to Fig. 3 below for some illustration.

The paper is organised as follows. In Sect. 2 we collect definitions and some ingredients. This includes wavelet characterisations and weighted generalisations $A^s_{p,q}({\mathbb R}^n, w_\alpha )$ of the above unweighted spaces $A^s_{p,q}({\mathbb R}^n)$, where the function $w_\alpha (x) = (1+|x |^2)^{\alpha /2}$, $\alpha \in \mathbb R$, is a so-called ‘admissible’ weight. In Sect. 3 we recall first some already known properties about nuclear embeddings between these spaces and prove Theorem 3.4. This will be complemented by related assertions for some limiting cases. Finally, in Sect. 4 we collect some more or less immediate consequences when $\mathcal {F}$ is considered as a mapping between weighted spaces of type $A^s_{p,q}({\mathbb R}^n, w_\alpha )$.

2 Definitions and Ingredients

2.1 Definitions and Some Basic Properties

We use standard notation. Let $\mathbb N$ be the collection of all natural numbers and $\mathbb N_0= \mathbb N\cup \{0 \}$. Let ${\mathbb R}^n$ be the Euclidean n-space where $n\in \mathbb N$. Put $\mathbb R= \mathbb R^1$. Let $\mathcal {S}({\mathbb R}^n)$ be the Schwartz space of all complex-valued rapidly decreasing infinitely differentiable functions on ${\mathbb R}^n$ and let $\mathcal {S}'({\mathbb R}^n)$ be the dual space consisting of all tempered distributions on ${\mathbb R}^n$. Furthermore, $L_p ({\mathbb R}^n)$ with $0< p \le \infty$, is the standard complex quasi-Banach space with respect to the Lebesgue measure, quasi-normed by

$$\begin{aligned} \Vert f \, \vert L_p ({\mathbb R}^n) \Vert = \Big ( \int _{{\mathbb R}^n} |f(x) |^p \, {\textrm{d}}x \Big )^{1/p} \end{aligned}$$

(2.1)

with the obvious modification if $p=\infty$. As usual, $\mathbb Z$ is the collection of all integers; and ${\mathbb Z}^n$, $n\in \mathbb N$, denotes the lattice of all points $m= (m_1, \ldots , m_n) \in {\mathbb R}^n$ with $m_k \in \mathbb Z$ for any $k=1,\ldots , n$.

If $\varphi \in \mathcal {S}({\mathbb R}^n)$, then

$$\begin{aligned} \widehat{\varphi } (\xi ) = (\mathcal {F}\varphi )(\xi ) = (2\pi )^{-n/2} \int _{{\mathbb R}^n} e^{-ix \xi } \varphi (x) \, {\textrm{d}}x, \qquad \xi \in {\mathbb R}^n, \end{aligned}$$

(2.2)

denotes the Fourier transform of $\varphi$. As usual, $\mathcal {F}^{-1}\varphi$ and $\varphi ^\vee$ stand for the inverse Fourier transform, given by the right-hand side of (2.2) with i in place of $-i$. Here $x \xi$ stands for the scalar product in ${\mathbb R}^n$. Both $\mathcal {F}$ and $\mathcal {F}^{-1}$ are extended to $\mathcal {S}'({\mathbb R}^n)$ in the standard way, i.e.,

$$\begin{aligned} (\mathcal {F}f)(\psi ) = f (\mathcal {F}\psi ), \qquad \text {if}\quad f\in \mathcal {S}'({\mathbb R}^n)\quad \text {and}\quad \psi \in \mathcal {S}({\mathbb R}^n), \end{aligned}$$

and similarly for $\mathcal {F}^{-1}$. Let $\varphi _0 \in \mathcal {S}({\mathbb R}^n)$ with

$$\begin{aligned} \varphi _0 (x) =1 \ \text {if}\quad |x |\le 1 \quad \text {and} \quad \varphi _0 (x) =0 \ \text {if}\quad |x | \ge 3/2, \end{aligned}$$

(2.3)

and let

$$\begin{aligned} \varphi _k (x) = \varphi _0 (2^{-k} x) - \varphi _0 (2^{-k+1} x ), \qquad x\in {\mathbb R}^n, \quad k\in \mathbb N. \end{aligned}$$

(2.4)

Since

$$\begin{aligned} \sum ^\infty _{j=0} \varphi _j (x) =1 \qquad \text {for} \quad x\in {\mathbb R}^n, \end{aligned}$$

(2.5)

$\varphi =\{ \varphi _j \}^\infty _{j=0}$ forms a smooth dyadic resolution of unity. Moreover, it follows from the Paley–Wiener–Schwartz theorem that the Fourier transform of the distribution $\varphi _j \widehat{f}$ as well as its inverse Fourier transform are entire analytic functions for any $f\in \mathcal {S}'({\mathbb R}^n)$. So the expression $(\varphi _j \widehat{f} )^\vee (x)$ makes sense pointwise in ${\mathbb R}^n$.

Definition 2.1

Let $\varphi = \{ \varphi _j \}^\infty _{j=0}$ be the above dyadic resolution of unity. Let $s\in \mathbb R$, $0<q\le \infty$.

• (i) Let $0<p \le \infty$. Then $B^s_{p,q}({\mathbb R}^n)$ is the collection of all $f \in \mathcal {S}'({\mathbb R}^n)$ such that

  $$\begin{aligned} \Vert f \, \vert B^s_{p,q}({\mathbb R}^n) \Vert _{\varphi } = \Big ( \sum ^\infty _{j=0} 2^{jsq} \big \Vert (\varphi _j \widehat{f})^\vee \, \vert L_p ({\mathbb R}^n) \big \Vert ^q \Big )^{1/q} \end{aligned}$$

  (2.6)

  is finite (with the usual modification if $q= \infty )$.

• (ii) Let $0<p<\infty$. Then $F^s_{p,q}({\mathbb R}^n)$ is the collection of all $f\in \mathcal {S}'({\mathbb R}^n)$ such that

  $$\begin{aligned} \Vert f \, \vert F^s_{p,q}({\mathbb R}^n) \Vert _{\varphi } = \Big \Vert \Big ( \sum ^\infty _{j=0} 2^{jsq} |(\varphi _j \widehat{f})^\vee (\cdot ) |^q \Big )^{1/q} \, \vert L_p ({\mathbb R}^n) \Big \Vert \end{aligned}$$

  (2.7)

  is finite (with the usual modification if $q=\infty )$.

Remark 2.2

These well-known inhomogeneous spaces are independent of the above resolution of unity $\varphi$ according to (2.3)-(2.5) in the sense of equivalent quasi-norms. This justifies the omission of the subscript $\varphi$ in (2.6), (2.7) in the sequel. Let us mention here, in particular, the series of monographs [20,21,22, 24], where also one finds further historical references, explanations and discussions. The above restriction to $p<\infty$ in case of $F^s_{p,q}{({\mathbb R}^n)}$ is the usual one, though many important results could be extended to $F^s_{\infty ,q}{({\mathbb R}^n)}$, cf. [24] for the definition and properties of the spaces as well as historical remarks. Here we stick to the above setting.

As usual we write $A^s_{p,q}({\mathbb R}^n)$, $A \in \{B,F \}$, if the related assertion applies equally to the B-spaces $B^s_{p,q}({\mathbb R}^n)$ and the F-spaces $F^s_{p,q}({\mathbb R}^n)$. We deal mainly with the B-spaces. The F-spaces can often be incorporated in related assertions using the continuous embeddings

$$\begin{aligned} B^s_{p, \min (p,q)} ({\mathbb R}^n) \hookrightarrow F^s_{p,q}({\mathbb R}^n) \hookrightarrow B^s_{p, \max (p,q)} ({\mathbb R}^n), \end{aligned}$$

(2.8)

$s\in \mathbb R$, $0<p<\infty$, $0<q \le \infty$. Occasionally we use also Sobolev-type embeddings for $F^s_{p,q}({\mathbb R}^n)$ spaces: If $0<p_1<p_2<\infty$, $0<q_1,q_2\le \infty$ and $s_1,s_2\in \mathbb R$, then

$$\begin{aligned} F^{s_1}_{p_1,q_1}({\mathbb R}^n)\hookrightarrow F^{s_2}_{p_2,q_2}({\mathbb R}^n) \end{aligned}$$

(2.9)

provided that $s_1-\frac{n}{p_1}\ge s_2-\frac{n}{p_2}$. Let

$$\begin{aligned} w_\alpha (x) = (1 + |x |^2 )^{\alpha /2}, \qquad x\in {\mathbb R}^n, \quad \alpha \in \mathbb R. \end{aligned}$$

(2.10)

Then $I_\alpha$,

$$\begin{aligned} I_\alpha : \quad f \mapsto \big ( w_\alpha \widehat{f}\, \big )^\vee = \big ( w_\alpha f^\vee \big )^\wedge , \qquad f\in \mathcal {S}'({\mathbb R}^n), \quad \alpha \in \mathbb R, \end{aligned}$$

(2.11)

is a lift in the spaces $A^s_{p,q}({\mathbb R}^n)$, $s\in \mathbb R$, $0<p<\infty$, $0<q \le \infty$, mapping $A^s_{p,q}({\mathbb R}^n)$ isomorphically onto $A^{s-\alpha }_{p,q} ({\mathbb R}^n)$,

$$\begin{aligned} I_\alpha A^s_{p,q}({\mathbb R}^n) = A^{s-\alpha }_{p,q} ({\mathbb R}^n), \quad \Vert (w_\alpha \widehat{f} \, )^\vee \vert A^{s-\alpha }_{p,q} ({\mathbb R}^n) \Vert \sim \Vert f \, \vert A^s_{p,q}({\mathbb R}^n) \Vert , \end{aligned}$$

(2.12)

equivalent quasi-norms, see [24, Theorem 1.22, p. 16] and the references given there. Of interest for us will be the Sobolev spaces (also called fractional Sobolev spaces or Bessel potential spaces)

$$\begin{aligned} H^s_p ({\mathbb R}^n) = F^s_{p,2} ({\mathbb R}^n), \qquad s\in \mathbb R, \quad 1<p<\infty , \end{aligned}$$

(2.13)

their Littlewood–Paley characterisations and

$$\begin{aligned} I_s H^s_p ({\mathbb R}^n) = L_p ({\mathbb R}^n), \quad \Vert (w_s \widehat{f})^\vee \vert L_p ({\mathbb R}^n) \Vert = \Vert f \, \vert H^s_p ({\mathbb R}^n) \Vert . \end{aligned}$$

(2.14)

Remark 2.3

For our arguments below we need the weighted counterparts of the spaces $A^s_{p,q}({\mathbb R}^n)$ as introduced in Definition 2.1. Let s, p, q be as there and let $w_\alpha$ be the weight according to (2.10). Then $A^s_{p,q}({\mathbb R}^n, w_\alpha )$ is the collection of all $f\in \mathcal {S}'({\mathbb R}^n)$ such that (2.6), (2.7) with $L_p ({\mathbb R}^n, w_\alpha )$ in place of $L_p ({\mathbb R}^n)$ is finite. Here $L_p ({\mathbb R}^n, w_\alpha )$ is the complex quasi-Banach space quasi-normed by

$$\begin{aligned} \Vert f \, \vert L_p ({\mathbb R}^n, w_\alpha ) \Vert = \Vert w_\alpha f \, \vert L_p ({\mathbb R}^n) \Vert , \qquad 0<p \le \infty , \quad \alpha \in \mathbb R. \end{aligned}$$

(2.15)

These spaces have some remarkable properties which will be of some use for us later on, see also [11] and [5, Sect. 4.2]. In particular, for all spaces $f \mapsto w_\alpha f$ is an isomorphic mapping,

$$\begin{aligned} \Vert w_\alpha f \, \vert A^s_{p,q}({\mathbb R}^n) \Vert \sim \Vert f \, \vert A^s_{p,q}({\mathbb R}^n, w_\alpha ) \Vert , \qquad \alpha \in \mathbb R, \end{aligned}$$

(2.16)

and for all spaces the lifting (2.12) can be extended from the unweighted spaces to their weighted counterparts,

$$\begin{aligned} \begin{aligned} I_\alpha A^s_{p,q}({\mathbb R}^n, w_\beta )&= A^{s-\alpha }_{p,q} ({\mathbb R}^n, w_\beta ), \\ \Vert (w_\alpha \widehat{f} )^\vee \vert A^{s-\alpha }_{p,q} ({\mathbb R}^n, w_\beta ) \Vert&\sim \Vert f\, \vert A^s_{p,q}({\mathbb R}^n, w_\beta ) \Vert , \end{aligned} \end{aligned}$$

(2.17)

$\alpha \in \mathbb R$, $\beta \in \mathbb R$. Both (substantial) assertions are covered by [22, Theorem 6.5, pp. 265–266] and the references given there. Note that weights of type $w_\alpha$ given by (2.10) are also special Muckenhoupt weights when $\alpha >-n$.

2.2 Wavelet Characterisations

Our arguments below rely on wavelet representations for some (unweighted) B-spaces. Here we collect what we need and refer to the standard monographs for this topic [4, 13, 14, 26], where one can find related definitions and explanations. We will follow the notation used in [24, Sect. 1.2.1, pp. 7–10]. Further remarks concerning wavelets in Besov and Triebel–Lizorkin spaces can be found in [22, Chap. 3] with a short summary given in [22, Sect. 1.7].

As usual, $C^{u} (\mathbb R)$ with $u\in \mathbb N$ collects all bounded complex-valued continuous functions on $\mathbb R$ having continuous bounded derivatives up to order u inclusively. Let

$$\begin{aligned} \psi _F \in C^{u} (\mathbb R), \qquad \psi _M \in C^{u} (\mathbb R), \qquad u \in \mathbb N, \end{aligned}$$

(2.18)

be real compactly supported Daubechies wavelets with $\Vert \psi _F\,\vert L_2(\mathbb R)\Vert =\Vert \psi _M\,\vert L_2(\mathbb R)\Vert =1$ and

$$\begin{aligned} \int _{\mathbb R} \psi _M (x) \, x^v \, {\textrm{d}}x =0 \qquad \text {for all}\quad v\in \mathbb N_0\quad \text {with}\quad v<u. \end{aligned}$$

(2.19)

This means, in particular, that the functions

$$\begin{aligned} \psi _{F,k}(x)=\psi _F(x-k),\quad \psi _{M,k}^j(x)= 2^{j/2}\psi _{M,k}^j(2^jx-k), \quad k\in {\mathbb Z},\ j\in \mathbb N_0, \end{aligned}$$

form an orthonormal basis in $L_2(\mathbb R)$. Let $n\in \mathbb N$ and, when $j=0$, let

$$\begin{aligned} G = (G_1, \ldots , G_n) \in G^0 = \{F,M \}^n, \end{aligned}$$

(2.20)

which means that $G_r$ is either F or M. Furthermore, for $j\in \mathbb N$, let

$$\begin{aligned} G= (G_1, \ldots , G_n) \in G^j = \{F, M \}^{n*}, \qquad j \in \mathbb N, \end{aligned}$$

(2.21)

which means that $G_r$ is either F or M, where $*$ indicates that at least one of the components of G must be an M. Note that the parameter j indicates that we take different sets $G^j$ in case of $j=0$ and $j\in \mathbb N$. Let

$$\begin{aligned} \psi ^j_{G,m} (x) = \prod ^n_{l=1} \psi _{G_l} \big (2^j x_l -m_l \big ), \qquad G\in G^j, \quad m \in {\mathbb Z}^n, \end{aligned}$$

(2.22)

$x\in {\mathbb R}^n$, where (now) $j \in \mathbb N_0$. Then

$$\begin{aligned} \big \{ 2^{jn/2} \psi ^j_{G,m}: \ j \in \mathbb N_0, \ G\in G^j, \ m \in {\mathbb Z}^n\big \} \end{aligned}$$

(2.23)

is an orthonormal basis in $L_2 ({\mathbb R}^n)$. Let

$$\begin{aligned} 1\le p,q \le \infty \qquad \text {and} \qquad s\in \mathbb R. \end{aligned}$$

(2.24)

Let $u\in \mathbb N$ be such that $|s | <u$, recall (2.18). Then $f\in B^s_{p,q}({\mathbb R}^n)$ can be represented as

$$\begin{aligned} f = \sum _{j=0}^\infty \sum _{G\in G^j} \sum _{m \in {\mathbb Z}^n} 2^{jn} \langle f, \psi ^j_{G,m} \rangle \, \psi ^j_{G,m} , \end{aligned}$$

(2.25)

unconditional convergence being in $\mathcal {S}'({\mathbb R}^n)$, with

$$\begin{aligned} \Vert f \, \vert B^s_{p,q}({\mathbb R}^n) \Vert \sim \bigg ( \sum _{j=0}^\infty 2^{j(s- \frac{n}{p})q} \sum _{G\in G^j} \Big ( \sum _{m\in {\mathbb Z}^n} 2^{jnp} | \langle f, \psi ^j_{G,m} \rangle |^p \Big )^{q/p} \bigg )^{1/q}, \end{aligned}$$

(2.26)

where the equivalence constants are independent of f, with the usual modification if $\max (p,q)=\infty$, cf. [22, Theorem 3.5] and [24, Sect. 1.2.1]. If $\max (p,q)<\infty$, then the series in (2.25) converges unconditionally in terms of the convergence in $B^s_{p,q}({\mathbb R}^n)$, hence also in terms of the convergence in $\mathcal {S}'({\mathbb R}^n)$. Furthermore (2.23) is a basis in $B^s_{p,q}({\mathbb R}^n)$ if $\max (p,q)<\infty$. From (2.26), (2.8) and the orthonormality of the system (2.23) it follows that

$$\begin{aligned} \Vert \psi ^j_{G,m} \, \vert A^s_{p,q}({\mathbb R}^n) \Vert \sim 2^{j(s- \frac{n}{p})}, \qquad j\in \mathbb N_0, \quad m\in {\mathbb Z}^n, \quad G\in G^j, \end{aligned}$$

(2.27)

$1 \le p,q \le \infty$, $s\in \mathbb R$, $A\in \{B,F \}$ (with $p<\infty$ when $A=F$), where the equivalence constants can be chosen independently of j, G, m.

2.3 Mappings

We recall some mapping properties of the Fourier transform $\mathcal {F}$ obtained in [25]. This covers also (more or less) what has already been said in the Introduction, (1.3)–(1.8).

Let $n\in \mathbb N$, $1<p<\infty$ and $s\in \mathbb R$. We use the notation

$$\begin{aligned} d^n_p = 2n \left( \frac{1}{p} - \frac{1}{2} \right) , \qquad 1<p < \infty , \quad n\in \mathbb N, \end{aligned}$$

(2.28)

and define

$$\begin{aligned} \tau ^{n+}_p = \max (0, d^n_p) \qquad \text {and} \qquad \tau ^{n-}_p = \min (0, d^n_p). \end{aligned}$$

(2.29)

We denote by

$$\begin{aligned} X^s_p ({\mathbb R}^n) = {\left\{ \begin{array}{ll} L_p ({\mathbb R}^n) &{}\text {if}\quad 2\le p<\infty , s=0, \\ {B^s_{p,p}} ({\mathbb R}^n) &{} \text {if}\quad 2 \le p<\infty , s>0, \\ {B^s_{p,p}} ({\mathbb R}^n) &{}\text {if}\quad 1<p \le 2, s \ge d^n_p, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} Y^s_p ({\mathbb R}^n) = {\left\{ \begin{array}{ll} {B^s_{p,p}} ({\mathbb R}^n) &{}\text {if}\quad 2 \le p<\infty , s \le d^n_p, \\ {B^s_{p,p}} ({\mathbb R}^n) &{}\text {if}\quad 1<p \le 2, s<0, \\ L_p ({\mathbb R}^n) &{}\text {if}\quad 1<p\le 2, s=0. \end{array}\right. } \end{aligned}$$

For convenience, we have sketched in the usual $(\frac{1}{p},s)$-diagram in Fig. 1 below the corresponding areas for the definition of $X^s_p$ and $Y^s_p$ indicating the space $B^s_{p,q}({\mathbb R}^n)$ by its parameters s and p, neglecting q.

Fig. 1

Parameter areas for the definition of spaces $X^s_p$ and $Y^s_p$, and their continuous embedding (2.31).

We collect what is already known about the continuity and compactness of the map $\mathcal {F}: X^{s_1}_p({\mathbb R}^n) \hookrightarrow Y^{s_2}_p({\mathbb R}^n)$.

Theorem 2.4

([25]) Let $1<p<\infty$, $s_1{\in \mathbb R}, s_2\in \mathbb R$ and $\tau ^{n+}_p$, $\tau ^{n-}_p$ be given by (2.29) with (2.28).

• (i) Then

  $$\begin{aligned} \mathcal {F}: \quad X^{s_1}_p ({\mathbb R}^n) \hookrightarrow Y^{s_2}_p ({\mathbb R}^n) \quad \text {with}\quad s_1 \ge \tau ^{n+}_p\quad \hbox {and} \quad s_2 \le \tau ^{n-}_p \end{aligned}$$

  (2.30)

  is continuous. This mapping is even compact if, and only if, both $s_1 > \tau ^{n+}_p$ and $s_2 < \tau ^{n-}_p$.

• (ii) Furthermore, if there is a continuous mapping

  $$\begin{aligned} \mathcal {F}: \quad B^{s_1}_{p,p} ({\mathbb R}^n) \hookrightarrow B^{s_2}_{p,p} ({\mathbb R}^n), \end{aligned}$$

  (2.31)

  then both $s_1 \ge \tau ^{n+}_p$ and $s_2 \le \tau ^{n-}_p$.

Remark 2.5

These assertions are covered by [25, Theorem 3.2, Corollary 3.3]. There one also finds results about the entropy numbers $e_k(\mathcal {F})$, $k\in \mathbb N$, of $\mathcal {F}$ which further characterise the ‘degree of compactness’, cf. [25, Theorem 4.8].

Corollary 2.6

Let $1<p<\infty$, $0<q_1,q_2\le \infty$, $s_1, s_2\in \mathbb R$. Let $A\in \{B, F\}$. Then

$$\begin{aligned} \mathcal {F}: \quad A^{s_1}_{p,q_1}({\mathbb R}^n) \hookrightarrow A^{s_2}_{p,q_2} ({\mathbb R}^n) \end{aligned}$$

(2.32)

is compact if both $s_1 > \tau ^{n+}_p$ and $s_2 < \tau ^{n-}_p$.

If $s_1 < \tau ^{n+}_p$ or $s_2 > \tau ^{n-}_p$, then there is no continuous map (2.32).

Proof

This is an immediate consequence of Theorem 2.4 together with the elementary embeddings $A^{s+\varepsilon }_{p,q_1}({\mathbb R}^n)\hookrightarrow B^s_{p,p}({\mathbb R}^n) \hookrightarrow A^{s-\varepsilon }_{p,q_2}({\mathbb R}^n)$, $\varepsilon >0$. If $s_1 > \tau ^{n+}_p$ and $s_2 < \tau ^{n-}_p$, then one can choose $\varepsilon >0$ such that $\widetilde{s_1}=s_1-\varepsilon > \tau ^{n+}_p$ and $\widetilde{s_2}=s_2+\varepsilon < \tau ^{n-}_p$. So by the elementary embeddings $A^{s_1}_{p,q_1}({\mathbb R}^n)\hookrightarrow B^{\widetilde{s_1}}_{p,p}({\mathbb R}^n)$ and $B^{\widetilde{s_2}}_{p,p}({\mathbb R}^n) \hookrightarrow A^{s_2}_{p,q_2}({\mathbb R}^n)$ the operator (2.32) can be factorised through the compact operator

$$\begin{aligned} \mathcal {F}: \quad B^{\widetilde{s_1}}_{p,p} ({\mathbb R}^n) \hookrightarrow B^{\widetilde{s_2}}_{p,p} ({\mathbb R}^n). \end{aligned}$$

(2.33)

On the other hand, if $s_1 < \tau ^{n+}_p$ and the operator (2.32) is continuous, then we can choose $\varepsilon >0$ such that $\widetilde{s_1}=s_1+\varepsilon < \tau ^{n+}_p$. If we also put $\widetilde{s_2}=s_2-\varepsilon$, then by the elementary embeddings the operator (2.33) can be factorised through the continuous operator (2.32). This contradicts the second statement of Theorem 2.4. A similar argument works if $s_2 > \tau ^{n+}_p$.

The above result shows that $s_1 = \tau ^{n+}_p$ and $s_2 = \tau ^{n-}_p$ are natural barriers if one wishes to study continuous and compact mappings of type (2.32). The observation justifies (1.6)–(1.8). It also implies that the compactness restrictions $s_1 > \tau ^{n+}_p$ and $s_2 < \tau ^{n-}_p$ in what follows are natural. We complement the above assertion in Sect. 3.3 where we shall also deal with the limiting cases $p=1$ and $p=\infty$.

3 Nuclear Mappings

3.1 Preliminaries

A linear continuous mapping $T: A \hookrightarrow B$ from the (complex) Banach space A into the (complex) Banach space B is called nuclear if it can be represented as

$$\begin{aligned} Tf = \sum _{k=1}^\infty \langle f, a_k'\rangle \, b_k, \qquad \{a_k' \} \subset A', \quad \{b_k \} \subset B, \end{aligned}$$

(3.1)

such that $\sum _{k=1}^\infty \Vert a_k' \vert A' \Vert \cdot \Vert b_k \vert B \Vert$ is finite. Here $A'$ is the dual of A. Then

$$\begin{aligned} \Vert T \, \vert \mathcal N(A,B)\Vert = \inf \sum _{k=1}^\infty \Vert a_k' \vert A' \Vert \cdot \Vert b_k \vert B \Vert \end{aligned}$$

(3.2)

is the related nuclear norm, where the infimum is taken over all representations (3.1). In particular any nuclear mapping is compact. The collection of all nuclear mappings between complex Banach spaces is a symmetric operator ideal, see [16, 8.2.6, p. 108], [17, p. 280]. Here symmetric means that $T': \, B' \hookrightarrow A'$ is nuclear if $T: \, A \hookrightarrow B$ is nuclear.

Remark 3.1

Grothendieck introduced the concept of nuclearity in [7] more than 60 years ago. It provided the basis for many famous developments in functional analysis afterwards, we refer to [16], and, in particular, to [17] for further historic details. In Hilbert spaces $H_1,H_2$, the nuclear operators $\mathcal {N}(H_1,H_2)$ coincide with the trace class $S_1(H_1,H_2)$, consisting of those T with singular numbers $(s_k(T))_{k\in \mathbb N} \in \ell _1$. It follows directly from the definition that nuclear operators can be approximated by finite-rank operators. However, it is well known from the remarkable Enflo result [6] that there are compact operators between Banach spaces which cannot be approximated by finite-rank operators. This led to a number of—meanwhile well-established and famous—methods to circumvent this difficulty and find alternative ways to ‘measure’ the compactness or ‘degree’ of compactness of an operator, e.g. the asymptotic behaviour of its approximation or entropy numbers. In all these problems, the decomposition of a given compact operator into a series is an essential proof technique. It turns out that in many of the recent contributions [2, 3, 8, 10, 23] studying nuclearity, a key tool in the arguments are new decomposition techniques as well, adapted to the different spaces. This is also our intention now.

In addition to the tools described above we will rely on the following two observations about nuclear embeddings between function spaces.

Let $\Omega$ be a bounded Lipschitz domain in ${\mathbb R}^n$, $n\in \mathbb N$, (bounded interval if $n=1$). Then $A^s_{p,q}(\Omega )$ is, as usual, the restriction of the spaces $A^s_{p,q}({\mathbb R}^n)$ as introduced in Definition 2.1 and Remark 2.2.

Proposition 3.2

Let

$$\begin{aligned} 1<p_1, p_2, q_1 , q_2 <\infty \qquad \text {and} \qquad s_1 \in \mathbb R, \quad s_2 \in \mathbb R. \end{aligned}$$

(3.3)

• (i) The embedding

  $$\begin{aligned} \textrm{id}: \quad A^{s_1}_{p_1, q_1} (\Omega ) \hookrightarrow A^{s_2}_{p_2,q_2} (\Omega ) \end{aligned}$$

  (3.4)

  is compact, if, and only if,

  $$\begin{aligned} s_1-s_2 > n \max \left( \frac{1}{p_1}-\frac{1}{p_2},0\right) . \end{aligned}$$

  (3.5)

• (ii) The embedding (3.4) is nuclear if, and only if,

  $$\begin{aligned} s_1 - s_2 > n -n \max \left( \frac{1}{p_2} - \frac{1}{p_1}, 0 \right) . \end{aligned}$$

  (3.6)

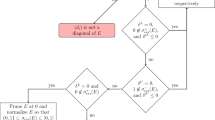
The classical condition (3.5) can be found e.g. in [5, p. 60]. Part (ii) of the proposition was proved in [23, Theorem, p. 3039], clarifying some limiting cases compared with what was already known before, cf. [15, 18]. In [10] we also dealt with the situations $p=1$ and $p=\infty$. Let us briefly illustrate the situation in Figure 2 above. This has to be understood in the sense that for a fixed source space $A^{s_1}_{p_1,q_1}(\Omega )$, that is, given parameters $s_1$, $p_1$ (and $q_1$ hidden), we indicate the area of parameters $s_2$ and $p_2$ (and $q_2$ hidden again) such that the embedding $\textrm{id}$, given by (3.4), in the corresponding target space $A^{s_2}_{p_2,q_2}(\Omega )$ is compact or nuclear, respectively.

Fig. 2

Parameter areas for the compactness and nuclearity of embedding (3.4).

Secondly we need the counterpart of this result for weighted spaces $A^s_{p,q}({\mathbb R}^n, w_\alpha )$ as introduced in Remark 2.3 with $w_\alpha$ as in (2.10). Let $p_1, p_2, q_1, q_2$ and $s_1, s_2$ be as in (3.3). Let $-\infty< \alpha _2 \le \alpha _1 <\infty$. We consider the embedding

$$\begin{aligned} \textrm{id}_\alpha : \quad A^{s_1}_{p_1,q_1}({\mathbb R}^n, w_{\alpha _1} ) \hookrightarrow A^{s_2}_{p_2,q_2}({\mathbb R}^n, w_{\alpha _2} )\quad \text {where}\quad \alpha =\alpha _1-\alpha _2 \ge 0, \end{aligned}$$

(3.7)

extended to the indicated limiting cases 1 and $\infty$ for the parameters $p_1$, $p_2$, $q_1$ and $q_2$.

Proposition 3.3

Let $1\le p_1<\infty ,\ 1\le p_2\le \infty$ (with $p_2<\infty$ for F-spaces), $1\le q_1,q_2\le \infty$, $s_1,s_2\in \mathbb R$, and $\alpha =\alpha _1-\alpha _2 \ge 0$.

• (i) $\textrm{id}_\alpha$ given by (3.7) is compact if, and only if,

  $$\begin{aligned} \alpha> n\max \left( \frac{1}{p_2}-\frac{1}{p_1},0\right) \quad \text {and} \quad s_1-s_2 > n\max \left( \frac{1}{p_1}-\frac{1}{p_2},0\right) . \end{aligned}$$

  (3.8)

• (ii) $\textrm{id}_\alpha$ given by (3.7) is nuclear if, and only if,

  $$\begin{aligned} \alpha> n+n\min \left( \frac{1}{p_2}-\frac{1}{p_1},0\right) \quad \text {and} \quad s_1-s_2> n+ n\min \left( \frac{1}{p_1}-\frac{1}{p_2},0\right) .\nonumber \\ \end{aligned}$$

  (3.9)

For the compactness result (i) we refer to [22, Prop. 6.29], [11, Thm. 2.3], [5, Thm. and Rem. 4.2.3] (in the context of so-called admissible weights) and [9, Prop. 2.8] (in the context of Muckenhoupt weights). The nuclearity part (ii) is covered by [10, Theorem 3.12, p. 14] combined with the lifting (2.17), see also [10, Cor. 3.15, p.22].

3.2 Main Assertion

We first restrict ourselves to the non-limiting situation, that is, we assume $1<p,q<\infty$. We consider the limiting cases when $p,q\in \{1,\infty \}$ in Sect. 3.3 below. Let $s\in \mathbb R$. Then

$$\begin{aligned} A^s_{p,q}({\mathbb R}^n)' = A^{-s}_{p',q'} ({\mathbb R}^n), \qquad \frac{1}{p} + \frac{1}{p'} = \frac{1}{q} + \frac{1}{q'} =1, \end{aligned}$$

(3.10)

is the well-known duality in the framework of the dual pairing $\big ( \mathcal {S}({\mathbb R}^n), \mathcal {S}'({\mathbb R}^n)\big )$, cf. [20, Theorem 2.11.2, p. 178]. Let $\mathcal {F}$ be the Fourier transform as introduced in Sect. 2.1 and let $\mathcal {F}f\in A^s_{p,q}({\mathbb R}^n)$ be expanded according to (2.25). Then

$$\begin{aligned} \begin{aligned} \mathcal {F}f&= \sum _{j=0}^\infty \sum _{G\in G^j} \sum _{m\in {\mathbb Z}^n} 2^{jn} \big \langle \mathcal {F}f, \psi ^j_{G,m} \big \rangle \, \psi ^j_{G,m} \\&= \sum _{j=0}^\infty \sum _{G\in G^j} \sum _{m\in {\mathbb Z}^n} 2^{jn} \big \langle f, \mathcal {F}\psi ^j_{G,m} \big \rangle \, \psi ^j_{G,m} \end{aligned} \end{aligned}$$

(3.11)

follows from $\mathcal {F}' = \mathcal {F}$ in the context of the dual pairing $\big ( \mathcal {S}({\mathbb R}^n), \mathcal {S}'({\mathbb R}^n)\big )$ and $\langle \mathcal {F}f, \psi ^j_{G,m} \rangle = \langle f, \mathcal {F}\psi ^j_{G,m}\rangle$ what can be justified by (3.10) and the properties of the wavelets $\psi ^j_{G,m}$.

Our main result in this paper reads as follows.

Theorem 3.4

Let $1<p,q_1,q_2<\infty$ and let $s_1 \in \mathbb R$, $s_2 \in \mathbb R$. Then

$$\begin{aligned} \mathcal {F}: \quad A^{s_1}_{p, q_1} ({\mathbb R}^n) \hookrightarrow A^{s_2}_{p, q_2} ({\mathbb R}^n) \end{aligned}$$

(3.12)

is nuclear if, and only if, both

$$\begin{aligned} s_1 > {\left\{ \begin{array}{ll} n &{}\text {for}\quad 1<p \le 2,\\ \frac{2n}{p} &{}\text {for}\quad 2 \le p<\infty , \end{array}\right. } \quad and \quad s_2< {\left\{ \begin{array}{ll} -2n (1 - \frac{1}{p}) &{}\text {for}\quad 1<p \le 2, \\ -n &{} \text {for}\quad 2 \le p <\infty . \end{array}\right. } \end{aligned}$$

(3.13)

Remark 3.5

Note that (3.13) can also be written as $s_1 > n- \tau ^{n+}_{p'}$ and $s_2<-n-\tau ^{n-}_{p'}$ with $\tau ^{n+}_{p'}$ and $\tau ^{n-}_{p'}$ as in (2.29) with (2.28), replacing p by $p'$ and using $\frac{1}{p}+\frac{1}{p'}=1$. We return to this observation in Remark 3.6 below. There one also finds some illustration of the corresponding parameter areas in Fig. 3. This discussion will be extended in Remark 3.15 to the limiting cases $p=1$ and $p=\infty$ where compactness and nuclearity coincide.

Proof

Step 1 First we prove that (3.13) ensures that $\mathcal {F}$ in (3.12) is nuclear. We choose $\widetilde{s_1}, \widetilde{s_2}\in \mathbb R$ such that $s_1>\widetilde{s_1}> n\min \big \{1,\frac{2}{p}\big \}$ and $s_2<\widetilde{s_2}< -n\min \big \{1,\frac{2}{p'}\big \}$. Then by elementary embeddings (monotonicity of the spaces $A^s_{p,q}({\mathbb R}^n)$ with respect to s) and (2.13) the operator (3.12) can be factorised in the following way,

$$\begin{aligned} A^{s_1}_{p, q_1} ({\mathbb R}^n) \hookrightarrow H^{\widetilde{s_1}}_p ({\mathbb R}^n) {\mathop {\hookrightarrow }\limits ^{\mathcal {F}}} H^{\widetilde{s_2}}_p ({\mathbb R}^n) \hookrightarrow A^{s_2}_{p, q_2} ({\mathbb R}^n). \end{aligned}$$

Thus, by the ideal property of $\mathcal N$, it is sufficient to prove that the operator

$$\begin{aligned} \mathcal {F}: \quad H^{s_1}_p ({\mathbb R}^n) \hookrightarrow H^{s_2}_p ({\mathbb R}^n), \qquad 1<p<\infty , \end{aligned}$$

(3.14)

is nuclear if the conditions (3.13) hold. We recall that $H^s_p ({\mathbb R}^n)$ are the Sobolev spaces according to (2.13), (2.14), normed by

$$\begin{aligned} \Vert f \, \vert H^s_p ({\mathbb R}^n) \Vert = \Vert (w_s \widehat{f})^\vee \, \vert L_p ({\mathbb R}^n) \Vert , \qquad 1<p<\infty , \quad s\in \mathbb R, \end{aligned}$$

(3.15)

with $w_s (x) = (1 + |x |^2 )^{s/2}$, $x\in {\mathbb R}^n$.

Step 2 Let $1<p \le 2$. We rely on (3.11). By (2.27) one has the following equivalence

$$\begin{aligned} 2^{jn} \Vert \psi ^j_{G,m} \, \vert H^{s_2}_p ({\mathbb R}^n) \Vert \sim 2^{j(s_2 +n - \frac{n}{p})}, \qquad j \in \mathbb N_0, \quad m\in {\mathbb Z}^n. \end{aligned}$$

(3.16)

It follows from the duality (3.10) and (2.13) that $H^{s_1}_p ({\mathbb R}^n)' = H^{-s_1}_{p'} ({\mathbb R}^n)$. Then one obtains from (3.15) and the Hausdorff–Young inequality (1.2) that

$$\begin{aligned} \begin{aligned} \Vert \mathcal {F}\psi ^j_{G,m} \, \vert H^{-s_1}_{p'} ({\mathbb R}^n) \Vert&= \, \Vert \mathcal {F}\big ( w_{-s_1} \psi ^j_{G,m} \big ) \, \vert L_{p'} ({\mathbb R}^n) \Vert \\&\le c_1 \, \Vert w_{-s_1} \psi ^j_{G,m} \, \vert L_p ({\mathbb R}^n) \Vert \\&\le c_2 (1 + 2^{-j} |m | )^{-s_1} \, 2^{-j \frac{n}{p}}, \end{aligned} \end{aligned}$$

(3.17)

$j \in \mathbb N_0$, $m\in {\mathbb Z}^n$, where we used that $\psi ^j_{G,m}$ given by (2.22) has a support within a ball centred at $2^{-j}m$ and with radius $c2^{-j}$. Then (3.11), (3.16), (3.17) applied to (3.1), (3.2) show that

$$\begin{aligned} \begin{aligned} \Vert \mathcal {F}\, \vert \mathcal N\big (H^{s_1}_p ({\mathbb R}^n), H^{s_2}_p ({\mathbb R}^n) \big ) \Vert&\le c \, \sum ^\infty _{j=0} \sum _{m \in {\mathbb Z}^n} (1 + 2^{-j} |m |)^{-s_1} 2^{j(s_2 +n - \frac{2n}{p})} \\&\le c' \, \sum ^\infty _{j=0} 2^{j(s_2 +n - \frac{2n}{p})} \sum _{k=0}^\infty \ \sum _{2^{-j}|m |\sim 2^k} (1 + 2^k)^{-s_1} \\&\le c'' \sum ^\infty _{j=0} 2^{j(s_2 +n- \frac{2n}{p})} \Big ( \sum _{|m | \le 2^j} 1 + \sum ^\infty _{k=1} 2^{-k s_1} 2^{(j+k)n} \Big ) \\&\le c''' \, \sum ^\infty _{j=0} 2^{js_2 + j 2n (1- \frac{1}{p})} \, \sum ^\infty _{k=0} 2^{-k(s_1 -n)} <\infty \end{aligned} \end{aligned}$$

(3.18)

if both $s_1 >n$ and $s_2 < -\frac{2n}{p'}$. Here we could omit the summation over $G\in G^j$ since it is finite for any j and has at most $2^n$ summands. Moreover, the third inequality follows from the elementary combinatorial estimate $\#\{m\in {\mathbb {Z}}^n: |m | \sim 2^\ell \} \sim 2^{n\ell }$. This proves that $\mathcal {F}$ is nuclear as claimed in (3.13) for $1<p \le 2$.

Step 3 Let $2 \le p <\infty$. As recalled in Sect. 3.1 the operator ideal $\mathcal N$ is symmetric. Then one obtains from the above-mentioned duality for $H^s_p ({\mathbb R}^n)$ and $\mathcal {F}= \mathcal {F}'$ that

$$\begin{aligned} \mathcal {F}: \quad H^{s_1}_p ({\mathbb R}^n) \hookrightarrow H^{s_2}_p ({\mathbb R}^n), \qquad 2< p <\infty , \end{aligned}$$

(3.19)

is nuclear if, and only if,

$$\begin{aligned} \mathcal {F}: \quad H^{-s_2}_{p'} ({\mathbb R}^n) \hookrightarrow H^{-s_1}_{p'} ({\mathbb R}^n), \qquad \frac{1}{p} + \frac{1}{p'} =1, \end{aligned}$$

(3.20)

is nuclear. So it follows from Step 2 that $\mathcal {F}$ is nuclear as claimed in (3.13) for $2\le p<\infty$.

Step 4 We prove in two steps that the conditions (3.13) are also necessary to ensure that $\mathcal {F}$ in (3.12) is nuclear. Let $2\le p <\infty$ and let

$$\begin{aligned} \mathcal {F}: \quad A^{s_1}_{p, q_1} ({\mathbb R}^n) \hookrightarrow A^{s_2}_{p, q_2} ({\mathbb R}^n), \qquad \end{aligned}$$

(3.21)

be nuclear. According to (3.13) we wish to prove that $s_2<-n$ and $s_1>\frac{2n}{p}$. Let us take $k\in \mathbb N$ such that $k>s_1$. Since we have an elementary continuous embedding $W^k_{p} ({\mathbb R}^n)=F^k_{p,2} ({\mathbb R}^n)\hookrightarrow A^{s_1}_{p,2}({\mathbb R}^n)$, by the ideal property of $\mathcal N$ it follows that the mapping

$$\begin{aligned} \mathcal {F}: \quad W^k_{p} ({\mathbb R}^n) \hookrightarrow A^{s_2}_{p, q_2} ({\mathbb R}^n) \end{aligned}$$

(3.22)

is nuclear. Now we proceed to the proof of the condition $s_2 <-n$ if the operator (3.22) is nuclear. Let $f\in L_{p'} ({\mathbb R}^n, w_k)$, $p'=\frac{p}{p-1}$, according to (2.15). Then for any multi-index $\alpha \in \mathbb N_0^n$ with $|\alpha |\le k$, the function $\xi \mapsto \xi ^\alpha f(\xi )$ belongs to $L_{p'}({\mathbb R}^n)$. So using the modification of the Hausdorff–Young inequality (1.2) for the inverse Fourier transform we get that

$$\begin{aligned} \textrm{D}^\alpha \mathcal {F}^{-1}f (x) = i^{|\alpha |} \, \mathcal {F}^{-1}\big (\xi ^\alpha f (\xi )\big ) (x) \in L_p ({\mathbb R}^n), \qquad |\alpha | \le k, \end{aligned}$$

(3.23)

and consequently $\mathcal {F}^{-1}: \, L_{p'}({\mathbb R}^n, w_k) \hookrightarrow W^k_{p}({\mathbb R}^n)$. Now (3.22) and $\mathcal {F}\mathcal {F}^{-1}= \textrm{id}$ imply that the mapping

$$\begin{aligned} \textrm{id}: \quad L_{p'} ({\mathbb R}^n, w_k) \hookrightarrow A^{s_2}_{p, q_2} ({\mathbb R}^n) \end{aligned}$$

(3.24)

is nuclear. But now $s_2<-n$ is an immediate consequence of Proposition 3.3(ii) applied to (3.24).

Step 5 We prove that $s_1>\frac{2n}{p}$ if the operator (3.12) is nuclear and $2\le p<\infty$. We proceed by contradiction. So let us assume that $s_1\le \frac{2n}{p}$. Let us choose an arbitrary $s<s_2$ and $q_0=\min \{p,q_1\}$. Then

$$\begin{aligned} B^{\frac{2n}{p}}_{p, q_0} ({\mathbb R}^n) \hookrightarrow A^{s_1}_{p,q_1} ({\mathbb R}^n) {\mathop {\hookrightarrow }\limits ^{\mathcal {F}}} A^{s_2}_{p,q_2} ({\mathbb R}^n) \hookrightarrow B^{s}_{p, p} ({\mathbb R}^n). \end{aligned}$$

So, we can factorise the operator

$$\begin{aligned} \mathcal {F}: \quad B^{\frac{2n}{p}}_{p,q_0} ({\mathbb R}^n) \hookrightarrow {B^s_{p,p}} ({\mathbb R}^n), \qquad 2\le p<\infty , \end{aligned}$$

(3.25)

through the nuclear operator (3.12) and in consequence the operator (3.25) is also nuclear by virtue of the ideal property of $\mathcal N$. Let us fix an arbitrary number $\alpha \in (-\infty ,s)$. The mappings $I_\alpha :\, {B^s_{p,p}} ({\mathbb R}^n)\hookrightarrow {B^{s-\alpha }_{p,p}} ({\mathbb R}^n)$ and $\mathcal {F}^{-1}:\, {B^{s-\alpha }_{p,p}}({\mathbb R}^n)\hookrightarrow {B^{d^n_p}_{p,p}} ({\mathbb R}^n)$ are both continuous. The continuity of the second operator follows from Theorem 2.4, since $s-\alpha >0=\tau ^{n+}_p$ and $d^n_p=\tau ^{n-}_p$. Using the ideal property of $\mathcal N$ again we obtain nuclearity of the mapping

$$\begin{aligned} \mathcal {F}^{-1}\circ I_\alpha \circ \mathcal {F}:\,B^{\frac{2n}{p}}_{p,q_0} ({\mathbb R}^n) \hookrightarrow {B^{d^n_p}_{p,p}} ({\mathbb R}^n). \end{aligned}$$

(3.26)

But $\mathcal {F}^{-1}\circ I_\alpha \circ \mathcal {F}$ is a factorisation of the mapping

$$\begin{aligned} W_\alpha : B^{\frac{2n}{p}}_{p,q_0} ({\mathbb R}^n) \hookrightarrow {B^{d^n_p}_{p,p}} ({\mathbb R}^n), \quad f\mapsto w_\alpha f,\end{aligned}$$

and $W_{-\alpha }: B^{\frac{2n}{p}}_{p,q_0} ({\mathbb R}^n, w_{-\alpha })\hookrightarrow B^{\frac{2n}{p}}_{p,q_0} ({\mathbb R}^n)$ is an isometry. This implies that the mapping

$$\begin{aligned}\textrm{id}= W_\alpha \circ W_{-\alpha }: B^{\frac{2n}{p}}_{p,q_0} ({\mathbb R}^n, w_{-\alpha }) \hookrightarrow {B^{d^n_p}_{p,p}} ({\mathbb R}^n)\end{aligned}$$

is nuclear. Therefore it follows from Proposition 3.3 that $\frac{2n}{p}-d^n_p>n$ which contradicts $\frac{2n}{p}-d^n_p=n$.

The corresponding assertions for $1<p \le 2$ are a matter of duality. The justification of $s_1 >n$ in (3.13) can be proved similarly as in Step 4. The corresponding assertion for $s_2$ is based on (3.10).

Remark 3.6

In the Fig. 3 below we sketched in the usual $\big (\frac{1}{p},s\big )$-diagram the parameter areas where the Fourier operator $\mathcal {F}$ is nuclear—as a proper subdomain of the compactness area, recall Fig. 1. Note that, using the notation (2.29) with (2.28), one could rewrite the condition (3.13) for the nuclearity of $\mathcal {F}$ in (3.12) as well as for the compactness in (2.32) as: $\mathcal {F}$ is compact, if

$$\begin{aligned} s_1> \tau ^{n+}_p\quad \text {and}\quad s_2<\tau ^{n-}_p \end{aligned}$$

and $\mathcal {F}$ is nuclear, if, and only if,

$$\begin{aligned} s_1 > n- \tau ^{n+}_{p'}\quad \text {and}\quad s_2<-n-\tau ^{n-}_{p'}. \end{aligned}$$

This explains somehow the reflected and shifted ‘nuclear’ parameter areas compared with the compactness areas, see also Fig. 2.

Fig. 3

Parameter areas for the compactness and continuity of $\mathcal {F}$ given by (3.10).

Remark 3.7

Let us briefly mention that the method from Step 5 of the proof of Theorem 3.4, that is, to ensure $s_1 > 2n/p$ for $2\le p <\infty$, can also be used if $1<p \le 2$. If we assume that $s_2\ge -2n\big (1-\frac{1}{p}\big )=d^n_p-n$ and fix arbitrary $s>s_1$, then we get the nuclearity of the mapping

$$\begin{aligned} \mathcal {F}:\, B^s_{p,p}({\mathbb R}^n) \hookrightarrow B^{d^n_p-n}_{p,\max (p,q_2)}({\mathbb R}^n), \end{aligned}$$

(3.27)

which is the counterpart of (3.25). Moreover, taking $\alpha < -s$ and using the continuity of the operators $\mathcal {F}^{-1}:\, B^{d^n_p}_{p,p}({\mathbb R}^n) \hookrightarrow B^{s+\alpha }_{p,p}({\mathbb R}^n)$ and $I_\alpha :\, B^{s+\alpha }_{p,p}({\mathbb R}^n) \hookrightarrow B^{s}_{p,p}({\mathbb R}^n)$ together with the factorisation $W_\alpha =\mathcal {F}\circ I_\alpha \circ \mathcal {F}^{-1}$, we prove the nuclearity of $W_\alpha :B^{d^n_p}_{p,p}({\mathbb R}^n)\hookrightarrow B^{d^n_p-n}_{p,\max (p,q_2)}({\mathbb R}^n)$. But this implies the nuclearity of the embedding

$$\begin{aligned}\textrm{id}:B^{d^n_p}_{p,p}({\mathbb R}^n,w_{-\alpha })\hookrightarrow B^{d^n_p-n}_{p,\max (p,q_2)}({\mathbb R}^n)\end{aligned}$$

which contradicts (3.9).

3.3 Limiting Cases

So far we excluded the values 1 and $\infty$ for the parameters $p, q_1, q_2$ in Theorem 3.4. We now collect what can be said about these limiting cases.

Proposition 3.8

Let $1<p<\infty$, $1\le q_1,q_2\le \infty$, and let $s_1 \in \mathbb R$, $s_2 \in \mathbb R$. Then

$$\begin{aligned} \mathcal {F}: \quad F^{s_1}_{p, q_1} ({\mathbb R}^n) \hookrightarrow F^{s_2}_{p, q_2} ({\mathbb R}^n) \end{aligned}$$

(3.28)

is nuclear if, and only if, (3.13) is satisfied.

Proof

Step 1 The sufficiency of the assumptions (3.13) follows by Theorem 3.4 together with the elementary embeddings for the spaces $F^s_{p,q}({\mathbb R}^n)$. We can take $\widetilde{s_1}$ and $\widetilde{s_2}$ such that $s_1>\widetilde{s_1}>n\min \{1,\frac{2}{p}\}$ and $s_2<\widetilde{s_2}< - n\min \{1,\frac{2}{p'}\}$. Then for any $\widetilde{q_1}$ and $\widetilde{q_2}$ such that $1<\widetilde{q_1}, \widetilde{q_2}<\infty$, we have

$$\begin{aligned} F^{s_1}_{p, q_1} ({\mathbb R}^n) \hookrightarrow F^{\widetilde{s_1}}_{p, \widetilde{q_1}} ({\mathbb R}^n) {\mathop {\hookrightarrow }\limits ^{\mathcal {F}}} F^{\widetilde{s_2}}_{p, \widetilde{q_2}} ({\mathbb R}^n) \hookrightarrow F^{s_2}_{p, q_2} ({\mathbb R}^n), \end{aligned}$$

where Theorem 3.4 ensures the nuclearity of the middle mapping, and thus also of (3.28).

Step 2  We prove the necessity of the condition (3.13). The case $1<q_1,q_2<\infty$ is covered by Theorem 3.4. So it remains to consider the situation when the parameters $q_1$ or $q_2$ attain the limiting values 1 or $\infty$. First we consider the following composition,

$$\begin{aligned} F^{\widetilde{s_1}}_{p,\widetilde{q_1}}({\mathbb R}^n) \hookrightarrow F^{s_1}_{p,q_1}({\mathbb R}^n) {\mathop {\hookrightarrow }\limits ^{\mathcal {F}}} F^{s_2}_{p, q_2} ({\mathbb R}^n) \hookrightarrow F^{\widetilde{s_2}}_{p, \widetilde{q_2}} ({\mathbb R}^n) , \end{aligned}$$

(3.29)

where the parameters $\widetilde{s_i}$, $\widetilde{q_i}$, $i=1,2$, will be chosen appropriately below. We would like to reduce the argument further and claim that it is sufficient to prove the necessity of the assumption concerning $s_2$ if $q_2=\infty$, and concerning $s_1$ if $q_1=1$. This can be seen as follows. Let $\varepsilon >0$. If $q_2=\infty$ and $q_1>1$, then we may choose $\widetilde{s_1}=s_1$ and $\widetilde{q_1}\le q_1$ such that $1<\widetilde{q_1}<\infty$, and $\widetilde{s_2}=s_2-\varepsilon$ and $1<\widetilde{q_2}<\infty$. Thus the necessity of the condition (3.13) for $s_1$ follows from Theorem 3.4 applied to (3.29). On the other hand, if $q_1=1$ and $q_2<\infty$, then we can take $\widetilde{s_1}=s_1+\varepsilon$, $1<\widetilde{q_1}< \infty$, $\widetilde{s_2}=s_2$ and $q_2\le \widetilde{q_2}$ such that $1<\widetilde{q_2}<\infty$. Then the necessity of the condition (3.13) for $s_2$ follows once more from Theorem 3.4 applied to (3.29). If $2\le p <\infty$ and $q_2=\infty$, then the argument that was used in Step 4 of the proof of Theorem 3.4 shows the necessity of $s_2<-n$ in this case. Here we benefit from the fact that in Proposition 3.3 the case $q_2=\infty$ is covered.

If $q_2<\infty$ and $1<p\le 2$, and the mapping

$$\begin{aligned} \mathcal {F}: \quad F^{s_1}_{p, 1} ({\mathbb R}^n) \hookrightarrow F^{s_2}_{p, q_2} ({\mathbb R}^n) \end{aligned}$$

is nuclear, then, by duality, the mapping

$$\begin{aligned} \mathcal {F}: \quad F^{-s_2}_{p', q'_2} ({\mathbb R}^n) \hookrightarrow F^{-s_1}_{p', \infty } ({\mathbb R}^n) \end{aligned}$$

is nuclear. So $-s_1<-n$ is a consequence of the last argument.

Now we consider the case $2<p<\infty$ and $q_1=1$. We choose r with $2<r<p$ and $s_3$ such that

$$\begin{aligned} s_3=s_1+\frac{n}{r} -\frac{n}{p} . \end{aligned}$$

(3.30)

Then by the Sobolev type embedding, cf. (2.9),

$$\begin{aligned} H^{s_3}_{r}({\mathbb R}^n)= F^{s_3}_{r,2}({\mathbb R}^n)\hookrightarrow F^{s_1}_{p,1}({\mathbb R}^n){\mathop {\hookrightarrow }\limits ^{\mathcal {F}}} F^{s_2}_{p, q_2} ({\mathbb R}^n) \end{aligned}$$

(3.31)

this implies that

$$\begin{aligned} \mathcal {F}:\quad H^{s_3}_r({\mathbb R}^n)\hookrightarrow F^{s_2}_{p,q_2}({\mathbb R}^n) \end{aligned}$$

(3.32)

is nuclear. Since $I_{s_3}(\mathcal {F}^{-1}(f))= \mathcal {F}^{-1}(w_{s_3}f)$ and $w_{s_3}f\in L_{r'}({\mathbb R}^n)$ if $f\in L_{r'}({\mathbb R}^n, w_{s_3})$, $r'<2$, it follows from the Hausdorff–Young inequality that

$$\begin{aligned} \begin{aligned} \Vert \mathcal {F}^{-1}f\, \vert H^{s_3}_{r} ({\mathbb R}^n) \Vert = \, \Vert \mathcal {F}^{-1}\big ( w_{s_3} f\big ) \, \vert L_{r} ({\mathbb R}^n) \Vert \le c \, \Vert w_{s_3} f \, \vert L_{r'} ({\mathbb R}^n) \Vert . \end{aligned} \end{aligned}$$

(3.33)

Now $\mathcal {F}\mathcal {F}^{-1}= \textrm{id}$ combined with (3.32) shows that

$$\begin{aligned} \textrm{id}: \quad L_{r'} ({\mathbb R}^n, w_{s_3}) \hookrightarrow F^{s_2}_{p, q_2} ({\mathbb R}^n) \end{aligned}$$

(3.34)

is nuclear if (3.32) was nuclear. Thus Proposition 3.3(ii) implies that

$$\begin{aligned} s_3>n-n\max \left( \frac{1}{r'}-\frac{1}{p}, 0\right) =n-\frac{n}{r'}+\frac{n}{p}= \frac{n}{r}+\frac{n}{p}, \end{aligned}$$

(3.35)

which leads to

$$\begin{aligned} s_1= s_3-\frac{n}{r}+\frac{n}{p}>\frac{n}{r}+\frac{n}{p}-\frac{n}{r}+\frac{n}{p}= \frac{2n}{p}. \end{aligned}$$

(3.36)

Analogously we can prove the necessity in the case $1<p<2$ and $q_2=\infty$. We choose r such that $p<r<2$ and $s_3$ given by

$$\begin{aligned} s_3=s_2+\frac{n}{r} -\frac{n}{p} . \end{aligned}$$

(3.37)

Now the Sobolev embeddings, recall (2.9), imply

$$\begin{aligned} F^{s_1}_{p,q_1}({\mathbb R}^n){\mathop {\hookrightarrow }\limits ^{\mathcal {F}}} F^{s_2}_{p, \infty } ({\mathbb R}^n) \hookrightarrow H^{s_3}_{r}({\mathbb R}^n), \end{aligned}$$

(3.38)

which finally leads to the nuclearity of

$$\begin{aligned} \mathcal {F}:\quad F^{s_1}_{p,q_1}({\mathbb R}^n) \hookrightarrow H^{s_3}_r({\mathbb R}^n). \end{aligned}$$

(3.39)

Thus in the same way as above, since $w_{s_3}\mathcal {F}(f)=\mathcal {F}(I_{s_3}(f))$ and $\Vert \mathcal {F}^{-1}f\vert L_{r'}({\mathbb R}^n,w_{s_3})\Vert = \Vert \mathcal {F}f\vert L_{r'}({\mathbb R}^n, w_{s_3})\Vert$, it follows from the Hausdorff–Young inequality that

$$\begin{aligned} \nonumber \Vert \mathcal {F}^{-1}f \, \vert L_{r'} ({\mathbb R}^n, w_{s_3} ) \Vert&= \Vert \mathcal {F}f \, \vert L_{r'} ({\mathbb R}^n, w_{s_3} ) \Vert \le c\, \Vert \mathcal {F}^{-1}( w_{s_3} \mathcal {F}f) \, \vert L_r({\mathbb R}^n) \Vert \\&= c \, \Vert f\, \vert H^{s_3}_{r} ({\mathbb R}^n) \Vert . \end{aligned}$$

(3.40)

Combined with $\mathcal {F}^{-1}\mathcal {F}= \textrm{id}$ and (3.39) this leads to the nuclearity of

$$\begin{aligned} \textrm{id}: \quad F^{s_1}_{p, q_1} ({\mathbb R}^n) \hookrightarrow L_{r'} ({\mathbb R}^n, w_{s_3}). \end{aligned}$$

(3.41)

Another application of Proposition 3.3(ii) implies

$$\begin{aligned} -s_3>n +\frac{n}{r'}-\frac{n}{p}. \end{aligned}$$

(3.42)

Consequently,

$$\begin{aligned} s_2< - 2n\left( 1-\frac{1}{p} \right) , \end{aligned}$$

(3.43)

which concludes the proof of the necessity of the conditions (3.13) in all cases.

Corollary 3.9

Let $1<p<\infty$, $1\le q_1,q_2\le \infty$ and let $s_1 \in \mathbb R$, $s_2 \in \mathbb R$. Then

$$\begin{aligned} \mathcal {F}: \quad B^{s_1}_{p, q_1} ({\mathbb R}^n) \hookrightarrow B^{s_2}_{p, q_2} ({\mathbb R}^n) \end{aligned}$$

(3.44)

is nuclear if (3.13) is satisfied.

Conversely, the nuclearity of (3.44) implies (3.13) in all cases apart from $2<p<\infty$ and $q_1=1$, or $1<p<2$ and $q_2=\infty$. In case of $2<p<\infty$ and $q_1=1$ the nuclearity of (3.44) implies $s_1\ge \frac{2n}{p}$, while in case of $1<p<2$ and $q_2=\infty$ the nuclearity of (3.44) implies $s_2\le -2n\big (1-\frac{1}{p}\big )$.

Proof

Step 1  The sufficiency of the assumptions (3.13) can be proved in exactly the same way as in Proposition 3.8, Step 1 of its proof by substituting F-spaces by corresponding B-spaces.

Step 2  As for the necessity we can use the same argument as in Step 2 of that proof, to reduce the argument to the assumption concerning $s_2$ if $q_2=\infty$, and concerning $s_1$ if $q_1=1$. In case of $q_1=1$, $1<p\le 2$, or $q_2=\infty$ and $2\le p<\infty$, we can follow the same arguments as presented at the beginning of Step 2 in the proof of Proposition 3.8. Since the argument works for any $\varepsilon >0$, it proves the inequality $s_1\ge \frac{2n}{p}$ if $2<p<\infty$, and $s_2\le -2n\big (1-\frac{1}{p}\big )$ if $1<p<2$. The strict inequalities in case of $2\le p<\infty$ and $q_2=\infty$, or $1<p\le 2$ and $q_1=1$, can be proved in the same way as in Step 2 of the above-mentioned proof.

Remark 3.10

To prove the necessity of the strict inequalities for F-spaces in the cases $1<p<2$ and $q_2=\infty$, or $2<p<\infty$ and $q_1=1$, we benefit from the independence of the Sobolev embeddings of the q-parameters, cf. (2.9) and (3.31). This holds for Triebel–Lizorkin spaces, unlike for Besov spaces. So our argument does not work in that context.

Next we consider the case $p=1$. If $1\le q_1,q_2<\infty$, we can extend Theorem 3.4 in the desired way.

Proposition 3.11

Let $1\le q_1,q_2<\infty$ and let $s_1,s_2 \in \mathbb R$. Then

$$\begin{aligned} \mathcal {F}: \quad A^{s_1}_{1, q_1} ({\mathbb R}^n) \hookrightarrow A^{s_2}_{1, q_2} ({\mathbb R}^n) \end{aligned}$$

(3.45)

is nuclear if, and only if,

$$\begin{aligned} s_1 > n \qquad \text {and}\qquad s_2<0 . \end{aligned}$$

(3.46)

Proof

It is sufficient to consider the Besov spaces, i.e.,

$$\begin{aligned} \mathcal {F}: \quad B^{s_1}_{1,q_1} ({\mathbb R}^n) \hookrightarrow B^{s_2}_{1,q_2} ({\mathbb R}^n), \qquad 1\le q_1,q_2<\infty , \end{aligned}$$

(3.47)

since $B^s_{1,1}({\mathbb R}^n)\hookrightarrow F^s_{1,q}({\mathbb R}^n)\hookrightarrow B^s_{1,q}({\mathbb R}^n)$ for any $s\in \mathbb R$ and $1\le q<\infty$. By [20, Thm. 2.11.2, p. 178] we have the following duality

$$\begin{aligned} B^{s_1}_{1,q_1} ({\mathbb R}^n)' = B^{-s_1}_{\infty ,q_1'} ({\mathbb R}^n)\end{aligned}$$

and according to (2.27) the estimates for the norms of the wavelets

$$\begin{aligned} 2^{jn} \Vert \psi ^j_{G,m} \, \vert B^{s_2}_{1,q_2} ({\mathbb R}^n) \Vert \sim 2^{j s_2}, \qquad j \in \mathbb N_0, \quad m\in {\mathbb Z}^n, \quad G\in G^j. \end{aligned}$$

(3.48)

First we assume that (3.46) holds and we prove the nuclearity of (3.45). As for $p\le 2$ we have the continuity of the Fourier transform $\mathcal {F}:\, L_p({\mathbb R}^n)\hookrightarrow B^0_{p',p}({\mathbb R}^n)$ (see [19, Theorem 1]) and we also have a continuous embedding $B^0_{\infty ,1}({\mathbb R}^n)\hookrightarrow B^0_{\infty ,q'_1}({\mathbb R}^n)$. Now using the lift property for Besov spaces we obtain that

$$\begin{aligned} \Vert \mathcal {F}\psi ^j_{G,m} \, \vert B^{-s_1}_{\infty ,q_1'} ({\mathbb R}^n) \Vert&= \Vert I_{-s_1}\mathcal {F}\psi ^j_{G,m}\vert B^{0}_{\infty ,q_1'} ({\mathbb R}^n) \Vert \\ \nonumber&\le c \Vert \mathcal {F}(w_{-s_1} \psi ^j_{G,m}) \, \vert B^{0}_{\infty , 1} ({\mathbb R}^n) \Vert \le c' \, \Vert w_{-s_1} \psi ^j_{G,m} \, \vert L_1 ({\mathbb R}^n) \Vert \\ \nonumber&\le c'' (1 + 2^{-j} |m | )^{-s_1} \, 2^{-j n}, \end{aligned}$$

(3.49)

where $j \in \mathbb N_0$, $m\in {\mathbb Z}^n$. Then (3.11), (3.48), (3.49) applied to (3.1), (3.2) show in the same way as in (3.18) that

$$\begin{aligned} \begin{aligned} \Vert \mathcal {F}\, \vert \mathcal N\big (B^{s_1}_{1,q_1} ({\mathbb R}^n), B^{s_2}_{1,q_2} ({\mathbb R}^n) \big ) \Vert&\le c_1 \, \sum ^\infty _{j=0} \sum _{m \in {\mathbb Z}^n} (1 + 2^{-j} |m |)^{-s_1} 2^{j(s_2 -n)} \\&\le c_2 \, \sum ^\infty _{j=0} 2^{js_2} \, \sum ^\infty _{k=0} 2^{-k(s_1 -n)} <\infty \end{aligned} \end{aligned}$$

(3.50)

as $s_1 >n$ and $s_2 < 0$. This proves that $\mathcal {F}$ is nuclear as claimed.

Now we assume that $\mathcal {F}$ given by (3.47) is a nuclear operator. Let $f\in B^{s_2}_{1,q_2}({\mathbb R}^n)$. Due to the continuous embedding $B^{s_2}_{1,q_2}({\mathbb R}^n)\hookrightarrow B^{s_2}_{1,\infty }({\mathbb R}^n)$ and the lift property for Besov spaces we obtain $I_{s_2}(f)\in B^{0}_{1,\infty }({\mathbb R}^n)$. Using the continuity of the Fourier transform $\mathcal {F}:\,B^0_{1,\infty }({\mathbb R}^n)\hookrightarrow L_\infty ({\mathbb R}^n)$ (see [19, Theorem 1]) and the mapping properties of $I_{s_2}$, cf. (2.12), we get

$$\begin{aligned} \Vert w_{s_2}\mathcal {F}^{-1}f\, \vert L_\infty ({\mathbb R}^n) \Vert&= \Vert w_{s_2}\mathcal {F}f\, \vert L_\infty ({\mathbb R}^n) \Vert = \Vert \mathcal {F}\mathcal {F}^{-1}w_{s_2}\mathcal {F}f\vert L_\infty ({\mathbb R}^n) \Vert \\&\le \, c\, \Vert I_{s_2}f \vert B^{0}_{1,\infty } ({\mathbb R}^n) \Vert \le c' \Vert f \vert B^{s_2}_{1,q_2} ({\mathbb R}^n) \Vert . \nonumber \end{aligned}$$

(3.51)

We combine (3.47) and (3.51) with the identity $\textrm{id}=\mathcal {F}^{-1}\circ \mathcal {F}$ and get the following nuclear embedding,

$$\begin{aligned} \textrm{id}:\; B^{s_1}_{1,q_1} ({\mathbb R}^n) {\mathop {\hookrightarrow }\limits ^{\mathcal {F}}} B^{s_2}_{1,q_2} ({\mathbb R}^n) {\mathop {\hookrightarrow }\limits ^{\mathcal {F}^{-1}}} L_\infty (w_{s_2},{\mathbb R}^n). \end{aligned}$$

(3.52)

Thus, the embedding $\textrm{id}:B^{s_1}_{1,q_1} ({\mathbb R}^n) \hookrightarrow L_\infty (w_{s_2},{\mathbb R}^n)$ and obviously also the embedding $\textrm{id}:B^{s_1}_{1,q_1} ({\mathbb R}^n,w_{-s_2}) \hookrightarrow L_\infty ({\mathbb R}^n)$ are nuclear. But $L_\infty ({\mathbb R}^n)\hookrightarrow B^{0}_{\infty ,\infty } ({\mathbb R}^n)$, therefore the embedding

$$\begin{aligned} \textrm{id}: \; B^{s_1}_{1,q_1} ({\mathbb R}^n, w_{-s_2}) \hookrightarrow B^0_{\infty ,\infty }({\mathbb R}^n)\end{aligned}$$

is also nuclear, and another application of Proposition 3.3(ii) implies $-s_2>0$ and $s_1>n$.

Remark 3.12

We would like to mention that one can also use a more direct argument to prove the above extensions. This would be based on the modifications

$$\begin{aligned} \mathcal {F}: \quad L_1 ({\mathbb R}^n) \hookrightarrow B^0_{\infty ,1} ({\mathbb R}^n) \end{aligned}$$

(3.53)

and

$$\begin{aligned} \mathcal {F}: \quad B^0_{1, \infty } ({\mathbb R}^n) \hookrightarrow L_\infty ({\mathbb R}^n) \end{aligned}$$

(3.54)

of the Hausdorff–Young mappings. Here (3.53) follows from

$$\begin{aligned} \begin{aligned} \Vert \mathcal {F}f \, \vert B^0_{\infty ,1} ({\mathbb R}^n)\Vert&\sim \sum ^\infty _{j=0} \Vert \mathcal {F}^{-1}(\varphi _j f)\, \vert L_\infty ({\mathbb R}^n) \Vert \\&\le c \sum ^\infty _{j=0} \Vert \varphi _j f \, \vert L_1 ({\mathbb R}^n) \Vert \\&\sim \Vert f \, \vert L_1 ({\mathbb R}^n) \Vert \end{aligned} \end{aligned}$$

(3.55)

where the last equivalence follows from the properties of the dyadic resolution of unity $\{\varphi _j\}$, cf. (2.3)–(2.5). In an analogous way (3.54) is a consequence of

$$\begin{aligned} \begin{aligned} \Vert \mathcal {F}f\, \vert L_\infty ({\mathbb R}^n) \Vert&\sim \sup _{j\in \mathbb N_0} \Vert \varphi _j \mathcal {F}f \, \vert L_\infty ({\mathbb R}^n) \Vert \\&\le c \, \sup _{j\in \mathbb N_0} \Vert \mathcal {F}^{-1}\varphi _j \mathcal {F}f \, \vert L_1 ({\mathbb R}^n) \Vert \\&= c \, \Vert f\, \vert B^0_{1,\infty } ({\mathbb R}^n) \Vert . \end{aligned} \end{aligned}$$

(3.56)

Now we can use (3.53) in (3.49) and (3.54) in (3.51).

Finally, by duality arguments, one can cover the case $p=\infty$, when $A=B$ and $1<q_1,q_2\le \infty$. But using Proposition 3.11, we even have a characterisation in this case.

Corollary 3.13

Let $1 < q_1,q_2\le \infty$ and $s_1,s_2 \in \mathbb R$. Then

$$\begin{aligned} \mathcal {F}: \quad B^{s_1}_{\infty , q_1} ({\mathbb R}^n) \hookrightarrow B^{s_2}_{\infty , q_2} ({\mathbb R}^n) \end{aligned}$$

(3.57)

is nuclear if, and only if,

$$\begin{aligned} s_1 > 0 \qquad \text {and}\qquad s_2<-n . \end{aligned}$$

(3.58)

Proof

Let $s_1>0$ and $s_2<-n$. Then by Proposition 3.11, the mapping $\mathcal {F}:\, B^{-s_2}_{1,q_2'}({\mathbb R}^n)\hookrightarrow B^{-s_1}_{1,q_1'}({\mathbb R}^n)$ is nuclear. So, a duality argument and symmetry of the ideal $\mathcal N$ imply nuclearity of (3.57).

We come to the necessity. Note first, that by Proposition 3.11

$$\begin{aligned} \mathcal {F}: \quad B^{s_1}_{1, q_1} ({\mathbb R}^n) \hookrightarrow B^{s_2}_{1, q_2} ({\mathbb R}^n), \qquad 1\le q_1, q_2 < \infty , \end{aligned}$$

(3.59)

is nuclear if, and only if, $s_1 >n$, $s_2 <0$. Then $\mathcal {F}$ is also compact. Conversely, if $\mathcal {F}$ in (3.59) is compact, then the decomposition in (3.52) implies the compactness of $\mathcal {F}:\, B^{s_1}_{1,q_1}({\mathbb R}^n,w_{-s_2})\hookrightarrow B^0_{\infty ,\infty }({\mathbb R}^n)$, which by Proposition 3.3 implies $s_1 >n$, $s_2 <0$. In other words, $\mathcal {F}$ in (3.59) is nuclear if, and only if, it is compact.

Let now, conversely, $\mathcal {F}$ in (3.57) for some $s_1 \in \mathbb R$ and $s_2 \in \mathbb R$, be nuclear. Then for the same $s_1 \in \mathbb R$ and $s_2 \in \mathbb R$ both $\mathcal {F}$ in (3.57) and

$$\begin{aligned} \mathcal {F}: \quad \overset{\circ }{B}{}^{s_1}_{\infty , q_1} ({\mathbb R}^n) \hookrightarrow \overset{\circ }{B}{}^{s_2}_{\infty ,q_2} ({\mathbb R}^n), \qquad 1<q_1, q_2 \le \infty , \end{aligned}$$

(3.60)

are compact. Here $\overset{\circ }{B}{}^{s}_{\infty , q}({\mathbb R}^n)$ stands for the closure of $\mathcal {S}({\mathbb R}^n)$ in $B^s_{\infty ,q}({\mathbb R}^n)$, which is a proper subspace of $B^s_{\infty ,q}({\mathbb R}^n)$. The Fourier transform $\mathcal {F}$ maps $\mathcal {S}({\mathbb R}^n)$ onto $\mathcal {S}({\mathbb R}^n)$. Therefore it follows from (3.57) that its restriction to $\overset{\circ }{B}{}^{s_1}_{\infty , q_1} ({\mathbb R}^n)$ is a continuous mapping into $\overset{\circ }{B}{}^{s_2}_{\infty ,q_2} ({\mathbb R}^n)$. Using the duality

$$\begin{aligned} \overset{\circ }{B}{}^s_{\infty , q} ({\mathbb R}^n)' = B^{-s}_{1, q'} ({\mathbb R}^n), \qquad s\in \mathbb R, \quad 1\le q \le \infty , \quad \frac{1}{q} + \frac{1}{q'} =1, \end{aligned}$$

(3.61)

cf. [20, Remark 2.11.2/2, p. 180], then

$$\begin{aligned} \mathcal {F}: \quad B^{-s_2}_{1, q'_2} ({\mathbb R}^n) \hookrightarrow B^{-s_1}_{1, q'_1} ({\mathbb R}^n), \qquad 1 \le q'_1, q'_2 <\infty , \end{aligned}$$

(3.62)

is compact. This requires $-s_2 >n$ and $-s_1 <0$.

Remark 3.14

Note that the nuclear counterpart of the argument in (3.60) is not clear, maybe not true, as there is no projection operator from $\ell _\infty$ onto $c_0$, [1, Corollary 2.5.6, p. 46], on which a related proof could be based. Furthermore, according to [17, p. 343] the operator ideal $\mathcal N$ is not injective which would otherwise ensure the nuclear version of (3.60).

Remark 3.15

Let us remark that

$$\begin{aligned} \mathcal {F}: \quad B^{s_1}_{1, q_1} ({\mathbb R}^n) \hookrightarrow B^{s_2}_{1, q_2} ({\mathbb R}^n), \qquad 1\le q_1, q_2 < \infty , \end{aligned}$$

(3.63)

is nuclear if, and only if, it is compact. The same phenomenon can be observed for

$$\begin{aligned} \mathcal {F}: \quad B^{s_1}_{\infty , q_1} ({\mathbb R}^n) \hookrightarrow B^{s_2}_{\infty , q_2} ({\mathbb R}^n), \qquad 1<q_1, q_2 \le \infty , \end{aligned}$$

(3.64)

which is nuclear if, and only if, it is compact. In view of Theorems 2.4 and 3.4 this is different from the situation for $1<p<\infty$, when the conditions for the nuclearity of $\mathcal {F}$ are indeed stronger than for its compactness. In other words, for $\mathcal {F}: B^{s_1}_{p,q_1}({\mathbb R}^n) \hookrightarrow B^{s_2}_{p,q_2}({\mathbb R}^n)$ compactness and nuclearity coincide if, and only if, $p=1$ or $p=\infty$ (with appropriately chosen $q_1,q_2$), as can be also seen from the reformulated conditions in Remark 3.6 or in Fig. 3. We always have $n-\tau ^{n+}_{p'}\ge \tau ^{n+}_p$ and $-n-\tau ^{n-}_{p'}\le \tau ^{n-}_p$, with both inequalities turning into equalities only in each of the cases $p=1$ and $p=\infty$.

A similar phenomenon was observed in [10, Cor. 3.16, Rem. 3.18] related to the situations on domains as described in Proposition 3.2, and for weighted spaces, recall Proposition 3.3.

4 Weighted Spaces

Let again $A^s_{p,q}({\mathbb R}^n, w_\alpha )$, $A \in \{B,F \}$, and s, p, q as in Definition 2.1 be the weighted spaces as introduced in Remark 2.3 where we restrict ourselves to the distinguished weights

$$\begin{aligned} w_\alpha (x) = \big ( 1 + |x |^2)^{\alpha /2}, \qquad x \in {\mathbb R}^n, \quad \alpha \in \mathbb R. \end{aligned}$$

(4.1)

So far we concentrated mainly on the unweighted spaces $A^s_{p,q}({\mathbb R}^n)$ and used their weighted generalisations as tools caused by the specific mapping properties of $\mathcal {F}$. But under these circumstances it is quite natural to ask how weighted counterparts of the main assertions obtained in the above Sect. 3 and in [25] may look like. Fortunately enough there is no need to extend the quite substantial machinery underlying the related theory for the spaces $A^s_{p,q}({\mathbb R}^n)$ to the weighted spaces $A^s_{p,q}({\mathbb R}^n, w_\alpha )$ (what might be possible), but there is an effective short-cut based on qualitative arguments which will be described below. We rely on the same remarkable properties of the spaces $A^s_{p,q}({\mathbb R}^n, w_\alpha )$ which we already described in Sect. 2.1 with a reference to [22, Theorem 6.5, pp. 265–266]. In particular, the multiplier

$$\begin{aligned} W_\beta : \ f \mapsto w_\beta f, \qquad f\in \mathcal {S}'({\mathbb R}^n), \quad \beta \in \mathbb R, \end{aligned}$$

(4.2)

is for all these spaces an isomorphic mapping,

$$\begin{aligned} \begin{aligned} W_\beta A^s_{p,q}\left( {\mathbb R}^n, w_{\alpha }\right)&= A^s_{p,q}({\mathbb R}^n, w_{{\alpha -\beta }}),\\ \Vert w_\beta f \, \vert A^s_{p,q}({\mathbb R}^n, w_{\alpha -\beta }) \Vert&\sim \Vert f \, \vert A^s_{p,q}({\mathbb R}^n, w_{\alpha }) \Vert , \qquad \alpha \in \mathbb R, \quad \beta \in \mathbb R, \end{aligned} \end{aligned}$$

(4.3)

and the lift $I_\gamma$, $\gamma \in \mathbb R$,

$$\begin{aligned} I_\gamma : \quad f \mapsto \big ( w_\gamma \widehat{f}\, \big )^\vee = \big ( w_\gamma f^\vee \big )^\wedge , \qquad f\in \mathcal {S}'({\mathbb R}^n), \quad \gamma \in \mathbb R, \end{aligned}$$

(4.4)

for the spaces $A^s_{p,q}({\mathbb R}^n)$ according to (2.12) generates also the isomorphic mappings

$$\begin{aligned} \begin{aligned} I_\gamma A^{{s}}_{p,q} ({\mathbb R}^n, w_\alpha )&= A^{s-\gamma }_{p,q} ({\mathbb R}^n, w_\alpha ), \\ \Vert (w_\gamma \widehat{f} )^\vee \vert A^{s-\gamma }_{p,q} ({\mathbb R}^n, w_\alpha ) \Vert&\sim \Vert f\, \vert A^s_{p,q} ({\mathbb R}^n, w_\alpha ) \Vert , \end{aligned} \end{aligned}$$

(4.5)

$\alpha \in \mathbb R$, $\gamma \in \mathbb R$, $s\in \mathbb R$ and $0<p,q \le \infty$ ($p<\infty$ for F-spaces).

Note that by the definitions of $W_\beta$ in (4.2) and $I_\gamma$ in (4.4),

$$\begin{aligned} \mathcal {F}\circ W_\beta \circ I_\gamma = I_\beta \circ W_\gamma \circ \mathcal {F}\quad \text {on}\quad \mathcal {S}'({\mathbb R}^n), \end{aligned}$$

which directly leads to the decomposition of $\mathcal {F}$ into

$$\begin{aligned} \mathcal {F}= W_{-\gamma } \circ I_{-\beta } \circ \mathcal {F}\circ W_\beta \circ I_\gamma \quad \text {on}\quad \mathcal {S}'({\mathbb R}^n). \end{aligned}$$

(4.6)

We shall benefit from this observation below, see also Remark 4.2.

Although not needed, it might illuminate what is going on that any $f\in \mathcal {S}'({\mathbb R}^n)$ belongs to a suitable weighted space of the above type. More precisely, one has for fixed $0<p,q \le \infty$ that

$$\begin{aligned} \mathcal {S}({\mathbb R}^n)= \bigcap _{\alpha \in \mathbb R, s\in \mathbb R} B^s_{p,q}({\mathbb R}^n, w_\alpha ) \quad \text {and} \quad \mathcal {S}'({\mathbb R}^n)= \bigcup _{\alpha \in \mathbb R, s\in \mathbb R} B^s_{p,q}({\mathbb R}^n, w_\alpha ). \end{aligned}$$

(4.7)

This is more or less known and was proved in [12].

In what follows we are not interested in generality. This may explain why we suppose as in Theorem 3.4 that $1<p,q_1,q_2 <\infty$, whereas it is quite clear that at least some of the arguments below apply also to a wider range of these parameters.

Proposition 4.1

Let $1<p,q_1,q_2 < \infty$ and $s_1 \in \mathbb R$, $s_2 \in \mathbb R$. Let $-\infty<\alpha _1, \alpha _2, \beta , \gamma <\infty$ and $A \in \{B,F \}$. Then there is a continuous mapping

$$\begin{aligned} \mathcal {F}: \quad A^{s_1+\gamma }_{p,q_1} ({\mathbb R}^n, w_{\alpha _1 + \beta }) \hookrightarrow A^{s_2 +\beta }_{p,q_2} ({\mathbb R}^n, w_{\alpha _2 +\gamma }) \end{aligned}$$

(4.8)

if, and only if, there is a continuous mapping

$$\begin{aligned} \mathcal {F}: \quad A^{s_1}_{p,q_1} ({\mathbb R}^n, w_{\alpha _1}) \hookrightarrow A^{s_2}_{p,q_2} ({\mathbb R}^n, w_{\alpha _2}). \end{aligned}$$

(4.9)

Furthermore, $\mathcal {F}$ in (4.8) is compact if, and only if, $\mathcal {F}$ in (4.9) is compact, and $\mathcal {F}$ in (4.8) is nuclear if, and only if, $\mathcal {F}$ in (4.9) is nuclear.

Proof

Step 1. Let $\mathcal {F}$ in (4.9) be continuous and let $f\in A^{s_1}_{p,q_1} ({\mathbb R}^n, w_{\alpha _1 +\beta })$. Then due to (4.3), $w_\beta f \in A^{s_1}_{p,q_1}({\mathbb R}^n,w_{\alpha _1})$, so

$$\begin{aligned} \Vert \mathcal {F}(w_\beta f) \, \vert A^{s_2}_{p,q_2} ({\mathbb R}^n, w_{\alpha _2}) \Vert \le c \, \Vert w_\beta f \, \vert A^{s_1}_{p,q_1} ({\mathbb R}^n, w_{\alpha _1}) \Vert . \end{aligned}$$

(4.10)

By (4.4) one has

$$\begin{aligned} \mathcal {F}\circ W_\beta = I_\beta \circ \mathcal {F}. \end{aligned}$$

(4.11)

Inserted in (4.10) one obtains by (4.3) and (4.5) that

$$\begin{aligned} \Vert \mathcal {F}f \, \vert A^{s_2 + \beta }_{p, q_2} ({\mathbb R}^n, w_{\alpha _2} ) \Vert \le c\, \Vert f \, \vert A^{s_1}_{p,q_1} ({\mathbb R}^n, w_{\alpha _1 +\beta }) \Vert . \end{aligned}$$

(4.12)

This proves the continuity of $\mathcal {F}$ in (4.8) with $\gamma =0$. Let again $\mathcal {F}$ in (4.9) be continuous and let $f \in A^{s_1 + \gamma }_{p, q_1} ({\mathbb R}^n, w_{\alpha _1} )$. Then due to (4.5), $I_\gamma f \in A^{s_1}_{p,q_1}({\mathbb R}^n,w_{\alpha _1})$, so

$$\begin{aligned} \Vert \mathcal {F}(I_\gamma f) \, \vert A^{s_2}_{p,q_2} ({\mathbb R}^n, w_{\alpha _2})\Vert \le c \, \Vert I_\gamma f\, \vert A^{s_1}_{p, q_1} ({\mathbb R}^n, w_{\alpha _1} ) \Vert . \end{aligned}$$

(4.13)

By (4.4) one has

$$\begin{aligned} \mathcal {F}\circ I_\gamma = W_\gamma \circ \mathcal {F}. \end{aligned}$$

(4.14)

Inserted in (4.13) one obtains by (4.3) and (4.5) that

$$\begin{aligned} \Vert \mathcal {F}f\, \vert A^{s_2}_{p, q_2} ({\mathbb R}^n, w_{\alpha _2 +\gamma }) \Vert \le c \, \Vert f \, \vert A^{s_1 +\gamma }_{p, q_1} ({\mathbb R}^n, w_{\alpha _1})\Vert . \end{aligned}$$

(4.15)

This proves the continuity of $\mathcal {F}$ in (4.8) with $\beta =0$. A combination of the above arguments for $\gamma =0$ and $\beta =0$ shows that $\mathcal {F}$ in (4.8) is continuous for all $\beta \in \mathbb R$ and $\gamma \in \mathbb R$ if $\mathcal {F}$ in (4.9) is continuous. But this covers also the reverse step from (4.8) to (4.9). Indeed, it is sufficient to take $\widetilde{s_1}=s_1-\gamma$, $\widetilde{s_2}=s_2-\beta$, $\widetilde{\alpha _1}=\alpha _1-\beta$, $\widetilde{\alpha _2}=\alpha _2-\gamma$ and then $A^{\widetilde{s_1}+\gamma }_{p,q_1}({\mathbb R}^n,w_{\widetilde{\alpha _1}+\beta }) = A^{s_1}_{p,q_1}({\mathbb R}^n,w_{\alpha _1})$ and $A^{\widetilde{s_2}+\beta }_{p,q_1}({\mathbb R}^n,w_{\widetilde{\alpha _2}+\gamma }) = A^{s_2}_{p,q_1}({\mathbb R}^n,w_{\alpha _2})$.

Step 2. The above arguments combine supposed mapping properties for $\mathcal {F}$ with isomorphisms of type (4.3) and (4.5). But then not only continuity is inherited, but also compactness and nuclearity.

Remark 4.2

The strategy of the above proof can be illustrated by the following commutative diagram:

Here the mappings (4.8) and (4.9) can be found on the left-hand and right-hand side of the diagram, while travelling around in the diagram is based on (4.6).

Now one can extend assertions about continuity, compactness and nuclearity for the unweighted spaces $A^s_{p,q}({\mathbb R}^n)$ to their weighted counterparts.

Theorem 4.3

Let $1< p, q_1, q_2 <\infty$ and $s_1 \in \mathbb R$, $s_2 \in \mathbb R$. Let $\beta \in \mathbb R$, $\gamma \in \mathbb R$ and $A \in \{B,F \}$.

• (i) Let $d^n_p$ and $\tau ^{n+}_p, \tau ^{n-}_p$ be as in (2.28), (2.29). Then

  $$\begin{aligned} \mathcal {F}: \quad A^{s_1 +\gamma }_{p, q_1} ({\mathbb R}^n, w_\beta ) \hookrightarrow A^{s_2 +\beta }_{p, q_2} ({\mathbb R}^n, w_\gamma ) \end{aligned}$$

  (4.16)

  is compact if both $s_1 > \tau ^{n+}_p$ and $s_2 < \tau ^{n-}_p$.

• (ii) Then $\mathcal {F}$ in (4.16) is nuclear if, and only if, both

  $$\begin{aligned} s_1 > {\left\{ \begin{array}{ll} n &{}\text {for}\quad 1<p \le 2, \\ \frac{2n}{p} &{}\text {for}\quad 2\le p<\infty , \end{array}\right. } \quad and \quad s_2< {\left\{ \begin{array}{ll} -2n (1 - \frac{1}{p}) &{}\text {for}\quad 1<p \le 2, \\ -n &{} \text {for}\quad 2 \le p <\infty . \end{array}\right. } \end{aligned}$$

  (4.17)

Proof

This follows immediately from Proposition 4.1 with $\alpha _1 = \alpha _2 =0$ combined with Corollary 2.6 and Theorem 3.4.

Remark 4.4

It was one of the main aims of [25] to measure the degree of compactness of

$$\begin{aligned} \mathcal {F}: \quad B^{s_1}_{p, q_1} ({\mathbb R}^n) \hookrightarrow B^{s_2}_{p,q_2} ({\mathbb R}^n), \end{aligned}$$

(4.18)

$1<p, q_1, q_2 <\infty$ and $s_1 > \tau ^{n+}_p$, $s_2 <\tau ^{n-}_p$ in terms of entropy numbers. Proposition 4.1 and its proof show that these assertions can also be extended to the compact mappings in (4.16).

Remark 4.5

It is quite obvious that one can relax the assumptions $1<q_1, q_2 <\infty$ for the compact mappings in (4.16) by $0<q_1, q_2 \le \infty$. This applies also to related entropy numbers as mentioned in Remark 4.4.