Phase Retrieval for $L^2([-\pi ,\pi ])$ via the Provably Accurate and Noise Robust Numerical Inversion of Spectrogram Measurements

Abstract

In this paper, we focus on the approximation of smooth functions $f: [-\pi , \pi ] \rightarrow {\mathbb {C}}$, up to an unresolvable global phase ambiguity, from a finite set of Short Time Fourier Transform (STFT) magnitude (i.e., spectrogram) measurements. Two algorithms are developed for approximately inverting such measurements, each with theoretical error guarantees establishing their correctness. A detailed numerical study also demonstrates that both algorithms work well in practice and have good numerical convergence behavior.

Appendices

Appendix A: The Proofs of Lemma 2.3

Proof

Let $g{:}{=}P_{\mathcal {S}}f$ and $h{:}{=}P_{\mathcal {R}}m$, where $P_{\mathcal {S}}$ and $P_{\mathcal {R}}$ are the Fourier projection operators defined as in (11). Since g and h are trigonometric polynomials and ${\mathcal {R}} + {\mathcal {S}} \subseteq {\mathcal {D}}$, we may write

$$\begin{aligned}&\int _{-\pi }^{\pi }g(x)h(x-{{\tilde{\ell }}})\mathbbm {e}^{-\mathbbm {i}x\omega }dx \\&\quad = \sum _{m\in {\mathcal {R}}} \sum _{n\in {\mathcal {S}}} {\widehat{g}}(n) {\widehat{h}}(m) \mathbbm {e}^{-\mathbbm {i}m{{\tilde{\ell }}}}\int _{-\pi }^{\pi } \mathbbm {e}^{\mathbbm {i}(m+n-\omega )x}dx\\&\quad =\sum _{m\in {\mathcal {R}}} \sum _{n\in {\mathcal {S}}} {\widehat{g}}(n) {\widehat{h}}(m) \mathbbm {e}^{-\mathbbm {i}m{{\tilde{\ell }}}} \frac{2\pi }{d}\sum _{p\in {\mathcal {D}}} \mathbbm {e}^{2\pi \mathbbm {i} p(n+m-\omega )/d}\\&\quad = \frac{2\pi }{d}\sum _{p\in {\mathcal {D}}}\left( \sum _{n\in {\mathcal {S}}} {\widehat{g}}(n) \mathbbm {e}^{2\pi \mathbbm {i} pn/d}\right) \left( \sum _{m\in {\mathcal {R}}}{\widehat{h}}(m) \mathbbm {e}^{\left( \left( \frac{2\pi \mathbbm {i}m}{d}\right) \left( p-\ell \right) \right) }\right) \mathbbm {e}^{-2\pi \mathbbm {i} m p\omega /d}\\&\quad = \frac{2\pi }{d}\sum _{p\in {\mathcal {D}}} g\left( \frac{2\pi p}{d}\right) h\left( \frac{2\pi (p-\ell )}{d}\right) \mathbbm {e}^{-2\pi \mathbbm {i} p\omega /d} \\&\quad =\frac{2\pi }{d}\sum _{p\in {\mathcal {D}}} x_p y_{p-\ell } \mathbbm {e}^{-2\pi \mathbbm {i} \omega p/d}. \end{aligned}$$

$\square$

Appendix B: The Proofs of Propositions 3.2 and 3.4

The Proof of Proposition 3.2

We first note that

$$\begin{aligned}{\widehat{z}}_q={\left\{ \begin{array}{ll}{\widehat{m}}(q)&{}\text {if } \vert q\vert \le \rho /2,\\ 0 &{}\text {if } \vert q\vert > \rho /2. \end{array}\right. } \end{aligned}$$

Therefore, for all $\vert p\vert \le \kappa -1$, we have

$$\begin{aligned} \left( \widehat{{\textbf{z}}}\circ S_{p}\overline{\widehat{{\textbf{z}}}^{}}\right) _{q}={\left\{ \begin{array}{ll} {\widehat{m}}(q){\widehat{m}}(p+q) &{} \text {if }-\rho /2\le q,\,p+q \le \rho /2,\\ 0 &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

For any $\vert p\vert \le \kappa -1,$ let

$$\begin{aligned} {\mathcal {I}}_{p}{:}{=}\{q\in {\mathcal {D}}:-\rho /2\le q\le \rho /2\quad \text {and } -\rho /2\le q+p\le \rho /2\}. \end{aligned}$$

One may check that

$$\begin{aligned} {\mathcal {I}}_{p} = {\left\{ \begin{array}{ll} {[}-\frac{\rho }{2}-p, \frac{\rho }{2}]\cap {\mathbb {Z}}&{}\text {if }p<0\\ {[}-\frac{\rho }{2}, \frac{\rho }{2}-p]\cap {\mathbb {Z}} &{}\text {if }p\ge 0 \end{array}\right. }. \end{aligned}$$

Therefore, making a simple change of variables in the case $p<0,$ we have that

$$\begin{aligned} \mathbf {F_{d}}\left( \widehat{{\textbf{z}}}\circ S_{p}\overline{\widehat{{\textbf{z}}}^{}}\right) _{q}&=\frac{1}{d}\sum _{\ell \in {\mathcal {I}}_{p}}{\widehat{m}}(\ell ){\widehat{m}}(p+\ell )\mathbbm {e}^{-2\pi \mathbbm {i}q\ell /d}=\frac{1}{d}\sum _{\ell =-\rho /2}^{\rho /2-\vert p\vert }{\widehat{m}}(\ell ){\widehat{m}}\left( \ell +\vert p\vert \right) \mathbbm {e}^{\mathbbm {i}\phi _{p,q,\ell }}, \end{aligned}$$

where $\mathbbm {e}^{\mathbbm {i}\phi _{p,q,\ell }}$ is a unimodular complex number depending on p, q and $\ell .$ Using the Assumptions (23) and (24), we see that

$$\begin{aligned} \bigg \vert \frac{1}{d}\sum _{\ell =-\rho /2+1}^{\rho /2-\vert p\vert }{\widehat{m}}(\ell ){\widehat{m}}(\ell +\vert p\vert )\mathbbm {e}^{\mathbbm {i}\phi _{p,q,\ell }}\bigg \vert&\le \frac{\rho }{d} \left| {\widehat{m}}\left( \frac{-\rho }{2}+1\right) \right| \left| {\widehat{m}}\left( \frac{-\rho }{2}+1+\vert p\vert \right) \right| \\&\le \frac{1}{2d} \left| {\widehat{m}}\left( \frac{-\rho }{2}\right) \right| \left| {\widehat{m}}\left( \frac{-\rho }{2}+\vert p\vert \right) \right| . \end{aligned}$$

With this, we may use the reverse triangle inequality to see

$$\begin{aligned} \bigg \vert \mathbf {F_{d}}\left( \widehat{{\textbf{z}}}\circ S_{p}\overline{\widehat{{\textbf{z}}}^{}}\right) _{q}\bigg \vert&=\bigg \vert \frac{1}{d}\sum _{\ell =-\rho /2}^{\rho /2-\vert p\vert }{\widehat{m}}(\ell ){\widehat{m}}(\ell +\vert p\vert )\mathbbm {e}^{\mathbbm {i}\phi _{p,q,\ell }}\bigg \vert \\&\ge \frac{1}{d} \bigg \vert {\widehat{m}}\left( \frac{-\rho }{2}\right) \bigg \vert \left| {\widehat{m}}\left( \frac{-\rho }{2}+\vert p\vert \right) \right| \\&\quad - \frac{1}{d}\bigg \vert \! \sum _{\ell =-\rho /2+1}^{\rho /2-\vert p\vert }\! \! \! \! \! {\widehat{m}}(\ell ){\widehat{m}}(\ell +\vert p\vert )\mathbbm {e}^{\mathbbm {i}\phi _{p,q,\ell }}\bigg \vert \\&\ge \frac{1}{2d} \left| {\widehat{m}}\left( \frac{-\rho }{2}\right) \right| \left| {\widehat{m}}\left( \frac{-\rho }{2}+\vert p\vert \right) \right| \\&\ge \frac{1}{2d} \left| {\widehat{m}}\left( \frac{-\rho }{2}\right) \right| \left| {\widehat{m}}\left( \frac{-\rho }{2}+\kappa -1\vert \right) \right| . \end{aligned}$$

$\square$

The Proof of Proposition 3.4

First, we note that by applying Lemma 3.3, and setting $p=\omega , q=\ell$, we have

$$\begin{aligned} \mu _2&= \inf _{\omega \in [2\kappa -1]_c,\ell \in [2s-1]_c} \vert (\mathbf {F_d}(\widehat{{\textbf{z}}}\circ S_{\ell }\overline{\widehat{{\textbf{z}}}^{}}))_\omega \vert \\ {}&=\frac{1}{d}\inf _{\omega \in [2\kappa -1]_c,\ell \in [2s-1]_c} \vert (\mathbf {F_d}({\textbf{z}}\circ S_{\omega }\overline{{\textbf{z}}}))_\ell \vert \\ {}&=\frac{1}{d}\inf _{p\in [2\kappa -1]_c,q\in [2s-1]_c} \vert (\mathbf {F_d}({\textbf{z}}\circ S_{p}\overline{{\textbf{z}}}))_q\vert . \end{aligned}$$

For $\vert p\vert \le \kappa -1$, we have

$$\begin{aligned} \left( {\textbf{z}}\circ S_{p}\overline{{\textbf{z}}}\right) _{q}={\left\{ \begin{array}{ll} z_q\overline{z_{p+q}} &{} \text {if }n\le q,p+q \le n+{{\tilde{\delta }}}-1,\\ 0 &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

For any $\vert p\vert \le \kappa -1,$ let

$$\begin{aligned} {\mathcal {I}}_{p}{:}{=}\{q\in {\mathcal {D}}:n\le q\le n+{{\tilde{\delta }}}-1\quad \text {and}\quad n\le q+p\le n+{\tilde{\delta }}-1\}. \end{aligned}$$

One may check that

$$\begin{aligned} {\mathcal {I}}_{p} = {\left\{ \begin{array}{ll} {[}n-p, n+{{\tilde{\delta }}}-1]\cap {\mathbb {Z}}&{}\text {if }p<0,\\ {[}n, n+{{\tilde{\delta }}}-1-p]\cap {\mathbb {Z}}&{}\text {if }p\ge 0. \end{array}\right. } \end{aligned}$$

Therefore, making a simple change of variables in the case $p<0,$ we have that in either case

$$\begin{aligned}\left| \mathbf {F_{d}}\left( {\textbf{z}}\circ S_{p}\overline{{\textbf{z}}}\right) _{q}\right|&=\frac{1}{d}\bigg \vert \sum _{\ell \in {\mathcal {I}}_{p}}z_\ell \overline{z_{p+\ell }}\mathbbm {e}^{-2\pi \mathbbm {i}\ell q/d}\bigg \vert =\frac{1}{d}\bigg \vert \sum _{\ell =n}^{n+{{\tilde{\delta }}}-1-\vert p\vert }z_{\ell }\overline{z_{\ell +\vert p\vert }}\mathbbm {e}^{\mathbbm {i}\phi _{p,q,\ell }}\bigg \vert , \end{aligned}$$

where $\mathbbm {e}^{\mathbbm {i}\phi _{p,q,\ell }}$ is a unimodular complex number depending on p, q and $\ell .$ Using the Assumptions (37) and (38) we see that

$$\begin{aligned} \bigg \vert \frac{1}{d}\sum _{\ell =n+1}^{n+{{\tilde{\delta }}}-1-\vert p\vert }z_\ell \overline{z_{\ell +\vert p\vert }}\mathbbm {e}^{\mathbbm {i}\phi _{p,q,\ell }}\bigg \vert \le \frac{{\tilde{\delta }} }{d} \left| z_{n+1}\right| \left| z_{n+1+\vert p\vert }\right| \le \frac{1}{2d} \vert z_n\vert \vert z_{n+\vert p\vert }\vert . \end{aligned}$$

With this,

$$\begin{aligned} \left| F_{d}\left( {\textbf{z}}\circ S_{p}\overline{{\textbf{z}}}\right) _{q}\right|&=\bigg \vert \frac{1}{d}\sum _{\ell =n}^{n+{{\tilde{\delta }}}-1-\vert p\vert }z_{\ell }\overline{z_{\ell +\vert p\vert }}\mathbbm {e}^{\mathbbm {i}\phi _{p,q,\ell }}\bigg \vert \\&\ge \frac{1}{d} \vert z_n\vert \vert z_{n+\vert p\vert }\vert - \bigg \vert \frac{1}{d}\sum _{\ell =n+1}^{n+{{\tilde{\delta }}}-1-\vert p\vert }z_\ell \overline{z_{\ell +\vert p\vert }}\mathbbm {e}^{\mathbbm {i}\phi _{p,q,\ell }}\bigg \vert \\&\ge \frac{1}{2d}\vert z_n\vert \vert z_{n+\vert p\vert }\vert \ge \frac{1}{2d}\vert z_n\vert \vert z_{n+\kappa -1}\vert . \end{aligned}$$

Thus, the proof is complete. $\square$

Appendix C: The Proof of Lemma 4.5

Proof

Our proof requires the following sublemma which shows that, if $n\in L_f$, then Algorithm 3 used in the definition of $\alpha _n$ will only select indices $n_\ell$ corresponding to large Fourier coefficients.

Lemma C.1

Let $n\in L_f$, and let $n_0,\ldots , n_\zeta$ be the sequence of indices as introduced in the definition of $\alpha _n$. Then

$$\begin{aligned} \vert {\widehat{f}}(n_\ell )\vert \ge \frac{\vert {\widehat{f}}(n)\vert }{2} \end{aligned}$$

for all $0\le \ell \le \zeta$.

Proof

When $\ell =\zeta$, the claim is immediate from the fact that $n_\zeta =n$. For all $0\le \ell \le \zeta -1$, the definition of $n_\ell$ implies that there exists an interval $I_\ell$, centered at some point a with $\vert a\vert \le \vert n\vert$, such that the length of $I_\ell$ is at most $\beta$ and

$$\begin{aligned} a_{n_\ell }=\max _{m\in I_\ell } a_m. \end{aligned}$$

Letting $\epsilon =\sqrt{3\Vert {\textbf{N}}\Vert _\infty }$, we see that by (45) and Remark 1.5

$$\begin{aligned} \vert {\widehat{f}}(n_\ell )\vert&\ge a_{n_\ell }-\epsilon =\max _{m\in I_\ell } a_m-\epsilon \ge \max _{m\in I_\ell } \vert {\widehat{f}}(m)\vert -2\epsilon \ge \vert {\widehat{f}}(n)\vert -2\epsilon . \end{aligned}$$

The result now follows from noting that $\epsilon <\frac{\vert {\widehat{f}}(n)\vert }{4}$ for all $n\in L_f$. $\square$

With Lemma C.1 established, we may now prove Lemma 4.5. Let $n\in L_f$ and let $n_0,\ldots n_\zeta$ be the sequence describe in the definition of $\alpha _n$. For $0\le \ell \le \zeta -1$, let $t_{\ell } {:}{=}{\widehat{f}}(n_{\ell +1})\overline{{\widehat{f}}(n_{\ell })^{}}$, $a'_{\ell } {:}{=}{\widehat{f}}(n_{\ell +1})\overline{{\widehat{f}^{}}(n_{\ell })}+N_{n_{\ell +1},n_{\ell }}$, and $N'_{\ell }{:}{=}N_{n_{\ell +1},n_{\ell }}$. Consider the triangle with sides $a'_{\ell }$, $t_{\ell }$, and $N'_{\ell }$ with angles $\theta _{\ell } =\vert \arg (a'_{\ell })-\arg (t_{\ell })\vert$ and $\phi _{\ell } = \vert \arg (a'_{\ell })-\arg (N'_{\ell })\vert$, as illustrated in Fig. 6.

Fig. 6

Triangle in the complex domain

By the law of sines and Lemma C.1, we get that

$$\begin{aligned} \vert \sin (\theta _{\ell })\vert = \left| \frac{N_{\ell }'}{t_{\ell }}\sin (\phi _{\ell })\right| \le \frac{\Vert {\textbf{N}}\Vert _\infty }{\vert {\widehat{f}}(n_{\ell })\vert \vert {\widehat{f}}(n_{\ell +1})\vert }\le \frac{4\Vert {\textbf{N}}\Vert _\infty }{\vert {\widehat{f}}(n)\vert ^2} \end{aligned}$$

(C1)

for all $0\le \ell \le \zeta$. By the definition of $L_f$ and Lemma C.1, we have that for all $\ell$

$$\begin{aligned} \vert N'_\ell \vert \le \Vert {\textbf{N}}\Vert _\infty \le \frac{\vert \widehat{f(n)}\vert ^2}{4}\le \vert {\widehat{f}}(n_\ell )\vert \vert {\widehat{f}}(n_{\ell +1})\vert =\vert t_\ell \vert . \end{aligned}$$

Therefore, $0\le \theta _\ell \le \frac{\pi }{2}$, and so by (C1), we have

$$\begin{aligned} \vert \theta _{\ell }\vert \le \frac{\pi }{2}\,\vert \sin (\theta _{\ell })\vert \le 2\pi \,\frac{\Vert {\textbf{N}}\Vert _\infty }{\vert {\widehat{f}}(n)\vert ^2}. \end{aligned}$$

By definition $\tau _{n}=\sum _{\ell =0}^{\zeta -1} \arg (t_{\ell })$ and $\alpha _{n}=\sum _{l=0}^{\zeta -1} \arg (a'_{\ell })$. Therefore, we have

$$\begin{aligned} \vert \mathbbm {e}^{\mathbbm {i}\tau _{n}}-\mathbbm {e}^{\mathbbm {i}\alpha _{n}}\vert \le \vert \alpha _{n}-\tau _{n}\vert&=\bigg \vert \sum _{\ell =0}^{\zeta -1} \arg (a'_{\ell })-\arg (t_{\ell }) \bigg \vert =\bigg \vert \sum _{\ell =0}^{\zeta -1} \theta _{\ell }\bigg \vert \le 2\pi b\frac{\Vert {\textbf{N}}\Vert _\infty }{\vert {\widehat{f}}(n)\vert ^2}. \end{aligned}$$

From the definition of $n_\ell$, we have

$$\begin{aligned} \vert n_\ell -n_{\ell -1}\vert \ge \gamma -\beta \ge \frac{\gamma }{2} \end{aligned}$$

for all $1\le \ell \le \zeta -1$. Therefore, the path length $\zeta$ is bounded by

$$\begin{aligned} \zeta \le \frac{\vert n-n_0\vert }{\min \vert n_\ell -n_{\ell -1}\vert }\le \frac{2d}{\gamma }. \end{aligned}$$

Thus, we have

$$\begin{aligned} \vert \mathbbm {e}^{\mathbbm {i}\tau _{n}}-\mathbbm {e}^{\mathbbm {i}\alpha _{n}}\vert \le 2\pi b\frac{\Vert {\textbf{N}}\Vert _\infty }{\vert {\widehat{f}}(n)\vert ^2} \le \frac{4\pi d}{\gamma }\frac{\Vert {\textbf{N}}\Vert _\infty }{\vert {\widehat{f}}(n)\vert ^2} \end{aligned}$$

as desired. $\square$

Appendix D: Additional Experiments

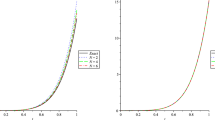
In this section, we provide additional numerical simulations studying the empirical convergence behavior of Algorithms 1 and 2. We start with a study of the convergence behavior of Algorithm 1. Here, we reconstruct the same test function using different discretization sizes d (with $\rho$ chosen to be $\min \{ (d-5)/2, 16\lfloor \log _2(d)\rfloor \}$ and $\kappa =\rho -1$), where the total number of phaseless measurements used is $Ld=(2\rho -1)d$. Figure 7 plots representative reconstructions (of the real part of the test function) for two choices of d ($d=33$ and $d=1025$). We note that the (smooth) test function illustrated in the figure has several sharp and closely separated gradients, making the reconstruction process challenging. This is evident in the partial Fourier sums ($P_Nf$) plotted for reference alongside the reconstructions from Algorithm 1 ($f_e$). For small d and $\rho$, we observe oscillatory behavior similar to that seen in the Gibbs phenomenon. Nevertheless, we see that the proposed algorithm closely tracks the performance of the partial Fourier sum, with reconstruction quality improving significantly as d (and $\rho$) increases.

Fig. 7

Evaluating the convergence behavior of Algorithm 1. Figure plots reconstructions of the real part of the test function at $d=33$ and $d=1025$ (along with an expanded view of the reconstruction in [0, 1]) on a discrete equispaced grid in $[-\pi , \pi ]$ of 7003 points; we set $\rho =\min \{ (d-5)/2, 16\lfloor \log _2(d)\rfloor \}$ and $\kappa =\rho -1$

Fig. 8

Evaluating the convergence behavior of Algorithm 2. Figure plots reconstructions of the real part of the test function at $d=57$ and $d=921$ (along with an expanded view of the reconstruction in [0, 1]) on a discrete equispaced grid in $[-\pi , \pi ]$ of 7003 points; we set $K=d/3,\delta =(K+1)/2$ and $\kappa =\delta -1$

We next evaluate the convergence behavior of Algorithm⁷ 2 by reconstructing the same test function using different discretization sizes d (with $K=d/3$, $\delta =(K+1)/2$, $\kappa =\delta -1$ and $s=\kappa -1$). Figure 8 plots representative reconstructions (of the real part of the test function) for two choices of d ($d=57$ and $d=921$). As in Fig. 7, we note that the (smooth) test function has several sharp and closely separated gradients, making the reconstruction process challenging. Again, the partial Fourier sums ($P_Nf$) plotted alongside the reconstructions from Algorithm 2 ($f_e$) exhibit Gibbs-like oscillatory behavior for small d and $\kappa$. Nevertheless, we see that the proposed algorithm closely tracks the performance of the partial Fourier sum, with reconstruction quality improving significantly as d (and $\delta ,\kappa$) increases.

Appendix E: Results from Previous Work

The following is a restatement of Theorem 4 of [26] updated to use the notation of this paper. Notably, in this paper we use a different normalization of the Fourier transform (our $\mathbf {F_d}$ is equal to the $F_d$ from [26] divided by d). We also note that the measurements ${\textbf{T}}'$ considered here differ by a factor of $\frac{4\pi }{d^2}$ from the measurements Y considered in [26]. Lastly, we note that the summations in [26] take place over a different string of d consecutive integers. However, this makes no difference do the the periodicity of the complex exponential function.

Theorem E.1

[26, Theorem 4] Let $\tilde{{\textbf{T}}}$ be as in (16). Then for any $\omega \in \left[ K\right] _{c}$ and $\ell \in \left[ L\right] _{c}$,

$$\begin{aligned}&\frac{{\widetilde{T}}_{\ell ,\omega }-{\widetilde{N}}_{\ell ,\omega }}{4\pi ^2}\\&\quad =d\sum _{p\in \left[ \frac{d}{K}\right] _c}\sum _{q\in \left[ \frac{d}{L}\right] _c}\left( {\textbf{F}}_{\textbf{d}}\left( \widehat{\textbf{x}}\circ S_{q L-\ell }\overline{{{\widehat{x}}}^{}}\right) \right) _{\omega -pK}\left( {\textbf{F}}_{\textbf{d}}\left( {{\widehat{m}}}\circ S_{\ell -q L}\overline{{{\widehat{m}}}}\right) \right) _{\omega -pK}\\&\quad =\frac{1}{d}\sum _{p\in \left[ \frac{d}{K}\right] _c}\sum _{q\in \left[ \frac{d}{L}\right] _c}\mathbbm {e}^{-2\pi \mathbbm {i}(q L-\ell )(\omega -pK)/d}\left( {\textbf{F}}_{\textbf{d}}\left( \widehat{\textbf{x}}\circ S_{q L-\ell }\overline{{{\widehat{x}}}^{}}\right) \right) _{\omega -pK}\left( {\textbf{F}}_{\textbf{d}}\left( \textbf{m}\circ S_{\omega -pK}\overline{\textbf{m}}\right) \right) _{q L-\ell }\\&\quad =\frac{1}{d}\sum _{p\in \left[ \frac{d}{K}\right] _c}\sum _{q\in \left[ \frac{d}{L}\right] _c}\mathbbm {e}^{2\pi \mathbbm {i}(q L-\ell )(\omega -pK)/d}\left( {\textbf{F}}_{\textbf{d}}\left( \textbf{x}\circ S_{\omega -pK}\overline{\textbf{x}}\right) \right) _{\ell -q L}\left( {\textbf{F}}_{\textbf{d}}\left( {{\widehat{m}}}\circ S_{\ell -q L}\overline{{{\widehat{m}}}^{}}\right) \right) _{\omega -pK}\\&\quad =\frac{1}{d}\sum _{p\in \left[ \frac{d}{K}\right] _c}\sum _{q\in \left[ \frac{d}{L}\right] _c}\left( {\textbf{F}}_{\textbf{d}}\left( \textbf{x}\circ S_{\omega -pK}\overline{\textbf{x}}\right) \right) _{\ell -q L}\left( {\textbf{F}}_{\textbf{d}}\left( \textbf{m}\circ S_{\omega -pK}\overline{\textbf{m}}\right) \right) _{q L-\ell }. \end{aligned}$$