Abstract
We prove resolvent estimates in \(L^p\)-spaces for time-harmonic Maxwell’s equations in two spatial dimensions and in three dimensions in the partially anisotropic case. In the two-dimensional case the estimates are sharp up to endpoints. We consider anisotropic permittivity and permeability, which are both taken to be time-independent and spatially homogeneous. For the proof we diagonalize time-harmonic Maxwell’s equations to equations involving Half-Laplacians. We apply these estimates to infer a Limiting Absorption Principle in intersections of \(L^p\)-spaces and to localize eigenvalues for perturbations by potentials.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and Main Results
Maxwell’s equations describe electromagnetic waves and consequently the propagation of light. We refer to the physics’ literature for further query (cf. [9, 20]). Time-dependent Maxwell’s equations in media in three spatial dimensions relate electric and magnetic field \(({\mathcal {E}},{\mathcal {B}}):{\mathbb {R}}\times {\mathbb {R}}^3 \rightarrow {\mathbb {C}}^3 \times {\mathbb {C}}^3\) with displacement and magnetizing fields \(({\mathcal {D}},{\mathcal {H}}):{\mathbb {R}}\times {\mathbb {R}}^3 \rightarrow {\mathbb {C}}^3 \times {\mathbb {C}}^3\), the electric and magnetic current \(({\mathcal {J}}_e,{\mathcal {J}}_m): {\mathbb {R}}\times {\mathbb {R}}^3 \rightarrow {\mathbb {C}}^3 \times {\mathbb {C}}^3 \), and electric and magnetic charges \((\rho _e,\rho _m): {\mathbb {R}}\times {\mathbb {R}}^3 \rightarrow {\mathbb {C}}\times {\mathbb {C}}\):
In physical contexts, fields, currents and charges are real-valued, and the magnetic charge and current vanish. We consider possibly non-vanishing magnetic charge and current to highlight symmetry between the electric and magnetic field. Moreover, \({\mathcal {J}}_e\) and \({\mathcal {J}}_m\) are typically taken with opposite signs.
In the following we consider the time-harmonic, monochromatic ansatz
with \(\omega \in {\mathbb {R}}\). We supplement (1) with the material laws
where \(\varepsilon = \text {diag}(\varepsilon _1,\varepsilon _2,\varepsilon _3) \in {\mathbb {R}}^{3 \times 3}, \; \varepsilon _i, \; \mu \in {\mathbb {R}}_{> 0}\). Requiring \(\varepsilon \) and \(\mu \) to be symmetric and positive definite is a physically natural assumption. The fully anisotropic case
is analyzed in joint work with Mandel [22], where we argue in detail how the analysis reduces in the general case to scalar \(\mu \) (see also [21, p. 63]). Material laws with scalar \(\mu \) are frequently used in optics (cf. [23, Section 2]). Then (1) becomes under (2) and (3) to relate E with D and H with B:
(2) can be explained by considering (1) under Fourier transforms in time: Letting
we find a solution to (1) provided that \(D(\omega ,\cdot )\),... solve (4). We focus on solenoidal currents, but shall also consider the effect of non-vanishing divergence. We deduce from the continuity equation for electric charges \(\partial _t \rho _e(t,x) - \nabla \cdot {\mathcal {J}}_e(t,x) = 0\) the following relation between \(J_e(\omega ,\cdot )\) and the time-dependent charges:
Since \(\omega \) will be fixed in the following analysis of the time-harmonic equation, we let
We consider Maxwell’s equations in two spatial dimensions and the partially anisotropic case in three dimensions. The time-dependent form of Maxwell’s equations in two dimensions corresponds to electric and magnetic fields and currents of the form
where \({\mathcal {D}},{\mathcal {E}},{\mathcal {J}}_e:{\mathbb {R}}\times {\mathbb {R}}^2 \rightarrow {\mathbb {C}}^2\), \({\mathcal {B}},{\mathcal {H}},{\mathcal {J}}_m: {\mathbb {R}}\times {\mathbb {R}}^2 \rightarrow {\mathbb {C}}\), \(\nabla _\perp = (\partial _2,-\partial _1)^t\), and we assume (3) with \(\mu > 0\), and \((\varepsilon ^{ij})_{i,j} \in {\mathbb {R}}^{2 \times 2}\) denoting a symmetric, positive definite matrix. We can rewrite (6) under (2) and (3) as
denoting with \(\varepsilon _{ij}\) the components of the inverse of \(\varepsilon \). In two dimensions, we let
In the following let \(d \in \{2,3\}\), \(m(2) = 3\), \(m(3) = 6\), and
In this paper we are concerned with the resolvent estimates
However, as will be clear from perceiving \(P(\omega ,D)\) as a Fourier multiplier, \(P(\omega ,D)^{-1}\) cannot even be understood in the distributional sense for \(\omega \in {\mathbb {R}}\). The remedy will be to consider \(\omega \in {\mathbb {C}}\backslash {\mathbb {R}}\) and prove estimates independent of the distance to the real axis. Then we can consider limits \(\Im (\omega ) \downarrow 0\) and \(\Im (\omega ) \uparrow 0\). This is presently referred to as Limiting Absorption Principle (LAP) in the \(L^p\)-\(L^q\)-topology. Moreover, the analysis yields explicit formulae for the resulting limits. It appears that this is the first contribution to resolvent estimates for the Maxwell operator in anisotropic media in the \(L^p\)-\(L^q\)-topology.
Recently, Cossetti–Mandel analyzed the isotropicFootnote 1, possibly spatially inhomogeneous case \(\varepsilon , \mu \in W^{1,\infty }({\mathbb {R}}^3; {\mathbb {R}}_{>0})\) in [5]. In the isotropic case, iterating (1) and using the divergence conditions yields Helmholtz-like equations for D and H. This approach was carried out in [5]. In the anisotropic case this strategy becomes less straight-forward. Instead we choose to diagonalize the Fourier multiplier to get into the position to use resolvent estimates for the fractional Laplacian. Kwon–Lee–Seo [19] previously used a diagonalization to prove resolvent estimates for the Lamé operator. However, there are degenerate components in the diagonalization of time-harmonic Maxwell’s operators, which do not occur for the Lamé operator. We use the divergence condition to ameliorate the contribution of the degeneracies. In case the currents have non-vanishing divergence, we can quantify this contribution with the charges.
We digress for a moment to elaborate on \(L^p\)-\(L^q\)-estimates for the fractional Laplacian and applications. Let \(s \in (0,d)\). For \(\omega \in {\mathbb {C}}\backslash [0,\infty )\) we consider the resolvents as Fourier multiplier:
for \(f: {\mathbb {R}}^d \rightarrow {\mathbb {C}}\) in some suitable a priori class, e.g., \(f \in {\mathcal {S}}({\mathbb {R}}^d)\). In the present context, resolvent estimates for the Half-Laplacian \(\Vert ((-\Delta )^{\frac{1}{2}}-\omega )^{-1} \Vert _{p \rightarrow q}\) are most important. There is a huge body of literature on resolvent estimates for the Laplacian \((-\Delta - \omega )^{-1}:L^p({\mathbb {R}}^d) \rightarrow L^q({\mathbb {R}}^d)\). This is due to versatile applications to uniform Sobolev estimates and unique continuation (cf. [17]), the localization of eigenvalues for Schrödinger operators with complex potential (cf. [6, 10, 11]), or LAPs in \(L^p\)-spaces (cf. [14]). Kenig–Ruiz–Sogge [17] showed that uniform resolvent estimates in \(\omega \in {\mathbb {C}}\backslash [0,\infty )\) for \(d \ge 3\) hold if and only if
By homogeneity and scaling, we find
Thus, it suffices to consider \(|\omega | = 1\) to discuss boundedness. Kwon–Lee [18] showed the currently widest range of resolvent estimates for the fractional Laplacian outside the uniform boundedness range (see [15] for a previous contribution). To state the range of admissible \(L^p\)-\(L^q\)-estimates, we shall use notations from [18]. Let \(I^2 = \{(x,y) \in {\mathbb {R}}^2 \, | \, 0 \le x,y \le 1 \}\), and let \((x,y)^\prime = (1-x,1-y)\) for \((x,y) \in I^2\). For \({\mathcal {R}} \subseteq I^2\) we set \({\mathcal {R}}^\prime = \{ (x,y)^\prime \, | \, (x,y) \in {\mathcal {R}} \}\).
The resolvent of the fractional Laplacian \(((-\Delta )^{\frac{s}{2}} - z)^{-1}\) is bounded for fixed \(z \in {\mathbb {C}}\backslash [0,\infty )\) if and only if \((1/p,1/q) \in {\mathcal {R}}_0^{\frac{s}{2}}\) with
see, e.g., [18, Proposition 6.1]. Gutiérrez showed in [14] that uniform estimates for \(\omega \in \{ z \in {\mathbb {C}}\, : \, |z| = 1, \, z \ne 1 \}\) hold if and only if (1/p, 1/q) lies in the set
Failure outside this range was known before (cf. [4, 17]) due to the connection to Bochner-Riesz operators with negative index. Clearly, there are more estimates available outside \({\mathcal {R}}_1\) if one allows for dependence on \(\omega \), e.g.,
Kwon–Lee [18] analyzed estimates outside the uniform boundedness range in detail and covered a wide range. Estimates with dependence on \(\omega \) can be used to localize eigenvalues for Schrödinger operators with complex potentials (cf. [6]), which is done for Maxwell operators in Sect. 4.
Diagonalizing the symbol of (4) to operators involving the Half-Laplacian works in the partially anisotropic case, i.e.,
This includes the isotropic case \(\varepsilon _1 = \varepsilon _2 = \varepsilon _3\), for which the results of Cossetti–Mandel [5] are recovered for constant coefficients, albeit via a different approach. It turns out that in the fully anisotropic case
diagonalizing the multiplier introduces singularities, and this case has to be treated differently (cf. [22]). The estimates proved in [22] for the fully anisotropic case are strictly weaker than in the partially anisotropic case. We connect resolvent bounds for the Maxwell operator with resolvent estimates for the Half-Laplacian:
Theorem 1.1
Let \(1< p,q < \infty \), \(d \in \{2,3\}\), and \(\omega \in {\mathbb {C}} \backslash {\mathbb {R}}\). Let \(\varepsilon \in {\mathbb {R}}^{d\times d}\) denote a symmetric positive definite matrix, and let \(P(\omega ,D)\) as in (7) for \(d=2\), and as in (4) for \(d=3\). For \(d=3\), we assume that \(\varepsilon =\text {diag}(\varepsilon _1,\varepsilon _2,\varepsilon _3)\) and satisfies (14).
Then, \(P(\omega ,D)^{-1}:L^p_0({\mathbb {R}}^d) \rightarrow L^q_0({\mathbb {R}}^d)\) is bounded if and only if \((1/p,1/q) \in {\mathcal {R}}_0^{\frac{1}{2}}(d)\), and we find the estimate
to hold.
If \(1 \le p \le \infty \) and \(1< q < \infty \), then we find the estimate
to hold with \(\rho _e\) and \(\rho _m\) defined as in (8) for \(d=2\) and (5) for \(d=3\). If \(\rho _e = \rho _m = 0\), \(1<p<\infty \), and \(q \in \{1,\infty \}\), then (16) also holds.
We cannot allow for \(p\in \{1, \infty \}\) or \(q \in \{1,\infty \}\) in the proof of
as multiplier bounds for Riesz transforms are involved. It is well-known that the Riesz transforms are bounded on \(L^p({\mathbb {R}}^d)\), \(1<p<\infty \), but neither on \(L^1\) nor on \(L^\infty \). In the proof of (16) for \(\rho _e = \rho _m = 0\), which covers the reverse estimate of the above display, we can overcome this possibly technical issue by arranging the Riesz transforms acting on a reflexive \(L^p\)-space. Hence, we can allow for either \(p \in \{1,\infty \}\) or \(q \in \{ 1, \infty \}\). For the sake of simplicity, in Corollary 1.2 we only consider \(1<p,q<\infty \) although (16) partially extends to \(p \in \{1, \infty \}\) or \(q \in \{1, \infty \}\).
Coming back to resolvent estimates for the Half-Laplacian, for \(d \in \{2,3\}\) and \((1/p,1/q) \in I^2\), define
Set
Kwon–Lee [18, Conjecture 3, p. 1462] conjectured for \((1/p,1/q) \in {\mathcal {R}}_0^{1/2}(d)\)
They verified the conjecture for \(d=2\) and for \(d = 3\) in the restricted range in \(\tilde{{\mathcal {R}}}_0^{1/2}(3)\) [18, Theorem 6.2, p. 1462]. We refer to [18] for the precise description. For notational convenience, let \(\tilde{{\mathcal {R}}}_0^{1/2}(2) = {\mathcal {R}}_0^{1/2}(2)\). By invoking the results from [18], we find the following:
Corollary 1.2
Let \(1< p,q < \infty \), \(d \in \{2,3\}\), and \(\omega \in {\mathbb {C}} \backslash {\mathbb {R}}\). Let \(\varepsilon \in {\mathbb {R}}^{d\times d}\) and \(P(\omega ,D)\) be as in Theorem 1.1. Then we find the following:
-
1.
If \(d=2\), then
$$\begin{aligned} \Vert P(\omega ,D)^{-1} \Vert _{L_0^p({\mathbb {R}}^d) \rightarrow L^q_0({\mathbb {R}}^d)} \sim \kappa _{p,q}(\omega ) \end{aligned}$$(18)is true for \((1/p,1/q) \in {\mathcal {R}}_0^{\frac{1}{2}}(2)\).
-
2.
If \(d=3\) with \(\varepsilon \) satisfying (14), then (18) is true for \((1/p,1/q) \in \tilde{{\mathcal {R}}}_0^{\frac{1}{2}}(3)\).
Turning to LAPs, we work with the following notions:
Definition 1.3
Let \(d \in \{2,3\}\), \(1 \le p,q \le \infty \), \(\omega \in {\mathbb {R}}\backslash 0\), and \(0< \delta < 1/2\). We say that a global \(L^p_0\)-\(L^q_0\)-LAP holds if \(P(\omega \pm i \delta ,D)^{-1}: L^p_0({\mathbb {R}}^d) \rightarrow L^q_0({\mathbb {R}}^d)\) are bounded uniformly in \(\delta > 0\), and there are operators \(P_{\pm }(\omega ) : L_0^p({\mathbb {R}}^d) \rightarrow L_0^q({\mathbb {R}}^d)\) such that
We say that a local \(L^p_0\)-\(L^q_0\)-LAP holds if for any \(\beta \in C^\infty _c({\mathbb {R}}^d )\), \(P(\omega \pm i \delta ,D)^{-1} \beta (D): L^p_0({\mathbb {R}}^d) \rightarrow L^q_0({\mathbb {R}}^d)\) are bounded uniformly in \(\delta > 0\), and there are operators \(P^{loc}_{\pm }(\omega ): L_0^p({\mathbb {R}}^d) \rightarrow L_0^q({\mathbb {R}}^d)\) such that
Remark 1.4
By the explicit formulae for \(P(\omega ,D)^{-1}\) for \(\omega \in {\mathbb {C}}\backslash {\mathbb {R}}\) we can also handle currents with non-vanishing divergence as in Theorem 1.1. We omitted this discussion for the sake of brevity.
We observe that \(\gamma _{p,q} > 0\) for p and q as in Corollary 1.2:
Corollary 1.5
Let \(d \in \{2,3\}\). For \(1<p,q<\infty \), \((1/p,1/q) \in \tilde{{\mathcal {R}}}_0^{\frac{1}{2}}(d)\), there is no global \(L^p_0\)-\(L^q_0\)-LAP for (7) or (4).
We show a local \(L^p_0\)-\(L^q_0\)-LAP for the Maxwell operator in Proposition 3.2. Roughly speaking, for low frequencies the resolvent estimates are equivalent to resolvent estimates for the Laplacian, and uniform estimates \(L^{p_1} \rightarrow L^q\) are possible for \((1/p_1,1/q) \in {\mathcal {P}}(d)\) (see Sect. 3). For the high frequencies, away from the singular set, the multiplier is smooth, but provides merely the smoothing of the Half-Laplacian. We use different \(L^{p_2} \rightarrow L^q\)-estimates for this region. This gives \(L^{p_1} \cap L^{p_2} \rightarrow L^q\)-estimates, which are uniform in \(\omega \) in a compact set away from the origin, and an LAP in the same spaces. The necessity of considering currents in intersections of \(L^p\)-spaces is shown in Corollary 1.5. Below for \(s \ge 0\) and \(1< q < \infty \), \(W^{s,q}({\mathbb {R}}^d)\) denotes the \(L^q\)-based Sobolev space:
Theorem 1.6
(LAP for Time-Harmonic Maxwell’s equations) Let \(1 \le p_1,p_2,q \le \infty \), and let \(d \in \{2,3\}\). If \((1/p_1,1/q) \in {\mathcal {P}}(d)\), \((1/p_2,1/q) \in {\mathcal {R}}_0^{\frac{1}{2}}(d)\), then \(P(\omega ,D)^{-1}: L_0^{p_1}({\mathbb {R}}^d) \cap L_0^{p_2}({\mathbb {R}}^d) \rightarrow L_0^q({\mathbb {R}}^d)\) is bounded uniformly for \(\omega \in {\mathbb {C}}\backslash {\mathbb {R}}\) in a compact set away from the origin. Furthermore, for \(\omega \in {\mathbb {R}}\backslash 0\) there are limiting operators \(P_{\pm }(\omega ): L_0^{p_1}({\mathbb {R}}^d) \cap L_0^{p_2}({\mathbb {R}}^d) \rightarrow L_0^{q}({\mathbb {R}}^d)\) with
such that \((D,B) = P_{\pm }(\omega ) (J_e,J_m)\) satisfy
Additionally, if \(q<\infty \), and \(s \in [1,\infty )\), then
Previously, Picard–Weck–Witsch [26] showed an LAP in weighted \(L^2\)-spaces (cf. [1]). Since the results in [26] are proved via Fredholm’s Alternative, the frequencies \(\omega \in {\mathbb {R}}\backslash 0\) are assumed not to belong to a discrete set of eigenvalues. In [26] \(\varepsilon \) and \(\mu \) are assumed to be positive-definite and isotropic, but allowed to depend on x as in [5]. Pauly [25] proved similar results as Picard–Weck–Witsch [26] in weighted \(L^2\)-spaces in the anisotropic case; see also [2, 24]. Much earlier, Eidus [8] already proved non-existence of eigenvalues of the Maxwell operator provided that \(\varepsilon \) and \(\mu \) are sufficiently smooth short-range perturbations of the identity and satisfy a repulsivity condition. Recently, D’Ancona–Schnaubelt [7] proved global-in-time Strichartz estimates from resolvent estimates in weighted \(L^2\)-spaces.
It appears that in the present work the role of the Half-Laplacian is explicitly identified for the analysis of the Maxwell operator the first time. We note that in [27, 28], in joint work with R. Schnaubelt, we apply a similar diagonalization to show Strichartz estimates for time-dependent Maxwell’s equations with rough coefficients. In these works, due to variable permittivity and permeability, the diagonalization is carried out with pseudo-differential operators, and the present role of the Half-Laplacian is played by the Half-Wave operator. Provided that suitable estimates for the Half-Laplacian with variable coefficients were at disposal, of which the author is not aware, it seems possible that the present approach extends to variable permittivity and permeability as well.
Outline of the Paper In Sect. 2 we diagonalize time-harmonic Maxwell’s equations in Fourier space to reduce the resolvent estimates to estimates for the Half-Laplacian. We also give examples for lower resolvent bounds in terms of the Half-Laplacian. In Sect. 3 we argue how an LAP fails in \(L^p\)-spaces, but can be salvaged in intersections of \(L^p\)-spaces. In Sect. 4 we show how the \(\omega \)-dependent resolvent estimates lead to localization of eigenvalues in the presence of potentials. We postpone technical computations to the Appendix, where we also give explicit solution formulae.
2 Reduction to Resolvent Estimates for the Half-Laplacian
Let \(\omega \in {\mathbb {C}}\backslash {\mathbb {R}}\). We diagonalize \(P(\omega ,D)\) defined in (7) or in (4) in the partially anisotropic case. We shall see that the transformation matrices are essentially Riesz transforms. This allows to bound the resolvents with estimates for the Half-Laplacian. We will make repeated use of the Mikhlin–Hörmander multiplier theorem (cf. [12, Theorem 6.2.7, p. 446]):
Theorem 2.1
(Mikhlin–Hörmander) Let \(1<p<\infty \) and \(m: {\mathbb {R}}^n \backslash 0 \rightarrow {\mathbb {C}}\) be a bounded function that satisfies
for \(|\alpha | \le \lfloor \frac{n}{2} \rfloor + 1\). Then, \({\mathfrak {m}}_p: L^p({\mathbb {R}}^n) \rightarrow L^p({\mathbb {R}}^n)\) given by \(f \mapsto (m {\hat{f}}) \check{\;}\) defines a bounded mapping with
where
As pointed out in [12], \(m \in C^k({\mathbb {R}}^n \backslash 0)\), \(k \ge \lfloor \frac{n}{2} \rfloor + 1\) is an \(L^p\)-multiplier for \(1<p<\infty \), if it is zero-homogeneous, i.e., there is \(\tau \in {\mathbb {R}}\) such that for any \(\lambda > 0\) and \(\xi \ne 0\), we have
Differentiating the above display with respect to \(\xi \), we obtain for \(\lambda > 0\)
and (23) is satisfied with \(D_\alpha = \sup _{|\theta | = 1} |\partial ^\alpha m(\theta )|\).
2.1 Proof of Theorem 1.1 for \(d=2\)
Let \(u = (D_1,D_2,B)\). We denote \((\varepsilon ^{-1})_{ij} = (\varepsilon _{ij})_{i,j}\). To reduce to estimates for the Half-Laplacian, we diagonalize the symbol associated with the operator defined in (7). We write \(\xi = (\xi _1,\xi _2) \in {\mathbb {R}}^2\):
Let \(\Vert \xi \Vert ^2_{\varepsilon ^\prime } = \langle \xi , \mu ^{-1} \det (\varepsilon )^{-1} \varepsilon \xi \rangle \), \(\xi ^\prime = \xi / \Vert \xi \Vert _{\varepsilon ^\prime }\), and define
We have the following lemma on diagonalization:
Lemma 2.2
For almost all \(\xi \in {\mathbb {R}}^2\) there is a matrix \(m(\xi ) \in {\mathbb {C}}^{3 \times 3}\) such that
with
Furthermore, the operators \(m_{ij}(D)\) and \(m^{-1}_{ij}(D)\) are \(L^p\)-bounded for \(1<p<\infty \).
Proof
It is straight-forward to check that the eigenvalues are as in (28) with the eigenvectors at hand. We align the corresponding eigenvectors as columns to
and note that \(\det m(\xi ) = - 1\) for \(\xi \ne 0\). For the inverse matrix we compute
\(L^p\)-boundedness is immediate from Theorem 2.1 because the components of m and \(m^{-1}\) are zero-homogeneous and smooth away from the origin. \(\square \)
In Proposition 5.2 we compute \(p^{-1}(\omega ,\xi )\) via this diagonalization. The diagonalization allows us to separate
with \(M^2_c v = 0\) for \(\xi _1 v_1 + \xi _2 v_2 = 0\) and
We can finish the proof of Theorem 1.1 for \(d=2\):
Proof of Theorem 1.1, d=2
We begin with the lower bound in (15). For u with \(\partial _1 u_1 +\partial _2 u_2 = 0\), we have
The entries of \(M^2(A,B)\) are linear combinations of \(e_{\pm }(\omega ,\xi )\) and \(\xi _i'\). The operators
are \(L^p\)-bounded for \(1<p<\infty \) with a constant only depending on \(p,\varepsilon ,\mu \) as the symbols are linear combinations of Riesz symbols after changes of variables. We find (see (27) for notations)
for \(1 \le p,q \le \infty \) with \((1< p < \infty \) or \(1<q<\infty )\). The reason we are not required to take \(1<p<\infty \) and \(1<q<\infty \) is that, if there is one reflexive \(L^p\)-space, then we can commute the Fourier multipliers after multiplying out the matrices such that the Riesz transforms act on a reflexive \(L^p\)-space.Footnote 2 This shows the lower bound in (15) for \(d=2\).
We turn to show the upper bound in (15), which is
for \(1<p,q<\infty \).
The operators \({\mathcal {R}}_j^{\varepsilon '}\) satisfy for \(1<p<\infty \)
In fact, as already used above, \(\Vert {\mathcal {R}}_j^{\varepsilon ^\prime } f \Vert _{L^p} \lesssim _{p,\varepsilon ,\mu } \Vert f \Vert _{L^p}\) for \(1<p<\infty \) as a consequence of Theorem 2.1. Let \(\chi _1\), \(\chi _2: {\mathbb {R}}/ (2 \pi {\mathbb {Z}}) \rightarrow [0,1]\) be a smooth partition of unity of the unit circle such that
We extend \(\chi _i\) to \({\mathbb {R}}^2 \backslash 0\) by zero-homogeneity.
For the reverse bound in (35), we decompose \(f=f_1+f_2\) as \(f_i = \chi _i(D) f\). Set \((({\mathcal {R}}_i^{\varepsilon ^\prime })^{-1} f) \widehat{(}\xi ) = \frac{\Vert \xi \Vert _{\varepsilon ^\prime }}{\xi _i} {\hat{f}}(\xi )\). Note that \(|\xi _i| \gtrsim \Vert \xi \Vert _{\varepsilon '}\) for \(\xi \in \text {supp}({\hat{f}}_i)\). By Theorem 2.1, we find the estimate
Consequently,
With (35) in mind, we show (34) by considering the data
Clearly, \(\partial _1 v_1 + \partial _2 v_2 = 0\). We compute
We further compute
and it follows by (35)
as claimed. Since \(\Vert v \Vert _{L^p} \sim \Vert f \Vert _{L^p}\), by choosing f suitably, we find
Finally, we turn to (16), which reads for \(d=2\)
We decompose writing \(J = (J_e,J_m)\)
as in (31). The arguments from above estimate the contribution of \((M^2(A,B) {\hat{J}})^{\vee }\). A computation yields
with \(\rho _e = \partial _1 J_{e1} + \partial _2 J_{e2}\). From this follows
by \(L^q\)-boundedness of \({\mathcal {R}}_i^{\varepsilon '}\) for \(1<q<\infty \) and \(\Vert \xi \Vert / \Vert \xi \Vert _{\varepsilon '}\) zero-homogeneous and smooth away from the origin. The proof is complete. \(\square \)
2.2 Proof of Theorem 1.1 for \(d=3\)
We consider \(P(\omega ,D)\) as in (4) with \(\varepsilon = \text {diag}(\varepsilon _1,\varepsilon _2,\varepsilon _3)\) and \(\mu > 0\). Here we consider the partially anisotropic case \(a^{-1}= \varepsilon _1 ; \quad \varepsilon _2 = \varepsilon _3 = b^{-1}\) and suppose that \(\mu = 1\) without loss of generality, to which we can reduce by linear substitution. The computation also covers the isotropic case \(a=b\), which was considered in [5]. For \(\xi \in {\mathbb {R}}^3\) we denote
We write further
We have the following lemma on diagonalization:
Lemma 2.3
For almost all \(\xi \in {\mathbb {R}}^3\) there is a matrix \({\tilde{m}}(\xi ) \in {\mathbb {C}}^{6 \times 6}\) such that
with
Furthermore, the components of \({\tilde{m}}\) and \({\tilde{m}}^{-1}\) are \(L^p\)-bounded Fourier multipliers for \(1<p<\infty \).
Proof
To verify that the diagonal entries of d are truly the eigenvalues of p, we record eigenvectors, which are normalized to zero-homogeneous entries. Eigenvectors to \(i \omega \) are
Eigenvectors to \(i\omega \mp i \sqrt{b} \Vert \xi \Vert \) are given by
Eigenvectors to \(i \omega \mp i \Vert \xi \Vert _{\varepsilon }\) are given by
Set
and
The determinant of \(m(\xi )\) is computed in Lemma 5.1 in the Appendix. We have
Furthermore, we find for \(\alpha \ne 0\):
Since \(\alpha (\xi ) \rightarrow 0\) as \(|\xi _2| + |\xi _3| \rightarrow 0\), m becomes singular along the \(\xi _1\)-axis, and the entries of \(m^{-1}(\xi )\) are no \(L^p\)-bounded Fourier multipliers anymore. This suggests to renormalize \(v_3,\ldots ,v_6\) with \(1/\alpha (\xi )\). We let
By Lemma 5.1, we have \(\det ({\tilde{m}}) \sim 1\) if and only if \(\xi \ne (\nu ,0,0)\) for some \(\nu \in {\mathbb {R}}\). Hence, \({\tilde{m}}\) and \({\tilde{m}}^{-1}\) are well-defined away from the \(\xi _1\)-axis. By Cramer’s rule, we obtain \({\tilde{m}}(\xi )^{-1}\) from \(m^{-1}(\xi )\) by modifying the rows 3-6:
Also by Cramer’s rule, it is enough to check that the Fourier multipliers associated with the entries in \({\tilde{m}}\) are \(L^p\)-bounded, for which we use Theorem 2.1.
For the first and second column this is evident since these are Riesz transforms up to change of variables. We turn to the proof that the entries of \(v_i/\alpha (\xi )\), \(i=3,\ldots ,6\), are multipliers bounded in \(L^p\) for \(1<p<\infty \). This follows by writing them as products of zero-homogeneous functions, which are smooth away from the origin, and Riesz transforms in two variables. We give the details for the entries of \(v_3/\alpha (\xi )\):
-
\((v_3)_2/\alpha (\xi )\): We have to show that
$$\begin{aligned} \frac{\xi _3 (\Vert \xi \Vert \Vert \xi \Vert _{{\tilde{\varepsilon }}})^{1/2} }{\Vert \xi \Vert (\xi _2^2 + \xi _3^2)^{1/2}} = \frac{\xi _3}{(\xi _2^2+ \xi _3^2)^{1/2}} \Big ( \frac{\Vert \xi \Vert _{\varepsilon }}{\Vert \xi \Vert } \Big )^{1/2} \end{aligned}$$is a multiplier. This is the case because \(\frac{i \xi _3}{(\xi _2^2+ \xi _3^2)^{1/2}}\) is a Riesz transform in \((x_2,x_3)\) and the second factor \(\big ( \frac{\Vert \xi \Vert _{\varepsilon }}{\Vert \xi \Vert } \big )^{1/2}\) is zero-homogeneous and smooth away from the origin, hence, in the scope of Theorem 2.1.
-
\((v_3)_3/\alpha (\xi )\) is a multiplier by symmetry in \(\xi _2\) and \(\xi _3\) and the previous considerations.
-
\((v_3)_4/\alpha (\xi )\): We find
$$\begin{aligned} \frac{(\xi _2^2 + \xi _3^2)}{\Vert \xi \Vert ^2 (\xi _2^2+ \xi _3^2)^{1/2}} \cdot (\Vert \xi \Vert \Vert \xi \Vert _{\varepsilon })^{1/2} = \frac{(\xi _2^2 + \xi _3^2)^{1/2}}{\Vert \xi \Vert } \cdot \Big ( \frac{\Vert \xi \Vert _{\varepsilon }}{\Vert \xi \Vert } \Big )^{1/2} \end{aligned}$$to be a Fourier multiplier as it is zero-homogeneous and smooth away from the origin.
-
\((v_3)_5/\alpha (\xi )\): Consider
$$\begin{aligned} \frac{\xi _1 \xi _2}{\Vert \xi \Vert ^2 (\xi _2^2 + \xi _3^2)^{1/2}} (\Vert \xi \Vert \Vert \xi \Vert _{\varepsilon })^{1/2} = \frac{\xi _1}{\Vert \xi \Vert } \cdot \frac{\xi _2}{(\xi _2^2 + \xi _3^2)^{1/2}} \cdot \Big ( \frac{\Vert \xi \Vert _{\varepsilon }}{\Vert \xi \Vert } \Big )^{1/2}, \end{aligned}$$which is again a Fourier multiplier because the first and third expression are zero-homogeneous and smooth in \({\mathbb {R}}^n \backslash 0\), the second is again a Riesz transform in two variables.
-
\((v_3)_6/\alpha (\xi )\) can be handled like the previous case.
The remaining entries of \({\tilde{m}}\) are treated similarly, which completes the proof.
\(\square \)
Remark 2.4
To compute the eigenvalues from scratch, it is perhaps easiest to use the block structure of \(p(\omega ,\xi )\) to find
Next, we can use the identity \({\mathcal {B}}^2(\xi ) = - \Vert \xi \Vert ^2 1_{3 \times 3} + \xi \otimes \xi \), after which there seems to be no further simplification but to compute the determinant brutely. Note that \(\det (i \lambda 1_{6 \times 6} - p(\omega ,\xi )) = \det (p(\lambda - \omega ,\xi ))\), which allows to find the eigenvalues from the zero locus of \(\det (p(\omega ,\xi ))\).
We prove Theorem 1.1 for \(d=3\) following along the argument for \(d=2\). Proposition 5.3 in the Appendix provides a decomposition
with \(M^3_c v = 0\) for \(\xi _1 v_1 + \xi _2 v_2 + \xi _3 v_3 = \xi _1 v_4 + \xi _2 v_5 + \xi _3 v_6 = 0\) and
Proof of Theorem 1.1, d=3
The estimate
for \(1 \le p,q \le \infty \) with \((1<p < \infty \) or \(1<q<\infty )\) follows from the same argument as in the two-dimensional case: The entries of \(M^3(A,B,C,D)\) are linear combinations of A,B,C,D multiplied with components of \({\tilde{m}}\) and \({\tilde{m}}^{-1}\), which yield Fourier multipliers by Lemma 2.3.
Below let \(({\mathcal {R}}_i f) \widehat{(}\xi ) = \frac{\xi _i}{\Vert \xi \Vert } {\hat{f}}(\xi ) \). To show the lower bound for \(1<p,q<\infty \), we consider the following initial data:
Note that \(\nabla \cdot J_{e} = 0\) and again, the initial data is also physically meaningful as the magnetic current vanishes.
Let \((e_{\pm } f) \widehat{(}\xi ) = (\omega \pm \sqrt{b} | \xi |)^{-1} {\hat{f}}(\xi )\). We compute with m as in (38):
We shall see that
either, if f has frequency support in a conic neighbourhood of the \(\xi _3\)-axis, or, if f is spherically symmetric.
Assume that \(g \in {\mathcal {S}}({\mathbb {R}}^3)\) and
By Theorem 2.1, we have for \(1<p<\infty \)
with \(C(c) \rightarrow 0\) as \(c \rightarrow 0\). If \(\text {supp}( {\hat{f}}) \subseteq E\), then also the Fourier support of \(e_- f \pm e_+ f\) is contained in E, and an application of (43) to \(D_2\) and \(B_1\) yields
which is (42).
Next, suppose that \(f \in L^p({\mathbb {R}}^3)\), \(1<p<\infty \) is spherically symmetric. Since \({\mathcal {R}}_1^2 + {\mathcal {R}}_2^2 + {\mathcal {R}}_3^2 = Id\) and \(\Vert {\mathcal {R}}_i^2 f \Vert _{L^p} = \Vert {\mathcal {R}}_j^2 f \Vert _{L^p}\) for \(i,j \in \{1,2,3\}\) by change of variables and rotation symmetry, we find \(\Vert {\mathcal {R}}_i^2 f \Vert _{L^p} \gtrsim \Vert f \Vert _{L^p}\). By \(L^p\)-boundedness, we have
Similarly,
and \(\Vert ({\mathcal {R}}_i^2 + {\mathcal {R}}_j^2) f \Vert _{L^p} = \Vert ({\mathcal {R}}_k^2 + {\mathcal {R}}_l^2) f \Vert _{L^p}\) again by change of variables and rotation symmetry. Hence, we also find
(45) and (46) together allow to argue as well in case of spherical symmetry as in (44). If we can choose f such that the operator norms of \(e_{\pm }\) are approximated, we find
Lastly, if \(\text {supp} ({\hat{f}}) \subseteq E\), i.e., the frequency support is in a conic neighbourhood of the \(\xi _3\)-axis, or is spherically symmetric, we find \(\Vert (J_{e},J_{m}) \Vert _{L^p_0} \sim \Vert f \Vert _{L^p}\). To see that it suffices to consider the frequency support of f as such, we recall the examples from [18, Section 5.2], giving the claimed lower bound for the operator norm of the resolvent of the fractional Laplacian: a Knapp type example, which can be realized with frequency support in a conic neighbourhood of the \(\xi _3\)-axis [18, p. 1458], and a spherically symmetric example related with the surface measure on the sphere [18, p. 1459].
We turn to the proof of (16) for \(d=3\):
This hinges again on the decomposition
The contribution of \(M^3(A,B,C,D)\) is estimated like in the first part of the proof. We compute
The claim follows by Theorem 2.1 because \(\Vert \xi \Vert / \Vert \xi \Vert _\varepsilon \) and \(\xi _i'\) and \({\tilde{\xi }}_i\) are zero-homogeneous and smooth away from the origin. The proof of Theorem 1.1 is complete. \(\square \)
3 Local and Global LAP
Let \(P(\omega ,D)\) be as in the previous section. In the following we want to investigate the limit of
by which we construct solutions to time-harmonic Maxwell’s equations. By scaling we see that the following estimates are uniform in \(\omega \), provided it varies in a compact set away from the origin. We further suppose that \(\omega > 0\); the case \(\omega < 0\) can be treated with the obvious modifications.
In the following let \(0<|\delta |<1/2\). By the above diagonalization, it is equivalent to consider uniform boundedness of
Hence, by the results of the previous section, the uniform \(L^p_0\)-\(L^q_0\)-LAP fails due to the lack of uniform resolvent estimates for the Half-Laplacian in \(L^p\)-spaces. This is recorded in Corollary 1.5.
Regarding the local \(L^p_0\)-\(L^q_0\)-LAP, we observe that the operator
for \(\beta \in C^\infty _c\), \(0<\delta <1/2\) is bounded from \(L^p \rightarrow L^q\) for \(1 \le p \le q \le \infty \) by Young’s inequality, with the obvious limit as \(\delta \rightarrow 0\). Thus, we focus on
with \(0< \delta < \delta _0 \ll 1\), where \(\beta \in C^\infty _c({\mathbb {R}}^n)\).
We can be more precise about the limiting operators: For \(t \in {\mathbb {R}}\) recall Sokhotsky’s formula, which hold in the sense of distributions:
where \(\delta _0\) denotes the delta-distribution at the origin.
Let
We find
and by the diagonalization formulae, we find that the limiting operators can be expressed as linear combinations involving possibly generalized Riesz transforms, \({\mathcal {R}}^{loc}_{\pm }\), and \(e_+\). We recall the \(L^p\)-\(L^q\)-mapping properties of \({\mathcal {R}}^{loc}_{\pm }\).
We observe that
This operator, modulo the bounded operator given by convolution with \({\mathcal {F}}^{-1} \beta \) and linear change of variables \(\xi \rightarrow \zeta \) such that \(\Vert \xi \Vert _{\varepsilon '} = \Vert \zeta \Vert \), is known as restriction-extension operator (cf. [16, 18]) and is a special case of the Bochner–Riesz operator of negative index:
\({\mathcal {B}}_\alpha \) is defined by analytic continuation for \(\alpha \ge 1\). Hence, for \(\alpha = 1\), it matches the restriction–extension operator. This operator is well-understood due to the works of Börjeson [4], Sogge [29], and Gutiérrez [13, 14]. The most recent results for Bochner–Riesz operators of negative index are due to Kwon–Lee [18]. Gutiérrez showed that \({\mathcal {B}}^1: L^p \rightarrow L^q\) is bounded if and only if \((1/p,1/q) \in {\mathcal {P}}(d)\) with
She used this to show uniform resolvent estimates for
We summarize the operator bounds for \(e_\delta \) and \({\mathcal {R}}_{\pm }^{\text {loc}}\).
Proposition 3.1
[18, Proposition 4.1] Let \(\omega > 0\), \(0<\delta <1/2\), \(\beta \in C^\infty _c({\mathbb {R}}^d)\) and \(d_\delta \) as in (48). Then, we find the following estimates to hold for \((1/p,1/q) \in {\mathcal {P}}(d)\):
We are ready for the proof of the local LAP:
Proposition 3.2
(Local LAP) We find a local \(L^p_0\)-\(L^q_0\)-LAP to hold provided that \((1/p,1/q) \in {\mathcal {P}}(d)\). This means that for \(\omega \in {\mathbb {R}}\backslash 0\) and \(\beta \in C^\infty _c({\mathbb {R}}^d)\), we find uniform (in \(0<\delta <1/2\)) resolvent bounds
and there are limiting operators \(P_{\pm }^{loc}: L^p_0 \rightarrow L^q_0\) such that
Proof
We assume that \(\omega > 0\) because \(\omega < 0\) can be treated mutatis mutandis. Recall the bounds for \(e_\delta \) recorded in Proposition 3.1, easier bounds for \(e_+^{\varepsilon '}\), and the diagonalization from Sect. 2, which decompose (cf. Lemmas 2.2, 2.3)
By these, (50) follows for \((1/p,1/q) \in {\mathcal {P}}(d)\) provided that \(1<p,q<\infty \) to bound the generalized Riesz transforms. We extend this to all \((1/p,1/q) \in {\mathcal {P}}(d)\) by Young’s inequality: For \((1/p,0) \in {\mathcal {P}}(d)\) we choose \(1<{\tilde{q}}<\infty \) such that \((1/p,1/{\tilde{q}}) \in {\mathcal {P}}(d)\). By Young’s inequality and the previously established bounds for \((1/p,1/{\tilde{q}}) \in {\mathcal {P}}(d)\) follows
The case \((1,1/q) \in {\mathcal {P}}(d)\) is treated by the dual argument.
By Sokhotsky’s formula and the diagonalization, we can consider the limiting operators
whose mapping properties follow again from Proposition 3.1 and the diagonalization as argued above. We give explicit formulae in Propositions 5.2 and 5.3; however, these are bulky and recorded in the Appendix. \(\square \)
We are ready for the proof of Theorem 1.6:
Proof of Theorem 1.6
Let \(1 \le p_1, p_2, q \le \infty \), and \(\omega \in {\mathbb {R}}\backslash 0\). Choose \(C=C(\varepsilon ,\omega )\) such that \(p(\omega ,\xi )^{-1}\) is regular for \(\Vert \xi \Vert \ge C\). Write \(J = (J_e,J_m)\) for the sake of brevity. Let \(\beta \in C^\infty _c\) with \(\beta \equiv 1\) on \(\{ \Vert \xi \Vert \le C \}\) and decompose
By Proposition 3.2, we find uniform bounds for \(0< \delta < 1/2\)
provided that \((\frac{1}{p_1},\frac{1}{q}) \in {\mathcal {P}}(d)\). The estimate
follows for \(0 \le \frac{1}{p_2} - \frac{1}{q} \le \frac{1}{d}\) and \((\frac{1}{p_2},\frac{1}{q}) \notin \{ (\frac{1}{d},0), (1,\frac{d-1}{d}) \}\) by properties of the Bessel kernel. The limiting operators \(P^{loc}_{\pm }(\omega )\) were described in Proposition 3.2: We have
The high frequency is limit is easier to analyze because the multiplier remains regular by construction. Let \(M^d \in {\mathbb {C}}^{m(d) \times m(d)}\) be as in Propositions 5.2 and 5.3. For \(d=2\), let
and we have
For \(d=3\), let
and we have with convergence in \( ({\mathcal {S}}'({\mathbb {R}}^3))^6\)
Let \(P_{\pm }(\omega ) = P_{\pm }^{loc}(\omega ) + P^{high}(\omega )\). By Proposition 3.2, and (51), (52), we have
Let \((D,B)^{\pm }_\delta = P(\omega \pm i \delta , D)^{-1} J\) and \((D,B)^{\pm } = P_{\pm }(\omega ) J\). At last, we show that
For this purpose, we show that for \(\delta \rightarrow 0\) we have
As \((D,B)^{\pm }_\delta \rightarrow (D,B)^{\pm }\) in \({\mathcal {S}}'({\mathbb {R}}^d)^{m(d)}\), (54) concludes the proof.
To show (54), we return to the diagonalizations (cf. Lemmas 2.2 and 2.3):
We find for \(\omega \in {\mathbb {R}}\):
Hence,
In particular, (54) holds true in \({\mathcal {S}}'({\mathbb {R}}^d)^{m(d)}\).
Next, we suppose additionally that \(J \in (W^{s-1,q}({\mathbb {R}}^d))^{m(d)}\) for \(s \ge 1\). By Young’s inequality, we have
Hence, the low frequencies can be estimated like before. For the high frequencies, we recall that the multipliers \(M^2\) and \(M^3\) yield smoothing of one derivative and by Theorem 2.1, we find
The proof of Theorem 1.6 is complete. \(\square \)
4 Localization of Eigenvalues
At last, we use the \(\omega \)-dependent resolvent estimates to localize eigenvalues for operators \(P(\omega ,D) + V\) acting in \(L^q\). For this purpose, we consider for \(\ell > 0\) and \((1/p,1/q) \in \tilde{{\mathcal {R}}}_0^{\frac{1}{2}}\) the region, where uniform resolvent estimates are possible:
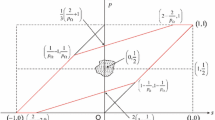
Describing the regions, we start with observing the symmetry in the real and imaginary part. For \(\alpha _{p,q} = 0\), \(\ell < 1\), we find \({\mathcal {Z}}_{p,q}(\ell ) = \emptyset \). For \(\ell \ge 1\), \({\mathcal {Z}}_{p,q}(\ell )\) describes a cone around the y-axis with aperture getting larger. For \(\alpha _{p,q} > 0\) the boundaries become slightly curved. Pictorial representations for \(\Re \omega > 0\) were provided in [18, Figures 9(a)–(c)]. The region in the left half plane is obtained by reflection along the imaginary axis. We shall see that eigenvalues of \(P(\omega ,D) + V\) must lie in \({\mathbb {C}}\backslash {\mathcal {Z}}_{p,q}(\ell )\). Previously in [11], for non-self-adjoint Schrödinger operators analogous arguments were used to show that in a range of (p, q), a sequence of eigenvalues \(\lambda _j\) with \(\Re \lambda _j \rightarrow \infty \) has to satisfy \(\Im \lambda _j \rightarrow 0\) as a consequence of the shape of \({\mathcal {Z}}_{p,q}(\ell )\). This is not the case presently and the shape of \({\mathcal {Z}}_{p,q}(\ell )\) only yields a bound for the asymptotic growth of \(|\Im \lambda _j|\) as \(|\Re \lambda _j| \rightarrow \infty \). This also raises the question for counterexamples, where the behavior \(\Re \lambda _j \rightarrow \infty \) and \(\Im \lambda _j \rightarrow 0\) fails. We also refer to Cuenin [6] for resolvent estimates for the fractional Laplacian in this context.
Let C be the constant such that
Corollary 4.1
Let \(d \in \{2,3\}\), \(\ell > 0\), and \(1<p,q<\infty \) such that \((1/p,1/q) \in \tilde{{\mathcal {R}}}_0^{1/2}\). Suppose that there is \(t \in (0,1)\) such that
If \(E \in {\mathbb {C}}\backslash {\mathbb {R}}\) is an eigenvalue of \(P+V\) acting in \(L^q_0\), then E must lie in \({\mathbb {C}}\backslash {\mathcal {Z}}_{p,q}(\ell )\).
Proof
The short argument is standard by now (cf. [18, 19]), but contained for the sake of completeness. Let \(u \in L_0^q({\mathbb {R}}^d)\) be an eigenfunction of \(P+V\) with eigenvalue \(E \in {\mathbb {C}}\backslash {\mathbb {R}}\) and suppose that \(E \in {\mathcal {Z}}_{p,q}(\ell )\). By Hölder’s inequality, we find \(-(P-E)u = (V-(P-E+V))u = Vu \in L^p\). By definition of \({\mathcal {Z}}_{p,q}(\ell )\), we find
By the triangle and Hölder’s inequality, we find
which implies \(u=0\) as \(t<1\). Hence, \(E \notin {\mathcal {Z}}_{p,q}(\ell )\). \(\square \)
Notes
In the isotropic case we identify \(\varepsilon = \lambda 1_{3 \times 3}\) with \(\lambda \in {\mathbb {R}}_{>0}\) and do likewise for \(\mu \).
I thank the referee for pointing this out.
References
Agmon, S.: Spectral properties of Schrödinger operators and scattering theory. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 2(2), 151–218 (1975)
Ben-Artzi, M., Nemirovsky, J.: Resolvent estimates for Schrödinger-type and Maxwell equations with applications. In: Spectral and Scattering Theory (Newark. DE, 1997), pp. 19–31. Plenum, New York (1998)
Boito, D., de Andrade, L.N.S., de Sousa, G., Gama, R., London, C.Y.M.: On Maxwell’s electrodynamics in two spatial dimensions. Revista Brasileira de Ensino de Física [online]
Börjeson, L.: Estimates for the Bochner-Riesz operator with negative index. Indiana Univ. Math. J. 35(2), 225–233 (1986)
Cossetti, L., Mandel, R.: A limiting absorption principle for Helmholtz systems and time-harmonic isotropic Maxwell’s equations. J. Funct. Anal. 281(11): Paper No. 109233 (2021)
Cuenin, J.-C.: Eigenvalue bounds for Dirac and fractional Schrödinger operators with complex potentials. J. Funct. Anal. 272(7), 2987–3018 (2017)
D’Ancona, P., Schnaubelt, R.: Global Strichartz estimates for an inhomogeneous Maxwell system. Commun. Partial Differ. Equ. (to appear)
Eidus, D.: On the spectra and eigenfunctions of the Schrödinger and Maxwell operators. J. Math. Anal. Appl. 106(2), 540–568 (1985)
Feynman, R.P., Leighton, R.B., Sands, M.: The Feynman lectures on physics. In: Mainly Electromagnetism and Matter, vol. 2. Addison-Wesley Publishing Co., Inc, Reading (1964)
Frank, R.L.: Eigenvalue bounds for Schrödinger operators with complex potentials. Bull. Lond. Math. Soc. 43(4), 745–750 (2011)
Frank, R.L.: Eigenvalue bounds for Schrödinger operators with complex potentials. III. Trans. Am. Math. Soc. 370(1), 219–240 (2018)
Grafakos, L.: Classical Fourier Analysis, volume 249 of Graduate Texts in Mathematics, 3rd ed. Springer, New York (2014)
Gutiérrez, S.: A note on restricted weak-type estimates for Bochner-Riesz operators with negative index in \({ R}^n, n\ge 2\). Proc. Am. Math. Soc. 128(2), 495–501 (2000)
Gutiérrez, S.: Non trivial \(L^q\) solutions to the Ginzburg-Landau equation. Math. Ann. 328(1–2), 1–25 (2004)
Huang, S., Yao, X., Zheng, Q.: Remarks on \(L^p\)-limiting absorption principle of Schrödinger operators and applications to spectral multiplier theorems. Forum Math. 30(1), 43–55 (2018)
Jeong, E., Kwon, Y., Lee, S.: Uniform Sobolev inequalities for second order non-elliptic differential operators. Adv. Math. 302, 323–350 (2016)
Kenig, C.E., Ruiz, A., Sogge, C.D.: Uniform Sobolev inequalities and unique continuation for second order constant coefficient differential operators. Duke Math. J. 55(2), 329–347 (1987)
Kwon, Y., Lee, S.: Sharp resolvent estimates outside of the uniform boundedness range. Commun. Math. Phys. 374(3), 1417–1467 (2020)
Kwon, Y., Lee, S., Seo, I.: Resolvent estimates for the Lamé operator and failure of Carleman estimates. J. Fourier Anal. Appl. 27(3): Paper No. 53, 27 (2021)
Landau, L.D., Lifschitz, E.M.: Lehrbuch der theoretischen Physik (“Landau-Lifschitz”). Band VIII. Akademie-Verlag, Berlin, fifth edition, (1990). Elektrodynamik der Kontinua. [Electrodynamics of Continua]
Liess, O.: Decay estimates for the solutions of the system of crystal optics. Asymptot. Anal. 4(1), 61–95 (1991)
Mandel, R., Schippa, R.: Time-Harmonic Solutions for Maxwell’s Equations in Anisotropic Media and Bochner-Riesz Estimates with Negative Index for Non-Elliptic Surfaces. Ann, Henri Poincaré (2021)
Moloney, J.V., Newell, A.C.: Nonlinear optics. Physica D 44(1–2), 1–37 (1990)
Pauly, D.: Niederfrequenzasymptotik der Maxwell-Gleichung im inhomogenen und anisotropen AuSSengebiet. Universität Essen (2002) (PhD thesis)
Pauly, D.: Low frequency asymptotics for time-harmonic generalized Maxwell’s equations in nonsmooth exterior domains. Adv. Math. Sci. Appl. 16(2), 591–622 (2006)
Picard, R., Weck, N., Witsch, K.-J.: Time-harmonic Maxwell equations in the exterior of perfectly conducting, irregular obstacles. Analysis (Munich) 21(3), 231–263 (2001)
Schippa, R.: Well-posedness for Maxwell equations with Kerr nonlinearity in three dimensions via Strichartz estimates. arXiv e-prints, arXiv:2108.07691 (2021)
Schippa, R., Schnaubelt, R.: On quasilinear Maxwell equations in two dimensions. Pure Appl. Anal. (to appear)
Sogge, C.D.: Oscillatory integrals and spherical harmonics. Duke Math. J. 53(1), 43–65 (1986)
Acknowledgements
Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) Project-ID 258734477 – SFB 1173. I would like to thank Lucrezia Cossetti and Rainer Mandel for helpful discussions about the results and context. Moreover, I am much obliged to the anonymous referees whose insightful comments clearly improved the presentation.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Andrei Shkalikov.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Lemma 5.1
With the notations from Section 2.2, let \(m(\xi )\) be as in (38) and \(\alpha (\xi )\) as in (39). Then, we have
Proof
We compute the determinant by taking linear combinations of the third and fourth column and fifth and sixth column, and aligning the columns as block matrices:
We find by noting that \((\xi _1')^2 + (\xi _2')^2 + (\xi _3')^2 = 1\)
Next, by a similar argument,
We use multilinearity to write
\(\square \)
In the following we give explicit formulae for the resolvents and for limiting operators in two dimensions:
Proposition 5.2
Let \(d=2\) and
furthermore,
Then, we have for \(\omega \in {\mathbb {C}}\backslash {\mathbb {R}}\) and almost all \(\xi \in {\mathbb {R}}^2\):
with
For \(\omega > 0\), \(\beta \in C^\infty _c({\mathbb {R}}^2)\), and \(u \in {\mathcal {S}}({\mathbb {R}}^2)^3\), we find
with
where
Proof
The first claim follows from computing \(p^{-1}(\omega ,\xi )\) (cf. Lemma 2.2). We decompose
based on the observation that \(m_2(\xi ) v(\xi ) = 0\) for \(\xi _1 v_1(\xi ) + \xi _2 v_2(\xi ) = 0\). We compute for A and B as in the first claim:
The computation is simplified by noting that:
We find for \(m(\xi ) d(\omega ,\xi )^{-1} m_1(\xi )\):
In \(M^2_c = m(\xi ) d(\omega ,\xi )^{-1} m_2(\xi )\) we have separated the contribution of non-trivial charges. The second claim follows with the same computation from Sokhotsky’s formula. \(\square \)
For \(d=3\), we define \(M^3(A,B,C,D) \in {\mathbb {C}}^{6 \times 6}\):
Furthermore,
Next,
Lastly,
We let moreover
We have the following analog of Proposition 5.2:
Proposition 5.3
Let \(d=3\). We find for \(\omega \in {\mathbb {C}}\backslash {\mathbb {R}}\) and almost all \(\xi \in {\mathbb {R}}^3\)
with
For \(\omega > 0\), \(\beta \in C^\infty _c({\mathbb {R}}^3)\), and \(u \in {\mathcal {S}}({\mathbb {R}}^3)^6\), we find
with
where
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schippa, R. Resolvent Estimates for Time-Harmonic Maxwell’s Equations in the Partially Anisotropic Case. J Fourier Anal Appl 28, 16 (2022). https://doi.org/10.1007/s00041-022-09912-y
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00041-022-09912-y