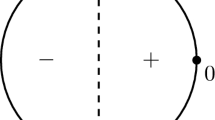Sign Retrieval in Shift-Invariant Spaces with Totally Positive Generator

Abstract

We show that a real-valued function f in the shift-invariant space generated by a totally positive function of Gaussian type is uniquely determined, up to a sign, by its absolute values $\{|f(\lambda )|: \lambda \in \Lambda \}$ on any set $\Lambda \subseteq {\mathbb {R}}$ with lower Beurling density $D^{-}(\Lambda )>2$.

We consider a totally positive function of Gaussian type, i.e., a function $g \in L^2({\mathbb {R}})$ whose Fourier transform factors as

$$\begin{aligned} \hat{g}(\xi )= \int _{{\mathbb {R}}} g(x) e^{-2\pi i x \xi } dx = C_0 e^{- \gamma \xi ^2}\prod _{\nu =1}^m (1+2\pi i\delta _\nu \xi )^{-1}, \quad \xi \in {\mathbb {R}}, \end{aligned}$$

(1)

with $\delta _1,\ldots ,\delta _m\in {\mathbb {R}}, C_0, \gamma >0, m \in {\mathbb {N}} \cup \{0\}$, and the shift-invariant space

$$\begin{aligned} V^\infty (g) = \Big \{ f=\sum _{k \in {\mathbb {Z}}} c_k\, g(\cdot -k): c \in \ell ^\infty ({\mathbb {Z}}) \Big \}, \end{aligned}$$

generated by its integer shifts within $L^\infty ({\mathbb {R}})$. As a consequence of (1), each $f \in V^\infty (g)$ is continuous, the defining series converges unconditionally in the weak$^*$ topology of $L^\infty$, and the coefficients $c_k$ are unique [6, Theorem 3.5].

The shift-invariant space $V^\infty (g)$ enjoys the following sampling property [4]: every separated set $\Lambda \subseteq {\mathbb {R}}$ with lower Beurling density

$$\begin{aligned} D^{-}(\Lambda ) := \liminf _{r \longrightarrow \infty } \inf _{x\in {\mathbb {R}}} \frac{\# \big [ \,\Lambda \cap [x-r,x+r] \,\big ]}{2r} \end{aligned}$$

strictly larger than 1 provides the norm equivalence

$$\begin{aligned} ||{f}||_{L^\infty ({\mathbb {R}})} \asymp ||{f|\Lambda }||_{\ell ^\infty ({\Lambda })}, \quad f \in V^\infty (g). \end{aligned}$$

(2)

(A similar property holds for all $L^p$ norms, $1 \le p \le \infty$; see [4, Theorems 5.2 and 3.1].)

In this article, we show the following uniqueness property for the absolute values of real-valued functions in $V^\infty (g)$.

FormalPara Theorem 1

(Sign retrieval) Let g be a totally positive function of Gaussian type, as in (1), and $\Lambda \subseteq {\mathbb {R}}$ with lower Beurling density

$$\begin{aligned} D^{-}(\Lambda )>2. \end{aligned}$$

(3)

Assume that $f_1, f_2 \in V^\infty (g)$ are real-valued and $\left| f_1 \right| \equiv \left| f_2 \right|$ on $\Lambda$. Then either $f_1 \equiv f_2$ or $f_1 \equiv - f_2$.

See [2] for motivation for sign retrieval in shift-invariant spaces. When g is a Gaussian function—corresponding to $m=0$ in (1)—Theorem 1 was recently obtained in [3, Theorem 1]. Here, that result is extended to all totally positive functions of Gaussian type.¹

The intuition behind Theorem 1 is as follows. Suppose that $\left| f_1 \right| \equiv \left| f_2 \right|$ on $\Lambda$, and split $\Lambda$ into

$$\begin{aligned} \begin{aligned} \Lambda _1&= \{ \lambda \in \Lambda : f_1(\lambda ) = f_2(\lambda )\},\\ \Lambda _2&= \{ \lambda \in \Lambda : f_1(\lambda ) = -f_2(\lambda )\}. \end{aligned} \end{aligned}$$

(4)

Then $f_1 - f_2$ vanishes on $\Lambda _1$ while $f_1 + f_2$ vanishes on $\Lambda _2$. Under (3), one may expect one of the two subsets $\Lambda _j$ to have lower Beurling density larger than 1. The sampling inequalities (2) would then imply that either $f_1 - f_2$ or $f_1 + f_2$ are identically zero. This argument breaks down, however, because Beurling’s lower density is not subadditive. For example, $\Lambda _1 := \Lambda \cap (-\infty ,0]$ and $\Lambda _2 := \Lambda \cap (0,\infty )$ have always zero lower Beurling density. The proof of the sign retrieval theorem for Gaussian generators in [3] resorts instead to a special property of the Gaussian function, namely that $V^\infty (g) \cdot V^\infty (g)$ is contained in a dilation of $V^\infty (\tilde{g})$ by a factor of 2, where $\tilde{g}$ is another Gaussian function. Thus, in the Gaussian case, the sampling theorem can be applied after rescaling to the set $\Lambda$ to conclude that $(f_1-f_2) \cdot (f_1+f_2) \equiv 0$, and, by analyticity, that either $f_1 \equiv f_2$ or $f_1 \equiv - f_2$. A similar argument applies to Paley–Wiener spaces [1, Theorem 2.5]. We are unaware of an analogous dilation property for general totally positive generators.

To prove Theorem 1 for all totally positive generators of Gaussian type we take a different route. We define the upper average circular density of a set $\Lambda \subseteq {\mathbb {R}}$ as

$$\begin{aligned} D^+_{\mathrm {circ}}(\Lambda ) = \limsup _{r \longrightarrow \infty } \frac{4}{\pi r^2} \int _0^r \sum _{\lambda \in \Lambda \cap [-t,t]} \sqrt{t^2 - \lambda ^2} \, \frac{dt}{t}, \end{aligned}$$

(5)

with the convention that $D^+_{\mathrm {circ}}(\Lambda )=\infty$, if $\Lambda$ is uncountably infinite. The density is named circular because, in (5), each point $\lambda \in [-t,t]$ is weighted with the measure of the largest vertical segment $\{\lambda \} \times (-a,a)$ contained in the two-dimensional open disk $B_t(0) \subseteq {\mathbb {R}}^2$.

The upper average circular density can be alternatively described as follows: as shown in Lemma 1 below, for any lattice $\alpha {\mathbb {Z}}$, $\alpha >0$,

$$\begin{aligned} D^+_{\mathrm {circ}}(\Lambda )= \limsup _{r \longrightarrow \infty } \frac{2\alpha }{\pi r^2} \int _0^r \# \big [ (\Lambda \setminus \{0\} \times \alpha {\mathbb {Z}}) \cap B_t(0)\big ] \,\frac{dt}{t}. \end{aligned}$$

(6)

From here, it follows easily that $D^+_{\mathrm {circ}}$ dominates Beurling’s lower density:

$$\begin{aligned} D^+_{\mathrm {circ}}(\Lambda ) \ge D^{-}(\Lambda ); \end{aligned}$$

(7)

see Lemma 1 below. We call $D^+_{\mathrm {circ}}$ an upper density because, due to the sublinearity of $\limsup$,

$$\begin{aligned} D^+_{\mathrm {circ}}(\Lambda _1 \cup \Lambda _2) \le D^+_{\mathrm {circ}}(\Lambda _1) + D^+_{\mathrm {circ}}(\Lambda _2), \end{aligned}$$

(8)

for any two sets $\Lambda _1, \Lambda _2 \subseteq {\mathbb {R}}$.

Below we prove the following uniqueness result formulated in terms of the upper average circular density of the zero set $\{f=0\}$ of a function f (counted without multiplicities).

FormalPara Theorem 2

(Uniqueness theorem) Let g be a totally positive function of Gaussian type, as in (1). Let $f \in V^\infty (g)$ be non-zero. Then $D^+_{\mathrm {circ}}(\{f=0\}) \le 1$.

The uniqueness theorem (which applies also to non-real-valued functions) allows one to carry out the following natural proof of the sign retrieval theorem.

FormalPara Proof

(Proof of Theorem 1, assuming Theorem 2) Assume that $D^{-}(\Lambda )>2$ and write $\Lambda = \Lambda _1 \cup \Lambda _2$ as in (4). Then, by (7) and (8), either $D^+_{\mathrm {circ}}(\Lambda _1) >1$ or $D^+_{\mathrm {circ}}(\Lambda _2) >1$ (possibly both). In the first case, Theorem 2 shows that $f_1 \equiv f_2$, while in the second, $f_1 \equiv -f_2$.$\square$

As the proof shows, Theorem 1 remains valid if (3) is relaxed to $D^+_{\mathrm {circ}}(\Lambda )>2$. Sign retrieval also holds under the same density condition for the shift-invariant spaces $V^p(g)$ defined with respect to $L^p$ norms, $1 \le p \le \infty$, as these are contained in $V^\infty (g)$.

Towards the proof of Theorem 2, we first prove (6) and (7).

FormalPara Lemma 1

Let $\Lambda \subseteq {\mathbb {R}}$ and $\alpha >0$. Then (6) and (7) hold true.

FormalPara Proof

We assume that $\Lambda$ has no accumulation points, since, otherwise, both sides of (6) are infinite. Denote provisionally the right hand side of (6) by ${\tilde{D}}^+_{\mathrm {circ}}(\Lambda )$, and set $\Lambda ' := \Lambda \setminus \{0\}$.

Step 1. Let $\varepsilon \in (0,1)$, and $C=C_{\alpha ,\varepsilon }>0$ a constant to be specified. We claim:

$$\begin{aligned}&D^+_{\mathrm {circ}}(\Lambda ) = \limsup _{r \longrightarrow \infty } \frac{4}{\pi r^2} \int _{C} ^r \sum _{\lambda \in \Lambda ' \cap [-t,t]} \sqrt{t^2 - \lambda ^2} \, \frac{dt}{t}, \end{aligned}$$

(9)

$$\begin{aligned}&(1+\delta )^{2} {\tilde{D}}^+_{\mathrm {circ}}(\Lambda ) = \limsup _{r \longrightarrow \infty } \frac{2\alpha }{\pi r^2} \int _{C}^r \# \big [ (\Lambda ' \times \alpha {\mathbb {Z}}) \cap B_{(1+\delta )t}(0) \big ] \,\frac{dt}{t}, \quad \delta =\pm \varepsilon . \end{aligned}$$

(10)

To prove the first claim, we first note that $D^+_{\mathrm {circ}}(\Lambda )=D^+_{\mathrm {circ}}(\Lambda ')$, since, if $0 \in \Lambda$, the contribution of the point $\lambda =0$ is

$$\begin{aligned} \frac{4}{\pi r^2} \int _0^r dt = \frac{4}{\pi r}, \end{aligned}$$

and does not affect the limit on r. Similarly, since $\sqrt{t^2 - \lambda ^2} \le t$,

$$\begin{aligned} \frac{4}{\pi r^2} \int _0^C \sum _{\lambda \in \Lambda ' \cap [-t,t]} \sqrt{t^2 - \lambda ^2} \frac{dt}{t} \le \# \big ( \Lambda ' \cap [-C,C]\big ) \cdot \frac{4C}{\pi r^2}. \end{aligned}$$

The last quantity is finite because $\Lambda$ has no accumulation points. This proves (9), because it shows that limiting the integral to [C, r] does not affect the limit on r. Second, a change of variables shows that (10) holds with C replaced by 0. In addition, since $\Lambda$ has no accumulation points, there exists $\eta >0$ such that $\Lambda '\cap (-\eta ,\eta )=\emptyset$. Therefore, we can estimate the part of the integral excluded in (10) as

$$\begin{aligned} \frac{2\alpha }{\pi r^2} \int _{0}^C \# \big [(\Lambda ' \times \alpha {\mathbb {Z}}) \cap B_{(1+\delta )t}(0) \big ]\,\frac{dt}{t} \le \# \big [ (\Lambda ' \times \alpha {\mathbb {Z}}) \cap B_{2C}(0) \big ] \cdot \frac{2\alpha }{\pi r^2} \int _{\frac{\eta }{1+\varepsilon }}^C \frac{dt}{t}, \end{aligned}$$

which is finite because $\eta >0$. This proves (10).

Step 2. For $t>0$, we note that

$$\begin{aligned} \# (\Lambda ' \times \alpha {\mathbb {Z}}) \cap B_t(0)&= \sum _{\lambda \in \Lambda ' \cap [-t,t]} \# \left\{ k \in {\mathbb {Z}}: \lambda ^2+\alpha ^2 k^2< t^2 \right\} \\&= \sum _{\lambda \in \Lambda ' \cap [-t,t]} \# \left\{ k \in {\mathbb {Z}}: \left| k \right| < \alpha ^{-1} \sqrt{t^2 - \lambda ^2} \right\} . \end{aligned}$$

Next, we choose the constant $C_{\alpha , \varepsilon }$ so that the following estimates hold for $t \ge C_{\alpha , \varepsilon }$:

$$\begin{aligned}&\# \big [ (\Lambda ' \times \alpha {\mathbb {Z}}) \cap B_{(1+\varepsilon )t}(0) \big ] \ge \sum _{\lambda \in \Lambda ' \cap [-t,t]} \left[ \frac{2}{\alpha } \sqrt{(1+\varepsilon )^2 t^2 - \lambda ^2} - 1\right] \\&\quad =\sum _{\lambda \in \Lambda ' \cap [-t,t]} \frac{2}{\alpha } \sqrt{(1+\varepsilon )^2 t^2 - \lambda ^2 - \alpha \sqrt{(1+\varepsilon )^2 t^2 - \lambda ^2} + \alpha ^2/4 }\\&\quad \ge \sum _{\lambda \in \Lambda ' \cap [-t,t]} \frac{2}{\alpha } \sqrt{(1+\varepsilon )^2 t^2 - \lambda ^2 - \alpha (1+\varepsilon )t + \alpha ^2/4 }\\&\quad \ge \sum _{\lambda \in \Lambda ' \cap [-t,t]} \frac{2}{\alpha } \sqrt{t^2 - \lambda ^2}, \end{aligned}$$

where the last estimate requires choosing $C_{\alpha , \varepsilon }$ large. Similarly,

$$\begin{aligned}&\# \big [(\Lambda ' \times \alpha {\mathbb {Z}}) \cap B_{(1-\varepsilon )t}(0)\big ] \le \sum _{\lambda \in \Lambda ' \cap [-(1-\varepsilon )t,(1-\varepsilon )t]} \left[ \frac{2}{\alpha } \sqrt{(1-\varepsilon )^2 t^2 - \lambda ^2} + 1\right] \\&\quad = \sum _{\lambda \in \Lambda ' \cap [-(1-\varepsilon )t,(1-\varepsilon )t]} \frac{2}{\alpha } \sqrt{(1-\varepsilon )^2 t^2 - \lambda ^2 + \alpha \sqrt{(1-\varepsilon )^2 t^2 - \lambda ^2} +\alpha ^2/4 } \\&\quad \le \sum _{\lambda \in \Lambda ' \cap [-(1-\varepsilon )t,(1-\varepsilon )t]} \frac{2}{\alpha } \sqrt{(1-\varepsilon )^2 t^2 - \lambda ^2 + \alpha {(1-\varepsilon ) t} +\alpha ^2/4 } \\&\quad \le \sum _{\lambda \in \Lambda ' \cap [-t,t]} \frac{2}{\alpha } \sqrt{t^2 - \lambda ^2}, \end{aligned}$$

where the last estimate requires choosing $C_{\alpha , \varepsilon }$ large. Combining the last two estimates with (9) and (10), and letting $\varepsilon \longrightarrow 0$, we deduce (6).

Step 3. To prove (7), let $r>s>0$ and use (6) with $\alpha =1$ to estimate

$$\begin{aligned} D^+_{\mathrm {circ}}(\Lambda )&\ge \liminf _{r \longrightarrow \infty } \frac{2}{\pi r^2} \int _s^r \inf _{z \in {\mathbb {R}}^2} \# \big [ (\Lambda ' \times {\mathbb {Z}}) \cap B_t(z) \big ] \,\frac{dt}{t} \\&\ge \inf _{t \ge s} \left[ \tfrac{1}{\left| B_t(0) \right| } \inf _{z \in {\mathbb {R}}^2} \# \big [ (\Lambda ' \times {\mathbb {Z}}) \cap B_t(z)\big ] \right] \liminf _{r \longrightarrow \infty } \frac{2}{\pi r^2} \int _s^r \left| B_t(0) \right| \,\frac{dt}{t} \\&=\inf _{t \ge s} \left[ \inf _{z \in {\mathbb {R}}^2} \tfrac{1}{\left| B_t(z) \right| } \# \big [ (\Lambda ' \times {\mathbb {Z}}) \cap B_t(z) \big ] \right] . \end{aligned}$$

Letting $s \longrightarrow \infty$, we see that

$$\begin{aligned} D^+_{\mathrm {circ}}(\Lambda ) \ge \liminf _{t \longrightarrow \infty } \inf _{z \in {\mathbb {R}}^2} \tfrac{1}{\left| B_t(z) \right| } \# \big [ (\Lambda ' \times {\mathbb {Z}}) \cap B_t(z) \big ] = D^{-}(\Lambda ') = D^{-}(\Lambda ), \end{aligned}$$

where we used that the two-dimensional lower Beurling density of $\Lambda ' \times {\mathbb {Z}}$ is $D^{-}(\Lambda )$.

$\square$

We can now prove the uniqueness Theorem. The proof builds on [4, Lemma 5.1] and [5, Theorems 4.3 and 4.9].

FormalPara Proof of Theorem 2

We proceed by induction on m in (1).

In the case $m=0$, the function g is a Gaussian $g(x) = C'_0 e^{-a x^2}$, with $a=\frac{\pi ^2}{\gamma }>0$. Let $f=\sum _k c_k g(\cdot -k)\in V^\infty (g)$ with c bounded be non-zero, and denote by $\Lambda \subseteq {\mathbb {R}}$ its zero set.

As shown in [5, Lemma 4.1], f possesses an extension to an entire function on $\mathbb {C}$, satisfying the growth estimate $|f(x+iy)| \lesssim e^{a y^2}$ for $x,y \in {\mathbb {R}}$, where the implied constant depends on f. Let $n \ge 0$ be the order of f at $z=0$, and consider the analytic function

$$F(z) := C_1 z^{-n} f(z) e^{\frac{a}{2} z^2},$$

where $C_1 \in \mathbb {C}$ is chosen so that $F(0)=1$. Then F satisfies

$$\begin{aligned} \left| F(x+iy) \right| \le C e^{ay^2} e^{\frac{a}{2} (x^2-y^2)} = C e^{\frac{a}{2} (x^2+y^2)}, \quad x,y \in {\mathbb {R}}, \end{aligned}$$

(11)

for some constant $C>0$. Moreover, the zero set of f is invariant under addition of $i\tfrac{\pi }{a}{\mathbb {Z}}$ [5, Lemma 4.2]. Therefore, the set of complex zeros of F contains $\big (\Lambda \setminus \{0\}\big ) + i\tfrac{\pi }{a}{\mathbb {Z}}$:

$$\begin{aligned} F \big (\lambda + i \tfrac{\pi }{a} k \big ) = 0, \quad \lambda \in \Lambda \setminus \{0\}, k \in {\mathbb {Z}}. \end{aligned}$$

By (6) with $\alpha =\tfrac{\pi }{a}$, the zero-counting function of F,

$$\begin{aligned} n_F(t) := \# \{ z \in \mathbb {C}: F(z)=0, \left| z \right| \le t \}, \end{aligned}$$

satisfies

$$\begin{aligned} \limsup _{r \longrightarrow \infty } \frac{1}{r^2} \int _0^r \frac{n_F(t)}{t} dt \ge \frac{a}{2} D^+_{\mathrm {circ}}(\Lambda ). \end{aligned}$$

(12)

On the other hand, by Jensen’s formula combined with (11), for all $r>0$,

$$\begin{aligned} \frac{1}{r^2} \int _0^r \frac{n_F(t)}{t} dt = \frac{1}{2\pi r^2} \int _0^{2\pi } \log |{F\big (r e^{i\theta }\big )}| d\theta \le \frac{\log (C)}{r^2} + \frac{a}{2}. \end{aligned}$$

(13)

By combining (12) and (13) we conclude that $D^+_{\mathrm {circ}}(\Lambda ) \le 1$, as claimed. Note, in particular, that $\Lambda$ has no accumulation points.

Inductive step. Let g be as in (1) and $f=\sum _k c_k g(\cdot -k) \in V^\infty (g)$ non-zero. Without loss of generality we assume that, in (1), $\delta _1, \ldots , \delta _m$ are non-zero. Since g is real-valued, by replacing $c_k$ with $\mathfrak {R}(c_k)$ or $\mathfrak {I}(c_k)$ if necessary, we may assume that f is real-valued. Let $g_1$ be given by (1), except that the product runs only up to $m-1$. Then

$$\begin{aligned} f_1 := f + \delta _m f' = \sum _{k\in {\mathbb {Z}}} c_k g_1(\cdot -k) \end{aligned}$$

belongs to $V^\infty (g_1)$ and is real-valued and non-zero, because the coefficients $c_k$ are real and at least one of them is non-zero. We assume by inductive hypothesis that $D^+_{\mathrm {circ}}(\{f_1=0\}) \le 1$.

Let $\Lambda =\{f=0\}$ and $\Gamma =\{f_1=0\}$. Suppose that $\Lambda$ has no accumulation points. Assume for the moment that, in addition, f has a non-negative zero, and order the set of non-negative zeros of f increasingly:

$$\begin{aligned} \Lambda \cap [0,\infty )=\{\lambda _k : k=0,\ldots ,N\}, \end{aligned}$$

where $N \in {\mathbb {N}}\cup \{0,\infty \}$, and we do not count multiplicities. Hence, $\lambda _k >0$, if $k>0$.

By Rolle’s Theorem applied to the differential operator $I + \delta _m \partial _x$, there is a sequence of zeros of $f_1$ that interlaces $\Lambda \cap [0,\infty )$. (Indeed, we note that $\frac{d}{dx} \big [ e^{x/\delta _m} f(x)\big ] = \frac{1}{\delta _m} e^{x/\delta _m} f_1(x)$ and apply the standard version of Rolle’s theorem; see [4, Lemma 5.1] or [5, Lemma 4.8] for details.) We parameterize that sequence as $\Gamma ^+=\big \{\gamma _k : k=1,\ldots ,N\}$, with

$$\begin{aligned} \lambda _{k-1}< \gamma _k < \lambda _k, \quad k>0. \end{aligned}$$

The set $\Gamma ^+$ is empty if $N=0$. For $t>0$, this ordering associates with each $\lambda _k \in (0,t]$, $k \not =0$, a distinct zero of $f_1$, $\gamma _k \in (0,t]$, such that the vertical segment through $\gamma _k$ contained in the disk $B_t(0)$ is longer than the corresponding segment through $\lambda _k$:

$$\begin{aligned} \sum _{k>0, \lambda _k \in (0,t] } \sqrt{t^2 - \lambda _k^2}&\le \sum _{k >0, \gamma _k \in (0,t] } \sqrt{t^2 - \gamma _k^2} \le \sum _{\gamma \in \Gamma \cap (0,t] } \sqrt{t^2 - \gamma ^2}; \end{aligned}$$

see Fig. 1.

Fig. 1

Each positive zero $\lambda _k$ of f is assigned to a zero $\gamma _k$ of $f_1$ in such a way that the corresponding vertical segments contained in the disk $B_t(0)$ become longer

We now add the term corresponding to $\lambda _0$, and bound $\sqrt{t^2 - \lambda _0^2} \le t$ to obtain

$$\begin{aligned} \sum _{\lambda \in \Lambda \cap [0,t] } \sqrt{t^2 - \lambda ^2} \le t + \sum _{\gamma \in \Gamma \cap (0,t] } \sqrt{t^2 - \gamma ^2}. \end{aligned}$$

The previous estimate is also trivially true is f has no non-negative zeros. Arguing similarly with the non-positive zeros of f we conclude that

$$\begin{aligned} \sum _{\lambda \in \Lambda \cap [-t,t] } \sqrt{t^2 - \lambda ^2} \le 2t + \sum _{\gamma \in \Gamma \cap [-t,t] } \sqrt{t^2 - \gamma ^2}. \end{aligned}$$

This shows that $D^+_{\mathrm {circ}}(\{f=0\}) \le D^+_{\mathrm {circ}}(\{f_1=0\})$. The latter quantity is bounded by 1 by inductive hypothesis. Finally, if $\Lambda =\{f=0\}$ has an accumulation point, Rolle’s theorem applied as before shows that so does $\Gamma =\{f_1=0\}$, and, therefore, $D^+_{\mathrm {circ}}(\{f_1=0\}) = \infty$ contradicting the inductive hypothesis. $\square$