Abstract
We refine a result of Matei and Meyer on stable sampling and stable interpolation for simple model sets. Our setting is model sets in locally compact abelian groups and Fourier analysis of unbounded complex Radon measures as developed by Argabright and de Lamadrid. This leads to a refined version of the underlying model set duality between sampling and interpolation. For rather general model sets, our methods also yield an elementary proof of stable sampling and stable interpolation sufficiently far away from the critical density, which is based on the Poisson Summation Formula.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Background and Plan of the Article
Sampling concerns the problem of reconstructing a function f from its restriction \(f|_\Lambda \) to a subdomain \(\Lambda \). Interpolation concerns the question of how to extend a function defined on the subdomain. For particular function spaces, both problems are classical in harmonic analysis. We are interested in irregular sampling domains arising from model sets in locally compact abelian (LCA) groups.
Let us explain our notation. For a subset \(A\subset X\) in some topological space X, we write \(A^c=X\setminus A\) for its complement in X. We will denote the topological closure and interior of A by \(\mathrm {cl}(A)\) and \(\mathrm {int}(A)\), respectively. We denote by \(\partial A=\mathrm {cl}(A)\setminus \mathrm {int}(A)\) the topological boundary of A. We denote by \(\mathbf{1}_{A}\) the indicator function of A. Let G be an LCA group with Haar measure \(\theta _G\). Following [16, 36], we say that \(A\subset G\) has almost no boundary if \(\theta _G(\partial A)=0\). We say that measurable \(A\subset G\) has almost no inner boundary if \(\theta _G(A\cap \partial A)=0\). A real-valued function \(f:G\rightarrow {\mathbb {R}}\) is Riemann integrable if for every \(\varepsilon >0\) there are continuous compactly supported functions \(u,v\in C_c(G)\) such that \(u\leqslant f \leqslant v\) and \(\int (v-u) \mathrm{d}\theta _{G}\leqslant \varepsilon \). We call \(f:G\rightarrow {\mathbb {C}}\) Riemann integrable if both its real and imaginary part are Riemann integrable. Consider relatively compact \(A\subset G\). Then A has almost no boundary if and only if \(\mathbf{1}_{A}\) is Riemann integrable.
1.1 Function Spaces
Consider an LCA group G and its dual group  . Later, we will sometimes require G to be \(\sigma \)-compact or metrizable. Note that \(\sigma \)-compactness and metrizability are dual notions [15, (24.48)], and that \(\sigma \)-compactness and metrizability is equivalent to second countability [6, Chapter IX, Sect. 2.9, Corollary]. As a consequence, second countability of G is equivalent to second countability of
. Later, we will sometimes require G to be \(\sigma \)-compact or metrizable. Note that \(\sigma \)-compactness and metrizability are dual notions [15, (24.48)], and that \(\sigma \)-compactness and metrizability is equivalent to second countability [6, Chapter IX, Sect. 2.9, Corollary]. As a consequence, second countability of G is equivalent to second countability of  . Fix Haar measures \(\theta _G\) on G and
. Fix Haar measures \(\theta _G\) on G and  on
on  such that the Fourier inversion theorem [33, Theorem 4.4.5] holds. Recall that for integrable \(f:G\rightarrow {\mathbb {C}}\), its Fourier transform is defined by
such that the Fourier inversion theorem [33, Theorem 4.4.5] holds. Recall that for integrable \(f:G\rightarrow {\mathbb {C}}\), its Fourier transform is defined by  for
for  . We also write
. We also write  for the inverse Fourier transform.
for the inverse Fourier transform.
Definition 1.1
(Paley–Wiener space) Let G be an LCA group. Consider  to be relatively compact and measurable. Then the translation invariant vector space of functions with restricted band width
to be relatively compact and measurable. Then the translation invariant vector space of functions with restricted band width

is called the Paley–Wiener space with respect to K.
Remark 1.2
-
(i)
We consider relatively compact K in this article only. Then G may be assumed to be metrizable. Indeed, for relatively compact K we may assume that
 is compactly generated without loss of generality, see [14, Sect. 8].
is compactly generated without loss of generality, see [14, Sect. 8]. -
(ii)
Note that \(f\in {{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) satisfies
 . Indeed,
. Indeed,  follows from Hölder’s inequality by assumption on K. We thus have
follows from Hölder’s inequality by assumption on K. We thus have  and
and  in \(L^2(G)\) by the Fourier inversion theorem. Hence any equivalence class \(f\in {{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) has a unique continuous representative. In this article, we will always consider \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) as a space of continuous functions.
in \(L^2(G)\) by the Fourier inversion theorem. Hence any equivalence class \(f\in {{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) has a unique continuous representative. In this article, we will always consider \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) as a space of continuous functions. -
(iii)
Note that \(({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K, \Vert \cdot \Vert _{L^2(G)})\) is a Hilbert space. Closedness is obvious from continuity of the map
 . The above definition is also used in [2, 19]. Another definition is used in [13, 23]. If K is closed in
. The above definition is also used in [2, 19]. Another definition is used in [13, 23]. If K is closed in  , then both definitions are equivalent. This is discussed in Sect. 8.
, then both definitions are equivalent. This is discussed in Sect. 8.
The following subspace of \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) will be central in our subsequent analysis, as it provides continuous test functions for complex Radon measures which are transformable in the sense of Argabright and de Lamadrid [3, 34]. It is defined to be

In this article, we consider \({{\,\mathrm{{\mathcal {S}}}\,}}_K\) as a space of continuous functions. Any \(f\in {{\,\mathrm{{\mathcal {S}}}\,}}_K\) satisfies \(f\in L^1(G)\cap L^2(G)\) and  . Note that \({{\,\mathrm{{\mathcal {S}}}\,}}_K\) is dense in \(({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K, \Vert \cdot \Vert _{L^2(G)})\) if and only if K has almost no inner boundary, see Proposition 8.1.
. Note that \({{\,\mathrm{{\mathcal {S}}}\,}}_K\) is dense in \(({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K, \Vert \cdot \Vert _{L^2(G)})\) if and only if K has almost no inner boundary, see Proposition 8.1.
1.2 Stable Sampling and Stable Interpolation
The stable sampling condition ensures that any (continuous) Paley–Wiener function is reconstructable in a stable way from its values on a given uniformly discrete point set. We say that \(\Lambda \subset G\) is uniformly discrete if there exists a compact zero neighborhood \(B\subset G\) such that \(\mathrm {card}(\Lambda \cap (x+B))\leqslant 1\) for all \(x\in G\).
Definition 1.3
(stable sampling) Let G be an LCA group and let  be relatively compact and measurable. A uniformly discrete set \(\Lambda \subset G\) is stable sampling for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) if and only if there exist positive finite constants A, B such that
be relatively compact and measurable. A uniformly discrete set \(\Lambda \subset G\) is stable sampling for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) if and only if there exist positive finite constants A, B such that
for all \(f\in {{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\).
If \(\Lambda \) is stable sampling for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\), then any \(f\in {{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) is uniquely determined by its values on \(\Lambda \). Indeed, for \(f_1,f_2\in {{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) satisfying \({f_1}|_\Lambda ={f_2}|_\Lambda \) we have \(f=f_1-f_2\in {{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\), too. Thus \(\Vert f\Vert _{L^2(G)}\leqslant 0\), which implies \(f=0\) pointwise by continuity of f.
For a uniformly discrete set \(\Lambda \), stable interpolation for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) may be described as follows: For every square integrable sequence \(\varphi \in \ell ^2(\Lambda )\) there exists at least one \(f\in {{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) such that \(f=\varphi \) on \(\Lambda \). As discussed in Remark 1.5, this interpolation property is rephrased in the following definition.
Definition 1.4
(stable interpolation) Let G be an LCA group and let \(K\subset {\widehat{G}}\) be relatively compact and measurable. A uniformly discrete set \(\Lambda \subset G\) is stable interpolating for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) if and only if there exist positive finite constants A, B such that

for all finitely supported \(\varphi \in \ell ^2(\Lambda )\). Here  is the discrete Fourier transform of \(\varphi \) given by \(f_\varphi (\chi )=\sum _{\lambda \in \Lambda }\varphi (\lambda )\overline{\chi (\lambda )}\).
is the discrete Fourier transform of \(\varphi \) given by \(f_\varphi (\chi )=\sum _{\lambda \in \Lambda }\varphi (\lambda )\overline{\chi (\lambda )}\).
Remark 1.5
As is well known, stable sampling and stable interpolating can be rephrased using Hilbert space techniques [38]. Let us briefly indicate this connection in order to clarify the above definitions. For relatively compact and measurable  consider the Hilbert space \(L^2(K)\), compare Lemma 8.4. The Fourier transform provides a norm preserving isomorphism between \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) and \(L^2(K)\). For \(x\in G\) consider the “exponential”
consider the Hilbert space \(L^2(K)\), compare Lemma 8.4. The Fourier transform provides a norm preserving isomorphism between \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) and \(L^2(K)\). For \(x\in G\) consider the “exponential”  defined by \(e_x(\chi ):=\chi (x)\) for all
defined by \(e_x(\chi ):=\chi (x)\) for all  . If \(\langle \cdot , \cdot \rangle \) denotes the usual scalar product in \(L^2(K)\), we then have for any \(f\in {{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) and any \(x\in G\) that
. If \(\langle \cdot , \cdot \rangle \) denotes the usual scalar product in \(L^2(K)\), we then have for any \(f\in {{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) and any \(x\in G\) that

For a uniformly discrete set \(\Lambda \subset G\) consider \(E(\Lambda )\subset L^2(K)\) defined by
The stable sampling inequalities say that \(E(\Lambda )\) is a so-called frame in \(L^2(K)\). In our setting frame theory provides a reconstruction algorithm for  , see e. g. [38, p. 159]. The interpolation property is equivalent to requiring that \(E(\Lambda )\) is a so-called Riesz–Fischer sequence. Hilbert space arguments for Riesz–Fischer sequences, see e. g. [38, p. 129], can be used to infer the following: The interpolation property is equivalent to the existence of a lower inequality in Eq. (1.2). Moreover, existence of an upper inequality in Eq. (1.2) is equivalent to the existence of an upper inequality in Eq. (1.1). Is is well known that the upper inequalities hold for uniformly discrete sets \(\Lambda \). We will give an elementary proof of the upper inequality for interpolation in Lemma 3.1.
, see e. g. [38, p. 159]. The interpolation property is equivalent to requiring that \(E(\Lambda )\) is a so-called Riesz–Fischer sequence. Hilbert space arguments for Riesz–Fischer sequences, see e. g. [38, p. 129], can be used to infer the following: The interpolation property is equivalent to the existence of a lower inequality in Eq. (1.2). Moreover, existence of an upper inequality in Eq. (1.2) is equivalent to the existence of an upper inequality in Eq. (1.1). Is is well known that the upper inequalities hold for uniformly discrete sets \(\Lambda \). We will give an elementary proof of the upper inequality for interpolation in Lemma 3.1.
1.3 Landau’s Necessity Conditions
In Euclidean space, necessary conditions for \(\Lambda \) to be a set of stable sampling or of stable interpolation for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) have been given by Landau [20]. These have been extended to general LCA groups in [14]. The conditions are formulated in terms of a particular uniform density.
In order to compute asymptotic frequencies, one often uses suitable averaging sequences generalizing balls, whose “boundary to bulk ratio” vanishes asymptotically. We will work with so-called van Hove sequences. For their definition, consider \(A\subset G\) and a compact set \(K\subset G\). The K-boundary of A is given by
Note that \(\partial ^K\!A\) is compact if A is relatively compact. As \(\partial A=\partial ^{\{e\}}A\subset \partial ^U\!A\) for U any compact zero neighborhood, the van Hove boundary may be considered as a thickened topological boundary in that case. The value \(\theta _G(\partial ^U \! A)\), where \(\theta _G\) is the chosen Haar measure on G and A is relatively compact, can be chosen arbitrarily close to \(\theta _G(\partial A)\) for sufficiently concentrated zero neighborhoods U, compare [16, Lemma 4.4]. A sequence \((A_n)_{n\in {\mathbb {N}}}\) of compact sets in G of positive Haar measure is van Hove if and only if
for every compact set K in G. Van Hove sequences have been introduced by Schlottmann [37] for model set analysis, where also their existence in \(\sigma \)-compact LCA groups is shown. In Euclidean space, any sequence of nonempty compact rectangular boxes of diverging positive inradius is a van Hove sequence, as well as any sequence of compact nonempty balls of diverging positive radius is a van Hove sequence. In general, note that the van Hove property is stable under shifting, i. e., for a van Hove sequence \((A_n)_{n\in {\mathbb {N}}}\) the sequence \((A_n+x_n)_{n\in {\mathbb {N}}}\) is still van Hove, for any shift sequence \((x_n)_{n\in {\mathbb {N}}}\). Further properties are collected in Sect. 9. For additional background, see e. g. [16, 22, 31] and references therein.
Definition 1.6
(Banach densities) Let \(\Lambda \) be a uniformly discrete set in a \(\sigma \)-compact LCA group G. Let \({{\mathcal {A}}}=(A_n)_{n\in {\mathbb {N}}}\) be any van Hove sequence in G. We define the lower and upper Banach densities
If \({{\mathcal {D}}}^-_{{\mathcal {A}}}(\Lambda )={{\mathcal {D}}}^+_{{\mathcal {A}}}(\Lambda )=:{{\mathcal {D}}}(\Lambda )\), we say that \(\Lambda \) has Banach density \({{\mathcal {D}}}(\Lambda )\).
The above densities are finite due to uniform discreteness of \(\Lambda \). In \(G={\mathbb {R}}^d\) and with centered n-balls \(A_n\), the above densities are also called Landau-Beurling densities, compare [14, Sect. 7]. In ergodic theory or number theory, the attribution to Banach is more common. Note that existence of a Banach density implies independence of the choice of the van Hove sequence. Banach densities exist for any regular model set by Fact 6.2, see Sect. 2 for definitions. In particular any lattice L in G, i. e., any discrete co-compact subgroup of G, has a Banach density, which equals the inverse measure of a measurable fundamental domain. For countable LCA groups and uniformly discrete \(\Lambda \), it has recently been shown that the lower and upper Banach densities exist as a limit [8, Sect. 2.2].
We rephrase Theorem 1” from [14] using upper and lower Banach densities. This is justified by Lemma 9.3.
Fact 1.7
(Landau’s necessity conditions) Let G be a \(\sigma \)-compact LCA group. Let  be a relatively compact measurable set. Let \(\Lambda \subset G\) be a uniformly discrete set and let \({{\mathcal {A}}}\) be any van Hove sequence in G. Then the following hold.
be a relatively compact measurable set. Let \(\Lambda \subset G\) be a uniformly discrete set and let \({{\mathcal {A}}}\) be any van Hove sequence in G. Then the following hold.
-
(a)
If \(\Lambda \) is stable sampling for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\), then
 .
. -
(b)
If \(\Lambda \) is stable interpolating for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\), then
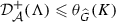 . \(\square \)
. \(\square \)
1.4 Sampling and Interpolation Near the Critical Density
An interesting problem concerns the question which point sets admit stable sampling or stable interpolation arbitrarily close to the above critical density value  . A classic result for subsets of the line traces back to works of Ingham, Beurling and Kahane. See [23, Theorems 4.3, 4.5] for the statement and a discussion.
. A classic result for subsets of the line traces back to works of Ingham, Beurling and Kahane. See [23, Theorems 4.3, 4.5] for the statement and a discussion.
Fact 1.8
(Stable sampling and stable interpolation on the line) Let \(I\subset {\mathbb {R}}\) be a bounded interval, and let \(\Lambda \subset {\mathbb {R}}\) be a uniformly discrete set. Let \({\mathcal {A}}\) be any van Hove sequence of intervals in \({\mathbb {R}}\).
-
(i)
If \({\mathcal {D}}_{{\mathcal {A}}}^-(\Lambda )>{|}I{|}\), then \(\Lambda \) is stable sampling for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_I\).
-
(ii)
If \({\mathcal {D}}_{{\mathcal {A}}}^+(\Lambda )<{|}I{|}\), then \(\Lambda \) is stable interpolating for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_I\). \(\square \)
For so-called simple model sets in Euclidean space, a corresponding result has been proved by Matei and Meyer [23, Theorem 3.2]. For general LCA groups, sampling and interpolation sets arbitrarily close to the critical density have been constructed in [1]. For simple model sets in general LCA groups, an extension of [23] has been suggested by Agora et al. [2, Theorem 6]. As emphasized in [13, 19], these results rely on a duality between stable sampling and stable interpolation for model sets having Euclidean internal space. This duality allows to transfer the general problem to the line, where Fact 1.8 can be invoked.
In Theorem 7.1, we will formulate the sampling and interpolation duality for model sets in the framework of LCA groups, where we use Fourier analysis of unbounded complex Radon measures as developed by Argabright and de Lamadrid [3]. This setting is well suited, since integrable Paley–Wiener functions are test functions for transformable measures. In our proof, we follow the constructions of Matei and Meyer but argue without Bruhat–Schwartz functions, which are used in [2]. A central part of the proof relies on mathematical diffraction theory as described in e.g. [30, 34], see also [35] for a recent review. In comparison to previous results, our approach yields additional structural insight, which results in a refined version of the duality theorem in a more general setting. See Sect. 7.1 for further discussion.
As an application, we obtain the following version of the stable sampling and stable interpolation theorem for simple model sets. Cut-and-project schemes and model sets will be defined in the following section. Note that the model sets in the theorem below have a Banach density.
Theorem 1.9
(Stable sampling and stable interpolation for simple model sets) Let \((G,H,{{\mathcal {L}}})\) be a complete cut-and-project scheme, where G is a \(\sigma \)-compact LCA group and where \(H={\mathbb {R}}\). Let \(I\subset H\) be a bounded nonempty interval and let \(\Lambda _I\subset G\) be the associated model set. Assume that  is relatively compact and measurable. Then the following hold.
is relatively compact and measurable. Then the following hold.
-
(i)
If
 , then \(\Lambda _{I}\) is stable sampling for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\).
, then \(\Lambda _{I}\) is stable sampling for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\). -
(ii)
If
 , then \(\Lambda _I\) is stable interpolating for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_{K}\).
, then \(\Lambda _I\) is stable interpolating for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_{K}\).
Remark 1.10
-
(i)
Let us compare the above result to [23, Theorem 3.2] and to [2, Theorem 6]. In those references, it is assumed that K is compact, and for (ii) it is assumed in addition that K has almost no boundary, i.e.,
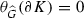 . However these assumptions are not necessary, as may be seen by approximation arguments using regularity of the Haar measure.
. However these assumptions are not necessary, as may be seen by approximation arguments using regularity of the Haar measure. -
(ii)
We can slightly relax the completeness assumption on the cut-and-project scheme, see Remark 7.3 and the proof of Theorem 1.9: From the four projection assumptions in the complete cut-and-project scheme \((G,H,{{\mathcal {L}}})\) described in Definition 2.1, the proof of (i) does not use that \({{\mathcal {L}}}\) projects densely to H. The proof of (ii) only uses that \({{\mathcal {L}}}\) projects densely to G and injectively to H.
-
(iii)
The works [13, 19] construct model sets \(\Lambda _I\) in Euclidean space which are simultaneously stable sampling and stable interpolating. This is possible if \(\Lambda _I\) has critical Banach density
 , if
, if  , and if K is a so-called bounded remainder set. In particular in [19, Lemma 2.1] and [13, Theorem 3.1], the arguments leading to [23, Theorem 3.2] are reviewed.
, and if K is a so-called bounded remainder set. In particular in [19, Lemma 2.1] and [13, Theorem 3.1], the arguments leading to [23, Theorem 3.2] are reviewed.
In fact, our methods also allow to prove stable sampling and stable interpolation for general weak model sets sufficiently far away from the critical density. This will be done in the first part of the article, see Propositions 4.3 and 3.2. That part will also serve as a preparation for the second part of the article, as some of the corresponding arguments will reappear in the proof of the duality theorem.
1.5 Outline of the Article
In Sect. 2, we review weighted model combs and introduce our notation. Section 3 is devoted to a proof of stable interpolation for weak model sets away from the critical density. Section 4 is devoted to a proof of stable sampling for weak model sets away from the critical density. Although we discuss in Sect. 5 that our results are not optimal, we believe that our techniques, which presently rely on standard estimates, may be substantially refined. Section 6 discusses density formulae for model sets. This is a preparation for the proof of the duality theorem, which uses a density formula with smooth averaging functions instead of van Hove sequences. Section 7 contains a proof of the duality theorem for stable sampling and stable interpolation. We conclude that section with a proof of Theorem 1.9. The last sections collect some facts about Paley–Wiener spaces, van Hove sequences and Banach densities.
Notes added in proof
-
(i)
After submitting this manuscript, the authors became aware of recent work by Meyer [28], where he reviews his constructions for simple model sets in Euclidean space and gives an alternative proof of [23, Theorem 3.2], again by reduction to the line. Meyer’s proof uses a duality principle from [27]. It differs from the Duality Theorem 7.1, which is based on square integrable Paley–Wiener functions.
-
(ii)
After submitting this manuscript, the authors observed that the Poisson Summation Formula of Lemma 2.7 actually holds for \(g\in S_0(G)\) and \(h\in S_0(H)\), where \(S_0(G)\) is Feichtinger’s Segal algebra [11], see [17] for a recent review. In fact, as kindly pointed out to us by Prof. Feichtinger, the Fourier theory of translation bounded Radon measures of Argabright and de Lamadrid is subsumed by distribution theory based on \(S_0(G)\), see [9, Anwendung (D)] and [10, Théorème C.1]. Also, the Banach Gelfand Triple based on \(S_0(G)\) provides a useful setting for sampling and interpolation problems, see e.g. [12]. Using that setting, one might obtain alternative derivations of results in this article. Indeed, steps into that direction appear in [24], where Gabor analysis is extended to simple model sets in Euclidean space.
2 Weighted Model Sets
In order to set up our notation, we recall relevant notions related to model sets, following the monograph [4] where possible.
2.1 Cut-and-Project Schemes and Weak Model Sets
Definition 2.1
(Cut-and-project scheme) Let G, H be LCA groups, and let \({{\mathcal {L}}}\subset G\times H\) be a lattice, i. e., a discrete co-compact subgroup in \(G\times H\). We then call \((G,H,{{\mathcal {L}}})\) a bare cut-and-project scheme. If \({{\mathcal {L}}}\) projects injectively to G and densely to H, then \((G,H,{{\mathcal {L}}})\) is called a cut-and-project scheme. If \({{\mathcal {L}}}\) projects injectively and densely to both G and H, we call \((G,H,{{\mathcal {L}}})\) a complete cut-and-project scheme.
Remark 2.2
For a (bare) cut-and-project scheme \((G,H,{{\mathcal {L}}})\), we will denote by \(\pi _G:G\times H\rightarrow G\) and \(\pi _H:G\times H\rightarrow H\) the canonical projections. Denseness of \(\pi _H({{\mathcal {L}}})\) can always be obtained by passing from H to the LCA group \(H'=\mathrm {cl}(\pi _H({{\mathcal {L}}}))\). Injectivity of \(\pi _G|_{{\mathcal {L}}}\) allows to identify \({{\mathcal {L}}}\) and \(\pi _G({{\mathcal {L}}})\). This identification will repeatedly be used below. The name complete cut-and-project scheme appears in [2], where also some structure theory is developed.
Model sets in G are obtained by “cutting from \({{\mathcal {L}}}\) all points inside some strip parallel to G” and projecting them to G. An analogous construction can be used to obtain point sets in H. This is the content of the following definition.
Definition 2.3
(Weak model set) Assume that \((G,H,{{\mathcal {L}}})\) is a bare cut-and-project scheme. Take a window \(W\subset H\) and consider the projection set \(\Lambda _W\subset G\) defined by
If \((G,H,{{\mathcal {L}}})\) is a cut-and-project scheme, then
-
(i)
\(\Lambda _W\) is called a weak model set if W is relatively compact.
-
(ii)
\(\Lambda _W\) is called a model set if \(\Lambda _W\) is a weak model set and if W has nonempty interior.
-
(iii)
\(\Lambda _W\) is called a regular model set if \(\Lambda _W\) is a model set and if \(\theta _H(\partial W)=0\).
We may take a window \(V\subset G\) and consider the projection set \(_V\Lambda \subset H\) defined by
If \((G,H,{{\mathcal {L}}})\) is a complete cut-and-project scheme, we call \(_V\Lambda \) a (weak, regular) model set depending on the corresponding properties of V.
Remark 2.4
(Elementary properties of projection sets) Any weak model set is uniformly discrete. More generally, any projection set with relatively compact window is uniformly discrete, compare to [29, Proposition 2.6(i)]. Any model set is relatively dense. The proof of the latter statement uses that \({{\mathcal {L}}}\) projects densely to H, compare the proof of [29, Proposition 2.6(i)]. For any regular model set in a \(\sigma \)-compact group G, all of its pattern frequencies exist as a limit which is uniform in shifts of the chosen averaging sequence, see also below. Projection sets \(\Lambda \) with relatively compact window are of finite local complexity, i. e., we have \(\Lambda -\Lambda \subset \Lambda +F\), where F is some finite set. One also says that \(\Lambda \) is an almost lattice.
Remark 2.5
(Star map) If \((G,H,{{\mathcal {L}}})\) is a bare cut-and-project scheme and if \({{\mathcal {L}}}\) projects injectively to G, then the star map
is well defined. Hence we can write \(\Lambda _W=\{g\in \pi _G({{\mathcal {L}}}):s(g)\in W\}\) in that case. If \((G,H,{{\mathcal {L}}})\) is a complete cut-and-project scheme, then the star map is a bijection. Hence in that case we may write \(_V \Lambda =\{h\in \pi _H({{\mathcal {L}}}):s^{-1}(h)\in V\}\).
2.2 Dual Cut-and-Project Scheme
We recall duality for cut-and-project schemes, compare [29]. Denote by \({{\mathcal {L}}}_0\subset {\widehat{G}}\times {\widehat{H}}\) the annihilator of \({\mathcal {L}}\), i. e.,
By Pontryagin duality, is a \({{\mathcal {L}}}_0\) is lattice in  ,
,  is one-to-one iff \(\pi _{{\widehat{H}}}({{\mathcal {L}}}_0)\) is dense in \({\widehat{H}}\), and \(\pi _H({{\mathcal {L}}})\) is dense in H iff \(\pi _{{\widehat{G}}}|_{{{\mathcal {L}}}_0}\) is one-to-one. Hence we can define
is one-to-one iff \(\pi _{{\widehat{H}}}({{\mathcal {L}}}_0)\) is dense in \({\widehat{H}}\), and \(\pi _H({{\mathcal {L}}})\) is dense in H iff \(\pi _{{\widehat{G}}}|_{{{\mathcal {L}}}_0}\) is one-to-one. Hence we can define
Lemma 2.6
(Dual cut-and-project scheme) Let \((G,H,{{\mathcal {L}}})\) be a bare cut-and-project scheme. Then \(({\widehat{G}},{\widehat{H}},{{\mathcal {L}}}_0)\) is a bare cut-and-project scheme, which we call the dual cut-and-project scheme. If \((G,H,{{\mathcal {L}}})\) is a (complete) cut-and-project scheme, then \(({\widehat{G}},{\widehat{H}},{{\mathcal {L}}}_0)\) is a (complete) cut-and-project scheme as well. \(\square \)
We write \({\widehat{s}}:\pi _{{\widehat{G}}}({{\mathcal {L}}}_0)\rightarrow \pi _{{\widehat{H}}}({{\mathcal {L}}}_0)\) for the star map in the dual cut-and-project scheme \(({\widehat{G}},{\widehat{H}},{{\mathcal {L}}}_0)\). In the following, given a relatively compact subset  , we will frequently consider the projection set
, we will frequently consider the projection set

2.3 Weighted Model Combs and Their Transforms
Instead of working with point sets in G, it is sometimes advantageous to consider associated weighted Dirac combs. Let us denote by \({\mathcal {M}}(G)\) the space of complex Radon measures on G. Assume that \((G,H,{{\mathcal {L}}})\) is a bare cut-and-project scheme and that \(h:H\rightarrow {\mathbb {C}}\) is a bounded function such that
is a complex Radon measure on G, i. e., we have \(\omega _h\in {\mathcal {M}}(G)\). Then \(\omega _h\) is called a weighted model comb, and h is called its weight function. Examples of weight functions are \(h\in C_c(H)\) and \(h=\mathbf{1}_{W}\) for relatively compact \(W\subset H\), see the proof of Lemma 4.8 in [35]. We have \(\Lambda _W={{\,\mathrm{supp}\,}}(\omega _{\mathbf{1}_{W}})\), where \({{\,\mathrm{supp}\,}}\) denotes the measure-theoretic support. Another example is \(h\in C_0(H)\) of sufficiently fast decay [22].
We will also consider weighted model combs \(_g\omega =\sum _{(x,y)\in {{\mathcal {L}}}} g(x)\delta _y\) for bounded \(g:G\rightarrow {\mathbb {C}}\) such that \(_g\omega \in {\mathcal {M}}(H)\). For relatively compact \(V\subset G\), we have \(_V \Lambda ={{\,\mathrm{supp}\,}}(_{\mathbf{1}_{V}}\omega )\).
Consider the associated dual cut-and-project scheme  . As no confusion may arise, we will denote weighted model combs in that scheme by the same symbol, i. e., we write
. As no confusion may arise, we will denote weighted model combs in that scheme by the same symbol, i. e., we write
for bounded  . If \(\psi =\mathbf{1}_{\Omega }\) for
. If \(\psi =\mathbf{1}_{\Omega }\) for  , we have \(\Lambda _\Omega ={{\,\mathrm{supp}\,}}(\omega _{\mathbf{1}_{\Omega }})\).
, we have \(\Lambda _\Omega ={{\,\mathrm{supp}\,}}(\omega _{\mathbf{1}_{\Omega }})\).
Recall that \(\mu \in {\mathcal {M}}(G)\) is translation bounded if \(\sup _{t\in G}{|}\mu {|}(K+t)<\infty \) for every compact \(K\subset G\), where \({|}\mu {|}\) is the total variation measure of \(\mu \), see e.g. [3, Chapter 1]. Let us denote by \({\mathcal {M}}^\infty (G)\) the space of translation bounded complex Radon measures on G. Observing that \({|}\omega _h{|}=\omega _{{|}h{|}}\), we conclude \(\omega _h\in {\mathcal {M}}^\infty (G)\) for \(h\in C_c(H)\) or for \(h=\mathbf{1}_{W}\) with relatively compact \(W\subset H\). We write \(L^1(\mu )\) for the space of \({|}\mu {|}\)-integrable functions.
As weighted model combs are complex Radon measures, one might apply Fourier analysis of complex Radon measures as developed by Argabright and de Lamadrid [3, 30, 34, 35]. Weighted model sets satisfy a Poisson Summation Formula for a large class of test functions. Consider the function spaces

and note \({{\,\mathrm{{\mathcal {S}}}\,}}_K\subset LK(G)\) for all measurable relatively compact  . Let us denote by \(KL(G)+LK(G)\) the vector space of linear combinations of functions from KL(G) or LK(G). We have the following result.
. Let us denote by \(KL(G)+LK(G)\) the vector space of linear combinations of functions from KL(G) or LK(G). We have the following result.
Lemma 2.7
(Transform of weighted model combs) Let \((G,H,{{\mathcal {L}}})\) be a bare cut-and-project scheme. Assume that \(h\in KL(H)+LK(H)\). Then both \(\omega _h\) and  are translation bounded complex Radon measures. Moreover the Poisson Summation Formula
are translation bounded complex Radon measures. Moreover the Poisson Summation Formula

holds for every \(g\in KL(G)+ LK(G)\).
Remark 2.8
Here \({{\,\mathrm{dens}\,}}({{\mathcal {L}}})\) is the reciprocal Haar measure of a measurable fundamental domain of \({{\mathcal {L}}}\). It coincides with the density of lattice points, evaluated on any van Hove sequence. Note that \({{\,\mathrm{dens}\,}}({{\mathcal {L}}})\cdot {{\,\mathrm{dens}\,}}({{\mathcal {L}}}_0)=1\).
Proof of Lemma 2.7
By linearity, it suffices to show the claim for \(g\in KL(G)\cup LK(G)\) and \(h\in KL(H)\cup LK(H)\). Assume that \(h\in KL(H)\). Then \(\omega _h\in {\mathcal {M}}^\infty (G)\). As \(\omega _h\) is transformable by [34, Theorem 4.10], also  is a translation bounded complex Radon measure. Note that the Poisson Summation Formula (2.1) holds for all \(g\in KL(G)\) and \(h\in KL(H)\) by [34, Theorem 4.10 (ii)]. In fact, the same formula also holds for \(g\in LK(G)\) and \(h\in KL(H)\). Indeed, as \(\omega _h\) is twice transformable by [34, Theorem 4.12] and
is a translation bounded complex Radon measure. Note that the Poisson Summation Formula (2.1) holds for all \(g\in KL(G)\) and \(h\in KL(H)\) by [34, Theorem 4.10 (ii)]. In fact, the same formula also holds for \(g\in LK(G)\) and \(h\in KL(H)\). Indeed, as \(\omega _h\) is twice transformable by [34, Theorem 4.12] and  by the Fourier inversion theorem, we have
by the Fourier inversion theorem, we have

where \(h^\dag (y)=h(-y)\). Here the first equation is double transformability of \(\omega _h\), and the second equation is transformability of  . The statement for \(h\in LK(H)\) now follows from the above arguments by double transformability of
. The statement for \(h\in LK(H)\) now follows from the above arguments by double transformability of  . \(\square \)
. \(\square \)
2.4 Averages and van Hove Sequences
With respect to Fourier analysis, characteristic functions of van Hove sequences behave similarly to rectangular functions of increasing width in \({\mathbb {R}}\).
Lemma 2.9
[34, Lemma, 3.14] Let G be a \(\sigma \)-compact LCA group and let \((A_n)_{n\in {\mathbb {N}}}\) be a van Hove sequence in G. We then have pointwise

where  denotes the identity character. \(\square \)
denotes the identity character. \(\square \)
3 Stable Interpolation by Model Sets
3.1 An Interpolation Upper Bound
As is well known, the interpolation upper bound holds for arbitrary uniformly discrete point sets. Here we give a short direct proof based on Dirac nets and Fourier analytic arguments. These will later reappear in the proof of the Duality Theorem 7.1. Recall that a Dirac net in a general LCA group G is a net \((v_j)_{j\in J}\) in G such that \(v_j\in C_c(G)\), \(v_j\geqslant 0\) and \(\int _{G} v_j\,{\mathrm d}\theta _{G}=1\) for all j. Furthermore the support of \(v_j\) shrinks, i. e., for every zero neighborhood \(U\subset G\) there exists \(j_0\in J\) such for all \(j\geqslant j_0\) we have \({{\,\mathrm{supp}\,}}(v_j)\subset U\). For the construction of such a net see e. g. [7, Lemma 1.6.5]. If the LCA group G is metrizable, we can work with Dirac sequences \((v_n)_{n\in {\mathbb {N}}}\) instead of Dirac nets.
Lemma 3.1
(Upper bound for interpolation from uniformly discrete sets) Let G be any LCA group. Let \(\Lambda \subset G\) be any uniformly discrete point set in G. Consider any measurable relatively compact  . Then there exists a finite constant \(B=B(\Lambda , K)\) such that
. Then there exists a finite constant \(B=B(\Lambda , K)\) such that

for all finitely supported \(\varphi :\Lambda \rightarrow {{\mathbb {C}}}\).
Recall that  denotes the discrete Fourier transform of \(\varphi \), which is defined by \(f_\varphi (\chi )=\sum _{\lambda \in \Lambda }\varphi (\lambda )\overline{\chi (\lambda )}\).
denotes the discrete Fourier transform of \(\varphi \), which is defined by \(f_\varphi (\chi )=\sum _{\lambda \in \Lambda }\varphi (\lambda )\overline{\chi (\lambda )}\).
Proof
Take any Dirac net \((v_j)_{j\in J}\) in G of positive definite functions, compare [7, Lemma 3.4.1]. Fix \(\varepsilon \in (0,1)\) and choose \(j=j(\Lambda , K, \varepsilon )\) sufficiently large such that the following two properties are satisfied.
-
(a)
For any \(\lambda \in \Lambda \), the set \({{\,\mathrm{supp}\,}}(v_j)+\lambda \) contains exactly one point of \(\Lambda \). This is possible as \(\Lambda \) is uniformly discrete.
-
(b)
We have
 on K. This is possible as
on K. This is possible as  is non-negative for every j and since
is non-negative for every j and since  converges locally uniformly to one by [7, Lemma 3.4.5].
converges locally uniformly to one by [7, Lemma 3.4.5].
Now take any \(\varphi \in \ell ^2(\Lambda )\) of finite support and define \(f_j\in L^2(G)\cap C_c(G)\) by
Note that by the support condition on \(v_j\) we have  . A straightforward calculation shows
. A straightforward calculation shows  , where
, where

We can thus conclude

Since  on K, we have
on K, we have

for every \(\varphi \in \ell ^2(\Lambda )\) of finite support. Thus \(B=\Vert v_j\Vert _{L^2(G)}^2/\varepsilon ^2\) gives an upper bound for stable interpolation. \(\square \)
3.2 An Interpolation Lower Bound
Proposition 3.2
(Interpolation lower bound) Consider any bare cut-and-project scheme \((G,H,{{\mathcal {L}}})\), where G is metrizable. Take any relatively compact \(W\subset H\) and consider the projection set \(\Lambda _W\subset G\). Then there exist a compact set  and a positive constant \(A=A(W,K)\) such that
and a positive constant \(A=A(W,K)\) such that

for all finitely supported \(\varphi :\Lambda _W\rightarrow {{\mathbb {C}}}\).
Remark 3.3
The following proof shows how to obtain suitable  . Here we summarize the construction. Fix any compact unit neighborhood
. Here we summarize the construction. Fix any compact unit neighborhood  and take non-negative and positive definite
and take non-negative and positive definite  such that \({{\,\mathrm{supp}\,}}(\varphi _V)\subset V\) and
such that \({{\,\mathrm{supp}\,}}(\varphi _V)\subset V\) and  . For any relatively compact
. For any relatively compact  the function \(g_K=\mathbf{1}_{K\setminus \partial ^V K}*\varphi _V\) satisfies
the function \(g_K=\mathbf{1}_{K\setminus \partial ^V K}*\varphi _V\) satisfies  by Hölder’s inequality and \(\mathbf{1}_{K}\geqslant g_K \geqslant 0\). Here we denote by \(f*g\) the convolution of f and g. Now fix a zero neighborhood \(B\subset G\) such that \((\Lambda _W-\Lambda _W)\cap B=\{0\}\) and choose relatively compact
by Hölder’s inequality and \(\mathbf{1}_{K}\geqslant g_K \geqslant 0\). Here we denote by \(f*g\) the convolution of f and g. Now fix a zero neighborhood \(B\subset G\) such that \((\Lambda _W-\Lambda _W)\cap B=\{0\}\) and choose relatively compact  such that
such that

The positive constant A in the proposition is then given by

For example, K may be taken as a member of any van Hove sequence \((K_n)_n\) of sufficiently large index. To see this, we may argue as in the proof of [34, Proposition 3.14]. Note first that van Hove sequences exist in  as G is metrizable. Furthermore \((K_n\setminus \partial ^V K_n)_{n\in {\mathbb {N}}}\) is also a van Hove sequence, which can be seen by straightforward estimates. We can then use Lemma 2.9 to infer
as G is metrizable. Furthermore \((K_n\setminus \partial ^V K_n)_{n\in {\mathbb {N}}}\) is also a van Hove sequence, which can be seen by straightforward estimates. We can then use Lemma 2.9 to infer  as \(n\rightarrow \infty \). Moreover the latter functions are dominated by the non-negative continuous function
as \(n\rightarrow \infty \). Moreover the latter functions are dominated by the non-negative continuous function  . In fact we have
. In fact we have  , since \(\mathbf{1}_{W-W}\) may be majorised by suitable \(h\in KL(H)\), and since we have
, since \(\mathbf{1}_{W-W}\) may be majorised by suitable \(h\in KL(H)\), and since we have  by Lemma 2.7. Hence the claim follows from dominated convergence.
by Lemma 2.7. Hence the claim follows from dominated convergence.
Proof of Proposition 3.2
Note \(\Lambda _W-\Lambda _W\subset \Lambda _{W-W}\), where the latter set is uniformly discrete as W is relatively compact. We may thus choose any zero neighborhood \(B\subset G\) such that \((\Lambda _W-\Lambda _W)\cap B=\{0\}\). Take any  such that \(\mathbf{1}_{K} \geqslant g_K\geqslant 0\), compare Remark 3.3. We can then write
such that \(\mathbf{1}_{K} \geqslant g_K\geqslant 0\), compare Remark 3.3. We can then write

The latter sum can be simplified as follows. We first note that for non-negative \(h:G\rightarrow {\mathbb {R}}\) we have uniformly in \(\lambda \in \Lambda _W\) the estimate
We can now estimate the above sum using an argument as in the proof of Young’s inequality [15, Theorem 20.18] where \(p=q=2\) and \(r=1\) by

If \({{\mathcal {L}}}\) projects injectively to G, then the last inequality is an equality. Collecting the above estimates, we arrive at

The term in brackets will be positive if K is a member of any van Hove sequence of sufficiently large index, compare Remark 3.3. \(\square \)
4 Stable Sampling by Model Sets
4.1 A Sampling Upper Bound
Since \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) is closed, Hilbert space techniques are available. One can show that the existence of an upper bound for stable sampling is equivalent to the existence of an upper bound for stable interpolation, see [38, p. 129]. A direct proof of an upper bound is, for general uniformly discrete sets, given in [14, Lemma 2]. In the following, we give an alternative argument for weak model sets based on the Poisson Summation Formula. It yields an explicit constant appearing in the upper bound. This serves as a preparation for the lower bound, where the following argument will be adapted.
Lemma 4.1
(Explicit sampling upper bound for weak model sets) Consider any bare cut-and-project scheme \((G,H,{{\mathcal {L}}})\). Take any relatively compact \(W\subset H\) and any relatively compact  . Define the finite constant \(B=B(W,K)\) by
. Define the finite constant \(B=B(W,K)\) by  , where \(h\in KL(H)\) is any function satisfying \(h \geqslant \mathbf{1}_{W}\). We then have
, where \(h\in KL(H)\) is any function satisfying \(h \geqslant \mathbf{1}_{W}\). We then have
for all \(f\in {{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\).
Remark 4.2
A suitable function \(h\geqslant \mathbf{1}_{W}\) may be constructed as follows. Take any compact zero neighborhood U in H and take non-negative \(\varphi _U\in L^2(H)\) such that \({{\,\mathrm{supp}\,}}(\varphi _U)\subset U\) and \(\int _H\varphi _U\,{\mathrm d}\theta _H=1\). Then \(h=\mathbf{1}_{W-U} * \varphi _U\) satisfies \(h\geqslant \mathbf{1}_{W}\) by construction, and we have \(h\in KL(H)\) by [34, Lemma 3.7].
Proof of Lemma 4.1
Fix any relatively compact window \(W\subset H\) and  . Take any \(h\in KL(H)\) such that \(h\geqslant \mathbf{1}_{W}\), compare Remark 4.2. Consider any \(f\in {{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\). Then \(g={|}f{|}^2\in LK(G)\), and we have
. Take any \(h\in KL(H)\) such that \(h\geqslant \mathbf{1}_{W}\), compare Remark 4.2. Consider any \(f\in {{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\). Then \(g={|}f{|}^2\in LK(G)\), and we have  . Here we used the notation \({\widetilde{f}}(x)=\overline{f(-x)}\). Using the Poisson Summation Formula Lemma 2.7, we can write
. Here we used the notation \({\widetilde{f}}(x)=\overline{f(-x)}\). Using the Poisson Summation Formula Lemma 2.7, we can write

This first inequality is an equality if \({{\mathcal {L}}}\) projects injectively to G. Now we can apply a standard estimate, using that  is a complex Radon measure and that
is a complex Radon measure and that  . We obtain
. We obtain

where the second estimate relies on Young’s inequality. The finite constant \(B=B(W,K)\) can be chosen independently of the continuous function \(f\in {{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) by  . \(\square \)
. \(\square \)
4.2 A Sampling Lower Bound
Proposition 4.3
(Sampling lower bound) Consider any bare cut-and-project scheme \((G,H,{{\mathcal {L}}})\). Assume that H is \(\sigma \)-compact and that \({{\mathcal {L}}}\) projects both injectively and densely to G. Take any relatively compact  . Then there exist compact \(W=W(K)\subset H\) and a positive constant \(A=A(K,W)\) such that
. Then there exist compact \(W=W(K)\subset H\) and a positive constant \(A=A(K,W)\) such that
for any \(f\in {{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\).
Remark 4.4
The following proof also shows how to obtain suitable windows W. Here we summarize the construction, which is analogous to that in Remark 3.3. Fix any compact zero neighborhood \(U\subset H\) and take non-negative and positive definite \(\varphi _U\in C_c(H)\) such that \({{\,\mathrm{supp}\,}}(\varphi _U)\subset U\) and \(\int _H\varphi _U\,{\mathrm d}\theta _H=1\). For given compact \(W\subset H\) define \(h_W=\mathbf{1}_{W\setminus \partial ^U W}*\varphi _U\). Then \(h_W\in KL(H)\) satisfies \(h_W\leqslant \mathbf{1}_{W}\) and  .
.
Choose some compact zero neighborhood  containing only the origin of the uniformly discrete projection set
containing only the origin of the uniformly discrete projection set  . Now take compact \(W\subset H\) such that
. Now take compact \(W\subset H\) such that

Note that H admits a Hove sequence \((W_n)_{n\in {\mathbb {N}}}\) since H is \(\sigma \)-compact. One may choose \(W=W_n\) for n sufficiently large, compare the arguments in Remark 3.3. In that case, the positive constant A can be chosen as

Proof of Proposition 4.3
Define \(h_W\in KL(H)\) as in Remark 4.4. Take \(f\in {{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) and note \(g={|}f{|}^2\in LK(G)\). Using the Poisson Summation Formula Lemma 2.7, we can write

In the first equation, we used that \({{\mathcal {L}}}\) projects injectively to G. Note that the projection set  is uniformly discrete as \(K-K\) is relatively compact. Take any relatively compact unit neighborhood
is uniformly discrete as \(K-K\) is relatively compact. Take any relatively compact unit neighborhood  containing only the unit in \(_{K-K}{\Lambda }\). Noting
containing only the unit in \(_{K-K}{\Lambda }\). Noting  and \(\check{h_W}(1)=\theta _H(W\setminus \partial ^U W)\), we can write
and \(\check{h_W}(1)=\theta _H(W\setminus \partial ^U W)\), we can write

In the second equality, we used that \({{\mathcal {L}}}_0\) projects injectively to  , which is equivalent to \(\pi ^G({{\mathcal {L}}})\) being dense in G. A standard estimate on the second term on the rhs of Eq. (4.1), which uses
, which is equivalent to \(\pi ^G({{\mathcal {L}}})\) being dense in G. A standard estimate on the second term on the rhs of Eq. (4.1), which uses  , yields
, yields

where we used Young’s inequality [15, Theorem 20.18] for the last estimate. Summarizing the above estimates, we get

The term in brackets will be positive if W is a member of any van Hove sequence of sufficiently large index, compare Remark 4.4. Here we use that H is \(\sigma \)-compact. \(\square \)
5 Lower Bounds and Critical Density
We analyze the above method for sampling using model sets in \(G={\mathbb {R}}\) which are simple, i. e., which satisfy \(H={\mathbb {R}}\) and \(W\subset H\) an interval. We will see that the method used above does not give sharp results.
5.1 Sampling Upper Bound
We give an explicit upper bound for the statement in Lemma 4.1. Choose centered intervals \(U=[-u,u]\) and \(W=[-w,w]\subset H\), where \(u,w>0\). Define \(\varphi _U=\frac{1}{2u}\mathbf{1}_{U}\) and \(h= \mathbf{1}_{W-U} *\varphi _U\). Then \(h\in KL(H)\) is piecewise linear, and we have \(h=1\) on W and \(h=0\) on \((W+U)^c\). The transform of h is given by

We have  , and we may later use the standard estimate
, and we may later use the standard estimate  . Due to uniform discreteness of the projection set \(_{K-K} \Lambda \), we may assume that \(b>0\) is sufficiently small such that any translation of
. Due to uniform discreteness of the projection set \(_{K-K} \Lambda \), we may assume that \(b>0\) is sufficiently small such that any translation of  contains at most one point of \(_{K-K} \Lambda \). Using an interval partition of
contains at most one point of \(_{K-K} \Lambda \). Using an interval partition of  by shifted copies of B, we can estimate
by shifted copies of B, we can estimate

Here we used \(\sum _{\ell \in {\mathbb {N}}} \frac{1}{(2\ell -1)^{2}}=\pi ^2/8\). Hence we may require the finite stable sampling upper bound to satisfy

At \(u=1/(4b)\), the latter expression takes its minimum \({{\,\mathrm{dens}\,}}({{\mathcal {L}}})\cdot (2w+1/b)\).
5.2 Sampling Lower Bound
We may proceed similarly for the upper bound case. Choose centered intervals \(W=[-w,w]\subset H\) and \(U=[-u,u]\) where \(0<u<w\). Define \(\varphi _U=\frac{1}{2u}\mathbf{1}_{U}\) and \(h_W= \mathbf{1}_{W\setminus \partial ^UW} *\varphi _U\). Then \(h_W\in KL(H)\) is piecewise linear, and we have \(h_W=1\) on \([-(w-u),w-u]\) and \(h_W=0\) on \(W^c\). We have  , and as above we have the standard estimate
, and as above we have the standard estimate  . Due to uniform discreteness of the projection set \(_{K-K} \Lambda \), we may assume that \(b>0\) is sufficiently small such that any translate of
. Due to uniform discreteness of the projection set \(_{K-K} \Lambda \), we may assume that \(b>0\) is sufficiently small such that any translate of  contains at most one point of \(_{K-K} \Lambda \). Using an interval partition of
contains at most one point of \(_{K-K} \Lambda \). Using an interval partition of  by shifted copies of B, we can estimate as above
by shifted copies of B, we can estimate as above

Using the Poisson Summation Formula, we thus get

A necessary condition for the rhs to be positive can be explicitly calculated as \(2w b> 1\). Let us rephrase this result in terms of the density of the regular model set \(\Lambda _W\), which is given by \({{\,\mathrm{dens}\,}}(\Lambda _W)={{\,\mathrm{dens}\,}}({{\mathcal {L}}})\cdot \theta _H(W)\), compare Fact 6.2. Assume that K is a centered interval and that \(_{K-K} \Lambda \) has maximal b, i. e.,  . We then get
. We then get

This is away from Landau’s necessity condition  by a factor of 4.
by a factor of 4.
6 Density Formulae for Weighted Model Combs
6.1 Point Densities
Regular model sets have a uniform point density. This result can be seen as a consequence of the Poisson Summation Formula, an approach employed by Meyer [25, 26, Sect. V.7.3], [23, Proposition 5.1]. The density formula for a weighted model comb \(\omega _h\) generalizes uniform point density of the underlying model set \({{\,\mathrm{supp}\,}}(\omega _h)\), see e.g . [35, Theorem 4.14].
Fact 6.1
(Density formula for Riemann integrable weight functions) Let \((G,H,{\mathcal {L}})\) be a bare cut-and-project scheme. Assume that G is \(\sigma \)-compact and that \({{\mathcal {L}}}\) projects densely to H. If \(h : H \rightarrow {\mathbb {C}}\) is Riemann integrable, then for every van Hove sequence sequence \((A_n)_{n\in {\mathbb {N}}}\) in G the density formula holds, i. e., for every \(s\in G\) we have
The convergence is uniform in \(s\in G\). \(\square \)
The density formula implies that any regular model set \(\Lambda _W\) has a uniform point density. Indeed, then \(h=\mathbf{1}_{W}\) is Riemann integrable. For a general weak model set, only upper and lower estimates can be given. The following result can be proved by approximation with regular model sets using the density formula, compare [16, Proposition 3.4]. A version for \(G={\mathbb {R}}\) was already used by Meyer in [27, Remarks 6.2].
Fact 6.2
Let \((G,H,{\mathcal {L}})\) be a bare cut-and-project scheme. Assume that G is \(\sigma \)-compact and that \({{\mathcal {L}}}\) projects densely to H. For any weak model set \(\Lambda _W\) in \((G,H,{{\mathcal {L}}})\), any van Hove sequence \({{\mathcal {A}}}\) in G and any \(t\in H\), we have the estimates
In particular if \(\theta _H(\partial W)=0\), then \({{\mathcal {D}}}(\Lambda _{W+t})={{\,\mathrm{dens}\,}}({{\mathcal {L}}}) \cdot \theta _H(W)\). \(\square \)
6.2 Density Formula for Continuous Test Functions
The density formula Fact 6.1 expresses that the weighted model comb \(\omega _h\) has a uniform density. Indeed we have \(\omega _h(g_n)\rightarrow {{\,\mathrm{dens}\,}}({{\mathcal {L}}})\cdot \theta _H(h)\) where \(g_n=\mathbf{1}_{s+A_n}/\theta _G(A_n)\). Below we need to compute the limit in the density formula on a sequence of continuous test functions \((g_n)_n\) of unbounded support. If G is \(\sigma \)-compact, then such sequences may be obtained using a Dirac sequence \((v_n)_n\) in  , as the sequence
, as the sequence  then converges locally uniformly to 1, see [7, Lemma 3.4.5]. We have the following result.
then converges locally uniformly to 1, see [7, Lemma 3.4.5]. We have the following result.
Proposition 6.3
(Density formula with continuous averaging functions) Let \((G,H,{{\mathcal {L}}})\) be a bare cut-and-project scheme. Assume that G is \(\sigma \)-compact and that \({{\mathcal {L}}}\) projects densely to H. Take a Dirac sequence \((v_n)_{n\in {\mathbb {N}}}\) in  and define \(g_n\in L^1(G)\) by
and define \(g_n\in L^1(G)\) by

Then for any Riemann integrable \(h: H\rightarrow {\mathbb {C}}\) and for every \(s\in G\) we have
The convergence is uniform in \(s\in G\).
The proof of Proposition 6.3 is based on a version of the Fourier–Bohr coefficient formula, compare [34, Proposition 3.12], for continuous averaging functions.
Proposition 6.4
(Fourier–Bohr coefficients with continuous averaging functions) Let G be a \(\sigma \)-compact LCA group. Take any Dirac sequence \((v_n)_{n\in {\mathbb {N}}}\) in  and define \(g_n\in L^1(G)\) by
and define \(g_n\in L^1(G)\) by

Let \(\mu \in {\mathcal {M}}^\infty (G)\) be twice transformable and consider  . We then have for every \(s\in G\)
. We then have for every \(s\in G\)

The convergence is uniform in \(s\in G\).
Proof of Proposition 6.4
We prove the proposition for \(\chi =1\), where 1 denotes the trivial character. The general case then follows from  and
and  , where \(*\) denotes measure convolution. Recall that
, where \(*\) denotes measure convolution. Recall that  is metrizable since G is \(\sigma \)-compact. Hence there exists a Dirac sequence \((v_n)_{n\in {\mathbb {N}}}\) in
is metrizable since G is \(\sigma \)-compact. Hence there exists a Dirac sequence \((v_n)_{n\in {\mathbb {N}}}\) in  . Note first that
. Note first that

We also have  and
and  by Young’s inequality. The function
by Young’s inequality. The function  is positive definite and compactly supported, and its Fourier transform \(g_n\) is integrable. As
is positive definite and compactly supported, and its Fourier transform \(g_n\) is integrable. As  is transformable, we thus have
is transformable, we thus have

by the inversion theorem for transformable measures [3, Theorem 3.4] and by definition of the Fourier transform [3, Chapter 2]. In Eq. (6.2), recall that \(e_s\) is the exponential \(e_s(\chi )=\chi (s)\). Let us consider the limit \(n\rightarrow \infty \) on the lhs. We first note  pointwise. Indeed, this is obvious for \(\chi =1\), and for \(\chi \ne 1\) we choose any compact unit neighborhood K in
pointwise. Indeed, this is obvious for \(\chi =1\), and for \(\chi \ne 1\) we choose any compact unit neighborhood K in  such that \(\chi \notin K\). Then
such that \(\chi \notin K\). Then  for finally all n, such that
for finally all n, such that  for finally all n. As
for finally all n. As  for finally all n, we can apply Lebesgue’s dominated convergence theorem to obtain
for finally all n, we can apply Lebesgue’s dominated convergence theorem to obtain  as \(n\rightarrow \infty \) uniformly in \(s\in G\). \(\square \)
as \(n\rightarrow \infty \) uniformly in \(s\in G\). \(\square \)
Proof of Proposition 6.3
Abbreviate \(c={{\,\mathrm{dens}\,}}({\mathcal {L}})>0\), take \(\varphi \in C_c(H)\) and consider \(h=\varphi *{\widetilde{\varphi }}\in C_c(H)\). Then \(\omega _h\) is twice transformable by [34, Theorem 4.12]. We can now argue

uniformly in \(s\in G\). In the first equation we used that  is a measure and that \({{\mathcal {L}}}_0\) projects injectively to
is a measure and that \({{\mathcal {L}}}_0\) projects injectively to  , which is equivalent to \({{\mathcal {L}}}\) projecting densely to H by Pontryagin duality. In the second equation, we used the generalized Poisson Summation Formula
, which is equivalent to \({{\mathcal {L}}}\) projecting densely to H by Pontryagin duality. In the second equation, we used the generalized Poisson Summation Formula  , see Lemma 2.7, and for the third equation we used Proposition 6.4 as \(\omega _h\in {\mathcal {M}}^\infty (G)\) is twice transformable.
, see Lemma 2.7, and for the third equation we used Proposition 6.4 as \(\omega _h\in {\mathcal {M}}^\infty (G)\) is twice transformable.
The general case follows by a standard approximation argument. Consider without loss of generality any Riemann integrable \(h:H\rightarrow {\mathbb {R}}\) and let \(\varepsilon >0\). Recall from [3] that \(K_2(H)={{\,\mathrm{span}\,}}\{\varphi *{\widetilde{\varphi }}: \varphi \in C_c(H)\}\) is dense in \(C_c(H)\) with respect to the supremum norm. Since h is Riemann integrable, there exist \(f_1,f_2 \in K_2(H)\) such that \(f_1 \leqslant h \leqslant f_2 \) and \(\int (f_2 -f_1)\,{\mathrm d}\theta _H \leqslant \frac{\varepsilon }{2c}\). By the above result there exists N such that for all \(n \geqslant N\) and \(i\in \{1,2\}\) we have
uniformly in \(t\in G\). Thus, as \(\omega _{f_1} \leqslant \omega _h \leqslant \omega _{f_2}\), for all \(n \geqslant N\) we have
and similarly
both uniformly in \(s\in G\). Hence the claim of the proposition follows. \(\square \)
7 Sampling and Interpolation Duality
7.1 Statement and Discussion of the Duality Theorem
Recall that  is a subspace of \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\), which is dense in \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) if and only if K has almost no inner boundary. The duality theorem relates, under suitable assumptions, sampling on \(\Lambda _W\) for \({{\,\mathrm{{\mathcal {S}}}\,}}_{K}\) to interpolation from \(_{K} \Lambda \) for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_{W}\). We say that \(\Lambda \) is stable sampling for \({{\,\mathrm{{\mathcal {S}}}\,}}_K\) if Eq. (1.1) holds for any \(f\in {{\,\mathrm{{\mathcal {S}}}\,}}_K\).
is a subspace of \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\), which is dense in \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) if and only if K has almost no inner boundary. The duality theorem relates, under suitable assumptions, sampling on \(\Lambda _W\) for \({{\,\mathrm{{\mathcal {S}}}\,}}_{K}\) to interpolation from \(_{K} \Lambda \) for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_{W}\). We say that \(\Lambda \) is stable sampling for \({{\,\mathrm{{\mathcal {S}}}\,}}_K\) if Eq. (1.1) holds for any \(f\in {{\,\mathrm{{\mathcal {S}}}\,}}_K\).
Theorem 7.1
(Sampling-interpolation duality for model sets) Let \((G,H,{\mathcal {L}})\) be a complete cut-and-project scheme. Let \(W\subset H\) and  both be relatively compact and measurable. Then the following hold.
both be relatively compact and measurable. Then the following hold.
-
(i)
Assume that G is \(\sigma \)-compact. Take any relatively compact and measurable neighborhood \(K'\) of K. If \(\Lambda _W\subset G\) is stable sampling for \({{\,\mathrm{{\mathcal {S}}}\,}}_{K'}\subset L^2(G)\), then
 is stable interpolating for
is stable interpolating for  .
. -
(ii)
Assume that H is metrizable. If
 is stable interpolating for
is stable interpolating for  , then \(\Lambda _{\mathrm {cl}(W)} \subset G\) is stable sampling for \({{\,\mathrm{{\mathcal {S}}}\,}}_K\subset L^2(G)\).
, then \(\Lambda _{\mathrm {cl}(W)} \subset G\) is stable sampling for \({{\,\mathrm{{\mathcal {S}}}\,}}_K\subset L^2(G)\).
Remark 7.2
In applications, it might be convenient to replace (i) by the following equivalent statement. It is obtained from (i) by exchanging the roles of G and H and using the dual cut-and-project scheme.
- (i’):
-
Assume that H is \(\sigma \)-compact. Take any relatively compact and measurable neighborhood \(W'\) of W. If
 is stable sampling for
is stable sampling for  , then \(\Lambda _W\subset G\) is stable interpolating for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_{K}\subset L^2(G)\).
, then \(\Lambda _W\subset G\) is stable interpolating for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_{K}\subset L^2(G)\).
The assumptions in the duality theorem may slightly be relaxed, as is seen by inspecting the proof of the duality theorem.
Remark 7.3
(Assumptions in the Duality Theorem)
-
(a)
The proof does not use all four projection assumptions in Definition 2.1. The proof of (i) only uses that \({{\mathcal {L}}}\) projects injectively to G and densely to H. The proof of (i’) only uses that \({{\mathcal {L}}}\) projects injectively to H and densely to G. The proof of (ii) does not use that \({{\mathcal {L}}}\) projects densely to H.
-
(b)
If K is open, we may take \(K'=K\) in (i). For more general K, assume that \(\partial K\) is nowhere dense. This comprises the cases K compact and K topologically regular, i. e., \(\mathrm {cl}(\mathrm {int}(K))=\mathrm {cl}(K)\). Then, without any projection assumption, nowhere denseness implies that the set of
 such that
such that  is dense \(G_\delta \) in
is dense \(G_\delta \) in  , see the proof of [18, Proposition 8.3] or [16, Proposition 2.12]. Thus by an arbitrarily small shift we may ensure
, see the proof of [18, Proposition 8.3] or [16, Proposition 2.12]. Thus by an arbitrarily small shift we may ensure  . In that case, we may take \(K'=K\) in (i). Analogous reasoning applies to (i’).
. In that case, we may take \(K'=K\) in (i). Analogous reasoning applies to (i’). -
(c)
If W is closed, we have \(\mathrm {cl}(W)=W\) in (ii). For more general W, assume that \(\partial W\) is nowhere dense, which comprises the case W topologically regular. Then, without any projection assumption, by an arbitrarily small shift we may ensure \(\partial W\cap \pi _{H}({{\mathcal {L}}})=\varnothing \). In that case \(\Lambda _{\mathrm {cl}(W)}=\Lambda _W\) in (ii).
-
(d)
Consider the case \(G={\mathbb {R}}\) or \(G={\mathbb {Z}}\) and assume that
 is a left-semiclosed multiband set, i. e., a union of finitely many pairwise disjoint intervals [a, b). In that situation one may take \(K'=K\). This is possible as the structure of K allows to approach any left interval endpoint in K from the right. Indeed, in the proof of part (i) of the Duality Theorem 7.1, one may take
is a left-semiclosed multiband set, i. e., a union of finitely many pairwise disjoint intervals [a, b). In that situation one may take \(K'=K\). This is possible as the structure of K allows to approach any left interval endpoint in K from the right. Indeed, in the proof of part (i) of the Duality Theorem 7.1, one may take  to be \(\eta _n=1/n\) in Eq. (7.3) to see that \(K'=K\) is a possible choice. This has been used in [19, Lemma 2.1] and generalized in [13] to the multi-dimensional case.
to be \(\eta _n=1/n\) in Eq. (7.3) to see that \(K'=K\) is a possible choice. This has been used in [19, Lemma 2.1] and generalized in [13] to the multi-dimensional case.
Note that our Duality Theorem relates \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_{K/W}\) and \({{\,\mathrm{{\mathcal {S}}}\,}}_{W/K}\) in a particular way. This is in contrast to the duality theorems in [2, 13, 19], which all relate \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_{K/W}\) and \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_{W/K}\). In fact those duality theorems are special cases of Theorem 7.1, as can be seen using Proposition 7.4 and the previous remark.
Proposition 7.4
Let G be an LCA group. Let \(\Lambda \subset G\) be uniformly discrete and let  be relatively compact, measurable having almost no inner boundary. If \(\Lambda \) is stable sampling for \({{\,\mathrm{{\mathcal {S}}}\,}}_K\), then \(\Lambda \) is stable sampling for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\).
be relatively compact, measurable having almost no inner boundary. If \(\Lambda \) is stable sampling for \({{\,\mathrm{{\mathcal {S}}}\,}}_K\), then \(\Lambda \) is stable sampling for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\).
Proof
Note that the \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) stable sampling upper bound in Eq. (1.1) holds for general uniformly discrete sets by [14, Lemma 2], see also Lemma 4.1 for weak model sets. It thus suffices to consider the lower bound. Assume that \(\Lambda \) is stable sampling for \({{\,\mathrm{{\mathcal {S}}}\,}}_K\) and that K has almost no inner boundary. Fix any \(f\in {{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\). Take \(\varepsilon >0\) and choose \(f_\varepsilon \in {{\,\mathrm{{\mathcal {S}}}\,}}_K\) such that \(\Vert f-f_\varepsilon \Vert _{L^2(G)}\leqslant \varepsilon \), which is possible due to Proposition 8.1. By the triangle inequality we then have
Moreover, using the upper bound, we can estimate
This leads to the following estimate for the lower bound:
As \(\varepsilon >0\) was arbitrary, the claim follows. \(\square \)
7.2 Proof of the Duality Theorem
We now give a proof of the Duality Theorem. Since the upper bounds for stable sampling and stable interpolation hold in general, see also Sects. 4.1 and 3.1 for model sets, we only discuss the lower bounds.
Proof of (i)
We assume that there is a positive constant \(A_S\) such that
for all \(f\in {{\,\mathrm{{\mathcal {S}}}\,}}_{K'}\), where \(K'\supset K\) is any given fixed relatively compact and measurable neighborhood of K. We will show that for arbitrary \(\varphi \in \ell ^2(_K\Lambda )\) with finite support we have
The strategy of the proof consists in associating to \(\varphi \in \ell ^2(_K\Lambda )\) suitable \(f_n\in {{\,\mathrm{{\mathcal {S}}}\,}}_{K'}\), which will be defined via their Fourier transform, compare Fig. 1.
Take any \(\varphi \in \ell ^2(_K \Lambda )\) of finite support. We consider certain  approximations to \(\varphi \circ {\widehat{s}}\), where \({\widehat{s}}\) denotes the star map \({{\widehat{s}}}:\pi _{{\widehat{G}}}({{\mathcal {L}}}_0)\rightarrow \pi _{{\widehat{H}}}({{\mathcal {L}}}_0)\). The latter is indeed well-defined as \({{\mathcal {L}}}_0\) projects injectively to
approximations to \(\varphi \circ {\widehat{s}}\), where \({\widehat{s}}\) denotes the star map \({{\widehat{s}}}:\pi _{{\widehat{G}}}({{\mathcal {L}}}_0)\rightarrow \pi _{{\widehat{H}}}({{\mathcal {L}}}_0)\). The latter is indeed well-defined as \({{\mathcal {L}}}_0\) projects injectively to  , which follows by Pontryagin duality as \({{\mathcal {L}}}\) projects densely to H. Take any sequence \((\eta _n)_n\) of characters in
, which follows by Pontryagin duality as \({{\mathcal {L}}}\) projects densely to H. Take any sequence \((\eta _n)_n\) of characters in  converging to the identity character, see Remark 7.3(d). Take a Dirac sequence \((v_n)_{n}\) in
converging to the identity character, see Remark 7.3(d). Take a Dirac sequence \((v_n)_{n}\) in  such that \(v_n\) is positive definite. This is possible as
such that \(v_n\) is positive definite. This is possible as  is metrizable by assumption. Define
is metrizable by assumption. Define  to be the finite sum
to be the finite sum

The latter sum is indeed finite as \(\varphi \) has finite support and as K is relatively compact. Note that the support of \(v_n\) is contained in any given unit neighborhood if n is sufficiently large. Thus  satisfies \(f_n\in {{\,\mathrm{{\mathcal {S}}}\,}}_{K'}\) for sufficiently large n. Note that if
satisfies \(f_n\in {{\,\mathrm{{\mathcal {S}}}\,}}_{K'}\) for sufficiently large n. Note that if  , we may choose \(K'=K\).
, we may choose \(K'=K\).
We argue that the functions \(f_n\) asymptotically provide the claimed duality. Note first that for sufficiently large n we have

by Eq. (7.1). Let us compute that the rhs is asymptotically bounded by the rhs of Eq. (7.2). We have the explicit expression

where \(f\in C(G)\). Now consider \(f_\varphi \in C(H)\) from Definition 1.4, which satisfies

Consider the star map \(s:\pi _G({{\mathcal {L}}})\rightarrow \pi _H({{\mathcal {L}}})\), which is well-defined as \({{\mathcal {L}}}\) projects injectively to G. Note that f coincides on \(\pi _G({{\mathcal {L}}})\) with \(f_\varphi \circ s\). Indeed, for \(\lambda \in \pi _G({{\mathcal {L}}})\) we have

Here we used that for any \(\chi \in \pi _{{\widehat{G}}}({{\mathcal {L}}}_0)\) and \(\lambda \in \pi _G({{\mathcal {L}}})\), we have  and \(\ell :=(\lambda ,s(\lambda ))\in {{\mathcal {L}}}\), and further
and \(\ell :=(\lambda ,s(\lambda ))\in {{\mathcal {L}}}\), and further

Now we can compute

By outer regularity of the Haar measure \(\theta _H\) on H and by [16, Lemma 3.6] there are windows \(W_\varepsilon \supset W\) such that \(\theta _H(\partial W_\varepsilon )=0\) and \(\theta _H(W_\varepsilon )-\theta _H(W)\leqslant \varepsilon \) for any \(\varepsilon >0\). We can thus apply the density formula Proposition 6.3 for unbounded averaging functions to conclude from Eq. (7.5) that

In order to apply the density formula Proposition 6.3, we worked in the bare cut-and-project scheme \((G,H,{{\mathcal {L}}})\), where we used that G is \(\sigma \)-compact and that \({{\mathcal {L}}}\) projects densely to H. This combined with Eq. (7.4) shows stable interpolation (i). \(\square \)
Proof of (ii)
The strategy of the proof is similar to that of (i). We will associate to any \(f\in {{\,\mathrm{{\mathcal {S}}}\,}}_K\) suitable \(\varphi _n\in \ell ^2(_K \Lambda )\) of finite support, compare Fig. 2. Our computations will then use diffraction theory of model sets. In particular, we will use commutativity of the modified Wiener diagram, as explained in [34, Sect. 2, Remarks 5.6].
Consider an arbitrary \(f\in {{\,\mathrm{{\mathcal {S}}}\,}}_K\). As \((G,H,{{\mathcal {L}}})\) is a bare cut-and-project scheme and  , we have that
, we have that

is a weighted model comb in  . Fix any van Hove sequence \((B_n)_{n\in {\mathbb {N}}}\) in
. Fix any van Hove sequence \((B_n)_{n\in {\mathbb {N}}}\) in  . Such a sequence indeed exists as H is assumed to be metrizable. Define
. Such a sequence indeed exists as H is assumed to be metrizable. Define  by
by

Then \(\varphi _n\) is finitely supported as  has compact support and \(B_n\) is compact. Here we use that the star map \({\widehat{t}}:\pi _{{\widehat{H}}}({{\mathcal {L}}}_0)\rightarrow \pi _{{\widehat{G}}}({{\mathcal {L}}}_0)\) is well-defined since \({{\mathcal {L}}}_0\) projects injectively to \({\widehat{H}}\), which holds by Pontryagin duality as lattice \({{\mathcal {L}}}\) projects densely to G. Now the density formula Fact 6.1 for
has compact support and \(B_n\) is compact. Here we use that the star map \({\widehat{t}}:\pi _{{\widehat{H}}}({{\mathcal {L}}}_0)\rightarrow \pi _{{\widehat{G}}}({{\mathcal {L}}}_0)\) is well-defined since \({{\mathcal {L}}}_0\) projects injectively to \({\widehat{H}}\), which holds by Pontryagin duality as lattice \({{\mathcal {L}}}\) projects densely to G. Now the density formula Fact 6.1 for  reads
reads

Here we used that  is \(\sigma \)-compact and that \({{\mathcal {L}}}_0\) projects densely to
is \(\sigma \)-compact and that \({{\mathcal {L}}}_0\) projects densely to  , which follows from injectivity of \(\pi _H|_{{{\mathcal {L}}}}\) by Pontryagin duality. Now the stable interpolation lower bound yields an inequality, and we show that the rhs of this inequality is asymptotically bounded from above by the expression needed for stable sampling.
, which follows from injectivity of \(\pi _H|_{{{\mathcal {L}}}}\) by Pontryagin duality. Now the stable interpolation lower bound yields an inequality, and we show that the rhs of this inequality is asymptotically bounded from above by the expression needed for stable sampling.
Consider the weighted model comb  in the bare cut-and-project scheme
in the bare cut-and-project scheme  . By standard reasoning, see e. g. [34, Proposition 5.1], its autocorrelation is
. By standard reasoning, see e. g. [34, Proposition 5.1], its autocorrelation is  , where we used that \({{\mathcal {L}}}_0\) projects densely to
, where we used that \({{\mathcal {L}}}_0\) projects densely to  , which follows from injectivity of \(\pi _H|_{{\mathcal {L}}}\) by Pontryagin duality. Moreover by [34, Theorem 4.10], its diffraction measure is
, which follows from injectivity of \(\pi _H|_{{\mathcal {L}}}\) by Pontryagin duality. Moreover by [34, Theorem 4.10], its diffraction measure is  , where \(_{{|}f{|}^2}\omega = \sum _{(x,y)\in {{\mathcal {L}}}} {|}f{|}^2(x) \delta _y\). Let us consider the normalized finite sample autocorrelations
, where \(_{{|}f{|}^2}\omega = \sum _{(x,y)\in {{\mathcal {L}}}} {|}f{|}^2(x) \delta _y\). Let us consider the normalized finite sample autocorrelations

where \(*\) denotes convolution of measures, and where \({\widetilde{\mu }}(g)=\mu ({\widetilde{g}})\) denotes measure reflection. As finite point measures satisfy the convolution theorem [3, Theorem 3.1], we have

where multiplication of absolutely continuous measures \(f\theta _H\) and \(g\theta _H\) is understood as \((f\theta _H)\cdot (g\theta _H)=(fg)\theta _H\). Here \(f_{\varphi _n}: H\rightarrow {\mathbb {C}}\) is the discrete Fourier transform associated to \(\varphi _n\), i. e., the finite trigonometric sum

We have argued that for every \(h\in C_c(H)\) we have

Note that the Fourier transform is continuous on the space of positive definite complex Radon measures, see [30, Lemma 1.26] for the general case and [5, Theorem 4.16] for positive measures. Since \(\lim _{n\rightarrow \infty } \gamma _n=\gamma \) vaguely, we thus also have  vaguely. Taking \(h_\varepsilon \in C_c(H)\) such that \(\mathbf{1}_{\mathrm {cl}(W)}\leqslant h_\varepsilon \) and \(h_\varepsilon \rightarrow \mathbf{1}_{\mathrm {cl}(W)}\) pointwise as \(\varepsilon \downarrow 0\), we can argue
vaguely. Taking \(h_\varepsilon \in C_c(H)\) such that \(\mathbf{1}_{\mathrm {cl}(W)}\leqslant h_\varepsilon \) and \(h_\varepsilon \rightarrow \mathbf{1}_{\mathrm {cl}(W)}\) pointwise as \(\varepsilon \downarrow 0\), we can argue

where we used dominated convergence for the last equality. We thus have shown

where in the last equation we again used that \(\pi _G|_{{\mathcal {L}}}\) is injective. We combine this with Eq. (7.6) and the definition of stable interpolating:

which finishes the proof that stable sampling is implied by stable interpolation. \(\square \)
Reinspecting the proof of part (ii) in the duality theorem, the following observations arise.
Remark 7.5
-
(i)
The argument in Eq. (7.7) can analogously be applied for W an open set. As a result, we have equality in Eq. (7.8) if
 , a condition which is satisfied if \(\partial W\cap \pi _H({{\mathcal {L}}})=0\). The latter property holds generically if \(\partial W\) is nowhere dense, compare Remark 7.3(c).
, a condition which is satisfied if \(\partial W\cap \pi _H({{\mathcal {L}}})=0\). The latter property holds generically if \(\partial W\) is nowhere dense, compare Remark 7.3(c). -
(ii)
By the Fourier–Bohr coefficient formula [21, Theorem 5], we have for every \(y\in H\) that

which implies
 . This differs from
. This differs from  in Eq. (7.8).
in Eq. (7.8).
7.3 Stable Sampling and Stable Interpolation for Simple Model Sets
Theorem 7.1 can now be used in conjunction with Fact 1.8 to give a proof of Theorem 1.9.
Proof of Theorem 1.9
Note that by Eq. (6.1) the weak model set  satisfies the density formula
satisfies the density formula

where \({{\mathcal {A}}}\) is any van Hove sequence in  .
.
(i) By assumption we have  , where the latter equality is the density formula for the regular model set \(\Lambda _I\). Choose any neighborhood \(K'\) of \(\mathrm {cl}(K)\) such that \(K'\) has almost no boundary and
, where the latter equality is the density formula for the regular model set \(\Lambda _I\). Choose any neighborhood \(K'\) of \(\mathrm {cl}(K)\) such that \(K'\) has almost no boundary and  . Such a neighborhood exists by [16, Lemma 3.6]. Then by the density formula Eq. (7.9) we have \({|}I{|}>{\mathcal {D}}^+_{{\mathcal {A}}}(_{K'}\Lambda )\). Choose compact \(I'\subset I\) such that \({|}I'{|}>{\mathcal {D}}^+_{{\mathcal {A}}}(_{K'}\Lambda )\). Then \(_{K'}\Lambda \subset {\widehat{H}} \cong {\mathbb {R}}\) is stable interpolating for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_{I'}\) by Fact 1.8(ii). We can now invoke the Duality Theorem 7.1(ii) to infer that \(\Lambda _{\mathrm {cl}(I')}=\Lambda _{I'}\) is stable sampling for \({{\,\mathrm{{\mathcal {S}}}\,}}_{K'}\). Since \(K'\) has almost no boundary, we have that \(\Lambda _{I'}\) is stable sampling for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_{K'}\) by Proposition 7.4. In particular, \(\Lambda _{I'}\) is stable sampling for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_{K}\). Since \(I'\subset I\), we have \(\Lambda _{I'}\subset \Lambda _{I}\). Hence also \(\Lambda _{I}\) is stable sampling for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_{K}\). Indeed, in Definition 1.3 the lower inequality continues to hold for any superset of \(\Lambda \), whereas an upper inequality is satisfied for general uniformly discrete sets.
. Such a neighborhood exists by [16, Lemma 3.6]. Then by the density formula Eq. (7.9) we have \({|}I{|}>{\mathcal {D}}^+_{{\mathcal {A}}}(_{K'}\Lambda )\). Choose compact \(I'\subset I\) such that \({|}I'{|}>{\mathcal {D}}^+_{{\mathcal {A}}}(_{K'}\Lambda )\). Then \(_{K'}\Lambda \subset {\widehat{H}} \cong {\mathbb {R}}\) is stable interpolating for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_{I'}\) by Fact 1.8(ii). We can now invoke the Duality Theorem 7.1(ii) to infer that \(\Lambda _{\mathrm {cl}(I')}=\Lambda _{I'}\) is stable sampling for \({{\,\mathrm{{\mathcal {S}}}\,}}_{K'}\). Since \(K'\) has almost no boundary, we have that \(\Lambda _{I'}\) is stable sampling for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_{K'}\) by Proposition 7.4. In particular, \(\Lambda _{I'}\) is stable sampling for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_{K}\). Since \(I'\subset I\), we have \(\Lambda _{I'}\subset \Lambda _{I}\). Hence also \(\Lambda _{I}\) is stable sampling for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_{K}\). Indeed, in Definition 1.3 the lower inequality continues to hold for any superset of \(\Lambda \), whereas an upper inequality is satisfied for general uniformly discrete sets.
(ii) By assumption we have  , where the latter equality is the density formula for the regular model set \(\Lambda _I\). Now choose an interval \(I'\supset I\) such that \({|}I'{|}>{|}I{|}\) and such that still
, where the latter equality is the density formula for the regular model set \(\Lambda _I\). Now choose an interval \(I'\supset I\) such that \({|}I'{|}>{|}I{|}\) and such that still  . Then by the density formula Eq. (7.9) we have \({|}I'{|}<{\mathcal {D}}^-_{{\mathcal {A}}}(_K\Lambda )\). Hence
. Then by the density formula Eq. (7.9) we have \({|}I'{|}<{\mathcal {D}}^-_{{\mathcal {A}}}(_K\Lambda )\). Hence  is stable sampling for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_{I'}\) by Fact 1.8(i). In particular \(_K\Lambda \) is stable sampling for \({{\,\mathrm{{\mathcal {S}}}\,}}_{I'}\). We can now invoke the Duality Theorem 7.1(i’) to infer that \(\Lambda _I\) is stable interpolating for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\). \(\square \)
is stable sampling for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_{I'}\) by Fact 1.8(i). In particular \(_K\Lambda \) is stable sampling for \({{\,\mathrm{{\mathcal {S}}}\,}}_{I'}\). We can now invoke the Duality Theorem 7.1(i’) to infer that \(\Lambda _I\) is stable interpolating for \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\). \(\square \)
8 Topological Properties of the Paley–Wiener Space
8.1 The Test Function Space \({{\,\mathrm{{\mathcal {S}}}\,}}_K\)
Proposition 8.1
Let G be an LCA group and assume that  is measurable and relatively compact. Then \({{\,\mathrm{{\mathcal {S}}}\,}}_K\) is dense in \(({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K,\Vert \cdot \Vert _{L^2(G)})\) if and only if A has almost no inner boundary, i.e.,
is measurable and relatively compact. Then \({{\,\mathrm{{\mathcal {S}}}\,}}_K\) is dense in \(({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K,\Vert \cdot \Vert _{L^2(G)})\) if and only if A has almost no inner boundary, i.e.,  .
.
Proof
Let us first assume that  . By weak inner regularity of the Haar measure, we find a compact set \(C\subset K\cap \partial K\) with positive Haar measure. Consider
. By weak inner regularity of the Haar measure, we find a compact set \(C\subset K\cap \partial K\) with positive Haar measure. Consider  . Note that for any \(g\in {{\,\mathrm{{\mathcal {S}}}\,}}_K\subset L^1(G)\) we have
. Note that for any \(g\in {{\,\mathrm{{\mathcal {S}}}\,}}_K\subset L^1(G)\) we have  as \({\widehat{g}}\) is continuous. We thus have
as \({\widehat{g}}\) is continuous. We thus have

Therefore  . In particular, \({{\,\mathrm{{\mathcal {S}}}\,}}_K\) is not dense in \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\).
. In particular, \({{\,\mathrm{{\mathcal {S}}}\,}}_K\) is not dense in \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\).
We now assume  . We will use the function space \(K_2(G)={{\,\mathrm{span}\,}}\{f*\widetilde{f}:f\in C_c(G)\}\), where \({\widetilde{f}}(x)=\overline{f(-x)}\), compare [3]. Take any \(f\in {{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) and assume \(f\ne 0\) without loss of generality. For any given \(\varepsilon >0\), we define an approximation \(f_\varepsilon \in {{\,\mathrm{{\mathcal {S}}}\,}}_K\) as follows. As
. We will use the function space \(K_2(G)={{\,\mathrm{span}\,}}\{f*\widetilde{f}:f\in C_c(G)\}\), where \({\widetilde{f}}(x)=\overline{f(-x)}\), compare [3]. Take any \(f\in {{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) and assume \(f\ne 0\) without loss of generality. For any given \(\varepsilon >0\), we define an approximation \(f_\varepsilon \in {{\,\mathrm{{\mathcal {S}}}\,}}_K\) as follows. As  is dense in
is dense in  and
and  is dense in
is dense in  and the embedding
and the embedding  is continuous, also
is continuous, also  is dense in
is dense in  . Hence we may choose
. Hence we may choose  such that
such that  . Choose any compact unit neighborhood
. Choose any compact unit neighborhood  such that
such that  . Such a neighborhood indeed exists: By \(f\in {{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) and Hölder’s inequality we have
. Such a neighborhood indeed exists: By \(f\in {{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) and Hölder’s inequality we have

By outer regularity of the Haar measure, we can choose U sufficiently concentrated around unity to achieve  , see [16, Lemma 4.4]. Now the claim follows from our assumption, as
, see [16, Lemma 4.4]. Now the claim follows from our assumption, as

Take any Dirac net \((v_j)_j\) in  . Choose j such that \({{\,\mathrm{supp}\,}}(v_j)\subset U\) and that
. Choose j such that \({{\,\mathrm{supp}\,}}(v_j)\subset U\) and that  . The latter can be achieved as
. The latter can be achieved as  converges locally to one. Consider now
converges locally to one. Consider now

Note that in fact  , as it is a convolution of two compactly supported functions in
, as it is a convolution of two compactly supported functions in  . By construction we have
. By construction we have  . Furthermore, we have
. Furthermore, we have  since
since

is a product of two functions in \(L^2(G)\). Indeed, the convolution is in \(L^2(G)\) by Young’s inequality, as  and
and  . Altogether we conclude \(f_\varepsilon \in {{\,\mathrm{{\mathcal {S}}}\,}}_K\). Now we can estimate
. Altogether we conclude \(f_\varepsilon \in {{\,\mathrm{{\mathcal {S}}}\,}}_K\). Now we can estimate

where we used Young’s inequality in the fourth line. As \(\varepsilon >0\) was arbitrary, this proves the claim of the proposition. \(\square \)
8.2 Another Definition of Paley–Wiener Space
If G is an LCA group and if  is closed, then there is another definition of Paley-Wiener space. Recall that for a function \(f\in L^2(G)\), its support is defined to be
is closed, then there is another definition of Paley-Wiener space. Recall that for a function \(f\in L^2(G)\), its support is defined to be
We consider the subspace \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}^\prime \!}\,}}_K\) of \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) defined by

Proposition 8.2
Let G be an LCA group. We have \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}^\prime \!}\,}}_K={{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) if and only if \({{\,\mathrm{supp}\,}}(\mathbf{1}_{K})\subset K\). In particular \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}^\prime \!}\,}}_K={{\,\mathrm{{\mathcal {P}}{\mathcal {W}}}\,}}_K\) if K is closed in  .
.
A proof will be given at the end of this section after Lemma 8.4. We first collect some topological properties of the support.
Lemma 8.3
Let G be an LCA group, and let \(K\subset G\) be measurable.
-
(i)
For all \(f\in L^2(G)\), \({{\,\mathrm{supp}\,}}(f)\subset G\) is closed.
-
(ii)
For all \(f\in L^2(G)\), we have \(f=f\cdot \mathbf{1}_{{{\,\mathrm{supp}\,}}(f)}\) almost everywhere.
-
(iii)
If K is closed, then \({{\,\mathrm{supp}\,}}(\mathbf{1}_{K})\subset K\).
-
(iv)
If K is open or \(\theta _G(K)<\infty \) or G is \(\sigma \)-finite, then \(\theta _G(K\setminus {{\,\mathrm{supp}\,}}(\mathbf{1}_{K}))=0\).
Proof
Ad (i). Fix \(f\in L^2(G)\). For all \(x\in G\setminus {{\,\mathrm{supp}\,}}(f)\), there is an open neighborhood \(U_x\) with \(\Vert f\cdot \mathbf{1}_{U}\Vert _2=0\). \(U_x\) is open, hence \(U_x\subset G\setminus {{\,\mathrm{supp}\,}}(f)\). Thus, \(G\setminus {{\,\mathrm{supp}\,}}(f)=\bigcup _{x\in G\setminus {{\,\mathrm{supp}\,}}(f)}U_x\) is open.
Ad (ii). Let \(f\in L^2(G)\). The measure \({|}f{|}^2\cdot \theta _G\) is a finite Radon measure. Indeed, the map \(C_c(G)\rightarrow {{\mathbb {C}}}\), defined by \(g\mapsto \theta _G({|}f{|}^2\cdot g)\), is a continuous linear functional, since for all \(g\in C_c(G)\) we have
where \(C=\Vert f\Vert _2^2<\infty \) is independent of g. By the Riesz representation theorem, \(B\mapsto \theta _G({|}f{|}^2\cdot \mathbf{1}_{B}) =\Vert f\cdot \mathbf{1}_{B}\Vert _2^2\) is a Radon measure.
We now turn to the support of f. Each \(x\in G\setminus {{\,\mathrm{supp}\,}}(f)\) has an open neighborhood \(U_x\) such that \(\Vert f\cdot \mathbf{1}_{U_x}\Vert _2=0\). Each compact \(C\subset G\setminus {{\,\mathrm{supp}\,}}(f)\) admits a finite subset \(I_C\subset C\) indexing the finite subcover \(\bigcup _{x\in I_C}U_x\supset C\). Thus, \(\Vert f\cdot \mathbf{1}_{C}\Vert _2^2\leqslant \sum _{x\in I_C}\Vert f\cdot \mathbf{1}_{U_x}\Vert _2^2=0\). We now use regularity to conclude
Ad (iii). For closed \(K\subset G\), the set \(U=G\setminus K\) is open, and we have \(\Vert \mathbf{1}_{K}\cdot \mathbf{1}_{U}\Vert _2=0\). By definition of \({{\,\mathrm{supp}\,}}\), we conclude \(U\subset G\setminus {{\,\mathrm{supp}\,}}(\mathbf{1}_{K})\). This is equivalent to \({{\,\mathrm{supp}\,}}(\mathbf{1}_{K})\subset K\). Ad (iv). Note that each \(x\in K\setminus {{\,\mathrm{supp}\,}}(\mathbf{1}_{K})\) has an open neighborhood \(U_x\) with \(\Vert \mathbf{1}_{U_x}\cdot \mathbf{1}_{K}\Vert _2=0\). For compact \(C\subset K\setminus {{\,\mathrm{supp}\,}}(\mathbf{1}_{K})\), there is a finite set \(I_C\subset C\) indexing a covering \(\bigcup _{x\in I_C}U_x\supset C\). We conclude
The Haar measure \(\theta _G\) is weakly inner regular, see e.g. [7, Theorem 1.3.4], so we have for all open K and all K with \(\theta _G(K)<\infty \)
If G is \(\sigma \)-finite, we exhaust \(K\setminus {{\,\mathrm{supp}\,}}(\mathbf{1}_{K})\) with countably many sets of finite measure. \(\square \)
Let \(K\subset G\) be measurable. We denote by \(L^2(G:K)\) the subspace of functions having support within K. In slight abuse of notation, we also write
The relation between these spaces is described by the following result.
Lemma 8.4
Let G be an LCA group and let \(K\subset G\) be measurable. Then the following hold.
-
(a)
We have \(\mathrm {cl}(L^2(G:K)) =L^2(K) \subset L^2(G:{{\,\mathrm{supp}\,}}(\mathbf{1}_{K}))\) with equality if and only if \(\theta _G({{\,\mathrm{supp}\,}}(\mathbf{1}_{K})\setminus K)=0\).
-
(b)
The following are equivalent:
-
(i)
\({{\,\mathrm{supp}\,}}(\mathbf{1}_{K})\subset K\).
-
(ii)
\(L^2(G:K)\) is a closed subspace of \(L^2(G)\).
-
(i)
In particular, if K is closed in G, then \(L^2(G:K)\) is closed in \(L^2(G)\), and the spaces in (a) coincide.
Proof
We begin with (a).
-
\(\mathrm {cl}(L^2(G:K))\subset L^2(K)\): Since \(L^2(G)\ni f\mapsto \Vert f\cdot \mathbf{1}_{G\setminus K}\Vert _2\in {{\mathbb {R}}}\) is continuous, the right hand side is closed. Fix \(f\in L^2(G:K)\). From Lemma 8.3(ii) and \({{\,\mathrm{supp}\,}}(f)\subset K\), we get \(\Vert f\cdot \mathbf{1}_{G\setminus K}\Vert _2 =\Vert f\cdot \mathbf{1}_{{{\,\mathrm{supp}\,}}(f)}\cdot \mathbf{1}_{G\setminus K}\Vert _2 =0\), which establishes the claim.
-
\(\mathrm {cl}(L^2(G:K))\supset L^2(K)\): Fix \(f\in L^2(K)\). Using the inner regularity of the Radon measure \({|}f{|}^2\cdot \theta _G\), compare the proof of Lemma 8.3(ii), we see that
$$\begin{aligned} \Vert f\Vert _2^2 =\Vert f\cdot \mathbf{1}_{K}\Vert _2^2+\Vert f\cdot \mathbf{1}_{G\setminus K}\Vert _2^2 =\sup _{\begin{array}{c} C\subset K\\ C\text { compact} \end{array}}\Vert f\cdot \mathbf{1}_{C}\Vert _2^2 =\lim _{n\rightarrow \infty }\Vert f\cdot \mathbf{1}_{C_n}\Vert _2^2 \end{aligned}$$for a suitable sequence of compact \(C_n\subset K\), \(n\in {\mathbb {N}}\). For all \(n\in {\mathbb {N}}\), we know by Lemma 8.3(iii) that \({{\,\mathrm{supp}\,}}(\mathbf{1}_{C_n})\subset C_n\subset K\) since \(C_n\) is closed, so \(f\cdot \mathbf{1}_{C_n}\in L^2(G:K)\). Now
$$\begin{aligned} \Vert f-f\cdot \mathbf{1}_{C_n}\Vert _2^2 =\int {|}f{|}^2\cdot (1-\mathbf{1}_{C_n})\,{\mathrm d}\theta _G =\Vert f\Vert _2^2-\Vert f\cdot \mathbf{1}_{C_n}\Vert _2^2 \xrightarrow {n\rightarrow \infty }0\,\text{. } \end{aligned}$$ -
\(L^2(K)\subset L^2(G:{{\,\mathrm{supp}\,}}(\mathbf{1}_{K}))\): Fix \(f\in L^2(G)\) with \(\Vert f\cdot \mathbf{1}_{G\setminus K}\Vert _2=0\) and define \(U=G\setminus {{\,\mathrm{supp}\,}}(\mathbf{1}_{K})\). Note that U is open and satisfies \(\Vert \mathbf{1}_{U}\cdot \mathbf{1}_{K}\Vert _2=0\). Then
$$\begin{aligned} \Vert f\cdot \mathbf{1}_{U}\Vert _2 = \Vert f\cdot \mathbf{1}_{K}\cdot \mathbf{1}_{U}\Vert _2+\Vert f\cdot \mathbf{1}_{G\setminus K}\cdot \mathbf{1}_{U}\Vert _2 =0\,\text{. } \end{aligned}$$Therefore, \(U\subset G\setminus {{\,\mathrm{supp}\,}}(f)\), which is equivalent to \({{\,\mathrm{supp}\,}}(f)\subset {{\,\mathrm{supp}\,}}(\mathbf{1}_{K})\).
-
If \(\theta _G({{\,\mathrm{supp}\,}}(\mathbf{1}_{K})\setminus K)=0\), then \(L^2(K)\supset L^2(G:{{\,\mathrm{supp}\,}}(\mathbf{1}_{K}))\): Fix \(f\in L^2(G:{{\,\mathrm{supp}\,}}(\mathbf{1}_{K}))\) and note that \( {{\,\mathrm{supp}\,}}(f)\cap (G\setminus K) \subset {{\,\mathrm{supp}\,}}(\mathbf{1}_{K})\setminus K \) is by assumption a set of Haar measure zero. Therefore, by Lemma 8.3(ii), \(\Vert f\cdot \mathbf{1}_{G\setminus K}\Vert _2 =\Vert f\cdot \mathbf{1}_{{{\,\mathrm{supp}\,}}(f)}\cdot \mathbf{1}_{G\setminus K}\Vert _2 =0\).
-
If \(\theta _G({{\,\mathrm{supp}\,}}(\mathbf{1}_{K})\setminus K)>0\), then \(L^2(K)\ne L^2(G:{{\,\mathrm{supp}\,}}(\mathbf{1}_{K}))\): By inner regularity of the Haar measure \(\theta _G\), we find a compact \(C\subset {{\,\mathrm{supp}\,}}(\mathbf{1}_{K})\setminus K\) with \(\theta _G(C)>0\). Define \(f=\mathbf{1}_{C} \in L^2(G)\) and note \(\Vert f\cdot \mathbf{1}_{G\setminus K}\Vert _2 =\Vert f\Vert _2 =\theta _G(C)>0\), but by Lemma 8.3(iii) \({{\,\mathrm{supp}\,}}f \subset C \subset {{\,\mathrm{supp}\,}}(\mathbf{1}_{K})\setminus K \subset {{\,\mathrm{supp}\,}}(\mathbf{1}_{K})\).
We now prove (b).
-
(i)\(\implies \)(ii): By (a) and (i), we have \(\mathrm {cl}(L^2(G:K)) \subset L^2(G:{{\,\mathrm{supp}\,}}(\mathbf{1}_{K})) \subset L^2(G:K) \).
-
(ii)\(\implies \)(i): For each compact subset \(C\subset G\), the measurable set \(C\cap K\) has finite Haar measure. Hence by weak inner regularity of the Haar measures \(\theta _G\), see e. g. [7, Theorem 1.3.4], we may take a sequence \((C_n)_{n\in {\mathbb {N}}}\) of compact sets \(C_n\subset C\cap K\) such that \(\theta _G(C\cap K)=\lim _{n\rightarrow \infty }\theta _G(C_n)\). This implies
$$\begin{aligned} \Vert \mathbf{1}_{C\cap K}-\mathbf{1}_{C_n}\Vert _2^2 =\theta _G(C\cap K)-\theta _G(C_n) \xrightarrow {n\rightarrow \infty }0\ , \end{aligned}$$so that \(\mathbf{1}_{C_n}\rightarrow \mathbf{1}_{C\cap K}\) in \(L^2(G)\). Also, since \(C_n\) is closed, we have \({{\,\mathrm{supp}\,}}(\mathbf{1}_{C_n})\subset C_n\subset C\cap K\subset K\) by Lemma 8.3(iii), so \(\mathbf{1}_{C_n}\in L^2(G:K)\). Now \(L^2(G:K)\) is closed by (ii), so \(\mathbf{1}_{C\cap K}\in L^2(G:K)\), too. This shows \({{\,\mathrm{supp}\,}}(\mathbf{1}_{C\cap K})\subset K\). Now note that
$$\begin{aligned} {{\,\mathrm{supp}\,}}(\mathbf{1}_{K}) \subset \bigcup _{C~\text {compact}}{{\,\mathrm{supp}\,}}(\mathbf{1}_{C\cap K}) \subset \bigcup _{C~\text {compact}}K =K\text { .} \end{aligned}$$Indeed, the first inclusion follows from the following fact: For each \(x\in {{\,\mathrm{supp}\,}}(\mathbf{1}_{K})\) and each compact neighborhood C of x we have \(x\in {{\,\mathrm{supp}\,}}(\mathbf{1}_{C\cap K})\). This is true as for every open neighborhood U of x we have \( \Vert \mathbf{1}_{C\cap K}\mathbf{1}_{U}\Vert _{2} =\Vert \mathbf{1}_{K}\mathbf{1}_{C\cap U}\Vert _{2} >0 \), since \(C\cap U\) contains an open neighborhood of \(x\in {{\,\mathrm{supp}\,}}(\mathbf{1}_{K})\). \(\square \)
Proof of Proposition 8.2
As the Fourier transform is a norm isomorphism between \(L^2(G)\) and  , see e. g. [33, Theorem 4.4.13], the space \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}^\prime \!}\,}}_K\) is closed if and only if
, see e. g. [33, Theorem 4.4.13], the space \({{\,\mathrm{{\mathcal {P}}{\mathcal {W}}^\prime \!}\,}}_K\) is closed if and only if  is closed. Now the claim is obvious from Lemma 8.4. \(\square \)
is closed. Now the claim is obvious from Lemma 8.4. \(\square \)
9 Van Hove Sequences and Banach Densities
We collect some properties of van Hove boundaries \(\partial ^KA=((K+\mathrm {cl}(A))\cap \mathrm {cl}(A^c)) \cup ((K+\mathrm {cl}(A^c))\cap \mathrm {cl}(A))\) that will be used in the sequel. As the following proof shows, Lemma 9.1 continues to hold in the non-abelian setting.
Lemma 9.1
Let G be an LCA group, and consider arbitrary sets \(A,K,L\subset G\). We then have
-
(i)
\(K+\mathrm {cl}(A)\subset \mathrm {int}(A) \cup \partial ^K A \subset (K\cup \{0\})+\mathrm {cl}(A)\)
-
(ii)
\(\mathrm {int}(A)\setminus \partial ^K A \subset \{x\in \mathrm {int}(A): -K+x \subset \mathrm {int}(A)\}\)
-
(iii)
\(\partial ^K(A+L)\subset (\partial ^K A) + \mathrm {cl}(L)\)
-
(iv)
\((L+(\partial ^K A))\subset (\partial ^{L+K}A) \cup (\partial ^L A)\)
Proof
We will use multiplicative notation for the group operation, which is more compact than additive notation.
“(i)” Assume that \(x\in K\mathrm {cl}(A)\) but \(x\notin \mathrm {int}(A)\). Then \(x\in K\mathrm {cl}(A) \cap \mathrm {int}(A)^c=K\mathrm {cl}(A)\cap \mathrm {cl}(A^c)\subset \partial ^KA\). The second statement is obvious.
“(ii)” We compute
Now the claim follows: Assume \(k^{-1}x\notin \mathrm {int}(A)\) for some \(k\in K\) and some \(x\in \mathrm {int}(A) \setminus \partial ^K A\). Then \(x\in k\mathrm {int}(A)^c\subset K\mathrm {cl}(A^c)\), which is a contradiction.
“(iii)” Let us first consider \(x\in K\mathrm {cl}(AL)\cap (\mathrm {int}(AL))^c\). Then \(x=ka\ell \) for some \(k\in K\), \(a\in \mathrm {cl}(A)\) and \(\ell \in \mathrm {cl}(L)\). We show \(ka \in \mathrm {int}(A)^c\), which results in \(x\in (K\mathrm {cl}(A) \cap \mathrm {int}(A)^c) \mathrm {cl}(L)\subset (\partial ^KA)\mathrm {cl}(L)\). Assume \(ka=x\ell ^{-1} \in \mathrm {int}(A)\). Then \(x\in \mathrm {int}(A)\ell \subset \mathrm {int}(A)\mathrm {cl}(L) \subset \mathrm {int}(AL)\), which is a contradiction. It remains to consider the case \(x\in K (\mathrm {int}(AL))^c \cap \mathrm {cl}(AL)\). Then \(x=a\ell \) for some \(a\in \mathrm {cl}(A)\) and some \(\ell \in \mathrm {cl}(L)\). We show \(a=x\ell ^{-1}\in K\mathrm {int}(A)^c\), which proves the claim. Indeed, assume \(x\ell ^{-1} \notin K \mathrm {int}(A)^c\). Then \(x\notin K(\mathrm {int}(A)\ell )^c \supset K (\mathrm {int}(A)\mathrm {cl}(L))^c \supset K (\mathrm {int}(AL))^c\), which is a contradiction.
“(iv)” This is proved in [31, Lemma 2.13]. \(\square \)
The following lemma shows that van Hove sequences may be nested and may have simple topological properties. In fact they may be supersets of any relatively compact seed.
Lemma 9.2
Let G be a \(\sigma \)-compact LCA group with Haar measure \(\theta _G\). Consider any relatively compact set \(A\subset G\). Then there exists a van Hove sequence \((A_n)_{n}\) such that \(A_n=\mathrm {cl}(\mathrm {int}(A_n))\), \(\theta _G(\partial A_n)=0\), \(A_n\subset \mathrm {int}(A_{n+1})\) and \(A\subset A_n\) for all n.
Proof
(i) We first prove the assertion of the lemma for \(A=\{e\}\). Take any van Hove sequence \((C_n)_n\). We will first use \((C_n)_n\) to construct a van Hove sequence \((B_n)_n\) satisfying \(B_n=\mathrm {cl}(\mathrm {int}(B_n))\) and \(\theta _G(\partial B_n)=0\). Passing to a suitable shifted subsequence will then yield \((A_n)_n\) with the claimed properties. Take any open relatively compact zero neighborhood \(U\subset G\). For every n, take a compact set \(B_n\) such that \(C_n\subset B_n\subset UC_n\), \(\theta _G(\partial B_n)=0\) and \(\mathrm {cl}(\mathrm {int}(B_n))=B_n\). This is possible by the construction given in the proof of [16, Lemma 3.6]. Consider any compact \(K\subset G\). We can now estimate
Since \(\theta _G(B_n)\geqslant \theta _G(C_n)\), the van Hove property \(\theta _G(\partial ^K B_n)/\theta _G(B_n)\rightarrow 0\) follows from the van Hove property of \((C_n)_n\). Next, we construct \((A_n)_n\) as follows. Take \(b\in B_1\) and define \(A_1=B_1b^{-1}\). Now assume that \(A_1, \ldots , A_k\) satisfying the properties claimed in the statement of the lemma have been chosen. We construct \(A_{k+1}\) following the proof of [32, Lemma 2.6(e)]. Take n such that \(\theta _G(\partial ^{A_k^{-1}}B_n)< \theta _G(\mathrm {int}(B_n))=\theta _G(B_n)\), which is possible due to the van Hove property of \((B_n)_n\). Then \(\mathrm {int}(B_n)\setminus \partial ^{A_k^{-1}}B_n \subset \{x\in \mathrm {int}(B_n): A_kx\subset \mathrm {int}(B_n)\}=:S_n\) by Lemma 9.1(ii) and
In particular, we may choose \(s\in S_n\) and define \(A_{k+1}=B_ns^{-1}\). Then \(A_ks\subset \mathrm {int}(B_n)\) implies \(A_k\subset \mathrm {int}(B_ns^{-1})=\mathrm {int}(A_{k+1})\). It is obvious that \((A_n)_n\) is van Hove, since it is a shifted subsequence of the van Hove sequence \((B_n)_n\).
(ii) Now choose any relatively compact set \(A\subset G\), which we assume to be nonempty without loss of generality. Take any van Hove sequence \((B_n)_n\) having the properties in part (i) of the proof. Then the sequence \((A_n)_n\) of compact sets defined by \(A_n=B_n\mathrm {cl}(A)\) satisfies \(A\subset A_n\) and \(A_n\subset \mathrm {int}(A_{n+1})\) for all n. Take any compact \(K\subset G\). By Lemma 9.1 and commutativity of G, we can estimate
This can be used to conclude that \((A_n)_n\) is van Hove. Indeed, we have
Here we used that the first factor on the rhs is bounded by 1 uniformly in n. Indeed, by translation invariance of the Haar measure we may assume \(e\in A\) without loss of generality. But then \(B_n\subset B_n\mathrm {cl}(A)\), implying \(\theta _G(B_n)/\theta _G(B_n\mathrm {cl}(A))\leqslant 1\). \(\square \)
Following [14], we consider a transitive relation \(\preceq \) between non-negative translation bounded measures. Let \(\mu , \nu \in {\mathcal {M}}^\infty (G)\) such that \(\mu ,\nu \geqslant 0\). Then \(\mu \preceq \nu \) iff for every \(\varepsilon >0\) there exists compact \(K\subset G\) such that for all compact \(A\subset G\) we have \((1-\varepsilon ) \mu (A)\leqslant \nu (K+A)\). Let us write \(\nu \succeq \mu \) iff \(\mu \preceq \nu \). We have the following result, which allows to rephrase Theorem 1” from [14] using upper and lower Banach densities.
Lemma 9.3
Let G be a \(\sigma \)-compact LCA group with Haar measure \(\theta _G\). Let \({\mathcal {A}}=(A_n)_{n\in {\mathbb {N}}}\) be any van Hove sequence in G. Then for any uniformly discrete set \(\Lambda \subset G\) with associated counting measure \(\delta _\Lambda \) and any \(\alpha \geqslant 0\) the following implications hold.
-
(i)
\(\delta _\Lambda \succeq \alpha \theta _G \Longrightarrow {{\mathcal {D}}}^-_{{\mathcal {A}}}(\Lambda )\geqslant \alpha \)
-
(ii)
\(\delta _\Lambda \preceq \alpha \theta _G \Longrightarrow {{\mathcal {D}}}^+_{{\mathcal {A}}}(\Lambda ) \leqslant \alpha \)
Proof
“(i)”: Consider arbitrary \(\varepsilon >0\). By assumption there exists compact \(K\subset G\) such that for all compact \(A\subset G\) we have \((1-\varepsilon )\alpha \theta _G(A)\leqslant \delta _\Lambda (KA)\). Letting \(A=A_ns\), we have
where we used Lemma 9.1 (i) and translation invariance of the Haar measure. Now the second term on the rhs vanishes as \(n\rightarrow \infty \) uniformly in s by [22, Lemma 9.2.(b)]. This implies \((1-\varepsilon )\alpha \leqslant {{\mathcal {D}}}^-_{{\mathcal {A}}}(\Lambda )\). As \(\varepsilon >0\) was arbitrary, the claim follows.
“(ii)”: Consider arbitrary \(\varepsilon >0\). By assumption there exists compact \(K\subset G\) such that for all compact \(A\subset G\) we have \((1-\varepsilon )\delta _\Lambda (A)\leqslant \alpha \theta _G(KA)\). Letting \(A=A_ns\), we have
where we used translation invariance of the Haar measure. Now the second factor on the rhs tends to unity as \(n\rightarrow \infty \) by the van Hove property. Indeed, we may assume \(0\in K\) and can then use Lemma 9.1(i). This implies \(\alpha \geqslant (1-\varepsilon ) {{\mathcal {D}}}^+_{{\mathcal {A}}}(\Lambda )\). As \(\varepsilon >0\) was arbitrary, the claim follows. \(\square \)
Change history
17 May 2021
A Correction to this paper has been published: https://doi.org/10.1007/s00041-021-09851-0
References
Agora, E., Antezana, J., Cabrelli, C.: Multi-tiling sets, Riesz bases, and sampling near the critical density in LCA groups. Adv. Math. 285, 454–477 (2015)
Agora, E., Antezana, J., Cabrelli, C., Matei, B.: Existence of quasicrystals and universal stable sampling and interpolation in LCA groups. Trans. Am. Math. Soc. 372, 4647–4674 (2019)
Argabright, L.N., Gil de Lamadrid, J.: Fourier Analysis of Unbounded Measures on Locally Compact Abelian Groups. American Mathematical Society, Providence (1974)
Baake, M., Grimm, U.: Aperiodic Order. Vol. 1 A Mathematical Invitation Encyclopedia of Mathematics and its Applications. Cambridge University Press, Cambridge (2013)
Berg, C., Forst, G.: Potential Theory on Locally Compact Abelian Groups. Springer, Berlin (1975)
Bourbaki, N.: General Topology, Chapters 5–10, Elements of Mathematics. Springer, Berlin (1998)
Deitmar, A., Echterhoff, S.: Principles of Harmonic Analysis. Springer, New York (2009)
Downarowicz, T., Huczek, D., Zhang, G.: Tilings of amenable groups. J. Reine Angew. Math. 747, 277–298 (2019)
Feichtinger, H.G.: Eine neue Segalalgebra mit Anwendungen in der harmonischen Analyse. In: Winterschule 1979: Internationale Arbeitstagung über topologische Gruppen und Gruppenalgebren, Institut für Mathematik der Universität Wien, pp. 23–26. (1980)
Feichtinger, H.G.: Un espace de Banach de distributions tempérés sur les groupes localement compacts abéliens. Compt. Rend. Acad. Sci. Paris Ser. A 290, 791–794 (1980)
Feichtinger, H.G.: On a new Segal algebra. Monatsh. Math. 92, 269–289 (1981)
Feichtinger, H.G., Luef, F., Cordero, E.: Banach Gelfand triples for Gabor analysis. In: Rodino, L., Wong, M.W. (eds.) Lecture Notes in Mathematics. Pseudo-Diffential Operators: Quantization and Signals, pp. 1–33. Springer, Berlin (2008)
Grepstad, S., Lev, N.: Riesz bases, Meyer’s quasicrystals, and bounded remainder sets. Trans. Am. Math. Soc. 370, 4273–4298 (2018)
Gröchenig, K., Kutyniok, G., Seip, K.: Landau’s necessary density conditions for LCA groups. J. Funct. Anal. 255, 1831–1850 (2008)
Hewitt, E., Ross, K.A.: Abstract Harmonic Analysis, vol. I. Springer, Berlin (1979)
Huck, C., Richard, C.: On pattern entropy of weak model sets. Discrete Comput. Geom. 54, 741–757 (2015)
Jakobsen, M.S.: On a (no longer) new Segal slgebra: a review of the Feichtinger algebra. J. Fourier Anal. Appl. 24, 1579–1660 (2018)
Keller, G., Richard, C.: Periods and factors of weak model sets. Israel J. Math. 229, 85–132 (2019)
Kozma, G., Lev, N.: Exponential Riesz bases, discrepancy of irrational rotations and BMO. J. Fourier Anal. Appl. 17, 879–898 (2011)
Landau, H.J.: Necessary density conditions for sampling and interpolation of certain entire functions. Acta Math. 117, 37–52 (1967)
Lenz, D.: Continuity of eigenfunctions of uniquely ergodic dynamical systems and intensity of Bragg peaks. Commun. Math. Phys. 287, 225–258 (2009)
Lenz, D., Richard, C.: Pure point diffraction and cut and project schemes for measures: the smooth case. Math. Z. 256, 347–378 (2007)
Matei, B., Meyer, Y.: Simple quasicrystals are sets of stable sampling. Complex Var. Elliptic Equ. 55, 947–964 (2010)
Matusiak, E.: Gabor frames for model sets. J. Fourier Anal. Appl. 25, 2570–2607 (2019)
Meyer, Y.: Nombres de Pisot, Nombres de Salem et Analyse Harmonique. Lecture Notes in Mathematics. Springer, Berlin (1970)
Meyer, Y.: Algebraic Numbers and Harmonic Analysis. North-Holland, Amsterdam (1972)
Meyer, Y.: Adeles et series trigonometriques speciales. Ann. Math. 97, 171–186 (1973)
Meyer, Y.: Mean-Periodic Functions and Irregular Sampling, pp. 5–23. Royal Norwegian Society of Sciences and Letters, Trondheim (2018)
Moody, R.V.: Meyer sets and their duals. In: Moody, R.V. (ed.) The Mathematics of Long-Range Aperiodic Order. NATO ASI Series, pp. 403–441. Kluwer, Dordrecht (1997)
Moody, R.V., Strungaru, N.: Almost Periodic Measures and Their Fourier Transform Aperiodic Order. Cambridge University Press, Cambridge (2017)
Müller, P., Richard, C.: Ergodic properties of randomly coloured point sets. Can. J. Math. 65, 349–402 (2013)
Pogorzelski, F., Schwarzenberger, F.: A Banach space-valued ergodic theorem for amenable groups and applications. J. Anal. Math. 130, 19–69 (2016)
Reiter, H., Stegeman, J.D.: Classical Harmonic Analysis and Locally Compact Groups. Clarendon Press, Oxford (2000)
Richard, C., Strungaru, N.: Pure point diffraction and Poisson summation. Ann. Henri Poincaré 18, 3903–3931 (2017)
Richard, C., Strungaru, N.: A short guide to pure point diffraction in cut-and-project sets. J. Phys. A 50, 154003 (2017)
Schlottmann, M.: Cut-and-project sets in locally compact Abelian groups. In: Patera, J. (ed.) Quasicrystals and Discrete Geometry, pp. 247–264. American Mathematical Society, Providence, RI (1998)
Schlottmann, M.: Generalized model sets and dynamical systems. In: Baake, M. (ed.) Directions in Mathematical Quasicrystals. CRM Monograph Series, pp. 143–159. American Mathematical Society, Providence, RI (2000)
Young, R.M.: An Introduction to Nonharmonic Fourier Series, revised, 1st edn. Academic Press, New York (2001)
Acknowledgements
The results of this article emerged from discussions during mutual visits of the authors at TU Chemnitz, FAU Erlangen-Nürnberg and TU Dortmund. The authors are grateful for support by their faculties. CS would like to thank Thomas Kalmes and Albrecht Seelmann for enlightening and fruitful discussions. CR would like to thank the participants of the conference Model sets and Aperiodic Order in Durham in September 2018, where parts of the above results were presented, for inspiring discussions. We thank the referees and Hans Georg Feichtinger for very helpful comments and suggestions.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Karlheinz Gröchenig.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article has been updated to publish as Open Access.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Richard, C., Schumacher, C. On Sampling and Interpolation by Model Sets. J Fourier Anal Appl 26, 39 (2020). https://doi.org/10.1007/s00041-020-09742-w
Received:
Revised:
Published:
DOI: https://doi.org/10.1007/s00041-020-09742-w




 is compactly generated without loss of generality, see [
is compactly generated without loss of generality, see [ . Indeed,
. Indeed,  follows from Hölder’s inequality by assumption on K. We thus have
follows from Hölder’s inequality by assumption on K. We thus have  and
and  in
in  . The above definition is also used in [
. The above definition is also used in [ , then both definitions are equivalent. This is discussed in Sect.
, then both definitions are equivalent. This is discussed in Sect.  .
. .
.  , then
, then  , then
, then  . However these assumptions are not necessary, as may be seen by approximation arguments using regularity of the Haar measure.
. However these assumptions are not necessary, as may be seen by approximation arguments using regularity of the Haar measure. , if
, if  , and if K is a so-called bounded remainder set. In particular in [
, and if K is a so-called bounded remainder set. In particular in [ on K. This is possible as
on K. This is possible as  is non-negative for every j and since
is non-negative for every j and since  converges locally uniformly to one by [
converges locally uniformly to one by [ is stable interpolating for
is stable interpolating for  .
. is stable interpolating for
is stable interpolating for  , then
, then  is stable sampling for
is stable sampling for  , then
, then  such that
such that  is dense
is dense  , see the proof of [
, see the proof of [ . In that case, we may take
. In that case, we may take  is a left-semiclosed multiband set, i. e., a union of finitely many pairwise disjoint intervals [a, b). In that situation one may take
is a left-semiclosed multiband set, i. e., a union of finitely many pairwise disjoint intervals [a, b). In that situation one may take  to be
to be 

 , a condition which is satisfied if
, a condition which is satisfied if 
 . This differs from
. This differs from  in Eq. (
in Eq. (