Abstract
We generalize three main concepts of Gabor analysis for lattices to the setting of model sets: fundamental identity of Gabor analysis, Janssen’s representation of the frame operator and Wexler–Raz biorthogonality relations. Utilizing the connection between model sets and almost periodic functions, as well as Poisson’s summations formula for model sets we develop a form of a bracket product that plays a central role in our approach. Furthermore, we show that, if a Gabor system for a model set admits a dual which is of Gabor type, then the density of the model set has to be greater than one.
Similar content being viewed by others

Avoid common mistakes on your manuscript.
1 Introduction
One of the central themes within Gabor analysis for lattices is a duality theory for Gabor frames, including Wexler–Raz biorthogonality relations [28] and Janssen’s representation of a Gabor frame operator [17]. These results are closely connected with the so-called fundamental identity of Gabor analysis, that can be derived from an application of Poisson’s summation formula for the symplectic Fourier transform [8]. These duality conditions allow us for example to specify whether a given Gabor system is a tight frame or whether two Gabor systems are dual to each other. An immediate consequence of the duality theory one can obtain necessary density conditions on a lattice so that a given Gabor system forms a frame. In this exposition we leave the setting of a lattice and consider a certain type of irregular sets of time-frequency shifts, namely model sets.
The first examples of model sets were studied by Meyer in [22]. Meyer thought of model sets as generalizations of lattices which retain enough lattice-like structure to be useful for studying sampling problems in harmonic analysis [20, 23]. The crucial property of model sets is that there exists a form of Poisson’s summation formula, which in turn will allow us to derive analogous duality theory as in the case of Gabor analysis for lattices.
First work on Gabor frames for model sets was done by Kreisel [18], where he showed how Gabor frames for a simple model set can be made compatible with its topological dynamics and derived existence conditions for multiwindow Gabor frames for model sets. We will use some of his results here. A constructive approach, that is a characterization of tight and dual frames of semi-regular Gabor systems (where time shifts come from a lattice, and frequency shifts come from a model set, or vice versa), was recently obtained in [21].
For general irregular sets of time-frequency shifts, that are however discrete and relatively separated, it is difficult to provide any constructive results as the tools to deal with such sets are missing. However, certain extensions into irregular Gabor frames were undertaken, for example in [9] or [12]. In [9], the author gave a characterization of the weighted irregular Gabor tight frame and dual systems in \({L^2}(\mathbb {R}^d)\) in terms of the distributional symplectic Fourier transform of a positive Borel measure on \(\mathbb {R}^{2d}\) in the case where the window belongs to the Schwartz class. More recently in [13] the authors study nonuniform sampling in shift invariant spaces and construct semi-regular Gabor frames with respect to the class of totally positive functions. Their results are Beurling type results, expressed by means of density of the sampling sets.
We utilize the connection between model sets and almost periodic functions and use harmonic analysis of the latter to develop a certain form of duality theory for Gabor frames for model sets. We rely strongly on Poisson’s summation formula for model sets to introduce the so-called bracket product, in analogy to the bracket product for lattices introduced in [6] to study shift-invariant spaces, or later in multi-dimensional setting to study frames of translates [14, 19].
Almost periodic functions were recently investigated in the connection with Gabor frames in [4, 10, 26]. As the space of almost periodic functions is non-separable, it can not admit countable frames, and the problem arises in which sense frame-type inequalities are still possible for norm estimation in this space [4, 10, 26]. In [4] the authors also provide Gabor frames for a suitable separable subspaces of the space of almost periodic functions. We, on the other hand, use almost periodic functions as a tool to develop existence results for irregular Gabor frames for the space of square integrable functions.
The article is organized as follows. In Sect. 2 we establish some notations and definitions that we will use throughout the article. In Sect. 3 we derive main identities of Gabor analysis for lattices using a different approach than the one presented in the literature, namely by constructing a certain bracket product. We introduce model sets in Sect. 4, and we also shortly present main facts from the theory of almost periodic functions and point out some connections between the two. Section 5 is devoted to developing a technical tool, that is a bracket product for model sets, that we later use in Sect. 6 to obtain fundamental identity of Gabor analysis, Janssen representation and Wexler–Raz biorthogonality relations for Gabor systems for model sets.
2 Notation and Preliminaries
We will work with the Hilbert space of square integrable functions on \({L^2}(\mathbb {R}^d)\). The key element in time-frequency analysis is the time-frequency shift operator\(\pi (z)\), \(z=(x,\omega )\in \mathbb {R}^{2d}\), which acts on \({L^2}(\mathbb {R}^d)\) by
Here \(M_\omega \) denotes the modulation operator and \(T_x\) the translation operator which are defined as
We define a Fourier transform on \({L^2}(\mathbb {R}^d)\) as
and denote the inverse Fourier transform of f by \(\check{f}\). In the sequel we will distinguish between Fourier transform on \({L^2}(\mathbb {R}^d)\) and Fourier transform on \({L^2}(\mathbb {R}^{2d})\) by writing \(\mathcal {F}f\) for the latter, \(f\in {L^2}(\mathbb {R}^{2d})\). The Fourier transform has a property of interchanging translation and modulation, that is
The translation and modulation operators obey the following commutation relation
Combining the last two properties, we have that
Given a non-zero function \(g\in {L^2}(\mathbb {R}^d)\), the short-time Fourier transform of \(f\in {L^2}(\mathbb {R}^d)\) with respect to the window g, is defined as
We define the modulation spaces as follows: fix a non-zero Schwartz function \(g\in \mathcal {S}(\mathbb {R}^d)\), and let
with the norm \(||f||_{M^p} = ||\mathcal {V}_g f||_p\). Different choices for g give rise to equivalent norms on \(M^p(\mathbb {R}^d)\). For \(p=2\), we have \(M^2(\mathbb {R}^d) = {L^2}(\mathbb {R}^d)\). The space \(M^1(\mathbb {R}^d)\), known as Feichtinger’s algebra, can also be characterized as
Proposition 2.1
[11] The space \(M^1(\mathbb {R}^d)\) has the following properties:
-
(i)
\(M^1(\mathbb {R}^d)\) is a Banach algebra under pointwise multiplication.
-
(ii)
\(M^1(\mathbb {R}^d)\) is a Banach algebra under convolution.
-
(iii)
\(M^1(\mathbb {R}^d)\) is invariant under time-frequency shifts.
-
(vi)
\(M^1(\mathbb {R}^d)\) is invariant under Fourier transform.
\(M^1(\mathbb {R}^d)\) contains the Schwartz space \(\mathcal {S}(\mathbb {R}^d)\) and it is dense in \(L^p(\mathbb {R}^d)\), \(1\le p < \infty \), therefore it is a very useful space in the time-frequency analysis. This will be the space of windows g.
Another collection of function spaces that will be useful in our calculations are the amalgam spaces \(\mathbf {W}(L^p,\ell ^q)(\mathbb {R}^d)\), \(1\le p,q \le \infty \). The amalgam space \(\mathbf {W}(L^p,\ell ^q)(\mathbb {R}^d)\) is the space of functions f such that
where \(\mathbb {1}_k\) is the characteristic function of the cube \([0,1]^d +k\), \(k\in \mathbb {Z}^d\). Different partitions of \(\mathbb {R}^d\) give equivalent norms. The space \(\mathbf {W}(L^{\infty },{\ell ^1})(\mathbb {R}^d)\), which is a subspace of \(L^1(\mathbb {R}^d)\), is referred to as Wiener’s algebra, and will be denoted by \(\mathbf {W}(\mathbb {R}^d)\). It consists of all \(f\in L^\infty (\mathbb {R}^d)\) such that
Moreover, we have \(\mathbf {W}(\mathbb {R}^d) \subseteq \mathbf {W}(L^{\infty },{\ell ^2})(\mathbb {R}^d)\). The following convolution relation will be often used:
For a function \(f\in M^1(\mathbb {R}^d)\) it follows that \(f\in \mathbf {W}(L^{\infty },{\ell ^1})(\mathbb {R}^d)\) and \({\widehat{f}} \in \mathbf {W}(L^{\infty },{\ell ^1})(\mathbb {R}^d)\), [11].
Let \(C_0(\mathbb {R}^d)\) be the space of all continuous functions that vanish at infinity. Then the closed subspace of \(\mathbf {W}(\mathbb {R}^d)\) consisting of continuous functions is \(\mathbf {W}(C_0,{\ell ^1})(\mathbb {R}^d)\). Continuity of elements in \(\mathbf {W}(L^{\infty },{\ell ^1})(\mathbb {R}^d)\) allows for pointwise evaluations, and we have (see Proposition 11.1.4 in [11]): if \(F\in \mathbf {W}(C_0,{\ell ^1})(\mathbb {R}^d)\), then \(F|\Lambda \in {\ell ^1}(\Lambda )\), for \(\Lambda \) any discrete relatively separated set in \(\mathbb {R}^d\) with the norm estimate
A discrete subset \(\Lambda \) of \(\mathbb {R}^d\) is relatively separated if
where B(x, 1) is a ball of radius 1 in \(\mathbb {R}^d\) centered at x.
There are two more time frequency representations of f that we will be using. For \(f,g\in {L^2}(\mathbb {R}^d)\), the cross-ambiguity function of f and g
and the cross-Wigner distribution of f and g
The three time-frequency representations, \(\mathcal {V}_gf\), \(\mathcal {A}(f,g)\) and \(\mathcal {W}(f,g)\) are related to each other. Before we state the relationships, we define the rotation \(\mathcal {U}= \mathcal {U}_J\) of a function F on \(\mathbb {R}^{2d}\) as
where I is the \(d\times d\) identity matrix. Then \(\mathcal {U}^{-1} = \mathcal {U}_J^{-1} = \mathcal {U}_{-J}\). In the following two propositions we list the properties of the cross-ambiguity function and the cross-Wigner distribution that we will be using throughout the exposition. For the proofs we refer the reader to [11].
Proposition 2.2
For \(f,g\in {L^2}(\mathbb {R}^d)\) the cross-ambiguity function has the following properties.
-
(a)
\(\mathcal {A}(f,g)\) is uniformly continuous on \(\mathbb {R}^{2d}\).
-
(b)
\(\mathcal {A}(f,g)(x,\omega ) = e^{\pi i x \cdot \omega } \mathcal {V}_g f(x,\omega )\).
-
(c)
\(\mathcal {A}(f,g)^* = \mathcal {A}(g,f)\), where \(\mathcal {A}(f,g)^*(x,\omega ) = \overline{\mathcal {A}(f,g)(-x,-\omega )}\) is the involution.
-
(d)
\(\mathcal {A}(\pi (x,\omega )f,g)(t,\zeta ) = e^{\pi i t \cdot \omega } e^{-\pi i x\cdot (\zeta -\omega )} \mathcal {A}(f,g) (t-x,\zeta -\omega )\) for \((x,\omega )\in \mathbb {R}^{2d}\).
-
(e)
\(\mathcal {A}(f,g) = \mathcal {F}^{-1} \mathcal {U}^{-1} \mathcal {W}(f,g)\).
Moreover, if \(f,g\in M^1(\mathbb {R}^d)\), then \(\mathcal {A}(f,g) \in \mathbf {W}(C_0,{\ell ^1})(\mathbb {R}^{2d})\), and by b), also \(\mathcal {V}_g f \in \mathbf {W}(C_0,{\ell ^1})(\mathbb {R}^{2d})\).
Proposition 2.3
For \(f,g\in {L^2}(\mathbb {R}^d)\) the cross-Wigner distribution has the following properties.
-
(a)
\(\mathcal {W}(f,g)\) is uniformly continuous on \(\mathbb {R}^{2d}\).
-
(b)
\(\mathcal {W}(f,g) = \overline{\mathcal {W}(g,f)}\).
-
(c)
\(\mathcal {W}({\widehat{f}},{\widehat{g}}) = \mathcal {U}^{-1} W(f,g)\).
-
(d)
\(\mathcal {W}(f,g) = \mathcal {F}\mathcal {U}\mathcal {A}(f,g)\).
-
(e)
For \((x,\omega )\in \mathbb {R}^{2d}\) and \((x',\omega ')\in \mathbb {R}^{2d}\), we have
$$\begin{aligned} \mathcal {W}(T_x M_\omega f,&T_{x'} M_{\omega '}g)(t,\zeta ) \\&= e^{-\pi i (x+x')\cdot (\omega -\omega ')} e^{2\pi i t\cdot (\omega -\omega ')} e^{-2\pi i \zeta \cdot (x-x')} \\&\quad \times \,\mathcal {W}(f,g)\Big (t - \frac{x+x'}{2},\zeta - \frac{\omega +\omega '}{2}\Big ) \end{aligned}$$ -
f)
Moyal’s formula: for \(f_1,g_1 \in {L^2}(\mathbb {R}^d)\),
$$\begin{aligned} \langle W(f,g),W(f_1,g_1)\rangle _{{L^2}(\mathbb {R}^{2d})} = \langle f,f_1\rangle \overline{\langle g,g_1\rangle }\,. \end{aligned}$$
Moreover, if \(f,g\in M^1(\mathbb {R}^d)\), then \(\mathcal {W}(f,g) \in \mathbf {W}(C_0,{\ell ^1})(\mathbb {R}^{2d})\).
We note here that Moyal’s formula also holds for the cross-ambiguity function and the short-time Fourier transform. We also mention the following tensor-product properties: if \(Z=(z,{\tilde{z}})\) with \(z\in \mathbb {R}^{2n}\), \({\tilde{z}}\in \mathbb {R}^{2d-2n}\) and \(\psi _1,\phi _1\in M^1(\mathbb {R}^n)\), \(\psi _2,\phi _2\in M^1(\mathbb {R}^{d-n})\), then
Similarly for the cross-Wigner distribution and short-time Fourier transform.
Before we turn to Gabor systems, we need one more result. It is originally stated for the short-time Fourier transform, but we state it here for the cross-ambiguity function. The proof is the same.
Lemma 2.4
[7] Let \(f,g\in M^1(\mathbb {R}^d)\). Then \(\mathcal {A}(f,g) \in M^1(\mathbb {R}^{2d})\).
The main object of our study here are Gabor systems. Let \(\Lambda \) be a relatively separated subset of \(\mathbb {R}^{2d}\). A Gabor system is a collection of time-frequency shifts of one or more window functions \(g_i\in M^1(\mathbb {R}^d)\), \(i=1,\ldots ,M\), with respect to \(\Lambda \subset \mathbb {R}^{2d}\), and it is denoted by
The analysis operator and the synthesis operator for a Gabor system \(\mathcal {G}(g_1,\ldots ,g_M;\Lambda )\) are defined as
are bounded between \(M^p(\mathbb {R}^d)\) and \(\ell ^p(\Lambda )\) spaces, with estimates
A Gabor system \(\mathcal {G}(g_1,\ldots ,g_M;\Lambda )\) with \(g_i\in M^1(\mathbb {R}^d)\), \(i=1,\ldots ,M\), will be called an \(M^p\)-frame if \(C_{g,\Lambda }\) is bounded below on \(M^p(\mathbb {R}^d)\). This is equivalent to having constants \(A_g,B_g>0\) so that for all \(f\in M^p(\mathbb {R}^d)\)
where \(S_g^{\Lambda }\) is a frame operator given by
In this case the frame operator is invertible on \(M^p(\mathbb {R}^d)\). Theorem 3.2 in [12] states that when each \(g_i\in M^1(\mathbb {R}^d)\), \(i=1,\ldots ,M\), then \(\mathcal {G}(g_1,\ldots ,g_M;\Lambda )\) is an \(M^p\)-frame for some \(p\in [1,\infty ]\), if and only if it is an \(M^p\)-frame for all p. The constants \(A_g\) and \(B_g\) are called lower and upper frame bounds, respectively. If \(A_g=B_g\) then the frame is called a tight Gabor frame, and if \(A_g=B_g=1\), a normalized tight Gabor frame.
When \(\mathcal {G}(g_1,\ldots ,g_M;\Lambda )\) is an \(M^p\)-frame for some \(p\in [1,\infty ]\), then we have a frame decomposition
The sequence \(\{\big (S_g^\Lambda \big )^{-1} \pi (\lambda ) g_i: i=1,\ldots , M,\, \lambda \in \Lambda \}\) is also a frame for \(M^p(\mathbb {R}^d)\), called the canonical dual frame of \(\mathcal {G}(g_1,\ldots ,g_M;\Lambda )\), and has upper and lower frame bounds \(B_g^{-1}\) and \(A_g^{-1}\), respectively. If the frame is tight, then \(\big (S_g^\Lambda \big )^{-1}= A_g^{-1} I\), where I is the identity operator, and the frame decomposition becomes
In order to use the representation (2) in practice, we need to be able to calculate \(\big (S_g^\Lambda \big )^{-1}\). While the existence of \(\big (S_g^\Lambda \big )^{-1}\) is guaranteed by the frame condition, it is usually tedious to find this operator explicitly. Moreover, if \(\Lambda \) is not a lattice in \(\mathbb {R}^d\), then the frame operator of \(S_g^{\Lambda }\) does not commute with time-frequency shifts, that is \(\pi (\beta ) S_g^\Lambda \ne S_g^\Lambda \pi (\beta )\) for \(\beta \in \Lambda \). Indeed, let \(\beta \in \Lambda \) and \(f\in {L^2}(\mathbb {R}^d)\), then
where \(\beta =(\beta _1,\beta _2)\) and \(\lambda =(\lambda _1,\lambda _2)\). On the other hand,
and the two expressions are not equal since \(\Lambda +\beta \ne \Lambda \). Therefore, the canonical dual frame \(\{ \big (S_g^{\Lambda }\big )^{-1} \pi (\lambda ) g_i:i=1,\ldots ,M,\, \lambda \in \Lambda \}\) does not have the same structure as \(\mathcal {G}(g_1,\ldots ,g_M;\Lambda )\), that is it is not a Gabor frame, and, in order to compute the canonical dual frame we would have to apply \(\big (S_g^{\Lambda } \big )^{-1}\) to \(\pi (\lambda ) g_i\), for all \(i=1,\ldots ,M\) and all \(\lambda \in \Lambda \). Hence, we search for a pair of dual frames, rather than just one frame. Let \(\mathcal {G}(g_1,\ldots ,g_M;\Lambda )\) and \(\mathcal {G}(h_1,\ldots ,h_M;\Lambda )\) be Gabor systems, then we can define a mixed frame operator
which is a bounded linear operator on \( M^p(\mathbb {R}^d)\). If \(S_{g,h}^{\Lambda } f = f\) for every \(f\in M^p(\mathbb {R}^d)\), then we call \(\mathcal {G}(h_1,\ldots ,h_M;\Lambda )\) a generalized dual Gabor frame of \(\mathcal {G}(g_1,\ldots ,g_M;\Lambda )\).
3 Gabor Frames for Lattices: Revised
Before we turn our attention to Gabor frames for model sets, we revisit here known results for regular Gabor frames, that is where time-frequency shifts come from a lattice. We present a different approach then the one presented in the literature, by constructing a bracket product for the time-frequency plane. Alternative, but in some sense similar approaches, were also developed in [8] and more recently in [16].
Throughout this section \(\Lambda \) will be a lattice, that is a discrete subgroup of \(\mathbb {R}^{2d}\). A lattice can be represented by an invertible matrix \(A\in GL(2d,\mathbb {R})\) and is then given by \(\Lambda = A \mathbb {Z}^{2d}\). We define the volume of a lattice \(\Lambda =A\mathbb {Z}^{2d}\) by \(\text {vol}(\Lambda ) = |\det (A)|\). The density of a lattice is given by the reciprocal of the volume, that is \(D(\Lambda ) = \text {vol}(\Lambda )^{-1}\). A dual lattice is defined as \(\Lambda ^*=A^{-T}\mathbb {Z}^{2d}\).
A tool that is heavily utilized in time-frequency analysis is the Poisson summation formula for functions on \(\mathbb {R}^d\). However, we will use here Poisson summation formula for functions on \(\mathbb {R}^{2d}\).
Theorem 3.1
(Poisson Summation Formula for Lattices) Let \(\Lambda \) be a lattice in \(\mathbb {R}^{2d}\). Then, for every \(F\in M^1(\mathbb {R}^{2d})\) we have
where \(\Lambda ^*\) is a dual lattice. The identity holds pointwise for all \(z\in \mathbb {R}^{2d}\), and both sums converge uniformly and absolutely \(z\in \mathbb {R}^{2d}\).
Let \(f,g,h\in M^1(\mathbb {R}^d)\). Then, by Lemma 2.4\(\mathcal {A}(f,g)\) and \(\mathcal {W}(f,g)\) belong to \(M^1(\mathbb {R}^{2d})\), and by Poisson summation formula,
where we used the relation \(\mathcal {A}(f,g) = \mathcal {F}^{-1} \mathcal {W}({\widehat{f}},{\widehat{g}})\) derived from Proposition 2.2 and Proposition 2.3. Assume that \(\Lambda = A\mathbb {Z}^{2d}\), then we can write (3) more explicitly as
We are now in the position to define a main ingredient in our approach, the bracket product. Let \(f\in {L^2}(\mathbb {R}^d)\) and \(g\in M^1(\mathbb {R}^d)\). For a fixed \(z=(x,\omega )\in \mathbb {R}^{2d}\), the generalized\(\Lambda -\)bracket product of \(\pi (z)f\) and g is defined as
where \(M_z\) denotes the \(\mathbb {R}^{2d}\) modulation by z. It follows from Monotone Convergence Theorem and the fact that \(\mathcal {W}({\widehat{f}},{\widehat{g}}) \in {L^1}(\mathbb {R}^{2d})\), that the series (5) converges absolutely to a function \({L^1}(\mathbb {T}_{\Lambda ^*})\), \(\mathbb {T}_{\Lambda ^*} = \mathbb {R}^{2d}/\Lambda ^*\). When \(\Lambda \) is represented by a matrix A, we have \(\mathbb {T}_{\Lambda ^*} = A^{-1}\mathbb {T}\) where \(\mathbb {T}\) is the torus in \(\mathbb {R}^{2d}\). Since \(\big [{\widehat{\pi (z)f}},{\widehat{g}}\big ]_\Lambda \in {L^1}(\mathbb {T}_{\Lambda ^*})\), we can compute the Fourier coefficients
Then the application of the Plancherel theorem for Fourier series, gives us the following proposition.
Proposition 3.2
Let \(\Lambda \) be a lattice in \(\mathbb {R}^{2d}\). Fix \(z\in \mathbb {R}^{2d}\). Then for all \(g,h\in M^1(\mathbb {R}^{2d})\) and \(f_1,f_2\in {L^2}(\mathbb {R}^{2d})\), we have
with the absolute convergence of the integral.
The following two results are the main ingredients in deriving Janssen representation of the Gabor frame operator \(S_{g,h}^\Lambda \) and successive characterization of tight and dual Gabor frames.
Proposition 3.3
Let \(\Lambda \) be a lattice in \(\mathbb {R}^{2d}\). Assume that \(f_1,f_2,g,h\in M^1(\mathbb {R}^d)\). Then the function
is continuous and periodic, and coincides pointwise with its Fourier series
Proof
Let \(\Lambda \) be a lattice and \(f_1,f_2,g,h\in M^1(\mathbb {R}^d)\). Using Proposition 3.2 and a change of index, we write explicitely
For a fixed \(\beta ^*\in \Lambda ^*\), consider the series
Since \(\mathcal {W}({\widehat{f_1}}, {\widehat{g}})\) and \(\mathcal {W}({\widehat{f_2}}, \widehat{h})\) lie in \(M^1(\mathbb {R}^{2d})\), their product as well. Moreover,
since \(\mathcal {A}(f_1,g),\mathcal {A}(f_2,h) \in M^1(\mathbb {R}^{2d})\). Therefore, by Poisson summation formula we can write \(F_{\beta ^*}({\tilde{z}})\) as
and \(F(z,{\tilde{z}})\) becomes
By Lemma 2.4, \(\mathcal {A}(f_1,g),\mathcal {A}(f_2,h) \in M^1(\mathbb {R}^{2d})\), and therefore,
Hence, \(\mathcal {V}_{\mathcal {A}(f_2,h)}( \mathcal {A}(f_1,g))\) restricted to \(\Lambda \times \Lambda ^*\) belongs to \({\ell ^1}(\Lambda \times \Lambda ^*)\), and as a consequence, the series (8) defining \(F(z,{\tilde{z}})\) is absolutely convergent. By the uniqueness of the Fourier series, (8) is the Fourier series of F. \(\square \)
Proposition 3.4
Let \(\Lambda \) be a lattice in \(\mathbb {R}^{2d}\). Assume that \(g_i,h_i\in M^1(\mathbb {R}^{2d})\), for every \(i=1,\ldots ,M\). Then for every \(f_1,f_2\in M^1(\mathbb {R}^{2d})\), the function
is continuous and periodic, and coincides pointwise with its Fourier series \(\sum _{\lambda ^\circ \in \Lambda ^\circ } {\widehat{\mathcal {N}}}(\lambda ^\circ ) e^{-2\pi i \sigma (\lambda ^\circ , z)}\), with
where \(\Lambda ^\circ = J\Lambda ^*\) is the adjoint lattice and \(\sigma \) a symplectic form defined as \(\sigma (\theta ,z) = \theta \cdot Jz\), with \(\theta \) and z seen as column vectors in \(\mathbb {R}^{2d}\).
Proof
Let \(\Lambda \) be a lattice in \(\mathbb {R}^{2d}\) and choose \(f_1,f_2 \in M^1(\mathbb {R}^{2d})\). Then the function \({\mathcal {N}}(z)\) is well defined and can be expressed using the mixed frame operator \(S_{g,h}^\Lambda \) as \({\mathcal {N}}(z) = \langle S_{g,h}^{\Lambda } \pi (z)f_1,\pi (z)f_2\rangle \). Moreover, using the relations between short time Fourier transform and cross-ambiguity function, we can write \({\mathcal {N}}\) as
For \(i=1,\ldots ,M\) fixed, let
which is a periodic function. Using Proposition 3.2 and Proposition 3.3, we have
The interchange of the integral and the sum is possible due to the Fubini’s Theorem. Now, since \(\Big \langle \mathcal {A}(f_1,g),T_\lambda M_{\beta ^*} \mathcal {A}(f_2,h) \Big \rangle _{{L^2}(\mathbb {R}^{2d})}\) are in \({\ell ^1}(\Lambda \times \Lambda ^*)\) by the proof of Proposition 3.3, the coefficients \(\Big \langle \mathcal {W}({\widehat{f_1}},{\widehat{g_i}}),T_{\beta ^*}\mathcal {W}({\widehat{f_2}},\widehat{h_i}) \Big \rangle _{{L^2}(\mathbb {R}^{2d})}\) are in \(\ell ^1(\Lambda ^*)\). Hence, for each \(i=1,\ldots ,M\), the function \({\mathcal {N}}_i\) is continuous, as it equals the absolutely convergent trigonometric series
The coefficients \(\Big \langle \mathcal {W}({\widehat{f_1}},{\widehat{g_i}}),T_{\beta ^*} \mathcal {W}({\widehat{f_2}},\widehat{h_i}) \Big \rangle _{{L^2}(\mathbb {R}^{2d})}\) can be simplified. Let \(\frac{\beta ^*}{2} = (\frac{\beta ^*_1}{2},\frac{\beta ^*_2}{2})\), then using Proposition 2.3 e), we have
and applying Moyal’s formula we obtain
where \(\lambda ^\circ = J \beta ^* \in J \Lambda ^* = \Lambda ^\circ \). We can then express \({\mathcal {N}}_i(z)\) as
and we have
The function \({\mathcal {N}}\) is continuous since it is a finite sum of continuous functions. By the uniqueness of the Fourier series, (26) is the Fourier series of \({\mathcal {N}}\). \(\square \)
We are now in the position to state the three main identities in Gabor analysis.
Theorem 3.5
Let \(\Lambda \) be a lattice in \(\mathbb {R}^{2d}\) with adjoint lattice \(\Lambda ^\circ \). Then for \(g_i,h_i\in M^1(\mathbb {R}^d)\), \(i=1,\ldots ,M\), the following hold.
-
(i)
Fundamental identity of Gabor analysis:
$$\begin{aligned} \sum _{i=1}^M \sum _{\lambda \in \Lambda } \langle f_1,\pi (\lambda )g_i\rangle \langle \pi (\lambda )h_i,f_2\rangle = \text {vol}(\Lambda )^{-1} \sum _{i=1}^M \sum _{\lambda ^\circ \in \Lambda ^\circ } \langle h_i,\pi (\lambda ^\circ )g_i\rangle \langle \pi (\lambda ^\circ )f_1,f_2\rangle \end{aligned}$$(12)for all \(f_1,f_2\in {L^2}(\mathbb {R}^d)\).
-
(ii)
Janssen Representation:
$$\begin{aligned} S_{g,h}^\Lambda = \text {vol}(\Lambda )^{-1} \sum _{i=1}^M \sum _{\lambda ^\circ \in \Lambda ^\circ } \langle h_i,\pi (\lambda ^\circ ) g_i\rangle \pi (\lambda ^\circ )\,, \end{aligned}$$(13)where the series converges unconditionally in the strong operator sense.
-
(iii)
Wexler–Raz Biorthogonality Relations:
$$\begin{aligned} S_{g,h}^\Lambda = I \text{ on } {L^2}(\mathbb {R}^d) \quad \Longleftrightarrow \quad \text {vol}(\Lambda )^{-1} \sum _{i=1}^M \langle h_i,\pi (\lambda ^\circ ) g_i\rangle = \delta _{\lambda ^\circ ,0} \quad \text{ for } \lambda ^\circ \in \Lambda ^\circ \,. \end{aligned}$$(14)
Proof
The Fundamental Identity of Gabor Analysis and Janssen representation follow directly from Proposition 3.4. It suffices to prove the statements on a dense subspace of \({L^2}(\mathbb {R}^d)\). Let \(f_1,f_2\in M^1(\mathbb {R}^d)\), then the left hand side of (12) equals the function \({\mathcal {N}}\) of Proposition 3.4 evaluated at \(z=0\). Since \({\mathcal {N}}\) equals its Fourier series expansion, we have
which gives (12).
As for Janssen representation, we observed in the proof of Proposition 3.4 that \({\mathcal {N}}(z) = \langle S_{g,h}^\Lambda \pi (z)f_1,\pi (z) f_2\rangle \) for fixed \(f_1,f_2\in M^1(\mathbb {R}^d)\). Evaluating \({\mathcal {N}}\) at \(z=0\) and using the Fourier series representation of \({\mathcal {N}}\), we obtain
which is the Janssen representation of the frame operator \(S_{g,h}^\Lambda \).
The implication \(\Longleftarrow \) of iii) follows trivially from the Janssen representation of \(S_{g,h}^\Lambda \). For the converse, assume that \(S_{g,h}^\Lambda = I\). Let \(f_1,f_2 \in M^1(\mathbb {R}^d)\), then \({\mathcal {N}}\) of Proposition 3.4 is a constant function. Indeed,
for every \(z\in \mathbb {R}^{2d}\). Since \({\mathcal {N}}\) is a constant function, it equals its 0th Fourier coefficient \({\widehat{\mathcal {N}}}(0) = \langle f_1,f_2\rangle \). By Proposition 3.4, we have
Fix \(\lambda ^\circ = (\lambda _1^\circ ,\lambda _2^\circ )\in \Lambda ^\circ \) and let \(f\in M^1(\mathbb {R}^d)\) be a nonzero function. By letting \(f_1 = T_{-\lambda _1^\circ } M_{-\lambda _2^\circ } f\) and \(f_2=f\), (15) becomes
and the right hand side of (14) holds. \(\square \)
In the subsequent sections we will turn our attention to Gabor frames for model sets by generalizing the construction we have just presented.
4 Almost Periodic Functions, Model Sets and Local Functions
The main object of our investigation are Gabor frames for model sets, and in the treatment of such frames, we naturally come across almost periodic functions. Therefore, we begin with the review of some basic facts about almost periodic functions and finish with a definition and some properties of model sets. For a detailed exposition on almost periodic functions we refer to [2, 3, 5].
We say that a bounded and continuous function \(f:\mathbb {R}^{2d}\rightarrow \mathbb {C}\) is almost periodic, if to every \(\epsilon >0\) there corresponds a relatively dense set \(E(f,\epsilon ) \subseteq \mathbb {R}^{2d}\), such that for every \(\tau \in E(f,\epsilon )\),
A subset D is called relatively dense in \(\mathbb {R}^{2d}\) when there exists \(r>0\), such that for all \(z\in \mathbb {R}^{2d}\), \(D\cap B(z,r) \ne \emptyset \), where B(z, r) is a ball of radius r in \(\mathbb {R}^{2d}\) centered at z. Each \(\tau \in E(f,\epsilon )\) is called an \(\epsilon \)-period of f. Let \(AP(\mathbb {R}^{2d})\) denote the space of almost periodic functions. Each almost periodic function is uniformly continuous and admits a formal Fourier series
where
are the Fourier coefficients of f, and \(\sigma (f)\) is the so-called Bohr spectrum of f,
and it forms a countable set, that is only for a countable number of \(\lambda \in \mathbb {R}^m\), \(a(\lambda ,f)\) is nonzero ([5]). The 0-th Fourier coefficient of f,
is called the mean value of f. If \(f(z,{\tilde{z}})\), with \((z,{\tilde{z}}) \in \mathbb {R}^{2d}\times \mathbb {R}^{2d}\), is almost periodic, then it is almost periodic with respect to each of the variables z and \({\tilde{z}}\). Moreover, \(\mathcal {M}_{{\tilde{z}}}\{ f(z,{\tilde{z}})\}\) is an almost periodic function of z.
We gather the important identities of almost periodic functions, that we will use throughout the article, in the following theorem.
Theorem 4.1
([5]) Let \(f\in AP(\mathbb {R}^{2d})\) with the Fourier series given by (16). Then the following hold.
-
(i)
Bohr’s Fundamental Theorem: \(\mathcal {M}_z\{|f(z)|^2\} = \sum _{\lambda \in \sigma (f)} |a(\lambda ,f)|^2\).
-
(ii)
Plancherel’s Theorem: \(\mathcal {M}_z\{ f(z)\, \overline{g(z)} \} = \sum _{\lambda \in \sigma (f)} a(\lambda ,f)\,\overline{a(\lambda ,g)}\) for all \(g\in AP(\mathbb {R}^{2d})\) with \(\sigma (f) = \sigma (g)\).
-
(iii)
If all the coefficients \(a(\lambda ,f)\) of \(f\in AP(\mathbb {R}^m)\) are zero, then the function \(f\equiv 0\).
-
(iv)
When f is non-negative, then \(\mathcal {M}\{ f \} = 0\) if and only if \(f\equiv 0\).
Throughout the exposition we will be encountering almost periodic functions whose spectrums lie in model set. We state the basic definitions and theorems for even dimensional model sets since only those we will use, however the same definitions and properties apply in any dimension.
We begin with a lattice in \(\Gamma \subset \mathbb {R}^{2d}\times \mathbb {R}^n\), where \(\mathbb {R}^{2d}\) and \(\mathbb {R}^n\) are equipped with Euclidean metrics and \(\mathbb {R}^{2d}\times \mathbb {R}^n\) is the orthogonal sum of the two spaces. Let \(p_1:\mathbb {R}^{2d}\times \mathbb {R}^n \rightarrow \mathbb {R}^{2d}\) and \(p_2: \mathbb {R}^{2d}\times \mathbb {R}^n \rightarrow \mathbb {R}^n\) be projection maps such that \(p_1|\Gamma \) is injective and \(L= p_1(\Gamma )\) is a dense subgroup of \(\mathbb {R}^{2d}\). We impose the same properties on \(p_2\). For the dual lattice of \(\Gamma \), denoted by \(\Gamma ^*\), let \(p_1^*,p_2^*\) be defined as \(p_1,p_2\). It holds then, that \(p_1^*|\Gamma ^*\) is injective and \(p_1^*(\Gamma ^*)\) is a dense subgroup of \(\mathbb {R}^{2d}\), and the same holds for \(p_2^*\). Moreover, for \(\gamma \in \Gamma \) and \(\gamma ^*\in \Gamma ^*\),
Let \(\Omega \subset \mathbb {R}^n\) be compact, equal to the closure of its interior and have boundary of measure 0. We call \(\Omega \) a window. Then a model set \(\Lambda (\Omega )\) is defined as
If \(\Omega \) is symmetric around the origin then \(0\in \Lambda (\Omega )\). Model set is generic if the boundary of \(\Omega \) has no common points with \(p_2(\Gamma )\). A model set is simple if \(n=1\). We will be working only with simple model sets. We assume, without loss of generality, that from now on \(\Omega \) is symmetric around the origin.
Model sets are a very natural generalizations of lattices, and for \(n=0\) they reduce to a lattice and, thus, the results that we develop later on in the article reduce to the known ones for lattices. If \(\Lambda (\Omega )\) is a model set, then it is uniformly discrete, relatively dense, and has a well defined density
where \(\#S\) denotes the cardinality of the set S and B(x, R) is a ball of radius R in \(\mathbb {R}^{2d}\) centered at x . The limit is independent of \(x\in \mathbb {R}^{2d}\). For a simple model set \(\Lambda (\Omega )\), we have \(D(\Lambda (\Omega )) = \text {vol}(\Gamma )^{-1} |\Omega |\), see [1].
Due to the underlying lattice structure of a model set, there exists a Poisson summation formula for \(\Lambda (\Omega )\). Let \(C_0^\infty (\Omega )\) be the space of all smooth, real valued functions on \(\mathbb {R}\) with support in \(\Omega \). Via the mapping \(p_2\circ (p_1|_\Gamma )^{-1}: L \rightarrow \mathbb {R}\) we obtain a space \(\mathcal {C}(\Lambda (\Omega ))\) of functions on L, vanishing off \(\Lambda (\Omega )\): for \(\psi \in C_0^\infty (\Omega )\), we define \(w_\psi \in \mathcal {C}(\Lambda (\Omega ))\) by
and \(w_\psi (\lambda )=0\) for \(\lambda \notin \Lambda (\Omega )\). If \(\psi \) were the indicator function of \(\Omega \), we would have \(w_\psi (\lambda ) = 1\) on \(\Lambda (\Omega )\) and \(w_\psi (\lambda )=0\) if \(\lambda \notin \Lambda (\Omega )\). However, the indicator function is not smooth. The Poisson summation formula for model sets was originally stated for the class of Schwartz functions in [23]. However, since it relies on the original Poisson summation formula, we can state it for a bigger space.
Theorem 4.2
(Poisson Summation Formula for Model Sets) Let \(\Lambda (\Omega )\) be a simple model set defined by a relatively compact set \(\Omega \subseteq \mathbb {R}\) of non-empty interior and a lattice \(\Gamma \subseteq \mathbb {R}^{2d}\times \mathbb {R}\). Let \(\psi \in C_0^\infty (\Omega )\), and the weight factors \(w_\psi (\lambda )\) on \(\Lambda (\Omega )\) be defined as in (17). Then, for every \(F\in M^1(\mathbb {R}^{2d})\), the following holds
where
The identity holds pointwise for all \(z\in \mathbb {R}^{2d}\), and both sums converge uniformly and absolutely for all \(t\in \mathbb {R}^{2d}\).
Meyer, in [23], originally stated the Poisson summation formula for model sets for functions in the Schwartz class \(\mathcal {S}(\mathbb {R}^{2d})\). As the Poisson summation formula for model sets follows from the ordinary Poisson summation formula, which holds not only for the elements from \(\mathcal {S}(\mathbb {R}^{2d})\) but also for functions in \(M^1(\mathbb {R}^{2d})\), we were able to extend the former one to a bigger class of functions.
Proof
Since \(w_\psi (\lambda ) = \psi (p_2(\gamma ))\) for \(\lambda =p_1(\gamma )\), one can forget about the restriction \(\lambda \in \Lambda \) which is given for free by the support of \(\psi \), and consider a function \(f=F \otimes \psi \). Since \(\psi \in C_0^\infty (\Omega ) \subset M^1(\mathbb {R})\), \(f\in M^1(\mathbb {R}^{2d}\times \mathbb {R})\) by the tensor product property of Feichtinger’s algebra \(M^1\). We can now apply the ordinary Poisson summation formula, Theorem 3.1, to the lattice \(\Gamma \), its dual lattice \(\Gamma ^*\) and the function f and obtain
Then (18) follows by taking \(z=(x,0)\in \mathbb {R}^{2d}\times \mathbb {R}\). \(\square \)
Remark 1
Poisson summation formula for model sets gives a method for constructing almost periodic functions with desired spectrum. Indeed, the function on the right hand side of (18) is almost periodic since it equals an absolutely convergent trigonometric series. By the property of almost periodic functions, the Fourier series of this function coincides with this trigonometric series. That means that the Fourier coefficients of the right hand side of (18) equal \(w_\psi (\lambda )F(\lambda )\).
On the collection of point sets in \(\mathbb {R}^{2d}\) that are relatively dense and uniformly separated, with minimal separation greater than r, denoted by \(D_r(\mathbb {R}^{2d})\), we can put a topology, called local topology: two sets \(\Lambda \) and \(\Lambda '\) of \(D_r(\mathbb {R}^{2d})\) are close if, for some large R and some small \(\epsilon \), one has
Thus for each point of \(\Lambda \) within the ball B(0, R), there is a point of \(\Lambda '\) within the distance \(\epsilon \) of that point, and vice versa. The pairs \((\Lambda ,\Lambda ')\) satisfying (20) are called \((R,\epsilon )\)-close. More formally, for \(\epsilon >0\) and a ball B(x, R), define
These sets form a fundamental system for a uniform structure on \(D_r(\mathbb {R}^{2d})\) whose topology has the sets
as a neighbourhood basis of \(\Lambda \). Note, all the point sets \(\Lambda \) from \(D_r(\mathbb {R}^{2d})\) have the same relative separation \(\text {rel}(\Lambda )\).
On the set \(D_r(\mathbb {R}^{2d})\) we can put a metric. Let \(\Lambda ,\Lambda ' \in D_r(\mathbb {R}^{2d})\), then
is a pseudometric on \(D_r(\mathbb {R}^{2d})\). We obtain a metric by defining the equivalence relation
Later in the article, we will work with a collection of model sets. Let \(\Omega \) be a window, then for each \((s,t)\in \mathbb {R}^{2d}\times \mathbb {R}\) we may define
Note that \(\Lambda (\Omega )\) and all its shifts have the same relative separation \(\text {rel}(\Lambda (\Omega ))\).
If \((s,t)\equiv (s',t') \mod \Gamma \), then \(\Lambda _{(s,t)}^\Omega =\Lambda _{(s',t')}^\Omega \), however the inverse is not necessarily true. In the sequel we will write \((s,t)_L\) for the congruence class \((s,t)\mod \Gamma \). These model sets are parametrized by the torus \(\mathbb {T}:=(\mathbb {R}^{2d}\times \mathbb {R}) / \Gamma = (\mathbb {R}/\mathbb {Z})^{2d+1}\). There is a natural measure, Haar measure, \(\theta \) on \(\mathbb {T}\). It is invariant under the action of \(\mathbb {R}^{2d}\) on \((\mathbb {R}^{2d}\times \mathbb {R})/\Gamma \) and it acts by
We can define an embedding \(\mathbb {R}^{2d}\rightarrow \mathbb {T}\), \(z\mapsto (z,0)_L\). The image of this embedding is dense in \(\mathbb {T}\).
Now, let \(\Lambda (\Omega )\) be a model set, and we translate it by elements \(z\in \mathbb {R}^{2d}\)
The closure of the set of all translates \(\Lambda _{(z,0)}^\Omega \) of \(\Lambda (\Omega )\) under the local topology (20) forms the so-called local hull \(X(\Lambda (\Omega ))\) of \(\Lambda (\Omega )\), \(X(\Lambda (\Omega )) = \overline{\{z+\Lambda (\Omega ):z\in \mathbb {R}^{2d}\}}\), ([25, 27]).
Proposition 4.3
[27] Let \(\Lambda (\Omega )\) be a model set. There is a continuous mapping
called the torus parametrization, such that (i) \(\beta \) is onto; (ii) \(\beta \) is injective almost everywhere with respect to the Haar measure \(\theta \); (iii) \(\beta (z+\Lambda ') = z+ \beta (\Lambda ')\) for all \(z\in \mathbb {R}^{2d}\) and all \(\Lambda '\in X(\Lambda )\); and (iv) \(\beta (z+\Lambda (\Omega )) = (z,0)_L\) for all \(z\in \mathbb {R}^{2d}\).
By injective almost everywhere, we mean that the set P of points \(z\in \mathbb {T}\), for which there is more than one point set of \(X(\lambda (\Omega ))\) over z, satisfies \(\theta (P)=0\).
There is a unique \(\mathbb {R}^{2d}\)-invariant measure \(\mu \) on \(X(\Lambda (\Omega ))\), with \(\mu (X(\Lambda (\Omega ))) = 1\), and \(\beta \) relates the Haar measure \(\theta \) and \(\mu \) through: \(\theta (P) = \mu (\beta ^{-1} P)\) for all measurable subsets P of \(\mathbb {T}\). Having \(\mu \) we can introduce the space \({L^2}(X(\Lambda (\Omega )),\mu )\) of square integrable functions on \(X(\Lambda (\Omega ))\). Square integrable functions on \(X(\Lambda (\Omega ))\) and square integrable functions on \(\mathbb {T}\) can be identified,
The mapping takes a function \({\mathfrak {N}}\in {L^2}(\mathbb {T},\theta )\) and creates \({\widetilde{\mathcal {N}}}={\mathfrak {N}} \circ \beta \in {L^2}(X(\Lambda (\Omega )),\mu )\), and since \(\beta \) is almost everywhere injective, the map is a bijection. This allows us to analyze functions on \(X(\Lambda (\Omega ))\) by treating them as functions on \(\mathbb {T}\).
Consider a function \({\widetilde{\mathcal {N}}}:X(\Lambda (\Omega )) \rightarrow \mathbb {C}\). We can define from it a function \({\mathcal {N}}:\mathbb {R}^{2d}\rightarrow \mathbb {C}\) by
If \({\widetilde{\mathcal {N}}}\) is continuous, then for all \(z_1,z_2\in \mathbb {R}^{2d}\), if \(z_1+\Lambda (\Omega )\) and \(z_2+\Lambda (\Omega )\) are close, then \({\widetilde{\mathcal {N}}}(z_1+\Lambda (\Omega ))\) and \({\widetilde{\mathcal {N}}}(z_2+\Lambda (\Omega ))\) are close, and as a consequence, \({\mathcal {N}}(z_1)\) and \({\mathcal {N}}(z_2)\) are close. Thus continuity of \({\widetilde{\mathcal {N}}}\) implies continuity of \({\mathcal {N}}\), or a certain locality. More formally, a function \({\mathcal {N}}:\mathbb {R}^{2d}\rightarrow \mathbb {C}\) is called local with respect to\(\Lambda (\Omega )\), if for all \(\delta >0\) there exists \(R>0\) and \(\epsilon >0\) so that whenever \(z_1+\Lambda (\Omega )\) and \(z_2+\Lambda (\Omega )\), for \(z_1,z_2\in \mathbb {R}^{2d}\), are \((R,\epsilon )\)-close, then
Intuitively, \({\mathcal {N}}\) looks very much the same at places where the local environment looks the same. It can be easily verified that local functions are continuous on \(\mathbb {R}^{2d}\) and almost periodic.
Using locality, we can go in the opposite direction. Let \({\mathcal {N}}\) be a local function with respect to \(\Lambda (\Omega )\). Define a function \({\widetilde{\mathcal {N}}}\) on the orbit of \(\Lambda (\Omega )\):
Then \({\widetilde{\mathcal {N}}}\) is uniformly continuous on \(\{ z+\Lambda (\Omega ):z\in \mathbb {R}^{2d}\}\) with respect to the local topology. The reason for this is that the continuity condition which defines the localness of \({\mathcal {N}}\) is based on the uniformity defining the local topology on \(\{ z+\Lambda (\Omega ):z\in \mathbb {R}^{2d}\}\). It follows that \({\widetilde{\mathcal {N}}}\) lifts uniquely to a continuous function on a local hull \(X(\Lambda (\Omega ))\).
Proposition 4.4
[24] For each local function \({\mathcal {N}}\) with respect to \(\Lambda (\Omega )\) there is a unique continuous function \({\widetilde{\mathcal {N}}}\) on a local hull \(X(\Lambda (\Omega ))\), whose restriction to the orbit of \(\Lambda (\Omega )\) is \({\mathcal {N}}\). Every continuous function on the local hull of \(\Lambda (\Omega )\) arises in this way.
The spectral theory of \({L^2}(X(\Lambda (\Omega )),\mu )\) allows us to analyze \({\mathcal {N}}\) by analyzing its corresponding function \({\widetilde{\mathcal {N}}}\) on \({L^2}(X(\Lambda (\Omega )),\mu )\). Suppose \({\mathcal {N}}\) is a local function with respect to the model set \(\Lambda (\Omega )\). From the locality of \({\mathcal {N}}\) we have its extension \({\widetilde{\mathcal {N}}}\in {L^2}(X(\Lambda (\Omega )),\mu )\) which is continuous. Then we obtain \({\mathfrak {N}}\in {L^2}(\mathbb {T},\theta )\), where
and since functions in \({L^2}(\mathbb {T},\theta )\) have Fourier expansions, we can write
almost everywhere, with
However, we know \({\mathfrak {N}}\) only on \((\mathbb {R}^{2d},0)_L\). To compute the coefficients \({\widehat{{\mathfrak {N}}}}(\eta )\) out of \({\mathcal {N}}\) alone, we can use the Birkhoff ergodic theorem
where we used \({\mathfrak {N}}((z,0)_L) = {\mathcal {N}}(z)\) and \(\eta = (p_1^*(\eta ),p_2^*(\eta ))\), so
If \( \sum _{\eta \in \Gamma ^*} |{\widehat{{\mathfrak {N}}}}(\eta )|<\infty \), then the Fourier series (22) converges absolutely to \({\mathcal {N}}(z)\) for all \(z\in \mathbb {R}^{2d}\).
5 Bracket Product on Model Sets
As described in the introduction, we are interested in the charaterization of tight and dual Gabor frames for simple model sets. We are going to imitate the approach presented in Sect. 3 for model sets, and like in the previous Section, the Poisson summation formula will play a crucial role.
We assume from now on that \(\Omega \) is symmetric around the origin and that \(p_2(\Gamma )\) and \(p_2^*(\Gamma ^*)\) have no common points with the boundary of \(\Omega \). Let \(\Lambda (\Omega )\) be a simple model set and \(\psi \in C_0^\infty (\Omega )\). Let \({\widetilde{w}}_\psi \) be a function defined as in Theorem 4.2. Then for a fixed \(z=(x,\omega )\in \mathbb {R}^{2d}\) the generalized \(\psi \)-bracket product of f and g is defined as
For \(f,g\in M^1(\mathbb {R}^d)\), we have \(\mathcal {W}({\widehat{f}},{\widehat{g}}) \in M^1(\mathbb {R}^{2d})\) and the bracket product is well defined. Moreover, \(\mathcal {F}^{-1} M_{-z}\mathcal {W}({\widehat{f}}, {\widehat{g}}) = T_z \mathcal {A}(f,g)\) and is also an element of \(M^1(\mathbb {R}^{2d})\), and by Remark 1, \(\big [{\widehat{\pi (z)f}},{\widehat{g}}\big ]_{\Lambda (\Omega )}^{\psi }\) is an almost periodic function represented by the trigonometric series
The Fourier coefficients are given by
We make the following useful observation that is in analogy with regular shifts.
Lemma 5.1
Let \(\Lambda (\Omega )\) be a simple model set and \(\psi \in C_0^\infty (\Omega )\). For all functions \(f_1,f_2,g,h\in M^1(\mathbb {R}^d)\), we have
Proof
The bracket products \(\big [{\widehat{\pi (z)f_1}},{\widehat{g}}\big ]_{\Lambda (\Omega )}^{\psi }\) and \(\big [{\widehat{\pi (z)f_2}},\widehat{h}\big ]_{\Lambda (\Omega )}^{\psi }\) are almost periodic function with Fourier coefficients given by \(w_{\psi }(\lambda ) \mathcal {A}(f_1,g)(\lambda - z)\) and \(w_{\psi }(\lambda ) \mathcal {A}(f_2,h) (\lambda - z)\), respectively. Using Plancherel Theorem for Fourier series of almost periodic functions and (24), we obtain
\(\square \)
The following result concerning the bracket product will be important in many calculations to follow.
Proposition 5.2
Let \(\Lambda (\Omega )\) be a simple model set and \(\psi \in C_0^\infty (\mathbb {R})\) be non-negative. Assume that \(g,h\in M^1(\mathbb {R}^d)\). Then, for \(f_1,f_2\in M^1(\mathbb {R}^d)\),
is an almost periodic function.
Proof
Let \(f_1,f_2\in M^1(\mathbb {R}^d)\). Moreover, for \(\eta \in \Gamma ^*\), we define \(\Psi _\eta \) such that \(\widehat{\Psi _\eta } = \widehat{\psi } \cdot T_{p^*_2(\eta )} \widehat{\psi }\). Then each \(\Psi _\eta \) belongs to \(C_0^\infty (\mathbb {R})\) and is compactly supported on \(\Omega +\Omega \), and we can define \({\widetilde{w}}_{\Psi _\eta }\) as \({\widetilde{w}}_{\Psi _\eta } (p^*_2(\gamma ^*))=\text {vol}(\Gamma )^{-1} \widehat{\Psi _\eta }(p^*_2(\gamma ^*))\), for all \(\gamma ^*\in \Gamma ^*\), as in (19). Then, by the change of index, we have
For a fixed \(\eta \in \Gamma ^*\), consider the series
Since \(\mathcal {W}({\widehat{f_1}}, {\widehat{g}})\) and \(\mathcal {W}({\widehat{f_2}}, \widehat{h})\) lie in \(M^1(\mathbb {R}^{2d})\), their product as well. Moreover,
which is in \(M^1(\mathbb {R}^{2d})\) since \(\mathcal {A}(f_1,g),\mathcal {A}(f_2,h) \in M^1(\mathbb {R}^{2d})\). Therefore, by Poisson summation formula for model sets we can write \(F_\eta ({\tilde{z}})\) as
and \(F(z,{\tilde{z}})\) becomes
The coefficients in the series defining \(F(z,{\tilde{z}})\) are in \({\ell ^1}(\Gamma \times \Gamma ^*)\), because \(\psi \otimes \mathcal {A}(f_1,g)\) and \(\psi \otimes \mathcal {A}(f_2,h)\) lie in \(M^1(\mathbb {R}\times \mathbb {R}^{2d})\), and hence
That means that F equals a generalized trigonometric polynomial, and therefore is almost periodic. \(\square \)
We need one more result that will be an important tool in the characterization of tight frames and dual frames.
Proposition 5.3
Let \(\Lambda (\Omega )\) be a simple model set and \(\psi \in C_0^\infty (\Omega )\) non-negative function. Assume that \(g_i,h_i\in M^1(\mathbb {R}^d)\) for every \(i=1,\ldots ,M\). Then, for every \(f_1,f_2\in M^1(\mathbb {R}^d)\), the function
is almost periodic and coincides pointwise with its Fourier series \(\sum _{\eta \in \Gamma ^*} {\widehat{\mathcal {N}}^\psi }(\eta ) e^{-2\pi i p^*_1(\eta ) \cdot z}\), with
where \(\eta \in \Gamma ^*\) and J is the symplectic matrix.
Proof
Let \(f_1,f_2 \in M^1(\mathbb {R}^d)\). Using the relationship between short time Fourier transform and cross-ambiguity function, we can express \({\mathcal {N}}^{\psi }\) as
For \(i=1,\ldots ,M\) fixed, let
By Lemma 5.1, we have
and by Proposition 5.2 and properties of almost periodic functions of two variables, \({\mathcal {N}}^\psi _i(z)\) is almost periodic. Moreover, using functions \(F_\eta \) and \(\Psi _\eta \) defined in the proof of Proposition 5.2, we have
where the last equality follows from relations between cross-ambiguity function, cross-Wigner distribution and Moyal’s formula, as in the proof of Proposition 3.4.
Now, since \({\mathcal {N}}\) is a finite sum of almost periodic functions, it is almost periodic and it equals a generalized trigonometric series
By the uniqueness of the Fourier series, (26) is the Fourier series of \({\mathcal {N}}^\psi (z)\). \(\square \)
6 Gabor Analysis for Model Sets
We first begin with weighted Gabor frames and characterize normalized tight and dual weighted Gabor frames. The characterization follows directly from the bracket product defined in the previous section. Next, we move to the non-weighted scenario, where we develop Fundamental Identity of Gabor Analysis for model sets, Janssen representation and Wexler–Raz orthogonality relations.
6.1 Weighted Gabor Systems
Let \(\Lambda (\Omega )\) be a simple model set, \(\psi \in C_0^\infty (\Omega )\) non-negative function and the windows \(g_1,\ldots , g_M\in M^1(\mathbb {R}^d)\). Then, a weighted Gabor system, denoted by \(\mathcal {G}_\psi (g_1,\ldots ,g_M;\Lambda (\Omega ))\), is a collection of elements \(w_\psi (\lambda ) \pi (\lambda ) g_i\), where \(\lambda \in \Lambda (\Omega )\), \(i=1,\ldots , M\) and \(w_\psi \) as defined in (17). The system \(\mathcal {G}_\psi (g_1,\ldots ,g_M;\Lambda (\Omega ))\) is a frame for \({L^2}(\mathbb {R}^d)\) if there exist constants \(A_g,B_g > 0\) such that
holds for all \(f\in {L^2}(\mathbb {R}^d)\). \(\mathcal {G}_\psi (g_1,\ldots ,g_M;\Lambda (\Omega ))\) is a normalized weighted tight Gabor frame if \(A_g=B_g=1\). As in the case of non-weighted Gabor systems, \(\mathcal {G}_\psi (g_1,\ldots ,g_M;\Lambda (\Omega ))\) is a Bessel sequence (only the right hand side of (27) holds) if all \(g_i\in M^1(\mathbb {R}^d)\), \(i=1,\ldots ,M\). Equipped with this notions, we can now characterize weighted tight Gabor frames.
Proposition 6.1
Let \(\Lambda (\Omega )\) be a simple model set and \(\psi \in C_0^\infty (\Omega )\) non-negative function. Then the family \(\mathcal {G}_\psi (g_1,\ldots ,g_M;\Lambda (\Omega ))\), with \(g_i\in M^1(\mathbb {R}^d)\) for every \(i=1,\ldots , M\), is a normalized weighted tight Gabor frame for \({L^2}(\mathbb {R}^m)\), that is
if and only if
for each \(\eta \in \Gamma ^*\), where \(\delta \) is the Kronecker delta.
Proof
By [15], it is sufficient to prove the theorem when \(f\in M^1(\mathbb {R}^d)\). Assume that \(\mathcal {G}_\psi (g_1,\ldots ,g_M;\Lambda (\Omega ))\) is a normalized weighted tight Gabor frame. Since \(g_i\in M^1(\mathbb {R}^d)\) for every \(i=1,\ldots , M\), by Proposition 5.3 with \(g_i=h_i\) for all \(i=1,\ldots ,M\) and \(f_1=f_2=f\), we can define a function \({\mathcal {O}}^\psi (z)\) as
By (28), this function is constant and equals \(||f||_2^2\). Let \(\mathcal {E}^\psi (z) = {\mathcal {O}}^\psi (z) - ||f||_2^2\). Then, \(\mathcal {E}^\psi (z)\) is almost periodic and \(\mathcal {E}^\psi = 0\). By the property of almost periodic function, it implies that the Fourier coefficients of \(\mathcal {E}^\psi (z)\),
are zero. By Proposition 5.3, we have then
with \(\eta \in \Gamma ^*\), for every \(f\in M^1(\mathbb {R}^d)\).
Let \(f\in M^1(\mathbb {R}^d)\setminus \{0\}\). Consider first \(\eta =0\). Then (31) becomes
and (29) follows. Now, let \(\eta \ne 0\) be fixed and take \(f(x) = e^{-\pi x^2}\), a Gausian. Then (31) implies
and since \(\Big \langle \pi \big (J p_1^*(\eta )\big ) f,f \Big \rangle \ne 0\), (29) is satisfied.
Conversely, assume that (29) holds. Since \(g_i\in M^1(\mathbb {R}^d)\) for every \(i=1,\ldots ,M\), by Proposition 5.3 with \(f_1=f_2=f\) and \(g_i=h_i\) for every \(i=1,\ldots ,M\), we can define function \({\mathcal {O}}^\psi (z)\) as in (30). Then, by Proposition 5.3 and relation (29), the function \({\mathcal {O}}^\psi (z)\) is given by the trigonometric series
for every \(z\in \mathbb {R}^d\), with
Hence, \({\mathcal {O}}^\psi (z)\) is constant and \({\mathcal {O}}^\psi (z) = ||f||_2^2\). Evaluating \({\mathcal {O}}^\psi (z)\) at \(z=0\), gives the claim. \(\square \)
We know state conditions for a weighted Gabor system \(\mathcal {G}_\psi (h_1,\ldots ,h_M;\Lambda (\Omega ))\) to be a dual system of \(\mathcal {G}_\psi (g_1,\ldots ,g_M;\Lambda (\Omega ))\).
Proposition 6.2
Let \(\Lambda (\Omega )\) be a simple model set and \(\psi \in C_0^\infty (\Omega )\) non-negative function. Let \(g_i\in M^1(\mathbb {R}^d)\) and \(h_i\in M^1(\mathbb {R}^d)\), for every \(i=1,\ldots , M\). Then \(\mathcal {G}_\psi (g_1,\ldots ,g_M;\Lambda (\Omega ))\) and \(\mathcal {G}_\psi (h_1,\ldots ,h_M;\Lambda (\Omega ))\) are weighted dual Gabor frames, that is
if and only if
for each \(\eta \in \Gamma ^*\), where \(\delta \) is the Kronecker delta.
Proof
The proof is analogous to the proof of Proposition 6.1 with obvious adjustments. \(\square \)
Based on the last proposition we can also derive density condition for weighted Gabor frames.
Proposition 6.3
Let \(\Lambda (\Omega )\) be a simple model set and \(\psi \in C_0^\infty (\Omega )\) a non-negative function such that \(||\psi ||_2=1\). If the Gabor frame \(\mathcal {G}_\psi (g;\Lambda (\Omega ))\), with \(g\in M^1(\Lambda (\Omega ))\) admits a weighted dual that is also a Gabor system, then \(D(\Lambda (\Omega ))\ge 1\).
Proof
Let \(g\in M^1(\mathbb {R}^d)\) and assume that the Gabor frame \(\mathcal {G}_\psi (g;\Lambda (\Omega ))\) admits a dual \(\mathcal {G}_\psi (h;\Lambda (\Omega ))\) with \(h\in M^1(\mathbb {R}^d)\). Let \(B_g\) be the upper frame bound of \(\mathcal {G}_\psi (g;\Lambda (\Omega ))\), and we can assume without loss of generality that \(||h||_2^2 = |\Omega |B_g^{-1}\). Then, by polarization, we have the frame decomposition
If we set \(f_1=h\) and \(f_2=g\), by the Bessel property of \(\mathcal {G}_\psi (g;\Lambda (\Omega ))\), we obtain
On the other hand, by Proposition 6.2 with \(M=1\), \( \text {vol}(\Gamma )^{-1} {\widehat{\psi ^2}}(0)\,\langle h,g\rangle = 1\), and therefore \(D(\Lambda (\Omega )) = \text {vol}(\Gamma )^{-1} |\Omega | \ge 1\) because \({\widehat{\psi ^2}}(0) = ||\psi ||_2^2 = 1\). \(\square \)
Gabardo, in [9], gave a characterization of the weighted irregular Gabor tight frames and dual systems in terms of the distributional symplectic Fourier transform of a positive Borel measure where the windows belong to the Schwartz class. It is possible to derive his results in the setting of model sets, using the characterization just presented.
6.2 (Nonweighted) Gabor Systems
Let \(g_i,h_i\in M^1(\mathbb {R}^d)\), \(i=1,\ldots ,M\), and \(\Lambda (\Omega )\) a simple model set. At the beginning of Sect. 2, we showed that the frame operator \(S_g^{\Lambda (\Omega )}\) of \(\mathcal {G}(g_1,\ldots ,g_M;\Lambda )\) does not commute with the time-frequency shifts taken from \(\Lambda (\Omega )\). The same holds in particular for any \(\Lambda \in X(\Lambda (\Omega ))\) and a time-frequency shift by \(z\in \mathbb {R}^{2d}\). Let \(S_{g,h}^{\Lambda -z}\) denote the mixed frame operator associated to \(\mathcal {G}(g_1,\ldots ,g_M;\Lambda -z)\) and \(\mathcal {G}(h_1,\ldots ,h_M;\Lambda -z)\). Then there is a covariance relation relating \(S_{g,h}^{\Lambda }\) and \(S_{g,h}^{\Lambda -z}\). The following result was obtained by Kreisel in [18]. We state it here for the mixed frame operators.
Proposition 6.4
[18] If \(\mathcal {G}(g_1,\ldots ,g_M;\Lambda )\) and \(\mathcal {G}(h_1,\ldots ,h_M;\Lambda )\) ,are Gabor systems for \(\Lambda \), and, \(\mathcal {G}(g_1,\ldots ,g_M;\Lambda -z)\) and \(\mathcal {G}(h_1,\ldots ,h_M;\Lambda -z)\) are Gabor systems for \(\Lambda -z\), then the mixed frame operators \(S_{g,h}^\Lambda \) and \(S_{g,h}^{\Lambda -z}\) satisfy
Moreover, the following continuity property holds.
Proposition 6.5
[18] Suppose \(\Lambda _n\rightarrow \Lambda \) in \(X(\Lambda (\Omega ))\) and the window functions \(g_i,h_i\) lie in \(M^1(\mathbb {R}^d)\), for each \(i=1,\ldots ,M\). Then \(S_{g,h}^{\Lambda _n} \rightarrow S_{g,h}^{\Lambda }\) in the strong operator topology on \(B(M^1(\mathbb {R}^d))\).
Even though the mapping \(\Lambda \rightarrow S_g^{\Lambda }\), \(\Lambda \in X(\Lambda (\Omega ))\) is not continuous when \(B(M^1(\mathbb {R}^d))\) is given the norm topology, all the frames \(\mathcal {G}(g_1,\ldots ,g_M;\Lambda )\) have the same optimal frame bounds.
Proposition 6.6
[18] Suppose \(\mathcal {G}(g_1,\ldots ,g_M;\Lambda )\) is a frame for each \(\Lambda \in X(\Lambda (\Omega ))\) and each \(g_i\in M^1(\mathbb {R}^d)\). For any \(\Lambda \in X(\Lambda (\Omega ))\) the optimal upper and lower frame bounds for \(\mathcal {G}(g_1,\ldots ,g_M;\Lambda )\) are the same as those for \(\mathcal {G}(g_1,\ldots ,g_M;\Lambda (\Omega ))\). As a result, \(||S_g^\Lambda ||_{M^1} = ||S_g^{\Lambda (\Omega )}||_{M^1}\) and \(||(S_g^\Lambda )^{-1}||_{M^1} = ||(S_g^{\Lambda (\Omega )})^{-1}||_{M^1}\), where \(||\cdot ||_{M^1}\) denotes the operator norm on \(B(M^1(\mathbb {R}^d))\).
As a result of the continuity property, we have the following Corollary.
Corollary 6.7
[18] Suppose \(g_1,\ldots ,g_M\in M^1(\mathbb {R}^d)\) and \(\mathcal {G}(g_1,\ldots ,g_M;\Lambda (\Omega ))\) is an \(M^1\)-frame. Then for any \(\Lambda \in X(\Lambda (\Omega ))\), \(\mathcal {G}(g_1,\ldots ,g_M;\Lambda )\) is also an \(M^1\)-frame.
Now, let \(f_1,f_2 \in M^1(\mathbb {R}^d)\) be fixed and let \(g_i,h_i\in M^1(\mathbb {R}^d)\) for \(i=1,\ldots ,M\). We define a function \({\widetilde{\mathcal {N}}} : X(\Lambda (\Omega )) \rightarrow \mathbb {C}\) through the mixed frame operator, as
Since, by Proposition 6.5, \(S_{g,h}^{\Lambda }\) is continuous, in the strong operator topology, over \(X(\Lambda (\Omega ))\), the function \({\widetilde{\mathcal {N}}}\) is continuous. As was presented in Sect. 4, we can define from \({\widetilde{\mathcal {N}}}\) a function \({\mathcal {N}} :\mathbb {R}^m\rightarrow \mathbb {C}\), by
and since \({\widetilde{\mathcal {N}}}\) is continuous, \({\mathcal {N}}\) is local with respect to \(\Lambda (\Omega )\). As was shown in Sect. 4, it has a Fourier expansion
where
Applying the tools developed in Sect. 5, we will be able to compute the Fourier coefficients \({\widehat{{\mathfrak {N}}}}(\eta )\) of \({\mathcal {N}}\).
Before we proceed further we introduce a sequence of auxiliary functions that will be crucial in proving our results. The following Lemma is a particular case of Prop 3.6 in [1].
Lemma 6.8
Let \(0<\epsilon <1\), \(\Omega \) be a compact subset of \(\mathbb {R}\), \({\widetilde{\Omega }} = (1-\epsilon )\Omega \) and \(f_s = \frac{\mathbb {1}_{\epsilon ^{s}{\widetilde{\Omega }}}}{|\epsilon ^{s}{\widetilde{\Omega }}|}\) for \(s\in \mathbb {N}\). Then,
-
(i)
the infinite convolution product
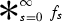 converges in \(L^1(\mathbb {R})\) and defines a non-negative smooth function
converges in \(L^1(\mathbb {R})\) and defines a non-negative smooth function 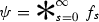 compactly supported on \(\Omega \), with \(||\psi ||_1 = 1\);
compactly supported on \(\Omega \), with \(||\psi ||_1 = 1\); -
(ii)
the Fourier transform of \(\psi \) is the smooth function \(\widehat{\psi } = \prod _{s=0}^{\infty } \,\widehat{f_s} \), with uniform convergence of the product, where \(\widehat{f_s}(t) = \text {sinc}(t\,|\epsilon ^{s} {\widetilde{\Omega }}|)\) and \(\text {sinc}(t) = \frac{\sin (\pi t)}{\pi t}\).
Now, for \(0<\epsilon <1\) and \(\Omega \) a compact subset of \(\mathbb {R}\), we define a sequence of compact sets \(\Omega _n = (1-\epsilon ^n)\Omega \). The sets \(\Omega _n\) are increasing and \(\overline{\bigcup _n \Omega _n} = \Omega \). Let \(\psi _n\) be an infinite convolution product

Then, by Lemma 6.8, each \(\psi _n\) is well defined and forms a sequence of \(C_0^\infty (\Omega )\) non-negative functions, with Fourier transform of \(\psi _n\) being
Lemma 6.9
With the above notation,
-
(i)
the sequence \(\{\psi _n\}_{n=1}^{\infty }\) converges pointwise to \(\frac{\mathbb {1}_\Omega }{|\Omega |}\) on \(\Omega \setminus \partial \Omega \), where \(\partial \Omega \) is the boundary of \(\Omega \);
-
(ii)
the sequence of Fourier transforms, \(\{{\widehat{\psi _n}}\}_{n=1}^{\infty }\), converges uniformly.
Proof
Let \(t_0\in \Omega \setminus \partial \Omega \) and \(\delta >0\). By the properties of the sets \(\Omega _n\) we have: \(\Omega _m \subset \Omega _n \subset \Omega \) and \(\epsilon ^{ns} \Omega _n \subset \epsilon ^{ms} \Omega _m\) for \(n\ge m\) and \(\epsilon ^{ns} \Omega _n \subset \epsilon ^{n(s+1)} \Omega _n\) for all n and s. Then, there exists \(N\ge 0\), such that for all \(n\ge N\), \(|\Omega \setminus \Omega _n| < \delta |\Omega |^2\) and \(t_0\in \Omega _n\). That means, for \(n\ge N\)
Then, for all \(n\ge N\),

and claim (i) follows.
For (ii) it suffices to show that the sequence of Fourier transforms \({\widehat{\psi _n}}\) is uniformly Cauchy. By (i) and Lemma 6.8, \(\{\psi _n\}_{n=1}^{\infty }\) is a sequence of \(L^1\) functions converging pointwise almost everywhere to \(\frac{\mathbb {1}_{\Omega }}{|\Omega |} \). Then by the \(L^1\) Dominated Convergence Theorem, \(\{\psi _n\}_{n=1}^{\infty }\) converges to \(\frac{\mathbb {1}_{\Omega }}{|\Omega |} \) in \(L^1\), and it follows that \(\{\psi _n\}_{n=1}^{\infty }\) is an \(L^1\) Cauchy sequence. Meaning, for \(\delta >0\) there exists \(N>0\) such that \(||\psi _n-\psi _m||_1 < \delta \) for all \(n,m\ge N\). Let \(n,m\ge N\), then
and \(\{{\widehat{\psi _n}}\}_{n=1}^{\infty }\) is uniformly Cauchy. By the completeness of \(L^{\infty }(\mathbb {R})\), it converges uniformly. \(\square \)
Let, \(\Psi \) denote the uniform limit of the sequence defined in (37). To make things more convenient later, we normalize \(\Psi \), and define a new function
Note that \(\Phi (0)=1\).
The following observation will be the main ingredient in our approach. It is analogous to the results for lattices developed in Sect. 3. With the above notation we have
Proposition 6.10
Let \(\Lambda (\Omega )\) be a simple generic model set. Assume that \(g_i,h_i\in M^1(\mathbb {R}^d)\) for every \(i=1,\ldots ,M\). Then, for every \(f_1,f_2\in M^1(\mathbb {R}^d)\), the function
is continuous and coincides pointwise with its Fourier series \(\sum _{\eta \in \Gamma ^*} {\widehat{\mathcal {N}}}(\eta ) e^{-2\pi i p_1^*(\eta ) \cdot z}\), with
where \(\eta \in \Gamma ^*\), \(\Phi \) defined in (38).
We can approximate function \({\mathcal {N}}\) with the desired accuracy by an almost periodic function whose spectrum lies in a ’dual’ model set. Let \(\epsilon >0\) and \(C=\max {||\mathcal {V}_{g_i} h_i||_{\mathbf {W}(L^\infty ,{\ell ^2})}}\). The function \(\Phi \) decays rapidly outside its essential support, hence, for the essential support, we can choose a compact interval \({\widetilde{\Omega }}_\epsilon \), depending on the windows \(g_i,h_i\), such that
where \(\big |\Phi \big |^*(x) = \big |\Phi \big |(-x)\) is the involution and \({\widetilde{\Omega }}_\epsilon ^c\) a complement of \({\widetilde{\Omega }}_\epsilon \). Let us define an \(\epsilon -\)dual model set \(\Lambda ^*({\widetilde{\Omega }}_\epsilon )\) originating from \(\Gamma ^*\) and \({\widetilde{\Omega }}_\epsilon \) by
We note here, that the concept of an \(\epsilon \)-dual model set defined here differs from the original \(\epsilon \)-dual model set definition by Meyer. Then, the function \({\mathcal {N}}_{\epsilon }\), given by the series
defines an almost periodic function with spectrum in \(\Lambda ^*({\widetilde{\Omega }}_\epsilon )\). Moreover, by Cauchy-Schwarz inequality, we have
By the property of tensor product and (39), we obtain
Proof of Proposition 6.10
Let \(f_1,f_2\in M^1(\mathbb {R}^d)\). Let \(\psi _n\) be a sequence of \(C_0^\infty (\Omega )\) non-negative functions defined in (36). By Proposition 5.3, for each \(n\in \mathbb {N}\), the functions
are well defined almost periodic functions that are pointwise equal to their Fourier series \(\sum _{\eta \in \Gamma ^*} {\widehat{\mathcal {N}}^{\psi _n}}(\eta ) e^{-2\pi i p_1^*(\eta ) \cdot z}\), where \({\widehat{\mathcal {N}}^{\psi _n}}(\eta )\) are given by
On the other hand, the series \(\sum _{\eta \in \Gamma ^*} {\widehat{\mathcal {N}}}(\eta ) e^{-2\pi i p_1^*(\eta ) \cdot z}\) converges absolutely (by a similar argument as in the proof of Proposition 5.3) and gives rise to a uniformly continuous function. By the uniform convergence of \(\widehat{\psi _n^2}\) to \({\Psi }\,*\,{\Psi }\), it can be easily verified that \({\mathcal {N}}^{\psi _n}\) converges uniformly to \(|\Omega |^{-2}\,\sum _{\eta \in \Gamma ^*} {\widehat{\mathcal {N}}}(\eta ) e^{-2\pi i p_1^*(\eta ) \cdot z}\), since \(D(\Lambda (\Omega )) = \text {vol}(\Gamma )^{-1} |\Omega |\) and \(\Phi = |\Omega | \cdot ({\Psi }\,*\,{\Psi })\).
Now, since \(\Lambda (\Omega )\) is genereic, that is the boundary \(\partial \Omega \) of \(\Omega \) has no common points with \(p_2(\Gamma )\), and \(\psi _n\) converges pointwise to \(\frac{\mathbb {1}_\Omega }{|\Omega |}\) on \(\Omega \setminus \partial \Omega \), by Lemma 6.8, we show that \({\mathcal {N}}(z)\) is a pointwise limit of \(|\Omega |^2 \,{\mathcal {N}}^{\psi _n}(z)\). Indeed, by the Lebesgue Dominated Convergence Theorem, we can move the limit inside the sum, and for every \(z\in \mathbb {R}^{2d}\), we have
By the uniqueness of the the limits, we must have \({\mathcal {N}}(z) = \sum _{\eta \in \Gamma ^*} {\widehat{\mathcal {N}}}(\eta ) e^{-2\pi i p_1^*(\eta ) \cdot z}\), and by the uniqueness of the Fourier series, (26) is the Fourier series of \({\mathcal {N}}(z)\). \(\square \)
For \(g_i,h_i\in M^1(\mathbb {R}^d)\) with \(i=1,\ldots ,M\), the function \({\mathcal {N}}(z)\) of Proposition 6.10 coincides with the function \({\mathcal {N}}(z)\) defined in (34). Indeed, using Proposition 6.4, we can write \({\mathcal {N}}(z)\) from (34) explicitly as
By the uniqueness of the Fourier coefficients, \({\widehat{{\mathfrak {N}}}}(\eta )\) in (35) equal \({\widehat{\mathcal {N}}}(\eta )\) from Proposition 6.10, for all \(\eta \in \Gamma ^*\).
We are now in the position to state the main results.
Theorem 6.11
Let \(\Lambda (\Omega )\) be a simple generic model set. Then for \(g_i,h_i\in M^1(\mathbb {R}^d)\), \(i=1,\ldots ,M\) the following hold.
-
(i)
Fundamental Identity of Gabor Analysis for Model Sets:
$$\begin{aligned} \sum _{i=1}^M \sum _{\lambda \in \Lambda (\Omega )}&\langle f_1,\pi (\lambda )g_i\rangle \langle \pi (\lambda )h_i,f_2\rangle \nonumber \\&= D(\Lambda (\Omega )) \sum _{\eta \in \Gamma ^*} \Phi \big (p_2^*(\eta )\big ) \Big \langle \pi \big (J p_1^*(\eta )\big ) f_1,f_2 \Big \rangle \,\sum _{i=1}^M \Big \langle h_i,\pi \big (J p_1^*(\eta )\big ) g_i \Big \rangle \end{aligned}$$(41)for all \(f_1,f_2\in M^1(\mathbb {R}^d)\).
-
(ii)
Janssen representation:
$$\begin{aligned} S_{g,h}^{\Lambda (\Omega )} =D(\Lambda (\Omega )) \sum _{i=1}^M \sum _{\eta \in \Gamma ^*} \Phi \big (p_2^*(\eta )\big ) \, \Big \langle h_i,\pi \big (J p_1^*(\eta )\big ) g_i \Big \rangle \, \pi \big (J p_1^*(\eta )\big )\,, \end{aligned}$$(42)where the series converges unconditionally in the strong operator topology.
-
(iii)
Wexler–Raz Biorthogonality Relations:
$$\begin{aligned} S_{g,h}^{\Lambda (\Omega )} = I \text{ on } M^1(\mathbb {R}^d) \quad \Longleftrightarrow \quad D(\Lambda (\Omega )) \sum _{i=1}^M \Phi \big (p_2^*(\eta )\big ) \, \Big \langle h_i,\pi \big (J p_1^*(\eta )\big ) g_i \Big \rangle = \delta _{\eta ,0} \end{aligned}$$(43)for \(\eta \in \Gamma ^*\).
The relation (41), as well as (42), can be written using dual model sets, and giving a better understanding of the above relations to the ones for regular lattices. Let \({\widetilde{\Omega }}\) be a compact subset of \(\mathbb {R}\), equal closure of its interior and with measure of the boundary equal to zero. We define a sequence of dual model sets as
Then, the right hand side of (41) equals
where \(w_{\Phi }\) is defined as in (17) for the function \(\Phi \). Since \(\Phi \) is well concentrated, with rapid decay outside its essential support, the sum over m has only a finite number of relevant terms, and we can approximate (41) as
Approximation depends on M and \({\widetilde{\Omega }}\). We can choose \({\widetilde{\Omega }}\) to be an \(\epsilon -\)essential support of \(\Phi \) in the sense of (39), that is \({\widetilde{\Omega }} = {\widetilde{\Omega }}_\epsilon \) and we have \(\Lambda ^*_1({\widetilde{\Omega }}) = \Lambda ^*({\widetilde{\Omega }}_\epsilon )\) as in (40). Then we obtain a good approximation already for \(M=1\)
-
(i)
Fundamental Identity of Gabor Analysis for Model Sets becomes
$$\begin{aligned} \sum _{i=1}^M \sum _{\lambda \in \Lambda (\Omega )} \langle f_1,\pi (\lambda )g_i\rangle&\langle \pi (\lambda )h_i,f_2\rangle \\&\approx D(\Lambda (\Omega )) \sum _{\beta \in \Lambda ^*({\widetilde{\Omega }}_\epsilon )} w_{\Phi }(\beta ) \Big \langle \pi (J \beta ) f_1,f_2 \Big \rangle \,\sum _{i=1}^M \Big \langle h_i,\pi (J \beta ) g_i \Big \rangle \,. \end{aligned}$$ -
(ii)
Janssen Representation gives us an approximation of the frame operator in the form of
$$\begin{aligned} S_{g,h}^{\Lambda (\Omega )} \approx D(\Lambda (\Omega )) \sum _{i=1}^M \sum _{\beta \in \Lambda ^*({\widetilde{\Omega }}_\epsilon )} w_{\Phi }(\beta ) \, \Big \langle h_i,\pi (J \beta ) g_i \Big \rangle \, \pi (J \beta )\,. \end{aligned}$$ -
(iii)
Wexler–Raz Biorthogonality Relations provide an approximation to the identity operator:
$$\begin{aligned} S_{g,h}^{\Lambda (\Omega )} \approx I \text{ on } M^1(\mathbb {R}^d) \quad \Longleftrightarrow \quad D(\Lambda (\Omega )) \sum _{i=1}^M w_{\Phi }(\beta ) \, \Big \langle h_i,\pi (J \beta ) g_i \Big \rangle = \delta _{\beta ,0} \end{aligned}$$for \(\beta \in \Lambda ^*({\widetilde{\Omega }}_\epsilon )\).
These relations resemble the relations of Gabor systems for lattices, where there is a connection between a lattice and its dual (or symplectic dual). Here \(\Lambda (\Omega )\) takes the place of a lattice, and an \(\epsilon -\)dual model set \(\Lambda ^*({\widetilde{\Omega }}_\epsilon )\) takes the place of a dual lattice, and depends on the desired accuracy of the approximation and window functions \(g_i,h_i\).
Proof
The Fundamental Identity of Gabor Analysis and Janssen representation follow directly from Proposition 6.10. Let \(f_1,f_2\in M^1(\mathbb {R}^d)\), then the left hand side of (41) equals the function \({\mathcal {N}}\) of Proposition 6.10 evaluated at \(z=0\). Since \({\mathcal {N}}\) equals its Fourier series expansion, we have
which gives (41).
As for Janssen representation, we observe that \({\mathcal {N}}(z) = \langle S_{g,h}^{\Lambda (\Omega )} \pi (z)f_1,\pi (z) f_2\rangle \) for fixed \(f_1,f_2\in M^1(\mathbb {R}^d)\). Evaluating \({\mathcal {N}}\) at \(z=0\) and using the Fourier series representation of \({\mathcal {N}}\), we obtain
which is the Janssen representation of the frame operator \(S_{g,h}^{\Lambda (\Omega )}\).
The implication \(\Longleftarrow \) of iii) follows trivially from the Janssen representation of \(S_{g,h}^{\Lambda (\Omega )}\). For the converse, assume that \(S_{g,h}^{\Lambda (\Omega )} = I\). Let \(f_1,f_2 \in M^1(\mathbb {R}^d)\), then \({\mathcal {N}}\) of Proposition 3.4 is a constant function. Indeed,
for every \(z\in \mathbb {R}^{2d}\). Since \({\mathcal {O}} = {\mathcal {N}} - \langle f_1,f_2\rangle \) is a zero function, all its Fourier coefficients
are zero. By Proposition 6.10, we have then
Fix \(J p_1^*(\eta )\in \mathbb {R}^{2d}\) and let f be a Gausian, that is \(f(x) = e^{-\pi x^2}\). Then \(\Big \langle \pi \big (J p_1^*(\eta )\big ) f_1,f_2 \Big \rangle = \Big \langle \pi \big (J p_1^*(\eta )\big ) f,f \Big \rangle \ne 0\) and the right hand side of (43) holds. \(\square \)
As a consequence of the Wexler–Raz biorthogonality relations we obtain a density result for Gabor systems for model sets.
Proposition 6.12
Let \(\Lambda (\Omega )\) be a simple generic model set. If the Gabor frame \(\mathcal {G}(g;\Lambda (\Omega ))\), with \(g\in M^1(\Lambda (\Omega ))\) admits a dual that is also a Gabor system, then \(D(\Lambda (\Omega ))\ge 1\).
Proof
Let \(g\in M^1(\mathbb {R}^d)\) and assume that the Gabor frame \(\mathcal {G}(g;\Lambda (\Omega ))\) admits a dual \(\mathcal {G}(h;\Lambda (\Omega ))\) with \(h\in M^1(\mathbb {R}^d)\). Let \(B_g\) be the upper frame bound of \(\mathcal {G}(g;\Lambda (\Omega ))\), and we can assume without loss of generality that \(||h||_2^2 = B_g^{-1}\). Then we have the frame decomposition
If we set \(f_1=h\) and \(f_2=g\), by the Bessel property of \(\mathcal {G}(g;\Lambda (\Omega ))\), we obtain
On the other hand, by Theorem 6.11 iii) with \(L=1\), \(D(\Lambda (\Omega )) \langle h,g\rangle = 1\), and therefore \(D(\Lambda (\Omega )) \ge 1\). \(\square \)
References
Baake, M., Moody, R.V.: Self-similar measures for quasicrystals. In: Baake, M. (ed.) Directions in Mathematical Quasicrystals. AMS, American Mathematical Society, Providence, RI (2000)
Besicovitch, A.: Almost Periodic Functions. Neudruck, vol. XIII. Dover Publications, Inc., New York (1955)
Besicovitch, A., Bohr, H.: Almost periodicity and general trigonometric series. Acta Math. 57, 203–292 (1931)
Boggiatto, P., Fernández, C., Galbis, A.: Gabor systems and almost periodic functions. Appl. Comput. Harmon. Anal. 42(1), 65–87 (2017)
Bohr, H.: Almost Periodic Functions. Chelsea Publishing Company, New York (1947)
de Boor, C., DeVore, R.A., Ron, A.: The structure of finitely generated shift-invariant spaces in \(L_2(\mathbb{R}^d)\). J. Funct. Anal. 119(1), 37–78 (1994)
Feichtinger, H.G.: On a new Segal algebra. Monatsh. Math. 92, 269–289 (1981)
Feichtinger, H.G., Luef, F.: Wiener amalgam spaces for the fundamental identity of Gabor analysis. Collect. Math. 57(Extra Volume (2006)), 233–253 (2006)
Gabardo, J.-P.: Weighted irregular Gabor tight frames and dual systems using windows in the Schwartz class. J. Funct. Anal. 256(3), 635–672 (2009)
Galindo, F.: Some remarks on “On the windowed Fourier transform and wavelet transform of almost periodic functions,” by J. R. Partington and B. Ünalmış. Appl. Comput. Harmon. Anal., 16(3), 174–181 (2004)
Gröchenig, K.: Foundations of Time-Frequency Analysis. Birkhäuser, Boston (2001)
Gröchenig, K., Ortega-Cerdà, J., Romero, J.L.: Deformation of Gabor systems. Adv. Math. 277, 388–425 (2015)
Gröchenig, K., Romero, J.L., Stöckler, J.: Sampling theorems for shift-invariant spaces, Gabor frames, and totally positive functions. Invent. Math. 211(3), 1119–11148 (2017)
Hernández, E., Labate, D., Weiss, G.: A unified characterization of reproducing systems generated by a finite family. II. J. Geom. Anal. 12(4), 615–662 (2002)
Hernández, E., Weiss, G.: A First Course on Wavelets. CRC Press, Boca Raton, FL (1996)
Jakobsen, M., Lemvig, J.: Co-compact Gabor systems on locally compact Abelian groups. J. Fourier Anal. Appl. 22(1), 36–70 (2016)
Janssen, A.: Duality and biorthogonality for Weyl-Heisenberg frames. J. Fourier Anal. Appl. 1(4), 403–436 (1995)
Kreisel, M.: Gabor frames for quasicrystals, \(K\)-theory, and twisted gap labeling. J. Funct. Anal. 270(3), 1001–1030 (2016)
Labate, D.: A unified characterization of reproducing systems generated by a finite family. J. Geom. Anal. 12(3), 469–491 (2002)
Matei, B., Meyer, Y.: Simple quasicrystals are sets of stable sampling. Complex Var. Elliptic Equ. 55(8–10), 947–964 (2010)
Matusiak, E.: Frames of translates for model sets. preprint (2018)
Meyer, Y.: Algebraic Numbers and Harmonic Analysis. North-Holland Mathematical Library, vol. 2. North-Holland Publishing Company, Amsterdam (1972)
Meyer, Y.: Quasicrystals, almost periodic patterns, mean-periodic functions and irregular sampling. Afr. Diaspora J. Math. 13(1), 1–45 (2012)
Moody, R., Nesterenko, M., Patera, J.: Computing with almost periodic functions. Acta Crystallogr. Sect. A 64(6), 654–669 (2008)
Moody, R.V.: Mathematical quasicrystals: a tale of two topologies. In: XIVth international congress on mathematical physics (ICMP 2003), Lisbon, Portugal, 28 July–2 August 2003. Selected papers based on the presentation at the conference., pp. 68–77. Hackensack, NJ: World Scientific (2005)
Partington, J., Ünalmış, B.: On the windowed Fourier transform and wavelet transform of almost periodic functions. Appl. Comput. Harmon. Anal. 10(1), 45–60 (2001)
Schlottmann, M.: Generalized model sets and dynamical systems. In: Baake, M. (ed.) Directions in Mathematical Quasicrystals, pp. 143–159. AMS, American Mathematical Society, Providence, RI (2000)
Wexler, J., Raz, S.: Discrete Gabor expansions. Signal Process. 21, 207–220 (1990)
Acknowledgements
Open access funding provided by University of Vienna. This research was supported by the Austrian Science Fund, FWF Project (V312-N25).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Massimo Fornasier.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Matusiak, E. Gabor Frames for Model Sets. J Fourier Anal Appl 25, 2570–2607 (2019). https://doi.org/10.1007/s00041-019-09674-0
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00041-019-09674-0


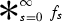 converges in
converges in 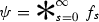 compactly supported on
compactly supported on