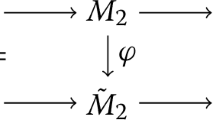A New Regularized Siegel-Weil Type Formula. Part I

Abstract

In this paper, we prove a formula, realizing certain residual Eisenstein series on symplectic groups as regularized kernel integrals. These Eisenstein series, as well as the kernel integrals, are attached to Speh representations. This forms an initial step to a new type of a regularized Siegel-Weil formula that we propose. This new formula bears the same relation to the generalized doubling integrals of Cai, Friedberg, Ginzburg and Kaplan, as does the regularized Siegel-Weil formula to the doubling integrals of Piatetski-Shapiro and Rallis.

1 Introduction

Our main guiding question in this work is whether there is a regularized Siegel-Weil type formula related to the generalized doubling integrals of Cai, Friedberg, Ginzburg and Kaplan [C+19], as the regularized Siegel-Weil formula is related to the doubling integrals of Piatetski-Shapiro and Rallis [PR87]. This formula resulted from the Rallis program of computing the L²-inner product of two theta lifts. Kudla and Rallis achieved this formula for symplectic-orthogonal dual pairs [KR94]. Their work was later generalized by Ikeda, Mœglin, Ichino, Yamana, Gan-Qiu-Takeda and others. See [GQT14] and the references therein. It turns out that the theta correspondence, the Rallis inner product formula, the Siegel-Weil formula, the doubling method, L-functions for symplectic (resp. metaplectic, orthogonal, unitary) groups and their poles are all beautifully related. In this paper, we consider an analog of the theta correspondence for symplectic groups. It yields, as in the case of Kudla and Rallis, a certain divergent integral, which we regularize and identify as a residue of an Eisenstein series. This will enable us to propose conjectures on a new regularized Siegel-Weil type formula that comes along with the generalized doubling integrals.

Let F be a number field and ${\mathbb{A}}$ its ring of adeles. We start with a correspondence of automorphic representations of symplectic groups, constructed by Ginzburg in [Gin03]. We like to think of it as an analog of the classical theta correspondence, although it is different. Attached to a given irreducible, self-dual, cuspidal, automorphic representation τ of ${\mathrm {GL}}_{d}({\mathbb{A}})$, there is a space of theta kernel functions on the adele points of a commuting pair of symplectic groups inside a larger symplectic group. This pair is not a reductive dual pair. We restrict ourselves to irreducible, cuspidal, automorphic representations τ of ${\mathrm {GL}}_{2}({\mathbb{A}})$, with trivial central character, and such that $L(\tau ,\frac{1}{2})\neq 0$. We keep this assumption throughout the paper. This case is already deep and challenging. We can formulate our program for any self-dual cuspidal τ and any d. This will be done elsewhere, but we will comment on this more general case in the end of the paper.

Let Δ(τ,k) (k, a positive integer) denote the Speh representation of ${\mathrm {GL}}_{2k}({\mathbb{A}})$, attached to τ. It was defined by Jacquet [Jac82]. See also [MW89]. Consider an Eisenstein series E(f_Δ(τ,k),s), induced from the Siegel parabolic subgroup Q_2k and Δ(τ,k), on ${\mathrm {Sp}}_{4k}({\mathbb{A}})$, and corresponding to f_Δ(τ,k),s, a smooth, holomorphic section of

$$ \rho _{\Delta (\tau ,k),s}={\mathrm {Ind}}_{Q_{2k}({\mathbb{A}})}^{{\mathrm {Sp}}_{4k}({\mathbb{A}})} \Delta (\tau ,k)|\det \cdot |^{s}. $$

(1.1)

By [JLZ13], Theorem 6.2, the largest pole of E(f_Δ(τ,k),s) is at $s=\frac{k}{2}$ (as the section varies) and it is simple. Denote by Θ_Δ(τ,k) the automorphic representation of ${\mathrm {Sp}}_{4k}({\mathbb{A}})$ generated by the residues $Res_{s=\frac{k}{2}}E(f_{\Delta (\tau ,k),s})$. The elements θ_Δ(τ,k)∈Θ_Δ(τ,k) will be our new “theta series”. Let n≤2k be a positive integer. Restrict θ_Δ(τ,k) to the image of the embedding of ${\mathrm {Sp}}_{2n}({\mathbb{A}})\times {\mathrm {Sp}}_{4k-2n}({\mathbb{A}})$ inside ${\mathrm {Sp}}_{4k}({\mathbb{A}})$. We use the functions θ_Δ(τ,ℓ)(g,h) as kernel functions. Let π be an irreducible, cuspidal, automorphic representation of ${\mathrm {Sp}}_{2n}({\mathbb{A}})$. Define, for $h\in {\mathrm {Sp}}_{4k-2n}({\mathbb{A}})$,

$$ T_{\tau}^{4k-2n}(\varphi _{\pi},\theta _{\Delta (\tau ,k)})(h)=\int _{{\mathrm {Sp}}_{2n}(F)\backslash {\mathrm {Sp}}_{2n}({\mathbb{A}})}\theta _{\Delta ( \tau ,k)}(g,h)\varphi _{\pi}(g)dg. $$

(1.2)

Let Θ_Δ(τ,k)(π) denote the representatation by right translations of ${\mathrm {Sp}}_{4k-2n}({\mathbb{A}})$ in the space generated by the functions (1.2). We call it the Θ_Δ(τ,k)-lift of π, from ${\mathrm {Sp}}_{2n}({\mathbb{A}})$ to ${\mathrm {Sp}}_{4k-2n}({\mathbb{A}})$. These representations satisfy the tower property (Theorem 5.3 in [Gin03]), namely at the first $k\geq \frac{n}{2}$, where Θ_Δ(τ,k)(π) is nontrivial, Θ_Δ(τ,k)(π) is cuspidal. We call k the first τ- occurrence of π. Computations of the correspondence above, at the unramified level, as in Sect. 6 in [Gin03], show

Theorem 1.1

1. If the first τ-occurrence of π is at $\frac{n}{2}\leq k< n$, and σ is an irreducible (cuspidal) subrepresentation of Θ_Δ(τ,k)(π), then π is CAP with respect to the parabolic data

$$ \Delta (\tau ,n-k)|\det \cdot |^{\frac{n-k}{2}}\otimes \sigma . $$

2. If the first τ-occurrence of π is at k>n, then any irreducible summand of Θ_Δ(τ,k)(π) is a CAP representation with respect to the parabolic data

$$ \Delta (\tau ,k-n)|\det \cdot |^{\frac{k-n}{2}}\otimes \pi . $$

3. If the first τ-occurrence of π is at k=n, then any irreducible summand of Θ_Δ(τ,k)(π) is nearly equivalent to π.

Thus, the Θ_Δ(τ,k)-correspondence helps detect CAP representations on symplectic groups. In the first case of Theorem 1.1, the fuctorial lift of π to ${\mathrm {GL}}_{2n+1}({\mathbb{A}})$ is Δ(τ,2(n−k))⊞L(σ), where L(σ) is the functorial lift of σ to ${\mathrm {GL}}_{4k-2n+1}({\mathbb{A}})$. In the second case of the theorem, the functorial lift to ${\mathrm {GL}}_{4k-2n+1}({\mathbb{A}})$ of each irreducible summand of Θ_Δ(τ,k)(π) is Δ(τ,2(k−n))⊞L(π).

The main object of our study is the Θ_Δ(τ,k)-lift of Θ_Δ(τ,ℓ), when ℓ<k. While this object is meaningful locally at each place, its global meaning, in terms of the correspondence (1.2) is problematic, since the integral there, when we replace π by the non-cuspidal Θ_Δ(τ,ℓ) diverges. One of our main results in this paper is a regularization of this integral. This is an analog of what Kudla and Rallis do in [KR94], Sect. 5, where they regularize the integral expressing the theta lift of the trivial representation of an orthogonal group ${\mathrm {O}}_{m}({\mathbb{A}})$ (assumed split, m≠2, for simplicity,) to ${\mathrm {Sp}}_{2n}({\mathbb{A}})$, when m≤n+1. This regularization is a key step in the work of Kudla and Rallis.

To explain our regularization, we will write k=m+ℓ. We are interested in our new theta lifts from a symplectic group to a larger symplectic group, and so we assume that ℓ≤m. Let θ_Δ(τ,m+ℓ)∈Θ_Δ(τ,m+ℓ) and θ_Δ(τ,ℓ)∈Θ_Δ(τ,ℓ). We want to regularize the following integral which might diverge. It is convenient to write it formally, and even have a notation for it. Alternatively, consider it when data is such that it converges absolutely. For $h\in {\mathrm {Sp}}_{4m}({\mathbb{A}})$, let

$$ E(\theta _{\Delta (\tau ,m+\ell )}, \theta _{\Delta (\tau ,\ell )};h)= \int _{{\mathrm {Sp}}_{4\ell}(F)\backslash {\mathrm {Sp}}_{4\ell}({\mathbb{A}})}\theta _{ \Delta (\tau ,m+\ell )}(g,h)\theta _{\Delta (\tau ,\ell )}(g)dg. $$

(1.3)

Our regularization of this integral is similar to the one carried out by Ichino for the regularization of the Siegel-Weil formula [Ich01]. We will choose a finite place v, where the factor at v of Θ_Δ(τ,m+ℓ), Θ_{Δ(τ,m+ℓ),v}, is unramified. Let $\xi _{v}\in \mathcal{H}({\mathrm {Sp}}_{4m}(F_{v})// K_{4m,v})$, the spherical Hecke algebra of Sp_4m(F_v). Here, K_4m,v denotes the standard maximal compact subgroup of Sp_4m(F_v). Denote

$$ ((1\otimes \xi _{v})\ast \theta _{\Delta (\tau ,m+\ell )})(x)=\int _{{\mathrm {Sp}}_{4m}(F_{v})}\xi _{v}(h_{v})\theta _{\Delta (\tau ,m+ \ell )}(x(1,h_{v}))dh_{v}. $$

(1.4)

Similarly, we can also consider, for $\eta _{v}\in \mathcal{H}({\mathrm {Sp}}_{4\ell}(F_{v})// K_{4\ell ,v})$,

$$ ((\eta _{v}\otimes 1)\ast \theta _{\Delta (\tau ,m+\ell )})(x)=\int _{{\mathrm {Sp}}_{4\ell}(F_{v})}\eta _{v}(g_{v})\theta _{\Delta (\tau ,m+ \ell )}(x(g_{v},1))dg_{v}. $$

(1.5)

Our first main result is the following analog of Howe duality.

Theorem 1.2

Assume that ℓ≤m. There is a homomorphism of algebras

$$ \eta _{m,\ell ,\tau _{v}}: \mathcal{H}({\mathrm {Sp}}_{4m}(F_{v})// K_{4m,v}) \rightarrow \mathcal{H}({\mathrm {Sp}}_{4\ell}(F_{v})// K_{4\ell ,v}), $$

such that, for any K_4m,v×K_4ℓ,v-fixed θ_Δ(τ,m+ℓ)∈Θ_Δ(τ,m+ℓ), we have

$$ (1\otimes \xi _{v})\ast \theta _{\Delta (\tau ,m+\ell )}=(\eta _{m, \ell ,\tau _{v}}(\xi _{v})\otimes 1)\ast \theta _{\Delta (\tau ,m+ \ell )}, $$

(1.6)

for all $\xi _{v}\in \mathcal{H}({\mathrm {Sp}}_{4m}(F_{v})// K_{4m,v})$.

Of course, the property (1.6) holds for the factor at v of Θ_Δ(τ,m+ℓ), and our proof will be purely local. Our second main result is the following rapid decrease property.

Theorem 1.3

Assume that ℓ≤m. There is a function $\xi _{m,\ell ,v}\in \mathcal{H}({\mathrm {Sp}}_{4m}(F_{v})// K_{4m,v})$, depending on τ_v, m, ℓ, such that the function on ${\mathrm {Sp}}_{4\ell}({\mathbb{A}})$,

$$ g\mapsto ((1\otimes \xi _{m,\ell ,v})\ast \theta _{\Delta (\tau ,m+ \ell )})(g,h) $$

is rapidly decreasing, uniformly in h varying in bounded subsets of ${\mathrm {Sp}}_{4m}(F)\backslash {\mathrm {Sp}}_{4m}({\mathbb{A}})$.

Thus, E((1⊗ξ_v)∗θ_Δ(τ,m+ℓ),θ_Δ(τ,ℓ);h) in (1.3) is an absolutely convergent integral. More generally, as Kudla and Rallis do in [KR94], Sect. 5, we replace θ_Δ(τ,ℓ) in E((1⊗ξ_v)∗θ_Δ(τ,m+ℓ),θ_Δ(τ,ℓ);h) by an Eisenstein series E(f_Δ(τ,ℓ),s) on ${\mathrm {Sp}}_{4\ell}({\mathbb{A}})$, corresponding to a smooth, holomorphic section f_Δ(τ,ℓ),s of ρ_Δ(τ,ℓ),s, such that

$$ \theta _{\Delta (\tau ,\ell )}=Res_{s=\frac{\ell}{2}}E(f_{\Delta ( \tau ,\ell ),s}). $$

Then we consider

$$ \int _{{\mathrm {Sp}}_{4\ell}(F)\backslash {\mathrm {Sp}}_{4\ell}({\mathbb{A}})}(1 \otimes \xi _{m,\ell ,v})\ast \theta _{\Delta (\tau ,m+\ell )}(g,h)E(f_{ \Delta (\tau ,\ell ),s};g)dg. $$

(1.7)

This is the analog of the integral (5.5.1) in [KR94]. In our third main result, we identify this integral as an Eisenstein series on ${\mathrm {Sp}}_{4m}({\mathbb{A}})$.

Theorem 1.4

Assume that θ_Δ(τ,m+ℓ) is K_4ℓ×K_4m-finite. There is an explicit K_4m-finite, meromorphic section $\varphi _{\Delta (\tau ,\ell )|\det \cdot |^{s}\otimes \Theta _{ \Delta (\tau ,m-\ell )}}$ of

$$ {\mathrm {Ind}}_{Q_{2\ell}^{4m}({\mathbb{A}})}^{{\mathrm {Sp}}_{4m}({\mathbb{A}})}\Delta (\tau ,\ell )| \det \cdot |^{s}\otimes \Theta _{\Delta (\tau ,m-\ell )}, $$

depending on θ_Δ(τ,m+ℓ), f_Δ(τ,ℓ),s, such that

$$ \int _{{\mathrm {Sp}}_{4\ell}(F)\backslash {\mathrm {Sp}}_{4\ell}({\mathbb{A}})}(1 \otimes \xi _{m,\ell ,v})\ast \theta _{\Delta (\tau ,m+\ell )}(g,h)E(f_{ \Delta (\tau ,\ell ),s};g)dg= $$

$$ =E(\varphi _{\Delta (\tau ,\ell )|\det \cdot |^{s}\otimes \Theta _{ \Delta (\tau ,m-\ell )}},h), $$

where $E(\varphi _{\Delta (\tau ,\ell )|\det \cdot |^{s}\otimes \Theta _{ \Delta (\tau ,m-\ell )}},h)$ denotes the Eisenstein series on ${\mathrm {Sp}}_{4m}({\mathbb{A}})$, corresponding to $\varphi _{\Delta (\tau ,\ell )|\det \cdot |^{s}\otimes \Theta _{ \Delta (\tau ,m-\ell )}}$. The poles of the section $\varphi _{\Delta (\tau ,\ell )|\det \cdot |^{s}\otimes \Theta _{ \Delta (\tau ,m-\ell )}}$ are contained in the set of poles of the L-function $L(\Delta (\tau ,\ell )\times \tau ,s+m-\ell +\frac{1}{2})$.

In order to obtain the regularization of (1.3), consider a case where θ_Δ(τ,m+ℓ) and f_Δ(τ,ℓ),s are such that the integral

$$ \int _{{\mathrm {Sp}}_{4\ell}(F)\backslash {\mathrm {Sp}}_{4\ell}({\mathbb{A}})}\theta _{ \Delta (\tau ,m+\ell )}(g,h)E(f_{\Delta (\tau ,\ell ),s};g)dg $$

(1.8)

converges absolutely. For example, this is the case when $\theta _{\Delta (\tau ,m+\ell )}=(1\otimes \xi _{m,\ell ,v})\ast \theta '_{\Delta (\tau ,m+\ell )}$. In this case, the integral (1.8) converges absolutely, for each s, which is not a pole of E(f_Δ(τ,ℓ),s;⋅). Then we prove that there is a polynomial $P(x, y)\in {\mathbb{C}}[x,y]$, depending on τ_v, ℓ, m, such that

$$\begin{gathered} \begin{gathered}[t] \int _{{\mathrm {Sp}}_{4\ell}(F)\backslash {\mathrm {Sp}}_{4\ell}({\mathbb{A}})}(1 \otimes \xi _{m,\ell ,v})\ast \theta _{\Delta (\tau ,m+\ell )}(g,h)E(f_{ \Delta (\tau ,\ell ),s};g)dg= \\ =P(q_{v}^{-s},q_{v}^{s})\int _{{\mathrm {Sp}}_{4\ell}(F)\backslash {\mathrm {Sp}}_{4 \ell}({\mathbb{A}})}\theta _{\Delta (\tau ,m+\ell )}(g,h)E(f_{\Delta (\tau , \ell ),s};g)dg, \end{gathered} \end{gathered}$$

(1.9)

for θ_Δ(τ,m+ℓ) which is K_4m,v×K_4ℓ,v-fixed, and a section f_Δ(τ,ℓ),s, which is K_4ℓ,v-fixed. Here, q_v is the number of elements in the residue field of F_v. This follows from Theorem 1.2. The polynomial is obtained by using (1.6) applied to ξ_m,ℓ,v and convolving $\eta _{m,\ell ,\tau _{v}}(\xi _{m,\ell ,v})$ against an unramified vector of the local factor at v of ρ_Δ(τ,ℓ),s. Thus, it is natural to consider

$\mathcal{E}(\theta _{\Delta (\tau ,m+\ell )},f_{\Delta (\tau ,\ell ),s};h)=$

$$ \frac{1}{P(q_{v}^{-s},q_{v}^{s})}\int _{{\mathrm {Sp}}_{4\ell}(F) \backslash {\mathrm {Sp}}_{4\ell}({\mathbb{A}})}(1\otimes \xi _{m,\ell ,v})\ast \theta _{ \Delta (\tau ,m+\ell )}(i(g,h))E(f_{\Delta (\tau ,\ell ),s};g)dg. $$

(1.10)

Now, we need to explain the choice of the place v in some more details. Since τ_v is unramified and self-dual, τ_v is induced from a character of the Borel subgroup of the form $\chi _{v}\otimes \chi _{v}^{-1}$, where χ_v is an unramified character of $F_{v}^{*}$. We require that v is such that χ_v is not quadratic. This is possible. We will prove

Theorem 1.5

With the above assumption on v, $P(q_{v}^{-\frac{\ell}{2}},q_{v}^{\frac{\ell}{2}})\neq 0$, for m≥2ℓ, and for ℓ≤m≤2ℓ−1, $P(q_{v}^{-s},q_{v}^{s})$ has a simple zero at $s=\frac{\ell}{2}$. Consider $\mathcal{E}(\theta _{\Delta (\tau ,m+\ell )},f_{\Delta (\tau ,\ell ),s}; h)$, which is (by Theorem 1.4) an Eisenstein series on ${\mathrm {Sp}}_{4m}({\mathbb{A}})$, corresponding to ${\mathrm {Ind}}_{Q_{2\ell}^{4m}({\mathbb{A}})}^{{\mathrm {Sp}}_{4m}({\mathbb{A}})}\Delta (\tau ,\ell )| \det \cdot |^{s}\otimes \Theta _{\Delta (\tau ,m-\ell )}$. At $s=\frac{\ell}{2}$, it has at most a simple pole, when m≥2ℓ, and at most a double pole, when ℓ≤m≤2ℓ−1.

Note the similarity between Theorem 1.5 and [KR94], (5.5.23), (5.5.24). Thus, we regularize the integral (1.3) as follows. Consider the Laurent expansion of (1.10) at $s=\frac{\ell}{2}$. The leading term when m≥2ℓ is the residue, which we denote by $B_{-1}(h, \theta _{\Delta (\tau ,m+\ell )},f_{\Delta (\tau ,\ell ), \frac{\ell}{2}})$. When m≤2ℓ−1, the leading term is the coefficient of $(s-\frac{\ell}{2})^{-2}$, which we denote by $B_{-2}(h, \theta _{\Delta (\tau ,m+\ell )},f_{\Delta (\tau ,\ell ), \frac{\ell}{2}})$. Thus, we regularize (1.3), by

$$ E_{reg}(\theta _{\Delta (\tau ,m+\ell )}, \theta _{\Delta (\tau , \ell )};h)= \textstyle\begin{cases} B_{-1}(h, \theta _{\Delta (\tau ,m+\ell )},f_{\Delta (\tau ,\ell ), \frac{\ell}{2}}),\ \ 2\ell \leq m \\ B_{-2}(h, \theta _{\Delta (\tau ,m+\ell )},f_{\Delta (\tau ,\ell ), \frac{\ell}{2}}),\ \ \ell \leq m\leq 2\ell -1 \end{cases}\displaystyle . $$

(1.11)

Plan of this paper: We set up notation and recall some preliminiaries in the end of this introduction. In Sect. 2, we prove Theorem 1.2. We describe the local unramified factor at a finite place v of Θ_Δ(τ,m+ℓ), describe the homomorphism from $\mathcal{H}({\mathrm {Sp}}_{4m}(F_{v})// K_{4m,v})$ to $\mathcal{H}({\mathrm {Sp}}_{4\ell}(F_{v})// K_{4\ell ,v})$ and prove the property (1.6). We then define the function $\xi _{m,\ell ,v}\in \mathcal{H}({\mathrm {Sp}}_{4m}(F_{v})// K_{4m,v})$. In Sect. 3, we write down the Fourier expansion of ((1⊗ξ_m,ℓ,v)∗θ_Δ(τ,m+ℓ)) along $U_{2\ell}^{4\ell}\times I_{4m}$. The convolution by 1⊗ξ_m,ℓ,v annihilates certain families of “low rank” Fourier coefficients (Theorem 3.2). In Sect. 4, we prove Theorem 1.3. For the proof, we use the results of Sect. 3. This and Sect. 2 allow us to introduce the regularization (1.11). In Sect. 5, we study the integral (1.7) and prove Theorem 1.4, and then Theorem 1.5 follows. In Sect. 6, we review the work of Kudla and Rallis [KR94] on the Siegel-Weil formula and point out the analogy of our work to some of the results in [KR94]. We then formulate a conjecture with our proposed new type of a Siegel-Weil formula (Conjecture 6.6). Finally, we comment on the general case, where τ is any irreducible, self-dual, cuspidal, automorphic representation of ${\mathrm {GL}}_{d}({\mathbb{A}})$, such that $L(\tau ,\frac{1}{2})\neq 0$.

We thank the anonymous referees for their careful reading and for their valuable, helpful comments, remarks, questions and suggestions.

Notation and some preliminaries: We write the symplectic group Sp_2k as the subgroup of GL_2k of matrices g satisfying

$$ {}^{t}gJ_{2k}g=J_{2k}, $$

where $J_{2k}= \begin{pmatrix} &w_{k} \\ -w_{k}\end{pmatrix}$, and w_k is the k×k permutation matrix with 1 along the anti-diagonal. Let 1≤r≤k be an integer. We denote by Q_r the standard parabolic subgroup of Sp_2k, with Levi decomposition Q_r=L_r⋉U_r, where L_r≅GL_r×Sp_2(k−r). The Siegel parabolic subgroup of Sp_2k is Q_k. The elements of its Levi part L_k are

$$ \hat{a}= \begin{pmatrix} a \\ &a^{*}\end{pmatrix} ,\ a^{*}=w_{k}{}^{t} a^{-1}w_{k},\ a\in {\mathrm {GL}}_{k}; $$

The elements of U_k are

$$ u_{k}(x)= \begin{pmatrix} I_{k}&x \\ &I_{k}\end{pmatrix} ,\ {}^{t}(w_{k}x)=w_{k}x. $$

For a∈GL_r, r≤k, we also denote

$$ \hat{a}= \begin{pmatrix} a \\ &I_{2(k-r)} \\ &&a^{*}\end{pmatrix} \in {\mathrm {Sp}}_{2k}, $$

when k is understood. More generally, for positive integers $\underline{i}=(i_{1},\ldots,i_{\ell})$, such that i=i₁+⋯+i_ℓ≤k, we denote by $Q_{\underline{i}}$ the standard parabolic subgroup of Sp_2k with Levi part $L_{\underline{i}}\cong {\mathrm {GL}}_{i_{1}}\times \cdots \times {\mathrm {GL}}_{i_{ \ell}}\times {\mathrm {Sp}}_{2(k-i)}$. We denote its unipotent radical by $U_{\underline{i}}$. When we want to recall that these are subgroups of Sp_2k, we sometimes denote $Q^{2k}_{\underline{i}}$, $L^{2k}_{\underline{i}}$, $U^{2k}_{ \underline{i}}$. For positive integers $\underline{j}=(j_{1},\ldots,j_{\ell})$, such that j₁+⋯+j_ℓ=k, we denote by $P_{\underline{j}}=M_{\underline{j}}\ltimes V_{\underline{j}}$ the standard parabolic subgroup of GL_k, with unipotent radical $V_{\underline{j}}$ and Levi part $M_{\underline{j}}\cong {\mathrm {GL}}_{j_{1}}\times \cdots \times {\mathrm {GL}}_{j_{ \ell}}$. We denote the standard Borel subgroups of Sp_2k, GL_k by $B_{{\mathrm {Sp}}_{2k}}$, $B_{{\mathrm {GL}}_{k}}$. We denote the corresponding diagonal subgroups by $T_{{\mathrm {Sp}}_{2k}}$, $T_{{\mathrm {GL}}_{k}}$. We sometimes denote $T_{{\mathrm {GL}}_{k}}=T_{k}$.

Let v be a place of F. We denote by K_2m,v the standard maximal compact subgroup of Sp_2m(F_v). Similarly, we denote by $K_{{\mathrm {GL}}_{m},v}$ the standard maximal compact subgroup of GL_m(F_v). When v is finite, we denote by $\mathcal{O}_{v}$ the ring of integers of F_v, and by $\mathcal{P}_{v}$ its maximal ideal. Denote by q_v the number of elements in the residue field $\mathcal{O}_{v}/\mathcal{P}_{v}$, and by p_v a generator of $\mathcal{P}_{v}$. Then $K_{2m,v}={\mathrm {Sp}}_{2m}(\mathcal{O}_{v})$, $K_{{\mathrm {GL}}_{m},v}={\mathrm {GL}}_{m}(\mathcal{O}_{v})$. We denote K_2m=∏_vK_2m,v, $K_{{\mathrm {GL}}_{m}}=\prod _{v}K_{{\mathrm {GL}}_{m},v}$.

For an F-variety X, we denote by $\mathcal{S}(X({\mathbb{A}}))$ the space of Schwartz functions on $X({\mathbb{A}})$. For a place ν of F, $\mathcal{S}(X(F_{\nu}))$ denotes the space of Schwartz functions on X(F_ν).

We use Ind to denote normalized induction.

In this paper, we fix an irreducible, cuspidal, automorphic representation τ of ${\mathrm {GL}}_{2}({\mathbb{A}})$, with trivial central character. (In this case, the property that the central character is trivial is equivalent to the property that L(τ,∧²,s) has a pole at s=1.) We assume also that $L(\tau ,\frac{1}{2})\neq 0$. Let k be a positive integer and let Δ(τ,k) denote the Speh representation of ${\mathrm {GL}}_{2k}({\mathbb{A}})$, attached to τ. See [Jac82], [MW89] (where, of course, the theory applies to any irreducible, cuspidal, automorphic representations of ${\mathrm {GL}}_{n}({\mathbb{A}})$.) This is the representation spanned by the (multi-) residues of Eisenstein series corresponding to the parabolic induction from

$$ \tau |\det \cdot |^{s_{1}}\times \tau |\det \cdot |^{s_{2}}\times \cdots \times \tau |\det \cdot |^{s_{k}}, $$

at the point

$$ (\frac{k-1}{2},\frac{k-3}{2},\ldots,\frac{1-k}{2}). $$

Consider an Eisenstein series, induced from Δ(τ,k), on the adelic symplectic group ${\mathrm {Sp}}_{4k}({\mathbb{A}})$. Let f_Δ(τ,k),s be a smooth, holomorphic section of

$$ \rho _{\Delta (\tau ,k),s}={\mathrm {Ind}}_{Q_{2k}({\mathbb{A}})}^{{\mathrm {Sp}}_{4k}({\mathbb{A}})} \Delta (\tau ,k)|\det \cdot |^{s}. $$

We denote the corresponding Eisenstein series by E(f_Δ(τ,k),s), and sometimes also by $E^{{\mathrm {Sp}}_{4k}}(f_{\Delta (\tau ,k),s})$. In [JLZ13], Theorem 6.2, the poles of the normalized Eisenstein series E^∗(f_Δ(τ,ℓ),s), in Re(s)≥0, are determined, and they are simple. The largest pole is at $s=\frac{k}{2}$ and the remaining poles are $\frac{k}{2}-1, \frac{k}{2}-2,\ldots$, up to 1, or $\frac{1}{2}$, according to whether k is even or odd, respectively. In fact, they are simple poles of E(f_Δ(τ,ℓ),s) (unnormalized), as the section varies. Denote by Θ_Δ(τ,k) the automorphic representation of ${\mathrm {Sp}}_{4k}({\mathbb{A}})$ generated by the residues $Res_{s=\frac{k}{2}}E(f_{\Delta (\tau ,\ell ,s})$. We note that

Proposition 1.6

The automorphic representation Θ_Δ(τ,k) is irreducible and square-integrable.

The square-integrability is proved in [JLZ13], Theorem 6.1. The irreducibility is proved in [Liu13], Theorem 7.1.

Let ℓ≤m be positive integers. The specific embedding ${\mathrm {Sp}}_{4\ell}({\mathbb{A}})\times {\mathrm {Sp}}_{4m}({\mathbb{A}})\hookrightarrow {\mathrm {Sp}}_{4(m+ \ell )}({\mathbb{A}})$ that we use in (1.2) is the following. Let $g\in {\mathrm {Sp}}_{4\ell}({\mathbb{A}})$, $h\in {\mathrm {Sp}}_{4m}({\mathbb{A}})$. Write g as

$$ g= \begin{pmatrix} g_{1}&g_{2} \\ g_{3}&g_{4}\end{pmatrix} , $$

where g_i are 2ℓ×2ℓ matrices. Then

$$ i(g,h)= \begin{pmatrix} g_{1}&&g_{2} \\ &h \\ g_{3}&&g_{4}\end{pmatrix} . $$

(1.12)

We, usually, simply write (g,h) instead of i(g,h). Thus, when we evaluate θ_Δ(τ,m+ℓ) at $i(g,h)\in i({\mathrm {Sp}}_{4\ell}({\mathbb{A}})\times {\mathrm {Sp}}_{4m}({\mathbb{A}}))$, we, usually, write θ_Δ(τ,ℓ)(g,h).

We finish this introduction with two facts that we need on the representations Θ_Δ(τ,k). For f∈Θ_Δ(τ,k), consider the constant term of f along the unipotent radical U_r, r≤2k,

$$ f^{U_{r}}(g)=\int _{U_{r}(F)\backslash U_{r}({\mathbb{A}})}f(ug)du. $$

(1.13)

Proposition 1.7

The constant term (1.13) is zero on Θ_Δ(τ,k), unless r=2i, 1≤i≤k, and then, for each f∈Θ_Δ(τ,k), the constant term $f^{U_{2i}}$, as a function on ${\mathrm {Sp}}_{4k}({\mathbb{A}})$, lies in the space of

$$ {\mathrm {Ind}}_{Q_{2i}({\mathbb{A}})}^{{\mathrm {Sp}}_{4k}({\mathbb{A}})}\Delta (\tau ,i)|\det \cdot |^{-k+ \frac{i}{2}}\otimes \Theta _{\Delta (\tau ,k-i)}. $$

This is Lemma 2.3 in [Liu13] (in the special case of GL₂). See also [JL16], Lemma 4.1.

Recall that Fourier coefficients supported by automorphic forms correspond to nilpotent orbits. See [GRS03]. In the case of the automorphic forms in the space of Θ_Δ(τ,k), we have

Proposition 1.8

There is a unique maximal nilpotent orbit in the Lie algebra of Sp_4k, over the algebraic closure of F, attached to Fourier coefficients admitted by Θ_Δ(τ,k). This is the orbit which corresponds to the partition ((2)^2k).

This was proved (in general) by Ginzburg in [Gin08]. See [Liu13] for a detailed proof. See also [GS22].

2 An analog of Howe duality in spherical Hecke algebras

The goal of this section is to prove Theorem 1.2. Fix a finite place v of F, where the factor at v of Θ_Δ(τ,m+ℓ), Θ_{Δ(τ,m+ℓ),v} is unramified. Since τ_v is unramified, write $\tau _{v}={\mathrm {Ind}}_{B_{{\mathrm {GL}}_{2}}(F_{v})}^{{\mathrm {GL}}_{2}(F_{v})}\chi _{v} \otimes \chi _{v}^{-1}$, where $B_{{\mathrm {GL}}_{2}}$ is the standard Borel subgroup of GL₂, and χ_v is an unramified character of $F_{v}^{*}$. Recall that the central charcater of τ is trivial. Denote, for short, χ=χ_v. Later on, we will need to assume that χ is not quadratic. (This will be needed only in Lemma 4.6, in order that the polynomial P(x,y) of (1.9) is such that $P(q_{v}^{-s},q_{v}^{s})$ has a simple zero at $s=\frac{\ell}{2}$, when m≤2ℓ−1.)

Lemma 2.1

Θ_{Δ(τ,m+ℓ),v} is isomorphic to

$$ \rho _{\chi}=\rho ^{4(m+\ell )}_{\chi}={\mathrm {Ind}}_{Q_{2(m+\ell )}(F_{v})}^{ {\mathrm {Sp}}_{4(m+\ell )}(F_{v})}\chi \circ \det . $$

Proof

This is a special case of Lemma 3.1 in [Gin03]. We bring it for convenience. Denote, for this proof, k=m+ℓ. The representation Θ_Δ(τ,k),v is the unramified constituent of the representation of Sp_4k(F_v), parabolically induced from the standard Borel subgroup $B_{{\mathrm {Sp}}_{4k}}(F_{v})$ and the character of the diagonal subgroup given by

$$ (\chi |\cdot |^{\frac{k-1}{2}+\frac{k}{2}}\otimes \chi ^{-1}|\cdot |^{ \frac{k-1}{2}+\frac{k}{2}})\otimes (\chi |\cdot |^{\frac{k-3}{2}+ \frac{k}{2}}\otimes \chi ^{-1}|\cdot |^{\frac{k-3}{2}+\frac{k}{2}}) \otimes \cdots $$

(2.1)

$$ \cdots \otimes (\chi |\cdot |^{\frac{1-k}{2}+\frac{k}{2}}\otimes \chi ^{-1}|\cdot |^{\frac{1-k}{2}+\frac{k}{2}}). $$

Conjugating by an appropriate Weyl element, the representation parabolically induced from (2.1) shares the same unramified constituent with the representation parabolically induced from the character

$$ (\chi |\cdot |^{k-\frac{1}{2}}\otimes \chi |\cdot |^{-k+\frac{1}{2}}) \otimes (\chi |\cdot |^{k-\frac{3}{2}}\otimes \chi |\cdot |^{-k+ \frac{3}{2}})\otimes \cdots \otimes (\chi |\cdot |^{\frac{1}{2}} \otimes \chi |\cdot |^{-\frac{1}{2}}). $$

(2.2)

We may permute the characters of $F_{v}^{*}$ in (2.2). Hence Θ_Δ(τ,k),v is the unramified constituent of the representation of Sp_4k(F_v), parabolically induced from $B_{{\mathrm {Sp}}_{4k}}(F_{v})$ and the character

$$ \chi |\cdot |^{k-\frac{1}{2}}\otimes \chi |\cdot |^{k-\frac{3}{2}} \otimes \cdots \otimes \chi |\cdot |^{\frac{1}{2}}\otimes \chi | \cdot |^{-\frac{1}{2}}\otimes \cdots \otimes \chi |\cdot |^{-k+ \frac{1}{2}}. $$

(2.3)

The character (2.3), when viewed as a character of the diagonal subgroup of GL_2k(F_v), is the product of $\delta _{B_{{\mathrm {GL}}_{2k}}}^{\frac{1}{2}}$ and the restriction of χ∘det. Since the trivial representation of GL_2k(F_v) is a quotient of ${\mathrm {Ind}}_{B_{{\mathrm {GL}}_{2k}(F_{v})}}^{GL_{2k}(F_{v})}\delta _{B_{{\mathrm {GL}}_{2k}}}^{ \frac{1}{2}}$, we see that Θ_Δ(τ,k),v is the unramified constituent of ρ_χ. Finally, by a theorem of Kudla and Rallis, ρ_χ is irreducible. See [KR92], p. 210. □

From this point until (almost) the end of this section, we work solely over F_v, and so we will drop the index v from our notation, writing F instead of F_v, K_4m instead of K_4m,v etc.

Assume that ℓ≤m. We have the following homomorphism of spherical Hecke algebras,

$$ \eta ^{\chi}_{m,\ell}: \mathcal{H}({\mathrm {Sp}}_{4m}(F)// K_{4m}) \longrightarrow \mathcal{H}({\mathrm {Sp}}_{4\ell}(F)// K_{4\ell}), $$

$$ \begin{gathered}[b] \eta ^{\chi}_{m,\ell}(\xi )(g)=\int _{{\mathrm {GL}}_{2(m-\ell )}(F)} \xi ^{U_{2(m-\ell )}}( \begin{pmatrix} b \\ &g \\ &&b^{*}\end{pmatrix} )\chi (\det (b))|\det (b)|^{-(m+\ell +\frac{1}{2})}db= \\ =\int _{{\mathrm {GL}}_{2(m-\ell )}(F)}(\delta ^{-\frac{1}{2}}_{Q_{2(m- \ell )}}\cdot \xi ^{U_{2(m-\ell )}})( \begin{pmatrix} b \\ &g \\ &&b^{*}\end{pmatrix} )\chi (\det (b))db. \end{gathered} $$

(2.4)

Here, for h∈Sp_4m(F), we denote

$$ \xi ^{U_{2(m-\ell )}}(h)=\int _{U_{2(m-\ell )}(F)}\xi (uh)du. $$

For a function f in the space of ρ_χ, we denote by (1⊗ξ)∗f and $(\eta ^{\chi}_{m,\ell}(\xi )\otimes 1)\ast f$ the functions in the space of ρ_χ given by

$$ (1\otimes \xi )\ast f(x)=\int _{{\mathrm {Sp}}_{4m}(F)}\xi (h)f(x\cdot i(I_{4 \ell},h))dh, $$

$$ (\eta ^{\chi}_{m,\ell}(\xi )\otimes 1)\ast f(x)=\int _{{\mathrm {Sp}}_{4 \ell}(F)}\eta ^{\chi}_{m,\ell}(\xi )(g)f(x\cdot i(g,I_{4m}))dg. $$

In this section, we prove the following analog of (spherical) Howe duality.

Theorem 2.2

Assume that m≥ℓ. For any i(K_4ℓ×K_4m)-fixed function f in the space of ρ_χ, and for any $\xi \in \mathcal{H}({\mathrm {Sp}}_{4m}(F)// K_{4m})$, we have

$$ (1\otimes \xi )\ast f=(\eta ^{\chi}_{m,\ell}(\xi )\otimes 1)\ast f. $$

Proof

We start with analyzing the restriction of ρ_χ to i(Sp_4ℓ(F)×Sp_4m(F)). Consider Q_2(m+ℓ)(F)∖Sp_4(m+ℓ)(F)/i(Sp_4ℓ(F)×Sp_4m(F)). By Lemma 2.2 in [GS211], we may take the following (slightly modified) representatives. For 0≤e≤2ℓ,

$$ \gamma _{e}=\gamma _{e}^{1}\gamma _{e}^{2}, $$

(2.5)

$$ \gamma _{e}^{1}= \begin{pmatrix} I_{e} \\ &I_{2(2\ell -e)} \\ &&I_{2(e+2(m-\ell ))} \\ &I_{2(2\ell -e)}&&I_{2(2\ell -e)} \\ &&&&I_{e}\end{pmatrix} , $$

$$ \gamma _{e}^{2}= \begin{pmatrix} I_{2\ell} \\ &&I_{2\ell -e} \\ &I_{e+2(m-\ell )} \\ &&&&I_{e+2(m-\ell )} \\ &&&I_{2\ell -e} \\ &&&&&I_{2\ell}\end{pmatrix} . $$

The orbit which corresponds to e=0 is the unique open orbit. Since it is dense, it is enough to show that, for f and ξ as in the theorem, and for (g,h)∈Sp_4ℓ(F)×Sp_4m(F), we have

$$ (1\otimes \xi )\ast f(\gamma _{0}i(g,h))=(\eta ^{\chi}_{m,\ell}(\xi ) \otimes 1)\ast f(\gamma _{0}i(g,h)). $$

(2.6)

We thank the referee for pointing to us that it suffices to consider the open orbit. Let

$$ Q_{m,\ell}(F)=\gamma _{0}^{-1}Q_{2(m+\ell )}(F)\gamma _{0}\cap i({\mathrm {Sp}}_{4 \ell}(F)\times {\mathrm {Sp}}_{4m}(F)). $$

For f in the space of ρ_χ, we have, for i(g₀,h₀)∈Q_m,ℓ(F),

$$ f(\gamma _{0} i(g_{0}g,h_{0}h))=(\delta _{Q_{2(m+\ell )}}^{ \frac{1}{2}}\chi \circ \det )(\gamma _{0}i(g_{0},h_{0})\gamma _{0}^{-1})f( \gamma _{0}i(g,h)). $$

(2.7)

The elements of Q_m,ℓ(F) have the form

$$ x=i(g, \begin{pmatrix} b&\ast &\ast \\ &g^{\iota}&\ast \\ &&b^{*}\end{pmatrix} )\in i({\mathrm {Sp}}_{4\ell}(F)\times {\mathrm {Sp}}_{4m}(F)), $$

(2.8)

where g∈Sp_4ℓ(F), b∈GL_2(m−ℓ)(F), and for g∈Sp_2k(F),

$$ g^{\iota}= \begin{pmatrix} &I_{k} \\ I_{k}\end{pmatrix} g \begin{pmatrix} &I_{k} \\ I_{k}\end{pmatrix} . $$

Now, (2.7), with the element x as in (2.8), gives

$$ f(\gamma _{0} xi(g,h))=\chi (\det (b))|\det (b)|^{m+\ell +\frac{1}{2}}f( \gamma _{0}i(g,h)). $$

(2.9)

Denote, for h∈Sp_4ℓ(F),

$$ \varphi _{f}(h)=f(\gamma _{0}i(I_{4\ell}, \begin{pmatrix} I_{2(m-\ell )} \\ &h \\ &&I_{2(m-\ell )}\end{pmatrix} )). $$

Since f is i(K_4ℓ×K_4m)-right invariant, by the Iwasawa decomposition in Sp_4m(F) and (2.9), f is determined by φ_f. Indeed, let g₁∈Sp_4ℓ(F), h′∈Sp_4m(F). Write the Iwasawa decomposition of h′,

$$ h'= \begin{pmatrix} b&\ast &\ast & \\ &g_{2} &\ast \\ &&b^{*}\end{pmatrix} \cdot r, $$

where b∈GL_2(m−ℓ)(F), g₂∈Sp_4ℓ(F), r∈K_4m. Then

$$ f(\gamma _{0}i(g_{1},h'))=\chi (\det (b))|\det (b)|^{m+\ell + \frac{1}{2}}\varphi _{f}((g^{\iota}_{1})^{-1}g_{2}). $$

Clearly, φ_f is bi- K_4ℓ invariant. Thus, to prove (2.6), it is enough to show that, for all h∈Sp_4ℓ(F),

$$ \varphi _{(1\otimes \xi )\ast f}(h)=\varphi _{(\eta ^{\chi}_{m,\ell}( \xi )\otimes 1)\ast f}(h). $$

(2.10)

By the Iwasawa decomposition in Sp_4m(F), with respect to Q_2(m−ℓ)(F), and (2.9), we have

$\varphi _{(1\otimes \xi )\ast f}(h)=(1\otimes \xi )\ast f(\gamma _{0}i((I_{4l}, \begin{pmatrix} I_{2(m-\ell )} \\ &h \\ &&I_{2(m-\ell )}\end{pmatrix} )))=$

$$ \int _{{\mathrm {GL}}_{2(m-\ell )}(F)\times {\mathrm {Sp}}_{4\ell}(F)} (\delta ^{- \frac{1}{2}}_{Q_{2(m-\ell )}}\cdot \xi ^{U_{2(m-\ell )}})( \begin{pmatrix} b \\ &x \\ &&b^{*}\end{pmatrix} )\chi (\det (b))\varphi _{f}(hx)dbdx= $$

(2.11)

$$ = \int _{{\mathrm {Sp}}_{4\ell}(F)}\eta ^{\chi}_{m,\ell}(\xi )(x)\varphi _{f}((hx)dx. $$

See (2.4). In the same way we have,

$\varphi _{(\eta ^{\chi}_{m,\ell}(\xi )\otimes 1)\ast f}(h)=(\eta ^{ \chi}_{m,\ell}(\xi )\otimes 1)\ast f(\gamma _{0}i((I_{4l}, \begin{pmatrix} I_{2(m-\ell )} \\ &h \\ &&I_{2(m-\ell )}\end{pmatrix} )))=$

$$ =\int _{{\mathrm {Sp}}_{4\ell}(F)}\eta ^{\chi}_{m,\ell}(\xi )(x)\varphi _{f}((x^{ \iota})^{-1}h)dx. $$

(2.12)

It is easy to see that for a bi-K_2r invariant function on Sp_2r(F), we have, for all g∈Sp_2r(F),

$$ \varphi (g)=\varphi (g^{-1})=\varphi (g^{\iota}). $$

Then the integral (2.12) becomes

$$ \int _{{\mathrm {Sp}}_{4\ell}(F)}\eta ^{\chi}_{m,\ell}(\xi )(x)\varphi _{f}((hx)dx, $$

which is the last integral in (2.11). This proves (2.10) and Theorem 2.2 is proved. □

Recall the Satake isomorphism

$$ \mathcal{H}({\mathrm {Sp}}_{4m}(F)// K_{4m})\cong {\mathbb{C}}[Z_{1}^{\pm 1},\ldots,Z_{2m}^{ \pm 1}]^{W_{{\mathrm {Sp}}_{4m}}}, $$

(2.13)

where $W_{{\mathrm {Sp}}_{4m}}$ is the Weyl group of Sp_4m. It is given as follows. Let, for $t\in T_{{\mathrm {Sp}}_{4m}}(F)$,

$$ \mathcal{S}(\xi )(t)=\delta _{B_{{\mathrm {Sp}}_{2m}}}^{-\frac{1}{2}}(t)\xi ^{U_{1^{2m}}}(t)= \delta _{B_{{\mathrm {Sp}}_{2m}}}^{-\frac{1}{2}}(t)\int _{U_{1^{2m}}(F)} \xi (ut)du. $$

(2.14)

This is the Satake transform of ξ. It defines an isomorphism

$$ \mathcal{H}({\mathrm {Sp}}_{4m}(F)// K_{4m})\cong \mathcal{H}(T_{{\mathrm {Sp}}_{4m}}(F)/ T_{ {\mathrm {Sp}}_{4m}}(\mathcal{O}))^{W_{{\mathrm {Sp}}_{4m}}}. $$

Let μ be an unramified character of $T_{{\mathrm {Sp}}_{4m}}(F)$,

$$ \mu ( \begin{pmatrix} t \\ &t^{*}\end{pmatrix} )=\mu _{1}(t_{1})\cdot \ldots \cdot \mu _{2m}(t_{2m}), \ t= \begin{pmatrix} t_{1} \\ &\ddots \\ &&t_{2m}\end{pmatrix} , $$

where μ₁,…,μ_2m are unramified characters of F^∗. Let f_μ be a spherical vector in the one dimensional subspace $({\mathrm {Ind}}_{B_{{\mathrm {Sp}}_{4m}}(F)}^{{\mathrm {Sp}}_{4m}(F)}\mu )^{K_{4m}}$. Then

$$ \xi \ast f_{\mu}=(\mathcal{S}(\xi ),\mu )f_{\mu}, $$

where

$$ (\mathcal{S}(\xi ),\mu )=\int _{T_{{\mathrm {Sp}}_{4m}}(F)}\mathcal{S}( \xi )(t)\mu (t)dt. $$

There is a unique element $\tilde{\mathcal{S}}(\xi )\in {\mathbb{C}}[Z_{1}^{\pm 1},\ldots,Z_{2m}^{\pm 1}]^{W_{ {\mathrm {Sp}}_{4m}}}$, such that

$$ (\mathcal{S}(\xi ),\mu )= \tilde{\mathcal{S}}(\xi )(\mu _{1}(p)^{\pm 1},\ldots, \mu _{2m}(p)^{\pm 1}), $$

(2.15)

where p=p_v is a generator of the maximal ideal of $\mathcal{O}$. The isomorphism (2.13) is given by $\xi \mapsto \tilde{\mathcal{S}}(\xi )$. It will be convenient to denote

$$ \tilde{\mathcal{S}}(\xi )(Z_{1}^{\pm 1},\ldots,Z_{2m}^{\pm 1})= \hat{\mathcal{S}}(\xi )(Z_{1},\ldots,Z_{2m}). $$

Note that (when m≥ℓ)

$\hat{\mathcal{S}}(\eta ^{\chi}_{m,\ell}(\xi ))(Z_{1},\ldots,Z_{2\ell})=$

$$ =\hat{\mathcal{S}}(\xi )(\chi (p)q^{-(m-\ell -\frac{1}{2})},\chi (p)q^{-(m- \ell -\frac{3}{2})},\ldots,\chi (p)q^{m-\ell -\frac{1}{2}},Z_{1},\ldots,Z_{2 \ell}). $$

(2.16)

We recall that in this section, we replaced the notation F_v by F. For the definition of the following function, we return to the notation F_v. We define the function $\xi _{m,\ell ,v}\in \mathcal{H}({\mathrm {Sp}}_{4m}(F_{v})// K_{4m,v})$ to be such that

$$ \hat{\mathcal{S}}(\xi _{m,\ell ,v})(Z_{1},\ldots,Z_{2m})=\prod _{i=1}^{2m}(Z_{i}- \chi (p_{v})q_{v}^{-m+\ell -\frac{1}{2}})(Z_{i}^{-1}-\chi (p_{v})q_{v}^{-m+ \ell -\frac{1}{2}}). $$

(2.17)

Convolving θ_Δ(τ,m+ℓ) with 1⊗ξ_m,ℓ,v will result in the rapid decrease stated in Theorem 1.3. By (2.16),

$$ \hat{\mathcal{S}}(\eta ^{\chi}_{m,\ell}(\xi _{m,\ell ,v}))(Z_{1},\ldots,Z_{2 \ell})=\alpha _{m,\ell ,v}\prod _{i=1}^{2\ell}(Z_{i}-\chi (p_{v})q_{v}^{-m+ \ell -\frac{1}{2}})(Z_{i}^{-1}-\chi (p_{v})q_{v}^{-m+\ell - \frac{1}{2}}), $$

(2.18)

where

$$ \alpha _{m,\ell ,v}=\prod _{j=1}^{2(m-\ell )}[(q_{v}^{-m+\ell +j- \frac{1}{2}}-q_{v}^{-m+\ell -\frac{1}{2}})(q_{v}^{m-\ell -j+ \frac{1}{2}}-\chi ^{2}(p_{v})q_{v}^{-m+\ell -\frac{1}{2}})]\neq 0. $$

(2.19)

When ℓ=m, we define α_m,m,v=1. The reason that α_m,ℓ,v is nonzero also for ℓ<m is that, for 1≤j≤2(m−ℓ), $q_{v}^{m-\ell -j+\frac{1}{2}}-\chi ^{2}(p_{v})q_{v}^{-m+\ell - \frac{1}{2}}\neq 0$. Otherwise, writing $|\chi (p_{v})|=q_{v}^{\alpha}$, we get that 2α=2(m−ℓ)−j+1, and hence $\frac{1}{2}\leq \alpha \leq m-\ell$. Recall that χ is obtained by considering our cuspidal representation τ at the finite place v, where τ_v is unramified and induced from the character χ⊗χ⁻¹ of $B_{{\mathrm {GL}}_{2}}(F_{v})$. In particular, we know that $-\frac{1}{2}<\alpha <\frac{1}{2}$, and so we get a contradiction.

3 The Fourier expansion of ((1⊗ξ _m,ℓ,v)∗θ _Δ(τ,m+ℓ)) along $i(U_{2\ell}^{4\ell}\times I_{4m})$

In this section, we write down the Fourier expansion of ((1⊗ξ_m,ℓ,v)∗θ_Δ(τ,m+ℓ)) along $i(U_{2\ell}^{4\ell}\times I_{4m})$. It turns out that convolving θ_Δ(τ,m+ℓ) with 1⊗ξ_m,ℓ,v annihilates Fourier coefficients which have a low rank in some sense. This will be needed in the proof of rapid decrease stated in Theorem 1.3.

The elements of the subgroup $i(U_{2\ell}^{4\ell}\times I_{4m})$ have the form

$$ i(u^{4\ell}_{2\ell}(x),I_{4m})= \begin{pmatrix} I_{2\ell}&0&x \\ &I_{4m}&0 \\ &&I_{2\ell}\end{pmatrix} ,\ \ u^{4\ell}_{2\ell}(x)= \begin{pmatrix} I_{2\ell}&x \\ &I_{2\ell}\end{pmatrix} ,\ {}^{t}(w_{2\ell}x)=w_{2\ell}x. $$

(3.1)

Denote by S_2ℓ(F) the subspace of matrices x∈M_2ℓ(F), such that w_2ℓx is symmetric. Fix a nontrivial character ψ of $F\backslash {\mathbb{A}}$. We start with the Fourier expansion of θ_Δ(τ,m+ℓ), along $i(U_{2\ell}^{4\ell}\times I_{4m})$, viewed, first, as a function of $b\in {\mathrm {Sp}}_{4(m+\ell )}({\mathbb{A}})$,

$$ \theta _{\Delta (\tau ,m+\ell )}(b)=\sum _{A\in S_{2\ell}(F)}\theta _{ \Delta (\tau ,m+\ell )}^{\psi _{A}}(b), $$

(3.2)

where

$$ \theta _{\Delta (\tau ,m+\ell )}^{\psi _{A}}(b)=\int _{S_{2 \ell}(F)\backslash S_{2\ell}({\mathbb{A}})}\theta _{\Delta (\tau ,m+\ell )}((u_{2 \ell}^{4\ell}(x),I_{4m})b)\psi ^{-1}(tr(Ax))dx. $$

We denote by ψ_A the character of $U^{4\ell}_{2\ell}({\mathbb{A}})$ given by $\psi _{A}(u^{4\ell}_{2\ell}(x))=\psi (tr(Ax))$. Consider the sum of the Fourier coefficients $\theta _{\Delta (\tau ,m+\ell )}^{\psi _{A}}$ over all A with rank c, 0≤c≤2ℓ. Consider the action of GL_2ℓ(F), γ⋅A=γ^∗Aγ⁻¹, γ∈GL_2ℓ(F), γ^∗=w_2ℓ^tγ⁻¹w_2ℓ. Then there is a diagonal matrix δ′=diag(δ_c,…,δ₁), δ_i∈F^∗, such that diag(δ′,0,…,0)w_2ℓ=γ^∗Aγ⁻¹ is in the orbit of A. In this case,

$\theta _{\Delta (\tau ,m+\ell )}^{\psi _{A}}(b)=$

$$ =\int _{S_{2\ell}(F)\backslash S_{2\ell}({\mathbb{A}})}\theta _{ \Delta (\tau ,m+\ell )}((u_{2\ell}^{4\ell}(x),I_{4m})b)\psi ^{-1}(tr( \begin{pmatrix} \delta ' \\ &0\end{pmatrix} w_{2\ell}\gamma x(\gamma ^{*})^{-1}))dx= $$

(3.3)

$$ =\int _{S_{2\ell}(F)\backslash S_{2\ell}({\mathbb{A}})}\theta _{ \Delta (\tau ,m+\ell )}((u_{2\ell}^{4\ell}(x)\hat{\gamma},I_{4m})b) \psi ^{-1}(tr( \begin{pmatrix} &w_{c}\delta \\ 0\end{pmatrix} x))dx, $$

where δ=w_cδ′w_c=diag(δ₁,…,δ_c). The stabilizer of diag(δ′,0,…,0)w_2ℓ inside GL_2ℓ(F) is

$$ P^{\delta}_{2\ell -c,c}(F)=\{ \begin{pmatrix} \gamma _{1}&\gamma _{2} \\ 0&\gamma _{4}\end{pmatrix} \in {\mathrm {GL}}_{2\ell}(F)\ |\ \gamma _{1}\in {\mathrm {GL}}_{2\ell -c}(F),\ \gamma _{4} \in {\mathrm {O}}_{c,\delta}(F) \}, $$

(3.4)

where O_c,δ denotes the F-orthogonal group in c variables corresponding to $\delta ^{w_{c}}=w_{c}\delta w_{c}$. Using (3.3), the expansion (3.2) becomes

$$ \theta _{\Delta (\tau ,m+\ell )}(b)=\sum _{c=0}^{2\ell}\sum _{[ \delta ]\in [T_{c}(F)]}\sum _{\gamma \in P^{\delta}_{2\ell -c,c}(F) \backslash {\mathrm {GL}}_{2\ell}(F)}\theta ^{\psi _{\delta}}_{\Delta (\tau ,m+ \ell )}((\hat{\gamma},I_{4m})b), $$

(3.5)

where

$\theta ^{\psi _{\delta}}_{\Delta (\tau ,m+\ell )}(b)=$

$$ =\int _{S_{2\ell}(F)\backslash S_{2\ell}({\mathbb{A}})}\theta _{ \Delta (\tau ,m+\ell )}( \begin{pmatrix} I_{2\ell -c}&0&0&x_{1}&x_{2} \\ &I_{c}&0&x_{3}&x'_{1} \\ &&I_{4m}&0&0 \\ &&&I_{c}&0 \\ &&&&I_{2\ell -c}\end{pmatrix} b)\psi ^{-1}(tr(w_{c}\delta x_{3}))dx. $$

(3.6)

In (3.5), [δ] varies over the equivalence classes of c×c diagonal, invertible matrices (over F), representing quadratic forms $\delta _{1}x_{1}^{2}+\cdots +\delta _{c}x_{c}^{2}$. We re-denote, for short, by ψ_δ, the character of $U_{2\ell}^{4\ell}({\mathbb{A}})$, which we denoted before by $\psi _{diag(w_{c}\delta w_{c},0,\ldots,0)w_{2\ell}}$. For fixed b, consider the smooth function on the compact abelian group

$M_{(2\ell -c)\times 4m}(F)\backslash M_{(2\ell -c)\times 4m}({\mathbb{A}})$, $\theta ^{\psi _{\delta}}_{\Delta (\tau ,m+\ell )}(b)(y)=$

$$ =\int _{S_{2\ell}(F)\backslash S_{2\ell}({\mathbb{A}})}\theta _{ \Delta (\tau ,m+\ell )}( \begin{pmatrix} I_{2\ell -c}&0&y&x_{1}&x_{2} \\ &I_{c}&0&x_{3}&x'_{1} \\ &&I_{4m}&0&y' \\ &&&I_{c}&0 \\ &&&&I_{2\ell -c}\end{pmatrix} b)\psi ^{-1}(tr(w_{c}\delta x_{3}))dx, $$

and write its Fourier expansion at y=0. Then

$$ \theta ^{\psi _{\delta}}_{\Delta (\tau ,m+\ell )}(b)=\sum _{B\in M_{4m \times (2\ell -c)}(F)}\theta ^{\psi _{\delta ,B}}_{\Delta (\tau ,m+ \ell )}(b), $$

(3.7)

where

$$ \theta ^{\psi _{\delta ,B}}_{\Delta (\tau ,m+\ell )}(b)=\int _{M_{(2 \ell -c)\times 4m}(F)\backslash M_{(2\ell -c)\times 4m}({\mathbb{A}})}\theta ^{ \psi _{\delta}}_{\Delta (\tau ,m+\ell )}(b)(y)\psi ^{-1}(tr(yB))dy. $$

(3.8)

Proposition 3.1

Assume that 0≤c<2ℓ and that $\theta ^{\psi _{\delta ,B}}_{\Delta (\tau ,m+\ell )}$ is nontrivial. Then the column space of B is a totally isotropic subspace of F^4m with respect to the synplectic form corresponding to J_4m.

Proof

Consider the smooth function on the compact abelian group $M_{(2\ell -c)\times c}(F)\backslash M_{(2\ell -c)\times c}({\mathbb{A}})$,

$$ \theta ^{\psi _{\delta ,B}}_{\Delta (\tau ,m+\ell )}(b)(z)=\theta ^{ \psi _{\delta ,B}}_{\Delta (\tau ,m+\ell )}(( \widehat{\begin{pmatrix}I_{2\ell -c}&z\\&I_{c}\end{pmatrix}},I_{4m})b). $$

We write its Fourier expansion at z=0,

$$ \theta ^{\psi _{\delta ,B}}_{\Delta (\tau ,m+\ell )}(b)=\sum _{D\in M_{c \times (2\ell -c)}(F)}\theta ^{\psi _{\delta ,B,D}}_{\Delta (\tau ,m+ \ell )}(b), $$

(3.9)

where

$$ \theta ^{\psi _{\delta ,B,D}}_{\Delta (\tau ,m+\ell )}(b)=\int _{M_{(2\ell -c)\times c}(F)\backslash M_{(2\ell -c)\times c}( {\mathbb{A}})}\theta ^{\psi _{\delta ,B}}_{\Delta (\tau ,m+\ell )}(b)(z)\psi ^{-1}(tr(zD))dz. $$

(3.10)

By our assumption, for the given B, one of the Fourier coefficients (3.10) is nontrivial. Then there is D∈M_{c×(2ℓ−c)}(F), such that the following Fourier coefficient, being an inner integral of (3.10), is nontrivial, for some automorphic form $\theta '_{\Delta (\tau ,m+\ell )}$ in the space of Θ_Δ(τ,m+ℓ),

$$ \int \theta '_{\Delta (\tau ,m+\ell )}( \begin{pmatrix} I_{2\ell -c}&e&t \\ &I_{4m+2c}&e' \\ &&I_{2\ell -c}\end{pmatrix} )\psi ^{-1}(tr(e \begin{pmatrix} D \\ B \\ 0\end{pmatrix} ))d(e,t)\neq 0, $$

(3.11)

where the integration is over $U^{4(m+\ell )}_{2\ell -c}(F)\backslash U^{4(m+\ell )}_{2\ell -c}( {\mathbb{A}})$. Consider the right action of GL_2ℓ−c(F)×Sp_4m+2c(F) on M_{(4m+2c)×(2ℓ−c)}(F), given by L⋅(α,β)=β⁻¹Lα. See Lemma 9.1 in [GS212] for representatives of this action. Exactly as in the proof of Prop. 9.2 in [GS212], using Prop. 1.8, we see that the GL_2ℓ−c(F)×Sp_4m+2c(F)-orbit of $\begin{pmatrix} D \\ B \\ 0\end{pmatrix}$ contains a matrix of the form

$$ \begin{pmatrix} I_{\ell _{1}}&0 \\ 0&0\end{pmatrix} ,\ \ \ell _{1}\leq 2\ell -c. $$

Thus, the column space of $\begin{pmatrix} D \\ B \\ 0\end{pmatrix}$ is a totally isotropic subspace of F^4m+2c of dimension ℓ₁. This implies that the column space of B is a totally isotropic subspace of F^4m of dimension rank(B)≤ℓ₁. □

Theorem 3.2

Assume that 0≤c<2ℓ, that the column space of B is totally isotropic and rank(B)<2ℓ−c. Then, for all $(g,h)\in {\mathrm {Sp}}_{4\ell}({\mathbb{A}})\times {\mathrm {Sp}}_{4m}({\mathbb{A}})$,

$$ (1\otimes \xi _{m,\ell ,v})\ast \theta ^{\psi _{\delta ,B}}_{\Delta ( \tau ,m+\ell )}(g,h)=0. $$

Proof

We start the proof with arbitrary θ_Δ(τ,m+ℓ), and later apply the convolution by 1⊗ξ_m,ℓ,v. Assume that rank(B)=k<2ℓ−c. By the last proposition, we may write

$$ B=\beta ^{-1} \begin{pmatrix} 0&I_{k} \\ 0&0\end{pmatrix} _{4m\times (2\ell -c)}\cdot \alpha , $$

where $(\alpha ,\beta )\in (P_{2\ell -c-k,k}(F)\times _{d} Q^{4m}_{k}(F)) \backslash (GL_{2\ell -c}(F)\times {\mathrm {Sp}}_{4m}(F))$, and $P_{2\ell -c-k,k}(F)\times _{d} Q^{4m}_{k}(F)$ denotes the subgroup of $P_{2\ell -c-k,k}(F)\times Q^{4m}_{k}(F)$, consisting of the elements

$$ ( \begin{pmatrix} \alpha _{1}&\ast \\ 0&\alpha _{2}\end{pmatrix} , \begin{pmatrix} \alpha _{2}&\ast &\ast \\ &\beta _{2}&\ast \\ &&\alpha _{2}^{*}\end{pmatrix} ),\ \ \alpha _{1}\in {\mathrm {GL}}_{2\ell -c-k}(F), \alpha _{2}\in {\mathrm {GL}}_{k}(F), \beta _{2}\in {\mathrm {Sp}}_{4m-2k}(F). $$

Then, for $b\in {\mathrm {Sp}}_{4(m+\ell )}({\mathbb{A}})$,

$\theta ^{\psi _{\delta ,B}}_{\Delta (\tau ,m+\ell )}(b)=$

$$ =\int \theta _{\Delta (\tau ,m+\ell )}( \begin{pmatrix} I_{2\ell -c}&0&y&x_{1}&x_{2} \\ &I_{c}&0&x_{3}&x'_{1} \\ &&I_{4m}&0&y' \\ &&&I_{c}&0 \\ &&&&I_{2\ell -c}\end{pmatrix} ((\hat{\alpha},\beta )b) $$

(3.12)

$$ \psi ^{-1}(tr(w_{c}\delta x_{3})+tr( \begin{pmatrix} 0&I_{k} \\ 0&0\end{pmatrix} y))dydx:=\theta ^{\psi _{\delta ,k}}_{\Delta (\tau ,m+\ell )}(( \hat{\alpha},\beta )b). $$

Next, we write the Fourier expansion of the function on $M_{k\times c}(F)\backslash M_{k\times c}({\mathbb{A}})$,

$$ t\mapsto \theta ^{\psi _{\delta ,k}}_{\Delta (\tau ,m+\ell )}( \widehat{\begin{pmatrix}I_{2\ell -c-k}\\&I_{k}&t\\&&I_{c}\end{pmatrix}}b), $$

at t=0,

$\theta ^{\psi _{\delta ,k}}_{\Delta (\tau ,m+\ell )}(b)=$

$$ =\sum _{e\in M_{c\times k}(F)}\int _{M_{k\times c}(F)\backslash M_{k \times c}({\mathbb{A}})}\theta ^{\psi _{\delta ,k}}_{\Delta (\tau ,m+\ell )}( \widehat{\begin{pmatrix}I_{2\ell -c-k}\\&I_{k}&t\\&&I_{c}\end{pmatrix}}b) \psi ^{-1}(tr(te))dt. $$

(3.13)

The summand in (3.13), corresponding to e, is, using (3.12), equal to

$$ \int \theta _{\Delta (\tau ,m+\ell )}( \begin{pmatrix} I_{2\ell -c-k}&0&0&y_{1}&y_{2}&y_{3}&x_{1}&x_{2}&x_{3} \\ &I_{k}&t&y_{4}&y_{5}&y_{6}&x_{4}&x_{5}&x'_{2} \\ &&I_{c}&0&0&0&x_{6}&x_{4}'&x_{1}' \\ &&&I_{k}&0&0&0&y'_{6}&y'_{3} \\ &&&&I_{4m-2k}&0&0&y'_{3}&y'_{2} \\ &&&&&I_{k}&0&y'_{4}&y'_{1} \\ &&&&&&I_{c}&t'&0 \\ &&&&&&&I_{k}&0 \\ &&&&&&&&I_{2\ell -c-k}\end{pmatrix} \hat{v_{1}}(e)b) $$

(3.14)

$$ \psi ^{-1}(tr(w_{c}\delta x_{6})+tr(y_{4}))d(x,y,t):=\theta ^{\psi _{ \delta ,k,0}}_{\Delta (\tau ,m+\ell )}(\hat{v_{1}}(e)b), $$

where $v_{1}(e)= \begin{pmatrix} I_{2\ell -c} \\ &I_{c}&-e \\ &&I_{k}\end{pmatrix}$. By Prop. 1.8, the unique maximal nilpotent orbit, attached to Fourier coefficients supported by Θ_Δ(τ,m+ℓ), corresponds to the partition (2^2(m+ℓ)). From this, it follows that $\theta ^{\psi _{\delta ,k,0}}_{\Delta (\tau ,m+\ell )}(b)$ is left invariant to $\hat{v}_{2}(u)$, where $v_{2}(u)= \begin{pmatrix} I_{2\ell -c-k}&0&u \\ &I_{k}&0 \\ &&I_{c}\end{pmatrix}$, $u\in M_{(2\ell -c-k)\times c}({\mathbb{A}})$. The reason is that in the Fourier expansion of $\theta ^{\psi _{\delta ,k,0}}_{\Delta (\tau ,m+\ell )}$ along the subgroup of the elements $\hat{v}_{2}(u)$, $u\in M_{(2\ell -c-k)\times c}(F)\backslash M_{(2\ell -c-k)\times c}( {\mathbb{A}})$, only the trivial character contributes. The Fourier coefficients with respect to nontrivial characters of $M_{(2\ell -c-k)\times c}(F)\backslash M_{(2\ell -c-k)\times c}({\mathbb{A}})$ give rise to Fourier coefficients on Θ_Δ(τ,m+ℓ) which correspond to a symplectic partition of 4(m+ℓ) which is strictly larger than (2^2(m+ℓ)). We omit the details here. We have used this argument many times before. See, for example, Theorems 8.2, 9.5 in [GS212], where we carry out similar proofs in full detail. We conclude that

$\theta ^{\psi _{\delta ,k,0}}_{\Delta (\tau ,m+\ell )}(b)=$

$$ \int \theta _{\Delta (\tau ,m+\ell )}( \begin{pmatrix} I_{2\ell -c-k}&0&u&y_{1}&y_{2}&y_{3}&x_{1}&x_{2}&x_{3} \\ &I_{k}&t&y_{4}&y_{5}&y_{6}&x_{4}&x_{5}&x'_{2} \\ &&I_{c}&0&0&0&x_{6}&x_{4}'&x_{1}' \\ &&&I_{k}&0&0&0&y'_{6}&y'_{3} \\ &&&&I_{4m-2k}&0&0&y'_{3}&y'_{2} \\ &&&&&I_{k}&0&y'_{4}&y'_{1} \\ &&&&&&I_{c}&t'&u' \\ &&&&&&&I_{k}&0 \\ &&&&&&&&I_{2\ell -c-k}\end{pmatrix} b) $$

(3.15)

$$ \psi ^{-1}(tr(w_{c}\delta x_{6})+tr(y_{4}))d(x,y,t,u). $$

(We take the measure of $F\backslash {\mathbb{A}}$ to be 1.) Apply a conjugation inside θ_Δ(τ,m+ℓ), in (3.15), by $\hat{\omega}= \widehat{\begin{pmatrix}I_{2\ell -c}\\&&I_{k}\\&I_{c}\end{pmatrix}}$. Then (3.15) becomes

$\theta ^{\psi _{\delta ,k,0}}_{\Delta (\tau ,m+\ell )}(b)=$

$$ \int \theta _{\Delta (\tau ,m+\ell )}( \begin{pmatrix} I_{2\ell -c}&y&x \\ &I_{4m+2c}&y' \\ &&I_{2\ell -c}\end{pmatrix} \begin{pmatrix} I_{2\ell -c+k} \\ &I_{c}&0&z \\ &&I_{4m-2k}&0 \\ &&&I_{c} \\ &&&&I_{2\ell -c+k}\end{pmatrix} \hat{\omega}b) $$

(3.16)

$$ \psi ^{-1}(tr(w_{c}\delta z)+tr(y \begin{pmatrix} 0&I_{k} \\ 0&0\end{pmatrix} _{(4m+2c)\times (2\ell -c)})d(x,y,z). $$

Repeating the last argument, several more times, using Prop. 1.8, it follows that the function

$$ b\mapsto \int \theta _{\Delta (\tau ,m+\ell )}( \begin{pmatrix} I_{2\ell -c}&y&x \\ &I_{4m+2c}&y' \\ &&I_{2\ell -c}\end{pmatrix} b) \psi ^{-1}(tr(y \begin{pmatrix} 0&I_{k} \\ 0&0\end{pmatrix} )d(x,y) $$

is invariant to left translations by the elements of the following subgroups. First, it is invariant to left translations by

$$ diag(I_{2\ell -c}, \begin{pmatrix} I_{k}&0&u_{2} \\ &I_{4m-2k+2c}&0 \\ &&I_{k}\end{pmatrix} ,I_{2\ell -c}), \ \ u_{2}\in S_{k}({\mathbb{A}}). $$

Then it is invariant to left translations by $(diag(I_{2\ell -c}, U^{4m+2c}_{k}({\mathbb{A}}),I_{2\ell -c})$, and, finally, it is also invariant to left translations by $\widehat{\begin{pmatrix}I_{2\ell -c-k}&v\\&I_{k}\end{pmatrix}}$, $v\in M_{(2\ell -c-k)\times k}({\mathbb{A}})$. Again, at each time, it follows that in the Fourier expansion along the corresponding subgroup, only the trivial character contributes. Going back to (3.12), we conclude that

$\theta ^{\psi _{\delta ,B}}_{\Delta (\tau ,m+\ell )}(g,h)=$

$$ \sum _{e\in M_{c\times k}(F)}\int \theta ^{U^{4(m+\ell )}_{2\ell -c+k}}_{ \Delta (\tau ,m+\ell )}( \begin{pmatrix} I_{2\ell -c-k}&a_{1}&a_{2} \\ &I_{k}&a_{3} \\ &&I_{k} \\ &&&I_{c}&0&z \\ &&&&I_{4m-2k}&0 \\ &&&&&I_{c} \\ &&&&&&I_{k}&a'_{3}&a'_{2} \\ &&&&&&&I_{k}&a'_{1} \\ &&&&&&&&I_{2\ell -c-k}\end{pmatrix} \cdot $$

(3.17)

$$ \widehat{\omega v_{1}(e)}(\hat{\alpha}g,\beta h))\psi ^{-1}(tr(w_{c} \delta z)+tr(a_{3}))d(a_{1},a_{2},a_{3},z). $$

All integrations are over variables in $F\backslash {\mathbb{A}}$. Recall that $U^{4(m+\ell )}_{2\ell -c+k}$ is the unipotent radical

$$ \left \{ \begin{pmatrix} I_{2\ell -c+k}&y&x \\ &I_{4m+2c-2k}&y' \\ &&I_{2\ell -c+k}\end{pmatrix} \in {\mathrm {Sp}}_{4(m+\ell )}\right \}. $$

Note that since τ is cuspidal on ${\mathrm {GL}}_{2}({\mathbb{A}})$, for the constant term $\theta ^{U^{4(m+\ell )}_{2\ell -c+k}}_{\Delta (\tau ,m+\ell )}$ to be nontrivial, 2ℓ−c+k must be even, and hence c+k must be even. By Prop. 1.7, the constant term $\theta _{\Delta (\tau ,m+\ell )}\mapsto \theta ^{U^{4(m+\ell )}_{2 \ell -c+k}}_{\Delta (\tau ,m+\ell )}$ projects Θ_Δ(τ,m+ℓ) into

$$ {\mathrm {Ind}}_{Q_{2\ell -c+k}({\mathbb{A}})}^{{\mathrm {Sp}}_{4(m+\ell )}({\mathbb{A}})}(\Delta (\tau , \ell +\frac{k-c}{2})||det\cdot |^{-m-\frac{\ell}{2}+\frac{k-c}{4}} \otimes \Theta _{\Delta (\tau ,m+\frac{c-k}{2})}). $$

In (3.17), we further take the constant term of $\Delta (\tau ,\ell +\frac{k-c}{2})$ along V_{2ℓ−c−k,2k}, followed by the Fourier coefficient with respect to the subgroup of elements $\begin{pmatrix} I_{2\ell -c-k} \\ &I_{k}&a_{3} \\ &&I_{k}\end{pmatrix}$ and the character ψ(tr(a₃)). This projects $\Delta (\tau ,\ell +\frac{k-c}{2})$ into

$$ {\mathrm {Ind}}_{P_{2\ell -c-k,2k}({\mathbb{A}})}^{{\mathrm {GL}}_{2\ell -c+k}({\mathbb{A}})}(\Delta ( \tau ,\ell -\frac{c+k}{2})|\det \cdot |^{-\frac{k}{2}}\otimes \Delta _{ \psi}(\tau ,k)|\det \cdot |^{\frac{2\ell -c-k}{4}}), $$

where Δ_ψ(τ,k) denotes the representation by right translations of ${\mathrm {GL}}_{2k}({\mathbb{A}})$ in the space of functions,

$$ x\mapsto \int _{M_{k}(F)\backslash M_{k}({\mathbb{A}})}\varphi ( \begin{pmatrix} I_{k}&a \\ &I_{k}\end{pmatrix} x)\psi ^{-1}(tr(a))da, \ \ \varphi \in \Delta (\tau ,k). $$

Denote by $\Theta ^{\psi _{\delta}}_{\Delta (\tau ,m+\frac{c-k}{2})}$ the representation by right translations of ${\mathrm {Sp}}_{4m+2c-2k}({\mathbb{A}})$ in the space of functions

$$ y\mapsto \int _{S_{c}(F)\backslash S_{c}({\mathbb{A}})}\theta _{\Delta (\tau ,m+ \frac{c-k}{2})}( \begin{pmatrix} I_{c}&0&z \\ &I_{4m-2k}&0 \\ &&I_{c}\end{pmatrix} y)\psi ^{-1}(tr(w_{c}\delta z))dz. $$

We identify here Sp_4m+2c−2k as the subgroup diag(I_2ℓ−c+k,Sp_4m+2c−2k,I_2ℓ−c+k) of Sp_4(m+ℓ. Then the integral in (3.17) projects Θ_Δ(τ,m+ℓ) into

$$ {\mathrm {Ind}}_{Q_{2\ell -c-k,2k}({\mathbb{A}})}^{{\mathrm {Sp}}_{4(m+\ell )}({\mathbb{A}})}(\Delta ( \tau ,\ell -\frac{c+k}{2})||det\cdot |^{-m-\frac{\ell}{2}- \frac{c+k}{4}}\otimes \Delta _{\psi}(\tau ,k)|\det \cdot |^{-m- \frac{c}{2}}\otimes \Theta ^{\psi _{\delta}}_{\Delta (\tau ,m+ \frac{c-k}{2})}). $$

(3.18)

Let f be a function in the space of (3.18). Denote, for $g\in {\mathrm {Sp}}_{4\ell}({\mathbb{A}})$, and fixed e₀∈M_c×k(F), $h_{0}\in {\mathrm {Sp}}_{4m}({\mathbb{A}})$,

$$ f_{e_{0},h_{0}}(g)=f(\hat{\omega}\widehat{ v_{1}(e_{0})}i(g,h_{0})). $$

(3.19)

Then by a simple check, we find that for $u\in U^{4\ell}_{2\ell -c-k}({\mathbb{A}})$ and $a\in {\mathrm {GL}}_{2\ell -c-k}({\mathbb{A}})$,

$$ f_{e_{0},h_{0}}(u \begin{pmatrix} a \\ &I_{2(c+k)} \\ &&a^{*}\end{pmatrix} g)=|\det (a)|^{m+\frac{\ell +1}{2}+\frac{c+k}{4}}\Delta (\tau ,\ell - \frac{c+k}{2})(a)f_{e_{0},h_{0}}(g). $$

(3.20)

Let f_v be a right K_4ℓ,v×K_4m,v-invariant function in the space of the v-component of (3.18). For a fixed h₀∈Sp_4m(F_v), consider the function on Sp_4ℓ(F_v), $f_{e_{0},h_{0},v}$ which is the local analog at v of (3.19), and convolve it with $\eta _{m,\ell}^{\chi}(\xi _{m,\ell ,v})$:

$$ \eta _{m,\ell}^{\chi}(\xi _{m,\ell ,v})\ast f_{e_{0},h_{0},v} (g_{0})= \int _{{\mathrm {Sp}}_{4\ell}(F_{v})} \eta _{m,\ell}^{\chi}(\xi _{m, \ell ,v})(g)f_{e_{0},h_{0},v}(g_{0}g)dg. $$

We will show that

$$ \eta _{m,\ell}^{\chi}(\xi _{m,\ell ,v})\ast f_{e_{0},h_{0},v}=0. $$

(3.21)

The proof of Theorem 3.2 will follow from (3.21). Indeed, we have, by Theorem 2.2,

$$ (1\otimes \xi _{m,\ell ,v})\ast \theta _{\Delta (\tau ,m+\ell )}^{ \delta ,B}=(\eta _{m,\ell}^{\chi}(\xi _{m,\ell ,v})\otimes 1)\ast \theta _{\Delta (\tau ,m+\ell )}^{\delta ,B} $$

(3.22)

Now, use (3.17), where we explained that the integral there projects Θ_Δ(τ,m+ℓ) into (3.18). Looking again at (3.17), we see that we need to prove that, for f in the space of (3.18), we have

$$ (\eta _{m,\ell}^{\chi}(\xi _{m,\ell ,v})\otimes 1)\ast f ( \hat{\omega}\widehat{ v_{1}(e_{0})}i(g,h_{0}))=0. $$

(3.23)

For this, using the definition (3.19), it is enough to prove (3.21), and then, by (3.22), we will achieve the proof of Theorem 3.2. Thus, let us prove (3.21).

Let $\Delta (\tau _{v}, \ell -\frac{c+k}{2})$ denote the local factor at v of $\Delta (\tau , \ell -\frac{c+k}{2})$. By our assumption on v, this representation is unramified. As in the proof of Lemma 2.1, it is the unramified component of the representation ${\mathrm {Ind}}_{P_{(\ell -\frac{c+k}{2})^{2}}(F_{v})}^{{\mathrm {GL}}_{2\ell -c-k}(F_{v})}( \chi \circ \det \otimes \chi ^{-1}\circ \det )$. Thus, the factor at v of (3.18) is the unramified component of the representation obtained by replacing in (3.18), at the place v, $\Delta (\tau _{v}, \ell -\frac{c+k}{2})|\det \cdot |^{-m- \frac{\ell}{2}-\frac{c+k}{4}}$ by

$$ {\mathrm {Ind}}_{P_{(\ell -\frac{c+k}{2})^{2}}(F_{v})}^{{\mathrm {GL}}_{2\ell -c-k}(F_{v})}(( \chi \circ \det ) |\det \cdot |^{-m-\frac{\ell}{2}-\frac{c+k}{4}} \otimes (\chi ^{-1}\circ \det ) |\det \cdot |^{-m-\frac{\ell}{2}- \frac{c+k}{4}}. $$

Thus, consider right K_4ℓ,v-invariant functions φ_v on Sp_4ℓ(F_v), which satisfy the local analog of (3.20), with $\Delta (\tau _{v}, \ell -\frac{c+k}{2})|\det \cdot |^{-m-\ell - \frac{c+k}{2}}$ replaced by the last representation. Then (3.20) is replaced by

$\varphi _{v}(u \begin{pmatrix} a_{1} \\ &a_{2} \\ &&I_{2(c+k)} \\ &&&a_{2}^{*} \\ &&&&a_{1}^{*}\end{pmatrix} g)=$

$$ =\chi (\det (a_{1}a^{-1}_{2}))|\det (a_{1})|^{m+\ell +\frac{1}{2}}| \det (a_{2})|^{m+\frac{c+k+1}{2}}\varphi _{v}(g), $$

(3.24)

for $u\in U^{4\ell}_{(\ell -\frac{c+k}{2})^{2}}(F_{v})$, $a_{1}, a_{2}\in {\mathrm {GL}}_{\ell -\frac{c+k}{2}}(F_{v})$. Note again, that for this calculation, we identify Sp_4ℓ as a subgroup of Sp_4(m+ℓ) via g↦i(g,I_4m), as we do in (3.19). In order to show (3.21), it is enough to show that for all φ_v, as above, satisfying (3.24),

$$ \eta _{m,\ell}^{\chi}(\xi _{m,\ell ,v})\ast \varphi _{v}(g_{0})=0,\ \ \ g_{0}\in {\mathrm {Sp}}_{4\ell}(F_{v}). $$

(3.25)

Recall that

$$ \eta _{m,\ell}^{\chi}(\xi _{m,\ell ,v})\ast \varphi _{v}(g_{0})=\int _{ {\mathrm {Sp}}_{4\ell}(F_{v})}\eta _{m,\ell}^{\chi}(\xi _{m,\ell ,v})(x) \varphi _{v}(g_{0}x)dx. $$

(3.26)

Denote, for short, $\eta _{m,\ell}^{\chi}(\xi _{m,\ell ,v})=\eta _{\xi _{v}}$. Writing the Iwasawa decomposition for g₀, with respect to $Q^{4\ell}_{(\ell -\frac{c+k}{2})^{2}}(F_{v})$, using that $\eta _{\xi _{v}}$ is left K_4ℓ,v invariant and changing variable in (3.26), we may assume that g₀ lies in the Levi part of $Q^{4\ell}_{(\ell -\frac{c+k}{2})^{2}}(F_{v})$. By (3.24), we may further assume that $g_{0}=diag (I_{\ell -c-k},b_{0},I_{\ell -c-k}):=\tilde{b}_{0}$, b₀∈Sp_2(c+k)(F_v). Now, write the dx-integration in (3.26) according to the Iwasawa decomposition with respect to $Q^{4\ell}_{(\ell -\frac{c+k}{2})^{2}}(F_{v})$. Using (3.24) and that $\eta _{\xi _{v}}$ is also right K_4ℓ,v invariant, (3.26) becomes

$\eta _{\xi _{v}}\ast \varphi _{v}(\tilde{b}_{0})=$

$$ =\int \eta _{\xi _{v}}^{U_{(\ell -\frac{c+k}{2})^{2}}}( \begin{pmatrix} a_{1} \\ &a_{2} \\ &&b \\ &&&a_{2}^{*} \\ &&&&a_{1}^{*}\end{pmatrix} )\chi (\det (a_{1}a^{-1}_{2}))|\det (a_{1})|^{m-2\ell - \frac{c+k+1}{2}} $$

(3.27)

$$ |\det (a_{2})|^{m-\ell -c-k-\frac{1}{2}}\varphi _{v}(\tilde{b}_{0} \tilde{b})da_{1}da_{2}db, $$

where the integration is over $a_{1}, a_{2}\in {\mathrm {GL}}_{\ell -\frac{c+k}{2}}(F_{v})$, b∈Sp_2(c+k)(F_v). Consider the inner da₁da₂-integration in (3.27). We claim that, for all 0≤k<2ℓ−c and all b∈Sp_2(c+k)(F_v),

$$ \int \eta _{\xi _{v}}^{U_{(\ell -\frac{c+k}{2})^{2}}}( \begin{pmatrix} a_{1} \\ &a_{2} \\ &&b \\ &&&a_{2}^{*} \\ &&&&a_{1}^{*}\end{pmatrix} )\chi (\det (a_{1}a^{-1}_{2}))|\det (a_{1})|^{m-2\ell - \frac{c+k+1}{2}} $$

(3.28)

$$ |\det (a_{2})|^{m-\ell -c-k-\frac{1}{2}}da_{1}da_{2}=0. $$

Using the Iwasawa decomposition in ${\mathrm {GL}}_{\ell -\frac{c+k}{2}}(F_{v})\times {\mathrm {GL}}_{\ell -\frac{c+k}{2}}(F_{v})$, the l.h.s. of (3.28) is equal to

$$\begin{aligned} \varphi _{\xi _{v}}(b)={}& \int \delta ^{-\frac{1}{2}}_{Q^{4\ell}_{1^{2 \ell -c-k}}}\eta _{\xi _{v}}^{U_{1^{2\ell -c-k}}}( \begin{pmatrix} t_{1} \\ &t_{2} \\ &&b \\ &&&t_{2}^{*} \\ &&&&t_{1}^{*}\end{pmatrix} )\\ &{}\times\chi (\det (t_{1}t^{-1}_{2}))|\det (t_{1}t_{2})|^{m-\frac{\ell}{2}- \frac{c+k}{4}} \end{aligned}$$

(3.29)

$$ \delta ^{-\frac{1}{2}}_{B_{{\mathrm {GL}}_{\ell -\frac{c+k}{2}}}}(t_{1}t_{2})dt_{1}dt_{2}. $$

Here, t₁, t₂ are integrated over $T_{\ell -\frac{c+k}{2}}(F_{v})$. The function $\varphi _{\xi _{v}}$ lies in $\mathcal{H}({\mathrm {Sp}}_{2(c+k)}(F_{v})/ / K_{2(c+k),v})$. It is enough to show that $\hat{\mathcal{S}}(\varphi _{\xi _{v}})=0$, that is the polynomial $\hat{\mathcal{S}}(\varphi _{\xi _{v}})(Z_{1},\ldots, Z_{c+k})\in {\mathbb{C}}[Z_{1}^{ \pm 1},\ldots,Z_{c+k}^{\pm 1}]^{W_{{\mathrm {Sp}}_{4(c+k)}}}$ is the zero polynomial. By (3.29) and (2.15), we have

$\hat{\mathcal{S}}(\varphi _{\xi _{v}})(Z_{1},\ldots,Z_{c+k})=$

$$ =\hat{\mathcal{S}}(\eta ^{\chi}_{m,\ell}(\xi _{m,\ell ,v}))(\chi (p_{v})q_{v}^{-m+ \ell -\frac{1}{2}},\chi (p_{v})q_{v}^{-m+\ell -\frac{3}{2}},\ldots,\chi (p_{v})q_{v}^{-m+ \frac{c+k+1}{2}}, $$

(3.30)

$$ \chi ^{-1}(p_{v})q_{v}^{-m+\ell -\frac{1}{2}},\chi ^{-1}(p_{v})q_{v}^{-m+ \ell -\frac{3}{2}},\ldots,\chi ^{-1}(p_{v})q_{v}^{-m+\frac{c+k+1}{2}},Z_{1},\ldots,Z_{c+k})=0. $$

The last equality follows from (2.18) since 2ℓ>c+k and one of the substitutions in the last polynomial is $\chi (p_{v})q_{v}^{-m+\ell -\frac{1}{2}}$. This completes the proof of Theorem 3.2. □

Going back to (3.7), Prop. 3.1 and Theorem 3.2 tell us that only the GL_2ℓ−c(F_v)×Sp_4m(F_v) – orbit of $B_{2\ell -c}= \begin{pmatrix} I_{2\ell -c} \\ 0\end{pmatrix}$ contributes to the expansion (3.7) of $(1\otimes \xi _{m,\ell ,v})\ast \theta ^{\psi _{\delta}}_{\Delta ( \tau ,m+\ell )}$. Thus,

$$ (1\otimes \xi _{m,\ell ,v})\ast \theta ^{\psi _{\delta}}_{\Delta ( \tau ,m+\ell )}(g,h)=\sum _{\beta \in Q'_{2\ell -c}(F)\backslash {\mathrm {Sp}}_{4m}(F)}(1 \otimes \xi _{m,\ell ,v})\ast \theta ^{\psi _{\delta},B_{2\ell -c}}_{ \Delta (\tau ,m+\ell )}(g,\beta h). $$

(3.31)

Here, $Q'_{2\ell -c}(F)$ is the subgroup of matrices in Sp_4m(F) of the form $\begin{pmatrix} I_{2\ell -c}&\ast &\ast \\ &b&\ast \\ &&I_{2\ell -c}\end{pmatrix}$, b∈Sp_{4(m−ℓ)+2c}(F). By (3.17),

$(1\otimes \xi _{m,\ell ,v})\ast \theta ^{\psi _{\delta ,B_{2\ell -c}}}_{ \Delta (\tau ,m+\ell )}(g,h)=$

$$\begin{aligned} &\sum _{e\in M_{c\times (2\ell -c)}(F)}\int (1\otimes \xi _{m,\ell ,v})\\ &\quad {}\ast \theta ^{U_{2(2\ell -c)}}_{\Delta (\tau ,m+\ell )}( \begin{pmatrix} I_{2\ell -c}&a \\ &I_{2\ell -c} \\ &&I_{c}&0&z \\ &&&I_{4(m-\ell )+2c}&0 \\ &&&&I_{c} \\ &&&&&I_{2\ell -c}&a' \\ &&&&&&I_{2\ell -c}\end{pmatrix} \cdot \end{aligned}$$

(3.32)

$$ \widehat{\omega v_{1}(e)}(g,h))\psi ^{-1}(tr(w_{c}\delta z)+tr(a))dadz. $$

Note the case where c=0, i.e. δ=0. We will need it later. Then $(1\otimes \xi _{m,\ell ,v})\ast \theta ^{\psi _{0}}_{\Delta (\tau ,m+ \ell )}$ is the constant term of (1⊗ξ_m,ℓ,v)∗θ_Δ(τ,m+ℓ) along $i(U^{4\ell}_{2\ell}\times 1)$. By (3.31), (3.32),

$(1\otimes \xi _{m,\ell ,v})\ast \theta ^{U^{4\ell}_{2\ell}\times 1}_{ \Delta (\tau ,m+\ell )}(g,h)=$

$$ =\sum _{\beta \in Q'_{2\ell}(F)\backslash {\mathrm {Sp}}_{4m}(F)}\int (1 \otimes \xi _{m,\ell ,v})\ast \theta ^{U_{4\ell}}_{\Delta (\tau ,m+ \ell )}( \begin{pmatrix} I_{2\ell}&a \\ &I_{2\ell} \\ &&I_{4(m-\ell )} \\ &&&I_{2\ell}&a' \\ &&&&I_{2\ell}\end{pmatrix} (g,\beta h))\cdot $$

(3.33)

$$ \cdot \psi ^{-1}(tr(a))da. $$

Denote the integral on the r.h.s. of (3.33) by $(1\otimes \xi _{m,\ell ,v})\ast \theta ^{U_{4\ell},\psi _{V_{(2\ell )^{2}}}}_{ \Delta (\tau ,m+\ell )}(g,\beta h)$. By an easy check, one can rewrite (3.33) as

$$ (1\otimes \xi _{m,\ell ,v})\ast \theta ^{U^{4\ell}_{2\ell}\times 1}_{ \Delta (\tau ,m+\ell )}(g,h)=\sum _{\beta \in Q_{2\ell}(F)\backslash {\mathrm {Sp}}_{4m}(F)}\sum _{\alpha \in {\mathrm {GL}}_{2\ell}(F)} (1\otimes \xi _{m, \ell ,v})\ast \theta ^{U_{4\ell},\psi _{V_{(2\ell )^{2}}}}_{\Delta ( \tau ,m+\ell )}(\hat{\alpha}g,\beta h). $$

(3.34)

4 Rapid decrease of (1⊗ξ _m,ℓ,v)∗θ _Δ(τ,m+ℓ)(g,h) in g and regularization

We keep the notation above. In this section, we prove Theorem 1.3 with the function ξ_m,ℓ,v above (defined by (2.17)).

Theorem 4.1

Assume that ℓ≤m. The function on ${\mathrm {Sp}}_{4\ell}(F)\backslash {\mathrm {Sp}}_{4\ell}({\mathbb{A}})$, g↦(1⊗ξ_m,ℓ,v)∗θ_Δ(τ,m+ℓ)(g,h) is rapidly decreasing, uniformly in h varying in bounded sets in ${\mathrm {Sp}}_{4m}(F)\backslash {\mathrm {Sp}}_{4m}({\mathbb{A}})$.

Fix a Siegel domain $\mathfrak{S}_{4\ell}=\Omega _{4\ell} T_{4\ell}^{+}(\epsilon _{0})K_{4 \ell}$ in ${\mathrm {Sp}}_{4\ell}({\mathbb{A}})$, where Ω_4ℓ is a sufficiently large compact subset of $B_{{\mathrm {Sp}}_{4\ell}}({\mathbb{A}})$, ϵ₀>0 is sufficiently small, and $T_{4\ell}^{+}(\epsilon _{0})$ is the subset of diagonal matrices $\hat{t}=diag(t_{1},\ldots,t_{2\ell},t^{-1}_{2\ell},\ldots,t_{1}^{-1})$, such that each $t_{i}=\prod _{\nu }t_{i,\nu}\in {\mathbb{A}}^{*}$ satisfies t_i,ν=1, for all ν<∞, and at the set of archimdean places, S_∞, t_i,ν=a_i, for all ν∈S_∞, where a_i>0, and we have,

$$ \frac{a_{i}}{a_{i+1}}>\epsilon _{0},\ \ i=1,2,\ldots,2\ell -1;\ \ a_{2 \ell}>\epsilon _{0}. $$

(4.1)

We will denote by ||⋅|| the norm on our adelic groups ${\mathrm {Sp}}_{2k}({\mathbb{A}})$, or ${\mathrm {GL}}_{k}({\mathbb{A}})$, as in [MW95], I.2.2. Similarly, fix a Siegel domain $\mathfrak{S}_{4m}=\Omega _{4m} T_{4m}^{+}(\epsilon _{0})K_{4m}$ in ${\mathrm {Sp}}_{4m}({\mathbb{A}})$. We will prove the rapid decrease in g, in Theorem 4.1, for a fixed $h\in \mathfrak{S}_{4m}$.

Assume that $g\in \mathfrak{S}_{4\ell}$. Since (1⊗ξ_m,ℓ,v)∗θ_Δ(τ,m+ℓ) is K_4ℓ×1-finite, we may assume that g=bt, where b∈Ω_4ℓ and $\hat{t}\in T^{+}(\epsilon _{0})$. We start with the Fourier expansion (3.5),

(1⊗ξ_m,ℓ,v)∗θ_Δ(τ,m+ℓ)(g,h)=

$$ =\sum _{c=0}^{2\ell}\sum _{[\delta ]\in [T_{c}(F)]}\sum _{\gamma \in P^{ \delta}_{2\ell -c,c}(F)\backslash {\mathrm {GL}}_{2\ell}(F)}(1\otimes \xi _{m, \ell ,v})\ast \theta ^{\psi _{\delta}}_{\Delta (\tau ,m+\ell )}(( \hat{\gamma}b\hat{t},h)). $$

(4.2)

In (4.2), consider the terms with 1≤c≤2ℓ, and let $P^{\delta}_{2\ell -c,c}(F)\gamma$ be a coset in $P^{\delta}_{2\ell -c,c}(F)\backslash {\mathrm {GL}}_{2\ell}(F)$. Write $\gamma = \begin{pmatrix} \gamma _{1} \\ \gamma _{2}\end{pmatrix}$, where γ₁∈M_{(2ℓ−c)×2ℓ}(F) and γ₂∈M_c×2ℓ(F). Denote by $\gamma _{2}^{1}$ the first column of γ₂. Although $\gamma _{2}^{1}$ depends on the representative γ, the property of being nonzero depends only on the coset $P^{\delta}_{2\ell -c,c}(F)\gamma$. We will prove that, for each 0≤c≤2ℓ, the corresponding term in (4.2) is rapidly decreasing in g. For 1≤c≤2ℓ, we will prove this separately for the corresponding sums over $\gamma _{2}^{1}\neq 0$ (Prop. 4.2) and then for $\gamma _{2}^{1}=0$ (Prop. 4.3). In Prop. 4.4, we will treat the case c=0.

Proposition 4.2

Let 1≤c≤2ℓ. There is A>0, and for every integer N≥1, there exists k_N>0, such that, for all b∈Ω_4ℓ, $\hat{t}\in T_{4\ell}^{+}(\epsilon _{0})$, $h\in {\mathrm {Sp}}_{4m}({\mathbb{A}})$,

$$ \sum _{[\delta ]\in [T_{c}(F)]}\sum _{\gamma \in P^{\delta}_{2\ell -c,c}(F) \backslash {\mathrm {GL}}_{2\ell}(F); \gamma _{2}^{1}\neq 0}|(1\otimes \xi _{m, \ell ,v})\ast \theta ^{\psi _{\delta}}_{\Delta (\tau ,m+\ell )}(( \hat{\gamma}b\hat{t},h))|\leq k_{N} a_{1}^{-N}||h||^{A} $$

Proof

We will prove the proposition with θ_Δ(τ,m+ℓ) in place of (1⊗ξ_m,ℓ,v)∗θ_Δ(τ,m+ℓ). Since θ_Δ(τ,m+ℓ) is smooth and of uniform moderate growth, there are k₁,A>0, such that,

$$ \sum _{[\delta ]\in [T_{c}(F)]} \sum _{\gamma \in P^{\delta}_{2\ell -c,c}(F) \backslash {\mathrm {GL}}_{2\ell}(F)}|\theta ^{\psi _{\delta}}_{\Delta (\tau ,m+ \ell )}((\hat{\gamma}b\hat{t},h))|\leq k_{1} || \begin{pmatrix} t \\ &h \\ &&t^{*}\end{pmatrix} ||^{A}. $$

(4.3)

Indeed, the series of absolute values (4.3) is part of the full series of absolute values resulting from the Fourier expansion of θ_Δ(τ,m+ℓ) along $U^{4\ell}_{2\ell}(F)\backslash U^{4\ell}_{2\ell}({\mathbb{A}})\times I_{4m}$. By (4.1),

$$ || \begin{pmatrix} t \\ &h \\ &&t^{*}\end{pmatrix} ||=max\{a_{1}^{\pm 1},\ldots,a_{2\ell}^{\pm 1},||h||\}\leq k_{2}a_{1}||h||, $$

where $k_{2}=\epsilon _{0}^{-4\ell}$. Thus, from (4.3), with $k=k_{1}k_{2}^{A}$,

$$ \sum _{[\delta ]\in [T_{c}(F)]} \sum _{\gamma \in P^{\delta}_{2\ell -c,c}(F) \backslash {\mathrm {GL}}_{2\ell}(F)}|\theta ^{\psi _{\delta}}_{\Delta (\tau ,m+ \ell )}((\hat{\gamma}b\hat{t},h))|\leq k (a_{1}||h||)^{A}. $$

(4.4)

Since θ_Δ(τ,m+ℓ) is smooth, we can write it, by the lemma of Dixmier-Malliavin, as a finite sum of convolutions

$$ \phi \ast \theta '_{\Delta (\tau ,m+\ell )}=\int _{S_{2\ell}({\mathbb{A}})} \phi (y)\rho ((u_{2\ell}^{4\ell}(y),I_{4m}))\theta '_{\Delta (\tau ,m+ \ell )}dy $$

where $\phi \in \mathcal{S}(S_{2\ell}({\mathbb{A}}))$ – the space of Schwartz functions on $S_{2\ell}({\mathbb{A}})$. Here, ρ(x) denotes the right translation by x. Thus, let us replace θ_Δ(τ,m+ℓ) by $\phi \ast \theta '_{\Delta (\tau ,m+\ell )}$ and consider

$\sum _{[\delta ]\in [T_{c}(F)]}\sum _{\gamma \in P^{\delta}_{2\ell -c,c}(F) \backslash {\mathrm {GL}}_{2\ell}(F); \gamma _{2}^{1}\neq 0} \phi \ast \theta ^{\prime \, \psi _{\delta}}_{\Delta (\tau ,m+\ell )}((\hat{\gamma}b\hat{t},h))=$

$$ =\sum _{[\delta ]\in [T_{c}(F)]}\sum _{\gamma \in P^{\delta}_{2\ell -c,c}(F) \backslash {\mathrm {GL}}_{2\ell}(F); \gamma _{2}^{1}\neq 0}\int \phi (y) \theta '_{\Delta (\tau ,m+\ell )}((u_{2\ell}^{4\ell}(x)\hat{\gamma}b \hat{t}u_{2\ell}^{4\ell}(y),h)) $$

(4.5)

$$ \psi ^{-1}_{\delta}(u_{2\ell}^{4\ell}(x))dydx, $$

where x is integrated along $S_{2\ell}(F)\backslash S_{2\ell}({\mathbb{A}})$ and y is integrated along $S_{2\ell}({\mathbb{A}})$. Write $b=\hat{b}_{1}u_{2\ell}^{4\ell}(e)$, where $b_{1}\in B_{{\mathrm {GL}}_{2\ell}}({\mathbb{A}})$. Simple conjugations inside (4.5) yield, with the same domains of summation and integrations,

$$ \sum \int \phi (y)\theta '_{\Delta (\tau ,m+\ell )}((u_{2\ell}^{4\ell}(x+ \gamma b_{1}(ty(t^{*})^{-1}+e)(\gamma ^{*}b_{1}^{*})^{-1}\hat{\gamma}b \hat{t},h))\psi _{\delta}^{-1}(x)dydx. $$

Switching the integration order and changing variables in x, the dy integration results in a Fourier transform of ϕ at

$$ (\gamma ^{*}b_{1}^{*}t^{*})^{-1} \begin{pmatrix} 0&w_{c}\delta \\ 0&0\end{pmatrix} \gamma b_{1}t=w_{2\ell}t{}^{t}b_{1}{}^{t}\gamma _{2}\delta \gamma _{2}b_{1}t. $$

Then (4.5) becomes $\sum _{[\delta ]\in [T_{c}(F)]}\sum _{\gamma \in P^{\delta}_{2\ell -c,c}(F) \backslash {\mathrm {GL}}_{2\ell}(F); \gamma _{2}^{1}\neq 0} \phi \ast \theta ^{\prime \, \psi _{\delta}}_{\Delta (\tau ,m+\ell )}((\hat{\gamma}b\hat{t},h))=$

$$ =\sum _{[\delta ]\in [T_{c}(F)]}\sum _{\gamma \in P^{\delta}_{2\ell -c,c}(F) \backslash {\mathrm {GL}}_{2\ell}(F); \gamma _{2}^{1}\neq 0}\psi _{\delta}( \gamma b_{1}e(\gamma ^{*}b_{1}^{*})^{-1})\hat{\phi}(w_{2\ell}t{}^{t}b_{1}{}^{t} \gamma _{2}\delta \gamma _{2}b_{1}t) $$

(4.6)

$$ \theta ^{\prime \,\psi _{\delta}}_{\Delta (\tau ,m+\ell )}((\hat{\gamma}b \hat{t},h)). $$

Since $\psi _{\delta}(\gamma b_{1}e(\gamma ^{*}b_{1}^{*})^{-1})$ has absolute value 1, the above calculation also shows that

$\sum _{[\delta ]\in [T_{c}(F)]}\sum _{\gamma \in P^{\delta}_{2\ell -c,c}(F) \backslash {\mathrm {GL}}_{2\ell}(F); \gamma _{2}^{1}\neq 0} |\phi \ast \theta ^{ \psi _{\delta}}_{\Delta (\tau ,m+\ell )}((\hat{\gamma}b\hat{t},h))|=$

$$ =\sum _{[\delta ]\in [T_{c}(F)]}\sum _{\gamma \in P^{\delta}_{2\ell -c,c}(F) \backslash {\mathrm {GL}}_{2\ell}(F); \gamma _{2}^{1}\neq 0}|\hat{\phi}(w_{2 \ell}{}^{t}(\gamma _{2}b_{1}t)\delta \gamma _{2}b_{1}t)| |\theta ^{\prime \, \psi _{\delta}}_{\Delta (\tau ,m+\ell )}((\hat{\gamma}b\hat{t},h))|. $$

(4.7)

Since γ₂ has rank c and $\gamma _{2}^{1}\neq 0$, the first column of ^tγ₂δγ₂ is nonzero. In (4.7), $\hat{\phi}$ being a Schwartz function, we can estimate in (4.7), for any integer N≥1,

$$ |\hat{\phi}(w_{2\ell}{}^{t}(\gamma _{2}b_{1}t)\delta \gamma _{2}b_{1}t)| \leq k'_{N} ||w_{2\ell}{}^{t}(\gamma _{2}b_{1}t)\delta \gamma _{2}b_{1}t||^{-N}_{max}, $$

(4.8)

for a suitable $k'_{N}>0$. Here, ||⋅||_max=∏_v||⋅||_max,v denotes the product over all places of the local maximum norms. We have, for a suitable k₃>0, and all t, b₁, γ₂ as in (4.7),

$$ ||w_{2\ell}{}^{t}(\gamma _{2}b_{1}t)\delta \gamma _{2}b_{1}t||_{max}=||{}^{t}(t^{-1}b_{1}t)t({}^{t} \gamma _{2}\delta \gamma _{2})t(t^{-1}b_{1}t)||_{max}\geq k_{3}||t{}^{t} \gamma _{2}\delta \gamma _{2})t||_{max}. $$

(4.9)

Indeed, since b₁ lies in a compact subset Ω₁ of $B_{{\mathrm {GL}}_{2\ell}}({\mathbb{A}})$, then, by (4.1), the conjugation t⁻¹b₁t shrinks the coordinates of b₁, and hence t⁻¹b₁t lies in a compact subset $\Omega '_{1}\subset \Omega _{1}$. Clearly,

$$ ||t{}^{t}\gamma _{2}\delta \gamma _{2})t||_{max}\geq max\{a_{1}a_{j} \cdot |{}^{t}\gamma _{2}^{1}\delta \gamma _{2}^{j}|\}_{j\leq 2\ell} \geq \epsilon _{0}^{2\ell}a_{1}\cdot max\{|{}^{t}\gamma _{2}^{1} \delta \gamma _{2}^{j}|\}_{j\leq 2\ell}, $$

where $\gamma _{2}^{j}$ denotes the j-th column of γ₂. By (4.9), there is k₄>0, such that, for t, b₁, γ₂ as in (4.7),

$$ ||w_{2\ell}{}^{t}(\gamma _{2}b_{1}t)\delta \gamma _{2}b_{1}t||_{max} \geq k_{4} a_{1}\cdot max\{|{}^{t}\gamma _{2}^{1}\delta \gamma _{2}^{j}| \}_{j\leq 2\ell}. $$

(4.10)

In (4.7), since $\hat{\phi}$ is a Schwartz function, the coordinates of ^t(γ₂b₁t)δγ₂b₁t) must lie in fixed compact subsets C_v⊂S_2ℓ(F_v), at each finite place v. Since b₁∈Ω₁, and since t_v=I_2ℓ, for all v<∞, we conclude that in (4.7), the coordinates of ^tγ₂δγ₂ must lie inside a lattice $L\subset {\mathbb{A}}_{\infty}$. (Recall that the coordinates of γ₂ and δ are in F.) Let k₀=min{|x|_∞}_0≠x∈L. Then k₀>0 and inside the support of $\hat{\phi}$ in (4.7), we have, by (4.10),

$$ ||w_{2\ell}{}^{t}(\gamma _{2}b_{1}t)\delta \gamma _{2}b_{1}t||_{max} \geq k_{5} a_{1}, $$

(4.11)

for a suitable positive constant k₅, which depends on ϕ and ϵ₀. Note, again, that in (4.7), we take $\gamma _{2}^{1}\neq 0$, and hence the r.h.s. of (4.10) is nonzero. Using (4.11) in (4.8), we get that for every positive integer N,

$$ |\hat{\phi}(w_{2\ell}{}^{t}(\gamma _{2}b_{1}t)\delta \gamma _{2}b_{1}t)| \leq k''_{N}a_{1}^{-N}, $$

(4.12)

for a suitable positive constant $k''_{N}$, which depends on ϕ, ϵ₀ and N. By (4.4), (4.7), (4.12), we get that there is A>0, and for every positive integer N, there is c_N>0, such that, for all b∈Ω_4ℓ, $\hat{t}\in T^{+}(\epsilon _{0})$, $h\in {\mathrm {Sp}}_{4m}({\mathbb{A}})$,

$$ \sum _{[\delta ]\in [T_{c}(F)]}\sum _{\gamma \in P^{\delta}_{2\ell -c,c}(F) \backslash {\mathrm {GL}}_{2\ell}(F); \gamma _{2}^{1}\neq 0} |\phi \ast \theta ^{\prime \,\psi _{\delta}}_{ \Delta (\tau ,m+\ell )}((\hat{\gamma}b\hat{t},h))|\leq k_{N}a_{1}^{-N+A}||h||^{A}. $$

This completes the proof of Proposition 4.2. □

We now consider the sum over the terms in (4.2) with $\gamma _{2}^{1}=0$. This forces c<2ℓ. For the next proposition, we take $h\in \mathfrak{S}_{4m}$, and, again, it is enough to take h of the form $h=b'\hat{t'}$, where b′∈Ω_4m, and $\hat{t'}=diag(t'_{1},\ldots,t'_{2m},(t')^{-1}_{2m},\ldots,(t')_{1}^{-1}) \in T^{+}_{4m}(\epsilon _{0})$. Thus, all finite coordinates of $t'_{i}$ are 1, and at v∈S_∞, $t'_{i,v}=a'_{i}>0$, satisfying the inequalities analogous to (4.1).

Proposition 4.3

Let 1≤c<2ℓ. There is A>0, and for every integer N≥1, there exists c_N>0, such that, for all b∈Ω_4ℓ, b′∈Ω_4m, $\hat{t}\in T_{4\ell}^{+}(\epsilon _{0})$, $\hat{t'}\in T_{4m}^{+}(\epsilon _{0})$,

$$ \sum _{[\delta ]\in [T_{c}(F)]}\sum _{\gamma \in P^{\delta}_{2\ell -c,c}(F) \backslash {\mathrm {GL}}_{2\ell}(F); \gamma _{2}^{1}= 0}|(1\otimes \xi _{m, \ell ,v})\ast \theta ^{\psi _{\delta}}_{\Delta (\tau ,m+\ell )}(( \hat{\gamma}b\hat{t},b'\hat{t'}))|\leq c_{N} a_{1}^{-N}(a_{1}')^{A+N} $$

Proof

For $\gamma \in P^{\delta}_{2\ell -c,c}(F)\backslash {\mathrm {GL}}_{2\ell}(F)$, with $\gamma _{2}^{1}=0$, we may take $\gamma = \begin{pmatrix} 1 \\ &\gamma '\end{pmatrix}$, $\gamma '\in P^{\delta}_{2\ell -1-c,c}(F)\backslash {\mathrm {GL}}_{2\ell -1}(F)$. By (3.31), the Fourier expansion of the following function on $F^{4m}\backslash {\mathbb{A}}^{4m}$,

$$\begin{gathered} x\mapsto (1\otimes \xi _{m,\ell ,v})\ast \theta ^{\psi _{\delta}}_{ \Delta (\tau ,m+\ell )}( \begin{pmatrix} 1&0&x&0&\ast \\ &I_{2\ell -1}&0&0&0 \\ &&I_{4m}&0&x' \\ &&&I_{2\ell -1}&0 \\ &&&&1\end{pmatrix} (\hat{\gamma}b\hat{t},h)):= \\ :=(1\otimes \xi _{m,\ell ,v})\ast \theta ^{\psi _{\delta}}_{\Delta ( \tau ,m+\ell )}(\bar{y}(x)(\hat{\gamma}b\hat{t},h)) \end{gathered}$$

at x=0 is

$$ \sum _{0\neq e\in F^{4m}}\int _{F^{4m}\backslash {\mathbb{A}}^{4m}}(1\otimes \xi _{m,\ell ,v})\ast \theta ^{\psi _{\delta}}_{\Delta (\tau ,m+\ell )}( \bar{y}(x)(\hat{\gamma}b\hat{t},h))\psi ^{-1}(x\cdot {}^{t}e)dx. $$

The point here is that the trivial character, i.e. e=0 does not contribute. Write, in the last sum, e=(1,0,…,0)^tη⁻¹, with $\eta \in Q'_{1}(F)\backslash {\mathrm {Sp}}_{4m}(F)$, where $Q'_{1}(F)$ is the subgroup of matrices in Sp_4m(F) of the form $\begin{pmatrix} 1&\ast &\ast \\ &\eta '&\ast \\ &&1\end{pmatrix} , \eta '\in {\mathrm {Sp}}_{4m-2}(F)$. Then the last Fourier expansion is

$(1\otimes \xi _{m,\ell ,v})\ast \theta ^{\psi _{\delta}}_{\Delta ( \tau ,m+\ell )}((\hat{\gamma}b\hat{t},h))=$

$$ \sum _{\eta \in Q'_{1}(F)\backslash {\mathrm {Sp}}_{4m}(F)}\int _{F^{4m} \backslash {\mathbb{A}}^{4m}}(1\otimes \xi _{m,\ell ,v})\ast \theta ^{\psi _{ \delta}}_{\Delta (\tau ,m+\ell )}(\bar{y}(x)(\hat{\gamma}b\hat{t}, \eta h))\psi ^{-1}(x_{1})dx. $$

(4.13)

By (4.13), it suffices to prove that, for a given $\theta '_{\Delta (\tau ,m+\ell )}\in \Theta _{\Delta (\tau ,m+\ell )}$, there is A>0, and for every integer N≥1, there exists k_N>0, such that, for all b∈Ω_4ℓ, $\hat{t}\in T^{+}(\epsilon _{0})$, $h\in {\mathrm {Sp}}_{4m}({\mathbb{A}})$,

$$ \sum _{[\delta ]\in [T_{c}(F)]}\sum _{\gamma \in P^{\delta}_{2\ell -c,c}(F) \backslash {\mathrm {GL}}_{2\ell}(F); \gamma _{2}^{1}= 0}\sum _{\eta \in Q'_{1}(F) \backslash {\mathrm {Sp}}_{4m}(F)}| (\theta ')^{\tilde{\psi}_{\delta}}_{\Delta ( \tau ,m+\ell )}((\hat{\gamma}b\hat{t},\eta h))| $$

(4.14)

$$ \leq k_{N} a_{1}^{-N}||h||^{A+N}, $$

where

$$ (\theta ')^{\tilde{\psi}_{\delta}}_{\Delta (\tau ,m+\ell )}(( \hat{\gamma}b\hat{t},\eta h))=\int _{F^{4m}\backslash {\mathbb{A}}^{4m}} ( \theta ')^{\psi _{\delta}}_{\Delta (\tau ,m+\ell )}(\bar{y}(x)( \hat{\gamma}b\hat{t},\eta h))\psi ^{-1}(x_{1})dx. $$

As in the proof of Prop. 4.2, by the lemma of Dixmier-Malliavin, it is enough to prove (4.14), with $\theta '_{\Delta (\tau ,m+\ell )}=f_{\phi ,\varphi}\ast \theta ''_{ \Delta (\tau ,m+\ell )}$, where

$$ f_{\phi ,\varphi}\ast \theta ''_{\Delta (\tau ,m+\ell )}=\int _{{\mathbb{A}}^{4m+1}} \phi (u)\varphi (z)\rho ( \begin{pmatrix} 1&0&u&0&z \\ &I_{2\ell -1}&0&0&0 \\ &&I_{4m}&0&u' \\ &&&I_{2\ell -1}&0 \\ &&&&1\end{pmatrix} )\theta ''_{\Delta (\tau ,m+\ell )}d(u,z), $$

$\phi \in \mathcal{S}({\mathbb{A}}^{4m})$, $\varphi \in \mathcal{S}({\mathbb{A}})$. We have, for $\gamma = \begin{pmatrix} 1 \\ &\gamma '\end{pmatrix}$, as in the beginning of the proof,

$$ \int _{F^{4m}\backslash {\mathbb{A}}^{4m}}(f_{\phi ,\varphi}\ast \theta ''_{ \Delta (\tau ,m+\ell )})^{\psi _{\delta}}(\bar{y}(x)(\hat{\gamma}b \hat{t},\eta h))\psi ^{-1}(x_{1})dx= $$

$$ =\alpha _{\varphi}\int _{F^{4m}\backslash {\mathbb{A}}^{4m}}\int _{{\mathbb{A}}^{4m}} \phi (u)(\theta '')^{\psi _{\delta}}_{\Delta (\tau ,m+\ell )}(\bar{y}(x+b_{1,1}t_{1}u( \eta h)^{-1})(\hat{\gamma}b\hat{t},\eta h))\psi ^{-1}(x_{1})dudx, $$

where $\alpha _{\varphi}=\int _{{\mathbb{A}}}\varphi (z)dz$. We may switch the order of integration since ϕ is a Schwartz function and x varies in a compact set. When we change variable x↦x−b_1,1t₁u(ηh)⁻¹, the du-integration gives the Fourier transform of ϕ at the point b_1,1t₁h⁻¹η⁻¹⋅e₁, where $e_{1}= \begin{pmatrix} 1 \\ 0 \\ \vdots \\ 0\end{pmatrix}$. We get

$$ \alpha _{\varphi}\hat{\phi}(b_{1,1}t_{1}h^{-1}\eta ^{-1}\cdot e_{1}) \int _{F^{4m}\backslash {\mathbb{A}}^{4m}} (\theta '')^{\psi _{\delta}}_{ \Delta (\tau ,m+\ell )}(\bar{y}(x)(\hat{\gamma}b\hat{t},\eta h))\psi ^{-1}(x_{1})dx. $$

Thus, we can majorize the l.h.s. of (4.14) by

$$ |\alpha _{\varphi}| \sum _{[\delta ]\in [T_{c}(F)]}\sum _{\gamma ' \in P^{\delta}_{2\ell -1-c,c}(F)\backslash {\mathrm {GL}}_{2\ell -1}(F)}\sum _{ \eta \in Q'_{1}(F)\backslash {\mathrm {Sp}}_{4m}(F)}|\hat{\phi}(b_{1,1}t_{1}h^{-1} \eta ^{-1}\cdot e_{1})|\cdot $$

(4.15)

$$ \cdot \int _{F^{4m}\backslash {\mathbb{A}}^{4m}}|(\theta '')^{\psi _{\delta}}_{ \Delta (\tau ,m+\ell )}(\bar{y}(x)( \widehat{\begin{pmatrix}1\\&\gamma '\end{pmatrix}}b\hat{t},\eta h))|dx. $$

Substitute $h=b'\hat{t'}$, b′∈Ω_4m, $\hat{t'}\in T^{+}_{4m}(\epsilon _{0})$. Exactly as in the last proof, since $\hat{\phi}$ is a Schwartz function, we conclude that the coordinates of $\eta ^{-1}\dot{e}_{1}$ in (4.15) must lie inside a lattice $L\subset {\mathbb{A}}_{\infty}$. In (4.15), inside the support of $\hat{\phi}$, we have, for positive constants k₁,…,k₄,

$$ ||b_{1,1}t_{1}(t')^{-1}(b')^{-1}\eta ^{-1}\cdot e_{1}||_{max}\geq k_{1}a_{1}||((t')^{-1}(b')^{-1}t')(t')^{-1} \eta ^{-1}\cdot e_{1}||_{max}\geq $$

$$ \geq k_{2}a_{1}||(t')^{-1}\eta ^{-1}\cdot e_{1}||_{max}\geq k_{3}a_{1}(a'_{1})^{-1}|| \eta ^{-1}\cdot e_{1}||_{max}\geq k_{4}a_{1}(a'_{1})^{-1}. $$

Here, we used that, since b∈Ω_4ℓ, b_1,1 lies in a compact subset of ${\mathbb{A}}^{*}$. Since b′∈Ω_4m, and the archimedean coordinates $a'_{i}$ satisfy the analog of (4.1), the conjugation (t′)⁻¹(b′)⁻¹t′) lies in a compact subset Ω′⊂Ω_4m. Finally, let k₀=min{|z|_∞| 0≠z∈L}. Then k₀>0 and $||\eta ^{-1}\cdot e_{1}||_{max}\geq k_{0}k_{0}'$, where $k'_{0}>0$ depends on the (compact) support of $\hat{\phi}$ at the finite places. We take $k_{4}=k_{0}k_{0}'k_{3}$. Thus, for every positive integer N,

$$ |\hat{\phi}(b_{1,1}t_{1}(t')^{-1}(b')^{-1}\eta ^{-1}\cdot e_{1})| \leq k'_{N}a_{1}^{-N}(a'_{1})^{N}, $$

(4.16)

for a suitable positive constant $k'_{N}$, which depends on ϕ, ϵ₀ and N. Put $k''_{N}=k'_{N}|\alpha _{\varphi}|$. Using (4.16), we can majorize (4.15) by

$$ k''_{N} a_{1}^{-N}(a'_{1})^{N}\sum _{[\delta ]\in [T_{c}(F)]} \sum _{ \gamma '}\sum _{\eta }\int _{F^{4m}\backslash {\mathbb{A}}^{4m}}|(\theta '')^{ \psi _{\delta}}_{\Delta (\tau ,m+\ell )}(\bar{y}(x)( \widehat{\begin{pmatrix}1\\&\gamma '\end{pmatrix}}b\hat{t},\eta b' \hat{t'}))|dx, $$

(4.17)

where γ′ runs over $P^{\delta}_{2\ell -1-c,c}(F)\backslash {\mathrm {GL}}_{2\ell -1}(F)$ and η – over $Q'_{1}(F)\backslash {\mathrm {Sp}}_{4m}(F)$. As in (4.3), there are k₅,k₆,A>0, such that the last triple series is majorized by

$$ k_{5}|| \begin{pmatrix} t \\ &b'\hat{t'} \\ &&t^{*}\end{pmatrix} ||^{A}\leq k_{6} a^{A}_{1}(a'_{1})^{A}. $$

This proves Proposition 4.3. □

It remains to consider the term in (4.2) with c=0. This is exactly $(1\otimes \xi _{m,\ell ,v})\ast \theta ^{U^{4\ell}_{2\ell}\times 1}_{ \Delta (\tau ,m+\ell )}(g,h)$.

Proposition 4.4

There is A>0, and for every integer N≥1, there exists k_N>0, such that, for all b∈Ω_4ℓ, b′∈Ω_4m, $\hat{t}\in T_{4\ell}^{+}(\epsilon _{0})$, $\hat{t'}\in T_{4m}^{+}(\epsilon _{0})$,

$$ |(1\otimes \xi _{m,\ell ,v})\ast \theta ^{U^{4\ell}_{2\ell}\times 1}_{ \Delta (\tau ,m+\ell )}(b\hat{t},b'\hat{t'})|\leq k_{N} a_{1}^{-N}(a_{1}')^{A+N}. $$

Proof

By (3.7) and Theorem 3.2 with c=0, we may use (3.14) with k=2ℓ, and hence it suffices to prove that, for a given $\theta '_{\Delta (\tau ,m+\ell )}\in \Theta _{\Delta (\tau ,m+\ell )}$, there is A>0, and for every integer N≥1, there exists k_N>0, such that, for b, t, b′, t′ as above,

$$ \sum |\int \theta '_{\Delta (\tau ,m+\ell )}( \begin{pmatrix} I_{2\ell}&y&z \\ &I_{4m}&y' \\ &&I_{2\ell}\end{pmatrix} (b\hat{t},\beta b'\hat{t'})) \psi ^{-1}(tr(y\cdot \begin{pmatrix} I_{2\ell} \\ 0\end{pmatrix} ))d(y,z)|\leq $$

(4.18)

$$ \leq k_{N} a_{1}^{-N}(a_{1}')^{A+N}, $$

where β runs over $Q'_{2\ell}(F)\backslash {\mathrm {Sp}}_{4m}(F)$. As in the proofs of the last two propositions, by the lemma of Dixmier-Malliavin, it is enough to prove (4.18) for $\theta '_{\Delta (\tau ,m+\ell )}=\varphi \ast \theta ''_{\Delta ( \tau ,m+\ell )}$, where $\varphi \in \mathcal{S}(U_{2\ell}^{4(m+\ell )}({\mathbb{A}}))$, and

$$ \varphi \ast \theta ''_{\Delta (\tau ,m+\ell )}(x)=\int _{U_{2\ell}^{4(m+ \ell )}({\mathbb{A}})}\varphi (u)\theta ''_{\Delta (\tau ,m+\ell )}(xu)du. $$

Denote, for $y\in M_{2\ell \times 4m}({\mathbb{A}})$,

$$ \phi (y)=\int _{S_{2\ell}({\mathbb{A}})}\varphi ( \begin{pmatrix} I_{2\ell}&0&z \\ &I_{4m}&0 \\ &&I_{2\ell}\end{pmatrix} \begin{pmatrix} I_{2\ell}&y&s(y) \\ &I_{4m}&y' \\ &&I_{2\ell}\end{pmatrix} )dz, $$

where we may take $s(y)=\frac{1}{2}yJ_{4m}{}^{t}yw_{2\ell}$. Then $\phi \in \mathcal{S}(M_{2\ell \times 4m}({\mathbb{A}}))$. Write $b=\hat{b}_{1}u_{2\ell}^{4\ell}(e)$, where $b_{1}\in B_{{\mathrm {GL}}_{2\ell}}({\mathbb{A}})$. Substituting $\varphi \ast \theta ''_{\Delta (\tau ,m+\ell )}$ in the integral in (4.18), the integral becomes

$$ \hat{\phi}((\hat{t'})^{-1}(b')^{-1}\beta ^{-1}\cdot \begin{pmatrix} I_{2\ell} \\ 0\end{pmatrix} b_{1}t)\int \theta ''_{\Delta (\tau ,m+\ell )}( \begin{pmatrix} I_{2\ell}&y&z \\ &I_{4m}&y' \\ &&I_{2\ell}\end{pmatrix} (b\hat{t},\beta b'\hat{t'}))\cdot $$

$$ \psi ^{-1}(tr(y\cdot \begin{pmatrix} I_{2\ell} \\ 0\end{pmatrix} ))d(y,z). $$

Thus,we can majorize the l.h.s. of (4.18) by,

$$ \sum |\hat{\phi}((\hat{t'})^{-1}(b')^{-1}\beta ^{-1}\cdot \begin{pmatrix} I_{2\ell} \\ 0\end{pmatrix} b_{1}t)|\int | \theta ''_{\Delta (\tau ,m+\ell )}( \begin{pmatrix} I_{2\ell}&y&z \\ &I_{4m}&y' \\ &&I_{2\ell}\end{pmatrix} (b\hat{t},\beta b'\hat{t'}))|d(y,z). $$

(4.19)

As in (4.16), for every positive integer N, there is a $k'_{N}>0$, such that

$$ |\hat{\phi}((\hat{t'})^{-1}(b')^{-1}\beta ^{-1}\cdot \begin{pmatrix} I_{2\ell} \\ 0\end{pmatrix} b_{1}t)|\leq k'_{N}a_{1}^{-N}(a'_{1})^{N}. $$

(4.20)

Now, we finish the proof as in the end of Proposition 4.3. □

The proof of Theorem 4.1 is now complete.

Let us introduce the polynomial appearing in (1.9), which will lead to the regularization of (1.3). Before that, we specify a little more our choice of the place v. Recall that at v, τ_v is induced from a character of the Borel subgroup

$$ \begin{pmatrix} a&x \\ 0&b\end{pmatrix} \mapsto \chi (ab^{-1}), \ \ a, b\in F_{v}^{*}, x\in F_{v}, $$

where χ=χ_v is an unramified character of $F_{v}^{*}$. We assume that χ²≠1. We can choose such a place v, since otherwise, at each finite place v, where τ_v is unramified, we would get that $L(\tau _{v}\times \tau _{v},s)=(1-q_{v}^{-s})^{-4}$, and hence the partial L-function, away from the finite set S of archimedean places and the finite places v′, where τ_v′ is ramified, L^S(τ×τ,s)=L^S(1,s)⁴ has a pole of order four at s=1, which is impossible, since τ is cuspidal. From now on, assume that v is a finite place, where τ_v is unramified and χ is not quadratic.

Let f_Δ(τ,ℓ),s be a smooth, holomorphic section of ρ_Δ(τ,ℓ),s. See (1.1). Recall that we denote by E(f_Δ(τ,ℓ),s;⋅) the corresponding Eisenstein series on ${\mathrm {Sp}}_{4\ell}({\mathbb{A}})$. Consider a case where θ_Δ(τ,m+ℓ) and f_Δ(τ,ℓ),s are such that the integral

$$ \int _{{\mathrm {Sp}}_{4\ell}(F)\backslash {\mathrm {Sp}}_{4\ell}({\mathbb{A}})}\theta _{ \Delta (\tau ,m+\ell )}(g,h)E(f_{\Delta (\tau ,\ell ),s};g)dg $$

(4.21)

converges absolutely. For example, this is the case when $\theta _{\Delta (\tau ,m+\ell )}=(1\otimes \xi _{m,\ell ,v})\ast \theta '_{\Delta (\tau ,m+\ell )}$. In this case, the integral (4.21) converges absolutely, for each s, which is not a pole of E(f_Δ(τ,ℓ),s;⋅). Assume that θ_Δ(τ,m+ℓ) is right i(K_4ℓ,v×K_4m,v)-invariant and that f_Δ(τ,ℓ),s is right K_4ℓ,v-invariant. By Theorem 4.1, the integral

$$ \int _{{\mathrm {Sp}}_{4\ell}(F)\backslash {\mathrm {Sp}}_{4\ell}({\mathbb{A}})}(1 \otimes \xi _{m,\ell ,v})\ast \theta _{\Delta (\tau ,m+\ell )}(g,h)E(f_{ \Delta (\tau ,\ell ),s};g)dg $$

(4.22)

converges absolutely, for each s, which is not a pole of E(f_Δ(τ,ℓ),s;⋅). By Theorem 2.2, the integral (4.22) is equal to

$$ \int _{{\mathrm {Sp}}_{4\ell}(F)\backslash {\mathrm {Sp}}_{4\ell}({\mathbb{A}})}(\eta ^{\chi}_{m, \ell}(\xi _{m,\ell ,v})\otimes 1)\ast \theta _{\Delta (\tau ,m+\ell )}(i(g,h))E(f_{ \Delta (\tau ,\ell ),s};g)dg= $$

$$ =\int _{{\mathrm {Sp}}_{4\ell}(F)\backslash {\mathrm {Sp}}_{4\ell}({\mathbb{A}})}\theta _{\Delta ( \tau ,m+\ell )}(i(g,h)) E(\eta ^{\chi}_{m,\ell}(\xi _{m,\ell ,v}) \ast f_{\Delta (\tau ,\ell ),s};g)dg. $$

(4.23)

Note that since f_Δ(τ,ℓ),s is right i(K_4ℓ,v)-invariant,

$$ \eta ^{\chi}_{m,\ell}(\xi _{m,\ell ,v})\ast f_{\Delta (\tau ,\ell ),s}=P(q_{v}^{-s},q_{v}^{s})f_{ \Delta (\tau ,\ell ),s}, $$

(4.24)

where

$$ P(q_{v}^{-s},q_{v}^{s})=\hat{\mathcal{S}}(\eta ^{\chi}_{m,\ell}(\xi _{m, \ell ,v}))(\chi (p_{v})q_{v}^{\pm (s+\frac{\ell -1}{2})},\chi (p_{v})q_{v}^{ \pm (s+\frac{\ell -3}{2})},\ldots,\chi (p_{v})q_{v}^{\pm (s+ \frac{1-\ell}{2})}). $$

(4.25)

Thus, by (2.19),

$$ P(q_{v}^{-s},q_{v}^{s})=\alpha _{m,\ell ,v}\prod _{i=1}^{\ell}(q_{v}^{-s- \frac{\ell -(2i-1)}{2}}-q_{v}^{-m+\ell -\frac{1}{2}})(q_{v}^{s+ \frac{\ell -(2i-1)}{2}}-\chi (p_{v})^{2}q_{v}^{-m+\ell -\frac{1}{2}}) \cdot $$

(4.26)

$$ \cdot \prod _{i=1}^{\ell}(q_{v}^{-s-\frac{\ell -(2i-1)}{2}}-\chi (p_{v})^{2}q_{v}^{-m+ \ell -\frac{1}{2}})(q_{v}^{s+\frac{\ell -(2i-1)}{2}}-q_{v}^{-m+\ell - \frac{1}{2}}). $$

Here, α_m,ℓ,v is nonzero. It is defined in (2.19). Summarizing, we proved (1.9).

Proposition 4.5

Assume that θ_Δ(τ,m+ℓ) and f_Δ(τ,ℓ),s are such that the integral (4.21) converges absolutely, and are right i(K_4ℓ,v×K_4m,v)-invariant and, respectively, right K_4ℓ,v-invariant. Then

$$ \int _{{\mathrm {Sp}}_{4\ell}(F)\backslash {\mathrm {Sp}}_{4\ell}({\mathbb{A}})}\theta _{ \Delta (\tau ,m+\ell )}(g,h)E(f_{\Delta (\tau ,\ell ),s};g)dg= $$

(4.27)

$$ \frac{1}{ P(q_{v}^{-s},q_{v}^{s})} \int _{{\mathrm {Sp}}_{4\ell}(F) \backslash {\mathrm {Sp}}_{4\ell}({\mathbb{A}})}(1\otimes \xi _{m,\ell ,v})\ast \theta _{ \Delta (\tau ,m+\ell )}(g,h)E(f_{\Delta (\tau ,\ell ),s};g)dg, $$

with $P(q_{v}^{-s},q_{v}^{s})\in {\mathbb{C}}[q_{v}^{-s},q_{v}^{s}]$ given by (4.26).

Note that the r.h.s. of (4.27) is an absolutely convergent integral, for all θ_Δ(τ,m+ℓ) and all f_Δ(τ,ℓ),s, except when s is a pole of E(f_Δ(τ,ℓ),s;⋅). Therefore we will think of it as a regularization of the l.h.s. of (4.27) in the cases where it diverges. We will consider this regularization in the next section and identify it as an Eisenstein series on ${\mathrm {Sp}}_{4m}({\mathbb{A}})$ induced from $Q_{2\ell}^{4m}({\mathbb{A}})$ and Δ(τ,ℓ)|det⋅|^s⊗Θ_{Δ(τ,m−ℓ)}. Thus, in the notation (1.10), denote

$\mathcal{E}(\theta _{\Delta (\tau ,m+\ell )},f_{\Delta (\tau ,\ell ),s};h)=$

$$ \frac{1}{P(q_{v}^{-s},q_{v}^{s})}\int _{{\mathrm {Sp}}_{4\ell}(F) \backslash {\mathrm {Sp}}_{4\ell}({\mathbb{A}})}(1\otimes \xi _{m,\ell ,v})\ast \theta _{ \Delta (\tau ,m+\ell )}(i(g,h))E(f_{\Delta (\tau ,\ell ),s};g)dg. $$

(4.28)

This will yield a regularization of the integral (1.3). For this, we need to consider the point $s=\frac{\ell}{2}$, which is a simple pole of the Eisenstein series E(f_Δ(τ,ℓ),s;⋅), as the section varies. Thus, we consider $P(q_{v}^{-\frac{\ell}{2}},q_{v}^{\frac{\ell}{2}})$.

Lemma 4.6

1. When m≥2ℓ, $P(q_{v}^{-\frac{\ell}{2}},q_{v}^{\frac{\ell}{2}})\neq 0$.

2. When ℓ≤m≤2ℓ−1, recall that we assume that v is such that χ is not quadratic. Then $P(q_{v}^{-s},q_{v}^{s})$ has a simple zero at $s=\frac{\ell}{2}$.

Proof

Substituting $s=\frac{\ell}{2}$ in (4.26), we need to solve one of the equations

$$ \pm (\frac{\ell}{2}+\frac{\ell -(2i-1)}{2})=-m+\ell -\frac{1}{2}, $$

or one of the equations

$$ \pm (\frac{\ell}{2}+\frac{\ell -(2i-1)}{2})=-m+\ell -\frac{1}{2}+2 \alpha , $$

for 1≤i≤ℓ, where $|\chi (p_{v})|=q_{v}^{\alpha}$. When we consider the plus sign, we get either m=i−1<ℓ, which is impossible, or m=i−1+2α, which implies that 2α is an integer. Since |2α|<1, we get that α=0, and then m=i−1<ℓ, which is impossible. Consider the equations with the minus sign. Then we get m=2ℓ−i, which is possible, when ℓ≤m≤2ℓ−1, exactly for one 1≤i≤ℓ. We also get m=2ℓ−i+2α, which, as before, forces α=0, and hence $\chi (p_{v})=q_{v}^{\frac{ k_{v}}{log(q_{v})}\pi i}$, for some integer k_v, and then χ(p_v)²=1, that is χ²=1, contrary to our assumption. This is the point where we need the assumption that χ is not quadratic. This guarantees that, when m≤2ℓ−1, $P(q_{v}^{-s},q_{v}^{s})$ has a simple zero at $s=\frac{\ell}{2}$. □

We obtain the following corollary, which proves Theorem 1.5 on the pole at $s=\frac{\ell}{2}$ of $\mathcal{E}(\theta _{\Delta (\tau ,m+\ell )},f_{\Delta (\tau ,\ell ),s};h)$.

Corollary 4.7

At the point $s=\frac{\ell}{2}$, $\mathcal{E}(\theta _{\Delta (\tau ,m+\ell )},f_{\Delta (\tau ,\ell ),s};h)$ has at most a simple pole, when m≥2ℓ, and at most a double pole, when ℓ≤m≤2ℓ−1.

As Kudla and Rallis do in [KR94], (5.5.23), (5.5.24), we regularize the integral (1.3) as follows. Consider the Laurent expansion of $\mathcal{E}(\theta _{\Delta (\tau ,m+\ell )},f_{\Delta (\tau ,\ell ),s};h)$ at $s=\frac{\ell}{2}$. The leading term, when m≥2ℓ, is the residue, which we denote by $B_{-1}(h, \theta _{\Delta (\tau ,m+\ell )},f_{\Delta (\tau ,\ell ), \frac{\ell}{2}})$. When m≤2ℓ−1, the leading term is the coefficient of $(s-\frac{\ell}{2})^{-2}$, which we denote by $B_{-2}(h, \theta _{\Delta (\tau ,m+\ell )},f_{\Delta (\tau ,\ell ), \frac{\ell}{2}})$. Thus, we regularize (1.3), by

$$ E_{reg}(\theta _{\Delta (\tau ,m+\ell )}, \theta _{\Delta (\tau , \ell )};h)= \textstyle\begin{cases} B_{-1}(h, \theta _{\Delta (\tau ,m+\ell )},f_{\Delta (\tau ,\ell ), \frac{\ell}{2}}),\ \ 2\ell \leq m \\ B_{-2}(h, \theta _{\Delta (\tau ,m+\ell )},f_{\Delta (\tau ,\ell ), \frac{\ell}{2}}),\ \ \ell \leq m\leq 2\ell -1 \end{cases}\displaystyle . $$

(4.29)

5 Proof of Theorem 1.4

Our goal in this section is to identify $\mathcal{E}(\theta _{\Delta (\tau ,m+\ell )},f_{\Delta (\tau ,\ell ),s};h)$ as an Eisenstein series on ${\mathrm {Sp}}_{4m}({\mathbb{A}})$, attached to ${\mathrm {Ind}}_{Q_{2\ell}({\mathbb{A}})}^{{\mathrm {Sp}}_{4m}({\mathbb{A}})}\Delta (\tau ,\ell )|\det \cdot |^{s}\otimes \Theta _{\Delta (\tau ,m-\ell )}$. In Theorem 5.1, we unfold $\mathcal{E}(\theta _{\Delta (\tau ,m+\ell )},f_{\Delta (\tau ,\ell ),s};h)$, for Re(s) sufficiently large, and write it as an “Eisenstein summation”, over Q_2ℓ(F)∖Sp_4m(F), of an explicit section. Later on, in Prop. 5.2-5.4, we show that this section is meromorphic and analyze its poles.

Theorem 5.1

Assume that θ_Δ(τ,m+ℓ) is i(K_4ℓ×K_4m)-finite. Let f_Δ(τ,ℓ),s be a smooth, holomorphic section of ρ_Δ(τ,ℓ),s (see (1.1)). Then, for Re(s) sufficiently large, we have, for all $h\in {\mathrm {Sp}}_{4m}({\mathbb{A}})$,

$$ \begin{gathered}[t] \int _{{\mathrm {Sp}}_{4\ell}(F)\backslash {\mathrm {Sp}}_{4\ell}({\mathbb{A}})}(1 \otimes \xi _{m,\ell ,v})\ast \theta _{\Delta (\tau ,m+\ell )}(i(g,h))E(f_{ \Delta (\tau ,\ell ),s};g)dg= \\ =\sum _{\gamma \in Q_{2\ell}(F)\backslash {\mathrm {Sp}}_{4m}(F)}F(f_{\Delta ( \tau ,\ell ),s},(1\otimes \xi _{m,\ell ,v})\ast \theta _{\Delta ( \tau ,m+\ell )};\gamma h), \end{gathered} $$

(5.1)

where

$$ F(f_{\Delta (\tau ,\ell ),s},\theta _{\Delta (\tau ,m+\ell )};h) = \int _{U_{2\ell}({\mathbb{A}})\backslash {\mathrm {Sp}}_{4\ell}({\mathbb{A}})}\theta ^{U_{4 \ell},\psi _{V_{(2\ell )^{2}}}}_{\Delta (\tau ,m+\ell )}(i(g,h))f_{ \Delta (\tau ,\ell ),s}(g)dg. $$

(5.2)

(See right after (3.33) for the definition of the Fourier coefficient $\theta ^{U_{4\ell},\psi _{V_{(2\ell )^{2}}}}_{\Delta (\tau ,m+\ell )}$.) The integral (5.2) converges absolutely for Re(s) sufficiently large and, in this domain of convergence, F(f_Δ(τ,ℓ),s,θ_Δ(τ,m+ℓ);⋅) defines a K_4m-finite, holomorphic section of

$$ \rho _{\Delta (\tau ,\ell )|\det \cdot |^{s}\otimes \Theta _{\Delta ( \tau ,m-\ell )}}={\mathrm {Ind}}_{Q_{2\ell}({\mathbb{A}})}^{{\mathrm {Sp}}_{4m}({\mathbb{A}})}\Delta ( \tau ,\ell )|\det \cdot |^{s}\otimes \Theta _{\Delta (\tau ,m-\ell )}. $$

Remark: Later on in this section, we will prove that F(f_Δ(τ,ℓ),s,θ_Δ(τ,m+ℓ);h) in (5.2) has a meromorphic continuation to the complex plane and that its poles are contained in the set of poles of the L-function $L(\Delta (\tau ,\ell )\times \tau ,s+m-\ell +\frac{1}{2})$.

Proof

Since g↦(1⊗ξ_m,ℓ,v)∗θ_Δ(τ,m+ℓ)(i(g,h)) is rapidly decreasing, for any given h, the integral (5.1) converges absolutely, for all s, which is not a pole of E(f_Δ(τ,ℓ),s). Since we assume that θ_Δ(τ,m+ℓ) is i(K_4ℓ×K_4m)-finite, we may assume that f_Δ(τ,ℓ),s is K_4ℓ-finite. (The integral (5.1) factors through such sections). Write, for Re(s) sufficiently large,

$$ E(f_{\Delta (\tau ,\ell ),s};g)=\sum _{\gamma \in Q_{2\ell}(F) \backslash {\mathrm {Sp}}_{4\ell}(F)}f_{\Delta (\tau ,\ell ),s}(\gamma g), $$

and substitute in the l.h.s. of (5.1), which yields

$$ \int _{Q_{2\ell}(F)U_{2\ell}({\mathbb{A}})\backslash {\mathrm {Sp}}_{4\ell}( {\mathbb{A}})}(1\otimes \xi _{m,\ell ,v})\ast \theta ^{U_{2\ell}^{4\ell} \times 1}_{\Delta (\tau ,m+\ell )}(i(g,h))f_{\Delta (\tau ,\ell ),s}(g)dg. $$

By (3.34), this is equal to

$$ \sum _{\gamma \in Q_{2\ell}(F)\backslash {\mathrm {Sp}}_{4m}(F)}\int _{U_{2 \ell}({\mathbb{A}})\backslash {\mathrm {Sp}}_{4\ell}({\mathbb{A}})}(1\otimes \xi _{m,\ell ,v}) \ast \theta ^{U_{4\ell},\psi _{V_{(2\ell )^{2}}}}_{\Delta (\tau ,m+ \ell )}(g,\gamma h)f_{\Delta (\tau ,\ell ),s}(g)dg. $$

(5.3)

This is (5.1). In order to justify the passage to (5.3), we will show that, for Re(s) sufficiently large,

$$ \int _{U_{2\ell}({\mathbb{A}})\backslash {\mathrm {Sp}}_{4\ell}({\mathbb{A}})}|\theta ^{U_{4 \ell},\psi _{V_{(2\ell )^{2}}}}_{\Delta (\tau ,m+\ell )}(g, h)f_{ \Delta (\tau ,\ell ),s}(g)|dg< \infty , $$

(5.4)

for all K_4ℓ-finite f_Δ(τ,ℓ),s and i(K_4ℓ×K_4m)-finite elements θ_Δ(τ,m+ℓ)∈Θ_Δ(τ,m+ℓ). We will then show the assertion that F(f_Δ(τ,ℓ),s,θ_Δ(τ,m+ℓ);h) is a section of $\rho _{\Delta (\tau ,\ell )|\det \cdot |^{s}\otimes \Theta _{\Delta ( \tau ,m-\ell )}}$, so that the summation over γ in (5.3) is the usual summation defining an Eisenstein series, and hence it converges absolutely, since Re(s) is sufficiently large. We may assume that h=I_4m. Using the Iwasawa decomposition in ${\mathrm {Sp}}_{4\ell}({\mathbb{A}})$, it is enough to consider the integral

$$ \int _{{\mathrm {GL}}_{2\ell}({\mathbb{A}})}|\theta ^{U_{4\ell},\psi _{V_{(2 \ell )^{2}}}}_{\Delta (\tau ,m+\ell )}(\hat{a}, I_{4m})\varphi _{ \Delta (\tau ,\ell )}(a)| |det(a)|^{Re(s)-\ell -\frac{1}{2}}da, $$

(5.5)

where φ_Δ(τ,ℓ) is an automorphic form in the space of Δ(τ,ℓ). By Prop. 1.7, we may consider in place of (5.5), the integral

$$ \int _{{\mathrm {GL}}_{2\ell}({\mathbb{A}})}|\varphi ^{\psi _{V_{(2\ell )^{2}}}}_{ \Delta (\tau ,2\ell )}( \begin{pmatrix} a \\ &I_{2\ell}\end{pmatrix} )\varphi _{\Delta (\tau ,\ell )}(a)| |det(a)|^{Re(s)+m-\ell}da, $$

(5.6)

where φ_Δ(τ,2ℓ) is an automorphic form in the space of Δ(τ,2ℓ), and, for $y\in {\mathrm {GL}}_{4\ell}({\mathbb{A}})$,

$$ \varphi ^{\psi _{V_{(2\ell )^{2}}}}_{\Delta (\tau ,2\ell )}(y)=\int _{M_{2\ell}(F)\backslash M_{2\ell}({\mathbb{A}})}\varphi ^{\psi _{V_{(2 \ell )^{2}}}}_{\Delta (\tau ,2\ell )}( \begin{pmatrix} I_{2\ell}&x \\ &I_{2\ell}\end{pmatrix} y)\psi ^{-1}(tr(x))dx. $$

Let us rewrite (5.6) using the Cartan decomposition. We get

$$ \begin{gathered}[t] \int _{K_{{\mathrm {GL}}_{2\ell}}}\int _{T^{+}_{2\ell}({\mathbb{A}})} \int _{K_{{\mathrm {GL}}_{2\ell}}}|\varphi ^{\psi _{V_{(2\ell )^{2}}}}_{ \Delta (\tau ,2\ell )}( \begin{pmatrix} k_{1}tk_{2} \\ &I_{2\ell}\end{pmatrix} )\varphi _{\Delta (\tau ,\ell )}(k_{1}tk_{2})|\\ {}\times |det(t)|^{Re(s)+m-\ell} \gamma (t)dk_{1}dtdk_{2}, \end{gathered} $$

(5.7)

where $T^{+}_{2\ell}({\mathbb{A}})$ denotes the set of diagonal matrices $t=diag(t_{1},\ldots,t_{2\ell})\in T_{2\ell}({\mathbb{A}})$, such that at any place ν, |t_1,ν|_ν≤|t_2,ν|_ν≤⋯≤|t_2ℓ,ν|_ν, and, for ν archimedean, t_1,ν,…,t_2ℓ,ν, are all positive. Finally, γ(a)=∏_vγ_ν(a_ν), where γ_ν is the positive weight function, which appears in the measure determined by the Cartan decomposition. By Lemma 12 in [C+21], we have in (5.7)

$$ \varphi ^{\psi _{V_{(2\ell )^{2}}}}_{\Delta (\tau ,2\ell )}( \begin{pmatrix} k_{1}tk_{2} \\ &I_{2\ell}\end{pmatrix} )=\varphi ^{\psi _{V_{(2\ell )^{2}}}}_{\Delta (\tau ,2\ell )}( \begin{pmatrix} tk_{2} \\ &k_{1}^{-1}\end{pmatrix} ). $$

Hence, due to the $K_{{\mathrm {GL}}_{4\ell}}$-finiteness of φ_Δ(τ,2ℓ), it is enough to consider

$$ \int _{T^{+}_{2\ell}({\mathbb{A}})}|\varphi ^{\psi _{V_{(2\ell )^{2}}}}_{ \Delta (\tau ,2\ell )}( \begin{pmatrix} t \\ &I_{2\ell}\end{pmatrix} )\xi _{\Delta (\tau ,\ell )}(t)| |det(t)|^{Re(s)+m-\ell}\gamma (t)dt, $$

(5.8)

where ξ_Δ(τ,ℓ) is a matrix coefficient of Δ(τ,ℓ). If $\varphi ^{\psi _{V_{(2\ell )^{2}}}}_{\Delta (\tau ,2\ell )}( \begin{pmatrix} t \\ &I_{2\ell}\end{pmatrix} )\neq 0$, then, for each finite place ν, |t_2ℓ,ν|_ν≤A_ν, and A_ν=1, for almost all finite ν. The argument is standard. We take a matrix z∈M_2ℓ(F_ν), close to zero. Think of z as an element of $M_{2\ell}({\mathbb{A}})$ having the zero coordinate at all places other than ν. We take z sufficiently close to zero, so that φ_Δ(τ,2ℓ) is fixed by the right translation by $\begin{pmatrix} I_{2\ell}&z \\ &I_{2\ell}\end{pmatrix}$. Then we get, for all such z,

$$ \varphi ^{\psi _{V_{(2\ell )^{2}}}}_{\Delta (\tau ,2\ell )}( \begin{pmatrix} t \\ &I_{2\ell}\end{pmatrix} )=\psi _{\nu}(tr(t_{\nu }z))\varphi ^{\psi _{V_{(2\ell )^{2}}}}_{ \Delta (\tau ,2\ell )}( \begin{pmatrix} t \\ &I_{2\ell}\end{pmatrix} ). $$

This necessarily bounds |t_2ℓ|_ν as we want. The analogue at an archimedean place ν is that $\varphi ^{\psi _{V_{(2\ell )^{2}}}}_{\Delta (\tau ,2\ell )}( \begin{pmatrix} t \\ &I_{2\ell}\end{pmatrix} )$ is rapidly decreasing as t_2ℓ,ν tends to infinity. We omit the details. Using the moderate growth of φ_Δ(τ,ℓ), ξ_Δ(τ,2ℓ), we may bound (5.8) by

$$ c'\int _{T^{+}_{2\ell}({\mathbb{A}})}\phi (t)||t||^{A} |det(t)|^{Re(s)+m- \ell}\gamma (t)dt, $$

(5.9)

where c′,A>0 and $\phi \in \mathcal{S}({\mathbb{A}}^{2\ell})$ is a positive Schwartz function. Let $t\in T^{+}_{2\ell}({\mathbb{A}})$. Then, for a finite place ν, $\gamma _{\nu}(t_{\nu})\leq \delta ^{-1}_{B_{{\mathrm {GL}}_{2\ell}}}(t_{\nu})$. For an archimedean place ν, there is c″>0, such that $\gamma _{\nu}(t_{\nu})\leq c''\delta ^{-1}_{B_{{\mathrm {GL}}_{2\ell}}}(t_{\nu})$. Thus, the integral (5.9) is majorized by

$$ c\int _{T^{+}_{2\ell}({\mathbb{A}})}\phi (t)||t||^{A} |det(t)|^{Re(s)+m- \ell}\delta ^{-1}_{B_{{\mathrm {GL}}_{2\ell}}}(t)dt,\ \ c,\ A>0. $$

(5.10)

The integral (5.10) converges for Re(s) sufficiently large. This proves (5.4).

Assume that Re(s) is sufficiently large, so that the integral (5.2) converges absolutely. We will show now that F(f_Δ(τ,ℓ),s,θ_Δ(τ,m+ℓ);h) is a section of $\rho _{\Delta (\tau ,\ell )|\det \cdot |^{s}\otimes \Theta _{\Delta ( \tau ,m-\ell )}}$. It is immediate to check that F(f_Δ(τ,ℓ),s,θ_Δ(τ,m+ℓ);h) is left invariant to $U_{2\ell}^{4m}({\mathbb{A}})$. Let $a\in {\mathrm {GL}}_{2\ell}({\mathbb{A}})$, $b\in {\mathrm {Sp}}_{4(m-\ell )}({\mathbb{A}})$. Then

$F(f_{\Delta (\tau ,\ell ),s},\theta _{\Delta (\tau ,m+\ell )}; \begin{pmatrix} a \\ &b \\ &&a^{*}\end{pmatrix} h)=$

$$ =\int _{U_{2\ell}({\mathbb{A}})\backslash {\mathrm {Sp}}_{4\ell}({\mathbb{A}})}\theta ^{U_{4 \ell},\psi _{V_{(2\ell )^{2}}}}_{\Delta (\tau ,m+\ell )}( \begin{pmatrix} I_{2\ell} \\ &a \\ &&b \\ &&&a^{*} \\ &&&&I_{2\ell}\end{pmatrix} i(g,h))f_{\Delta (\tau ,\ell ),s}(g)dg. $$

(5.11)

As in (5.6), using Prop. 1.7, the first factor of the integrand in (5.11) has the form

$$ q( \begin{pmatrix} I_{2\ell} \\ &a \\ &&b \\ &&&a^{*} \\ &&&&I_{2\ell}\end{pmatrix} i(g,h)), $$

(5.12)

where q is a function in the space of

$$ {\mathrm {Ind}}_{Q_{4\ell}({\mathbb{A}})}^{{\mathrm {Sp}}_{4(m+\ell )}({\mathbb{A}})}\Delta _{\psi}(\tau ,2 \ell )|\det \cdot |^{-m}\otimes \Theta _{\Delta (\tau ,m-\ell )}. $$

(5.13)

Here, Δ_ψ(τ,2ℓ) denotes the representation of ${\mathrm {GL}}_{4\ell}({\mathbb{A}})$, by right translations in the space of functions $\varphi ^{\psi _{V_{(2\ell )^{2}}}}_{\Delta (\tau ,2\ell )}$, where φ_Δ(τ,2ℓ) lies in the space of Δ(τ,2ℓ). By Lemma 12 in [C+21], (5.12) is equal to

$$ |\det (a)|^{2m+1}q(i(\hat{a}^{-1}g, \begin{pmatrix} I_{2\ell} \\ &b \\ &&I_{2\ell}\end{pmatrix} h)). $$

Substituting in (5.11), and changing variable $g\mapsto \hat{a}g$, we get

$$ |\det (a)|^{2(m-\ell )}\int _{U_{2\ell}({\mathbb{A}})\backslash {\mathrm {Sp}}_{4 \ell}({\mathbb{A}})}\theta ^{U_{4\ell},\psi _{V_{(2\ell )^{2}}}}_{\Delta ( \tau ,m+\ell )}(i(g, \begin{pmatrix} I_{2\ell} \\ &b \\ &&I_{2\ell}\end{pmatrix} h))f_{\Delta (\tau ,\ell ),s}(\hat{a}g)dg. $$

(5.14)

We may take h=I_4m. Using the Iwasawa decomposition in ${\mathrm {Sp}}_{4\ell}({\mathbb{A}})$, the K_4ℓ-finiteness of the integrand, and (5.13), we get that (5.14) is a finite sum

$\delta _{Q_{2\ell}^{4m}}^{\frac{1}{2}}( \begin{pmatrix} a \\ &I_{4(m-\ell )} \\ &&a^{*}\end{pmatrix} )|\det (a)|^{s}\sum _{j=1}^{N}\theta ^{(j)}_{\Delta (\tau ,m-\ell )}(b) \cdot$

$$ \cdot \int _{{\mathrm {GL}}_{2\ell}({\mathbb{A}})}\varphi ^{(j)}_{\Delta (\tau , \ell )}(ac)(\varphi _{\Delta (\tau ,2\ell )}^{(j)})^{\psi _{V_{(2 \ell )^{2}}}}( \begin{pmatrix} c \\ &I_{2\ell}\end{pmatrix} )|\det (c)|^{s+m-\ell}dc. $$

(5.15)

Here, $\varphi ^{(j)}_{\Delta (\tau ,\ell )}$, $\varphi _{\Delta (\tau ,2 \ell )}^{(j)}$, $\theta ^{(j)}_{\Delta (\tau ,m-\ell )}$ are K-finite elements of Δ(τ,ℓ), Δ(τ,2ℓ), Θ_{Δ(τ,m−ℓ)}, respectively. The integral in (5.15), as a function of a, defines a function in the space of Δ(τ,ℓ). Formally, this is clear. To justify this, we use the Cartan decomposition, exactly as we did in the first part of the proof, and express the integral in (5.15) as a finite sum of the form

$$ \sum _{j'} \int _{T^{+}_{2\ell}({\mathbb{A}})}\xi ^{(j')}_{\Delta ( \tau ,\ell )}(t)(\tilde{\varphi}_{\Delta (\tau ,2\ell )}^{(j')})^{ \psi _{V_{(2\ell )^{2}}}}( \begin{pmatrix} t \\ &I_{2\ell}\end{pmatrix} )\gamma (t) |\det (t)|^{s+m-\ell}dt\cdot \tilde{\varphi}^{(j')}_{ \Delta (\tau ,\ell )}(a), $$

(5.16)

where $\xi ^{(j')}_{\Delta (\tau ,\ell )}$ are matrix coefficients of Δ(τ,ℓ), and $\tilde{\varphi}_{\Delta (\tau ,2\ell )}^{(j')}$, $\tilde{\varphi}_{ \Delta (\tau ,\ell )}^{(j')}$ are elements of Δ(τ,2ℓ), Δ(τ,ℓ), respectively. Recall that we have seen in the first part of the proof that the integrals in (5.16) converge absolutely, for Re(s) sufficiently large. This shows that F(f_Δ(τ,ℓ),s,θ_Δ(τ,m+ℓ);h) is a section of $\rho _{\Delta (\tau ,\ell )|\det \cdot |^{s}\otimes \Theta _{\Delta ( \tau ,m-\ell )}}$, and the proof of the theorem is complete. □

We note that without using the Cartan decomposition, we can express the integral in (5.15), as a finite sum, as follows, instead of (5.16),

$$ \sum _{j} \int _{{\mathrm {GL}}_{2\ell}({\mathbb{A}})}\eta ^{(j)}_{\Delta ( \tau ,\ell )}(c)(\phi _{\Delta (\tau ,2\ell )}^{(j)})^{\psi _{V_{(2 \ell )^{2}}}}( \begin{pmatrix} c \\ &I_{2\ell}\end{pmatrix} )|\det (c)|^{s+m-\ell}dc\cdot \phi ^{(j)}_{\Delta (\tau ,\ell )}(a), $$

(5.17)

where $\eta ^{(j)}_{\Delta (\tau ,\ell )}$ are matrix coefficients of Δ(τ,ℓ), and $\phi _{\Delta (\tau ,2\ell )}^{(j)}$, $\phi _{\Delta (\tau ,\ell )}^{(j)}$ are elements of Δ(τ,2ℓ), Δ(τ,ℓ), respectively.

We now address the issue of analytic continuation of F(f_Δ(τ,ℓ),s,θ_Δ(τ,m+ℓ);h). We view $\theta ^{U_{4\ell},\psi _{V_{(2\ell )^{2}}}}_{\Delta (\tau ,m+\ell )}$ as an element in the space of (5.13). Let ν be a place of F. Denote the local factor at ν of Δ(τ,2ℓ) by Δ(τ_ν,2ℓ), realized in a space $V_{\Delta (\tau _{\nu},2\ell )}$. Denote the local factor at ν of Θ_{Δ(τ,m−ℓ)} by Θ_{Δ(τ,m−ℓ),ν}, realized in a space $V_{\Theta _{\Delta (\tau ,m-\ell )},\nu}$. Note that, up to scalars, there is a unique (continuous when ν is archimedean) linear functional $C^{\psi _{\nu}}$ on $V_{\Delta (\tau _{\nu},2\ell )}$, such that, for all $\xi \in V_{\Delta (\tau _{\nu},2\ell )}$,

$$ C^{\psi _{\nu}}(\Delta (\tau _{\nu},2\ell )( \begin{pmatrix} I_{2\ell}&x \\ &I_{2\ell}\end{pmatrix} )\xi )=\psi _{\nu}(tr(x))C^{\psi _{\nu}}(\xi ). $$

The uniqueness property is proved in [C+21], Theorem 4. We may then realize Δ(τ_ν,2ℓ) in the space C(Δ(τ_ν,2ℓ),ψ_ν) of functions on GL_2ℓ(F_ν), $a\mapsto C^{\psi _{\nu}}(\Delta (\tau _{\nu},2\ell )(a)u_{\nu})$, $u_{\nu}\in V_{\Delta (\tau _{\nu},2\ell )}$. Thus, we can write the analogous local sections of F(f_Δ(τ,ℓ),s,θ_Δ(τ,m+ℓ);h) at each place and consider them for decomposable data. For this, we fix isomorphisms p_τ,2ℓ, p_τ,ℓ, q_τ,m−ℓ of $\otimes _{\nu}'\Delta (\tau _{\nu},2\ell )$, $\otimes '_{\nu}\Delta ( \tau _{\nu},\ell )$, $\otimes '_{\nu}\Theta _{\Delta (\tau _{,}m-\ell ),\nu}$ with Δ(τ,2ℓ), Δ(τ,ℓ), Θ_{Δ(τ,m−ℓ)}, respectively. Let S₀ be a finite set of places of F, containing the infinite places, outside which τ is unramified. For ν∉S₀, fix unramified vectors $v^{0}_{\tau _{\nu},\ell}\in V_{\Delta (\tau _{\nu},\ell )}$, $\eta ^{0}_{\tau _{\nu},m-\ell}\in V_{\Theta _{\Delta (\tau ,m-\ell )}, \nu}$, and $W^{0}_{\Delta (\tau _{\nu},2\ell )}\in C(\Delta (\tau _{\nu},2\ell ), \psi _{\nu})$, such that $W^{0}_{\Delta (\tau _{\nu},2\ell )}(I_{4\ell})=1$. For each place ν, let $f_{\Delta (\tau _{\nu},\ell ),s}$ be a K_4ℓ,ν-finite, holomorphic section of $\rho _{\Delta (\tau _{\nu},\ell ),s}$, and let $f_{C(\Delta (\tau _{\nu},2\ell ),\psi _{\nu}),\Theta _{\Delta (\tau ,m- \ell )},\nu}$ be a K_4ℓ,ν×K_4m,ν-finite function in the space of

$$ {\mathrm {Ind}}_{Q_{4\ell}(F_{\nu})}^{{\mathrm {Sp}}_{4(m+\ell )}(F_{\nu})}C(\Delta ( \tau _{\nu},2\ell ),\psi _{\nu})|\det \cdot |^{-m}\otimes \Theta _{ \Delta (\tau ,m-\ell ),\nu}. $$

(5.18)

Denote by $f'_{C(\Delta (\tau _{\nu},2\ell ),\psi _{\nu}),\Theta _{\Delta ( \tau ,m-\ell )},\nu}$ the function $f_{C(\Delta (\tau _{\nu},2\ell ),\psi _{\nu}),\Theta _{\Delta (\tau ,m- \ell )},\nu}$ composed with the evaluation at a=I_4ℓ in the GL_4ℓ(F_ν) factor. Let S be a finite set of places, containing S₀. Assume that for ν∉S, $f_{\Delta (\tau _{\nu},\ell ),s}=f^{0}_{\Delta (\tau _{\nu},\ell ),s}$ is the unramified section, such that $f^{0}_{\Delta (\tau _{\nu},\ell ),s}(I_{4\ell})=v^{0}_{\tau _{\nu}, \ell}$, and, similarly, $f_{C(\Delta (\tau _{\nu},2\ell ),\psi _{\nu}),\Theta _{\Delta (\tau ,m- \ell )},\nu}=f^{0}_{C(\Delta (\tau _{\nu},2\ell ),\psi _{\nu}), \Theta _{\Delta (\tau ,m-\ell )},\nu}$ is the unramified vector taking the value $W^{0}_{\Delta (\tau _{\nu},2\ell )}\otimes \eta ^{0}_{\tau _{\nu},m- \ell}$ at I_4(m+ℓ). Define, for a place ν of F, and for h∈Sp_4m(F_ν),

$F_{\nu}(f_{\Delta (\tau _{\nu},\ell ),s},f_{C(\Delta (\tau _{\nu},2 \ell ),\psi _{\nu}),\Theta _{\Delta (\tau ,m-\ell )},\nu};h)=$

$$ =\int _{U_{2\ell}(F_{\nu})\backslash {\mathrm {Sp}}_{4\ell}(F_{\nu})} f_{ \Delta (\tau _{\nu},\ell ),s}(g)\otimes f'_{C(\Delta (\tau _{\nu},2 \ell ),\psi _{\nu}),\Theta _{\Delta (\tau ,m-\ell )},\nu}(i(g,h))dg. $$

(5.19)

For given g, h, the integrand is an element of Δ(τ_ν,ℓ)⊗Θ_{Δ(τ,m−ℓ),ν}. Assume that in (5.2),

$$ f_{\Delta (\tau ,\ell ),s}=p_{\tau ,\ell}\circ (\otimes _{\nu }f_{ \Delta (\tau _{\nu},\ell ),s}), $$

$$ \theta _{\Delta (\tau ,m+\ell )}^{U_{4\ell},\psi _{V_{(2\ell )^{2}}}}=(p_{ \tau ,2\ell}\otimes q_{\tau ,m-\ell})\circ (\otimes _{\nu }f_{C( \Delta (\tau _{\nu},2\ell ),\psi _{\nu}),\Theta _{\Delta (\tau ,m- \ell )},\nu}). $$

Then

$$\begin{aligned} &F(f_{\Delta (\tau ,\ell ),s},\theta _{\Delta (\tau ,m+\ell )};h)\\ &\quad =(p_{ \tau ,\ell}\circ q_{\tau ,m-\ell})(\otimes _{\nu }F_{\nu}(f_{\Delta ( \tau _{\nu},\ell ),s},f_{C(\Delta (\tau _{\nu},2\ell ),\psi _{\nu}), \Theta _{\Delta (\tau ,m-\ell )},\nu};h_{\nu})). \end{aligned}$$

In complete analogy with the last part of the proof of Theorem 5.1, we see that $F_{\nu}(f_{\Delta (\tau _{\nu},\ell ),s},f_{C(\Delta (\tau _{\nu},2 \ell ),\psi _{\nu}),\Theta _{\Delta (\tau ,m-\ell )},\nu};\cdot )$, for Re(s) sufficiently large, is a K_4m,ν-finite section of ${\mathrm {Ind}}_{Q_{2\ell}(F_{\nu})}^{{\mathrm {Sp}}_{4m}(F_{\nu})}\Delta (\tau _{\nu}, \ell )|\det \cdot |^{s}\otimes \Theta _{\Delta (\tau ,m-\ell ),\nu}$. In fact, analogously with (5.15), (5.16) (and notation as well), we get, for a∈GL_2ℓ(F_ν), b∈Sp_4(m−ℓ)(F_ν), that it is a finite sum

$F_{\nu}(f_{\Delta (\tau _{\nu},\ell ),s},f_{C(\Delta (\tau _{\nu},2 \ell ),\psi _{\nu}),\Theta _{\Delta (\tau ,m-\ell )},\nu}; \begin{pmatrix} a \\ &b \\ &&a^{*}\end{pmatrix} )=\delta _{Q_{2\ell}^{4m}}^{\frac{1}{2}}(\hat{a})|\det (a)|^{s}$

$$ \sum _{r} (\int _{T^{+}_{2\ell}(F_{\nu})}\xi ^{(r)}_{\Delta ( \tau _{\nu},\ell )}(t)W^{(r)}_{\Delta (\tau _{\nu},2\ell )}( \begin{pmatrix} t \\ &I_{2\ell}\end{pmatrix} )\gamma _{\nu}(t)|\det (t)|^{s+m-\ell}dt)\cdot $$

(5.20)

$$ \Delta (\tau _{\nu},\ell )(a)\varphi ^{(r)}_{\Delta (\tau _{\nu}, \ell )}\otimes \Theta _{\Delta (\tau ,m-\ell ),\nu}(b)\theta ^{(r)}_{ \Delta (\tau _{\nu},m-\ell )}. $$

As in (5.17), we can write the following expression instead of (5.20),

$F_{\nu}(f_{\Delta (\tau _{\nu},\ell ),s},f_{C(\Delta (\tau _{\nu},2 \ell ),\psi _{\nu}),\Theta _{\Delta (\tau ,m-\ell )},\nu}; \begin{pmatrix} a \\ &b \\ &&a^{*}\end{pmatrix} )=\delta _{Q_{2\ell}^{4m}}^{\frac{1}{2}}(\hat{a})|\det (a)|^{s}$

$$ \sum _{r'} (\int _{{\mathrm {GL}}_{2\ell}(F_{\nu})}\xi ^{(r')}_{\Delta ( \tau _{\nu},\ell )}(g)W^{(r')}_{\Delta (\tau _{\nu},2\ell )}( \begin{pmatrix} g \\ &I_{2\ell}\end{pmatrix} )|\det (g)|^{s+m-\ell}dg)\cdot $$

(5.21)

$$ \Delta (\tau _{\nu},\ell )(a)\varphi ^{(r')}_{\Delta (\tau _{\nu}, \ell )}\otimes \Theta _{\Delta (\tau ,m-\ell ),\nu}(b)\theta ^{(r')}_{ \Delta (\tau _{\nu},m-\ell )}. $$

Denote

$$ \mathcal{L}(\xi _{\Delta (\tau _{\nu},\ell )},W_{\Delta (\tau _{\nu},2 \ell )},s)=\int _{{\mathrm {GL}}_{2\ell}(F_{\nu})}\xi _{\Delta (\tau _{ \nu},\ell )}(g)W_{\Delta (\tau _{\nu},2\ell )}( \begin{pmatrix} g \\ &I_{2\ell}\end{pmatrix} )|\det (g)|^{s+m-\ell}dg. $$

We note that, for ν∉S₀, when data are unramified, normalized, and with the measure of K_4ℓ,ν taken to be 1, (5.21), evaluated at the identity, becomes

$$ F_{\nu}(f^{0}_{\Delta (\tau _{\nu},\ell ),s},f^{0}_{C(\Delta (\tau _{ \nu},2\ell ),\psi _{v}),\Theta _{\Delta (\tau ,m-\ell )},\nu};I_{4m})= \mathcal{L}(\xi ^{0}_{\Delta (\tau _{\nu},\ell )},W^{0}_{\Delta ( \tau _{\nu},2\ell )},s)\cdot (v^{0}_{\tau _{\nu},\ell}\otimes \eta ^{0}_{ \tau _{\nu},m-\ell}). $$

(5.22)

Here, $\xi ^{0}_{\Delta (\tau _{\nu},\ell )}$ is the spherical matrix coefficient of Δ(τ_ν,ℓ). Assume, also, that, for ν∉S, ψ_ν is normalized. As in the last proof, the integrals in (5.20), (5.21), converge absolutely for Re(s) sufficiently large. The integrals $\mathcal{L}(\xi _{\Delta (\tau _{\nu},\ell )},W_{\Delta (\tau _{\nu},2 \ell )},s)$ appear in the local theory of global integrals considered in [Gin18]. They are also a special case of the local integrals considered in Appendix C of [CFK18]. We thank the referee for pointing this to us, which made the proofs of the following three propositions just a matter of quoting [CFK18], for the first two, and quoting [Ito21], for the third.

Proposition 5.2

In the notation of (5.22), for Re(s) sufficiently large,

$$ \mathcal{L}(\xi ^{0}_{\Delta (\tau _{\nu},\ell )},W^{0}_{\Delta ( \tau _{\nu},2\ell )},s)=L(\Delta (\tau _{\nu},\ell )\times \tau _{\nu},s+m- \ell +\frac{1}{2}). $$

(5.23)

Proof

The proof follows by applying inductively the computation (C.10) in [CFK18] in the unramified case, with unramified data. For our case, take in [CFK18], Appendix C, π=Δ(τ_ν,ℓ), c=2ℓ, k=2 and τ in [CFK18] is τ_ν here. Also, in this case, the complex parameter considered in [CFK18] (appearing in the power of |det(g)| in the integral) is $s-\frac{1}{2}$, while here, it is s+m−ℓ. In our case, we get

$\mathcal{L}(\xi ^{0}_{\Delta (\tau _{\nu},\ell )},W^{0}_{\Delta ( \tau _{\nu},2\ell )},s)=$

$$ \prod _{i=1}^{\ell}\int _{F_{\nu}^{*}}W^{0}_{\tau _{\nu}, \psi _{\nu}}( \begin{pmatrix} t_{2i-1} \\ &1\end{pmatrix} )\chi _{\nu}(t_{2i-1})|t_{2i-1}|^{s+m-\ell +\frac{2i-1-\ell}{2}}d^{*}t_{2i-1} \cdot $$

$$ \cdot \prod _{i=1}^{\ell}\int _{F_{\nu}^{*}}W^{0}_{\tau _{\nu}, \psi _{\nu}}( \begin{pmatrix} t_{2i} \\ &1\end{pmatrix} )\chi _{\nu}^{-1}(t_{2i})|t_{2i}|^{s+m-\ell +\frac{2i-1-\ell}{2}}d^{*}t_{2i}. $$

The factors in the last products are the Jacquet-Langlands local unramified integrals for $\tau _{\nu}\times \chi _{\nu}^{\pm 1}$, which give

$$ \prod _{i=1}^{\ell }L(\tau _{\nu}\times \chi _{\nu},s+m-\ell + \frac{2i-\ell}{2})L(\tau _{\nu}\times \chi ^{-1}_{\nu},s+m-\ell + \frac{2i-\ell}{2})= $$

(5.24)

$$ =L(\Delta (\tau _{\nu},\ell )\times \tau _{\nu},s+m-\ell +\frac{1}{2}). $$

 □

More generally, we have

Proposition 5.3

In the previous notation, for a given place ν, assume that $\tau _{\nu}={\mathrm {Ind}}_{B_{{\mathrm {GL}}_{2}}}^{{\mathrm {GL}}_{2}(F_{v})}\chi _{\nu}\times \chi _{\nu}^{-1}$ (χ_ν is not necessarily unramified, and ν is not necessarily finite). Then $\mathcal{L}(\xi _{\Delta (\tau _{\nu},\ell )},W_{\Delta (\tau _{\nu},2 \ell )},s)$ is a meromorphic function. It is a finite sum of the form

$$ \sum \prod _{i=1}^{\ell }L(W_{i},\chi _{\nu},s+m-\ell + \frac{2i-1-\ell}{2})L(W'_{i},\chi ^{-1}_{\nu},s+m-\ell + \frac{2i-1-\ell}{2}), $$

where $W_{i},W'_{i}\in W(\tau _{\nu},\psi _{\nu})$, and L(W_i,χ_ν,z) is the analytic continuation of the Jacquet-Langlands local integral, which converges absolutely for Re(z) large,

$$ \int _{F_{\nu}^{*}}W_{i}( \begin{pmatrix} t \\ &1\end{pmatrix} )\chi _{\nu}(t)|t|^{z}d^{*}t. $$

Proof

Again, the proof follows from the identity (C.10) in [CFK18], applied inductively. It implies that, in our case, $\mathcal{L}(\xi _{\Delta (\tau _{\nu},\ell )},W_{\Delta (\tau _{\nu},2 \ell )},s)$ can be expressed as a sum of products of the integrals considered in [CFK18], Appendix C, corresponding to the “most basic” parabolic data inducing π=Δ(τ_ν,ℓ). Thus, we get the products of integrals corresponding to χ_ν×τ_ν at $s+m-\ell +\frac{2i-\ell}{2}$ and $\chi ^{-1}_{\nu}\times \tau _{\nu}$ at $s+m-\ell +\frac{2i-\ell}{2}$, i=1,2,…,ℓ. Each such integral is a local Jacquet-Langlands integral. This also provides the meromorphic continuation of $\mathcal{L}(\xi _{\Delta (\tau _{\nu},\ell )},W_{\Delta (\tau _{\nu},2 \ell )},s)$. □

The last case to consider is a finite place ν where τ_ν is supercuspidal, and then we have

Proposition 5.4

Assume that τ_ν is supercuspidal. Then $\mathcal{L}(\xi _{\Delta (\tau _{\nu},\ell )},W_{\Delta (\tau _{\nu},2 \ell )},s)$ is a rational function of $q_{\nu}^{-s}$. Moreover,

$$ \mathcal{L}(\xi _{\Delta (\tau _{\nu},\ell )},W_{\Delta (\tau _{\nu},2 \ell )},s)\in {\mathbb{C}}[q_{\nu}^{-s},q_{\nu}^{s}]L(\Delta (\tau _{\nu}, \ell )\times \tau _{\nu},s+m-\ell +\frac{1}{2}). $$

Proof

This follows from Theorem 0.1 (i), (iii) of Ito in [Ito21]. □

Altogether, Propositions 5.2–5.4 give,

Corollary 5.5

In the notation of (5.19)–(5.22), consider a decomposable section F(f_Δ(τ,ℓ),s,θ_Δ(τ,m+ℓ);h) corresponding to $\otimes _{\nu }F_{\nu}(f_{\Delta (\tau _{\nu},\ell ),s},f_{C(\Delta ( \tau _{\nu},2\ell ),\psi _{\nu}),\Theta _{\Delta (\tau ,m-\ell )},\nu}; h_{ \nu})$. Then each local section $F_{\nu}(f_{\Delta (\tau _{\nu},\ell ),s},f_{C(\Delta (\tau _{\nu},2 \ell ),\psi _{\nu}),\Theta _{\Delta (\tau ,m-\ell )},\nu};h_{\nu})$ is meromorphic in the complex plane. Moreover,

$$ \frac{F_{\nu}(f_{\Delta (\tau _{\nu},\ell ),s},f_{C(\Delta (\tau _{\nu},2\ell ),\psi _{\nu}),\Theta _{\Delta (\tau ,m-\ell )},\nu};h_{\nu})}{L(\Delta (\tau _{\nu},\ell )\times \tau _{\nu},s+m-\ell +\frac{1}{2})} $$

is holomorphic, and, for ν finite, it lies in ${\mathbb{C}}[q_{\nu}^{-s},q_{\nu}^{s}]$. For ν∉S,

$F_{\nu}(f^{0}_{\Delta (\tau _{\nu},\ell ),s},f^{0}_{C(\Delta (\tau _{ \nu},2\ell ),\psi _{\nu}),\Theta _{\Delta (\tau _{\nu},m-\ell )}};I_{4m})=$

$$ =L(\Delta (\tau _{\nu},\ell )\times \tau _{\nu},s+m-\ell +\frac{1}{2}) \cdot (v^{0}_{\tau _{\nu},\ell}\otimes \eta ^{0}_{\tau _{\nu},m-\ell}). $$

Theorem 5.1 and Corollary 5.5 prove Theorem 1.4, and together with Corollary 4.7, we also get Theorem 1.5.

6 An analogy with the work of Kudla-Rallis, conjectural new Siegel-Weil formulas and applications

In this section, we review the work of Kudla and Rallis on the Siegel formula, mainly from [KR94], focusing on and connecting, as in the introduction of [GQT14], the theta correspondence, Rallis inner product formula, Siegel-Weil formula, the doubling method and L-functions. We will point the analogy with our work, formulate conjectures and potential applications.

6.1 The work of Kudla and Rallis

Consider a dual pair (Sp_2n,O_2m) inside Sp_4mn, where O_2m is an orthogonal group corresponding to a 2m-dimensional space V over F, equipped with a nondegenerate, symmetric bilinear F-form, with Witt index r. We assume that O_2m is not binary and split. Denote by χ_V the corresponding quadratic character of $F^{*}\backslash {\mathbb{A}}^{*}$. Fix ψ, a nontrivial character of $F\backslash {\mathbb{A}}$. Let π be an irreducible, cuspidal, automorphic representation of ${\mathrm {Sp}}_{2n}({\mathbb{A}})$, and consider θ_ψ,2m(π) – the theta lift (with respect to ψ) of π to ${\mathrm {O}}_{2m}({\mathbb{A}})$. Its space is spanned by the functions on ${\mathrm {O}}_{2m}({\mathbb{A}})$,

$$ \theta _{\psi ,2m}^{\phi}(\varphi _{\pi})(h)=\int _{{\mathrm {Sp}}_{2n}(F) \backslash {\mathrm {Sp}}_{2n}({\mathbb{A}})}\theta _{\psi ,4mn}^{\phi}(g,h)\varphi _{ \pi}(g)dg, $$

(6.1)

where φ_π is a cusp form in the space of π, $\phi \in \mathcal{S}(V({\mathbb{A}})^{n})$, and $\theta _{\psi ,4mn}^{\phi}(g,h)$ is the pullback to ${\mathrm {Sp}}_{2n}({\mathbb{A}})\times {\mathrm {O}}_{2m}({\mathbb{A}})$ of the theta series on the double cover $\widetilde{{\mathrm {Sp}}}_{4mn}({\mathbb{A}})$ of ${\mathrm {Sp}}_{4mn}({\mathbb{A}})$,

$$ \theta _{\psi ,4mn}^{\phi}(x)=\sum _{\alpha \in V(F)^{n}} \omega _{\psi ,4mn}(x)\phi (\alpha ),\ \ x\in \widetilde{{\mathrm {Sp}}}_{4mn}( {\mathbb{A}}). $$

Here, ω_ψ,4mn denotes the Weil representation of $\widetilde{{\mathrm {Sp}}}_{4mn}({\mathbb{A}})$, corresponding to ψ, acting in $\mathcal{S}(V({\mathbb{A}})^{n})$. Our $T_{\tau}^{4k-2n}(\varphi _{\pi},\theta _{\Delta (\tau ,k)})$ in (1.2) is an analog of (6.1). To study the question of non-vanishing of θ_ψ,2m(π), consider, formally, the L²-inner product of two theta lifts of the form (6.1). Applying one more formal manipulation, we get

$$\begin{aligned} &(\theta _{\psi ,2m}^{\phi _{1}}(\varphi _{\pi}), \theta _{\psi ,2m}^{ \phi _{2}}(\varphi '_{\pi}))= \\ &\quad =\int \varphi _{\pi}(g_{1})\bar{\varphi}'_{\pi}(g_{2})(\int _{ {\mathrm {O}}_{2m}(F)\backslash {\mathrm {O}}_{m}({\mathbb{A}}) }\theta _{\psi ,4mn}^{\phi _{1}}(g_{1},h) \theta _{\psi ^{-1},4mn}^{\bar{\phi _{2}}}(g_{2},h)dh)dg_{1}dg_{2}, \end{aligned}$$

(6.2)

where g₁ and g₂ are integrated over ${\mathrm {Sp}}_{2n}(F)\backslash {\mathrm {Sp}}_{2n}({\mathbb{A}})$. The goal is to make sense out of the integral (6.2), which may diverge. The first thing is to note that the dh-integrand in (6.2) can be expressed as one theta series. This is the multiplicative property of theta series, which is easy to establish, namely, for $g_{1},g_{2}\in {\mathrm {Sp}}_{2n}({\mathbb{A}})$, $h\in {\mathrm {O}}_{2m}({\mathbb{A}})$,

$$ \theta _{\psi ,4mn}^{\phi _{1}}(g_{1},h)\theta _{\psi ^{-1},4mn}^{ \bar{\phi _{2}}}(g_{2},h)=\theta _{\psi ,8mn}^{\phi _{1}\otimes \bar{\phi}_{2}}((g_{1},g_{2}),h). $$

(6.3)

The r.h.s. of (6.3) is a theta series on $\widetilde{{\mathrm {Sp}}}_{8mn}({\mathbb{A}})$, pulled back, first, to ${\mathrm {Sp}}_{4n}({\mathbb{A}})\times {\mathrm {O}}_{2m}({\mathbb{A}})$, and then to $({\mathrm {Sp}}_{2n}({\mathbb{A}})\times {\mathrm {Sp}}_{2n}({\mathbb{A}}))\times {\mathrm {O}}_{2m}({\mathbb{A}})$. In our case, we don’t have presently an analog of (6.3). Later on, we will comment on a possible analog in our case, which seems to be quite involved. The next step in figuring out the meaning of (6.2) is to interpret the dh-inner integral, using (6.3), that is, for $g\in {\mathrm {Sp}}_{4n}({\mathbb{A}})$, $\Phi \in \mathcal{S}(V({\mathbb{A}})^{2n})$ ($\Phi = \phi _{1}\otimes \bar{\phi}_{2}$ in (6.2)), we want to interpret

$$ I(\Phi ,g)=\int _{{\mathrm {O}}_{2m}(F)\backslash {\mathrm {O}}_{2m}({\mathbb{A}})} \theta _{\psi ,8mn}^{\Phi}(g,h)dh. $$

(6.4)

The integral (6.4) is absolutely convergent when r=0, or when 2m−r>2n+1. In this range, we have the Siegel-Weil formula, proved by Weil and Kudla-Rallis,

$$ I(\Phi ,g)=\kappa E(f_{\Phi ,s},g)\Big|_{s=s_{0}}, $$

(6.5)

where $s_{0}=m-n-\frac{1}{2}$, κ=1,2 and E(f_Φ,s) is the Eisenstein series on ${\mathrm {Sp}}_{4n}({\mathbb{A}})$, attached to the Siegel-Weil section f_Φ,s of the parabolic induction ${\mathrm {Ind}}_{Q_{2n}({\mathbb{A}})}^{{\mathrm {Sp}}_{4n}({\mathbb{A}})}(\chi _{V}\circ \det ) |\det \cdot |^{s}$,

$$ f_{\Phi ,s}(g)=\omega _{\psi ,8mn}(g,I_{2m})\Phi (0)a(g)^{s-s_{0}}. $$

(6.6)

Here, a(g) is obtained by writing the Iwasawa decomposition $g=\hat{m}_{g}u_{g}k_{g}$, where k_g∈K_4n, $u_{g}\in U_{2n}({\mathbb{A}})$, $m_{g}\in {\mathrm {GL}}_{2n}({\mathbb{A}})$. Then a(g)=|det(m_g)|. Note that ω_ψ,8mn(x)Φ(0) is the constant term at x of $\theta _{\psi ,8mn}^{\Phi}$ along the Siegel radical $U^{8mn}_{4mn}$,

$$ \int _{U_{4mn}(F)\backslash U_{4mn}({\mathbb{A}})}\theta _{\psi ,8mn}^{ \Phi}(ux)du= \omega _{\psi ,8mn}(x)\Phi (0). $$

(6.7)

When we substitute (6.5), with $\Phi =\phi _{1}\otimes \bar{\phi}_{2}$, in (6.2), we get

$(\theta _{\psi ,2m}^{\phi _{1}}(\varphi _{\pi}), \theta _{\psi ,2m}^{ \phi _{2}}(\varphi '_{\pi}))=$

$$ =\kappa \int _{{\mathrm {Sp}}_{2n}(F)\times {\mathrm {Sp}}_{2n}(F)\backslash {\mathrm {Sp}}_{2n}( {\mathbb{A}})\times {\mathrm {Sp}}_{2n}({\mathbb{A}})}\varphi _{\pi}(g_{1})\bar{\varphi}'_{\pi}(g_{2})E(f_{ \Phi ,s},(g_{1},g_{2}))\Big|_{s=s_{0}}dg_{1}dg_{2}. $$

(6.8)

This is the global integral of the doubling method of Piatetski-Shapiro and Rallis [PR87], at s=s₀. This global integral represents $L(\pi \times \chi _{V},s+\frac{1}{2})$, up to normalization. In our case, the analogous integrals of the generalized doubling method of [C+19] show up.

Regularization: In the range 2m−r≤2n+1, r≥1, Kudla and Rallis found explicit nonzero elements $z\in \mathfrak{z}_{\scriptstyle{sp_{4n}(F_{\nu})}}$, $z'\in \mathfrak{z}_{\scriptstyle{o_{2m}(F_{\nu})}}$, in the centers of the enveloping algebras of the Lie algebras of Sp_4n(F_ν), O_2m(F_ν), at one archimedean place ν, such that the following theorem holds.

Theorem 6.1

[Kudla, Rallis] For all $\Phi \in \mathcal{S}(V({\mathbb{A}})^{2n})$,

$$ \omega _{\psi ,8mn}(z)\Phi =\omega _{\psi ,8mn}(z')\Phi , $$

(6.9)

and $\theta _{\psi ,8mn}^{\omega _{\psi ,8mn}(z)\Phi}(g,h)$ is rapidly decreasing in $h\in {\mathrm {O}}_{2m}(F)\backslash {\mathrm {O}}_{2m}({\mathbb{A}})$.

Ichino obtained a similar result by convolving Φ against a function in the spherical Hecke algebra of Sp_4n(F_v), at one nonarchimedean place v. See [Ich01], Sect. 1. Our Theorems 2.2, 4.1 are the analogs of Theorem 6.1. Next, Kudla and Rallis took an Eisenstein series E(h,ζ) on ${\mathrm {O}}_{2m}({\mathbb{A}})$, attached to the maximal parabolic subgroup with Levi part isomorphic to GL_r×O_2(m−r) and the character $|\det _{{\mathrm {GL}}_{r}}\cdot |^{\zeta}$. This Eisenstein series has a simple pole at $\zeta _{0}=m-\frac{r+1}{2}$, with constant residue. Then they introduce

$$ \mathcal{E}(g,\Phi ,\zeta )=\frac{1}{P(\zeta )}\int _{{\mathrm {O}}_{2m}(F) \backslash {\mathrm {O}}_{2m}({\mathbb{A}})}\theta _{\psi ,8mn}^{\omega _{\psi ,8mn}(z) \Phi}(g,h)E(h,\zeta )dh, $$

(6.10)

where P(ζ) is the polynomial obtained by the action of z′ on E(h,ζ). Note that the integral (6.10) converges absolutely, away from the poles of E(h,ζ).

Theorem 6.2

[Kudla, Rallis] $\mathcal{E}(g,\Phi ,\zeta )$ is an Eisenstein series on ${\mathrm {Sp}}_{4n}({\mathbb{A}})$ attached to Q_r and the representation $|\det _{{\mathrm {GL}}_{r}}\cdot |^{\zeta }\otimes \theta _{\psi , 2(2n-r)}(1_{ {\mathrm {O}}(V_{an})})$, where $\theta _{\psi , 2(2n-r)}(1_{{\mathrm {O}}(V_{an})})$ denotes the theta lift to ${\mathrm {Sp}}_{2(2n-r)}({\mathbb{A}})$ of the trivial representation of the adele points of the orthogonal group of the anisotropic kernel V_an of V.

Our analog of (6.10) is the integral (4.28) and the analog of Theorem 6.2 is Theorem 1.4. Note, again, that in (6.10), the residue of E(h,ζ) at ζ₀ is constant. Our analog is that the residue of E(f_Δ(τ,ℓ),s) at $s=\frac{\ell}{2}$ is θ_Δ(τ,ℓ),s. The integral in (1.7) is formed out of the integral (1.3) exactly as the integral in (6.10) is formed out of the integral (6.4). The analog of the polynomial P(ζ) is our polynomial $P(q_{v}^{-s},q_{v}^{s})$. Kudla and Rallis compute P(ζ) explicitly and find out that when m≤n (and then 2m−r≤2n+1), P(ζ₀)≠0, so that $\mathcal{E}(g,\Phi ,\zeta )$ has at most a simple pole at ζ₀, and then

$$ Res_{\zeta =\zeta _{0}} \mathcal{E}(g,\Phi ,\zeta )= \frac{c}{P(\zeta _{0})}\int _{{\mathrm {O}}_{2m}(F)\backslash {\mathrm {O}}_{2m}( {\mathbb{A}})}\theta _{\psi ,8mn}^{\omega _{\psi ,8mn}(z)\Phi}(g,h)dh, $$

(6.11)

where $c=Res_{\zeta =\zeta _{0}}E(h,\zeta )$. This is the interpretation, or the regularization of the integral (6.4). Denote $B_{-1}(g,\Phi )=Res_{\zeta =\zeta _{0}} \mathcal{E}(g,\Phi ,\zeta )$. When m>n and 2m−r≤2n+1, P(ζ₀)=0, so that $\mathcal{E}(g,\Phi ,\zeta )$ has at most a double pole at ζ₀. Denote by B₋₂(g,Φ) the leading term of the Laurent expansion of $\mathcal{E}(g,\Phi ,\zeta )$ about ζ₀. Our analog to this is Corollary 4.7. In (4.29), we used a similar notation for the leading term of the Laurent series. The generalization of the Siegel-Weil formula (6.5), in the convergence range, is the following theorem with formulation (partly) adapted from [GQT14], p. 746, 747.

Theorem 6.3

The regularized Siegel-Weil formula: first term identity

1. Assume that m≤n, so that $s_{0}\leq -\frac{1}{2}$. Then E(f_Φ,s,g) is holomorphic at s₀ and

$$ B_{-1}(g,\Phi )=\frac{1}{2}Value_{s=s_{0}}E(f_{\Phi ,s},g). $$

2. Assume that 1≤r≤2n and 2n+2≤2m≤2n+r+1, so that $s_{0}\geq \frac{1}{2}$. Then

$$ B_{-2}(g,\Phi )=Res_{s=s_{0}}E(f_{\Phi ,s},g)=B_{-1}(g,\Phi '), $$

where Φ′ is an appropriate function in $\mathcal{S}(V'({\mathbb{A}})^{2n})$, and V′ is the complementary space of V.

See [KR94], p. 4, for the notion of complementary spaces. We also recall that $s_{0}=m-n+\frac{1}{2}$ and $\zeta _{0}=m-\frac{r+1}{2}$. Now, as in (6.8), assume that χ is a quadratic character of $F^{*}\backslash {\mathbb{A}}^{*}$, such that the partial L-function L^S(π×χ,s) has a pole at s=k, a positive integer. Kudla and Rallis show that these are the only possible poles, and that necessarily $k\leq [\frac{n}{2}]+1$. Let $\tilde{m}=n+k$. Using the doubling integral, as in (6.8), to represent this L-function, they show that there is a quadratic space $\tilde{V}$ over F, of dimension $2\tilde{m}$, with $\chi =\chi _{\tilde{V}}$, and $\tilde{\Phi}\in \mathcal{S}(\tilde{V}({\mathbb{A}})^{2n})$, such that the following integral is not (identically) zero,

$$ \int _{{\mathrm {Sp}}_{2n}(F)\times {\mathrm {Sp}}_{2n}(F)\backslash {\mathrm {Sp}}_{2n}( {\mathbb{A}})\times {\mathrm {Sp}}_{2n}({\mathbb{A}})}\varphi _{\pi}(g_{1})\bar{\varphi}'_{\pi}(g_{2}) {\mathrm {Res}}_{s=\tilde{s_{0}}}(E(f_{\tilde{\Phi},s},(g_{1},g_{2})))dg_{1}dg_{,} $$

where $\tilde{s_{0}}=\tilde{m}-n-\frac{1}{2}$. By Theorem 6.3(2), the following integral is not identically zero,

$$ \int _{{\mathrm {Sp}}_{2n}(F)\times {\mathrm {Sp}}_{2n}(F)\backslash {\mathrm {Sp}}_{2n}( {\mathbb{A}})\times {\mathrm {Sp}}_{2n}({\mathbb{A}})}\varphi _{\pi}(g_{1})\bar{\varphi}'_{\pi}(g_{2})B_{-1}( \Phi ,(g_{1},g_{2})))dg_{1}dg_{2}, $$

where $\Phi \in \mathcal{S}(V({\mathbb{A}})^{2n})$, and V is the quadratic space, complementary to $\tilde{V}$; $dim(V)=4n+2-2\tilde{m}=2n+2-2k:=2m$. Kudla and Rallis show that there are $\phi _{1}, \phi _{2}\in \mathcal{S}(V({\mathbb{A}})^{n})$, such that we may replace in the last integral Φ′ by $\phi _{1}\otimes \bar{\phi}_{2}$. Using (6.10), (6.3), we conclude that the theta lift of π to ${\mathrm {O}}_{2m}({\mathbb{A}})$ (corresponding to V) is nontrivial. This was one of the main goals of Kudla and Rallis, that is

Theorem 6.4

Kudla, Rallis

Let π be an irreducible, cuspidal, automorphic representation of ${\mathrm {Sp}}_{2n}({\mathbb{A}})$, and χ, a quadratic character of $F^{*}\backslash {\mathbb{A}}^{*}$. Assume that L^S(π×χ,s) has a pole at s=k, a positive integer. Then $k\leq [\frac{n}{2}]+1$, and there is a quadratic space V, over F, of dimension 2m, m=n+1−k, and χ_V=χ, such that the theta lift of π, θ_ψ,2m(π), to ${\mathrm {O}}_{2m}({\mathbb{A}})$, corresponding to V, is nontrivial.

6.2 Conjectures

Our program follows a similar itinerary, guided by the poles of the L-functions for ${\mathrm {Sp}}_{2n}({\mathbb{A}})\times {\mathrm {GL}}_{d}({\mathbb{A}})$, L(π×τ,s), where π, τ are irreducible, cuspidal, automorphic representations of ${\mathrm {Sp}}_{2n}({\mathbb{A}})$, ${\mathrm {GL}}_{d}({\mathbb{A}})$, respectively. We use the generalized doubling integrals of Cai, Friedberg, Ginzburg and Kaplan [C+19] in order to represent L(π×τ,s). In this paper, we considered the case d=2. As we explained before, the role of the theta correspondence is played by the Θ_Δ(τ,ℓ)-correspondence from ${\mathrm {Sp}}_{2n}({\mathbb{A}})$ to ${\mathrm {Sp}}_{4\ell -2n}({\mathbb{A}})$. The analog of characterizing the poles of L(π×χ,s) by the theta correspondence from a smaller orthogonal group will be that the poles of L(π×τ,s) are characterized by the new theta correspondence with respect to τ, and also by the property that π is CAP, as in Theorem 1.1. Then we ask whether there is a related new Siegel-Weil formula. Thus, let us consider the question of nonvanishing of Θ_Δ(τ,ℓ)(π). As in (6.2), we consider, formally, the inner product of two functions of the form (1.2),

$$\begin{aligned} &( T_{\tau}^{4\ell -2n}(\varphi _{\pi},\theta _{\Delta (\tau ,\ell )}),T_{ \tau}^{4\ell -2n}(\varphi '_{\pi},\theta '_{\Delta (\tau ,\ell )}))= \\ &\quad =\int _{[{\mathrm {Sp}}_{2n}\times {\mathrm {Sp}}_{2n}]}\varphi _{\pi}(g_{1}) \bar{\varphi}'_{\pi}(g_{2})(\int _{[{\mathrm {Sp}}_{4\ell -2n}]}\theta _{ \Delta (\tau ,\ell )}(g_{1},h) \overline{\theta '_{\Delta (\tau ,\ell )}(g_{2},h)}dh)dg_{1}dg_{2}. \end{aligned}$$

(6.12)

Here, we used the short-hand notation $[G]=G(F)\backslash G({\mathbb{A}})$. Of course, all of (6.12) is formal, and we want to make sense out of the r.h.s. of (6.12). For this, we need to interpret the inner dh-integration. Thus, we would like to have an analog of the multiplicative property (6.3) of classical theta series. Then we would like to find an analog of the regularized Siegel-Weil formula, Theorem 6.3, which will interpret and relate the inner product (6.12), as in (6.8) and the proof of Theorem 6.4, to the generalized doubling integrals [C+19], representing L(π×τ,s).

Assume that π is as in the first case of Theorem 1.1. In particular, $\frac{n}{2}\leq \ell < n$. Let S be a finite set of places of F, containing the archimedean places, outside which π is unramified. Assume also that L^S(σ×τ,s) is holomorphic and nonzero at $s=n-\ell +\frac{1}{2}$, for example, when σ is generic. (The representation σ is related to π as in Theorem 1.1(1).) Then L^S(π×τ,s) has a simple pole at $s=n-\ell +\frac{1}{2}$. Let us represent $L^{S}(\pi \times \tau ,s+\frac{1}{2})$ by the generalized doubling integrals. These have the form

$$ \mathcal{L}(\varphi _{\pi},\varphi '_{\pi},f_{\Delta (\tau ,2n),s})= \int _{[{\mathrm {Sp}}_{2n}\times {\mathrm {Sp}}_{2n}]}\varphi _{\pi}(g_{1}) \bar{\varphi}'_{\pi}(g_{2})E^{\psi _{U_{2n}}}(f_{\Delta (\tau ,2n),s})(t(g_{1},g_{2}))dg_{1}dg_{2}, $$

(6.13)

where $E^{\psi _{U_{2n}}}(f_{\Delta (\tau ,2n),s})$ denotes the following Fourier coefficient along $U^{8n}_{2n}$,

$$ E^{\psi _{U_{2n}}}(f_{\Delta (\tau ,2n),s})(x)=\int _{U_{2n}(F) \backslash U_{2n}({\mathbb{A}})}E(f_{\Delta (\tau ,2n),s})(ux)\psi ^{-1}_{U_{2n}}(u)du, $$

and $\psi _{U_{2n}}$ is the following character of $U_{2n}({\mathbb{A}})$. Let

$$ u= \begin{pmatrix} I_{2n}&y&z \\ &I_{4n}&y' \\ &&I_{2n}\end{pmatrix} \in U_{2n}({\mathbb{A}}). $$

Then, when we write y=(y₁,y₂,y₃), $y_{1},y_{3}\in M_{2n\times n}({\mathbb{A}})$,

$$ \psi _{U_{2n}}(u)=\psi (tr([y_{1},y_{3}])). $$

(6.14)

Finally, for $g_{i}\in {\mathrm {Sp}}_{2n}({\mathbb{A}})$, i=1,2, and $g_{1}= \begin{pmatrix} a_{1}&b_{1} \\ c_{1}&d_{1}\end{pmatrix}$, with n×n blocks,

$$ t(g_{1},g_{2})= \begin{pmatrix} g_{1} \\ &a_{1}&&b_{1} \\ &&g_{2} \\ &c_{1}&&d_{1} \\ &&&&g_{1}^{*}\end{pmatrix} . $$

We conclude that there exist data, such that

$$ \int _{[{\mathrm {Sp}}_{2n}\times {\mathrm {Sp}}_{2n}]}\varphi _{\pi}(g_{1}) \bar{\varphi}'_{\pi}(g_{2})Res_{s=n-\ell}(E(f_{\Delta (\tau ,2n),s}))^{ \psi _{U_{2n}}}(t(g_{1},g_{2}))dg_{1}dg_{2}\neq 0. $$

(6.15)

This line of thought suggests that the inner dh-integral in the r.h.s. of (6.12) should be related to the residue inside the integral (6.15), namely, for some choice of data

$$ \int _{[{\mathrm {Sp}}_{4\ell -2n}]}\theta _{\Delta (\tau ,\ell )}(g_{1},h) \overline{\theta '_{\Delta (\tau ,\ell )}(g_{2},h)}dh=Res_{s=n-\ell}(E(f_{ \Delta (\tau ,2n),s}))^{\psi _{U_{2n}}}(t(g_{1},g_{2})). $$

(6.16)

We are still at the formal level since the l.h.s. of (6.16) may diverge. Let us apply, still formally, the Θ_{Δ(τ,2n+ℓ)}-correspondence (1.2) to the non-cuspidal representation Θ_Δ(τ,ℓ), that is, for $h\in {\mathrm {Sp}}_{8n}({\mathbb{A}})$,

$$ T^{8n}(\theta _{\Delta (\tau ,\ell )}, \theta _{\Delta (\tau ,2n+ \ell )})(h)=\int _{{\mathrm {Sp}}_{4\ell}(F)\backslash {\mathrm {Sp}}_{4\ell}( {\mathbb{A}})}\theta _{\Delta (\tau ,2n+\ell )}(g,h)\theta _{\Delta (\tau , \ell )}(g)dg. $$

(6.17)

When one examines the proof of Theorem 1.1, one can see that the unramified parameters of the representation of ${\mathrm {Sp}}_{8n}({\mathbb{A}})$ generated by the functions T⁸ⁿ(θ_Δ(τ,ℓ),θ_{Δ(τ,2n+ℓ)}), that is Θ_{Δ(τ,2n+ℓ)}(Θ_Δ(τ,ℓ)) (pretending that it exists), are identical to those of the representation generated by the residues Res_s=n−ℓ(E(f_Δ(τ,2n),s)). Thus, we expect the following crude, formal type of a Siegel-Weil formula,

Conjecture 6.5

(Siegel-Weil formula; formal, crude form) Assume that 1≤ℓ<n. Given θ_Δ(τ,ℓ), θ_{Δ(τ,2n+ℓ)}, there is a section $f'_{\Delta (\tau ,2n),s}$, such that, for $h\in {\mathrm {Sp}}_{8n}({\mathbb{A}})$,

$$ \int _{{\mathrm {Sp}}_{4\ell}(F)\backslash {\mathrm {Sp}}_{4\ell}({\mathbb{A}})}\theta _{ \Delta (\tau ,2n+\ell )}(g,h)\theta _{\Delta (\tau ,\ell )}(g)dg =Res_{s=n- \ell}(E(f'_{\Delta (\tau ,2n),s}))(h). $$

(6.18)

The main work of this paper was to regularize the l.h.s. of (6.18) and interprate it in terms of the Eisenstein series $\mathcal{E}(\theta _{\Delta (\tau ,m+\ell )},f_{\Delta (\tau ,\ell ),s};h)$ at the point $s=\frac{\ell}{2}$. Also, since (6.18) is independent of π, we replaced 2n by m (which now can be odd). The integral (6.18) becomes now E(θ_Δ(τ,m+ℓ),θ_Δ(τ,ℓ);h) in (1.3), which we regularized as E_reg(θ_Δ(τ,m+ℓ),θ_Δ(τ,ℓ);h) in (1.11) (also (4.29)). We played informally with experiments trying to prove Conjecture 6.5, such as comparing certain constant terms of both sides of (5.18) (with the l.h.s. regularized). As a result, and with an analogy to the regularized Siegel-Weil formula for classical dual pairs, we came up with a more precise formulation of the last conjecture. In order to write it down, we need to propose, first, an explicit expression of $f'_{\Delta (\tau ,2n),s}$ depending on θ_Δ(τ,ℓ), θ_{Δ(τ,2n+ℓ)} in Conjecture 6.5. Is there an analog of the Siegel-Weil section as in (6.6)? We propose the following analog which can be tracked down to a certain term in the Fourier expansion of the constant term along the Siegel radical of the Eisenstein series $\mathcal{E}(\theta _{\Delta (\tau ,m+\ell )},f_{\Delta (\tau ,\ell ),s};h)$. Consider the constant term of θ_Δ(τ,m+ℓ), along the unipotent radical $U_{2m}=U_{2m}^{4(m+\ell )}$,

$$ \theta ^{U_{2m}}_{\Delta (\tau ,m+\ell )}(x)=\int _{U_{2m}(F) \backslash U_{2m}({\mathbb{A}})}\theta _{\Delta (\tau ,m+\ell )}(ux)dx. $$

Define

$$ \Phi (\theta _{\Delta (\tau ,\ell )}, \theta _{\Delta (\tau ,m+\ell )})(h)= \int _{{\mathrm {Sp}}_{4\ell}(F)\backslash {\mathrm {Sp}}_{4\ell}({\mathbb{A}})}\theta ^{U_{2m}}_{ \Delta (\tau ,m+\ell )}(i^{*}(g,h)w)\theta _{\Delta (\tau ,\ell )}(g)dg, $$

(6.19)

where, in the notation of (1.12), i^∗(g,h) is obtained from i(g,h) by switching g and h, and w is a Weyl element which does this switch by conjugating i(g,h). Thus, writing $h= \begin{pmatrix} h_{1}&h_{2} \\ h_{3}&h_{4}\end{pmatrix}$, where h_i, 1≤i≤4, are 2m×2m matrices,

$$ i^{*}(g,h)= \begin{pmatrix} h_{1}&&h_{2} \\ &g \\ h_{3}&&h_{4}\end{pmatrix} . $$

The integral (6.19) converges absolutely. Indeed, it is enough to consider (6.19) when h=I_4m. By Prop. 1.7, the function $g\mapsto \theta ^{U_{2m}}_{\Delta (\tau ,m+\ell )}(i^{*}(g,I_{4m})w)$ lies in the space of Θ_Δ(τ,ℓ), which, by Prop. 1.6, is square-integrable.

Define

$$ \Phi (\theta _{\Delta (\tau ,\ell )}, \theta _{\Delta (\tau ,m+\ell )},s)(h)=a(h)^{s+ \frac{m-2\ell}{2}}\Phi (\theta _{\Delta (\tau ,\ell )}, \theta _{ \Delta (\tau ,m+\ell )})(h), $$

(6.20)

where a(h) is as in the definition of the Siegel-Weil section (6.6). One can check that Φ(θ_Δ(τ,ℓ),θ_Δ(τ,m+ℓ),s) is a section of ρ_Δ(τ,m),s. This is our proposed analog of a Siegel-Weil section. Note the analogy with the Siegel-Weil section (6.6). It depends on the constant term (6.7) of $\theta ^{\Phi}_{\psi ,8mn}$ along U_4mn and the section (6.20) depends on the constant term $\theta ^{U_{2m}}_{\Delta (\tau ,m+\ell )}$.

Consider the Eisenstein series on ${\mathrm {Sp}}_{4m}({\mathbb{A}})$ attached to the section Φ(θ_Δ(τ,ℓ),θ_Δ(τ,m+ℓ),s), E(Φ(θ_Δ(τ,ℓ),θ_Δ(τ,m+ℓ),s)). Then a more precise form of Conjecture 6.5 is

Conjecture 6.6

1. Assume that m≥2ℓ. Then E(Φ(θ_Δ(τ,ℓ),θ_Δ(τ,m+ℓ),s)) is holomorphic at $s=\frac{2\ell -m}{2}$, and, up to a possible constant, for all $h\in {\mathrm {Sp}}_{4m}({\mathbb{A}})$,

$$ B_{-1}(h, \theta _{\Delta (\tau ,m+\ell )},f_{\Delta (\tau ,\ell ), \frac{\ell}{2}}) =Value_{s=\frac{2\ell -m}{2}}E(\Phi (\theta _{ \Delta (\tau ,\ell )}, \theta _{\Delta (\tau ,m+\ell )},s))(h). $$

2. Assume that ℓ≤m≤2ℓ−1. Then, up to a possible constant, for all $h\in {\mathrm {Sp}}_{4m}({\mathbb{A}})$,

$$ B_{-2}(h, \theta _{\Delta (\tau ,m+\ell )},f_{\Delta (\tau ,\ell ), \frac{\ell}{2}}) =Res_{s=\frac{2\ell -m}{2}}E(\Phi (\theta _{\Delta ( \tau ,\ell )}, \theta _{\Delta (\tau ,m+\ell )},s))(h). $$

We remark that in comparing (1) in the last conjecture with Conjecture 6.5, when m>2ℓ, we expect that the value on the r.h.s. of (1) is equal to the residue at $s=\frac{m-2\ell}{2}$ of the Eisenstein series of some corresponding section $f'_{\Delta (\tau ,m),s}$. In view of (6.16), in case m=2n is even, we expect

Conjecture 6.7

crude, formal form

Assume that $\frac{n}{2}\leq \ell < n$. Given θ_{Δ(τ,2n+ℓ)}, θ_Δ(τ,ℓ), there exist $\theta '_{\Delta (\tau ,\ell )}$, $\theta ''_{\Delta (\tau ,\ell )}$, such that

$$ \int _{U_{2n}^{8n}(F)\backslash U_{2n}^{8n}({\mathbb{A}})}\int _{{\mathrm {Sp}}_{4\ell}(F)\backslash {\mathrm {Sp}}_{4\ell}({\mathbb{A}})}\theta _{ \Delta (\tau ,2n+\ell )}(g,u\cdot t(g_{1},g_{2}))\theta _{\Delta ( \tau ,\ell )}(g)\psi ^{-1}_{U_{2n}}(u)dgdu= $$

$$ =\int _{{\mathrm {Sp}}_{4\ell -2n}(F)\backslash {\mathrm {Sp}}_{4\ell -2n}({\mathbb{A}})} \theta '_{\Delta (\tau ,\ell )}(g_{1},h) \overline{\theta ''_{\Delta (\tau ,\ell )}(g_{2},h)}dh. $$

Both sides of the last equality should be regularized. We view Conjecture 6.7 as an analog of the multiplicative property (6.3) of theta series. As an application that we expect, we will have the following analog of Theorem 6.4.

Conjecture 6.8

Let π be an irreducible, cuspidal, automorphic representation of ${\mathrm {Sp}}_{2n}({\mathbb{A}})$. Assume that L^S(π×τ,s) has its largest pole at $s=n-\ell +\frac{1}{2}$, where ℓ<n. Then $\ell \geq \frac{n}{2}$ and Θ_Δ(τ,ℓ)(π) is nonzero and cuspidal, so that by Theorem 1.1, π is CAP with respect to

$$ {\mathrm {Ind}}^{{\mathrm {Sp}}_{2n}({\mathbb{A}})}_{Q_{2(n-\ell )}({\mathbb{A}})}\Delta (\tau ,n-\ell )| \det \cdot |^{\frac{n-\ell}{2}}\otimes \sigma , $$

where σ is an irreducible (cuspidal) subrepresentation of Θ_Δ(τ,ℓ)(π).

We sketch some ideas for a possible proof of this conjecture, based on the conjectures above. By [GS212], Prop. 3.3, we have $n-\ell \leq \frac{n}{2}$, and hence $\ell \geq \frac{n}{2}$. As we explained before, we conclude that (6.15) is satisfied. Assuming that the section $f'_{\Delta (\tau ,2n),s}$ obtained in Conjecture 6.5 is sufficiently general, we conclude from Conjecture 6.6 and then Conjecture 6.7, that there exist $\theta '_{\Delta (\tau ,2n+\ell )}$, $\theta ''_{\Delta (\tau ,\ell )}$, such that

$$ \int _{[{\mathrm {Sp}}_{2n}\times {\mathrm {Sp}}_{2n}]}\int _{[{\mathrm {Sp}}_{4 \ell -2n}] }\varphi _{\pi}(g_{1})\bar{\varphi}'_{\pi}(g_{2})\theta '_{ \Delta (\tau ,\ell )}(g_{1},h) \overline{\theta ''_{\Delta (\tau ,\ell )}(g_{2},h)}dhdg_{1}dg_{2} \neq 0. $$

This is (6.12), and hence the Θ_Δ(τ,ℓ)-correspondence of π to ${\mathrm {Sp}}_{4n-2\ell}({\mathbb{A}})$ is nontrivial. Since $s=n-\ell +\frac{1}{2}$ is the largest pole of L^S(π×τ,s), one can show that Θ_Δ(τ,ℓ)(π) is cuspidal. Now we apply Theorem 1.1.

6.3 Generalizations

We comment on generalizations of the above conjectures. First, we may consider any irreducible, cuspidal, automorphic representation τ of GL_2d(A), such that L(τ,1/2)≠0 and L(τ,∧²,s) has a pole at s=1. Consider the irreducible, automorphic representations Θ_Δ(τ,ℓ), Θ_{Δ(τ,2n+(2d−1)ℓ)} of ${\mathrm {Sp}}_{4d\ell}({\mathbb{A}})$, ${\mathrm {Sp}}_{4d(2n+(2d-1)\ell )}({\mathbb{A}})$, respetively. Let $U=U_{(4d\ell )^{d-1}}^{4d(2n+(2d-1)\ell )}$ (the unipotent radical of the parabolic subgroup $Q_{(4d\ell )^{d-1}}\subset {\mathrm {Sp}}_{4d(2n+(2d-1)\ell )}$). Consider the unipotent orbit of Sp_{4d(2n+(2d−1)ℓ)} corresponding to the partition ((2d−1)^4dℓ1^8dn). Then one can define a character ψ_U of $U({\mathbb{A}})$, trivial on U(F), corresponding to this orbit, such that the stabilizer of this character, inside $GL_{4d\ell}^{d-1}({\mathbb{A}})\times Sp_{4d(2n+\ell )}({\mathbb{A}})$, is isomorphic to $Sp_{4d\ell}({\mathbb{A}})\times Sp_{8dn}({\mathbb{A}})$. For θ_{Δ(τ,2n+(2d−1)ℓ)}∈Θ_{Δ(τ,2n+(2d−1)ℓ)}, consider the Fourier coefficient

$$ \theta _{\Delta (\tau ,2n+(2d-1)\ell )}^{\psi _{U}}(x)=\int _{U(F) \backslash U({\mathbb{A}})}\theta _{\Delta (\tau ,2n+(2d-1)\ell )}(ux)\psi ^{-1}_{U}(u)du. $$

Recall that the Eisenstein series on $Sp_{8dn}({{\mathbb{A}}})$, E(f_Δ(τ,2n),s), has its positive poles at s=1,2,…,n. Our analog of Conjecture 6.6 (crude form and formal) is

Conjecture 6.9

Let θ_Δ(τ,ℓ)∈Θ_Δ(τ,ℓ), θ_{Δ(τ,2n+(2d−1)ℓ)}∈Θ_{Δ(τ,2n+(2d−1)ℓ)}.

1. Assume that 1≤ℓ≤n. Then there is a section f_Δ(τ,2n),s, such that E(f_Δ(τ,2n),s) is holomorphic at s=ℓ−n and

$$ \int _{Sp_{4d\ell}(F)\backslash Sp_{4d\ell}({{\mathbb{A}}})} \theta _{ \Delta (\tau ,2n+(2d-1)\ell )}^{\psi _{U}}((h,g))\theta _{\Delta ( \tau ,\ell )}(g)dg=Value_{s=\ell -n}E(f_{\Delta (\tau ,2n),s},h). $$

2. Assume that n<ℓ≤2n. Then there is a section f_Δ(τ,2n),s, such that

$$ \int _{Sp_{4d\ell}(F)\backslash Sp_{4d\ell}({{\mathbb{A}}})} \theta _{ \Delta (\tau ,2n+(2d-1)\ell )}^{\psi _{U}}((h,g))\theta _{\Delta ( \tau ,\ell )}(g)dg=Res_{s=\ell -n}E(f_{\Delta (\tau ,2n),s},h). $$

The previous case corresponds to d=1. The technical difference and difficulty here is the presence of the unipotent integration.

The next generalization to consider is for an irreducible, cuspidal, automorphic representation τ of ${\mathrm {GL}}_{d}({\mathbb{A}})$, such that L(τ,1/2)≠0 and L(τ,sym²,s) has a pole at s=1. In this case, we replace our “theta series” corresponding to τ by the following residual representation of the double cover ${\mathrm {Sp}}^{(2)}_{2dr}({\mathbb{A}})$ of ${\mathrm {Sp}}_{2dr}({\mathbb{A}})$. Consider the representation

$$ \rho ^{(2)}_{\Delta (\tau ,r),s;\psi}={\mathrm {Ind}}_{Q^{(2)}_{rd}({\mathbb{A}})}^{ {\mathrm {Sp}}^{(2)}_{2dr}({\mathbb{A}})}\Delta (\tau ,r)|\det \cdot |^{s}\gamma _{\psi}, $$

where γ_ψ is the Weil factor composed with the determinant. Let f_{Δ(τ,r),s;ψ} be a K_2dr-finite, holomorphic section of $\rho ^{(2)}_{\Delta (\tau ,r),s;\psi}$, and denote by E⁽²⁾(f_{Δ(τ,r),s;ψ}) the corresponding Eisenstein series on ${\mathrm {Sp}}^{(2)}_{2dr}({\mathbb{A}})$. Then, as the section varies, its positive poles are at $s=\frac{r}{2},\frac{r}{2}-1,\frac{r}{2}-2,\ldots$. We let $\Theta ^{(2)}_{\Delta (\tau ,r),\psi}$ denote the automorphic representation of ${\mathrm {Sp}}^{(2)}_{2dr}({\mathbb{A}})$ generated by the residues at the largest pole $Res_{s=\frac{r}{2}}E^{(2)}(f_{\Delta (\tau ,r),s;\psi})$. See [GS22]. Similarly, we can write theta representations corresponding to τ, self-dual and cuspidal, on split orthogonal groups, general linear groups and also on higher covers of all the groups above, and outline a similar program. We will deal with these in the future.