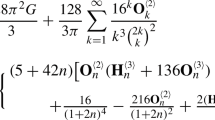Abstract
We examine the remarkable connection, first discovered by Beukers, Kolk and Calabi, between ζ(2n), the value of the Riemann Zeta-function at an even positive integer, and the volume of some 2n-dimensional polytope. It can be shown that this volume is equal to the trace of a compact self-adjoint operator. We provide an explicit expression for the kernel of this operator in terms of Euler polynomials. This explicit expression makes it easy to calculate the volume of the polytope and hence ζ(2n). In the case of odd positive integers, we rediscover an integral representation for ζ(2n + 1), obtained by a different method by Cvijović and Klinowski. Finally, we indicate that the origin of the miraculous Beukers–Kolk–Calabi change of variables in the multidimensional integral, which is at the heart of this circle of ideas, can be traced to the amoeba associated with the certain Laurent polynomial. The article is dedicated to the memory of Vladimir Arnold (1937–2010).
Similar content being viewed by others
Suggested Reading
V I Arnold, Problems for Kids from 5 to 15, MCNMO, Moscow, 2004, (in Russian).
A M Yaglom and I M Yaglom, Elementary Presentation of Nonelementary Problems, problem 143, Gostekhizdat, Moscow, 1954, (in Russian).
D Kalman, Six Ways to Sum a Series, College Math. J., Vol.24, pp.402–421, 1993.
K P Kokhas, Sum of inverse squares, Mathematicheskoe Prosveshenie, Vol.8, pp.142–163, 2004, (in Russian). See also informal notes by R Chapman, Evaluating ζ(2), http://www.secamlocal.ex.ac.uk/~rjc/etc/ zeta2.pdf
J Hofbauer, A simple proof of \(1 + \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \ldots = \frac{{{\pi ^2}}}{6}\) and related identities, Am. Math. Mon, Vol.109, pp.196–200, 2002.
M D Hirschhorn, A simple proof that ζ(2)=n 2/6, Math. Intelligencer, Vol.33N3, pp.81–82, 2011.
N Lord, Yet another proof that \(\Sigma \frac{1}{{{n^2}}} = \frac{1}{6}{\pi ^2}\), Math. Gazette, Vol.86, pp.477–479, 2002.
J T D'Avanzo and N A Krylov, ζ(n) via hyperbolic functions, Involve, Vol.3, pp.289–296, 2010.
F M S Lima, New definite integrals and a two-term dilogarithm identity, Indag. Math., Vol.23, pp.1–9, 2012.
M Passare, How to compute \(\Sigma \frac{1}{{{n^2}}}\) by solving triangles, Am. Math. Mon., Vol.115, pp.745–752, 2008.
F Beukers, J A C Kolk and E Calabi, Sums of generalized harmonic series and volumes, Nieuw Archief voor Wiskunde, fourth series, Vol.11, pp.217–224, 1993.
N D Elkies, On the sums \(\sum\limits_{k = - \infty }^\infty {{{(4k + 1)}^{ - n}}} \), Am. Math. Mon., Vol.110, pp.561–573, 2003; Corr. ibid., Vol.111, p.456, 2004.
D Cvijovic and J Klinowski, Integral representations of the Riemann zeta function for odd-integer arguments, J Comput. Appl. Math., Vol.142, pp.435–439, 2002.
M Aigner and G M Ziegler, Proofs from THE BOOK, Springer-Verlag, Berlin Heidelberg, third edition, p.38, 2004.
D Cvijovic and H M Srivastava, Closed-form evaluations of certain definite integrals by employing the Cauchy integral theorem, Numer. Algor., Vol.49, pp.129–141, 2008.
D Cvijovic, Closed-form evaluation of some families of cotangent and cosecant integrals, Integral Transform. Spec. Funct., Vol.19, pp.147–155, 2008.
D Cvijovic, Closed-form evaluation of some families of definite tangent and secant integrals, Integral Transform. Spec. Funct., Vol.18, pp.569–579, 2007.
J Kubilius, Estimating the second central moment for strongly additive arithmetic functions, Lithuanian Mathematical Journal, Vol.23, pp.61–69, 1983.
Z K Silagadze, Comment on the sums S (n) = \(\sum\limits_{k = - \infty }^\infty {\frac{1}{{{{(4k + 1)}^n}}}} \), Georgian Math. J., Vol.19, pp.587–595, 2012.
See, B K Karande and N K Thakare, On the unification of Bernoulli and Euler polynomials, Indian J. Pure Appl. Math., Vol.6, pp.98–107, 1975
G Bretti and P E Ricci, Euler polynomials and the related quadrature rule, Georgian Math. J., Vol.8, pp.447–453, 2001.
V I Arnold, Mathematics and Physics, G Boniolo, P Budinich and M Trobok (Eds.) The Role of Mathematics in Physical Sciences, pp.225–233, Springer, Dordrecht, 2005.
O Viro, WHAT IS an amoeba?, Notices Amer. Math. Soc., Vol.49, pp.916–917, 2002.
M Passare and A Tsikh, Amoebas: their spines and their contours, Contemp. Math., Vol.377, pp.275–288, 2005.
I M Gelfand, M M Kapranov and A V Zelevinsky, Discriminants, Resultants, and Multidimensional Determinants, Birkhäuser, Boston, 1994.
Author information
Authors and Affiliations
Corresponding author
Additional information
Zurab Silagadze graduated from the Tbilisi State University in 1979. He got his PhD from Novosibirsk in theoretical and mathematical physics. Currently, he works as senior researcher at Budker Institute of Nuclear Physics and as assistant professor at Novosibirsk State University.
Rights and permissions
About this article
Cite this article
Silagadze, Z. Sums of generalized harmonic series. Reson 20, 822–843 (2015). https://doi.org/10.1007/s12045-015-0241-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12045-015-0241-0