Symplectic mapping class groups of K3 surfaces and Seiberg–Witten invariants

Abstract

The purpose of this note is to prove that the symplectic mapping class groups of many K3 surfaces are infinitely generated. Our proof makes no use of any Floer-theoretic machinery but instead follows the approach of Kronheimer and uses invariants derived from the Seiberg–Witten equations.

1 Main Result

Let $(X,\omega )$ be a symplectic manifold, $\text {Symp}(X,\omega )$ the symplectomorphism group of $(X,\omega )$, and $\text { {Diff}}(X)$ the diffeomorphism group of X. Define

$$\begin{aligned} K(X,\omega ) = \text {ker}\,\left[ \pi _0 \text {Symp}(X,\omega ) \rightarrow \pi _0 \text { {Diff}}(X) \right] . \end{aligned}$$

In his thesis [Sei08], Seidel found examples where $K(X,\omega )$ is non-trivial: If $(X,\omega )$ is a complete intersection that is neither ${\mathbb P}^2$ nor ${\mathbb P}^1 \times {\mathbb P}^1$, then there exists a symplectomorphism $\tau :(X,\omega ) \rightarrow (X,\omega )$ called the four-dimensional Dehn twist such that $\tau ^2$ is smoothly isotopic to the identity but not symplectically so. Seidel also proved [Sei00] that for certain symplectic K3 surfaces $(X,\omega )$ the group $K(X,\omega )$ is infinite. Results of Tonkonog [Ton15] show that $K(X,\omega )$ is infinite for most hypersurfaces in Grassmannians. Until recently, however, it was unknown whether $K(X,\omega )$ can be infinitely generated. The question has been answered in the positive by Sheridan and Smith [SS20], who gave examples of algebraic K3 surfaces $(X,\omega )$ with $K(X,\omega )$ infinitely generated. The present paper aims to extend their result to a large class of K3 surfaces, including some non-algebraic K3 surfaces.

Let $(X,\omega )$ be a Kähler K3 surface, and let $\kappa = [\omega ] \in H^{1,1}(X;{\mathbb R})$ be the corresponding Kähler class. We set

$$\begin{aligned} \Delta _{\kappa } = \left\{ \delta \in H^2(X;{\mathbb Z}) \ |\ \langle \kappa , \delta \rangle = 0,\ \langle \delta , \delta \rangle = -2 \right\} , \end{aligned}$$

where $\langle , \rangle$ denotes the cup product pairing.

Our goal in this note is to prove the following statement:

Theorem 1

If $\Delta _{\kappa }$ is infinite, then $K(X,\omega )$ is infinitely generated.

The plan of the proof is as follows: We start from the results of [Kro97] and construct a homomorphism

$$\begin{aligned} q :K(X,\omega ) \rightarrow \prod _{\delta \in {\overline{\Delta }}_{\kappa }} {\mathbb Z}_2,\quad \text {where } {\overline{\Delta }}_{\kappa } \text { is defined as } \Delta _{\kappa }/\sim \text { with } \delta \sim (-\delta ). \end{aligned}$$

We then consider the moduli space B of marked ($\kappa$-)polarized K3 surfaces. This moduli space is a smooth manifold and has the following properties:

• (1) B is a fine moduli space, meaning it carries a universal family of K3 surfaces $\left\{ X_t \right\} _{t \in B}$ together with a family of fiberwise cohomologous Kähler forms $\left\{ \omega _t \right\} _{t \in B}$.

• (2) $H_1(B;{\mathbb Z}_2) = \bigoplus _{\delta \in {\overline{\Delta }}_{\kappa }} {\mathbb Z}_2$¹.

Fix a basepoint $t_0 \in B$. Identify $(X,\omega )$ with $(X_t,\omega _{t_0})$. Provided by Moser’s theorem, there is a monodromy homomorphism

$$\begin{aligned} \pi _1(B, t_0) \rightarrow \pi _0 \text {Symp}(X,\omega ). \end{aligned}$$

We shall prove that the image of this homomorphism is contained in $K(X,\omega )$ and that the composite homomorphism

$$\begin{aligned} \pi _1(B, t_0) \rightarrow \pi _0 \text {Symp}(X,\omega ) \xrightarrow {q} \prod _{\delta \in {\overline{\Delta }}_{\kappa }} {\mathbb Z}_2 \end{aligned}$$

surjects onto $\bigoplus _{\delta \in {\overline{\Delta }}_{\kappa }} {\mathbb Z}_2 \subset \prod _{\delta \in {\overline{\Delta }}_{\kappa }} {\mathbb Z}_2$.

Remark 1

Theorem 1 has a natural generalization, with practically identical proof: There is a homomorphism

$$\begin{aligned} q :K(X,\omega ) \rightarrow \prod _{\delta \in {\overline{\Delta }}_{\kappa }} {\mathbb Z}, \end{aligned}$$

such that the subgroup $\bigoplus _{\delta \in {\overline{\Delta }}_{\kappa }} {\mathbb Z}\subset \prod _{\delta \in {\overline{\Delta }}_{\kappa }} {\mathbb Z}$ is in the image of q. This stronger version of Theorem 1 can be proved by using Seiberg–Witten invariants taking values in ${\mathbb Z}$.

2 Family Seiberg–Witten Invariants

Here, we briefly recall the definition of the Seiberg–Witten invariants in the family setting. The given exposition is extremely brief, meant mainly to fix notations. We refer the reader to [Nic00, Mor96] for a comprehensive introduction to four-dimensional gauge theory. The Seiberg–Witten equations for families of smooth 4-manifolds have been studied in various works including [Kro97, Rub98, Rub01, LL01, Nak03, BK20, Bar19].

Let X be a closed oriented simply-connected 4-manifold, B a closed n-manifold, ${\mathcal X}\rightarrow B$ a fiber bundle with fiber X. Choose a family of fiberwise metrics $\left\{ g_b \right\} _{b \in B}$. Pick a spin$^{\mathbb C}$ structure ${\mathfrak {s}}$ on the vertical tangent bundle $T_{{\mathcal X}/B}$ of ${\mathcal X}$. By restricting ${\mathfrak {s}}$ to a fiber $X_b$ at $b \in B$, we get a spin$^{\mathbb C}$ structure ${\mathfrak {s}}_b$ on $X_b$. Hereafter, for any object on the total space ${\mathcal X}$, the object with subscript b stands for the restriction of the object to the fiber $X_b$. Conversely: Suppose we are given a spin$^{\mathbb C}$ structure ${\mathfrak {s}}_b$ on $X_b$. When can we find a spin$^{\mathbb C}$ structure on $T_{{\mathcal X}/B}$ whose restriction to $X_b$ is ${\mathfrak {s}}_b$? The following is a sufficient condition: B is a homotopy $S^2$. (This is the only case we will be considering in the sequel.) Let us briefly sketch why this is sufficient. Chapter 3 in [Mor96] presents necessary preliminaries on spin$^{\mathbb C}$ structures.

Lemma 1

Let ${\mathcal X}\rightarrow B$ be a fiber bundle whose fiber $X_b$ is a closed simply-connected 4-manifold, and whose base B is a homotopy $S^2$. Suppose we are given a spin$^{\mathbb C}$ structure ${\mathfrak {s}}_b$ on $X_b$. Then there exists a spin$^{\mathbb C}$ structure ${\mathfrak {s}}$ on $T_{{\mathcal X}/B}$ extending the spin$^{\mathbb C}$ structure ${\mathfrak {s}}_b$ on $X_b$.

Proof

We begin with a general result on spin$^{\mathbb C}$ structures. Let Y be an orientable manifold, which does not need to be four-dimensional nor closed. Let $V \rightarrow Y$ be a real oriented rank 4 vector bundle over Y. Endow V with a positive-definite inner product so that the structure group of V is ${\varvec{SO}}(4)$. Suppose that its Stiefel-Whitney class $w_2(V) \in H^2(Y;{\mathbb Z}_2)$ can be lifted to an integral class $c_1({\mathcal L})$, for some complex line bundle ${\mathcal L}\rightarrow Y$. Then there is a spin$^{\mathbb C}$ structure ${\mathfrak {s}}$ whose determinant line bundle is ${\mathcal L}$; that is, we have

$$\begin{aligned} c_1({\mathfrak {s}}) = c_1({\mathcal L}). \end{aligned}$$

On the other hand, if a bundle carries one spin$^{\mathbb C}$ structure, it carries many; they are parameterized by the elements in $H^2(Y;{\mathbb Z})$. In particular, if $H^2(Y;{\mathbb Z})$ has no 2-torsion, then the Chern class $c_1({\mathfrak {s}})$ determines uniquely the spin$^{\mathbb C}$ structure ${\mathfrak {s}}$.

Specialize to the case of $Y = {\mathcal X}$. What remains is to show that $w_2(T_{{\mathcal X}/B}) \in H^2({\mathcal X};{\mathbb Z}_2)$ lifts to a class $a \in H^2({\mathcal X};{\mathbb Z})$ whose restriction to $X_b$ is equal to $c_1({\mathfrak {s}}_b)$. Since X is simply-connected, the group $H^2(Y;{\mathbb Z})$ has no 2-torsion. Thus, we may choose ${\mathfrak {s}}$ such that $c_1({\mathfrak {s}}) = a \in H^2({\mathcal X};{\mathbb Z})$, and the extension is done.

Using a Mayer-Vietoris argument, we obtain the following exact sequence:

$$\begin{aligned} 0 \rightarrow H^2(B;{\mathbb Z}) \rightarrow H^2({\mathcal X};{\mathbb Z}) \rightarrow H^2(X_b;{\mathbb Z}) \rightarrow 0. \end{aligned}$$

Here the first arrow comes from the projection ${\mathcal X}\rightarrow B$, whereas the latter arrow is induced by the inclusion $X_b \rightarrow {\mathcal X}$. This exact sequence provides a lift of $c_1({\mathfrak {s}}_b) \in H^2(X_b;{\mathbb Z})$ to a class $a \in H^2({\mathcal X};{\mathbb Z})$. Such a lift is not unique; however, letting e denote the generator of $H^2(B;{\mathbb Z})$, one writes all other lifts as translates $a + k\,e$ by k’s from ${\mathbb Z}$. It is clear that either a or $a + e$ has to be an integral lift of $w_2(T_{{\mathcal X}/B})$.$\square$

Fix a spin$^{\mathbb C}$ structure ${\mathfrak {s}}$ on $T_{{\mathcal X}/B}$. Associated to ${\mathfrak {s}}$, there are spinor bundles $W^{\pm } \rightarrow B$ and determinant line bundle ${\mathcal L}$, which we regard as families of bundles

$$\begin{aligned} W^{\pm } = \bigcup _{b \in B} W^{\pm }_b,\quad {\mathcal L}= \bigcup _{b \in B} {\mathcal L}_{b}. \end{aligned}$$

Let ${\mathcal A}_{b}$ be the space of ${\varvec{U}}(1)$-connections on ${\mathcal L}_b$, ${\mathcal U}_b$ the gauge groups acting on $(W^{\pm }_b,{\mathcal A}_b)$ as follows:

$$\begin{aligned} \text {for } u_b = e^{-i f_b} \in {\mathcal U}_b \text { and } (\varphi _b,A_b) \in W^{+}_b \times {\mathcal A}_b,\quad u_b \cdot (\varphi _b,A_b) = (e^{-i f_b} \varphi _b, A_b + 2 i \text { {d}}\,f_b). \end{aligned}$$

Given $b \in B$, let $\Pi _b$ be the space of $g_b$-self-dual forms on $X_b$, $\Pi _b^{*} \subset \Pi _b$ be the subset of $\Pi _b$ given by

$$\begin{aligned} \langle \eta _b \rangle _{g_b} + \langle 2 \pi c_1({\mathcal L}_b) \rangle _{g_b} \ne 0, \end{aligned}$$

(2.1)

where $\langle \eta _b \rangle _{g_b}$ is the harmonic part of $\eta _b$ and $\langle 2 \pi c_1({\mathcal L}_b) \rangle _{g_b}$ is the self-dual part of the harmonic representative of the class $2 \pi [c_1({\mathcal L}_b)] \in H^2(X_b;{\mathbb R})$. For the family of metrics $\left\{ g_b \right\} _{b \in B}$, let $\Pi ^{*}$ be the set of all pairs $(g_b, \eta _b)$ where $\eta _b \in \Pi _b^{*}$ and $g_b$ varies with $b \in B$. $\Pi ^{*}$ may be thought of as the fiber bundle over B whose fiber over $b \in B$ is the space $\Pi _b^{*}$.

Given a family of fiberwise self-dual 2-forms $\left\{ \eta _b \right\} _{b \in B}$ satisfying (2.1), the Seiberg–Witten equations with perturbing terms $\left\{ \eta _b \right\} _{b \in B}$ are equations for a family $\left\{ (\varphi _b,A_b)\right\}$. The equations are:

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal D}_{A_b} \varphi _b = 0, \\ F^{+}_{A_{b}} = \sigma (\varphi _b) + i\,\eta _b, \end{array}\right. } \end{aligned}$$

(2.2)

where ${\mathcal D}_{A_b} :\Gamma (W_{b}^{+}) \rightarrow \Gamma (W_{b}^{-})$ is the Dirac operator, $\sigma (\varphi )$ is the squaring map, and $F^{+}_{A_{b}}$ is the self-dual part of the curvature of $A_b$. Letting

(2.3)

we define the parametrized moduli space as:

We let $\pi _{{\mathfrak {s}}} :{\mathfrak {M}}^{{\mathfrak {s}}} \rightarrow \Pi ^{*}$ be the projection whose fiber over $(g,\eta ) \in \Pi ^{*}$ is . It is shown in [KM94] that $\pi _{{\mathfrak {s}}}$ is a smooth and proper Fredholm map. The index of $\pi _{{\mathfrak {s}}}$ is given by:

$$\begin{aligned} \text {ind}\,\pi _{{\mathfrak {s}}} = \frac{1}{4}( c_1^2({\mathfrak {s}}_b) - 3 \sigma (X) -2 \chi (X) ), \end{aligned}$$

where $c_1({\mathfrak {s}}_b) = c_1({\mathcal L}_b)$ is the Chern class of ${\mathfrak {s}}_b$.

Fix a family of fiberwise self-dual 2-forms $\left\{ \eta _b \right\} _{b \in B}$ satisfying (2.1), and consider it as a section of $\Pi ^{*}$. If $\left\{ \eta _b \right\} _{b \in B}$ is chosen generic, then the moduli space

$$\begin{aligned} {\mathfrak {M}}_{(g_b,\eta _b)}^{{\mathfrak {s}}} = \bigcup _{b \in B} \pi ^{-1}_{{\mathfrak {s}}} (g_b,\eta _b) \end{aligned}$$

is either empty or a compact manifold of dimension

$$\begin{aligned} d({\mathfrak {s}},B) = \frac{1}{4}( c_1^2({\mathfrak {s}}_b) - 3 \sigma (X) -2 \chi (X) ) + n. \end{aligned}$$

Now suppose that $d({\mathfrak {s}},B) = 0$. Then ${\mathfrak {M}}_{(g_b,\eta _b)}^{{\mathfrak {s}}}$ is zero-dimensional, and thus consists of finitely-many points. We call

$$\begin{aligned} {\mathsf {FSW}}_{(g_b,\eta _b)}({\mathfrak {s}}) = \# \left\{ \text {points of } {\mathfrak {M}}_{(g_b,\eta _b)}^{{\mathfrak {s}}} \right\} \,{\mathsf {mod}}\,2 \end{aligned}$$

(2.4)

the family (${\mathbb Z}_2$-)Seiberg–Witten invariant for the spin$^{\mathbb C}$ structure ${\mathfrak {s}}$ with respect to the family $\left\{ (g_b,\eta _b) \right\} _{b \in B}$. The following properties of family invariants are well-known:

• (1) There is a “charge conjugation” involution ${\mathfrak {s}} \rightarrow -{\mathfrak {s}}$ on the set of spin$^{\mathbb C}$ structures that changes the sign of $c_1({\mathfrak {s}})$. This involution provides us with a canonical isomorphism between

  $$\begin{aligned} {\mathfrak {M}}_{(g_b,\eta _b)}^{{\mathfrak {s}}}\quad \text {and}\quad {\mathfrak {M}}_{(g_b,-\eta _b)}^{-{\mathfrak {s}}}. \end{aligned}$$

  Hence,

  $$\begin{aligned} {\mathsf {FSW}}_{(g_b,\eta _b)}({\mathfrak {s}}) = {\mathsf {FSW}}_{(g_b,-\eta _b)}(-{\mathfrak {s}}). \end{aligned}$$

  (2.5)

  See, e.g., Proposition 2.2.22 in [Nic00]. The corresponding ${\mathbb Z}$-valued Seiberg–Witten invariants are also equal to each other, but only up to sign. See Proposition 2.2.26 in [Nic00] for the precise statement.

• (2) If ${\mathfrak {s}}$, ${\mathfrak {s}}'$ are two spin$^{\mathbb C}$ structures on $T_{{\mathcal X}/B}$ that are isomorphic on $X_b$ for each $b \in B$, then

  $$\begin{aligned} {\mathsf {FSW}}_{(g_b,\eta _b)}({\mathfrak {s}}) = {\mathsf {FSW}}_{(g_b,\eta _b)}({\mathfrak {s}}'), \end{aligned}$$

  in fact, the corresponding moduli spaces ${\mathfrak {M}}_{(g_b,\eta _b)}^{{\mathfrak {s}}}$ and ${\mathfrak {M}}_{(g_b,\eta _b)}^{{\mathfrak {s}}'}$ are canonically diffeomorphic. See [Bar19, § 2.2] for details.

• (3) Suppose we have two families $\left\{ \eta _{b} \right\} _{b \in B}$, $\left\{ \eta '_{b} \right\} _{b \in B}$ of $g_b$-self-dual 2-forms satisfying (2.1). Suppose further that they are homotopic, when considered as sections of $\Pi ^{*}$; then

  $$\begin{aligned} {\mathsf {FSW}}_{(g_b,\eta _b)}({\mathfrak {s}}) = {\mathsf {FSW}}_{(g_b,\eta '_b)}({\mathfrak {s}}). \end{aligned}$$

  This is proved by applying the Sard-Smale theorem. See [LL01, § 2] for details. More generally, the family Seiberg–Witten invariants are unchanged under the homotopies of $\left\{ (g_b, \eta _{b}) \right\} _{b \in B}$ that satisfy (2.1).

3 Unwinding Families

Let ${\mathcal X}$ be a fiber bundle over B with fiber X. From now on, we assume that B is the 2-sphere $S^2$ and X is the K3 surface. Pick a family $\left\{ g_b \right\} _{b \in B}$ of fiberwise metrics on the fibers of ${\mathcal X}$. Let ${\mathfrak {s}}_b$ be a spin$^{{\mathbb C}}$ structure on a fiber $X_b$, and let ${\mathfrak {s}}$ be a spin$^{{\mathbb C}}$ structure on $T_{{\mathcal X}/B}$ extending ${\mathfrak {s}}_b$.

The group $H_2(X;{\mathbb Z})$ is a free abelian group of rank 22 which, when endowed with the bilinear form coming from the cup product, becomes a unimodular lattice of signature (3, 19). Let us fix (once and for all) an abstract lattice $\Lambda$ which isometric to $H^2(X;{\mathbb Z})$ and an isometry $\alpha :H^2(X_b;{\mathbb Z}) \rightarrow \Lambda$, where $b \in B$ is some fixed base-point. Since B is simply-connected, the groups $\left\{ H^2(X_b;{\mathbb Z}) \right\} _{b \in B}$ are all canonically isomorphic to each other, and hence they are isomorphic to $\Lambda$ through the isometry $\alpha$. Let ${\mathbf {K}} \subset \Lambda \otimes {\mathbb R}$ be the (open) positive cone:

$$\begin{aligned} {\mathbf {K}} = \left\{ \kappa \in \Lambda \otimes {\mathbb R}\,|\, \kappa ^2 > 0 \right\} , \end{aligned}$$

which is homotopy-equivalent to $S^2$.

Let $H_b$ be the space of $g_b$-self-dual harmonic forms on $X_b$, and let ${\mathcal H}\rightarrow B$ be the vector bundle whose fiber over $b \in B$ is $H_b$. Pick a family $\left\{ \eta _b \right\} _{b \in B}$ of $g_b$-self-dual forms. Suppose that $(g_b,\eta _b)$ satisfies

$$\begin{aligned} \langle \eta _b \rangle _{g_b} \ne 0\quad \text {for each } b \in B, \end{aligned}$$

so that the correspondence $b \rightarrow \langle \eta _b \rangle _{g_b}$ yields a non-vanishing section of ${\mathcal H}$. Then, associated to such a section, there is a map:

$$\begin{aligned} B \rightarrow {\mathbf {K}} - \left\{ 0 \right\} ,\quad b \rightarrow [\langle \eta _b \rangle _{g_b}], \end{aligned}$$

where the brackets $[\,]$ signify the cohomology class of $\langle \eta _b \rangle$. Since both B and ${\mathbf {K}}$ are homotopy $S^2$, this map has a degree, called the winding number of the family $(g_b,\eta _b)$.

Lemma 2

Suppose that the winding number of $(g_b,\eta _b)$ vanishes. Then

$$\begin{aligned} {\mathsf {FSW}}_{(g_b,\lambda \eta _b)}({\mathfrak {s}}) = {\mathsf {FSW}}_{(g_b,-\lambda \eta _b)}({\mathfrak {s}}) \end{aligned}$$

(3.1)

for $\lambda$ sufficiently large.

Proof

By choosing $\lambda$ large enough, we can make

$$\begin{aligned} \lambda ^2\, {\mathsf {min}}_{b \in B} \int _{X_b} \langle \eta _b \rangle _{g_b}^2 > 4\,\pi ^2 {\mathsf {max}}_{b \in B} \int _{X_b} \langle c_1({\mathfrak {s}}_b) \rangle _{g_b}^2, \end{aligned}$$

(3.2)

so that both $(g_b,\lambda \eta _b)$ and $(g_b,-\lambda \eta _b)$ satisfies (2.1) for $\lambda$ large enough, and both sides of (3.1) are well defined. Let us show that there exists a homotopy between $\left\{ (g_b,\lambda \eta _b) \right\} _{b \in B}$ and $\left\{ (g_b,-\lambda \eta _b) \right\} _{b \in B}$ that satisfies (2.1).

To begin with, we can assume that $\eta _b = \langle \eta _b \rangle _{g_b}$ for each $b \in B$. This can be assumed because:

If $\eta _b$ satisfies (2.1), then so does $\eta _b + \text {Image}\,\text {d}^{+}$.

If (3.2) holds, then the range of both maps

$$\begin{aligned} b \rightarrow \lambda [\eta _b],\quad b \rightarrow -\lambda [\eta _b] \end{aligned}$$

(3.3)

lies in the complement of the ball $O \subset {\mathbf {K}}$,

$$\begin{aligned} O = \left\{ \kappa \in {\mathbf {K}}\ |\ \kappa ^2 < 4\,\pi ^2\,{\mathsf {max}}_{b \in B} \langle c_1({\mathfrak {s}}_b) \rangle ^{2}_{g_b} \right\} . \end{aligned}$$

(3.4)

For every map $\chi :B \rightarrow {\mathbf {K}}$, there exists a unique section ${\tilde{\chi }} :B \rightarrow {\mathcal H}$ such that the diagram

is commutative. If the range of $\chi$ is contained in ${\mathbf {K}} - O$, then ${\tilde{\chi }}(b)$ satisfies (2.1) for each $b \in B$. To conclude the proof, it suffices to show that the maps (3.3) are homotopic as maps from B to ${\mathbf {K}} - O$. Since ${\mathbf {K}} - O$ is a homotopy $S^2$, the maps (3.3) are homotopic iff their degrees are equal to each other. This is the case, as the winding number of $(g_b,\pm \lambda \eta _b)$ is equal to that of $(g_b,\pm \eta _b)$, and the latter is zero. $\square$

Combining (3.1) and (2.5), we obtain

$$\begin{aligned} {\mathsf {FSW}}_{(g_b,\lambda \eta _b)}(-{\mathfrak {s}}) = {\mathsf {FSW}}_{(g_b,\lambda \eta _b)}({\mathfrak {s}})\quad \text {for } \lambda \text { sufficiently large.} \end{aligned}$$

(3.5)

4 Seiberg–Witten for Symplectic Manifolds

The following material is well-known; see, e.g., [Nic00, § 3.3], [Mor96, Ch. 7] for details. On a symplectic 4-manifold $(X,\omega )$ endowed with a compatible almost-complex structure J and the associated Hermitian metric $g(\cdot ,\cdot ) = \omega (\cdot ,J\cdot )$, each spin$^{{\mathbb C}}$ structure has the following form:

$$\begin{aligned} W^{+} = L_{\varepsilon } \oplus \left( \Lambda ^{0,2} \otimes L_{\varepsilon } \right) ,\quad W^{-} = \Lambda ^{0,1} \otimes L_{\varepsilon }, \end{aligned}$$

(4.1)

where $L_{\varepsilon }$ is a line bundle on X with $c_1(L_{\varepsilon }) = \varepsilon \in H^2(X;{\mathbb Z})$. $K^{*}_X$ denotes the anticanonical bundle of X. We parameterize all connections on ${\mathcal L}= K_{X}^{*} \otimes L_{\varepsilon }^2$ as $A = A_0 + 2\,B$, where B is a $\varvec{U}(1)$-connection on $L_{\varepsilon }$ and $A_0$ is the Chern connection on $K_{X}^{*}$. We also write $\varphi = (\ell ,\beta )$ for $\varphi \in W^{+}$. Following Taubes, we choose the perturbation

$$\begin{aligned} i\,\eta = F^{+}_{A_0} - i\, \rho \, \omega . \end{aligned}$$

(4.2)

Note that $\omega$ is g-self-dual and of type (1, 1) with respect to J. The Seiberg–Witten equations are:

$$\begin{aligned} {\left\{ \begin{array}{ll} {\bar{\partial }}_{B} \ell + {\bar{\partial }}_{B}^{*} \beta = 0, \\ F^{0,2}_{A_0} + 2\,F^{0,2}_{B} = \dfrac{\ell ^{*} \beta }{2} + i \eta ^{0,2}, \\ (F_{A_0}^{+})^{1,1} + 2 (F^{+}_{B})^{1,1} = \dfrac{i}{4}\,(|\ell |^2 - |\beta |^2) \omega + i \eta ^{1,1}\,. \end{array}\right. } \end{aligned}$$

(4.3)

Theorem 2

(Taubes [Tau95]). Suppose that

$$\begin{aligned} \varepsilon \ne 0\quad \text {and}\quad \int _X \varepsilon \cup \omega \leqslant 0. \end{aligned}$$

Then the equations (4.3) with the perturbing term (4.2) have no solutions for $\rho$ positive sufficiently large.

Proof

See Theorem 3.3.29 in [Nic00]. $\square$

When $(X,\omega )$ is Kähler we have the following result: Set

$$\begin{aligned} \rho _0 = 4 \pi \left( \int _X \varepsilon \cup \omega \right) \left( \int _X \omega \cup \omega \right) ^{-1}. \end{aligned}$$

Theorem 3

Let $\eta$ be as in (4.2). If , then the equations (4.3) have no solutions. If $\varepsilon \in H^{1,1}(X;{\mathbb R})$ and $\rho > \rho _0$, then solutions to (4.3) are irreducible and, modulo gauge transformations, are in one-to-one correspondence with the set of effective divisors in the class $\varepsilon$.

Proof

See [Mor96, Ch. 7]. $\square$

5 The Homomorphism q

Consider the following fibration, introduced in [Kro97] and studied in [McD01]:

$$\begin{aligned} \text {Symp}(X,\omega ) \rightarrow \text { {Diff}}(X) \xrightarrow {\psi \rightarrow (\psi ^{-1})^{*} \omega } S_{[\omega ]}, \end{aligned}$$

(5.1)

where $\text {Symp}(X,\omega )$ is the symplectomorphism group of $(X,\omega )$, $\text { {Diff}}(X)$ the diffeomorphism group of X, and $S_{[\omega ]}$ is the space of those symplectic forms which can be joined with $\omega$ through a path of cohomologous symplectic forms. We first recall the construction of Kronheimer’s homomorphism [Kro97]:

$$\begin{aligned} Q :\pi _1(S_{[\omega ]}) \rightarrow {\mathbb Z}_2, \end{aligned}$$

and then define the homomorphism q afterwards. Kronheimer’s original construction restricts to the case of $b^{+}_{2}(X) > 3$, and a mild refinement of his argument is given here in order to deal with $b^{+}_{2}(X) = 3$.

Let $\left\{ \omega _t \right\} _{t \in S^1}$ be a loop in $S_{[\omega ]}$. $\left\{ \omega _t \right\} _{t \in S^1}$ can always be equipped with a family of $\omega _t$-compatible almost-complex structures $\left\{ J_t \right\} _{t \in S^1}$ on X. This follows from the fact that the space of compatible almost-complex structures is non-empty and contractible; see, e.g., [MS17, Prop. 4.1.1]. We let $\left\{ g_t \right\} _{t \in S^1}$ be the associated family of Hermitian metrics on X.

Let ${\mathcal X}$ be a trivial bundle over the 2-disc D with fiber X. Let $\left\{ g_b \right\} _{b \in D}$ be a family of fiberwise metrics on ${\mathcal X}$, providing a nullhomotopy of the family $\left\{ g_t \right\} _{t \in S^1}$ in the space of all Riemannian metrics on X. Pick a class $\varepsilon \in H^2(X;{\mathbb Z})$ that satisfies:

$$\begin{aligned} \int _X \varepsilon \cup \omega = 0,\quad \int _X \varepsilon \cup \varepsilon = -2. \end{aligned}$$

(5.2)

These include, for examples, those classes represented by smooth Lagrangian spheres in $(X,\omega )$. Let ${\mathfrak {s}}_{\varepsilon }$ be the spin$^{{\mathbb C}}$ structure on X given by (4.1). We have $c_1({\mathfrak {s}}_{\varepsilon }) = c_1(X) + 2\,\varepsilon$. Choose a spin$^{{\mathbb C}}$ structure on $T_{{\mathcal X}/D}$ extending ${\mathfrak {s}}_{\varepsilon }$. We shall use ${\mathfrak {s}}_{\varepsilon }$ to denote this spin$^{{\mathbb C}}$ structure also.

As in (3.4), set:

$$\begin{aligned} O = \left\{ \kappa \in {\mathbf {K}}\ |\ \kappa ^2 < 4\,\pi ^2\,{\mathsf {max}}_{t \in S^1} \langle c_1({\mathfrak {s}}_{\varepsilon }) \rangle ^{2}_{g_t} \right\} . \end{aligned}$$

Let ${A_0}_t$ denote the Chern connection on $K^{*}_X$ determined by $g_t$. As in (4.2), set:

$$\begin{aligned} \eta _{t} = -i F_{{A_0}_t}^{+} - \rho \, \omega _t. \end{aligned}$$

(5.3)

Choosing $\rho$ large enough, we can assume that

$$\begin{aligned} {}[\langle \eta _t \rangle _{g_t}] \in {\mathbf {K}} - O\quad \text {for each } t \in S^1. \end{aligned}$$

Note that ${\mathbf {K}} - O$ has the homotopy type of the sphere $S^{b_{2}^{+}(X) - 1}$; hence, $\pi _i({\mathbf {K}} - O) = 0$ for $i < b_{2}^{+}(X) - 1$.

Let $\left\{ \eta _b \right\} _{b \in D}$ be a family of fiberwise $g_b$-self-dual forms on ${\mathcal X}$ that agree with $\eta _t$ on $\partial D$. We call $\left\{ \eta _b \right\} _{b \in D}$ an admissible extension of $\left\{ \eta _t \right\} _{t \in S^1}$ if

$$\begin{aligned}{}[\langle \eta _b \rangle _{g_b}] \in {\mathbf {K}} - O\quad \text {for each } b \in D. \end{aligned}$$

(5.4)

If $b_2^{+}(X) > 2$, then $\pi _1({\mathbf {K}} - O) = 0$ and an admissible extension always exists. Moreover, if $b_2^{+}(X) > 3$, an admissible extension is essentially unique: Suppose we are given another admissible extension $\left\{ \eta '_b \right\} _{b \in D}$ of $\left\{ \eta _t \right\} _{t \in S^1}$. Using the fact that $\pi _2({\mathbf {K}} - O) = 0$ and then arguing as in the proof of Lemma 2, one shows that there exists a homotopy $\left\{ \eta _b^{s} \right\} _{b \in D}$ from $\left\{ \eta _b \right\} _{b \in D}$ to $\left\{ \eta '_b \right\} _{b \in D}$ that agrees with $\left\{ \eta _t \right\} _{t \in S^1}$ at each stage and such that $[\langle \eta _b^s \rangle _{g_b}] \in {\mathbf {K}} - O$.

Fix an admissible extension $\left\{ \eta _b \right\} _{b \in D}$ of $\left\{ \eta _t \right\} _{t \in S^1}$. By (5.4),

$$\begin{aligned} \langle \eta _b \rangle _{g_b} + 2 \pi \langle c_1({\mathfrak {s}}_{\varepsilon }) \rangle _{g_b} \ne 0\quad \text {for each } b \in D. \end{aligned}$$

(5.5)

Now we consider the Seiberg–Witten equations parametrized by the family $\left\{ (g_b, \eta _b) \right\} _{b \in D}$. By (5.5), for all $b \in B$, these equations have no reducible solutions. By Theorem 2, for $\rho$ large enough, it is true that

$$\begin{aligned} \pi ^{-1}_{{\mathfrak {s}}_{\varepsilon }} (g_t,\eta _t) = \varnothing \quad \text {for all } t \in S^1. \end{aligned}$$

Here, following the notation of § 2, we let $\pi ^{-1}_{{\mathfrak {s}}_{\varepsilon }} (g_t,\eta _t)$ stand for the moduli space of solutions of the Seiberg–Witten equations parameterized by $(g_t,\eta _t)$.

Now the relative version of Sard-Smale theorem is applied: By perturbing $\left\{ \eta _b \right\} _{b \in D}$, we can assume that the moduli space ${\mathfrak {M}}^{{\mathfrak {s}}_{\varepsilon }}_{(g_b,\eta _b)}$, lying over D, is a manifold of dimension $d({\mathfrak {s}}_{\varepsilon }, D) = 0$. Now set:

$$\begin{aligned} Q_{\varepsilon }(\left\{ \omega _t \right\} _{t \in S^1}) = \# \left\{ \text {points of } {\mathfrak {M}}_{(g_b,\eta _b)}^{{\mathfrak {s}}_{\varepsilon }} \right\} \,{\mathsf {mod}}\,2. \end{aligned}$$

This gives an element of ${\mathbb Z}_2$ depending only on the homotopy class of $\left\{ \omega _t \right\} _{t \in S^1}$ but not on our choice of an admissible extension. Thus, $Q_{\varepsilon }$ gives a group homomorphism $\pi _1(S_{[\omega ]}) \rightarrow {\mathbb Z}_2$.

One can extend the above definition of Q to the case of $b_{2}^{+}(X) = 3$. Letting

$$\begin{aligned} N_{\omega } = \left\{ \kappa \in {\mathbf {K}}\ |\ \int _X \kappa \cup \omega = 0 \right\} , \end{aligned}$$

the complement of $N_{\omega }$ in ${\mathbf {K}}$ has two connected components ${\mathbf {K}}^{\pm }$, each being contractible; the component ${\mathbf {K}}^{+}$ is specified by the condition $[\omega ] \in {\mathbf {K}}^{+}$. With $\eta _{t}$ as in (5.3), we choose $\rho$ large enough so that $[\langle \eta _t \rangle _{g_t}] \in {\mathbf {K}} - O$ for each $t \in S^1$. Observe that $\langle -i F_{{A_0}_t}^{+} \rangle _{g_t} = 0$ because $K_{X}^{*}$ is topologically trivial. Thus $\langle \eta _t \rangle _{g_t} = -\rho \langle \omega _t \rangle _{g_t}$, and we have the inequality:

$$\begin{aligned} \int _X \langle \eta _t \rangle _{g_t} \wedge \omega _t < 0,\quad \text {and thus}\quad [\langle \eta _t \rangle _{g_t}] \in {\mathbf {K}}^{-} - O\quad \text {for each } t \in S^1. \end{aligned}$$

An admissible extension of $\left\{ \eta _t \right\} _{t \in S^1}$ is now defined as follows: An extension $\left\{ \eta _b \right\} _{b \in D}$ is admissible if it satisfies

$$\begin{aligned}{}[\langle \eta _b \rangle _{g_b}] \in {\mathbf {K}}^{-} - O\quad \text {for each } b \in D. \end{aligned}$$

Since ${\mathbf {K}}^{-} - O$ is contractible, an admissible extension exists and it is unique up to homotopy. The rest of the definition of Q goes just as before.

Note that if $\varepsilon$ satisfies (5.2), then so does $(-\varepsilon )$. Define $q_{\varepsilon } :\pi _1(S_{[\omega ]}) \rightarrow {\mathbb Z}_2$ as:

$$\begin{aligned} q_{\varepsilon } = Q_{\varepsilon } - Q_{-\varepsilon }. \end{aligned}$$

(5.6)

Lemma 3

The composite homomorphism

$$\begin{aligned} \pi _1 \text { {Diff}}(X) \rightarrow \pi _1(S_{[\omega ]}) \xrightarrow {q_{\varepsilon }} {\mathbb Z}_2 \end{aligned}$$

is a nullhomomorphism.

Proof

Assume that there is a family of symplectomorphisms

$$\begin{aligned} f_t :(X,\omega _t) \rightarrow (X,\omega )\quad \text {for } t \in \partial D. \end{aligned}$$

Via the clutching construction, the family $\left\{ f_t \right\} _{t \in \partial D}$ corresponds to the quotient space:

$$\begin{aligned} {\mathcal Y}= {\mathcal X}\cup X/\sim ,\quad \text {where } (t,x) \sim f_t(x) \text { for each } t \in \partial D \text { and } x \in X, \end{aligned}$$

which is a fiber bundle over the 2-sphere $B = D/\partial D$. Pick an $\omega$-compatible almost-complex structure J on X. Let g be the associated Hermitian metric. Now let $J_t = (f_t^{-1})_* \circ J\circ (f_t)_*$, $g_t = g \circ (f_t)_{*}$. Then, there is a g-self-dual form $\eta$ on X such that:

$$\begin{aligned} (f^{-1}_t)^{*} \eta _t = \eta \quad \text {for each } t \in \partial D. \end{aligned}$$

Let $\left\{ g_b \right\} _{b \in D}$ be a family of Riemannian metrics on X that agree with $\left\{ g_t \right\} _{t \in \partial D}$ at each $t \in \partial D$. We repeat the above construction of the family $\left\{ \eta _b \right\} _{b \in D}$, and observe that we get a family $\left\{ (g_b,\eta _b) \right\} _{b \in B}$ on ${\mathcal Y}$. By definition, we have

$$\begin{aligned} q_{\varepsilon }(\left\{ \omega _t \right\} _{t \in S^1}) = {\mathsf {FSW}}_{(g_b, \eta _b)}({\mathfrak {s}}_{\varepsilon }) - {\mathsf {FSW}}_{(g_b, \eta _b)}({\mathfrak {s}}_{-\varepsilon }). \end{aligned}$$

The Chern classes $c_1({\mathfrak {s}}_{-\varepsilon })$ and $c_1(-{\mathfrak {s}}_{\varepsilon })$ are equal to each other, when restricted to $X_b$, and hence:

$$\begin{aligned} q_{\varepsilon }(\left\{ \omega _t \right\} _{t \in S^1}) = {\mathsf {FSW}}_{(g_b, \eta _b)}({\mathfrak {s}}_{\varepsilon }) - {\mathsf {FSW}}_{(g_b, \eta _b)}(-{\mathfrak {s}}_{\varepsilon }). \end{aligned}$$

Recall that $\eta _b$ satisfies (5.5), and so does $\lambda \eta _b$ for all $\lambda > 1$, and hence:

$$\begin{aligned} {\mathsf {FSW}}_{(g_b, \eta _b)}({\mathfrak {s}}_{\varepsilon }) = {\mathsf {FSW}}_{(g_b, \lambda \eta _b)}({\mathfrak {s}}_{\varepsilon })\quad \text {for } \lambda \text { positive arbitrary large,} \end{aligned}$$

and likewise for $-{\mathfrak {s}}_{\varepsilon }$. Since $[\langle \eta _b \rangle ] \in {\mathbf {K}}^{-}$ for each $b \in B$, it follows that the winding number of $\left\{ (g_b,\eta _b) \right\} _{b \in B}$ vanishes. The lemma now follows by (3.5). $\square$

Let $\Delta _{[\omega ]}$ be the (possibly infinite) set of classes satisfying (5.2), and let ${\overline{\Delta }}_{[\omega ]}$ be defined as: ${\overline{\Delta }}_{[\omega ]} = \Delta _{[\omega ]}/\sim$, where $\varepsilon \sim -\varepsilon$. Set: ${\mathbb Z}^{\infty }_{2} = \prod _{\varepsilon \in {\overline{\Delta }}_{[\omega ]}} {\mathbb Z}_2$. For $\varepsilon _k \in {\overline{\Delta }}_{[\omega ]}$, let $q_{\varepsilon _k}$ be the homomorphism defined by (5.6) above. Extending $q_{\varepsilon _{k}}$ as

$$\begin{aligned} \pi _1(S_{[\omega ]}) \rightarrow {\mathbb Z}_2 \xrightarrow {I_{\varepsilon _{k}}} {\mathbb Z}_{2}^{\infty }, \end{aligned}$$

where $I_{\varepsilon _{k}} :{\mathbb Z}_2 \rightarrow {\mathbb Z}^{\infty }_2$ is the inclusion homomorphism, we define $q :\pi _1(S_{[\omega ]}) \rightarrow {\mathbb Z}_{2}^{\infty }$ as the (infinite) sum:

$$\begin{aligned} q = \oplus _{\varepsilon _k \in {\overline{\Delta }}_{[\omega ]}} q_{\varepsilon _k}. \end{aligned}$$

The fibration (5.1) leads to the following long exact sequence:

$$\begin{aligned} \cdots \rightarrow \pi _1 \text { {Diff}}(X) \rightarrow \pi _1 (S_{[\omega ]}, \omega ) \rightarrow \pi _0 \text {Symp}(X,\omega ) \rightarrow \pi _0 \text { {Diff}}(X) \rightarrow \cdots . \end{aligned}$$

It follows from Lemma 3 that q gives a homomorphism:

$$\begin{aligned} q :\pi _1 (S_{[\omega ]}, \omega )/\pi _1 \text { {Diff}}(X) \cong K(X,\omega ) \rightarrow {\mathbb Z}^{\infty }_2. \end{aligned}$$

6 Period Domains for K3 Surfaces

The following material is well-known; see, e.g., [Huy16, LP80, BR75]. A K3 surface is a simply-connected compact complex surface X that has trivial canonical bundle. By a theorem of Siu [Siu83] every K3 surface X admits a Kähler form. Fix an even unimodular lattice $\left( \Lambda , \langle , \rangle \right)$ of signature (3, 19). (All such lattices are isometric: see [MH73]). Set: $\Lambda _{{\mathbb R}} = \Lambda \otimes {\mathbb R}$ and $\Lambda _{{\mathbb C}} = \Lambda \otimes {\mathbb C}$. Given a K3 surface X, there are isometries $\alpha :H^2(X;{\mathbb Z}) \cong \Lambda$; a choice of such an isometry is called a marking of X. The isometry $\alpha$ determines the subspace $H^{2,0}(X) \subset H^2(X;{\mathbb C}) \cong \Lambda _{{\mathbb C}}$. If $\varphi _X \in H^{2,0}(X)$ is a generator, then $\langle \varphi _X, \varphi _X \rangle = 0$ and $\langle \varphi _X, {\bar{\varphi }}_X \rangle > 0$. The period map associates to a marked K3 surface $(X,\alpha )$ a point in the period domain

$$\begin{aligned} \Phi = \left\{ \varphi \in \Lambda _{{\mathbb C}}\ |\ \langle \varphi _X, \varphi _X \rangle = 0,\ \langle \varphi _X, {\bar{\varphi }}_X \rangle > 0 \right\} /{\mathbb C}^{*} \subset {\mathbb P}^{21}, \end{aligned}$$

which is a complex manifold of dimension 20. Every point $\varphi \in \Phi$ determines the Hodge structure on $\Lambda _{{\mathbb C}}$ as follows:

$$\begin{aligned} H^{2,0} = {\mathbb C}\varphi ,\quad H^{0,2} = {\mathbb C}{\bar{\varphi }},\quad H^{1,1} = \left( H^{2,0} \oplus H^{0,2} \right) ^{\bot }. \end{aligned}$$

Define ${\overline{M}}$ as:

$$\begin{aligned} {\overline{M}} = \left\{ (\varphi ,\kappa ) \in \Phi \times \Lambda _{{\mathbb R}}\ |\ \langle \varphi , \kappa \rangle = 0,\ \langle \kappa , \kappa \rangle > 0 \right\} . \end{aligned}$$

We set $\Delta = \left\{ \delta \in \Lambda \ |\ \langle \delta , \delta \rangle = -2 \right\}$. Define $M \subset {\overline{M}}$ as:

$$\begin{aligned} M = \left\{ (\varphi ,\kappa ) \in {\overline{M}}\ |\ \text {for all } \delta \in \Delta \text { if } \langle \varphi , \delta \rangle = 0\text { then } \langle \kappa , \delta \rangle \ne 0\right\} . \end{aligned}$$

Letting

$$\begin{aligned} \text {pr} :M \rightarrow \Phi ,\quad \text {pr}(\varphi ,\kappa ) = \varphi , \end{aligned}$$

we define an equivalence relation on M as follows: $(\varphi ,\kappa ) \sim (\varphi ,\kappa ')$ iff $\kappa$ and $\kappa '$ are in the same connected component of the fiber $\text {pr}^{-1}(\varphi ) \subset M$. We call

$$\begin{aligned}{\widetilde{\Phi }} = M/\sim \end{aligned}$$

the Burns-Rapoport period domain. In [BR75] Burns and Rapoport prove that ${\widetilde{\Phi }}$ is a (non-Hausdorff) complex-analytic space. A point $(\varphi ,\kappa ) \in {\widetilde{\Phi }}$ gives rise to:

• (1) the Hodge structure on $\Lambda _{{\mathbb C}}$ determined by $\varphi$,

• (2) a choice $V^{+}(\varphi )$ of one of the two connected components of

  $$\begin{aligned} V(\varphi ) = \left\{ \kappa \in H^{1,1} \cap \Lambda _{{\mathbb R}}\ |\ \langle \kappa ,\kappa \rangle > 0 \right\} , \end{aligned}$$

  (6.1)

• (3) a partition of $\Delta (\varphi ) = \Delta \cap H^{1,1}$ into $P = \Delta ^{+}(\varphi ) \cup \Delta ^{-}(\varphi )$ such that:

  • (a) if $\delta _1,\ldots ,\delta _k \in \Delta ^{+}(\varphi )$ and $\delta = \sum n_i \delta _i \in \Delta (\varphi )$ with $n_i \geqslant 0$, then $\delta \in \Delta ^{+}(\varphi )$, and

  • (b) $V_{P}^{+}(\varphi ) = \left\{ \kappa \in V^{+}(\varphi )\ |\ \langle \kappa ,\delta \rangle > 0\ \text { for all } \delta \in \Delta ^{+}(\varphi ) \right\}$ is not empty.

The Burns-Rapoport period map associates to a marked K3 surface $(X,\alpha )$ the point of $(\varphi ,\kappa ) \in {\widetilde{\Phi }}$ determined by

• (1) the Hodge structure of $H^2(X;{\mathbb C})$,

• (2) the component $V^{+}(X)$ of $V(X) = \left\{ \kappa \in H^{1,1}(X;{\mathbb R})\ |\ \langle \kappa , \kappa \rangle > 0 \right\}$ containing the cohomology class of any Kähler form on X,

• (3) the partition of

  $$\begin{aligned} \Delta (X) = \left\{ \delta \in H^{1,1}(X;{\mathbb R}) \cap H^2(X;{\mathbb Z})\ |\ \langle \delta ,\delta \rangle = -2 \right\} \end{aligned}$$

  into $P = \Delta ^{+}(X) \cup \Delta ^{-}(X)$, where

  $$\begin{aligned} \Delta ^{+}(X)= & {} \left\{ \delta \in \Delta (X)\ |\ \delta \text { is an effective divisor}\right\} ,\nonumber \\ \Delta ^{-}(X)= & {} \left\{ \delta \in \Delta (X)\ |\ -\delta \in \Delta ^{+}(X) \right\} . \end{aligned}$$

  (6.2)

It follows from the Riemann-Roch formula that either $\delta$ or $-\delta$ is effective for each $\delta \in \Delta (X)$, hence (6.2) is indeed a partition. Finally, we set:

$$\begin{aligned} V^{+}_{P}(X) = \left\{ \kappa \in V^{+}(X)\ |\ \langle \kappa , \delta \rangle > 0\ \text { for all } \delta \in \Delta ^{+}(X)\right\} . \end{aligned}$$

An element $\kappa \in V^{+}_P(X)$ is called a Kähler polarization on X. If X is given a Kähler form, then the cohomology class of this form gives a polarization. Conversely, every class $\kappa \in V^{+}_P(X)$ is a cohomology class of some Kähler form on X. We call X polarized if the choice of $\kappa \in V^{+}_P(X)$ has been specified. A classical result (see, e.g., [Siu81]) is that every point $(\varphi ,\kappa ) \in M$ is a period of some marked $\kappa$-polarized K3 surface. Two smooth marked K3 surfaces with the same Burns-Rapoport periods are isomorphic. In other words, we have:

Theorem 4

(Burns-Rapoport [BR75]). Let X and $X'$ be two non-singular K3 surfaces. If $\theta :H^2(X;{\mathbb Z}) \rightarrow H^2(X';{\mathbb Z})$ is an isometry which preserves the Hodge structures, maps $V^{+}(X)$ to $V^{+}(X')$ and $\Delta ^{+}(X)$ to $\Delta ^{+}(X')$, then there is a unique isomorphism $\Theta :X' \rightarrow X$ with $\Theta ^{*} = \theta$.

More generally, we have:

Theorem 5

(Burns-Rapoport [BR75]). Let S be a complex-analytic manifold, and let $p :{\mathcal X}\rightarrow S$ and $p' :{\mathcal X}' \rightarrow S$ be two families of non-singular K3 surfaces. If

$$\begin{aligned} \theta :{\mathcal R}^2 p_*({\mathbb Z}) \rightarrow {\mathcal R}^2 p'_*({\mathbb Z}) \end{aligned}$$

is an isomorphism of second cohomology lattices which preserves the Hodge structures, maps $V^{+}(X_s)$ to $V^{+}(X'_s)$ and $\Delta ^{+}(X_s)$ to $\Delta ^{+}(X'_s)$, then there is a unique family isomorphism $\Theta :{\mathcal X}' \rightarrow {\mathcal X}$, with $\Theta ^{*} = \theta$, such that the following diagram is commutative:

Let us show how this theorem is used to construct a fine moduli space of polarized K3 surfaces.

7 Universal Family of Marked Polarized K3’s

Let $p :{\mathcal X}\rightarrow S$ be a complex-analytic family of K3 surfaces. Regarding $\Lambda$ as a group, let ${\overline{\Lambda }}_{S}$ be a locally-constant sheaf on S taking values in $\Lambda$. If ${\mathcal R}^2 p({\mathbb Z})$ is globally-constant, then there are isomorphisms $\alpha :{\mathcal R}^2 p({\mathbb Z}) \rightarrow {\overline{\Lambda }}_{S}$. A choice of an isomorphism $\alpha :{\mathcal R}^2 p({\mathbb Z}) \rightarrow {\overline{\Lambda }}_{S}$ is called a marking of ${\mathcal X}$. A marked family of K3 surfaces $({\mathcal X},\alpha )$ carries a holomorphic map $\mathrm {T}_{({\mathcal X},\alpha )} :S \rightarrow \Phi$ which associates to each marked fiber $X_s$ the corresponding point of $\varphi$. This map is called the period map for the family ${\mathcal X}$. A polarization of ${\mathcal X}$ is a section $\kappa \in \Gamma (S,{\overline{\Lambda }}_{S} \otimes {\mathbb R})$ such that $\kappa |_s \in V^{+}_{P}(X_s)$ for each $s \in S$. The period map $\mathrm {T}_{({\mathcal X},\alpha )}$ together with $\kappa$ gives a map $S \rightarrow \Phi \times \Lambda _{{\mathbb R}}$, whose image is contained in M; the composite map

$$\begin{aligned} S \xrightarrow {\ \left( \mathrm {T}_{({\mathcal X},\alpha )}, \kappa \right) \ } M \xrightarrow {\ /\sim \ } {\widetilde{\Phi }}. \end{aligned}$$

is called the polarized period map for the family ${\mathcal X}$. This map is independent of the choice of $\kappa$, because $V^{+}_{P}(X_s)$ is connected. We can restate Theorem 5 as follows: Let $({\mathcal X},\alpha )$ and $({\mathcal X}',\alpha ')$ be two marked families of K3 surfaces over a complex-analytic manifold S. Suppose that their polarized period maps agree on S. Then there exists a unique family isomorphism $\Theta :{\mathcal X}' \rightarrow {\mathcal X}$, with $\alpha ' \circ \Theta ^{*} = \alpha$, such that diagram (6.3) is commutative.

Fix $\kappa \in \Lambda _{{\mathbb R}}$ with $\kappa ^2 > 0$. Letting

$$\begin{aligned} \Delta _{\kappa } = \left\{ \delta \in \Delta \ |\ \langle \kappa , \delta \rangle = 0 \right\} , \end{aligned}$$

we define two complex manifolds $M_{\kappa } \subset {\overline{M}}_{\kappa }$ as:

$$\begin{aligned} {\overline{M}}_{\kappa } \!=\! \left\{ \varphi \!\in \! \Phi \ |\ \langle \varphi ,\kappa \rangle \!=\! 0 \right\} ,\quad M_{\kappa } \!=\! \left\{ \varphi \!\in \! \Phi \ |\ \langle \varphi ,\kappa \rangle \!= \!0, \text { and } \langle \varphi , \delta \rangle \ne 0 \text { for all } \delta \!\in \! \Delta _{\kappa }\right\} . \end{aligned}$$

Setting $H_{\delta } = \left\{ \varphi \in {\overline{M}}_{\kappa }\ |\ \langle \delta , \varphi \rangle = 0 \right\}$, where $\delta \in \Delta _{\kappa }$, we have $M_{\kappa } = {\overline{M}}_{\kappa } - \cup _{\Delta _{\kappa }} H_{\delta }$.

Lemma 4

([BR75]) Let $\kappa _0 \in \Lambda _{{\mathbb R}}$, and assume $\kappa _0^2 > 0$. Let $\varphi _0 \in {\overline{M}}_{\kappa _0}$. Then there is a neighbourhood U of $\varphi _0$ in ${\overline{M}}_{\kappa }$ and a neighbourhood K of $\kappa _0$ in $\Lambda _{{\mathbb R}}$ such that for all $(\varphi , \kappa ) \in U \times K$,

if $\delta \in \Delta$ satisfies $\langle \delta , \kappa \rangle = \langle \delta , \varphi \rangle = 0$, then $\langle \delta , \kappa _0 \rangle = \langle \delta , \varphi _0 \rangle = 0$.

Proof

See Proposition 2.3 in [BR75] and also see the proof of Lemma 5 below. $\square$

In particular, we have:

Lemma 5

Every $\varphi \in {\overline{M}}_{\kappa }$ has neighbourhood U such that $H_{\delta } \cap U = \varnothing$ for all but finitely many $\delta \in \Delta _{\kappa }$. Hence, in particular, $M_{\kappa }$ is an open submanifold of ${\overline{M}}_{\kappa }$.

Proof

We let $x \in \Lambda _{{\mathbb C}}$ be the vector corresponding to the point $\varphi \in \Phi$. Letting $x = x_1 + i x_2$, $x_i \in \Lambda _{{\mathbb R}}$, we obtain three pairwise orthogonal vectors $(\kappa ,x_1,x_2)$ in $\Lambda _{{\mathbb R}}$ such that

$$\begin{aligned} \kappa ^2> 0,\quad x_1^2> 0,\quad x_2^2 > 0. \end{aligned}$$

Fix some euclidean norm $||\, ||$ on $\Lambda _{{\mathbb R}}$. It is clear that any ball (with respect to the norm $||\, ||$) contains only finitely many elements of $\Delta _{\kappa }$. Suppose, contrary to our claim, that there is an unbounded sequence $\left\{ \delta _i \right\} _{k=1}^{\infty }$ such that:

$||\delta _i|| \rightarrow \infty$ and $\left( \delta _i, x_1 \right) , \left( \delta _i, x_2 \right) , \left( \delta _i, \kappa \right) \rightarrow 0$ as $i \rightarrow \infty$.

Assuming, as we may, that $\left\{ \left\{ \delta _i \right\} /||\delta _i|| \right\} _{i=1}^{\infty } \rightarrow \delta _{\infty } \in \Lambda _{{\mathbb R}}$ as $i \rightarrow \infty$, we obtain four pairwise orthogonal non-zero vectors $(\delta _{\infty },\kappa ,x_1,x_2)$ such that

$$\begin{aligned} \delta _{\infty }^{2} = 0\quad \text {and}\quad \kappa ^2> 0,\quad x_1^2> 0,\quad x_2^2 > 0. \end{aligned}$$

Such a configuration of vectors, however, is not realizable in the space of signature (3, 19). $\square$

For a point $\varphi \in M_{\kappa }$, let $(X,\alpha )$ be a marked K3 surface whose Burns-Rapoport period is $(\kappa ,\varphi )$. Let $p :({\mathcal S},X) \rightarrow (S,*)$ be its Kuranishi family. By restricting to smaller neighbourhoods of $*$, we may assume that S is contractible. Then the family ${\mathcal S}$ has a natural marking $\alpha :{\mathcal R}^2p_{*}({\mathbb Z}) \rightarrow H^2(X;{\mathbb Z})$, uniquely determined by the marking of X. The corresponding period map $\mathrm {T}_{({\mathcal S},\alpha )} :S \rightarrow \Phi$ is a local isomorphism at $*$ (the local Torelli theorem). Thus, $M_{\kappa }$ admits an open cover $\left\{ U_i \right\}$ such that: for each $U_i$, there is a marked family ${\mathcal X}_{i} \rightarrow U_i$ with $\mathrm {T}_{({\mathcal X}_i,\alpha _i)} = \text {id}$. Each $({\mathcal X}_i,\alpha _i)$ is polarized by the constant section $\kappa \in \Gamma (U_i,{\overline{\Lambda }}_{U_i} \otimes {\mathbb R})$. Applying the Burns-Rapoport theorem for families, one can construct a global marked family ${\mathcal X}\rightarrow M_{\kappa }$ by gluing all the ${\mathcal X}_i$’s; namely, the families ${\mathcal X}_i$ and ${\mathcal X}_j$ can be uniquely identified over $U_i \cap U_j$ by a morphism $\Theta _{ij} :{\mathcal X}_j \rightarrow {\mathcal X}_i$ such that $\Theta _{ij}^{*} \circ \alpha _j = \alpha _i$ and such that $\Theta _{ij}$ fits into the diagram:

We call the family ${\mathcal X}\rightarrow M_{\kappa }$ the universal family of marked ($\kappa$-)polarized K3’s.

8 Proof of Theorem 1

Given $\kappa \in \Lambda _{{\mathbb R}}$, with $\kappa ^2 > 0$, the space ${\overline{M}}_{\kappa }$ consists of two connected components ${\overline{M}}_{\kappa }^{\,\pm }$, each being contractible; they are interchanged by the mapping $\varphi \rightarrow {\bar{\varphi }}$. $M_{\kappa }$ also consists of two connected components $M_{\kappa }^{\pm }$, which, however, are not contractible.

Lemma 6

$H_1(M_{\kappa }^{+};{\mathbb Z}) = \bigoplus _{\delta \in {\overline{\Delta }}_{\kappa }} {\mathbb Z}$, and likewise for $M_{\kappa }^{-}$. ${\overline{\Delta }}_{\kappa }$ denotes the quotient space obtained by identifying the elements $\delta \in \Delta _{\kappa }$ and $(-\delta ) \in \Delta _{\kappa }$.

Proof

Let $\gamma :[0,1] \rightarrow M_{\kappa }^{+}$ be a loop. Since ${\overline{M}}_{\kappa }^{+}$ is contractible, it follows that $\gamma$ is nullhomotopic in ${\overline{M}}_{\kappa }^{+}$. Let $\psi :D \rightarrow {\overline{M}}_{\kappa }^{+}$, where D is a 2-disc, be a nullhomotopy of $\gamma$ in ${\overline{M}}_{\kappa }^{+}$. Since ${\overline{M}}_{\kappa }^{+}$ is contractible, it follows that such a map $\psi$ is unique up to homotopies that agree with $\psi$ on $\partial D$. By Lemma 5, there are but finitely many $\delta \in \Delta _{\kappa }$ such that $\psi (D) \cap H_{\delta }$ is not empty. Each $H_{\delta }$ is a smooth codimension-2 subvariety of ${\overline{M}}_{\kappa }^{+}$. Hence, we may perturb $\psi$ so as it is transverse to each $H_{\delta }$. Setting

$$\begin{aligned} \ell _{\delta }(\gamma ) = \#\left\{ \text {points of } \psi ^{-1}(H_{\delta })\right\} \,{\mathsf {mod}}\,2, \end{aligned}$$

we associate to $\gamma$ a sequence $\left\{ \ell _{\delta }(\gamma ) \right\} _{\delta \in {\overline{\Delta }}_{\kappa }}$, which is an element of $\bigoplus _{\delta \in {\overline{\Delta }}_{\kappa }} {\mathbb Z}$. It is clear that $\ell _{\delta }(\gamma )$ depends only on the homology class of $\gamma$, so the correspondence

$$\begin{aligned} \ell :\gamma \rightarrow \left\{ \ell _{\delta }(\gamma ) \right\} _{\delta \in {\overline{\Delta }}_{\kappa }} \end{aligned}$$

(8.1)

gives a group homomorphism. It is easy to show that (8.1) is an isomorphism. $\square$

Fix a basepoint $b_0 \in M_{\kappa }^{+}$. We now specify “generators” for $\pi _1(M_{\kappa }^{+}, b_0)$. For each $H_{\delta }$ we pick a loop $\gamma _{\delta }$ such that there exists a nullhomotopy of $\gamma _{\delta }$ in $M_{\kappa }^{+} \cup H_{\delta }$ that intersects $H_{\delta }$ transversally at a single point.

Lemma 7

$\pi _1(M_{\kappa }^{+},b_0)$ is normally-generated by the set $\left\{ \gamma _{\delta } \right\} _{\delta \in {\overline{\Delta }}_{\kappa }}$.

Proof

Throughout the proof, all loops are based at $b_0$. Let $\mu$ be a loop in $M_{\kappa }^{+}$ such that there exists $H_{\delta _{0}}$ and a nullhomotopy of $\mu$ in $M_{\kappa }^{+} \cup H_{\delta _{0}}$ that intersects $H_{\delta _{0}}$ transversally at a single point. Such a $\mu$ is called a meridian. Since $H_{\delta _{0}}$ is connected, it follows that $\mu$ and $\gamma _{\delta _{0}}$ are conjugate in $\pi _1(M_{\kappa }^{+},b_0)$. Let $\gamma$ be an arbitrary loop in $M_{\kappa }^{+}$. Since $M_{\kappa }^{+}$ is contractible, the loop $\gamma$ bounds a disc. We may assume that this disc is transverse to each $H_{\delta }$, $\delta \in \Delta _{\kappa }$. It clear now that $\gamma$ is a product of a bunch of meridians, each being a conjugate of some $\gamma _{\delta }$. $\square$

Fix $\kappa _0 \in \Lambda _{{\mathbb R}}$ with $\langle \kappa _0, \kappa _0 \rangle$ > 0. From now on, we write B (resp. ${\overline{B}}$) for $M_{\kappa _0}^{\,+}$ (resp. ${\overline{M}}_{\kappa _0}^{\,+}$). Let ${\mathcal X}\rightarrow B$ the universal family of polarized K3 surfaces, defined in § 7. Each fiber $X_b$ admits a Kähler form in the class $\kappa _0 \in V^{+}_P(X_b)$. Since the space of Kähler forms representing a given Kähler class is convex and therefore contractible, we may assume given a family of fiberwise Kähler forms $\left\{ \omega _b \right\} _{b \in B}$ which varies smoothly with b ( [KS60]). Thus, there is a monodromy map

$$\begin{aligned} \pi _1(B, b_0) \rightarrow \pi _0 \text {Symp}(X_{b_0},\omega _{b_0}). \end{aligned}$$

(8.2)

We shall prove:

• (a) $\pi _1(B, b_0) \xrightarrow {\,(8.2)\,} \pi _0 \text {Symp}(X_{b_0},\omega _{b_0}) \rightarrow \pi _0 \text { {Diff}}(X_{b_0})$ is a nullhomomorphism.

• (b) The following diagram is commutative:

  

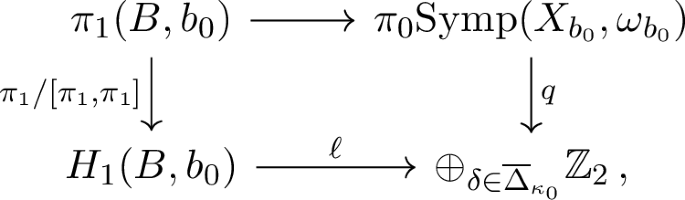
  where $\ell$ is the homomorphism defined in Lemma 6.

Before proving (a) we make a definition: Given $\delta _0 \in \Delta _{\kappa _0}$ and a point $\varphi \in {\overline{B}}$, with $\langle \varphi , \delta _0 \rangle = 0$, we say that $\varphi$ is good if $\langle \varphi , \delta \rangle \ne 0$ for all $\delta \in \Delta _{\kappa _0} - \left\{ \delta _0 \right\}$. The subset of $H_{\delta _0}$ consisting of good points is the complement of a collection of proper analytic subvarieties, and hence it is open and dense.

To prove (a), it suffices by Lemma 7 to show that the restriction of ${\mathcal X}$ to each $\gamma _{\delta }$ is $C^{\infty }$-trivial. Fix $\delta _0 \in \Delta _{\kappa _{0} }$. Considering $\gamma _{\delta _0}$ as a free loop we find a homotopy of $\gamma _{\delta _0}$ into a loop so small that it becomes the boundary of a holomorphic disc D transverse to $H_{\delta _0}$. By perturbing D, we may arrange that it intersects $H_{\delta _0}$ at a good point; that is, setting $\varphi _0 = D \cap H_{\delta _{0}}$, we get:

$$\begin{aligned} \langle \varphi _0, \delta \rangle \ne 0\quad \text{ for } \text{ each } \delta \in \Delta _{\kappa _0} - \left\{ \delta _0 \right\} . \end{aligned}$$

By Lemma 5, D can be chosen small enough so that:

$$\begin{aligned} D \cap H_{\delta _{0}} = \left\{ \varphi _0 \right\} \quad \text {and}\quad D \cap H_{\delta } = \varnothing \ \text {for each } \delta \in \Delta _{\kappa _0} - \left\{ \delta _0 \right\} . \end{aligned}$$

(8.3)

Choose a coordinate t on D such that $\varphi _0$ is given by $t = 0$. Let $D^{*} = D - \left\{ 0 \right\}$. Let ${\mathcal Y}= {\mathcal X}|_{D^{*}}$ be the restriction of ${\mathcal X}$ to $D^{*}$, and let $p :{\mathcal Y}\rightarrow D^{*}$ be the projection. The family ${\mathcal X}$ carries a canonical marking. So does ${\mathcal Y}$, being a subfamily of ${\mathcal X}$; call this marking $\alpha :{\mathcal R}^2p_{*}({\mathbb Z}) \rightarrow {\overline{\Lambda }}_{D^{*}}$. We shall prove that there is a marked family of non-singular K3 surfaces ${\mathcal Y}' \rightarrow D$ whose restriction to $D^{*}$ coincides with ${\mathcal Y}$. Let $(Y'_0,\alpha ')$ be a marked K3 surface whose Burns-Rapoport period is given by

$$\begin{aligned} (\varphi _0,\kappa _0 - \hslash \, \delta _0)\quad \text{ for } \hslash \, \text{ positive } \text{ small } \text{ enough }. \end{aligned}$$

Let S be a sufficiently small neighbourhood of $\varphi _0$ in $\Phi$. Let $p' :({\mathcal Y}', Y'_0) \rightarrow (S,\varphi _0)$ be the Kuranishi family of $(Y'_0,\alpha ')$, endowed with a natural marking ${\mathcal R}^2p'_{*}({\mathbb Z}) \rightarrow H^2(Y'_0;{\mathbb Z})$. We assume (by further shrinking D toward $t = 0$) that $D \subset S$. Now consider the restriction ${\mathcal Y}'|_{D}$. We shall use ${\mathcal Y}'$ to denote this family, also.

Lemma 8

There is a neighbourhood U of $0 \in D$ such that for each $t \in U - \left\{ 0 \right\}$, the class $\kappa _0$ gives a polarization on $Y'_t$.

Proof

It is enough to prove that there is a neighbourhood U of $0 \in D$ such that for each $t \in U - \left\{ 0 \right\}$,

$$\begin{aligned} \langle \kappa _0, \delta \rangle > 0\quad \text {for all } \delta \in \Delta ^{+}(Y'_t). \end{aligned}$$

(8.4)

We first show that there is a neighbourhood U of $0 \in D$ and $\hslash ^{*} > 0$ such that for each $t \in U - \left\{ 0 \right\}$,

$$\begin{aligned} \text { if } \delta \in \Delta ^{+}(Y'_{t}) \text { and } \langle \kappa _0 - \hslash \,\delta _0, \delta \rangle = 0, \text { then } |\hslash | \geqslant \hslash ^{*}. \end{aligned}$$

(8.5)

Suppose, contrary to our claim, that there is a sequence

$$\begin{aligned} (t_k,\delta _k,\hslash _k), t_k \in D - \left\{ 0 \right\} , \delta _k \in \Delta ^{+}(Y'_{t_{k}}) \quad \text {with } t_k \rightarrow 0, \hslash _k \rightarrow 0, \end{aligned}$$

where $\hslash _k$ is the unique solution to the following equation:

$$\begin{aligned} \langle \kappa _0 - \hslash _k\,\delta _0, \delta _k \rangle = 0. \end{aligned}$$

We have, by (8.3), that

$$\begin{aligned} \langle \kappa _0, \delta _k \rangle \ne 0\quad \text {for all } (t_k,\delta _k). \end{aligned}$$

Thus, $\hslash _k$, for all $(t_k,\delta _k)$, is non-zero. Observe that if $\hslash _k \ne 0$, then our sequence contains infinitely many pairwise distinct values of $\hslash _k$, and hence it contains infinitely many pairwise distinct classes $\delta _k \in \Delta$. The rest of the proof is similar to that of Lemma 5. Fix some euclidean norm $||\, ||$ on $\Lambda _{{\mathbb R}}$. The set of numbers $||\delta _k||$ is unbounded for otherwise we would have only finitely many $\delta _k$ in our sequence; thus $\delta _k/||\delta _k||$ converges to a class $\delta _{\infty }$ such that:

$$\begin{aligned} \delta _{\infty }^2 = 0,\quad \langle \delta _{\infty }, \kappa _0 \rangle = 0,\quad \langle \delta _{\infty }, \varphi _0 \rangle = 0. \end{aligned}$$

But this is impossible. Therefore we may choose a small enough U so that (8.5) holds true.

Now choose $\hslash > 0$ so small that $\hslash < \hslash ^{*}$ and also that the class $\kappa _0 - \hslash \,\delta _0$ is a polarization on $Y'_0$; the latter is needed to claim that for each $Y'_t$, sufficiently close to $Y'_0$, we have that

$$\begin{aligned} \langle \kappa _0 - \hslash \,\delta _0, \delta \rangle > 0\quad \text {for each } \delta \in \Delta ^{+}(Y'_t). \end{aligned}$$

(8.6)

Make U small enough so that (8.6) holds for each $t \in U$. Then (8.4) holds for each $t \in U - \left\{ 0 \right\}$, because $\hslash < \hslash ^{*}$. This completes the proof. $\square$

We make D still smaller so that the neighbourhood U may be chosen to cover the whole of D. Then both ${\mathcal Y}$ and ${\mathcal Y}'$ are polarized by the constant section $\kappa _0 \in \Gamma (D^{*},{\overline{\Lambda }}_{D^{*}} \otimes {\mathbb R})$; therefore, their polarized period maps agree over $D^{*}$. Then there exists a canonical family isomorphism $\Theta :{\mathcal Y}' \rightarrow {\mathcal Y}$, with $\alpha ' \circ \Theta ^{*} = \alpha$, that fits into the diagram:

In other words, the family ${\mathcal Y}$, which is defined over $D - \left\{ 0 \right\}$, extends to a family of non-singular surfaces defined for all $t \in D$. Conclusion: the fiber bundle ${\mathcal Y}\rightarrow D - \left\{ 0 \right\}$ is $C^{\infty }$-trivial, and (a) follows.

Abusing notation, we write ${\mathcal Y}$ for the extension of ${\mathcal Y}\rightarrow D^*$ to the whole disc D. We write $Y_0$ instead of $Y'_0$ for the central fiber of this extension. Let $\left\{ \omega _t \right\} _{t \in \partial D}$ be a family of cohomologous Kähler forms, with $[\omega _t] = \kappa _0$, on the fibers $Y_t$ over $\partial D$. To prove (b), it suffice to show that

$$\begin{aligned} q_{\delta }( \left\{ \omega _t \right\} _{t \in \partial D } ) = {\left\{ \begin{array}{ll} 1 &{}{} \text{ for } \delta = \delta _0,\\ 0 &{}{} \text{ for } \text{ all } \delta = {\overline{\Delta }}_{\kappa _0 } - \left\{ \delta _0 \right\} . \end{array}\right. } \end{aligned}$$

To begin with, we choose an extension of $\left\{ \omega _t \right\} _{t \in \partial D}$ to a family of non-cohomologous Kähler forms $\left\{ \omega _t \right\} _{t \in D}$ over the whole of D. Such an extension always exists, and may be defined by using partitions of unity in local charts on D.

We claim that for each $t \in D$,

$$\begin{aligned} \int _{Y_t} [\omega _t] \cup \kappa _0 > 0. \end{aligned}$$

(8.8)

To see this, recall that for each $t \in D$, we have,

$$\begin{aligned}{}[\omega _t]^2> 0,\ \kappa _0^2 > 0 \quad \text {and}\quad [\omega _t], \kappa _0 \in H^{1,1}(Y_t;{\mathbb R}). \end{aligned}$$

Then for each $t \in D - \left\{ 0 \right\}$, and hence, by continuity, for $t = 0$, we have,

$$\begin{aligned}{}[\omega _t], \kappa _0 \in V^{+}(Y_t). \end{aligned}$$

Since neither $[\omega _t]$ nor $\kappa _0$ is isotropic, it follows that their cup product must be positive.

Observe that

$$\begin{aligned} \langle -\delta _0, \kappa _0 - \hslash \,\delta _0\rangle = -2\,\hslash < 0, \end{aligned}$$

hence $\delta _0$ lies in $\Delta ^{+}(Y_0)$ and $(-\delta _0)$ does not. It follows then that

$$\begin{aligned} \Delta ^{+}(Y_0) \cap \Delta _{\kappa _0} = \left\{ \delta _0 \right\} . \end{aligned}$$

Recall that, by (8.3), we get:

$$\begin{aligned} \Delta ^{+}(Y_t) \cap \Delta _{\kappa _0} = \varnothing \quad \text {for each } t \in D^{*}. \end{aligned}$$

Let $\left\{ g_t \right\} _{t \in D}$ be the family of fiberwise Hermitian metrics on ${\mathcal Y}$ associated to $\left\{ \omega _t \right\} _{t \in D}$. Pick a spin$^{{\mathbb C}}$ structure ${\mathfrak {s}}_{\delta }$ on $T_{{\mathcal Y}/D}$ which, when restricted to $Y_0$, satisfies:

$$\begin{aligned} c_1({\mathfrak {s_{\delta }}}) = c_1(Y_0)(=0) + 2\, \delta . \end{aligned}$$

(8.9)

Note that (8.9) specifies ${\mathfrak {s_{\delta }}}$ uniquely. As in (4.2), set:

$$\begin{aligned} \eta _{t} = -i F_{{A_0}_t}^{+} - \rho \, \omega _t. \end{aligned}$$

(8.10)

By (8.8), there is $\rho$ so large that $\left\{ \eta _{t} \right\} _{t \in D}$ becomes an admissible extension of $\left\{ \eta _{t} \right\} _{t \in \partial D}$. Let us consider the Seiberg–Witten equations parametrized by the family $\left\{ (g_t, \eta _t) \right\} _{t \in D}$. To describe their solutions, we use Theorem 3. Let $\Pi ^{*}$, ${\mathfrak {M}}^{{\mathfrak {s}}_{\delta }}$, and $\pi _{{\mathfrak {s}}_{\delta }} :{\mathfrak {M}}^{{\mathfrak {s}}_{\delta }} \rightarrow \Pi ^*$ be as in § 2. We embed D into $\Pi ^{*}$ by the map

$$\begin{aligned} t \rightarrow (g_t,\eta _t),\quad \text {where } \eta _t \text { is given by } (8.10). \end{aligned}$$

If $\delta \ne \pm \delta _0$ and $\delta \in \Delta _{\kappa _0}$, then for all $t \in D$, and we have (by Theorem 3)

$$\begin{aligned} \bigcup _{t \in D} \pi ^{-1}_{{\mathfrak {s}}_{\delta }} (g_t,\eta _t) = \varnothing \quad \text {for all } \delta \in \Delta _{\kappa _0} - \left\{ \pm \delta _0 \right\} . \end{aligned}$$

(8.11)

Hence,

$$\begin{aligned} Q_{\delta }( \left\{ \omega _t \right\} _{t \in \partial D } ) = 0\quad \text{ for } \text{ all } \delta \in \Delta _{\kappa _0 } - \left\{ \pm \delta _0 \right\} , \end{aligned}$$

(8.12)

and $q_{\delta }( \left\{ \omega _t \right\} _{t \in \partial D } ) = 0$ for all $\delta \in {\overline{\Delta }}_{\kappa } - \left\{ \delta _0 \right\}$.

Now let $\delta = \pm \delta _0$. Making $\rho$ so large that

$$\begin{aligned} \rho > \rho _0 = 4 \pi \left( \int _X \delta _0 \cup [\omega _t] \right) \left( \int _X [\omega _t] \cup [\omega _t] \right) ^{-1}, \end{aligned}$$

we insure that the corresponding Seiberg–Witten equations have no reducible solutions. Since for all $t \in D$, , it follows that (8.11) still holds for $\delta = -\delta _0$. Hence,

$$\begin{aligned} Q_{(-\delta _0)}( \left\{ \omega _t \right\} _{t \in \partial D } ) = 0. \end{aligned}$$

unless $t = 0$. Let C be a divisor in $Y_0$ representing $\delta _0$. The divisor C is irreducible. Moreover, C is a smooth rational curve. This follows upon applying the adjunction formula to C. If $C'$ is another effective divisor in the class $\delta _0$, then $C' = C$. This is proved by observing that C is irreducible and has negative self-intersection number. Thus, if we abbreviate ${\mathfrak {s}}_{\delta _0}$ to ${\mathfrak {s}}_0$, we have

$$\begin{aligned} \pi ^{-1}_{{\mathfrak {s}}_{0}} (g_0,\eta _0) = \text {pt},\quad \pi ^{-1}_{{\mathfrak {s}}_{0}} (g_t,\eta _t) = \varnothing \quad \text {for all } t \in D^{*}. \end{aligned}$$

In order to prove that $Q_{\delta _0}( \left\{ \omega _t \right\} _{t \in \partial D } ) = 1$ it suffice to show that $\pi _{{\mathfrak {s}}_{0}}$ is transverse to D. Identifying the groups $\left\{ H^2(Y_t;{\mathbb C}) \right\} _{t \in D}$, we consider the infinitesimal variation of Hodge structures ( [Gri68]):

$$\begin{aligned} \Omega _{*} :T_{D} \rightarrow \text {Hom}\,(H^{1,1}, H^{0,2}),\quad \text {where } H^{p,q} = H^{p,q}(Y_0;{\mathbb C}). \end{aligned}$$

It was shown in [Smi21, § 6] that $\pi _{{\mathfrak {s}}_{0}}$ is transverse to D, provided

(8.13)

This last condition is equivalent to the condition that the period map

$$\begin{aligned} \mathrm {T}_{({\mathcal Y},\alpha )} :D \rightarrow \Phi \end{aligned}$$

is transverse to the divisor $H_{\delta _0}$. This is the case by our choice of D.