Abstract
We show that non-collapsed Gromov–Hausdorff limits of polarized Kähler manifolds, with Ricci curvature bounded below, are normal projective varieties, and the metric singularities of the limit space are precisely given by a countable union of analytic subvarieties. This extends a fundamental result of Donaldson–Sun, in which 2-sided Ricci curvature bounds were assumed. As a basic ingredient we show that, under lower Ricci curvature bounds, almost Euclidean balls in Kähler manifolds admit good holomorphic coordinates. Further applications are integral bounds for the scalar curvature on balls, and a rigidity theorem for Kähler manifolds with almost Euclidean volume growth.
Similar content being viewed by others
References
S. Boucksom. Finite generation for Gromov–Hausdorff limits, unpublished note. http://sebastien.boucksom.perso.math.cnrs.fr/notes/Donaldsun.pdf.
F. Cavelletti and A. Mondino. Almost Euclidean isoperimetric inequalities in spaces satisfying local Ricci curvature lower bounds. Int. Math. Res. Not., (5) (2020), 1481–1510
J. Cheeger. Degeneration of Riemannian metrics under Ricci curvature bounds, Lezioni Fermiane, Scuola Normale Superiore, Pisa (2001). ii+77 pp.
J. Cheeger and T. Colding. Lower bounds on Ricci curvature and the almost rigidity of warped products. Ann. Math. (2), (1)144 (1996), 189–237
J. Cheeger and T. Colding. On the structure of spaces with Ricci curvature bounded below. I. J. Differ. Geom., (3)46 (1997), 406–480
J. Cheeger and T. Colding. On the structure of spaces with Ricci curvature bounded below. II. J. Differ. Geom., (1)54 (2000), 13–35
J. Cheeger and T. Colding. On the structure of spaces with Ricci curvature bounded below. III. J. Differ. Geom., (1)54 (2000), 37–74
J. Cheeger, T. Colding, and W. Minicozzi. Linear growth harmonic functions on complete manifolds with nonnegative Ricci curvature. Geom. Funct. Anal., 5 (1995), 948–954
J. Cheeger, T. Colding, and G. Tian. On the singularities of spaces with bounded Ricci curvature. Geom. Funct. Anal., 12 (2002), 873–914
J. Cheeger, W. Jiang, and A. Naber. Rectifiability of singular sets in spaces with Ricci curvature bounded below, preprint.
J. Cheeger and A. Naber. Lower bounds on Ricci curvature and quantitative behavior of singular sets. Invent. Math., (2)191 (2013), 321–339
J. Cheeger and A. Naber. Regularity of Einstein manifolds and the codimension 4 conjecture. Ann. Math. (2), 182 (2015), 1093–1165
T. Colding and A. Naber. Sharp Hölder continuity of tangent cones for spaces with a lower Ricci curvature bound and applications. Ann. Math. (2), (2)176 (2012), 1173–1229
T. Colding and A. Naber. Characterization of tangent cones of noncollapsed limits with lower Ricci bounds and applications. Geom. Funct. Anal., (1) 23 (2013), 134–148
J.-P. Demailly. Analytic Methods in Algebraic Geometry. Surveys of Modern Mathematics, 1. International Press, Somerville.
X.-X. Chen, S. Donaldson, and S. Sun. Kähler–Einstein metrics on Fano manifolds. II: limits with cone angle less than \(2\pi \). J. Am. Math. Soc., (1)28 (2015), 199–234
X.-X. Chen, S. Donaldson, and S. Sun. Kähler–Einstein metrics on Fano manifolds. III: limits as cone angle approaches \(2\pi \) and completion of the main proof. J. Am. Math. Soc., (1)28 (2015), 235–278
X.X. Chen and B. Wang. Space of Ricci flows (II). Forum Math. Sigma, 5 (2017), e32
S.-Y Cheng and S.-T. Yau. Differential equations on Riemannian manifolds and their geometric applications. Commun. Pure Appl. Math., 28 (1975), 333–354
T. Colding. Ricci curvature and volume convergence. Ann. Math. (2), 145 (1997), 477–501
Y. Ding. The gradient of certain harmonic functions on manifolds of almost nonnegative Ricci curvature. Israel J. Math., 129 (2002), 241–251
S.-K Donaldson and S. Sun. Gromov–Hausdorff limits of Kähler manifolds and algebraic geometry. Acta Math., (1)213 (2014), 63–106
S.-K Donaldson and S. Sun. Gromov–Hausdorff limits of Kähler manifolds and algebraic geometry II. J. Differ. Geom., (2)107 (2017), 327–371
L. Evans and R. Gariepy. Measure Theory and Fine Properties of Functions. Studies in Advanced Mathematics. CRC Press, Boca Raton (1992).
F. He. Existence and applications of Ricci flows via pseudolocality. arXiv:1610.01735.
R. Hochard. Short-time existence of the Ricci flow on complete, non-collapsed 3-manifolds with Ricci curvature bounded from below. arXiv:1603.08726.
L. Hörmander. The Analysis of Linear Partial Differential Operators I. Distribution Theory and Fourier Analysis, 2nd ed. Springer, Berlin (1990).
L. Hörmander. An Introduction to Complex Analysis in Several Variables, D. Van Nostrand Co. (1966).
S. Huang and L.-F. Tam. Kähler–Ricci flow with unbounded curvature. Am. J. Math., (1)140 (2018), 189–220
W. Jiang. Bergman kernel along the Kähler Ricci flow and Tian’s conjecture. J. Reine Angew. Math., 717 (2016), 195–226
B. Kotschwar. Hamilton’s gradient estimate for the heat kernel on complete manifolds. Proc. Am. Math. Soc., (9)135 (2007), 3013–3019
B. Kotschwar. Kählerity of shrinking gradient Ricci solitons asymptotic to Kähler cones. arXiv:1701.08486.
B. Kotschwar. Ricci flow and the holonomy group. J. Reine Angew. Math., 690 (2014), 133–161.
N. Li and A. Naber. Quantitative estimates on the singular sets of Alexandrov spaces, preprint.
G. Liu. Gromov–Hausdorff limits of Kähler manifolds with bisectional curvature lower bound. Commun. Pure Appl. Math., (2)71 (2018), 267–303
G. Liu. Gromov–Hausdorff limits of Kähler manifolds and the finite generation conjecture. Ann. Math. (2), (3)184 (2016), 775–815
G. Liu. On Yau’s uniformization conjecture. Camb. J. Math., 7 (2019), 33–70
G. Liu. Compactification of certain Kähler manifolds with nonnegative Ricci curvature. arXiv:1706.06067.
P. Li and S.-T. Yau. On the parabolic kernel of the Schrödinger operator. Acta Math. (3-4)156 (1986), 153–201
P. Li and G. Tian. On the heat kernel of the Bergmann metric on algebraic varieties. J. Am. Math. Soc., (4)8 (1995), 857–877
N. Mok, Y.T. Siu, and S.T. Yau. The Poincaré–Lelong equation on complete Kähler manifolds. Compos. Math., (1–3)44 (1981), 183–218.
G. Perelman. The entropy formula for the Ricci flow and its geometric applications. arXiv:math.DG/0211159.
A.M. Petrunin. An upper bound for the curvature integral. Algebra i Analiz (2)20 (2008), 134–148
D.H. Phong, J. Song, and J. Sturm, Degenerations of Kähler–Ricci solitons on Fano manifolds. Univ. Iagel. Acta Math., 52 (2015), 29–43
W.X. Shi. Ricci deformation of the metric on complete noncompact Riemannian manifolds. J. Differ. Geom., 30 (1989), 303–394
W.X. Shi. Ricci flow and the uniformization on complete noncompact Kähler manifolds. J. Differ. Geom., 45 (1997), 94–220
Y.-T. Siu. Analyticity of sets associated to Lelong numbers and the extension of meromorphic maps. Bull. Am. Math. Soc., 79 (1973), 1200–1205
Y.-T. Siu. Analyticity of sets associated to Lelong numbers and the extension of closed positive currents. Invent. Math., 27 (1974), 53–156
G. Székelyhidi. The partial \(C^0\)-estimate along the continuity method. J. Am. Math. Soc., (2)29 (2016), 537–560
G. Tian. Kähler–Einstein metrics on algebraic manifolds. In: Proceedings of the International Congress of Mathematicians, Kyoto (1990).
G. Tian. On Calabi’s conjecture for complex surfaces with positive first Chern class. Invent. Math., (1)101 (1990), 101–172
G. Tian and B. Wang. On the structure of almost Einstein manifolds. J. Am. Math. Soc., 28 (2015), 1169–1209
G. Tian and Z. Zhang. On the Kähler–Ricci flow on projective manifolds of general type. Chin. Ann. Math. Ser. B, 27 (2006), 179–192
P. Topping. Ricci flow compactness via pseudolocality, and flows with incomplete initial metrics. J. Eur. Math. Soc. (JEMS), (6)12 (2010), 1429–1451
S.-T. Yau. Open problems in geometry. Chern–a great geometer of the twentieth century. International Press, Hong Kong (1992), pp. 275–319.
Acknowledgements
We would like to thank Jeff Cheeger and John Lott for their interest in this work. We also thank Aaron Naber for many fruitful discussions, as well as Richard Bamler and Peter Topping for helpful suggestions. Special thanks also goes to Yum-Tong Siu for the proof of Lemma 4.6.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Gang Liu is partially supported by the Science and Technology Commission of Shanghai Municipality No. 18dz2271000, NSFC No. 12071140, Program of Shanghai Academic/ Technology Research Leader 20XD1401500, as well as the Xplore Prize by Tencent. Gábor Székelyhidi is supported in part by NSF Grant DMS-1350696.
Appendix
Appendix
In the proof of Proposition 3.1 we used the estimate of Cheeger–Jiang–Naber [CJN] for the volumes of tubular neighborhoods of the singular set, in order to control the cutoff functions \(\psi ^3_i\). In this appendix we first give an alternative argument, following the approach of Chen–Donaldson–Sun [CDS15a], which is independent of the results in [CJN]. First note that the cone \(V = {\mathbb {R}}^{2n-2} \times W\) for a two-dimensional cone \((W,o')\) has singular set \({\mathbb {R}}^{2n-2} \times \{o'\}\), and so we can directly see the required estimate for the volumes of its tubular neighborhoods. Therefore Propositions 3.4 and 3.5 hold without appealing to [CJN].
We can now argue similarly to [CDS15a] to show that the singular sets in any cone (V, o) arising in Proposition 3.1 have good cutoff functions (even closer to what we do are Propositions 12, 13 and 14 of the arXiv version of [Sze16]). More precisely, suppose that \((M_i, L_i, \omega _i)\) is a sequence as in Proposition 3.1 such that \((M_i, p_i)\) converges to a cone (V, o) for some \(p_i\in M_i\). Recall that the singular set is \(\Sigma \subset V\), consisting of points \(q\in V\) such that \(\lim _{r\rightarrow 0} r^{-2n}\mathrm {vol}(B(q,r)) \le \omega _{2n}-\epsilon \), where \(\epsilon \) is obtained from Theorem 1.5. We then have the following.
Proposition 5.1
For any compact set \(K\subset V\) and \(\kappa > 0\) there is a function \(\chi \) on V, equal to 1 on a neighborhood of \(K\cap \Sigma \), supported in the \(\kappa \)-neighborhood of \(K\cap \Sigma \), and such that \(\int _K |\nabla \chi |^2 < \kappa \).
Proof
Let us fix \(K, \kappa \). Suppose that we have distance functions \(d_i\) on \(B(p_i,2R) \sqcup B(o,2R)\), realizing the Gromov–Hausdorff convergence, where R is large so that \(K\subset B(o,R)\). For \(q\in B(o,R)\), and \(\rho \in (0,1)\), define
where \(U_i(q,\rho ) = \{x \in B(p_i,2)\,:\, d_i(x, q) < \rho \}\). Note that \(S_i + 2n \ge 0\).
Let us denote by \({\mathcal {D}}\subset K\cap \Sigma \) the set of points which have a tangent cone splitting off \({\mathbb {R}}^{2n-2}\), and let \(S_2 = \Sigma {\setminus } {\mathcal {D}}\). Proposition 3.5 implies that for any \(x\in {\mathcal {D}}\) there exists a \(\rho _x > 0\) such that \(V(i,x,\rho _x) < A\) for a fixed constant A, for sufficiently large i. At the same time by Proposition 3.5 we also have a constant \(c_0 > 0\) (depending on \(n, v, d, \epsilon \)) such that for any \(x\in {\mathcal {D}}\) and \(\delta > 0\) there is an \(r_x < \delta \) such that \(V(i,x,r_x) > c_0\) for sufficiently large i (here note that the two dimensional cones appearing in tangent cones of points in \({\mathcal {D}}\) have cone angles bounded strictly away from \(2\pi \)).
By Cheeger–Colding’s [CC97] the Hausdorff dimension of \(S_2\) is at most \(2n-4\), so for any small \(\epsilon > 0\) we can cover \(S_2\cap K\) with balls \(B_\mu \) such that
The set
is compact, \(J\subset {\mathcal {D}}\), and so it is covered by the balls \(B(x,\rho _x)\) with \(x\in {\mathcal {D}}\). We choose a finite subcover corresponding to \(x_1,\ldots , x_N\), and set
For sufficiently large i we then get an estimate
where C depends on \(\epsilon , N\), but not on i.
We claim that the compact set \( J \subset {\mathcal {D}}\) has finite \((2n-2)\)-dimensional Hausdorff measure. To prove this, recall that for any small \(\delta > 0\) and all \(x\in {\mathcal {D}}\cap J\) we have \(r_x < \delta \) such that \(V(i,x,r_x) > c_0\) for large i. By a Vitali type covering argument we can find a disjoint, finite sequence of balls \(B(y_k, r_{y_k})\) in W, for \(k=1,\ldots , N'\) such that \(B(y_k, 5r_{y_k})\) cover all of J. It follows that
At the same time for each \(y_k\), we have the estimate
for sufficiently large i. Taking i even larger we can assume that the \(U_i(y_k, r_{y_k})\) are disjoint, since they converge in the Gromov–Hausdorff sense to the disjoint balls \(B(y_k, r_{y_k})\). Using (5.1) we therefore have
Since \(\delta \) was arbitrary (and C is independent of \(\delta \)), this implies that \({\mathcal {H}}^{2n-2}(J) \le C'\).
It follows that J has capacity zero, in the sense that for any \(\kappa > 0\) we can find a cutoff function \(\eta _1\) supported in the \(\kappa \)-neighborhood of J, such that \(\Vert \nabla \eta _1\Vert _{L^2} \le \kappa /2\), and \(\eta _1 = 1\) on a neighborhood U of J (see for instance [Bou, Lemma 2.2] or [EG92, Theorem 3, p. 154]). The set \((K\cap \Sigma ) {\setminus } U\) is compact, and so it is covered by finitely many of our balls \(B_\mu \) from before. Because of this, as in [DS14], we can find a good cutoff function \(\eta _2\), with \(\Vert \nabla \eta _2\Vert _{L^2} \le \kappa /2\) (if \(\epsilon \) at the beginning was sufficiently small), such that \(\eta _2\) is supported in the \(\kappa \)-neighborhood of \((K\cap \Sigma ){\setminus } U\) and with \(\eta _2 = 1\) on a neighborhood of \((K\cap \Sigma ){\setminus } U\). Then \(\eta = 1 - (1-\eta _1)(1-\eta _2)\) gives the required cutoff function. \(\square \)
We next prove a result essentially contained in Cheeger–Colding–Minicozzi [CCM95], that we used in the proof of Proposition 4.1.
Proposition 5.2
Let (V, o) denote a tangent cone of a non-collapsed limit space of manifolds with Ricci curvature bounded from below. Suppose that there are k linearly independent harmonic functions \(u^1,\ldots , u^k\) on V that are homogeneous of degree one. Then we have a splitting \(V = {\mathbb {R}}^k \times Y\).
Proof
By assumption we have a sequence \(B(p_i, 2)\) of balls in Riemannian manifolds with \(\mathrm {Ric} > -i^{-1}\), such that \(B(p_i,2)\rightarrow B(o,2)\) in the Gromov–Hausdorff sense. We will prove the following: for any \(\delta > 0\), we can find an \(r > 0\) and \(\delta \)-splitting maps \(u_i : B(p_i, r) \rightarrow {\mathbb {R}}^k\) for sufficiently large i. Since V is a cone, after scaling up by \(r^{-1}\) and taking a diagonal sequence, we find a sequence \(B(p_i', 1)\rightarrow B(o, 1)\) such that each \(B(p_i', 1)\) admits an \(i^{-1}\)-splitting map. From this it follows that B(o, 1/2) splits an isometric factor of \({\mathbb {R}}^k\). For this, see Cheeger–Colding [CC96], or Cheeger–Naber [CN15, Definition 1.20, Lemma 1.21].
Before we begin let us recall the notion of a \(\delta \)-splitting map. A map \(u=(u^1, \ldots , u^k): B(p,r) \rightarrow {\mathbb {R}}^k\) is a \(\delta \)-splitting map, if it is harmonic, and satisfies
-
(1)
\(|\nabla u| < 1 + \delta \),
-
(2)
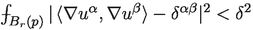 ,
, -
(3)
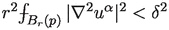 .
.
Consider again our sequence \(B(p_i, 2) \rightarrow B(o,2)\). We can assume that

and since the \(u^\alpha \) are homogeneous, this implies that for all r we have

We can find a sequence of harmonic functions \(u_i^{\alpha }\) on \(B(p_i, 2)\) such that under the Gromov–Hausdorff convergence we have \(u_i^\alpha \rightarrow u^\alpha \) uniformly on each compact set, and moreover for any \(0< r < 2\),

Let \(f_i\) denote a harmonic function of the form \(u^\alpha _i\) or \(\frac{1}{\sqrt{2}} (u_i^\alpha \pm u_i^\beta )\) for \(\alpha \not = \beta \). By the Bochner formula \(\Delta |\nabla f_i|^2 \ge -\Psi (i^{-1}) |\nabla f_i|^2\), and so by the mean value inequality, for sufficiently large i we have
It follows that for any \(0< r < 1.5\) we have

As the gradient of \(f_i\) is uniformly bounded, we find the above convergence is uniform on the interval \(a<r<1\), where \(a>0\) is any constant.
Note that \(\sup _{B(p_i, r)} |\nabla f_i|^2 \ge 1/2\), and so for large i
Given \(\epsilon > 0\), we can then choose \(r_0 > 0\) depending on \(\epsilon , C\), such that for all sufficiently large i there is some \(r \in (r_0, 1/10)\), perhaps depending on i, satisfying
Consider now the functions \(v_i = \sup _{B(p_i, 3r)}|\nabla f_i|^2 - |\nabla f_i|^2\). Then on \(B(p_i, 3r)\), \(v_i \ge 0\),
and
From the weak Harnack inequality, once i is sufficiently large,

This implies

where C depends only on the non-collapsing constant, through the Sobolev inequality. Recall r (depending on i) has a lower bound \(r_0\), and so by (5.3),

It follows that for sufficiently large i we have
Therefore,

We now apply this to \(f_i = u^\alpha _i\), and to \(f_i = \frac{1}{\sqrt{2}}(u_i^\alpha \pm u_i^\beta )\), and use the polarization identity
Using also (5.2) we find that for sufficiently large i (depending on \(\epsilon \)), we have

Since at the same time \(|\nabla u_i^\alpha |^2 \le 1 + \Psi (\epsilon )\), we can use the Bochner formula, using a cutoff function \(\phi \) as in Cheeger–Colding [CC96] supported in \(B(p_i, 2r_0)\), equal to 1 in \(B(p_i, r_0)\). We find that for sufficiently large i,

If \(\epsilon \) is chosen sufficiently small, depending on \(\delta > 0\), then this shows that \(u_i = (u_i^1,\ldots , u_i^k)\) is a \(\delta \)-splitting map on \(B(p_i, r_0)\), for sufficiently large i.\(\square \)
Rights and permissions
About this article
Cite this article
Liu, G., Székelyhidi, G. Gromov–Hausdorff limits of Kähler manifolds with Ricci curvature bounded below. Geom. Funct. Anal. 32, 236–279 (2022). https://doi.org/10.1007/s00039-022-00594-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00039-022-00594-8




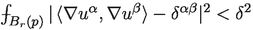 ,
,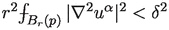 .
.