1 Introduction

Active noise and vibration control (ANVC) or simply active noise control (ANC) [11, 12, 15, 17, 23, 24, 33, 42] is a class of methods to reduce noise and vibration by generating an anti-noise signal with a phase opposite to the original noise so that both interfere destructively, reducing the noise level. ANC works best at low frequencies where passive techniques are less effective and can be used together with the last. It is finding applications in many fields like noise reduction in cars [40], homes [8], headphones [10, 25, 39], and even vibration of airplane tails [35].

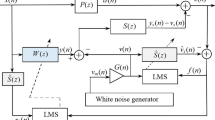
ANC methods can be divided into two categories [23], feedforward ANC and feedback ANC. In feedforward ANC, a reference sensor captures a reference signal early in the noise path. Then a controller uses information from this sensor to generate an anti-noise signal that is fed to an actuator to reduce the noise. The residual noise level is measured by an error sensor and used by the controller when generating the anti-noise. In feedback ANC, there is no reference sensor, and the anti-noise signal is generated using only the information from the error sensor. This work focuses on feedback ANC since in many applications may be difficult to obtain a good reference. Feedback ANC has been extensively applied to ANC headphones, for instance, [22, 41, 43, 44] and many other systems [21, 35].

Most feedforward and feedback ANC algorithms (like the filtered-x least mean squares (FxLMS) algorithm[32]) require a model of the secondary path. This model may be obtained offline before the ANC controller starts to reduce noise or online during the operation of the ANC controller. Online secondary path modeling allows the ANC system to cope with slow changes in the secondary path. However, only a few algorithms can cope with fast changes. Eriksson [13] first proposed online secondary path modeling using a small auxiliary white noise signal as input to an adaptive filter. After this, it was proposed to improve the modeling by using an additional adaptive filter to remove the primary noise from the secondary path model error signal [5, 45]. The auxiliary noise power can be chosen so that residual noise to auxiliary noise at the error sensor is constant [9] and it can also be turned off after convergence has been reached [2, 26] and on after the secondary path changes. Finally, it can also be used to model the path from the anti-noise transducer to the reference sensor (feedback path) [1].

In feedforward ANC, the secondary path can also be modeled without the auxiliary noise by the simultaneous equations method [14] or the overall modeling algorithm (OMA) [23]. However, the secondary path model of the OMA algorithm may be incorrect [6, 23, 27]. Nevertheless, even with an incorrect secondary path model, the resulting overall model (primary and secondary path) can be used to determine the optimum controller as in the mirror-modified FxLMS (MMFxLMS) algorithm [27, 28].

There is very little work on online secondary path modeling for feedback ANC. However, when using auxiliary noise, the same algorithms as in feedforward ANC can be used [18, 43]. Unfortunately, to the authors’ knowledge, there is no work on online secondary path modeling for feedback ANC without auxiliary noise. Moreover, the anti-noise signal and the (unknown) disturbance signal are usually highly correlated, making it difficult to use the first to obtain an accurate secondary path model.

This work proposes to use a variant of adaptive model predictive control (MPC) [30, 38] to determine the anti-noise signal. In MPC, the plant output (the ANC error signal) future values are predicted using a model and set close to a predetermined signal (zero in ANC) by carefully selecting the present and future values of the plant input signal (anti-noise). The predictions consider the effect that present inputs have on future outputs. The ANC’s primary noise signal is the MPC disturbance. However, unlike standard model predictive control applications, in ANC, the plant plus disturbance model is unknown and needs to be estimated, making this an adaptive model predictive control application [30, 38] that has yet to receive much attention. Nevertheless, the model is linear, allowing for simpler solutions, as shown in this work. ANC also falls in the more general field of adaptive control [4] and stochastic adaptive control [7] that, in general, requires complex solutions with caution and probing (a dual controller) [20]. Adaptive model predictive control applications have been presented in [34] and [31] for ANC. This work builds on these two papers but presents a different approach with lower computational complexity.

Regarding notation, vectors are boldface lowercase letters as \(\textbf{u}\). Given a signal u(n), \(\textbf{u}(n)\) is the vector with its past samples \(\textbf{u}(n)=[u(n) \dots u(n-N+1)]^\textrm{T}\) where N is the vector length, which should be determined from context. The operator \(*\) stands for convolution.

2 Proposed Algorithm

In feedback ANC, the residual noise signal e(n) is given by the sum of the primary noise signal d(n) (disturbance) with the anti-noise signal u(n) after passing through the secondary path (or plant) with impulse response s(n)

$$\begin{aligned} e(n) = d(n) + s(n) * u(n). \end{aligned}$$
(1)

In the proposed algorithm, d(n) is modeled by an order \(N_\textrm{d}\) autoregressive (AR) model:

$$\begin{aligned} d(n)=\tilde{d}(n) - \textbf{a}_\textrm{dx}^\textrm{T}(n) \textbf{d}(n-1) \end{aligned}$$
(2)

or \(\textbf{a}_\textrm{d}^\textrm{T}(n) \textbf{d}(n)=\tilde{d}(n)\) where \(\tilde{d}(n)\) is a white noise process and \(\textbf{a}_\textrm{d}=[1, \textbf{a}_\textrm{dx}]\). The signal \(\tilde{d}(n)\) is taken to have small power making d(n) predictable. This happens in narrowband systems, for instance. The secondary path is modeled by an autoregressive exogenous input (ARX) model so that the anti-noise signal \(y(n) = s(n) * u(n)\) is also given by

$$\begin{aligned} \textbf{a}_s(n) \textbf{y}(n) = \textbf{b}_s(n) \textbf{u}(n) \end{aligned}$$
(3)

assuming the model coefficients are constant or slowly varying. Taking the z-transform [36] results in

$$\begin{aligned} a_\textrm{d}(z) a_\textrm{s}(z) e(z) = a_\textrm{d}(z) b_\textrm{s}(z) u(z) + a_\textrm{s}(z) \tilde{d}(z) \end{aligned}$$
(4)

and taking the inverse z-transform result in

$$\begin{aligned} \textbf{a}^\textrm{T}\textbf{e}(n) = \textbf{b}^\textrm{T}\textbf{u}(n) + \textbf{a}_\textrm{s}^\textrm{T}\tilde{\textbf{d}}(n) \end{aligned}$$
(5)

where \(\textbf{a}= \textbf{a}_\textrm{s}* \textbf{a}_\textrm{d}\) and \(\textbf{b}= \textbf{b}_\textrm{s}* \textbf{a}_\textrm{d}\).

Estimates for \(\textbf{a}\) and \(\textbf{b}\), \(\hat{\textbf{a}}\), and \(\hat{\textbf{b}}\) can be obtained by minimizing the residual noise estimation error square sum \(\xi (n)=\sum _{i=0}^{\infty } j^2(n-i) \lambda ^i\) where

$$\begin{aligned} j(n) = e(n) - (\hat{\textbf{b}}^\textrm{T}(n) \textbf{u}(n) - \hat{\textbf{a}}_\textrm{x}^\textrm{T}(n) \textbf{e}(n-1)). \end{aligned}$$
(6)

These estimates can be obtained using the RLS algorithm [19, 31]. The vectors \(\hat{\textbf{b}}\) and \(\hat{\textbf{a}}_\textrm{x}\) have length \(N+1\) and N resulting in a order N model. For small \(\tilde{\textbf{d}}(n)\) (as in narrowband disturbances), persistent excitation, and N large enough, the minimization results in \(\hat{\textbf{a}}=\textbf{a}\) and \(\hat{\textbf{b}}=\textbf{b}\). The resulting model has canceling poles and zeros at the zeros of \(a_\textrm{d}(z)\) and uncontrollable states that are only excited by \(\tilde{d}(n)\) in the original model, which may be described by a zero input filter in the new model.

This model is the least-squares (LS) one-step-ahead predictor of e(n) given u(n), and it can be used to predict future values of e(n). Replacing the LS with the least mean squares (LMS) predictor (since they are equivalent for large M and stationary signals) and since the last is given by the expected value [3] results in the following. Using measures up to time n, the predicted residual noise at time \(n+1\) is

$$\begin{aligned} \hat{e}(n+1,n)=\textrm{E}[e(n+1)\mid n]= \hat{\textbf{b}}^\textrm{T}(n) \textbf{u}(n+1) - \hat{\textbf{a}}_\textrm{x}^\textrm{T}(n) \textbf{e}(n). \end{aligned}$$
(7)

The predicted residual noise at time \(n+2\) is

$$\begin{aligned} \hat{e}(n+2,n)&= \textrm{E}[e(n+2)\mid n]\nonumber \\&= \hat{\textbf{b}}^\textrm{T}(n) \textbf{u}(n+2) - \hat{\textbf{a}}_\textrm{x}^\textrm{T}(n) [\textrm{E}[e(n+1)\mid n], \textbf{e}(n)] \nonumber \\&= \hat{\textbf{b}}^\textrm{T}(n) \textbf{u}(n+2) - \hat{\textbf{a}}_\textrm{x}^\textrm{T}(n) [\hat{e}(n+1), \textbf{e}(n)], \end{aligned}$$
(8)

etc. So, \(\hat{e}(n+i)\) given u(n) can be obtained simply by iterating the difference equation of the estimated model. Namely,

$$\begin{aligned} \hat{e}(n+i+1,n) = \hat{\textbf{b}}^\textrm{T}(n) \textbf{u}(n+i+1) - \hat{\textbf{a}}_\textrm{x}^\textrm{T}(n) \hat{e}(n+i,n), \end{aligned}$$
(9)

where

$$\begin{aligned} \hat{e}(n+i,n)=\textrm{E}[e(n+i)\mid n]=\left\{ \begin{matrix} e(n+i) &{} \text {for } i\le 0 \\ \textrm{E}[e(n+i)\mid n] &{} \text {otherwise} \\ \end{matrix}\right. . \end{aligned}$$
(10)

Note, however, that the model formed by \(\hat{\textbf{a}}_\textrm{x}\) and \(\hat{\textbf{b}}\) is the LS predictor of e(n) and may not be the best predictor of \(e(n+i)\) even for \(i=1\). It can be tuned to a set of u(n) components that change in \(u(n+i)\), especially after fast changes. Regardless, this work will use this predictor in the remaining text.

Let \(u(n) = u_0(n)+u_1(n)\) where

$$\begin{aligned} u_0(n+i)=\left\{ \begin{matrix} u(n+i) &{} \text {for } i\le 0 \\ 0 &{} \text {otherwise} \\ \end{matrix}\right. \end{aligned}$$
(11)

and

$$\begin{aligned} u_1(n+i)=\left\{ \begin{matrix} u(n+i) &{} \text {for } i > 0 \\ 0 &{} \text {otherwise} \\ \end{matrix}\right. . \end{aligned}$$
(12)

Then, since (9) describes a linear IIR filter [36], then

$$\begin{aligned} \hat{e}(n+i,n)=\hat{e}_0(n+i,n) + \hat{s}(i) * u_1(n+i) \end{aligned}$$
(13)

where \(i>0\), \(\hat{s}(i)\) is the impulse response of the IIR filter, and the signal \(\hat{e}_0(n+i)\) can be obtained from iterating the difference equation

$$\begin{aligned} \hat{e}_0(n+i,n) = \hat{\textbf{b}}^\textrm{T}(n) \textbf{u}_0(n+i) - \hat{\textbf{a}}_\textrm{x}^\textrm{T}(n) \hat{\textbf{e}}_0(n+i-1,n), \end{aligned}$$
(14)

with \(\hat{e}(n+i)=e(n+i)\) for \(i\le 0\). Finally, let

$$\begin{aligned} e_0(n+i)=\left\{ \begin{matrix} e(n+i) &{} \text {for } i \le 0 \\ 0 &{} \text {otherwise} \\ \end{matrix}\right. . \end{aligned}$$
(15)

Since the goal is to drive \(\hat{e}(n+i,n)\) to \(e_0(n+i)\), keeping past values and driving future values to zero, then \(u_1(n)\) should be

$$\begin{aligned} u_1(n+i) = -\hat{s}^{-1}(n) * (\hat{e}_0(n+i,n)-e_0(n+i)) \end{aligned}$$
(16)

where \(\hat{s}^{-1}(n)\) is the impulse response of the inverse of the IIR filter in (9). Let \(\hat{s}(z)=\hat{b}(z)/\hat{a}(z)\) and \(\hat{s}^{-1}(z)=1/\hat{s}(z)\) be the z-transform of \(\hat{s}(n)\) and \(\hat{s}^{-1}(n)\), then \(\hat{s}^{-1}(n)\) can be obtained using the inverse z-transform of \(\hat{s}^{-1}(z)\). To obtain a finite energy signal (and a stable filter), the region of convergence (ROC) of the z-transform should be selected to include the unit circle resulting in general in a non-causal signal (and filter). This (non-causal) filter can be implemented since \(\hat{e}_0(n)\) is known for past and future. Finally, \(u(n+1)\) is set to \(u_1(n+1)\) and used as input to the plant at time \(n+1\).

In the proposed algorithm, the non-causal filter \(\hat{s}^{-1}(z)=\hat{a}(z)/\hat{b}(z)\) is implemented by numerically calculating the roots of \(\hat{b}(z)\), \(z_i\). Then forming \(\hat{b}_\textrm{st}(z)\) by the set of roots with \(|z_i |< \alpha \) with \(\alpha \) slightly greater than one (inside the unit circle or close), and \(\hat{b}_\textrm{ut}(z)\) by the set of roots with \(|z_i |\ge \alpha \) (outside the unit circle). Choosing \(\alpha >1\) assures that canceling poles and zeros at the unit circle (that form oscillators to predict sinusoidal signals) stay in the same filtering operation. Then \(\hat{e}_0(n+i,n)-e_0(n+i)\) is filtered by \(1/\hat{b}_\textrm{ut}(z)\) by flipping (time reversing, \(x(-n)\)) all the signals to make the filter stable; and then by \(\hat{a}(z)/b_\textrm{st}(z)\). All the signals extend from \(n-L+1\) to \(n+L\) (length 2L) with L large enough so that the transients of the filters are negligible at time \(n+1\). The source code for the proposed algorithm is available in [29].

3 Computational Complexity

The computational complexity of the proposed algorithm is approximately (for large N and L) \(32N^2\) for the system identification component, \(4/3N^3\) for the calculation of the b(z) polynomial roots by calculating the eigenvalues of the companion matrix [16, 37] and 16LN for filtering and prediction. This results in a total of \(32N^2+4/3N^3+16LN\). As a comparison, Mohseni’s algorithm [31] has a computational complexity of \(L_\textrm{h}N^2 + (8/3+6)L_\textrm{h}^3\), where \(L_\textrm{h}\) is the horizon length. Using the same parameters as in the simulation section, \(f_\textbf{s}=2000\) Hz, \(N=16\), \(L=64\), \(L_\textrm{h}=64\) results in 60 MFLOPS for the proposed algorithm and 4577 MFLOPS for Mohseni’s algorithm.

Note that it is still possible to reduce the computational complexity by noting that \(\hat{e}_0(z,n)-e_0(z) = g(z)/\hat{a}(z)\) where g(z) is an order N polynomial related to the initial conditions for \(\hat{e}_0(n+i,n)\) and that \(u_1(n+i) = -\hat{b}^{-1}(n) * g(z)\) but this will not be further discussed in this work.

4 Simulation Results

Table 1 Algorithm’s parameters
Full size table

This section presents a set of simulation results. In the simulations, the sampling frequency is \(f_\textbf{s}=2000\) Hz. The plant is formed by an order \(N_\textbf{x}=6\) IIR filter. The plant parameters \(\textbf{a}_\textrm{s}\) and \(\textbf{b}_\textrm{s}\) coefficients are initially set Gaussian random values with zero mean and variance \(1/N_\textbf{x}^2\) and one, respectively, with \(\textbf{a}_\textrm{s}\) first coefficient equal to one. The parameters change during the simulation according to random walk model (\(\textbf{a}_\textrm{s}(n+1)=\textbf{a}_\textrm{s}(n)+\textbf{r}_\textrm{a}(n)\), \(\textbf{b}_\textrm{s}(n+1)=\textbf{b}_\textrm{s}(n)+\textbf{r}_\textrm{b}(n)\)) where the state noise \(\textbf{r}_\textrm{a}\) and \(\textbf{r}_\textrm{b}\) is formed by a set independent white noise signals with variance \(q_r(n)\). The plant changes fast from 2 to 3 s with \(q_\textbf{r}= 1/fs\) and slowly for the remaining time with \(q_\textbf{r}(n) = 1/(400 f_\textbf{s})\). The filter poles and zeros are kept at a distance greater than \(\beta =0.1\) of the unit circle at any time n. Three sinusoidal signals with frequencies of 200, 400, and 600 Hz and amplitudes of 0.5, 1.3, and 0.3 plus white background noise with variance \(q_\textbf{v}=0.01\) are added at the plant’s output. The charts plot the result for 100 simulations of several algorithms. The anti-noise signal saturates at 10 and \(-10\). Before ANC is started, at 0.5 s, the input of the plant is set to a unit-power white noise signal, and the model identification component of the algorithm is left running. The percentile charts show the percentile 10%, 25%, 50%, 75%, 90%, and 99% residual noise level at each time, given some information about its probability density function (PDF). The algorithms parameters are presented in Table 1. These are based on the values presented in the corresponding papers and tuned by trial and error. In Carini’s algorithm, the step size \(\mu \) was scaled by the factor \(\mu _\textrm{SC}\) to improve stability.

Figure 1 shows the residual noise level power versus time of three typical simulations of the proposed algorithm. As can be seen, the residual noise quickly settles to the minimum value after ANC is started, rises while the plant changes fast, and settles to the minimum again as desired. However, there are some narrow spikes and even divergence (not shown). Figure 2 shows the percentile chart for the 100 simulations. As can be seen, performance is not always as good as in Fig. 1. The residual noise power takes large values in less than 10% of the simulations. Narrow spikes contribute to a rise in the percentile curves, but they are not visible on the plots. The very high percentile 99% curve is primarily due to divergence in some simulations. Nevertheless, the residual noise takes low values (at each time instant) in more than 90% of the simulations. This is confirmed by the histogram of the residual noise power at the simulation end, as shown in Fig. 3. It shows that the final residual noise power in 10 out of 100 simulations is considerably larger than the minimum value (with 6 divergence cases), while in the remaining 90, it is close to the optimum.

Figures  4 and 5 show percentile plots of the residual noise power versus time of Carini’s[9] and Lopes’ [26] algorithms simulation results when used in feedback ANC. The reference signal equals the estimated primary noise signal [23]. This signal equals the error signal minus the anti-noise signal filtered by the plant estimate. These algorithms have very low computational complexity. They deal well with slow plant changes and are intended for feedforward (not feedback) ANC systems. So, performance is not good and considerably worse than the proposed algorithm, as can be seen by comparing (for instance) the percentile 90% curve.

Fig. 1
figure 1

Three typical simulations residual noise power versus time

Full size image
Fig. 2
figure 2

Residual noise power percentile curves versus time. Curves for percentile 10%, 25%, 50% (solid), 75%, 90%, and 99% (gray)

Full size image
Fig. 3
figure 3

Final residual noise power histogram

Full size image
Fig. 4
figure 4

Carini’s algorithm residual noise power percentile curves versus time. Curves for percentile 10%, 25%, 50% (solid), 75%, 90%, and 99% (gray)

Full size image
Fig. 5
figure 5

Lopes’s algorithm residual noise power percentile curves versus time. Curves for percentile 10%, 25%, 50% (solid), 75%, 90%, and 99% (gray)

Full size image
Fig. 6
figure 6

Mohseni’s algorithm residual noise power percentile curves versus time. Curves for percentile 10%, 25%, 50% (solid), 75%, 90%, and 99% (gray)

Full size image

Figure 6 shows the same results for Mohseni’s algorithm [31]. Performance is much better than Carini’s and Lopes’s algorithms, in fact also better than the proposed algorithm, but at the expense of higher computational complexity, much larger than the last. However, the residual noise is still high, at least in 1% of the simulations (and at each time n), as seen by the percentile 99% curve. Also, there is a degradation of performance with time, as seen by the 90% curve.

5 Conclusion

This work presents an algorithm for narrowband feedback ANC systems that improves the performance of state-of-the-art algorithms when dealing with fast secondary path changes while keeping a moderate computational complexity. However, performance is as good as desired in every case. This algorithm uses an estimated model to predict the primary noise and the same model to estimate a non-causal secondary path inverse that filters the predicted noise to calculate the anti-noise signal.