Fooling the Big Picture in Classification Tasks

Abstract

Minimally perturbed adversarial examples were shown to drastically reduce the performance of one-stage classifiers while being imperceptible. This paper investigates the susceptibility of hierarchical classifiers, which use fine and coarse level output categories, to adversarial attacks. We formulate a program that encodes minimax constraints to induce misclassification of the coarse class of a hierarchical classifier (e.g., changing the prediction of a ‘monkey’ to a ‘vehicle’ instead of some ‘animal’). Subsequently, we develop solutions based on convex relaxations of said program. An algorithm is obtained using the alternating direction method of multipliers with competitive performance in comparison with state-of-the-art solvers. We show the ability of our approach to fool the coarse classification through a set of measures such as the relative loss in coarse classification accuracy and imperceptibility factors. In comparison with perturbations generated for one-stage classifiers, we show that fooling a classifier about the ‘big picture’ requires higher perturbation levels which results in lower imperceptibility. We also examine the impact of different label groupings on the performance of the proposed attacks.

1 Introduction

There has been enormous progress in the design and development of powerful classifiers in numerous applications of machine learning and artificial intelligence, including modern techniques that make use of deep learning architectures [2, 30, 32, 45]. However, recent literature has revealed the fragility of one-stage classifiers (OSCs) given their susceptibility to imperceptible, crafted perturbation attacks [5, 14, 18, 62]. Understanding the impact of adversarial attacks is both critical and momentous considering the envisioned mass adoption of such classifiers in safety-critical systems, such as in autonomous driving and surveillance applications [8].

There are several taxonomies one could use to categorize adversarial attacks based on attacker’s side information, goal of the attack, attack scenario, and scope of the attack. In the side information-based taxonomy, adversarial attacks can be characterized as black (white) box attacks when the attacker has no (full) access to the classifier’s function [3] and semi-black-box attacks when the attacker has partial access [44]. The strongest adversary is the white-box attacker given its full knowledge of the target model. As such, defense methods that succeed against black-box/semi-black-box attacks could be vulnerable to an efficient white-box attack [46]. Depending on the goal of the attack, attacks can be classified into non-targeted, targeted, and confidence reduction attacks. The goal of non-targeted attacks is to modify the input in such a way that it is misclassified, whereas targeted attacks seek to alter the output prediction to a predefined target class [41]. Confidence reduction attacks aim to reduce the confidence in the label estimation of the target model to introduce ambiguity [60]. In the context of the attack scenario, evasion attacks refer to scenarios where the adversary attempts to evade the detection system during the system operation when samples are modified at test time, while poisoning attack (also known as contamination attack) is when the adversary attempts to poison the data during the training phase [13]. Attacks can also be assorted into individual or universal attacks based on their scope. Individual attacks generate perturbations against every input feature vector, while universal perturbations are designed against the entire dataset [60]. In terms of the nature of the perturbations, they can be additive when perturbations are added to the example, or non-additive where techniques such as rotation, inversion, and other transformations are applied to the original sample [19, 20]. In this paper, we assume a white-box, non-targeted, evasion, individual, and additive attack scenario.

The vast majority of existing studies have focused on adversarial attacks on OSCs. In sharp contrast, in this paper we focus on hierarchical classifiers (HCs) that make use of coarse and fine level predictions. A wide range of real-world problems can be naturally described using a hierarchical classification framework where sample labels to be estimated are categorized into a class hierarchy.

HCs have direct bearing on numerous important applications. Examples include text categorization, protein function prediction, musical genre classification, speech classification, computer vision, COVID-19 identification, marine benthic biota, satellite spectral images, and forensics [29, 37, 43, 49, 53, 61]. We refer the reader to the recent survey [52] and references therein for more details.

In this paper, we develop and analyze attacks against HCs consisting of a OSC and a function that maps the predicted label to its corresponding super-class. We focus on the ‘direct’ approach (also known in the literature as global classifier, or bottom-up approach, or flat HC [11, 57]), in which, for every feature vector, the basic genre is first classified, and then, the corresponding super-class is obtained accordingly. This is in sharp distinction to the top-down approach wherein an example is first classified in line with the coarser genres followed by a finer level prediction [49].

The proposed HC formulation is applicable to OSCs if the attacker’s goal is to fool the ‘big picture.’ In other words, the perturbations are generated such that the prediction of the sample of interest is outside a given set of labels (including the ground truth)—for instance, changing the classification of a ‘dog’ to a ‘car’ but not a ‘cat.’ It is important to note that while targeted attacks such as Carlini and Wagner [12] can be leveraged to perform such task, our approach is more general and has the advantage of being flexible. In particular, unlike targeted attacks which need to specify the target label, our approach allows us to select any label as long as it is outside the true super-class set. As a result, our methods yield performance gains in terms of attack perceptibility which is at the heart of designing and generating undetectable attacks. In addition, the methods developed are amenable to efficient online implementations in view of their low computational complexity.

Our approach applies to both simple classifiers (i.e., ones based on simple hypothesis testing (SHT) such as trained neural networks) and composite classifiers (i.e., ones based on composite hypothesis testing (CHT)) [63]. A composite hypothesis can be thought of as a union of many simple point hypotheses covering a set of values from a parameter space and hence can be particularly useful when the data models involve some unknown parameters. While CHT-based classifiers continue to play an important role in many applications, such as medical imaging [55] and digital communications [4], a methodical study of their robustness against adversarial attacks is largely lacking. Here, we show the applicability of our framework to CHT classifiers, thereby providing an approach to study their robustness.

In order to reduce the complexity of obtaining optimal solutions, we develop a solver that uses the alternating direction method of multipliers (ADMM), which has shown great promise in developing fast solvers for convex programs in various tasks [42].

1.1 Summary of Contributions

The main contributions of this paper are summarized below.

• We formulate a program to generate perturbations aimed at fooling the super-class of HCs using minimax constraints to ensure the coarse classification is altered.

• We obtain efficient approximations suitable for online implementations to reduce complexity based on convex relaxations of said program.

• We develop an ADMM-based solver to the proposed formulations shown to outperform popular solvers such as the solvers in Diamond and Boyd [17], Grant and Boyd [26].

• We demonstrate the applicability of our approach to both SHT- and CHT-based classifiers.

• We present a comprehensive comparison to existing attacks in terms of super classification accuracy and imperceptibility, which is gauged using a set of performance measures.

• We quantify the perturbation levels required to fool HCs and demonstrate that such perturbations are more perceptible than ones targeting OSCs.

• We demonstrate the impact of using various mappings (in turn, label groupings) on fooling the big picture in classification tasks.

1.2 Related Work

The literature abounds with approaches for generating individual perturbations against OSCs in white-box settings. Optimization-based techniques, such as the Carlini and Wagner attack [12], the box-constrained Limited-Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) attack [51], Deepfool [39], and saliency map attack [41], generate adversarial examples by optimizing a cost function expressed in terms of the perturbation norm and/or the model’s loss subject to misclassifications of the adversarial examples. Other methods, such as the fast gradient sign method (FGSM) [25], compute the gradient of the loss function with respect to (w.r.t.) the input vector—which can be computed efficiently using backpropagation—to generate perturbations. An iterative version (I-FGSM) is proposed in [33] to ensure the perturbations result in mistaking the input examples for less likely classes by taking iterative steps in the direction of the negative gradient of the loss function. An approach that integrates a momentum term (which accumulates previous gradients) into the iterative procedure to escape local maxima is presented in Kurakin et al. [18], thereby boosting the adversarial attacks. The approach proposed in Rony et al. [47] decouples the norm and the direction of the perturbation to avert the expensive iterations of optimization-based techniques. In order to constrain the norm of the adversarial perturbation while also ensuring it induces a misclassification, the algorithm projects the generated perturbation on a sphere centered at the original example of varying radius. The elastic-net attack generates perturbations that achieve the twin objective of low $L_1$ distortion and good visual quality using regularization with a mixture of $L_1$ and $L_2$ penalty functions [15]. Generative methods have also been used to generate adversarial examples [34, 59]. For example, generative adversarial networks (GANs) train a generator model to generate adversarial examples along with a discriminator model to encourage that the generated examples are indistinguishable from the original instances. For image classification, there are also non-additive methods that apply various transformations to an image in order to induce misclassifications [56].

This paper extends the scope of our recent work [7], which presents attacks on image HCs. An important distinction is that Alkhouri and Matloub et al. [7] make use of off-the-shelf targeted attack generators such as Papernot et al. [41] and Carlini and Wagner [12] to induce incorrect predictions of coarse labels. In sharp contrast, here we take a principled approach in which we formulate a constrained program to craft adversarial perturbations capable of fooling the coarse predictions and develop several one-step and iterative solutions of various relaxations of said program. Further, we consider both SHT and CHT models and develop a competitive ADMM-based solution. A case study on the impact of various groupings on the classifier robustness is also presented. In the context of CHT, we expand on the hierarchical CHT-based model introduced in our earlier work [6] by proposing two additional methods. To the best of our knowledge, this line of work is the first to study perturbation attacks against HCs.

1.3 Notation and Organization

Throughout the paper, we use boldface uppercase letters (e.g., ${\textbf{X}}$) to denote matrices, boldface lowercase letters (e.g., ${\textbf{x}}$) to denote vectors, and Roman lowercase letters (e.g., x) to represent scalars. Discrete linear convolution is denoted by $*$. The operator $|. |$ is used for the cardinality of a set, as well as the absolute value, which will be clear from the context. Given a set S, the set $S^{'}$ denotes its complement. The p-norm of a vector ${\textbf{x}} = (x_1, \ldots , x_n)$ is defined as $\Vert {\textbf{x}} \Vert _p:= (\sum _{i=1}^n |x_i |^p)^{1/p}$ for $p\in [1,\infty )$. For any positive integer M, the index set $[M]:=\{1,\ldots ,M\}$. The set difference of sets A and B is the set of elements in A that are not in B which is denoted as $A\setminus B$. Given vector ${\textbf{x}}$, vector ${\textbf{y}}$, and matrix ${\textbf{Z}}$, the notation ${\textbf{Z}} = [{\textbf{x}} ~~ {\textbf{y}}]$ refers to the matrix obtained by concatenating columns ${\textbf{x}}$ and ${\textbf{y}}$. The matrices ${\textbf{Z}}^T$, ${\textbf{Z}}^{-1}$, and ${\textbf{Z}}^{\dagger }$ represent the transpose, inverse, and pseudo-inverse of matrix ${\textbf{Z}}$, respectively. We use $\text {sign(.)}$ to denote the signum function, and ${\textbf{I}}_N$ denotes the identity matrix of size $N \times N$.

The rest of the paper is organized as follows. Section 2 presents the main formulation of adversarial attacks on HCs. The proposed solutions are presented in Sect. 3. In Sect. 4, we present our ADMM-based solver. Instances of classifier models are presented in Sect. 5. The experimental results are presented in Sect. 6, followed by the conclusion in Sect. 7.

2 Formulation of Attacks

Define $k:{\mathbb {R}}^N\rightarrow [M]$ as a classifier function that maps the input signal ${\textbf{x}}\in {\mathbb {R}}^N$ to its predicted label out of M candidate classes. To determine the prediction, we assume there exist M discriminant functionals $J_i:{\mathbb {R}}^N\rightarrow {\mathbb {R}}, i\in [M]$ such that

$$\begin{aligned} k({\textbf{x}}) = \underset{i\in [M]}{\mathop {\textrm{argmin}}\limits }\ \,{J}_i({\textbf{x}}). \end{aligned}$$

(1)

The detector in (1) represents the first stage of our HC. The second stage uses a mapping T(.) which maps the predicted fine label to a coarser super-class $i\in [M_c]$, where $M_c$ is the total number of super-classes. A block diagram of the HC is shown in Fig. 1.

Fig. 1

Hierarchical classifier block diagram consisting of the discriminant functionals generator, selecting the best candidate, and mapping the predicted label to its super-class

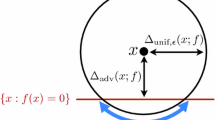
Given an input example ${\textbf{x}}$, the attacker seeks to generate an additive perturbation $\varvec{\varvec{\eta }}\in {\mathbb {R}}^N$ to fool the classifier about the coarse class of said example while also being imperceptible. For imperceptibility, $\varvec{\varvec{\eta }}$ must be bounded to ensure that the original and perturbed examples are not too dissimilar. To this end, we define a distance function $D({\textbf{x}}, {\textbf{x}}+{\varvec{\eta }})$ between the original and perturbed samples. For simplicity, we use the shorthand notation $D(\varvec{\varvec{\eta }}):=D({\textbf{x}}, {\textbf{x}}+{\varvec{\eta }})$.

We can readily formulate the program in (2), which the attacker solves to fool the super-class of a HC.

$$\begin{aligned} \begin{aligned} \min _{{\varvec{\eta }}} D({\varvec{\eta }}) \quad \text {subject to}~~~ T(k({\textbf{x}}+{\varvec{\eta }})) \ne T(k({\textbf{x}}))\,. \end{aligned} \end{aligned}$$

(2)

The solution to (2) is an additive perturbation ${\varvec{\eta }}\in {\mathbb {R}}^N$ that not only fools the coarse classification as captured by the constraint, but also ensures that the perturbed example is at a small distance from the original example as required by the minimization of the objective. If the mapping $T=\textrm{id}_M$, where $\textrm{id}_M$ is the identity function on the range of k, the formulation in (2) reduces to generation of perturbations for a OSC.

Proposition 1

Let ${\varvec{\eta }}^*(T)$ be the optimal solution to (2) for a given mapping function T. Then, $D({\varvec{\eta }}^*(\textrm{id}_M)) \le D({\varvec{\eta }}^*(T))$.

In other words, perturbations needed to fool the OSC are smaller than those needed to fool the super-class of a HC.

Proof

Suppose there exists an optimal solution ${\varvec{\eta }}^*$ to (2) such that $T(k({\textbf{x}}+{\varvec{\eta }}^*)) \ne T(k({\textbf{x}}))$. It follows that $k({\textbf{x}}+{\varvec{\eta }}^*) \ne k({\textbf{x}})$. Hence, the feasible set of (2) is a subset of the feasible region of the program (2) in which T is replaced with the identity mapping $\textrm{id}_M$. Thus, $D({\varvec{\eta }}^*(\textrm{id}_M)) \le D({\varvec{\eta }}^*(T))$. $\square$

In lieu of the formulation in (2), which is generally intractable, we reformulate the constraint on the coarse class using constraints on the discriminant functionals. First, let us define the super-class sets

$$\begin{aligned} S_i = \{l\in [M]:T(l)=i\}\,, ~i\in [M_c]\,, \end{aligned}$$

(3)

to group the labels such that $S_i$ consists of all the fine labels that belong to super-class i. To yield an incorrect prediction of the coarse class, the label with the smallest discriminant value must not be in the true super-class set, i.e.,

$$\begin{aligned} \exists j\in S^{'}_{T(k({\textbf{x}}))}: J_j({\textbf{x}}+{\varvec{\eta }}) < J_l({\textbf{x}}+{\varvec{\eta }}), \forall l\in S_{T(k({\textbf{x}}))}. \end{aligned}$$

(4)

Therefore, unlike requirements found in earlier works that can be expressed in terms of the true class [8], the generated perturbation must be such that a discriminant function of a label in some alternative super-class dominates all values associated with every label in the true super-class.

Therefore, it follows that the program in (2) can be reformulated to the equivalent program ($\textrm{FC}$) given in (5), where the appellation ‘FC’ refers to fooling the coarse class.

$$\begin{aligned} (\textrm{FC}) \begin{aligned}&\qquad \qquad \min _{{\varvec{\eta }}} D(\varvec{\eta }) \quad \text {subject to} \\ \min _{j\in S^{'}_{T(k({\textbf{x}}))}}&\max _{l\in S_{T(k({\textbf{x}}))}} J_j({\textbf{x}}+{\varvec{\eta }})-J_l({\textbf{x}}+{\varvec{\eta }})<0 \end{aligned} \end{aligned}$$

(5)

Henceforth, we assume D is a convex function of $\varvec{\eta }$. But even then, a key challenge still lies in handling the minimax constraint in (5). Devising solutions to the main program in (5) is the primary focus of the next section.

3 Proposed Solutions

In this paper, we develop three approaches to the solution of ($\textrm{FC}$) in (5) presented in the next three subsections.

3.1 Algorithmic Approach

As our first approach to solving ($\textrm{FC}$), we propose an algorithm that iterates over all labels, $j\in S^{'}_{T(k({\textbf{x}}))}$, in the complement set of the true super-class set in order to find the smallest perturbation (in the sense of minimizing D) satisfying the condition $T(k({\textbf{x}}+{\varvec{\eta }})) \ne T(k({\textbf{x}}))$. In other words, for each $j\in S^{'}_{T(k({\textbf{x}}))}$, we solve the program $(\textrm{FC}_j)$,

$$\begin{aligned} (\textrm{FC}_j)\quad \begin{aligned}&\qquad \min _{{\varvec{\eta }}} D({\varvec{\eta }}) \quad \text {subject to} \\ J_j({\textbf{x}}&+{\varvec{\eta }}) < J_l({\textbf{x}}+{\varvec{\eta }}), \forall l\in S_{T(k({\textbf{x}}))}\, \\ \end{aligned} \end{aligned}$$

(6)

to generate perturbations for each label outside the true super-class and then select the minimum w.r.t. the distance function D. Algorithm 1 presents the procedure.

Theorem 1 establishes the correctness of Algorithm 1.

Theorem 2

Let ${\varvec{\eta }}^{*}_{\text {alg}}$ be the output of Algorithm 1. If (5) is feasible, then ${\varvec{\eta }}^{*}_{\text {alg}}$ is an optimal solution of (5).

Proof

Let ${\varvec{\eta }}^{*}$ be an optimal solution of (5), and assume for the sake of contradiction that ${\varvec{\eta }}^{*}_{\text {alg}}$ is not optimal. Then, $D(\varvec{\eta }^*) < D(\varvec{\eta }^{*}_{\text {alg}})$. Since $\varvec{\eta }^*$ is a feasible solution of ($\textrm{FC}$), it satisfies (4), i.e., $\exists j_0\in S^{'}_{T(k({\textbf{x}}))}: J_{j_0}({\textbf{x}} + \varvec{\eta }^*)< J_l({\textbf{x}} + \varvec{\eta }^*), \forall l\in S_{T(k({\textbf{x}}))}$. Thus, the feasible set of ($\textrm{FC}$) is a subset of the feasible region of $(\textrm{FC}_{j_0})$ defined in (6). It follows that $D(\varvec{\eta }^*_{j_0})\le D(\varvec{\eta }^*)$, where $\varvec{\eta }^*_{j}$ is the optimal solution to $(\textrm{FC}_{j})$. Algorithm 1 solves $(\textrm{FC}_j)$ for all $j\in S^{'}_{T(k({\textbf{x}}))}$ and chooses the one corresponding to the smallest value of the objective (last step), thus $D({\varvec{\eta }}^{*}_{\text {alg}}) \le D({\varvec{\eta }}^{*}_{j}), \forall j\in S^{'}_{T(k({\textbf{x}}))}$. Hence, $D({\varvec{\eta }}^{*}_{\text {alg}}) \le D({\varvec{\eta }}^{*}_{j_0})\le D(\varvec{\eta }^*)$, yielding a contradiction. Therefore, ${\varvec{\eta }}^{*}_{\text {alg}}$ is an optimal solution of (5). $\square$

There are still two more difficulties with regard to implementing Algorithm 1. First, the discriminant functionals in the constraint set of $(\textrm{FC}_j)$ are generally non-convex. To address this issue, we utilize the first-order Taylor series expansion, $J({\textbf{x}}+{\varvec{\eta }}) \approx J({\textbf{x}})+{\varvec{\eta }}^T \nabla _{\textbf{x}} J({\textbf{x}})$, to yield the approximate program in (7) which uses linear constraints as a convex relaxation of $(\textrm{FC}_j)$.

$$\begin{aligned} \begin{aligned}&\qquad \min _{{\varvec{\eta }}} D({\varvec{\eta }}) \quad \text {subject to} \\ {\varvec{\eta }}^T(\nabla _{\textbf{x}}J_{j}({\textbf{x}})&-\nabla _{\textbf{x}}J_l({\textbf{x}})) < J_l({\textbf{x}}) - J_{j}({\textbf{x}})\,, \forall l\in S_{T(k({\textbf{x}}))}\,. \end{aligned} \end{aligned}$$

(7)

In practice, an arbitrarily small constant $\epsilon _c > 0$ is used to transform the strict inequalities in (7) for which the feasible region is an open set [26] to bounded inequalities, i.e., the constraints in (7) become

$$\begin{aligned} {\varvec{\eta }}^T(\nabla _{\textbf{x}}J_{j}({\textbf{x}})-\nabla _{\textbf{x}}J_l({\textbf{x}})) \le J_l({\textbf{x}}) - J_{j}({\textbf{x}})-\epsilon _c\,,\forall l\in S_{T(k({\textbf{x}}))}. \end{aligned}$$

The second difficulty stems from the computational complexity of Algorithm 1 since it iterates over all fine labels $j\in S^{'}_{T(k({\textbf{x}}))}$, which limits its applicability when M is large. To reduce complexity, we propose an enhanced algorithm (Algorithm 2) which rests on three complementary ingredients described next.

• 1. Verifying OSC attack: Generate perturbation ${\varvec{\eta }}_\text {SC} = R_\text {SC}({\textbf{x}})$, where $R_\text {SC}(.)$ is a perturbation generator function of a non-targeted attack against classifier k. If the constraint in (2) is satisfied and ${\varvec{\eta }}_\text {SC}$ yields a distance measure that is sufficiently small, the search concludes. This step facilitates the generation of a perturbed example without iterating over all labels $j\in S^{'}_{T(k({\textbf{x}}))}$ (if one exists). This corresponds to steps 1–3 of Algorithm 2.

• 2. Reducing size of candidate set: We sort $j\in S^{'}_{T(k({\textbf{x}}))}$ in ascending order according to their $J_j$ values. The idea is to obtain the labels outside the estimated super-class set with the lowest cost. Subsequently, we select the Q labels with the smallest values to iterate over. Therefore, we define the reduced candidate set $S^{'*}_{T(k({\textbf{x}}))}:= \{q_i\}_{i\in [Q]} \subset S^{'}_{T(k({\textbf{x}}))}$, with cardinality $|S^{'*}_{T(k({\textbf{x}}))} |= Q$, where

  $$\begin{aligned} \begin{aligned} q_i = \underset{l\in S^{'}_{T(k({\textbf{x}}))}\setminus \{q_{i-1},q_{i-2},\ldots ,q_1\}}{\mathop {\textrm{argmin}}\limits } \,{J}_l({\textbf{x}}), \forall i\in [Q]\,, \end{aligned} \end{aligned}$$

  (8)

  which Algorithm 2 iterates over to generate perturbations.

• 3. Stopping criterion: We conclude the search if the distance achieved by the perturbed example falls below a predefined threshold $\epsilon _D$. This helps accelerate the search as shown in steps 2 and 10 of Algorithm 2.

3.2 Reduced Set Approximation

The minimax constraint in ($\textrm{FC}$) can be viewed in the lens of two-player finite games, where one of the players seeks to minimize the value of the game over the choice of labels in the complement set $S^{'}_{T(k({\textbf{x}}))}$, while the other player chooses the worst label from $S_{T(k({\textbf{x}}))}$ that maximizes the value of the game. Therefore, one of the main difficulties lies in the selection of $j\in S^{'}_{T(k({\textbf{x}}))}$. In this section, we describe our second method in which we obtain a set $S^{'*}_{T(k({\textbf{x}}))} \subset S^{'}_{T(k({\textbf{x}}))}$ (with $|S^{'*}_{T(k({\textbf{x}}))} |= Q$ and $Q > 1$) from (8) and include all linear constraints corresponding to $j\in S^{'*}_{T(k({\textbf{x}}))}$ in the program. Therefore, we term this approach the reduced set extended constraints approximation (REC). The REC program can be written as

$$\begin{aligned} \begin{aligned} \min _{{\varvec{\eta }}} D(\varvec{\eta }) \quad \text {subject to} \qquad \qquad \qquad \qquad \\ {\varvec{\eta }}^T(\nabla _{\textbf{x}}J_{j}({\textbf{x}})-\nabla _{\textbf{x}}J_l({\textbf{x}})) \le J_l({\textbf{x}}) - J_{j}({\textbf{x}})-\epsilon _c\,,\\ \qquad \qquad \qquad \qquad \qquad \forall l\in S_{T(k({\textbf{x}}))}, \forall j\in S^{'*}_{T(k({\textbf{x}}))}\,, \end{aligned} \end{aligned}$$

(9)

which is a convex program with $Q |S_{T(k({\textbf{x}}))} |$ linear constraints. In comparison with the algorithmic approach of Sect. 3.1 in which we need to solve multiple programs, the advantage is that we only need to solve a single program.

3.3 Nearest Label Approximation

In this section, we describe another approach to selecting $j\in S^{'}_{T(k({\textbf{x}}))}$ to approximate the constraint set of ($\textrm{FC}$) in (5). Since $J_i, \forall i\in [M]$, represents the class membership, we identify the index

$$\begin{aligned} j^* = \underset{j\in S^{'}_{T(k({\textbf{x}}))}}{\mathop {\textrm{argmin}}\limits } \,{J}_j({\textbf{x}}), \end{aligned}$$

(10)

corresponding to the lowest discriminant functional (without perturbations) outside the true super-class given the example ${\textbf{x}}$. This can be viewed as a special case of REC with $Q=1$. The resulting program, given in (11), only has $|S_{T(k({\textbf{x}}))} |$ linear constraints, thereby yielding further reduction in complexity compared to the previous two methods. We term this approximation NOC, since it uses the nearest label outside the super-class set constraints.

$$\begin{aligned} \begin{aligned}&\qquad \qquad \min _{{\varvec{\eta }}} D(\varvec{\eta }) \quad \text {subject to} \\ {\varvec{\eta }}^T(\nabla _{\textbf{x}}J_{j^*}({\textbf{x}})&-\nabla _{\textbf{x}}J_l({\textbf{x}})) \le J_l({\textbf{x}}) - J_{j^*}({\textbf{x}})-\epsilon _c\,, \forall l\in S_{T(k({\textbf{x}}))}\,. \end{aligned} \end{aligned}$$

(11)

Proposition 3

Let ${\varvec{\eta }}^*_{\text {alg}}$, ${\varvec{\eta }}^*_{\text {REC}}$, and ${\varvec{\eta }}^*_{\text {NOC}}$ be the optimal solutions of Algorithm 1, (9), and (11), respectively. Then, $D({\varvec{\eta }}^*_{\text {alg}}) \le D({\varvec{\eta }}^*_{\text {NOC}}) \le D({\varvec{\eta }}^*_{\text {REC}})$.

According to Proposition 3, perturbations generated from the REC approximation are more perceptible than those obtained from the NOC approximation. Also, Algorithm 1 yields the most imperceptible perturbations.

Proof

Recall that program (7) is solved in the j-th iteration of Algorithm 1, for every $j\in S^{'}_{T(k({\textbf{x}}))}$. Since $j^*\in S^{'}_{T(k({\textbf{x}}))}$ as defined in (10), the NOC program defined in (11) is solved in one of these iterations. However, the algorithm selects the minimizing perturbation in its final step, and thus, $D({\varvec{\eta }}^*_{\text {alg}}) \le D({\varvec{\eta }}^*_{\text {NOC}})$. Given the definition of $S^{'*}_{T(k({\textbf{x}}))}$ in (8), we have that $j^*\in S^{'*}_{T(k({\textbf{x}}))}$. Hence, the feasible set of the REC program in (9) is a subset of the feasible region of the NOC program in (11). Hence, $D({\varvec{\eta }}^*_{\text {NOC}})\le D({\varvec{\eta }}^*_{\text {REC}})$. $\square$

4 ADMM-Based Solver

In this section, we develop an ADMM-based solver [10] for the programs presented in the previous sections. To simplify notation, we use $S_T, S^{'}_T$, and $S^{'*}_T$ as short for $S_{T(k({\textbf{x}}))}$, $S^{'}_{T(k({\textbf{x}}))}$, and $S^{'*}_{T(k({\textbf{x}}))}$, respectively. First, we define matrix ${\textbf{G}} \in {\mathbb {R}}^{N\times V}$ whose columns are obtained as the difference of the gradients of the discriminant functionals w.r.t. the input feature vector as,

$$\begin{aligned} {\textbf{G}} = {\left\{ \begin{array}{ll} \Big [ \nabla _{\textbf{x}}J_{j}({\textbf{x}}) - \nabla _{\textbf{x}}J_{l}({\textbf{x}})\Big ], \forall l\in S_T, \\ \text {for iteration } j\in S^{'}_T \text { of Algorithm~1} \\ \Big [ \nabla _{\textbf{x}}J_{j}({\textbf{x}}) - \nabla _{\textbf{x}}J_{l}({\textbf{x}})\Big ], \forall l\in S_T, \forall j\in S^{'*}_T, \\ \text {for REC method} \\ \Big [ \nabla _{\textbf{x}}J_{j^*}({\textbf{x}}) - \nabla _{\textbf{x}}J_{l}({\textbf{x}})\Big ], \forall l\in S_T, \\ j^* \text { as in (10)}, \text {for NOC method}. \end{array}\right. } \end{aligned}$$

(12)

Hence, $V=Q\, |S_T |$ for the REC approximation and $V= |S_T |$ otherwise. Similarly, we define the vector ${\textbf{b}} \in {\mathbb {R}}^{V}$ whose entries are given by

$$\begin{aligned} {\textbf{b}} = {\left\{ \begin{array}{ll} \Big [ J_l({\textbf{x}}) - J_j({\textbf{x}}) - \epsilon _c \Big ]^T, \forall l\in S_T,\\ \text {for iteration } j\in S^{'}_{T(k({\textbf{x}}))}\text {of Algorithm 1} \\ \Big [ J_l({\textbf{x}}) - J_j({\textbf{x}}) - \epsilon _c \Big ]^T, \forall l\in S_T, \forall j\in S^{'*}_T, \\ \text {for REC method} \\ \Big [ J_l({\textbf{x}}) - J_{j^*}({\textbf{x}}) - \epsilon _c \Big ]^T, \forall l\in S_T, \\ j^* \text { as in (10)}, \text {for NOC method}. \end{array}\right. } \end{aligned}$$

(13)

Our convex approximations to program (5) can now be written as

$$\begin{aligned} \min _{{\varvec{\eta }}} D({\varvec{\eta }}) \quad \text {subject to}\quad {{\textbf{G}}^T}{\varvec{\eta }} - {\textbf{b}} \le {\textbf{0}}\,. \end{aligned}$$

(14)

We introduce a slack variable ${\textbf{z}}\in {\mathbb {R}}^{V}$ [23] and rewrite the minimization in the standard form of ADMM as Boyd et al. [10]

$$\begin{aligned} \begin{aligned} \min _{{\varvec{\eta }},{\textbf{z}}} D({\varvec{\eta }})+E({\textbf{z}}) \quad \text {subject to} \quad {{\textbf{G}}^T}{\varvec{\eta }} - {\textbf{b}} + {\textbf{z}} = {\textbf{0}}, \end{aligned} \end{aligned}$$

(15)

where $E({\textbf{z}})$ is a penalty function and given as

$$\begin{aligned} E({\textbf{z}}) = {\left\{ \begin{array}{ll} 0,&{} \text {if } {\textbf{z}} \ge {\textbf{0}}\\ +\infty , &{} \text {otherwise}\,. \end{array}\right. } \end{aligned}$$

(16)

As an instance of this proposed solver, consider $D({\varvec{\eta }})= \Vert \varvec{\varvec{\eta }} \Vert ^2_2$. The augmented Lagrangian can be written as

$$\begin{aligned} \begin{aligned} {\mathcal {L}}_r({\varvec{\eta }},{\textbf{z}},{\varvec{\mu }}) = \Vert {\varvec{\eta }} \Vert _2^2 + E({\textbf{z}})+\frac{r}{2} \Big ( \Vert {{\textbf{G}}^T}{\varvec{\eta }} - {\textbf{b}} + {\textbf{z}} - {\varvec{\mu }} \Vert _2^2 - \Vert {\varvec{\mu }} \Vert _2^2 \Big ), \end{aligned} \end{aligned}$$

(17)

where r is a penalty factor and ${\varvec{\mu }}\in {\mathbb {R}}^{V}$ is the vector of Lagrange multipliers. Define the $N \times V$ matrix ${\varvec{\Delta }}$ as,

$$\begin{aligned} {\varvec{\Delta }} = (2{\textbf{I}}_N + r\mathbf {{G}} \mathbf {{G}}^T)^{-1} \mathbf {{G}}. \end{aligned}$$

(18)

We can readily formulate the steps of the ADMM for each iteration t [10]:

• 1. Given that $\nabla _{{\varvec{\eta }}}D({\varvec{\eta }}) = 2{\varvec{\eta }}$, we obtain ${\varvec{\eta }}^{(t)}$ by minimizing the Lagrangian function w.r.t ${\varvec{\eta }}$, while variables ${\textbf{z}}$ and ${\varvec{\mu }}$ are held constant. The closed-form solution is found as

  $$\begin{aligned} {\varvec{\eta }}^{(t+1)} = r{\varvec{\Delta }} ({\textbf{b}} - {\textbf{z}}^{(t)} - {\varvec{\mu }}^{(t)}). \end{aligned}$$

  (19)

• 2. Similarly, update the slack variable ${\textbf{z}}$ as

  $$\begin{aligned} {\textbf{z}}^{(t+1)} = \max ({\textbf{0}}, {{\textbf{G}}^T}{\varvec{\eta }}^{(t)} - {\textbf{b}} - {\varvec{\mu }}^{(t)}). \end{aligned}$$

  (20)

• 3. Update the Lagrangian as

  $$\begin{aligned} {\varvec{\mu }}^{(t+1)} = {\varvec{\mu }}^{(t)} + {{\textbf{G}}^T}{\varvec{\eta }}^{(t+1)} - {\textbf{b}} + {\textbf{z}}^{(t+1)}. \end{aligned}$$

  (21)

These steps are repeated for a predefined number of iterations ${\mathcal {T}}$. We call this version of the algorithm the regular-ADMM (rADMM) algorithm. We also propose a version of the algorithm, termed enhanced ADMM (eADMM), that utilizes a stopping criterion. Specifically, in each iteration t of eADMM, we check if ${\varvec{\eta }}^{(t)}$ is successful at fooling the super-class and whether the corresponding distance falls below a predefined threshold $\epsilon _A$, in which case the search stops. The steps are presented in Algorithm 3.

4.1 Complexity

Our formulations entail solving convex programs with N variables and $|S_T |\ll M$ linear constraints. The complexity of an iterative solver to said programs is measured by the complexity of the initialization procedure, the worst case complexity per iteration for a given target precision [24], and the convergence rate. Given our rADMM, the initialization process consists of calculating the matrix ${\textbf{G}}$ and computing the matrix ${\varvec{\Delta }}$, which has computational complexity ${\mathcal {O}}(\max (N^3,N^2|S_T |)) = {\mathcal {O}}(N^3)$ for Algorithm 1 and the NOC approximation, and ${\mathcal {O}}(\max (N^3, QN^2 |S_T |)) \approx {\mathcal {O}}(N^3)$ for the REC method.

The order complexity per iteration is ${\mathcal {O}}(N |S_T |)$. For each step, the complexity is linear in the length of the primal N and the number of labels inside the true super-class set $|S_T |$. For the REC method, the complexity is ${\mathcal {O}}(NQ |S_T |)$, which is linear in the number of constraints $Q |S_T |$. The algorithm can obtain an $\epsilon _1$-approximate solution in ${\mathcal {O}}(1/\epsilon _1)$ iterations [28].

Note that Algorithm 1 solves $|S^{'}_T |$ convex programs with $|S_T |$ linear constraints, while Algorithm 2 only solves $Q\ll |S^{'}_T |$ programs per feature vector. In the REC and NOC methods, we only solve one convex program with $Q |S_T |$ and $|S_T |$ linear constraints, respectively, per feature vector.

5 Instantiations of the Approach Proposed

In this section, we present instantiations of the approach proposed using different classifiers. The first is a trained neural network (NN) in which the classification function and model amount to a SHT problem. The second is a composite detector which corresponds to a CHT problem. We remark that our formulation and proposed ADMM-based solutions are applicable to any classification setting in which the attacker has access to the discriminant functionals, their gradients w.r.t. the input observation vector, and the mapping function.

5.1 Hierarchical Neural Network Classifier

We consider a trained convolutional neural network (CNN) with a vectorized input image ${\textbf{x}}\in {\mathbb {R}}^N$ given the effectiveness of such networks in image classification tasks [50]. During the training phase, a loss function is minimized to update the trainable parameters $\phi$ of the NN using labeled training samples. To train the NN, we leverage existing optimization algorithms such as ADAM [31], which is an adaptive learning rate optimization algorithm designed for training deep NNs.

Given our assumption of a white-box attack and the fact that the softmax layer acts as a probability distribution over the predicted classes, we can choose the discriminant functionals to correspond to the output of the softmax layer or the output of the last dense layer (the input to the softmax layer) [27]. In this paper, we select $J_i({\textbf{x}}), i\in [M]$ as the negative of the input to the softmax layer due to the simplicity and efficiency of computing the gradients w.r.t. the input feature vectors.

The CNN acts as the first stage of our HC. The predicted output of the NN is the input to a mapper (the second stage of our hierarchical classification) to assign feature vectors to their super-classes. The trained CNN can be seen as an instance of a SHT formulation. Therefore, we call this classifier the hierarchical simple hypothesis testing classifier (HSC). Gradients of the discriminant functionals w.r.t. the input images are calculated using TensorFlow [1].

OSC-based NN adversarial training is known to be among the most effective defense methods in the class of white-box defenses [36]. The effectiveness of our attack in fooling the big picture against an adversarially trained OSC-model depends on the mapping function T. This means that if the OSC classifier is trained using adversarial examples that are classified inside $S_T$, then fooling the bigger picture is supposed to require the same amount of perturbation. If the adversarial examples are classified outside of $S_T$, then more perturbations are required to fool the big picture. Thus, in order to fully defend against our approach, the mapping function must be taken into account so as to generate perturbations that not only fool the classification, but also ensure that the adversarial example is classified outside $S_T$. Analysis of defense mechanisms against our attack is an interesting avenue for future work.

5.2 Hierarchical Composite Detector

To show the versatility of our framework, we also apply our approach to a composite hypothesis testing model. Specifically, consider a linear time invariant (LTI) system with an unknown impulse response ${\varvec{\theta }} \in {\mathbb {R}}^{q}$. The input sequence is ${\textbf{a}}_i \in {\mathbb {R}}^{L}$, and the output ${\textbf{v}} \in {\mathbb {R}}^{N}$, where $N=L+q-1$, is observed in noise and the goal is to detect the sequence ${\textbf{a}}_i, i\in [M]$. Under the $i^\text {th}$ hypothesis,

$$\begin{aligned} {\textbf{x}} = {\textbf{v}} + {\textbf{w}} = {\textbf{a}}_i * {\varvec{\theta }} + {\textbf{w}} \,, ~ i \in [M] \end{aligned}$$

(22)

where ${\textbf{x}}$ is the observed feature vector and ${\textbf{w}}$ is a zero-mean additive white Gaussian noise (AWGN) with covariance matrix $\delta ^{2}_w{\textbf{I}}_N$. We can rewrite the model in (22) as,

$$\begin{aligned} {\textbf{x}} = {\textbf{A}}_i {\varvec{\theta }} + {\textbf{w}}\,, \end{aligned}$$

(23)

where ${\textbf{A}}_i \in {\mathbb {R}}^{N\times q}$ is a zero-padded Toeplitz matrix representing the sequence ${\textbf{a}}_i$ [9].

Since the system’s response $\varvec{\theta }$ is unknown, we have an instance of CHT. Our classifier is based on a generalized likelihood ratio test (GLRT) detector [5], in which the likelihoods are evaluated at the maximum likelihood estimate (MLE) of the unknown parameters $\varvec{\theta }$. Therefore, the cost functions $J_i$ in (1) are defined as

$$\begin{aligned} J_i({\textbf{x}})= \Vert {\textbf{x}} - {\textbf{A}}_i{\varvec{\theta }}_i^*\Vert _{2}^{2}, \end{aligned}$$

(24)

where $\varvec{\theta }_i^*$ is the MLE estimate of $\varvec{\theta }$ under the $i^\text {th}$ hypothesis, obtained as ${\varvec{\theta }}_{i}^{*} = ({{\textbf{A}}_{i}^{T}{\textbf{A}}_{i}})^{\dagger }{\textbf{A}}_{i}^{T}{\textbf{x}}$. Defining the $N \times N$ matrix, ${\varvec{\Gamma }}_{i} = {\textbf{A}}_{i}({{\textbf{A}}_{i}^{T}{\textbf{A}}_{i}})^{\dagger }{\textbf{A}}_{i}^{T}$, we obtain

$$\begin{aligned} J_i({\textbf{x}})=\ \Vert ({\textbf{I}}_N - {\varvec{\Gamma }}_i){\textbf{x}}\ \Vert _{2}^{2}. \end{aligned}$$

(25)

The output of the LTI system is the input to the HC as in Fig. 1. We term this model the hierarchical composite hypothesis testing classifier (HCC). The gradients can be obtained as

$$\begin{aligned} \nabla _{\textbf{x}}J_i({\textbf{x}}) = 2({\textbf{I}}_N - {\varvec{\Gamma }}_i)({\textbf{x}}-{\varvec{\Gamma }}_i{\textbf{x}}). \end{aligned}$$

(26)

Remark 1

While this HCC considers a linear model with unknown impulse response as an instance of models with unknown parameters, extending the methods of this paper to other composite models is straightforward. For example, if a closed form of the MLE is elusive, it can be replaced with an approximation such as the estimate of the iterative expectation–maximization (EM) algorithm [16].

6 Experimental Results

In this section, we present numerical experiments to investigate the performance of the proposed methods. First, we define the performance metrics used and then compare the performance of our methods against state-of-the-art attacks on OSCs in terms of their ability to fool the super-class, for both the HSC and HCC models presented in Sect. 5. Additionally, we examine the impact of various mappings on the performance of the attacks. In the supplementary document, we present two experiments to tune the parameters of the algorithms.

6.1 Performance Metrics

We use three measures to evaluate the performance degradation caused by the attacks and assess the robustness of the classifier to these attacks. The first measure is the fooling ratio or the relative loss of accuracy $\zeta =( {\text {CA}}-{\text {CA}}_{\text {pert}} )/ {\text {CA}}$, defined in Moosavi-Dezfooli et al. [40] as the percentage of correctly classified data that are misclassified after the perturbation is added. The second measure is the equalized loss of accuracy $\xi =( 1-{\text {CA}}_{\text {pert}} )/ {\text {CA}}$, defined in in Sáez, Luengo and Herrera [48] as the loss of performance at a controlled perturbation level. Both parameters provide comprehensive performance degradation measures in the presence of imperfect data. Each parameter, $\zeta$ and $\xi$, is a function of the classification accuracy without perturbation ($\text {CA}$) and the classification accuracy with the perturbation $({\text {CA}}_{{\text {pert}}})$. The third measure is the perceptibility (or relative perturbation) $\rho _p = \ \Vert {\varvec{\eta }}\ \Vert _{p} / \ \Vert {\textbf{x}}\ \Vert _{p}$, defined as the ratio of the p-norms of the added perturbation and the observation vector as a measure of perturbation detectability [58]. All three measures are computed for the one-stage and the hierarchical classifiers.

We use the parameter $\sigma _p$ derived from $\rho _p$ as a measure of robustness of a given classifier as suggested by Fawzi, Moosavi-Dezfooli, and Frossard [22], which can also represent the average detectability/perceptibility of an attack w.r.t. the observations of interest.

$$\begin{aligned} \sigma _p = \frac{1}{ |{\mathcal {X}} |} \sum _{{\textbf{x}}\in {\mathcal {X}}} \rho _p({\textbf{x}}), \end{aligned}$$

(27)

where $\rho _p({\textbf{x}})$ refers to the detectability measure of observation vector ${\textbf{x}}$, and ${\mathcal {X}}$ is the set of observations used to measure robustness.

We examine the performance of perturbations generated to fool the big picture of the OSC and the HC using the multi-class confusion matrix ${\textbf{C}} \in {\mathbb {N}}^{M_c\times M_c}$ [21].

In addition to the $l_p$-norm, we also use the structural similarity index (SSIM). The SSIM returns values in the interval [0, 1], with 1 indicating two identical images. The advantage of the SSIM is that it does not only account for pixel differences, but also accounts for luminance, contrast, and structural measurements [54]. We use $D_s({\textbf{x}},{\textbf{x}}+{\varvec{\eta }})$ to denote the SSIM index reflecting the similarity between an example ${\textbf{x}}$ and its perturbed version ${\textbf{x}}+{\varvec{\eta }}$. As such, a robustness measure using the SSIM index can be obtained as

$$\begin{aligned} \sigma _s = \frac{1}{ |{\mathcal {X}} |} \sum _{{\textbf{x}}\in {\mathcal {X}}} D_s({\textbf{x}},{\textbf{x}}+{\varvec{\eta }}). \end{aligned}$$

(28)

6.2 Experimental Setup

For the HSC, we use the MNIST fashion dataset [56] in which each observation vector is a grayscale image of $28 \times 28$ pixels. The labels are defined as (from 0 to 9): ‘T-shirt,’ ‘Trouser,’ ‘Pullover,’ ‘Dress,’ ‘Coat,’ ‘Sandal,’ ‘Shirt,’ ‘Sneaker,’ ‘Bag,’ and ‘Ankle boot.’ The trained CNN consists of 8 layers with 10 outputs representing the discriminant functionals. The configuration of the CNN is given in Table 1. The trained CNN scores a classification accuracy $\text {CA}=90.09\%$ and a super classification accuracy $\text {CA}^{\text {sup}}=97.27\%$ against the test dataset ${\mathcal {X}}_{\text {sc}}$ with $|{\mathcal {X}}_{\text {sc}} |=10,000$. TensorFlow [1] is used to build and train the CNN with the cross-entropy loss function. When we generate perturbations $\varvec{\eta }$, we enforce that ${{\textbf {0}}} \le {\textbf{x}}+{\varvec{\eta }} \le {{\textbf {1}}}$, through the CVXPY tool. For ADMM, these constraints are encoded in ${\textbf{G}}$ and ${\textbf{b}}$.

Based on the results of the experiments presented in the supplementary material, we choose $\epsilon _c = 10$ for the HSC and $\epsilon _c = 2.15$ for the HCC. For the ADMM parameters, $r = 0.0075$ and ${\mathcal {T}} = 10$ for the HSC, and $r = 0.003$ and ${\mathcal {T}} = 180$ for the HCC. The selection of these parameters satisfies the two goals of high fooling ratio and low detectability.

Table 1 CNN Architecture used for the HSC

For the HCC described in Sect. 5.2, we generate the entries of the M sequences ${\textbf{a}}_i$ from a discrete uniform distribution over $\{-0.5,0.5\}$. The parameter vector ${\varvec{\theta }}$ and the noise vector ${\textbf{w}}$ are generated from the Gaussian distributions ${\mathcal {N}}(0,{\textbf{I}}_q)$ and ${\mathcal {N}}(0,0.25 {\textbf{I}}_N)$, respectively. The length of sequences $L=10$, the number of unknown parameters $q=30$, and the number of hypotheses $M=15$. The composite classifier scores a classification accuracy $\text {CA}=81.1\%$ and a super classification accuracy against the synthetic dataset ${\mathcal {X}}_{\text {cc}}$ with $|{\mathcal {X}}_{\text {cc}} |=1000$.

For the HSC, the function T(.) maps labels to their super-classes: $S_0 = \{0,2,4,6\}$ as ‘top,’ $S_1 = \{1\}$ as ‘bottom,’ $S_2 = \{5,7,9\}$ as ‘shoes,’ $S_3 = \{3\}$ as ‘dress,’ and $S_4 = \{8\}$ as ‘other.’ For the HCC, the function T(.) maps the labels into their super-classes as follows: $S_1 = \{1,2,3,4\}$, $S_2 = \{5,6,7,8,9,10\}$, $S_3 = \{11,12\}$, and $S_4 = \{13,14,15\}$. The experiments are run on Intel(R) Core(TM) i7-7700 CPU @ 3.60GHz with 16GB of RAM machine. Our code is publicly available through the Code Ocean repository.¹

6.3 Comparison of Methods

Recalling that Theorem 2 established the correctness of Algorithm 1, in the first experiment of this section we validate the approximations proposed to solve (5) in relation to Algorithm 1. We first run Algorithm 1 and record the best (winning) label, w, among all labels $j\in S^{'}_T$. Then, we consider the following three cases:

• Case (1): Labels satisfy the approximation in the NOC method, i.e., $w=j^*$, defined in (10).

• Case (2): Labels are such that w is a member of the sorted/reduced set $S^{'*}_T$ of length Q, as suggested by the approximation of Algorithm 2 and the REC method, but is not the same label of the first case.

• Case (3): The selected label w is not a member of set $S^{'*}_T$.

Table 2 shows the results for the proposed models using the rADMM solver. We observe that the winning label is the same one selected by the NOC method for 788 (799) times out of 1000 for the HSC (HCC). Also, when $w\ne j^*$, 176 (195) examples were classified inside the set $S^{'*}_T$ and only 36 (6) were outside $S^{'*}_T$ for HSC (HCC). Therefore, in almost $80\%$ of the trials, the best label could be selected using (10), and for $96\%$ of the trials, the winning label w falls inside the set $S^{'*}_T$, which verifies the validity of our label selection criterion for the REC method and Algorithm 2.

Table 2 Winning label w for the HSC and HCC models for 1000 observations

In the next experiment, we present comprehensive comparisons between the attacks proposed targeting the coarse classification. Comparisons are given in terms of the proposed model, the approach to solving (5), and the solver used (rADMM and eADMM in comparison with the state-of-the-art tools such as CVX and CVXPY). The evaluation is based on the degradation in the classification accuracy of the super-class measured by the fooling ratio $\zeta ^{\text {sup}}$, the perceptibility (captured by $\sigma _2$ and $\sigma _s$ for the HSC and $\sigma _2$ and $\sigma _\infty$ for the HCC), and the run time to generate perturbations. Table 3 and Table 4 present the results for the HSC and HCC, respectively. To simplify the exposition and comparisons, the ID number in the first column of both tables is used to refer to a combination of method, parameters, and solver used for the experiment. A set of observations follow.

• Regardless of the used solver, Algorithm 1 always yields the best performance in terms of the fooling ratio and perceptibility, but not in terms of run time. This is due to the fact that Algorithm 1 iterates over all labels outside the true super-class set. This can be seen by comparing ID 1–3 to all others in Tables 3 and 4 for the HSC and HCC classifiers, respectively.

• The performance of Algorithm 2 is very similar to that of Algorithm 1 regarding the fooling ratio and perceptibility, while also reducing the run time. This can be seen for both classifier models (e.g., ID 2 versus ID 5 in Tables 3 and 4). The reduction in run time is because Algorithm 2 iterates over a reduced set $S^{'*}_T$ instead of the entire set of labels in $S^{'}_T$.

• Comparing the REC and NOC methods, we observe that NOC outperforms REC in terms of perceptibility and fooling ratio, while the run time is relatively similar. For example, see ID 7 versus ID 10 in Table 3 and ID 8 versus ID 11 in Table 4. The perceptibility is higher in the REC method because the formulated program has Q times more constraints to satisfy in comparison with the NOC method as shown in (9). This observation is an empirical verification of proposition 3.

• Regardless of the solver, the NOC method performs relatively similar to Algorithm 2 in terms of perceptibility and fooling ratio with a decrease in run time for the HSC (HCC) classifiers as observed when comparing ID 4 (5) versus ID 10 (11) of Table 3 (4). The run time is reduced since we only solve one convex program in the NOC method.

• Regardless of the formulation and the solution method of (5), our proposed solvers (rADMM and eADMM) either outperform, or perform on par with, state-of-the-art solvers such as CVXPY [17] and CVX [26]. For the HSC, the run time and fooling ratio are similar, while we observe lower perceptibility (higher SSIM) by comparing ID 10 versus ID 11 of Table 3. For the HCC, rADMM yields very similar results to CVX in terms of perceptibility and fooling ratio but with a significant reduction in run time, for example, by comparing ID 1 and ID 2 of Table 4. When comparing eADMM and CVX, we observe similarity in terms of the fooling ratio, with eADMM outperforming in perceptibility for the HCC. For the HSC model, eADMM outperforms CVXPY in every aspect other than the run time. The eADMM solver incurs a longer execution time since it checks the stopping criterion at each iteration t as described in Algorithm 3. This highlights a tradeoff for eADMM between performance (perceptibility/fooling ratio) and computation time (to generate perturbations).

Table 3 HSC proposed attacks comparison with $\epsilon _c=10$ and over 1000 trials

Table 4 HCC proposed attacks comparison with $\epsilon _c=2.15$ and over 1000 trials

6.4 Generators for OSCs Versus Proposed Methods

In this section, we compare the performance of attacks generated from OSC models and our formulations. The goal is to assess the ability of perturbation generators to fool the coarse class. Figure 2 presents samples of the original and perturbed images for the HSC model, and Fig. 3 shows examples of the original and perturbed observations for each of the super-classes for the HCC.

For OSCs, we use MIFGSM [18] being one of the state-of-the-art iterative gradient-based methods that support targeted and non-targeted white-box attacks. In this paper, we use the non-targeted version. The iterations of MIFGSM can be written as

$$\begin{aligned}{} & {} {\textbf{x}}_{*}^{(t+1)} = {\textbf{x}}_{*}^{(t)} + \frac{\epsilon _M}{{\mathcal {T}}} \text { sign}({\textbf{g}}^{(t+1)}), \end{aligned}$$

(29)

$$\begin{aligned}{} & {} {\textbf{g}}^{(t+1)} = \mu _M {\textbf{g}}^{(t)} + \frac{\nabla _{{\textbf{x}}} {\mathcal {J}}({\textbf{x}}_{*}^{(t)},k^*({\textbf{x}}))}{\Vert \nabla _{{\textbf{x}}} {\mathcal {J}}({\textbf{x}}_{*}^{(t)},k^*({\textbf{x}}))\Vert _{1}} \,, \end{aligned}$$

(30)

where ${\textbf{x}}_{*}$, t, $\epsilon _M$, $\mu _M$, $k^*({\textbf{x}})$, and ${\mathcal {T}}$ are the perturbed image, iteration index, perturbations bound, decay factor, the true label, and number of iterations, respectively. Also, ${\mathcal {J}}(.,.)$ denotes the loss function during the training phase. Here, we use ${\mathcal {T}} = 10$, $\mu _M = 1$, and $\epsilon _M = 0.3$. The algorithm initializes ${\textbf{x}}_{*}^{(0)} = {\textbf{x}}$ and ${\textbf{g}}^{(0)} = {\textbf{0}}$.

In addition to the MIFGSM attack, we report results from the $l_2$ version of the well-known projected gradient descent (PGD) attack [36]. We use the unrestricted variant in which the amount of allowable perturbation is increased in every iteration. We start by $\epsilon _P = 0.1$ and increase it by 0.05.

The first three columns of Fig. 2 illustrate the original image, the perturbation, and the perturbed image generated by MIFGSM to fool the OSC. The following two columns show the perturbation and the perturbed image generated by Algorithm 1 and rADMM to fool the HSC. The last two columns show the perturbations and the perturbed image generated by Algorithm 1 from our prior work [7], which uses the novel targeted saliency map attack [41], to fool the HSC. Results from Alkhouri et al. [7] are included to compare against our proposed attack. The rows show images selected from each of the super-classes. For instance, the label of the first image is $k=2$ and the super label $T=0$. As shown, while MIFGSM is able to change the label from $k=2$ to a predicted label ${\hat{k}} = 6$, it does not change the super label (3rd column), where ${\hat{k}}:=k({\textbf{x}}+{\varvec{\eta }})$ and ${\hat{T}}:=T(k({\textbf{x}}+{\varvec{\eta }}))$. On the other hand, our proposed method (Algorithm 1+rADMM) changes the super-class from 0 to 4 (5th column) and the attack from Alkhouri et al. [7] (7th column) changes the super-label from 0 to 3. Similar behavior is observed in the third row, where MIFGSM obtains ${\hat{T}} = T = 2$, while our proposed method changes the predicted super-label from 2 to 4.

Our proposed methods and Alkhouri et al. [7] achieve similar performance in terms of fooling the coarse class and perceptibility. A main difference is that attacks from Alkhouri et al. [7] are limited to the task of image classification using NNs (since they utilize off-the-shelf targeted OSC perturbation generators such as Carlini and Wagner [41] and Papernot et al. [12]), while our formulation is applicable to any classifier that can be modeled as a ‘direct approach’ HC.

Fig. 2

Samples from each super-class (rows) for the MNIST dataset. Columns 1–7: original image, perturbations needed to fool the OSC, perturbed image that fooled the OSC, perturbations needed to fool the HSC with Algorithm 1 + NOC, perturbed image by proposed method that fooled the HSC, perturbations needed to fool the HSC generated by Alkhouri et al. [7], and perturbed image that fooled the HSC. The values of k and T show whether classes belonging to same coarse level are semantically related or not relative to T. While MIFGSM is only able to change the coarse classification in the cases of $S_1$, $S_2$, and $S_3$, our proposed attack is able to change the coarse classification in all the cases

Fig. 3

Samples from each super-class. For each observation vector, k, T, ${\hat{k}}$, and ${\hat{T}}$ represent the predicted label, predicted super-label, predicted label with perturbations, and predicted super-label with perturbations, respectively. As we consider an LTI system for the HCC model, the ‘Amplitude’ (y-axis) measures the input signal strength w.r.t. the ‘Discrete Time’ (x-axis)

Fig. 4

Confusion matrices of the true super-labels versus the predicted ones of the HSC (top) and HCC (bottom) for the no perturbations case (left), perturbed with OSC generator (middle), and perturbed with HC (right)

For our composite model, we perform the comparison based on perturbations generated by the NOC method and the rADMM solver. For the OSC, they are generated as Alkhouri et al. [5],

$$\begin{aligned} {\varvec{\eta }} = - \epsilon _{s} \text { sign}(\nabla _{{\textbf{x}}}J_{{\hat{i}}}({\textbf{x}}) - \nabla _{{\textbf{x}}}J_{k^*({\textbf{x}})}({\textbf{x}})), \end{aligned}$$

(31)

where $\epsilon _{s}$ is a predefined perturbation bound (here, we use $\epsilon _s = 0.19$), and

$$\begin{aligned} {\hat{i}} = \underset{{i}\ne k^*({\textbf{x}})}{\mathop {\textrm{argmin}}\limits } \frac{ |J_{{i}}({\textbf{x}}) - J_{k^*({\textbf{x}})}({\textbf{x}}) |}{\Vert \nabla _{x}J_{{i}}({\textbf{x}}) - \nabla _{x}J_{k^*({\textbf{x}})}({\textbf{x}})\Vert _{1}} \,, \end{aligned}$$

(32)

where $|. |$ in the numerator denotes the absolute value.

Figure 3 (left) presents an observation from super-class set $S_1$, which has predicted label $k=2$ and super-class $T=1$ (without perturbations). The attack derived from (31) is able to change the output of the classifier from $k=2$ to ${\hat{k}} = 3$, but does not change the super-label, so $T = {\hat{T}} = 1$. Our proposed approach changes the super-label $T=1$ to ${\hat{T}}=2$. A similar behavior is exhibited in Fig. 3 second from left, second from right, and (right) for $S_2$, $S_3$, and $S_4$, respectively.

We also evaluate the performance using the confusion matrices. In the matrices of Fig. 4, the rows correspond to the true super-classes and the columns to the predicted super-classes for the HSC (top) and HCC (bottom) models. The diagonal of the confusion matrix is an indicator of the attack’s success in fooling the super-label. For the HSC model (top), the matrices on the left, middle, and right represent results with no perturbations, MIFGSM [18], and our NOC+rADMM, respectively. Our proposed attack only fails to fool the super-class for 194 feature vectors out of 10, 000, while nearly $50\%$ of the instances fail using perturbations from the OSC generator. For the HCC, the matrices on the left, middle, and right correspond to results with no perturbations, the method in Alkhouri et al.[5], and our proposed method (NOC+rADMM), respectively. As observed, the proposed attack only fails to confuse the classifier for 8 observations out of 1000, versus nearly 400 instances using the method in Alkhouri et al. [5]. These two examples illustrate the success of our method in fooling the super-label (confusing the big picture).

We evaluate in detail the performance of our proposed method (Algorithm 2 + rADMM) attacking the HSC in comparison with perturbations generated for the one-stage simple hypothesis testing classifier (OSSC) (Dong et al. [18]) using MIFGSM. In addition, we compare with the algorithm from Alkhouri et al. [7] which uses off-the-shelf, state-of-the-art targeted attack generators [12, 41]. The results are given in Table 5 and are averaged over 1000 trials. The comparison against MIFGSM and PGD-$l_2$ demonstrates the degradation in the super classification accuracy (captured by $\zeta ^{\text {sup}}$ and $\xi ^{\text {sup}}$), and the perceptibility factors (represented by $\sigma _2$). As observed, our method causes a significant misclassification of the super-labels yielding $\zeta ^{\text {sup}}=95.81\%$ and $\xi ^{\text {sup}}=98.6\%$ compared with $\zeta ^{\text {sup}}=41.95\%$ ($\zeta ^{\text {sup}}=40.1\%$) and $\xi ^{\text {sup}}=44.75\%$ ($\xi ^{\text {sup}}=40.1\%$) using MIFGSM (PGD-$l_2$) against the OSSC. Our proposed method and Alkhouri et al. [7] achieve similar performance.

Table 5 Comprehensive attacks results

Additionally, we examine the performance of our proposed method (NOC + rADMM) targeting the HCC against [5] which generates perturbations to fool a one-stage composite hypothesis testing classifier (OSCC). The results are presented in Table 5 averaged over 1000 trials. The comparison shows the degradation in the super classification accuracy (represented by $\zeta ^{\text {sup}}$ and $\xi ^{\text {sup}}$), and the perceptibility factors (represented by $\sigma _2$ and $\sigma _\infty$). As observed, for $\sigma _2 \approx 12\%$, our method inflicts a massive misclassification of the super-labels with $\zeta ^{\text {sup}}=99.07\%$ and $\xi ^{\text {sup}}=100\%$ in comparison with $\zeta ^{\text {sup}}=54.79\%$ and $\xi ^{\text {sup}}=71.61\%$ reported from the method attacking the OSCC.

We show the perceptibility measured by the SSIM index $(D_s)$ of the first 100 images of the MNIST fashion dataset for the HSC model. Figure 5(left) shows the SSIM index for MIFGSM and our proposed method (NOC + rADMM). As observed, the perturbed images to fool the super-class have lower SSIM compared with those generated from MIFGSM. Hence, fooling the big picture captured by the coarser classification requires larger perturbations (lower SSIM). We also show the cumulative distribution function (CDF) of the SSIM index $D_s$ in Fig. 5 (right) in which we can also observe that fooling the super-class requires higher perturbations. We can also visually identify that perturbations needed to fool the big picture are more perceptible by comparing the 2nd (MIFGSM) and 4th columns (our proposed method) of Fig. 2.

Fig. 5

SSIM ($D_s$) of the first 100 examples with MIFGSM and our proposed method (left) and CDF of $D_s$ (right). The thicker lines in the left plot are the smoothed average for each case with moving average window of length 25

In the last experiment of this subsection, we present the perceptibility factor $\rho _\infty$ for OSC and our method (NOC + rADMM) for the HCC. The results are shown in Fig. 6(left). On average, the perturbations required to fool the HCC are larger with a higher variance than those needed to fool the OSC. Additionally, we show the complementary CDF (CCDF) of the perceptibility factor $\rho _\infty$ in the cases of OSC and HCC in Fig. 6(right). As shown, fooling the HCC generally requires higher perturbations than those needed in the OSC case.

Fig. 6

Perceptibility factor ($\rho _{\infty }$) of the first 200 examples with perturbations from Alkhouri et al.[5] and our proposed method (left) and CCDF of $\rho _{\infty }$ (right). The thicker lines in the left figure reflect the smoothed average (moving average window of 25) for each case

6.5 Impact of Label Grouping

In this section, we study the impact of label grouping on the attack performance. Specifically, we utilize different mapping functions T(.) to map labels to their super-classes and show the impact on perceptibility and fooling ratio for the HSC model using the MNIST fashion dataset. In other words, the idea is to show the impact of using different grouping functions given a fixed OSC-classifier and an attack method. Let $T_{L}$ represent the mapping used in the previous subsection, in which the grouping of the labels depends on the location of the item relative to the body (e.g., ‘T-shirt’ is mapped to ‘top’). In addition to the location semantic, we define three other mappings based on state-of-the-art clustering visualization techniques/tools: $T_{t}$ represents the t-distributed stochastic neighbor embedding (tSNE)-based mapping [35], $T_{P}$ represents the mapping based on principal component analysis (PCA), and $T_{U}$ represents the mapping based on the uniform manifold approximation and projection for dimension reduction tool (UMAP) [38]. For each method, we have used the resultant maps to obtain the grouping visually. The grouping for each method is defined as follows: $T_{t}:$ $S_0=\{0,3\}$, $S_1=\{1\}$, $S_2=\{2,4,6\}$, $S_3=\{5,7,9\}$, and $S_4=\{8\}$, $T_{P}:$ $S_0=\{0\}$, $S_1=\{1,3\}$, $S_2=\{2,4,6\}$, $S_3=\{5,7\}$, and $S_4=\{8,9\}$, and $T_{U}:$ $S_0=\{0,2,4\}$, $S_1=\{1\}$, $S_2=\{3,5,6,7,9\}$, and $S_3=\{8\}$.

In Table 6, we show that with similar perceptibility measure $\sigma _2\approx 15\%$ and $\sigma _s\approx 81\%$, different misclassification performance is observed (as seen from $\zeta ^{\text {sup}}$ and $\xi ^{\text {sup}}$). With UMAP, we observe that our attack performs the best in the sense of generating the smallest perturbations to fool the super-class (low $\sigma _2$ and high $\sigma _s$). The location and tSNE bases yield good results unlike PCA. Results illustrate that different mappings can yield different results for the same imperceptibility. In this experiment, we used the rADMM+NOC combination with $\epsilon _c=10$ to generate the perturbations.

Furthermore, we report results from the MIFGSM attack against the OSSC model. In terms of the fooling ratio for the super label, we observe that irrespective of the mapping used and the number of super-classes, the OSSC attack is only successful, in terms of $\zeta ^{\text {su[}}$, to fool, on average, nearly 55% only. A similar observation is also seen for the values of $\xi ^{\text {sup}}$.

Table 6 Performance using different mapping functions averaged for 100 observations

We also conduct another experiment in which we study the perturbation level (in terms of detectability) given a pre-specified fooling level. The results are shown in Fig. 7. The perturbations are generated to achieve $\zeta ^{\text {sup}}\approx 90\%$ and $\xi ^{\text {sup}}\approx 94\%$ for each mapping. To this end, we use $\epsilon _c$ as 10, 15, 17, and 10 for the mappings based on location, tSNE, PCA, and UMAP, respectively. As can be observed from the CCDF in Fig. 7, higher levels of perturbation (increased perceptibility) are needed for PCA and tSNE in comparison with UMAP or the location based mappings.

Fig. 7

CCDF of the perceptibility ($\rho _2$) of the proposed mappings

The former experiments show that the performance of the attacks is highly dependent on the mapping used. This suggests that the grouping of the labels can be designed to enable more robust HCs that are harder to fool, in the sense of requiring more perceptible perturbations.

7 Conclusion

Studies on adversarial perturbation attacks have largely focused on one-stage classifiers (OSCs). In this paper, we advanced a new formulation that uses minimax constraints to attack hierarchical classifiers (HCs). We derived several convex relaxations to said formulation to obtain approximate solutions. An alternating direction method of multipliers (ADMM) solver is proposed for the resulting convex programs. The framework can be broadly applied to implement attacks on both simple and composite classifiers. Performance was evaluated in terms of the degradation in classification accuracy and perceptibility of the added perturbations. Among the lessons learned is that HCs are inherently more robust than OSCs in the sense that fooling the big picture generally requires higher levels of perturbation. Also, the attack performance is highly dependent on the function used to map labels to super-classes, which can provide guidelines for designing robust HCs.