1 Introduction

Point cloud feature extraction has become a research hotspot in 3D digital geometry processing techniques. This technology is widely used in sectors such as industrial design [15, 26], medical research [10, 28], shape recognition [20], spatiotemporal analysis [5, 13], and digital protection of cultural relics [27, 31]. High-quality feature extraction can provide strong support for subsequent point cloud registration, splicing, and surface reconstruction [18, 35]. At present, much intensive research has been conducted on the feature extraction of 3D models, which can be mainly divided into feature extraction based on the mesh model and feature extraction based on the point cloud. The mesh model consists of many triangular patches and weakens some of the distinctive features of the model, which is a considerable challenge for feature extraction and subsequent applications. Most researchers are now performing processing directly on point cloud data, which can describe the model intuitively, and point cloud feature extraction is the basis of 3D geometric processing. It is concentrated mainly on feature point extraction and feature line extraction.

As for feature point extraction, most existing methods focus on using the geometric parameter features of the local neighborhood of the point cloud to detect feature points. Zhang et al. [41] proposed a local reconstruction method to extract feature points using Laplace operators. This method needed to perform point cloud data meshing. Moreover, additional operations were needed to increase the amount of calculation, and the sampling quality of the point cloud would directly affect the reconstruction effect which, in turn, affected the accuracy of subsequent feature extraction. Fu and Wu [9] used the geometric relationship between adjacent points to calculate the line-to-intercept ratio, based on which the feature points of the model could be identified. Moreover, multi-scale feature extraction technology improved the accuracy of feature recognition and enhanced the noise resistance of the algorithm [3, 14, 16, 19, 29].

Feature point extraction is a vital part of the feature line extraction in the 3D point cloud model; it is the accuracy of which directly affects feature lines. At present, the method for extracting feature points of the point cloud model is mainly analyzing the neighborhood of sampling points and selecting local feature extreme points as model feature points. Some researchers have realized multi-scale feature point extraction by changing the size of the neighborhood to reduce the impact of noise on the accuracy of feature point extraction [4]. Feature line extraction is an essential operation of 3D geometric model processing to express the surface structure and geometric shape of 3D models [24]. For the 3D point cloud model, the feature line is the orderly connection of a series of feature points [37]. As there is no topological connection among the point cloud data itself, together with the problems such as uneven sampling, noise, and missing data, further discussion and research are still required on how to extract the feature points of the point cloud model quickly and with high quality [7, 30].

He et al. [11] proposed a feature line extraction method for the point cloud based on the covariance matrix. First, the feature values of the covariance matrix of the sampling points were clustered to extract the feature points according to the main direction in each strip region, which were projected onto the local surface to obtain a smooth feature line. For more complex models, this method would present more irregular strip features, so that the primary direction trend obtained was not obvious and ultimately affected the extraction effect of feature lines. Erdenebayar and Konno [6] proposed a feature line extraction algorithm based on the Mahalanobis metric which recognized the potential feature points of the model according to the multi-scale surface change degree. This framework used the weighted Laplace algorithm to refine the feature points that were connected into lines according to polyline propagation. Fu and Wu [8] located the feature areas of the model according to the spatial grid dynamic division method using the Laplace operators to refine the feature points, which were finally connected into feature lines based on the improved lines by the polyline propagation method. This method could effectively improve the speed of feature line extraction. Wang et al. [33] proposed a feature extraction method for point cloud based on region clustering segmentation, which used region clustering to divide the model into several regions, perform the surface reconstruction of each region to estimate the curvature information, and, based on which, identify feature points. The effect of this method was not ideal for models with complex shapes.

In summary, the connection method of feature lines is divided into the minimum spanning tree and the polyline propagation method [32, 40]. However, since the construction of the minimum spanning tree is relatively time-consuming, this method is less efficient, so it is more suitable in cases of fewer real-time requirements. The method proposed in this paper mainly includes the steps of feature point extraction, clustering, refinement, and connection. First, the projection distance feature of the point cloud model was calculated to identify the potential feature points of the model, and local information of the possible feature points was used to construct the adaptive neighborhoods. Then, the neighborhoods of the model were utilized to identify the feature points of the model. Because the identified feature points were distributed on the model in an arbitrary, scattered manner and the feature lines extracted were distributed at the junctions between faces, it was necessary to cluster the feature points. Then, feature point sets were obtained according to the discrimination threshold of feature points, based on which the clustering fusion of feature points was proposed to ensure a comprehensive recognition of model features. As the feature points still had a certain width after clustering, a certain degree of difficulty was undoubtedly added to the connection of subsequent feature lines. Therefore, the Laplace thinning method was performed to refine the feature points, and finally, the feature points were connected in an orderly manner to form smooth feature lines.

2 Material and Methods

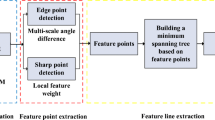
Compared with the complete model, the fragment model has richer surface information and contains a lot of noise, whose sharp features will be decreased by wear, making feature extraction more difficult. Therefore, a feature point extraction algorithm based on adaptive neighborhood is proposed in this paper to address the problem of incomplete extraction of detailed features in the point cloud fragment model, based on which the feature points are clustered, refined, and connected. An overview of the specific algorithm flow is shown in Fig. 1.

Fig. 1
figure 1

Overview of the method in this article

Full size image

2.1 Feature Point Extraction

In the three-dimensional point cloud model, the extraction of feature points is mostly aimed at calculating the geometric parameters of the point cloud based on the local neighborhoods of the sampling points and, thus, to identify the feature points. A neighborhood is a topological relationship established between each point and its consecutive point that can effectively improve the speed and efficiency of point cloud data processing. The geometric information of feature points is often from other points in the neighborhood. Therefore, an adaptive neighborhood feature point extraction method is proposed in this paper based on the local geometric information of the point.

2.1.1 Potential Feature Point Extraction

The steps of specifying the point cloud \(P = \left\{ {p_{1} , \cdots ,p_{i} , \cdots ,p_{m} } \right\}\) are: 1. selecting Point pi randomly, 2. r0 is considered as the initial radius, 3. the spherical neighborhood is calculated as \(NBHD\left( {p_{i} } \right) = \left\{ {p_{ij} \left| {\left\| {p_{ij} - p_{i} } \right\| \le r_{0} ,j = 1 \cdots k} \right.} \right\}\), and 4. the normal vector \(n_{{p_{i} }}\) corresponding to each point is calculated according to the PCA method [38]. The distance \(DIS\left( {p_{i} } \right)\) is formed when the vector \(\overrightarrow {{p_{i} \overline{p}_{i} }}\) is projected onto the normal vector and \(n_{{p_{i} }}\) is calculated. This projection distance is used to describe the local information at Point \(p_{i}\) as shown in Fig. 2. The closer the local surface of Point \(p_{i}\) is to the plane, the closer the distance \(DIS\left( {p_{i} } \right)\) is to 0.

Fig. 2
figure 2

Neighborhood feature of Point \(p_{i}\)

Full size image

For Point \(p_{i}\), the projection distance \(DIS\left( {p_{i} } \right)\) of the point is described according to the features of its corresponding neighborhood Point \(p_{ij}\), as shown in Eq. (1).

$$ \begin{gathered} DIS\left( {p_{i} } \right) = \left| {\left( {p_{i} - \overline{p}_{i} } \right) \cdot n_{{p_{i} }} } \right| \hfill \\ \overline{p}_{i} = \frac{1}{N}\sum\limits_{j = 1}^{N} {p_{ij} } \hfill \\ \end{gathered} $$
(1)

where \(\overline{p}_{i}\) = the centroid of the neighborhood Point \(p_{ij}\), and \(N\) = the number of neighborhood points of Point \(p_{i}\). When \(DIS\left( {p_{i} } \right)\) is larger than a certain threshold value, Point \(p_{i}\) is regarded as a potential feature point; otherwise, it is a non-feature point. Therefore, the set of potential feature points \(P^{\prime}_{F} = \left\{ {p^{\prime}_{1} , \cdots ,p^{\prime}_{i} , \cdots ,p^{\prime}_{n} } \right\}\) is obtained, and \(n\) is the number of potential feature points.

2.1.2 Adaptive Neighborhood Construction

Currently, the most widely used methods for neighborhood search include k-nearest neighbor and R-radius neighborhood, for which the choice of parameters is critical [33, 39]. The radius neighborhood search method is used to identify the point cloud neighborhood, which is more effective for evenly distributed point cloud data [17]. For models with complex surface information, the neighborhood scale will directly affect the algorithm [21, 43]. The features of the point cloud cannot be identified effectively by a single scale. Although the multi-scale neighborhood search can improve the accuracy of feature detection, it takes more time [36]. All existing methods rely on experience when choosing neighborhood parameters. A neighborhood with an inappropriate radius can slow down the calculation speed of the algorithm and increase the time cost exponentially [44, 45]. Compared with the complete model, the fragment model studied in this paper has more abundant features. The effective recognition of model features is a problem worthy of attention for subsequent fragment splicing. Because of the difference in the local information distribution of the point cloud, the influence of noise is effectively overcome. Moreover, an adaptive neighborhood is constructed to identify point cloud features with high efficiency and high quality.

For the set of potential feature points \(P^{\prime}_{F} = \left\{ {p^{\prime}_{1} , \cdots ,p^{\prime}_{i} , \cdots ,p^{\prime}_{n} } \right\}\), taking Point \(p^{\prime}_{i}\) as the center O, its corresponding normal vector as \(Y\) axis creates a local coordinate system with \(OX\) axis located on the tangent plane of Point \(p^{\prime}_{i}\) (Fig. 3). As shown in Fig. 3, \(p^{\prime}_{ij}\) is the neighborhood point of \(p^{\prime}_{i}\).

Fig. 3
figure 3

Establishment of the local coordinate system

Full size image

Function \(y = f\left( x \right)\) is constructed, of which \(f\left( x \right)\) is unknown, let \(y^{\prime} = 0\). Such a function is subjected to second-order Taylor expansion [2] to obtain Eq. (2):

$$ y = f\left( 0 \right) + \frac{1}{2}y^{\prime\prime}x^{2} = \varepsilon + \frac{1}{2}y^{\prime\prime}x^{2} $$
(2)

where \(\varepsilon\) is constant. If \(y^{\prime} = 0\), then \(\varepsilon = 0\). By the definition of curvature [1], the following can be derived:

$$ \omega = \left| {y^{\prime\prime}} \right| = \mathop {\lim }\limits_{x \to 0} \frac{2\left| y \right|}{{x^{2} }} $$
(3)

where \(\omega\) is curvature. It can be seen from Fig. 3 that \(\omega \left( {p^{\prime}_{ij} } \right) = \mathop {\lim }\limits_{x \to 0} \frac{2h}{{\left| l \right|^{2} }}\), wherein \(l\) denotes the distance from Point \(p^{\prime}_{ij}\) to Y axis, h denotes the distance from Point \(p^{\prime}_{ij}\) to \(OX\) axis.

It is expected that a high-quality neighborhood can describe as many points as possible and can effectively describe the features. From Fig. 4, the relationship between the local feature of each point and the radius neighborhood in the point cloud model can be seen more intuitively. As shown in Fig. 4a, the selection relationship between neighborhood features and radius is described, while in Fig. 4b, Point \(p_{i}\) located in the sensitive area corresponds to the optimal radius \(r_{i} \left( {r_{i} < y_{i} } \right)\). In contrast, Point \(p_{j}\) located in the relatively flat area corresponds to the optimal radius \(r_{j} \left( {r_{j} > y_{j} } \right)\).

Fig. 4
figure 4

The relationship between neighborhood radius and local features

Full size image

The above analysis clearly indicates that a mathematical expression can be established based on the relationship between the local feature of the point cloud and the radius to adjust the neighborhood of each point adaptively. It can be derived from Eq. (3).

$$ \omega = \frac{2\left| y \right|}{{r^{2} }} \Rightarrow \left| y \right| = \frac{{\omega r^{2} }}{2} $$
(4)

where y = the projection distance of each neighborhood point on the normal vector, and \(\omega\) = the corresponding curvature. It can be seen from Eq. (4) that the selection of the neighborhood radius of each point is closely related to the projection distance and curvature.

Assuming that Point \(p^{\prime}_{i}\) is located in a flat area (Fig. 4b), if \(r_{i} \ge y_{i}\), Eq. (5) may be built to ensure that the radius of the point located in the feature area can be shrunk until the radius \(r_{i}\) is larger than \(y_{i}\), to obtain the optimal radius corresponding to Point \(p^{\prime}_{i}\).

$$ \left| {y_{i} \left( {p^{\prime}_{i} } \right)} \right| \le {{\omega r_{i}^{2} \left( {p^{\prime}_{i} } \right)} \mathord{\left/ {\vphantom {{\omega r_{i}^{2} \left( {p^{\prime}_{i} } \right)} 2}} \right. \kern-\nulldelimiterspace} 2} $$
(5)

To sum up, Eq. (5) can be used to adaptively adjust the selection of the optimal radius. By the projection distance defined in Eq. (1), it can be inferred from Eq. (5).

$$ \left| {\left( {p^{\prime}_{i} - p^{\prime}_{ij} } \right) \cdot n_{{p^{\prime}_{i} }} } \right| \le \frac{{\omega \left( {p^{\prime}_{ij} } \right)}}{2}r_{i}^{2} \left( {p^{\prime}_{i} } \right) $$
(6)

where \(p^{\prime}_{ij}\) = the neighborhood point of \(p^{\prime}_{i}\), and \(\omega \left( {p^{\prime}_{ij} } \right)\) = the curvature of Point \(p^{\prime}_{ij}\). The approximate calculation can be performed for the curvature according to the method in He et al. [12], as shown in Eq. (7).

$$ \omega \left( {p^{\prime}_{ij} } \right) = \frac{{\lambda_{0} }}{{\lambda_{0} + \lambda_{1} + \lambda_{2} }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\lambda_{0} \le \lambda_{1} \le \lambda_{2} } \right) $$
(7)

The process of performing adaptive adjustment to the neighborhood of potential feature points is described as follows: First, the initial radius is set to calculate the features of the normal vector and curvature corresponding to each point in the set of potential feature points. Then, inequality (6) is calculated; if the condition is not met, the point with the largest radius in the current neighborhood is removed until inequality (6) is satisfied. The details are presented in Algorithm 1.

figure a

2.1.3 Feature Point Optimization

From the previous section, the optimal neighborhood size corresponding to each point in the set of potential feature points can be obtained, of which the neighborhood size has a close relationship with the local features of the point cloud. Therefore, the more prominent the area where the point cloud features are located is, the smaller the radius will be. Conversely, the larger the area with the radius is, the smoother the point cloud will be. Feature points generally appear in areas with significant feature changes. According to this principle, it can be concluded that a point with a smaller radius is more likely to become a feature point. Therefore, the optimal radius of each point is used as one of the elements to detect the feature points in this paper. If the radius of the points in the potential feature point set \(P^{\prime}_{F}\) is less than threshold t, these points are stored in the enhanced feature point set, denoted as \(P_{F} = \left\{ {p_{1} , \cdots ,p_{i} , \cdots ,p_{n} } \right\}\), where \(n\) is the number of feature points. The results of the feature points extracted in this paper are presented in Fig. 5. Figure 5a represents the original model, and Fig. 5b represents the feature point extraction results. The blue points represent the detected feature points, from which it can be seen that feature points are distributed more in the sensitive area and less in the smooth area.

Fig. 5
figure 5

Feature point extraction results of the brick model

Full size image

2.2 Feature Line Construction

2.2.1 Feature Point Clustering and Refinement

As can be seen from Fig. 5b, the finally extracted feature points are scattered on the model. To avoid the existence of false feature points (such as noise points), the current paper conducted cluster partition for the detected feature points to divide the points into multiple point sets independent from one another, so that more accurate feature lines can be generated.

The classic distance-based clustering algorithm [11] is used to perform cluster partition for feature point \(P_{F} = \left\{ {p_{1} , \cdots ,p_{i} , \cdots ,p_{n} } \right\}\). The main idea is to randomly select a feature point as an initial value to determine other feature points according to the corresponding adaptive radius in the neighborhood. If this condition is met, the current cluster is added until all points in the feature point set are identified, and clustering is completed.

The wide recognition of feature points is a prerequisite for effectively connecting feature lines. If the threshold value is selected too strictly, more regular clustering will be obtained, which may not be good for the extraction of sharp features of the model. On the contrary, more clustering can be obtained to describe the sharp features of the model well, which affects the accuracy of the extracted feature points. The accuracy was evaluated based on the definition expressed by Reinders et al. [25]. Therefore, the fusion of feature point clustering at two scales [22] is employed in this paper, which can effectively make up for the incompleteness of feature point clustering at a single scale and can provide better support for the subsequent connection of feature points.

Assuming that the discrimination thresholds of the feature points are \(t_{1} ,t_{2} \left( {t_{1} < t_{2} } \right)\), respectively, based on which two different feature point sets \(P_{F}^{1}\) and \(P_{F}^{2}\) can be obtained, the distance cluster is performed for the feature sets, respectively, to obtain two cluster set \(cluster1 = \left\{ {cluster1_{i} } \right\}\),\(i = 1, \cdots ,m\) and \(cluster2 = \left\{ {cluster2_{j} } \right\},j = 1, \cdots ,n\), wherein \(m,n\) represent the number of clusters, respectively. The number of the feature points contained in each cluster is \(cluster1\_num_{i}\) and \(cluster2\_num_{j}\).

In this paper, the fusion is performed according to the degree of coincidence of the feature point clusters, which can be divided into three situations: (a) \(cluster1\) contains multiple clusters in \(cluster2\), which directly retains the clusters in \(cluster2\); (b) \(cluster1\) in \(cluster1\) and one of the clusters \(cluster2_{j}\) in \(cluster2_{j}\) overlap with each other, which needs to be judged according to the degree of overlapping; and (c) the cluster \(cluster1\) in \(cluster1\) is entirely contained in one of the clusters \(cluster2_{j}\) in \(cluster2_{j}\), which indicates that the features contained in \(cluster1_{i}\) are more complete than those contained in \(cluster2\), and \(cluster2\) can be replaced by \(cluster1_{i}\) directly. For different degrees of coincidence, the feature point clustering fusion algorithm is presented explicitly in Algorithm 2, where \(Count2_{j}\) is the counter corresponding to \(cluster2_{j}\).

figure b

As can be seen from Fig. 6a, the clustered feature points still present a certain width, which may bring a particular challenge to the connection of subsequent feature lines. The extracted feature points are generally distributed on both sides of the feature lines. When connecting directly based on the extracted feature points, the generated feature lines may deviate from the original feature lines. Therefore, it is necessary to refine the feature points. In this paper, inspired by the method in Erdenebayar and Konno [6], the feature points are iteratively refined so that the feature points can be closer to the original feature lines.

Fig. 6
figure 6

The feature point clustering and refinement results of brick model

Full size image

The cluster set of feature points finally obtained is \(cluster = \left\{ {cluster_{i} } \right\}\), and the refinement method for feature points is mainly divided into two steps, specifically described as follows:

Step 1: The corresponding adaptive neighborhood is calculated for each feature point \(p_{y}\) in \(cluster_{i}\), and Eq. (8) is used to calculate the average value \(\overline{p}_{y}\) of the neighborhood points, where \(\overline{p}_{y}\) is a new position corresponding to Point \(p_{y}\), \(n\) represents the number of the feature points in the corresponding neighborhood, and \(Q_{c}\) represents the feature point corresponding to the neighborhood point.

$$ \overline{p}_{y} = \frac{1}{n}\sum\limits_{c = 1}^{n} {Q_{c} } $$
(8)

Step 2: The projection distance corresponding to each point is calculated according to the newly obtained feature point \(\overline{p}_{y}\) and Eq. (1), and the points with the most significant projection distance in the neighborhood are used to replace all the points in the neighborhood.

2.2.2 Feature Line Connection

The feature points are scattered and disorderly without any topological connection relationship, unable to describe the features of the model intuitively. Therefore, the appropriate feature points in this paper are selected to be connected into smooth feature lines to reflect the distribution of model features at a higher level. Though the number of refined feature points has been reduced, the locations have been updated, which is more conducive to efficiently generating high-quality feature lines. The polyline propagation method is used in this paper to connect the feature points. The propagation first starts from the points with prominent features to ensure better tracking results, as the propagation process of the feature line is irreversible.

The feature point with the largest projection distance is taken as the first seed Point \(p_{seed}\). This current seed Point \(p_{seed}\) is taken as the center to search for its corresponding neighborhood point in the feature point set. The neighborhood point is projected into the direction \({\mathbf{d}}_{{\mathbf{s}}}\) formed by Point \(p_{seed}\) and the feature vector corresponding to the most significant feature value. The point with the largest projection distance is used as the next propagation point. To avoid the direction of the propagation point deviating from the main direction, the range \(\left\langle {{\mathbf{p}}_{{{\mathbf{seed}}}} {\mathbf{q}}_{{\mathbf{i}}} ,{\mathbf{d}}_{{\mathbf{s}}} } \right\rangle < \theta\) is taken as the prediction range of the next propagation point, wherein \(\theta = 30^{ \circ }\) is taken, as shown in Fig. 7. The blue points are the feature points, and the red points are the connected feature points. The predicted range of the next propagation point for \(p_{seed}\) is the shaded area in the figure, and the obtained propagation points are sequentially connected to obtain a set of feature polylines (\(Ployline = \left\{ {f_{i} } \right\}\)).

Fig. 7
figure 7

An example of constructing feature lines

Full size image

3 Results and Discussion

The proposed feature extraction method includes feature point extraction and feature line connection, which are analyzed separately. The proposed algorithms were implemented in C++ using the PCL. The experiment was performed on an Intel Core i7-9700 3.0 GHz machine with 16 GB of RAM. In this paper, models with different structures and features were used as experimental models to verify the effectiveness of this algorithm, of which the box model had a simple structure and distinct features. In contrast, the fragment model had complex features, mainly based on the fragment data set published by the Technical University of Vienna.

3.1 The Experiment and Analysis of Feature Point Extraction

3.1.1 The Neighborhood Sensitivity

Feature point extraction is the key to feature line extraction, the accuracy of which directly affects the accuracy of the feature line connection. Therefore, the robustness of feature point extraction and the ability to recognize subtle features are analyzed herein. In this section, the parameters with different neighborhood radii are set to analyze the performance of feature point extraction. Figure 8 shows the results of feature point extraction for different models on different scales. The extraction results at feature points r = 0.03, r = 0.15, r = 0.03, 0.15 and for adaptive neighborhood are shown in Fig. 8a–d, respectively.

Fig. 8
figure 8

Feature point extraction results of different models at different scales, a r = 0.03, b r = 0.15, c r = 0.03, 0.15; d based on adaptive neighborhood

Full size image

As can be seen from Fig. 8, the multi-scale method can extract more comprehensive features compared to the fixed-scale feature extraction method. The method used herein is able not only to extract the feature points of the model more concisely and accurately, but also to identify subtle features with high quality, such as the area marked by the red rectangle. For different point cloud models, multiple attempts are required to select the best neighborhood. This method can describe the features of the model more comprehensively, but it is time-consuming. In contrast, the adaptive selection model only needs to set the initial neighborhood radius to obtain the best neighborhood of each point on the model and thus to better identify each point, which indicates that the method in this paper helps to improve the accuracy of feature extraction for the point cloud.

Table 1 shows the numerical results of feature recognition of models with different neighborhood radii. #model = the point cloud model corresponding to the model in Fig. 8; #NR = the size of the selected neighborhood radius; #P = the number of points contained in the original model; #F = the number of identified feature points; #Rate = the recognition rate of feature points, obtained by Eq. (9); and #Timing = the time spent for feature recognition. A more intuitive illustration from Table 1 indicates the effectiveness of the adaptive neighborhood method. It can be observed that it is difficult for the artificially set global neighborhood to give an appropriate value. In contrast, too large a neighborhood radius may spend too much time for model feature extraction, but a too small neighborhood radius can increase the speed of feature extraction. In this paper, two scales of \(r =\) 0.03 and 0.15 were selected to extract feature points of the model, and five scales of \(r =\) 0.03, 0.06, 0.09, 0.12, and 0.15 were selected for analysis for multi-scale feature point extraction. It can be observed that compared with the multi-scale method, the feature points extracted by the proposed method are more concise and can effectively express the features of the model through a limited number of points. Although the single-scale feature extraction method takes a shorter time, the accuracy is also lower. A multi-scale method came into being, which achieves more accurate results at the cost of time and includes some redundancy points to improve the accuracy of feature extraction. However, the method in this paper can achieve a better balance between time efficiency and the accuracy of feature extraction.

$$ rate = \frac{\# F}{{\# P}} $$
(9)
Table 1 Numerical results of recognition rate of feature points of different models (seconds)
Full size table

3.1.2 Results of Comparison with Existing Methods

To further verify the robustness of the proposed algorithm, a brick model containing six fragments is selected herein, with Gaussian white noises at different intensities being added. The noise deviation is set to [0.1, 0.5]. Under the same hardware environment, the methods in Zhang et al. [41], Xia and Wang [34], and Jia et al. [14] are used together with the method proposed in this paper to calculate the feature point extraction rates, respectively, to conduct an experimental comparative analysis, the results of which are shown in Fig. 9.

Fig. 9
figure 9

Comparison of feature point extraction results of brick model

Full size image

It can be seen intuitively from Fig. 9, under different noise conditions, for the recognition rate of feature points, the performance of the proposed method is better than the methods of Zhang et al. [41] and Xia and Wang [34]. It changes slowly with the increase of noise. The method of Zhang et al. [41] is more sensitive to noise, which is to extract model features based on the method of local reconstruction, needing to construct a triangular mesh based on the extracted data to extract the model features. The method of Xia and Wang [34] detects feature points by calculating the gradient of the point cloud and analyzing the ratio between the feature values. Both methods in Zhang et al. [41] and Xia and Wang [34] are based on the distribution features of the point cloud to define the local detection operator. They need to manually adjust multiple parameters and set the global threshold value to detect the feature points of the model. This type of method is more sensitive to parameters and threshold values, and setting the size of a single neighborhood for different areas of the point cloud is not suitable for identifying features. Compared with the method in Jia et al. [14], the recognition rate of the method in this paper is relatively decreased because of the generation of some false feature points caused by the redundancy of feature points when selecting the parameters by the multi-scale neighborhood method. The sensitivity to noise is relatively increased because the proposed method in Jia et al. [14] used the multi-scale neighborhood method to calculate the point cloud features. Furthermore, the proposed method not only reduces the parameter setting, but also improves the robustness to noise at a certain degree, which effectively enhances the adaptability of the algorithm.

3.2 The Experiment and Analysis of Feature Line Extraction

3.2.1 Results of Feature Line Extraction

Figure 10 shows the results of feature line extraction by this method on different models, where (a) represents the extraction results from model feature points, (b) represents the results from feature point clustering, (c) shows the results from feature point refinement, and (d) represents the connection results from the feature lines. As shown in Fig. 10, the box model has a simple structure and distinct boundary features, obtaining precise feature line results. The fragments with complex structures and abundant features are used as experimental models to verify the versatility of the algorithm. As can be seen in Fig. 10, good extraction results have still been obtained using the proposed method, indicating that the method in this paper not only can extract the features of simple structure models, but also be somewhat feasible for fragment models with abundant features.

Fig. 10
figure 10

Experimental results of feature line extraction based on different models

Full size image

3.2.2 Effectiveness Analysis

Different models are used to further verify the superiority of this proposed algorithm, which is compared with the methods in Nie [23] and He et al. [11]. The results are shown in Fig. 11, of which (1), (2), (3), and (4), respectively, represent the results of feature line extraction from the models of brick 1, brick 2, pebble, and box one. Figure 11a represents the original model; (b), (c), and (d) represent the connection results of the feature lines from Nie [23], He et al. [11], and the method in this paper, respectively.

Fig. 11
figure 11

Experimental comparison of feature line connection results

Full size image

For the simple box model, the feature line extraction results obtained by the three methods are relatively straightforward and continuous (Fig. 11). For the fragment model, the surface information is more complex, including not only sharp features, but also transitional features with weaker features. For example, the method in this paper can effectively identify the detailed features of complex models which are connected into more complete feature lines. However, some of the feature lines extracted by the method in Nie [23] are incomplete, as shown by the blue rectangle box in Fig. 11b. This is because the developed method in Nie [23] performs the feature point segmentation of the model based on the degree of surface variation. The use of the local surface reconstruction method to identify the regional boundary points may lead to some minor details. This is another reason for the breakage and defect of the feature lines. As shown in Fig. 11c, the results from the method in He et al. [11] have wrong lines that deviate from the original model. This is because the method only distinguishes feature points based on the size of neighborhood feature values and can identify more redundancy points, which leads to the inaccuracy of the calculation of the main direction and the deviation of the feature lines.

3.2.3 Parameter Setting and Time Efficiency Analysis

Table 2 records the parameter settings and running time for different model execution steps, and threshold represents the threshold values set for feature point discrimination; (a) and (b), respectively, represent the time spent for feature point identification and feature line connection. Total timing indicates the time spent executing the algorithm. According to Table 2, the time efficiency of the method in this paper is better than that of methods in Zhang et al. [42] and He et al. [11]. In He et al. [11], simple plane fitting is performed on adjacent points, which has a negligible extraction effect for features formed by complex curved surfaces and requires the moving least squares method to perform local surface fitting. Zhang et al. [42] improved the threshold value to extract feature points according to the Poisson boundary region propagation method and used the median value of L1 to reconstruct the shape of each boundary point cluster approximately to complete the connection of the feature lines.

Table 2 Parameter settings and running time of different model execution steps
Full size table

4 Conclusion

Feature extraction is not only the basis of point cloud model processing, but also the key to research on the segmentation of 3D fragments, fragment splicing, and model restoration. Considering the problem that existing methods need to manually set the global neighborhood that makes the model sensitive to sharp feature recognition, a feature extraction method based on the adaptive neighborhood was proposed in this paper. First, the projection distance feature of the point cloud model was calculated to identify the potential feature points of the model. Moreover, the local information of the potential feature points was used to construct the adaptive neighborhoods to identify the feature points of the model based on different neighborhoods. Next, the clustering fusion of the feature points was performed according to the discrimination threshold values of feature points to effectively remove some false feature points, thereby improving the efficiency. Finally, the Laplace operator was utilized to refine and connect the feature points orderly to form smooth feature lines. The analysis of multiple sets of experimental data indicated that the method proposed in this paper is simple and effective, can retain the detailed features of the model as much as possible, reduces the manual setting of parameters, and has a certain degree of robustness. In this paper, the local neighborhood was adaptively adjusted according to the distribution of different regions of the point cloud model, thereby improving the accuracy of feature point recognition. For a model with abundant features, it was difficult to effectively describe the local features of the model by using fixed neighborhoods in different regions. Therefore, in this paper, different radii were set according to the feature distribution of each area of the point cloud model to realize the adaptive adjustment of the neighborhoods, so that the algorithm can find the feature points of the point cloud model more accurately and efficiently. Although calculating the unique neighborhood size of each point in the point cloud will lead to additional calculation time, adaptive neighborhoods can avoid the undesirable effects caused by unreasonable parameter settings, which can make up for the time cost defect.