Designing a Winner–Loser Gap for WTA in Subthreshold. Resolution Performance Revisited

Abstract

The paper pioneers a thorough mathematical approach for the Lazzaro variant of the W(inner) T(ake) A(ll) maximum rank and amplitude analog selector. Two exact levels of output which split the maximum and determine the resolution, are found for the first time. At the input, a list of currents $\left( I_{1},I_{2},\ldots ,I_{N}\right)$ from a large family ${{\mathcal {L}}}$ with smallest relative distance $\Delta$ on a $\left[ 0,I_{M}\right]$ scale is applied. To distinguish the largest current $I_{w}$ (the winner) from the second largest $I_{l}$ (the loser), the paper proposes two decision levels, ${\overline{D}}$ and ${\underline{D}}$, for the output voltage list $\left( U_{1},U_{2},\ldots ,U_{N}\right)$. The upper level ${\overline{D}}$ is surpassed only by the $U_{w}$ winner and encodes the winning rank w. All other ranks are placed under the lower level ${\underline{D}}$. Two rigorously treated optimization problems with inequality constraints lead to the identification of two input lists that yield the levels ${\overline{D}}$ and ${\underline{D}}$ as outputs. They are valid for processing any list in the ${\mathcal {L}}$ family. The index $\left( {\overline{D}}-{\underline{D}}\right) /U_{M}$—“the output resolution”—expresses how large the gap between the first and the second component on the $\left[ 0,U_{M}\right]$ scale is. It exceeds “the input resolution,” i.e., the similar index $\Delta /I_{M}$ at the input and the two depend monotonically on each other. Widely commented numerical examples are presented.

1 Introduction

The MOS-based WTA (Winner Take All) circuit—[14]—emerged when the neural-inspired VLSI analog circuits were launched [2, 22]. By making full use of its parallelism and compactness, the initial Lazzaro circuit and its variants have been implemented in a large diversity of applications such as image, sound and odor processing, classification, biomedical implants, motion control, computer memory, and neuromorphic circuits [1,2,3,4,5].

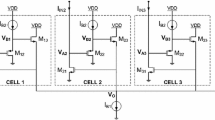
In this work, we apply a Lazzaro circuit as a current-voltage maximum rank selector. The circuit has N identical cells, among which Fig. 1 shows two consecutive cells. The cells share a common voltage V where the bias (tail) current $I_{C}$ is connected. Fed with tiny currents $I_{1},I_{2},\ldots ,I_{N}$ (for example, at the order of nanoamps), the circuit should signal the rank $w\in \overline{1,N}$ of the largest current $I_{w}$. Dissociating “the winner” $I_{w}$ from “the loser” $I_{l}$—which is the second-largest current—becomes difficult when $I_{w}$ and $I_{l}$ are small currents with very close amplitudes. To resolve this issue, WTA provides an output list of voltages $U_{1},U_{2},\ldots ,U_{N}$ identically ordered by size as the currents. The difference is that the winning rank w is unambiguously separated from the loser rank l. An input difference $I_{w}-I_{l}$, which is very small in comparison with the largest possible current $I_{M}$, yields a large output difference $U_{w}-U_{l}$ relative to the largest possible output $U_{M}$.

Fig. 1

Lazzaro WTA j-th and $\left( j+1\right)$-th cells. $I_{1},I_{2},\ldots ,I_{N}$—input currents; $U_{1},U_{2},\ldots ,U_{N}$—output voltages; V—cell common voltage

Now, consider that at input are applied successively all the lists of class ${{\mathcal {L}}}$ of currents, with maximum value $I_{M}$ and with mutual distance al least $\Delta$. Each list of currents produces at the output a list of voltages that has a $U_{w}$ winner and a $U_{l}$ loser. Our main achievement is the determination of three values ${\overline{D}}$, ${\underline{D}}$ and $U_{M}$ against which $U_{w}$ and $U_{l}$ of any processed list have the following positioning: $U_{M}\ge U_{w}\ge {\overline{D}}>{\underline{D}}\ge U_{l}\ge 0$. Out of all possible outputs (when current lists in ${{\mathcal {L}}}$ are at the input), ${\overline{D}}$ is the smallest of winners. To find it, we construct a classic optimization problem with inequality constraints. Solving this problem leads to a semi-analytical solution in the form of a concrete list ${\overline{C}}$ of currents that applied to the input gives an output winner ${\overline{D}}$. The lower level ${\underline{D}}$ is obtained by a similar reasoning from another list ${\underline{C}}$ at input. Together with ${\widehat{C}}$ which yields the highest winner $U_{M}$, we have three tools ${\overline{C}}$, ${\underline{C}}$ and ${\widehat{C}}$ to control by parameters the level of any maximum and its separation interval $\left[ {\underline{D}},{\overline{D}}\right]$ from the second rank. So, we built a rank filter with fixed parameters to process the lists in ${{\mathcal {L}}}$.

Once we have the decision levels clearly found, they can be used for WTA subsequent connections in an analog or digital way. For instance, ${\overline{D}}$ can operate as a comparison level for each output voltages—Fig. 2. Only one of these voltages surpasses ${\overline{D}}$, and this encodes the winning rank w. All other ranks—the losers—are situated below ${\underline{D}}$. On the other hand, it is pretty apparent that the decision levels can be exploited to define a measure of the winner separation. Thus, if $\omega =\Delta /I_{M}$ is the “input resolution” meaning a measure of the separation of $I_{w}$ from $I_{l}$ on the $\left[ 0,I_{M}\right]$ scale, then $\Omega =\left( {\overline{D}}-{\underline{D}}\right) /U_{M}$ is the “output resolution” meaning a measure of the separation of $U_{w}$ from $U_{l}$ on the $\left[ 0,U_{M}\right]$ scale of the output, for any input list in ${{\mathcal {L}}}$. The low value of $\omega$ combined with the high value of $\Omega$ indicates the high capacity of the circuit to detach the winning rank even for crowded input lists. The possibility of error is small. We rigorously prove that the $\Omega \left( \omega \right)$ function is monotonically increasing and that the WTA always “amplifies” the resolution. Detailed examples motivate and verify the theory.

Fig. 2

The WTA + N comparators. $I_{w}$ is the largest input, and $U_{w}$ is the only output that surpasses ${\overline{D}}$. $I_{l}$ is the second-largest input, and $U_{l}$ is the largest output less than ${\underline{D}}$. All other ranks are smaller than $I_{l}$ and $U_{l}$, respectively

Everywhere in our work, we consider all MOS in subthreshold. To ensure this regime, Theorem 1 limits the values of the maximum current $I_{M}$ and the bias current $I_{C}$. These constraints, together with those of Theorem 4, which ensure the ordering of decision levels, prove easy in the examples provided.

Many researchers have studied and modified the original Lazzaro circuit to improve its performance. Let us refer briefly to some of the papers where resolution (accuracy) is of particular concern in the context of a weak inversion regime.

Thus, one of the first findings was that local excitatory feedback improves the resolution [27]. The same effect has been reported when distributed “hysteresis” (using a resistive network) were implemented [7]. It avoids resetting after each processed list when the winning input shifts between adjacent pixels. Next, by adding local inhibitory feedback, flexible functioning was obtained [11]. The selective enlargement of the input range (“adaptive thresholding”) when changing the input list has also led to enhanced resolution [8]. A circuit with good performance for rank order operation has been reported in [29]. It selects the winner with cells in parallel, while the other ranks are treated sequentially. Time domain encoding was proposed in [23] for resolution improvement. Preamplification of the input signals has the same effect [10]. The extensive use of Lazzaro type WTA in visual attention, target tracking and centroid computation can be seen in [3, 7, 21]. Let us also mention a WTA application to rank-read circuitry from multilevel-cell computer memories [13]. The parallelism of WTA cells makes the circuit sensitive to mismatch and process variations. These result in errors of selection. Mismatch compensation techniques using floating gate programming [26], or $N-P$ MOS pairs instead of the original $N-MOS$, Sundararajan and Winstead [28], reduce the threshold and zero-current deviation influence. In [9], the Lazzaro WTA circuit classifies the brain generated spikes as part of a neuromorphic sensor. Specific problems of analog classifiers for low-resolution images or for remote wireless sensors can be found in [4]. In [25] five WTA configurations are compared in terms of resolution, speed, compactness and power dissipation. A combination of Matrix-Multiply and WTA is presented in [24]. It is concluded that any perceptron can be modeled in this way. An extended plea for biological neural circuits (where WTA is also a key element) can be found in [12]. Costea and Marinov [6] deals with the correctness of the subthreshold dynamic model of Lazzaro circuit. Very recent papers are Lohmiller et al. [16] and Akbari et al. [1]. Finally, for classification problems in OpAmp Hopfield type neural networks see [18,19,20].

It seems that our work opens a new topic in analog circuits. It is about accurate determining of WTA output which leads to a new and exact definition of resolution. Our approach is detailed and mathematically rigorous.

Our paper is organized as follows.

Section 2 defines the ${{\mathcal {L}}}$-class of currents. In Sect. 3, Theorem 1 contains sufficient constraints to ensure the subthreshold regime, and also two useful properties of the solution. Section 4 contains the main results. Section 4.2 addresses the upper decision level ${\overline{D}}$, which is found in Theorem 2. Section 4.3 with Theorem 3 finds the lower decision level ${\underline{D}}$. Section 5 proves that, with a certain inequality restriction on parameters, the decision levels are properly positioned ${\overline{D}}>{\underline{D}}$—Theorem 4. Example 1 shows a case when ${\overline{D}}<{\underline{D}}$, while Example 2 confirms Theorem 4. In Section 6, the monotonic behaviors of ${\overline{D}}$, ${\underline{D}}$, $U_{M}$ and $\Omega$ as functions of $\omega$, are proven in Theorem 5. These properties are checked in Example 3 by solving the model equations. Section 7 summarizes the results. Some general conclusion can be found in Section 8. Our proofs imply extensive analytical derivations. Most are relegated to seven Appendices, out of which Appendix A contains the notations used in all the others.

2 The Family ${{\mathcal {L}}}\left( N,I_{M},\Delta \right)$ of Input Currents

The currents to be processed by the WTA machine are grouped in vectors with N components and called “lists” here. If $1,2,\ldots ,N$ are the input terminals, then $I=\left( I_{1},I_{2},\ldots ,I_{N}\right)$ is such a list, whose N currents are simultaneously fed into the circuit. We suppose that the currents are nonnegative, limited by $I_{M}$ and mutually distinct. Their relative distance is at least $\Delta$, a positive “input separation”:

$$\begin{aligned}&0\le I_{j}\le I_{M},\,\,\,j\in \overline{1,N} \end{aligned}$$

(1)

$$\begin{aligned}&\mid I_{j}-I_{k}\mid \ge \Delta >0,\,\,\,j,k\in \overline{1,N},\,\,\,j\ne k \end{aligned}$$

(2)

The above three numbers N, $I_{M}$, and $\Delta$ characterize the set of lists we process. We denote this by ${{\mathcal {L}}}\left( N,I_{M},\Delta \right)$—or simply ${{\mathcal {L}}}$ if confusion is not possible—and refer to it as the ${{\mathcal {L}}}$-family of lists. Certainly, we must have

$$\begin{aligned} \Delta \left( N-1\right) \le I_{M} \end{aligned}$$

(3)

Let us denote by ${{\mathcal {S}}}$ the set of all possible permutations of natural numbers $1,2,\ldots ,N$ denoting the terminals.

For each list $I=\left( I_{1},I_{2},\ldots ,I_{N}\right) \in {{\mathcal {L}}}$, there exists a unique index permutation $\sigma =\left( \sigma _{1},\sigma _{2},\ldots ,\sigma _{N}\right) \in {{\mathcal {S}}}$ such that

$$\begin{aligned} I_{M}\ge I_{\sigma 1}>I_{\sigma 2}>\cdots >I_{\sigma N}\ge 0 \end{aligned}$$

(4)

That is, $\sigma$ arranges the components of I in decreasing order, or we say that the vector I “has the $\sigma$-order.” We write $I^{\sigma }=\left( I_{\sigma 1},I_{\sigma 2},\ldots ,I_{\sigma N}\right)$ for the $\sigma$-ordered vector with the currents in $I=\left( I_{1},I_{2},\ldots ,I_{N}\right)$. If the vector I has no superscript, it is considered by convention as the vector with components in terminal order $I=\left( I_{1},I_{2},\ldots ,I_{N}\right)$. If we write “$I\in {{\mathcal {L}}}$ with order $\sigma \in {{\mathcal {S}}}$,” this will be equivalent to $I^{\sigma }\in {{\mathcal {L}}}$. The largest current $I_{\sigma 1}$ is called “the winner.” When the permutation $\sigma$ is not important, the largest current will be generically denoted by $I_{w}$. Similarly, $I_{\sigma 2}$, the second largest current of the list will be called “the loser”. When $\sigma$ is not important, $I_{\sigma 2}$ will be denoted by $I_{l}$. We also refer to $I_{\sigma 2},I_{\sigma 3},\ldots ,I_{\sigma N}$ as “losers.” This language is used for the output lists of voltages as well. If $I^{\sigma }\in {{\mathcal {L}}}$, (2) becomes

$$\begin{aligned} I_{\sigma j}-I_{\sigma \left( j+1\right) }\ge \Delta >0,\,\,\,j\in \overline{1,N-1} \end{aligned}$$

(5)

From (4) and (5), we immediately derive

$$\begin{aligned} \left( N-j\right) \Delta \le I_{\sigma j}\le I_{M}-\left( j-1\right) \Delta \end{aligned}$$

(6)

Thus, for each $j\in \overline{1,N}$, (6) reveals two special currents $C_{jm}$ and $C_{jM}$, where

$$\begin{aligned} C_{jm}=\left( N-j\right) \Delta ,\,\,\,j\in \overline{1,N} \end{aligned}$$

(7)

and

$$\begin{aligned} C_{jM}=I_{M}-\left( j-1\right) \Delta ,\,\,\,j\in \overline{1,N} \end{aligned}$$

(8)

They depend on N, $I_{M}$, $\Delta$ and rank j only, and do not depend on the particular list $I^{\sigma }$. We will call $C_{jm}$ and $C_{jM}$ “characteristic currents” of family ${{\mathcal {L}}}$, and they will serve an important role below. Thus, for each rank of the descending order, we have

$$\begin{aligned} I_{\sigma j}\in \left[ C_{jm},C_{jM}\right] \end{aligned}$$

(9)

that is, each current in ${\mathcal {L}}$ belongs to a “characteristic interval”.

3 The Subthreshold MOS Model

If $V_{G}$, $V_{S}$, and $V_{D}$ are the MOS terminal voltages, the subthreshold (weak inversion) domain is defined by

$$\begin{aligned} V_{GS}\le V_{T}\,\,\,\,{\mathrm{and}}\,\,\,\,V_{DS}\ge 0 \end{aligned}$$

(10)

where $V_{T}$ is “the threshold voltage.” A common steady-state model of this regime—[2, 15, 30]—takes the gate current as zero and provides the drain-to-source current by

$$\begin{aligned} I_{DS}=I_{0}\left[ \exp \left( -\displaystyle \frac{V_{S}}{V_{t}}\right) -\exp \left( -\displaystyle \frac{V_{D}}{V_{t}}\right) \right] \exp \left( k\displaystyle \frac{V_{G}}{V_{t}}\right) \end{aligned}$$

(11)

Here, $I_{0}$ is “the zero current,” k is “the slope factor,” $k<1$ and $V_{t}$ is the “thermal voltage.” From Fig. 1, we have $I_{j}=I_{T_j}$ and $I_{C}=\displaystyle \sum _{j=1}^{N} I_{T_{j}^{\star }}$, where $I_{T_j}$ and $I_{T_{j}^{\star }}$ are the $I_{DS}$ currents for $T_{j}$ and $T_{j}^{\star }$ transistors, respectively. Thus, we find

$$\begin{aligned} I_{j}=I_{0}\left[ 1-\exp \left( -\displaystyle \frac{U_{j}}{V_{t}}\right) \right] \exp \left( k\displaystyle \frac{V}{V_{t}}\right) ,\,\,\,j\in \overline{1,N} \end{aligned}$$

(12)

$$\begin{aligned} I_{C}=I_{0}\left[ \exp \left( -\displaystyle \frac{V}{V_{t}}\right) -\exp \left( -\displaystyle \frac{V_{DD}}{V_{t}}\right) \right] \displaystyle \sum _{j=1}^{N}\exp \left( k\displaystyle \frac{U_{j}}{V_{t}}\right) \end{aligned}$$

(13)

Here, $V_{DD}$ is the supply voltage, $I_{C}>0$ is the “bias” or “tail” current and V is the common voltage of cells.

The subthreshold conditions (10) for $T_{j}$ and $T_{j}^{\star }$ can be written as

$$\begin{aligned}&0\le V\le {\mathrm{min}}\left\{ V_{DD},V_{T}\right\} \end{aligned}$$

(14)

$$\begin{aligned}&0\le U_{j}\le V_{T}+V,\,\,\,j\in \overline{1,N} \end{aligned}$$

(15)

For further reference, let us group the parameters $I_{0}$, $V_{T}$, k, $V_{t}$ and $V_{DD}$ into a set ${{\mathcal {P}}}=\left\{ I_{0},V_{T},k,V_{t},V_{DD}\right\}$. Let us take an input list $I\in {{\mathcal {L}}}\left( N,I_{M},\Delta \right)$ with $\sigma \in {{\mathcal {S}}}$ its order.

If we denote

$$\begin{aligned} V_{0}\left( I_{\sigma 1}\right) =\displaystyle \frac{V_{t}}{k}\ln \left( \displaystyle \frac{I_{\sigma 1}}{I_{0}}\right) \end{aligned}$$

(16)

, then for V belonging to the following interval,

$$\begin{aligned} V\in \left( V_{0}\left( I_{\sigma 1}\right) ,+\infty \right) \end{aligned}$$

(17)

we can solve (12) for $U_{j}$ and get

$$\begin{aligned} U_{j}=V_{t}\ln \left[ 1-\displaystyle \frac{I_{j}}{I_{0}}\exp \left( -k\displaystyle \frac{V}{V_{t}}\right) \right] ^{-1},\,\,\,\,j\in \overline{1,N} \end{aligned}$$

(18)

By insertion into (13), we obtain

$$\begin{aligned} I_{C}=G\left( V,I\right) \end{aligned}$$

(19)

where

$$\begin{aligned} G\left( V,I\right)= & {} I_{0}\left[ \exp \left( -\displaystyle \frac{V}{V_{t}}\right) -\exp \left( -\displaystyle \frac{V_{DD}}{V_{t}}\right) \right] \nonumber \\&\times \displaystyle \sum _{j=1}^{N}\left[ 1-\displaystyle \frac{I_{j}}{I_{0}}\exp \left( -k\displaystyle \frac{V}{V_{t}}\right) \right] ^{-k} \end{aligned}$$

(20)

is a scalar function defined on $\left( V;I\right) \in \left( V_{0}\left( I_{\sigma 1}\right) ,+\infty \right) \times {{\mathcal {L}}}$.

We see that (18) + (19) is an input–output description of our WTA circuit: for $I=\left( I_{1},I_{2},\ldots ,I_{N}\right)$, and given ${{\mathcal {P}}}$ and $I_{C}>0$, (19) yields the scalar function $V\left( I\right) =V\left( I_{1},I_{2},\ldots ,I_{N}\right)$, and then (18) relates each pair $\left( V\left( I_{1},I_{2},\ldots ,I_{N}\right) ,I_{j}\right)$ with the j-th output $U_{j}\left( I\right) =U_{j}\left( V\left( I_{1},I_{2},\ldots ,I_{N}\right) ,I_{j}\right)$. For simplicity, we write $U_{j}\left( I\right) =U_{j}\left( I_{1},I_{2},\ldots ,I_{N}\right)$ and denote the solution of (18) + (19) by $\left( V;U\right)$.

For a given ${{\mathcal {L}}}\left( N,I_{M},\Delta \right)$ class, let us denote by $\widehat{{\widehat{C}}}$ the vector of maximum characteristic currents

$$\begin{aligned} \widehat{{\widehat{C}}}=\left( C_{1M},C_{2M},\ldots ,C_{NM}\right) \end{aligned}$$

(21)

and by ${\widehat{C}}$, the vector with all components being the minimum characteristic current except for the first component, which is the maximum characteristic current

$$\begin{aligned} {\widehat{C}}=\left( C_{1M},C_{2m},\ldots ,C_{Nm}\right) \end{aligned}$$

(22)

Let us also denote by $U_{M}$ the first component of the solution of (18) + (19) when the input currents are those in ${\widehat{C}}$

$$\begin{aligned} U_{M}=U_{1}\left( {\widehat{C}}\right) \end{aligned}$$

(23)

We are now prepared to prove the results of this section grouped in the following theorem.

Theorem 1

We take the sets ${{\mathcal {P}}}$ and ${{\mathcal {L}}}\left( N,I_{M},\Delta \right)$ and the bias $I_{C}$ under the following assumptions:

$$\begin{aligned}&V_{T}<V_{DD} \end{aligned}$$

(24)

$$\begin{aligned}&I_{0}\le I_{M}\le I_{0}\exp \displaystyle \frac{kV_{T}}{V_{t}} \end{aligned}$$

(25)

$$\begin{aligned}&\displaystyle \frac{I_{0}}{N-1}\le \Delta \le \displaystyle \frac{I_{M}}{N-1} \end{aligned}$$

(26)

$$\begin{aligned}&I_{C}\ge G\left( V_{T},\widehat{{\widehat{C}}}\right) \end{aligned}$$

(27)

Then,

• (a) For a certain $I^{\sigma }\in {{\mathcal {L}}}\left( N,I_{M},\Delta \right)$, the circuit model (18) + (19) has a unique solution $\left( V;U\right) =\left( V,U_{1},U_{2},\ldots ,U_{N}\right) \in \Re \times \Re ^{N}$ that fulfills the subthreshold conditions (14) and (15) and also

  $$\begin{aligned}&V\in \left( V_{0}\left( I_{\sigma 1}\right) ,V_{T}\right] \subset \left( 0,V_{T}\right] \end{aligned}$$

  (28)
  $$\begin{aligned}&U_{M}\ge U_{\sigma 1}>U_{\sigma 2}>\cdots >U_{\sigma N}\ge 0 \end{aligned}$$

  (29)

• (b) For any $I\in {{\mathcal {L}}}\left( N,I_{M},\Delta \right)$, we have

  $$\begin{aligned}&\displaystyle \frac{\partial U_{j}}{\partial I_{p}}\left( I\right) <0,\,\,\mathrm{where}\,\,j,p\in \overline{1,N},\,\,j\ne p,\,\,j\ne \sigma N \end{aligned}$$

  (30)
  $$\begin{aligned}&\displaystyle \frac{\partial U_{j}}{\partial I_{j}}\left( I\right) >0,\,\,\mathrm{if}\,\,j\in \overline{1,N},\,\,j\ne \sigma N \end{aligned}$$

  (31)

Proof

From (9), (16), (24) and (25), we have

$$\begin{aligned} V_{0}\left( \left( N-1\right) \Delta \right) \le V_{0}\left( I_{\sigma 1}\right) \le V_{0}\left( I_{M}\right) \le V_{T}< V_{DD} \end{aligned}$$

(32)

On the interval $\left( V_{0}\left( I_{\sigma 1}\right) ,V_{DD}\right]$, G monotonically decreases with V from $+\infty$ to 0—Fig. 3. Thus, for any $I_{C}\ge 0$. (19) has a unique solution V. From (18), we obtain unique $U_{j}\ge 0$, $j\in \overline{1,N}$, and the order of $U_{j}$ is the same as the order of $I_{j}$, which is in (29). To restrict the V-part of solution to the interval $\left( V_{0}\left( I_{\sigma 1}\right) , V_{T}\right]$ we take $I_{C}\ge G\left( V_{T},I^{\sigma }\right)$—Fig. 3. To make this inequality valid for all $I^{\sigma }\in {{\mathcal {L}}}\left( N,I_{M},\Delta \right)$, we take into account that $I_{\sigma j}\le C_{jM}$ from (9) and that G increases with each $I_{\sigma j}$. Thus, (27) is sufficient for $V\le V_{T}$, proving (28). For the proof of (30) and (31), see Appendix B.

Due to (30) and (31), we infer that the largest component of U when ${\widehat{C}}$ is the input is exactly $U_{M}$—the maximum value of outputs when all of $I\in {{\mathcal {L}}}$ are processed. Thus, (29) is fully proven.

Fig. 3

V is the solution of $I_{C}=G\left( V,I^{\sigma }\right)$, $V\in \left( V_{0}\left( I_{\sigma 1}\right) ,V_{T}\right]$

Going further, the left-hand side of (26) implies $V_{0}\left( \left( N-1\right) \Delta \right) \ge 0$, and from (32), $V_{0}\left( I_{\sigma 1}\right) \ge 0$ such that $V\ge 0$. Thus, the left-hand side of subthreshold condition (14) is fulfilled. Still to be proven is the right-hand side of (15), $U_{j}\le V_{T}+V$, $j\in \overline{1,N}$. This means $U_{\sigma 1}\le V_{T}+V$ and from (18), we derive the condition

$$\begin{aligned} \displaystyle \frac{I_{\sigma 1}}{I_{0}}\exp \left[ \left( 1-k\right) \displaystyle \frac{V}{V_{t}}\right] \le \exp \left( \displaystyle \frac{V}{V_{t}}\right) -\exp \left( -\displaystyle \frac{V_{T}}{V_{t}}\right) \end{aligned}$$

(33)

To avoid unnecessary (and long) details, let us observe that even for the small practical values of $V_{T}$, such as $V_{T}=0.1\,\,Volt$, we have $\exp \left( -\displaystyle \frac{V_{T}}{V_{t}}\right) =0.02136$ (when $V_{t}=0.026V$). Therefore, with reasonable approximation $\exp \left( -\displaystyle \frac{V_{T}}{V_{t}}\right)$—is negligible against $\exp \left( \displaystyle \frac{V}{V_{t}}\right) >1$. This reduces (33) to $V_{0}\left( I_{\sigma 1}\right) \le V$, already met. Thus, the subthreshold conditions (14) and (15) are fulfilled.

Remarks:

• For practical values of $I_{0}$—see [30]—the limitation $I_{0}\le \Delta \left( N-1\right)$ in (26) is totally acceptable.

• Due to assumption $I^{\sigma }\in {{\mathcal {L}}}\left( N,I_{M},\Delta \right)$, the inequality $\Delta \left( N-1\right) \le I_{M}$ in (26) is in fact redundant—see (3).

• From (30) and (31), we see that the $j-$th output voltage increases with the $j-$th input and decreases with other currents. These will be essential for finding the decision levels.

• (30) and (31) imply that an increase in the winner input $I_{\sigma 1}$ leads to an increase in $U_{\sigma 1}$output and to a decrease in all other outputs. This is the Winner Take All effect. In particular, it shows that in (23) $U_{M}$ is the largest voltage.

$\square$

4 Decision Levels

4.1 Generalities: Formulation of Mathematical Problem

Let us consider our WTA in the particular case $N=3$ fed with the infinite number of lists in ${{\mathcal {L}}}\left( 3,I_{M},\Delta \right)$. The first list $I=\left( I_{1},I_{2},I_{3}\right)$ with the (decreasing) order $\sigma =\left( 3,1,2\right)$ arrives at the WTA input—see Fig. 4. The goal is to signal the “winning” rank $\sigma 1=3$ of the largest current $I_{3}$, even in the extreme case when “the loser”—which is the second largest current $I_{1}$—is at the minimum distance $\Delta$, $I_{3}-I_{1}=\Delta$ and $\Delta$ is so small that the two are not distinguishable on the $\left[ 0,I_{M}\right]$ scale.

The WTA circuit translates the reading of the winner rank to the output list of voltages $U=\left( U_{1},U_{2},U_{3}\right)$, which has the same order $\sigma =\left( 3,1,2\right)$—Theorem 1. However, the winner $U_{3}$ is now split from the loser $U_{1}$ by a gap ${\overline{D}}-{\underline{D}}$, which is sufficiently large on the $\left[ 0,U_{M}\right]$ scale.

In fact, we have to have $U_{3}\ge {\overline{D}}>{\underline{D}}\ge U_{1}>U_{2}$. ${\overline{D}}$ is called “the upper decision level” and has the property that it is surpassed only by the winner. Thus, the outputs $\left( U_{1},U_{2},U_{3}\right)$ are compared with ${\overline{D}}$—see Fig. 4—and rank 3 will be the unique winner.

Fig. 4

The input list $\left( I_{1},I_{2},I_{3}\right)$ yields the output list $\left( U_{1},U_{2},U_{3}\right)$; the input list $\left( J_{1},J_{2},J_{3}\right)$ yields the output list $\left( W_{1},W_{2},W_{3}\right)$. The winning ranks are “3” in the first case and “2” in the second, since $U_{3}$ and $W_{2}$ surpass ${\overline{D}}$

Furthermore, ${\underline{D}}$ is called “the lower decision level,” and all the “losers” ($U_{1}$ and $U_{2}$ here) are under it. The distance ${\overline{D}}-{\underline{D}}$ is significant on the scale $\left[ 0,U_{M}\right]$, where $U_{M}$ is the maximum voltage. Returning to Fig. 4, let us consider a second list $\left( J_{1},J_{2},J_{3}\right)$ from ${{\mathcal {L}}}\left( 3,I_{M},\Delta \right)$ applied at the input. Suppose that $J_{2}>J_{3}>J_{1}$ and the winner rank “2” has to be signaled. This is done by obtaining the output voltages $\left( W_{1},W_{2},W_{3}\right)$ arranged as $W_{2}\ge {\overline{D}}>{\underline{D}}\ge W_{3}\ge W_{1}$, where the only rank surpassing the upper decision level ${\overline{D}}$ is “2”, the winner. The losers are below the lower decision level ${\underline{D}}$. The processing should be similar for any list from ${{\mathcal {L}}}\left( 3,I_{M},\Delta \right)$ when using the same decision level ${\overline{D}}$ and ${\underline{D}}$ and the same circuit parameters.

We are now prepared to formulate our general problem of finding ${\overline{D}}$ and ${\underline{D}}$.

Let us consider the WTA circuit in Fig. 1, with N identical MOS devices, the set of parameters ${{\mathcal {P}}}$ and the bias $I_{C}$ and the class ${{\mathcal {L}}}\left( N,I_{M},\Delta \right)$ of input lists. Let also the restrictions (24)–(27) be valid such that for any input list $I=\left( I_{1},I_{2},\ldots ,I_{N}\right)$ in ${{\mathcal {L}}}\left( N,I_{M},\Delta \right)$ with $\sigma$ order

$$\begin{aligned} I_{M}\ge I_{\sigma 1}>I_{\sigma 2}>\cdots >I_{\sigma N}\ge 0 \end{aligned}$$

(34)

the circuit has a subthreshold solution. Moreover, the output list of voltages $U=\left( U_{1},U_{2},\ldots ,U_{N}\right)$ repeats the $\sigma$ order of input. Let us denote by $U^{\sigma }\left( I^{\sigma }\right) =\left( U_{\sigma 1}\left( I^{\sigma }\right) ,U_{\sigma 2}\left( I^{\sigma }\right) ,\ldots ,U_{\sigma N}\left( I^{\sigma }\right) \right)$ the $\sigma$-ordered output. We are looking for two voltage values ${\overline{D}}$—“the upper decision level”—and ${\underline{D}}$—“the lower decision level”—such that

$$\begin{aligned} U_{M}\ge & {} U_{\sigma 1}\left( I^{\sigma }\right) \ge {\overline{D}}>{\underline{D}}>U_{\sigma 2}\left( I^{\sigma }\right) \nonumber \\> & {} U_{\sigma 3}\left( I^{\sigma }\right)>\cdots >U_{\sigma N}\left( I^{\sigma }\right) \ge 0 \end{aligned}$$

(35)

Taking into account that (35) should work with unchanged ${\overline{D}}$ and ${\underline{D}}$, regardless of whether $I\in {{\mathcal {L}}}\left( N,I_{M},\Delta \right)$, $\sigma \in {{\mathcal {S}}}$, we see that ${\overline{D}}$ has to be the smallest possible winner while ${\underline{D}}$ has to be the largest possible loser. Thus, we define

$$\begin{aligned} {\overline{D}}=min\left\{ U_{\sigma 1}\left( I^{\sigma }\right) \,\,{{\mathrm{for\,\,all}}}\,\,I\in {{\mathcal {L}}}\left( N,I_{M},\Delta \right) ,\,\,\sigma \in {{\mathcal {S}}}\right\} \end{aligned}$$

(36)

and

$$\begin{aligned} {\underline{D}}=max\left\{ U_{\sigma 2}\left( I^{\sigma }\right) \,\,{\mathrm{for\,\,all}}\,\,I\in {{\mathcal {L}}}\left( N,I_{M},\Delta \right) ,\,\,\sigma \in {{\mathcal {S}}}\right\} \end{aligned}$$

(37)

In this section, we find concrete lists in ${{\mathcal {L}}}$ that provide outputs ${\overline{D}}$ and ${\underline{D}}$.

4.2 The Upper Decision Level

According to definition (36), we search for the minimum of function $U_{\sigma 1}$ on the set ${{\mathcal {L}}}\left( N,I_{M},\Delta \right)$ of $\Re ^{N}$.

Our result is

Theorem 2

Let ${{\mathcal {P}}}$, $I_{C}$ and ${{\mathcal {L}}}\left( N,I_{M},\Delta \right)$ under hypotheses (24)–(27).

Let

$$\begin{aligned} {\overline{C}}=\left( C_{1m},C_{2m},\ldots ,C_{Nm}\right) \end{aligned}$$

(38)

be the input list from ${{\mathcal {L}}}\left( N,I_{M},\Delta \right)$ consisting of all lower characteristic currents. We denote by

$$\begin{aligned} U\left( {\overline{C}}\right) =\left( U_{1}\left( {\overline{C}}\right) ,U_{2}\left( {\overline{C}}\right) ,\ldots ,U_{N}\left( {\overline{C}}\right) \right) \end{aligned}$$

(39)

its corresponding output.

Then, the upper decision level is the highest voltage in (39), namely,

$$\begin{aligned} {\overline{D}}=U_{1}\left( {\overline{C}}\right) \end{aligned}$$

(40)

Proof

Our idea is to write the fact that a list belongs to the class ${{\mathcal {L}}}\left( N,I_{M},\Delta \right)$ as a set of inequalities. Thus, minimizing $U_{\sigma 1}\left( I^{\sigma }\right)$ on ${{\mathcal {L}}}\left( N,I_{M},\Delta \right)$ becomes a classical optimization problem with inequality constraints.

Let us denote by $I^{\gamma }=\left( I_{\gamma 1},I_{\gamma 2},\ldots ,I_{\gamma N}\right)$ the vector in ${{\mathcal {L}}}\left( N,I_{M},\Delta \right)$, $\gamma \in { {\mathcal {S}}}$ giving the minimum of all $U_{\sigma 1}\left( I^{\sigma }\right)$. The fact that $I^{\gamma }\in {{\mathcal {L}}}\left( N,I_{M},\Delta \right)$ leads to a set of $N+1$ restrictions—see (4) and (5):

$$\begin{aligned} \left\{ \begin{array}{ll} H_{1}=I_{\gamma 1}-I_{M}\le 0\\ H_{2}=I_{\gamma 2}-I_{\gamma 1}+\Delta \le 0\\ H_{3}=I_{\gamma 3}-I_{\gamma 2}+\Delta \le 0\\ \vdots \\ H_{N}=I_{\gamma N}-I_{\gamma \left( N-1\right) }+\Delta \le 0\\ H_{N+1}=-I_{\gamma N}\le 0 \end{array} \right. \end{aligned}$$

(41)

The Kuhn–Tucker necessary conditions for this problem, Luenberger [17], ensure the existence of the nonnegative numbers $\eta _{1},\eta _{2},\ldots ,\eta _{N+1}$ such that

$$\begin{aligned} \nabla U_{\gamma 1}\left( I^{\gamma }\right)&+\eta _{1}\nabla H_{1}\left( I^{\gamma }\right) +\eta _{2}\nabla H_{2}\left( I^{\gamma }\right) +\cdots \nonumber \\&+\eta _{N+1}\nabla H_{N+1}\left( I^{\gamma }\right) =0 \end{aligned}$$

(42)

and

$$\begin{aligned} \eta _{j}H_{j}\left( I^{\gamma }\right) =0,\,\,\,j\in \overline{1,N+1} \end{aligned}$$

(43)

In (42), by $\nabla$, we understand the N-dimensional vector of derivatives with respect to currents. Since $\nabla H_{1}\left( I^{\gamma }\right) =\left( 1,0,0,\ldots ,0\right)$, $\nabla H_{2}\left( I^{\gamma }\right) =\left( -1,1,0,0,\ldots ,0\right)$, $\cdots$, $\nabla H_{N+1}\left( I^{\gamma }\right) =\left( 0,0,\ldots ,0,-1\right)$, the N equalities in (42) are

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial U_{\gamma 1}}{\partial I_{\gamma 1}}\left( I^{\gamma }\right) +\eta _{1}-\eta _{2}=0\\ \displaystyle \frac{\partial U_{\gamma 1}}{\partial I_{\gamma 2}}\left( I^{\gamma }\right) +\eta _{2}-\eta _{3}=0\\ \displaystyle \frac{\partial U_{\gamma 1}}{\partial I_{\gamma 3}}\left( I^{\gamma }\right) +\eta _{3}-\eta _{4}=0\\ \vdots \\ \displaystyle \frac{\partial U_{\gamma 1}}{\partial I_{\gamma N}}\left( I^{\gamma }\right) +\eta _{N}-\eta _{N+1}=0\\ \end{array} \right. \end{aligned}$$

(44)

From (31), Theorem 1, we know that $\displaystyle \frac{\partial U_{\gamma 1}}{\partial I_{\gamma 1}}\left( I^{\gamma }\right) >0$, and adding the fact that $\eta _{1}\ge 0$, from the first equation in (44), we find $\eta _{2}>0$. Then, (43) yields $H_{2}=0$. In the third equation in (44), with $\displaystyle \frac{\partial U_{\gamma 1}}{\partial I_{\gamma 3}}\left( I^{\gamma }\right) <0$ (see Theorem 1) and $\eta _{4}\ge 0$, we obtain $\eta _{3}>0$. Then, $H_{3}=0$. Similarly, we find $H_{4}=0$, $H_{5}=0$, $\cdots$, $H_{N}=0$. Therefore, (41) gives

$$\begin{aligned} I_{\gamma 1}-I_{\gamma 2}=\Delta , I_{\gamma 2}-I_{\gamma 3}=\Delta ,\ldots ,I_{\gamma \left( N-1\right) }-I_{\gamma N}=\Delta \end{aligned}$$

(45)

On the other hand, we know that $I^{\gamma }\in {{\mathcal {L}}}\left( N,I_{M},\Delta \right)$ implies that $I_{\gamma p}$ belongs to a feature interval $I_{\gamma p}\in \left[ C_{pm},C_{pM}\right]$ for all $p\in \overline{1,N}$—see (9). This is equivalent to the existence of $\varepsilon _{p}\in \left[ 0,1\right]$ such that $I_{\gamma p}=C_{pm}+\varepsilon _{p}\left( C_{pM}-C_{pm}\right) =C_{pm}+\varepsilon _{p}B$, where $B=I_{M}-\left( N-1\right) \Delta$ does not depend on p. By using (45), we infer that $\varepsilon _{1}=\varepsilon _{2}=\cdots =\varepsilon _{N}$, and we denote by $\varepsilon$ this common value. Thus,

$$\begin{aligned} I_{\gamma p}=C_{pm}+\varepsilon B \end{aligned}$$

(46)

which shows that the $\gamma$-order is in fact the order of terminals $I^{\gamma }=I$, $I_{p}=C_{pm}+\varepsilon B$, with $\varepsilon \in \left[ 0,1\right]$. Now, we can show—see Appendix C—that the function $\varepsilon \longrightarrow U_{1}\left( I\left( \varepsilon \right) \right) =U_{1}\left( C_{1m}+\varepsilon B,C_{2m}+\varepsilon B,\ldots ,C_{Nm}+\varepsilon B\right)$ increases with $\varepsilon$. Thus, the minimum point of $U_{1}\left( I\right)$ occurs when $\varepsilon =0$, and this minimum point is $I=\left( C_{1m},C_{2m},\ldots ,C_{Nm}\right)$, which is exactly ${\overline{C}}$. $\square$

4.3 The Lower Decision Level

Here, we are looking for the lower decision level ${\underline{D}}$. Definition (37) states that we must find the second-highest output component when all inputs in ${{\mathcal {L}}}\left( N,I_{M},\Delta \right)$ are considered.

Theorem 3

Let ${{\mathcal {P}}}$, $I_{C}$ and ${{\mathcal {L}}}\left( N,I_{M},\Delta \right)$ under hypotheses (24)–(27).

Consider

$$\begin{aligned} {\underline{C}}=\left( C_{1M},C_{2M},C_{3m},\ldots ,C_{Nm}\right) \end{aligned}$$

(47)

a particular list of characteristic currents at the input: all of them are the minimum currents except the first two, which are the maximum currents.

When ${\underline{C}}$ is at the input, let us denote the output by

$$\begin{aligned} U\left( {\underline{C}}\right) =\left( U_{1}\left( {\underline{C}}\right) ,U_{2}\left( {\underline{C}}\right) ,\ldots ,U_{N}\left( {\underline{C}}\right) \right) \end{aligned}$$

(48)

Then, the lower decision level is

$$\begin{aligned} {\underline{D}}=U_{2}\left( {\underline{C}}\right) \end{aligned}$$

(49)

which is the second-largest voltage in (48).

Proof

The method is the same as before, namely, to write the Kuhn–Tucker necessary conditions for the minimum of function $\left( -\right) U_{\sigma 2}\left( I^{\sigma }\right)$ under $H_{1},H_{2},\ldots ,H_{N+1}$ constraints. If $I^{\gamma }=\left( I_{\gamma 1},I_{\gamma 2},\ldots ,I_{\gamma N}\right)$ is the minimum point of this function under the constraints in (41), the same reasoning as in Theorem 2 yields

$$\begin{aligned} \left\{ \begin{array}{ll} -\displaystyle \frac{\partial U_{\gamma 2}}{\partial I_{\gamma 1}}\left( I^{\gamma }\right) +\eta _{1}-\eta _{2}=0\\ -\displaystyle \frac{\partial U_{\gamma 2}}{\partial I_{\gamma 2}}\left( I^{\gamma }\right) +\eta _{2}-\eta _{3}=0\\ -\displaystyle \frac{\partial U_{\gamma 2}}{\partial I_{\gamma 3}}\left( I^{\gamma }\right) +\eta _{3}-\eta _{4}=0\\ \vdots \\ -\displaystyle \frac{\partial U_{\gamma 2}}{\partial I_{\gamma N}}\left( I^{\gamma }\right) +\eta _{N}-\eta _{N+1}=0 \end{array} \right. \end{aligned}$$

(50)

From Theorem 1, we know that $-\displaystyle \frac{\partial U_{\gamma 2}}{\partial I_{\gamma 2}}\left( I^{\gamma }\right) <0$ and $-\displaystyle \frac{\partial U_{\gamma 2}}{\partial I_{\gamma j}}\left( I^{\gamma }\right) >0$ for all other j-s.

Since $\eta _{j}\ge 0$, from the first of (50), we obtain $\eta _{2}>0$, while the third of (50) gives $\eta _{4}>0$. Furthermore, we obtain $\eta _{5}>0,\eta _{6}>0,\ldots ,\eta _{N+1}>0$. Thus, $H_{2}=H_{4}=H_{5}=\cdots =H_{N+1}=0$ and (41) gives $I_{\gamma 1}-I_{\gamma 2}=\Delta ,I_{\gamma 3}-I_{\gamma 4}=\Delta ,I_{\gamma 4}-I_{\gamma 5}=\Delta ,\ldots ,I_{\gamma \left( N-1\right) }-I_{\gamma N}=\Delta ,I_{\gamma N}=0$. Then, we obtain $I_{\gamma \left( N-1\right) }=\Delta ,I_{\gamma \left( N-2\right) }=2\Delta ,\ldots ,I_{\gamma 3}=\left( N-3\right) \Delta$, and, in addition, $I_{\gamma 1}-I_{\gamma 2}=\Delta$. Now, we use the feature intervals $\left[ C_{jm},C_{jM}\right]$ and observe that $I_{\gamma N}=C_{Nm}=0,I_{\gamma \left( N-1\right) }=C_{\left( N-1\right) m},\ldots ,I_{\gamma 3}=C_{3m}$. On the other hand, for $I_{\gamma 1}$ and $I_{\gamma 2}$, there exists $\varepsilon _{1},\varepsilon _{2}\in \left[ 0,1\right]$ such that $I_{\gamma 1}=C_{1M}-\varepsilon _{1}B$, $I_{\gamma 2}=C_{2M}-\varepsilon _{2}B$. Here, $B=I_{M}-\left( N-1\right) \Delta$. From $I_{\gamma 1}-I_{\gamma 2}=\Delta$, we derive $\varepsilon _{1}=\varepsilon _{2}$ and denote by $\varepsilon$ their common value $\varepsilon _{1}=\varepsilon _{2}=\varepsilon$. All of these results show that the maximum point for $U_{\sigma 2}$ is of the form $I^{\gamma }=\left( C_{1M}-\varepsilon B,C_{2M}-\varepsilon B, C_{3m},\ldots ,C_{Nm}\right)$. Since the currents are decreasing, we see that the order $\gamma$ of the maximum point is exactly the terminal order such that the maximum point is $I=(C_{1M}-\varepsilon B,C_{2M}-\varepsilon B,C_{3m},\ldots ,C_{Nm})$. Now, we can prove (Appendix D) that the function $\varepsilon \longrightarrow U_{2}\left( \varepsilon \right) = U_{2}(C_{1M}-\varepsilon B,C_{2M}-\varepsilon B,C_{3m},\ldots ,C_{Nm} )$ decreases with $\varepsilon$. Thus, the maximum value is attained for $\varepsilon =0$, showing that $I={\underline{C}}=\left( C_{1M},C_{2M},C_{3m},\ldots ,C_{Nm}\right)$. $\square$

5 A Gap between ${\overline{D}}$ and ${\underline{D}}$

5.1 A Motivation Example

The previous section has proven that, regardless of which list $I^{\sigma }$ in ${{\mathcal {L}}}\left( N,I_{M},\Delta \right)$ is processed, the highest output $U_{\sigma 1}\left( I^{\sigma }\right)$ always surpasses the upper decision level ${\overline{D}}=U_{1}\left( {\overline{C}}\right)$. The second-highest output $U_{\sigma 2}\left( I^{\sigma }\right)$ always falls beneath the lower decision level ${\underline{D}}=U_{2}\left( {\underline{C}}\right)$. The next example shows that, for certain parameters, the upper decision level can be smaller than the lower decision level, ${\underline{D}}>{\overline{D}}$. The output voltages do not fulfill (35). Consequently, the circuit cannot separate the highest output.

Example 1

We take $N=10$, $I_{0}=10^{-18}\,\,Amp$, $I_{C}=2\times 10^{-15}I_{0}$, $I_{M}=10^{11}I_{0}$, $\Delta =\displaystyle \frac{0.5}{9}I_{M}$, $V_{T}=1V$, $k=0.7$, $V_{t}=0.026V$, and $V_{DD}=1.5V$. The list ${\overline{C}}=\left( C_{1m},C_{2m},C_{3m},\ldots ,C_{Nm}\right)$ in Theorem 2 is ${\overline{C}}=10^{11}\times \displaystyle \frac{1}{9}\times I_{0}\times \left( 4.5,4,3.5,3,\ldots ,0.5,0\right)$.

By numerically solving the 11-equation system in (18) + (19), we find

$$\begin{aligned} U\left( {\overline{C}}\right)= & {} \left( U_{1}\left( {\overline{C}}\right) ,U_{2}\left( {\overline{C}}\right) ,\ldots ,U_{10}\left( {\overline{C}}\right) \right) \nonumber \\= & {} \left( 15.37,13.14,\ldots ,0\right) {\mathrm{in}}\,\,\,{\mathrm{mV}} \end{aligned}$$

From here, we find ${\overline{D}}=U_{1}\left( {\overline{C}}\right) =15.37\,\,\,\mathrm{mV}$.

Furthermore, the list ${\underline{C}}=\left( C_{1M},C_{2M},C_{3m},\ldots ,C_{Nm}\right)$ in Theorem 3 is

$$\begin{aligned} {\underline{C}}=10^{11}\times \displaystyle \frac{1}{9}\times I_{0}\times \left( 9,8.5,3.5,3,\ldots ,0\right) \end{aligned}$$

Solving (18) + (19) with these input currents, we obtain

$$\begin{aligned} U\left( {\underline{C}}\right)= & {} \left( U_{1}\left( {\underline{C}}\right) ,U_{2}\left( {\underline{C}}\right) ,\ldots ,U_{10}\left( {\underline{C}}\right) \right) =\\= & {} \left( 40.15,35.31,\ldots \right) \,\,\,{\mathrm{mV}} \end{aligned}$$

From here, ${\underline{D}}=U_{2}\left( {\underline{C}}\right) =35.31{\mathrm{mV}}$, which is larger than the ${\overline{D}}=15.37\,\,{\mathrm{mV}}$ obtained above. The wrong order means that the circuit is not a rank selector.

5.2 Sufficient Conditions for a Gap between ${\overline{D}}$ and ${\underline{D}}$

This paragraph finds additional restrictions such that the decision levels are in good order. We need the following notation:

$$\begin{aligned} F\left( \Delta \right)= & {} I_{0}^{\left( 1+\displaystyle \frac{1}{k}\right) }\Delta ^{-\displaystyle \frac{1}{k}}\left( N-1\right) ^{-\displaystyle \frac{1}{k}}\left[ \Delta ^{-k}I_{M}^{k}+\left( N-1\right) ^{k}\displaystyle \sum _{j=1}^{N-1} j^{\left( -k\right) }\right] \end{aligned}$$

(51)

The result is in the next Theorem.

Theorem 4

With all assumptions in (24)–(27) in addition to

$$\begin{aligned} I_{C}>F\left( \Delta \right) , \end{aligned}$$

(52)

we have

$$\begin{aligned} {\overline{D}}>{\underline{D}} \end{aligned}$$

(53)

For the Proof, see Appendix E.

The theorem stipulates that a sufficiently large bias current pushes the higher decision level ${\overline{D}}$ above the lower decision level ${\underline{D}}$. It creates a “gap” interval $\left[ {\underline{D}},{\overline{D}}\right]$ where none of the output voltages are placed. The lower bound $F\left( \Delta \right)$ of $I_{C}$ provided by the result is higher when the processed lists have higher currents and/or smaller separations. Indeed, due to Theorems 2 and 3, the above result implies that any $I^{\sigma }\in {{\mathcal {L}}}\left( N,I_{M},\Delta \right)$ at the input will produce a list $U^{\sigma }$ of output voltages such that

$$\begin{aligned} U_{M}\ge U_{\sigma 1}\ge {\overline{D}}>{\underline{D}}\ge U_{\sigma 2}>U_{\sigma 3}>\cdots >U_{\sigma N} \end{aligned}$$

(54)

Thus, the fact that $U_{\sigma 1}$ is the only component above the upper decision level ${\overline{D}}$ signals that the same rank input component $I_{\sigma 1}$ is the highest one of the $I^{\sigma }$ lists. The WTA circuit reaches its goal. In addition, “the gap interval” $\left[ {\underline{D}},{\overline{D}}\right]$ measures the level of error in detecting $I_{\sigma 1}$. A larger gap means a smaller error. Example 2 makes the above facts clearer.

Example 2

The ${{\mathcal {L}}}$ family has $N=5$, $I_{M}=100\,\,{\mathrm{nA}}$, $\Delta =2.5\,\,{\mathrm{nA}}$. The parameters in ${{\mathcal {P}}}$ are $I_{0}=10^{-18}\,\,{\mathrm{Amps}}$, $k=0.7$, $V_{T}=1\,\,{\mathrm{Volt}}$, $V_{t}=26\,\,{\mathrm{mV}}$, and $V_{DD}=1.5\,\,{\mathrm{Volt}}$.

Since $I_{M}=10^{-7}\in \left[ I_{0},I_{0}\times 10^{11.71}\right]$ (25) is fulfilled. Also, $\Delta =2.5\times 10^{-9}\in \left[ I_{0}/4,10^{-7}/4\right]$, i.e., (26) is valid. We also find $G\left( V_{T},\widehat{{\widehat{C}}}\right) =I_{0}\times 10^{-16}$ and $F\left( \Delta \right) =I_{0}\times 10^{-6.58}$. We choose $I_{C}=I_{0}\times 10^{-6}\,\,Amp$, which fulfils both (27) and (52).

Next, we compute the decision levels. For ${\overline{D}}$, we need the input ${\overline{C}}=\left( C_{1m},C_{2m},C_{3m},C_{4m},C_{5m}\right) =\left( 10,7.5,5,2.5,0\right)$ in ${\mathrm{nA}}$. After numerically solving (18) + (19), we find $U\left( {\overline{C}}\right) =\left( 709,72,24,5,0\right)$ in $\mathrm{mV}$. According to Theorem 2, ${\overline{D}}$ is the largest voltage in this list ${\overline{D}}=709\,\,{\mathrm{mV}}$. Theorem 3 states that for ${\underline{D}}$, we need the input ${\underline{C}}=\left( C_{1M},C_{2M},C_{3m},C_{4m},C_{5m}\right) =\left( 100,97.5, 5,2.5,0\right)$. After solving (18)+(19), we obtain $U\left( {\underline{C}}\right) =\left( 727,95,52,28,0\right)$, and the second largest voltage is ${\underline{D}}=95\,\,{\mathrm{mV}}$; see Fig. 5.

Finally, we solve for ${\widehat{C}}=\left( C_{1M},C_{2m},C_{3m},C_{4m},C_{5m}\right) =\left( 100,7.5,5,2.5,0\right)$ and find the largest possible voltage $U_{M}=830\,\,{\mathrm{mV}}$. At this stage, our circuit is able to process any list in ${{\mathcal {L}}}\left( 5,100\,\,{\mathrm{nA}},2.5\,\,{\mathrm{nA}}\right)$. On an output scale of $830\,\,{\mathrm{mV}}$, each winner will surpass ${\overline{D}}=709\,\,{\mathrm{mV}}$, while the losers will be below ${\underline{D}}=95\,\,{\mathrm{mV}}$. Once we have designed “the machine,” let us choose to process the input list $I=\left( 45,10,50,5,47.5\right)$ written in the terminal order and in ${\mathrm{nA}}$. The list in decreasing order is $I^{\sigma }=\left( I_{3},I_{5},I_{1},I_{2},I_{4}\right)$. Clearly, it belongs to the family ${{\mathcal {L}}}\left( 5,100,2.5\right)$, since $I_{\sigma 1}=50<I_{M}=100$ and the minimum distance between currents is $2.5\,\,{\mathrm{nA}}$, which is exactly $\Delta$. By numerically solving equations (18) + (19), where $\frac{I_{C}}{I_{0}}=10^{-6}$ as above, we obtain $U\left( I\right) =\left( 60,6,794,3,78\right)$ in ${\mathrm{mV}}$. We see first that the voltages exhibit the same order of amplitudes as the currents $\sigma =\left( \sigma 1,\sigma 2,\sigma 3,\sigma 4,\sigma 5\right) =\left( 3,5,1,2,4\right)$, $U^{\sigma }=\left( U_{3},U_{5},U_{1},U_{2},U_{4}\right)$. Figure 5 separately shows the input currents and the output voltages. Thus, a difficult “reading” of the largest current of $50\,\,{\mathrm{nA}}$ against loser $47.5\,\,{\mathrm{nA}}$ is transformed through facile discernment of $794\,\,{\mathrm{mV}}$ of the winner against $78\,\,{\mathrm{mV}}$ of the loser.

Fig. 5

Example 2. $N=5$, $I_{M}=100\,\,{\mathrm{nA}}$, $\Delta =2.5\,\,{\mathrm{nA}}$, $\omega =1/40$. Left: input currents in ${\mathrm{nA}}$ on the $\left[ 0,100\right]$ scale; right: output voltages in mV on the $\left[ 0,830\right]$ scale, ${\overline{D}}-{\underline{D}}=614\,\,{\mathrm{mV}}$

6 Input and Output Resolutions and their Connection

The family ${{\mathcal {L}}}\left( N,I_{M},\Delta \right)$ contains lists of currents on the $\left[ 0,I_{M}\right]$ scale, whose cramming is measured by $\Delta$. The difference between the largest and the second largest current of any list is at least $\Delta$. The coefficient $\omega$ defined by

$$\begin{aligned} \omega =\displaystyle \frac{\Delta }{I_{M}} \end{aligned}$$

(55)

which will be called “the input resolution.” When $\omega$ is very small, perceiving $I_{w}$ (the winner) and $I_{l}$ (the loser) as distinct from each other is difficult and prone to error. On the output side, the voltages are similarly arranged on the $\left[ 0,U_{M}\right]$ scale—see (54). However, the positions of the w and l ranks are now controlled by the decision levels ${\overline{D}}$ and ${\underline{D}}$:

$$\begin{aligned} U_{M}\ge U_{w}\ge {\overline{D}}>{\underline{D}}\ge U_{l}>0 \end{aligned}$$

(56)

${\overline{D}}$ and ${\underline{D}}$ do not change when a new list arrives. Under constraints in (24)–(27) and (52), ${\overline{D}}$ and ${\underline{D}}$ are fixed by Theorems 2 and 3. Each winner of each list surpasses ${\overline{D}}$. Each loser of each list in ${{\mathcal {L}}}\left( N,I_{M},\Delta \right)$ falls under ${\underline{D}}$. ${\overline{D}}-{\underline{D}}$ will be called “output separation,” and its ratio to the maximum output voltage $U_{M}$ will be denoted by $\Omega$ and called “the output resolution”:

$$\begin{aligned} \Omega =\displaystyle \frac{{\overline{D}}-{\underline{D}}}{U_{M}} \end{aligned}$$

(57)

The similarity between $\omega$ at input and $\Omega$ at output is complete. Both of them indicate how much of the “reading scale” is taken up by the smallest possible size difference between the w and l ranks. The circuit is effective if the $\Omega /\omega$ ratio is larger than 1—in other words, “if it amplifies” the resolution of the input list. The large values for $\Omega /\omega$ mean that the winning rank is highly distinct. To understand the WTA input-output mechanism, we study the function $\Omega (\omega )$ when $I_{M}$ and $I_{C}$ are unchanged. For clarity, we will translate the results obtained so far in terms of $\omega$, where $\omega =\Delta /I_{M}$. Thus, the family ${{\mathcal {L}}}\left( N,I_{M},\omega I_{M}\right)$ provides the currents for the model (18) + (19), which also contains $I_{C}$ and the set ${{\mathcal {P}}}$ of parameters. The hypotheses (24) and (25) are the same. With $\Delta =\omega I_{M}$, (26) will be replaced by

$$\begin{aligned} \omega _{0}\le \omega \le \displaystyle \frac{1}{N-1} \end{aligned}$$

(58)

where $\omega _{0}=I_{0}/I_{M}\left( N-1\right)$.

We denote ${\widehat{{\widehat{C}}}}\left( \omega \right) =\left( C_{1M},C_{2M},C_{3M},\ldots ,C_{NM}\right)$ where $C_{jM}=I_{M}-\left( j-1\right) \omega I_{M}$, as in (8). Additionally, below we use ${\widehat{C}}\left( \omega \right) =(C_{1M},C_{2m},C_{3m},\ldots ,C_{Nm})$, ${\overline{C}}\left( \omega \right) =\left( C_{1m},C_{2m},C_{3m},\ldots ,C_{Nm}\right)$, ${\underline{C}}\left( \omega \right) =\left( C_{1M},C_{2M},C_{3m},\ldots ,C_{Nm}\right)$, where $C_{jm}=\left( N-j\right) \omega I_{M}$ as in (7).

To gather together the assumptions (27) and (52), we observe first that $G(V_{T},{\widehat{{\widehat{C}}}}\left( \omega \right) )$ from (20) and $F\left( \omega I_{M}\right)$ from (51) both decrease with $\omega$. This means that both (27) and (52) are fulfilled on $\left[ \omega _{0},1/N-1\right]$ if we take $\omega =\omega _{0}$. Since $\omega _{0}$ is usually a very small number, we are led to very large values for $I_{C}$. Therefore, we choose a $\omega _{min}\in \left( \omega _{0},1/N-1\right)$ and perform our study on the $\left[ \omega _{min},1/N-1\right]$ interval for $\omega$. Then, the following inequality

$$\begin{aligned} I_{C}\ge I_{C0}=max\left\{ G\left( V_{T},{\widehat{{\widehat{C}}}}\left( \omega _{min}\right) \right) ;F\left( \omega _{min}I_{M}\right) \right\} \end{aligned}$$

(59)

is sufficient to fulfill (27) and (52).

Let $C\left( \omega \right)$ be a generic notation for the particular lists ${\widehat{{\widehat{C}}}}\left( \omega \right) ,{{\widehat{C}}}\left( \omega \right) ,{\overline{C}}\left( \omega \right) ,{\underline{C}}\left( \omega \right)$. If $C\left( \omega \right)$ is applied at input, the model (18)+(19) furnishes the solution $U\left( C\left( \omega \right) \right) =\left( U_{1}\left( C\left( \omega \right) \right) ,U_{2}\left( C\left( \omega \right) \right) ,\ldots ,U_{N}\left( C\left( \omega \right) \right) \right)$ with properties (28)–(31) and (53). We are interested in studying the particular functions:

$$\begin{aligned} \begin{array}{ll} {\overline{D}}\left( \omega \right) =U_{1}\left( {\overline{C}}\left( \omega \right) \right) ,\,\,\,{\mathrm{see\,\,\,Theorem}}\,\,\,2\\ {\underline{D}}\left( \omega \right) =U_{2}\left( {\underline{C}}\left( \omega \right) \right) ,\,\,\,{\mathrm{see\,\,\,Theorem}}\,\,\,3\\ U_{M}\left( \omega \right) =U_{1}\left( {{\widehat{C}}}\left( \omega \right) \right) \\ \Omega \left( \omega \right) =\left[ {\overline{D}}\left( \omega \right) -{\underline{D}}\left( \omega \right) \right] /U_{M}\left( \omega \right) \,\,\,\mathrm{positive\,\,\,by\,\,\,\,Theorem}\,\,\,4 \end{array} \end{aligned}$$

The results are in the following Theorem:

Theorem 5

Under the restrictions (24), (25), (59) and for any $\omega \in \left[ \omega _{min},1/N-1\right]$ where $\omega _{min}>\omega _{0}$, we have

$$\begin{aligned}&\displaystyle \frac{d{\overline{D}}\left( \omega \right) }{d\omega }>0 \end{aligned}$$

(60)

$$\begin{aligned}&\displaystyle \frac{d{\underline{D}}\left( \omega \right) }{d\omega }<0 \end{aligned}$$

(61)

$$\begin{aligned}&\displaystyle \frac{d U_{M}\left( \omega \right) }{d\omega }<0 \end{aligned}$$

(62)

$$\begin{aligned}&\displaystyle \frac{d\Omega \left( \omega \right) }{d\omega }>0 \end{aligned}$$

(63)

There always exists $\omega _{1}\in \left[ \omega _{min},1/N-1\right)$ such that on $\left[ \omega _{1},1/N-1\right]$ we have

$$\begin{aligned} \displaystyle \frac{\Omega \left( \omega \right) }{\omega }>1 \end{aligned}$$

(64)

Proof

(60)–(62) are proven in Appendix F, while (63) derives readily from them. (64) is proven in Appendix G. This ends the proof. $\square$

(60) and (61) show that with $\omega$ increasing (i.e., by processing less crammed lists), the upper decision level becomes larger, while the lower decision level decreases. Thus, the winning rank detaches clearly from the other ranks. Moreover, (63) shows that the proportion of the $\left[ 0,U_{M}\right]$ scale filled by the $\left[ {\underline{D}},{\overline{D}}\right]$ gap is larger for less crowded currents. Another encouraging fact is the certainty of existence of the interval $\left[ \omega _{1},1/N-1\right]$ where the circuit amplifies the resolution—see (64). Although at this point we cannot theoretically evaluate $\omega _{1}$, the next example will show that its value can be few orders of magnitude beneath $1/N-1$. Certainly, apart from $\Omega$ being large enough, the winner identification needs a maximum voltage $U_{M}$ as high as possible. Although the result in (62) seems to endanger the $U_{M}$ value, the next example shows that the variation of $U_{M}$ with $\omega$ is very small. The example will also verify the dependencies described in Theorem 5.

Example 3

Let us take a WTA with $N=100$ cells and characteristic parameters in Table 1. Consider 3 values of $I_{M}$, $10\,\,\mathrm{nA}$, $100\,\,{\mathrm{nA}}$, and $1\,\,{\mathrm{\mu A}}$. They satisfy (24), i.e., $10^{-18}\le I_{M}\le 10^{-2.95}$. The $\omega _{0}$ computed for $I_{M}=10\,\,{\mathrm{nA}}$ is $\displaystyle \frac{1}{99}10^{-10}$. We choose $\omega _{min}=10^{-5}$. Next, we observe that $G\left( V_{T},{\widehat{{\widehat{C}}}}\left( \omega _{min}\right) \right)$ increases with $I_{M}$. To choose an $I_{C}$ valid for any of the three values of $I_{M}$, we use $I_{M}=1\,\,{\mathrm{\mu A}}$ for the maximum of $G\left( V_{T},{\widehat{{\widehat{C}}}}\left( \omega _{min}\right) \right)$ and find it to be $10^{-31.2}$. On the other hand, $F\left( \omega _{min} I_{M}\right)$ decreases with $I_{M}$ such that, for its maximum we use $I_{M}=10\,\,{\mathrm{nA}}$ and obtain $10^{-21.28}$ for the largest value. According to (59), we should have $I_{C}\ge I_{C0}=10^{-21.28}$. We choose $I_{C}=10^{-20}=I_{0}\times 10^{-2}$. Inside the interval $\left[ \omega _{min},\omega _{max}\right]$ where $\omega _{max}=\frac{1}{N-1}=\frac{1}{99}$, we choose 4 values of $\omega$, namely, $10^{-5}\simeq 10^{-3}\omega _{max}$, $10^{-4}\simeq 10^{-2}\omega _{max}$, $10^{-3}\simeq 10^{-1}\omega _{max}$ and $10^{-2}\simeq \omega _{max}$. Next, for each of the 12 pairs $\left( \omega ;I_{M}\right)$, we numerically solve the 101 equations in (18) + (19) three times: with currents in ${\overline{C}}$ to obtain ${\overline{D}}$, with ${\underline{C}}$ to obtain ${\underline{D}}$ and with ${{\widehat{C}}}$ to obtain $U_{M}$. Then, $\Omega$ and $\Omega /\omega$ are computed. See Table 1 for the results.

The monotonic behaviors of ${\overline{D}}$, ${\underline{D}}$, $U_{M}$ and $\Omega$ with respect to $\omega$ are confirmed. We also observe that, for each $I_{M}$, the decrease in $U_{M}$ with $\omega$ is insignificant. Since $\Omega /\omega >1$ for all input resolutions we have considered, the value of $\omega _{1}$ equals $\omega _{min}=10^{-5}$. Surprisingly, the amplification ratio $\Omega /\omega$ decreases steeply with $\omega$, at least for the interval $\left[ \omega _{min},\omega _{max}\right]$ chosen here. The minimum value is approximately 80 at $\omega _{max}$ and reaches large values of $14\times 10^{3}$, $23\times 10^{3}$ and $31\times 10^{3}$ at $\omega _{min}=10^{-5}$ (for the three $I_{M}$, respectively). Indeed, the fact that the crammed lists are processed so efficiently seems to be favorable for applications. On the other hand, in practice it can be important that the winner in output list (located in $\left[ {\overline{D}},U_{M}\right]$ interval) should be as close as possible to $U_{M}$. Unfortunately, the lower $\omega$ the lower $\Omega$. Thus, a balance between $\Omega /\omega$ and $\Omega$ is necessary. The matter merits theoretical investigation.

Table 1 Example 3: $N=100$, $I_{0}=10^{-18}$, $k=0.9$, $V_{T}=1V$, $V_{t}=0.026V$, $V_{DD}=1.5V$, $I_{C}=10^{-2}I_{0}$, $\omega _{max}=1/N-1$, $\Omega \%=\displaystyle \frac{{\overline{D}}-{\underline{D}}}{U_{M}}100$, ${\overline{D}}\%=\displaystyle \frac{{\overline{D}}}{U_{M}}100$

Based on the results in Table 1, Fig. 6 explains, (for the case $I_{M}=100\,\,{\mathrm{nA}}$) how decision levels divide the range $\left[ 0,U_{M}\right]$. With the increase in $\omega$, the winner placed in the interval $\left[ {\overline{D}},U_{M}\right]$ is pushed toward its maximum value $U_{M}$. The 99 losers from the interval $\left[ 0,{\underline{D}}\right]$ are increasingly crowded with $\omega$, below $18\%$ of $U_{M}$.

Thus, for the ideal case at $\omega \simeq \omega _{max}$, the gap between the winner and losers is $81\%$, and the winner is at its highest level between $99\%$ and $100\%$. The worst case here, at $\omega =10^{-3}\omega _{max}$, has a gap of $23\%$, and the winner is at $67\%$.

Fig. 6

$N=100$, $I_{M}=100\,\,{nA}$, $\omega _{min}=10^{-5}$, $\omega _{max}=1/99$. Distribution of decision levels: $\left[ {\overline{D}},U_{M}\right]$—the winners placement, $\left[ {\underline{D}},{\overline{D}}\right]$—the splitting gap (output separation), $\left[ 0,{\underline{D}}\right]$—the losers placement. The output resolution $\Omega =\left( {\overline{D}}-{\underline{D}}\right) /U_{M}=23, 43, 62, 81$% for the four cases

The fact that the decision levels computed at $\omega _{min}$ work for the entire interval $\left[ \omega _{min},\omega _{max}\right]$ gives a certain flexibility for design. Referring to the example in Fig. 6, the interval of resolution $Q=\left[ 10^{-5},1/99\right]$ can be processed with ${\overline{D}}=67\%$, ${\underline{D}}=44\%$ and $\Omega =23\%$, all computed with $\omega =10^{-5}$. These performances can partially improve if we divide Q into the two intervals $Q^{a}=\left[ 10^{-5},10^{-3}\right]$ and $Q^{b}=\left[ 10^{-3},1/99\right)$. For $Q^{a}$, we use the above parameters computed with $\omega =10^{-5}$. For $Q^{b}$, we compute ${\overline{D}}=89\%$, ${\underline{D}}=27\%$ and $\Omega =62\%$ with $\omega =10^{-3}$. Thus, if we pay the price of changing ${\overline{D}}$ and ${\underline{D}}$ at an intermediate point, the lists from the second interval are processed much more accurately.

7 Summary of Results

The following “design scenario” summarizes the paper results:

Give the circuit in Fig. 1 with 2N identical MOS having the parameters $I_{0}$, $V_{T}$, k, $V_{t}$, $V_{DD}$. Give an infinite set ${{\mathcal {L}}}$ of input currents with N, $I_{M}$ and $\omega$ be known.

We aim to solve the following three issues:

• 1. to establish two levels ${\overline{D}}$ and ${\underline{D}}$ of the output voltages in such a way that for any list in ${{\mathcal {L}}}$ at the input, the first two largest outputs $U_{w}$ and $U_{l}$ are split by ${\overline{D}}$ and ${\underline{D}}$: $U_{M}\ge U_{w}\ge {\overline{D}}>{\underline{D}}\ge U_{l}\ge 0$;

• 2. to be able to control ${\overline{D}}$ and ${\underline{D}}$ such that ${\overline{D}}$ is as close as possible to the maximum voltage $U_{M}$, and the output resolution $\Omega =\left( {\overline{D}}-{\underline{D}}\right) /U_{M}$ increases with its input correspondent $\omega _{min}$;

• 3. to find consistent conditions for operating in subthreshold for all MOS

We found, respectively, the following answers:

• 1. ${\overline{D}}=U_{1}\left( {\overline{C}}\right)$ from (40), ${\underline{D}}=U_{2}\left( {\underline{C}}\right)$ from (49) and $U_{M}=U_{1}\left( {\widehat{C}}\right)$ from (23) where ${\overline{C}}$, ${\underline{C}}$ and ${\widehat{C}}$ are three special lists in ${{\mathcal {L}}}$;

• 2. ${\overline{D}}>{\underline{D}}$ if (52) is met; $\Omega$ monotonically increases with $\omega$—see (63); $\Omega /\omega >1$—see (64). Examples show that $\Omega /\omega$ is much higher than 1.

• 3. Mild restrictions (24)-(27) and (52) on $V_{T}$, $V_{DD}$, $I_{M}$, $\Delta =\omega I_{M}$ and $I_{C}$;

8 Conclusion

The above article considers the WTA subthreshold circuit as a rank separator and claims originality both as a subject and as a mathematical treatment. It deals with finding two levels of decision that separate the winner from losers and that depend semi-analytically on the input parameters. This is found by the analytical solution of two optimization problem with inequality constraints. A performance criterion of design interest is established. It is about the correspondence between the density of the input list of currents (“input resolution”) and the density of the output list voltages (“output resolution”). Detailed numerical examples motivate and verify the theory.

To conclude, a new idea for WTA output control was presented. It is about finding two levels that separate the winner from losers and allow the precise design and the calculation of the split performance. For this purpose, the paper formulates and rigorously solves two optimization problems with inequality constraints.

Appendices

Appendix A

For proving our Theorems, we use a simpler form for writing the models (18) and (19). It requires the following notations:

$i_{j}=\displaystyle \frac{I_{j}}{I_{0}}$, $i_{C}=\displaystyle \frac{I_{C}}{I_{0}}$, $i=\left( i_{1},i_{2},\ldots ,i_{N}\right)$, $i_{\sigma j}=\displaystyle \frac{I_{\sigma j}}{I_{0}}$, $i^{\sigma }=\left( i_{\sigma 1},i_{\sigma 2},\ldots ,i_{\sigma N}\right)$, $i_{M}=\displaystyle \frac{I_{M}}{I_{0}}$, $\delta =\displaystyle \frac{\Delta }{I_{0}}$, $c_{jm}=\displaystyle \frac{C_{jm}}{I_{0}}=\left( N-j\right) \delta$, $c_{jM}=\displaystyle \frac{C_{jM}}{I_{0}}=i_{M}-\left( j-1\right) \delta$, ${\overline{c}}=\left( c_{1m},c_{2m},c_{3m},\ldots ,c_{Nm}\right)$, ${\underline{c}}=\left( c_{1M},c_{2M},c_{3m},\ldots ,c_{Nm}\right)$.

$v=\exp \left( \displaystyle \frac{V}{V_{t}}\right)$, $x=\exp \left( -k\displaystyle \frac{V}{V_{t}}\right) =v^{-k}$, $u_{j}=\exp \left( \displaystyle \frac{U_{j}}{V_{t}}\right)$, $d=\exp \left( \displaystyle \frac{V_{DD}}{V_{t}}\right)$, $v_{T}=\exp \left( \displaystyle \frac{V_{T}}{V_{t}}\right)$, $u=\left( u_{1},u_{2},\ldots ,u_{N}\right)$, $u^{\sigma }=\left( u_{\sigma 1},u_{\sigma 2},\ldots ,u_{\sigma N}\right)$.

If $a\ne 0$ is a real number, we assign $sgn\left( a\right) =+1$ when $a>0$ and $sgn\left( a\right) =-1$ when $a<0$.

With

$$\begin{aligned} g\left( x,i\right) =\left( x^{1/k}-d^{-1}\right) \displaystyle \sum _{j=1}^{N}\left( 1-i_{j}x\right) ^{-k} \end{aligned}$$

(A1)

our model (18) + (19) becomes

$$\begin{aligned}&u_{j}=\left( 1-i_{j}x\right) ^{-1},\,\,j\in \overline{1,N} \end{aligned}$$

(A2)

$$\begin{aligned}&i_{C}=g\left( x,i\right) \end{aligned}$$

(A3)

The properties $V\in \left( V_{0}\left( I_{\sigma 1}\right) ,V_{T}\right]$ from (28) and $V_{T}<V_{DD}$ from (24) translate into

$$\begin{aligned} d^{-k}\le v^{-k}_{T}\le x<i^{-1}_{\sigma 1}\le i^{-1}_{j},\,\,\,j\in \overline{1,N} \end{aligned}$$

(A4)

where $i_{\sigma 1}$ is the highest of $i_{j}$.

In (A4), x is the solution of the scalar equation (A3). Our subsequent proofs need its derivatives. We differentiate both parts of (A3) with respect to $i_{p}$, $p\in \overline{1,N}$, take into account that $i_{C}$ is constant and obtain

$$\begin{aligned} \displaystyle \frac{\partial x}{\partial i_{p}}=-kx\left( x^{1/k}-d^{-1}\right) \left( 1-xi_{p}\right) ^{\left( -k-1\right) }/S \end{aligned}$$

(A5)

where

$$\begin{aligned} S=S_{1}+S_{2} \end{aligned}$$

(A6)

and

$$\begin{aligned}&S_{1}=\displaystyle \sum _{j=1}^{N}\displaystyle \frac{1}{k}x^{\left( \displaystyle \frac{1}{k}-1\right) }\left( 1-xi_{j}\right) ^{\left( -k\right) } \end{aligned}$$

(A7)

$$\begin{aligned}&S_{2}=\displaystyle \sum _{j=1}^{N}ki_{j}\left( x^{1/k}-d^{-1}\right) \left( 1-xi_{j}\right) ^{-k-1} \end{aligned}$$

(A8)

Appendix B

Here, we prove (30) and (31) in Theorem 1.

For the input currents $I_{1},I_{2},\ldots ,I_{N}$, let $U_{1},U_{2},\ldots ,U_{N}$ be the output voltages. With notations from Appendix A, we have $\displaystyle \frac{\partial u_{j}}{\partial i_{p}}=\displaystyle \frac{I_{0}}{V_{t}}\left( \exp \displaystyle \frac{U_{j}}{V_{t}}\right) \displaystyle \frac{\partial U_{j}}{\partial I_{p}}$ such that $sgn\left( \displaystyle \frac{\partial U_{j}}{\partial I_{p}}\right) =sgn\left( \displaystyle \frac{\partial u_{j}}{\partial i_{p}}\right)$ when $u_{j}\ne 0$.

Thus, for any $j\not \in \sigma N$, by using (A2), we obtain

$$\begin{aligned} sgn\displaystyle \frac{\partial U_{j}}{\partial I_{p}}=sgn\displaystyle \frac{\partial }{\partial i_{p}}\left( xi_{j}\right) =sgn E_{jp} \end{aligned}$$

(B1)

where

$$\begin{aligned} E_{jp}=\displaystyle \frac{\partial i_{j}}{\partial i_{p}}S-ki_{j}\left( x^{1/k}-d^{-1}\right) \left( 1-xi_{p}\right) ^{-k-1} \end{aligned}$$

(B2)

Here, x is the solution of (A3) with currents $i_{1},i_{2},\ldots ,i_{N}$, and S is that in (A6)–(A8).

For $j\ne p$ and $j\ne \sigma N$, (B2) immediately gives $E_{jp}=0$. Thus, (30) comes from (B1).

For $j=p$, again from (B2) and by using (A6), we obtain $E_{jj}>0$. Thus, (31) comes from (B1) with $j=p$.

Appendix C

Here, we show that the function $\varepsilon \longrightarrow U_{1}\left( C_{1m}+\varepsilon B,C_{2m}+\varepsilon B,\cdots \right)$ (from the proof of Theorem 2) is monotonically increasing. With $A=\frac{\partial U_{1}}{\partial \varepsilon }(C_{1m}+\varepsilon B,C_{2m}+\varepsilon B,\cdots )$ and $b=\frac{B}{I_{0}}$, we obtain $sgn A=sgn\frac{\partial u_{1}}{\partial \varepsilon }\left( c_{1m}+\varepsilon b,c_{2m}+\varepsilon b,\cdots \right)$ and from (A2) $sgn A=sgn\frac{\partial }{\partial \varepsilon }\left[ x\left( c_{1m}+\varepsilon b\right) \right]$, where x is the solution of (A3) with $c_{jm}+\varepsilon b$ as currents. Further on, $sgn A=sgn\left[ bx+b\left( c_{1m}+\varepsilon b\right) \sum _{j=1}^{N}\displaystyle \frac{\partial x}{\partial i_{j}}\right]$. After replacing $\frac{\partial x}{\partial i_{j}}$ with (A5), we get

$$\begin{aligned} sgn A= & {} sgn\displaystyle \frac{bx}{S}\displaystyle \sum _{j=1}^{N}\left( 1-xi_{j}\right) ^{-k-1}\left[ \displaystyle \frac{1}{k}x^{\left( \frac{1}{k}-1\right) }\left( 1-xi_{j}\right) -k\left( x^{\frac{1}{k}}-d^{-1}\right) \left( i_{1}-i_{j}\right) \right] \end{aligned}$$

By using $i_{j}=c_{jm}+\varepsilon b$, $\left( 1/k\right) \ge k$ and $x^{-1}>i_{1}$ from (A4), we find $sgn A=+1$.

Appendix D

Here, we show that the function $\varepsilon \longrightarrow U_{2}\left( \varepsilon \right)$ from the proof of Theorem 3 is monotonically decreasing.

With notations in Appendix A and the same reasoning as in Appendix C, we have $A=\frac{\partial U_{2}}{\partial \varepsilon }\left( C_{1M}-\varepsilon B,C_{2M}-\varepsilon B,C_{3m},C_{4m},\cdots \right)$ and $sgn A=sgn\frac{\partial }{\partial \varepsilon }[\left( c_{2M}-\varepsilon b\right) x]$, where x is the solution of (A3) with $c_{1M}-\varepsilon b,c_{2M}-\varepsilon B,c_{3m},\ldots ,c_{Nm}$ as currents.

Further on, $sgn A=sgn\left[ -bx+\left( c_{2M}-\varepsilon b\right) \frac{\partial x}{\partial \varepsilon }\right] =sgn\Big [-bx-b\left( c_{2M}-\varepsilon b\right) \sum _{j=1}^{2}\frac{\partial x}{\partial i_{j}}\Big ]$. After inserting $\frac{\partial x}{\partial i_{j}}$ from (A5), we easily obtain $sgn A=-1$.

Appendix E

Here, we prove Theorem 4. See notations in Appendix A. According to Theorem 2, ${\overline{D}}$ is the first component of solution $U\left( {\overline{C}}\right)$ of (18) + (19), where ${\overline{C}}=\left( C_{1m},C_{2m},C_{3m},\ldots ,C_{Nm}\right)$. In terms of “small letter” notation, ${\overline{c}}=\left( c_{1m},c_{2m},\ldots ,c_{Nm}\right)$ yields ${\overline{x}}$ via (A3) and $u_{j}=\left( 1-{\overline{x}}c_{jm}\right) ^{-1}$ via (A2). Thus,

$$\begin{aligned} i_{C}=\left( {\overline{x}}^{1/k}-d^{-1}\right) \left[ u_{1}^{k}+\displaystyle \sum _{j=2}^{N}\left( 1-c_{jm}{\overline{x}}\right) ^{-k}\right] \end{aligned}$$

(E1)

Now, from (A4) we have ${\overline{x}}\le c_{1m}^{-1}=\left[ \left( N-1\right) \delta \right] ^{-1}$ and (E1) gives

$$\begin{aligned} i_{C}\le \left( N-1\right) ^{-1/k}\delta ^{-1/k}\left[ u_{1}^{k}+\displaystyle \sum _{j=2}^{N}\left( \displaystyle \frac{j-1}{N-1}\right) ^{-k}\right] \end{aligned}$$

(E2)

Note that $u_{1}=\exp \left( \displaystyle \frac{{\overline{D}}}{V_{t}}\right)$ from Theorem 2. On the other hand, ${\underline{D}}$ is the second component of the solution $U\left( {\underline{C}}\right)$ of (18) + (19). In terms of “small letter” notation, ${\underline{c}}=\left( c_{1M},c_{2M},c_{3m},\ldots ,c_{Nm}\right)$ yields ${\underline{x}}$ via (A3) and $u_{2}=\left( 1-c_{2M}{\underline{x}}\right) ^{-1}$ from (A2). We use (A4) to obtain ${\underline{x}}\le c_{1M}^{-1}=i_{M}^{-1}$. Then,

$$\begin{aligned} u_{2}\le \left( 1-\displaystyle \frac{i_{M}-\delta }{i_{M}}\right) ^{-1}=\delta ^{-1}i_{M} \end{aligned}$$

(E3)

where $u_{2}=\exp \left( \displaystyle \frac{{\underline{D}}}{V_{t}}\right)$. Now, to obtain ${\overline{D}}>{\underline{D}}$, we have to have ${\underline{u}}_{1}^{k}>{\overline{u}}_{2}^{k}$, where ${\underline{u}}_{1}^{k}$ is the lower bound of $u_{1}^{k}$ derived from (E2) and ${\overline{u}}^{k}_{2}=\delta ^{-k}i_{M}^{k}$ is the upper bound of $u_{2}^{k}$ from (E3). This results in (52).

Appendix F

We prove Theorem 5. See notations in Appendix A. Proving $\displaystyle \frac{\partial {\overline{D}}}{\partial \omega }>0$ means showing $\displaystyle \frac{\partial U_{1}}{\partial \omega }\left( {\overline{C}}\right) >0$, equivalent to $\displaystyle \frac{\partial u_{1}}{\partial \omega }\left( {\overline{c}}\right) >0$ where ${\overline{c}}=\left( c_{1m},c_{2m},\ldots ,c_{Nm}\right)$. By (A2), it is sufficient to prove $\displaystyle \frac{\partial }{\partial \omega }\left( c_{1m}x\right) >0$, where x is the solution of (A3) with ${\overline{c}}$ as currents. It comes out that $\displaystyle \frac{\partial }{\partial \omega }\left( c_{1m}x\right) =\left( N-1\right) i_{M}x+\left( N-1\right) \omega i_{m}\displaystyle \sum _{j=1}^{N}\displaystyle \frac{\partial x}{\partial i_{j}}\left( N-j\right) i_{M}$ and with (A5), we obtain the result.

Proving $\displaystyle \frac{\partial {\underline{D}}}{\partial \omega }<0$ means showing that $\displaystyle \frac{\partial U_{2}}{\partial \omega }\left( {\underline{C}}\right) <0$ or $\displaystyle \frac{\partial u_{2}}{\partial \omega }\left( {\underline{c}}\right) <0$, where ${\underline{c}}=\left( c_{1M},c_{2M},c_{3m},\ldots ,c_{Nm}\right)$. By (A2), it is sufficient to prove $\displaystyle \frac{\partial }{\partial \omega }\left( c_{2M}x\right) <0$. By using (A5) here, we straightforwardly obtain the result. To prove $\displaystyle \frac{\partial U_{M}}{\partial \omega }<0$ means to show that $\displaystyle \frac{\partial U_{1}}{\partial \omega }\left( {\widehat{C}}\right) <0$, where ${\widehat{C}}=\left( C_{1M},C_{2m},C_{3m},\ldots \right)$. Then, $\displaystyle \frac{\partial U_{1}}{\partial \omega }=\displaystyle \frac{\partial U_{1}}{\partial I_{1}}\left( {\widehat{C}}\right) \displaystyle \frac{\partial C_{1M}}{\partial \omega }+\displaystyle \sum _{j=2}^{N}\displaystyle \frac{\partial U_{1}}{\partial I_{j}}\left( {\widehat{C}}\right) \displaystyle \frac{\partial C_{jm}}{\partial \omega }$. Now, $\displaystyle \frac{\partial C_{1M}}{\partial \omega }=\displaystyle \frac{\partial I_{M}}{\partial \omega }=0$ and $\displaystyle \frac{\partial U_{1}}{\partial I_{j}}\left( {\widehat{C}}\right) <0$ for $j\ge 2$ by (30) Theorem 1. Then, with $\displaystyle \frac{\partial C_{jm}}{\partial \omega }=\left( N-j\right) I_{M}>0$, we get $\displaystyle \frac{\partial U_{1}}{\partial \omega }<0$.

Appendix G

Here, we prove (64) in Theorem 5.

If we show that

$$\begin{aligned} \Omega \left( 1/N-1\right) >1/N-1 \end{aligned}$$

(G1)

, then (64) comes from the (left) continuity of $\Omega$ in $1/N-1$. Translated in small letter notation, (64) is

$$\begin{aligned} u_{1}\left( {\overline{c}}\right) >u_{2}\left( {\underline{c}}\right) \left[ u_{1}\left( {{\widehat{c}}}\right) \right] ^{\omega } \end{aligned}$$

(G2)

For $\omega =1/N-1$, we denote by c the common value ${\overline{c}}={\underline{c}}={{\widehat{c}}}=\left( i_{M},i_{M}\frac{N-2}{N-1},i_{M}\frac{N-3}{N-1},\ldots ,0\right)$. If x is the solution of $i_{C}=g\left( x,c\right)$, we have $u_{1}\left( {\overline{c}}\right) =u_{1}\left( c\right) =\frac{1}{1-xi_{M}}$, $u_{2}\left( {\underline{c}}\right) =u_{2}\left( c\right) =\frac{1}{1-x\frac{N-2}{N-1}i_{M}}$, $u_{1}\left( {{\widehat{c}}}\right) =u_{M}=u_{1}\left( c\right) =\frac{1}{1-xi_{M}}$. Thus, (G2) reduces to $\left( 1-xi_{M}\right) ^{\frac{N-2}{N-1}}<1-x\frac{N-2}{N-1}i_{M}$, which is the well-known Bernoulli inequality.