1 Introduction

ARX model is an AutoRegressive model with eXogenous terms [31]. Because of its simplicity and easy parameterization, the ARX model has been widely used to model a lot of real systems, such as micro-turbines, data improving, fault detection, biomedical signals, COVID-19 case forecasting and communication systems  [1, 3, 7, 28, 34, 44].

Much research has been performed to identify ARX models in the last five decades. A piecewise auto-regressive exogenous structure was adopted to forecast the river floods [18]. A novel automated framework based on generalized spectral decomposition was proposed to estimate the parameters of an ARX model [33]. A new method based on the expectation–maximization (EM) algorithm was utilized for the identification of ARX models subject to missing data [24]. A recursive EM algorithm based on Student’s t-distribution was used for robust identification of ARX models [8]. A modified momentum gradient descent algorithm was investigated to identify ARX models [50]. A three-stage algorithm was studied for the identification of fractional differencing ARX with errors in variables [25].

However, most of the noises considered in the aforementioned papers are white noises or Gaussian noises. Random impulse signals can often be found in industrial signals, such as image signals, audio signals and communication signals  [2, 9, 46].

Identification criteria play an important role in system identification. The classical identification criteria include the least square criterion, maximum likelihood criterion and so on. These criteria have the advantages of simple calculation and easy theoretical analysis. However, the performance of the least-squares algorithm is poor for the non-Gaussian case, and the maximum likelihood algorithm needs to know the conditional probability density of the sample. Because of these problems, many researchers have put forward many other criteria, such as \(p-\)norm error criterion and mixed-norm error criterion [39, 53]. In recent years, information criteria have become more widespread in signal processing and system identification [14, 23, 32]. Compared with mean square error (MSE) criterion, which focuses on second-order statistics, the information-theoretic criterion (e.g., minimum error entropy (MEE) [4], Renyi’s entropy [15, 41], fixed-point maximum correntropy [21]) is related to various statistical behaviors of the probability density function (pdf) of the error. Algorithms based on information-theoretic criterion may have better performance than MSE-based algorithms [6, 15, 16].

In the last decade, entropy has found significant applications in system identification. A maximum correntropy criterion (MCC) algorithm was proposed for sparse system identification based on normalized adaptive filter theory [30]. An extended version of correntropy, whose center can be located at any position, and a new optimization criterion based on MCC with a variable center, were proposed [5]. A blocked proportionate normalized maximum correntropy algorithm and a separable maximum correntropy adaptive algorithm were presented to identify dynamic systems [29, 45].

To decrease the entropy estimators’ complexity, a stochastic information gradient (SIG) algorithm was proposed and its performance was investigated [14]. To improve the estimates, a joint stochastic gradient algorithm based on MSE and MEE was proposed and applied to identify an RBF network [4]. Though having less complexity, the SIG converges very slowly. To speed up the SIG, like the multi-innovation used in [12], a multi-error strategy is adopted and a feasible equation for calculation of the step size is introduced.

Since its introduction in 2003, the SIG algorithm has been widely used in system identification and machine learning. For example, a kernel-based gradient descent algorithms based on MEE was proposed to find nonlinear structures in the data, and its convergence rate was deduced [22]. A kernel adaptive filter for quaternion data was developed, and a new algorithm based on the SIG approach was applied to this filter [37]. To avoid unstable training or poor performance in deep learning, a strategy of directly estimating the gradients of information measures with respect to model parameters was explored, and a general gradient estimation method for information measures was proposed [52]. To avoid potentially sub-optimal solutions with respect to class separability, a dimensionality reduction network training procedure based on the stochastic estimate of the mutual information gradient was presented [38].

For several decades, data-driven techniques have been used in modeling and fault detection. For example, a surrogate model was developed based on a data-driven approach, and it can facilitate the design and optimization processes of permanent magnet systems [36]. A Matlab toolbox for data-based fault detection was developed in a unified data-driven framework. [27]. A new recursive total principle component regression-based design and implementation approach was proposed for efficient data-driven fault detection and applied to vehicular cyber-physical systems [26].

In this paper, the problem of parameter identification of the ARX model disturbed by random impulse noise is studied. The premise is that the structure of the model is known, the type of noise is known, the identification data are normal measurement data, and there are no outliers except impulse noise. The possible outliers, modeling errors, and other uncertainties in practice are not considered. Interested readers can refer to the recent literature [13, 47,48,49]. The main contributions of this work are as follows:

  1. (1)

    For the SIG algorithm, a simple step size method is proposed.

  2. (2)

    To make the algorithm faster, a multi-error method that uses stack error instead of instantaneous scalar error is applied.

  3. (3)

    Since the stack length can only be taken as an integer, a forgetting factor is used to further accelerate the algorithm.

  4. (4)

    The proposed algorithm is utilized to estimate the parameters of an ARX model with random impulse noise. Several numerical simulations and a case study show the effectiveness of the algorithm.

The rest of this work is organized as follows. In the next section, we describe the ARX model to be estimated. Based on an SIG algorithm in Sect. 3, a multi-error SIG with a forgetting factor is presented in Sect. 4. The convergence and the computational cost are analyzed in Sect. 5. Then, parameter estimation of an ARX model with a random impulse noise and a gas furnace dataset from the literature [42] is used to validate the proposed algorithm in Sect. 6. Finally, conclusions are presented in Sect. 7.

2 Problem Description

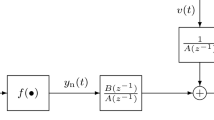
Consider an ARX model depicted in Fig. 1, where u(k) is the input and y(k) is the output. \(A({z^{ - 1}})\) and \(B({z^{ - 1}})\) are two polynomials with respect to \(z^{-1}\), and their degrees are \(n_a\) and \(n_b\), respectively. The model is polluted by a random impulse noise v(k).

Fig. 1
figure 1

Block diagram of an ARX model

Full size image

It is easy to find that

$$\begin{aligned} y(k)=\frac{B({{z}^{-1}})}{A({{z}^{-1}})}u(k)+\frac{1}{A({{z}^{-1}})}v(k). \end{aligned}$$
(1)

Multiplying both sides of Eq. 1 by \({A({{z}^{-1}})}\) gives

$$\begin{aligned} A({{z}^{-1}})y(k)=B({{z}^{-1}})u(k)+v(k). \end{aligned}$$
(2)

Suppose \(A({z^{ - 1}})=1+a_1 z^{-1}+a_2 z^{-2}+\cdots +a_{n_a}z^{-{n_a}}\) and \(B({z^{ - 1}})=b_1 z^{-1}+b_2 z^{-2}+\cdots +b_{n_b}z^{-{n_b}}\), then we can directly parameterize the model as follows,

$$\begin{aligned} \begin{aligned} y(k)&=\left( 1-A({{z}^{-1}}) \right) y(k)+B({{z}^{-1}})u(k)+v(k), \\&={{{\varphi }}^T}(k){{\theta }}+v(k), \end{aligned} \end{aligned}$$
(3)

with

$$\begin{aligned} \left\{ \begin{array}{l} {{\theta }} = {\left[ a_1,\cdots , a_{n_a}, b_1,\cdots , b_{n_b} \right] ^T} \in {{\mathbb {R}}^{n \times 1}},\\ {{{\varphi }}}(k) = {\left[ -y(k-1),\cdots , -y(k-n_a), u(k-1),\cdots , u(k-n_b) \right] ^T} \in {{\mathbb {R}}{^{{n} \times 1}}},\\ n = {n_a} + {n_b } . \end{array} \right. \end{aligned}$$
(4)

Then, the identification of the ARX model shown in Fig. 1 can be transformed into the estimation of the parameters \({{{\theta }}}\) based on the observations \(\left\{ {u(k),y(k)} \right\} _{k = 1}^N\) , where N is the data length.

However, traditional identification algorithms, such as the least-square algorithm and the mean square error algorithm, only consider the second moment of the error, and in some cases (such as the presence of random impulse noise) identification results deteriorate further. The information criterion algorithm based on a probability density function (pdf) considers the statistical information of each order of the error and is expected to achieve better estimates.

Next, we introduce the SIG algorithm and then describe our algorithm based on information gradient, which is integrated with the multi-error and a forgetting factor.

3 SIG of Shannon’s Error Entropy

Consider the parameterized system in Eq. 3, and denote a random error e(k) as

$$\begin{aligned} e(k)=y^*(k)-{{{\varphi }}^{T}}(k){\theta }, \end{aligned}$$
(5)

where \(y^*(k)\) is the system output without noise.

Shannon’s entropy for e with pdf f(e) is [43]

$$\begin{aligned} H(e)=-\int _{-\infty }^{\infty } f(e) \log f(e) d e=E\left[ -\log f(e)\right] . \end{aligned}$$
(6)

In practice, the pdf of e, i.e., f(e), is unknown. Thus, Eq. 6 cannot be used to calculate the entropy of e directly. One way is to utilize a Parzen window to approximate the unknown pdf underlying the N observations by [41]

$$\begin{aligned} {\hat{f}}(e)=\frac{1}{N} \sum _{i=1}^{N} \kappa _{\sigma }\left( e-e(i)\right) , \end{aligned}$$
(7)

where \(\kappa _{\sigma }(\cdot )\) is the kernel function with size \(\sigma \) [40].

At time k, a Parzen window estimate of e with window length L is

$$\begin{aligned} {\hat{f}}\left( e(k)\right) =\frac{1}{L} \sum _{i=k-L}^{k-1} \kappa _{\sigma }\left( \varDelta _{ki}\right) , \end{aligned}$$
(8)

where \(\varDelta _{ki} \text {=}e(k)-e(i)\), and e(k), e(i) denote the error at time k, i, respectively.

Thus, the stochastic entropy estimate at time k becomes

$$\begin{aligned} {\hat{H}} (e(k))=E\left[ -\log \left( \frac{1}{L} \sum _{i=k-L}^{k-1} \kappa _{\sigma }\left( \varDelta _{ki}\right) \right) \right] . \end{aligned}$$
(9)

Dropping the expectation in Eq. 9 [14], we obtain

$$\begin{aligned} {\hat{H}} (e(k))\approx -\log \left( \frac{1}{L} \sum _{i=k-L}^{k-1} \kappa _{\sigma }\left( \varDelta _{ki}\right) \right) . \end{aligned}$$
(10)

The stochastic gradient of Shannon entropy concerning \({\theta }\) at time k, \({\mathbf {g}}\), is

$$\begin{aligned} {\mathbf {g}}=-\frac{\sum \limits _{i=k-L}^{k-1} \kappa _{\sigma }^{\prime }\left( \varDelta _{ki}\right) \left( \frac{\partial e(k)}{\partial {\theta }}-\frac{\partial e(i)}{\partial {\theta }}\right) }{\sum \limits _{i=k-L}^{k-1} \kappa _{\sigma }\left( \varDelta _{ki}\right) }, \end{aligned}$$
(11)

where \(\kappa _{\sigma }^{\prime }(\cdot )\) is the derivative of the kernel function.

Using the following Gaussian kernel with variance \(\sigma ^2\), i.e.,

$$\begin{aligned} \kappa _{\sigma }\left( {\varDelta _{ki}}\right) =\exp \left( -\frac{\left\| {\varDelta _{ki}}\right\| ^{2}}{2 \sigma ^{2}}\right) , \end{aligned}$$
(12)

Equation 11 becomes

$$\begin{aligned} {\mathbf {g}}=\frac{\sum \limits _{i=k-L}^{k-1}{{{\kappa }_{\sigma }}\left( {{\varDelta }_{ki}} \right) {{\epsilon }_{ki}}{{\varDelta }_{ki}}}}{\sigma ^2\sum \limits _{i=k-L}^{k-1}{{{\kappa }_{\sigma }}\left( {{\varDelta }_{ki}} \right) }}, \end{aligned}$$
(13)

with

$$\begin{aligned} \epsilon _{ki}={\varphi }(k)-{\varphi }(i). \end{aligned}$$
(14)

The SIG for estimating the parameter vector \({\theta }\) is obtained as follows:

$$\begin{aligned} {\hat{\theta }}(k)={\hat{\theta }}(k-1)+ {\eta (k)} {\mathbf {g}}, \end{aligned}$$
(15)

where \( \eta (k)\) is the step size and is critical for convergence speed. However, equations to calculate the step size in [4] and [14] are too complicated to operate online. Here, we utilize the equation in stochastic gradient [10]:

$$\begin{aligned} \left\{ \begin{aligned}&r(k)=r(k-1)+\left\| {\varphi }(k) \right\| ^2, \quad r(0)=1,\\&\eta (k)=\frac{1}{r(k)}. \end{aligned} \right. \end{aligned}$$
(16)

In practice, the \({\theta }\) and the output without noise \(y^{*}(k)\) in Eq. 5 are unknown. A feasible way is to replace them by \(\hat{{\theta }}(k-1)\) and y(k), respectively. Thus, Eq. 5 becomes

$$\begin{aligned} e(k)=y(k)-{{{\varphi }}^{T}}(k)\hat{{\theta }}(k-1). \end{aligned}$$
(17)

4 Forgetting Factor Multi-error SIG Algorithm

One drawback of the SIG algorithm is its slow convergence. To enable the algorithm converge faster, a multi-error strategy is adopted and Eq. 13 is rewritten as follows:

$$\begin{aligned} {\mathbf {g}}=\frac{\sum \limits _{i=k-L}^{k-1} \kappa _{\sigma }\left( \varDelta _{ki}\right) \varDelta {\varvec{\Phi } }(p;k,i)\varDelta {\mathbf {E}}(p;k,i)}{\sigma ^2\sum \limits _{i=k-L}^{k-1} \kappa _{\sigma }\left( \varDelta _{ki}\right) } \end{aligned}$$
(18)

with

$$\begin{aligned} \left\{ \begin{aligned}&\varDelta {\varvec{\Phi } }(p;k,i)\text {=}{\varvec{\Phi } }(p,k)-{\varvec{\Phi } }(p,i), \\&\varDelta {\mathbf {E}}(p;k,i)\text {=}{\mathbf {E}}(p,k)-{\mathbf {E}}(p,i), \\ \end{aligned} \right. \end{aligned}$$
(19)

where p is the stack length and \({\mathbf {E}}(p,k)\) and \({\varvec{\Phi } }(p,k)\) are the stacked error vector and stacked information matrix, respectively,

$$\begin{aligned} {\mathbf {E}}(p, k)=\left[ \begin{array}{c} e(k) \\ e(k-1) \\ \vdots \\ e(k-p+1) \end{array}\right] \in {\mathbb {R}}^{p \times 1}, \end{aligned}$$
(20)

and

$$\begin{aligned} \varvec{\Phi }(p, k)= [{\varphi }(k), {\varphi }(k-1), \cdots , {\varphi }(k-p+1)] \in {\mathbb {R}}^{n \times p}. \end{aligned}$$
(21)

Note that the scalar error \(\varDelta _{ki}\) in Eq. 13 is replaced by the vector error \(\varDelta {\mathbf {E}}(k,i)\) in Eq. 18. In other words, multi-error takes the place of a single error. Thus, the algorithm is named a multi-error SIG algorithm (ME-SIG).

The stack length p can only be a positive integer. To make the ME-SIG faster, a forgetting factor (FF) \(\lambda \) is introduced. The first equation of Eq. 16 becomes

$$\begin{aligned} r(k)=\lambda r(k-1)+\left\| {{\varphi }(k)} \right\| ^2, \quad r(0)=1. \end{aligned}$$
(22)

Equations 15 and 17–22 construct the FF-ME-SIG algorithm.

5 Performance Analysis

5.1 Convergence Analysis

The approximate linearization approach [17] is used to analyze the convergence of the proposed ME-SIG algorithm in Eq. (15) with Eqs. (18) and (19).

Subtracting \({\theta }_0\) from both sides of Eq. (15), we obtain

$$\begin{aligned} {{\tilde{\theta }}}(k)={{\tilde{\theta }}}(k-1)+ {\eta (k)} {\mathbf {g}}, \end{aligned}$$
(23)

where \({{\tilde{\theta }}}(k)={\hat{\theta }}(k)-{{\theta }}_{0}\) is the estimation error vector of the parameter.

Approximating the gradient \({\mathbf {g}}\) in Eq. (18) using the first-order Taylor expansion:

$$\begin{aligned} \begin{aligned} {\mathbf {g}}&\approx {\mathbf {g}}(\theta _0)+{H}_1 \left( {\hat{\theta }}(k-1)-{{\theta }_0}\right) \\&={H}_1 \left( {\hat{\theta }}(k-1)-{{\theta }_0}\right) \\&={H}_1 {{\tilde{\theta }}}(k-1), \end{aligned} \end{aligned}$$
(24)

where \(H_1=\frac{\partial {\mathbf {g}}^{T}(\theta _0)}{\partial {\theta }}\) is the Hessian matrix and is expressed as

$$\begin{aligned} \begin{aligned} {H}_1=&\frac{\sum \limits _{i=k-L}^{k-1} \kappa _{\sigma }\left( \varDelta _{ki}\right) {\left( \varDelta {\mathbf {E}}^T(p;k,i)\right) }'\varDelta {\varvec{\Phi }}^T(k,i) }{\sigma ^2\sum \limits _{i=k-L}^{k-1} \kappa _{\sigma }\left( \varDelta _{ki}\right) }\\&+\frac{\sum \limits _{i=k-L}^{k-1} \kappa _{\sigma }\left( \varDelta _{ki}\right) {\varDelta {\mathbf {E}}^T(p;k,i)\left( \varDelta {\varvec{\Phi }}^T(k,i) \right) }'}{\sigma ^2\sum \limits _{i=k-L}^{k-1} \kappa _{\sigma }\left( \varDelta _{ki}\right) }\\&-\frac{\sum \limits _{i=k-L}^{k-1} \kappa _{\sigma }\left( \varDelta _{ki}\right) {\varDelta {\mathbf {E}}^T(p;k,i) \varDelta {\varvec{\Phi }}^T(k,i) } \sum \limits _{i=k-L}^{k-1} \kappa '_{\sigma }\left( \varDelta _{ki}\right) }{\sigma ^2\sum \limits _{i=k-L}^{k-1} \kappa _{\sigma }^2\left( \varDelta _{ki}\right) }.\\ \end{aligned} \end{aligned}$$
(25)

Substituting Eq. (24) into Eq. (23), we obtains

$$\begin{aligned} {{\tilde{\theta }}}(k)={{\tilde{\theta }}}(k-1)+ {\eta (k)} {{H}_1 }{{{\tilde{\theta }}}(k-1)}, \end{aligned}$$
(26)

We analyze the convergence of Eq. 26 by borrowing the results from the LMS convergence theory [19, 20]. Assuming that the Hessian matrix \(H_1\) is a normal matrix and can be decomposed into the following normal form:

$$\begin{aligned} {H}_1=Q_1 \varLambda _1 Q_1^{-1}, \end{aligned}$$
(27)

where \(Q_1\) is an \( m \times m \) orthogonal matrix, \( \varLambda _1=diag[\gamma _1, \gamma _2, \cdots , \gamma _m], \gamma _i\) is the eigenvalue of \(H_1\). Then, the recursive Eq. 26 can be expressed as

$$\begin{aligned} \begin{aligned} {{{\tilde{\theta }}}(k)}&=Q_1\left[ I+\eta (k) \varLambda _1\right] Q_1^{-1} {{{\tilde{\theta }}}(k-1)}\\&=Q_1\left[ \prod \limits _{i=1}^{k}{\left( I+\eta (i)\varLambda _1 \right) }\right] Q_1^{-1} {{{\tilde{\theta }}}(0)}.\\ \end{aligned} \end{aligned}$$
(28)

Clearly, if the following conditions are satisfied, \({{{\tilde{\theta }}}(k)}\rightarrow {\mathbf {0}}\) , i.e., \({\hat{\theta }}(k)\rightarrow {\theta }_0\):

$$\begin{aligned} \left| 1+\eta (i) \gamma _{j}\right| <1, \quad i=1,2,\cdots ,k, \quad j=1, 2,\ldots , m. \end{aligned}$$
(29)

Thus, a sufficient condition that ensures the convergence of the algorithm is as follows:

$$\begin{aligned} \left\{ \begin{aligned}&\gamma _j<0, j=1,2,\cdots , m,\\&0<\eta (i)<\frac{2}{\underset{j}{\mathop {\max }}\,\vert {{\gamma }_{j}} \vert }. \end{aligned} \right. \end{aligned}$$
(30)

5.2 Computational Analysis

According to the calculation method of [11], the calculation amount of each iteration of the three algorithms is shown in Table 1, where \(e^x\) is calculated by its Taylor expansion, and the first three terms are used. ‘Time’ denotes the time that the numerical example consumes.

Table 1 Computational cost of SIG, ME-SIG and FF-ME-SIG
Full size table

From the calculation of complexity and running time, we can see that the former algorithm has lower values than the others, while the latter two algorithms have little difference. The computational complexity of the two algorithms proposed in this paper is larger than that of the first algorithm, because the latter two algorithms need the calculation of multi-error. In terms of running time, the latter two algorithms take approximately 4% more time than the previous SIG algorithm, which is not a significant difference.

6 Experimental Results

Consider the ARX model depicted in Fig. 1 with

$$\begin{aligned} \left\{ \begin{array}{l} A(z^{-1})=1.0-1.5z^{-1}+0.7z^{-2},\\ B(z^{-1})=1.0z^{-1}+0.5z^{-2},\\ \end{array} \right. \end{aligned}$$
(31)

where input data u(k) are an M-sequence and v(k) is a random impulse noise. 5% of the output data (30 outputs) are randomly selected, and 30 noises with random amplitude between 0 and 1 are added, respectively. The curves of input u(k) and output y(k) are shown in Fig. 2. All simulation experiments use this model.

Fig. 2
figure 2

Curves of input–output data

Full size image

6.1 Numerical Simulation

(1) Results using SIG algorithm

The parameter estimates using the SIG with window length \(L=3\) are shown in Table 2, where the estimation error \(\delta \) is defined as \(\delta \text {=}\frac{\left\| {\hat{\theta }}(k)\text {-}{{{\theta }}_{0}} \right\| }{\left\| {{{\theta }}_{0}} \right\| }\times 100\). It is easy to determine that estimation error decreases as data length k increases (for a given L). However, the errors are very large (38.9319%) at the end of the estimation.

Table 2 Results using SIG algorithm (\(L=5\))
Full size table

(2) Results using ME-SIG algorithm

The parameter estimates using the proposed ME-SIG with stack length \(p=5\) and \(L=3\) are shown in Table 3. The estimation errors with different p are depicted in Fig. 3 (\(L=3\)). It can be seen that:

  1. (1)

    Estimation error of a given p decreases when data length k increases;

  2. (2)

    With stack length p increasing, the estimation error decreases quickly.

Table 3 Results using ME-SIG algorithm (\(p=5, L=3\))
Full size table
Fig. 3
figure 3

Estimation errors using ME-SIG with different stack length p

Full size image

(3) Results using FF-ME-SIG algorithm

The parameter estimates using proposed FF-ME-SIG with forgetting factor \(\lambda =0.99\) are shown in Table 4, where \(L=3\) and \(p=5\). It can be seen that:

  1. (1)

    Estimation error decreases when data length k increases;

  2. (2)

    Compared with Table 3, the estimation error of the FF-ME-SIG is smaller at the same data length k.

Table 4 Results using FF-ME-SIG algorithm (\(p=5, L=3, \lambda =0.99\))
Full size table

(4) Comparison of the results of SIG, ME-SIG and FF-ME-SIG algorithms

The estimation errors using SIG, ME-SIG and FF-ME-SIG are depicted in Fig. 4. It can be seen that:

Fig. 4
figure 4

Estimation errors using SIG, ME-SIG, FF-ME-SIG

Full size image
  1. (1)

    All curves decrease when data length k increases;

  2. (2)

    The estimation error of the SIG algorithm is larger than that of ME-SIG, which means that multi-error can improve the accuracy of the SIG’s estimate;

  3. (3)

    The estimate of the FF-ME-SIG is the most accurate one of the three. In other words, the introduction of the forgetting factor improves the accuracy of the estimation.

(5) Results using FF-ME-SIG algorithm under different noise additions

To test the performance of the algorithm under different noise levels, we add 5%, 10%, 30%, and 50% of noises to the samples. The mean of the noise is 0.5, and the amplitude is between 0 and 1. The estimation results when \(k=600\) are shown in Table 5, where \(p=5, L=3, \lambda =0.99\). The estimation error curve is shown in Fig. 5. It can be seen from Table 5 and Fig. 5 that with the increase in the added noise, the estimation error tends to increase, but the change is small, which indicates that the proposed algorithm has strong adaptability to noise.

Table 5 Results using FF-ME-SIG algorithm under different noise additions (\(p=5, L=3, \lambda =0.99\))
Full size table
Fig. 5
figure 5

Estimates of FF-ME-SIG using samples with different noise additions

Full size image

(6) Results using the FF-ME-SIG for the identification of the Narendra difference equations

To support this paper’s argument, we add further simulation examples involving synthetic input–output relations such as the Narendra difference equations proposed in [35, 51]:

$$\begin{aligned} {\varvec{y}}(n+1)=0.3 {\varvec{y}}(n)+0.6 {\varvec{y}}(n-1)+f[{\varvec{e}}(n)], \end{aligned}$$
(32)

where

$$\begin{aligned} \left\{ \begin{aligned}&f(e)=0.6 \sin (\pi e)+0.3 \sin (3 \pi e)+0.1 \sin (5 \pi {\varvec{e}}) \\&{\varvec{e}}(n)=\sin \left[ (1+{\varvec{a}}) \omega _{0} n\right] . \end{aligned} \right. \end{aligned}$$
(33)

Using the following structure to the model above equation:

$$\begin{aligned} y(k)=a_1y(k-1)+a_2y(k-2)+a_3y(k-3)+a_4y^2(k-1)+a_5y^2(k-2) \end{aligned}$$
(34)

Let the data length be 240. The estimate using the proposed algorithm is \( \left[ 0.3084,0.3255,0.3641,-0.0264,0.0372\right] \) (when \(k=240\)). The predicted y(k) and observed y(k) are depicted in Fig. 6.

Fig. 6
figure 6

Predicted and observed output using FF-ME-SIG for Eqs. 32–33

Full size image

(7) Results using FF-ME-SIG algorithm and RLS, SG algorithm

To prove the superiority of the proposed algorithm, the identification results of the stochastic gradient (SG) algorithm and recursive least squares (RLS) algorithm are compared with that of the proposed algorithm. Figure 7 shows the estimation error curves of the three algorithms. When \(k=600\), the estimation error of the SG, RLS and FF-ME-SIG is 55.5395%, 5.2045% and 4.8337%, respectively. It can be seen that the estimation error of SG is very large, and the estimation error of the RLS algorithm is slightly larger than that of the proposed algorithm. However, due to the impulse noise, the estimation error of the RLS algorithm changes dramatically, which indicates that the estimates given by the RLS algorithm change significantly.

Fig. 7
figure 7

Estimate errors using SG, RLS and FF-ME-SIG

Full size image
Fig. 8
figure 8

Curves of the input and output data of a gas furnace

Full size image
Table 6 Results using SIG, ME-SIG and FF-ME-SIG algorithm
Full size table
Fig. 9
figure 9

Curves of the outputs and prediction errors of a gas furnace

Full size image

6.2 Case Study

The data set of a gas furnace from the literature [42] is used to validate the proposed algorithm. These data were continuously collected from a gas furnace and then read every 9 s. The air feed of the furnace was kept constant, but the methane feed rate was varied and the resulting \(\text {CO}_2\) concentration in the off gases was measured. There are 296 input–output data in this set. The first 200 data are adopted to estimate the parameters. The curves of the input and output are shown in Fig. 8. The estimation results and the prediction errors using SIG, ME-SIG and FF-ME-SIG are listed in Table 6. The outputs y(k) and the prediction errors pe(k) using the proposed algorithm are shown in Fig. 9.

  1. (1)

    It can be seen from Table 6 that among three algorithms, the proposed FF-ME-SIG algorithm has the smallest RMSE, which means that the proposed algorithm can give the most accurate estimate.

  2. (2)

    As shown in Fig. 9, the outputs of the obtained model using the proposed algorithm can predict the observations well.

7 Conclusions

In this paper, a novel SIG algorithm based on minimum error entropy is presented. The traditional SIG algorithm needs less computation than the MSE algorithm. However, it converges slowly. A multi-error strategy and a forgetting factor are introduced to speed up the SIG. We compared the results of SIG, ME-SIG and FF-ME-SIG by estimating the parameters of an ARX model with random impulse noise and through a case study. It is found that SIG with ME and FF can obtain accurate estimates, and it has a quick convergence rate.