1 Introduction

Kernelized processing algorithms provide an attractive framework for dealing with many nonlinear problems in signal processing and machine learning. The fundamental mathematical notion of these technologies is to transform low-dimensional data into high-dimensional reproducing kernel Hilbert spaces (RKHSs) [28]. Nevertheless, the batch form of these algorithms usually requires a large amount of memory and computational complexity [27]. Kernel adaptive filters (KAFs) for online kernel processing have been studied extensively [9,10,11,12, 14, 15, 17,18,19,20, 26, 31, 33,34,35, 37, 38], including the kernel least mean square (KLMS) [17], kernel affine projection (KAP) [18, 26], kernel conjugate gradient (KCG) [38] and kernel recursive least squares (KRLS) [14].

As far as we know, most of the KAFs construct a real RKHS by real kernels, which are designed to process real data. However, complex-valued signals are also very common in practical nonlinear applications. For example, in communication system, when a QPSK signal passes through a nonlinear channel, the in-phase and quadrature components of the signal can be expressed compactly by a complex-value signal. In nonlinear electromagnetic calculation problems, the amplitude and phase of an electromagnetic wave can also be equivalent to a complex-value form. Therefore, several complex KAFs have recently been proposed [3,4,5,6,7,8, 22, 24]. The complex KLMS (CKLMS) was first proposed in [5, 6], which uses Wirtinger’s calculus to generalize a complex RKHS. The authors proposed two CKLMS algorithms. One is CKLMS1, which uses real kernels to model the complex RKHS, called complexification of the real RKHSs. The other is CKLMS2, which uses the pure complex kernel. However, the convergence rate of CKLMS decreases from circular (proper) to highly non-circular (improper) complex inputs [25]. The widely linear approach is a generalized way to process the complex signal [30]. In [7], by employing this approach, the authors proposed an augmented CKLMS (ACKLMS) algorithm, in which the streams of input and desired signal pairs have the augmented vector form, which stacks the standard complex representation on top of its complex conjugate. Nevertheless, the ACKLMS algorithm exploits the same kernel for both real and imaginary parts. It is proved to be the same as CKLMS1. In [2], the widely linear reproducing kernel Hilbert space (WL-RKHS) theory was developed, in which a new pseudo-kernel was introduced to complement the standard kernel for a complete representation of the complex Hilbert space. In [3], the authors borrowed from the results on the WL-RKHS for nonlinear regression and proposed the generalized CKLMS (GCKLMS). That algorithm can provide a better representation of complex-valued signal than the pure complex and complexified methods and perform the independent learning of the real and the imaginary parts. Meanwhile, it is concluded that the previous version of the CKLMS can be expressed as particular cases of the GCKLMS.

Other complex KAFs have also been discussed. The linearly complex affine projection (CAP) algorithm, which uses the widely linear approach, was proposed in [13, 36]. In [22], the authors introduced the CAP algorithm into the feature space and proposed the complex kernel affine projection (CKAP) algorithm. However, it is limited in a pure complex RKHS or a complexified RKHS (which uses real kernels to model the complex RKHS), and only circular complex signals are considered. When dealing with a non-circular complex signal, it is well known that widely linear minimum mean-squared error (MSE) estimation has many performance advantages over traditional linear MSE estimation. Meanwhile, the widely linear representation in the RKHS has been proved to be more powerful and convenient than the pure complex and the complexified representations [21, 30].

Therefore, by employing the WL-RKHS theory in [2], we propose the generalized CKAP (GCKAP) algorithms. This is the first and the main contribution of this paper. The GCKAP algorithms have two main notable features. One is that they provide a complete solution for both circular and non-circular complex nonlinear problems, and show many performance improvements over the CKAP algorithms. The other is that the GCKAP algorithms inherit the simplicity of the CKLMS algorithm while reducing its gradient noise and boosting its convergence.

The affine projection algorithms use more recent augmented inputs in the current iteration to achieve the affine projection of weights onto the affine subspace [1, 23]. During this process, the inverse of the Gram matrix (or kernel matrix) is needed for calculating the expansion coefficients. The forms of the augmented input and desired signal pairs determine the Gram matrix in GCKAP also has the augmented form. This leads to the second contribution of this paper: the development of second-order statistical characteristics of WL-RKHS. An augmented Gram matrix is introduced which consists of a standard Gram matrix and a pseudo-Gram matrix. This decomposition provides more underlying information when the real and imaginary parts of the signal are correlated and learning is independent. If the pseudo-Gram matrix vanishes, the input signal is proper; otherwise, it is improper. Improper can arise due to imbalance between the real and imaginary parts of a complex vector.

In addition, the inverse operation of the Gram matrix in the traditional KAP algorithm can no longer be solved by the previous iteration method [23] at the GCKAP iteration. To overcome this problem, we propose a decomposition method to reduce its complexity cost. This is the third contribution. Moreover, both the basic and the regularized GCKAP algorithms are proposed, named GCKAP-1 and GCKAP-2, respectively. Furthermore, it is found that the previous CKAP algorithms can be expressed as particular cases of the GCKAP algorithms. In addition, some online sparsification criteria are compared comprehensively in the GCKAP-2 algorithm, including the novelty criterion [19], the coherence criterion [26], and the angle criterion [38].

The rest of this paper is organized as follows. Section 2 discusses the theory of the WL-RKHS. Section 3 describes the details of the proposed GCKAP algorithms. Two simulation experiments are presented in Sect. 4. Finally, Sect. 5 summarizes the conclusions of this paper.

Notations We use bold lower-case letters to denote vectors and bold upper-case letters to denote matrices. The superscripts \((\cdot )^T\), \((\cdot )^H\) and \((\cdot )^*\) denote the transpose, Hermitian transpose, and complex conjugate, respectively. The inner product is denoted by \(\langle \cdot ,\cdot \rangle \); in the Hilbert space, it is denoted by \(\langle \cdot ,\cdot \rangle _{{\mathcal {H}}}\). The expectation is denoted by \({\mathbb {E}}(\cdot )\).

2 Widely Linear RKHS

Let \({\mathcal {X}}\) be a nonempty set of \({\mathbb {F}}^M\), where \({\mathbb {F}}\) can be the field of real numbers \({\mathbb {R}}\) or complex numbers \({\mathbb {C}}\), and \({\mathcal {H}}\) be a Hilbert space of functions \(f:{\mathcal {X}}\rightarrow {\mathbb {F}}\). \({\mathcal {H}}\) is called the reducing kernel Hilbert space endowed with the inner product \(\langle \cdot ,\cdot \rangle _{\mathcal {H}}\) and the norm \(\Vert \cdot \Vert _{\mathcal {H}}\) if there exists a kernel function \(\kappa :{\mathcal {X}}\times {\mathcal {X}}\rightarrow {\mathbb {F}}\) that satisfies the following properties.

  1. 1.

    For every \({\mathbf {x}}\), \(\kappa ({\mathbf {x}},{\mathbf {x}}')\) as a function of \({\mathbf {x}}'\) belongs to \({\mathcal {H}}\).

  2. 2.

    The kernel function satisfies the reproducing property

    $$\begin{aligned} f({\mathbf {x}})=\langle f(\cdot ), \kappa ({\mathbf {x}}, \cdot ) \rangle _{{\mathcal {H}}}\quad {\mathbf {x}}\in {\mathcal {X}}. \end{aligned}$$
    (1)

    In particular, \(\langle \kappa ({\mathbf {x}},\cdot ), \kappa ({\mathbf {x}}', \cdot ) \rangle _{{\mathcal {H}}} = \kappa ({\mathbf {x}}, {\mathbf {x}}')\).

In the RKHS, a complex function is in a closed linear combination of the kernels at the training points

$$\begin{aligned} f({\mathbf {x}}')=\sum _{i=1}^{K}\alpha _{i} \kappa ({\mathbf {x}}',{\mathbf {x}}(i)) ={\varvec{\kappa }}({\mathbf {x}}',{\mathbf {X}}){\varvec{\alpha }}, \end{aligned}$$
(2)

where \(\alpha _{i}\in {\mathbb {F}}\) is the linear combination coefficient of a kernel, \({\varvec{\alpha }}=[\alpha _1,\ldots , \alpha _K]^T\), K is the number of training points, and \({\varvec{\kappa }}({\mathbf {x}}',{\mathbf {X}}) = [\kappa ({\mathbf {x}}',{\mathbf {x}}_1),\ldots , \kappa ({\mathbf {x}}',{\mathbf {x}}_K)]\) is a row vector. The kernel trick states that we can construct a q-dimensional (possible infinite) mapping \({\varvec{\varphi }}(\cdot )\) into the RKHS \({\mathcal {H}}\) such that \(\kappa ({\mathbf {x}}',{\mathbf {x}})= \langle {\varvec{\varphi }} ({\mathbf {x}}'), {\varvec{\varphi }} ({\mathbf {x}})\rangle _{{\mathcal {H}}}\). If \({\varvec{\varphi }}(\cdot )\) is the complex mapping \({\varvec{\varphi }}(\cdot ) = {\varvec{\varphi }}_r(\cdot ) + j{\varvec{\varphi }}_j(\cdot )\), then the complex function \(f({\mathbf {x}}')\) can be denoted by

$$\begin{aligned} \begin{aligned}&f({\mathbf {x}}') = \left[ {{\varvec{\varphi }}}_{r'}^T{\varvec{\varPhi }}_r + {{\varvec{\varphi }}}_{j'}^T{\varvec{\varPhi }}_j - j({{\varvec{\varphi }}}_{j'}^T{\varvec{\varPhi }}_r - {{\varvec{\varphi }}}_{r'}^T{\varvec{\varPhi }}_j) \right] {\varvec{\alpha }}, \end{aligned} \end{aligned}$$
(3)

where the coefficient vector is \({\varvec{\alpha }} = {\varvec{\alpha }}_r + j{\varvec{\alpha }}_j\) and the real and imaginary mappings are \({\varvec{\varphi }}_{r'}={\varvec{\varphi }}_r({\mathbf {x}}')\) and \({\varvec{\varphi }}_{j'}={\varvec{\varphi }}_j({\mathbf {x}}')\), respectively. \({\varvec{\varPhi }}_r=[{\varvec{\varphi }}_r({\mathbf {x}}_1),\ldots , {\varvec{\varphi }}_r({\mathbf {x}}_K)]\), and \({\varvec{\varPhi }}_j=[{\varvec{\varphi }}_j({\mathbf {x}}_1),\ldots , {\varvec{\varphi }}_j({\mathbf {x}}_K)]\). The complex function \(f({\mathbf {x}}')= f_r({\mathbf {x}}') + j f_j({\mathbf {x}}')\) can be represented by a real vector-valued function \({\mathbf {f}}_{\mathbb {R}}({\mathbf {x}}')= [f_r({\mathbf {x}}'),~f_j({\mathbf {x}}')]^T \in {\mathbb {R}}^2\), which is composed of its real and imaginary parts. The real vector-valued function in the RKHS can be represented by the product of the real transformation matrix and the real coefficient vector:

$$\begin{aligned} \begin{aligned} {\mathbf {f}}_{\mathbb {R}}({\mathbf {x}}')&=\begin{bmatrix} {\varvec{\varphi }}_{r'}^T{\varvec{\varPhi }}_r + {\varvec{\varphi }}_{j'}^T{\varvec{\varPhi }}_j &{} ~-{\varvec{\varphi }}_{r'}^T{\varvec{\varPhi }}_j + {\varvec{\varphi }}_{j'}^T{\varvec{\varPhi }}_r \\ {\varvec{\varphi }}_{r'}^T{\varvec{\varPhi }}_j - {\varvec{\varphi }}_{j'}^T{\varvec{\varPhi }}_r &{}~ {\varvec{\varphi }}_{r'}^T{\varvec{\varPhi }}_r + {\varvec{\varphi }}_{j'}^T{\varvec{\varPhi }}_j \end{bmatrix} \begin{bmatrix} {\varvec{\alpha }}_r \\ {\varvec{\alpha }}_j \end{bmatrix} \\&\triangleq \begin{bmatrix}{\varvec{\kappa }}_{rr} &{} {\varvec{\kappa }}_{rj} \\ {\varvec{\kappa }}_{jr} &{}{\varvec{\kappa }}_{jj} \end{bmatrix} \begin{bmatrix} {\varvec{\alpha }}_r \\ {\varvec{\alpha }}_j \end{bmatrix} \triangleq {\mathbf {K}}{\varvec{\alpha }}_{{\mathbb {R}}}, \end{aligned} \end{aligned}$$
(4)

where \({\mathbf {K}}\) denotes the real transformation matrix and \({\varvec{\alpha }}_{{\mathbb {R}}}\) denotes the real vector-valued expansion coefficient. This is a real vector linear system. It is observed that the complex RKHS of the real vector-valued functions is limited as \({\varvec{\kappa }}_{rr} = {\varvec{\kappa }}_{jj},~ {\varvec{\kappa }}_{rj} = -{\varvec{\kappa }}_{jr}\). However, in general, this limitation does not always hold. By employing the widely linear approach, the WL-RKHS theory [2] breaks this limitation. In the WL-RKHS, a complex vector-valued function \(f({\mathbf {x}}')\) can be represented by an augmented form obtained by stacking the complex function \(f({\mathbf {x}}')\) on top of its complex conjugate \(f({\mathbf {x}}')^*\) with the expression \(\underline{{\mathbf {f}}}({\mathbf {x}}') = \left[ f({\mathbf {x}}'),~f({\mathbf {x}}')^*\right] ^T\in {\mathbb {C}}^2\). Therefore, a widely linear system \( \underline{{\mathbf {f}}}({\mathbf {x}}') = {\mathbf {K}}_A \underline{{\varvec{\alpha }}}\) is modeled, where \(\underline{{\varvec{\alpha }}} = \left[ {\varvec{\alpha }}^T,~{\varvec{\alpha }}^H \right] ^T\) is the augmented expansion coefficient and \({\mathbf {K}}_A \in {\mathbb {C}}^{2\times 2K} \) is the augmented transformation matrix defined as

$$\begin{aligned} {\mathbf {K}}_A = \begin{bmatrix} {\varvec{\kappa }}&{} \tilde{{\varvec{\kappa }}}\\ \tilde{{\varvec{\kappa }}}^*&{} {\varvec{\kappa }}^* \end{bmatrix}, \end{aligned}$$
(5)

where

$$\begin{aligned}&{\varvec{\kappa }} = \tfrac{1}{2} \left[ {\varvec{\kappa }}_{rr} + {\varvec{\kappa }}_{jj} + j ({\varvec{\kappa }}_{jr} - {\varvec{\kappa }}_{rj}) \right] , \end{aligned}$$
(6)
$$\begin{aligned}&\tilde{{\varvec{\kappa }}}= \tfrac{1}{2} \left[ {\varvec{\kappa }}_{rr} - {\varvec{\kappa }}_{jj} + j ({\varvec{\kappa }}_{jr} + {\varvec{\kappa }}_{rj}) \right] . \end{aligned}$$
(7)

Here, \({\varvec{\kappa }}_{rr}\), \({\varvec{\kappa }}_{jj}\), \({\varvec{\kappa }}_{jr}\), and \({\varvec{\kappa }}_{rj}\) are different row vectors that are defined in the same way as \({\varvec{\kappa }}({\mathbf {x}}',{\mathbf {X}})\). The complex function in (2) is represented by the first row of the widely linear system as

$$\begin{aligned} f({\mathbf {x}}') ={\varvec{\kappa }}({\mathbf {x}}',{\mathbf {X}}){\varvec{\alpha }} + \tilde{{\varvec{\kappa }}}({\mathbf {x}}',{\mathbf {X}}){\varvec{\alpha }}^*, \end{aligned}$$
(8)

where \({\varvec{\kappa }}({\mathbf {x}}',{\mathbf {X}})\) is the standard kernel vector and \(\tilde{{\varvec{\kappa }}}({\mathbf {x}}',{\mathbf {X}}) = [{\tilde{\kappa }}({\mathbf {x}}',{\mathbf {x}}_1),\ldots , {\tilde{\kappa }}({\mathbf {x}}',{\mathbf {x}}_K)]\) is defined as the pseudo-kernel vector. The augmented representation in the WL-RKHS obviously has some built-in redundancy, but it is very powerful and convenient, as we have to deal with non-circular complex signals.

Next, the second-order statistical properties of the widely linear system are discussed. Suppose the complex input \({\varvec{\varPhi }} = {\varvec{\varPhi }}_r + j{\varvec{\varPhi }}_j\) in the RKHS has a zero mean. The real correlation matrix of \({\varvec{\varPhi }}_{\mathbb {R}} = \left[ {\varvec{\varPhi }}_r^T, {\varvec{\varPhi }}_j^T\right] ^T\) is

$$\begin{aligned} {\mathbf {R}}_{\mathbb {R}} = \begin{bmatrix} {\mathbf {R}}_{rr} &{} {\mathbf {R}}_{rj} \\ {\mathbf {R}}_{rj}^T &{} {\mathbf {R}}_{jj} \end{bmatrix}, \end{aligned}$$
(9)

where \({\mathbf {R}}_{rr} = {\mathbb {E}}\left[ {\varvec{\varPhi }}_r{\varvec{\varPhi }}_r^T \right] , ~{\mathbf {R}}_{rj} = {\mathbb {E}}\left[ {\varvec{\varPhi }}_r{\varvec{\varPhi }}_j^T \right] = {\mathbf {R}}_{jr}^T\), and \({\mathbf {R}}_{jj} = {\mathbb {E}}\left[ {\varvec{\varPhi }}_j{\varvec{\varPhi }}_j^T \right] \). Define the real-to-complex transformation matrix \({\mathbf {T}}\) as

$$\begin{aligned} {\mathbf {T}} = \begin{bmatrix} {\mathbf {I}}&{} j{\mathbf {I}}\\ {\mathbf {I}}&{} -j{\mathbf {I}} \end{bmatrix} \in {\mathbb {C}}^{2q\times 2q}, \end{aligned}$$
(10)

which is unitary up to a factor of 2, that is, \({\mathbf {T}}{\mathbf {T}}^H = {\mathbf {T}}^H{\mathbf {T}} = 2{\mathbf {I}}\). The augmented input \(\underline{{\varvec{\varPhi }}} = \left[ {\varvec{\varPhi }}^T, ~ {\varvec{\varPhi }}^H \right] ^T\) can be expressed by the transformation of \(\underline{{\varvec{\varPhi }}} = {\mathbf {T}} {\varvec{\varPhi }}_{\mathbb {R}}\). Then, the augmented correlation matrix can be derived as

$$\begin{aligned} \underline{{\mathbf {R}}} = {\mathbf {T}} {\mathbf {R}}_{\mathbb {R}} {\mathbf {T}}^H = \begin{bmatrix} {\mathbf {R}} &{} \tilde{{\mathbf {R}}} \\ \tilde{{\mathbf {R}}}^* &{}{\mathbf {R}}^* \end{bmatrix}, \end{aligned}$$
(11)

where \({\mathbf {R}}\) is the standard correlation matrix

$$\begin{aligned} {\mathbf {R}} = {\mathbf {R}}_{rr} + {\mathbf {R}}_{jj} + j({\mathbf {R}}_{jr} - {\mathbf {R}}_{rj}) = {\mathbf {R}}^H \end{aligned}$$
(12)

and \(\tilde{{\mathbf {R}}}\) is the pseudo-correlation matrix

$$\begin{aligned} \tilde{{\mathbf {R}}} = {\mathbf {R}}_{rr} - {\mathbf {R}}_{jj} + j({\mathbf {R}}_{jr} + {\mathbf {R}}_{rj}) = \tilde{{\mathbf {R}}}^T. \end{aligned}$$
(13)

It is worth noting that both \({\mathbf {R}}\) and \(\tilde{{\mathbf {R}}}\) are required for a complete second-order characterization of the WL-RKHS. The degree of impropriety can be measured by the complex correlation coefficient \({\underline{\rho }}\) between \({\varvec{\varPhi }}\) and \({\varvec{\varPhi }}^*\). Many correlation analysis techniques transform \({\varvec{\varPhi }}\) and \({\varvec{\varPhi }}^*\) into internal representations \({\varvec{\xi }} = {\varvec{A\varPhi }}\) and \({\varvec{\psi }} = {\varvec{B\varPhi }}^*\). The full-rank matrices \({\mathbf {A}}\) and \({\mathbf {B}}\) are chosen to maximize all partial sums over the absolute values of the correlations \(\eta _i = {\mathbb {E}}[\xi _i\psi _i]\),

$$\begin{aligned} \max _{{\mathbf {A}},{\mathbf {B}}} = \sum _{i=1}^r |\eta _i|,\quad r = 1\cdots p_r, \end{aligned}$$
(14)

subject to the following constraints that determine three popular correlation analysis techniques: canonical correlation analysis (CCA), multivariate linear regression (MLR), and partial least squares (PLS) [29]. Some expressions of correlation coefficient \({\underline{\rho }}\) are

$$\begin{aligned} \begin{aligned} {\underline{\rho }}_1&= 1 - \prod _{i=1}^{r}(1-\eta _i^2) = 1 - \frac{\det \underline{{\mathbf {R}}} }{\det ^2{\mathbf {R}}},\\ {\underline{\rho }}_2&= \prod _{i=1}^{r}\eta _i^2 = \frac{\det (\tilde{{\mathbf {R}}}{\mathbf {R}}^{-*}\tilde{{\mathbf {R}}})}{\det {\mathbf {R}}},\\ {\underline{\rho }}_3&= \frac{1}{n}\sum _{i=1}^{r}\eta _i^2 = \frac{1}{n} tr({\mathbf {R}}^{-1}\tilde{{\mathbf {R}}}{\mathbf {R}}^{-*}\tilde{{\mathbf {R}}}), \end{aligned} \end{aligned}$$
(15)

where \({\mathbf {R}}^{-*}\) denotes \(({\mathbf {R}}^{-1})^*\). These correlation coefficients all satisfy \(0 \le {\underline{\rho }} \le 1\).

However, the dimensionality of \({\varvec{\varphi }}(\cdot )\) is generally high, this leads to the operation of correlation matrix unacceptable in practical kernel algorithms. Fortunately, using Gram matrix is an alternative way to solve this problem. Similar to the derivation of the correlation matrix, we firstly define the real Gram matrix of \({\varvec{\varPhi }}_{\mathbb {R}}' = \left[ {\varvec{\varPhi }}_r, {\varvec{\varPhi }}_j\right] \) as

$$\begin{aligned} {\mathbf {G}}_{\mathbb {R}} = {\varvec{\varPhi }}_{\mathbb {R}}'^T {\varvec{\varPhi }}_{\mathbb {R}}' = \begin{bmatrix} {\mathbf {G}}_{rr} &{} {\mathbf {G}}_{rj} \\ {\mathbf {G}}_{rj}^T &{} {\mathbf {G}}_{jj} \end{bmatrix}, \end{aligned}$$
(16)

where \({\mathbf {G}}_{rr} = {\mathbb {E}}\left[ {\varvec{\varPhi }}_r^T{\varvec{\varPhi }}_r \right] , ~{\mathbf {G}}_{rj} = {\mathbb {E}}\left[ {\varvec{\varPhi }}_r^T{\varvec{\varPhi }}_j \right] = {\mathbf {G}}_{jr}^T\), and \({\mathbf {G}}_{jj} = {\mathbb {E}}\left[ {\varvec{\varPhi }}_j^T{\varvec{\varPhi }}_j \right] \). The elements of these Gram matrix can be denoted as kernel functions \([{\mathbf {G}}_{rr}]_{m,n} = \kappa _{rr}({\mathbf {x}}_m,{\mathbf {x}}_n), ~ [{\mathbf {G}}_{rj}]_{m,n} = \kappa _{rj}({\mathbf {x}}_m,{\mathbf {x}}_n), ~ [{\mathbf {G}}_{jj}]_{m,n} = \kappa _{jj}({\mathbf {x}}_m,{\mathbf {x}}_n)\). The augmented form of \({\varvec{\varPhi }}_{\mathbb {R}}'\) is \(\underline{{\varvec{\varPhi }}}' = {\mathbf {T}} {\varvec{\varPhi }}_{\mathbb {R}}'\). Then, the augmented Gram matrix can be derived as.

$$\begin{aligned} \underline{{\mathbf {G}}} = \begin{bmatrix} {\mathbf {G}} &{} \tilde{{\mathbf {G}}} \\ \tilde{{\mathbf {G}}}^* &{}{\mathbf {G}} \end{bmatrix}, \end{aligned}$$
(17)

where the standard Gram matrix \({\mathbf {G}}\) and the new pseudo-Gram matrix \(\tilde{{\mathbf {G}}}\) are defined as

$$\begin{aligned}&{\mathbf {G}} = {\mathbf {G}}_{rr} + {\mathbf {G}}_{jj} + j({\mathbf {G}}_{jr} - {\mathbf {G}}_{rj}), \end{aligned}$$
(18)
$$\begin{aligned}&\tilde{{\mathbf {G}}} = {\mathbf {G}}_{rr} - {\mathbf {G}}_{jj} + j({\mathbf {G}}_{jr} + {\mathbf {G}}_{rj}). \end{aligned}$$
(19)

As a complement to the standard Gram matrix, the pseudo-Gram matrix provides the variance between the real and imaginary parts of the non-circular complex signal.

3 Algorithm Design

In this section, we discuss the generalized complex kernel affine projection algorithms and the online sparsification methods.

3.1 Generalized Complex Kernel Affine Projection Algorithms

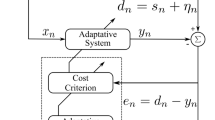
To gain insight, we employ the affine subspace method [23] to derive the AP algorithms. In linear adaptive filters, let \(({\mathbf {x}}_1,d_1), ({\mathbf {x}}_2,d_2),\ldots ({\mathbf {x}}_K,d_K)\) be a stream of input and desired signal pairs. At the kth instant, we can define a hyperplane \(\varPi _{k} = \left\{ {\mathbf {w}}\in {\mathbb {C}}^M |\langle {\mathbf {x}}_{k},{\mathbf {w}} \rangle = d_{k} \right\} \), which is orthogonal to \({\mathbf {x}}_{k}\) and passes through the point \(\frac{d_{k}}{\Vert {\mathbf {x}}_{k}\Vert ^2}{\mathbf {x}}_{k}\). Figure 1 shows a geometric description of the AP algorithms, which uses more recent inputs \({\mathbf {x}}_{k}, {\mathbf {x}}_{k-1}, {\mathbf {x}}_{k-P}\) and carries out the affine projection of \({\mathbf {w}}_{k}\) onto the affine subspace \(\varPi ^{(k)} = \varPi _{k}\cap \varPi _{k-1}\cap \cdots \cap \varPi _{k-(P-1)}\) to generalize the update process of weights as

$$\begin{aligned} \begin{aligned} {\mathbf {w}}_{k+1}&= {\mathbf {w}}_{k} + \mu \varDelta {\mathbf {w}}_{k}\\ \varDelta {\mathbf {w}}_{k}&= \text {Proj}_{\varPi ^{(k)}} {\mathbf {w}}_{k} - {\mathbf {w}}_{k} = {\mathbf {X}}_{k}^\dag \left( {\mathbf {d}}_{k} - {\mathbf {X}}_{k}{\mathbf {w}}_{k}\right) , \end{aligned} \end{aligned}$$
(20)

where \({\mathbf {d}}_k = \left[ d_{k}, d_{k-1}, \ldots , d_{k-P+1}\right] ^T\), \( {\mathbf {X}}_{k} = \left[ {\mathbf {x}}_{k}, {\mathbf {x}}_{k-1}, \ldots , {\mathbf {x}}_{k-P+1} \right] ^T\), \(\mu \) denotes step update factor, and \(\text {Proj}_{\varPi ^{(k)}} {\mathbf {w}}_{k}\) denotes the projection of \({\mathbf {w}}_{k}\) onto the affine subspace \(\varPi ^{(k)}\). The Moore–Penrose pseudo-inverse [16] of \({\mathbf {X}}_{k}\) is \({\mathbf {X}}_{k}^\dag = {\mathbf {X}}_{k}^H\left( {\mathbf {X}}_{k}{\mathbf {X}}_{k}^H\right) ^{-1}\). Therefore, the basic AP algorithm, named AP-1, can be derived as

$$\begin{aligned} {\mathbf {w}}_{k+1} = {\mathbf {w}}_{k} + \mu {\mathbf {X}}_{k}^H\left( {\mathbf {X}}_{k}{\mathbf {X}}_{k}^H\right) ^{-1} {\mathbf {e}}_{k}, \end{aligned}$$
(21)

where \({\mathbf {e}}_{k}\) is the error defined by

$$\begin{aligned} \begin{aligned} {\mathbf {e}}_{k}&\triangleq {\mathbf {d}}_{k}-{\mathbf {X}}_{k}{\mathbf {w}}_{k}\\&=\begin{bmatrix} d_k-\langle {\mathbf {x}}_{k}, {\mathbf {w}}_{k} \rangle \\ d_{k-1}-\langle {\mathbf {x}}_{k-1}, {\mathbf {w}}_{k} \rangle \\ \vdots \\ d_{k-P+1}-\langle {\mathbf {x}}_{k-P+1}, {\mathbf {w}}_{k} \rangle \end{bmatrix}. \end{aligned} \end{aligned}$$
(22)
Fig. 1
figure 1

The geometric description of affine projection algorithms

Full size image

Adding the regularized item \(\delta {\mathbf {I}}_P\) to \({\mathbf {X}}_{k}{\mathbf {X}}_{k}^H\) to stabilize the numerical inversion process, we obtain the regularized AP algorithm, named AP-2, which can be derived as

$$\begin{aligned} {\mathbf {w}}_{k+1} = {\mathbf {w}}_{k} + \mu {\mathbf {X}}_{k}^H\left( {\mathbf {X}}_{k}{\mathbf {X}}_{k}^H + \delta {\mathbf {I}}_P\right) ^{-1} {\mathbf {e}}_{k}. \end{aligned}$$
(23)

AP-2 reduces to AP-1 when \(\delta =0\). We can map all the inputs into the complex RKHS using the complex feature mapping \({\varvec{\varphi }}\). The update equation of AP-2 in the complex RKHS is

$$\begin{aligned} {\varvec{\omega }}_{k+1} = {\varvec{\omega }}_{k} + \mu {\varvec{\varPhi }}_{k}^H({\varvec{\varPhi }}_{k}{\varvec{\varPhi }}_{k}^H+\delta {\mathbf {I}}_P)^{-1} {\varvec{\varepsilon }}_{k}, \end{aligned}$$
(24)

where \( {\varvec{\varPhi }}_{k} = [{\varvec{\varphi }}({\mathbf {x}}_{k}), {\varvec{\varphi }}({\mathbf {x}}_{k-1}), \ldots , {\varvec{\varphi }}({\mathbf {x}}_{k-P+1})]^T\) and

$$\begin{aligned} {\varvec{\varepsilon }}_{k} = {\mathbf {d}}_{k}-{\varvec{\varPhi }}_{k}{\varvec{\omega }}_{k} =\begin{bmatrix} d_{k}-f_{k}({\mathbf {x}}_{k})\\ d_{k-1}-f_{k}({\mathbf {x}}_{k-1})\\ \vdots \\ d_{k-P+1}-f_{k}({\mathbf {x}}_{k-P+1}) \\ \end{bmatrix}. \end{aligned}$$
(25)

The output \(f_{k}({\mathbf {x}}')\) in (25) follows the inner product of \({\varvec{\varphi }}({\mathbf {x}}')\) and \({\varvec{\omega }}_{k}\) in RKHS

$$\begin{aligned} f_{k}({\mathbf {x}}') = \langle {\varvec{\varphi }}({\mathbf {x}}'),{\varvec{\omega }}_{k} \rangle _{\mathcal {H}}, \end{aligned}$$
(26)

where the weight \({\varvec{\omega }}_k\) can be expressed as a linear combination of mapped inputs \({\varvec{\varphi }}({\mathbf {x}}(i))\) in the RKHS

$$\begin{aligned} {\varvec{\omega }}_k = \sum _{j=-P+1}^{k-1} a_{k,j} {\varvec{\varphi }}({\mathbf {x}}_j). \end{aligned}$$
(27)

Define a Gram matrix \({\mathbf {G}}_k \triangleq {\varvec{\varPhi }}_k{\varvec{\varPhi }}_k^H\in {\mathbb {C}}^{P\times P}\), where \( [{\mathbf {G}}_k]_{m-k+P,~n-k+P} = \kappa ({\mathbf {x}}_m,{\mathbf {x}}_n), ~k-P+1\le m,n\le k\), and a new vector

$$\begin{aligned} {\mathbf {b}}_{k} \triangleq \mu ({\mathbf {G}}_k + \delta {\mathbf {I}}_P)^{-1}{\varvec{\varepsilon }}_k. \end{aligned}$$
(28)

Then, the update of the weight in (24) can be rewritten as

$$\begin{aligned} \begin{aligned} {\varvec{\omega }}_{k+1}&= \sum _{j=-P+1}^{k-1} a_{k,j} {\varvec{\varphi }}({\mathbf {x}}_j) + {\varvec{\varPhi }}_k^H {\mathbf {b}}_{k} \\&= \sum _{j=-P+1}^{k-1} a_{k,j} {\varvec{\varphi }}({\mathbf {x}}_j) + \sum _{j=k-P+1}^{k} b_{k,j} {\varvec{\varphi }}({\mathbf {x}}_j)\\&= \sum _{j=-P+1}^{k} a_{k+1,j} {\varvec{\varphi }}({\mathbf {x}}_j), \end{aligned} \end{aligned}$$
(29)

where

$$\begin{aligned} a_{k+1,j} = {\left\{ \begin{array}{ll} a_{k,j} &{} -P+1\le j\le k-P\\ a_{k,j} + b_{k,j-k} &{} k-P+1\le j\le k-1\\ b_{k,k} &{} j=k \end{array}\right. }. \end{aligned}$$
(30)

The output can be rewritten as a linear combination of kernels

$$\begin{aligned} f_k({\mathbf {x}}') =\langle {\varvec{\varphi }}({\mathbf {x}}'),{\varvec{\omega }}_{k} \rangle _{\mathcal {H}} = \sum _{j=-P+1}^{k-1}a_{k,j}\kappa ({\mathbf {x}}',{\mathbf {x}}_j). \end{aligned}$$
(31)

This describes the direct form of the regularized CKAP algorithm, named CKAP-2, in which \(\kappa ({\mathbf {x}}',{\mathbf {x}}_j)\) is a complex kernel function. When \(\delta =0\), CKAP-2 reduces to the basic CKAP algorithm, named CKAP-1. Next, we use the widely linear approach in (8) to obtain the output of the GCKAP algorithms:

$$\begin{aligned} \begin{aligned} f_k({\mathbf {x}}')&= {\varvec{\kappa }}({\mathbf {x}}',{\mathcal {D}}_{k-1}){\mathbf {a}}_k + \tilde{{\varvec{\kappa }}}({\mathbf {x}}',{\mathcal {D}}_{k-1}) {\mathbf {a}}_k^*\\&= \sum _{j=-P+1}^{k-1} \left[ a_{k,j}\kappa ({\mathbf {x}}',{\mathbf {x}}_j) + a^*_{k,j}{\tilde{\kappa }}({\mathbf {x}}',{\mathbf {x}}_j)\right] , \end{aligned} \end{aligned}$$
(32)

where \({\mathcal {D}}_{k-1} = \{{\mathbf {x}}_j\}_{j=-P+1}^{k-1}\) is the training dictionary set when all the inputs are added. The augmented coefficient vector \(\underline{{\mathbf {b}}}_{k} = \left[ {\mathbf {b}}_{k}^T,~ {\mathbf {b}}_{k}^H \right] ^T\) can be calculated by

$$\begin{aligned} \underline{{\mathbf {b}}}_{k} = \mu (\underline{{\mathbf {G}}} + \delta {\mathbf {I}}_{2P})^{-1} \underline{{\varvec{\varepsilon }}}_k, \end{aligned}$$
(33)

where \(\underline{{\varvec{\varepsilon }}}_k = \left[ {\varvec{\varepsilon }}_k^T,~{\varvec{\varepsilon }}_k^H \right] ^T\) is the augmented error vector. Let \(\underline{{\varvec{\varPhi }}}_k = \left[ {\varvec{\varPhi }}^T_k, ~ {\varvec{\varPhi }}^H_k \right] ^T\) be the augmented inputs. The augmented Gram matrix can be denoted as \(\underline{{\mathbf {G}}} = \underline{{\varvec{\varPhi }}}_k \underline{{\varvec{\varPhi }}}_k^H\in {\mathbb {C}}^{2P\times 2P}\). The inverse operation of \(\underline{{\mathbf {G}}} + \delta {\mathbf {I}}_{2P}\) can no longer be solved by the iteration method in [23]. However, the directly inverse operation of the augmented Gram matrix requires the complexity of \({\mathcal {O}}(8P^3)\). We propose a decomposition method to reduce the complexity. We rewrite the block form of \(\underline{{\mathbf {G}}}\) as

$$\begin{aligned} \underline{{\mathbf {G}}} =\begin{bmatrix} {\mathbf {G}}_{} &{} \tilde{{\mathbf {G}}} \\ \tilde{{\mathbf {G}}}^* &{}{\mathbf {G}}_{} \end{bmatrix}, \end{aligned}$$
(34)

where the standard Gram matrix \({\mathbf {G}}\) and the pseudo-Gram matrix \(\tilde{{\mathbf {G}}}\) are

$$\begin{aligned} {\mathbf {G}}&= {\mathbf {G}}_{rr} + {\mathbf {G}}_{jj} + j({\mathbf {G}}_{jr} - {\mathbf {G}}_{rj}),\end{aligned}$$
(35)
$$\begin{aligned} \tilde{{\mathbf {G}}}&= {\mathbf {G}}_{rr} - {\mathbf {G}}_{jj} + j({\mathbf {G}}_{jr} + {\mathbf {G}}_{rj}). \end{aligned}$$
(36)

The real Gram matrices are defined as

$$\begin{aligned} \begin{aligned}&[{\mathbf {G}}_{rr}]_{m-k+P,~n-k+P} = \kappa _{rr}({\mathbf {x}}_m,{\mathbf {x}}_n),\\&[{\mathbf {G}}_{rj}]_{m-k+P,~n-k+P} = \kappa _{rj}({\mathbf {x}}_m,{\mathbf {x}}_n), \quad {\mathbf {G}}_{jr} = {\mathbf {G}}_{rj}^T,\\&[{\mathbf {G}}_{jj}]_{m-k+P,~n-k+P} = \kappa _{jj}({\mathbf {x}}_m,{\mathbf {x}}_n), \quad k-P+1\le m,n\le k. \end{aligned} \end{aligned}$$
(37)

The inverse of \(\underline{{\mathbf {G}}}\) can be factored as

$$\begin{aligned} \underline{{\mathbf {G}}}_{}^{-1} = \begin{bmatrix} {\mathbf {I}} &{} {\mathbf {0}} \\ -{\mathbf {W}}^H &{} {\mathbf {I}} \end{bmatrix} \begin{bmatrix} {\mathbf {V}}^{-1} &{} {\mathbf {0}} \\ {\mathbf {0}} &{} {\mathbf {G}}_{}^{-*} \end{bmatrix} \begin{bmatrix} {\mathbf {I}} &{} -{\mathbf {W}} \\ {\mathbf {0}} &{} {\mathbf {I}} \end{bmatrix} , \end{aligned}$$
(38)

where \({\mathbf {W}} = \tilde{{\mathbf {G}}} {\mathbf {G}}_{}^{-*}\), \({\mathbf {V}} = {\mathbf {G}}_{} - {\mathbf {W}} \tilde{{\mathbf {G}}}^*\) denotes the Schur complement [16] of \( {\mathbf {G}}_{}^{*} \) within \(\underline{{\mathbf {G}}}\), and \({\varvec{G^{-*}}}\) denotes \(({\varvec{G}}^{-1})^*\). Using the factor of (38), the augmented vector \(\underline{{\mathbf {b}}}_k\) can be derived as

$$\begin{aligned} \begin{aligned} \underline{{\mathbf {b}}}_k&= \mu \left( \underline{{\mathbf {G}}} + \delta {\mathbf {I}}_{2P}\right) ^{-1} \underline{{\varvec{\varepsilon }}}_k\\&= \mu \begin{bmatrix} {\mathbf {G}} + \delta {\mathbf {I}}_{P} &{} \tilde{{\mathbf {G}}} \\ \tilde{{\mathbf {G}}}^* &{}{\mathbf {G}} + \delta {\mathbf {I}}_{P} \end{bmatrix}^{-1} \underline{{\varvec{\varepsilon }}}_k \\&= \mu \begin{bmatrix} {\mathbf {I}} &{} {\mathbf {0}} \\ -{\mathbf {W}}_d^H &{} {\mathbf {I}} \end{bmatrix} \begin{bmatrix} {\mathbf {V}}_d^{-1} &{} {\mathbf {0}} \\ {\mathbf {0}} &{} {\mathbf {G}}_{d}^{-*} \end{bmatrix} \begin{bmatrix} {\mathbf {I}} &{} -{\mathbf {W}}_d \\ {\mathbf {0}} &{} {\mathbf {I}} \end{bmatrix} \begin{bmatrix} {\varvec{\varepsilon }}_k \\ {\varvec{\varepsilon }}_k^* \end{bmatrix}\\&= \mu \begin{bmatrix} {\mathbf {V}}_d^{-1} &{} {\mathbf {0}} \\ -{\mathbf {W}}_d^H {\mathbf {V}}_d^{-1} &{} {\mathbf {G}}_{d}^{-*} \end{bmatrix} \begin{bmatrix} {\mathbf {I}} &{} -{\mathbf {W}}_d \\ {\mathbf {0}} &{} {\mathbf {I}} \end{bmatrix} \begin{bmatrix} {\varvec{\varepsilon }}_k \\ {\varvec{\varepsilon }}_k^* \end{bmatrix}\\&= \mu \begin{bmatrix} {\mathbf {V}}_d^{-1} &{} -{\mathbf {V}}_d^{-1}{\mathbf {W}}_d \\ -{\mathbf {W}}_d^H {\mathbf {V}}_d^{-1} &{} ~~{\mathbf {W}}_d^H {\mathbf {V}}_d^{-1}{\mathbf {W}}_d + {\mathbf {G}}_{d}^{-*} \end{bmatrix} \begin{bmatrix} {\varvec{\varepsilon }}_k \\ {\varvec{\varepsilon }}_k^* \end{bmatrix}\\&= \begin{bmatrix} \mu {\mathbf {V}}_d^{-1}({\varvec{\varepsilon }}_k - {\mathbf {W}}_d {\varvec{\varepsilon }}_k^*) \\ -\mu {\mathbf {W}}_d^H {\mathbf {V}}_d^{-1}({\varvec{\varepsilon }}_k - {\mathbf {W}}_d {\varvec{\varepsilon }}_k^*) + \mu {\mathbf {G}}_{d}^{-*} {\varvec{\varepsilon }}_k^* \end{bmatrix}, \end{aligned} \end{aligned}$$
(39)

where \({\mathbf {G}}_{d} = {\mathbf {G}}_{} + \delta {\mathbf {I}}_P\) is the regularized Gram matrix, \({\mathbf {W}}_d = \tilde{{\mathbf {G}}} {\mathbf {G}}_{d}^{-*}\), and \({\mathbf {V}}_d = {\mathbf {G}}_{d} - {\mathbf {W}}_d \tilde{{\mathbf {G}}}^*\). Therefore, by the upper part of the representation of \(\underline{{\mathbf {b}}}_k\), the complex coefficient \({\mathbf {b}}_k\) can be further simplified as

$$\begin{aligned} {\mathbf {b}}_k =\mu {\mathbf {V}}_d^{-1}({\varvec{\varepsilon }}_k - {\mathbf {W}}_d {\varvec{\varepsilon }}_k^*). \end{aligned}$$
(40)

The vector form iteration of \({\mathbf {a}}_k\) can be derived from (30):

$$\begin{aligned} {\mathbf {a}}_{k+1} = [{\mathbf {a}}_k^T,~0]^T + [{\mathbf {0}},~{\mathbf {b}}_k^T]^T. \end{aligned}$$
(41)

The final GCKAP-2 algorithm is summarized in Algorithm 1. If the current input satisfies some sparsification criteria, \(({\mathbf {x}}_i, d_i)\) is added to the dictionary. Note that GCKAP-2 reduces to GCKAP-1 when the regularized factor \(\delta =0\). In addition, the CKAP algorithms can be denoted as particular cases of the GCKAP algorithms when the pseudo-kernel vanishes. The inverse operation of the standard regularized Gram matrix \({\mathbf {G}}_d^{-1}\) can be substituted by the iteration form [32], which requires the complexity \({\mathcal {O}}(P^2)\). Through the decomposition method, the complexity of calculating the coefficient vector \({\mathbf {b}}_k\) is reduced to \({\mathcal {O}}(3P^3)\). In general, this complexity is acceptable for the AP algorithms because of the limited projection order. The computational costs of complex KAF algorithms are summarized in Table 1, where N denotes the dictionary size at current iteration and P denotes the projection order of AP algorithms. As presented in this table, compared with CKAP algorithm, GCKAP algorithm does not add much extra computational cost for small projection order. Widely linear KAF algorithms (GCKLMS and GCKAP) have almost the same computational cost to the pure complex KAF algorithms.

figure a
Table 1 Computational cost of complex KAF algorithms
Full size table

3.2 Online Sparsification Methods

Several online sparsification methods have been proposed to overcome the infinite growth of the dictionary set while keeping the remaining data sufficiently well. The novelty criterion (NC) calculates the distance from a new data point to the current dictionary. The approximate linear dependency (ALD) criterion measures how well the data can be approximated in the RKHS as a linear combination of the dictionary set. However, the ALD criterion is not suitable for KLMS and KAP due to the quadratic complexity. The coherence sparsification (CS) criterion checks the similarity by the kernel function between the new data and the dictionary set. Recently, the angle sparsification (AS) criterion was proposed in [38], which defined the geometric structure in the RKHS by inner production. We add this criterion to the GCKAP algorithms.

The basic idea of the angle criterion is to define the angles among functions in the feature space as the sparsification criterion. The cosine of the angle between \({\varvec{\varphi }}({\mathbf {x}})\) and \({\varvec{\varphi }}({\mathbf {y}})\) is defined by

$$\begin{aligned} \nu (\mathbf {x,y}) = \frac{\langle {\varvec{\varphi }}({\mathbf {x}}),{\varvec{\varphi }}({\mathbf {y}}) \rangle _{{\mathcal {H}}}}{\Vert {\varvec{\varphi }}({\mathbf {x}})\Vert _{{\mathcal {H}}}\Vert {\varvec{\varphi }}({\mathbf {y}})\Vert _{{\mathcal {H}}}} = \frac{\kappa (\mathbf {y,x})}{\sqrt{\kappa (\mathbf {x,x})\kappa (\mathbf {y,y})}}. \end{aligned}$$
(42)

Suppose the current dictionary is \({\mathcal {D}}=\{({\varvec{\varphi }}(\tilde{{\mathbf {x}}}_k),{\tilde{d}}_k)\}_{k=1}^N\) and a new sample \(({\mathbf {x}}_i,d_i)\) is coming. The procedure of the angle criterion can be described as follows. First, the parameter

$$\begin{aligned} \nu _i = \max _{1\le k\le N} |\nu ({\mathbf {x}}_i,\tilde{{\mathbf {x}}}_k)| \in [0,1] \end{aligned}$$
(43)

is calculated. Second, if \(\nu _i\) is smaller than a predefined threshold \(\nu _0\), \(({\varvec{\varphi }}({\mathbf {x}}_i),d_i)\) is added to \({\mathcal {D}}\); otherwise, it is discarded. The parameter \(\nu _0\) controls the level of similarity among the elements in \({\mathcal {D}}\) and is called the similarity parameter.

4 Simulation Experiments

In this section, we compare the performance of the proposed GCKAP algorithms with that of the CKLMS2 [6], GCKLMS [3], CKAP-1 and CKAP-2 [22] algorithms in nonlinear channel equalization, as shown in Fig. 2. The nonlinear channel consists of a linear filter followed by a memoryless strong or soft nonlinearity. At the end of the channel, the signal is corrupted by additive noise. The equalizer performs an inverse filtering of the received signal \(r_k\) to recover the input signal \(s_k\) with as small error as possible. Two experiments are considered: (a) a strong nonlinear channel equalization with non-circular Gaussian distributed signal input and (b) a soft nonlinear channel equalization with QPSK input. In all experiments, the complex Gaussian kernel functions [6] are used in CKLMS2, CKAP-1 and CKAP-2:

$$\begin{aligned} \kappa _{{\mathbb {C}}} = \exp \left( -({\mathbf {x}} - {\mathbf {x}}'^*)^T({\mathbf {x}} - {\mathbf {x}}'^*) / \gamma ^2 \right) , \end{aligned}$$
(44)

where \(\gamma \) is the kernel parameter. The real Gaussian kernel functions [3] with complex inputs are used in GCKLMS, GCKAP-1 and GCKAP-2:

$$\begin{aligned} \kappa _{{\mathbb {R}}} = \exp \left( -({\mathbf {x}} - {\mathbf {x}}')^H({\mathbf {x}} - {\mathbf {x}}') / \gamma ^2 \right) . \end{aligned}$$
(45)
Fig. 2
figure 2

The nonlinear channel equalization

Full size image

4.1 Strong Nonlinear Channel Equalization

In the first experiment, we reproduce the nonlinear channel equalization task in [7]. The channel consists of a linear filter

$$\begin{aligned}\begin{aligned} t_k&= (-0.9+0.8j)s_{k} + (0.6-0.7j)s_{k-1}\\&\quad +(-0.4+0.3j)s_{k-2}+(0.3-0.2j)s_{k-3}\\&\quad +(-0.1-0.2j)s_{k-4} \end{aligned} \end{aligned}$$

and a memoryless nonlinearity

$$\begin{aligned} q_{k} = t_{k} + (0.2+0.25j)t^2_{k} + (0.08+0.09j)t^3_{k}. \end{aligned}$$

At the end of the channel, the signal is corrupted by white circular Gaussian noise and then observed as \(r_{k}\). The signal-to-noise ratio (SNR) is set to 15 dB. The non-circular Gaussian distributed signal as the input is fed into the channel:

$$\begin{aligned} s_{k} = 0.7(\sqrt{1-\rho ^2} \cdot x_{k} + j\rho \cdot y_{k}), \end{aligned}$$

where \(x_{k}\) and \(y_{k}\) are independent Gaussian random variables, with \(\rho = 0.1\) for non-circular input signals. The vector \({\mathbf {x}} = \left[ r_{k+D},~ r_{k+D-1},\ldots , r_{k+D-L+1} \right] ^T\) is the training samples of the equalizer, where L and D are the length and delay of the equalizer, respectively. Here, we set \(L=5,~D=2\). The equalizer is conducted on 100 independent trails of 10000 samples of the input signal. The purpose of the equalizer is to estimate the original input signal. We set the step update factor \(\mu = 1/6\) for all algorithms. In the AP algorithms, we set the order of projection \(P = 4\). The kernel parameters are set as \(\gamma = 4\) for a complex kernel and as \(\gamma _r = 5,~\gamma _j = 3\) for a real kernel and pseudo-kernel, respectively.

The average MSEs are shown in Fig. 3. The novelty criterion is used for the sparsification of all algorithms with \(\delta _1 = 0.15,~ \delta _2 = 0.2\). It can be seen that the convergence rates of the CKAP and GCKAP algorithms are faster than that of the CKLMS algorithms. In addition, the GCKAP algorithms provide the smallest steady-state MSE. To compare the online sparsification criteria, the dictionary size and growth rate of GCKAP-2 are shown in Fig. 4. The similarity parameter is chosen as \(\nu _0 = 0.9\) for the coherence and the angle criteria. It can be seen that the growth rate drops dramatically from around 1 to 0.1. To achieve almost the same steady-state MSE, more data are selected for the dictionary with the novelty criterion. Only round 1030 inputs out of 10,000 (10.3%) are eventually selected into the dictionary with the coherence criterion and angle criterion. We know that the coherence and the angle criteria perform in the RKHS, while the novelty criterion works in the original space. Therefore, the criterion in the RKHS can represent the space more accurately than that in the original space.

The simulations of the effect of step size factor and projection order of the GCKAP-2 are shown in Figs. 5 and 6, respectively. The step size factor is set to 0.03, 0.15, 0.5 from small to large. The simulation results show that the larger the step size factor, the faster the convergence rate of the algorithm, and vice versa. The projection order of the algorithm is set to 1, 2, and 5, respectively. The GCKAP algorithm reduces to GCKLMS when the projection order is 1. The simulation results show that the larger the projection order, the faster the convergence rate of the algorithm. It can be seen that the effect of step size factor and projection order of the GCKAP-2 algorithm is consistent with the traditional AP algorithm. However, in the RKHS, the kernel algorithms need to use the growing dictionary set to construct the nonlinear feature space. It will further lead to an increase in the misadjustment in steady state. This stack effect reduces the difference between the misadjustment behaviors under the various parameter settings.

Fig. 3
figure 3

Learning curves of CKLMS and CKAP for strong nonlinear channel equalization with the novelty criterion

Full size image
Fig. 4
figure 4

Dictionary size and growth rate of GCKAP-2 with the novelty criterion, coherence criterion, and angle criterion

Full size image
Fig. 5
figure 5

The effect of step size factor of the GCKAP-2 algorithm

Full size image
Fig. 6
figure 6

The effect of projection number of the GCKAP-2 algorithm

Full size image

4.2 Soft Nonlinear Channel Equalization with the QPSK Input

In this experiment, we consider a soft nonlinear channel equalization task with the QPSK input. The channel consists of a linear filter

$$\begin{aligned} t_{k} = s_{k} + (0.5-0.5j)s_{k-1}+(0.1+0.1j)s_{k-2} \end{aligned}$$

and a memoryless nonlinearity

$$\begin{aligned} q_{k} = t_{k} + (0.1+0.15j)t^2_{k}. \end{aligned}$$

The QPSK input signal is \(s_{k} = x_{k} + jy_{k}\), where \(x_{k}\) and \(y_{k}\) are independent binary \(\{-1, +1\}\) data streams. The channel parameters are set the same as strong nonlinear channel equalization. The step update factor and the order of projection also remain the same. We set the kernel parameter \(\gamma = 2.7\) for the complex kernel and \(\gamma _r = 2.3,~\gamma _j = 2.1\) for the real kernel and pseudo-kernel, respectively.

The average MSE learning curves are plotted in Fig. 7. It can be shown that the proposed GCKAP-1 and GCKAP-2 algorithms outperform the other algorithms. This reflects the main advantage of GCKAP algorithms: the kernel and pseudo-kernel provide more representation to the QPSK improper signal. The estimated symbols from the training data are shown in Fig. 8. As can be seen, the linear AP algorithm produces a poor estimation of the symbols; however, the GCKAP-2 algorithm can model and invert this nonlinear behavior.

Fig. 7
figure 7

Learning curves of CKLMS and CKAP for soft nonlinear channel equalization with the QPSK input

Full size image
Fig. 8
figure 8

Estimated symbols from the training data by the linear AP (left) and GCKAP-2 (right)

Full size image

5 Conclusions

The generalized complex affine projection algorithms in the WL-RKHS were developed in this paper. The proposed GCKAP algorithms retain the simplicity while outperforming the performance of the CKLMS algorithms. In addition, they work in the WL-RKHS, providing the complete solution for both circular and non-circular complex nonlinear problems. After discussing the statistical properties of the WL-RKHS, the augmented Gram matrix, which includes the standard Gram matrix and the pseudo-Gram matrix, was proposed to calculate the expansion coefficients in the GCKAP algorithms. As a complement to the standard Gram matrix, the pseudo-Gram matrix provides the variance between the real and imaginary parts of a non-circular signal. In addition, with the proposed decomposition method, the complexity of the inverse operation of the augmented Gram matrix is reduced. Finally, our simulation results show that the sparsification criterion in the RKHS can represent the space more accurately than that in the original space.