1 Introduction

Phase velocities of elastic waves propagating with waveguides, such as layered media, depend on the wave number, indicating that these waves exhibit dispersive characteristics. These types of dispersive elastic waves have been the subject of many studies due to their significant applications in various fields such as geophysics, non-destructive testing of materials, and electronic signal processing devices. In [1,2,3,4,5,6,7,8,9,10,11,12,13,14], the propagation of nonlinear shear waves has been studied in a layered medium made of different homogeneous elastic materials, whereas the propagation of in-plane waves in a layered medium made of similar materials has been discussed in [15, 16]. In Teymur’s study [11], nonlinear Love waves have been examined in the context of the propagation in a half-space covered with a uniform finite thickness layer made of different isotropic and compressible materials. By employing asymptotic analysis to balance the nonlinearity and dispersion, it has been shown that the nonlinear self-modulation of Love waves is governed by an NLS equation. Subsequently, building upon this study as a reference, the propagation of Love waves in a nonlinear half-space covered with a nonlinear thin layer has been examined by using the same asymptotic expansion, as detailed in [10], and the NLS equation describing the self-modulation of waves has been derived. The results of the nonlinear thin layer approach have been compared with the results obtained in [14] for the linear thin layer approach and with the results obtained in [11] for the finite layer. Even at small wave numbers, it has been observed that the propagation is significantly influenced by nonlinear material parameters of the layer.

Numerous studies have also been conducted on investigating the effects of the constitutional linearity and nonlinearity, as well as the inhomogeneity of materials in the layered medium on wave propagation [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34]. The initial works in this scope focused on linear wave propagation in an elastic medium where material heterogeneity (or inhomogeneity) depends on the depth variable. In [17], Hudson concentrated on the existence of Love waves in a layer with finite depth characterized by a stress-free upper surface and a rigidly fixed lower boundary with the assumption that the density and rigidity of the medium are chosen as a random function of the depth variable. In [18], Avtar derived the dispersion relation governing the propagation of Love waves in a semi-infinite, double-layered heterogeneous medium characterized by variations in both the density and rigidity with depth. In [19], the author examined the linear SH wave propagating in a vertically heterogeneous elastic isotropic medium, and derived solutions for the SH wave equation for the rigidity and density. These solutions were expressed in terms of hypergeometric, Whittaker, Bessel and exponential functions. Singh et al. performed an analysis on the dispersion relation of Love waves in media with n layers, considering the rigidity and density to be functions of both the propagation and depth directions [20]. Wuttke et al. have investigated the scattering and diffraction phenomena of SH waves in a quadratically depth-dependent, inhomogeneous half-plane with canyon [22]. In the context of a periodically stratified elastic half-space with a coating layer, where the shear modulus and mass density exhibit variations described by a power function with respect to distance, Kowalczyk et al. have derived the frequency equation [23]. Subsequently, they provide a numerical analysis of how the mechanical properties of the medium affect wave velocity. Kumari et al. explained the impact of both the heterogeneity and thickness ratio of layers on the phase velocity of Love waves propagating in a half-space coated by two distinct layers of varying thickness. In this scenario, the rigidity and density of the top layer vary linearly, while only the rigidity of the intermediate layer experiences quadratic changes [24].

In the aforementioned studies, the constituent materials of the stratified medium are heterogeneous with linear properties. However, the literature also includes researches that investigate the impact of both the linear and nonlinear characteristics of heterogeneous materials that constitute stratified media on the propagation of nonlinear Love waves. Demirkus examined the influence of both heterogeneity and nonlinearity on the propagation of bright solitary Love waves in a nonhomogeneous layer where the constituent materials change as a hyperbolic function of the depth variable [29]. Then, a similar investigation is undertaken to analyze the propagation of nonlinear antisymmetric SH waves within a nonlinear plate composed of heterogeneous materials of finite thickness [30]. Subsequent works by the same researcher have systematically compared the effects of heterogeneity and nonlinearity in scenarios involving layered media composed of both homogeneous and heterogeneous nonlinear materials [31,32,33]. The propagation of nonlinear SH waves in media composed of different elastic materials but with the same type of heterogeneity has been investigated in [34]. In this work, the effect of both the layer’s heterogeneity properties and nonlinear material properties on wave propagation has been observed.

In the models of semi-infinite spaces, the previously employed inhomogeneity functions, though mathematically straightforward and widely recognized, pose the challenge of portraying a somewhat unrealistic degree of heterogeneity. This stems from their tendency to either diverge or vanish as \(x_2\) approaches infinity, or to exhibit same patterns periodically. These challenges can be addressed by taking into account that they emerge at a significant distance from the interface and by focusing on the wave localized near the surface [26]. However, in this article, the inhomogeneities in rigidity and density are modeled as exponential functions. Notably, these functions are bounded throughout the semi-infinite space and bear physical significance (refer to Eq. (3.3)) [27, 28]. The exact solution of the linear model describing the wave motion for exponential-type heterogeneous function models given by (3.3) is provided in [28].

There are few works that examine the effect of weak inhomogeneity on the propagation of waves in a layered medium composed of elastic materials [35,36,37]. In [35], the authors derived the first-order asymptotic solutions for the plane-wave response of a vertically heterogeneous elastic medium by using weak plane inhomogeneities. Additionally, in [36], the interaction of two longitudinal waves in a weakly inhomogeneous nonlinear elastic material is studied. In another work [37], the authors investigated the shear elastic wave propagation in a layer characterized by continuously changing periodical weak heterogeneity along the layer.

In our research, we will employ the heterogeneity model introduced in [27], with a specific emphasis on considering the heterogeneity effect as weak. Under this assumption, we will investigate the modulation of SH waves in a semi-infinite space composed of heterogeneous material covered by a thin elastic layer made of homogeneous material. Initially, by employing the thin layer approximation method as presented in [10], a reduced boundary value problem is derived from the problem of SH wave propagation in a nonlinear semi-infinite space characterized by weak heterogeneity in the vertical direction covered by distinct homogeneous isotropic nonlinear finite thickness layer. Subsequently, an NLS equation including an external force term has been obtained for the propagation of nonlinear SH waves by employing an asymptotic perturbation expansion. The weak inhomogeneity of the semi-infinite space is observed solely in this external force term. Both the effect of the nonlinearity of the thin layer and the heterogeneity and constitutional nonlinearity of the semi-infinite space on wave propagation have been examined numerically for real material models.

2 Love waves in a heterogeneous half-space covered by a homogeneous finite layer

Let \((x_1,x_2,x_3)\) and \((X_1,X_2,X_3)\) refer to the spatial and material coordinates of a point, respectively in three-dimensional space with respect to the same perpendicular Cartesian coordinate system. We consider a continuous medium consisting of a heterogeneous half-space that is covered with a uniformly finite-thickness layer made of homogeneous elastic material filling the following regions in the initial state

$$\begin{aligned} P_{1} =\{ ( X_{1},X_{2},X_{3}) \mid \quad 0\le X_{2}\le h, -\infty< (X_{1}, X_3)< \infty \}, \end{aligned}$$
(2.1)
$$\begin{aligned} P_{2} =\{ ( X_{1},X_{2},X_{3}) \mid \quad - \infty \le X_{2}\le 0, -\infty< (X_{1}, X_3)< \infty \} \end{aligned}$$
(2.2)

where h represents the constant thicknesses of the layer. We assume that the displacements and stresses are continuous in the interface \( X_{2}=0\), and the free surface \( X_{2}=h\) is free of traction. The anti-plane deformations are described by

$$\begin{aligned} x_{1}=X_{1},\qquad x_2=X_2,\qquad x_3=X_3+u^{(\alpha )}(X_1,X_2,t), \quad \alpha =1,2 \end{aligned}$$
(2.3)

which produce the shear wave propagation in the direction of \(X_1\). Here, t is the time, and \(u^{(\alpha )}\) denotes the particle’s displacement in region \(P_\alpha \) in the direction of \(X_3\) due to the polarization of waves [9]. The constituent material of the layer is incompressible, homogeneous, isotropic and elastic while that of the half-space is incompressible, heterogeneous, isotropic and elastic. In this study, the strain energy function associated with the layer is in the form of \(\Sigma _{1}\!=\!\Sigma _{1}(I_{1})\), while the strain energy function associated with the half-space is in the form of \(\Sigma _{2}\!=\!\Sigma _{2}(I_{1},X_2)\). Here, \(I_1\) is the first invariant of the Green’s deformation tensor \(C_{KL}\!=\!x_{k,K}x_{k,L}\) [9].

We define \(X_1=X\), \(X_2=Y\), and \(X_3=Z\), and consider that an elastic half-space occupies the region \(Y\le 0\) and it is covered by a layer consisting of a different elastic material with a uniform thickness of h. We assume that the free surface is free of traction, the stresses and displacements are continuous at the interface \(Y=0\) and the displacement in the half-space approaches to zero as \(Y\rightarrow -\infty \). In such conditions, we suppose that a surface SH wave having displacement component in the direction of Z propagates along the direction of X in the layered half-space. The displacement of a particle is denoted by \(u=u(X,Y,t)\) in the layer and by \(v=v(X,Y,t)\) in the half-space. Then, the approximate governing equations of motion and boundary conditions involving terms not higher than the third degree in the deformation gradients are as follows:

$$\begin{aligned}{} & {} \frac{{\partial }^{2}u}{\partial {t}^{2}}-{c}_{1}^{2}\left( \frac{{\partial }^{2}u}{\partial {X}^{2}}+\frac{{\partial }^{2}u}{\partial {Y}^{2}}\right) = {n}_{1}\left[ {\frac{\partial }{\partial X} \left( \frac{\partial u}{\partial X} Q(u)\right) }+{\frac{\partial }{\partial Y} \left( \frac{\partial u}{\partial Y} Q(u)\right) }\right] \qquad \text{ in } \qquad {\mathcal {P}}_{1}, \end{aligned}$$
(2.4)
$$\begin{aligned}{} & {} \frac{{\partial }^{2}v}{\partial {t}^{2}}-{c}_{2}^{2}\left( \frac{{\partial }^{2}v}{\partial {X}^{2}}+\frac{{\partial }^{2}v}{\partial {Y}^{2}}\right) -\frac{1}{{\rho }_{2}}\left( \frac{\textrm{d}\left( {\rho }_{2}{c}_{2}^{2}\right) }{dY}\frac{\partial v}{\partial Y}\right) \nonumber \\{} & {} \quad ={n}_{2}\left[ {\frac{\partial }{\partial X}\left( \frac{\partial v}{\partial X} Q(v)\right) }+{\frac{\partial }{\partial Y} \left( \frac{\partial v}{\partial Y} Q(v)\right) }\right] + \frac{1}{{\rho }_{2}} Q(v)(\frac{\partial }{\partial Y}\left( {\rho }_{2}{n}_{2}\right) \frac{\partial v}{\partial Y}) \qquad \text{ in } \qquad {\mathcal {P}}_{2}, \end{aligned}$$
(2.5)
$$\begin{aligned}{} & {} \frac{\partial u }{\partial Y}+\theta _{1}Q\left( u\right) \frac{\partial u}{\partial Y}=0 \qquad \text{ on }\qquad {Y}={h}, \end{aligned}$$
(2.6)
$$\begin{aligned}{} & {} {u}-{v}=0, \qquad \frac{\partial u}{\partial Y}-\gamma \frac{\partial v}{\partial Y}=\theta _{2}\gamma \, Q\left( v\right) \frac{\partial v}{\partial Y}-\theta _{1}Q\left( u\right) \frac{\partial u}{\partial Y}\qquad \text{ on }\qquad {Y}=0, \end{aligned}$$
(2.7)
$$\begin{aligned}{} & {} v\rightarrow 0\quad \text{ as }\quad Y\rightarrow -\infty \end{aligned}$$
(2.8)

where \(Q(\psi )={\left( \frac{\partial \psi }{\partial X}\right) }^{2}+{\left( \frac{\partial \psi }{\partial Y}\right) }^{2} \). Here, \(\mu _\alpha =2\frac{\textrm{d} \Sigma _\alpha }{\textrm{d} I}\) and \(n_\alpha \) are the second and third-order elastic constants corresponding to the usual one of Lamé constants called as linear shear modulus and to the one of the Murnaghan constants (see e.g., [38]), respectively. Densities of the layers, \(\rho _\alpha \), \(\gamma =\frac{{\mu }_{2}}{{\mu }_{1}}\), \(n_\alpha \), \(\theta _{\alpha } =\frac{{ n_{\alpha } }}{{c}_{\alpha }^{2}}\) are functions of Y if \(\alpha =2\), whereas they are constants if \(\alpha =1\). \(c_{\alpha }\) is the linear shear velocity in the relevant medium \(\mathcal {P}_\alpha \) such that \({c}_{\alpha }^{2} =\frac{{\mu }_{\alpha }}{{\rho }_{\alpha }}\). The nonlinear parameters \(n_1=2\frac{\textrm{d}^2 \Sigma _1(3)}{\rho _1 \textrm{d}I^2 }\) and \(n_2=2\frac{\textrm{d}^2 \Sigma _1(3,Y)}{\rho _2 \textrm{d}I^2 }\) exhibit the nonlinear characteristics of the materials. When \(n_\alpha >0\), the relevant medium is hardening in shear, but if \(n_\alpha <0\), then it is softening.

2.1 Nonlinear thin layer approximation

Equations from (2.4) to (2.8) describe Love waves propagating in a half-space that is covered by a finite uniform layer. Constituent materials of the layer and the half-space are cubically nonlinear homogeneous elastic material and cubically nonlinear heterogeneous elastic material, respectively. As previously mentioned, our aim is to observe the effect of the layer’s nonlinear parameter on the propagation of a weakly nonlinear surface SH wave with slowly varying amplitude by employing the nonlinear thin layer assumption. Consequently, we will derive an approximate equation representing the layer as h approaches zero. With this aim, we initially integrate the equation of the motion of the layer (2.4) with respect to Y over the interval [0, h], and next, use the boundary condition (2.6). Then, we obtain the following equation

$$\begin{aligned} \frac{\partial ^2}{\partial t^2}\int \limits _0^h u \textrm{d}Y-c_1^2 \frac{\partial ^2}{\partial X^2}\int \limits _0^h u \textrm{d}Y+c_1^2\left[ \frac{\partial u}{\partial Y}\big (1+\frac{n_1}{c_1^2}Q(u)\big )\right] _{Y=0}=n_1\frac{\partial }{\partial X}\int \limits _0^h \frac{\partial u}{\partial X}Q(u)\textrm{d}Y. \end{aligned}$$
(2.9)

Using the condition of continuity of stresses at the interface \(Y=0\), (2.9) reduces to the following

$$\begin{aligned} \frac{\partial ^2}{\partial t^2}\int \limits _0^h u \textrm{d}Y-c_1^2 \frac{\partial ^2}{\partial X^2}\int \limits _0^h u \textrm{d}Y+c_1^2\gamma \left[ \frac{\partial v}{\partial Y}\big (1+\frac{n_2}{c_2^2}Q(v)\big )\right] _{Y=0}=n_1\frac{\partial }{\partial X}\int \limits _0^h \frac{\partial u}{\partial X}Q(u)\textrm{d}Y. \end{aligned}$$
(2.10)

Subsequently, we will express the terms involving the displacement function u of the layer in equation (2.1) in terms of the displacement function v of the half-space. At \(Y=0\), the following can be used

$$\begin{aligned} \left( \frac{\partial u}{\partial Y} \bigg |_{Y=0}\right) ^2 \simeq \gamma ^2 \left( \frac{\partial u}{\partial Y} \bigg |_{Y=0}\right) ^2. \end{aligned}$$
(2.11)

This approximation is consistent with the one employed to express equations of motion and boundary conditions from (2.4) to (2.7). Furthermore, considering small values of h, we can use the following approximation

$$\begin{aligned} \int \limits _0^h f(X,Y,t)\textrm{d}Y \simeq \int \limits _0^h f(X,0,t)\textrm{d}Y=h f(X,0,t). \end{aligned}$$
(2.12)

Utilizing the equations (2.11) and (2.12) in (2.7), we obtain the following modified boundary condition for the thin layer on the half-space

$$\begin{aligned} h \frac{\partial ^2 v}{\partial t^2}-h c_1^2 \frac{\partial ^2 v}{\partial X^2}+c_1^2\gamma \frac{\partial v}{\partial Y}\left( 1+\frac{n_2}{c_2^2} Q(v)\right) =h n_1\frac{\partial }{\partial X}\Biggl \{ \frac{\partial v}{\partial X}\left( \left( \frac{\partial v}{\partial X}\right) ^2+\gamma ^2 \left( \frac{\partial v}{\partial Y}\right) ^2 \right) \Biggl \} \qquad \text{ on }\quad Y=0.\nonumber \\ \end{aligned}$$
(2.13)

For small values of h, this equation replaces for the equation of motion (2.4) governing the finite layer, as well as the free surface boundary condition (2.6) and the interface conditions (2.7). The term on the right-hand side of (2.13) reflects the nonlinear behavior of the layer material. Due to the heterogeneous nature of the half-space, we will express the new boundary value problem in the following form to simplify further investigation

$$\begin{aligned}{} & {} h \rho _1 \frac{\partial ^2 v}{\partial t^2}-h \mu _1 \frac{\partial ^2 v}{\partial X^2}+\mu _2 \frac{\partial v}{\partial Y}\left( 1+\frac{\rho _2 n_2}{\mu _2} Q(v)\right) =h \rho _1 n_1\frac{\partial }{\partial X}\Biggl \{ \frac{\partial v}{\partial X}\left( \left( \frac{\partial v}{\partial X}\right) ^2+\frac{\mu _2^2}{\mu _1^2}\left( \frac{\partial v}{\partial Y}\right) ^2 \right) \Biggl \} \text{ on } Y=0 \end{aligned}$$
(2.14)
$$\begin{aligned}{} & {} \rho _2\frac{{\partial }^{2}v}{\partial {t}^{2}}-\mu _2\left( \frac{{\partial }^{2}v}{\partial {X}^{2}}+\frac{{\partial }^{2}v}{\partial {Y}^{2}}\right) -\frac{1}{{\rho }_{2}}\left( \frac{\textrm{d}\left( {\rho }_{2}{c}_{2}^{2}\right) }{\textrm{d}Y}\frac{\partial v}{\partial Y}\right) \nonumber \\{} & {} \qquad ={n}_{2}\left[ {\frac{\partial }{\partial X}\left( \frac{\partial v}{\partial X} Q(v)\right) }+{\frac{\partial }{\partial Y} \left( \frac{\partial v}{\partial Y} Q(v)\right) }\right] + \frac{1}{{\rho }_{2}} Q(v)\left( \frac{\partial }{\partial Y}\left( {\rho }_{2}{n}_{2}\right) \frac{\partial v}{\partial Y}\right) \qquad \text{ in } \qquad {\mathcal {P}}_{2}. \end{aligned}$$
(2.15)

If the half-space is homogeneous; that is, the material parameters of the half-space are constant, (2.14) and (2.15) reduce to the problem studied in [10]. If the thin layer is linear; that is, the right-hand side of (2.14) is neglected, then the boundary condition takes the form of the condition derived in [14].

3 The nonlinear modulation of surface SH waves in a heterogeneous half-space covered with a thin layer.

The primary objective of the present study is to examine the self-modulation of the slowly varying amplitude of weakly nonlinear surface SH waves in the half-space covered by a nonlinear thin layer. In addition, we aim to observe the effects of the nonlinearity of the thin layer and heterogeneous material properties of the nonlinear half space on this modulation. For this observation, we employ the method of multiple scales [39], which involves introducing the following new independent variables that capture the slow variation of wave amplitude

$$\begin{aligned} {x}_{i} = {\varepsilon }^{i}X, \quad {t}_{i} = {\varepsilon }^{i}t, \quad y= Y,\quad i=0,1,2. \end{aligned}$$
(3.1)

Here, \(\varepsilon >0\) is a small parameter measuring the strength of nonlinearity. \(({x}_{0}, y, {t}_{0})\) represents rapid changes in the propagation while \(({x}_{1},{x}_{2}, {t}_ {1},{t}_{2})\) represents slow variations. Then, v as a function of these new variables is expanded in the following asymptotic series in \(\varepsilon \)

$$\begin{aligned} {v}= \sum _{n=1}^{\infty }\varepsilon ^{n}{v}_{n}({x}_{0},{x}_{1},{x}_{2},y,{t}_{0}, {t}_{1},{t}_{2}). \end{aligned}$$
(3.2)

If the effect of heterogeneity is weak, the material parameters associated with the half-space depend on the variable y in the following form

$$\begin{aligned} \mu _{2}={\mu }_{{20}}+\varepsilon ^2{\mu }_{{21}}(y),\quad \rho _{2}={\rho }_{{20}}+\varepsilon ^2{\rho }_{{21}}(y) \end{aligned}$$
(3.3)

where \(\,{\mu }_{{21}}(y)=-{\mu }_{{20}}{e}^{{dy}},\,{\rho }_{21}={\rho }_{{20}}{e}^{{dy}}\) and \(\,n_{{2}}(y)={n}_{{20}}{e}^{{dy}}\). In other words, we assume that the heterogeneity for the half-space is weak in the order of \(\epsilon ^2\). By substituting the expansion (3.2) into the equations (2.14)–(2.15) and subsequently equating the coefficients of similar powers of \(\varepsilon \), a series of problems is obtained. Solving these problems successively allows us to determine the value of \(v_n\). As our objective is to examine the nonlinear waves with small but finite amplitudes, it is adequate to precisely determine the solution function \(v_1\), which corresponds to the first-order perturbation problem. Therefore, it is more convenient to concentrate on the first three problems in the hierarchy, as follows

\({ O}({\varepsilon })\):

$$\begin{aligned}{} & {} \rho _{20} \frac{\partial ^2 {v}_{1}}{\partial t_0^2}-\mu _{20} \frac{\partial ^2 {v}_{1}}{\partial y^2}-\mu _{20} \frac{\partial ^2 {v}_{1}}{\partial x_0^2}=0 \quad \text{ on } \quad y<0, \end{aligned}$$
(3.4)
$$\begin{aligned}{} & {} h\rho _{10} \frac{\partial ^2 {v}_{1}}{\partial t_0^2}-h\mu _{10} \frac{\partial ^2 {v}_{1}}{\partial x_0^2}+\mu _{20} \frac{\partial {v}_{1}}{\partial y}=0 \quad \text{ on } \quad y=0, \end{aligned}$$
(3.5)
$$\begin{aligned}{} & {} v_1\rightarrow 0\hspace{1cm}\text{ as }\hspace{1cm} y\rightarrow -\infty \end{aligned}$$
(3.6)

\({ O}({\varepsilon ^2 })\):

$$\begin{aligned}{} & {} \rho _{20} \frac{\partial ^2 {v}_{2}}{\partial t_0^2}-\mu _{20} \frac{\partial ^2 {v}_{2}}{\partial y^2}-\mu _{20} \frac{\partial ^2 {v}_{2}}{\partial x_0^2}=2 \biggl (\mu _{20} \frac{\partial ^2 {v}_{1}}{\partial x_0 \partial x_1} -\rho _{20}\frac{\partial ^2 {v}_{1}}{\partial t_0 \partial t_1} \biggr ) \quad \text{ on } \quad y<0, \end{aligned}$$
(3.7)
$$\begin{aligned}{} & {} h\rho _{10} \frac{\partial ^2 {v}_{2}}{\partial t_0^2}+\mu _{20}\frac{\partial {v}_{2}}{\partial y}-h\mu _{10} \frac{\partial ^2 {v}_{2}}{\partial x_0^2}+\mu _{20} =2h\biggl (\mu _{10} \frac{\partial ^2 {v}_{1}}{\partial x_0 \partial x_1}-\rho _{10} \frac{\partial ^2 {v}_{1}}{\partial t_0 \partial t_1} \biggr ) \quad \text{ on } \quad y=0, \end{aligned}$$
(3.8)
$$\begin{aligned}{} & {} v_2\rightarrow 0\hspace{1cm}\text{ as }\hspace{1cm} y\rightarrow -\infty \end{aligned}$$
(3.9)

\({ O}(\varepsilon ^3)\):

$$\begin{aligned}{} & {} \rho _{20} \frac{\partial ^2 {v}_{3}}{\partial t_0^2}-\mu _{20} \frac{\partial ^2 {v}_{3}}{\partial y^2}-\mu _{20} \frac{\partial ^2 {v}_{3}}{\partial x_0^2}=-2\rho _{20} \frac{\partial ^2 {v}_{2}}{\partial t_0 \partial t_1}+2\mu _{20} \frac{\partial ^2 {v}_{2}}{\partial x_0 \partial x_1}-\rho _{20} \frac{\partial ^2 {v}_{1}}{\partial t_1^2} +\mu _{20}\frac{\partial ^2 {v}_{1}}{\partial x_1^2}\nonumber \\{} & {} -2\rho _{20}\frac{\partial ^2 {v}_{1}}{\partial t_0 \partial t_2}+2\mu _{20}\frac{\partial ^2 {u}_{1}}{\partial x_0 \partial x_2} -\rho _{21}(y)\frac{\partial ^2 {v}_{1}}{\partial t_0^2}+\mu _{21}(y)\bigg ( \frac{\partial ^2 {v}_{1}}{\partial x_0^2} +\frac{\partial ^2 {v}_{1}}{\partial y^2}\bigg )+ \frac{\partial \mu _{21}}{\partial y}\frac{\partial {v}_{1}}{\partial y}\nonumber \\{} & {} +n_{20}\rho _{20} \bigg [ 3\frac{\partial {v}_{1}}{\partial y}\frac{\partial ^2 {u}_{1}}{\partial y^2}+\frac{\partial ^2 {v}_{1}}{\partial y^2}(\frac{\partial {v}_{1}}{\partial x_0})^2+ 4\frac{\partial {v}_{1}}{\partial x_0}\frac{\partial {u}_{1}}{\partial y}\frac{\partial ^2 {v}_{1}}{\partial x_0 \partial y}+(\frac{\partial {v}_{1}}{\partial y})^2 \frac{\partial ^2 {u}_{1}}{\partial x_0^2} +3(\frac{\partial {v}_{1}}{\partial x_0})^2 \frac{\partial ^2 {v}_{1}}{\partial x_0^2} \bigg ] \quad \text{ on } \quad y<0, \end{aligned}$$
(3.10)
$$\begin{aligned}{} & {} h \rho _{10}\frac{\partial ^2 {v}_{3}}{\partial t_0^2}+\mu _{20} \frac{\partial {v}_{3}}{\partial y}-h \mu _{10}\frac{\partial ^2 {v}_{3} }{\partial x_0^2}=2h \mu _{10} \frac{\partial ^2 {v}_{2} }{\partial x_0\partial x_1}-2h \rho _{10} \frac{\partial ^2 {v}_{2} }{\partial t_0 \partial t_1} \nonumber \\{} & {} \quad - h\rho _{10} \frac{\partial ^2 {v}_{1} }{\partial t_1^2}-2h\rho _{10}\frac{\partial {v}_{1}}{\partial t_0 \partial t_2}+h \mu _{10} \frac{\partial ^2 {v}_{1}}{\partial x_1^2}+2h \mu _{10} \frac{\partial ^2 {v}_{1}}{\partial x_0 \partial x_2}+\mu _{21}(y)\frac{\partial {v}_{1}}{\partial y} \nonumber \\{} & {} \quad +\frac{1}{\mu _{10}^2} \biggl (-n_{20} \rho _{20}\mu _{10}^2(\frac{\partial v_{1}}{\partial y})^3+ 2h n_{10} \mu _{20}^2 \rho _{10} \frac{\partial v_{1}}{\partial y} \frac{\partial v_1}{\partial x_0} \frac{\partial ^2 v_1}{\partial x_0 \partial y} + h n_{10} \mu _{20}^2 \rho _{10} (\frac{\partial v_{1}}{\partial y})^2 \frac{\partial ^2 v_1}{\partial x_{0}^2} \nonumber \\{} & {} \quad +3h n_{10} \mu _{10}^2\rho _{10}(\frac{\partial v_1}{\partial x_0})^2 \frac{\partial ^2 v_1}{\partial x_{0}^2}-n_{20}\mu _{10}^2 \rho _{20} \frac{\partial v_1}{\partial y} (\frac{\partial v_1}{\partial x_{0}})^2 \biggr ) \quad \text{ on } \quad {y=0}. \end{aligned}$$
(3.11)
$$\begin{aligned}{} & {} v_3\rightarrow 0\hspace{1cm}\text{ as }\hspace{1cm} y\rightarrow -\infty \end{aligned}$$
(3.12)

The perturbation problems above exhibit linearity at each step in the hierarchy. The first-order problem, in particular, addresses the propagation of surface SH waves in a layered half-space covered by a thin linear layer. For the existence of surface SH waves, the phase velocity c of the wave must satisfy the inequality \(c_1<c<c_2\) where \(c_{1}\) and \(c_2\) are the linear shear velocity of the thin layer and half-space, respectively (see e.g., [40]). Then, the solution of Eq. (3.4) satisfying the radiation condition (3.6) can be expressed as

$$\begin{aligned} {v_1}= \sum _{n=1}^{\infty } A_1^{(n)}(x_1,x_2,t_1,t_2)e^{npy}e^{in(kx_0-\omega t_0)}+c.c. \end{aligned}$$
(3.13)

where

$$\begin{aligned} p=\sqrt{1-\frac{c^2}{c_{20}^2}}. \end{aligned}$$
(3.14)

Here, \(A_1^{(n)}\) is the first-order amplitude function, k is the wave number and \(\omega \) is the angular frequency. Using this solution in the boundary condition (3.5), we obtain the following

$$\begin{aligned} W_n \,A_1^{(n)}=0 \end{aligned}$$
(3.15)

where \(W_n= -h n^2\omega ^2 \rho _{1}+ k n^2 p \mu _{20} +h n k^2 \mu _{1}\), \(\gamma =\frac{\mu _{20}}{\mu _{1}}\) and \(c_{1}^2=\frac{\mu _{1}}{\rho _{1}}\). We note that \(W_1=0\) gives the following dispersion relation of the linear surface SH waves for the thin layer approximation

$$\begin{aligned} W_1:-h \omega ^2 \rho _{1}+ k p \mu _{20} +h k^2 \mu _{1}=0. \end{aligned}$$
(3.16)

For small values of kh, it approximates closely to the classical linear dispersion relation of Love waves on its first branch [10]. It is to be observed that the dispersion relation has no dependency on the heterogeneous properties of the half-space, but rather it is subject to the linear material properties of both the thin layer and half-space. We focus on the nonlinear self-modulation of a group of waves centered around a wave number k and corresponding frequency \(\omega \), which satisfy the dispersion relation (3.15). To avoid harmonic resonance, it is necessary to assume that \(W_n\) is not zero for \(n\ne 1\) (or equivalently, \(n\ge 2\)). Consequently, \(A_1^{(1)} = \mathcal {A}_1\) and \(A_1^{(n)} \equiv 0\) for \(n\ge 2\). Here, \(\mathcal {A}_1\) is a complex function of slow variables, representing the first-order slowly varying amplitude of the self-modulation. Therefore, the explicit expression for the first-order solution \(v_1\) is written as follows

$$\begin{aligned} v_1=\mathcal {A}_1 e^{kpy}e^{i(k x_0-\omega t_0)}+c.c. \end{aligned}$$
(3.17)

To finalize the first-order solution, we will proceed by examining the higher-order perturbation problems. Substitution of (3.17) into (3.7) yields

$$\begin{aligned} \rho _{20} \frac{\partial ^2 {v}_{2}}{\partial t_0^2}-\mu _{20} \frac{\partial ^2 {v}_{2}}{\partial y^2}-\mu _{20} \frac{\partial ^2 {v}_{2}}{\partial x_0^2}= \biggl (2 i \omega \rho _{20} \frac{\partial \mathcal {A}_1}{\partial t_1} +2 i k \mu _{20}\frac{\partial \mathcal {A}_1}{\partial x_1} \biggr )+c.c. \end{aligned}$$
(3.18)

Solution of the equation is categorized into two groups

$$\begin{aligned} v_2=\bar{v}_2+\tilde{v}_2 \end{aligned}$$
(3.19)

such that \(\bar{v}_2\) is the particular solution of (3.18) and \(\tilde{v}_2\) is the solution of corresponding homogeneous equation. The particular solution can be found by means of the method of undetermined coefficients as

$$\begin{aligned} \bar{v}_2= \frac{-i}{kp \mu _{20}} \biggl (\omega \rho _{20} \frac{\partial \mathcal {A}_1}{\partial t_1}+k \mu _{20}\frac{\partial \mathcal {A}_1}{\partial x_1}\biggr ) e^{i(k x_0-\omega t_0)}+c.c. \end{aligned}$$
(3.20)

The solution of the corresponding homogeneous equation, \(\widetilde{v}_2\), can be expressed as in the first-order solution by replacing \(A_1^{(n)}\) in (3.13) with the second-order amplitude function \(A_2^{(n)}\) which can be determined from higher order perturbation problems when necessary. However, since this work is concentrated on the propagation of weakly nonlinear waves, it is reasonable to obtain just the uniformly valid first-order solution. Therefore, using (3.19) together with \(v_1\) given by (3.17) in the boundary condition (3.11) of the second order problem yields

$$\begin{aligned} W_1 A_2^{(1)}=-i\biggl (\frac{\partial W_1}{\partial \omega } \frac{\partial \mathcal {A}_1}{\partial t_1}- \frac{\partial W_1}{\partial k} \frac{\partial \mathcal {A}_1}{\partial x_1}\biggr ), \qquad W_n {A}_2^{(n)}=0,\quad n>1. \end{aligned}$$
(3.21)

Since \(W_1=0\), the following condition holds

$$\begin{aligned} \biggl (\frac{\partial W_1}{\partial \omega } \frac{\partial \mathcal {A}_1}{\partial t_1}- \frac{\partial W_1}{\partial k} \frac{\partial \mathcal {A}_1}{\partial x_1}\biggr )=0. \end{aligned}$$
(3.22)

Thus, the group velocity of the self-modulated waves, \(V_{g}\), is

$$\begin{aligned} V_{g}=\frac{\partial \omega }{\partial k}=-\frac{\partial W}{\partial k} / \frac{\partial W}{\partial \omega }=\frac{k}{\omega } \frac{(2hkp \mu _{10}+\mu _{20})}{(2hkp \rho _{10}+\rho _{20})} \end{aligned}$$
(3.23)

and as a result, we obtain

$$\begin{aligned} \frac{\partial \mathcal {A}_1}{\partial t_1} +V_{g} \frac{\partial \mathcal {A}_1}{\partial x_1}=0. \end{aligned}$$
(3.24)

The equation above indicates that the first order amplitude \(\mathcal {A}_1\) remains constant in a frame of reference moving with the group velocity \(V_{g}\) of waves i.e., \(\mathcal {A}_1=\mathcal {A}_1(x_1-V_{g}\,t_1,x_2,t_2)\). Then, the solution of (3.21) is

$$\begin{aligned} A_2^{(1)}=\mathcal {A}_2(x_1,x_2,t_1,t_2),\qquad A_2^{(n)}=0,\quad n>1 \end{aligned}$$
(3.25)

and hence

$$\begin{aligned} v_2=\biggl [\mathcal {A}_2-\frac{i}{kp\mu _{20}} \biggl (\omega \rho _{20} \frac{\partial \mathcal {A}_1}{\partial t_1} +k \mu _{20} \frac{\partial \mathcal {A}_1}{\partial x_1}\biggr )y\biggr ]e^{kpy}e^{i(k x_0-\omega t_0)}+c.c. \end{aligned}$$
(3.26)

To fully determine the structure of \(\mathcal {A}_1\), we extend the analysis by incorporating the third-order problem. Substituting the solutions of the first and second-order solutions into the third-order equation (3.10), we obtain

$$\begin{aligned} \begin{aligned} \rho _{20} \frac{\partial ^2 v_3}{\partial t_{0}^2}- \mu _{20} \frac{\partial ^2 v_3}{\partial y^2}-\mu _{20} \frac{\partial ^2 v_3}{\partial x_{0}^2}&=\bigl [(D_{1}+D_2 y)e^{kpy}+D_3 e^{dy+kpy} \mathcal {A}_1 \\&\quad +D_4 e^{3kpy}\mathcal {A}_1^2\mathcal {A}_{1e}\bigr ]e^{i(kx_0-\omega t_0)}+D_5 \mathcal {A}_1^3 e^{3i(k x_0-\omega t_0)}+c.c. \end{aligned} \end{aligned}$$
(3.27)

The explicit forms of \(D_i\) for \(i=1,2,\ldots ,5\) are given in the “Appendix”. As in (3.19), \(v_3\) is decomposed as \(v_3 = \bar{v}_3 + \tilde{v}_3\) where the particular solution \(\bar{v}_3\) corresponds to the non-homogeneous equation (3.27), while \(\tilde{v}_3\) represents the solution of the corresponding homogeneous equation, subject to the non-homogeneous boundary condition derived from the boundary condition (3.11) of the third-order problem. The particular solution \(\bar{v}_3\) is expressed as

$$\begin{aligned} \bar{v}_3= g^{(1)}(x_1,x_2,y,t_1,t_2)e^{i\phi }+ g^{(3)}(x_1,x_2,y,t_1,t_2)e^{3i\phi }+c.c. \end{aligned}$$
(3.28)

While the term \(g^{(1)}\) is associated with the self-interaction of waves, the term \(g^{(3)}\) represents the third harmonic interaction effects. Given our specific focus on self-interaction in this context, the explicit form of the term \(g^{(3)}\) is unnecessary for further analysis. Therefore, we solely focus on calculating \(g^{(1)}\). Consequently, the following solution is obtained by the method of undetermined coefficients

$$\begin{aligned} {g}^{\left( 1\right) }=[(\mathcal {C}_{1}+y \mathcal {C}_{2})y{e}^{k p y}+\mathcal {C}_{3}e^{dy+kpy}+ \mathcal {C}_{4}{e}^{kpy}]e^{i(k x_0-\omega t_0)}+c.c. \end{aligned}$$
(3.29)

where \(C_i\) is given in the “Appendix”. On the other hand, the solution of the corresponding homogeneous equation obeying the radiation condition (3.12) can be expressed as follows

$$\begin{aligned} \tilde{v}_3= \sum _{n=1}^{\infty } A_3^{(n)}(x_1,x_2,t_1,t_2)e^{npy}e^{in(kx_0-\omega t_0)}+c.c. \end{aligned}$$
(3.30)

where \(A_3^{(n)}\) is the third order slowly varying amplitude function. Then, we use this solution, \(v_1\) and \(v_2\) together with \(\bar{v}_3\) in the boundary condition (3.11) of the third-order problem to determine \(A_3^{(n)}\). Thus

$$\begin{aligned} W_1 A_3^{(1)}=b_1, \qquad W_3 A_3^{(3)}=b_3,\quad \qquad W_n A_3^{(n)}=0,\quad n\ne 1,3 \end{aligned}$$
(3.31)

where

$$\begin{aligned} \begin{aligned} b_{1}&= -i\left( \frac{\partial W_1}{\partial \omega }\frac{\partial \mathcal {A}_2}{\partial {t}_{1}}-\frac{\partial W_1}{\partial k}\frac{\partial \mathcal {A}_2}{\partial x_1}\right) -i\left( \frac{\partial W_{1}}{\partial \omega }\frac{\partial \mathcal {A}_1}{\partial t_2}-\frac{\partial W_{1}}{\partial k}\frac{\partial \mathcal {A}_{1}}{\partial x_2}\right) \\&\quad + \frac{1}{2}\left( \frac{{\partial }^{2}W_{1}}{\partial \omega ^{2}}\frac{{\partial }^{2}\mathcal {A}_1}{\partial {t_1}^{2}}-{2}\frac{{\partial }^{2} W_{1}}{\partial \omega \partial k}\frac{{\partial }^{2}\mathcal {A}_{1}}{\partial {x_{1}}\partial {t_{1}}}+\frac{{\partial }^{2} W_1}{\partial k^{2}}\frac{{\partial }^{2}\mathcal {A}_1}{\partial x_{1}^2}\right) +F{|\mathcal {A}_{1}|}^{2}\mathcal {A}_{1}+G \mathcal {A}_{1}. \end{aligned} \end{aligned}$$
(3.32)

Here F and G are given by

$$\begin{aligned} \begin{aligned} F&=-\frac{k^3}{\mu _{10}^2(k^2 \mu _{20}(-1+9p^2)+\omega ^2 \rho _{20})} \bigl [n_{20}p\mu _{10}^2\rho _{20}(8k^2\mu _{20}+(1+3p^2)\omega ^2 \rho _{20}) \\&\quad +\!hk(\omega ^2((3n_{10}\!+\!n_{20}(-3\!+\!2p^2\!+\!9p^4))\mu _{10}^2\!+\!n_{10}p^2\mu _{20}^2)\bigr ] \rho _{10}\rho _{20} \\&\quad +\!k^2(n_{10}\mu _{20}\rho _{10}(\!-\!1\!+\!9p^2)(3 \mu _{10}^2\!+\!p^2\mu _{20}^2)\!+\!n_{20}\mu _{10}^3 \rho _{20}(3-2p^2-9p^4))\bigl ], \\ G&=\frac{-h(k^2\mu _{10}-\omega ^2\rho _{10})[k(dp+k(-1+p^2))\mu _{20}-\omega ^2\rho _{20}]+\mu _{20}[k^2d \mu _{20}+(d+2kp)\omega ^2\rho _{20}]}{[d+k(-1+p)](d+k+kp)\mu _{20}+\omega ^2\rho _{20}}. \end{aligned} \end{aligned}$$
(3.33)

Upon closer examination, it is apparent that the wave number F depends on the angular frequency and the nonlinear material parameters of both the thin layer and half-space, whereas the wave number G depends on the angular frequency and the linear material parameters of both the thin layer and half-space as well as the heterogeneity parameter of the material of the half-space. The explicit form of \(b_3\) is not provided here, as it will not be required in subsequent calculations. The existence of a solution to the equation \(W_1 \mathcal {A}_3^{(1)}=b_1\), the condition \(b_1 = 0\) must hold, given that \(W_1=0\). Under this condition, the value of \({A}_3^{(1)}\) remains arbitrary. If we assume that \(\mathcal {A}_2\) also satisfies the condition given by (3.24), then the condition \(b_1=0\) can be expressed as follows

$$\begin{aligned} \begin{aligned} b_{1}&= -i\left( \frac{\partial \mathcal {A}_1}{\partial t_2}+V_g\frac{\partial \mathcal {A}_{1}}{\partial x_2}\right) + {\tilde{\Gamma }}\frac{{\partial }^{2}\mathcal {A}_1}{\partial x_{1}^2} +{\tilde{\Delta }}{|\mathcal {A}_{1}|}^{2}\mathcal {A}_{1}+{\tilde{\Lambda }} \mathcal {A}_{1}=0 \end{aligned} \end{aligned}$$
(3.34)

where

$$\begin{aligned} {\tilde{\Gamma }}=\left( V_g^2\frac{{\partial }^{2}W_{1}}{\partial \omega ^{2}}+2 V_g\frac{{\partial }^{2} W_{1}}{\partial \omega \partial k}+\frac{{\partial }^{2} W_1}{\partial k^{2}}\right) /\left( 2 \frac{\partial W_1}{\partial \omega }\right) ,\,\, {\tilde{\Delta }}=F/\frac{\partial W_1}{\partial \omega },\,\, {\tilde{\Lambda }}=G/\frac{\partial W_1}{\partial \omega }. \end{aligned}$$
(3.35)

Here, \({\tilde{\Gamma }}\) is the linear dispersion coefficient, \({\tilde{\Delta }}\) is the nonlinear coefficient describing the self-modulation and \({\tilde{\Lambda }}\) is the external potential. We now introduce the following non-dimensional variables

$$\begin{aligned} \begin{aligned} \tau =\omega t_{2},\quad&\xi =k\varepsilon ^{-1}(x_{2}-V_{g}t_{2})=k(x_{1}-V_{g}t_{1}),\quad \mathcal {A}=k\mathcal {A}_{1}. \end{aligned} \end{aligned}$$
(3.36)

(3.34) yields the following nonlinear Shrödinger equation for \(\mathcal {A}\)

$$\begin{aligned} i\frac{\partial {\mathcal {A}}}{\partial \tau }+\Gamma \frac{\partial ^2 {\mathcal {A}}}{\partial \xi ^2}+\Delta |{\mathcal {A}}|^2{A}+\Lambda \mathcal {A}=0 \end{aligned}$$
(3.37)

where

$$\begin{aligned} {\Gamma }=-\frac{k^2}{\omega }{\tilde{\Gamma }},\,\, \,{\Delta }=-\frac{1}{k^2\omega }{\tilde{\Delta }},\,\,\, \Lambda =-\frac{1}{\omega }{\tilde{\Lambda }}. \end{aligned}$$
(3.38)

Over the past few decades, there has been a growing interest in NLS equations with external potentials, driven by their potential applications in soliton shaping and management. Cubic NLS equation with external potential appears in the explanation of various physical phenomena such as Bose-Einstein Condensates (BEC), nonlinear optics, fiber optics, condensed matter physics, plasma physics, etc. [41,42,43,44,45]. Here, Bose-Einstein condensates in the study of ultra-cold atomic gases can be defined by a form of cubic NLS equation with an external potential called the Gross-Pitaevskii equation. In nonlinear optics, the cubic NLS equation can be used to model the propagation of intense laser beams through nonlinear media. In the study of optical fiber communications, the cubic NLS equation describes the propagation of optical pulses through fiber optic cables, whereas in plasma physics, it can be used for the propagation of intense Langmuir waves or envelope solitons in plasma under the influence of external fields. The motivation for studying such equations stems from the desire to explain and understand the behavior of wave-like phenomena in nonlinear systems under the influence of an external force or potential. For more details, refer to [45]. We note that the external potential term can be eliminated under the substitution of

$$\begin{aligned} \mathcal {A}=\mathcal {B}e^{i \Lambda \tau }, \end{aligned}$$
(3.39)

and consequently, the equation (3.37) reduces to the following cubic NLS equation

$$\begin{aligned} i\frac{\partial {\mathcal {B}}}{\partial \tau }+\Gamma \frac{\partial ^2 {\mathcal {B}}}{\partial \xi ^2}+\Delta |{\mathcal {B}}|^2\mathcal {B}=0. \end{aligned}$$
(3.40)

Here, the coefficients \(\Gamma \) and \(\Delta \) are identical to the coefficients in (3.37). For an initial condition in the form of \(\mathcal {B}(\xi ,0)=\mathcal {B}_0(\xi )\), the first-order solution \(v_1\) by the solution of the equation (3.40) can be constructed by (3.17). The NLS equation emerges in many areas as an equation defining the self-modulation of monochromatic planar waves in dispersive media. Furthermore, the sign of \(\Gamma \Delta \) plays a crucial role in determining how specific initial conditions will evolve for the asymptotic wave field guided by an NLS equation [46, 47]. An initial disturbance vanishing as \(|\xi |\rightarrow \infty \) tends to become a series of envelope solitary waves if \(\Gamma \Delta >0\), while it evolves into decaying oscillations if \(\Gamma \Delta <0\). On the other hand, for disturbances that tend towards a uniform state at infinity, the envelope dark solitons exist for \(\Gamma \Delta <0\).

Fig. 1
figure 1

For the dispersion relations (4.94.10) and (4.12), the variation of nondimensional a phase velocity C and b group velocity \(V_{G}\) versus nondimensional wave number K for three different material models: Copper (softening layer)-Armco Iron (softening half-space);  Glass (Pyrex) (hardening layer)-Acrylic Plastic (hardening half-space;  Fused Quartz (softening layer)-Acrylic Plastic (hardening half-space)

Full size image
Fig. 2
figure 2

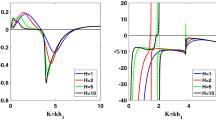
The variation of coefficients of the NLS equation (3.37), a \(\Gamma \),  b \(\Delta \) and c \(\Gamma \Delta \) versus nondimensional wave number K for the models Copper-Armco Iron, Glass (Pyrex)-Acrylic Plastic and Fused Quartz-Acrylic Plastic

Full size image
Fig. 3
figure 3

The deformations in the plane \(Z=0\) in the half-space covered by a thin layer for the envelope solitary wave solution (4.2) when \(K=0.0474\), \(C=1.14\), \(\epsilon =0.1\), \(t=1\) and \(\phi _0=1\) for Glass–Acrylic Plastic without translation a The envelope of the wave, b The wave packet

Full size image
Fig. 4
figure 4

The deformations in the plane \(Z=0\) in the half-space covered by a thin layer for the envelope solitary wave solution (4.2) when \(K=0.0921\), \(C=1.0626\), \(\epsilon =0.1\), \(t=1\) and \(\phi _0=1\) for Quartz-Acrylic Plastic without translation a The envelope of the wave, b The wave packet

Full size image
Fig. 5
figure 5

The deformations in the plane \(Z=0\) in the half-space covered by a thin layer for the dark solitary wave solution (4.3) for copper-armco iron without translation when \(K=0.100157\), \(C=1.39665\), \(\epsilon =0.1\), \(t=1\) and \(\phi _0=1\)

Full size image
Fig. 6
figure 6

The deformations in the plane \(Z=0\) in the half-space covered by a thin layer for the envelope solitary wave solution (4.2) when \(K=0.0474\), \(C=1.14\), \(\epsilon =0.1\), \(D=0.0001\), \(t=1\) and \(\phi _0=1\) for Glass-Acrylic Plastic. a Homogenous case (top View), b heterogenous case (top view), c the difference between homogenous and heterogenous cases (top view), d three-dimensional version of figure (c)

Full size image

4 The existence of bright and dark solitary waves

The sign of \(\Gamma \Delta \) affects the nature of traveling wave solutions of an NLS equation which has the following form [47]

$$\begin{aligned} \mathcal {B}(\xi ,\tau )=\phi (\eta )e^{i(K\xi -\Omega \tau )},\qquad \eta =\xi -V_0\tau ,\qquad V_0=constant. \end{aligned}$$
(4.1)

For instance, if \(\phi \rightarrow 0\) and \(d\phi /d\eta \rightarrow 0\) as \(\eta \rightarrow \infty \) for \(\Gamma \Delta >0\), then the corresponding equation is in the following form

$$\begin{aligned} \mathcal {B}(\xi ,\tau )=\phi _0 sech[(\Delta /2\Gamma )^{1/2}\phi _0 \eta ] e^{i(K\xi -\Omega \tau )} \end{aligned}$$
(4.2)

where \(V_0=2K\Gamma \) and \(\Omega =\Gamma K^2-\Delta \phi _0^2/2\). This solution is the envelope soliton or bright soliton in the optical context. When \(\Gamma \Delta <0\), a solution of the following form exists approaching to the uniform solution \(\phi _0 e^{i\Gamma ^2\Delta \phi _0^2\tau }\) as \(|\eta |\rightarrow \infty \) [47]

$$\begin{aligned} \mathcal {B}(\xi ,\tau )=\phi (\eta ) e^{i\Gamma ^2\Delta \phi _0^2\tau -iH(\eta )}. \end{aligned}$$
(4.3)

Here, the solutions for \(\phi \) and H are found as

$$\begin{aligned} \phi ^2=\phi _0^2(1-\sin ^2(B)sech^2(\psi ),\qquad H=\arctan (\tan A \tanh \psi ) \end{aligned}$$
(4.4)

where A is a constant, and \(\psi \) and \(V_0\) are given as

$$\begin{aligned} \psi =\left( -\frac{\Gamma \Delta }{2}\right) ^{1/2}\phi _0 \eta \sin B,\qquad V_0=\pm 2^{-3/2}\Gamma (-\Gamma \Delta )^{1/2}\phi _0. \end{aligned}$$
(4.5)

This solution corresponding to the dark soliton possesses all the typical soliton features as shown by Zakharov and Shabat [48]. For negative values of \(\Gamma \Delta \) and for \((\Gamma K^2-\Omega )/\Delta \phi _0^2=1\), if \(\phi \rightarrow \phi _0\) as \(\eta \) approaches negative infinity, then the solution for \(\phi \) is

$$\begin{aligned} \phi (\eta )=\phi _0 \tanh ((-\Delta /2\Gamma )^{1/2}\phi _0 \eta ),\qquad V_0=2K\Gamma \end{aligned}$$
(4.6)

which corresponds to the propagation of a phase jump. Here, we define the dimensionless variables, dimensionless linear and nonlinear material parameters and heterogeneity parameters as follows:

$$\begin{aligned}{} & {} \omega =c\, k,\, C=\frac{c}{c_{1}}, \, K=k\,h,\, D=d\,h, \end{aligned}$$
(4.7)
$$\begin{aligned}{} & {} c_{20}^2=\frac{\mu _{20}}{\rho _{20}},\, c_{1}^2=\frac{\mu _{1}}{\rho _{1}},\, \gamma _0=\frac{\mu _{20}}{\mu _{1}}, \, R=\frac{\rho _2}{\rho _1}, \, \beta _1=\frac{n_{1}}{c_{1}^2}, \,\beta _2=\frac{n_{20}}{c_{20}^2}, \, M=\frac{c_{1}}{c_{20}}. \end{aligned}$$
(4.8)

The inequality \(c_1<c<c_2\) can be expressed in terms of dimensionless variables as \(1<C<1/M\). For numerical evaluations, we will use the real material parameters for the thin layer and half-space, and their properties are provided in Table 1 [50]. We note that the nonlinear elastic material parameter n is negative for both Copper and Armco Iron. Therefore, the medium with these type of materials is a softening medium in shear. In contrast, the parameter n for Glass (Pylex), Acrylic Plastic and Fused Quartz is positive, indicating that the medium with these type of materials is a hardening in shear. We proceed by considering the following cases:

  • Case 1: Copper (softening layer)-Armco Iron (softening half-space)

  • Case 2: Glass (Pyrex) (hardening layer)-Acrylic Plastic (hardening half-space)

  • Case 3: Fused Quartz (softening layer)-Acrylic Plastic (hardening half-space)

Initially, we will examine the dimensionless dispersion relation in (3.16) by expressing it in terms of dimensionless quantities in (4.7) and (4.8) as follows

$$\begin{aligned} K(1-C^2)+p \gamma _0=0,\qquad p=\sqrt{1-M^2C^2} \end{aligned}$$
(4.9)

or

$$\begin{aligned} K=\frac{\gamma _0\sqrt{1-M^2C^2}}{C^2-1}. \end{aligned}$$
(4.10)

In a similar manner, we define the dimensionless group velocity as follows

$$\begin{aligned} V_G=\frac{V_g}{c_1}=\frac{2K p +\gamma _0 }{C (2 K p+R)}. \end{aligned}$$
(4.11)

On the other hand, the first branch of the dispersion relation corresponding to the finite layer can be expressed in terms of the same dimensionless quantities as follows [11]

$$\begin{aligned} K=\frac{1}{\sqrt{C^{2}-1}}\arctan \Bigg (\gamma _{0}\sqrt{\frac{1-M^2C^2}{C^2-1}}\Bigg ) \end{aligned}$$
(4.12)

that has infinitely many branches. Graphs for the two dispersion relations and for the related group velocities are shown respectively, in Fig. 1a, b, corresponding to the real material parameter cases presented above. The dispersion relation given by (3.16) has a unique branch on the half-space covered by a thin layer, and for smaller values of wave numbers, this branch corresponds to the first branch for the case of a finite layer. As K tends to zero, the phase velocity C for the two dispersion relations approaches to \(M=0.511\) for the first model, \(M=0.769\) for the second one and \(M=0.88\) for the third model. Therefore, we perform the numerical analysis for smaller values of K (\(0\le K<1\)), within the range where the thin-layer approximation remains valid.

Table 1 Linear and nonlinear material parameters [50]
Full size table

To examine the effects of material parameters on the existence of solitary waves, the graphs versus K of the coefficients \(\Gamma \), \(\Delta \) and \(\Gamma \Delta \) of the equation (3.40), corresponding to three different cases defined above are given in Fig. 2a–c, respectively. In addition, curves in the same figures corresponding to the case where the thin layer is linear have been plotted in dashed format to observe the influence of nonlinearity of the thin layer on wave propagation. Indeed, it is observed that the effect of the layer’s nonlinearity diminishes significantly for very small values of K (\(0<K<<1\)). As can be seen, all the \(\Gamma \) curves depending on the linear material parameters are negative for all values of K, whereas the \(\Delta \) curves depending on both the linear and nonlinear material parameters are remarkably different for each model, being positive for case 1, negative for case 2 and changing its sign about the critical value \(K_c=0.536567\) for case 3. Since \(\Gamma <0\) and \(\Delta >0\), and consequently \(\Gamma \Delta <0\) in case 1, it can be observed in Fig. 3 that an envelope solitary wave solution defined by (4.2) can not exist, but only the dark solitary waves (4.3) can be observed. For case 2, since \(\Delta <0\) and hence \(\Gamma \Delta >0\), there will be only an envelope solitary wave solution for all values of K. For case 3, there exist envelope solitary waves since \(\Delta <0\) and \(\Gamma \Delta >0\) for \(K<K_c\). On the other hand, they can not be observed for \(K>K_c\) yielding \(\Delta >0\) and \(\Gamma \Delta <0\). We note that the modulation instability of the plane-wave solution of the NLS equation is determined by the sign of \(\Gamma \Delta \). The marginal state of the modulation instability is determined by the condition that either of \(\Delta \) or \(\Gamma \) vanishes [49]. In case 3, the coefficient \(\Delta \) of the nonlinear term of the NLS equation vanishes at a certain wave number of the carrier wave, \(K_c\). Since the nonlinear term of the NLS equation vanishes at this critical wave number, and hence a marginal state occurs, a new ordering is necessary in order to balance the nonlinearity and dispersion.

We now examine the deformations in the plane \(Z=0\) in the half-space covered by a thin layer for each case. For case 2, the deformations in the plane \(Z=0\) for the envelope solitary wave solution (4.2) are shown in Fig. 3 for \(K=0.0474\), \(C=1.14\), \(\epsilon =0.1\), \(t=1\) and \(\phi _0=1\). Wave envelope and wave packet can be observed in Fig. 3a and Fig. 3b, respectively. Similarly, the deformations in the plane \(Z=0\) for the envelope solitary wave solution (4.2) for case 3 is shown in Fig. 4 for the values \(K=0.0921\), \(C=1.0626\), \(\epsilon =0.1\), \(t=1\) and \(\phi _0=1\). On the other hand, the deformations in the same plane for the dark soliton solution (4.3) are shown in Fig. 5 for the values \(K=0.0057\), \(C=1.3988\), \(\epsilon =0.1\), \(t=1\) and \(\phi _0=1\) for case 1.

As can be observed from these figures, there exists dense wave propagation at the surface for which the displacements vanish as the depth increases. In fact, we observe that the nonlinear material parameter of the thin layer at small wave numbers affects significantly the wave propagation. We now investigate the effects of heterogeneity of the half-space on the wave propagation. The external potential term \(\Lambda \) of the NLS equation (3.37) depends on the linear material parameters of both the thin layer and half-space as well as the parameter d corresponding to the heterogeneity of the half-space. Considering the substitution (3.39), the parameter d appears in the term \(e^{i \Lambda \tau }\). In the case of bright solitary waves, the term \(e^{i \Lambda \tau }\) only affects the term \(e^{i(K\xi -\Omega \tau )}\) in (4.2). Thus, in the case of bright solitary waves, the heterogeneity of the semi-infinite space only results in a temporal shift along the direction of wave propagation in the wave packet, while the envelope of waves remains unchanged and unaffected by the material’s heterogeneity. To observe this shift, the terms \(\mu _{21}(y)\) and \(\rho _{21}(y)\) in the material model in (3.3) for the semi-infinite space were set to zero (corresponding to a homogeneous material scenario). As a result, deformation in the plane \(Z=0\) associated with the bright solitary wave was obtained (for the top view, see Fig. 6a). Furthermore, by selecting an appropriate heterogeneity parameter in the material model in (3.3), the calculation was repeated by adding the parameter value of \(D=0.0001\), and deformation associated with the effect of heterogeneity was determined in the plane \(Z=0\) (for the top view, see Fig. 6b). The difference between these two deformations was computed for the parameter values used for case 2 and the top view is shown in Fig. 6c, whereas the three-dimensional version of Fig. 6c is given in Fig. 6d. We observe in this figure that a significant difference exists between these two deformations, indicating that the heterogeneity of the semi-infinite space has an effect on the propagation of waves in the stationary envelope of bright solitary waves.

The effect of heterogeneity is different for the dark solitary wave. For the solution, the term, \(e^{i \Lambda \tau }\) results in a shift of the entire wave in the direction of propagation over time. To observe this effect, a similar approach to that used for the bright solitary wave has been followed. For this purpose, deformations in the plane \(Z=0\) for homogeneous and heterogeneous material models have been obtained by adding \(D=0.001\) to the parameter values used for case 1. These two deformations and their difference have been calculated and their difference is presented in Fig. 7a. In addition, the three-dimensional image of this difference is provided in Fig. 7b, revealing a significant distinction between the two deformations. It is observed from this difference that the heterogeneity of the semi-infinite space has an effect on the propagation of dark solitary waves.

Fig. 7
figure 7

The deformations in the plane \(Z=0\) in the half-space covered by a thin layer for the dark solitary wave solution (4.3) when \(K=0.100157\), \(C=1.39665\), \(\epsilon =0.1\), \(D=0.0001\), \(t=1\) and \(\phi _0=1\) for copper-armco iron. a The difference between the homogenous case and the heterogenous case for the cross section \(Y=0\). b Three-dimensional version of figure (a)

Full size image

5 Conclusion

In this article, we investigate the propagation of nonlinear shear horizontal waves in a half-space covered by a thin layer. We assume that the constituent material of the layer is homogeneous, isotropic, and hyperelastic, and for the half-space, it is heterogeneous. For the existence of surface SH waves in such a medium, the inequality \(c_1<c<c_2\) must hold for the phase velocity of waves, c. Here, \(c_{1}\) and \(c_2\) are the linear shear velocities of the thin layer and half-space, respectively. We also assume that the linear and nonlinear elastic material parameters of the half-space depend on the depth variable in terms of exponential functions. We perform the analysis by employing a perturbation method, and obtain a nonlinear Schrödinger equation (NLS) with external potential, defining the self-modulation of waves asymptotically. As a result of the asymptotic expansion with the assumption of weak heterogeneity of the half-space, the parameter representing the heterogeneity exists only in the external potential term of the NLS equation.

For numerical evaluations of both the dispersion relation and the NLS equation, the following three real material models are used

  • Case 1: Copper (softening layer)- Armco Iron (softening half-space)

  • Case 2: Glass (Pyrex) (hardening layer)- Acrylic Plastic (hardening half-space)

  • Case 3: Fused Quartz (softening layer)-Acrylic Plastic (hardening half-space)

Since the heterogeneity of the half-space is assumed to be weak in the order of \(\epsilon ^2\), we do not observe this term in the dispersion relation in the thin-layer approximation but rather observe in the external potential term of the NLS equation.

The dispersion relation of the surface waves propagating in a half-space covered by a thin layer possesses a single branch, and in the case of small wave numbers, this branch corresponds to the first branch of the dispersion relation when the layer is finite. Therefore, the observations in this study are only valid for small non-dimensional wave numbers (\(0<K<<1\)).

We obtain the following by analyzing the solutions of the NLS equation for three real material models:

  • For all values of real material models, the dispersion term \(\Gamma \) of the NLS equation takes negative values.

  • The effect of the layer’s nonlinear parameters on wave propagation has also been observed through a comparison between the nonlinear thin layer case and the linear case. It has been observed that this effect diminishes as the dimensionless wave number approaches zero.

  • For case 1, since the coefficient of the nonlinear term, \(\Delta \) in the NLS equation is positive, and hence \(\Gamma \Delta <0\), an envelope solitary wave solution defined by (4.2) can not exist, but only the dark solitary waves can be observed for all non-dimensional wave numbers K.

  • For case 2, since \(\Delta <0\), and hence \(\Gamma \Delta >0\), there will be an envelope solitary wave solution for all values of K.

  • For case 3, as K increases, \(\Delta \) changes its sign from negative to positive, and \(\Delta =0\) at the critical value \(K=K_c= 0.536567\). Since \(\Delta <0\), and hence \(\Gamma \Delta >0\) for \(K<K_c\), there will be an envelope solitary wave solution. Furthermore, since \(\Delta >0\), and hence \(\Gamma \Delta <0\) for \(K>K_c\), the dark solitary waves can be observed.

  • For the bright solitary wave, the term \(e^{i \Lambda \tau }\) representing the effect of heterogeneity in the solution (4.2) affects only the term \(e^{i(K\xi -\Omega \tau )}\). Therefore, in the case of a bright solitary wave, the heterogeneity of the semi-infinite space results only in a temporal shift along the propagation direction of waves in the wave packet, while the envelope of waves remains unchanged and unaffected by the material’s heterogeneity.

  • In the cases of both bright and dark solitary waves, the term \(e^{i \Lambda \tau }\) representing the effect of heterogeneity, causes a shift of the entire wave along the propagation direction over time.

Since the inhomogeneity functions in this study remain bounded with respect to the depth variable, they have the importance in terms of their physical validity for models involving an elastic layer in semi-infinite space. Furthermore, the weak inhomogeneity approach has applications in various problems related to the propagation of nonlinear elastic waves in waveguides of all types of geometries and with different polarizations.

Another problem that can be explored concerning the thin-layer approach is the reevaluation of the problem in the long-wave limit by considering the layer thickness as a small parameter. A similar analysis has been conducted by assuming the materials constituting the layered half-space as linear and using a small parameter defined based on the layer thickness [51]. Furthermore, the propagation of nonlinear SH waves in a two-layered elastic medium has also been investigated in the long-wave limit [9]. However, achieving the same analysis for nonlinear SH waves propagating in a layered half-space in the long-wave limit continues to pose an unresolved challenge, even under the condition of material homogeneity. For this new problem, we made various attempts with different scaling alternatives on h/L by assuming \(\epsilon =(h/L)^{\alpha }\) to construct a uniformly valid asymptotic expansion using the method of multiple scales with the goal of deriving an evolutionary type equation in the long-wave limit. Here, h and L denote characteristic width and characteristic wavelength, respectively. Initially, we considered the parameter \(\alpha \) as a variable. In the leading-order problem, we successfully identified non-trivial solutions for the displacements that satisfy both the radiation condition at \(-\infty \) and the boundary conditions. However, determining an appropriate value for \(\alpha \) to obtain non-trivial solutions in the subsequent order perturbation problems proved challenging. If the half-space is inhomogenous, as in our problem, the propagation problem in the long-wave limit will become more complex.

Therefore, such problems provide rich content for future research.

6 Appendix

The right-hand side of the second-order non-homogeneous equation (3.27):

$$\begin{aligned} \begin{aligned} D_1&=\biggl (2i\omega \rho _{20} \frac{\partial \mathcal {A}_1}{\partial t_2}+2ik\mu _{20} \frac{\partial \mathcal {A}_1}{\partial x_2}\biggr )+\biggl (2i\omega \rho _{20} \frac{\partial \mathcal {A}_2}{\partial t_1}+2ik\mu _{20} \frac{\partial \mathcal {A}_2}{\partial x_1}\biggr )-\rho _{20}\frac{\partial ^2 \mathcal {A}_1}{\partial t_{1}^2}+\mu _{20}\frac{\partial ^2 \mathcal {A}_1}{\partial x_{1}^2}, \\ D_2&=\frac{2\omega ^2 \rho _{20}^2}{kp \mu _{20}}\frac{\partial ^2 \mathcal {A}_1}{\partial t_{1}^2}+\frac{4\omega \rho _{20}}{p}\frac{\partial ^2 \mathcal {A}_1}{\partial x_{1} \partial t_{1}}+\frac{2k \mu _{20}}{p}\frac{\partial ^2 \mathcal {A}_1}{\partial x_{1}^2}, \\ D_3&=-dkp \mu _{20}+k^2 \mu _{20}(1-p^2)+\omega ^2 \rho _{20}, \\ D_4&=k^4n_{20}(-3+2p^2+9p^4)\rho _{20}, \\ D_5&=3k^4n_{20}(-1+p^2)^2 \rho _{20}. \end{aligned} \end{aligned}$$
(6.1)

The coefficients of the second-order particular solution (3.29):

$$\begin{aligned} \begin{aligned} \mathcal {C}_{1}&=-\frac{2kp \mathcal {K}_1-\mathcal {K}_2}{k^2\mu _{20}+3k^2p^2\mu _{20}-\omega ^2\rho _{20}}, \\ \mathcal {C}_{2}&=-\frac{2kp\mu _{20}\mathcal {K}_2+\mathcal {K}_1(k^2\mu _{20}-k^2 p^2\mu _{20}-\omega ^2\rho _{20})}{2\mu _{20}(k^2\mu _{20}+3k^2p^2\mu _{20}-\omega ^2\rho _{20})}, \\ \mathcal {C}_{3}&=-\frac{\mathcal {K}_3}{d^2\mu _{20}-k^2\mu _{20}+2dkp\mu _{20}+k^2p^2\mu _{20}+\omega ^2 \rho _{20}}B_1, \\ \mathcal {C}_{4}&=-\frac{\mathcal {K}_4}{(-k^2\mu _{20}+9k^2p^2 \mu _{20}+\omega ^2 \rho _{20})}B_{1}^2 B_{1e}. \end{aligned} \end{aligned}$$
(6.2)