1 Introduction

An understanding of the stress distribution in rotating discs plays a crucial role in ensuring their structural integrity and overall performance. For example, excessive stress concentrations at specific locations can cause material fatigue, cracks, or even catastrophic rupture. By identifying high stress concentration areas, appropriate design modifications such as varying thickness, using reinforcing materials, or adding structural features (like ribs or spokes) can be applied as mitigating factors. This optimisation process allows for reducing unnecessary material usage and weight, resulting in more efficient and cost-effective design without compromising the structural integrity (e.g. see [1,2,3]).

In linear elasticity, there are several well-established elementary strategies for dealing with the calculation of stress distributions in rotating discs. Typically, for a thin disc the variation of radial and tangential stresses through the thickness is ignored and the problem is solved as a special case of the usual plane-stress approximation. The classical situation discussed in most textbooks (e.g. see [4,5,6,7]) pertains to uniform speeds and is based on setting the appropriate component of the body force equal to the centrifugal force; as a result, the obtained stress distribution turns out to be radially symmetric. For thick discs, the situation is a bit more complicated and relies on making suitable a priori symmetry assumptions in the three-dimensional Beltrami-Michell system (e.g. see [8], pp. 388–390). The simplified thin-disc solution mentioned above was extended in the mid-1960s/early 1970s to cope with nonzero angular accelerations [9, 10] (for discs of variable thickness, see [11, 12]). A key ingredient in the proposed new solution strategy was the observation that the angular acceleration contributes only to the azimuthal component of the body force; dynamic stress propagation effects were ignored, with the corresponding final formulae depending on either the instantaneous speed of the disc (normal stresses) or the acceleration (shear stress). The resulting approximate expression of the in-plane stress distribution is still of practical value as demonstrated in [13], where these new results were used to estimate the least time in which a relatively thin disc can be run up to its maximum speed without producing plastic deformations.

The existence of a closed-form solution for the acceleration stresses in rotating thin discs brings up additional open questions regarding its stability with respect to out-of-plane infinitesimal perturbations. A particular such scenario has been partly addressed in a recent numerical study by Sader et al. [14], who have considered the possibility of buckling in a related configuration; this consisted of an in-plane spinning annular thin plate having the inner rim clamped and the outer edge stress-free. The corresponding mathematical model was obtained by coupling together the usual Föppl–von Kármán buckling equation (e.g. [15,16,17]) with an inhomogeneous basic state given by the explicit solutions derived by Stern [9] and Tang [10]. It was noted by the authors of [14] that in certain cases the shear-induced buckling patterns observed in their numerical simulations had the tendency to concentrate near the clamped edge when the rotational speeds were sufficiently large. However, this feature was not entirely conspicuous since the magnitude of the chosen speeds was only moderate. One of the main objectives of the present investigation is to shed further light on the work reported in [14] by exploring its connection to a couple of prior studies [18, 19]. In order to motivate our forthcoming developments, it is necessary to offer some background regarding these last two papers.

The words ‘buckling’ and ‘wrinkling’ are often used interchangeably in the literature on thin-walled structures; occasionally, the latter term is reserved exclusively for elastic instabilities caused by non-compressive loads (e.g. [20, 21]) or characterised by a short-wavelength deformation pattern, but we will not make that distinction here. Our earlier studies mentioned above (i.e. [18, 19]) were concerned with the development of an asymptotic framework for the so-called partial wrinkling of pre-stressed annular plates undergoing azimuthal shearing (e.g. see [22,23,24,25]). The annular domain was stretched by applying a uniform in-plane displacement field to the outer boundary while the inner rim was subjected to a small torque. Even though the radial and hoop pre-buckling stresses corresponding to this loading are tensile throughout the plate, for a sufficiently large torque one of the principal stresses becomes negative in a concentric region adjacent to the inner rim of the plate—see Fig. 1. Subsequently, once the torque has exceeded a critical threshold, a local buckling pattern emerges in the vicinity of the central hole as seen in the two contour plots included in the same Figure. It was shown in [18, 19] that the spatial extent of the region affected by this out-of-plane deformations depends on a suitably defined non-dimensional asymptotic parameter that could be regarded as a combined measure of the relative thinness of the plate and its background tension due to the applied in-plane displacement field.

Fig. 1
figure 1

Examples of localised eigenmodes in the azimuthal shearing of a pre-stressed annular thin plate (see [18, 19]). Here, \(\sigma _j\) (\(j=1,2\)) represent the principal stresses prior to buckling. As illustrated by the two contour plots, the transverse deformations of the plate are concentrated near the central hole, while the outer regions (in pale green) are virtually undeformed (color figure online)

Full size image

The numerical study by Sader et al. [14] is qualitatively identical to the scenario outlined above; while the specific expressions of the pre-buckling stresses in their spinning plate are somewhat different from those derived in [18, 19], the asymptotic structure of the two problems is not, as we will confirm in the next sections.

The paper is organised as follows. A few key facts and notations relevant to the bifurcation equation governing the wrinkling instabilities of the spinning plate are gathered together in the next section. One of the main goals is to express the pertinent boundary-value problem in a manner that highlights its clear connection with our previous studies [18, 19]. The subsequent section (Sect. 3) includes a brief discussion of the zero bending-rigidity case; while this is essentially a plane-stress scenario, which is thus not suitable for the description of out-of-plane deformations experienced by the plate, simple calculations lead to a lower bound for the critical angular accelerations that trigger such transverse deformations. Direct numerical simulations are employed in Sect. 4 to explore further the dependence of the critical load on the various parameters present in the bifurcation equation. We also confirm the localised nature of the eigenmodes, as well as its relation to the aforementioned physical and geometrical parameters. Informed by the numerical evidence gathered in that section, we then proceed to elaborate on the details of the asymptotic structure underpinning the behaviour of the spinning plate in Sect. 5. This structure consists of two interactive boundary-layers adjacent to the inner rim of the plate; outside those regions the out-of-plane deformations are exponentially small. By using the method of matched asymptotics the corresponding boundary-layer solutions are pieced together in order to obtain an asymptotic formula for the critical load. The theoretical results are compared against the direct numerical simulations touched upon earlier in Sect. 4, while their accuracy and limitations are also discussed in some detail. The paper concludes with a number of further remarks and some future work.

2 The linearised BVP

A succinct description of the relevant boundary-value problem (BVP) that will be used in the rest of the paper is included below. We will be content with just a few highlights required to set the stage and make this work reasonably self-contained.

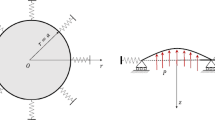
The situation of interest involves a flat annular thin elastic disc spinning about its vertical axis of symmetry with angular speed \(\widetilde{\omega }\) and acceleration \(\widetilde{\Omega }\) (see Fig. 2). With the former parameter fixed, the main question here concerns finding the critical value of the acceleration for which the disc will experience out-of-plane deformations (i.e. buckling takes place). As already mentioned in the Introduction, the problem was solved numerically by Sader et al. [14] with the help of some simplifying assumptions that will be also employed tacitly in what follows.

The annular geometry of the disc is characterised by an inner radius \(R_1\), outer radius \(R_2\), and thickness h (with \(0<h/R_2\ll {1}\)). Linear elasticity is assumed for the constitutive behaviour of the plate material, with E being its Young’s modulus and \(\nu \) the corresponding Poisson’s ratio; \(\rho _m\) denotes the mass density of the plate. We define a cylindrical coordinate system \((r,\theta ,z)\) that rotates with the disc and having the vertical axis coincident with the disc’s symmetry axis, as shown in Fig. 2. In this reference frame the two-dimensional stress distribution in the disc, \(\mathring{\varvec{\sigma }}=(\mathring{\sigma }_{\alpha \beta })\) (\(\alpha ,\beta \in \{r,\theta \}\)), can be found by solving \(\varvec{\nabla }\cdot \mathring{\varvec{\sigma }}= -\rho _m\left[ (r\widetilde{\omega }^2)\varvec{e}_r-(r\widetilde{\Omega })\varvec{e}_\theta \right] \), where \(\{\varvec{e}_r,\varvec{e}_\theta \}\) are the usual unit polar vectors (e.g. see [26]). The solution of this plane-stress problem does not pose any particular challenges and it is relegated to “Appendix A”.

Fig. 2
figure 2

The geometry of the spinning annular disc considered in the main text. Its mid-surface is parametrised by the polar coordinates \((r,\theta )\) with \(R_1\le {r}\le R_2\) and \(0\le \theta <2\pi \). The disc is clamped to a vertical rigid shaft of radius \(R_1\) passing through the centre of the circular domain

Full size image

The buckling analysis in [14] was conducted upon the linearised Föppl–von Kármán equation (e.g. [15,16,17]) for the incremental out-of-plane displacement \(w\equiv w(r,\theta )\),

$$\begin{aligned} \nabla ^4 w - \dfrac{h}{D}\varvec{\nabla }\cdot \big (\mathring{\varvec{\sigma }}\cdot \varvec{\nabla }w\big ) = 0, \end{aligned}$$
(2.1)

where the constant \(D\equiv Eh^3/12(1-\nu ^2)\) represents the usual bending rigidity of the plate. By making use of the identity \(\varvec{\nabla }\cdot (\mathring{\varvec{\sigma }}\cdot \varvec{\nabla }{w}) =\big (\varvec{\nabla }\cdot \mathring{\varvec{\sigma }}\big )\cdot \varvec{\nabla }{w} + \mathring{\varvec{\sigma }}:(\varvec{\nabla }\otimes \varvec{\nabla }{w})\) and the equation satisfied by \(\mathring{\varvec{\sigma }}\) mentioned earlier, (2.1) can be cast as

(2.2)

all the symbols/notations in (2.2) have their usual meaning (e.g. see Chapter 1 in [26]). We mention in passing that the spinning action of the disc is responsible for generating the two underlined terms in (2.2). This equation can be simplified further by introducing the non-dimensional quantities

$$\begin{aligned}{} & {} \rho :=\dfrac{r}{R_2},\quad \eta :=\dfrac{R_1}{R_2},\quad \big \{\Omega ,\,\omega ^2\big \}:= \dfrac{\rho _m R_2^2}{E}\big \{\widetilde{\Omega },\,\widetilde{\omega }^2\big \}, \end{aligned}$$
(2.3a)
$$\begin{aligned}{} & {} \dfrac{1}{E}\big \{\mathring{\sigma }_{rr},\mathring{\sigma }_{\theta \theta }\big \}=: \omega ^2\big \{{\mathring{\Sigma }}_{rr}, {\mathring{\Sigma }}_{\theta \theta }\big \},\quad \dfrac{1}{E}\,\mathring{\sigma }_{r\theta }=:\Omega \,{\mathring{\Sigma }}_{r\theta },\quad \mu ^2:=12(1-\nu ^2)\left( \dfrac{R_2}{h}\right) ^2.\end{aligned}$$
(2.3b)

For future reference, we note that \(\eta<\rho <1\) and \(\mu \gg {1}\).

On substituting (2.3) in (2.2), routine manipulations then show that the bifurcation equation can be arranged in the non-dimensional form

$$\begin{aligned}{} & {} {} \left( \dfrac{\partial ^2}{\partial \rho ^2} +\dfrac{1}{r}\dfrac{\partial }{\partial \rho } +\dfrac{1}{\rho ^2}\dfrac{\partial ^2}{\partial \theta ^2}\right) ^2w -\mu ^2\Omega \left[ \dfrac{\partial w}{\partial \theta } +2{\mathring{\Sigma }}_{r\theta }\dfrac{\partial }{\partial \rho } \left( \dfrac{1}{\rho }\dfrac{\partial w}{\partial \theta }\right) \right] \nonumber \\ {}{} & {} {} \quad +\mu ^2\omega ^2\left[ \rho \dfrac{\partial w}{\partial \rho } -{\mathring{\Sigma }}_{rr}\dfrac{\partial ^2w}{\partial \rho ^2} -{\mathring{\Sigma }}_{\theta \theta }\dfrac{1}{\rho }\left( \dfrac{\partial w}{\partial \rho } +\dfrac{1}{\rho }\dfrac{\partial ^2w}{\partial \theta ^2}\right) \right] =0, \end{aligned}$$
(2.4)

where the first term is easily recognised as being the usual bi-Laplacian operator expressed in polar coordinates. Solutions \(w\equiv w(\rho ,\theta )\) of this last equation will be sought by looking for a function with separable variables. To this end, we write

$$\begin{aligned} w = \mathfrak {Re}\left\{ W(\rho )\textrm{e}^{\textrm{i}{m}\theta }\right\} , \qquad W(\rho ):=W_R(\rho )+\textrm{i}W_I(\rho ), \end{aligned}$$
(2.5)

in which the notation \(\mathfrak {Re}\{z\}\) stands for the real part of \(z\in {\mathbb {C}}\), and the radial amplitude functions \(W_j\) (\(j\in \{R,I\}\)) are both real-valued. The arbitrary integer \(m\ge {0}\), referred to as the mode number henceforth, will be determined subject to additional constraints that will be spelled out shortly.

Performing the requisite calculations, it turns out that the unknown complex amplitude in (2.5) satisfies the linear ordinary differential equation

$$\begin{aligned} W'''' + \mathcal {A}_3(\rho )W''' + \mathcal {A}_2(\rho )W''+\mathcal {A}_1(\rho )W'+\mathcal {A}_0(\rho )W = 0, \qquad \eta<\rho <1, \end{aligned}$$
(2.6)

where

$$\begin{aligned}&\mathcal {A}_3(\rho ):=\dfrac{2}{\rho },\qquad \mathcal {A}_2(\rho ):=-\left[ \left( \dfrac{2m^2+1}{\rho ^2}\right) +\mu ^2\omega ^2{\mathring{\Sigma }}_{rr}\right] , \end{aligned}$$
(2.7a)
$$\begin{aligned}&\mathcal {A}_1(\rho ):=\left( \dfrac{2m^2+1}{\rho ^3}\right) +\mu ^2\omega ^2\left( \rho -\dfrac{{\mathring{\Sigma }}_{\theta \theta }}{\rho }\right) -2\text {i}\mu ^2{m}\Omega \left( \dfrac{{\mathring{\Sigma }}_{r\theta }}{\rho }\right) , \end{aligned}$$
(2.7b)
$$\begin{aligned}&\mathcal {A}_0(\rho ):= \dfrac{m^2}{\rho ^2}\left[ \left( \dfrac{m^2-4}{\rho ^2}\right) +\mu ^2\omega ^2{\mathring{\Sigma }}_{\theta \theta }\right] -\text {i}{m}\mu ^2\Omega \left( 1-\dfrac{2{\mathring{\Sigma }}_{r\theta }}{\rho ^2}\right) , \end{aligned}$$
(2.7c)

and \(\textrm{i}\equiv \sqrt{-1}\) is the usual imaginary unit. The physical solution is obtained from (2.5) as

$$\begin{aligned} w(\rho ,\theta ) = W_R(\rho )\cos (m\theta )-W_I(\rho )\sin (m\theta ), \end{aligned}$$
(2.8)

with \(W_R\) and \(W_I\) satisfying two coupled fourth-order differential equations akin to (2.6)—we refer to “Appendix B” for more details.

Finally, Eq. (2.6) is to be solved subject to an appropriate set of boundary conditions (e.g. see [14]). At its inner rim, the plate is assumed to be clamped, so

$$\begin{aligned} W = \dfrac{\textrm{d}W}{\textrm{d}\rho } = 0,\qquad {\text{ for }}\quad \rho =\eta , \end{aligned}$$
(2.9)

while the outer edge (\(\rho =1\)) is traction-free, which translates into

$$\begin{aligned}&\dfrac{\textrm{d}^2W}{\textrm{d}\rho ^2}+\nu \dfrac{\textrm{d}W}{\textrm{d}\rho }-\nu {m^2}W=0, \end{aligned}$$
(2.10a)
$$\begin{aligned}&\dfrac{\textrm{d}^3W}{\textrm{d}\rho ^3}+\dfrac{\textrm{d}^2W}{\textrm{d}\rho ^2} -\big [1+(2-\nu )m^2\big ]\dfrac{\textrm{d}W}{\textrm{d}\rho }+\big [(3-\nu )m^2\big ] W=0. \end{aligned}$$
(2.10b)

This completes the description of the bifurcation problem that constitutes the departure point for the subsequent asymptotic developments. The (instantaneous) angular speed \(\omega \) is assumed to be given, while \(\Omega \equiv \Omega (m;\omega ,\mu )\) represents the unknown eigenvalue. It is further noted that \(m\in {\mathbb {N}}\) is also unknown at this stage and, for each fixed \(\omega \) and \(\mu \), this parameter will have to be determined so that it renders the global minimum of the curves \(\Omega \) versus m. Although strictly speaking the mode number is a discrete quantity, here it will be regarded as a positive continuous parameter, i.e. \(m\in {\mathbb {R}}_+\). To summarise, for each fixed \(\omega >0\) and \(\mu \gg {1}\) the critical (wrinkling) eigenvalue, \(\Omega _{\textrm{c}}\), and the critical mode number, \(m_{\textrm{c}}\), will be identified by the conditions

$$\begin{aligned} \Omega _{\textrm{c}} = \min _{m>0}\Omega (m;\omega ,\mu ),\qquad \text{ with }\quad \Omega _{\textrm{c}} = \Omega (m_{\textrm{c}};\omega ,\mu ). \end{aligned}$$
(2.11)

Our main interest is in exploring the dependence of \(\Omega _{\textrm{c}}\) on \(\mu \gg {1}\). To gain further insight into the mathematical structure of Eq. (2.6) in the large-\(\mu \) limit, it is profitable to first examine closely the membrane problem (i.e. zero bending rigidity); this is our next step.

3 A particular scenario: zero bending rigidity

The relevant equation for the limiting case of interest in this section is readily obtained from the bifurcation Eq. (2.4) by multiplying the whole lot by \(\mu ^{-2}\), and then letting \(\mu \rightarrow \infty \). As a result, the bi-Laplacian drops out of the equation and the remaining terms become \(\mu \)-independent.

Letting \(\sigma _j\equiv \sigma _j(\rho )\) (\(j=1,2\)) denote the non-dimensional principal stresses in the unwrinkled plate, we have

$$\begin{aligned} \sigma _1 + \sigma _2 = \omega ^2\left( {\mathring{\Sigma }}_{rr}+{\mathring{\Sigma }}_{\theta \theta }\right) ,\qquad \sigma _1\cdot \sigma _2 = \omega ^4\left( {\mathring{\Sigma }}_{rr}\right) \left( {\mathring{\Sigma }}_{\theta \theta }\right) -\Omega ^2\left( {\mathring{\Sigma }}_{r\theta }\right) ^2. \end{aligned}$$
(3.1)

Using the expressions from “Appendix A”, routine algebraic manipulations indicate that

$$\begin{aligned} \sigma _1(\rho )+\sigma _2(\rho )= & {} \dfrac{1}{2}\omega ^2(1+\nu )\left\{ \dfrac{1}{2} \left[ \dfrac{(3+\nu )+\eta ^4(1-\nu )}{(1+\nu )+\eta ^2(1-\nu )}\right] -\rho ^2\right\} \\> & {} \dfrac{1}{2}\omega ^2(1+\nu )(1-\rho ^2)>0,\qquad \text{ for } \text{ all }\quad \eta \le \rho <{1}, \end{aligned}$$

but the sign of \(\sigma _1(\rho )\cdot \sigma _2(\rho )\) depends on the ratio \(\Omega /\omega ^2\), and this product may become negative in some parts of the annular domain of the plate under certain conditions. When this happens, one of the two principal stresses, either \(\sigma _1\) or \(\sigma _2\), is compressive and the spinning plate will experience compression in the direction of the negative principal stress. However, if the bending rigidity is not negligible, buckling will not be initiated as soon as the plate experiences compression; this compression needs to be sufficiently strong in order to trigger out-of-plane deformations. We will deal directly with the specifics of this situation later in Sect. 5, but for now we will focus on the zero bending rigidity case.

The partial differential equation that results from passing to the limit as explained at the beginning of this section is of second order and has variable coefficients. Although it cannot be used to describe the out-of-plane wrinkling of our spinning circular configuration, one can formulate a simplified criterion as suggested by Simmonds [27] in his pioneering study of a normally pressurised spinning nonlinear membrane (see also [19,20,21, 28, 29]). Transplanted to the situation of interest here, this result stipulates that a lower bound for the wrinkling load, (say), corresponds to the vanishing of the second expression in (3.1) when \(\rho =\eta \). Re-arranging the corresponding algebraic equation yields

$$\begin{aligned} \Omega \ge \Omega _{\small {\text {low}}}\equiv \omega ^2\sqrt{\dfrac{\big (\Sigma _{rr}^0\big )\big (\Sigma _{\theta \theta }^0\big )}{\big (\Sigma _{r\theta }^0\big )^2}}, \end{aligned}$$
(3.2)

where we have introduced the simplifying notations

$$\begin{aligned} \Sigma _{\alpha \beta }^0:={\mathring{\Sigma }}_{\alpha \beta }(\eta ),\qquad \alpha ,\beta \in \{r,\theta \}. \end{aligned}$$
(3.3)

When \(\Omega =\Omega _{\small {\text {low}}}\) we have \(\sigma _1(\eta )\cdot \sigma _2(\eta )=0\) and \(\sigma _1(\rho )\cdot \sigma _2(\rho )>0\) for all \(\eta<\rho <1\). For \(\Omega >\Omega _{\small {\text {low}}}\) one of the two principal stresses becomes strictly negative near the inner rim, and the annular domain of the disc develops a concentric sub-region of compressive stresses adjacent to \(\rho =\eta \); as \(\Omega \) is further increased, the extent of this region grows uniformly.

A close inspection of the coefficients of the bifurcation Eq. (2.6) suggests that their dependence on \(\mu \) and \(\omega \) is symmetric if we replace the original eigenvalue \(\Omega \) with

$$\begin{aligned} \lambda :=\dfrac{\Omega }{4\omega ^2} \end{aligned}$$
(3.4)

and modify the expressions of \(\mathcal {A}_j\) (\(j=0,1\)) accordingly. It will become apparent shortly that it is more convenient to work with the new eigenparameter \(\lambda \) instead of \(\Omega \), a convention that will be adopted for the rest of the paper. Note also that the criterion (3.2) leads to an alternative formulation, .

In Fig. 3 we illustrate the change of signs in the (non-dimensional) principal stresses for \(\eta =0.1\) and \(\eta =0.5\) (with \(\nu =0.25\)); the red curves correspond to the case , while the rest of the other curves are obtained for a suitably chosen monotonic increasing sequence of arbitrary \(\lambda \)-values (see caption for details); in both windows, the black circular markers indicate the transition between \(\sigma _1\cdot \sigma _2<0\) (left to the marker) and \(\sigma _1\cdot \sigma _2>0\) (right to the marker). We also mention in passing that for \(\eta =0.1\) and for \(\eta =0.5\).

Fig. 3
figure 3

Illustration of the dependence of the product \(\sigma _1\cdot \sigma _2\) on : \(\eta =0.1\) (left) and \(\eta =0.5\) (right). In both windows, we show \(D_{\pm }\equiv (\rho /\omega )^4\left\{ ({\mathring{\Sigma }}_{rr})({\mathring{\Sigma }}_{\theta \theta }) -16\lambda ^2\big ({\mathring{\Sigma }}_{r\theta }\big )^2\right\} \) as a function of \(\eta \le \rho \le {1}\) (\(\nu =0.25\)). The red curves correspond to , while the blue ones are obtained for with \(k=1,2,\ldots ,9\); the arrows show the direction in which \(\lambda \) increases (color figure online)

Full size image

Later, in Sect. 5, it will be shown how the results of this section can be linked to the case of a thin plate with very small (nonzero) bending rigidity. To prepare the stage for those developments, in the next section we will probe further into the behaviour of the critical load and mode number by looking at a small selection of direct numerical simulations regarding the bifurcation problem defined in Sect. 2. These results complement those reported by Sader et al. [14] and highlight some new features of the problem at hand.

4 Further numerical results

Past experience with similar type of wrinkling problems suggests that a natural choice of an asymptotic parameter in Eq. (2.6) would be the quantity \(\mu \gg {1}\) defined in (2.3b). However, in the light of the remarks made vis-à-vis the new eigenparameter \(\lambda \)—see (3.4), it is more advantageous to work with the combination \((\mu \omega )\). Thus, we introduce

$$\begin{aligned} \varepsilon :=(\mu \omega )^{-1} \end{aligned}$$
(4.1)

and note that \(0<\varepsilon \ll {1}\) provided that \(\omega \gg {\mu ^{-1}}\), an assumption that will be enforced tacitly in what follows. It is clear that if one succeeds in finding an asymptotic approximation for \(\lambda _{\textrm{c}}\equiv \lambda _{\textrm{c}}(\varepsilon )\), then it is entirely a routine task to express the corresponding formula as \(\Omega _{\textrm{c}}=\Omega _{\textrm{c}}(\mu )\); similar remarks apply for the mode number as well.

The numerical findings described in this section have been obtained with standard built-in routines available in MATLAB. The method of compound matrices (e.g. see [19]) was also used as an additional sanity check.

A first set of results is included in Fig. 4, in which we illustrate the dependence of \(\lambda _{\textrm{c}}\) and \(m_{\textrm{c}}\) on \(\varepsilon \) for three different values of the annular aspect ratio \(\eta \) (and \(\nu =0.25\)); we use \(\varepsilon ^{-1}\) on the horizontal axes of those plots because this parameter coincides with \(\overline{\omega }\) used in [14]. As \(\varepsilon ^{-1}\rightarrow +\infty \), the curves \(\lambda _{\textrm{c}}\equiv \lambda _{\textrm{c}}(\varepsilon ^{-1})\) in the left window asymptotically approach mentioned in Sect. 3, albeit at a very slow rate (this feature will be confirmed later on, in Sect. 5). It is also clear that the effect of increasing \(\eta \) translates into a sizeable shift upwards in the stability curves. Changing the Poisson’s ratio to other values has only a very minor effect on the quantitative data presented in the left window of Fig. 4, so in the interest of brevity those results are omitted. The other set of plots in the same Figure suggest that for fixed \(\eta \) and \(\nu \), the critical mode number \(m_{\textrm{c}}\equiv m_{\textrm{c}}(\varepsilon ^{-1})\) increases with \(\varepsilon ^{-1}\). All the features described above are somewhat unsurprising and mirror closely those encountered in similar contexts (e.g. see [18,19,20,21, 29]).

Fig. 4
figure 4

The dependence of the lowest positive critical eigenvalue \(\lambda _{\textrm{c}}\) (left) and the critical mode number \(m_{\textrm{c}}\) (right) on the asymptotic parameter defined in (4.1). The three curves included in each window correspond to \(\eta \in \big \{0.1,0.3, 0.5\big \}\); in all of these numerical results \(\nu =0.25\)

Full size image

A less obvious trait of the response curves for the bifurcation problem of the accelerating annular disc is related to the global minima of the functions \(\lambda \equiv \lambda (m)\) for a given/fixed \(0<\varepsilon \ll {1}\). According to the representative data included in Fig. 5, the bottom parts of the graphs of these functions happen to be very flat over extended regions. We consider the same \(\eta \)-values as in the previous figure and show the relevant portions of the \(\lambda -m\) curves (\(2\le m\le 30\)) for \(\varepsilon =1/250\simeq 0.004\) and \(\varepsilon =1/350\simeq 0.0029\); these appear as the continuous and the dashed curves, respectively. Numerical optimisation techniques for identifying minima situated in such flat regions of the graph of a given function are typically associated with slow convergence. Broadly speaking, this aspect is also likely to impact the asymptotic approximations of such critical points, as we will discover in the next section.

Fig. 5
figure 5

Sample of response curves for \(\varepsilon =1/250\) (continuous) and \(\varepsilon =1/350\) (dashed) for three different values of \(0<\eta <1\). The round markers on each curve identify the global minima of the functions \(\lambda =\lambda (m)\) with \(2\le m\le 30\). Here \(\nu =0.25\)

Full size image

Finally, in closing this section we illustrate briefly the localised nature of the critical eigenmodes of the differential Eq. (2.6) subject to the boundary constraints (2.9) and (2.10). Figure 6 includes the real (\(W_R\)) and imaginary (\(W_I\)) parts of those functions for \(\eta =0.1\) corresponding to three different choices of the small asymptotic parameter \(\varepsilon \). For all values of \(\varepsilon \) considered here, the out-of-plane deformations experienced by the wrinkled annulus are concentrated near the left edge where the plate is clamped to the vertical shaft. This is not a by-product of the usual bending boundary layer normally encountered in the literature on plates and shells (e.g. [30, 31]), but the corresponding eigendeformations are confined to a larger concentric region adjacent to the inner rim. By increasing \(\eta \)—see Fig. 7, the localisation becomes less pronounced than before; it also seems that \(\varepsilon \) needs to be much smaller in order for the localisation of the eigenmodes to visibly kick in. Such behaviour is to be expected due to the decrease in size of the radial span of the annular disc in the scenario illustrated in Fig. 7. These observations indicate that the specific behaviour exhibited by our eigenmodes can be attributed to the combined effect of two separate influences. One is the thin-plate effect (controlled by \(\varepsilon \)), while the other corresponds to the size of the central hole (of radius \(\eta \)) and can be likened to the Saint-Venant’s principle in linear elasticity—this will be referred to as the local effect. For \(0<\eta \ll {1}\), it is the latter that plays a dominant role, whereas the former becomes more significant when the central hole is sufficiently large (roughly, \(\eta > rsim 0.3\)). It is well known that the asymptotic description of each of the two effects mentioned above requires rather different mathematical strategies (e.g. see [32] for the buckling of an annular plate in the limit \(\eta \rightarrow {0}^+\)). For this reason, in this work we will focus exclusively on the thin-plate effect.

The re-assessment of the various numerical results in this section has shed further light on the localised nature of the critical eigenmodes, as well as the dependence of the \(\lambda _{\textrm{c}}\) and \(m_{\textrm{c}}\) in terms of the asymptotic parameter introduced in (4.1). With this in mind, we are now ready to tackle the details of the asymptotic structure for the wrinkling problem.

Fig. 6
figure 6

A representative sequence of critical eigenmodes for \(\eta =0.1\) showing the tendency to localisation as \(\varepsilon \rightarrow {0}^+\). Here \(\nu =0.25\), but these results are rather insensitive to the particular value chosen for the Poisson’s ratio

Full size image
Fig. 7
figure 7

The same as per Fig. 6, except that here \(\eta =0.5\)

Full size image

5 Asymptotic approximations

According to the direct numerical simulations discussed in the preceding section, the critical eigenmodes of the wrinkling problem under consideration display a multiple-scale structure in which a fast spatial oscillation is modulated over a relatively narrow region adjacent to the inner rim of the disc; this localisation becomes more pronounced as \(\varepsilon \rightarrow {0^+}\). Although not immediately apparent in Figs. 6 and 7, the shape of the eigenmodes involves another key spatial lengthscale, one that is essentially the result of a boundary layer originating in the clamped edge constraint at \(\rho =\eta \)—see (2.9). The details of the latter (secondary) effect will be taken up in Sect. 5.3 after we first pin down the multiple-scale asymptotic structure mentioned above.

5.1 The main structure

Standard scaling arguments similar to those discussed at length in [18, 19] can help establish the relevant orders of magnitude of the key terms in Eq. (2.6). In particular, this suggests the introduction of the re-scaled variable \(Y>0\) defined by

$$\begin{aligned} \rho = \eta + \varepsilon ^{1/2}Y,\qquad \text{ with }\qquad Y=\mathcal {O}(1). \end{aligned}$$
(5.1)

We then start by writing

$$\begin{aligned} m = m_0\,\varepsilon ^{-3/4} \end{aligned}$$
(5.2)

for some \(m_0=\mathcal {O}(1)\) (to be determined), and look for solutions of (2.6) satisfying an ansatz of the form

$$\begin{aligned} W = V(Y)\exp \big (\textrm{i}\kappa \,\varepsilon ^{-1/4}Y\big ),\qquad (\textrm{i}\equiv \sqrt{-1}), \end{aligned}$$
(5.3)

where

$$\begin{aligned}&V(Y) = V_{0}(Y) + \varepsilon ^{1/4}V_1(Y) + \varepsilon ^{1/2} V_{2}(Y) + \varepsilon ^{3/4} V_{3}(Y) + \varepsilon V_4(Y) + \dots , \end{aligned}$$
(5.4a)
$$\begin{aligned}&\lambda = \lambda _0 + \lambda _1\,\varepsilon ^{1/2} + \lambda _2\,\varepsilon ^{3/4} + \lambda _3\,\varepsilon + \lambda _4\varepsilon ^{5/4} + \lambda _5\varepsilon ^{3/2} + \dots . \end{aligned}$$
(5.4b)

The constant \(\kappa \in {\mathbb {R}}\) is unknown at this stage but will be found as part of the solution, and the same applies to the coefficients \(\lambda _j\in {\mathbb {R}}\) (\(j=0,1,2,\dots \)). The complex exponential term in (5.3) accounts for the fast spatial oscillations of the eigenmodes depicted in Sect. 4. These oscillations take place on a \(\mathcal {O}(\varepsilon ^{3/4})\) scale which is much shorter than that described by the re-scaled independent variable Y in (5.1).

On substituting (5.4) and (5.3) in (2.6), we find at the leading and next-to-leading orders the following relations

$$\begin{aligned} \mathcal {D}_1(\lambda _0,m_0,\kappa )V_0 = 0\qquad \text{ and }\qquad \mathcal {D}_1(\lambda _0,m_0,\kappa )V_1 +\textrm{i}\mathcal {D}_2(\lambda _0,m_0,\kappa )V_0' = 0, \end{aligned}$$
(5.5)

where the ‘dash’ stands for differentiation with respect to Y, a convention that will be employed from now on. The quantities \(\mathcal {D}_j\) (\(j=1,2\)) correspond to the definitions

$$\begin{aligned}{} & {} \mathcal {D}_1:=\kappa ^2\Sigma _{rr}^0 + 8\kappa \lambda _0\left( \dfrac{m_0}{\eta }\right) \Sigma _{r\theta }^0 + \left( \dfrac{m_0}{\eta }\right) ^2\Sigma _{\theta \theta }^0,\\ {}{} & {} \mathcal {D}_2:=-2\kappa \Sigma _{rr}^0 - 8\lambda _0\left( \dfrac{m_0}{\eta }\right) \Sigma _{r\theta }^0. \end{aligned}$$

As a side note, we mention that the values of the pre-buckling stresses at the inner rim satisfy the identity

$$\begin{aligned} \left( 1-\dfrac{\Sigma _{\theta \theta }^0}{\eta ^2}\right) -\dfrac{2}{\eta ^2}\left( \dfrac{B_1}{\eta ^2}-B_2\eta ^2\right) +\dfrac{\Sigma _{rr}^0}{\eta ^2} = 0, \end{aligned}$$
(5.6)

where the definitions of \(B_1\) and \(B_2\) can be found in “Appendix A”.

Since \(V_0\) cannot be identically zero, the two relations in (5.5) will be satisfied provided that \(\mathcal {D}_1(\lambda _0,m_0,\kappa ) = \mathcal {D}_2(\lambda _0,m_0,\kappa )=0\). From the first of these two equations it follows immediately that

$$\begin{aligned} \lambda _0 = -\dfrac{1}{8}\left[ \dfrac{\eta \kappa }{m_0}\left( \dfrac{\Sigma _{rr}^0}{\Sigma _{r\theta }^0}\right) +\dfrac{m_0}{\eta \kappa }\left( \dfrac{\Sigma _{\theta \theta }^0}{\Sigma _{r\theta }^0}\right) \right] , \end{aligned}$$
(5.7)

and it is also clear that \(\lambda _0\equiv \lambda _0(\kappa , m_0)\). As we are looking for the smallest \(\lambda _0>0\), one of the usual criticality conditions, \(\partial \lambda _0/\partial \kappa =0\), yields the solution \(\kappa =\kappa _*\) with

$$\begin{aligned} \kappa _* = \pm \dfrac{m_0}{\eta }\left( \dfrac{\Sigma _{\theta \theta }^0}{\Sigma _{rr}^0}\right) ^{1/2}\qquad \Longrightarrow \qquad \lambda _0^*:=\lambda _0\Big |_{\kappa =\kappa _*} = \dfrac{1}{4}\sqrt{\dfrac{\big (\Sigma _{rr}^0\big )\big (\Sigma _{\theta \theta }^0\big )}{\big (\Sigma _{r\theta }^0\big )^2}}. \end{aligned}$$
(5.8)

The dependence of \(\lambda _0\) on \(\kappa \) and \(m_0\) is symmetric and homogeneous, so the other criticality condition, \(\partial \lambda _0/\partial m_0 = 0\), does not yield any new information. We also note that the equation \(\mathcal {D}_2=0\) is identically satisfied when \(\lambda _0=\lambda _0^*\) and \(\kappa =\kappa _*\). Furthermore, a comparison between the critical value of \(\lambda _0\) in (5.8) and the lower bound mentioned in Sect. 3 reveals that these two quantities are in fact identical, i.e. .

The spatial structure of the critical eigenmode of (2.6) is fixed at the next order. For \(\kappa \) and \(\lambda _0\) as found in (5.8), it turns out that

$$\begin{aligned} \mathcal {L}[V_0]\equiv V_0'' - (\Gamma _1 Y + \Gamma _2)V_0 = 0, \end{aligned}$$
(5.9)

with

$$\begin{aligned}&\Gamma _1:=-\dfrac{2m_0^2}{\eta ^3\Sigma _{rr}^0}\left[ \left( \dfrac{B_1}{\eta ^2}-B_2\eta ^2\right) \dfrac{\Sigma _{\theta \theta }^0}{\Sigma _{rr}^0} +\dfrac{1}{4}\left( \eta ^2+\dfrac{3}{\eta ^2}\right) \dfrac{\Sigma _{\theta \theta }^0}{\Sigma _{r\theta }^0} +\left( \dfrac{2C_1}{\eta ^2}+C_3\right) \right] , \end{aligned}$$
(5.10a)
$$\begin{aligned}&\Gamma _2:=\dfrac{m_0^2}{\eta ^2\Sigma _{rr}^0}\left[ \dfrac{m_0^2}{\eta ^2} \left( \dfrac{\Sigma _{\theta \theta }^0}{\Sigma _{rr}^0}+1\right) ^2 +2\lambda _1\left( \eta ^2-\dfrac{1}{\eta ^2}\right) \sqrt{\dfrac{\Sigma _{\theta \theta }^0}{\Sigma _{rr}^0}}\right] . \end{aligned}$$
(5.10b)

We are going to see shortly that Eq. (5.9) can help establish a closed-form relationship between \(\lambda _1\) and \(m_0\), whereby the corresponding values associated with the minimum-energy configurations of the spinning disc can be obtained via routine calculations.

A further simplification of (5.9) is possible by adopting the re-scaling

$$\begin{aligned} Z:=\Gamma _1^{1/3}Y+\dfrac{\Gamma _2}{\Gamma _1^{2/3}}, \end{aligned}$$
(5.11)

whereupon it follows that \({\textrm{d}}^2\widehat{V}_0/{\textrm{d}}Z^2 - Z\widehat{V}_0=0\), with \(\widehat{V}_0(Z)\equiv V_0(Y(Z))\). The solution of interest is \(\widehat{V}_0 = (1+\textrm{i})\textrm{Ai}(Z)\), where ‘\(\textrm{Ai}\)’ denotes the usual Airy function that decays exponentially quickly as \(Z\rightarrow +\infty \).

The boundary conditions \(W=({\textrm{d}}W/{\textrm{d}}\rho )=0\) at \(\rho =\eta \) (i.e. at \(Y=0\)) cannot both be imposed; this suggests that the main \(Y=\mathcal {O}(1)\) region must be supplemented by an inner zone, but for the time being we will demand that \(V_0\rightarrow {0}\) as \(Y\rightarrow {0}^+\). We recall in passing that, in addition to decaying exponentially as \(Z\rightarrow +\infty \), the Airy function possesses a countable set of zeros along the negative Z-axis; the first occurs at \((-\zeta _0)\simeq -2.338\), so we can ensure that \(V_0(Y)=0\) at \(Y=0\) by requiring that \(\Gamma _1^{-2/3}\Gamma _2 = -\zeta _0\). If the expressions (5.10) are substituted in this relation, after some algebra it follows that

$$\begin{aligned} 2\lambda _1\left( \dfrac{1}{\eta ^2}-\eta ^2\right) = \left[ \zeta _0 m_0^{-2/3}(2\Delta )^{2/3}\left( \Sigma _{rr}^0\right) ^{1/3} +\dfrac{m_0^2}{\eta ^2}\left( \dfrac{\Sigma _{\theta \theta }^0}{\Sigma _{rr}^0}+1\right) ^2\right] \left( \dfrac{\Sigma _{rr}^0}{\Sigma _{\theta \theta }^0}\right) ^{1/2}, \end{aligned}$$

where \(\Delta \) represents the negative of the square-bracket on the right-hand side of (5.10a). The correction term \(\lambda _1\) varies with \(m_0\) and grows without bound when both \(m_0\rightarrow {0}^+\) and \(m_0\rightarrow +\infty \). It is a simple matter to check that \(\lambda _1\) is minimised when \(m_0=m_0^*\), where

$$\begin{aligned} m_0^*=\eta ^{3/4}\left( \dfrac{\zeta _0}{3}\right) ^{3/8}(2\Delta )^{1/4}\left( \Sigma _{rr}^0\right) ^{1/8} \left( \dfrac{\Sigma _{\theta \theta }^0}{\Sigma _{rr}^0}+1\right) ^{-3/4}, \end{aligned}$$
(5.12)

and then

$$\begin{aligned} \lambda _1^*:=\lambda _1\Big |_{m_0=m_0^*} =\dfrac{2\eta ^{3/2}}{1-\eta ^4}\left( \dfrac{\zeta _0}{3}\right) ^{3/4}(2\Delta )^{1/2} \left( \Sigma _{rr}^0\right) ^{1/4}\left( \dfrac{\Sigma _{rr}^0}{\Sigma _{\theta \theta }^0}+1\right) ^{1/2}. \end{aligned}$$
(5.13)

The result (5.12) completely determines the approximation of the mode number considered in (5.2). For \(\eta =0.1\) and \(\nu =0.25\), we get \(m_{\textrm{c}}^*\equiv m_0^*\varepsilon ^{-3/4}\simeq 6.88\) when \(\varepsilon =1/200\), while \(m_{\textrm{c}}^*\simeq 10.47\) for \(\varepsilon =1/350\); the corresponding direct numerical simulations predict critical mode numbers (approximately) equal to 7.2 and 11.0, respectively. Comparable results are obtained for other values of \(\nu \) and \(\eta \). In contrast to our earlier studies [18, 19], here a simplified approach is employed for the expression of the critical mode number (5.12). The reason for this will become clear in Sect. 5.5 when we will examine the nature of the asymptotic approximation for \(\lambda _{\textrm{c}}\).

5.2 Higher-order terms

Our predictions for the critical load so far are formally valid as \(\varepsilon \equiv (\mu \omega )^{-1}\rightarrow 0^+\), but given that the proposed asymptotic developments require \(0<\varepsilon ^{1/4}\ll {1}\)—see (5.3), it is quite unlikely that they are useful for all but very small \(\varepsilon \). In an attempt to potentially improve the accuracy of these results, we are going to calculate a few more correction terms \(\lambda _j\) (\(j=2,3,\dots \)) in the original ansatz (5.4b). The main steps of the calculations are outlined below.

The equation for \(V_1\equiv V_1(Y)\) in (5.4a) satisfies an inhomogeneous version of (5.9) in which \(V_0\rightarrow V_1\); more specifically,

$$\begin{aligned} \mathcal {L}[V_1]=\alpha _0V_0(Y) +\big (\alpha _1 + \alpha _2 Y\big )V_0'(Y), \end{aligned}$$
(5.14)

where the expressions of the coefficients \(\alpha _j\) (\(j=0,1,2\)) can be found in “Appendix C”. Further use of the change of variable (5.11) shows that (5.14) can be cast as an inhomogeneous Airy-type equation

$$\begin{aligned} \dfrac{\textrm{d}^2\widehat{V}_1}{\textrm{d}Z^2}-Z\widehat{V}_1 = a_0\widehat{V}_0(Z) + \big (a_1 + a_2 Z\big )\widehat{V}_0^{(1)}(Z), \end{aligned}$$
(5.15)

where \(\widehat{V}_1(Z)\equiv V_1(Y(Z))\) and the superscript on \(\widehat{V}_0\) indicates differentiation with respect to Z. The new coefficients on the right-hand side of (5.15) correspond to

$$\begin{aligned} a_0:= \alpha _0\Gamma _1^{-2/3},\quad a_1:= \alpha _1\Gamma _1^{-1/3}+\alpha _2\zeta _0\Gamma _1^{-2/3},\quad a_2:= \alpha _2\Gamma _1^{-2/3}. \end{aligned}$$
(5.16)

A particular integral of (5.15) is readily identified as

$$\begin{aligned} \widehat{V}_1(Z) = (a_0 - a_2)\widehat{V}_0^{(1)}(Z) + \dfrac{1}{2}a_1\widehat{V}_0^{(2)}(Z) +\dfrac{1}{4} a_2 \widehat{V}_0^{(4)}(Z). \end{aligned}$$
(5.17)

Since \(V_1(Y)\rightarrow {0}\) as \(Y\rightarrow {0}^+\), it is necessary to evaluate \(\widehat{V}_1\) at \(Z=-\zeta _0\); this is routinely found by taking advantage of the properties of the Airy operator present in (5.15), with the final result

$$\begin{aligned} \widehat{V}_1\big |_{Z=-\zeta _0} = (1+\textrm{i})\left( a_0-\dfrac{1}{2}a_2\right) \textrm{Ai}_0', \end{aligned}$$
(5.18)

where \(\textrm{Ai}_0'\equiv \textrm{Ai}'(-\zeta _0)\). To satisfy the aforementioned boundary condition, we need to require that the right-hand side of the relation (5.18) vanishes identically. In principle, as the expression in question is complex-valued, there will be two relations coming out of (5.18) that correspond to its real and imaginary parts, respectively. However, use of the earlier identity (5.6) shows that the second bracket in (5.18) is in fact real-valued since

$$\begin{aligned} {\mathfrak {Im}}\left\{ a_0-\dfrac{1}{2}a_2\right\} \equiv {0}, \end{aligned}$$

where \({\mathfrak {Im}}\{z\}\) stands for the imaginary part of \(z\in {\mathbb {C}}\). Thus, there is just one (linear) equation that follows from (5.18), and that amounts to

$$\begin{aligned} \lambda _2 = 0. \end{aligned}$$

This prompts the need for considering the governing differential equations for the subsequent terms in the ansatz (5.4a). It will become apparent shortly that it is helpful to have alternative expressions for \(\widehat{V}_1\) and \(\widehat{V}_1^{(1)}\) in terms of \(\widehat{V}_0\) and its derivative; these results are listed below for convenience

$$\begin{aligned}&\widehat{V}_1(Z) = \big (\gamma _0 Z + \gamma _1 Z^2\big )\widehat{V}_0(Z), \end{aligned}$$
(5.19a)
$$\begin{aligned}&\widehat{V}_1^{(1)}(Z)=\big (\gamma _0 + 2\gamma _1{Z}\big )\widehat{V}_0(Z) + \left( \gamma _0 Z + \gamma _1 Z^2\right) \widehat{V}_0^{(1)}(Z), \end{aligned}$$
(5.19b)

where

$$\begin{aligned} \gamma _0:=\dfrac{a_1}{2}\qquad \text{ and }\qquad \gamma _1:=\dfrac{a_2}{4}. \end{aligned}$$

The governing equation for \(V_2\equiv V_2(Y)\) assumes the form

$$\begin{aligned} \mathcal {L}[V_2]= & {} \left( \beta _1 + \beta _2 Y + \beta _3 Y^2\right) V_0(Y) + \beta _4 V_0'(Y) + (\beta _{5}+\beta _{6}Y)V_0''(Y)\nonumber \\{} & {} \quad +\beta _{7}V_1(Y) +\left( \beta _{8}+\beta _{9}Y\right) V_1'(Y), \end{aligned}$$
(5.20)

where the expressions of \(\beta _j\) (\(j=1,2,\dots ,9\)) can be found in “Appendix D”. As already explained, (5.20) can be cast in terms of Z so that the right-hand side depends only on the first-order solution and its derivative,

$$\begin{aligned} \dfrac{\textrm{d}^2\widehat{V}_2}{\textrm{d}Z^2}-Z\widehat{V}_2 = \mathcal {P}(Z)\widehat{V}_0(Z) + \mathcal {Q}(Z)\widehat{V}_0^{(1)}(Z), \end{aligned}$$
(5.21)

with

$$\begin{aligned} \mathcal {P}(Z):=\sum _{j=0}^2 p_j Z^j\qquad \text{ and }\qquad \mathcal {Q}(Z):=\sum _{j=0}^3 q_j Z^j, \end{aligned}$$

in which (some of the) \(p_j\) and \(q_j\) depend on \(m_0\) as well as \(\lambda _k\) (\(k=0,1,3\)); the rather intricate expressions of the coefficients of these two polynomials are included in “Appendix D”.

Before we can take full advantage of Eq. (5.21), we have to explore briefly a secondary asymptotic structure associated with the original bifurcation Eq. (2.6).

5.3 The bending layer

It was noted while trying to solve Eq. (5.9) that the derivative condition part of (2.9) had to be dropped. This is due to the presence of the usual boundary-layer associated with clamped boundary conditions for thin plates and shells. In replacing the initial fourth-order differential Eq. (2.6) with the sequence of second-order problems for the terms \(V_j(Y)\) in the ansatz (5.4a), one has to “give up” some of the original boundary constraints. Experience with similar situations [18, 33] suggests that such issues admit a satisfactory resolution within a thinner bending layer of size \(\mathcal {O}(\varepsilon )\). This motivates the introduction of a new re-scaled coordinate X such that

$$\begin{aligned} \rho = \eta + \varepsilon X,\qquad X = \mathcal {O}(1). \end{aligned}$$
(5.22)

The inner-layer solution, \(W_{\small {\text {inn}}}\) (say), will be sought with an ansatz of the form

$$\begin{aligned} W_{\small {\text {inn}}}= U(X)\exp (\textrm{i}\kappa \,\varepsilon ^{1/4} X), \end{aligned}$$
(5.23)

in which we assume that

$$\begin{aligned} U = \varepsilon ^{1/2}U_0(X) + \varepsilon ^{3/4} U_1(X)+\dots . \end{aligned}$$
(5.24)

The functions \(U_j\) (\(j=0,1,\dots \)) can be determined sequentially by solving a hierarchy of fourth-order ordinary differential equations. The one for \(U_0\) is readily found to satisfy

$$\begin{aligned} \dfrac{\textrm{d}^4U_0}{\textrm{d}X^4}-K^2\dfrac{\textrm{d}^2U_0}{\textrm{d}X^2}=0,\qquad K\equiv \sqrt{\Sigma _{rr}^0}. \end{aligned}$$
(5.25)

The solution of this equation is subject to the boundary conditions on the inner rim of the plate, \(U_0=dU_0/dX=0\) at \(X=0\), as well as the requirement that it does not grow exponentially as \(X\rightarrow +\infty \). Straightforward manipulations give

$$\begin{aligned} U_0(X) = \gamma _0\left[ X-\dfrac{1}{K}\big (1-\textrm{e}^{-KX}\big )\right] ,\qquad (\gamma _0\in {\mathbb {C}}), \end{aligned}$$
(5.26)

whereby the asymptotic behaviour of this function as \(X\rightarrow +\infty \) is immediately inferred.

5.4 Matching and the critical value of \(\lambda _3\)

The fix \(\lambda _3\) we must ensure that the solution in the main layer (see Sect. 5.1) matches with the bending-layer solution of the previous section. Defining \(W_{\small {\text {out}}}\) as the solution W in the ansatz (5.3) and noting that \(Y = \varepsilon ^{1/2}X\), we have

$$\begin{aligned} W_{\small {\text {out}}}= \bigg \{\varepsilon ^{1/2}\left( \Pi _{20}+\Gamma _1^{1/3}\Pi _{01}X\right) +\mathcal {O}(\varepsilon ^{3/4})\bigg \}\exp (\textrm{i}\kappa \varepsilon ^{1/4}X), \end{aligned}$$
(5.27)

where the constants \(\Pi _{kj}\in {\mathbb {C}}\) are defined by

$$\begin{aligned} \Pi _{kj}:={\left\{ \begin{array}{ll} \dfrac{\textrm{d}^j\widehat{V}_k}{\textrm{d}Z^j}\Big |_{Z=-\zeta _0}\quad \qquad &{}\text{ if }\quad j\ge {1},\\ \\ \widehat{V}_k(-\zeta _0)\quad \qquad &{}\text{ if }\quad j=0. \end{array}\right. } \end{aligned}$$

Comparing the \(\mathcal {O}(\varepsilon ^{1/2})\) terms in (5.23) and (5.27), we conclude that

$$\begin{aligned} \widehat{V}_2\big |_{Z=-\zeta _0}\equiv \Pi _{20} = -(1+\textrm{i})\dfrac{\Gamma _1^{1/3}\textrm{Ai}_0'}{\sqrt{\Sigma _{rr}^0}}. \end{aligned}$$
(5.28)

Finally, to find \(\lambda _3\), Eq. (5.21) is multiplied by \(\widehat{V}_0(Z)\), followed by integrating the corresponding result between \((-\zeta _0)\) and \(+\infty \). Repeated integration by parts in combination with (5.28) then yields

$$\begin{aligned} -\dfrac{\Gamma _1^{1/3}\textrm{Ai}_0'^{\,2}}{\sqrt{\Sigma _{rr}^0}} = \sum _{k=0}^{2}p_k\mathcal {I}_k + \sum _{k=0}^3q_k\mathcal {J}_k, \end{aligned}$$
(5.29)

with

$$\begin{aligned} \mathcal {I}_k:=\mathop {\int }\limits _{-\zeta _0}^{\infty }Z^k\textrm{Ai}^2(Z)\,\textrm{d}{Z},\qquad \mathcal {J}_k:=\mathop {\int }\limits _{-\zeta _0}^{\infty }Z^k\textrm{Ai}(Z)\textrm{Ai}'(Z)\,\textrm{d}{Z},\qquad (k=0,1,2,\dots ). \end{aligned}$$

These two sets of integrals can be evaluated in closed form as explained in [34] (see also [35]). It is noted that (5.29) represents an algebraic relation that depends linearly on \(\lambda _3\) and so the critical value of this parameter could be readily identified. The resulting expression is recorded below, and we recall that “Appendix D” contains the precise form of the various expressions that enter into this formula,

$$\begin{aligned} \lambda _3^* = -\dfrac{1}{\overline{\beta }_1}\left[ \dfrac{1}{4}\alpha _1\beta _{8}+\dfrac{\Gamma _1}{K} +\Lambda _1\zeta _0\Gamma _1^{-1/3} + \Lambda _2\zeta _0^2\Gamma _1^{-2/3}\right] ; \end{aligned}$$
(5.30)

here, we have written \(\beta _1=\lambda _3\overline{\beta }_1\) and

$$\begin{aligned} \Lambda _1{} & {} :=\dfrac{2\beta _2}{3}+ \dfrac{\alpha _1}{12}\left( 3\beta _{9}-2\beta _7\right) +\dfrac{1}{6}\alpha _2\beta _8 - \dfrac{1}{3}\beta _5\Gamma _1, \end{aligned}$$
(5.31a)
$$\begin{aligned} \Lambda _2{} & {} := \dfrac{8\beta _3}{15}-\dfrac{\alpha _2}{120}\left( 14\beta _{7}-23\beta _9\right) -\dfrac{2}{15}\beta _6\Gamma _1. \end{aligned}$$
(5.31b)

A brief evaluation of the accuracy of our results up to this point will be undertaken in the next section.

5.5 Asymptotics versus numerics

Based on the calculations outlined above, it follows that for \(0<\varepsilon \ll {1}\) the critical load can be approximated according to the following formula

$$\begin{aligned} \lambda _{\textrm{c}} = \lambda _0^* + \lambda _1^*\varepsilon ^{1/2}+\lambda _3^*\varepsilon + \mathcal {O}(\varepsilon ^{5/4}), \end{aligned}$$
(5.32)

where the coefficients on the right-hand side in (5.32) are given by (5.8), (5.13), and (5.30). In order to assess the usefulness of our predictions, it is necessary to compare the asymptotics with some direct numerical simulations. A first set of comparisons is illustrated in Fig. 8 for \(\eta =0.3\) (left window) and \(\eta =0.5\) (right window), where we have included one-, two-, and three-term truncations of the right-hand side of (5.32). It is apparent that the \(\mathcal {O}(\varepsilon )\) contribution in our approximation adds only a modest improvement to the overall relative accuracy (RA). This is related to the “flat” minima of the curves \(\lambda \) versus m (recall the discussion vis-à-vis Fig. 5 in Sect. 4). Given that the asymptotic work was carried out under the assumption that \(0<\varepsilon ^{1/4}\ll {1}\), the full three-term formula (5.32) performs reasonably well; for example, if \(\eta =0.5\) then RA\(\,\simeq 1.7\%\) for \(\varepsilon =1/600\), which increases to RA\(\,\simeq 2.13\%\) for \(\varepsilon =1/500\), and RA\(\,\simeq 3.75\%\) for \(\varepsilon =1/300\). For \(\eta =0.3\) these results change to RA\(\,\simeq 2.5\%\) and \(3.1\%\) when \(\varepsilon =1/600\) and \(\varepsilon =1/500\), respectively. Comparable relative accuracies are found for \(\eta =0.4\) and \(\eta =0.6\), but in the interest of brevity we do not include further details here.

Fig. 8
figure 8

Comparisons of the asymptotic formula (5.32) with direct numerical simulations of the buckling equations described in Sect. 2; \(\eta =0.3\) (left) and \(\eta =0.5\) (right). In both windows \(\nu =0.25\), and the horizontal dashed line corresponds to the lower bound discussed in Sect. 3

Full size image

For \(0<\eta \lesssim {0.3}\), the accuracy of (5.32) deteriorates quickly when \(150\le \varepsilon ^{-1}\le 600\); e.g. the corresponding RAs range between \(23\%\) and \(11\%\) when \(\eta =0.1\). The origin of this behaviour is partly related to the presence of the independent parameter \(\eta \) in the coefficients of the approximation for \(\lambda _{\textrm{c}}\), that is \(\lambda _j^*\equiv \lambda _j^*(\eta )\) for \(j=0,1,3\). In order for (5.32) to be considered a valid asymptotic expansion, it is essential that \(|T_0|\gg |T_1|\gg |T_3|\gg \dots \) (as \(\varepsilon \rightarrow {0}^+\)), where \(T_0:=\lambda _0^*\), \(T_1:=\lambda _1^*\varepsilon ^{1/2}\), \(T_3:=\lambda _3^*\varepsilon \), and so on. In theory, this requirement will always hold true for sufficiently small \(\varepsilon \)—due to the particular form of the ansatz (5.4b). However, from a practical point of view the situation is rather different. The effectiveness of an asymptotic series relies primarily on its capability to offer satisfactory precision for a small (yet finite) perturbation parameter, without necessarily requiring it to be infinitely small. In light of the remarks made at the end of Sect. 3 regarding the numerical values of , it is likely that the constraint \(T_0\gg T_1\) will only be valid for a restricted set of values of \(\eta \) if \(\varepsilon \) is not arbitrarily small. To gain a better perspective on this issue, in Fig. 9 we plot the dependence of \(T_0\) and \(T_1\) on \(\eta \) for a sequence of decreasing values of \(\varepsilon \) (see caption for further details). The former quantity (\(T_0\)) is independent of \(\varepsilon \) and is represented by the dashed red line, while the curves corresponding to the latter expression (\(T_1\)) appear in blue (continuous lines). These two families of curves intersect each other, with some of the intersection points for \(\varepsilon ^{-1}=300,400,500,600\) being indicated explicitly by black circular markers. For a given \(\varepsilon \), the inequality \(T_0>T_1\) will be satisfied only for \(\eta >\eta _{\,\varepsilon }\), where \(\eta _{\,\varepsilon }\) is the horizontal coordinate of the intersection point between \(T_0\) and \(T_1\equiv T_1(\varepsilon )\).

The global picture that transpires from the numerical data in Fig. 9 is quite informative as it highlights some of the limitations of the approximation for \(\lambda _{\textrm{c}}\) in terms of \(\varepsilon \). In particular, it becomes clear that for \(\eta \) between 0.1 and 0.2, the inequality \(T_0>T_1\) is satisfied only for \(\varepsilon \lesssim \mathcal {O}(10^{-3})\). Therefore, the larger relative errors mentioned above in connection to this range of \(\eta \)-values are not at all unexpected. We remark in passing that for other choices of Poisson’s ratio there are no significant qualitative changes in the topology of the curves shown in Fig. 9.

Fig. 9
figure 9

The dependence of \(T_0\equiv \lambda _0^*\) and \(T_1\equiv \lambda _1^*\varepsilon ^{1/2}\) on \(\eta \in [0.1,0.6]\) for \(\varepsilon =(1/j)\times {10^{-2}}\) (with \(j=1,2,\ldots ,20\)) and \(\nu =0.25\). In this plot, the arrow shows the direction in which \(\varepsilon \) decreases; further details are included in the main text

Full size image

Despite the limitations mentioned earlier regarding the asymptotic developments for the problem at hand, it is still feasible to propose an ad-hoc approximation for the critical eigenvalue when \(0.1\lesssim \eta \lesssim {0.2}\). While the empirical accuracy of this new formula turns out to be comparable to what we have already seen in Fig. 8, it is no longer an asymptotic approximation in the strictest sense. The general idea is to suitably modify the expression of \(\lambda _3^*\) in formula (5.32). To this end, we note that in matching the solutions between the two layers we only used information coming from \(V_0\) and \(V_2\), but \(V_1\) was not directly involved as this latter function already satisfied \(V_1=0\) for \(Y=0\). We also recall that \(\lambda _2\), the eigenvalue associated with \(V_1\), was found to be zero so, to a certain extent, \(V_1\) plays only a passive role as far as the original ansatz (5.4b) is concerned. With these observations in mind, we choose to take \(V_1(Y)\equiv {0}\) and set \(\alpha _j=0\) for \(j=0,1,2\). This change of tack will not impact \(\lambda _0^*\) and \(\lambda _1^*\), but it will eventually alter the expression of \(\lambda _3^*\) because the original right-hand side of the governing equation for \(V_2\) depends on \(V_1\). By implementing the steps outlined above, we arrive at a modified version for \(\lambda _3^*\), which will be denoted \(\lambda _3^{\dagger }\) and corresponds to

$$\begin{aligned} \lambda _3^{\dagger }:= -\dfrac{1}{\overline{\beta }_1}\left[ \dfrac{\Gamma _1}{K} +\dfrac{\zeta _0}{3\Gamma _1^{1/3}}\left( 2\beta _2 - \Gamma _1\beta _5\right) + \dfrac{2\zeta _0^2}{15\Gamma _1^{2/3}}\left( 4\beta _3-\Gamma _1\beta _6\right) \right] . \end{aligned}$$
(5.33)

For convenience, the modified (ad-hoc) new formula for \(0.1\lesssim \eta \lesssim {0.2}\) is recorded below

$$\begin{aligned} \lambda _{\textrm{c}} \simeq \lambda _0^* + \lambda _1^*\varepsilon ^{1/2}+\lambda _3^{\dagger }\varepsilon , \end{aligned}$$
(5.34)

where \(\lambda _0^*\), \(\lambda _1^*\) are still given by (5.8) and (5.13), respectively, while \(\lambda _3^{\dagger }\) has just been defined above.

The accuracy of the proposed modification for \(\lambda _{\textrm{c}}\) is illustrated in Fig. 10 for \(\eta =0.1\) (left window) and \(\eta =0.2\) (right window). For the smaller \(\eta \) the formula (5.34) delivers similar RA as the approximations included in Fig. 8; as \(\eta \) increases, the ad-hoc formula gets even better as it is already apparent for \(\eta =0.2\). However, the predictions of this new approximation tend to slightly overtake the numerical results as \(\varepsilon \) gets smaller (but the corresponding RAs are still less than \(0.1\%\)). For example, in the right window of Fig. 10 this happens only for \(\varepsilon \lesssim (1/350)\simeq 0.0029\). For larger values of \(\eta \) (e.g. those used in the earlier comparisons), one finds that \(\lambda _{\textrm{c}}\) given by (5.34) represents a tight upper bound for the values coming from the direct numerical simulations of the bifurcation equation. Given that formula (5.34) is merely a heuristic/speculative result, we do not include further numerical evidence regarding its accuracy or lack thereof.

Fig. 10
figure 10

Comparisons of the ad-hoc new formula (5.34) with direct numerical simulations of the buckling equations described in Sect. 2; \(\eta =0.1\) (left) and \(\eta =0.2\) (right). In both windows \(\nu =0.25\), and the horizontal dashed line corresponds to the lower bound discussed in Sect. 3

Full size image

6 Concluding remarks

This work has re-visited the shear-induced wrinkling instabilities of an accelerated spinning annular disc/plate [14] by exploring several new asymptotic features of the associated bifurcation equation. With the help of a general singular-perturbation strategy originally developed in our earlier studies (e.g. [20, 21, 36]), we have demonstrated that the problem studied by Sader et al. in [14] shares the same asymptotic structure as the scenario explored in [18, 19]. More precisely, the critical wrinkling eigenmodes turned out to have a multiple-scale structure consisting of a fast spatial oscillation modulated by a slowly varying envelope described by a re-scaled Airy function (of the first kind). This solution was attached to the inner edge of the annular region via an intermediary asymptotic structure that accounted for the minor bending effects resulting from the clamped constraint at the inner rim of the spinning plate. An approximation of the critical wrinkling load (the angular acceleration of the disc) was constructed by using a formal asymptotic expansion in powers of a suitably defined non-dimensional parameter (\(0<\varepsilon \ll {1}\)). The first two nonzero terms in this expansion were independent of the secondary asymptotic structure mentioned above, while the determination of the subsequent terms required the asymptotic matching between the two solutions (e.g. see [33] for a recent similar scenario). We have worked out just one such term, but there is no particular challenge in calculating further contributions (other than the increasing amount of algebra, of course).

Although the two problems considered in [14, 18, 19], respectively, are asymptotically equivalent, certain quantitative differences present in the specific form of the bifurcation equations and the expressions of the basic state impose stricter limitations on the accuracy of the asymptotic results for the former problem. Some of the issues that have transpired are not entirely surprising since the asymptotic analysis was conducted under the implicit assumption that \(0<\varepsilon ^{1/4}\ll {1}\). Another factor that contributes to the loss of accuracy mentioned here is re-iterated below.

Fig. 11
figure 11

A comparison between (6.1) and direct numerical simulations of the full wrinkling problem discussed in Sect. 2. The former data is shown as the (blue) continuous curve, while the latter results correspond to the (red) circular markers; the dashed (red) curve is obtained by interpolating the data points shown as markers. Here \(\varepsilon =1/400\), \(0.1\le \eta \le {0.5}\), and \(\nu =0.25\) (color figure online)

Full size image

In this paper, we have dealt exclusively with the thin-plate asymptotics of the wrinkled plate; in other words, the size \(\eta \in (0,1)\) of the central hole was assumed to be an \(\mathcal {O}(1)\) quantity which did not interfere with the expansions in \(\varepsilon \). The results obtained have not only confirmed the validity of this assumption within the range \(0.3\lesssim \eta \lesssim 0.6\), but have also exposed some of its limitations. As noticed in Sect. 5.5, the asymptotic approximations deteriorate as \(\eta \) gets progressively smaller, an observation that indicates the necessity of addressing the local effect introduced by the central hole of the annular disc through the adoption of a modified form of the ansatz (e.g. in suitable powers of \(\eta \) rather than \(\varepsilon \)). We note in passing that the leading-order term of our proposed approximation (5.32) is formally \(\mathcal {O}(\eta ^2)\) for \(0<\eta \ll {1}\). The asymptotic regime \(\eta \rightarrow {0}^+\) involves a singular perturbation of the plate domain, a situation that demands a somewhat different approach from that used in the present study (e.g. see [32] for such a related scenario). We hope to report the relevant details for this new case in the near future.

A final observation, which reinforces the remarks made above, is related to the choice of the small parameter in the present study. Motivated by the form of Eq. (2.6) and its close analogy with our earlier works [18, 19], we have used \(\varepsilon \) defined in (4.1). However, the particular expressions of the coefficients in the asymptotic formula (5.32) suggest that a more appropriate choice would be \(\delta :=\varepsilon /\eta \). By re-scaling the quantities of interest as indicated below

$$\begin{aligned} \widetilde{\lambda }_{\textrm{c}}:= \lambda _{\textrm{c}}/\eta ^2,\qquad \widetilde{\lambda }_0^*:=\lambda _0^*/\eta ^2,\qquad \widetilde{\lambda }_1^*:= \lambda _1^*/\eta ^{3/2},\qquad \widetilde{\lambda }_3^*:=\lambda _3^*/\eta , \end{aligned}$$

we find the equivalent representation of (5.32)

$$\begin{aligned} \widetilde{\lambda }_{\textrm{c}} = \widetilde{\lambda }_0^* + \widetilde{\lambda }_1^*\,\delta ^{1/2} + \widetilde{\lambda }_3^*\,\delta + \mathcal {O}(\delta ^{5/4}). \end{aligned}$$
(6.1)

Note that this alternative approximation for the critical loads will have an asymptotic character as long as \(0<\delta \ll {1}\). But from a practical point of view one has to resort to direct numerical computations in order to realistically ascertain how small \(\delta \) should be. In Fig. 11, we compare the three-term formula (6.1) with the direct numerical simulations of the original wrinkling problem (see Sect. 2) for \(\varepsilon =1/400\) and \(0.1\le \eta \le 0.5\). It is clear that for sufficiently small \(\delta \)-values the predictions of our asymptotic formula match very closely the numerical results (in the lower left-hand corner). On the other hand, for \(0.1\le \eta \lesssim {0.3}\), the smallness of \(\varepsilon \) is offset by \(\eta ^{-1}\) in the definition of \(\delta \), and the agreement within that range deteriorates. We also remark that (6.1) ceases to be an asymptotic approximation when \(\delta =\mathcal {O}(1)\) or, equivalently, when \(\varepsilon = \mathcal {O}(\eta )\).