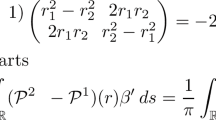Abstract
We consider the quasistationary Stokes flow that describes the motion of a two-dimensional fluid body under the influence of surface tension effects in an unbounded, infinite-bottom geometry. We reformulate the problem as a fully nonlinear parabolic evolution problem for the function that parameterizes the boundary of the fluid with the nonlinearities expressed in terms of singular integrals. We prove well-posedness of the problem in the subcritical Sobolev spaces \(H^s(\mathbb {R})\) up to critical regularity, and establish parabolic smoothing properties for the solutions. Moreover, we identify the problem as the singular limit of the two-phase quasistationary Stokes flow when the viscosity of one of the fluids vanishes.
Similar content being viewed by others
1 Introduction
In this paper we consider the two-dimensional flow of a fluid layer \(\Omega (t) \) of infinite depth in the case when the motion of the incompressible fluid is governed by the quasistationary Stokes equations and the motion is driven by surface tension at the free boundary \(\Gamma (t)=\partial \Omega (t)\). We consider the one-phase problem, i.e., no forces are exerted on the liquid by the medium above it. The mathematical model is given by the following system of equations
for \(t>0\), where the interface \(\Gamma (t)\) at time t is given as a graph of a function \(f(t,\cdot ):{\mathbb {R}}\longrightarrow {\mathbb {R}}\), i.e., the fluid domain \(\Omega (t)\) and its boundary \(\Gamma (t)\) are defined by
Additionally, the interface \(\Gamma (t)\) is assumed to be known at time \({t=0}\), i.e.
In Eq. (1.1a) above, \(v=v(t):\Omega (t)\longrightarrow {\mathbb R}^2 \) and \(p=p(t):\Omega (t)\longrightarrow {\mathbb R}\) are the velocity and the pressure of the Newtonian fluid, \({\tilde{\nu }}=({\tilde{\nu }}^1, {\tilde{\nu }}^2)\) is the unit exterior normal to \(\partial \Omega \), \({\tilde{\kappa }}\) denotes the curvature of the interface (negative where \(\Omega (t)\) is convex), and \(T_\mu (v,p)=(T_{\mu ,ij}(v,p))_{1\le i,\, j\le 2}\) is the stress tensor which is given by
Moreover, \(V_n\) is the normal velocity of the interface \(\Gamma (t)\), \(a\cdot b\) denotes the Euclidean scalar product of two vectors \(a,\, b\in {\mathbb R}^2\), \(E_2\in {\mathbb R}^{2\times 2}\) is the identity matrix, and the positive constants \(\mu \) and \(\sigma \) are the dynamic viscosity of the fluid and the surface tension coefficient at the interface \(\Gamma (t),\) respectively.
Previous analysis related to (1.1a) considered mainly the case of a sufficiently regular bounded fluid domain \(\Omega (t)\). More precisely, in [14] the authors studied the quasistationary motion of a free capillary liquid drop in \({\mathbb R}^d\) for initial data in \(H^{s+1}(\Sigma )\), \(s\ge s_1,\) \(s_1\) being the smallest integer that satisfies \(s_1>3+(d-1)/2\) and \(\Sigma \subset {\mathbb R}^d\) the smooth boundary of a strictly star shaped domain in \({\mathbb R}^d\). The authors established in [14] the well-posedness of the problem and they also showed that the equilibria of the problem, which are balls, are exponentially stable. In the context when \(\Sigma \) is the boundary of the unit ball, it is proven in [9] (for \(d=2\)) that solutions corresponding to small data in \(H^5(\Sigma )\) exist globally and converge to a ball, while in [8] (for \(d=3\)) the authors established the same result for small data in \(H^6(\Sigma ).\) Finally, in three space dimensions and for an initially bounded geometry possessing a \(\textrm{C}^{3+\alpha }\)-boundary, \(\alpha >0\), it was shown in [27] that the quasistationary Stokes flow is well-posed, and in [28] the same author has rigorously justified this problem as the singular limit of Navier–Stokes flow when the Reynolds number vanishes. The local well-posedness and the stability issue for the two-phase quasistationary Stokes flow (with or without phase transitions) in a bounded geometry in \({\mathbb R}^d\), with \(d\ge 2\), has been recently studied in [26] in the phase space \(W^{2+\mu -2/p}_p(\Sigma )\), with \(1\ge \mu >(d+2)/p\), by using a maximal \(L_p\)-regularity approach. In the context of [26], \(\Sigma \) is a real analytic hypersurface over which the boundary between the two fluid phases is parameterized.
Local well-posedness and stability results for the quasistationary two-phase spatially periodic Stokes flow in \({\mathbb R}^2\) with gravity effects and zero surface tension were established only recently in [11]. We emphasize that in contrast to the present analysis, where we deal with a parabolic problem, see Sect. 4, the problem considered in [11] is of hyperbolic type. A further related and very recent direction of research, see, e.g., [13, 17, 24], is focused on the study of the transport Stokes system which was derived in [15, 23] as a model for the sedimentation of a cloud of rigid particles in a viscous fluid. In this context the inhomogeneous density is transported by the velocity field which solves the gravity-driven Stokes boundary value problem in the entire space \({\mathbb R}^3\). At a formal level the transport Stokes system in \({\mathbb R}^2\) with initial density constant above and below a graph is equivalent to the quasistationary two-phase Stokes flow in \({\mathbb R}^2\) with gravity effects and zero surface tension (in the case of two fluids with equal viscosities).
We emphasize that in the references [8, 9, 14, 26,27,28] the moving interface is at least of class \(\textrm{C}^2\), whereas the critical \(L_2\)-Sobolev space for (1.1) is \(H^{3/2}({\mathbb R})\), see [21, 22]. Our goal is to establish the well-posedness of (1.1) in the subcritical spaces \(H^{s}({\mathbb R})\) with \(s\in (3/2,2)\), see Theorem 1.1. One of the obvious difficulties lies in the fact that, for \(f\in H^{s}({\mathbb R})\), the curvature term in (1.1a)\(_3\) is merely a distribution. To handle this issue we use a strategy inspired by the approach in the papers [4, 21, 22] where, for the corresponding two-phase problem, potential theory was used to determine the velocity and pressure fields in terms of f. Such a strategy was applied also in the context of the Muskat problem, see the surveys [10, 12], and it provides quite optimal results as the mathematical reformulations of the problems obtained by using this strategy require less smallness and regularity assumptions on the data compared to other approaches based on Lagrangian or Hanzawa transformations.
The first goal of this paper is to show that, at each time instant \(t>0\), the free boundary, given via \({f=f(t)}\), identifies the velocity field \(v=v(t)\) and the pressure \(p=p(t)\) uniquely. More precisely, as shown in Theorem 2.1, if \(f\in H^3({\mathbb R})\), then (v, p) is given by the hydrodynamic single-layer potential with a density \(\beta =(\beta _1,\beta _2)^\top \) which satisfies
where \((\cdot )'\) is the derivative with respect to the spatial coordinate \(\xi \in {\mathbb R}\) and \(g=g(f)\) is defined in (2.4) below. Furthermore, \(\mathbb {D}(f)^*\) is the \(L_2\)-adjoint of the double layer potential \(\mathbb {D}(f)\), see (2.8), and \(\omega :=(1+f'^2)^{1/2}\), see (2.2). Concerning (1.3), the following issues need to be clarified:
-
(i)
The invertibility of the operators \(\pm 1/2- \mathbb {D}(f)\) (and \(\pm 1/2- \mathbb {D}(f)^*\)) in \(\mathcal {L}(H^1({\mathbb R})^2)\);
-
(ii)
the question whether \((\frac{1}{2}- \mathbb {D}(f)^*)^{-1}g'\) is the derivative of some \(\beta \in (H^2({\mathbb R}))^2\).
We remark that these issues are new compared to the treatment of the two-phase problem.
With respect to (i), the main step is performed in Theorem 3.1 where the invertibility in \({\mathcal {L}(L_2({\mathbb R})^2)}\) is established for each \(f\in \textrm{BUC}^1({\mathbb R})\). At this point, we rely on the Rellich identities (3.12)–(3.16) for the Stokes boundary value problem which have been exploited, in a bounded geometry in \({\mathbb R}^n\) with \(n\ge 3\), also in [7]. In the unbounded two-dimensional setting considered in the present paper we provide new arguments which use, among others, also a Rellich identity obtained in [19] in the context of the Muskat problem. Based on Theorem 3.1, we then show that these operators are invertible in \(\mathcal {L}(H^k({\mathbb R})^2)\), \({k=1,\, 2}\), provided that \({f\in H^{k+1}({\mathbb R})}\), see Lemma 3.3, and in \(\mathcal {L}(H^{s-1}({\mathbb R})^2)\) when \(f\in H^{s}({\mathbb R})\), see Lemma 3.4.
Concerning (ii), we prove in Lemma 4.1 that, given \(f\in H^s({\mathbb R})\) and \(\beta \in H^1({\mathbb R})^2\), the function \({\mathbb {D}(f)[\beta ]}\) belongs to \({H^1({\mathbb R})^2}\) and
This relation and the observation that the right side of (1.3) is a derivative enables us to essentially replace, for \(f\in H^3({\mathbb R})\), Eq. (1.3) by
see Corollary 4.3. These properties, in particular Lemma 3.3 and the equivalence of (1.3) and (1.5), are then used to reformulate the one-phase Stokes flow (1.1) as the evolution problem (4.9), which has only f as unknown. Its well-posedness properties are summarized in Theorem 1.1 below.
Our second main result concerns the limit behavior for \(\mu ^+\rightarrow 0\) of the two-phase quasistationary Stokes problem
for \(t>0\) and
with \(\mu ^-=\mu \) fixed. In (1.6a) it is again assumed that \(\Gamma (t)\) is the graph of a function \({f(t,\cdot )}\),
and \({\tilde{\nu }}\) is the unit exterior normal to \(\partial \Omega ^-(t)\). Moreover, \(w^\pm (t)\) and \( q^\pm (t)\) represent the velocity and pressure fields in \(\Omega ^\pm (t)\), respectively, and [w] (respectively \([T_\mu (w, q)]\)) is the jump of the velocity (respectively stress tensor) across the moving interface, see (2.14) below. We emphasize that the limit \(\mu ^+\rightarrow 0\) in the formulation (1.6) is singular because ellipticity of the underlying boundary value problem is lost in this limit.
In [22], we reformulated the two-phase Stokes problem (1.6) as a nonlinear evolution equation for f, see (4.10) below. In Sects. 4.3 and 4.4 of the present paper we prove that the right side of (4.10) has a limit for \(\mu ^+\rightarrow 0\), and the limit is the right side of (4.9). In this sense, we show that the moving boundary problem (1.1) represents the “regular limit” of (1.6) for \(\mu ^-=\mu \) and \(\mu ^+\rightarrow 0\). This property is used in Sect. 4.4 to introduce the common formulation (4.23) that contains both evolution problems. It reads
where \(\mu ^+\ge 0\) is viewed as a parameter. We point out that though this common formulation has been derived from the Stokes flow equations under the assumption that \({f(t)\in H^3({\mathbb R})}\), the nonlinear and nonlocal operator \(\Phi \) is well-defined when assuming only \(f\in H^s({\mathbb R})\), \({s\in (3/2,2)}\), and this allows us to consider (1.7) under these lower smoothness assumptions. The regularity of the limit is now seen in the fact that \(\Phi \) is smooth on \([0,\infty )\times H^s({\mathbb R})\). For any fixed \({\mu ^+>0}\) we investigated the problem (1.7) in [22]. In particular, we showed in [22, Theorem 1.1] that, given \(f^{(0)}\in H^{s}({\mathbb R})\), there exists a unique maximal solution \((f_{\mu ^+},w_{\mu ^+}^\pm ,q_{\mu ^+}^\pm )\) to (1.6) such that
-
\(f_{\mu ^+}=f_{\mu ^+}(\cdot , f^{(0)})\in \textrm{C}([0,T_{+,\mu ^+}), H^{s}(\mathbb {R}))\cap \textrm{C}^1([0,T_{+,\mu ^+}), H^{s-1}(\mathbb {R})),\)
-
\(w_{\mu ^+}^\pm (t)\in \textrm{C}^2(\Omega ^\pm (t))\cap \textrm{C}^1(\overline{\Omega ^\pm (t)})\), \(q_{\mu ^+}^\pm (t)\in \textrm{C}^1(\Omega ^\pm (t))\cap \textrm{C}(\overline{\Omega ^\pm (t)})\) for all \({t\in (0,T_{+,\mu ^+})}\),
-
\( w_{\mu ^+}^\pm (t)|_{\Gamma (t)}\circ \Xi _{f(t)}\in H^2({\mathbb R})^2\) for all \(t\in (0,T_{+,\mu ^+})\),
where \(T_{+,\mu ^+}=T_{+,\mu ^+}( f^{(0)})\in (0,\infty ]\) is the maximal existence time and \(\Xi _{f(t)}(\xi ):=(\xi , f(t,\xi ))\) for \(\xi \in {\mathbb R}.\)
Our first main result is based on the fact that the properties of \(\Phi (\mu ^+,\cdot )\) and of its Fréchet derivative \(\partial _f\Phi (\mu ^+,\cdot )\) which were used to prove [22, Theorem 1.1] remain valid also when \({\mu ^+=0}\).
Theorem 1.1
Let \(s\in (3/2,2) \) be given. Then, the following statements hold true:
-
(i)
(Well-posedness) Given \(f^{(0)}\in H^{s}(\mathbb {R})\), there exists a unique maximal solution (f, v, p) to (1.1) such that
-
\(f=f(\cdot ;f^{(0)})\in \textrm{C}([0,T_+), H^{s}(\mathbb {R}))\cap \textrm{C}^1([0,T_+), H^{s-1}(\mathbb {R})),\)
-
\(v(t)\in \textrm{C}^2(\Omega (t))\cap \textrm{C}^1(\overline{\Omega (t)})\), \(p(t)\in \textrm{C}^1(\Omega (t))\cap \textrm{C}(\overline{\Omega (t)})\) for all \({t\in (0,T_+)}\),
-
\( v(t)|_{\Gamma (t)}\circ \Xi _{f(t)}\in H^2({\mathbb R})^2\) for all \(t\in (0,T_+)\),
where \(T_+=T_+( f^{(0)})\in (0,\infty ]\) is the maximal existence time. Moreover, the set
$$\begin{aligned} \mathcal {M}:=\{(t, f^{(0)}):\, f^{(0)}\in H^s({\mathbb R}),\,0< t<T_+( f^{(0)})\} \end{aligned}$$is open in \({(0,\infty )\times H^s({\mathbb R})}\), and \([(t, f^{(0)})\longmapsto f(t; f^{(0)})]\) is a semiflow on \(H^s({\mathbb R})\) which is smooth in \(\mathcal {M}\).
-
-
(ii)
(Parabolic smoothing)
-
(iia)
The map \([(t,\xi )\longmapsto f(t,\xi )]:(0,T_+)\times \mathbb {R}\longrightarrow \mathbb {R}\) is a \(\textrm{C}^\infty \)-function.
-
(iib)
For any \(k\in {\mathbb N}\), we have \(f\in \textrm{C}^\infty ((0,T_+), H^k(\mathbb {R})).\)
-
(iia)
-
(iii)
(Global existence) If
$$\begin{aligned} \sup _{[0,T]\cap [0,T_+( f^{(0)}))} \Vert f(t)\Vert _{H^s}<\infty \end{aligned}$$for each \(T>0\), then \(T_+(f^{(0)})=\infty .\)
Observe, in particular, that by Theorem 1.1 (iib) we have \(f(t)\in H^3({\mathbb R})\) for \({t>0}\), which justifies the assumptions that were made when deriving the reformulation (4.9). Thus, the solutions we construct correspond to one-phase Stokes flows, starting from initial domains whose boundaries might have a curvature in distribution sense only.
Our second main result gives a precise formulation of the limit result announced above. We point out that Theorem 1.2 is the first result in the literature which addresses the vanishing viscosity limit in the two-phase quasistationary Stokes flow. We recall the notation \({(f_{\mu ^+}(\cdot ; f^{(0)}),w^\pm _{\mu ^+},q^\pm _{\mu ^+})}\) for solutions to the two-phase problem (1.6).
Theorem 1.2
Let \(s\in (3/2,2) \) and \( f^{(0)}\in H^{s}(\mathbb {R})\) be given. Let further \((f(\cdot ; f^{(0)}),v,p)\) denote the maximal solution to (1.1) identified in Theorem 1.1 and choose \(T\in (0,T_+( f^{(0)}))\). Then, there exist constants \(\varepsilon >0\) and \(M>0\) such that for all \(\mu ^+\in (0, \varepsilon ]\) we have \(T<T_{+,\mu ^+}( f^{(0)})\) and
The proofs of the main results are presented in Sect. 4.5 which concludes the paper.
2 The Stokes boundary value problem in a fixed domain
In this section we fix \(f\in H^3({\mathbb R})\) and we consider the Stokes boundary value problem
where \(\Omega :=\{x=(x_1,x_2)\in {\mathbb R}^2\,:\, x_2<f(x_1)\}\) and \(\Gamma :=\{(\xi , f(\xi ))\,:\, \xi \in {\mathbb R}\}\). The main goal is to show that (2.1) has a unique solution (v, p), see Theorem 2.1 below.
We start by introducing some notation. Since \(\Gamma \) is a graph over \({\mathbb R}\), it is natural to view \(\Gamma \) as is the image of \({\mathbb R}\) under the diffeomorphism \(\Xi :=\Xi _f:=(\textrm{id}_\mathbb {R},f).\) Let now \(\nu \) and \(\tau \) denote the componentwise pull-back under \(\Xi \) of the unit normal \({\tilde{\nu }}\) on \(\Gamma \) exterior to \(\Omega \) and of the unit tangent vector \({\tilde{\tau }}\) to \(\Gamma \), i.e.
Observe that the pull-back \(\kappa :=\omega ^{-3}f''\in H^1({\mathbb R})\) of the curvature \({\tilde{\kappa }}\) satisfies
where \(g:=g(f)\) is given by
We further recall that the fundamental solutions \((\mathcal {U}^k,\mathcal {P}^k):\mathbb {R}^2\setminus \{0\}\longrightarrow \mathbb {R}^2\times \mathbb {R},\) \(k=1,\,2,\) where \(\mathcal {U}^k=(\mathcal {U}^k_1, \mathcal {U}^k_2)^\top \), to the Stokes equations
are given by
for \( y=(y_1,y_2)\in {\mathbb R}^2\setminus \{0\}\), see [16].
Finally, defining the mapping \(r:=(r^1,r^2):{\mathbb R}^2\longrightarrow {\mathbb R}^2\) by the formula
we introduce the double-layer potential \(\mathbb {D}(f)\) for the Stokes equations associated to the hypersurface \(\Gamma \) and its \(L_2\)-adjoint \(\mathbb {D}(f)^*\) by the formulas
for \(\beta =(\beta _1,\beta _2)^\top \in L_2({\mathbb R})^2\) and \(\xi \in {\mathbb R}\).
In (2.8), the integrals are absolutely convergent whenever \(f'\) is Hölder continuous. We prefer the definition as principal value integral because we will consider \(f\in \textrm{BUC}^1({\mathbb {R}})\) later. Given \({k\in {\mathbb N}}\), \(\textrm{BUC}^k({\mathbb {R}})\) is the Banach space consisting of functions with bounded and uniformly continuous derivatives up to order k. It is well-known that the intersection of all these spaces, denoted by \(\textrm{BUC}^\infty ({\mathbb {R}})\), is a dense subspace of \(\textrm{BUC}^k({\mathbb {R}})\) for each \(k\in {\mathbb N}\).
Both operators \(\mathbb {D}(f)\), \(\mathbb {D}(f)^*\) can be expressed in terms of the family \({\{B_{n,m}^0(f):\, n,\, m\in {\mathbb N}\}}\) of singular integral operators introduced in [19, 20], see (2.10) and (3.2) below. We now introduce these operators in a more general context. More precisely, given \({n,\,m\in {\mathbb N}}\) and Lipschitz continuous functions \({a_1,\ldots , a_{m},\, b_1, \ldots , b_n:\mathbb {R}\longrightarrow \mathbb {R}}\), we define
where \(\delta _{[\xi ,\eta ]}u:=u(\xi )-u(\xi -\eta )\). For brevity we set
We note that \(B^0_{0,0}=H\), where H denotes the Hilbert transform.
We now prove that the boundary value problem (2.1) is uniquely solvable and that the solution is given by the hydrodynamic single-layer potential with a suitable density function \(\beta \).
Theorem 2.1
Given \(f\in H^3({\mathbb R})\), the boundary value problem (2.1) has a unique solution (v, p) such that
Moreover, letting \(\beta =(\beta _1,\beta _2)^\top \in H^2({\mathbb R})^2\) denote the unique solution to the equation
where \(g\in H^2({\mathbb R})^2\) is defined in (2.4), we have
Proof
The unique solvability of Eq. (2.11) is established in Sect. 4 and is taken for granted in this proof. We divide the proof in two steps.
Step 1: Uniqueness. It suffices to show that the homogeneous boundary value problem (2.1) (with the right side of (2.1)\(_3\) set to be zero) has only the trivial solution. Let thus (v, p) be a solution to the homogeneous system (2.1) with regularity as prescribed above. We then set \({\Omega ^-:=\Omega }\), \(\Omega ^+:={\mathbb R}^2\setminus \overline{\Omega }\), and we define \({(w^\pm ,q^\pm ):\Omega ^\pm \longrightarrow {\mathbb R}^2\times {\mathbb R}}\) by
Clearly, it holds
Moreover, it can be easily checked that \((w^\pm ,q^\pm )\) solves the boundary value problem
with \(\gamma :=-w^-|_\Gamma \circ \Xi \in H^2({\mathbb R})^2\). Given \(z^\pm \in \textrm{C} (\overline{\Omega ^\pm }),\) we define [z] as being the jump
According to [22, Proposition 2.1], the system (2.13) has a unique solution. Moreover, we have
see [22, Lemma A.1]. Since \(w^+=0\) and \(1/2-\mathbb {D}(f)\in \mathcal {L}(L_2({\mathbb R})^2)\) is invertible, see Theorem 3.1 below, we conclude that \(\gamma =0\). Consequently \((w^\pm ,q^\pm )\) is the trivial solution and this establishes the uniqueness claim.
Step 2: Existence. We are going to verify that (v, p) from (2.12) with \(\beta \) from (2.11) has the announced regularity and satisfies (2.1). Recalling (2.6), we have
for \(y\ne 0\). A direct consequence of (2.12) is that (v, p) is defined as an integral of the form
where, for every \(\alpha \in {\mathbb N}^2,\) we have \(\partial ^\alpha _x K(x,s)=O(s^{-1})\) for \(|s|\rightarrow \infty \) and locally uniformly in \({x\in \Omega }\). This shows that v and p are well-defined by (2.12), and that integration and differentiation with respect to x may be interchanged. Hence, \((v,p)\in \textrm{C}^\infty (\Omega ,{\mathbb R}^2\times {\mathbb R})\), and, since \(\partial _j(\mathcal {U}^{k},\mathcal {P}^{k}),\) \(j=1,\, 2\), solve (2.5), we deduce that (v, p) is a solution to (2.1)\(_1\)–(2.1)\(_2\).
In view of [5, Lemma A.1] it holds that \(p\in \textrm{C}(\overline{\Omega })\) and
Given \(\phi \in H^1({\mathbb R})\), let \(Z_j[\phi ]:\Omega \longrightarrow {\mathbb R}\), \(j=0,\ldots ,3,\) be given by
Since
we obtain, due to (2.16), the following formulas
Since \( Z_j[\phi ]\in \textrm{C}({\overline{\Omega }})\), see the proof of [21, Lemma A.1], we obtain in view of the latter identities that \({v\in \textrm{C}^1(\overline{\Omega })}\). Moreover, the formula derived in the proof of [21, Lemma A.1] for the traces \({Z_j[\phi ]|_\Gamma }\), \(j=0,\ldots ,3,\) leads us to
It is now a matter of direct computation to infer from (1.2), (2.3), (2.8), (2.17), and (2.18) that the equation (2.1)\(_3\) is equivalent to (2.11), hence also (2.1)\(_3\) is satisfied. It remains to check that the far field boundary condition (2.1)\(_4\) holds true. To this end we infer directly from [5, Lemma A.4] and (2.12)\(_2\) that p vanishes at infinity. Moreover, since by (2.12)\(_1\) we have
for \(x\in \Omega \), where \(R=(R_1,R_2)\) is given by
we infer from [5, Lemma A.4] and [21, Lemma B.2] that also v vanishes at infinity.
In order to show that \(v|_\Gamma \circ \Xi \in H^2({\mathbb R})^2\) we conclude from (2.12)\(_1\), (2.16), and the formula derived in the proof of [21, Lemma A.1] for the traces \({Z_j[\phi ]|_\Gamma }\), \(j=0,\ldots ,3,\) that
Since \(B_{n,m}^0(f)\in \mathcal {L}(H^2({\mathbb R}))\), see Lemma 3.2 (iv) below, we immediately deduce from (2.19) that indeed \(v|_\Gamma \circ \Xi \in H^2({\mathbb R})^2\). \(\square \)
3 On the invertibility of \(\pm 1/2+\mathbb {D}(f)\) and \(\pm 1/2+\mathbb {D}(f)^*\)
In this section we establish the invertibility of the operators \(\pm 1/2-\mathbb {D}(f)\) and \({\pm 1/2-\mathbb {D}(f)^*}\) in \(\mathcal {L}(H^k({\mathbb R})^2)\), \(k=0,\, 1,\, 2\), and \(\mathcal {L}(H^{s-1}({\mathbb R})^2)\), \({s\in (3/2,2)},\) under suitable regularity assumptions on f. These properties are needed on the one hand in the proof of Theorem 2.1, see (2.11), and on the other hand when formulating the Stokes flow as an evolution problem for f, see Sect. 4. The main step is provided by Theorem 3.1 below.
Theorem 3.1
Given \(\delta \in (0,1)\), there exists a constant \(C_0=C_0(\delta )\ge 1\) such that for all \({f\in \textrm{BUC}^1({\mathbb R})}\) with \({\Vert f'\Vert _\infty \le 1/\delta }\) and all \(\beta \in L_2({\mathbb R})^2\) we have
Moreover, \(\pm 1/2-\mathbb {D}(f)^*\) and \(\pm 1/2-\mathbb {D}(f)\) are invertible in \(\mathcal {L}(L_2({\mathbb R}))^2\).
The present section is devoted mainly to the proof of this theorem, which is split up in a number of steps.
3.1 Preliminaries
To start, we reexpress the operators \(\mathbb {D}(f)\) and \(\mathbb {D}(f)^*\) by using the family of singular integral operators defined in (2.10) as follows
for \(\beta =(\beta _1,\beta _2)^\top \in L_2({\mathbb R})^2\).
Since the operators \(B_{n,m}\) are well-studied by now, mapping properties for the operators \(\mathbb {D}(f)\) and \(\mathbb {D}(f)^*\) can be obtained by using the representation (3.2) and Lemma 3.2 below (which collects some important properties of the operators \(B_{n,m}\)). In the following, for \(n\in {\mathbb N}\) and Banach spaces E and F, we define \(\mathcal {L}^n_\textrm{sym}(E,F)\) as the Banach space of n-linear, bounded, and symmetric maps \(A: E^n\rightarrow F\). Moreover, \(\textrm{C}^{1-}(E,F)\) (resp. \({\textrm{C}^{\infty }(E,F)}\)) is the space of locally Lipschitz continuous (resp. smooth) mappings from E to F.
Lemma 3.2
-
(i)
Given Lipschitz continuous functions \(a_1,\ldots , a_{m},\, b_1, \ldots , b_n:\mathbb {R}\longrightarrow \mathbb {R}\), there exists a constant C depending only on \(n,\, m\) and \(\max _{i=1,\ldots , m}\Vert a_i'\Vert _{\infty }\), such that
$$\begin{aligned} \Vert B_{n,m}(a_1,\ldots , a_m)[b_1,\ldots ,b_n,\,\cdot \,]\Vert _{\mathcal {L}(L_2(\mathbb {R}))}\le C\prod _{i=1}^{n} \Vert b_i'\Vert _{\infty }. \end{aligned}$$Moreover, \(B_{n,m}\in \textrm{C}^{1-}((W^1_\infty (\mathbb {R}))^{m},\mathcal {L}^n_\textrm{sym}(W^1_\infty (\mathbb {R}), \mathcal {L}(L_2(\mathbb {R})))).\)
-
(ii)
Let \(n\ge 1,\) \(s\in (3/2,2),\) and \(a_1,\ldots , a_m\in H^s({\mathbb R})\) be given. Then, there exists a constant C, depending only on \(n,\, m\), s, and \(\max _{1\le i\le m}\Vert a_i\Vert _{H^s}\), such that
$$\begin{aligned}&\Vert B_{n,m}(a_1,\ldots , a_{m})[b_1,\ldots , b_n,h]\Vert _2\le C\Vert b_1\Vert _{H^1}\Vert h\Vert _{H^{s-1}}\prod _{i=2}^{n}\Vert b_i\Vert _{H^s} \end{aligned}$$(3.3)for all \(b_1,\ldots , b_n\in H^s({\mathbb R})\) and \(h\in H^{s-1}({\mathbb R}).\)
-
(iii)
Given \(s\in (3/2,2)\) and \(a_1,\ldots , a_m, b_1,\ldots , b_n\in H^s(\mathbb {R})\), there exists a constant C, depending only on \(n,\, m,\, s\), and \(\max _{1\le i\le m}\Vert a_i\Vert _{H^s},\) such that
$$\begin{aligned} \Vert B_{n,m}(a_1,\ldots , a_{m})[b_1,\ldots , b_n,\cdot ]\Vert _{\mathcal {L}(H^{s-1}(\mathbb {R}))}\le C \prod _{i=1}^{n}\Vert b_i\Vert _{H^{s}}. \end{aligned}$$Moreover, \( B_{n,m}\in \textrm{C}^{1-}((H^s(\mathbb {R}))^m, \mathcal {L}^n_\textrm{sym}(H^s(\mathbb {R}), \mathcal {L}(H^{s-1}(\mathbb {R})))).\)
-
(iv)
Let \(a_1,\ldots , a_m\in H^2({\mathbb R})\) be given. Then, there exists a constant C, depending only on \(n,\, m\), and \(\max _{1\le i\le m}\Vert a_i\Vert _{H^2}\), such that
$$\begin{aligned} \Vert B_{n,m}(a_1,\ldots , a_{m})[b_1,\ldots , b_n,h]\Vert _{H^1}\le C \Vert h\Vert _{H^1}\prod _{i=1}^{n}\Vert b_i\Vert _{H^2} \end{aligned}$$(3.4)for all \(b_1,\ldots , b_n\in H^2({\mathbb R})\) and \(h\in H^1({\mathbb R}) \), with
$$\begin{aligned} \begin{aligned}&(B_{n,m}(a_1,\ldots , a_{m})[b_1,\ldots , b_n,h])'\\&\quad =B_{n,m}( a_1,\ldots , a_m) [b_1,\ldots , b_n, h' ]\\&\qquad +\sum _{i=1}^nB_{n,m}(a_1,\ldots ,a_m)[b_1,\ldots ,b_{i-1}, b_i',b_{i+1},\ldots b_n, h]\\&\qquad -2\sum _{i=1}^mB_{n+2,m+1}( a_1,\ldots , a_i, a_i,\ldots ,a_m) [b_1,\ldots ,b_n, a_i',a_i, h ]. \end{aligned} \end{aligned}$$(3.5)Moreover, \(B_{n,m}\in \textrm{C}^{1-}(H^2({\mathbb R})^m,\mathcal {L}^{n}_\textrm{sym}(H^2({\mathbb R}),\mathcal {L}(H^1({\mathbb R})))).\)
Proof
The claims (i) and (ii) are established in [19, Lemmas 3.1 and 3.2], the property (iii) is proven in [1, Lemmas 5], and (iv) is established in [22, Lemma 4.3]. \(\square \)
As a direct consequence of (3.2) and Lemma 3.2 (i) we obtain that
Moreover, by Lemma 3.2 (iv), we have
3.2 Rellich identities on \(\Gamma \)
The proof of Theorem 3.1 relies on several Rellich identities for the Stokes problem, (3.12)–(3.16) below, which hold also in a bounded geometry in \({\mathbb R}^n\), \(n\ge 3\), see [7].
Let \(f\in \textrm{BUC}^\infty ({\mathbb {R}})\) and \(\beta =(\beta _1,\beta _2)^\top \in \textrm{C}_c^\infty ({\mathbb {R}})^2\). Using the notation from Sect. 2, we set \({\Omega ^-:=\Omega }\), \(\Omega ^+:={\mathbb R}^2\setminus \overline{\Omega }\), and we define the hydrodynamic single-layer potential \((u, \Pi )\) by the formula
where \(\mathcal {U}^k\) and \(\mathcal {P}^k\) are defined in (2.6) (with \(\mu =1\)). Since \(\beta \) is compactly supported, it is not difficult to see that the functions \((u,\Pi )\) are well-defined, smooth in \(\Omega ^\pm \), and satisfy
as well as
Moreover, [5, Lemma A.1] and the arguments in the proof of [21, Lemma A.1] enable us to conclude that \( \Pi ^\pm :=\Pi |_{\Omega ^\pm }\) and \(u^\pm :=u|_{\Omega ^\pm }\) satisfy \(\Pi ^\pm \in \textrm{C}(\overline{\Omega ^\pm })\) and \(u^\pm \in \textrm{C}^1(\overline{\Omega ^\pm })\), with
for \(\xi \in {\mathbb {R}}\), with \(r=r(\xi ,s)\) defined in (2.7).
Recalling the definition (1.2) of the stress tensor, we then compute in view of (3.9)
where \(\Vert \cdot \Vert _F\) denotes as usual the Frobenius norm of matrices. Using (3.10), we may integrate the latter identities over \(\Omega ^\pm \) to obtain, in view of Gauss’ theorem, the Rellich identities
We now subtract (3.12) from (3.13) multiplied by 4 to get
Furthermore, from
we obtain, after taking the difference of (3.14) and (3.15),
3.3 Transformation to the real axis
To represent the pull-backs of the one-sided traces of \((\nabla u)_{ij}\) and \(\Pi \) on \(\Gamma \) as singular integral operators, we define, for \(f\in W^1_\infty ({\mathbb {R}})\), \({\beta \in L_2}({\mathbb {R}})^2\), and \(\theta \in L_2({\mathbb R})\), the singular integral operators \({\mathbb {T}}_i\), \(\mathbb {B}_i\), \(i=1,\,2\), as follows:
in the notation introduced in (2.7). Since the components of these operators may be expressed by using only the singular operators \({B^{0}_{n,m}(f)}\), we infer from Lemma 3.2 (i) that
It follows from (2.6), (2.16) (with \({\mu =1}\)) and (3.11) that for \({f\in \textrm{BUC}^\infty ({\mathbb {R}})}\) and \(\beta \in \textrm{C}_c^\infty ({\mathbb {R}})^2\) we have (in matrix notation)
the right sides of (3.18) being meaningful whenever \(f\in W^1_\infty ({\mathbb {R}})\) and \(\beta \in L_2({\mathbb {R}})^2\). To translate the Rellich identities of the previous subsection to identities for integral operators on \({\mathbb R}\) it is convenient to additionally introduce the operators \(\widetilde{T_1^\pm }\) and \(\widetilde{\partial _2u^\pm }\) by
where \(e_2:=(0,1)^\top \).
From (3.17) we immediately get
It is not difficult to check that
Parameterizing \(\Gamma \) over \({\mathbb R}\) via \([s\longmapsto (s,f(s))]\) and using (3.18) and (3.20), we find from (3.12) that
where \(\langle \cdot |\cdot \rangle \) denotes the \(L_2({\mathbb R})^2\) scalar product. Similarly, from (3.13) and (3.16) we get
and
respectively.
By a standard density argument, it follows from (3.6) and (3.19) that (3.21)–(3.23) hold for any functions \(f\in \textrm{BUC} ^1 ({\mathbb {R}})\) and \(\beta \in L_2({\mathbb R})^2\).
3.4 Completion of the proof of Theorem 3.1
We divide the remaining arguments in the proof of Theorem 3.1 in three steps.
Step 1. Fix \(\delta \in (0,1)\) and \({f\in \textrm{BUC}^1({\mathbb {R}})}\) such that \(\Vert f'\Vert _\infty \le 1/\delta \). In the sequel, we are going to write \(C(\delta )\) for different positive constants that depend on \(\delta \) only. Let \(\beta \in L_2({\mathbb R})^2\). Using Lemma 3.2 (i), we find a constant \(C(\delta )\) such that the right side of (3.21) satisfies
For the left side of (3.21) we have, in view of (3.20) and Lemma 3.2 (i),
These estimates show that there exists a constant \( C(\delta )\) with the property that
for all \(\beta \in L_2({\mathbb R})^2\).
Step 2. It follows from (3.23) that
hence
Furthermore, as
we infer from (3.25) that
The identity (3.22) implies the estimate
and together with (3.26) this yields
Multiplying the identity (3.18)\(_1\) by \(e_2\) and taking subsequently the scalar product with \(\beta \), we observe that
The second term on the right vanishes as \({\mathbb {T}}_2(f)^*=-{\mathbb {T}}_2(f)\), and thus
Next, we rewrite (3.18)\(_2\) as
Letting \({\mathbb {A}}(f):=\mathbb {B}_1(f)^*\), it follows from the Rellich identity for the Muskat problem established in the proof of [19, Theorem 3.5] that the operator \({(\pm 1-{\mathbb {A}}(f))\in \mathcal {L}(L_2({\mathbb R}))}\) is an isomorphism with
This implies that also its adjoint \((\pm 1- \mathbb {B}_1(f))\in \mathcal {L}(L_2({\mathbb R}^2))\) is an isomorphism and
Using this and Lemma 3.2 (i) we get
and together with (3.28) and Young’s inequality we arrive at
In view of (3.27) we infer from the latter inequality that
and together with (3.24) and Young’s inequality we finally obtain
Step 3. In view of the identity
we deduce from (3.29) that
and therefore
Now (3.30) together with the estimate [22, (3.15)] shows there exists a constant \({C_0=C_0(\delta )\ge 1}\) such that
As \(\mathbb {D}(f)^*\) is in \(\mathcal {L}(L_2({\mathbb R})^2),\) the shift \(\lambda -\mathbb {D}(f)^*\in \mathcal {L}(L_2({\mathbb R})^2)\) is an isomorphism if \(|\lambda |\) is sufficiently large. The method of continuity, cf. e.g. [2, Proposition I.1.1.1], implies now that \({\pm 1/2-\mathbb {D}(f)^*}\), and hence also \(\pm 1/2-\mathbb {D}(f)\), are isomorphisms as well. This completes the proof of Theorem 3.1.
3.5 Spectral properties in Sobolev spaces
In Lemma 3.3 we establish the invertibility of the operators considered in Theorem 3.1 in the Banach algebras \(\mathcal {L}(H^k({\mathbb R})^2)\), \(k=1,\, 2\).
Lemma 3.3
For \(f\in H^{k+1}({\mathbb R})\), \(k=1,\, 2\), the operators \({\pm 1/2-\mathbb {D}(f)}\) and \({\pm 1/2-\mathbb {D}(f)^*}\) are invertible in \(\mathcal {L}(H^k({\mathbb R})^2)\).
Proof
Fix \(f\in H^{k+1}({\mathbb R})\). The representation (3.2) and Lemma 3.2 (iv) then immediately imply that \(\mathbb {D}(f)\) and \(\mathbb {D}(f)^*\) belong to \(\mathcal {L}(H^k({\mathbb R})^2)\).
Let first \(k=1\). Using (3.5), we compute that the components of
are (finite) linear combination of terms of the form
with \(n,\,m\le 5\), \(\ell =0,\, 1,\) and \(i=1,\, 2\). Choosing \(s\in (3/2,2)\), it follows from Lemma 3.2 (i)-(ii) that there exists a constant \(C_1>0\) such that
This property together with (3.1) now leads to
The latter estimate, an interpolation argument, and Young’s inequality imply there exists a further constant \({C_2=C_2(\delta )\ge 1}\) such that
for all \(\beta \in H^1({\mathbb R})^2\). This estimate combined with (3.1) now yields
for all \(\beta \in H^1({\mathbb R})^2\). The invertibility of \(\pm 1/2-\mathbb {D}(f)\) in \(\mathcal {L}(H^1({\mathbb R})^2)\) follows from this estimate and the invertibility property in \(\mathcal {L}(L_2({\mathbb R})^2)\). The invertibility of \(\pm 1/2-\mathbb {D}(f)^*\) in \(\mathcal {L}(H^1({\mathbb R})^2)\) may be established by using the same arguments and therefore we omit the details.
Finally, when \(k=2\), the invertibility of \(\pm 1/2-\mathbb {D}(f)\) and \(\pm 1/2-\mathbb {D}(f)^*\) in \(\mathcal {L}(H^2({\mathbb R})^2)\) may be obtained by arguing along the same lines as above (see the proof of [22, Theorem 4.5] for some details). \(\square \)
The next invertibility result is used in Sect. 4.4 when we consider our evolution problems in \({H^{s-1}({\mathbb R})}\) with \({s\in (3/2,2)}\).
Lemma 3.4
Given \(\delta \in (0,1)\) and \(s\in (3/2,2),\) there exists a positive constant \({C=C(\delta ,s)\ge 1}\) such that for all \({f\in H^s({\mathbb R})}\) with \({\Vert f \Vert _{H^s}\le 1/\delta }\) and all \(\beta \in H^{s-1}({\mathbb R})^2\) we have
Moreover, \(\pm 1/2-\mathbb {D}(f)^*\) and \(\pm 1/2-\mathbb {D}(f)\) are invertible in \(\mathcal {L}(H^{s-1}({\mathbb R})^2)\).
Proof
As a direct consequence of Lemma 3.2 (iii) we get \(\mathbb {D}(f),\,\mathbb {D}(f)^*\in \mathcal {L}(H^{s-1}({\mathbb R}))^2\). The remaining claims follow from Lemma 3.2, (3.1), and Theorem 3.1, by arguing as in the proof of [22, Theorem 4.2] and Lemma 3.3. \(\square \)
4 Equivalent formulation and proof of the main results
In this section we formulate the quasistationary Stokes flow (1.1) as an evolution problem for f. The main step is established in Corollary 4.3, which provides the unique solvability of Eq. (2.11), as announced in Theorem 2.1. Using this, in Sect. 4.2 we derive the evolution problem (4.9) for the Stokes flow (1.1). This is in analogy to the problem (4.10) obtained in [22] for the corresponding two-phase Stokes flow (1.6). In Sect. 4.3, Problem (4.9) is then shown to be the limit \(\mu _+\rightarrow 0\) of (4.10). This is based on a commutator type identity provided in Proposition 4.4. Finally, in Sect. 4.4, we introduce the general evolution problem (4.23) with parameter \(\mu _+\ge 0\). This formulation enables us to treat both one- and two-phase flows simultaneously for initial data in \(H^s({\mathbb R})\), \({s\in (3/2,2)}\), and to establish the main results.
4.1 A relation connecting \((\mathbb {D}(f)[\beta ])'\) and \(\mathbb {D}(f)^*[\beta ']\)
The following identity is, besides Lemma 3.3, the main ingredient in the proof of Corollary 4.3.
Lemma 4.1
Given \(f\in H^{\tau }({\mathbb R})\), \(\tau \in (3/2,2)\), and \(\beta \in H^1({\mathbb R})^2\), we have \({\mathbb {D}(f)[\beta ]\in H^1({\mathbb R})^2}\) with
In order to prepare the proof of Lemma 4.1, which is presented below, we set
and define
where \(r=r(\xi ,s)\) is defined in (2.7). The double-layer potential \(\mathbb {D}(f)\) and its \(L_2\)-adjoint \(\mathbb {D}(f)^*\) can now be expressed as follows:
for \(\beta \in L_2({\mathbb R})^2\), see (2.8). Both integrals converge when \(f\in H^\tau ({\mathbb R})\), with \(\tau \in (3/2,2),\) since there exists a constant \(C>0\) such that
Here, \(\Vert \cdot \Vert _F\) is again the Frobenius norm. Motivated by (4.3), we establish the following auxiliary result.
Lemma 4.2
Let \(A\in \textrm{C}({\mathbb R}^2)\cap \textrm{C}^1({\mathbb R}^2\setminus D)\), \(u\in \textrm{C}_c({\mathbb R})\), and assume there exist constants \({C>0}\) and \(\alpha \in (0,1)\) such that
Then, the function \(\psi :{\mathbb R}\longrightarrow {\mathbb R}\) given by
belongs to \(\textrm{C}^1({\mathbb R})\) and
Proof
Given \({\varepsilon \in (0,1)}\), let \(\psi _\varepsilon \in \textrm{C}({\mathbb R})\) be given by
Since u has compact support and \(A\in \textrm{C}({\mathbb R}^2)\cap \textrm{C}^1({\mathbb R}^2{\setminus } D)\), we have \(\psi _\varepsilon \in \textrm{C}^1({\mathbb R})\) and \(\psi _\varepsilon \rightarrow \psi \) for \( \varepsilon \rightarrow 0\) uniformly on compact subsets of \({\mathbb R}\). By closedness of the differentiation, the lemma is proved once we show
uniformly on compact subsets of \({\mathbb R}\). Indeed, given \(\xi \in {\mathbb R}\), it holds that
and therefore
which implies the announced convergence. \(\square \)
We are now in a position to prove Lemma 4.1.
Proof of Lemma 4.1
We first establish the result for \(\beta \in \textrm{C}_c^\infty ({\mathbb R})^2\). To this end we define the function \(S:=S(f)\in \textrm{C}({\mathbb R}^2)\) by
The function S is continuously differentiable in \({\mathbb R}^2{\setminus } D\), where again \({D:=\{(\xi ,\xi )\,:\,\xi \in {\mathbb R}\}}\), with partial derivatives expressed, in the notation (2.7), as
Now (with arguments \((\xi ,s)\) partly suppressed), the kernel K defined in (4.2) can be expressed as
where \(G\in \textrm{C}^\infty ({\mathbb R},{\mathbb R}^{2\times 2})\) is a primitive of the smooth matrix valued function
Thus, after integration by parts,
We next observe that \(A:=G\circ S\) is continuous on \({\mathbb R}^2\) and \(A\in \textrm{C}^1({\mathbb R}^2\setminus D)\) with
Moreover, since \(f\in \textrm{BUC}^{\tau -1/2}({\mathbb R})\), setting \(\alpha :=\tau -3/2\in (0,1)\), we obtain from (4.3) that there exists \(C>0\) such that
We may now infer from Lemma 4.2 that \(\mathbb {D}(f)[\beta ]\in \mathrm{C^1}({\mathbb R})\) and
Let now \(\beta \in H^1({\mathbb R})^2\) arbitrary, and let \((\beta _n)\) be a sequence in \(\textrm{C}^\infty _c({\mathbb R})^2\) with \(\beta _n\rightarrow \beta \) in \({H^1({\mathbb R})^2}\). Then, by \(L_2\)-continuity of \(\mathbb {D}(f)\), see (3.6),
and, by \(L_2\)-continuity of \(\mathbb {D}(f)^*\), see (3.6),
Now the result follows by closedness of the derivative operator. \(\square \)
We are now in a position to establish the solvability of (2.11).
Corollary 4.3
Given \(f\in H^3({\mathbb R})\) and \(g\in H^2({\mathbb R})^2\), let \(\beta \in H^2({\mathbb R})^2\) denote the unique solution to the equation
Then \(\alpha :=\beta '\in H^1({\mathbb R})^2\) is the unique solution to
Proof
The claim is a direct consequence of Lemmas 3.3 and 4.1. \(\square \)
4.2 The evolution problem for f
Let \( T_+>0\) and (f, v, p) be a solution to (1.1) such that for all \(t\in (0,T_+)\) we have \(f(t)\in H^3({\mathbb R})\) and
Define \(\beta (t):=\beta (f(t))\in H^{2}({\mathbb R})^2\) by
with \(g(t)=g(f(t))\) as defined in (2.4). Then, by Corollary 4.3, \(\beta (t)'\) is the unique solution to
with the prime denoting the spatial derivative along \({\mathbb R}\). Theorem 2.1, in particular (2.19), then implies that
where, given \(f\in H^3({\mathbb R})\), the operator \({\mathbb {V}}(f)\in \mathcal {L}(H^{2}({\mathbb R})^2)\) (see (3.7)) is defined by
for \(\beta =(\beta _1,\beta _2)^\top \in H^{2}({\mathbb R})^2 \). Recalling (1.1a)\(_5\) and (1.1b), we may thus recast (1.1) as the following evolution problem
where the evolution equation should be satisfied pointwise with values in \(H^2({\mathbb R})\).
4.3 Problem (4.9) as the limit \(\mu _+\rightarrow 0\) of the two-phase Stokes problem
In [22] it is shown that if \(T_{+}>0\) and \((f, w^\pm ,q^\pm )\) is a solution to the two-phase quasistationary Stokes flow (1.6) such that for all \(t\in (0,T_{+})\) we have \(f(t)\in H^3({\mathbb R})\), \( w^\pm (t)|_{\Gamma (t)}\circ \Xi _{f(t)}\in H^2({\mathbb R})^2\), and
then \(f=f(t)\) solves the evolution problem
where \(\gamma (t):=\gamma (f(t))\in H^2({\mathbb R})^2\) is given by
and
In (4.11), \(g(f(t))\in H^2({\mathbb R})^2\) and \({\mathbb {V}}(f(t))\in \mathcal {L}(H^{2}({\mathbb R})^2)\), \(t\in (0,T_+)\), are defined in (2.4) and (4.8), respectively, and the evolution equation should be again satisfied pointwise with values in \(H^2({\mathbb R}), \) see [22, Theorem 4.5].
We next prove that the formulation (4.9) coincides with the limit \(\mu _+\rightarrow 0\) of (4.10) with \({\mu ^-=\mu }\) fixed. Then \(a_\mu \rightarrow -1\), and as Lemma 3.3 and [22, Theorem 4.5] show, this limit can be taken by continuity in (4.10).
Proposition 4.4
Given \(f\in H^3({\mathbb R})\), it holds that
Proof
We are going to prove the more compact identity
which is equivalent to (4.12) in view of Lemma 3.3.
Let \(\beta \in H^2({\mathbb R})^2\) be arbitrary and let \((v,p):=(v,p)(f)[\beta ]\) be defined by (2.12) (with \(\mu =1\)). Then, as shown in Theorem 2.1, it holds that
and, recalling also Corollary 4.3, (v, p) solves the boundary value problem
where
We next define \({(w^\pm ,q^\pm ):\Omega ^\pm \longrightarrow {\mathbb R}^2\times {\mathbb R}}\) by \((w^-,w^+)=( v,0)\) and \((q^-,q^+)=(p,0)\). Then
and \((w^\pm ,q^\pm )\) solves the boundary value problem
Similarly as in the proof of [22, Proposition 5.1], we decompose \((w^\pm ,q^\pm )\) as a sum
where \((w^\pm _s,q^\pm _s)\) solves
The system (4.18) has been studied in [21] and, according to [21, Theorem 2.1 and Lemma A.1], it has a unique solution which satisfies
and which has the same regularity as (w, q), see (4.16). Consequently, \((w^\pm _d,q^\pm _d)\) enjoys also the regularity (4.16) and moreover it solves
Since \(v|_\Gamma \circ \Xi \in H^2({\mathbb R})^2\), also (4.20) has a unique solution, see [22, Proposition 2.1], and, according to [22, Lemma A.1] we have
Since \({\mathbb {V}}(f)[\beta ]=v|_\Gamma \circ \Xi =(w^-_s+w^-_d)|_\Gamma \circ \Xi ,\) we infer from (4.15), (4.19), and (4.21) that
and (4.13) is now a direct consequence of this identity. \(\square \)
4.4 The common equivalent formulation for (1.1) and (1.6)
We are now able to simultaneously consider the evolution equations (4.9) and (4.10) that, respectively, encode the one-phase problem (1.1) and the two-phase problem (1.6). For this purpose we set
and view \(\mu ^+\in [0,\infty )\) as a parameter.
For \(f\in H^3({\mathbb R})\), we set
with g(f) defined in (2.4) and \({\mathbb {V}}(f)\) in (4.8).
Now, in view of Proposition 4.4, the parameter-dependent evolution equation
is identical to (4.9) for \(\mu ^+=0\) and to (4.10) for \(\mu ^+>0\).
Though (4.23) has been derived under the assumption that the solution lies in \( H^3({\mathbb R})\) for positive times, this equation may be viewed in a more general analytic setting. Indeed, given \(f\in H^{s}({\mathbb R})\), \(s\in (3/2,2)\), we first deduce from [21, Lemma 3.5] that \({g(f)\in H^{s-1}({\mathbb R})^2}\) and
Moreover, since
see [21, Corollary C.5], (3.2)\(_1\) and (4.8) yield
The properties (4.24), (4.25), Lemma 3.4 (for \(\mu ^+=0\)) and [22, Theorem 4.2] (for \(\mu ^+>0\)) ensure now that the operator \({\Phi :[0,\infty )\times H^s({\mathbb R})\longrightarrow H^{s-1}({\mathbb R})}\) is well-defined. Moreover, the smoothness of the function which maps an isomorphism to its inverse together with (4.24) and (4.25) implies that
We conclude this section with the observation that \(\Phi (\mu ^+,\cdot )\) maps bounded sets of \(H^s({\mathbb R})\) to bounded sets of \(H^{s-1}({\mathbb R}).\) This property is a consequence of the fact that g maps bounded sets of \(H^{s}({\mathbb R})\) to bounded sets of \(H^{s-1}({\mathbb R})^2\), of Lemma 3.2 (iii), and of Lemma 3.4 (for \(\mu ^+=0\)) or [22, Theorem 4.2] (for \(\mu ^+>0\)).
4.5 The proofs of the main results
In the case \(\mu ^+>0\), we shown in [22, Theorem 6.1] that the Fréchet derivative \(\partial _f\Phi (\mu ^+,f)\) is, for each \(f\in H^{s}({\mathbb R}),\) the generator of an analytic semigroup in \(\mathcal {L}(H^{s-1}({\mathbb R})).\) This property, the observation that \(\Phi (\mu ^+,\cdot )\) maps bounded sets of \({H^s({\mathbb R})}\) to bounded sets of \(H^{s-1}({\mathbb R}),\) the smoothness of \(\Phi (\mu ^+,\cdot )\), the fully nonlinear parabolic theory from [18], and a parameter trick used also for other problems, see, e.g., [3, 6, 20, 25], were then exploited in [22] to establish the well-posedness of the two-phase quasistationary Stokes flow (1.6), see [22, Theorem 1.1]. All these properties are satisfied also when \(\mu ^+=0\). Indeed, using Lemma 3.4 instead of [22, Theorem 4.2], the arguments in the proof of [22, Theorem 6.1] remain valid also if \(\mu ^+=0\), hence also \(\partial _f\Phi (0,f)\) is the generator of an analytic semigroup in \({\mathcal {L}(H^{s-1}({\mathbb R}))}\) for each \(f\in H^{s}({\mathbb R})\). In view of these facts we have:
Proof of Theorem 1.1
The proof is identical to that of [22, Theorem 1.1] and therefore we omit the details. \(\square \)
For the proof of Theorem 1.2 we consider \(\mu ^+\) as a parameter and we use a result on the continuous dependence of the solutions to abstract parabolic problems on parameters provided in [18, Theorem 8.3.2]
Proof of Theorem 1.2
In view of (4.26) and of the fact that Fréchet derivative \(\partial _f\Phi (\mu ^+,f)\) is, for each \((\mu ^+,f)\in [0,\infty )\times H^{s}({\mathbb R}),\) the generator of an analytic semigroup in \(\mathcal {L}(H^{s-1}({\mathbb R}))\) we find that all the assumptions of [18, Theorem 8.3.2] are satisfied in the context of (4.23).
Let thus \(f(\cdot ;f^{(0)}):[0,T_+( f^{(0)}))\longrightarrow {\mathbb R}\) denote the maximal solution to (4.23) with \(\mu ^+=0\) and fix \({T\in (0,T_+( f^{(0)}))}\). In view of [18, Theorem 8.3.2] there exist constants \(\varepsilon >0\) and \({M>0}\) such that for each \(\mu ^+ \in (0,\varepsilon ]\) the solution \(f_{\mu ^+}(\cdot ; f^{(0)})\) to (4.23) found in [22, Theorem 6.1] satisfies \(T_{+,\mu ^+}( f^{(0)})>T\) and
This completes the proof. \(\square \)
Data availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Abels, H., Matioc, B.-V.: Well-posedness of the Muskat problem in subcritical \(L_p\)-Sobolev spaces. Eur. J. Appl. Math. 33, 224–266 (2022)
Amann, H.: Linear and Quasilinear Parabolic Problems. Vol. I, vol. 89 of Monographs in Mathematics, Birkhäuser Boston, Inc., Boston (1995). Abstract linear theory
Angenent, S.B.: Nonlinear analytic semiflows. Proc. R. Soc. Edinb. Sect. A 115, 91–107 (1990)
Badea, A., Duchon, J.: Capillary driven evolution of an interface between viscous fluids. Nonlinear Anal. 31, 385–403 (1998)
Bierler, J., Matioc, B.-V.: The multiphase Muskat problem with equal viscosities in two dimensions. Interfaces Free Bound. 24, 163–196 (2022)
Escher, J., Simonett, G.: Analyticity of the interface in a free boundary problem. Math. Ann. 305, 439–459 (1996)
Fabes, E.B., Kenig, C.E., Verchota, G.C.: The Dirichlet problem for the Stokes system on Lipschitz domains. Duke Math. J. 57, 769–793 (1988)
Friedman, A., Reitich, F.: Quasi-static motion of a capillary drop. II. The three-dimensional case. J. Differ. Equ. 186, 509–557 (2002)
Friedman, A., Reitich, F.: Quasistatic motion of a capillary drop. I. The two-dimensional case. J. Differ. Equ. 178, 212–263 (2002)
Gancedo, F.: A survey for the Muskat problem and a new estimate. SeMA J. 74, 21–35 (2017)
Gancedo, F., Granero-Belinchón, R., Salguero, E.: Long time interface dynamics for gravity Stokes flow (2023). arXiv:2211.03437
Granero-Belinchón, R., Lazar, O.: Growth in the Muskat problem. Math. Model. Nat. Phenom., 15 , pp. Paper No. 7, 23 (2020)
Grayer, H.: Dynamics of density patches in infinite Prandtl number convection. Arch. Ration. Mech. Anal. 247 (2023)
Günther, M., Prokert, G.: Existence results for the quasistationary motion of a free capillary liquid drop. Z. Anal. Anwendungen 16, 311–348 (1997)
Höfer, R.M.: Sedimentation of inertialess particles in Stokes flows. Commun. Math. Phys. 360, 55–101 (2018)
Ladyzhenskaya, O.A.: The mathematical theory of viscous incompressible flow, Revised English edition. Translated from the Russian by Richard A. Silverman. Gordon and Breach Science Publishers, New York (1963)
Leblond, A.: Well-posedness of the Stokes-transport system in bounded domains and in the infinite strip (2021). arXiv:2103.16305
Lunardi, A.: Analytic Semigroups and Optimal Regularity in Parabolic Problems, Progress in Nonlinear Differential Equations and their Applications, 16. Birkhäuser Verlag, Basel (1995)
Matioc, B.-V.: Viscous displacement in porous media: the Muskat problem in 2D. Trans. Am. Math. Soc. 370, 7511–7556 (2018)
Matioc, B.-V.: The Muskat problem in two dimensions: equivalence of formulations, well-posedness, and regularity results. Anal. PDE 12, 281–332 (2019)
Matioc, B.-V., Prokert, G.: Two-phase Stokes flow by capillarity in full 2d space: an approach via hydrodynamic potentials. Proc. R. Soc. Edinb. Sect. A 151, 1815–1845 (2021)
Matioc, B.-V., Prokert, G.: Two-phase Stokes flow by capillarity in the plane: the case of different viscosities. NoDEA Nonlinear Differ. Equ. Appl. 29, pp. Paper No. 54, 34 (2022)
Mecherbet, A.: Sedimentation of particles in Stokes flow. Kinet. Relat. Models 12, 995–1044 (2019)
Mecherbet, A., Sueur, F.: A few remarks on the transport-Stokes system (2022). arXiv:2209.11637
Prüss, J., Shao, Y., Simonett, G.: On the regularity of the interface of a thermodynamically consistent two-phase Stefan problem with surface tension. Interfaces Free Bound. 17, 555–600 (2015)
Prüss, J., Simonett, G.: Moving Interfaces and Quasilinear Parabolic Evolution Equations, vol. 105 of Monographs in Mathematics. Birkhäuser/Springer, Cham (2016)
Solonnikov, V.A.: On quasistationary approximation in the problem of motion of a capillary drop. In: Topics in Nonlinear Analysis, vol. 35 of Progr. Nonlinear Differential Equations Appl., pp. 643–671. Birkhäuser, Basel (1999)
Solonnikov, V.A.: On the justification of the quasistationary approximation in the problem of motion of a viscous capillary drop. Interfaces Free Bound. 1, 125–173 (1999)
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflicts of interest to declare that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Partially supported by DFG Research Training Group 2339 “Interfaces, Complex Structures, and Singular Limits in Continuum Mechanics—Analysis and Numerics”.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Matioc, BV., Prokert, G. Capillarity-driven Stokes flow: the one-phase problem as small viscosity limit. Z. Angew. Math. Phys. 74, 212 (2023). https://doi.org/10.1007/s00033-023-02101-x
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00033-023-02101-x