Asymmetric equilibrium configurations of a body immersed in a 2d laminar flow

Abstract

We study the equilibrium configurations of a possibly asymmetric fluid–structure interaction problem. The fluid is confined in a bounded planar channel and is governed by the stationary Navier–Stokes equations with laminar inflow and outflow. A body is immersed in the channel and is subject to both the lift force from the fluid and to some external elastic force. Asymmetry, which is motivated by natural models, and the possibly non-vanishing velocity of the fluid on the boundary of the channel require the introduction of suitable assumptions to prevent collisions of the body with the boundary. With these assumptions at hand, we prove that for sufficiently small inflow/outflow there exists a unique equilibrium configuration. Only if the inflow, the outflow and the body are all symmetric, the configuration is also symmetric. A model application is also discussed.

1 Introduction

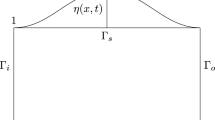
Let $L>H>0$ and consider the rectangle $R=(-L,L)\times (-H,H)$. Let $B\subset R$ be a closed smooth domain having barycenter at the origin $(x_1,x_2)=(0,0)$ such that $\textrm{diam}(B)\ll L,H$. We study the behavior of a stationary laminar (horizontal) fluid flow going through R and filling the domain $\Omega _h= R\setminus B_h$, where $B_h=B+he_2$ for some h (a vertical translation of B), see Fig. 1. Note that $B_0=B$.

The fluid is governed by the stationary 2D Navier–Stokes equations

$$\begin{aligned} -\mu \Delta u+u\cdot \nabla u+ \nabla p = 0,\quad \nabla \cdot u =0\quad \text{ in }\quad \Omega _h,\end{aligned}$$

(1.1)

complemented with inhomogeneous Dirichlet boundary conditions on $\partial \Omega _h=\partial B_h\cup \partial R$, see (2.4). Here, $\mu >0$ is the kinematic viscosity, u is the velocity vector field, p is the scalar pressure.

The body B is subject to two vertical forces. The first force (the lift) is due to the fluid flow and tends to move B away from its original position $B_0$; it is expressed through a boundary integral over $\partial B$, see (3.1). The second force is mechanical (elastic) and acts as a restoring force tending to maintain B in $B_0$. When there is no inflow/outflow, the body is only subject to the restoring force and remains in $B_0$ which is the unique equilibrium position. But, as soon as there is a fluid flow, these two forces start competing and one may wonder if the body remains in $B_0$ or, at least, if the equilibrium position remains unique.

We show that if the inflow/outflow is sufficiently small, then the equilibrium position of B remains unique and coincides with $B_h$ for some h close to zero. We point out that, contrary to [3, 8, 10], we make no symmetry assumptions neither on B nor on the laminar inflow/outflow. Therefore, not only the overall configuration will be asymmetric but also some of the techniques developed in these papers do not work and $B_h$ may be different from $B_0$. The motivation for studying asymmetric configurations comes from nature. Only very few bodies are perfectly symmetric, and most fluid flows, although laminar in the horizontal direction, are asymmetric in the vertical direction: think of an horizontal wind depending on the altitude or the water flow in a river depending on the distance from the banks. Figure 2 shows two front waves in sandstorms that have no vertical symmetry although the wind is (almost) horizontally laminar.

Fig. 1

Rectangle R and the body B with its vertical displacements $B_h$

Fig. 2

Front wave of two wind storms

In Sect. 2, we give a detailed description of our model and we prove that, for small Reynolds numbers, the Navier–Stokes equations are uniquely solvable in any $\Omega _h$, see Theorem 2.2. The related a priori bounds depend on h, and this is one crucial difference compared to the (symmetric) Poiseuille inflow/outflow considered in [3]. It is well known [5] that to solve inhomogeneous Dirichlet problems for the Navier–Stokes equations, one needs to find a solenoidal extension of the boundary data and to transform the original problem in an homogeneous Dirichlet problem with an additional source term. For the existence issue, one can use the classical Hopf extension, but there are infinitely many other possible choices for the solenoidal extension. One of them, introduced in [12], was used in [3] to write the lift force as a volume integral by means of the solution of an auxiliary Stokes problem. For asymmetric flows, the same solenoidal extension does not allow to estimate all the boundary terms and, in order to obtain refined bounds for the solution to the Navier–Stokes equations in $\Omega _h$, we build a new explicit solenoidal extension that also plays a fundamental role in the analysis of the subsequent fluid–structure interaction (FSI) problem.

The main physical interest in FSI problems is to determine the $\omega$-limit of the associated evolution equations because this allows to forecast the long-time behavior of the structure. Since the evolution Navier–Stokes equations are dissipative, one is led to investigate if the global attractor exists, see [7, 15]: the main difficulty is that the corresponding phase space is time dependent and semigroup theory does not apply. The global attractor contains stationary solutions of the evolution FSI problem that we call equilibrium configurations, which are investigated in the present work.

In Sect. 3, we introduce the lift force and the restoring force and we set up the steady-state FSI problem. Our main result, namely Theorem 3.1, states that, for small Reynolds numbers, the equilibrium position is unique and may differ from $B_0$. By exploiting the strength of the restoring force, uniqueness for the FSI problem is obtained without assuming uniqueness for (1.1). To prove this result, we need some bounds on the lift force in proximity of collisions of $B_h$ with $\partial R$: these bounds are collected in Theorem 3.2 and proved in Sect. 4 by using the very same solenoidal extension introduced in Sect. 2. The remaining part of the proof of Theorem 3.1 is divided in two steps. In Subsection 5.1, we prove some properties of the global force exerted on the body B. These properties are then used in Subsection 5.2 to complete the proof by means of an implicit function argument, combined with some delicate bounds involving derivatives of moving boundary integrals. We emphasize that for our FSI problem we cannot use the explicit expression of the lift derivative as in [17] because the displacements $B_h$ within R do not follow the normal of $\partial B_h$, in particular if $\partial B_h$ contains some vertical segments. Instead, based on the general approach introduced in [2] (see also the previous work [14]), we compute with high precision the lift variation with respect to the vertical displacement parameter h of $B_h$ by acting directly on the strong form of the FSI problem.

Section 6 contains the symmetric version of Theorem 3.1, see Theorem 6.1 which states that, under symmetry assumptions on the inflow/outflow and on B, for small Reynolds numbers the equilibrium position is unique and coincides with $B_0$. This extends former results in [3, 8, 10] to a wider class of symmetric frameworks.

As an application of our results, in Sect. 7 we consider a model where $B_h$ represents the cross-section of the deck of a suspension bridge [6], while $\Omega _h$ is filled by the air and represents either a virtual box around the deck or a wind tunnel around a scaled model of the bridge. Since the deck may have a nonsmooth boundary, we also explain how to extend our results to the case where B is merely Lipschitz.

2 Fluid boundary value problem

Let R and B be as in Sect. 1 (Fig. 1) with

$$\begin{aligned} B \text{ of } \text{ class } W^{2,\infty }. \end{aligned}$$

(2.1)

On the one hand, (2.1) ensures the regularity $(u,p)\in H^2(\Omega _h)\times H^1(\Omega _h)$ for the solutions to (1.1), see [14, Theorem 2.1] and Theorem 2.2. On the other hand, in engineering applications B is usually a polygon with rounded corners, see Sect. 7, which belongs to $W^{2,\infty }$ but not to $C^2$. Let

$$\begin{aligned} \delta _b:= -\min _{(x_1,x_2)\in \partial B}x_2>0, \quad \delta _t:= \max _{(x_1,x_2)\in \partial B}x_2>0, \quad \tau := \max _{(x_1,x_2)\in \partial B}|x_1|. \end{aligned}$$

(2.2)

Since we consider vertical displacements $B_h$ within R, we have $h\in (-H+\delta _b,H-\delta _t)$ and $B_h \subset [-\tau ,\tau ]\times [h-\delta _b, h +\delta _t]$ for any such h. Then, $\partial \Omega _h=\partial B_h\cup \partial R$. The bottom and top parts of $\partial R$ are, respectively,

$$\begin{aligned} \Gamma _b=[-L,L]\times \{-H\} \quad \text{ and } \quad \Gamma _t=[-L,L]\times \{H\}, \end{aligned}$$

while its lateral left and right parts are, respectively,

$$\begin{aligned} \Gamma _l=\{-L\}\times [-H,H]\quad \text{ and } \quad \Gamma _r=\{L\}\times [-H,H]. \end{aligned}$$

Let $V_\textrm{in}, V_\textrm{out}\in W^{2,\infty }(-H,H)\subset C^0[-H,H]$ satisfy

$$\begin{aligned} \begin{aligned} V_\text {in}(-H)&=V_\text {out}(-H)=0, \quad V_\text {in}(H)=V_\text {out}(H)=U\ge 0, \\ {}&\qquad \int \limits _{-H}^H V_\text {in}(x_2) \text {d}x_2= \int \limits _{-H}^H V_\text {out}(x_2) \text {d}x_2.\end{aligned} \end{aligned}$$

(2.3)

For some $\lambda \ge 0$, we consider the boundary value problem

$$\begin{aligned} {}&{} -\mu \Delta u + u\cdot \nabla u + \nabla p = 0,\qquad \nabla \cdot u =0\quad \text { in }\quad \Omega _h,\nonumber \\ \quad u_{|_{\partial B_h}}={}&{}u_{|_{\Gamma _b}}=0, \quad u_{|_{\Gamma _t}}=\lambda Ue_1,\quad u_{|_{\Gamma _l}}=\lambda V_\text {in}(x_2)e_1,\quad u_{|_{\Gamma _r}}=\lambda V_\text {out}(x_2)e_1. \end{aligned}$$

(2.4)

Note that $u_{|_{\partial R}}\in C^0(\partial R)$ and (2.3)-(2.4) are compatible with the Divergence Theorem. The role of $\lambda \ge 0$ in the boundary conditions is to measure with a unique parameter the strength of both the inflow and the outflow. Hence, $\lambda \asymp \textrm{Re}$ where $\textrm{Re}$ is the Reynolds number.

Definition 2.1

We say that $(u,p)\in H^2(\Omega _h)\times H^1(\Omega _h)$ is a strong solution to (2.4) if the differential equations are satisfied a.e. in $\Omega _h$ and the boundary conditions are satisfied as restrictions (recall that $H^2(\Omega _h)\subset C^0(\overline{\Omega _h})$).

We now state an apparently classical existence and uniqueness result which, however, has some novelties. First, since the domain $\Omega _h$ is only Lipschitzian, the regularity of the solution is obtained through a geometric reflection. More importantly, the explicit upper bound for the blow-up of the $H^1$-norm of the unique solution to (2.4) in proximity of collision: when B approaches $\Gamma _t$, the norm remains bounded while when B approaches $\Gamma _b$ we estimate its blow-up. This refined bound requires the construction of a suitable solenoidal extension of the boundary data. Note that, up to normalization, we can reduce to the cases where

$$\begin{aligned} U\in \{0,1\}. \end{aligned}$$

(2.5)

In order to state the result, we define the distances of the body $B_h$ to $\Gamma _b$ and $\Gamma _t$, respectively, by

$$\begin{aligned} \varepsilon _b(h):= H-\delta _b + h, \qquad \varepsilon _t(h):= H-\delta _t -h. \end{aligned}$$

(2.6)

Hence, $0<\varepsilon _b(h),\varepsilon _t(h) \le 2H -\delta _b -\delta _t$ for any $h\in (-H+\delta _b, H-\delta _t)$. Throughout the paper, any (positive) constant depending only on $\mu$, $B_0$, L, H will be denoted by C and, when it depends also on h, by $C_h$. We may now state

Theorem 2.2

Let $h\in (-H+\delta _b,H-\delta _t)$ and assume (2.3) with (2.5). Then, (2.4) admits a strong solution (u, p) for any $\lambda \ge 0$ and there exists $\Lambda =\Lambda (h)>0$ such that the solution is unique if $\lambda \in [0,\Lambda (h))$; if $U=0$, $\Lambda (h)$ can be chosen independent of h, i.e., $\Lambda (h)\equiv \Lambda >0$. Moreover, there exist $C>0$ and $C_h>0$ such that the unique solution (when $\lambda <\Lambda (h)$) satisfies

$$\begin{aligned}&\Vert u\Vert _{H^1(\Omega _h)} \le C (1+U(\varepsilon _t(h))^{-3/2})\lambda , \end{aligned}$$

(2.7)

$$\begin{aligned}&\Vert u\Vert _{H^2(\Omega _h)} + \Vert p\Vert _{H^1(\Omega _h)} \le C_h \lambda . \end{aligned}$$

(2.8)

A priori bounds such as (2.7) and (2.8) are available for any $\lambda \ge 0$ and any strong solution of (2.4), but with different powers of $\lambda$.

Before giving the proof, let us explain qualitatively the main differences between the cases $U=0$ and $U=1$. For $U=0$, the a priori bound (2.7) is independent of h, so that the graph of $\Lambda (h)$ looks like Fig. 3 (left). For $U=1$, (2.7) depends on h and $\Lambda (h)$ itself may depend on h, see Fig. 3 (right) and (2.20).

Fig. 3

Qualitative behavior of $\Lambda =\Lambda (h)$ for $U=0$ (left) and $U=1$ (right)

Proof

Existence of weak solutions. For later use, we first define weak solution for the forced Navier–Stokes equations

$$\begin{aligned} -\mu \Delta u + u\cdot \nabla u + \nabla p = f,\qquad \nabla \cdot u =0\quad \text{ in }\quad \Omega _h, \end{aligned}$$

(2.9)

which reduces to (2.4) when $f=0$. We say that $u\in H^1(\Omega _h)$ is a weak solution to (2.9) with $f\in L^2(\Omega _h)$ if u is a solenoidal vector field satisfying the boundary conditions in the trace sense and

$$\begin{aligned} \mu \int \limits _{\Omega _h} \nabla u : \nabla \varphi +\int \limits _{\Omega _h} u \cdot \nabla u \cdot \varphi =\int \limits _{\Omega _h}f\cdot \varphi \end{aligned}$$

(2.10)

for all $\varphi \in W(\Omega _h):=\{\varphi \in H^1_0(\Omega _h): \nabla \cdot \varphi =0 \ \text{ a.e. } \text{ in } \ \Omega _h\}$. For any weak solution u, there exists a unique associated $p\in L^2_0(\Omega _h)$ (i.e., with zero mean value), satisfying

$$\begin{aligned} \mu \int \limits _{\Omega _h}\nabla u : \nabla \psi +\int \limits _{\Omega _h} u\cdot \nabla u\cdot \psi -\int \limits _{\Omega _h} p \nabla \cdot \psi =\int \limits _{\Omega _h}f\cdot \psi \end{aligned}$$

(2.11)

for all $\psi \in H^1_0(\Omega _h)$ (Lemma IX.1.2, [5]). In (2.24), we introduce an ad-hoc solenoidal extension matching our geometric framework which is not optimal for our current purpose. This is why we use here the well-known Hopf’s extension s that reduces the effect of the nonlinearity and allows to prove existence for any $\lambda \ge 0$. Hence, we recast (2.4) as (2.9) with homogeneous boundary conditions, namely

$$\begin{aligned} -\mu \Delta v + v\cdot \nabla v +\nabla p =f,\quad \nabla \cdot v =0\quad \text{ in }\quad \Omega _h,\qquad v_{|_{\partial \Omega _h}}=0, \end{aligned}$$

(2.12)

where $f=\mu \Delta s -s\cdot \nabla v - v\cdot \nabla s-s\cdot \nabla s$. Then, there exists $v\in W(\Omega _h)$ satisfying (2.10) for any $\lambda \ge 0$ (Theorem IX.4.1, [5]). This is equivalent to say that the vector field $u=v+s\in H^1(\Omega _h)$ and the associated pressure $p\in L^2(\Omega _h)$ satisfy (2.10)-(2.11) with $f=0$. Moreover, $\nabla \cdot u=0$, $u_{|_{\partial \Omega _h}}= s_{|_{\partial \Omega _h}}$ and

$$\begin{aligned} \Vert u\Vert _{H^1(\Omega _h)}\le & {} C(\Vert \nabla v \Vert _{L^2(\Omega _h)}+\Vert s\Vert _{H^1(\Omega _h)})\nonumber \\\le & {} C\left( \left( 1+ \tfrac{1}{\mu }\right) \Vert s\Vert _{H^1(\Omega _h)}+\tfrac{1}{\mu }\Vert s\Vert ^2_{H^1(\Omega _h)}\right) \le C_h(\lambda + \lambda ^2)\,, \end{aligned}$$

(2.13)

$$\begin{aligned} \Vert p\Vert _{L^2(\Omega _h)}\le & {} C (\mu \Vert u\Vert _{H^1(\Omega _h)} + \Vert u\Vert ^2_{H^1(\Omega _h)})\le C_h (\lambda +\lambda ^4). \end{aligned}$$

(2.14)

In these bounds and the ones below, we only emphasize the smallest and largest powers of $\lambda$, as for any polynomial. These bounds are not part of the statement, but they will be used later in the present proof.

Regularity. We claim that any weak solution (u, p) to (2.4) satisfies $(u,p)\in H^2(\Omega _h)\times H^1(\Omega _h)$. This would be straightforward if $\Omega _h\in W^{2,\infty }$, see [14], but R is only Lipschitzian. Here, we take advantage of the particular shape of R and use a reflection argument as in [9]. We construct a new domain $\Omega ^t_h=R^t\setminus B^t_h$, obtained by reflecting $\Omega _h$ across $\Gamma _t$, where $R^t=(-L,L)\times [H,3H)$ and $B^t_h$ is the reflection of $B_h$ with respect to $\Gamma _t$. Define $(u^t, p^t): \Omega ^t_h \rightarrow \mathbb {R}^2\times \mathbb {R}$ by

$$\begin{aligned} \begin{aligned} u_1^t(x_1,H+x_2)&= u_1(x_1, H-x_2), \quad u_2^t(x_1,H+x_2)= -u_2(x_1, H-x_2),\\ p^t(x_1, H+x_2)&= p(x_1,H-x_2)\quad \ \ \text { for } \text { all } (x_1,x_2)\in (-L,L)\times [0,2H),\end{aligned} \end{aligned}$$

which satisfies

$$\begin{aligned} -\mu \Delta u^t+ u^t\cdot \nabla u^t + \nabla p^t = 0,\quad \nabla \cdot u^t =0\quad \text{ in }\quad \Omega ^t_h. \end{aligned}$$

(2.15)

Therefore, the couple

$$\begin{aligned} (\overline{u},\overline{p})={\left\{ \begin{array}{ll} (u,p) \ {} &{}\text{ in } \quad \Omega _h,\\ (u^t,p^t) \ {} &{}\text{ in } \quad \Omega ^t_h, \end{array}\right. } \end{aligned}$$

satisfies the Navier–Stokes equations

$$\begin{aligned} -\mu \Delta \overline{u}+ \overline{u}\cdot \nabla \overline{u} + \nabla \overline{p} = 0,\quad \nabla \cdot \overline{u} =0\quad \text{ in }\quad \big \{(-L,L)\times (-H,3H)\big \} \setminus \{B_h \cup B_h^t\} . \end{aligned}$$

Similarly, let $\Omega ^b_h=R^b\setminus B^b_h$ with $R^b=(-L,L)\times (-3H,-H]$ and $B^b_h$ is the reflection of $B_h$ with respect to $\Gamma _b$. Define $(u^b, p^b): \Omega ^b_h \rightarrow \mathbb {R}^2\times \mathbb {R}$ by

$$\begin{aligned}\begin{aligned} u_1^b(x_1,-H-x_2)&= u_1(x_1, -H+x_2), \quad u_2^b(x_1,-H-x_2)= -u_2(x_1, -H+x_2),\\ p^b(x_1, -H-x_2)&= p(x_1,-H+x_2) \quad \ \ \text { for } \text { all } (x_1,x_2)\in (-L,L)\times [0,2H), \end{aligned} \end{aligned}$$

which satisfies the corresponding of (2.15) in $\Omega ^b_h$. Thanks to these two vertical reflections, we obtain a solution in $\Omega ^s_h=\big \{(-L,L)\times (-3\,H,3\,H)\big \} {\setminus } \{B_h \cup B_h^t\cup B_h^b\}$.

With the same principle, we then perform two horizontal reflections of $\Omega ^s_h$ with respect to $x_1=\pm L$. At the end of this procedure, let

$$\begin{aligned} \widetilde{\Omega }_h=\big \{(-3L,3L)\times (-3H,3H)\big \} \setminus \{B_h \text{ and } \text{ its } \text{ eight } \text{ reflections }\} \end{aligned}$$

and $(\widetilde{u}, \widetilde{p}): \widetilde{\Omega }_h \rightarrow \mathbb {R}^2\times \mathbb {R}$ be the extension of (u, p), so that

$$\begin{aligned} -\mu \Delta \widetilde{u}+ \widetilde{u}\cdot \nabla \widetilde{u} + \nabla \widetilde{p} = 0,\quad \nabla \cdot \widetilde{u}=0\quad \text{ in }\quad \widetilde{\Omega }_h,\qquad \widetilde{u}_{|_{\partial B_h}}=0 \end{aligned}$$

(2.16)

and $\tilde{u}$ satisfies further boundary conditions that we do not need to make explicit. After introducing a suitable solenoidal extension, we can proceed as in the first part of the proof and obtain the existence of a solution $(\widetilde{u}, \widetilde{p})\in H^1(\widetilde{\Omega }_h)\times L^2(\widetilde{\Omega }_h)$ satisfying the bounds (2.13)-(2.14). Hence, $\widetilde{u}\cdot \nabla \widetilde{u} \in L^{3/2}(\widetilde{\Omega }_h)$ and

$$\begin{aligned} \begin{aligned} \Vert \widetilde{u}\cdot \nabla \widetilde{u} \Vert _{L^{3/2}(\widetilde{\Omega }_h)}\le \Vert \widetilde{u}\Vert _{L^6(\widetilde{\Omega }_h)} \Vert \nabla \widetilde{u} \Vert _{L^2(\widetilde{\Omega }_h)}\le C\Vert \widetilde{u}\Vert ^2_{H^1(\widetilde{\Omega }_h)} \le C_h(\lambda ^2 + \lambda ^4) \end{aligned} \end{aligned}$$

(2.17)

with $C_h=C(\widetilde{\Omega }_h)$. By applying [14] and [5, Theorems IV.4.1 and IV.5.1] to the Stokes problem (2.16), we infer that $(\widetilde{u}, \widetilde{p})\in W^{2,3/2}(\Omega ')\times W^{1,3/2}(\Omega ')$ for any $\Omega '\subset \widetilde{\Omega }_h$ and

$$\begin{aligned} \begin{aligned}&\Vert \widetilde{u}\Vert _{W^{2,3/2}(\Omega ')} + \Vert \widetilde{p}\Vert _{W^{1,3/2}(\Omega ')}\\ {}&\le C_h(\Vert \widetilde{u}\cdot \nabla \widetilde{u} \Vert _{L^{3/2}(\widetilde{\Omega }_h)} + \Vert \widetilde{u}\Vert _{W^{1,3/2}(\widetilde{\Omega }_h)}+ \Vert \widetilde{p}\Vert _{L^{3/2}(\widetilde{\Omega }_h)})\le C_h(\lambda + \lambda ^4) \end{aligned} \end{aligned}$$

(2.18)

with $C_h=C( \Omega ', \widetilde{\Omega }_h)$. We recall that $(\widetilde{u}, \widetilde{p})=(u,p)$ in $\Omega _h$. Then, using Sobolev embedding $W^{2,3/2}\hookrightarrow W^{1,6}$ in $\mathbb {R}^2$ and a bootstrap argument we obtain that $(u,p)\in H^2(\Omega _h)\times H^1(\Omega _h)$. Moreover, from (2.17)-(2.18) we get

$$\begin{aligned}\begin{aligned} \Vert u\Vert _{H^2(\Omega _h)} + \Vert p\Vert _{H^1(\Omega _h)}&\le C_h(\Vert \widetilde{u}\cdot \nabla \widetilde{u} \Vert _{L^{2}( \Omega ')} +\Vert \widetilde{u}\Vert _{H^1(\Omega ')} + \Vert \widetilde{p}\Vert _{L^2(\Omega ')})\\&\le C_h( \Vert \widetilde{u}\Vert _{L^3(\Omega ')}\Vert \nabla \widetilde{u}\Vert _{L^6(\Omega ')} +\Vert \widetilde{u}\Vert _{H^1(\Omega ')} + \Vert \widetilde{p}\Vert _{L^2(\Omega ')})\\&\le C_h(\Vert \widetilde{u}\Vert _{H^1(\Omega ')}\Vert \widetilde{u}\Vert _{W^{2,3/2}(\Omega ')}+\Vert \widetilde{u}\Vert _{H^1(\Omega ')} + \Vert \widetilde{p}\Vert _{L^2(\Omega ')})\\&\le C_h(\lambda +\lambda ^4) \end{aligned} \end{aligned}$$

with $C_h=C( \Omega _h, \widetilde{\Omega }_h)$. This also proves (2.8) whenever $\lambda < \Lambda (h)$.

Uniqueness. Let $u_1$ and $u_2$ be two weak solutions to (2.4), let $w=u_1-u_2$, then

$$\begin{aligned} \mu \int \limits _{\Omega _h}\nabla w: \nabla \varphi + \int \limits _{\Omega _h}w\cdot \nabla w \cdot \varphi =- \int \limits _{\Omega _h}\left( w\cdot \nabla u_2 + u_2\cdot \nabla w \right) \cdot \varphi \end{aligned}$$

for all $\varphi \in W(\Omega _h)$. Then, take $\varphi = w$ so that the latter yields

$$\begin{aligned} \begin{aligned} \mu \Vert \nabla w \Vert _{L^2(\Omega _h)}^2&= - \int \limits _{\Omega _h} w\cdot \nabla u_2 \cdot w \le \Vert \nabla u_2\Vert _{L^2(\Omega _h)}\Vert w\Vert _{L^4(\Omega _h)}^2 \\&\le C_h(1+\tfrac{1}{\mu }) (\lambda + \lambda ^2)\Vert \nabla w\Vert _{L^2(\Omega _h)}^2, \end{aligned} \end{aligned}$$

(2.19)

where we used Hölder, Ladyzhenskaya and Poincaré inequalities and (2.13). Hence, there exists $\Lambda =\Lambda (h)>0$ (uniformly upper-bounded with respect to h) such that

$$\begin{aligned} \lambda \in [0,\Lambda (h))\ \Longleftrightarrow \ C_h(1+\tfrac{1}{\mu })(\lambda +\lambda ^2)<\mu \end{aligned}$$

(2.20)

and this condition implies $\Vert \nabla w\Vert _{L^2(\Omega _h)}=0$ and, in turn, $w=0$ since $w_{|_{\partial \Omega _h}}=0$.

Refined bounds. For $\lambda \in [0,\Lambda (h))$, in all the above bounds we can drop the largest power of $\lambda$ and they all become linear upper bounds. We treat separately the cases $U=1$ and $U=0$ and we make explicit the dependence of the constant $C_h$ in (2.13) on h.

When $U=1$, we claim that the unique strong solution u to (2.4) satisfies

$$\begin{aligned} \Vert u\Vert _{H^1(\Omega _h)} \le C\big (1+(\varepsilon _t(h))^{-3/2}\big )\lambda \end{aligned}$$

(2.21)

with $C>0$ independent of h. To this end, we introduce a different (and explicit) solenoidal extension. Consider the cutoff functions $\zeta _l,\zeta _r\in C^\infty (\mathbb {R}^2)$, with $0\le \zeta _{ l}, \zeta _r\le 1$, defined piece-wise in the rectangles of Fig. 4 by

$$\begin{aligned} \zeta _l(x_1,x_2)={\left\{ \begin{array}{ll} 0 \quad &{}\text{ in } \quad [-\tau ,\tau ]\times \left[ -H, H -\tfrac{\varepsilon _t(h) }{2}\right] , \\ 0 \quad &{}\text{ in } \quad [\tau , L]\times [-H,H] ,\\ 1 \quad &{}\text{ in } \quad [-L,-2\tau ]\times [-H,H],\\ \zeta ^0_l(x_1)\quad &{}\text{ in }\quad [-2\tau ,-\tau ]\times \left[ -H,H-\tfrac{\varepsilon _t(h)}{2}\right] ,\\ C^\infty \text{-completion }\quad &{}\text{ in } \quad [-2\tau ,-\tau ]\times \left[ H-\tfrac{\varepsilon _t(h)}{2},H\right] , \end{array}\right. } \end{aligned}$$

(2.22)

where $\zeta ^0_l$ is a function only of $x_1$, and

$$\begin{aligned} \zeta _r(x_1,x_2)={\left\{ \begin{array}{ll} 0 \quad &{}\text{ in } \quad [-\tau ,\tau ]\times \left[ -H, H -\tfrac{\varepsilon _t(h)}{2}\right] , \\ 0 \quad &{}\text{ in } \quad [-L, -\tau ]\times \left[ -H,H-\tfrac{ \varepsilon _t(h)}{4}\right] ,\\ 1\quad &{}\text{ in } \quad [2\tau , L]\times \left[ -H,H-\tfrac{ \varepsilon _t(h)}{4}\right] ,\\ \zeta ^0_r(x_1)\quad &{}\text{ in }\quad [\tau ,2\tau ]\times \left[ -H,H-\tfrac{ \varepsilon _t(h)}{2}\right] ,\\ 1-\zeta _l(x_1,x_2)&{} \text{ in } \quad [-L,L]\times \left[ H -\tfrac{\varepsilon _t(h)}{4},H \right] ,\\ C^\infty \text{-completion } \quad &{}\text{ in }\quad [-\tau ,2\tau ]\times \left[ H-\tfrac{ \varepsilon _t(h)}{2}, H-\tfrac{ \varepsilon _t(h)}{4}\right] , \end{array}\right. } \end{aligned}$$

(2.23)

where $\zeta ^0_r$ is a function only of $x_1$.

Fig. 4

Cutoff functions $\zeta _l$ (left) and $\zeta _r$ (right) on $\overline{ R}$ when $U=1$

Then, letting $\nabla ^\perp =(-\partial _2,\partial _1)$, consider the vector field $s: R\rightarrow \mathbb {R}^2$ defined by

$$\begin{aligned} \begin{aligned} s(x_1,x_2):=-\lambda \nabla ^\perp \left( \zeta _l(x_1,x_2)\int \limits _{-H}^{x_2} V_\textrm{in}(z)\textrm{d}z + \zeta _r(x_1,x_2)\int \limits _{-H}^{x_2} V_\textrm{out}(z)\textrm{d}z\right) , \end{aligned} \end{aligned}$$

(2.24)

which is solenoidal and satisfies the boundary conditions in (2.4). Rewriting s as

$$\begin{aligned} \begin{aligned} s(x_1,x_2)= \lambda \left( -\nabla ^\perp \zeta _l \int \limits _{-H}^{x_2}V_\textrm{in} - \nabla ^\perp \zeta _r \int \limits _{-H}^{x_2}V_\textrm{out}+ (\zeta _l V_\textrm{in} + \zeta _r V_\textrm{out}) e_1\right) , \end{aligned} \end{aligned}$$

its partial derivatives read

$$\begin{aligned} \begin{aligned} \partial _1 s&= \lambda \left( -\nabla ^\perp \partial _1 \zeta _l \int \limits _{-H}^{x_2}V_\textrm{in} - \nabla ^\perp \partial _1\zeta _r \int \limits _{-H}^{x_2}V_\textrm{out} + (\partial _1 \zeta _l V_\textrm{in} + \partial _1 \zeta _r V_\textrm{out})e_1\right) \, ,\\ \partial _2 s&= \lambda \bigg ( -\nabla ^\perp \partial _2 \zeta _l \int \limits _{-H}^{x_2}V_\textrm{in} - \nabla ^\perp \partial _2\zeta _r \int \limits _{-H}^{x_2}V_\textrm{out} - \nabla ^\perp \zeta _l V_\textrm{in} -\nabla ^\perp \zeta _r V_\textrm{out} \\&\quad + (\partial _2 \zeta _l V_\textrm{in} + \partial _2 \zeta _r V_\textrm{out} +\zeta _l \tfrac{d}{dx_2}V_\textrm{in} + \zeta _r \tfrac{d}{dx_2}V_\textrm{out})e_1\bigg ). \end{aligned} \end{aligned}$$

Using that $V_\textrm{in},V_\textrm{out}\in W^{2,\infty }(-H,H)$ and that $\zeta _l,\zeta _r$ are smooth, it follows that

$$\begin{aligned} \begin{aligned}\Vert s\Vert _{L^\infty (\Omega _h)}, \Vert s\Vert&_{L^2(\Omega _h)}, \Vert s\Vert _{L^4(\Omega _h)} , \Vert \nabla s\Vert _{L^2(\Omega _h)}, \Vert \Delta s\Vert _{L^2(\Omega _h)}\le C_h\lambda ,\\ {}&\Vert s\cdot \nabla s\Vert _{L^2(\Omega _h)}\le C_h\lambda ^2\le C_h\lambda . \end{aligned} \end{aligned}$$

(2.25)

We need to quantify the dependence of $C_h>0$ on $\varepsilon _b(h)$ and $\varepsilon _t(h)$. On the one hand, we notice that, by construction, both $\zeta _l$ and $\zeta _r$ depend on $x_2$ only in

$$\begin{aligned} \Omega _{\varepsilon _t(h)}:=[-2\tau , 2\tau ] \times \left[ H-\tfrac{\varepsilon _t(h)}{2},H\right] . \end{aligned}$$

(2.26)

In this domain, the $x_1$-derivatives of $\zeta _{l}$ and $\zeta _r$ are uniformly bounded with respect to h while the $x_2$-derivatives blow-up as $\varepsilon _t(h)$ goes to zero, for instance, we have

$$\begin{aligned} |\partial _2 \zeta _{l}|, |\partial _2 \zeta _{r}|\le C (\varepsilon _t(h))^{-1},\qquad |\partial ^2_2 \zeta _{r}|, |\partial ^2_2 \zeta _{l}|\le C (\varepsilon _t(h))^{-2}. \end{aligned}$$

Therefore, in $\Omega _{\varepsilon _t(h)}$

$$\begin{aligned} \begin{aligned} |s|\le C (1&+(\varepsilon _t(h))^{-1})\lambda , \quad |\partial _1 s|\le C (1+(\varepsilon _t(h))^{-1})\lambda ,\\ {}&|\partial _2 s|\le C ( (\varepsilon _t(h))^{-1}+(\varepsilon _t(h))^{-2})\lambda . \end{aligned} \end{aligned}$$

On the other hand, the cutoff functions depend only on $x_1$ in $\Omega _h\setminus \Omega _{\varepsilon _t(h)}$ and their $x_1$ and $x_2$-derivatives are uniformly bounded with respect to h. Therefore, in $\Omega _h\setminus \Omega _{\varepsilon _t(h)}$

$$\begin{aligned} |s|, |\partial _1 s|, |\partial _2 s|\le C \lambda . \end{aligned}$$

Gathering all together, we refine the bounds in (2.25) as

$$\begin{aligned} \begin{aligned}&\Vert s\Vert _{L^\infty (\Omega _h)}\le C (1+(\varepsilon _t(h))^{-1})\lambda ,\\ {}&\Vert s\Vert _{L^2(\Omega _h)} \le C\lambda + C \left( \int \limits _{\Omega _{\varepsilon _t(h)}}( \varepsilon _t(h))^{-2}\right) ^{1/2}\lambda \le C (1+(\varepsilon _t(h))^{-1/2})\lambda ,\\ {}&\Vert s\Vert _{L^4(\Omega _h)}\le C (1+(\varepsilon _t(h))^{-3/4})\lambda ,\qquad \Vert \nabla s\Vert _{L^2(\Omega _h)} \le C (1+(\varepsilon _t(h))^{-3/2})\lambda ,\\ {}&\Vert \Delta s\Vert _{L^2(\Omega _h)}, \ \Vert s\cdot \nabla s\Vert _{L^2(\Omega _h)}\le C (1+(\varepsilon _t(h))^{-5/2})\lambda ,\end{aligned} \end{aligned}$$

(2.27)

with all the constants $C>0$ independent of h. Then, testing (2.12) with $v=u-s$ we obtain

$$\begin{aligned} \begin{aligned} \mu \Vert \nabla v\Vert _{L^2(\Omega _h)}^2= - \int \limits _{\Omega _h} v\cdot \nabla s\cdot v -\int \limits _{\Omega _h}s\cdot \nabla s \cdot v - \mu \int \limits _{\Omega _h}\nabla s : \nabla v \end{aligned} \end{aligned}$$

(2.28)

We want to estimate, when possible, only s and not $\nabla s$ since the bounds for s are less singular in terms of $\varepsilon _t(h)$. Hence, since $\nabla \cdot v=\nabla \cdot s=0$ and using integration by parts, we rewrite (2.28) as

$$\begin{aligned} \begin{aligned} \mu \Vert \nabla v\Vert _{L^2(\Omega _h)}^2=&\int \limits _{\Omega _h} v\cdot \nabla v\cdot s +\int \limits _{\Omega _h}s\cdot \nabla v \cdot s - \mu \int \limits _{\Omega _h}\nabla s : \nabla v. \end{aligned} \end{aligned}$$

(2.29)

We split the first integral in the right-hand side over $\Omega _{\varepsilon _t(h)}$ and $\Omega _h \setminus \Omega _{\varepsilon _t(h)}$. On the one hand, since $v_{|_{\Gamma _t}}=0$, Poincaré inequality

$$\begin{aligned} \Vert v\Vert _{L^2{(\Omega _{\varepsilon _t(h)}})}\le \frac{\varepsilon _t(h) }{2}\Vert \nabla v\Vert _{L^2{(\Omega _{\varepsilon _t(h)}})}, \end{aligned}$$

and Hölder inequality yield

$$\begin{aligned} \begin{aligned} \int \limits _{\Omega _{\varepsilon _t(h)}}( v \cdot \nabla v )\cdot s&\le \Vert v\Vert _{L^2{(\Omega _{\varepsilon _t(h)}})} \Vert \nabla v\Vert _{L^2{(\Omega _{\varepsilon _t(h)}})} \Vert s\Vert _{L^\infty {(\Omega _{\varepsilon _t(h)}})}\\&\le C\varepsilon _t(h) \Vert \nabla v\Vert ^2_{L^2{(\Omega _{\varepsilon _t(h)}})} (1+ (\varepsilon _t(h))^{-1})\lambda \le C \lambda \Vert \nabla v\Vert ^2_{L^2{(\Omega _{\varepsilon _t(h)}})}, \end{aligned} \end{aligned}$$

where we used that $\Vert s\Vert _{L^\infty (\Omega _{\varepsilon _t(h)})}\le C(1+ (\varepsilon _t(h))^{-1})\lambda$ and $\varepsilon _t(h)\le 2\,H-\delta _b -\delta _t$. On the other hand, since $v_{|_{\Gamma _l, \Gamma _r}}=0$, Poincaré and Hölder inequalities yield

$$\begin{aligned}\begin{aligned} \int \limits _{\Omega _h \setminus \Omega _{\varepsilon _t(h)}}( v \cdot \nabla v )\cdot s&\le \Vert v\Vert _{L^2(\Omega _h\setminus \Omega _{\varepsilon _t(h)})} \Vert \nabla v\Vert _{L^2{(\Omega _h \setminus \Omega _{\varepsilon _t(h)})}} \Vert s\Vert _{L^\infty (\Omega _h \setminus \Omega _{\varepsilon _t(h)})}\\&\le C\lambda \Vert \nabla v\Vert ^2_{L^2{(\Omega _h \setminus \Omega _{\varepsilon _t(h)})}}, \end{aligned} \end{aligned}$$

where we used that $\Vert s\Vert _{L^\infty (\Omega _h {\setminus }\Omega _{\varepsilon _t(h)})}\le C\lambda$. Therefore, from (2.27) and (2.29) we infer

$$\begin{aligned}\begin{aligned} \mu \Vert \nabla v\Vert ^2_{L^2(\Omega _h)}&\le C\lambda \Vert \nabla v\Vert ^2_{L^2(\Omega _h)} + \Vert s\Vert _{L^4(\Omega _h)}^2 \Vert \nabla v\Vert _{L^2(\Omega _h)} +\mu \Vert \nabla s\Vert _{L^2(\Omega _h)}\Vert \nabla v\Vert _{L^2(\Omega _h)}\\&\le C\lambda \Vert \nabla v\Vert ^2_{L^2(\Omega _h)}+ C (1+( \varepsilon _t(h))^{-3/2})(\lambda +\lambda ^2)\Vert \nabla v\Vert _{L^2(\Omega _h)}. \end{aligned} \end{aligned}$$

Then, for $\lambda \in [0,\Lambda (h))$ with $\Lambda (h)$ as in (2.20) we have

$$\begin{aligned} \begin{aligned} \Vert \nabla v\Vert _{L^2(\Omega _h)} \le C(1+ (\varepsilon _t(h))^{-3/2})\lambda \end{aligned} \end{aligned}$$

(2.30)

and

$$\begin{aligned}\begin{aligned} \Vert u\Vert _{H^1(\Omega _h)}\le \Vert \nabla v\Vert _{L^2(\Omega _h)} + \Vert s\Vert _{H^1(\Omega _h)}\le C(1+(\varepsilon _t(h))^{-3/2})\lambda , \end{aligned} \end{aligned}$$

which proves (2.21).

When $U=0$, we claim that the unique strong solution u to (2.4) satisfies

$$\begin{aligned} \Vert u\Vert _{H^1(\Omega _h)} \le C\lambda \end{aligned}$$

(2.31)

with $C>0$ independent of h, which will imply that $\Lambda (h)\equiv \Lambda$ can be also taken independent of h. In this case, we shall define the cut-off functions and the solenoidal extension differently depending if $h\le 0$ or $h>0$. If $h\le 0$, we define $\zeta _l$, $\zeta _r$ as in (2.22)-(2.23) (see Fig. 5) replacing $\varepsilon _t(h)$ with the distance of $B_0$ to $\Gamma _t$, namely $\varepsilon _t(0)=H-\delta _t$. The solenoidal extension s is then defined as in (2.24). By construction both $\zeta _l$ and $\zeta _r$ depend on $x_2$ only in $\Omega _{\varepsilon _t(0)}$, defined as in (2.26) with $\varepsilon _t(h)$ replaced by $\varepsilon _t(0)$. In this domain, both $x_1$ and $x_2$-derivatives of $\zeta _l$ and $\zeta _r$ are uniformly bounded with respect to h, for instance, we have

$$\begin{aligned} |\partial _2 \zeta _{l}|, |\partial _2 \zeta _{r}|\le C( \varepsilon _t(0))^{-1}\le C,\qquad |\partial ^2_2 \zeta _{r}|, |\partial ^2_2 \zeta _{l}|\le C (\varepsilon _t(0))^{-2}\le C. \end{aligned}$$

Since in $\Omega _h \setminus \Omega _{\varepsilon _t(0)}$ the cutoff functions depend only on $x_1$, we infer that s, $\partial _1 s$ and $\partial _2 s$ are uniformly bounded with respect to h in all $\Omega _h$ and

$$\begin{aligned} \Vert s\Vert _{L^\infty (\Omega _h)}, \Vert s\Vert _{L^2(\Omega _h)}, \Vert s\Vert _{L^4(\Omega _h)}, \Vert \nabla s\Vert _{L^2(\Omega _h)} \le C\lambda . \end{aligned}$$

(2.32)

Repeating the same computations as in the case $U=1$ and using (2.32), we obtain (2.31) for $h\le 0$.

If $h>0$, we make a vertical reflection $x_2\mapsto -x_2$ and we consider the new cutoff functions defined piece-wise in the rectangles of Fig. 5, where $\varepsilon _b(0)=H-\delta _b$.

Fig. 5

Cutoff functions $\zeta _l$ (left) and $\zeta _r$ (right) on $\overline{ R}$ when $U=0$ for $h>0$

Then, we consider the vector field $s: R\rightarrow \mathbb {R}^2$ defined by

$$\begin{aligned}\begin{aligned} s(x_1,x_2):=\lambda \nabla ^\perp \left( \zeta _l(x_1,x_2)\int \limits _{x_2}^{H} V_\textrm{in}(z)\textrm{d}z + \zeta _r(x_1,x_2)\int \limits _{x_2}^{H} V_\textrm{out}(z)\textrm{d}z\right) , \end{aligned} \end{aligned}$$

which is solenoidal and satisfies the boundary conditions in (2.4). By the same argument used when $h\le 0$, s, $\partial _1 s$ and $\partial _2 s$ are uniformly bounded with respect to h in $\Omega _h$. Therefore, using again (2.32), we obtain (2.31) for $h<0$.$\square$

Remark 2.3

We stated (2.7) and (2.8) only in case of uniqueness because, in what follows, $\lambda$ will be taken small and higher powers of $\lambda$ can be upper estimated with the first power.

The reflection method used to obtain the regularity result has its own interest. The rectangular shape of the domain is crucial and the technique fails for other polygons. However, in the case of convex polygons, in particular also for a rectangle, one can obtain the more $C^\infty$-regularity result by using Theorem 2 in [13], see also [11, Section 7.3.3] and [4].

3 Equilibrium configurations of a FSI problem

By Theorem 2.2, for any ${(\lambda , h)\in [0,+\infty )\times (-H+\delta _b, H-\delta _t)}$ there exists at least a strong solution $(u,p)=(u(\lambda , h), p(\lambda , h))$ to (2.4). The fluid described by (u, p) in $\Omega _h$ exerts on $B_h$ a force perpendicular to the direction of the inflow, called lift (see [16]). Since the inflow in (2.4) is horizontal, the lift is vertical and given by

$$\begin{aligned} \mathcal {L}(\lambda , h)=-e_2\cdot \int \limits _{\partial B_h} \mathbb {T}(u,p)n, \end{aligned}$$

(3.1)

where $\mathbb {T}$ is the fluid stress tensor, namely

$$\begin{aligned} \mathbb {T}(u,p):= \mu (\nabla u + \nabla u^T) -p\mathbb {I}\, , \end{aligned}$$

and n is the unit outward normal vector to $\partial \Omega _h$, which, on $\partial B_h$, points toward the interior of $B_h$. In fact, $\mathcal {L}(\lambda , h)$ is a multi-valued function when uniqueness for (2.4) fails. However, we keep this simple notation instead of writing $\mathcal {L}(\lambda , h, u(\lambda , h), p(\lambda , h)),$ in which also the dependence on the particular solution (u, p) is emphasized. The regularity of the solution (see Theorem 2.2) and the smoothness of $\partial B_h$ yield $\mathbb {T}(u,p)_{|_{\partial B_h}}\in H^{1/2}(\partial B_h)\subset L^1(\partial B_h)$; hence, the integral in (3.1) is finite. In fact, the lift can also be defined for merely weak solutions, see (7.5) in Sect. 7. Note that (3.1) holds for any $\lambda \ge 0$ and any solution to (2.4), but our main result on the FSI problem focuses on small inflows, see Theorem 3.1.

Aiming to model, in particular, a wind flow hitting a suspension bridge, the body B may also be subject to a (possibly nonsmooth) vertical restoring force f tending to maintain B in the equilibrium position $B_0$ (for $h=0$); see Sect. 7. We assume that f depends only on the position h, that $f\in C^0(-H+\delta _b,H-\delta _t)$ with $f(0)=0$ and

$$\begin{aligned} \exists \gamma >0\quad \text{ s.t. }\quad \frac{f(h_1)-f(h_2)}{h_1-h_2}\ge \gamma \quad \forall h_1,h_2 \in (-H+\delta _b,H-\delta _t), \ h_1\ne h_2. \end{aligned}$$

(3.2)

Moreover, we assume that there exists $K>0$ such that

$$\begin{aligned} \begin{aligned}&\limsup \limits _{h\rightarrow -H+\delta _b} \ f(h)(H-\delta _b+h)^{3/2}\le -K,\\ {}&\liminf \limits _{h\rightarrow H-\delta _t} \ \frac{f(h)}{\max \{(H-\delta _t-h)^{-3/2},U(H-\delta _t-h)^{-3}\}}\ge K. \end{aligned}\end{aligned}$$

(3.3)

The assumption (3.3) is somehow technical and prevents collisions of B with the horizontal boundary $\Gamma _b\cup \Gamma _t$, at least for small inflow/outflow. It can probably be relaxed but, so far, only few (numerical) investigations on the effect of proximity to collisions of hydrodynamic forces (such as the lift), acting on non-spherical bodies, have been tackled, see [20] and references therein. The presence of U in (3.3) highlights the different behavior of f when B is close to $\Gamma _t$ for $U=0$ or $U=1$. In the first case, f has the same strength close to $\Gamma _b$ and $\Gamma _t$. Conversely, for $U=1$, the asymmetry of the boundary conditions requires a different strength of f, which is stronger when B is close to $\Gamma _t$ than when B is close to $\Gamma _b$. Overall, (3.2)-(3.3) model the fact that B is not allowed to go too far away from the equilibrium position $B_0$.

Since we are interested in the equilibrium configurations of the FSI problem, we consider the boundary-value problem (2.4) coupled with a compatibility condition stating that the restoring force balances the lift force, namely

$$\begin{aligned} {}&{} -\mu \Delta u + u\cdot \nabla u + \nabla p = 0,\quad \nabla \cdot u =0\quad \text { in }\quad \Omega _h\nonumber \\ u_{|_{\partial B_h}}=u_{|_{\Gamma _b}}&=0, \quad u_{|_{\Gamma _t}}=\lambda Ue_1,\quad u_{|_{\Gamma _l}}=\lambda V_\text {in}(x_2)e_1,\quad u_{|_{\Gamma _r}}=\lambda V_\text {out}(x_2)e_1, \nonumber \\{}&{} \qquad \qquad \quad f(h)=-e_2\cdot \int \limits _{\partial B_h} \mathbb {T}(u,p)n. \end{aligned}$$

(3.4)

Our main result concerns the existence and uniqueness of the solution to (3.4) for small values of $\lambda$ that we expect to be stable.

Theorem 3.1

Let $f\in C^0(-H+\delta _b, H-\delta _t)$ satisfy (3.2)-(3.3) with $f(0)=0$ and $V_\textrm{in}$, $V_\textrm{out}\in W^{2,\infty }(-H,H)$ satisfy (2.3) with (2.5). There exist $\Lambda _1>0$ and a unique $\mathfrak {h}\in C^0[0, \Lambda _1)$ such that for $\lambda \in [0,\Lambda _1)$ the FSI problem (3.4) admits a unique solution $(u(\lambda ,h), p(\lambda ,h),h)\in H^2(\Omega _h)\times H^1(\Omega _h)\times (-H+\delta _b, H-\delta _t)$ given by

$$\begin{aligned} (u(\lambda ,\mathfrak {h}(\lambda )), p(\lambda ,\mathfrak {h}(\lambda )),\mathfrak {h}(\lambda )). \end{aligned}$$

We emphasize that Theorem 3.1 ensures uniqueness of the equilibrium configuration for the FSI problem (3.4) in the uniform interval $[0, \Lambda _1)$ even in absence of uniqueness for (2.4) that, instead, is only ensured in the possibly non-uniform interval $[0,\Lambda (h))$. The proof of Theorem 3.1 is given in Sect. 5. It is fairly delicate because if $U=0$ (as for symmetric inflow/outflow), then from (2.21) we infer that the $H^1$-norm is uniformly bounded with respect to h. However, if $U=1$, the same norm obviously blows up when $B_h$ approaches $\Gamma _t$, which affects the bounds for the lift in (3.1). As already mentioned, very little is known when a body approaches a collision, see again [20] and references therein. Therefore, the next statement has its own independent interest; it provides some upper bounds and shows that, probably, the lift behaves differently for homogeneous and inhomogeneous boundary data.

Theorem 3.2

Assume (2.5) and let $\lambda \in [0,\Lambda _0]$ for some $\Lambda _0>0$. Let (u, p) be a strong solution to (2.4) (see Theorem 2.2) and let $\mathcal {L}(\lambda , h)$ be as in (3.1). There exists $C>0$ (independent of $\lambda , h, u, p$) such that, for any $(\lambda ,h )\in [0,\Lambda _0]\times (-H+\delta _b, H-\delta _t)$,

$$\begin{aligned} |\mathcal {L}(\lambda , h)|\le C \Big ((\varepsilon _b(h))^{-3/2}+ \max \{(\varepsilon _t(h))^{-3/2},U (\varepsilon _t(h))^{-3} \}\Big )\lambda \end{aligned}$$

(3.5)

with $\varepsilon _b(h)$ and $\varepsilon _t(h)$ defined in (2.6). In fact, $\mathcal {L}(\lambda , h)$ is defined in all $[0,+\infty )\times (-H+\delta _b, H-\delta _t)$, possibly as a multi-valued function, but (3.5) would hold with different powers of $\lambda$.

The proof of Theorem 3.2 is given in the next section.

4 Proof of theorem 3.2

We rewrite the lift (3.1), which is a boundary integral, as a volume integral. This can be done by considering $w\in H^1(\Omega _h)$ that satisfies

$$\begin{aligned} \nabla \cdot w=0\quad \text{ in }\quad \Omega _h,\qquad w_{|_{\partial B_h}}=e_2,\qquad w_{|_{\partial R}}=0. \end{aligned}$$

(4.1)

The divergence theorem ensures that (4.1) admits infinitely many solutions. Testing (2.4) with one such solution w (recall that $\nabla \cdot \mathbb {T}=\mu \Delta u -\nabla p$) yields

$$\begin{aligned} \int \limits _{\Omega _h} u\cdot \nabla u \cdot w = \int \limits _{\Omega _h}\nabla \cdot \mathbb {T}(u,p)\cdot w=-\mu \int \limits _{\Omega _h}\nabla u : \nabla w + \int \limits _{\partial \Omega _h}\mathbb {T}(u,p)n \cdot w \end{aligned}$$

and, using the boundary conditions on w,

$$\begin{aligned} -e_2\cdot \int \limits _{\partial B_h}\mathbb {T}(u,p)n = -\int \limits _{\Omega _h} u\cdot \nabla u \cdot w - \mu \int \limits _{\Omega _h}\nabla u : \nabla w. \end{aligned}$$

(4.2)

Among the infinitely many solutions of (4.1), we select one obtained by using a solenoidal extension similar to the ones introduced in Sect. 2. We consider a cutoff function $\chi \in C^\infty (\overline{R})$ with $0\le \chi \le 1$ such that

$$\begin{aligned}\begin{aligned} \chi (x_1,x_2)={\left\{ \begin{array}{ll} 1 \quad &{}\text{ in } \quad [-\tau , \tau ]\times [h-\delta _b, h+\delta _t],\\ 0 \quad &{}\text{ in } \quad \Omega _h \setminus \left( [-2\tau , 2\tau ]\times \left[ h-\delta _b- \tfrac{\varepsilon _b(h)}{2}, h+\delta _t + \tfrac{\varepsilon _t(h)}{2}\right] \right) ,\\ \chi ^0(x_1) \quad &{}\text{ in }\quad ([-2\tau ,-\tau ]\cup [\tau ,2\tau ])\times [h-\delta _b, h+\delta _t], \\ C^\infty \text{-completion } \quad &{}\text{ elsewhere }. \end{array}\right. } \end{aligned} \end{aligned}$$

We put $w=\nabla ^\perp (x_1 \chi )$. Clearly $w\in H^1(\Omega _h)$ satisfies (4.1) and $\textrm{supp} \ w \subseteq \Omega _w= \Omega _{w,b} \cup \Omega _{w,c} \cup \Omega _{w,t}$ with

$$\begin{aligned} \begin{aligned} \Omega _{w,b}:=[-2\tau ,2\tau ]\times \left[ h-\delta _b- \tfrac{\varepsilon _b(h)}{2}, h-\delta _b\right]&,\qquad \Omega _{w,c}:=[-2\tau ,2\tau ]\times [h-\delta _b, h+\delta _t],\\ \Omega _{w,t}:=[-2\tau ,2\tau ]\times&\left[ h+\delta _t, h+\delta _t + \tfrac{\varepsilon _t(h)}{2}\right] . \end{aligned} \end{aligned}$$

Moreover, from the definition of $\chi$ it follows that w and its $x_1$ and $x_2$-derivatives are uniformly bounded with respect to h in $\Omega _{w,c}$, while in $\Omega _{w,b}$

$$\begin{aligned} \begin{aligned}|w|\le C (1&+(\varepsilon _b(h))^{-1}), \quad |\partial _1 w|\le (1+(\varepsilon _b(h))^{-1}),\\ {}&|\partial _2 w|\le ((\varepsilon _b(h))^{-1}+(\varepsilon _b(h))^{-2}) \end{aligned}\end{aligned}$$

(4.3)

and in $\Omega _{w,t}$

$$\begin{aligned} \begin{aligned}|w|\le C (1&+(\varepsilon _t(h))^{-1}), \quad |\partial _1 w|\le (1+(\varepsilon _t(h))^{-1}),\\ {}&|\partial _2 w|\le ((\varepsilon _t(h))^{-1}+(\varepsilon _t(h))^{-2}). \end{aligned} \end{aligned}$$

(4.4)

$B_h$ close to $\Gamma _b$. We consider the case when h is close to $-H+\delta _b$; hence, $\varepsilon _b(h)$ is close to zero. This implies that $\varepsilon _t(h)\ge 1$ and the bounds in (4.4) become uniform. Choosing in (4.2) the previously constructed w, we observe that the integrals in the right-hand side are defined only on $\Omega _w$. Let us split these integrals over the regions $\Omega _{w,b}$, which is shrinking as $\varepsilon _b(h)$ goes to zero, and $\Omega _w\setminus \Omega _{w,b}$. On the one hand, Hölder inequality and (2.7) yield

$$\begin{aligned} \begin{aligned}&\left| \ \int \limits _{\Omega _{w} \setminus \Omega _{w,b}} u\cdot \nabla u \cdot w + \mu \int \limits _{\Omega _{w} \setminus \Omega _{w,b}} \nabla u : \nabla w \right| \\ {}&\le C \Vert u\Vert ^2_{H^1(\Omega _h}\Vert w\Vert _{L^\infty (\Omega _{w} \setminus \Omega _{w,b})}+\mu \Vert \nabla u\Vert _{L^2(\Omega _h)}\Vert \nabla w \Vert _{L^2(\Omega _{w} \setminus \Omega _{w,b})} \\ {}&\le C(\Vert u\Vert ^2_{H^1(\Omega _h)}+\Vert u\Vert _{H^1(\Omega _h)}) \le C\lambda \end{aligned} \end{aligned}$$

(4.5)

for $\lambda \in [0,\Lambda _0]$, using that w and its derivatives are uniformly bounded with respect to h in $\Omega _{w} {\setminus } \Omega _{w,b}$. On the other hand, since $w\equiv 0$ in $\Omega ^0_{w, b}:=[-2\tau ,2\tau ]\times [-H,h-\delta _b-\tfrac{\varepsilon _b(h)}{2}]$ and $u_{|_{\Gamma _b}}=0$, Poincaré inequality for u in $\Omega _{w, b}\cup \Omega ^0_{w, b}$, the Hölder inequality and (2.7) yield

$$\begin{aligned} \begin{aligned}&\left| \ \int \limits _{\Omega _{w,b}} u\cdot \nabla u \cdot w \right| =\left| \ \int \limits _{\Omega _{w,b}\cup \Omega ^0_{w,b}} u\cdot \nabla u \cdot w \right| \\ {}&\le \varepsilon _b(h) \Vert \nabla u\Vert ^2_{L^2(\Omega _{w,b}\cup \Omega ^0_{w,b})} \Vert w\Vert _{L^\infty (\Omega _{w,b})} \le C\Vert u\Vert ^2_{H^1(\Omega _h)} \le C\lambda \end{aligned} \end{aligned}$$

(4.6)

and

$$\begin{aligned} \left| \ \int \limits _{\Omega _{w,b}} \nabla u : \nabla w\right| \le \Vert u\Vert _{H^1(\Omega _h)}\Vert \nabla w\Vert _{L^2(\Omega _{w,b})}\le C(\varepsilon _b(h))^{-3/2}\lambda , \end{aligned}$$

(4.7)

for $\lambda \in [0,\Lambda _0]$, using that $\Vert w\Vert _{L^\infty (\Omega _{w,b})}\le C (\varepsilon _b(h))^{-1}$ and $\Vert \nabla w\Vert _{L^2(\Omega _{w,b})}\le C (\varepsilon _b(h))^{-3/2}$ for $\varepsilon _b(h)$ close to zero, due to (4.3).

Putting together (4.5)-(4.7), then there exists $\eta _b>0$ sufficiently small such that, for any $(\lambda ,h)\in [0,\Lambda _0]\times (-H+\delta _b, -H+\delta _b+\eta _b),$

$$\begin{aligned} |\mathcal {L}(\lambda , h)|\le C (\varepsilon _b(h))^{-3/2} \lambda . \end{aligned}$$

(4.8)

We remark that the same blow-up rate in (4.8) could be obtained without taking advantage of Poincaré inequality in (4.6) but using directly $u\in H^1\subset L^4$. This idea, however, will be crucial to obtain a better blow-up rate for the lift in the case when the body is close to $\Gamma _t$, that we now analyze.

$B_h$ close to $\Gamma _t$. We consider the case when h is close to $H-\delta _t$; hence, $\varepsilon _t(h)$ is close to zero. Analogously to what done in the previous case, we split the integrals over the regions $\Omega _{w,t}$, which is shrinking as $\varepsilon _t(h)$ goes to zero, and $\Omega _w\setminus \Omega _{w,t}$. On the one hand, Hölder inequality yields

$$\begin{aligned}\begin{aligned}&\left| \ \int \limits _{\Omega _w\setminus \Omega _{w,t}} u\cdot \nabla u \cdot w + \mu \int \limits _{\Omega _w\setminus \Omega _{w,t}} \nabla u : \nabla w\right| \\ {}&\le C \Vert u\Vert ^2_{H^1(\Omega _h)}\Vert w\Vert _{L^\infty (\Omega _w\setminus \Omega _{w,t})}+\mu \Vert \nabla u\Vert _{L^2(\Omega _h)}\Vert \nabla w \Vert _{L^2(\Omega _w\setminus \Omega _{w,t})} \\ {}&\le C( \Vert u\Vert ^2_{H^1(\Omega _h)}+\Vert u\Vert _{H^1(\Omega _h)}) \end{aligned} \end{aligned}$$

using that w and its derivatives are uniformly bounded with respect to h in $\Omega _{w} \setminus \Omega _{w,t}$. On the other hand, since $w\equiv 0$ in $\Omega ^0_{w, t}:=[-2\tau ,2\tau ]\times [h+\delta _t+\tfrac{\varepsilon _t(h)}{2}, H]$ and $u=v+s$ with $v_{|_{\Gamma _t}}=0$, Poincaré inequality for v in $\Omega _{w,t}\cup \Omega ^0_{w,t}$ and Hölder inequality yield

$$\begin{aligned} \begin{aligned}&\left| \ \int \limits _{\Omega _{w,t}} u\cdot \nabla u \cdot w \right| = \left| \ \int \limits _{\Omega _{w,t}\cup \Omega ^0_{w,t}} v\cdot \nabla u \cdot w + \int \limits _{\Omega _{w,t}\cup \Omega ^0_{w,t}} s\cdot \nabla u \cdot w\right| \\ {}&\le \varepsilon _t(h) \Vert \nabla v\Vert _{L^2(\Omega _h)} \Vert \nabla u\Vert _{L^2(\Omega _h)}\Vert w\Vert _{L^\infty (\Omega _{w,t})} + \Vert s\Vert _{L^2(\Omega _h)}\Vert \nabla u\Vert _{L^2(\Omega _h)}\Vert w\Vert _{L^\infty (\Omega _{w,t})}\\ {}&\le C\Vert \nabla v \Vert _{L^2(\Omega _h)}\Vert u \Vert _{H^1(\Omega _h)} + C\Vert s\Vert _{L^2(\Omega _h)}\Vert u\Vert _{H^1(\Omega _h)}(\varepsilon _t(h))^{-1} \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \left| \ \int \limits _{\Omega _{w,t}} \nabla u : \nabla w\right| \le \Vert u \Vert _{H^1(\Omega _h)}\Vert \nabla w\Vert _{L^2(\Omega _{w,t})}\le \Vert u \Vert _{H^1(\Omega _h)}(\varepsilon _t(h))^{-3/2}, \end{aligned}$$

using that $\Vert w\Vert _{L^\infty (\Omega _{w,t})}\le C (\varepsilon _t(h))^{-1}$ and $\Vert \nabla w\Vert _{L^2(\Omega _{w,t})}\le C (\varepsilon _t(h))^{-3/2}$ for $\varepsilon _t(h)$ close to zero, due to (4.4). Now we shall distinguish the cases $U=1$ and $U=0$. When $U=1$, using (2.7), (2.27) and (2.30) we obtain, for $\lambda \in [0,\Lambda _0]$,

$$\begin{aligned} \begin{aligned}&\left| \,\, \int \limits _{\Omega _w\setminus \Omega _{w,t}} u\cdot \nabla u \cdot w + \mu \int \limits _{\Omega _w\setminus \Omega _{w,t}} \nabla u : \nabla w \right| \le C(\varepsilon _t(h))^{-3}\lambda \end{aligned} \end{aligned}$$

(4.9)

and

$$\begin{aligned} \left| \,\, \int \limits _{\Omega _{w,t}} u\cdot \nabla u \cdot w \right| \le C(\varepsilon _t(h))^{-3} \lambda , \quad \left| \,\, \int \limits _{\Omega _{w,t}} \nabla u : \nabla w \right| \le C (\varepsilon _t(h))^{-3}\lambda . \end{aligned}$$

(4.10)

When $U=0$, using (2.7) and (2.32), we obtain, for $\lambda \in [0,\Lambda _0]$,

$$\begin{aligned} \left| \,\, \int \limits _{\Omega _w\setminus \Omega _{w,t}} u\cdot \nabla u \cdot w + \mu \int \limits _{\Omega _w\setminus \Omega _{w,t}} \nabla u : \nabla w \right| \le C\lambda \end{aligned}$$

(4.11)

and

$$\begin{aligned} \left| \,\, \int \limits _{\Omega _{w,t}} u\cdot \nabla u \cdot w\right| \le C(\varepsilon _t(h))^{-1}\lambda , \ \ \ \left| \,\, \int \limits _{\Omega _{w,t}} \nabla u : \nabla w \right| \le C(\varepsilon _t(h))^{-3/2}\lambda . \end{aligned}$$

(4.12)

Putting together (4.9)-(4.12), then there exists $\eta _t>0$ sufficiently small such that, for $(\lambda ,h)\in [0,\Lambda _0]\times (H-\delta _t-\eta _t, H-\delta _t),$

$$\begin{aligned} |\mathcal {L}(\lambda , h)|\le C\max \{(\varepsilon _t(h))^{-3/2},U (\varepsilon _t(h))^{-3}\}\lambda . \end{aligned}$$

(4.13)

For $h\in [-H+\delta _b + \eta _b, H-\delta _t-\eta _t]$, $\varepsilon _b(h)$ and $\varepsilon _t(h)$ are uniformly bounded from below with respect to h. Therefore, by combining (4.8) and (4.13), there exists $C>0$ independent of h such that, for any $(\lambda ,h)\in [0,\Lambda _0]\times (-H+\delta _b, H-\delta _t)$,

$$\begin{aligned} |\mathcal {L}(\lambda , h)|\le C ((\varepsilon _b(h))^{-3/2}+ \max \{(\varepsilon _t(h))^{-3/2},U (\varepsilon _t(h))^{-3} \})\lambda . \end{aligned}$$

5 Proof of theorem 3.1

5.1 Continuity and monotonicity of the global force

In Sect. 3, we have defined the lift $\mathcal {L}(\lambda ,h)$ as a possibly multi-valued function of $(\lambda , h)\in [0,+\infty )\times (-H+\delta _b,H-\delta _t)$. Let f be the restoring force satisfying (3.2)-(3.3). Then, the global force acting on $B_h$ is the function $\phi : [0,+\infty )\times (-H+\delta _b,H-\delta _t) \rightarrow \mathbb {R}$ defined by

$$\begin{aligned} \phi (\lambda , h)=f(h) - \mathcal {L}(\lambda , h).\end{aligned}$$

(5.1)

We first focus on the $\lambda$-dependence by maintaining h fixed, and we prove the Lipschitz-continuity of the map $\lambda \mapsto \phi (\lambda , h)$.

Proposition 5.1

Let $\overline{h}=H-\max \{\delta _b,\delta _t\}$. There exist $\overline{\lambda }>0$ and $h^*\in (0, \overline{h})$ such that $\lambda \mapsto \phi (\lambda , h)$ is Lipschitz continuous in $[0,\overline{\lambda })$ for all $h\in [-h^*, h^*]$.

Proof

To begin, let us take $\overline{\lambda }$ and $h^*$ sufficiently small so that Theorem 2.2 guarantees the uniqueness for (2.4) whenever $\lambda < \overline{\lambda }$ and $|h|\le h^*$ (see Fig. 3). Hence, $\mathcal {L}(\lambda , h)$ is a one-valued function on $[0,\overline{\lambda })\times [-h^*, h^*]$. Since f does not depend on $\lambda$, we only need to show that $\lambda \mapsto \mathcal {L}(\lambda ,h)$ is Lipschitz continuous in a neighborhood of $\lambda =0$, possibly smaller than $[0, \overline{\lambda })$.

For $\lambda _1, \lambda _2\in [0,\overline{\lambda })$ consider, respectively, the solutions $(u(\lambda _1), p(\lambda _1))$ and $(u(\lambda _2), p(\lambda _2))$ to (2.4). Let

$$\begin{aligned} v:= u(\lambda _1) - u(\lambda _2), \qquad q:= p(\lambda _1) - p(\lambda _2), \end{aligned}$$

(5.2)

so that (v, q) satisfies

$$\begin{aligned} \begin{aligned}-\mu \Delta v+v\cdot \nabla v+\nabla q&=-v\cdot \nabla u(\lambda _2)-u(\lambda _2)\cdot \nabla v,\qquad \nabla \cdot v=0\quad \text { in }\quad \Omega _h,\\ v_{|_{\Gamma _t}}=(\lambda _{ 1}-\lambda _{ 2} )Ue_1&,\ v_{|_{\Gamma _l}}=(\lambda _{ 1}-\lambda _{ 2} )V_\text {in}(x_2)e_1,\ v_{|_{\Gamma _r}}=(\lambda _{ 1}-\lambda _{ 2} )V_\text {out}(x_2)e_1,\\ {}&\qquad \qquad v_{|_{\partial B_h}}=v_{|_{\Gamma _b}}=0. \end{aligned} \end{aligned}$$

(5.3)

Let $v_\lambda :=v-s_\lambda$, where $s_\lambda \in W^{1,\infty }(\Omega _h)\cap H^2(\Omega _h)$ is a solenoidal extension of v that can be constructed as s in (2.24) and, hence, it satisfies the estimates (2.25), namely

$$\begin{aligned} \begin{array}{rl} \Vert \nabla s_\lambda \Vert _{L^2(\Omega _h)}\le C_h|\lambda _1-\lambda _2|,\quad &{} \Vert \Delta s_\lambda \Vert _{L^2(\Omega _h)} \le C_h|\lambda _1-\lambda _2|,\\ \Vert s_\lambda \Vert _{L^\infty (\Omega _h)}\le C_h|\lambda _1-\lambda _2|,\quad &{} \Vert s_\lambda \cdot \nabla s_\lambda \Vert _{L^2(\Omega _h)}\le C_h|\lambda _{ 1}-\lambda _{ 2} |^2. \end{array} \end{aligned}$$

(5.4)

We then rewrite (5.3) as

$$\begin{aligned} -\mu \Delta v_\lambda + v_\lambda \cdot \nabla v_\lambda + \nabla q =g,\quad \nabla \cdot v_\lambda =0\quad \text{ in }\quad \Omega _h, \qquad {v_\lambda }_{|_{\partial \Omega _h}}=0, \end{aligned}$$

(5.5)

where

$$\begin{aligned} g:=\mu \Delta s_\lambda -v\cdot \nabla (u(\lambda _2)+s_\lambda )-u(\lambda _2)\cdot \nabla v+s_\lambda \cdot \nabla s_\lambda -s_\lambda \cdot \nabla v. \end{aligned}$$

From Theorem 2.2, we know that $v,u(\lambda _2)\in H^2(\Omega _h)\hookrightarrow L^\infty (\Omega _h)$, so that $g\in L^2(\Omega _h)$. Moreover,

$$\begin{aligned} \Vert g\Vert _{L^2(\Omega _h)}&\le \mu \Vert \Delta s_\lambda \Vert _{L^2(\Omega _h)} +\big (\Vert \nabla u(\lambda _2)\Vert _{L^2(\Omega _h)} +\Vert \nabla s_\lambda \Vert _{L^2(\Omega _h)}\big )\Vert v\Vert _{L^\infty (\Omega _h)}\\&\quad +\Vert u(\lambda _2)\Vert _{L^\infty (\Omega _h)}\Vert \nabla v\Vert _{L^2(\Omega _h)}+\Vert s_\lambda \cdot \nabla s_\lambda \Vert _{L^2(\Omega _h)} +\Vert s_\lambda \Vert _{L^\infty (\Omega _h)}\Vert \nabla v\Vert _{L^2(\Omega _h)}\\&\le C_h|\lambda _1-\lambda _2| +C_h(\lambda _2+|\lambda _1-\lambda _2|\big )\Vert v\Vert _{H^2(\Omega _h)}\\&\quad +C_h\lambda _2\Vert v\Vert _{H^2(\Omega _h)}+C_h|\lambda _{ 1}-\lambda _{ 2} |^2 +C_h|\lambda _{ 1}-\lambda _{ 2} |\cdot \Vert v\Vert _{H^2(\Omega _h)}, \end{aligned}$$

where we used Hölder inequality (first step), the estimates (2.7)-(2.8)-(5.4) and the embeddings $H^2\hookrightarrow H^1,L^\infty$ (second step). Thus, by extending the solution as in the proof of Theorem  2.2, recalling [14] and applying [5, Theorem IV.5.1] to (5.5), we obtain

$$\begin{aligned} \Vert v_\lambda \Vert _{H^2(\Omega _h)}+\Vert q\Vert _{H^1(\Omega _h)}\le C_h|\lambda _1-\lambda _2| +C_h\big (\lambda _2+|\lambda _1-\lambda _2|\big )\Vert v\Vert _{H^2(\Omega _h)}. \end{aligned}$$

(5.6)

Hence, there exists a possibly smaller $\overline{\lambda }>0$ such that if $\lambda _1, \lambda _2 \in [0,\overline{\lambda })$, the second term in the right-hand side of (5.6) can be absorbed in the left-hand side and

$$\begin{aligned} \Vert v_\lambda \Vert _{H^2(\Omega _h)} + \Vert q\Vert _{H^1(\Omega _h)} \le C_h|\lambda _1-\lambda _2|, \end{aligned}$$

(5.7)

for some $C_h>0$ also depending on $\overline{\lambda }$. Since the lift (3.1) is linear with respect to u and p, we have

$$\begin{aligned} \mathcal {L}(\lambda _1,h)-\mathcal {L}(\lambda _2,h)= -e_2 \cdot \int \limits _{\partial B_h}\mathbb {T}(v,q) n \end{aligned}$$

with v and q defined in (5.2). Therefore, using the Trace Theorem and (5.7), we infer that, for any $\lambda _1,\lambda _2\in [0,\overline{\lambda })$ and a fixed $h\in [-h^*,h^*]$, we have

$$\begin{aligned} \begin{aligned} |\mathcal {L}(\lambda _1, h)-\mathcal {L}(\lambda _2,h)|&\le C_h\left( \Vert \nabla v\Vert _{L^1(\partial B_h)} + \Vert q\Vert _{L^1(\partial B_h)}\right) \\&\le C_h\left( \Vert v\Vert _{H^2(\Omega _h)} + \Vert q\Vert _{H^1( \Omega _h)}\right) \le C_h|\lambda _1-\lambda _2|. \end{aligned} \end{aligned}$$

This shows that $\lambda \mapsto \mathcal {L}(\lambda , h)$ is Lipschitz continuous in $[0,\overline{\lambda })$ for all $h\in [-h^*,h^*]$. $\square$

We now focus on the h-dependence of $\phi$ by maintaining $\lambda$ fixed. Although we prove a slightly stronger result, we state:

Proposition 5.2

Let $\overline{h}=H-\max \{\delta _b,\delta _t\}$. There exist $h_0\in (0,h^*]$ and $\lambda _0\in (0, \overline{\lambda }]$ (see Proposition 5.1) such that $h\mapsto \phi ( \lambda , h)$ is continuous and strictly increasing in $[-h_0, h_0]$ for all $\lambda \in [0,\lambda _0)$.

Proof

Recall that $R=(-L,L)\times (-H,H)$. Let $0<r_1<r_2$ and $D_{r_i}(0)$ be the open disk centered at (0, 0) with radius $r_i$. Choose $h_0\in (0, h^*)$ in such a way that $B_h\subset D_{r_1}(0)\subset D_{r_2}(0)\subset R$ whenever $|h|\le h_0$; in later steps, we may need to choose a possibly smaller $h_0$ that, however, we continue calling $h_0$. Let $\sigma \in W^{2,\infty }(R, \mathbb {R}^2)$ be defined by

$$\begin{aligned} \sigma (x_1,x_2)= F(|x|) e_2 , \end{aligned}$$

(5.8)

with $F\equiv 1$ in $[0,r_1]$, $F\equiv 0$ in $[r_2, +\infty )$ and $F\in W^{2,\infty }(r_1,r_2)$ is the polynomial of third degree such that $F(r_1)=1$ and $F(r_2)=F'(r_1)=F'(r_2)=0$. For $h\in [-h_0, h_0]$, with $h_0$ small, we view the fluid domain $\Omega _h$ as a variation of $\Omega _0$ via the diffeomorphism $\textrm{Id}+h\sigma$, that is,

$$\begin{aligned} \Omega _h=(\textrm{Id}+h\sigma )(\Omega _0). \end{aligned}$$

In particular, $\partial B_h = \partial B_0 + he_2$ with unit outer normal vector $n(h)=n(0)\circ (\textrm{Id}+ he_2)$. Let J(h) denote the Jacobian matrix of the diffeomorphism $\textrm{Id} + h\sigma$, that is,

$$\begin{aligned} J(h)=I + h \frac{F'(|x|)}{|x|}\left( \begin{matrix} 0&{}0\\ x_1&{}x_2 \end{matrix}\right) \end{aligned}$$

with I the $2\times 2$ identity matrix. Fixing $\lambda \in [0,\overline{\lambda })$, the lift in (3.1) can be written as

$$\begin{aligned} \mathcal {L}(\lambda , h)=-e_2\cdot \int \limits _{\partial B_0+he_2}\mathbb {T}(u(h), p(h))n(h) \end{aligned}$$

with $\mathbb {T}(u(h), p(h))=\mathbb {T}(u( \lambda , h), p( \lambda , h))$. Letting

$$\begin{aligned} U( h )= u(h)\circ (\textrm{Id} + h\sigma ), \quad P(h )= p(h )\circ (\textrm{Id} + h\sigma ) \end{aligned}$$

with $\sigma$ as in (5.8), we transform the moving boundary integral into a fixed boundary integral, namely

$$\begin{aligned} \mathcal {L}(\lambda , h)=-e_2\cdot \int \limits _{\partial B_0} \mathbb {T}(U(h),P(h)) (n(0)\circ (\textrm{Id}+he_2)). \end{aligned}$$

Note that $(U(0), P(0))=(u(0), p(0))$. We now claim that

$$\begin{aligned} h\mapsto (U(h),P(h))\in H^2(\Omega _0) \times H^1(\Omega _0) \text{ belongs } \text{ to } C^1(-h_0, h_0). \end{aligned}$$

(5.9)

To this end, let $M(h)=(J^{-1}(h))^T$ and we rewrite (2.4) as

$$\begin{aligned} \begin{aligned}&-\mu \nabla \cdot (|\det J(h)|M^T(h) M(h)\nabla U(h))\quad \\ {}&+ U(h)\cdot |\det J(h)|M(h)\nabla U(h) + \nabla \cdot (|\det J(h)| M(h)P(h) ) =0 \quad&\text { in } \quad \Omega _0,\\&\ |\det J(h)| M(h)\nabla \cdot U(h) =0 \quad&\text { in } \quad \Omega _0, \end{aligned} \end{aligned}$$

complemented with the same boundary conditions. This can also be expressed as

$$\begin{aligned} \mathcal {H}(h,U(h), P(h))=0 \end{aligned}$$

(5.10)

where $\mathcal {H}:(-h_0,h_0)\times H^2(\Omega _0)\times H^1(\Omega _0) \rightarrow L^2(\Omega _0)\times H^1(\Omega _0)$ is defined by $\mathcal {H}(h, \xi , \varpi )=(\mathcal {H}_1(h, \xi , \varpi ), \mathcal {H}_2(h, \xi , \varpi ))$ with

$$\begin{aligned} \begin{aligned} \mathcal {H}_1(h, \xi , \varpi )=&-\mu \nabla \cdot (|\det J(h)|M^T(h) M(h)\nabla \xi )\quad \\&+ \xi \cdot |\det J(h)|M(h)\nabla \xi + \nabla \cdot (|\det J(h)| M(h)\varpi ),\\ \mathcal {H}_2(h, \xi , \varpi )=&\ |\det J(h)| M(h)\nabla \cdot \xi . \end{aligned} \end{aligned}$$

(5.11)

Due to the expression (5.8), we are able to compute $|\det J(h)|M(h)$ and $|\det J(h)|M^T(h)M(h)$ explicitly at second order for $h\rightarrow 0$. In fact,

$$\begin{aligned} \begin{aligned} |\det J(h)|&= 1 + h \frac{F'(|x|)}{|x|}x_2,\\ M(h)&= I +\frac{h}{|\det J(h)|} \frac{F'(|x|)}{|x|}\left( \begin{matrix} 0 &{} -x_1\\ 0 &{} -x_2 \end{matrix}\right) =I +h \frac{F'(|x|)}{|x|}\left( \begin{matrix} 0 &{} -x_1\\ 0 &{} -x_2 \end{matrix}\right) + O(h^2) \end{aligned} \end{aligned}$$

yield

$$\begin{aligned} \begin{aligned} |\det J(h)|M(h)&= I + h \frac{F'(|x|)}{|x|} \left( \begin{matrix}x_2&{}{}-x_1\\ 0&{}{}0\end{matrix}\right) =: I + h R_0,\\ |\det J(h)| M^T(h)M(h)&= I + h \frac{F'(|x|)}{|x|} \left( \begin{matrix} x_2 &{}{} -x_1\\ -x_1&{}{} -x_2 \end{matrix}\right) + h^2 (F'(|x|))^2\left( \begin{matrix} 0&{}{}0\\ 0&{}{}1 \end{matrix}\right) +O(h^3)\\ {}&=: I + h R_1 + h^2 R_2 +O(h^3), \end{aligned} \end{aligned}$$

(5.12)

where $O(h^3)$ contains terms having at least third order with respect to h as $h\rightarrow 0$. Note that the expression of $|\det J(h)|M(h)$ in (5.12) is exact and obtained without any Taylor expansion for $h\rightarrow 0$. We have that $\mathcal {H}$ is $C^1$ in a neighborhood of (0, U(0), P(0)) since the mappings $h\mapsto \det J(h)$ and $h\mapsto M(h)$ are $C^1(-h_0,h_0)$ with values in $C^1(R, \mathbb {R}^4)$.

For $h\in (-h_0, h_0)$, we consider the linearized operator $\Upsilon = D_{(\xi , \varpi )}\mathcal {H} (h, U(h), P(h))$ defined through the Jacobian matrix of $\mathcal {H}$. For any

$$\begin{aligned} (\chi , \Pi )\in \mathcal {X}\times \mathcal {Y}:=(H^2(\Omega _0)\cap H^1_0(\Omega _0))\times (H^1(\Omega _0)\cap L^2_0(\Omega _0)), \end{aligned}$$

we have $\Upsilon (\chi , \Pi )=( \Upsilon _1(\chi , \Pi ),\Upsilon _2(\chi , \Pi ) )$ with

$$\begin{aligned}\begin{aligned} \Upsilon _1( \chi , \Pi )=&-\mu \nabla \cdot (|\det J(h)|M^T(h) M(h)\nabla \chi ) + \chi \cdot |\det J(h)|M(h)\nabla U(h) \\ {}&+ U(h) \cdot |\det J(h)|M(h)\nabla \chi + \nabla \cdot (|\det J(h)| M(h)\Pi ),\\ \Upsilon _2( \chi , \Pi )=&|\det J(h)| M(h)\nabla \cdot \chi . \end{aligned} \end{aligned}$$

The linear operator $\Upsilon$ is bounded from $\mathcal {X}\times \mathcal {Y}$ into $L^2(\Omega _0)\times \mathcal {Y}$. To show that $\Upsilon$ is an isomorphism, given $(\varphi _1, \varphi _2)\in L^2(\Omega _0)\times \mathcal {Y}$, we have to prove that there exists a unique solution $(\chi , \Pi )\in \mathcal {X}\times \mathcal {Y}$ to

$$\begin{aligned} \begin{aligned}&-\mu \Delta \chi + \chi \cdot \nabla U(h)+ U(h) \cdot \nabla \chi + \nabla \Pi \\ {}&+ h \left( -\mu \nabla \cdot R_1 \nabla \chi +\chi \cdot R_0 \nabla U(h) + U(h)\cdot R_0\nabla \chi + \nabla \cdot (R_0 \Pi ) \right) \\ {}&-h^2 \mu \nabla \cdot R_2 \nabla \chi + O(h^3)= \varphi _1\quad&\text { in } \, \Omega _0, \\&\nabla \cdot \chi + h R_0 \nabla \cdot \chi = \varphi _2 \quad&\text { in } \ \Omega _0. \end{aligned} \end{aligned}$$

This linear elliptic problem admits a unique solution provided that

$$\begin{aligned} |h|<h_0\qquad \text{ and } \quad \Vert U(h)\Vert _{H^2(\Omega _0)}< r \end{aligned}$$

for $h_0, r>0$ small enough. For $|h|<h_0$ and $\sigma$ as in (5.8), we have

$$\begin{aligned} \begin{aligned} c\Vert u(h)\Vert _{H^2(\Omega _h)}\le&\Vert U(h)\Vert _{H^2(\Omega _0)}\le C\Vert u(h)\Vert _{H^2(\Omega _h)},\\ c\Vert p(h)\Vert _{H^1(\Omega _h)}\le&\Vert P(h)\Vert _{H^1(\Omega _0)}\le C\Vert p(h)\Vert _{H^1(\Omega _h)}, \end{aligned} \end{aligned}$$

(5.13)

with constants $0<c\le C$ independent of h. Then, by taking $\lambda \in [0,\overline{\lambda })$, the bound (2.8), where the constant $C_h$ is uniformly bounded for $|h|<h_0$, yields the needed smallness condition for U(h), so that $\Upsilon$ is an isomorphism. Therefore, by applying the Implicit Function Theorem to (5.10), we conclude (5.9).

Moreover, the derivatives $U'(h)$ and $P'(h)$, whose existence follows from (5.9), satisfy

$$\begin{aligned} \Upsilon (U'(h), P'(h))= - \partial _h \mathcal {H} (h,U(h), P(h)). \end{aligned}$$

(5.14)

From (5.12), we know that for any h (resp. $h\rightarrow 0$)

$$\begin{aligned} \frac{d}{dh}(|\det J(h)| M(h))=R_0, \quad \frac{d}{dh}(|\det J(h)| M^T(h)M(h))=R_1+2hR_2 + O(h^2). \end{aligned}$$

Then, recalling the definition (5.11), (5.14) and the fact that $\Upsilon$ is an isomorphism imply that $(U'(h), P'(h))$ is uniquely determined by the linear elliptic problem

$$\begin{aligned} \begin{aligned}&-\mu \Delta U'(h) +U'(h)\cdot \nabla U(h) +U(h)\cdot \nabla U'(h)+ \nabla P'(h) \\ {}&= S_0(U(h), P(h)) + hS_1(U'(h), P'(h), U(h))+O(h^2)&\text { in } \ \Omega _0, \\&\ \nabla \cdot U'(h) = -R_0 \nabla \cdot U(h) - h R_0 \nabla \cdot U'(h) \quad&\text { in } \ \Omega _0,\\&(U'(h), P'(h))\in \mathcal {X}\times \mathcal {Y}, \end{aligned} \end{aligned}$$

(5.15)

with

$$\begin{aligned}\begin{aligned} S_0(U(h), P(h))=&\mu \nabla \cdot R_1 \nabla U(h) - U(h)\cdot R_0 U(h) - \nabla \cdot (R_0 P(h)), \\ S_1(U'(h), P'(h), U(h))=&\mu \nabla \cdot (R_1 \nabla U'(h) + 2R_2\nabla U(h))- U'(h)\cdot R_0 \nabla U(h)\\&- U(h)\cdot R_0 \nabla U'(h) - \nabla \cdot (R_0 P'(h)). \end{aligned} \end{aligned}$$

For $h\in (-h_0,h_0)$, with $h_0$ small, we have

$$\begin{aligned}\begin{aligned}&\Vert U'(h)\Vert _{H^2(\Omega _0)} + \Vert P'(h)\Vert _{H^1(\Omega _0)} \\ {}&\le C( \Vert U'(h)\cdot \nabla U(h) +U(h) \cdot \nabla U'(h) + S_0( U(h),P(h))\Vert _{L^2(\Omega _0)} + \Vert R_0\nabla \cdot U(h)\Vert _{H^1(\Omega _0)}). \end{aligned} \end{aligned}$$

Since $(U(h),P(h))\in H^2(\Omega _0)\times H^1(\Omega _0)$ due to (5.13) and Theorem 2.2, we bound the right-hand side of the above expression as

$$\begin{aligned}\begin{aligned}&\Vert U'(h)\cdot \nabla U(h)+ U(h)\cdot \nabla U'(h)\Vert _{L^2(\Omega _0)}\le C \Vert \nabla U'(h)\Vert _{L^2(\Omega _0)}\Vert U(h)\Vert _{H^2(\Omega _0)},\\ {}&\Vert S_0( U(h), P(h))\Vert _{L^2(\Omega _0)}+ \Vert R_0\nabla \cdot U(h)\Vert _{H^1(\Omega _0)} \le C(\Vert U(h)\Vert _{H^2(\Omega _0)} + \Vert P(h)\Vert _{H^1(\Omega _0)}),\end{aligned} \end{aligned}$$

where in the second inequality we used that $\sigma \in W^{2,\infty }(R, \mathbb {R}^2)$, see (5.8). Testing the first equation in (5.15) with $U'(h)$, using (5.13) and (2.13)-(2.14) yield

$$\begin{aligned}\begin{aligned} \Vert \nabla U'(h)\Vert _{L^2(\Omega _0)}&\le C(\Vert U(h)\Vert _{H^1(\Omega _0)}+\Vert U(h)\Vert ^2_{H^1(\Omega _0)} + \Vert P(h)\Vert _{L^2(\Omega _0)} )\\ {}&\le C (\Vert U(h)\Vert _{H^1(\Omega _0)}+\Vert U(h)\Vert ^2_{H^1(\Omega _0)}). \end{aligned} \end{aligned}$$

Summarizing, we obtain

$$\begin{aligned} \begin{aligned}&\Vert U'(h)\Vert _{H^2(\Omega _0)} + \Vert P'(h)\Vert _{H^1(\Omega _0)}\\ {}&\le C\left( \Vert U(h)\Vert _{H^2(\Omega _0)}(1+\Vert U(h)\Vert _{H^1(\Omega _0)}+\Vert U(h)\Vert ^2_{H^1(\Omega _0)}) + \Vert P(h)\Vert _{H^1(\Omega _0)}\right) \\ {}&\le C(\lambda + \lambda ^3)\le C\lambda \end{aligned} \end{aligned}$$

(5.16)

for any $\lambda \in [0,\overline{\lambda })$, where in the second inequality we used (5.13) and (2.7)-(2.8).

Finally, we estimate the variation in the lift for small values of h, say $|h|< h_0$. By taking $h_1,h_2\in (-h_0,h_0)$, from the trace theorem we have

$$\begin{aligned}\begin{aligned}| \mathcal {L}(\lambda , h_1) - \mathcal {L}(\lambda , h_2) |&=\left| \ \int \limits _{\partial B_0} \mathbb {T}(U(h_1),P(h_1)) (n(0)\circ (\text {Id}+h_1e_2) )- \mathbb {T}(U(h_2),P(h_2)) (n(0)\circ (\text {Id}+h_2e_2) )\right| \\ {}&\le \int \limits _{\partial B_0}| \mathbb {T}(U(h_1),P(h_1)) - \mathbb {T}(U(h_2),P(h_2))| \\ {}&\quad + \int \limits _{\partial B_0} | \mathbb {T}(U(h_2),P(h_2))| \cdot |n(0)\circ (\text {Id} + h _1e_2)-n(0)\circ (\text {Id} + h_2 e_2)|\\ {}&\le C(\Vert U(h_1)- U(h_2)\Vert _{H^2(\Omega _0)}+ \Vert P(h_1)-P(h_2)\Vert _{H^1(\Omega _0)}) \\ {}&\quad +C(\Vert U(h_2)\Vert _{H^2(\Omega _0)}+ \Vert P(h_2)\Vert _{H^1(\Omega _0)})|h_1-h_2|. \end{aligned} \end{aligned}$$

Then, (5.16) and the mean value theorem yield

$$\begin{aligned}\begin{aligned}&| \mathcal {L}(\lambda , h_1) - \mathcal {L}(\lambda , h_2) |\\ {}&\le C\lambda |h_1-h_2| + C(\Vert u(h_2)\Vert _{H^2(\Omega _{h_2})}+ \Vert p(h_2)\Vert _{H^1(\Omega _{h_2})})|h_1-h_2|\le C\lambda |h_1-h_2| \end{aligned} \end{aligned}$$

using (5.13) and (2.8) in $\Omega _{h_2}$. Then, the monotonicity property (3.2) ensures that, if $-h_0<h_2< h_1< h_0$,

$$\begin{aligned}\begin{aligned} \phi (\lambda , h_1) - \phi (\lambda , h_2)&= f( h_1) - f ( h_2) - \mathcal {L}(\lambda , h_1) + \mathcal {L}(\lambda ,h_2) \ge (\gamma -C\lambda )(h_1-h_2). \end{aligned} \end{aligned}$$

There exists $\lambda _0\in (0,\overline{\lambda }]$ such that $\gamma -C\lambda _0\ge \gamma /2$. Therefore, $h\mapsto \phi (\lambda , h)$ is continuous and strictly increasing in $[-h_0,h_0]$ (with a possible smaller $h_0$) for all $\lambda \in [0,\lambda _0).$ $\square$

5.2 Conclusion of the proof

Let $(u(\lambda ,h), p(\lambda , h))$ be a solution to (2.4), and let $\phi (\lambda , h)$ be the corresponding global force in (5.1). Then, the triple (u, p, h) is a solution to (3.4) if and only if

$$\begin{aligned} (u(\lambda ,h), p(\lambda , h))\, \hbox {solves (2.4) and}\, \phi (\lambda ,h)=0. \end{aligned}$$

Therefore, Theorem 3.1 follows once we prove:

Proposition 5.3

Let $\phi$ be as in (5.1) and $(\lambda _0,h_0)$ be as in Proposition 5.2. Then, there exist $\Lambda _1\in (0,\lambda _0]$ and a unique $\mathfrak {h}\in C^0[0,\Lambda _1)$ such that, for all $\lambda \in [0,\Lambda _1)$, $\phi (\lambda , h)=0$ if and only if $h=\mathfrak {h}(\lambda ).$ Moreover, $\Vert \mathfrak {h}\Vert _{L^\infty (0, \Lambda _1)}\le h_0$.

Proof

We prove the result in two steps, namely by analyzing the behavior of $\phi$ in two different subregions of $[0,\lambda _0)\times (-H+\delta _b, H-\delta _t)$.

We start by considering the case when |h| is close to 0. Let again $\overline{h}=H-\max \{\delta _b,\delta _t\}$. We claim that there exists $\widetilde{\lambda }\in (0,\lambda _0]$ and a unique $\mathfrak {h}\in C^0[0,\widetilde{\lambda })$ such that

$$\begin{aligned} \forall (\lambda ,h)\in [0, \widetilde{\lambda })\times [-h_0,h_0]\qquad \phi (\lambda , h)=0\ \Longleftrightarrow \ h=\mathfrak {h}(\lambda ). \end{aligned}$$

(5.17)

To this end, we notice that Theorem 2.2 implies that, when $\lambda =0$, the unique solution to (2.4) is $(u,p)=(0,0)$, regardless of the value of $h\in (-H+\delta _b, H-\delta _t)$. Hence, $\phi (0,0)=0$. Moreover, by Proposition 5.2 we know that $h\mapsto \phi (0,h)$ is continuous and strictly increasing in $[-h_0,h_0]$. These two facts imply that

$$\begin{aligned} \phi (0,-h_0)<0<\phi (0,h_0). \end{aligned}$$

(5.18)

In turn, by Proposition 5.1 we know that $\lambda \mapsto \phi (\lambda ,h)$ is continuous in $[0,\overline{\lambda })$ for all $h\in [-h_0,h_0]$. By (5.18) and by compactness, we then infer that there exists $\widetilde{\lambda }\in (0,\lambda _0]$ such that

$$\begin{aligned} \phi (\lambda ,-h_0)<0<\phi (\lambda ,h_0)\qquad \forall \lambda \in [0,\widetilde{\lambda }) \end{aligned}$$

(5.19)

and, by invoking again Proposition 5.2, that $h\mapsto \phi (\lambda ,h)$ is continuous and strictly increasing in $[-h_0,h_0]$ for all $\lambda \in [0,\widetilde{\lambda })$. Together with (5.19), this implies that for all $\lambda \in [0,\widetilde{\lambda })$ there exists a unique $\mathfrak {h}(\lambda )\in [-h_0,h_0]$ such that $\phi (\lambda ,\mathfrak {h}(\lambda ))=0$. This defines the function $\lambda \mapsto \mathfrak {h}(\lambda )$ in the interval $[0,\widetilde{\lambda })$. Its continuity follows by the (separated) continuities proved in Propositions 5.1 and 5.2. The proof of (5.17) is so complete.

We now claim that there exists $\Lambda _1\in (0,\widetilde{\lambda }]$ such that

$$\begin{aligned} \phi ( \lambda ,h)\ne 0\qquad \forall ( \lambda ,h) \in [0, \Lambda _1)\times \Big [(-H+\delta _b, H-\delta _t)\setminus [-h_0,h_0]\Big ]. \end{aligned}$$

(5.20)

Recall that in this set $\phi (\lambda , h)$ may be multi-valued, see Theorem 3.2. In order to prove (5.20), from (3.2)-(3.3) we know that there exists $K_0\in (0,K]$ such that

$$\begin{aligned} \begin{aligned} f(h) \le -K_0(\varepsilon _b(h))^{-3/2} \qquad&\text{ for } \quad h\in (-H+ \delta _b,-h_0),\\ f(h)\ge K_0\max \{ (\varepsilon _t(h))^{-3/2}, U(\varepsilon _t(h))^{-3}\} \qquad&\text{ for } \quad h\in (h_0, H-\delta _t), \end{aligned} \end{aligned}$$

(5.21)

while from Theorem 3.2 there exists (a different) $C>0$ such that

$$\begin{aligned} \begin{aligned} \mathcal {L}(\lambda ,h) \ge -C(\varepsilon _b(h))^{-3/2} \ \lambda \qquad&\text{ for } \quad h\in (-H+ \delta _b,-h_0), \\ \mathcal {L}(\lambda ,h) \le C\max \{(\varepsilon _t(h))^{-3/2}, U(\varepsilon _t(h))^{-3}\} \ \lambda \qquad&\text{ for } \quad h\in (h_0, H-\delta _t). \end{aligned} \end{aligned}$$

(5.22)

Gathering (5.21)-(5.22) together yields

$$\begin{aligned} \begin{aligned} \phi (\lambda , h)\le ( -K_0 +C\lambda )(\varepsilon _b(h))^{-3/2} \qquad&\text{ for } \quad h\in (-H+ \delta _b,-h_0), \\ \phi (\lambda ,h)\ge ( K_0-C\lambda )\max \{(\varepsilon _t(h))^{-3/2}, U(\varepsilon _t(h))^{-3} \} \qquad&\text{ for } \quad h\in (h_0, H-\delta _t). \end{aligned} \end{aligned}$$

Then, there exists $\Lambda _1\in (0,\widetilde{\lambda }]$ such that (5.20) holds and the statement of the proposition follows from (5.17) and (5.20). $\square$

Remark 5.4

In fact, the proof of (5.20) shows that if $\lambda >0$ is small, then

$$\begin{aligned} h_0<h<H-\delta _t\ \Longrightarrow \ \phi (\lambda ,h)>0\quad \text{ and }\quad -H+\delta _b<h<-h_0\ \Longrightarrow \ \phi (\lambda ,h)<0. \end{aligned}$$

From a physical point of view, this means that, for small Reynolds numbers, the global force $\phi =\phi (\lambda , h)$ in (5.1) pushes downwards the body if $B_h$ is close to the upper boundary $\Gamma _t$, whereas it pushes the body upwards if $B_h$ is close to the lower boundary $\Gamma _b$.

6 Symmetric configuration

We consider here a symmetric framework for (3.4), that is, when

$$\begin{aligned} (x_1,x_2)\in \partial B \iff (x_1,-x_2)\in \partial B \end{aligned}$$

and the boundary data are symmetric with respect to the line $x_2=0$. Therefore, the FSI problem (3.4) is modified on $\Gamma _b$ and reads

$$\begin{aligned} {}&{} -\mu \Delta u +u\cdot \nabla u + \nabla p = 0,\qquad \nabla \cdot u =0\quad \text { in }\quad \Omega _h\nonumber \\ \quad u_{|_{\partial B_h}}=0,&\quad u_{|_{\Gamma _b}}= u_{|_{\Gamma _t}}=\lambda Ue_1,\quad u_{|_{\Gamma _l}}=\lambda V_\text {in}(x_2)e_1,\quad u_{|_{\Gamma _r}}=\lambda V_\text {out}(x_2)e_1,\nonumber \\{}&{} \qquad \qquad \qquad f(h)=-e_2\cdot \int \limits _{\partial B_h} \mathbb {T}(u,p)n,\end{aligned}$$

(6.1)

with $\lambda \ge 0$, $U\in \{0,1\}$ (up to normalization). Here, $V_\textrm{in},V_\textrm{out}\in W^{2,\infty }(-H,H)$ are now even functions satisfying

$$\begin{aligned} V_\textrm{in} (\pm H)= V_\textrm{out}(\pm H)=U,\qquad \int \limits _{-H}^H V_\textrm{in}(x_2) \textrm{d}x_2=\int \limits _{-H}^H V_\textrm{out}(x_2) \textrm{d}x_2. \end{aligned}$$

(6.2)

In this symmetric framework, $\delta _b=\delta _t=\delta$ and $h\in (-H+\delta , H-\delta ).$ Then, we prove that the unique curve $\mathfrak {h}(\lambda )$ found in Theorem 3.1 reduces to $\mathfrak {h}(\lambda )\equiv 0$, namely that the unique equilibrium position is symmetric. Again, we expect this position to be stable, at least for small $\lambda .$

Theorem 6.1

Let $V_\textrm{in}$, $V_\textrm{out}\in W^{2,\infty }(-H,H)$ be even functions satisfying (6.2) and $f\in C^0(-H+\delta , H-\delta )$ satisfying $f(0)=0$ and (3.2)-(3.3) with $\delta _b=\delta _t=\delta$. There exists $\Lambda _1 >0$ such that for $\lambda \in [0,\Lambda _1)$ the FSI problem (6.1) admits a unique strong solution $(u(\lambda ,h), p(\lambda ,h),h)\in H^2(\Omega _h)\times H^1(\Omega _h)\times (-H+\delta , H-\delta )$ given by

$$\begin{aligned} \big (u^0(\lambda ,0), p^0(\lambda ,0),0\big ), \end{aligned}$$

where $(u^0(\lambda ,0), p^0(\lambda ,0))$ is the unique solution to the first two lines in (6.1) for $h=0$ and has the following symmetries:

$$\begin{aligned} u^0_1(x_1,-x_2)=u^0_1(x_1, x_2), \quad u^0_2(x_1,-x_2)=-u^0_2(x_1, x_2), \quad p^0(x_1,-x_2)=p^0(x_1,x_2). \end{aligned}$$

Proof

The first step is to obtain the counterpart of Theorem 2.2. The case $U=0$ is already included in the original statement. When $U=1$, we construct the cutoff functions $\zeta _l$ and $\zeta _r$ in a slightly different way with Fig. 4 replaced by Fig. 6. We define the solenoidal extension as in (2.24), which satisfies the boundary conditions in (6.1).

Fig. 6

Cutoff functions $\zeta _l$ (left) and $\zeta _r$ (right) on $\overline{ R}$ when $U=1$ for the symmetric configuration

With this construction, the refined bound (2.7) is replaced by

$$\begin{aligned} \Vert u\Vert _{H^1(\Omega _h)} \le C ((\varepsilon _b(h))^{-3/2}+(\varepsilon _t(h))^{-3/2})\lambda . \end{aligned}$$

Hence, in both cases $U\in \{0,1 \}$, by arguing as in the proof of Theorem 2.2, we infer that there exists $\Lambda =\Lambda (h)>0$ such that for $\lambda \in [0,\Lambda (h))$ the solution (u, p) to

$$\begin{aligned} {}&{} -\mu \Delta u+u\cdot \nabla u + \nabla p = 0,\qquad \nabla \cdot u =0\quad \text { in }\quad \Omega _h\nonumber \\ u_{|_{\partial B_h}}=0,&\quad {} u_{|_{\Gamma _b}}= u_{|_{\Gamma _t}}=\lambda Ue_1,\quad u_{|_{\Gamma _l}}=\lambda V_\text {in}(x_2)e_1,\quad u_{|_{\Gamma _r}}=\lambda V_\text {out}(x_2)e_1, \end{aligned}$$

(6.3)

is unique for any $h\in (-H+\delta ,H-\delta )$. This proves the counterpart of Theorem 2.2.

In particular, for $h=0$ there exists a unique solution $(u^0,p^0)$ to (6.3) in $\Omega _0$. Since $\Omega _0$ is symmetric with respect to the line $x_2=0$, the couple $(u^*, p^*): \Omega _0 \rightarrow \mathbb {R}^2\times \mathbb {R}$ defined by

$$\begin{aligned}\begin{aligned} u_1^*(x_1,x_2)= u^0_1(x_1, -x_2), \quad u_2^*(x_1,x_2)= -u^0_2(x_1, -x_2),\quad p^*(x_1, x_2)= p^0(x_1,-x_2), \end{aligned} \end{aligned}$$

also satisfies (6.3) for $h=0$ (see also [10]). Therefore, by uniqueness $(u^0, p^0)=(u^*, p^*)$ is also symmetric and, thanks to all these symmetries, we obtain

$$\begin{aligned} \mathcal {L}(\lambda , 0)=-e_2\cdot \int \limits _{\partial B_0} \mathbb {T}(u^0(\lambda , 0), p^0(\lambda , 0))n= 0, \end{aligned}$$

which implies

$$\begin{aligned} \phi (\lambda ,0)= f(0)=0 \qquad \text{ for } \quad \lambda \in [0,\Lambda (h)). \end{aligned}$$

(6.4)

From Theorem 3.1, we know that there exist $\Lambda _1>0$ and a unique curve $\mathfrak {h}\in C^0[0,\Lambda _1)$ such that for $\lambda \in [0,\Lambda _1)$ the unique solution to (6.1) is given by

$$\begin{aligned} (u(\lambda ,\mathfrak {h}(\lambda )), p(\lambda ,\mathfrak {h}(\lambda )),\mathfrak {h}(\lambda )). \end{aligned}$$

Thanks to (6.4), $\mathfrak {h}(\lambda )\equiv 0$ and this solution coincides with $(u^0(\lambda ,0), p^0(\lambda ,0),0)$. $\square$

7 An application: equilibrium positions of the deck of a bridge

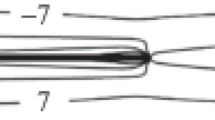
A suspension bridge is usually erected starting from the anchorages and the towers. Then, the sustaining cables are installed between the two couples of towers and the hangers are hooked to the cables. Once all these components are in position, they furnish a stable working base from which the deck can be raised from floating barges. We refer to [18, Section 15.23] for full details. The deck segments are put in position one aside the other (see Fig. 7, left) and have the shape of rectangles while their cross-section resembles to smoothened irregular hexagons (see Fig. 7, right) that satisfy (2.1).

Fig. 7

Left: erection of a suspension bridge. Right: sketch of a cross section

This cross section B plays the role of the obstacle in (2.4) while $\Omega _h$ is the region filled by the air. This region can be either be a virtual box around the deck of the bridge or a wind tunnel around a scaled model of the bridge. In both cases, we may refer to inflow and outflow also as windward and leeward, respectively: $\lambda V_\textrm{in}e_1$ represents the laminar horizontal windward while $\lambda V_\textrm{out}e_1$ is the leeward. Typically, the higher is the altitude the stronger is the wind. Therefore, in this application we consider specific laminar shear flows, which are the Couette flows. Thus, the inflow and outflow now read

$$\begin{aligned} V_\textrm{in}(x_2)= V_\textrm{out}(x_2)=\frac{U}{2H}(x_2+H) \qquad \text{ for }\qquad x_2\in [-H,H], \end{aligned}$$

(7.1)

and satisfy (2.3). The windward creates both vertical and torsional displacements of the deck. However, the cross section of the suspension bridge is also subject to some elastic restoring forces tending to maintain the deck in its original position $B_0$. These forces are of three different kinds. There is an upwards restoring force due to the elastic action of both the hangers and the sustaining cables of the bridge. The hangers behave as nonlinear springs which may slacken [1, 9-VI] so that they have no downwards action and they be nonsmooth. There is the weight of the deck which acts constantly downwards: this is why there is no odd requirement on the restoring force considered in the model. There is also a nonlinear resistance to both elastic bending and stretching of the whole deck for which B merely represents a cross-section. Moreover, since the boundary of the channel R is virtual and our physical model breaks down in case of collision of B with $\partial R$, we require that there exists an “unbounded force” preventing collisions.

Overall, the position of B depends on both the displacement parameter h and the angle of rotation $\theta$ with respect to the horizontal axis. With the addition of this second degree of freedom, we have $B=B_{h,\theta }$ and $\Omega =\Omega _{h,\theta }$. A “plastic” regime leading to the collapse of the bridge is reached when $\theta =\pm \tfrac{\pi }{4}$ (see [1]) since the sustaining cables of the bridge attain their maximum elastic tension. The strong point of the analysis carried out in this paper is that it applies independently of the part of $\partial B$ closest to $\partial R$. Therefore, for any $\theta \in (-\tfrac{\pi }{4}, \tfrac{\pi }{4})$, we can apply our general theory considering the family of bodies $B_{h,\theta }$ simply by adapting it to the rotating scenario. The only difference now is that, when the body is free to rotate, the collision with $\Gamma _b$ and $\Gamma _t$ occurs at $h=-H+\delta _b(\theta )$ and $h= H-\delta _t(\theta )$, where $\delta _b(\theta )$ and $\delta _t(\theta )$ are positive functions of $\theta$. For $\theta =0$, $\delta _b(0)$ and $\delta _t(0)$ are as in (2.2) while, for $\theta \ne 0$,

$$\begin{aligned} \delta _b(\theta ):= -\min _{(x_1,x_2)\in \partial B_{0,\theta }}x_2>0, \qquad \delta _t(\theta ):= \max _{(x_1,x_2)\in \partial B_{0,\theta }}x_2>0, \end{aligned}$$

both being independent of h. Due to the possible complicated shape of B, these functions are not easy to be determined explicitly. For this reason, we define the set of non-contact values of $(h,\theta )$ by

$$\begin{aligned} A=\{(h,\theta )\in (-H,H)\times (-\tfrac{\pi }{4}, \tfrac{\pi }{4}) \ : \ B_{h,\theta } \subset R \}. \end{aligned}$$

(7.2)

Clearly, $(0,0) \in A$ and $(h,\theta )\in \partial A$ if and only if $B_{h,\theta }\cap \partial R \ne \emptyset .$ We assume that, for some $K>0$, $f\in C^0(A)$ satisfies

$$\begin{aligned} \begin{aligned}&\limsup \limits _{ d( B_{h,\theta }, \Gamma _b)\rightarrow 0} \ f(h,\theta )(d( B_{h,\theta }, \Gamma _b))^{3/2}\le -K,\\ {}&\liminf \limits _{d( B_{h,\theta }, \Gamma _t)\rightarrow 0} \ \frac{f(h,\theta )}{\max \{(d( B_{h,\theta }, \Gamma _t))^{-3/2},U(d( B_{h,\theta }, \Gamma _t))^{-3}\}}\ge K, \end{aligned} \end{aligned}$$

(7.3)

where $d( \cdot , \cdot )$ is the distance function. Assumption (7.3) generalizes (3.3) taking into account the rotational degree of freedom. Moreover, we assume that

$$\begin{aligned} \begin{aligned}&\exists \gamma>0\quad \text{ s.t. }\quad \frac{f(h_1,\theta )-f(h_2, \theta )}{h_1-h_2}\ge \gamma \qquad \forall (h_1,\theta ),(h_2,\theta ) \in A,\\&f(0,0)=0, \qquad f(h,\theta )\theta >0 \quad \forall (h,\theta )\in A \quad \text{ with } \quad \theta \ne 0. \end{aligned} \end{aligned}$$

(7.4)

In fact, the second line in (7.4) is not mathematically needed, but, from a physical point of view, it states that the restoring force does not act at equilibrium and tends to maintain B in an horizontal position. A straightforward consequence of Theorem 3.1, in the case of the interaction between the wind and the deck of a suspension bridge, is the following:

Corollary 7.1

Let $V_\textrm{in}$, $V_\textrm{out}$ be as in (7.1) and $f\in C^0(A)$ satisfy (7.3)-(7.4). There exist $\Lambda _1>0$ and a unique $\mathfrak {h}\in C^0[0, \Lambda _1)$ such that, for $\lambda \in [0,\Lambda _1)$ and $\theta \in (-\tfrac{\pi }{4}, \tfrac{\pi }{4})$, the FSI problem (3.4) admits a unique solution $(u_\theta (\lambda ,h), p_\theta (\lambda ,h),h)\in H^2(\Omega _{h,\theta })\times H^1(\Omega _{h,\theta })\times (-H,H)$, with $(h,\theta )\in A$, given by

$$\begin{aligned} (u_\theta (\lambda ,\mathfrak {h}(\lambda )), p_\theta (\lambda ,\mathfrak {h}(\lambda )),\mathfrak {h}(\lambda )). \end{aligned}$$

Here, (3.4) is understood with h replaced by the couple $(h, \theta )$.

The deck of a suspension bridge, in particular its cross section, may have a nonsmooth boundary. If B is not $W^{2,\infty }$, but it is only Lipschitzian, Theorem 2.2 ceases to hold and we only know that (u, p) is a weak solution to (2.4) so that (3.1) does not hold in a “strong” sense. Indeed, since $u\in H^1(\Omega _h)$, see (2.7), we may rewrite the first equation in (2.4) as $-\mu \Delta u+\nabla p=f$ with $f\in L^q(\Omega _h)$ for all $q<2$. Hence, $f\in H^{-\epsilon }(\Omega _h)$ for any $\epsilon >0$. By applying [19, Theorem 7], we then deduce that $u\in H^{1+s}(\Omega _h)$ and $p\in H^s(\Omega _h)$ for all $s<1/2$, but, still, this does not allow to consider the trace of $\mathbb {T}(u,p)$ as an integrable function over $\partial B_h$. However, following [10] we may define the lift L through a generalized formula. Indeed, from $u \in H^1(\Omega _h)$ we know that $\mathbb {T}(u,p)\in L^2(\Omega _h)$ and, since $\Omega _h$ is a bounded domain, $\mathbb {T}(u,p)\in L^{3/2}(\Omega _h)$. Moreover, from the first equation in (2.4) we obtain $\nabla \cdot \mathbb {T}(u,p) \in L^{3/2}(\Omega _h)$. Therefore, $\mathbb {T}(u,p)\in E_{3/2}(\Omega _h):=\{f\in L^{3/2}(\Omega _h) \ | \ \nabla \cdot f\in L^{3/2}(\Omega _h)\}$. By Theorem III.2.2 in [5], we know that $\mathbb {T}(u,p)n_{|_{\partial \Omega _h}}\in W^{-2/3, 3/2}(\partial \Omega _h)$. Hence, if $\partial B_h$ is Lipschitzian and (u, p) is a weak solution to (2.4), then the lift exerted by the fluid over $B_h$ is

$$\begin{aligned} \mathcal {L}(\lambda ,h)=-e_2 \ \cdot \langle \mathbb {T}(u,p)n,1\rangle _{\partial B_h}, \end{aligned}$$

(7.5)

where $\langle \cdot ,\cdot \rangle _{\partial B_h}$ denotes the duality pairing between $W^{-2/3,3/2}(\partial B_h)$ and $W^{2/3, 3}(\partial B_h)$.