Fluid–structure system with boundary conditions involving the pressure

Abstract

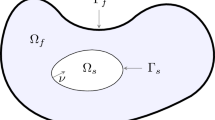
We study a coupled fluid–structure system involving boundary conditions on the pressure. The fluid is described by the incompressible Navier–Stokes equations in a 2D rectangular-type domain where the upper part of the domain is described by a damped Euler–Bernoulli beam equation. Existence and uniqueness of local strong solutions without assumptions of smallness on the initial data are proved.

Appendix

1.1 Steady Stokes equations

Consider the steady Stokes equations

$$\begin{aligned} \begin{aligned}&-\nu \Delta \mathbf{u }+ \nabla p={\mathbf{f }},\,\,\,\text {div }\mathbf{u }=0\,\text { in }\Omega _{0},\\&\mathbf{u }=\mathbf{g }\,\text { on }\Gamma _{0},\,\mathbf{u }=0\,\text { on }\Gamma _{b},\,u_2=0\,\text { and }\,p=h\,\text { on }\Gamma _{i,o},\\ \end{aligned} \end{aligned}$$

(5.1)

with $\mathbf{f }\in \mathbf{L }^{2}(\Omega _{0})$, $\mathbf{g }=(0,g)^{T}\in {\mathcal {H}}^{3/2}_{00}(\Gamma _{0})$ and $h\in H^{1/2}(\Gamma _{i,o})$. We prove in Theorem 5.4 the existence and uniqueness of a pair $(\mathbf{u },p)\in \mathbf{H }^{2}(\Omega _{0})\times H^{1}(\Omega _{0})$ solution to (5.1). An existence and uniqueness result for (5.1) with weaker data is given in Theorem 5.7. The non-homogeneous boundary condition on the pressure is handled directly with a lifting operator ${\mathcal {R}}\in {\mathcal {L}}(H^{1/2}(\Gamma _{i,o}),H^{1}(\Omega _{0}))$. For the non-homogeneous Dirichlet boundary condition, we use the following theorem.

Theorem 5.1

For all $\mathbf{g }=(0,g)^{T}\in {\mathcal {H}}^{3/2}_{00}(\Gamma _{0})$, the system

$$\begin{aligned} \begin{array}{l} \text {div }\mathbf{w }=0\,\text { in }\Omega _{0},\\ \mathbf{w }=\mathbf{g }\,\text { on }\Gamma _{0},\,\mathbf{w }=0\,\text { on }\Gamma _{b},\,w_2=0\,\text { on }\Gamma _{i,o},\\ \end{array} \end{aligned}$$

(5.2)

admits a solution $\mathbf{w }\in \mathbf{H }^{2}(\Omega _{0})$ satisfying the estimate

$$\begin{aligned} \left\| \mathbf{w }\right\| _{\mathbf{H }^{2}(\Omega _{0})}\le C\left\| \mathbf{g }\right\| _{{\mathcal {H}}^{3/2}_{00}(\Gamma _{0})}. \end{aligned}$$

Proof

We look for $\mathbf{w }$ under the form $\mathbf{w }=(-\partial _{2}\phi ,\partial _{1}\phi )^{T}$, which ensures the property $\text {div }\mathbf{w }=0$. The boundary conditions on $\mathbf{w }$ imply the following conditions on $\phi$

$$\begin{aligned} \begin{array}{lr} \partial _{2}\phi =0\text { and }\partial _{1}\phi =g\text { on }\Gamma _{0},\\ \frac{\partial \phi }{\partial \mathbf{n }}=\partial _{1}\phi =0\text { on }\Gamma _{i,o},\,\partial _{2}\phi =\partial _{1}\phi =0\text { on }\Gamma _{b}. \end{array} \end{aligned}$$

(5.3)

Let $\eta ^{0}_{e}$ be an $H^{3}({\mathbb {R}})$ extension of $\eta ^{0}$. We consider the change of variables

$$\begin{aligned} \psi ^{\pm } : {\left\{ \begin{array}{ll} \begin{array}{lr} {\mathbb {R}}^{2}\longrightarrow {\mathbb {R}}^{2}\\ (x,y)\mapsto (x,y\pm \eta ^{0}_{e}(x)).\\ \end{array} \end{array}\right. } \end{aligned}$$

Let ${\widehat{v}}$ be a function in $H^{3}({\mathbb {R}}^{2})$. Thanks to the $H^{3}$-regularity of $\eta ^{0}_{e}$, the function ${\widehat{v}}\circ \psi ^{\pm }$ is still in $H^{3}({\mathbb {R}}^{2})$. We search for $\phi$ solution to (5.3) under the form $\phi ={\widehat{\phi }}\circ \psi ^{-}$ with ${\widehat{\phi }}\in H^{3}((0,L)\times (-\infty ,1))$ satisfying

$$\begin{aligned} \begin{array}{lr} \partial _{2}{\widehat{\phi }}=0\text { and }\partial _{1}{\widehat{\phi }}={\widehat{g}}\text { on }\Gamma _{s},\\ \partial _{1}{\widehat{\phi }}=0\text { on }\Gamma _{i,o},\,{\widehat{\phi }}=0\text { on }(0,L)\times (-\infty ,1-\delta ), \end{array} \end{aligned}$$

(5.4)

with ${\widehat{g}}=g\circ \psi ^{+}$ and

$$\begin{aligned} \delta = {\left\{ \begin{array}{ll} \begin{array}{lr} \displaystyle \min _{x\in (0,L)}(1+\eta ^{0}(x))\text { if }\min _{x\in (0,L)}(1+\eta ^{0}(x))<1,\\ \displaystyle \alpha \text { if }\min _{x\in (0,L)}(1+\eta ^{0}(x))\ge 1,\\ \end{array} \end{array}\right. } \end{aligned}$$

(5.5)

for a fixed $\alpha \in (0,1)$. This condition is used to ensure that the function $\phi ={\widehat{\phi }}\circ \psi ^{-}$ is equal to zero near $\Gamma _{b}$, in order to fulfil the boundary conditions $\partial _{1}\phi =\partial _{2}\phi =0$ on $\Gamma _{b}$. To build ${\widehat{\phi }}$, we first search for ${\widehat{\phi }}_{o}$ such that

$$\begin{aligned} \begin{array}{lr} \frac{\partial {\widehat{\phi }}_{o}}{\partial \mathbf{n }}=0\text { on }\Gamma _{s}\cup \Gamma _{o},\\ {\widehat{\phi }}_{o}(x,y)=G(x,y)={\int }_{0}^{x}{\widehat{g}}(s)ds\text { for }(x,y)\in \Gamma _{s},\\ {\widehat{\phi }}_{o}=0\text { on }(0,L)\times (-\infty ,1-\delta ), \end{array} \end{aligned}$$

(5.6)

The boundary conditions on $\Gamma _{s}$ are handled directly thanks to a lifting and a symmetry argument is used to obtain the homogeneous Neumann boundary condition on $\Gamma _{o}$. We set

$$\begin{aligned} G^{*}: {\left\{ \begin{array}{ll} \begin{array}{lr} G^{*}(x,y)=G(x,y)\text { for }(x,y)\in \Gamma _{s},\\ G^{*}(x,y)=G(2L-x,y)\text { for }(x,y)\in (L,2L)\times \{1\}.\\ \end{array} \end{array}\right. } \end{aligned}$$

Denote by ${\widehat{g}}_{s}$ the odd extension of ${\widehat{g}}$ on $\Gamma _{s,s}=(0,2L)\times \{1\}$. As ${\widehat{g}}\in H^{3/2}_{00}(\Gamma _{s})$, the function ${\widehat{g}}_{s}$ belongs to $H^{3/2}(\Gamma _{s,s})$. Indeed, odd and even symmetries preserve the $H^1$-regularity (resp. $H^2$-regularity) for functions in $H^{1}_{0}(\Gamma _{0})$ (resp. in $H^{2}_{0}(\Gamma _{0})$); thus, by interpolation, the $H^{3/2}$-regularity is also preserved for functions in $H^{3/2}_{00}(\Gamma _{0})=[H^{1}_{0}(\Gamma _{0}),H^{2}_{0}(\Gamma _{0})]_{1/2}$.

As $\partial _{1}G^{*}(\cdot ,1)={\widehat{g}}_{s}(\cdot )$, we have $G^{*}\in H^{5/2}(\Gamma _{s,s})$. We still denote by $G^{*}$ a regular extension of $G^{*}$ on ${\mathbb {R}}\times \{1\}$. The lifting results in [18] in the case of the half-plan give a function ${\widehat{\phi }}_{1}\in H^{3}({\mathbb {R}}\times (-\infty ,1))$ such that ${\widehat{\phi }}_{1}=G^{*}$ and $\frac{\partial {\widehat{\phi }}_{1}}{\partial \mathbf{n }}=0$ on ${\mathbb {R}}\times \{1\}$. We then use cut-off functions to ensure that ${\widehat{\phi }}_{1}=0$ on $(0,2L)\times (-\infty ,1-\delta )$.

Introduce the symmetric function ${\widehat{\phi }}_{2}$ to ${\widehat{\phi }}$ with respect to the axis $x=L$ defined by ${\widehat{\phi }}_{2}(x,y)={\widehat{\phi }}_{2}(2L-x,y)$ for $(x,y)\in (0,2L)\times (-\infty ,1)$. As the Dirichlet boundary condition $G^{*}$ is symmetric, ${\widehat{\phi }}_{2}$ satisfies the same boundary conditions as ${\widehat{\phi }}_{1}$ on $\Gamma _{s,s}$. We finally set ${\widehat{\phi }}_{o}=\frac{{\widehat{\phi }}_{1}+{\widehat{\phi }}_{1,s}}{2}$. The function ${\widehat{\phi }}_{o}$ belongs to $H^{3}((0,2L)\times (-\infty ,1))$ and admits $x=L$ as an axis of symmetry. Hence, we have $\frac{\partial {\widehat{\phi }}_{o}}{\partial \mathbf{n }}=0$ on $\Gamma _{o}$ and the restriction on $(0,L)\times (-\infty ,1)$ is a solution to (5.6).

Using the same tools, we obtain a function ${\widehat{\phi }}_{i}\in H^{3}((0,L)\times (-\infty ,1))$ such that

$$\begin{aligned} \begin{array}{lr} \frac{\partial {\widehat{\phi }}_{i}}{\partial \mathbf{n }}=0\text { on }\Gamma _{s}\cup \Gamma _{i},\\ {\widehat{\phi }}_{i}(x,y)=G(x,y)={\int }_{0}^{x}{\widehat{g}}(s)ds\text { for }(x,y)\in \Gamma _{s},\\ {\widehat{\phi }}_{i}=0\text { on }(0,L)\times (-\infty ,1-\delta ). \end{array} \end{aligned}$$

(5.7)

Then, we combine ${\widehat{\phi }}_{o}$ and ${\widehat{\phi }}_{i}$. Let $\alpha$ be a function defined on [0, L] such that $\alpha =1$ near $\Gamma _{i}$, $\alpha =0$ near $\Gamma _{o}$ and $\alpha \in {\mathcal {C}}^{\infty }([0,L])$. The function ${\widehat{\phi }}$ defined by

$$\begin{aligned} {\widehat{\phi }}(x,y)=\alpha (x) {\widehat{\phi }}_{i}(x,y) + (1-\alpha (x)){\widehat{\phi }}_{o}(x,y)\text { for all }(x,y)\in (0,L)\times (-\infty ,1), \end{aligned}$$

is a solution to (5.4). Finally, the restriction to $\Omega _{0}$ of the function $\phi ={\widehat{\phi }}\circ \psi ^{-}$ is a solution to (5.3). Indeed,

$$\begin{aligned} \begin{array}{lr} \partial _{2}\phi =\partial _{2}{\widehat{\phi }}\circ \psi ^{-}=0\,\text { on }\Gamma _{0},\\ \partial _{1}\phi =\partial _{1}{\widehat{\phi }}\circ \psi ^{-} -\eta ^{0}_{x}\partial _{2}{\widehat{\phi }}\circ \psi ^{-}= \partial _{1}{\widehat{\phi }}\circ \psi ^{-}={\widehat{g}}\circ \psi ^{-}=g\text { on }\Gamma _{0},\\ \frac{\partial \phi }{\partial \mathbf{n }}=\partial _{1}\phi =0\text { on }\Gamma _{i,o},\,\partial _{2}\phi =\partial _{1}\phi =0\text { on }\Gamma _{b}. \end{array} \end{aligned}$$

and $\mathbf{w }=(-\partial _2 \phi ,\partial _1 \phi )^{T}$ is a solution of (5.2). We have $\mathbf{w }\in \mathbf{H }^{2}(\Omega _{0})$ and the estimate follows from the continuity of the lifting operator in [18]. $\square$

Let $\mathbf{w }\in \mathbf{H }^{2}(\Omega _{0})$ be the lifting of $\mathbf{g }$ given by Theorem 5.1 and $H={\mathcal {R}}(h)$. By setting $(\mathbf{v },q)=(\mathbf{u },p)-(\mathbf{w },H)$, the Stokes system (5.1) is equivalent to

$$\begin{aligned} \begin{aligned}&-\nu \Delta \mathbf{v }+\nabla q=\overline{\mathbf{f }},\,\,\,\,\text {div }\mathbf{v }=0\,\text { in }\Omega _{0},\\&\mathbf{v }=0\,\text { on }\Gamma _{d},\,\,\,v_{2}=0\,\text { and }q=0\,\text { on }\Gamma _{i,o},\\ \end{aligned} \end{aligned}$$

(5.8)

with $\overline{\mathbf{f }}=\mathbf{f }+\nu \Delta \mathbf{w }-\nabla H$. Using Green formula, one can derive the following variational formulation for (5.8).

Theorem 5.2

Let $(\mathbf{v },q)\in \mathbf{H }^{2}(\Omega _{0})\times H^{1}(\Omega _{0})$ be a solution to (5.8). Then, $\mathbf{v }$ satisfies the variational formulation:

Find $\mathbf{v }\in V$ such that $\quad \displaystyle \nu {\int }_{\Omega _{0}}\nabla \mathbf{v }:\nabla \varvec{\varphi }={\int }_{\Omega _{0}}\overline{\mathbf{f }}\cdot \varvec{\varphi }\text { for all }\varvec{\varphi }\in V.\quad (\star )$

Theorem 5.3

The variational formulation $(\star )$ admits a unique solution $\mathbf{v }\in V$. Moreover, there exists a pressure ${\mathcal {Q}}\in L^{2}(\Omega _{0})$, unique up to an additive constant, such that $\displaystyle -\nu \Delta \mathbf{v }+\nabla {\mathcal {Q}} = \overline{\mathbf{f }}\,$ in $\mathbf{H }^{-1}$.

The pressure ${\mathcal {Q}}$ is mentioned as a pressure associated with $\mathbf{v }$.

Proof

As the only constant in V is the null function, we can use a Poincaré inequality to prove that the bilinear form

$$\begin{aligned} a(\mathbf{v },\varvec{\varphi })=\nu {\int }_{\Omega _{0}}\nabla \mathbf{v }:\nabla \varvec{\varphi }, \end{aligned}$$

is coercive on V. Hence, the Lax–Milgram lemma gives us the existence of a unique solution $\mathbf{v }\in V$ to the variational formulation $(\star )$. For the pressure, we use the equality

$$\begin{aligned} \left\langle -\nu \Delta \mathbf{v }- \overline{\mathbf{f }},\varvec{\varphi } \right\rangle _{\mathbf{H }^{-1},\mathbf{H }^{1}_{0}}=0 \text {, for all }\varvec{\varphi }\in ({H}^{1}_{0}(\Omega _{0}))^{2}\text { such that }\text {div }\varvec{\varphi }=0, \end{aligned}$$

and [10, Chap 4, Theorem 2.3] to prove the existence of ${\mathcal {Q}}\in L^{2}(\Omega _{0})$, unique up to an additive constant and such that $-\nu \Delta \mathbf{v }+\nabla {\mathcal {Q}} = \overline{\mathbf{f }}$ in $\mathbf{H }^{-1}$. $\square$

We now state the main theorem of this section.

Theorem 5.4

For all $(\mathbf{f },\mathbf{g },h)\in \mathbf{L }^{2}(\Omega _{0})\times {\mathcal {H}}^{3/2}_{00}(\Gamma _0)\times H^{1/2}(\Gamma _{i,o})$, equation (5.1) admits a unique solution $(\mathbf{u },p)\in \mathbf{H }^{2}(\Omega _{0})\times H^{1}(\Omega _{0})$. This solution satisfies the estimate

$$\begin{aligned} \left\| \mathbf{u }\right\| _{\mathbf{H }^{2}(\Omega _{0})}+\left\| p\right\| _{H^{1}(\Omega _{0})}\le C(\left\| \mathbf{f }\right\| _{\mathbf{L }^{2}(\Omega _{0})}+ \left\| \mathbf{g }\right\| _{{\mathcal {H}}^{3/2}_{00}(\Gamma _0)}+ \left\| h\right\| _{H^{1/2}(\Gamma _{i,o})}). \end{aligned}$$

Proof

Let us work directly on the homogeneous system (5.8). We prove the existence of a unique pair $(\mathbf{v },q)\in \mathbf{H }^{2}(\Omega _{0})\times H^{1}(\Omega _{0})$ solution to this system. According to Theorems 5.2 and 5.3, $\mathbf{v }$ has to solve the variational formulation $(\star )$. Hence, we start with the solution of the variational formulation $(\star )$ and we prove that it is the solution to (5.8). The plan is the following:

• Step 1: We extend the variational formulation $(\star )$ on a larger domain $\Omega _{0,e}$ with a solution denoted by $\mathbf{v }_{e}$.

• Step 2: We prove that the solution $\mathbf{v }_{e}$ to this new variational formulation is in $\mathbf{H }^{2}$ in a neighbourhood of $\Gamma _{i}$.

• Step 3: We prove that the restriction of $\mathbf{v }_{e}$ to the initial domain $\Omega _{0}$ is the solution $\mathbf{v }$ to $(\star )$, which implies that $\mathbf{v }$ is $\mathbf{H }^{2}$ in a neighbourhood of $\Gamma _{i}$, and finally that $\mathbf{v }\in \mathbf{H }^{2}(\Omega _{0})$.

• Step 4: We prove that all the pressures associated with $\mathbf{v }$ are in $H^{1}(\Omega _{0})$ and are constant on $\Gamma _{i,o}$.

• Step 5: We conclude by taking the pressure satisfying $q=0$ on $\Gamma _{i,o}$, so that the pair $(\mathbf{v },q)$ is the unique solution to (5.8).

Step 1: Let $\eta ^{0}_{e}$ be the function defined by

$$\begin{aligned} \eta ^{0}_{e}: {\left\{ \begin{array}{ll} \begin{array}{lr} \eta ^{0}(x)\,\text { for all }x\in (0,L),\\ \eta ^{0}(-x)\,\text { for all }x\in (-L,0). \end{array} \end{array}\right. } \end{aligned}$$

We recall that $\eta ^{0}$ is in $H^{3}(0,L)$ and that $\eta ^{0}(0)=\eta ^{0}_{x}(0)=0$. Due to the even symmetry, we have $\eta ^{0}_{e}(0^{-})=\eta ^{0}_{e}(0^{+})=0$, $\eta ^{0}_{e,x}(0^{-})=\eta ^{0}_{e,x}(0^{+})=0$, $\eta ^{0}_{e,xx}(0^{-})=\eta ^{0}_{e,xx}(0^{+})$ and thus we obtain $\eta ^{0}_{e}\in H^{3}(-L,L)$ and the curve $\Gamma _{0,e}=\{(x,y)\in {\mathbb {R}}^{2}\mid x\in (-L,L),\,y=1+\eta ^{0}_{e}(x)\}$ is ${\mathcal {C}}^{2}$. We set $\Omega _{0,e}=\{(x,y)\in {\mathbb {R}}^{2}\mid x\in (-L,L),\,0<y<1+\eta ^{0}_{e}(x)\}$.

Let $\mathbf{v }_e$ be the solution to

$$\begin{aligned} \nu {\int }_{\Omega _{0,e}}\nabla \mathbf{v }_e:\nabla \psi ={\int }_{\Omega _{0,e}}\overline{\mathbf{f }}_e\cdot \psi \,\text { for all }\psi \in V_{e}, \end{aligned}$$

where

$$\begin{aligned}&V_{e}=\{\mathbf{v }\in \mathbf{H }^{1}(\Omega _{0,e})\mid \text {div }\mathbf{v }=0\text { in }\Omega _{0,e}, \,\mathbf{v }=0\text { on }\Gamma _{d,e}, \,v_2=0\text { on }\Gamma _{i,o,e}\},\\&\Gamma _{d,e}=(-L,L)\times \{0\}\cup \Gamma _{0,e},\,\,\,\Gamma _{i,e}=\{-L\} \times (0,1),\,\,\,\Gamma _{i,o,e}=\Gamma _{i,e}\cup \Gamma _{o},\\ \end{aligned}$$

and $\overline{\mathbf{f }}_e$ is the function defined by

$$\begin{aligned} \overline{\mathbf{f }}_e:{\left\{ \begin{array}{ll} \begin{aligned} \overline{\mathbf{f }}_e&{}=\overline{\mathbf{f }}\,\text { in }\Omega _{0},\\ \overline{\mathbf{f }}_e(x,y)&{}= \begin{pmatrix} 1&{}0\\ 0&{}-1\\ \end{pmatrix}\overline{\mathbf{f }}(-x,y)\,\text { for all }(x,y)\in \Omega _{0,s},\\ \end{aligned} \end{array}\right. } \end{aligned}$$

with $\Omega _{0,s}=\{(x,y)\in {\mathbb {R}}^{2}\mid x\in (-L,0),\,0<y<1+\eta ^{0}_{e}(x)\}$ .

Step 2: We use cut-off functions to prove the $\mathbf{H }^{2}$ regularity result near $\Gamma _{i}$. Let $\varphi$ be a function in ${\mathcal {C}}^{\infty }_{0}({\mathbb {R}}^{2})$ such that $\varphi =1$ on $\Omega _{\varphi ,1}$ and $\text {support}(\varphi )\subset \Omega _{\varphi ,2}$, with $\Omega _{\varphi ,1}$ and $\Omega _{\varphi ,2}$ two open sets with smooth boundaries such that $\overline{\Omega _{\varphi ,1}}\subset \overline{\Omega _{\varphi ,2}}\subset \Omega _{0,e}$ and $\Omega _{\varphi ,1}$ containing a neighbourhood of $\Gamma _i$.

Let ${\mathcal {Q}}_{e}$ be a pressure associated to $\mathbf{v }_{e}$. The pair $(\mathbf{v }_{c},q_{c})=(\varphi \mathbf{v }_{e},\varphi {\mathcal {Q}}_{e})$ satisfies, in $\mathbf{H }^{-1}(\Omega _{\varphi ,2})$,

$$\begin{aligned} -\nu \Delta \mathbf{v }_{c} +\nabla q_{c}=-\nu \Delta \varphi \mathbf{v }_{e} - 2\nu \nabla \mathbf{v }_{e}\text { }\nabla \varphi +{\mathcal {Q}}_{e}\nabla \varphi +\varphi \overline{\mathbf{f }}_e. \end{aligned}$$

Since $(\mathbf{v }_{c},q_{c})$ belongs to $\mathbf{H }^{1}_{0}(\Omega _{\varphi ,2})\times L^{2}(\Omega _{\varphi ,2})$, the previous equality implies that $(\mathbf{v }_{c},q_{c})$ is a solution to the following Stokes equations (in the usual variational sense)

$$\begin{aligned} \begin{aligned} -\nu \Delta \mathbf{v }_{c} +\nabla q_{c}&{}=-\nu \Delta \varphi \mathbf{v }_{e} - 2\nu \nabla \mathbf{v }_{e}\text { }\nabla \varphi +{\mathcal {Q}}_{e}\nabla \varphi +\varphi \overline{\mathbf{f }}_e\,\text { in }\Omega _{\varphi ,2},\\ \text {div }\mathbf{v }_{c}&=\mathbf{v }_{e}\cdot \nabla \varphi \,\text { in }\Omega _{\varphi ,2},\,\mathbf{v }_c=0\,\text { on }\partial \Omega _{\varphi ,2}. \end{aligned} \end{aligned}$$

(5.9)

We then use known results for Stokes equations with Dirichlet boundary conditions (see, for example, [10, Chap IV, Theorem 5.8]) to obtain $(\mathbf{v }_{c},q_{c})\in \mathbf{H }^{2}(\Omega _{\varphi ,2})\times H^{1}(\Omega _{\varphi ,2})$. As $(\mathbf{v }_{c},q_{c})$ is equal to $(\mathbf{v }_{e},{\mathcal {Q}}_{e})$ on $\Omega _{\varphi ,1}$, we obtain the regularity result for $(\mathbf{v }_{e},{\mathcal {Q}}_{e})$ in a neighbourhood of $\Gamma _{i}$.

Step 3: We want to prove that the restriction to $\Omega _{0}$ of $\mathbf{v }_{e}$ is the solution $\mathbf{v }$ to the variational formulation $(\star )$. Using the Lax–Milgram lemma, we know that $\mathbf{v }_{e}$ satisfies

$$\begin{aligned} \frac{1}{2}\nu {\int }_{\Omega _{0,e}}\vert \nabla \mathbf{v }_{e}\vert ^{2} - {\int }_{\Omega _{0,e}}\overline{\mathbf{f }}_e\cdot \mathbf{v }_{e}= \min _{\varvec{\varphi }\in V_{e}}\left( \frac{1}{2}\nu {\int }_{\Omega _{0,e}} \vert \nabla \varvec{\varphi }\vert ^{2}- {\int }_{\Omega _{0,e}}\overline{\mathbf{f }}_e\cdot \varvec{\varphi }\right) .\nonumber \\ \end{aligned}$$

(5.10)

Hence, using the symmetry properties of $\overline{\mathbf{f }}_e$ we can prove that the function $\mathbf{v }_s$ defined by

$$\begin{aligned} \mathbf{v }_s(x,y)=\begin{pmatrix} 1&{}0\\ 0&{}-1\\ \end{pmatrix}\mathbf{v }_{e}(-x,y)\,\text { for all }(x,y)\in \Omega _{0,e}, \end{aligned}$$

is also a solution to the minimization problem (5.10). As (5.10) admits a unique solution, we obtain that $\mathbf{v }_s=\mathbf{v }_{e}$. The symmetry properties and the regularity of $\mathbf{v }_{e}$ imply that $v_{e,2}=0$ on $\Gamma _{i}$. We can now prove that the restriction to $\Omega _{0}$ of $\mathbf{v }_{e}$ is the solution $\mathbf{v }$ to $(\star )$. Let $\varvec{\varphi }$ be a test function in V and denote by $\varvec{\varphi }_{e}$ the function defined by

$$\begin{aligned} \varvec{\varphi }_{e}:{\left\{ \begin{array}{ll} \begin{aligned} \varvec{\varphi }_{e}&{}=\varvec{\varphi }\text { on }\Omega _{0},\\ \varvec{\varphi }_{e}(x,y)&{}=\begin{pmatrix} 1&{}0\\ 0&{}-1\\ \end{pmatrix}\varvec{\varphi }(-x,y)\,\text { for all }(x,y)\in \Omega _{0,s}. \end{aligned} \end{array}\right. } \end{aligned}$$

Thanks to the condition $\varphi _{2}=0$ on $\Gamma _{i,o}$, we notice that $\varvec{\varphi }_{e}$ is in $\mathbf{H }^{1}(\Omega _{0,e})$ and more precisely in $V_{e}$. Hence, we can use $\varvec{\varphi }_{e}$ as a test function in the variational formulation satisfied by $\mathbf{v }_{e}$, we obtain

$$\begin{aligned} \nu {\int }_{\Omega _{0,e}}\nabla \mathbf{v }_{e}:\nabla \varvec{\varphi }_{e}={\int }_{\Omega _{0,e}} \overline{\mathbf{f }}_e\cdot \varvec{\varphi }_{e}. \end{aligned}$$

Using the symmetry properties of $\mathbf{v }_{e}$, $\varvec{\varphi }_{e}$ and $\overline{\mathbf{f }}_e$, we have

$$\begin{aligned} {\int }_{\Omega _{0,s}}\nabla \mathbf{v }_{e}:\nabla \varvec{\varphi }_{e}={\int }_{\Omega _{0}}\nabla \mathbf{v }_{e}:\nabla \varvec{\varphi }_{e}, \end{aligned}$$

and

$$\begin{aligned} {\int }_{\Omega _{0,s}}\overline{\mathbf{f }}_e\cdot \varvec{\varphi }_{e}={\int }_{\Omega _{0}} \overline{\mathbf{f }}_e\cdot \varvec{\varphi }_{e}. \end{aligned}$$

Hence,

$$\begin{aligned} \nu {\int }_{\Omega _{0}}\nabla \mathbf{v }_{e}:\nabla \varvec{\varphi }={\int }_{\Omega _{0}} \overline{\mathbf{f }}\cdot \varvec{\varphi }, \end{aligned}$$

for all $\varvec{\varphi }$ in V, which proves that the restriction to $\Omega _{0}$ of $\mathbf{v }_{e}$ is the solution $\mathbf{v }$ to the variational formulation $(\star )$. Hence, $\mathbf{v }$ is $\mathbf{H }^{2}$ in a neighbourhood of $\Gamma _{i}$. The same technique works for the boundary $\Gamma _{o}$, which implies the regularity result on the whole domain $\Omega _{0}$.

Step 4: Let ${\mathcal {Q}}$ be a pressure associated with $\mathbf{v }$. The regularity of $\mathbf{v }$ and the equality (in the sense of the distributions)

$$\begin{aligned} -\nu \Delta \mathbf{v }+ \nabla {\mathcal {Q}}=\overline{\mathbf{f }}, \end{aligned}$$

imply that ${\mathcal {Q}}$ belongs to $H^{1}(\Omega _{0})$. We now have to prove that ${\mathcal {Q}}$ is equal to a constant on $\Gamma _{i,o}$. Thanks to the regularity of $(\mathbf{v },{\mathcal {Q}})$, the equality $-\Delta \mathbf{v }+ \nabla {\mathcal {Q}}=\overline{\mathbf{f }}$ holds in $\mathbf{L }^{2}(\Omega _{0})$. For all $\varvec{\psi }$ in V, we have

$$\begin{aligned} {\int }_{\Omega _{0}}\mathbf{f }\cdot \varvec{\psi } ={\int }_{\Omega _{0}}(-\nu \Delta \mathbf{v }+ \nabla {\mathcal {Q}})\cdot \varvec{\psi }={\int }_{\Omega _{0}}\nu \nabla \mathbf{v }: \nabla \varvec{\psi } + {\int }_{\Gamma _{i,o}}{\mathcal {Q}}(\varvec{\psi }\cdot \mathbf{n }), \end{aligned}$$

and, using the definition of $\mathbf{v }$,

$$\begin{aligned} {\int }_{\Gamma _{i,o}}{\mathcal {Q}}(\varvec{\psi }\cdot \mathbf{n })=0. \end{aligned}$$

This implies that ${\mathcal {Q}}$ is constant on $\Gamma _{i,o}$. To see this, it is sufficient to prove that for all $\phi \in {\mathcal {C}}^{\infty }_{c}(\Gamma _{i,o})$ satisfying

$$\begin{aligned} {\int }_{\Gamma _{i,o}}\phi =0, \end{aligned}$$

there exists $\varvec{\psi }\in V$ such that $\varvec{\psi }\cdot \mathbf{n }=\phi$ on $\Gamma _{i,o}$. Let $\varvec{\phi }$ be the function defined by

$$\begin{aligned} \varvec{\phi }:{\left\{ \begin{array}{ll} \begin{aligned} \varvec{\phi }&{}=0 \text { on }\Gamma _{d},\\ \varvec{\phi }&{}=\begin{pmatrix} \phi \\ 0\\ \end{pmatrix} \text { on }\Gamma _{i,o}.\\ \end{aligned} \end{array}\right. } \end{aligned}$$

Using [13, Lemma 2.2], the equations

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{array}{rr} \begin{aligned} \text {div }\varvec{\psi }&{}=0 \\ \varvec{\psi }&{}=\varvec{\phi }\\ \end{aligned} &{} \begin{aligned} &{}\Omega _{0},\\ &{}\Gamma _{0},\\ \end{aligned} \end{array} \end{array}\right. } \end{aligned}$$

admit a solution $\varvec{\psi }$ in $\mathbf{H }^{1}(\Omega _{0})$. Such a $\varvec{\psi }$ belongs to V and satisfies $\varvec{\psi }\cdot \mathbf{n }=\phi$ on $\Gamma _{i,o}$. Hence, ${\mathcal {Q}}$ is constant on $\Gamma _{i,o}$.

Step 5: Among the pressures ${\mathcal {Q}}$ associated with $\mathbf{v }$, there exists a unique q in $H^{1}(\Omega _{0})$ satisfying $q=0$ in $\Gamma _{i,o}$ in the sense of the trace for Sobolev functions. The pair $(\mathbf{v },q)$ in $\mathbf{H }^{2}(\Omega _{0})\times H^{1}(\Omega _{0})$ is the unique solution to (5.8) and $(\mathbf{u },p)=(\mathbf{v },q)+(\mathbf{w },H)$ is the unique solution to (5.1). The estimate on $(\mathbf{u },p)$ follows from classical estimate for the Stokes equations (5.9) and Theorem 5.1 to estimate $\mathbf{w }$. $\square$

According to Theorem 5.4, the Stokes operator A associated with (5.1) with homogeneous boundary condition is defined by

$$\begin{aligned} {\mathcal {D}}(A)=\mathbf{H }^{2}(\Omega _{0})\cap V, \end{aligned}$$

and for all $\mathbf{u }\in {\mathcal {D}}(A)$, $A\mathbf{u }=\nu \Pi \Delta \mathbf{u }$.

Theorem 5.5

The operator $(A,{\mathcal {D}}(A))$ is the infinitesimal generator of an analytic semigroup on $\mathbf{V }^{0}_{n,\Gamma _{d}}(\Omega _{0})$. Moreover, we have ${\mathcal {D}}(A^{1/2})=V$.

Proof

The bilinear form associated with the operator A defined by

$$\begin{aligned} \forall (\mathbf{v },\varvec{\varphi })\in V\times V,\,\,\, a(\mathbf{v },\varvec{\varphi })=\nu {\int }_{\Omega _{0}}\nabla \mathbf{v }:\nabla \varvec{\varphi }, \end{aligned}$$

is continuous and coercive; hence, [7, Part 2, Theorem 2.2] proves that the operator A is the infinitesimal generator of an analytic semigroup. For the second part of the theorem, we have, for all $\mathbf{u }\in {\mathcal {D}}(A)$,

$$\begin{aligned} \left\| \mathbf{u }\right\| _{V}=\langle -A\mathbf{u },\mathbf{u }\rangle =\left\| (-A)^{1/2}\mathbf{u }\right\| _{\mathbf{V }^{0}_{n,\Gamma _{d}}(\Omega _{0})}. \end{aligned}$$

By density, the previous equality is still true for $\mathbf{u }\in V$, which concludes the proof. $\square$

We now want to study (5.1) for weaker data using transposition method. The following lemma, used to solve nonzero divergence Stokes equations, is needed to obtain weak estimates on the pressure in Theorem 5.6.

Lemma 5.1

For all $\Phi \in H^{1}_{0}(\Omega _{0})$, the system

$$\begin{aligned} \begin{array}{l} \text {div }\mathbf{w }=\Phi \,\text { in }\Omega _{0},\\ \mathbf{w }=0\,\text { on }\Gamma _{d},\,w_2=0\,\text { on }\Gamma _{i,o},\\ \end{array} \end{aligned}$$

(5.11)

admits a solution $\mathbf{w }\in \mathbf{H }^{2}(\Omega _{0})$ satisfying the estimate

$$\begin{aligned} \left\| \mathbf{w }\right\| _{\mathbf{H }^{2}(\Omega _{0})}\le C\left\| \Phi \right\| _{H^{1}_{0}(\Omega _{0})}. \end{aligned}$$

Proof

If $\Phi$ has a zero average, the result comes directly from [23, Chap II.2, Lemma 2.3.1]. This lemma gives the existence of a function $\mathbf{w }\in \mathbf{H }^{2}_{0}(\Omega _{0})$ such that $\text {div }\mathbf{w }=\Phi$. In the general case, the idea is to find a pair $(\mathbf{w }_{0},\Phi _{0})$ solution to (5.11), where $\Phi _{0}$ has a nonzero average, and to use it to come back to the previous framework.

Let $\delta >0$ be the constant defined by (5.5) in Theorem 5.1 and $\rho \in {\mathcal {C}}^{\infty }({\mathbb {R}})$ be a nonzero non-negative function compactly supported in $(0,\delta )$. Let $\theta \in {\mathcal {C}}^{\infty }(0,L)$ be such that $\theta =0$ near 0 and $\theta =1$ near L. Define $\mathbf{w }_{0}(x,y)=(\rho (y)\theta (x),0)^{T}$ for all $(x,y)\in \Omega _{0}$. The function $\mathbf{w }_{0}$ is smooth and satisfies the boundary conditions in (5.11). Finally, set $\Phi _{0}(x,y)=\text {div }\mathbf{w }_{0}(x,y)=\rho (y)\theta '(x)$ for all $(x,y)\in \Omega _{0}$ and remark that $\Phi _{0}\in H^{1}_{0}(\Omega _{0})$ and

$$\begin{aligned} {\int }_{\Omega _{0}}\rho (y)\theta '(x)dxdy={\int }_{0}^{\delta }\rho (y)dy>0. \end{aligned}$$

We look for a solution to (5.11) under the form $\mathbf{w }={\widetilde{\mathbf{w }}}+c\mathbf{w }_{0}$ with $c={\int }_{\Omega _{0}}\Phi /{\int }_{\Omega _{0}}\Phi _{0}$. The function ${\widetilde{\mathbf{w }}}$ needs to satisfy

$$\begin{aligned} \begin{array}{l} \text {div }{\widetilde{\mathbf{w }}}=\Phi -c\Phi _{0}\,\text { in }\Omega _{0},\\ {\widetilde{\mathbf{w }}}=0\,\text { on }\Gamma _{d},\,{\widetilde{w}}_2=0\,\text { on }\Gamma _{i,o}.\\ \end{array} \end{aligned}$$

The function ${\widetilde{\Phi }}=\Phi -c\Phi _{0}$ is in $H^{1}_{0}(\Omega _{0})$ and has a zero average. The existence of ${\widetilde{\mathbf{w }}}$ follows from [23, Chap II.2, Lemma 2.3.1]. To prove the estimate on $\mathbf{w }$, remark that

$$\begin{aligned} c\le \frac{\sqrt{\mu (\Omega _{0})}}{{\int }_{\Omega _{0}} \Phi _{0}}\left\| \Phi \right\| _{H^{1}_{0}(\Omega _{0})}. \end{aligned}$$

$\square$

Theorem 5.6

For all $(\mathbf{f },\mathbf{g },h)\in \mathbf{L }^{2}(\Omega _{0})\times {\mathcal {H}}^{3/2}_{00}(\Gamma _{0})\times H^{1/2}(\Gamma _{i,o})$, the solution $(\mathbf{u },p)$ of equation (5.1) satisfies the estimate

$$\begin{aligned} \left\| \mathbf{u }\right\| _{\mathbf{L }^{2}(\Omega _{0})}+\left\| p\right\| _{H^{-1}(\Omega _{0})}\le C(\left\| \mathbf{f }\right\| _{(\mathbf{H }^{2}(\Omega _{0}))'}+ \left\| \mathbf{g }\right\| _{({\mathcal {H}}^{1/2}(\Gamma _0))'}+ \left\| h\right\| _{(H^{3/2}(\Gamma _{i,o}))'}).\nonumber \\ \end{aligned}$$

(5.12)

Proof

The fluid part estimate is similar to [21, Lemma A.3] using as test function the solution $(\varvec{\Psi },\pi )$, given by Theorem 5.4, to

$$\begin{aligned} \begin{aligned}&-\nu \Delta \varvec{\Psi } +\nabla \pi =\varvec{\varphi },\,\,\, \text {div }\varvec{\Psi }=0\,\text { in }\Omega _{0},\\&\varvec{\Psi }=0\,\text { on }\Gamma _{d},\,\,\,\Psi _2=0\,\text { and }\,\pi =0\,\text { on }\Gamma _{i,o}, \end{aligned} \end{aligned}$$

(5.13)

with $\varvec{\varphi }\in \mathbf{L }^{2}(\Omega _{0})$. Let us prove the pressure estimate. For all $\Phi \in H^{1}_{0}(\Omega _{0})$, consider the system

$$\begin{aligned} \begin{aligned}&-\nu \Delta \mathbf{v }+\nabla q=0,\,\,\,\text {div }\mathbf{v }=\Phi \,\text { in }\Omega _{0},\\&\mathbf{v }=0\,\text { on }\Gamma _{d},\,\,\,v_2=0\,\text { and }\,q=0\,\text { on }\Gamma _{i,o}. \end{aligned} \end{aligned}$$

(5.14)

Using Lemma 5.1 and Theorem 5.4, this system admits a unique solution $(\mathbf{v },q)$ in $\mathbf{H }^{2}(\Omega _{0})\times H^{1}(\Omega _{0})$, which satisfies

$$\begin{aligned} \left\| \mathbf{v }\right\| _{\mathbf{H }^{2}(\Omega _{0})}+\left\| q\right\| _{H^{1}(\Omega _{0})}\le C\left\| \Phi \right\| _{H^{1}_{0}(\Omega _{0})}. \end{aligned}$$

Using Green’s formula, the following computations hold

$$\begin{aligned} 0&={\int }_{\Omega _{0}}(-\nu \Delta \mathbf{v }+ \nabla q)\cdot \mathbf{u }\\&=-\nu {\int }_{\Omega _{0}}\Delta \mathbf{u }\cdot \mathbf{v }-\nu {\int }_{\partial \Omega _{0}}\mathbf{u }\cdot (\nabla \mathbf{v }\,\mathbf{n }) +\nu {\int }_{\partial \Omega _{0}}\mathbf{v }\cdot (\nabla \mathbf{u }\,\mathbf{n }) + {\int }_{\partial \Omega _{0}}q(\mathbf{u }\cdot \mathbf{n })\\&={\int }_{\Omega _{0}}\mathbf{f }\cdot \mathbf{v }- {\int }_{\Omega _{0}}\nabla p\cdot \mathbf{v }+\nu {\int }_{\partial \Omega _{0}}\mathbf{u }\cdot (\nabla \mathbf{v }\,\mathbf{n }) + {\int }_{\Gamma _{0}}q(\mathbf{u }\cdot \mathbf{n })\\&={\int }_{\Omega _{0}}\mathbf{f }\cdot \mathbf{v }+ {\int }_{\Omega _{0}}p\,\Phi - {\int }_{\Gamma _{i,o}}h(\mathbf{v }\cdot \mathbf{n }) +\nu {\int }_{\partial \Omega _{0}}\mathbf{u } \cdot (\nabla \mathbf{v }\,\mathbf{n })+{\int }_{\Gamma _{0}}q(\mathbf{g }\cdot \mathbf{n }), \end{aligned}$$

and

$$\begin{aligned} {\int }_{\partial \Omega _{0}}\mathbf{u }\cdot (\nabla \mathbf{v }\, \mathbf{n })&={\int }_{\Gamma _{0}}\mathbf{g }\cdot (\nabla \mathbf{v }\,\mathbf{n }) + {\int }_{\Gamma _{i,o}}\mathbf{u }\cdot (\nabla \mathbf{v }\,\mathbf{n })\\&={\int }_{\Gamma _{0}}g \,P_{2}(\nabla \mathbf{v }\,\mathbf{n }) + {\int }_{\Gamma _{i,o}}u_1\partial _1 v_1, \end{aligned}$$

where $\mathbf{g }=(0,g)^{T}$ and $P_{2}$ is the vectorial projection on the second component. As $\partial _1 v_1+\partial _2 v_2=\Phi$ and $v_2=0$ on $\Gamma _{i,o}$, we notice that $\partial _1 v_1=\Phi$ on $\Gamma _{i,o}$, and as $\Phi \in H^{1}_{0}(\Omega _{0})$, we obtain $\partial _1 v_1=0$ on $\Gamma _{i,o}$. Finally,

$$\begin{aligned} \left| {\int }_{\Omega _{0}}p\,\Phi \right|&\le C(\left\| \mathbf{f }\right\| _{(\mathbf{H }^{2}(\Omega _{0}))'} \left\| \mathbf{v }\right\| _{\mathbf{H }^{2}(\Omega _{0})}+ \left\| h\right\| _{(H^{3/2}(\Gamma _{i,o}))'}\left\| \mathbf{v }\cdot \mathbf{n }\right\| _{H^{3/2}(\Gamma _{i,o})}\\&\quad +\left\| \mathbf{g }\right\| _{({\mathcal {H}}^{1/2}(\Gamma _0))'} \left\| P_{2}(\nabla \mathbf{v }\,\mathbf{n })\right\| _{{\mathcal {H}}^{1/2}(\Gamma _{0})}+ \left\| \mathbf{g }\right\| _{({\mathcal {H}}^{1/2}(\Gamma _{0}))'} \left\| P_{2}(q\mathbf{n })\right\| _{{\mathcal {H}}^{1/2}(\Gamma _{0})}),\\&\le C(\left\| \mathbf{f }\right\| _{(\mathbf{H }^{2}(\Omega _{0}))'}+ \left\| \mathbf{g }\right\| _{({\mathcal {H}}^{1/2}(\Gamma _0))'}+ \left\| h\right\| _{(H^{3/2}(\Gamma _{i,o}))'})\left\| \Phi \right\| _{H^{1}_{0}(\Omega _{0})}, \end{aligned}$$

which implies the pressure estimate. $\square$

As for [21, Theorem A.1], we now define a notion of weak solutions for (5.1). For $(\mathbf{f },\mathbf{g },h)$ in $(\mathbf{H }^{2}(\Omega _{0}))'\times ({\mathcal {H}}^{1/2}(\Gamma _0))'\times (H^{3/2}(\Gamma _{i,o}))'$, consider the following variational formulation:

Find $(\mathbf{u },p)\in \mathbf{L }^{2}(\Omega _{0})\times H^{-1}(\Omega _{0})$ such that

$$\begin{aligned} \begin{aligned} {\int }_{\Omega _{0}}\mathbf{u }\cdot \varvec{\varphi }={}&\langle \mathbf{f },\varvec{\Psi }\rangle _{(\mathbf{H }^{2} (\Omega _{0}))',\mathbf{H }^{2}(\Omega _{0})} + \langle h,\varvec{\Psi }\cdot \mathbf{n }\rangle _{(H^{3/2} (\Gamma _{i,o}))',H^{3/2}(\Gamma _{i,o})}\\&- \langle \mathbf{g },P_{2}(\nabla \varvec{\Psi }\,\mathbf{n }) \rangle _{({\mathcal {H}}^{1/2}(\Gamma _{0}))',{\mathcal {H}}^{1/2}(\Gamma _{0})} +\langle \mathbf{g },P_{2}(\pi \mathbf{n }) \rangle _{({\mathcal {H}}^{1/2} (\Gamma _{0}))',{\mathcal {H}}^{1/2}(\Gamma _{0})},\\ \end{aligned} \end{aligned}$$

(5.15)

for all $\varvec{\varphi }\in \mathbf{L }^{2}(\Omega _{0})$ and $(\varvec{\Psi },\pi )$ solution of (5.13), and

$$\begin{aligned} \begin{aligned} \langle p,\Phi \rangle _{H^{-1}(\Omega _{0}),H^{1}_{0}(\Omega _{0})}={}&-\langle \mathbf{f },\mathbf{v }\rangle _{(\mathbf{H }^{2}(\Omega _{0}))', \mathbf{H }^{2}(\Omega _{0})} + \langle h,\mathbf{v }\cdot \mathbf{n }\rangle _{(H^{3/2}(\Gamma _{i,o}))',H^{3/2}(\Gamma _{i,o})}\\&-\langle \mathbf{g },P_{2}(\nabla \mathbf{v }\,\mathbf{n })\rangle _{({\mathcal {H}}^{1/2} (\Gamma _{0}))',{\mathcal {H}}^{1/2}(\Gamma _{0})} \\&+\langle \mathbf{g }, P_{2}(q\mathbf{n })\rangle _{({\mathcal {H}}^{1/2}(\Gamma _{0}))', {\mathcal {H}}^{1/2}(\Gamma _{0})}, \end{aligned} \end{aligned}$$

(5.16)

for all $\Phi \in H^{1}_{0}(\Omega _{0})$ and $(\mathbf{v },q)$ solution of (5.14).

Theorem 5.7

For all $(\mathbf{f },\mathbf{g },h)\in (\mathbf{H }^{2}(\Omega _{0}))'\times ({\mathcal {H}}^{1/2}(\Gamma _0))'\times (H^{3/2}(\Gamma _{i,o}))'$, there exists a unique solution $(\mathbf{u },p)\in \mathbf{L }^{2}(\Omega _{0})\times H^{-1}(\Omega _{0})$ of (5.1) in the sense of the variational formulation (5.15)–(5.16). This solution satisfies the following estimate

$$\begin{aligned} \left\| \mathbf{u }\right\| _{\mathbf{L }^{2}(\Omega _{0})}+\left\| p\right\| _{H^{-1} (\Omega _{0})}\le & {} C(\left\| \mathbf{f }\right\| _{(\mathbf{H }^{2}(\Omega _{0}))'}+ \left\| \mathbf{g }\right\| _{({\mathcal {H}}^{1/2}(\Gamma _0))'} \nonumber \\&+ \left\| h\right\| _{(H^{3/2}(\Gamma _{i,o}))'}). \end{aligned}$$

(5.17)

Proof

See [21, Theorem A.1]. $\square$

1.2 Unsteady Stokes equations

Consider the unsteady Stokes equations

$$\begin{aligned} \begin{aligned}&\mathbf{u }_{t}-\nu \Delta \mathbf{u }+\nabla p={\mathbf{f }},\,\,\,\text {div }\mathbf{u }=0\,\text { in }Q_{T},\\&\mathbf{u }=\mathbf{g }\,\text { on }\Sigma ^{0}_{T},\,\mathbf{u }=0\,\text { on }\Sigma ^{b}_{T},\\&u_2=0\,\text { and }\,p=0\,\text { on }\Sigma ^{i,o}_{T},\\&\mathbf{u }(0)=\mathbf{u }^{0}\,\text { on }\Omega _{0}.\\ \end{aligned} \end{aligned}$$

(5.18)

As for the steady Stokes equations, a non-homogeneous boundary condition on the pressure $p=h$ in (5.18) can be handled directly with a lifting; hence, through this section, we assume that $h=0$. We prove the existence and uniqueness of a solution to (5.18) in Theorem 5.8. Then, we transform (5.18) to prove existence uniqueness and regularity result when the Dirichlet boundary condition $\mathbf{g }$ is less regular (see Theorem 5.9). We use this result to prove Lemma 3.2. Finally, we specify the regularity result used in the study of the fluid–structure system in Theorem 5.11 and we apply this result in Lemma 5.3.

Writing the equations satisfied by $\mathbf{u }-D\mathbf{g }$ and using standard semigroup techniques, we obtain the following theorem. Remark that the assumption $\mathbf{u }^0-D\mathbf{g }(0)\in V$ is equivalent to $\mathbf{u }^{0}\in \mathbf{V }^{1}(\Omega _{0})$, $\mathbf{u }^{0}=\mathbf{g }$ on $\Gamma _{0}$ and $u^{0}_{2}=0$ on $\Gamma _{i,o}$.

Theorem 5.8

For all $\mathbf{g }\in L^{2}(0,T;{\mathcal {H}}^{3/2}_{00}(\Gamma _0))\cap H^{1}(0,T;({\mathcal {H}}^{1/2}(\Gamma _0))')$, $\mathbf{f }\in \mathbf{L }^{2}(Q_{T})$ and $\mathbf{u }^0\in \mathbf{H }^{1}(\Omega _{0})$ satisfying the compatibility condition $\mathbf{u }^0-D\mathbf{g }(0)$ belongs to V, equation (5.18) admits a unique solution $(\mathbf{u },p)\in \mathbf{H }^{2,1}(Q_{T})\times L^{2}(0,T;H^{1}(\Omega _{0}))$. This solution satisfies the following estimate

$$\begin{aligned}&\left\| \mathbf{u }\right\| _{\mathbf{H }^{2,1}(Q_{T})}+\left\| p\right\| _{L^2(0,T;H^{1}(\Omega _{0}))}\\&\quad \le C(\Vert \mathbf{u }^0\Vert _{\mathbf{H }^{1}(\Omega _{0})}+ \left\| \mathbf{g }\right\| _{L^2(0,T;{\mathcal {H}}^{3/2}_{00}(\Gamma _0))}+ \left\| \mathbf{g }'\right\| _{L^{2}(0,T;({\mathcal {H}}^{1/2}(\Gamma _0)))'}+ \left\| \mathbf{f }\right\| _{\mathbf{L }^{2}(Q_{T})}). \end{aligned}$$

We now want to study (5.18) for $\mathbf{g }\in L^{2}(0,T;{\mathcal {L}}^{2}(\Gamma _0))$. We follow the approach of [21]. The operator A, using extrapolation method, can be extended to an unbounded operator $\overset{\sim }{A}$ defined on $({\mathcal {D}}(A^{*}))'$ with domain ${\mathcal {D}}(\overset{\sim }{A})=\mathbf{V }^{0}_{n,\Gamma _{d}}(\Omega _{0})$.

Definition 5.1

A function $\mathbf{u }\in \mathbf{L }^{2}(Q_{T})$ is called a weak solution to (5.18) if $\Pi \mathbf{u }$ is a weak solution to the evolution equation

$$\begin{aligned} \Pi \mathbf{u }'=\overset{\sim }{A}\Pi \mathbf{u }+(-\overset{\sim }{A})\Pi D\mathbf{g }+\Pi \mathbf{f },\,\,\Pi \mathbf{u }(0)=\Pi \mathbf{u }^0, \end{aligned}$$

(5.19)

and $({\mathbb {I}}-\Pi )\mathbf{u }$ is given by

$$\begin{aligned} ({\mathbb {I}}-\Pi )\mathbf{u }=({\mathbb {I}}-\Pi )D\mathbf{g }\,\text { in }\mathbf{L }^{2}(Q_{T}). \end{aligned}$$

(5.20)

Remark that $A=A^{*}$ (the operator A is symmetric and onto from ${\mathcal {D}}(A)$ into $\mathbf{V }^{0}_{n,\Gamma _{d}}(\Omega _{0})$). By definition to a weak solution for (5.19) (see [7]), $\Pi \mathbf{u }\in L^{2}(0,T,\mathbf{V }^{0}_{n,\Gamma _{d}}(\Omega _{0}))$ is solution to (5.19) if and only if for all $\Phi \in {\mathcal {D}}(A^{*})={\mathcal {D}}(A)$ the map $t\mapsto {\int }_{\Omega _{0}}\Pi \mathbf{u }\cdot \Phi$ belongs to $H^{1}(0,T)$ and

$$\begin{aligned} \frac{d}{dt}{\int }_{\Omega _{0}}\Pi \mathbf{u }\cdot \Phi= & {} \langle \overset{\sim }{A}\Pi \mathbf{u },\Phi \rangle _{{\mathcal {D}}(A)',{\mathcal {D}}(A)} + \langle -\overset{\sim }{A}\Pi D\mathbf{g }, \Phi \rangle _{{\mathcal {D}}(A)',{\mathcal {D}}(A)} \nonumber \\&+\langle \Pi \mathbf{f }, \Phi \rangle _{{\mathcal {D}}(A)',{\mathcal {D}}(A)}. \end{aligned}$$

(5.21)

Using Green formula, we compute the adjoint of the operator D.

Lemma 5.2

For all $\mathbf{f }\in \mathbf{L }^{2}(\Omega _{0})$, the adjoint operator $D^{*}$ of D is defined by

$$\begin{aligned} D^{*}\mathbf{f }=(-\nu \nabla \mathbf{v }+q)\,\mathbf{n }, \end{aligned}$$

where $(\mathbf{v },q)\in \mathbf{H }^{2}(\Omega _{0})\times H^{1}(\Omega _{0})$ is the solution to

$$\begin{aligned} \begin{aligned}&-\nu \Delta \mathbf{v }+\nabla q=\mathbf{f },\,\,\,\text {div }\mathbf{v }=0\,\text { in }\Omega _{0},\\&\mathbf{v }=0\,\text { on }\Gamma _{d},\,\,\,v_{2}=0\,\text { and }q=0\,\text { on }\Gamma _{i,o}. \end{aligned} \end{aligned}$$

Using that $\overset{\sim }{A}^{*}=A$ on ${\mathcal {D}}(A)$, the variational formulation (5.21) becomes

$$\begin{aligned} \frac{d}{dt}{\int }_{\Omega _{0}}\Pi \mathbf{u }\cdot \Phi&={\int }_{\Omega _{0}}\Pi \mathbf{u }\cdot A\Phi +{\int }_{\Gamma _0}\mathbf{g }\cdot D^{*}(-A)\Phi +{\int }_{\Omega _{0}}\Pi \mathbf{f }\cdot \Phi \\&={\int }_{\Omega _{0}}\Pi \mathbf{u }\cdot A\Phi +{\int }_{\Gamma _0}\mathbf{g }\cdot (-\nu \nabla \Phi +q)\,\mathbf{n },+{\int }_{\Omega _{0}}\Pi \mathbf{f }\cdot \Phi , \end{aligned}$$

with $\nabla q=\nu ({\mathbb {I}}-\Pi )\Delta \Phi$. The previous equality follows from the uniqueness of the stationary Stokes system and the identity $-\nu \Delta \Phi + \nu ({\mathbb {I}}-\Pi )\Delta \Phi =-A\Phi$. Finally, $\Pi \mathbf{u }$ is a weak solution to 5.19 if and only if

$$\begin{aligned} \frac{d}{dt}{\int }_{\Omega _{0}}\Pi \mathbf{u }\cdot \Phi= & {} {\int }_{\Omega _{0}}\Pi \mathbf{u }\cdot A\Phi +{\int }_{\Gamma _0}\mathbf{g }\cdot (-\nu \nabla \Phi +q)\,\mathbf{n }\nonumber \\&+{\int }_{\Omega _{0}}\Pi \mathbf{f }\cdot \Phi \,\text { for all }\Phi \in {\mathcal {D}}(A). \end{aligned}$$

(5.22)

We can now state a theorem analogue to [21, Theorem 2.3].

Theorem 5.9

For all $\Pi \mathbf{u }^0\in \mathbf{V }^{0}_{n,\Gamma _{d}}(\Omega _{0})$, $\mathbf{g }\in L^{2}(0,T;{\mathcal {L}}^{2}(\Gamma _0))$ and $\mathbf{f }\in \mathbf{L }^{2}(Q_{T})$, equation (5.18) admits a unique weak solution $\mathbf{u }$ in the sense Definition 5.1. This solution satisfies the following estimate

$$\begin{aligned} \begin{aligned}&\left\| \Pi \mathbf{u }\right\| _{L^{2}(0,T;\mathbf{V }^{1/2-\varepsilon }_{n,\Gamma _{d}} (\Omega _{0}))}+\left\| \Pi \mathbf{u }\right\| _{H^{1/4-\varepsilon /2}(0,T;\mathbf{V }^{0} (\Omega _{0}))}+\left\| ({\mathbb {I}}-\Pi )\mathbf{u }\right\| _{L^{2}(0,T;\mathbf{V }^{1/2}(\Omega _{0}))}\\&\quad \le C\left( \Vert \Pi \mathbf{u }^0\Vert _{\mathbf{V }^{0}_{n,\Gamma _{d}}(\Omega _{0})}+ \left\| \mathbf{g }\right\| _{L^{2}(0,T;{\mathcal {L}}^{2}(\Gamma _0))}+ \left\| \Pi \mathbf{f }\right\| _{L^{2}(0,T;\mathbf{V }^{0}_{n,\Gamma _{d}} (\Omega _{0}))}\right) ,\text { for all }\varepsilon >0. \end{aligned}\nonumber \\ \end{aligned}$$

(5.23)

Proof

See [21, Theorem 2.3]. $\square$

As in [21] we can prove that for $\mathbf{g }\in L^{2}(0,T;{\mathcal {H}}^{3/2}_{00}(\Gamma _0))\cap H^{1}(0,T;{\mathcal {H}}^{-1/2}(\Gamma _0))$ a function $\mathbf{u }$ is solution to (5.18) in the sense of Theorem 5.8 if and only if $\mathbf{u }$ is a weak solution to (5.18)(in the sense of Definition 5.1). The following theorem characterizes the pressure.

Theorem 5.10

For all $\mathbf{g }\in L^{2}(0,T;{\mathcal {H}}^{3/2}_{00}(\Gamma _0))\cap H^{1}(0,T;({\mathcal {H}}^{1/2}(\Gamma _0))')$, $\mathbf{f }\in \mathbf{L }^{2}(Q_{T})$ and $\mathbf{u }^0\in \mathbf{H }^{1}(\Omega _{0})$ satisfying the compatibility condition $\mathbf{u }^0-D\mathbf{g }(0)$ belongs to V, a pair $(\mathbf{u },p)\in \mathbf{H }^{2,1}(Q_{T})\times L^{2}(0,T;H^{1}(\Omega _{0}))$ is solution of (5.18) if and only if

$$\begin{aligned}&\Pi \mathbf{u }'=A\Pi \mathbf{u }+ (-A)\Pi D\mathbf{g }+\Pi \mathbf{f },\,\,\,\mathbf{u }(0)=\mathbf{u }^{0},\\&(I-\Pi )\mathbf{u }=(I-\Pi )D\mathbf{g },\,\,\,p=\rho -q_{t}+p_{\mathbf{f }}, \end{aligned}$$

where

• $q\in H^{1}(0,T;H^{1}(\Omega _{0}))$ is the solution to

  $$\begin{aligned} \Delta q=0\,\text { in }Q_{T},\,\,\,\rho =0\,\text { on }\Sigma ^{i,o}_{T},\,\,\,\frac{\partial q}{\partial \mathbf{n }}=\mathbf{g }\cdot \mathbf{n }\,\text { on }\Sigma ^{0}_{T},\,\,\,\frac{\partial q}{\partial \mathbf{n }}=0\,\text { on }\Sigma ^{b}_{T}. \end{aligned}$$

  (5.24)

• $\rho \in L^{2}(0,T;H^{1}(\Omega _{0}))$ is the solution to

  $$\begin{aligned} \Delta \rho =0\,\text { in }Q_{T},\,\,\,\rho =0\,\text { on }\Sigma ^{i,o}_{T},\,\,\,\frac{\partial \rho }{\partial \mathbf{n }}=\nu \Delta \Pi \mathbf{u }\cdot \mathbf{n }\,\text { on }\Sigma ^{d}_{T}, \end{aligned}$$

  (5.25)

  where $\nu \Delta \Pi \mathbf{u }\cdot \mathbf{n }$ is in $L^{2}(0,T;H^{-1/2}(\Gamma _{d}))$ thanks to the divergence theorem.

• $p_{\mathbf{f }}\in L^{2}(0,T;H^{1}(\Omega _{0}))$ is given by the identity $(I-\Pi )\mathbf{f }=\nabla p_{\mathbf{f }}$.

Proof

Writing $\mathbf{u }=\Pi \mathbf{u }+ ({\mathbb {I}}-\Pi )\mathbf{u }$ in Equation (5.18), we have

$$\begin{aligned} \mathbf{u }_t -\nu \Delta \mathbf{u }+\nabla p =\Pi \mathbf{u }_{t}+({\mathbb {I}}-\Pi )\mathbf{u }_t -\nu \Delta \Pi \mathbf{u }-\nu \Delta ({\mathbb {I}}-\Pi )\mathbf{u }+\nabla p=0. \end{aligned}$$

By definition of $({\mathbb {I}}-\Pi )$, there exists $q\in H^{1}_{\Gamma _{i,o}}(\Omega _{0})$ such that $\nabla q=({\mathbb {I}}-\Pi )\mathbf{u }$. Using the condition $\text {div }\mathbf{u }=0$ and $({\mathbb {I}}-\Pi )\mathbf{u }=({\mathbb {I}}-\Pi )D\mathbf{g }$, we obtain that q is solution to (5.24). As $\mathbf{g }\in H^{1}(0,T;{\mathcal {H}}^{-1/2}(\Gamma _0))$, the function q belongs to $H^{1}(0,T;H^{1}(\Omega _{0}))$.

The function $\Pi \mathbf{u }$ is solution to the equation

$$\begin{aligned} \Pi \mathbf{u }_{t}-\nu \Delta \Pi \mathbf{u }+\nabla \rho =0, \end{aligned}$$

with $\rho = p-\nu \Delta q + q_t=p+q_t$. Taking the divergence of the previous equation and the normal trace on $\Gamma _{d}$ (which is well defined as $\Delta \Pi \mathbf{u }$ is in $L^{2}(0,T;\mathbf{L }^{2}(\Omega _{0}))$ with a divergence equal to zero), we obtain (5.25) and $\rho \in L^{2}(0,T;H^{1}(\Omega _{0}))$. $\square$

We conclude this section with a regularity result, coming from the interpolation of the regularity results stated in Theorem 5.8 and Theorem 5.9, and an application to the operator ${\mathcal {A}}_{1}$ defined in Section 3.3.

Theorem 5.11

For all $\mathbf{g }\in L^{2}(0,T;{\mathcal {H}}^{1}_{0}(\Gamma _0))\cap H^{1/2}(0,T;{\mathcal {L}}^{2}(\Gamma _0))$, $\mathbf{f }=0$ and $\Pi \mathbf{u }^{0}=0$, the solution $\mathbf{u }$ to (5.19)–(5.20) satisfies the estimate

$$\begin{aligned} \left\| \Pi \mathbf{u }\right\| _{\mathbf{H }^{3/2-\varepsilon ,3/4-\varepsilon /2}(Q_{T})}\le C(\left\| \mathbf{g }\right\| _{L^{2}(0,T;{\mathcal {H}}^{1}_{0}(\Gamma _0))} + \left\| \mathbf{g }\right\| _{H^{1/2}(0,T;{\mathcal {L}}^{2}(\Gamma _0))}),\text { for all }\varepsilon >0. \end{aligned}$$

Lemma 5.3

The operator $({\mathcal {A}}_{1},{\mathcal {D}}({\mathcal {A}}_{1}))$ is the infinitesimal generator of a strongly continuous semigroup on $\mathbf{H }$.

Proof

The first part is to prove that the unbounded operator $(\overset{\sim }{{\mathcal {A}}_1},{\mathcal {D}}(\overset{\sim }{{\mathcal {A}}_1}))$, defined by

$$\begin{aligned} {\mathcal {D}}(\overset{\sim }{{\mathcal {A}}_1})= & {} \{(\Pi \mathbf{u },\eta _1,\eta _2)\in \mathbf{V }^{1}_{n,\Gamma _{d}}(\Omega _{0})\times (H^{4}(\Gamma _s)\cap H^{2}_{0}(\Gamma _s)) \\&\quad \times H^{2}_{0}(\Gamma _s)\mid \Pi \mathbf{u }-\Pi D_s(\eta _2)\in V\} \end{aligned}$$

and

$$\begin{aligned} \overset{\sim }{{\mathcal {A}}_1}= \begin{pmatrix} A&{}0&{}(-A)\Pi D_s\\ 0&{}0&{}I\\ 0&{}A_{\alpha ,\beta }&{}\delta \Delta _s\\ \end{pmatrix}, \end{aligned}$$

is the infinitesimal generator of a strongly continuous semigroup on $V^{-1}\times H_s$. Here, $V^{-1}$ is the dual of V endowed with the norm

$$\begin{aligned} \mathbf{v }\mapsto \left( \left\langle (-A)^{-1}\mathbf{v },\mathbf{v }\right\rangle _{V,V^{-1}}\right) ^{1/2}. \end{aligned}$$

This proof is similar to [22, Theorem 3.5]. Then, we consider the evolution equation

$$\begin{aligned} \frac{d}{dt}\begin{pmatrix} \Pi \mathbf{u }\\ \eta _{1}\\ \eta _{2}\\ \end{pmatrix} =\overset{\sim }{{\mathcal {A}}_1} \begin{pmatrix} \Pi \mathbf{u }\\ \eta _{1}\\ \eta _{2}\\ \end{pmatrix},\,\, \begin{pmatrix} \Pi \mathbf{u }(0)\\ \eta _{1}(0)\\ \eta _{2}(0)\\ \end{pmatrix} =\begin{pmatrix} \Pi \mathbf{u }^0\\ \eta ^{0}_{1}\\ \eta ^{0}_{2}\\ \end{pmatrix}. \end{aligned}$$

(5.26)

The solution to (5.26) can be found in two steps. First, we determine $(\eta _{1},\eta _{2})$ and then $\Pi \mathbf{u }$. We recall that $(A_s,{\mathcal {D}}(A_s))$ is the infinitesimal generator of an analytic semigroup on $H_s$ (see [11]). Let $(\Pi \mathbf{u }^{0},\eta ^{0}_{1},\eta ^{0}_{2})$ be in $V^{-1}\times H_s$. Using [7, Chap 3, Theorem 2.2], we obtain $\eta _{1}\in H^{3,3/2}(\Sigma ^{s}_{T})$ and $\eta _{2}\in H^{1,1/2}(\Sigma ^{s}_{T})$. Now let us assume that $(\Pi \mathbf{u }^{0},\eta ^{0}_{1},\eta ^{0}_{2})\in \mathbf{H }$. We have to solve

$$\begin{aligned} (\Pi \mathbf{u })'=A\Pi \mathbf{u }+ (-A)\Pi D_s(\eta _2),\,\, \Pi \mathbf{u }(0)=\Pi \mathbf{u }^{0}. \end{aligned}$$

We split this equation into two parts $\Pi \mathbf{u }=\Pi \mathbf{u }_{1} + \Pi \mathbf{u }_{2}$ with

$$\begin{aligned} (\Pi \mathbf{u }_{1})'=A\Pi \mathbf{u }_{1} + (-A)\Pi D_s(\eta _2),\,\, \Pi \mathbf{u }_{1}(0)=0, \end{aligned}$$

and

$$\begin{aligned} (\Pi \mathbf{u }_2)'=A\Pi \mathbf{u }_{2},\,\, \Pi \mathbf{u }(0)=\Pi \mathbf{u }^{0}. \end{aligned}$$

Using Theorem 5.11, we remark that $\Pi \mathbf{u }_{1}\in \mathbf{H }^{3/2-\varepsilon ,3/4-\varepsilon /2}(Q_{T})$. For $\Pi \mathbf{u }_{2}$, [7, Chap 3, Theorem 2.2] shows that $\Pi \mathbf{u }_{2}\in L^{2}(0,T;V)\cap H^{1}(0,T;V^{-1})$. Interpolation result [18, Theorem 3.1] ensures that $\Pi \mathbf{u }_{2}\in {\mathcal {C}}([0,T];\mathbf{V }^{0}_{n,\Gamma _{d}}(\Omega _{0}))$.

Hence, $(\Pi \mathbf{u },\eta _{1},\eta _2)\in {\mathcal {C}}([0,T];\mathbf{H })$ and the restriction to the semigroup $(e^{t\overset{\sim }{{\mathcal {A}}_1}})_{t\in {\mathbb {R}}^{+}}$ to $\mathbf{H }$ is a strongly continuous semigroup on $\mathbf{H }$. Finally, we can verify that the infinitesimal generator associated with this restriction is exactly the operator $({\mathcal {A}}_1,{\mathcal {D}}({\mathcal {A}}_{1}))$.

$\square$

1.3 Elliptic equations for the projector $\Pi$

In this section, we prove higher regularity result for an elliptic equation, which implies the regularity result on the projector $\Pi$ given in Lemma 3.1.

Lemma 5.4

Let f be in $H^{1}(\Omega _{0})$ such that $f=0$ on $\Gamma _{i,o}$ and g be in $H^{3/2}_{00}(\Gamma _{0})$. Then, the elliptic equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}\Delta \rho =f\,\text { in }\Omega _{0},\\ &{}\frac{\partial \rho }{\partial \mathbf{n }}=g(1+(\eta ^{0})^{2})^{-1/2}\,\text { on }\Gamma _{0}\text { and }\frac{\partial \rho }{\partial \mathbf{n }}=0\,\text { on }\Gamma _{b},\\ &{}\rho =0\,\text { on }\Gamma _{i,o},\\ \end{aligned} \end{array}\right. } \end{aligned}$$

(5.27)

admits a unique solution $\rho \in H^{3}(\Omega _{0})$.

Proof

$H^{3}$ regularity far from the corners of $\Omega _{0}$ is obtained through classical arguments. To prove the $H^{3}$ regularity at the corners, say along $x=0$, we first perform a symmetry with respect to $x=0$ (step 1) and then a change of variables to transport the PDE on $(-L,L)\times (0,1)$ (step 2).

Step 1: Using the notations of step 1 in the proof of Theorem 5.4 for $\eta ^{0}_{e}$, $\Gamma _{0,e}$, $\Omega _{0,s}$ and $\Omega _{0,e}$ we define $f_{e}$ and $g_{e}$ by

$$\begin{aligned} \begin{array}{cc} f_{e}:{\left\{ \begin{array}{ll} \begin{aligned} &{}f_{e}=f\text { in }\Omega _{0},\\ &{}f_{e}(x,y)=-f(-x,y)\,\text { in }\Omega _{0,s}, \end{aligned} \end{array}\right. }&{} g_{e}: {\left\{ \begin{array}{ll} \begin{aligned} &{}g_{e}=g\text { in }\Gamma _{0},\\ &{}g_{e}(x,y)=g(-x,y)\,\text { in }\Gamma _{0,e}\setminus \Gamma _{0}. \end{aligned} \end{array}\right. } \end{array} \end{aligned}$$

Assumptions on f and g ensure that $(f_{e},g_{e})$ is in $H^{1}(\Omega _{0,e})\times \mathbf{H }^{3/2}(\Gamma _{0,e})$. Define $\rho _{e}$ by

$$\begin{aligned} \rho _{e}:{\left\{ \begin{array}{ll} \begin{aligned} &{}\rho _{e}=\rho \text { in }\Omega _{0},\\ &{}\rho _{e}=-\rho (-x,y)\,\text { for all }(x,y)\in \Omega _{0,s}.\\ \end{aligned} \end{array}\right. } \end{aligned}$$

Then, $\rho _{e}\in H^{2}(\Omega _{0,e})$ and satisfies

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}\Delta \rho _{e} =f_{e}\,\text { in }\Omega _{0},\\ &{}\frac{\partial \rho _{e}}{\partial \mathbf{n }}=g_{e}(1+(\eta ^{0}_{e})^{2})^{-1/2}\,\text { on }\Gamma _{0,e}\text { and }\frac{\partial \rho _{e}}{\partial \mathbf{n }}=0\,\text { on }(-L,L)\times \{0\},\\ &{}\rho _e=0\,\text { on }\left( \{-L\}\times (0,1)\right) \cup \Gamma _{o}.\\ \end{aligned} \end{array}\right. } \end{aligned}$$

Step 2: Let $\Omega _{e}=(-L,L)\times (0,1)$ and $\varphi$ be the change of variables

$$\begin{aligned} \varphi :{\left\{ \begin{array}{ll} \begin{aligned} &{}\Omega _{0,e}\longrightarrow \Omega _{e},\\ &{}(x,y)\mapsto (x,z)=\left( x,\frac{y}{1+\eta ^{0}_{e}(x)}\right) .\\ \end{aligned} \end{array}\right. } \end{aligned}$$

As in Theorem 5.1, the function $\varphi$ transports $H^{3}(\Omega _{0,e})$ to $H^{3}(\Omega _{e})$. Hence, it is sufficient to prove the $H^{3}$ regularity after transport. Let $\mathbf{J }_{\varphi }$ be the Jacobian matrix of $\varphi$. Setting $\widetilde{\rho _{e}}=\rho \circ \varphi ^{-1}$, $\widetilde{f_{e}}=\vert \mathbf{J }_{\varphi }\vert ^{-1} f_{e}\circ \varphi ^{-1}$ and $\displaystyle \widetilde{g_{e}}(x,1)=g_{e}(x,1+\eta ^{0}_{e }(x))$ the function $\widetilde{\rho _{e}}$ is solution to

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}\text {div}(A\nabla \widetilde{\rho _{e}})=\widetilde{f_{e}}\,\text { in }\Omega _{e},\\ &{}A\nabla {\widetilde{\rho }}_{e}\cdot \mathbf{n }=\widetilde{g_{e}}\,\text { on }(-L,L)\times \{1\}\text { and }A(x,z)\nabla {\widetilde{\rho }}_{e}\cdot \mathbf{n }=0\,\text { on }(-L,L)\times \{0\},\\ &{}\widetilde{\rho _e}=0\,\text { on }\left( \{-L\}\times (0,1)\right) \cup \Gamma _{o},\\ \end{aligned} \end{array}\right. }\nonumber \\ \end{aligned}$$

(5.28)

where the matrix $A=(A_{i,j})_{1\le i,j\le 2}=\vert \text {det}(\mathbf{J }_{\varphi }) \vert ^{-1}\mathbf{J }_{\varphi }\mathbf{J }_{\varphi }^{T}$ is uniformly positive definite symmetric with coefficients in $W^{1,\infty }\cap H^{2}$.

Step 3: Deriving (5.28) with respect to x shows that $\partial _{x}\widetilde{\rho _{e}}$ satisfies (with $\partial _{1}=\partial _{x}$ and $\partial _{2}=\partial _{z}$)

$$\begin{aligned} \text {div}(A\nabla (\partial _{x}\widetilde{\rho _e}))=\partial _{x} \widetilde{f_e}-F(A,\widetilde{\rho _e}), \end{aligned}$$

(5.29)

with

$$\begin{aligned} F(A,\widetilde{\rho _e})=&\left( \partial _{11}A_{11}\right) \partial _{1} \widetilde{\rho _e}+\left( \partial _{1}A_{11}\right) \partial _{11} \widetilde{\rho _e}+\left( \partial _{11}A_{12}\right) \partial _{2} \widetilde{\rho _e}+\left( \partial _{1}A_{12}\right) \partial _{12}\widetilde{\rho _e}\\&+\left( \partial _{12}A_{21}\right) \partial _{1}\widetilde{\rho _e}+\left( \partial _{1} A_{21}\right) \partial _{21}\widetilde{\rho _e}+\left( \partial _{12}A_{22}\right) \partial _{2}\widetilde{\rho _e}+\left( \partial _{1}A_{22}\right) \partial _{22}\widetilde{\rho _e}, \end{aligned}$$

in the sense of the distributions on $\Omega _{e}$. From here on, we localize near (0, 1).

Step 4: We use a bootstrap argument. The first step is to find an $L^{\infty }$ estimate on $\nabla \widetilde{\rho _e}$. In the right hand-side of (5.29) the least regular terms are under the form $\left( \partial _{11}A_{11}\right) \partial _{x}\widetilde{\rho _e}$ or $\left( \partial _{12}A_{22}\right) \partial _{z}\widetilde{\rho _e}$. Sobolev embeddings show that these terms are in $L^{r}$ for all $1<r<2$. Moreover, the Neumann boundary condition involves $\partial _{x}\widetilde{g_e}-\left( \partial _{1}A_{21}\right) \partial _{x}\widetilde{\rho _e}-\left( \partial _{1}A_{22}\right) \partial _{z}\widetilde{\rho _e}$, where the least regular terms are traces of $W^{1,r}$ functions. Using the results of [2] and [3], we obtain that $\partial _{x}\widetilde{\rho _e}$ is in $W^{2,r}$. Then, the embeddings $W^{2,r}\subset W^{1,r^{*}}\subset L^{\infty }$ with $r^{*}=\frac{2r}{2-r}>2$ show that the terms under the form $\left( \partial _{11}A_{11}\right) \partial _{x}\widetilde{\rho _e}$ are in $L^{2}$ and $\left( \partial _{1}A_{21}\right) \partial _{x}\widetilde{\rho _e}$ is in $H^{1/2}$ (on the boundary). Moreover, using equation (5.28) we obtain that $\partial _{zz}\widetilde{\rho _e}$ is in $L^{r^{*}}$ and thus $\partial _{z}\widetilde{\rho _e}\in W^{1,r^{*}}\subset L^{\infty }$. Finally, the right-hand side is in $L^{2}$ and the Neumann boundary condition in $H^{1/2}$ and thus $\partial _{x}\widetilde{\rho _e}$ is $H^{2}$ near (0, 1). For the regularity with respect to z, we can use equation (5.28) and $\widetilde{\rho _e}$ is $H^{3}$ in a neighbourhood of (0, 0).

Step 5: The strategy applies for (0, 0). If we come back to the initial equation on the domain $\Omega _{0}$, we have proved that $\rho$ is $H^{3}$ near $\Gamma _{i}$. The same proof can be used for the regularity near $\Gamma _{o}$ and finally $\rho \in H^{3}(\Omega _{0})$. $\square$