Can large inhomogeneities generate target patterns?

Abstract

We study the existence of target patterns in oscillatory media with weak local coupling and in the presence of an impurity, or defect. We model these systems using a viscous eikonal equation posed on the plane and represent the defect as a perturbation. In contrast to previous results, we consider large defects, which we describe using a function with slow algebraic decay, i.e., $g \sim \textrm{O}(1/|x|^m)$ for $m \in (1,2]$. We prove that these defects are able to generate target patterns and that, just as in the case of strongly localized impurities, their frequency is small beyond all orders of the small parameter describing their strength. Our analysis consists of finding two approximations to target pattern solutions, one which is valid at intermediate scales and a second one which is valid in the far field. This is done using weighted Sobolev spaces, which allow us to recover Fredholm properties of the relevant linear operators, as well as the implicit function theorem, which is then used to prove existence. By matching the intermediate and far-field approximations, we then determine the frequency of the pattern that is selected by the system.

Appendix

In [10], it was shown that the following amplitude equation governs the dynamics of one-armed spiral waves in nonlocal oscillatory media,

$$\begin{aligned} 0 = \beta \Delta _1 w + \lambda w + \alpha |w|^2w + N(w,\varepsilon ), \quad r\in [0,\infty ).\end{aligned}$$

Here, w is a radial and complex-valued function, and

$$\begin{aligned} \beta = ( \sigma - \varepsilon \lambda ), \quad \lambda , \alpha \in \mathbb {C},\quad N \sim \textrm{O}(|\varepsilon ||w|^4). \end{aligned}$$

It was also established in [10] that the constant $\lambda _I$ is an unknown parameter that needs to be determined when solving the equation.

In this section, a multiple-scale analysis is used to derive a steady-state viscous eikonal equation from the above expression. We will see that this eikonal equation is of the form considered in this paper and that it involves an inhomogeneity that decays at order $\textrm{O}(1/|x|^2)$.

To accomplish this task, we first let $w = A {\tilde{w}}$, with $A^2 =- \lambda _R/\alpha _R$. This change of variables is done for convenience and leads to the following equation,

$$\begin{aligned} 0 = \beta \Delta _1 {\tilde{w}} + \lambda {\tilde{w}} + (-\lambda _R + \textrm{i}{\tilde{\alpha }}_I) |{\tilde{w}}|^2{\tilde{w}} + N({\tilde{w}},\varepsilon ), \qquad {\tilde{\alpha }}_I = - \alpha \lambda _R/\alpha _R.\end{aligned}$$

Letting ${\tilde{w}} = \rho \textrm{e}^{\textrm{i}\phi }$ and separating the real and imaginary parts of the above expression, one finally obtains the system

$$\begin{aligned} 0= & {} \beta _R \left[ \Delta _1 \rho - (\partial _r \phi )^2 \rho \right] - \beta _I \left[ \Delta _0 \phi \rho + 2\partial _r \phi \partial _r \rho \right] + \lambda _R \rho - \lambda _R \rho ^3 + \textrm{Re}\left[ N({\tilde{w}}; \varepsilon ) \textrm{e}^{-\textrm{i}\phi } \right] \end{aligned}$$

(20)

$$\begin{aligned} 0= & {} \beta _R \left[ \Delta _0 \phi \rho + 2\partial _r \phi \partial _r \rho \right] + \beta _I \left[ \Delta _1 \rho - (\partial \phi )^2 \rho \right] + \lambda _I \rho + {\tilde{\alpha }}_I \rho ^3 + \textrm{Im}\left[ N({\tilde{w}}; \varepsilon ) \textrm{e}^{-\textrm{i}\phi } \right] . \end{aligned}$$

(21)

Next, we proceed with a perturbation analysis following [4]. We rescale the variable r by defining $S = \delta r$, where $\delta$ is assumed to be a small positive parameter. We also use the following expressions for the unknown functions:

$$\begin{aligned}\begin{array}{r l c l } \rho = &{} \rho _0 + \delta ^2 (R_0 + \delta R_1), &{} \rho _0= \rho _0(r),&{} R_i = R_i(\delta r) \quad i=0,1\\ \phi = &{} \phi _0 + \delta \phi _1, &{} &{} \phi _i = \phi _i(\delta r) i =0,1. \end{array}\end{aligned}$$

And for the parameter, we choose $\lambda _I = -{\tilde{\alpha }}_I + \delta ^2 {\tilde{\lambda }}_I,$ with ${\tilde{\alpha }}$ as above and ${\tilde{\lambda }}_I$ a free parameter.

Inserting the above ansatz into Eqs. (20) and (21), we obtain a set of equations in powers of $\delta$. To write this equations more compactly, we use the subscript S to distinguish operators that are applied to functions that depend on this variable, i.e., $\Delta _{0,S}$. The absence of this subscript indicates that the operator is applied to a function of the original variable r.

At order $\textrm{O}(1)$, we find that $\rho _0$ must satisfy,

$$\begin{aligned} 0&= \beta _R \Delta _1\rho _0 + \lambda _R \rho _0 - \lambda _R \rho _0^3,\\ 0&= \beta _I \Delta _1 \rho _0 - {\tilde{\alpha }}_I \rho _0 + {\tilde{\alpha }}_I \rho _0^3. \end{aligned}$$

At the next order, $\textrm{O}(\delta ^2)$, we find two equations involving $R_0$ and $\phi _0$,

$$\begin{aligned} 0&= - \beta _I \rho _0 \Delta _{0,S} \phi _0 - 2\beta _I \partial _S \phi _0 \partial _S \rho _0 - \beta _R \rho _0 (\partial _S \phi _0)^2 + \lambda _R R_0( 1- 3 \rho _0^2),\\ 0&= \beta _R \rho _0 \Delta _{0,S} \phi _0 + 2\beta _R \partial _S \phi _0 \partial _S \rho _0 -\beta _I \rho _0 (\partial _S \phi _0)^2 + {\tilde{\alpha }}_I R_0 ( 3 \rho _0^2-1) + {\tilde{\lambda }}_I \rho _0 . \end{aligned}$$

For our purposes, it is enough to stop at this stage and not list higher-order terms.

We first focus on the order $\textrm{O}(1)$ system. The first equation can be solved, provided $\beta _R, \lambda _R>0$. This equation falls into a broader family of o.d.e. which were solved in [16]. In this reference, the authors showed that such equations posses a unique solution $\rho _*$ satisfying

$$\begin{aligned} \rho _* \rightarrow 1 \quad \text{ as } \quad r\rightarrow \infty , \qquad \rho _*(r) \sim br \quad \text{ when } \quad r \sim 0\end{aligned}$$

Of course, the solution $\rho _*$ would not satisfy the second equation in the system. So, we let

$$\begin{aligned} G = \beta _I \Delta _1 \rho _* - {\tilde{\alpha }}_I \rho _* + {\tilde{\alpha }}_I \rho _*^3 = \left( \frac{\beta _I}{\beta _R} \lambda _R + {\tilde{\alpha }}_I \right) \rho _* ( \rho _*^2-1),\end{aligned}$$

and add these terms to the order $\textrm{O}(\delta ^2)$ system.

Fig. 3

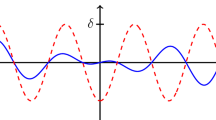
Solution to the boundary value problem (22)

Going back to the order $\textrm{O}(\delta ^2)$ system, we first notice that because $\rho _0 =\rho _* \sim br = bS/\delta$ near the origin, then the terms that involve this variable are in fact ‘large’ when compared to the terms that do not. Concentrating only on these large terms, we find that in the first equation we can solve for $R_0$ in terms of the variable $\phi _0$. Inserting this result into the second equation gives us the viscous eikonal equation,

$$\begin{aligned} \Delta _{0,S} \phi _0 - b (\partial _S \phi _0)^2 +\Omega - c g=0\end{aligned}$$

as expected, where

$$\begin{aligned} b = \frac{\beta _I \lambda _R - \beta _R {\tilde{\alpha }}_I}{{\tilde{\alpha }}_I \beta _I + \lambda _R \beta _R},\qquad \Omega = \frac{{\tilde{\lambda }}_I\lambda _R}{{\tilde{\alpha }}_I \beta _I + \lambda _R \beta _R}, \qquad c = -\frac{ \beta _I \lambda _R + {\tilde{\alpha }}_I \beta _R}{ \beta _R( {\tilde{\alpha }}_I \beta _I + \lambda _R \beta _R)},\qquad g = (1 - \rho _*^2 ).\end{aligned}$$

Numerical simulations show that the perturbation g decays at order $\textrm{O}(1/r^2)$ as r goes to infinity, see Fig. 3. To obtain these results, we solved the boundary value problem

$$\begin{aligned} 0 = \partial _{rr} \rho + \frac{1}{r} \partial _r \rho - \frac{1}{r^2} \rho + \rho - \rho ^3,\qquad \rho (\infty ) = 1, \quad \rho (0) =0, \end{aligned}$$

(22)

treating the equation as a system of o.d.e. and using a shooting method with condition

$$\begin{aligned} \rho (r) \sim br \quad \text{ when } \quad r \sim 0.\end{aligned}$$