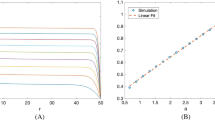
The spectral problem for an infinite periodic medium perturbed by a compact defect is considered. For a high contrast small ε-size periodicity and a finite size defect we consider the critical ε2-scaling for the contrast. We employ two-scale homogenization for deriving asymptotically explicit limit equations for the localized modes and associated eigenvalues. Those are expressed in terms of the eigenvalues and eigenfunctions of a perturbed version of a two-scale limit operator introduced by V. V. Zhikov with an emergent explicit nonlinear dependence on the spectral parameter for the spectral problem at the macroscale. Using the method of asymptotic expansions supplemented by a high contrast boundary layer analysis, we establish the existence of the actual eigenvalues near the eigenvalues of the limit operator, with “ε square root” error bounds. An example for circular or spherical defects in a periodic medium with isotropic homogenized properties is given.
Similar content being viewed by others
References
V. V. Zhikov, “On an extension of the method of two-scale convergence and its applications,” Sb. Math. 191, No. 7, 973–1014 (2000).
V. V. Zhikov, “On spectrum gaps of some divergent elliptic operators with periodic coefficients,” St. Petersb. Math. J. 16, No. 5, 773–790 (2005).
V. V. Zhikov and S. E. Pastukhova, “On gaps in the spectrum of the operator of elasticity theory on a high contrast periodic structure,” J. Math. Sci., New York 188, No. 3, 227–240 (2013).
V. V. Zhikov and S. E. Pastukhova, “Operator estimates in homogenization theory,” Russ. Math. Surv. 71, No. 3, 417–511 (2016).
V. V. Jikov, S. M. Kozlov, and O. A. Olejnik, Homogenization of Differential Operators and Integral Functionals, Springer, Berlin (1994).
V. V. Zhikov, “On operator estimates in homogenization theory,” Dokl. Math. 72, No. 1, 534–538 (2005).
P. Kuchment, “The mathematics of photonic crystals,” In: Mathematical Modeling in Optical Science, pp. 207–272, SIAM, Front. Appl. Math., Philadelphia, PA (2001).
J. D. Joannopoulos, R. D. Meade, and J. N. Winn, Photonic Crystals, Molding the Flow of Light, Princeton Univ. Press, Princeton, NJ (1995).
P. Russell, “Photonic crystal fibers,” Science 299, No. 5605, 358–362 (2003).
J. Pottage et al. “Robust photonic band gaps for hollow core guidance in PCF made from high index glass,” Optics Express 11, No. 22, 2854–2861 (2003).
A. Figotin and P. Kuchment, “Band-gap structure of spectra of periodic dielectric and acoustic media. II: Two-dimensional photonic crystals,” SIAM J. Appl. Math. 56, No. 6, 1561–1620 (1996).
R. Hempel and K. Lienau, “Spectral properties of periodic media in the large coupling limit,” Commun. Partial Differ. Equations 25, No. 7-8, 1445–1470 (2000).
G. Bouchitté and D. Felbacq, “Homogenization near resonances and artificial magnetism from dielectrics,” C. R., Math., Acad. Sci. Paris 339, No. 5, 377–382 (2004).
S. E. Golowich and M.I. Weinstein, Scattering resonances of microstructures and homogenization theory, Multiscale Model. Simul. 3, No. 3, 477–521 (2005).
G. Nguetseng, “A general convergence result for a functional related to the theory of homogenization,” SIAM J. Math. Anal. 20, No. 3, 608–623 (1989).
G. Allaire. “Homogenization and two-scale convergence,” SIAM J. Math. Anal. 23, No. 6, 1482–1518 (1992).
M. Sh. Birman, “The spectrum of singular boundary problems,” Am. Math. Soc., Transl., II. Ser. 53, 23-80 (1966).
A. Alama, M. Avellaneda, P. A. Deift, and R. Hempel, “On the existence of eigenvalues of a divergence-form operator A+λB in a gap of σ(A),” Asymptotic Anal. 8, No. 4, 311–344 (1994).
A. Figotin and A. Klein, “Localized classical waves created by defects,” J. Stat. Phys. 86, No. 1-2, 165–177 (1997).
A. Bensoussan, J.-L. Lions, and G. C. Papanicolaou, Asymptotic Analysis for Periodic Structures, North Holland, Amsterdam etc. (1978).
E. Sanchez-Palencia, Nonhomogeneous Media and Vibration Theory, Springer, Berlin etc. (1980).
N. S. Bakhvalov and G.P. Panasenko, Homogenization: Averaging Processes in Periodic Media. Mathematical Problems in the Mechanics of Composite Materials, Kluwer Acad., Dordrecht etc. (1989).
G. V. Sandrakov, “Averaging of nonstationary problems in the theory of strongly nonhomogeneous elastic media,” Dokl. Math. 57, No. 1, 54–57 (1998).
A. Yu. Belyaev, “Compression waves in a fluid with gas bubbles” J. Appl. Math. Mech. 52, No. 3, 344–348 (1988).
V. V. Zhikov, “Spectral approach to asymptotic diffusion problems,” Differ. Equations 25, No. 1, 33–39 (1989).
G. Allaire, and C. Conca, “Bloch wave homogenization and spectral asymptotic analysis,” J. Math. Pures Appl., IX. Sér. 77, No. 2, 153–208 (1998).
M. Sh. Birman and T. A. Suslina, “Second order periodic differential operators. Threshold properties and homogenization,” St. Petersbg. Math. J. 15, No. 5, 639–714 (2004).
V. V. Zhikov, “Spectral method in homogenization theory,” Proc. Steklov Inst. Math. 250, 85-94 (2005).
M. Cherdantsev, “Spectral convergence for high-contrast elliptic periodic problems with a defect via homogenization,” Mathematika 55, No. 1-2, 29–57 (2009).
M. Neuss-Radu, “A result on the decay of the boundary layers in the homogenization theory,” Asymptotic Anal. 23, No. 3-4, 313–328 (2000).
M.I. Vishik and A. A. Lyusternik, “Regular degeneration and boundary layer for linear differential equations with small parameter” [in Russian], Usp. Mat. Nauk 12, No. 5, 3–122 (1957).
E. Stein, Singular Integrals and Differentiability Properties of Functions, Princeton Univ. Press, Princeton, NJ (1970).
N. O. Babych, I. V. Kamotski, and V. P. Smyshlyaev, “Homogenization in periodic media with doubly high contrasts,” Netw. Heterog. Media 3, No. 3, 413–436 (2008).
M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions, Dover, New York (1965).
Author information
Authors and Affiliations
Corresponding author
Additional information
We dedicate this work to the memory of Professor V. V. Zhikov
Translated from Problemy Matematicheskogo Analiza 92, 2018, pp. 123-145.
Rights and permissions
About this article
Cite this article
Kamotski, I.V., Smyshlyaev, V.P. Localized Modes Due to Defects in High Contrast Periodic Media Via Two-Scale Homogenization. J Math Sci 232, 349–377 (2018). https://doi.org/10.1007/s10958-018-3877-y
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10958-018-3877-y