Skip to main content
SpringerLink
Log in

Fractional entropy-based modeling of suspended concentration distribution of type I and type II and sediment discharge in pipe and open-channel turbulent flows

  • Published:
Zeitschrift für angewandte Mathematik und Physik Aims and scope Submit manuscript

Abstract

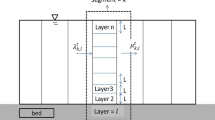
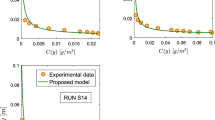
Fractional entropy based on probability concept is applied to study the type I and type II suspended particle concentration distribution along the vertical direction in pipe and open-channel turbulent flows. Taking dimensionless concentration as a random variable and maximizing the fractional entropy, proposed models for suspension distribution of both the types are derived by considering a realistic nonzero particle concentration at the free surface. At first, the model of type I is developed by considering the whole flow depth as one region; and then, for the type II profile, the flow zone is divided into two regions. Finally, using the concept of the asymptotic matching method, the model for the whole flow depth of the type II profile is obtained. To get the model, at first the density function and cumulative distribution functions are derived in the concentration domain, and then the cumulative distribution function of concentration is described in the spatial domain. This study introduces for the first time a type II model using the fractional entropy-based probability density function for suspension distribution. Apart from it, a new cumulative distribution function for suspension distribution based on the Mittag–Leffler function is suggested for further generalization and application of the study. The derived sediment concentration distribution models for both type I and II are validated with experimental and field data, and good agreement is obtained for both the models. Further, the proposed models are also compared with existing Renyi entropy-based concentration model of type I profile and with a deterministic model of type II. Comparison results and error analysis show that for both types of concentration distribution, fractional entropy-based models have better prediction accuracy than the existing entropy-based model and the deterministic concentration model. Finally, the model is applied to compute sediment discharge. The computed values using the model and observed values from experimental data of sediment discharge show a good agreement, and the present study improves the result of previous predictions using Renyi entropy.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26

Similar content being viewed by others

Data availability

All data used in this study are electronically available.

References

  1. Ahamed, N., Kundu, S.: Application of the fractional entropy for one-dimensional mean velocity distribution with dip-phenomenon in open-channel turbulent flows. Stoch. Environ. Res. Risk Assess. 36(5), 1289–1312 (2022)

  2. Almedeij, J.: Asymptotic matching with a case study from hydraulic engineering. In: Recent Advances in Water Resources, pp. 71–76. Hydraulics & Hydrology, Cambridge (2009)

  3. Bouvard, M., Petkovic, S.: Vertical dispersion of spherical, heavy particles in turbulent open channel flow. J. Hydraul. Res. 23(1), 5–20 (1985)

    Article  Google Scholar 

  4. Chanson, H.: The Hydraulics of Open Channel Flow: An Introduction, 2nd edn. Elsevier, Kidlington (2004)

    Google Scholar 

  5. Chen, D., Sun, H.G., Zhang, Y.: Fractional dispersion equation for sediment suspension. J. Hydrol. 491, 13–22 (2013)

    Article  Google Scholar 

  6. Chiu, C., Jin, W., Chen, Y.: Mathematical models for distribution of sediment concentration. J. Hydraul. Eng. 126(1), 16–23 (2000)

    Article  Google Scholar 

  7. Chiu, C.L.: Entropy and probability concepts in hydraulics. J. Hydraul. Eng. 16(9), 725–735 (1987)

    Google Scholar 

  8. Choo, T.H.: An efficient method of the suspended sediment discharge measurement using entropy concept. Water Eng. Res. 1(2), 95–105 (2000)

    Google Scholar 

  9. Coleman, N.: Effects of suspended sediment on the open-channel velocity distribution. Water Resour. Res. 22(10), 1377–1384 (1986)

    Article  Google Scholar 

  10. Cui, H., Singh, V.P.: On the cumulative distribution function for entropy-based hydrologic modeling. Trans. ASABE 55(2), 429–438 (2012)

    Article  Google Scholar 

  11. Cui, H., Singh, V.P.: Suspended sediment concentration in open channels using tsallis entropy. J. Hydrol. Eng. 19(5), 966–977 (2014)

    Article  Google Scholar 

  12. Dey, S.: Fluvial Hydrodynamics: Hydrodynamic and Sediment Transport Phenomena. Springer, Berlin (2014)

    Book  Google Scholar 

  13. Einstein, H., Chien, N.: Effects of heavy sediment concentration near the bed on velocity and sediment distribution. Us army corps of engineers, Missouri River Division, Report No 8 (1955)

  14. Ghoshal, K., Kumbhakar, M., Singh, V.P.: Suspended sediment concentration and discharge in open channels using Renyi entropy. J. Hydrol. Eng. 23(9), 04018038 (2018)

    Article  Google Scholar 

  15. Greimann, B., Holly, F.: Two-phase analysis of concentration profiles. J. Hydraul. Eng. 127(9), 753–762 (2001)

    Article  Google Scholar 

  16. Jaynes, E.: Information theory and statistical mechanics: I. Phys. Rev. 106, 620–930 (1957)

    Article  MathSciNet  MATH  Google Scholar 

  17. Jaynes, E.: Information theory and statistical mechanics: II. Phys. Rev. 108, 171–190 (1957)

    Article  MathSciNet  MATH  Google Scholar 

  18. Jaynes, E.: On the rationale of maximum entropy methods. Proc. IEEE 70, 939–952 (1982)

    Article  Google Scholar 

  19. Julien, P.Y.: Erosion and Sedimentation. Cambridge University Press, New York (2010)

    Book  Google Scholar 

  20. Kaushal, D., Tomita, Y.: Experimental investigation for near-wall lift of coarse particles in slurry pipeline using \(\gamma \)-ray densitometer. Powder Technol. 172, 177–187 (2007)

    Article  Google Scholar 

  21. Kumbhakar, M., Ghoshal, K.: One dimensional velocity distribution in open channels using Renyi entropy. Stoch. Environ. Res. Risk Assess. 31, 949–959 (2017)

    Article  MATH  Google Scholar 

  22. Kumbhakar, M., Ghoshal, K., Singh, V.P.: Derivation of rouse equation for sediment concentration using Shannon entropy. Physica A Stat. Mech. Appl. (accepted article) (2016)

  23. Kundu, S.: Theoretical study on velocity and suspension concentration in turbulent flow. Ph.D. thesis, Indian Institute of Technology Kharagpur, West Bengal, India (2015)

  24. Kundu, S.: Prediction of velocity-dip-position at the central section of open channels using entropy theory. J. Appl. Fluid Mech. (2017). https://doi.org/10.18869/acadpub.jafm.73.238.26403

  25. Kundu, S., Ghoshal, K.: Effects of secondary current and stratification on suspension concentration in an open channel flow. Environ. Fluid Mech. 14(6), 1357–1380 (2014)

    Article  Google Scholar 

  26. Kundu, S., Ghoshal, K.: A mathematical model for Type II profile of concentration distribution in turbulent flows. Environ. Fluid Mech. 17(449–472), 1–18 (2017)

    Google Scholar 

  27. Luo, H., Singh, V.P.: Entropy theory for two-dimensional velocity distribution. J. Hydrol. Eng. 16(4), 303–315 (2011)

    Article  Google Scholar 

  28. McQuivey, R.S.: Summary of turbulence data from rivers, conveyance channels and laboratory flumes. Tech. rep., U.S. Government Printing Office, Washington, DC (1973)

  29. Michalik, A.: Density patterns of the inhomogeneous liquids in the industrial pipeline measured by means of radiometric scanning. La Houille Blanche 1, 53–59 (1973)

    Article  Google Scholar 

  30. Ni, J., Wang, G.: On the two patterns of vertical distribution of sediment concentration and their formation causes. J. Hydraul. Eng. 7, 60–68 (1987)

    Google Scholar 

  31. Ni, J., Wang, G., Borthwick, A.: Kinetic theory for particles in dilute and dense solid-liquid flows. J. Hydraul. Eng. 126(12), 893–903 (2000)

    Article  Google Scholar 

  32. Ni, J., Huang, X., Borthwick, A.: Characteristics of hyperconcentrated sediment-laden flows. J. Eng. Mech. 129(12), 1489–1493 (2003)

    Article  Google Scholar 

  33. O’Brien, M.P.: Review of the theory of turbulent flow and its relation to sediment transport. Trans. Am. Geophys. Union 14(1), 487–491 (1933)

    Article  Google Scholar 

  34. Podlubny, I.: Fractional Differential Equations. Academic Press, Berkeley (1999)

    MATH  Google Scholar 

  35. Renyi, A.: On measures of entropy and information. In: Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960, University of California Press, Berkeley, CA, USA, pp 547–561 (1961)

  36. Rouse, H.: Modern concepts of the mechanics of turbulence. Trans. ASCE 102, 463–543 (1937)

    Google Scholar 

  37. Shafee, F.: Lambert function and a new non-extensive form of entropy. IMA J. Appl. Math. 72, 785–800 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  38. Shannon, C.E.: The mathematical theory of communications, I and II. Bell Syst. Tech. J. 27, 379–423 (1948)

    Article  Google Scholar 

  39. Singh, V.P.: Derivation of the Singh-Yu infiltration equation using entropy theory. J. Hydrol. Eng. 16, 187–191 (2011)

    Article  Google Scholar 

  40. Singh, V.P.: Hydrologic synthesis using entropy theory: Review. J. Hydrol. Eng. 16(5), 421–433 (2011)

    Article  Google Scholar 

  41. Singh, V.P., Luo, H.: Entropy theory for distribution of one-dimensional velocity in open channels. J. Hydrol. Eng. 16(9), 725–735 (2011)

    Article  Google Scholar 

  42. Tsallis, C.: Possible generalization of Boltzmann–Gibbs statistics. J. Stat. Phys. 52(1–2), 479–487 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  43. Valluri, S.R., Jeffrey, D.J., Corles, R.M.: Some applications of the Lambert W function to physics. Can. J. Phys. 78(9), 823–831 (2000)

    Google Scholar 

  44. Wang, G., Ni, J.: Kinetic theory for particle concentration distribution in two-phase flows. J. Eng. Mech. 116(12), 2738–2748 (1990)

    Article  Google Scholar 

  45. Wang, Q.A.: Extensive generalization of statistical mechanics based on incomplete information theory. Entropy 5, 220–232 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  46. Wang, X., Qian, N.: Turbulence characteristics of sediment-laden flows. J. Hydraul. Eng. 115(6), 781–799 (1989)

    Article  Google Scholar 

  47. Yalin, M.: Mechanics of Sediment Transport, 2nd edn. Pegramon Press, New York (1977)

    Google Scholar 

  48. Zhong, D., Wang, G., Sun, Q.: Transport equation for suspended sediment based on two-fluid model of solid/liquid two-phase flows. J. Hydraul. Eng. 137(5), 530–542 (2011)

    Article  Google Scholar 

Download references

Author information

Author notes

  1. Nizamuddin Ahamed

    Present address: Triveni Devi Bhalotia College, Raniganj, West Bengal, 713347, India

Authors and Affiliations

  1. Department of Mathematics, NIT Jamshedpur, Jamshedpur, Jharkhand, 831014, India

    Nizamuddin Ahamed & Snehasis Kundu

Authors
  1. Nizamuddin Ahamed
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Snehasis Kundu
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Dr. Kundu originally formulated the idea of the work. Mr. Ahamed initiated and contributed to the preliminary concept of the study under the supervision of Dr. Kundu. Afterward, Mr. Ahamed prepared the initial mathematical models and Dr. Kundu modified and corrected them. Mr. Ahamed completes the data analysis, modeling, programming and fitting parts and prepared the initial draft of the paper. Dr. Kundu edited, revised and completed the final draft. Finally, both the authors approved the final version.

Corresponding author

Correspondence to Snehasis Kundu.

Ethics declarations

Conflict of interest

The authors declare that they do not have any conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ahamed, N., Kundu, S. Fractional entropy-based modeling of suspended concentration distribution of type I and type II and sediment discharge in pipe and open-channel turbulent flows. Z. Angew. Math. Phys. 74, 101 (2023). https://doi.org/10.1007/s00033-023-01988-w

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00033-023-01988-w

Keywords

Mathematics Subject Classification

Search

Navigation