Derivation of different suspension equations in sediment-laden flow from Shannon entropy

Abstract

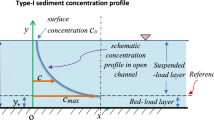
In this study the well-known Rouse equation and Barenblatt equation for suspension concentration distribution in a sediment-laden flow is derived using Shannon entropy. Considering dimensionless suspended sediment concentration as a random variable and using principle of maximum entropy, probability density function of suspension concentration is obtained. A new and general cumulative distribution function for the flow domain is proposed which can describe specific previous forms reported in the literature. The cumulative distribution function is tested with a variety sets of experimental data and also compared with previous models. The test results ensure the superiority of the new cumulative distribution function. Further a modified form of the cumulative distribution function is discussed and used to derive the suspension model of Greimann et al. The model parameters are expressed in terms of the Rouse number to show the effectiveness of this study using entropy based approach. Finally a non-linear equation in the Rouse number has been suggested to compute it from the experimental data.

Appendix

Let if $c_i$ are some values of the suspension concentration with corresponding weight $f(c_i)$ where f denotes the probability density function and $f(c_i )$ denotes the probability of the observation $c_i$ for $i=1,2,\ldots ,n$. Then the weighted geometric mean is calculated as

$$\begin{aligned} c = \left( \prod _{i=1}^n c_i^{f(c_i)} \right) ^{1/(\sum _{i=1}^n f(c_i))} = \exp \left( \frac{\sum \nolimits _{i=1}^n \ln c_i f(c_i)}{\sum \nolimits _{i=1}^n f(c_i)}\right) \end{aligned}$$

(47)

It can be written as

$$\begin{aligned} \ln c = \frac{\sum \nolimits _{i=1}^n \ln c_i f(c_i)}{\sum \nolimits _{i=1}^n f(c_i)} \end{aligned}$$

(48)

This equation shows that $\ln c$ is the weighted arithmetic mean of $\ln c_i$ values. Therefore we can denote and write it as

$$\begin{aligned} \overline{\ln c} = \frac{\frac{1}{n}\sum \nolimits _{i=1}^n \ln c_i f(c_i)}{\frac{1}{n}\sum \nolimits _{i=1}^n f(c_i)} \end{aligned}$$

(49)

Now taking the limit as $n\rightarrow \infty$ and using

$$\begin{aligned} \displaystyle \lim _{n\rightarrow \infty }\frac{1}{n} \sum _{i=1}^n f(c_i) = \int _0^1 f(c)~dc=1 \end{aligned}$$

(50)

we have

$$\begin{aligned} \overline{\ln c} = \lim _{n\rightarrow \infty } \frac{1}{n} \sum _{i=1}^n \ln c_i f(c_i) = \int _0^1 \ln c f(c)~dc \end{aligned}$$

(51)