Abstract
An energy for first-order structured deformations in the context of periodic homogenization is obtained. This energy, defined in principle by relaxation of an initial energy of integral-type featuring contributions of bulk and interfacial terms, is proved to possess an integral representation in terms of relaxed bulk and interfacial energy densities. These energy densities, in turn, are obtained via asymptotic cell formulae defined by suitably averaging, over larger and larger cubes, the bulk and surface contributions of the initial energy. The integral representation theorem, the main result of this paper, is obtained by mixing blow-up techniques, typical in the context of structured deformations, with the averaging process underlying the theory of homogenization.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The mathematical modeling of materials has interested scientists for many centuries. In the last decades, the accuracy of these models has considerably increased as an effect of more sophisticated measuring instruments, on the experimental side, and of the availability of sound mathematical abstract frameworks, on the theoretical side. Classical theories of continuum mechanics provide a good description of many phenomena such as elasticity, plasticity, and fracture and are susceptible of incorporating fine structures at the microscopic level. A mathematical process through which the effects of a preassigned microstructure emerge at the macroscopic level is called homogenization: this procedure provides an effective macroscopic description as the result of averaging out the heterogeneities.
By contrast, structured deformations [14] provide a mathematical framework to capture the effects at the macroscopic level of geometrical changes at submacroscopic levels. The availability of this framework, especially in its variational formulation [9], leads naturally to the enrichment of the energies and force systems that underlie variational and field-theoretic descriptions of important physical phenomena without having to commit at the outset to any of the existing prototypical mechanical theories, such as elasticity or plasticity. A (first-order) structured deformation is a pair \((g,G)\in SBV(\Omega ;{\mathbb {R}}^d)\times L^1(\Omega ;{\mathbb {R}}^{d\times N})=:SD(\Omega )\), where \(g:\Omega \rightarrow {\mathbb {R}}^d\) is the macroscopic deformation and \(G:\Omega \rightarrow {\mathbb {R}}^{d\times N}\) is the microscopic deformation tensor. As opposed to classical theories of mechanics, in which g and its gradient \(\nabla g\) alone characterize the deformations of the body \(\Omega \), the additional geometrical field G captures the contributions at the macroscopic level of the smooth submacroscopic changes. The difference \(\nabla g-G\) captures the contributions at the macroscopic level of slips and separations occurring at the submacroscopic level (which are commonly referred to as disarrangements [15]). Heuristically, the disarrangement tensor \(M:=\nabla g-G\) is an indication of how nonclassical a structured deformation is: should \(M=0\) and if g is a Sobolev field, then the field G is simply the classical deformation gradient; on the contrary, if \(M\ne 0\), there is a macroscopic bulk effect of submacroscopic slips and separations, which are phenomena involving interfaces. This fact will be made precise in Approximation Theorem 2.5.
In order to assign an energy to a structured deformation \((g,G)\in SD(\Omega )\), the proposal has been made in [9] to take the energetically most economical way to reach (g, G) by means of SBV fields \(u_n\): according to the Approximation Theorem [9, Theorem 2.12], we say that a sequence \(\{u_n\}\subset SBV(\Omega ;{\mathbb {R}}^d)\) converges to (g, G) if
where \({\mathcal {M}}(\Omega ;{\mathbb {R}}^{d\times N})\) is the set of bounded matrix-valued Radon measures on \(\Omega \), and we denote this convergence by  . We let the initial energy of a deformation \(u\in SBV(\Omega ;{\mathbb {R}}^d)\) be
. We let the initial energy of a deformation \(u\in SBV(\Omega ;{\mathbb {R}}^d)\) be
which is determined by the bulk and surface energy densities \(W:{\mathbb {R}}^{d\times N}\rightarrow [0,+\infty )\) and \(\psi :{\mathbb {R}}^d\times {\mathbb {S}}^{N-1}\rightarrow [0,+\infty )\). In formula (1.2), \(\mathrm dx\) and \(\mathrm d{\mathcal {H}}^{N-1}(x)\) denote the N-dimensional Lebesgue and \((N-1)\)-dimensional Hausdorff measures, respectively; [u](x) and \(\nu _u(x)\) denote the jump of u and the normal to the jump set for each \(x\in S_u\), the jump set.
In mathematical terms, the process just described to assign an energy to a structured deformation \((g,G)\in SD(\Omega )\) reads

In the language of calculus of variations, the operation described in (1.3) is called relaxation and the main result in [9] was to prove that the functional I admits an integral representation, that is, there exist functions \(H:{\mathbb {R}}^{d\times N}\times {\mathbb {R}}^{d\times N}\rightarrow [0,+\infty )\) and \(h:{\mathbb {R}}^d\times {\mathbb {S}}^{N-1}\rightarrow [0,+\infty )\) such that
In this work, we focus on submacroscopically heterogeneous, hyperelastic, defective materials featuring a fine periodic microstructure. Our scope is to provide an asymptotic analysis of the energies associated with these materials, as the fineness of their microstructure vanishes, in the variational context of structured deformations [9].
The initial energy functionals that we consider involve a bulk contribution and a surface contribution, each of which is described by an energy density which depends explicitly on the spatial variable in a periodic fashion, namely the energy associated with a deformation \(u\in SBV(\Omega ;{\mathbb {R}}^d)\) has the expression
where \(W:{\mathbb {R}}^N\times {\mathbb {R}}^{d\times N}\rightarrow [0,+\infty )\) and \(\psi :{\mathbb {R}}^N\times {\mathbb {R}}^d\times {\mathbb {S}}^{N-1}\rightarrow [0,+\infty )\) are Q-periodic in the first variable (Q being the unit cube in \({\mathbb {R}}^N\)), and \(\varepsilon >0\) is the length scale of the microscopic heterogeneities (see Assumptions 3.1 for the precise assumptions on W and \(\psi \)). We will perform a relaxation analogous to that in (1.3) for \(\varepsilon \)-dependent initial energy (1.5). In particular, we aim at assigning an energy to structured deformation (g, G) where the geometric field G is p-integrable for some \(p>1\). As proved in [9], this has the effect that the submacroscopic slips and separations diffuse in the bulk and contribute to determining the relaxed bulk energy density, whereas the relaxed surface energy density is determined alone by optimizing the initial surface energy density. The mechanical interpretation of this fact, which is also the motivation for our choice, is that the relaxed surface energy is not influenced by the initial bulk energy in the limit.
We define the class of admissible sequences for the relaxation by

and for every sequence \(\varepsilon _n\rightarrow 0\), we define
The main result of this work is the following theorem, which provides a representation result analogous to that in (1.4), for structured deformations \((g,G)\in SD_p(\Omega ):=SBV(\Omega ;{\mathbb {R}}^d)\times L^p(\Omega ;{\mathbb {R}}^{d\times N})\). Indeed, the convergence  and the uniform control on the \(L^p\) norm of the gradients \(\nabla u_n\) required in (1.6) imply that the gradients in (1.1) converge weakly in \(L^p(\Omega ;{\mathbb {R}}^{d\times N})\) to G, instead of converging weakly-* in the sense of measures (see our Approximation Theorem 2.5 below). Therefore, it makes sense to actually define
and the uniform control on the \(L^p\) norm of the gradients \(\nabla u_n\) required in (1.6) imply that the gradients in (1.1) converge weakly in \(L^p(\Omega ;{\mathbb {R}}^{d\times N})\) to G, instead of converging weakly-* in the sense of measures (see our Approximation Theorem 2.5 below). Therefore, it makes sense to actually define
where
Theorem 1.1
Let \(p>1\) and let us assume that Assumptions 3.1 hold; let \(u\in SBV(\Omega ;{\mathbb {R}}^d)\) and let \(E_\varepsilon (u)\) be the energy defined by (1.5). Then, for every \((g,G)\in SD_p(\Omega )\), and for each sequence \(\varepsilon _n\rightarrow 0\), the homogenized functional \(I_{\hom }^{\{\varepsilon _n\}}(g,G)\) defined in (1.8) admits the integral representation
The relaxed energy densities \(H_{\hom }:{\mathbb {R}}^{d\times N}\times {\mathbb {R}}^{d\times N}\rightarrow [0,+\infty )\) and \(h_{\hom }:{\mathbb {R}}^d\times {\mathbb {S}}^{N-1}\rightarrow [0,+\infty )\) are independent of \(\{\varepsilon _n\}\) and are given by the formulae
for every \(A,B\in {\mathbb {R}}^{d\times N}\), and
for every \((\lambda ,\nu )\in {\mathbb {R}}^d\times {\mathbb {S}}^{N-1}\), where \(Q_\nu \) is any rotated unit cube so that two faces are perpendicular to \(\nu \). Consequently, \(I_{\hom }^{\{\varepsilon _n\}}\), itself, is independent of \(\{\varepsilon _n\}\), and we write \(I_{\hom }\) in place of \(I_{\hom }^{\{\varepsilon _n\}}\).
The independence of \(h_{\hom }(\lambda ,\nu )\) from the specific choice of the cube \(Q_\nu \) can be deduced from Proposition 3.5. In (1.11) and (1.12), we have defined, for \(A,B\in {\mathbb {R}}^{d\times N}\), \((\lambda ,\nu )\in {\mathbb {R}}^d\times {\mathbb {S}}^{N-1}\), and \(R,R_\nu \subset {\mathbb {R}}^N\) cubes,


where
is the elementary jump of amplitude \(\lambda \) across the hyperplane perpendicular to \(\nu \). In formula (1.13), we denote by \(SBV_{\#}(R;{\mathbb {R}}^d)\) the set of \({\mathbb {R}}^d\)-valued SBV functions with equal traces on opposite faces of the cube R.
We notice that (1.11) and (1.12) are asymptotic cell formulae, as it is expected in the context of homogenization when no convexity assumptions are made on the initial energy densities (see, e.g., [6]). In the special case of functions W and \(\psi \) which are convex in the gradient and jump variable, respectively, we are able to show that (1.11) reduces to a cell problem in the unit cell (see Proposition 3.4 below); whether the same result holds for \(h_{\hom }\) is still unknown.
Since, in a structured deformation \((g,G)\in SD(\Omega )\), the field G is generally different from \(\nabla g\), convergence (1.1) generally entails the discontinuity sets of \(u_n\) diffusing in the bulk, namely \({\mathcal {H}}^{N-1}(S_{u_n})\rightarrow +\infty \) as \(n\rightarrow \infty \) (so that the hypotheses of Ambrosio’s compactness theorem in SBV [2] are in general not satisfied). This is reflected in the form of the relaxed bulk energy density in (1.11), where we point out that both the initial bulk and surface energy densities contribute to \(H_{\hom }\), with both undergoing the bulk rescaling. On the contrary, the coercivity assumption (see Assumption 3.1-(iv) below) yields an \(L^p\) constraint on the gradients of the approximating sequences which avoids the appearance of any bulk contributions in the relaxed surface energy density \(h_{\hom }\) in (1.12).
The proof of (1.10), to which whole Sect. 4 is devoted, is obtained by computing the \(\Gamma \)-limit in (1.8) by combining blow-up techniques à la Fonseca-Müller [19, 20] with rescaling techniques typically used in homogenization problems. This will be especially visible in the construction of the recovery sequences for proving that the densities in (1.10) are indeed given by (1.11) and (1.12). To deduce the upper bound for the homogenized surface energy density \(h_{\hom }\) we also make use of comparison results in a \(\Gamma \)-convergence setting (see [7, 11]).
We would like to close this introduction by mentioning two alternative possibilities for identifying relaxed energies for this problem that have analogues in the context of dimension reduction (see [8], where \(\varepsilon \) denotes the thickness of a body in a preassigned direction), namely to carry out successively the “partial relaxations” that fix either \(\varepsilon \) or n, i.e., (i) first relax with respect to structured deformations and second homogenize, or (ii) first homogenize and then relax with respect to structured deformations. These alternative possibilities have interest not only from the point of view of variational analysis, but they also may enlarge the class of multiscale problems in mechanics to which homogenization and relaxation to structured deformations can be applied. Consider, for example, a system for which the variables \(\nabla u\) and [u] for simple deformations u are expected to vary only over length scales much larger than the period \(\varepsilon \) of the microstructure. In this case, it would seem reasonable to first homogenize and then relax to structured deformations. This iterated relaxation procedure presumably would, in general, assign a larger energy to structured deformations, and such examples provide a motivation for future research on the alternatives (i) and (ii).
We will collect some preliminary results in Sect. 2, where we also prove Approximation Theorem 2.5 which guarantees the nonemptiness of the class \({\mathcal {R}}_p\) introduced in (1.6). Section 3 contains the precise formulation of the standing assumptions on the initial energy densities W and \(\psi \) and a collection of results on the homogenized energy densities \(H_{\hom }\) and \(h_{\hom }\) which can be deduced from definitions (1.11) and (1.12). For the reader’s convenience, we present in Appendix A some technical measure-theoretical results which are by now standard.
2 Preliminaries
2.1 Notation
We will use the following notations
-
\({\mathbb {N}}\) denotes the set of natural numbers without the zero element;
-
\(\Omega \subset {\mathbb {R}}^{N}\) is a bounded connected open set with Lipschitz boundary;
-
\({\mathbb {S}}^{N-1}\) denotes the unit sphere in \({\mathbb {R}}^N\);
-
For any \(r>0\), \(B_r\) denotes the open ball of \({\mathbb {R}}^{N}\) centered at the origin of radius r; for any \(x\in {\mathbb {R}}^{N}\), \(B_r(x) :=x+ B_r\) denotes the open ball centered at x of radius r; \(Q:=(-\tfrac{1}{2},\tfrac{1}{2})^N\) denotes the open unit cube of \({\mathbb {R}}^{N}\) centered at the origin; for any \(\nu \in {\mathbb {S}}^{N-1}\), \(Q_\nu \) denotes any open unit cube in \({\mathbb {R}}^{N}\) with two faces orthogonal to \(\nu \); for any \(x\in {\mathbb {R}}^{N}\) and \(\delta >0\), \(Q(x,\delta ):=x+\delta Q\) denotes the open cube in \({\mathbb {R}}^{N}\) centered at x with side \(\delta \);
-
\({{\mathcal {A}}}(\Omega )\) is the family of all open subsets of \(\Omega \);
-
\({\mathcal {L}}^{N}\) and \({\mathcal {H}}^{N-1}\) denote the N-dimensional Lebesgue measure and the \(\left( N-1\right) \)-dimensional Hausdorff measure in \({\mathbb {R}}^N\), respectively; the symbol \(\mathrm dx\) will also be used to denote integration with respect to \({\mathcal {L}}^{N}\);
-
\({\mathcal {M}}(\Omega ;{\mathbb {R}}^{d\times N})\) is the sets of finite matrix-valued Radon measures on \(\Omega \); \({\mathcal {M}}^+(\Omega )\) is the set of non-negative finite Radon measures on \(\Omega \); given \(\mu \in {\mathcal {M}}(\Omega ;{\mathbb {R}}^{d\times N})\), the measure \(|\mu |\in {\mathcal {M}}^+(\Omega )\) denotes the total variation of \(\mu \);
-
\(SBV(\Omega ;{\mathbb {R}}^d)\) is the set of vector-valued special functions of bounded variations defined on \(\Omega \). Given \(u\in SBV(\Omega ;{\mathbb {R}}^d)\), its distributional gradient Du admits the decomposition
 , where \(S_u\) is the jump set of u, [u] denotes the jump of u on \(S_u\), and \(\nu _u\) is the unit normal vector to \(S_u\); finally, \(\otimes \) denotes the dyadic product; for \(Q\subset {\mathbb {R}}^N\) a cube, we denote by \(SBV_{\#}(Q;{\mathbb {R}}^d)\) the set of \({\mathbb {R}}^d\)-valued SBV functions with equal traces on opposite faces of Q;
, where \(S_u\) is the jump set of u, [u] denotes the jump of u on \(S_u\), and \(\nu _u\) is the unit normal vector to \(S_u\); finally, \(\otimes \) denotes the dyadic product; for \(Q\subset {\mathbb {R}}^N\) a cube, we denote by \(SBV_{\#}(Q;{\mathbb {R}}^d)\) the set of \({\mathbb {R}}^d\)-valued SBV functions with equal traces on opposite faces of Q; -
\(L^p(\Omega ;{\mathbb {R}}^{d\times N})\) is the set of matrix-valued p-integrable functions; for \(p>1\) we denote by \(p'\) its Hölder conjugate;
-
For \(p\geqslant 1\), \(SD_p(\Omega ):=SBV(\Omega ;{\mathbb {R}}^d)\times L^p(\Omega ;{\mathbb {R}}^{d\times N})\) is the space of structured deformations (g, G) (notice that \(SD_1(\Omega )\) is the space \(SD(\Omega )\) introduced in [9]);
-
C represents a generic positive constant that may change from line to line;
-
For every \(x \in {\mathbb {R}}^N\), the symbol \(\lfloor x\rfloor \in {\mathbb {Z}}^N\) denotes the integer part of the vector x, namely that vector whose components are the integer parts of each component of x. We denote by \( \langle x \rangle \) the fractional part of x, i.e., \(\langle x \rangle :=x-\lfloor x\rfloor \in [0,1)^N\).
2.2 Function spaces
The following proposition serves as a definition of Lebesgue points for \(L^p\) functions (see [16, Theorem 1.33] for a more general statement).
Proposition 2.1
(Lebesgue points) Let \(p\geqslant 1\) and let \(u\in L^p(\Omega )\). Then for \({\mathcal {L}}^N\)-a.e. \(x_0\in \Omega \), the following equality holds

The following theorem collects some facts about BV functions. Its proof can be found, e.g., in [4, Sections 3.6 and 3.7], [16, Section 6.1], and [17, Theorem 4.5.9].
Theorem 2.2
Let \(u\in BV(\Omega ;{\mathbb {R}}^{d})\). Then
-
(i)
(Approximate differentiability) for \({\mathcal {L}}^{N}\)-a.e. \(x_0\in \Omega \)

-
(ii)
(Jump points) for every \(x_0\in S_u\) , there exist \(u^{+}(x_0), u^{-}(x_0)\in {\mathbb {R}}^{d}\) and \(\nu (x_0) \in {\mathbb {S}}^{N-1}\) normal to \(S_u\) at \(x_0\) such that
$$\begin{aligned} \lim _{r\rightarrow 0^{+}}\frac{1}{r^{N}}\int \limits _{Q_{\nu (x_0)}^{\pm }(x_0;r)}\big \vert u(x) -u^{\pm }(x_0)\big \vert \, \mathrm dx=0, \end{aligned}$$where \(Q_{\nu (x_0)}^{\pm }(x_0;r) :=\{x\in Q_{\nu (x_0)}(x_0;r) : (x-x_0) \cdot \nu (x_0) \gtrless 0\}\);
-
(iii)
(Lebesgue points) for \({\mathcal {H}}^{N-1}\)-a.e. \(x_0\in \Omega \setminus S_u\) , (2.1) holds true.
Observe that (i) above entails
2.3 The approximation theorem in \(SD_p(\Omega )\)
In this section, we prove the approximation theorem for structured deformations in \(SD_p(\Omega )\). This result will be useful for the proof of our homogenization Theorem 1.1 and rests on the following two statements.
Theorem 2.3
[1, Theorem 3] Let \(f \in L^1(\Omega ; {\mathbb {R}}^{d\times N})\). Then there exist \(v \in SBV(\Omega ; {\mathbb {R}}^d)\) and a Borel function \(\beta :\Omega \rightarrow {\mathbb {R}}^{d\times N}\) such that

where \(C_N>0\) is a constant depending only on N.
Theorem 2.4
[9, Lemma 2.9] Let \(v \in BV(\Omega ; {\mathbb {R}}^d)\). Then there exist piecewise constant functions \({\bar{v}}_n\in SBV(\Omega ;{\mathbb {R}}^d)\) such that \({\bar{v}}_n \rightarrow v\) in \(L^1(\Omega ; {\mathbb {R}}^d)\) and
One of the main results in the theory developed by Del Piero and Owen was the Approximation Theorem, stating that any structured deformation can be approximated, in the \(L^\infty \) sense, by a sequence of simple deformations (see [14] for the details, in particular Theorem 5.8). For structured deformations \((g,G)\in SD(\Omega )\), the corresponding result is obtained in [9, Theorem 2.12]. Here we prove a version in \(SD_p(\Omega )\), which is the natural framework for the integral representation of the functional \(I_{\hom }\) defined in (1.8).
Theorem 2.5
(Approximation Theorem) For every \((g,G)\in SD_p(\Omega )\) there exists a sequence \(u_n\in SBV(\Omega ;{\mathbb {R}}^d)\) such that  , namely
, namely
Moreover, there exists \(C>0\) such that, for all \(n\in {\mathbb {N}}{}\),
In particular, this implies that, up to a subsequence,
Proof
Let \((g,G)\in SD_p(\Omega )\) and, by Theorem 2.3 with \(f:=\nabla g-G\), let \(v\in SBV(\Omega ;{\mathbb {R}}^{d})\) be such that \(\nabla v=\nabla g-G\). Furthermore, let \({\bar{v}}_n\in SBV(\Omega ;{\mathbb {R}}^{d})\) be a sequence of piecewise constant functions approximating v, as per Lemma 2.4. Then, the sequence of functions
is easily seen to approximate (g, G) in the sense of (2.5). In fact, \( u_n \rightarrow g\) in \(L^1(\Omega ;{\mathbb {R}}^d)\) and \(\nabla u_n(x) = G(x)\) for \({\mathcal {L}}^N\)-a.e. \(x\in \Omega \). Estimate (2.6) follows from the inequality in (2.3) and from (2.4); finally, (2.5) and (2.6) imply (2.7). \(\square \)
In light of convergence (2.5), class (1.9) of admissible sequences for relaxation problem (1.8) can be written as

which is not empty because of the Approximation Theorem just proved.
3 Standing assumptions and properties of the homogenized densities
In this section we present the hypotheses on the initial energy densities W and \(\psi \) and we prove some properties of the homogenized densities \(H_{\hom }\) and \(h_{\hom }\) defined in (1.11) and (1.12), respectively.
Assumption 3.1
Let \(p>1\) and let \(W:{\mathbb {R}}^N \times {\mathbb {R}}^{d\times N} \rightarrow [0,+\infty )\) and \(\psi :{\mathbb {R}}^N\times {\mathbb {R}}^d \times {\mathbb {S}}^{N-1}\rightarrow [0,+\infty )\) be continuous functions such that
-
(i)
For every \(\xi \in {\mathbb {R}}^{d\times N}\) and for every \((\lambda ,\nu )\in {\mathbb {R}}^d\times {\mathbb {S}}^{N-1}\), the functions \(x\mapsto W(x,\xi )\) and \(x\mapsto \psi (x, \lambda , \nu )\) are Q-periodic, namely \(W(x+q,\xi )=W(x,\xi )\) and \(\psi (x+q,\lambda ,\nu )=\psi (x,\lambda ,\nu )\) for every \(q\in {\mathbb {Z}}^{N}\);
-
(ii)
There exists \(C_W > 0\) such that, for every \(x\in {\mathbb {R}}^N\) and for every \(\xi _1,\xi _2\in {\mathbb {R}}^{d\times N}\),
$$\begin{aligned} |W(x,\xi _1) - W(x,\xi _2)| \leqslant C_W|\xi _1-\xi _2|( 1 + |\xi _1|^{p-1} + |\xi _2|^{p-1}); \end{aligned}$$ -
(iii)
There exists a function \(\omega _W:[0,+\infty )\rightarrow [0,+\infty )\) such that \(\omega _W(s)\rightarrow 0\) as \(s\rightarrow 0^+\) such that for every \(x_1,x_2\in {\mathbb {R}}^{N}\) and \(\xi \in {\mathbb {R}}^{d\times N}\)
$$\begin{aligned} |W(x_1,\xi )-W(x_2,\xi )|\leqslant \omega _W(|x_1-x_2|)(1+|\xi |^p); \end{aligned}$$ -
(iv)
There exist \(C'_W>0\), and \(c'_W>0\) such that \(W(x,\xi )\geqslant C'_W |\xi |^p- c'_W\) for every \(\xi \in {\mathbb {R}}^{d\times N}\) and a.e. \(x\in \Omega \).
-
(v)
There exist \(c_\psi , C_\psi > 0\) such that, for every \((x,\lambda ,\nu )\in {\mathbb {R}}^N\times {\mathbb {R}}^d\times {\mathbb {S}}^{N-1}\),
$$\begin{aligned} c_\psi |\lambda | \leqslant \psi (x, \lambda , \nu ) \leqslant C_\psi |\lambda |; \end{aligned}$$ -
(vi)
There exists a function \(\omega _\psi :[0,+\infty )\rightarrow [0,+\infty )\) such that \(\omega _\psi (s)\rightarrow 0\) as \(s\rightarrow 0^+\) such that for every \(x_1,x_2\in {\mathbb {R}}^{N}\) and \((\lambda ,\nu )\in {\mathbb {R}}^{d}\times {\mathbb {S}}^{N-1}\)
$$\begin{aligned} |\psi (x_1,\lambda ,\nu )-\psi (x_2,\lambda ,\nu )|\leqslant \omega _\psi (|x_1-x_2|)|\lambda |; \end{aligned}$$ -
(vii)
For every \((x,\nu )\in {\mathbb {R}}^N\times {\mathbb {S}}^{N-1}\), the function \(\lambda \mapsto \psi (x,\lambda ,\nu )\) is positively homogeneous of degree one, i.e., for every \(\lambda \in {\mathbb {R}}^d\) and \(t>0\),
$$\begin{aligned} \psi (x, t\lambda , \nu ) = t\psi (x, \lambda , \nu ); \end{aligned}$$ -
(viii)
For every \((x,\nu )\in {\mathbb {R}}^N\times {\mathbb {S}}^{N-1}\), the function \(\lambda \mapsto \psi (x,\lambda ,\nu )\) is subadditive,i.e., for every \(\lambda _1,\lambda _2\in {\mathbb {R}}^d\),
$$\begin{aligned} \psi (x, \lambda _1 + \lambda _2, \nu ) \leqslant \psi (x, \lambda _1, \nu ) + \psi (x, \lambda _2, \nu ); \end{aligned}$$ -
(ix)
For every \(x\in {\mathbb {R}}^N\), the function \((\lambda ,\nu )\mapsto \psi (x,\lambda ,\nu )\) is symmetric, i.e., for every \((\lambda ,\nu )\in {\mathbb {R}}^d\times {\mathbb {S}}^{N-1}\),
$$\begin{aligned} \psi (x, \lambda , \nu ) = \psi (x, - \lambda , - \nu ); \end{aligned}$$
Remark 3.2
We make the following observations.
-
(A)
The p-Lipschitz continuity in (ii) jointly with (i) and (iii) implies that W has p-growth from above in the second variable, namely that there exists \(C_W>0\) such that for every \((x,\xi )\in {\mathbb {R}}^N\times {\mathbb {R}}^{d\times N}\)
$$\begin{aligned} W(x,\xi )\leqslant C_{W}(1+|\xi |^p). \end{aligned}$$(3.1)On the contrary, p-growth from above jointly with the quasiconvexity of the bulk energy density in the gradient variable (which is the natural assumption in equilibrium problems in elasticity) returns the p-Lipschitz continuity.
-
(B)
Condition (v) does not allow for a control on the \({\mathcal {H}}^{N-1}\)-measure of the jump set, which, in the spirit of Approximation Theorem 2.5, is crucial in the context of structured deformations.
-
(C)
Conditions (v) and (viii) imply Lipschitz continuity of the function \(\lambda \mapsto \psi (x,\lambda ,\nu )\), i.e., for every \((x,\nu )\in {\mathbb {R}}^N\times {\mathbb {S}}^{N-1}\) and for every \(\lambda _1,\lambda _2\in {\mathbb {R}}^d\),
$$\begin{aligned} |\psi (x,\lambda _1, \nu )- \psi (x,\lambda _2, \nu )| \leqslant C_\psi |\lambda _1- \lambda _2|, \end{aligned}$$(3.2) -
(D)
Conditions (vii), (viii), and (ix) are natural ones for fractured materials; in particular, condition (ix) is compatible with the specification \(\psi (x,\lambda ,\nu )={\widetilde{\psi }}(x,\lambda \otimes \nu )\), for a suitable function \({\widetilde{\psi }}:{\mathbb {R}}^N\times {\mathbb {R}}^{d\times N}\rightarrow [0,+\infty )\).
-
(E)
We notice that conditions (v) and (vii) are better suited for the case \(p=1\). Indeed, if \(p>1\) they can be weakened to
-
(v’)
There exist \(C_\psi > 0\) such that, for every \((x,\lambda ,\nu )\in {\mathbb {R}}^N\times {\mathbb {R}}^d\times {\mathbb {S}}^{N-1}\),
$$\begin{aligned} 0 \leqslant \psi (x, \lambda , \nu ) \leqslant C_\psi |\lambda |; \end{aligned}$$ -
(vii’)
There exist constants \(C,l,\alpha >0\) such that for every \((x,\lambda ,\nu )\in {\mathbb {R}}^N\times {\mathbb {R}}^d\times {\mathbb {S}}^{N-1}\) with \(|\lambda |=1\) and for \(0<t<l\),
$$\begin{aligned} \bigg |\psi _0(x,\lambda ,\nu )-\frac{\psi (x,t\lambda ,\nu )}{t}\bigg |\leqslant Ct^\alpha , \end{aligned}$$where \(\psi _0\) is the positively homogeneous function of degree one defined by
$$\begin{aligned} \psi _0(x,\lambda ,\nu ):=\limsup _{t\rightarrow 0^+}\frac{\psi (x,t\lambda ,\nu )}{t}. \end{aligned}$$
As a consequence of this weakening, to recover the boundedness of the BV norm of the approximating sequences, the class \({\mathcal {R}}_p\) of admissible sequences for the relaxation introduced in (1.6) must be adapted to include also the uniform control \(\sup _{n\in {\mathbb {N}}} \Vert u_n\Vert _{BV(\Omega ;{\mathbb {R}}^{d})}<+\infty \,;\) moreover, the relaxed energy density \(H_{\hom }\) in (1.11) must be redefined with \(\psi _0\) in place of \(\psi \), see [9, Remark 3.3].
-
(v’)
We now present a translation invariance property of \(H_{\hom }\) and \(h_{\hom }\).
Proposition 3.3
(Translation invariance) For \(A,B\in {\mathbb {R}}^{d\times N}\), let \(H_{\hom }(A,B)\) be defined by (1.11). Then for every \(\tau \in Q\), we have \(H_{\hom } (A, B) = H^\tau _{\hom }(A,B)\), where
where \({\mathcal {C}}_p^{\mathrm {bulk}}(A,B;kQ)\) is defined in (1.13).
For \((\lambda ,\nu )\in {\mathbb {R}}^d\times {\mathbb {S}}^{N-1}\), let \(h_{\hom }(\lambda ,\nu )\) be defined by (1.12). Then for every \(\tau \in Q\), we have \(h_{\hom } (\lambda ,\nu ) = h^\tau _{\hom }(\lambda ,\nu )\), where
where \({\mathcal {C}}^{\mathrm {surf}}(\lambda ,\nu ;kQ_\nu )\) is defined in (1.14).
Proof
The proof of both (3.3) and (3.4) is a straightforward adaptation of the proof of [21, Proposition 2.15]. \(\square \)
The next proposition shows that if the initial bulk and surface energy densities W and \(\psi \) are convex in the gradient and jump variable, respectively, then asymptotic cell formula (1.11) for the homogenized bulk energy density reduces to a cell formula in the unit cube.
Proposition 3.4
Let W and \(\psi \) satisfy Assumptions 3.1, let us assume that the functions \(\xi \mapsto W(x,\xi )\) and \(\lambda \mapsto \psi (x,\lambda ,\nu )\) are convex for every \(x\in {\mathbb {R}}^d\) and every \(\nu \in {\mathbb {S}}^{N-1}\), and let
Then \(H_{\hom }(A,B)=H_{\hom }^{\mathrm {cell}}(A,B)\) for every \(A,B\in {\mathbb {R}}^{d\times N}\).
Proof
Let \(A,B\in {\mathbb {R}}^{d\times N}\) be given and let us denote by \(m_k(A,B)\) the inner infimization problem in the definition of \(H_{\hom }(A,B)\), so that (1.11) reads \(H_{\hom }(A,B)=\inf _{k\in {\mathbb {N}}} m_k(A,B)\). With this position, we also have \(H_{\hom }^{\mathrm {cell}}(A,B)=m_1(A,B)\).
We obtain the desired result if we prove that \(m_k(A,B)=m_1(A,B)\). To this aim, let \(u\in {\mathcal {C}}_p^{\mathrm {bulk}}(A,B;Q)\) be an admissible function for \(m_1(A,B)\). By extending u by Q-periodicity on kQ, we obtain a function in \({\mathcal {C}}_p^{\mathrm {bulk}}(A,B;kQ)\) which is a competitor for \(m_k(A,B)\), whence \(m_k(A,B)\leqslant m_1(A,B)\). To show the reverse inequality, we consider \(u\in {\mathcal {C}}_p^{\mathrm {bulk}}(A,B;kQ)\) a competitor for \(m_k(A,B)\) and we use the standard method of averaging its translates to produce a competitor \(v\in {\mathcal {C}}_p^{\mathrm {bulk}}(A,B;Q)\) for \(m_1(A,B)\), see [6, proof of Theorem 14.7], and using Jensen’s inequality. By letting \(J:=\{0,1,\ldots ,k-1\}^N\), it is easy to see that the function \(v:{\mathbb {R}}^{N}\rightarrow {\mathbb {R}}^{d}\) defined by
and extended by periodicity is Q-periodic and satisfies

so that \(v\in {\mathcal {C}}_p^{\mathrm {bulk}}(A,B;Q)\) and therefore \(m_1(A,B)\leqslant m_k(A,B)\), yielding the sought-after equality \(m_k(A,B)=m_1(A,B)\) and the independence of the size of the cube. The thesis follows. \(\square \)
The next proposition contains further properties of \(h_{\hom }\).
Proposition 3.5
Let \(\psi \) satisfy Assumptions 3.1 and let \({\widehat{h}}_{\hom }:{\mathbb {R}}^d\times {\mathbb {S}}^{N-1}\rightarrow [0,+\infty )\) be the function defined by
Then the following properties hold true:
-
(i)
The function \({\widehat{h}}_{\hom }\) is a limit which is independent of the choice of the cube \(Q_\nu \), once \(\nu \in {\mathbb {S}}^{N-1}\) is fixed;
-
(ii)
The function \({\widehat{h}}_{\hom }\) is continuous on \({\mathbb {R}}^d\times {\mathbb {S}}^{N-1}\) and for every \((\lambda , \nu ) \in {\mathbb {R}}^d\times {\mathbb {S}}^{N-1}\)
$$\begin{aligned} c_{\psi }|\lambda |\leqslant {\widehat{h}}_{\hom }(\lambda ,\nu ) \leqslant C_{\psi }|\lambda |, \end{aligned}$$(3.6)where \(c_\psi \) and \(C_\psi \) are the constants in Assumptions 3.1-(v);
-
(iii)
For every \((\lambda ,\nu )\in {\mathbb {R}}^d\times {\mathbb {S}}^{N-1}\), we have \(h_{\hom }(\lambda ,\nu )={\widehat{h}}_{\hom }(\lambda ,\nu )\), where \(h_{\hom }\) is the function defined in (1.12).
Proof
The proofs of items (i) and (ii) are essentially the same as that of [7, Proposition 2.2], upon observing that our density \(\psi \) satisfies (3.2), which is a stronger continuity assumption than condition [7, (iii) page 304]. Conclusion (i) is obtained verbatim as in [7, proof of Proposition 2.2, Steps 1–4]; we sketch here a proof of conclusion (ii) for the reader’s convenience.
The continuity of \({\widehat{h}}_{\hom }\) can be obtained by arguing in the following way:
-
(a)
One shows that the function \({\widehat{h}}_{\hom }(\lambda ,\cdot )\) is continuous on \({\mathbb {S}}^{N-1}\), uniformly with respect to \(\lambda \), when \(\lambda \) varies on bounded sets;
-
(b)
One shows that for every \(\nu \in {\mathbb {S}}^{N-1}\), the function \({\widehat{h}}_{\hom }(\cdot ,\nu )\) is continuous on \({\mathbb {R}}^d\);
-
(c)
One shows that \({\widehat{h}}_{\hom }\) is continuous in the pair \((\lambda ,\nu )\).
The proof of point (a) above relies on the fact that for every fixed \(\lambda \in {\mathbb {R}}^d\), formula (3.5) does not depend on the cube \(Q_\nu \) once the direction \(\nu \) is prescribed, by (i). For the proof of point (b), we can argue as in [7, proof of Proposition 2.2, Step 6] (here we exploit Assumptions 3.1-(v) and the Lipschitz continuity of \(\psi \), see (3.2)). Point (c) can be obtained by arguing as in [12, proving (ii) from (i) in Theorem 2.8].
To conclude the proof of (ii), we need to prove (3.6). The estimate from above can be easily obtained from the very definition of \({\widehat{h}}_{\hom }\) in (3.5), by using Assumptions 3.1-(v). Concerning the estimate from below, it is sufficient to observe that the functional \(SBV(\Omega ;{\mathbb {R}}^d)\ni u\mapsto \int \limits _{S_u}|[u](x)|\,\mathrm d{\mathcal {H}}^{N-1}(x)\) is lower semicontinuous with respect to the convergence  , with g a pure jump function, as it follows from the lower semicontinuity of the total variation with respect to the weak-* convergence and, again, from Assumptions 3.1-(v).
, with g a pure jump function, as it follows from the lower semicontinuity of the total variation with respect to the weak-* convergence and, again, from Assumptions 3.1-(v).
To prove (iii), we take inspiration from the proof of [10, Lemma 2.1]: we show that \({\widehat{h}}_{\hom }\) is an infimum over the integers. Together with (i), we will conclude that \({\widehat{h}}_{\hom }=h_{\hom }\), as desired. Let \(g_T:{\mathbb {R}}^d\times {\mathbb {S}}^{N-1}\rightarrow [0,+\infty )\) be defined by
so that we can write (3.5) as \({\widehat{h}}_{\hom }(\lambda ,\nu )=\limsup _{T\rightarrow +\infty } g_T(\lambda ,\nu )\).
We start by proving a monotonicity property of \(g_T\) over multiples of integer values of T, namely we prove that, for every \((\lambda ,\nu )\in {\mathbb {R}}^d\times {\mathbb {S}}^{N-1}\),
To this end, let \(u\in {\mathcal {C}}^{\mathrm {surf}}(\lambda ,\nu ;kQ_\nu )\) be a competitor for \(g_k(\lambda ,\nu )\) and consider the function \({\bar{u}}:hkQ_\nu \rightarrow {\mathbb {R}}^d\) defined by
obtained by replicating u by periodicity in the \((N-1)\)-dimensional strip perpendicular to \(\nu \) and extending it to 0 and \(\lambda \) appropriately. It is immediate to see that \({\bar{u}}\in {\mathcal {C}}^{\mathrm {surf}}(\lambda ,\nu ;hkQ_\nu )\), so that (3.8) follows.
We now consider two integers \(0<m<n\) and a function \(u\in {\mathcal {C}}^{\mathrm {surf}}(\lambda ,\nu ,mQ_\nu )\); we define \({\tilde{u}}:nQ_\nu \rightarrow {\mathbb {R}}^d\) by
and notice that \({\tilde{u}}\in {\mathcal {C}}^{\mathrm {surf}}(\lambda ,\nu ;nQ_\nu )\). Then, invoking Assumptions 3.1-(v),
so that, by infimizing first over \({\tilde{u}}\in {\mathcal {C}}^{\mathrm {surf}}(\lambda ,\nu ;nQ_\nu )\) and then over \(u\in {\mathcal {C}}^{\mathrm {surf}}(\lambda ,\nu ;mQ_\nu )\), we obtain
Using [n/m]m in place of m and (3.8), we get
By (i), \({\widehat{h}}_{\hom }(\lambda ,\nu )=\lim _{T\rightarrow +\infty } g_T(\lambda ,\nu )\), so that, by taking the limit as \(n\rightarrow \infty \) in the inequality above, we can write
this yields, by taking the infimum over the integers,
the first inequality being obvious. Recalling definition (1.12) of \(h_{\hom }(\lambda ,\nu )\), this gives the equality \({\widehat{h}}_{\hom }=h_{\hom }\) of (iii) and concludes the proof. \(\square \)
4 Proof of Theorem 1.1
This section is entirely devoted to the proof of Theorem 1.1. The proof is achieved by obtaining upper and lower bounds for the Radon–Nikodým derivatives of the functional \(I_{\hom }^{\{\varepsilon _n\}}\) defined in (1.8) with respect to the Lebesgue measure \({\mathcal {L}}^N\) and to the Hausdorff measure \({\mathcal {H}}^{N-1}\) in terms of the homogenized bulk and surface energy densities \(H_{\hom }\) and \(h_{\hom }\) defined in (1.11) and (1.12), respectively. To keep the notation lighter, and in view of the fact that the dependence on the vanishing sequence \(\{\varepsilon _n\}\) is only illusory, in the following we will just write \(I_{\hom }\) .
4.1 The bulk energy density
We tackle here the bulk energy density \(H_{\hom }\). In the next two subsections, we assume that \(x_0\in \Omega \) is a point of approximate differentiability for g and a Lebesgue point for G, namely, Theorem 2.2(i) and (iii) hold for g and (2.1) holds for G (notice that \({\mathcal {L}}^N\)-a.e. \(x_0\in \Omega \) satisfies these properties).
4.1.1 The bulk energy density: lower bound
Let \(\{u_n\}\in {\mathcal {R}}_p(g,G;\Omega )\), and let \(\mu _n\in {\mathcal {M}}^+(\Omega )\) be the Radon measure defined by

Without loss of generality, we can assume that \(\sup _{n\in {\mathbb {N}}} \mu _n(\Omega ) < + \infty \), so that there exists \(\mu \in {\mathcal {M}}^+(\Omega )\) such that (up to a not relabeled subsequence) \(\mu _n {\mathop {\rightharpoonup }\limits ^{*}}\mu \).
We will prove that
Let \(\{r_k\}\) be a vanishing sequence of radii such that \(\mu (\partial Q(x_0; r_k)) = 0\); then we have
where we have changed variables in the last equality. Upon defining, for every \(y\in Q\),
and
we have that
and
(for any \(\varphi \in L^{p'}(Q;{\mathbb {R}}^{d \times N}\)), where we used the fact that  and Theorems 2.2 and 2.1. Thus, (4.2) becomes
and Theorems 2.2 and 2.1. Thus, (4.2) becomes
where we have used the positive 1-homogeneity of \(\psi \) (see (vii)). By writing
and using the 1-periodicity of W and \(\psi \) (see (i)), (4.8) becomes
We now choose n(k) so that, setting \(s_k :=r_k/\varepsilon _{n(k)}\), we have that \(\lim _{k\rightarrow \infty } s_k = +\infty \). By defining \(v_k (y) :=u_{n(k),k}(y)\) for every \(y\in Q\), (4.9) becomes
where \(\gamma _k:=\langle x_0/\varepsilon _{n(k)}\rangle \). By (4.6) we have that \(\nabla v_k(y)=\nabla _x u_{n(k)} (x_0 + r_k y) - \nabla g(x_0)\); from (4.5) and (4.7) the sequence \(\{v_k\}\) satisfies
It is now possibleFootnote 1 to replace the sequence \(\{v_k\}\) with a sequence \(\{w_k\}\subset SBV(Q;{\mathbb {R}}^d)\) still satisfying the convergences in (4.11), such that
and such that
so that (4.10) becomes
By changing variables, setting \(z:=s_ky\) and \(U_k(z):=s_kw_k(x/s_k)\), so that
we obtain
where we have used the positive 1-homogeneity of \(\psi \) once again (see (vii)).
In order to comply with the definition of \(H_{\hom }(\nabla g(x_0), G(x_0))\) (see (1.11)), we need to integrate over integer multiples of Q. To this aim, we extend \(U_k\) to the cube \((\lfloor s_k\rfloor +1)Q\) by setting
Notice that, by the first condition in (4.14) no further jumps are created, so that \([{\hat{U}}_k](z)=[U_k](z)\) for every \(z\in S_{{\hat{U}}_k}=S_{U_k}\). Moreover, if follows from (4.16), the definition of \(U_k\) and the second condition in (4.12) that

so that \(\{{\hat{U}}_k\}\subset {\mathcal {C}}_p^{\mathrm {bulk}}\big (\nabla g(x_0),G(x_0);(\lfloor s_k\rfloor +1)Q\big )\) (see (1.13)). Then, using (3.1) and the linear growth of \(\psi \) (see (v)), we can continue with (4.15) and obtain
where we have used Proposition 3.3 for the last equality. \(\square \)
4.1.2 The bulk energy density: upper bound
Here we prove that
Let \(k\in {\mathbb {N}}\setminus \{0\}\) and \(u\in {\mathcal {C}}_p^{\mathrm {bulk}}(\nabla g(x_0),G(x_0);kQ)\) (see (1.13)). Let us consider a sequence of radii \(r_j\rightarrow 0\) as \(j\rightarrow \infty \), and let \(h_j\in SBV(Q_{rj}(x_0);{\mathbb {R}}^d)\) be a function provided by Theorem 2.3 such that
finally, let \(\{h_{j,n}\}\) be a piecewise constant approximation of \(h_j\) in \(L^1(Q_{r_j}(x_0);{\mathbb {R}}^d)\) provided by Theorem 2.4. We notice that, thanks to Proposition 2.1 and Theorem 2.2,
where \(\alpha _j :=C\big ( \big \Vert |G-G(x_0)|^p \big \Vert _{L^1(Q_{r_j}(x_0))} + \Vert \nabla g - \nabla g(x_0)\Vert _{L^1(Q_{r_j}(x_0);{\mathbb {R}}^d)}\big )\). For every \(j,n\in {\mathbb {N}}{}\), we define the function \(u_{j,n}\in SBV(Q_{r_j}(x_0);{\mathbb {R}}^d)\) by
where \(\{m_n\}\) is a diverging sequence of integers to be defined later. By defining \(kQ\ni y:=k(x-x_0)/r_j\), and by applying the Riemann–Lebesgue lemma to the sequence of functions \(kQ\ni y\mapsto u^{(n)}(y):=u(m_ny)\), we obtain that \(u^{(n)}\) converges weakly in \(L^p(kQ;{\mathbb {R}}^d)\) to  , so that
, so that
moreover, recalling (4.19), we have
so that, by applying the Riemann–Lebesgue lemma to the sequence \(kQ\ni y\mapsto \nabla u^{(n)}(y):=\nabla u(m_ny)\), we obtain that \(\nabla u^{(n)}\) converges weakly in \(L^p(kQ;{\mathbb {R}}^{d\times N})\) to  , yielding
, yielding

The convergences in (4.22) and (4.24) show that the sequence \(\{u_{j,n}\}\) is admissible for the definition of \(I_{\hom }(g,G;Q_{r_j}(x_0))\), for every \(j\in {\mathbb {N}}{}\).
Recalling that the localization \({\mathcal {O}}(\Omega )\ni A\mapsto I_{\hom }(g,G;A)\) is the trace of a Radon measure on the open subsets of \(\Omega \) (see Proposition A.2), we can estimate
where we have used the subadditivity and the positive 1-homogeneity of \(\psi \) (see (vii) and (viii)) to obtain the second inequality. Now, using, in order, (v), the estimate in (2.3) and (2.4), and finally (4.20), the last three integrals above vanish as first \(n\rightarrow \infty \) and then \(j\rightarrow \infty \).
We are left with one volume integral and one surface integral; by adding and subtracting \(W(x/\varepsilon _n,\nabla g(x_0)+\nabla u(m_nk(x-x_0)/r_j))\) in the volume integral and using (ii), Hölder’s inequality, and (4.20), and by changing variables according to
we have
where we have defined \(\gamma _n:=\langle x_0/\varepsilon _n\rangle \) and \(m_n:=\lfloor r_j/k\varepsilon _n\rfloor \), and used the decomposition
to get the first equality; the second equality follows from the kQ-periodicity of u and from the Q-periodicity in the first variable of W and \(\psi \) (see (i)).
Upon noticing that \(m_n^{-1}\langle r_j/k\varepsilon _n\rangle \rightarrow 0\) as \(n\rightarrow \infty \), we can extract a subsequence \(j\mapsto n(j)\) such that \(\big |m_n^{-1}\langle r_j/k\varepsilon _n\rangle z\big |<1/j\), so that, upon diagonalization and invoking (iii) and (vi), we can write
moreover, by using the definition of infimum in \(H_{\hom }^{\tau }\) in (3.3) (for \(\tau =\gamma _{n(j)}\)), both \(k\in {\mathbb {N}}{}\) and \(u\in SBV_{\#}(kQ;{\mathbb {R}}^d)\) can be chosen in such a way that
where we have used the translation invariance property of \(H_{\hom }\) (see Proposition 3.3) to obtain the last equality. \(\square \)
Putting (4.1) and (4.18) together, we obtain that
for all the points \(x_0\in \Omega \) satisfying the conditions stated at the beginning of Sect. 4.1, thus proving the first part of integral representation (1.10).
4.2 The surface energy density
We tackle here the surface energy density \(h_{\hom }\). From now on, we consider a point \(x_0\in S_g\). Recalling Proposition A.2, for every \(U\in {\mathcal {O}}(\Omega )\) and for every \((g,G)\in SD_p(U)\), the functional \(U\mapsto I_{\hom }(g,G;U)\) in (1.8) is a measure. In particular, (see (A.2)) there exists \(C>0\) such that
Observe that (4.26) guarantees that, for every \(g \in SBV(\Omega ;{\mathbb {R}}^d)\), the computation of the Radon–Nikodým derivative \(\displaystyle \frac{\mathrm dI_{\hom }(g, G)}{\mathrm d|D^s g|}(x_0)\) does not depend on G. Indeed, let us consider \(\{u_k\}\in {\mathcal {R}}_p(g,G;U)\) a recovery sequence for \(I_{\hom }(g, G; U)\) and, by Theorems 2.3 and 2.4, let us consider \(v\in SBV(U;{\mathbb {R}}^d)\) such that \(\nabla v=-G\) and piecewise constant functions \(v_k\in SBV(U;{\mathbb {R}}^d)\) such that \(v_k\rightarrow v\) in \(L^1(U;{\mathbb {R}}^d)\). Finally, let us define \(w_k:=u_k+v-v_k\), so that  and therefore
and therefore
Thus, by invoking (ii) and Hölder’s inequality for the volume integrals, and first the sub-additivity of \(\psi \) (see (viii)) then the linear growth of \(\psi \) (see (v)) for the surface integrals, we can estimate
where \(C>0\) is a suitable constant. By virtue of the estimate in (2.3) and by (2.4), the two surface integrals in the last line above are bounded by the volume integral, so that, by exchanging the roles of \(I_{\hom }(g,G; U)\) and \(I_{\hom }(g, 0; U)\), we arrive at the conclusion that
for every \(U \in {\mathcal {O}}(\Omega )\). In turn, this guarantees that, for \({\mathcal {H}}^{N-1}\)-a.e. \(x_0 \in S_g\),
In view of this, without loss of generality, we will consider \(G=0\) for the rest of the proof. The lower bound (see (4.28)) below will be obtained considering g of the type \(s_{\lambda ,\nu }\) in (1.15), with \((\lambda ,\nu )\in ({\mathbb {R}}^d\setminus \{0\})\times {\mathbb {S}}^{n-1}\); the upper bound (see (4.37) below) will be obtained considering g taking finitely many values, that is \(g\in BV(\Omega ;L)\) where \(L\subset {\mathbb {R}}^d\) is a set with finite cardinality. In particular, the upper bound will also hold for functions of the type \(g=s_{\lambda ,\nu }\). To conclude, the general case will be obtained via standard approximation results as in [9, Theorem 4.4, Step 2] (stemming from the ideas [5, Proposition 4.8]), so that this part of the proof (which relies on the continuity properties of \(h_{\hom }\), see Proposition 3.5) will be omitted.
4.2.1 The surface energy density: lower bound
In this section we prove that
by following the lines of [7, Proposition 6.2]. Without loss of generality, we can suppose that \(\nu _g(x_0)=e_1\) (the first vector of the canonical basis) and we denote \(s_\lambda :=s_{\lambda ,e_1}\), so that \(\lambda =[g](x_0)\). Let \(\sigma \in (0,1)\) and define \(Q_\sigma :=(-\sigma /2,\sigma /2) \times (-1/2,1/2)^{N-1}\). By the definition of relaxation in (1.8), let \(\{u_n\}\subset {\mathcal {R}}_p(g,0;\Omega )\) be a recovery sequence such that  and
and
We now substitute the sequence \(\{u_n\}\) by a new sequence \(\{{\bar{u}}_n\}\in SBV(\Omega ;{\mathbb {R}}^d)\cap L^\infty (\Omega ;{\mathbb {R}}^d)\) (this is possible thanks to Lemma A.3) with the following properties:  ; given \(\{m_n\}\) a diverging sequence of integers such that \(\beta _n:=m_n\varepsilon _n\rightarrow 0\) as \(n\rightarrow \infty \), there holds
; given \(\{m_n\}\) a diverging sequence of integers such that \(\beta _n:=m_n\varepsilon _n\rightarrow 0\) as \(n\rightarrow \infty \), there holds
(the latter convergence is due to the metrizability of the weak convergence on bounded sets); and for every \(\eta >0\),
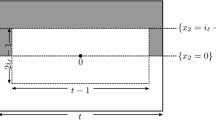
For \(\tau \in \{0\}\times {\mathbb {Z}}^{N-1}\), let \(x_{n,\tau }:=\beta _n \tau \) and \(Q_{n,\tau }:=x_{n,\tau }+ \beta _n Q_\sigma =\beta _n(Q_\sigma +\tau )\). Let \(\tau (n)\) be the index corresponding to a ’minimal cube’ such that
for every \(\tau \in \{0\}\times {\mathbb {Z}}^{N-1}\) and \(Q_{n,\tau } \subset Q_\sigma \). We now define \(Q_{n}:=Q_{n,\tau (n)}\), \(x_n:=x_{n,\tau (n)}\), and, for every \(x \in Q_\sigma \), we let \(w_n(x):={\bar{u}}_n (x_n+ \beta _n x)\). We claim that \(w_n \in SBV(Q_\sigma ;{\mathbb {R}}^d)\cap L^\infty (Q_\sigma ;{\mathbb {R}}^d)\) and
Indeed, (4.32)(i) follows by construction and (4.32)(ii) is obtained by changing variables according to \(y=x_n+\beta _nx\in Q_n\), by the definition of \(w_n\), by the choice of \(\tau \), by the inclusion \(Q_n\subset Q_\sigma \), and finally by the first limit in (4.29).
In order to prove (4.32)(iii), we observe that, by the boundedness of the energy, there exists a constant \(C>0\) such that
where the second inequality is due to the fact the cubes \(Q_{n,\tau }\) are disjoint; the third inequality follows from counting them; in the fourth inequality we have used the non-negativity of \(\psi \); in the last inequality we have exploited (iv). Next, observe that (using the change of variables \(y=x_n+\beta _nx\in Q_n\) and the inclusion \(Q_n\subset Q_\sigma \) again)
(where in the second integrand we computed the gradient of the composed function),
whence
We now prove (4.32)(iv) with \(\alpha _n= \varepsilon _n/\beta _n\). To this end, we observe that \(x_n/\varepsilon _n= m_n\tau (n)\in \{0\}\times {\mathbb {Z}}^{N-1}\) and so, by using the change of variables \(y=x_n+\beta _nx\in Q_n\), the non-negativity of W, and the periodicity of \(\psi \) (see (i)), we obtain
Thus (4.32)(iv) follows from (4.30) since
The sequence \(\{w_n\}\) can now be modified into a new sequence \(\{{\tilde{v}}_n\}\) such that \(\nabla {\tilde{v}}_n=0\) a.e. in \(Q_\sigma \) as follows: for every \(n\in {\mathbb {N}}\), we approximate via Theorem 2.5 the pair \((0,-\nabla w_n)\in SD_p(Q_\sigma )\) by a sequence \({\hat{w}}_{n,k}\), so that \({\hat{v}}_{n,k}:=w_n+{\hat{w}}_{n,k}\in SBV(Q_\sigma ;{\mathbb {R}}^d)\) is such that
moreover, invoking (4.32)(ii), we have that
Now, by (v), (viii), (2.3) and (2.4), we have
Hence, by a standard diagonalization argument, by defining \({\tilde{v}}_n:={\hat{v}}_{n, k(n)}\), we have that  , \(\nabla {\tilde{v}}_n =0\), and
, \(\nabla {\tilde{v}}_n =0\), and
The next step is to modify the sequence \(\{{\tilde{v}}_n\}\) into a new sequence \(\{v_n\}\) such that \(v_n|_{\partial Q_\sigma }=s_\lambda |_{\partial Q_\sigma }\). This can be achieved by defining the function
where \(\{r_n\}\subset (0,1)\) is a sequence such that \(\lim _{n \rightarrow \infty }r_n=1^-\) and, by (4.33),
Clearly \(\nabla v_n=0\) a.e. in \(Q_\sigma \) and, again by (4.33), \(\lim _{n \rightarrow \infty } v_n =s_\lambda \) in \(L^1(Q_\sigma ;{\mathbb {R}}^d)\). Moreover, by (3.2), (4.34), and (4.32)(iv), we have
and the latter limit is 0 by the choice of \(r_n\), as consequence of (4.35) and (4.36).
We conclude the proof by extending, without relabeling it, \(v_n\) to the whole unit cube Q by defining it as \(s_\lambda \) in \(Q\setminus Q_\sigma \), so that the previous inequality becomes
By Proposition 3.5 and the change of variables \(y=\alpha _n^{-1}x\in \alpha _n^{-1}Q\), the function \({\bar{v}}_n(y):=v_n(\alpha _ny)\) belongs to \({\mathcal {C}}^{\mathrm {surf}}(\lambda ,e_1;\alpha _n^{-1}Q)\) (see (1.14)), so that, recalling that we had set \(\lambda =[g](x_0)\) and letting \(\eta \rightarrow 0\), we obtain (4.28). \(\square \)
4.2.2 The surface energy density: upper bound
In this section we prove that
by following the lines of [7, Proposition 6.2]. Recall that by the preliminary discussion we made at the beginning of the section we will restrict ourselves to the case of piecewise constant functions g, that is \(g\in BV(\Omega ;L)\), where \(L\subset {\mathbb {R}}^d\) has finite cardinality; naturally, such a function g is also an element of \(SBV(\Omega ;{\mathbb {R}}^{d})\). We will obtain estimate (4.37) by using the abstract representation result contained in Theorem A.4, for which we need to prove that our (localized) functional \(I_{\hom }:SD_p(\Omega )\times {\mathcal {O}}(\Omega )\rightarrow [0,+\infty )\) satisfies hypotheses (i)–(v) of Theorem A.4.
As a consequence of (4.26), for every \(g \in BV(\Omega , L)\) and for every \(U\in {\mathcal {O}}(\Omega )\), the inequality \(I_{\hom }(g, 0; U \cap S_g)\leqslant C|D^s g|(U \cap S_g)\) holds true, giving (i). By Proposition A.2, for every \(g \in BV(\Omega ; L)\), the set function \({\mathcal {O}}(\Omega )\ni U\mapsto I_{\hom }(g, 0; U \cap S_g)\) is a measure, giving (ii). From definition (1.8) of \(I_{\hom }\) and from the locality property of the (sequence of) energies \(\{E_{\varepsilon _n}\}\), we obtain that \(I_{\hom }(g, 0; U\cap S_g) = I_{\hom }(g_1,0; U\cap S_{g_1})\) whenever \(g= g_1\) a.e. in \(U\in {\mathcal {O}}(\Omega )\). Indeed, it suffices to notice that the competitors for \(I_{\hom }(g,0)\) and \(I_{\hom }(g_1,0)\) are the same. Therefore, condition (iii) is satisfied. To show that condition (iv) holds, let us consider a sequence \(\{g_n\}\subset SBV(\Omega ;L)\) such that \(g_n\rightarrow g\) pointwise a.e.; then, the fact that L has finite cardinality entails that \(g_n\rightarrow g\) in \(L^1(\Omega ;{\mathbb {R}}^d)\), and therefore that  . Since \(g\mapsto I_{\hom }(g,0;U)\) is lower semicontinuous for every \(U\in {\mathcal {O}}(\Omega )\) by definition of \(\Gamma \)-liminf, the desired inequality
. Since \(g\mapsto I_{\hom }(g,0;U)\) is lower semicontinuous for every \(U\in {\mathcal {O}}(\Omega )\) by definition of \(\Gamma \)-liminf, the desired inequality
follows immediately. It remains to prove (v): as a matter of fact, we will prove a stronger condition, as it is obtained in the proof of [7, Proposition 4.2]. This translation invariance result, which is obtained following the argument in [7, Lemma 3.7], provides then a sufficient condition for (v). We claim that, for every \(z\in {\mathbb {R}}^N\) and every \(U\in {\mathcal {O}}(\Omega )\), we have
Indeed, let \(z\in {\mathbb {R}}^N\) be given and observe that it can be approximated by means of a sequence of integers in the sense that there exists \(\{z_n\}\subset {\mathbb {Z}}^{N}\) such that \(\varepsilon _nz_n\rightarrow z\) as \(n\rightarrow \infty \). Let now \(U\in {\mathcal {O}}(\Omega )\) be fixed, let \(\{u_n\}\in {\mathcal {R}}_p(g,0;U)\) be a recovery sequence for \(I_{\hom }(g,0;U)\), and define \(v_n:=u_n(\cdot -\varepsilon _n z_n):U+z_n\rightarrow {\mathbb {R}}^d\). Then, by using the Q-periodicity assumptions (i) on W and \(\psi \), we have
Let now \(V \subset \subset U\), so that, for n sufficiently large we may assume \(U + \varepsilon _n z_n \supseteq V + z\); hence, invoking the non-negativity of W and \(\psi \),
which yields \(I_{\hom }(g, 0;U) \geqslant I_{\hom }(g(\cdot -z), 0;V+z)\), since  . By the arbitrariness of \(V \subset \subset U\) we obtain that \(I_{\hom }(g, 0; U) \geqslant I_{\hom }(g(\cdot - z), 0;U+z)\). The reverse inequality can be obtained with the same reasoning, by defining \(v_n:=u_n(\cdot +\varepsilon z_n)\). Translation invariance (4.38) is proven, and this implies condition (v).
. By the arbitrariness of \(V \subset \subset U\) we obtain that \(I_{\hom }(g, 0; U) \geqslant I_{\hom }(g(\cdot - z), 0;U+z)\). The reverse inequality can be obtained with the same reasoning, by defining \(v_n:=u_n(\cdot +\varepsilon z_n)\). Translation invariance (4.38) is proven, and this implies condition (v).
We are in position to apply Theorem A.4 and conclude that there exists a function \({\tilde{\psi }}:\Omega \times L\times L\times {\mathbb {S}}^{N-1}\rightarrow [0,+\infty )\) such that the integral representation
holds for every \(g \in BV(\Omega ;L)\) and for every \(U\in {\mathcal {O}}(\Omega )\). Exactly with the same proof as in [7, Lemma 3.7] and [7, Equation (4.6)], one can prove that the density \({\tilde{\psi }}\) does not depend on the x variable and depends on g only through its jump, so that there exists \({\bar{h}}_{\hom }:{\mathbb {R}}^d\times {\mathbb {S}}^{N-1}\rightarrow [0,+\infty )\) such that
On the other hand, we can get a precise estimate from above arguing as in [7]. Upon defining the functional \(J_{\hom }:BV(\Omega ;L)\times {\mathcal {O}}(\Omega )\rightarrow [0,+\infty )\) as
we obtain
for every \(g \in BV(\Omega ; L)\) and every \(U\in {\mathcal {O}}(\Omega )\). Now, [7, Proposition 6.1] grants thatFootnote 2
where \(h_{\hom }:{\mathbb {R}}^d\times {\mathbb {S}}^{N-1}\rightarrow [0,+\infty )\) is the functions defined in (1.12); in turn, together with (4.40), we obtain
whence
which is (4.37) when \(g \in BV(\Omega , L)\). Putting (4.28) and (4.37) together and keeping (4.27) into account, we obtain that, for \(g=s_{\lambda ,\nu }\in BV(\Omega ;L)\) and for all \(G \in L^p(\Omega ;{\mathbb {R}}^{d \times N})\), the equality
holds for all the points \(x_0\in \Omega \) satisfying the conditions stated at the beginning of Sect. 4.2. To conclude, the equality in the general case, that is, for every \(g\in SBV(\Omega ;{\mathbb {R}}^d)\), is obtained via standard approximation results as in [9, Theorem 4.4, Step 2] (stemming from the ideas [5, Proposition 4.8]), so that this part of the proof, which relies on the continuity properties of \(h_{\hom }\) stated in Proposition 3.5, will be omitted.
Theorem 1.1 is now completely proved. \(\square \)
Notes
This is achieved, following the strategy in [9, Proposition 3.1 Step 2], by constructing a double-indexed sequence that gradually makes a transition from \(v_k\) to its limit. The transition takes place across a suitably located frame of vanishing thickness 1/m (independent of k) and is obtained via convex combination (see also the construction in [9, Lemma 2.21] where suitable truncations of the approximating sequences are considered; [9, Lemma 2.20] (see Lemma A.3) states that it is possible to work on bounded sequences). A sequence \({\tilde{w}}_k\) is then obtained by a diagonalization argument. Finally, the condition on the average in (4.12) is enforced by a further modification of the sequence \({\tilde{w}}_k\) into \(w_k\) by modification with a linear function on cubes that invade Q. The difference between our problem and that in [9] is the explicit dependence on the spatial variable that we have; nonetheless, our assumptions (ii) and (v) allow us to estimate the vanishing terms independently of the spatial variable.
We observe that in [7] the standing hypothesis on the growth of the surface energy density \(\psi \) is of the type \(c(1+|\lambda |)\leqslant \psi (\lambda , \nu )\leqslant C(1+|\lambda |)\), in contrast with our (v), the difference being that the measure \({\mathcal {H}}^{N-1}(S_{u_n})\) cannot be controlled in our case. Nonetheless, this is circumvented by the introduction of the functional \(J_{\hom }\) in (4.39), which provides an upper bound to \(I_{\hom }\) and to which we can apply [7, Proposition 6.1].
References
Alberti, G.: A Lusin type theorem for gradients. J. Funct. Anal. 100, 110–118 (1991)
Ambrosio, L.: Compactness for a special case of functions of bounded variation. Boll. Un. Mat. Ital. 3-B 7, 857–881 (1989)
Ambrosio, L., Braides, A.: Functionals defined on partitions in sets of finite perimeter I. Integral representation and \(\Gamma \)-convergence. J. Math. Pures Appl. 69(3), 285–305 (1990)
Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and Free Discontinuity Problems, Oxford Mathematical Monographs. The Clarendon Press, Oxford University Press, New York (2000)
Ambrosio, L., Mortola, S., Tortorelli, V.M.: Functionals with linear growth defined on vector valued \(BV\) functions. J. Math. Pures Appl. 70(3), 269–323 (1991)
Braides, A., Defranceschi, A.: Homogenization of Multiple Integrals. Oxford Lecture Series in Mathematics and its Applications, vol. 12. The Clarendon Press, Oxford University Press, New York (1998)
Braides, A., Defranceschi, A., Vitali, E.: Homogenization of free discontinuity problems. Arch. Ration. Mech. Anal. 135(4), 297–356 (1996)
Carita, G., Matias, J., Morandotti, M., Owen, D.R.: Dimension reduction in the context of structured deformations. J. Elast. 133(1), 1–35 (2018)
Choksi, R., Fonseca, I.: Bulk and interfacial energy densities for structured deformations of continua. Arch. Ration. Mech. Anal. 138(1), 37–103 (1997)
Cioranescu, D., Damlamian, A., De Arcangelis, R.: Homogenization of quasiconvex integrals via the periodic unfolding method. SIAM J. Math. Anal. 37(5), 1435–1453 (2006)
Dal Maso, G.: An Introduction to \(\Gamma \)-Convergence. Progress in Nonlinear Differential Equations and their Applications, vol. 8. Birkhäuser Boston Inc., Boston (1993)
De Giorgi, E: Semicontinuity theorems in the calculus of variations. Quaderni dell’accademia pontaniana. 56 (2009)
De Giorgi, E., Letta, G.: Une notion générale de convergence faible pour des fonctions croissantes d’ensemble. Ann. Sc. Norm. Sup. Pisa Cl. Sci. 4, 61–99 (1977)
Del Piero, G., Owen, D.R.: Structured deformations of continua. Arch. Ration. Mech. Anal. 124(2), 99–155 (1993)
Deseri, L., Owen, D.R.: Invertible structured deformations and the geometry of multiple slip in single crystals. Int. J. Plast. 18, 833–849 (2002)
Evans, L.C., Gariepy, R.F.: Measure Theory and Fine Properties of Functions, Textbooks in Mathematics. CRC Press, Boca Raton (2015)
Federer, H.: Geometric Measure Theory Die. Grundlehren der mathematischen Wissenschaften, vol. 153. Springer, New York (1969)
Fonseca, I., Malý, J.: Relaxation of multiple integrals in Sobolev spaces below the growth exponent for the energy density. Ann. Inst. H. Poncaré, Anal. Non Linéaire. Sect. C 14(3), 309–338 (1997)
Fonseca, I., Müller, S.: Quasi-convex integrands and lower semicontinuity in \(L^1\). SIAM J. Math. Anal. 23(5), 1081–1098 (1992)
Fonseca, I., Müller, S.: Relaxation of quasiconvex functionals in \({\rm BV}(\Omega ,{{\mathbf{R}}}^p)\) for integrands \(f(x, u,\nabla u)\). Arch. Ration. Mech. Anal. 123(1), 1–49 (1993)
Matias, J., Morandotti, M., Santos, P.M.: Homogenization of functionals with linear growth in the context of \({\cal{A}}\)-quasiconvexity. Appl. Math. Optim. 72(3), 523–547 (2015)
Matias, J., Morandotti, M., Zappale, E.: Optimal design of fractured media with prescribed macroscopic strain. J. Math. Anal. Appl. 449(2), 1094–1132 (2017)
Ziemer, W.P.: Weakly Differentiable Functions, Graduate Texts in Mathematics, vol. 120. Springer, New York (1989)
Acknowledgements
MA, MM, and EZ are members of the Gruppo Nazionale per l’Analisi Matematica, la Probabilità e le loro Applicazioni (GNAMPA) of the Instituto Nazionale di Alta Matematica “F. Severi” (INdAM). JM acknowledges support from FCT/Portugal through CAMGSD, IST-ID, projects UIDB/04459/2020 and UIDP/04459/2020. MM and EZ acknowledge funding from the GNAMPA Project 2020 Analisi variazionale di modelli non locali nelle scienze applicate. MM is a member of the Integrated Additive Manufacturing center at Politecnico di Torino. MM acknowledges both that the present research fits in the scopes of the MIUR Grant Dipartimenti di Eccellenza 2018-2022 (E11G18000350001) and partial support from the Starting grant per giovani ricercatori of Politecnico di Torino. The authors wish to thank the anonymous referee for their useful suggestions to improve the readability of the paper.
Funding
Open access funding provided by Politecnico di Torino within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: Some technical results
Appendix A: Some technical results
This appendix contains some technical results that are either reported here with no proof or proved for the reader’s convenience since their proof is quite standard but in some measure different from the analogous results in the literature.
We start by showing that, for every \(U \in {\mathcal {O}}(\Omega )\) and for every \((g,G) \in SD_p(U)\), the localization \(U\mapsto I_{\hom }(g, G; U)\) of the functional \( I_{\hom }^{\{\varepsilon _n\}}\) of (1.8), defined as
(recalling the definition of the set \({\mathcal {R}}_p\) in (2.8)), is the trace of a Radon measure which is absolutely continuous with respect to \({\mathcal {L}}^N + |D^s g|\).
To this end we recall a by now classical result of Fonseca and Malý [18], which refines the De Giorgi–Letta criterion [13] to establish sufficient conditions under which a functional is the restriction to open sets of a bounded Radon measure.
Lemma A.1
[18] Let X be a locally compact Hausdorff space, let \(\Pi :{\mathcal {O}}(X) \rightarrow [0,+\infty ]\) be a set function, and let \(\mu \) be a finite Radon measure on X satisfying
-
(i)
For every \(U, V, Z \in {\mathcal {O}}(X)\) such that \(U \subset \subset V \subset \subset Z\), the following nested subadditivity property holds: \(\Pi (Z) \leqslant \Pi (V) + \Pi (Z\setminus {\overline{U}})\);
-
(ii)
For every \(U \in {\mathcal {O}}(X)\) and for every \(\varepsilon > 0\) there exists \(U_\varepsilon \in {\mathcal {O}}(X)\) such that \(U_\varepsilon \subset \subset U\) and \(\Pi (U \setminus \overline{U_\varepsilon })\leqslant \varepsilon \);
-
(iii)
\(\Pi (X)\geqslant \mu (X)\);
-
(iv)
For every \(U \in {\mathcal {O}}(X)\), there holds \(\Pi (U) \leqslant \mu ({\overline{U}})\).
Then \(\Pi \) is the restriction of the finite Radon measure \(\mu \) to the open subsets of X.
The following proposition is in the spirit of [9, Proposition 2.22].
Proposition A.2
Assume that Assumptions 3.1 hold and let \((g, G) \in SD_p(\Omega )\). Then the localized functional \({\mathcal {O}}(\Omega )\ni U\mapsto I_{\hom }(g, G;U)\) defined in (A.1) is the trace on \({\mathcal {O}}(\Omega )\) of a finite Radon measure on \({\mathcal {B}}(\Omega )\).
Proof
The proof relies on Lemma A.1: we will show that its hypotheses are satisfied by \(\Pi (U)= I_{\hom }(g,G;U)\) and \(\mu ={\mathcal {L}}^N+|D^sg|\). First we prove that for every \(U\in {\mathcal {O}}(\Omega )\) and for every \((g, G)\in SD_p(\Omega )\) there exists a constant \(C>0\) such that
We observe that by Theorem 2.5 there exists \(\{u_n\} \subset SBV(U;{\mathbb {R}}^d)\) such that  and such that (2.6) and (2.7) hold. Thus, the definition of \(I_{\hom }(g, G; U)\), the linear growth condition (v) of \(\psi \), and (3.1) entail that
and such that (2.6) and (2.7) hold. Thus, the definition of \(I_{\hom }(g, G; U)\), the linear growth condition (v) of \(\psi \), and (3.1) entail that
which implies (A.2).
We start proving condition (iv) in Lemma A.1. By the definition of \(\Gamma \)-limit , there exists a sequence \(\{u_n\}\subset SBV(\Omega ;{\mathbb {R}}^d)\) such that  and along which
and along which
Upon the extraction of a subsequence, we know that

and
On the other hand, for every \(U \in {\mathcal {O}}(\Omega )\) we have that
Next we prove condition (i) in Lemma A.1. Consider \(U,V,Z \in {\mathcal {O}}(\Omega )\) such that \(U\subset \subset V\subset \subset Z\). Fix \(\eta >0\) and consider two sequences \(\{u_n\}\subset SBV(V;{\mathbb {R}}^d)\) and \(\{v_n\} \in SBV(Z\setminus {\overline{U}};{\mathbb {R}}^d)\) which are almost minimizing for \(I_{\hom }\), that is,
with  ,
,  .
.
In order to connect the functions without adding more interfaces, we argue as in the proof of [22, Proposition 5.1]. For \(\delta > 0\) small enough, consider
For \(x \in Z\), let \(d(x) :={\text {dist}}(x,U)\). Since the distance function to a fixed set is Lipschitz continuous (see [23, Exercise 1.1]), we can apply the change of variables formula (see [16, Theorem 2, Section 3.4.3]), to obtain
and, since the Jacobian determinant Jd(x) is bounded and \(u_n - v_n \rightarrow 0\) in \(L^1(V \cap (Z \setminus {\overline{U}});{\mathbb {R}}^d)\), it follows that for almost every \(\varrho \in [0, \delta ]\) we have
Fix \(\varrho _0\in [0; \delta ]\) such that (A.6) holds. We observe that \(U_{\varrho _0}\) is a set with locally Lipschitz boundary since it is a level set of a Lipschitz function (see, e.g., [16]). Hence we can consider \(u_n\) and \(v_n \) on \(\partial U_{\varrho _0}\) in the sense of traces and we can define
By the choice of \(\varrho _0\), the function \(w_n\) is admissible for \(I_{\hom }(g, G;Z)\); in particular  . Thus we have
. Thus we have
Observing that, by (v), and (A.6), the last surface integral converges to 0, condition (i) follows by letting \(\eta \rightarrow 0^+\).
It remains to prove conditions (ii) and (iii) in Lemma A.1. To this end, fix \(\eta >0\) and take \(V\subset \subset Z\) such that \(\mu (Z \setminus V)<\eta \). By (i), (A.4), and (A.5), it results
Letting \(\eta \rightarrow 0^+\), we obtain \(\mu (Z)\leqslant I_{\hom }(g, G; Z)\), which proves (ii).
Finally, fix \(\eta >0\) and \(Z\in {\mathcal {O}}(\Omega )\) and take K a compact set such that \(K \subset \subset Z\) with \(\lambda (Z\setminus K)<\eta \) (with \(\lambda \) the measure in the right-hand side of (A.3)), and \(V\in {\mathcal {O}}(\Omega )\) an open set such that \(K\subset \subset V\subset \subset Z\). Using (i) and (A.5) we have
and (iii) follows by taking the limit \(\eta \rightarrow 0^+\). The proposition is fully proved. \(\square \)
We now report a result stating that the functional \(I_{\hom }\) in (1.8) can be obtained along sequences that are bounded in \(L^\infty \). Let \(E_n\) be as in (1.5) and for every \(g \in L^\infty (\Omega ;{\mathbb {R}}^d)\cap SBV(\Omega ;{\mathbb {R}}^d)\), and \(G \in L^p(\Omega ;{\mathbb {R}}^{d \times N})\) define
Following the same arguments as in [9, Lemma 2.20] one can prove that \(I_{\hom }(g, G) = I^\infty _{\hom }(g,G)\) when \(g \in L^\infty (\Omega ;{\mathbb {R}}^d)\cap SBV(\Omega ;{\mathbb {R}}^d)\), i.e., the additional \(L^\infty \) bound on admissible sequences for (1.8) does not increase the energy, and it is used both in Sects. 4.1 and 4.2.
Lemma A.3
Let \(p > 1\), \((g, G)\in \big (SBV(\Omega ;{\mathbb {R}}^{d})\cap L^\infty (\Omega ;{\mathbb {R}}^d)\big ) \times L^p(\Omega ;{\mathbb {R}}^{d \times N})\), and assume that Assumptions 3.1 hold. Then
Finally, in the proof of upper bound (4.37) for the surface energy density \(h_{\hom }\), we used the integral representation result on partitions stated in [3, Theorem 3.1], which we recall here for the reader’s convenience.
Theorem A.4
Let \(L \subset {\mathbb {R}}^m\) be a subset with finite cardinality, and let \(F:BV (\Omega ;L) \times {\mathcal {O}}(\Omega )\rightarrow [0, +\infty )\) be a functional satisfying the following conditions:
-
(i)
There exists \(\Lambda >0\) such that \(0 \leqslant F(u; U) \leqslant \Lambda {\mathcal {H}}^{N-1}(U \cap S_u)\) for every \(u \in BV(\Omega ;L)\) and for every \(U \in {\mathcal {O}}(\Omega )\);
-
(ii)
\(F(u;\cdot )\) is a measure for every \(u \in BV (\Omega ; L)\);
-
(iii)
\(F(u; U) = F(v; U)\) whenever \(u = v\) almost everywhere in \(U\in {\mathcal {O}}(\Omega )\);
-
(iv)
\(u_h \rightarrow u\) a.e. in U implies that \(F(u; U) \leqslant \liminf _{h \rightarrow +\infty }F(u_h;U)\) for every \(U \in {\mathcal {O}}(\Omega )\);
-
(v)
For every \(U \subset \subset \Omega \), there exists a continuous function \(\omega _U:[0, +\infty ) \rightarrow [0, +\infty )\) such that \(\omega _U(0) = 0\) and \(|F(u, V) - F(v, V+ z)|\leqslant \omega _U(|z|){\mathcal {H}}^{N-1}(U \cap S_u)\) whenever \(V \in {\mathcal {O}}(U)\), \(z \in {\mathbb {R}}^N\), \(|z|<\frac{{\text {dist}}(U,\partial \Omega )}{2}\), and \(v(x + z) = u(x)\) in V.
Then there exists a unique continuous function \(f :\Omega \times L \times L\times {\mathbb {S}}^{N-1}\rightarrow [0,\Lambda ]\) such that \(f(x, i, j, \nu ) = f(x, j, i, -\nu )\), and the function \(\displaystyle p \mapsto f\Big (x, i, j,\frac{p}{|p|}\Big ) |p|\) is convex in \({\mathbb {R}}^N\) for every \(x \in \Omega \), \(i, j \in L\), and F(u; U) is representable as
for every \(u \in BV (\Omega ; L)\) and for every \(U \in {\mathcal {O}}(\Omega )\).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Amar, M., Matias, J., Morandotti, M. et al. Periodic homogenization in the context of structured deformations. Z. Angew. Math. Phys. 73, 173 (2022). https://doi.org/10.1007/s00033-022-01817-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00033-022-01817-6



 , where
, where 