Abstract
The onset of thermal convection in anisotropic rotating bidisperse porous media is investigated. The optimal result concerning the coincidence between linear instability and nonlinear stability thresholds with respect the \(L^2\)-norm is obtained.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The onset of thermal convection for both clear fluids (see [7, 20]) and fluids saturating porous materials (see [19, 25]) has been widely studied by many scientists—in the past as nowadays—due to its relevant applications in different fields, such as geophysics (geothermal reservoirs, geological storage of carbon dioxide), astrophysics (pore water convection within carbonaceous chondrite parent bodies), engineering and industrial process (water treatment process, nuclear waste disposal, chemical reactor engineering, and the storage of heat-generating materials such as grain and coal) (see [14] and references therein). In [1, 19] numerical studies of fluid flows through porous media have been performed; then in [5, 6, 12] the onset of convection in anisotropic porous media under various assumptions has been analyzed. Moreover, [13, 31] investigated clear fluid flows with pressure dependent viscosity, while [21,22,23] deal with the same problem but through porous media. Finally, [11, 20, 24, 30] analyze the onset of convection of a binary mixture in a porous medium, of a non-Newtonian fluid between two vertical plate, of a fluid saturating a porous medium under LTNE assumption and of fluids saturating rotating porous media, respectively.
However, in recent times, double-porosity materials have attracted the attention of a large number of researchers. A double-porosity material is also referred to as bidisperse porous medium (BDPM): it has the normal pore structure, but the solid skeleton has cracks or fissures in it. In particular, a BDPM is composed of clusters of large particles that are agglomerations of small particles, there are macropores between the clusters and micropores within them, and in particular the macropores are referred to as f-phase, while the remainder of the structure is referred to as p-phase. The reason of this nomenclature is that one can think of the f-phase as being a fracture phase, the p-phase as a porous phase [17].
Let \(\varphi \) be the porosity of the macropores and \(\epsilon \) be the porosity of the micropores, thus \((1- \varphi ) \epsilon \) is the fraction of volume occupied by the micropores, \(\varphi + (1- \varphi ) \epsilon \) is the fraction of volume occupied by the fluid, \((1- \epsilon )(1-\varphi )\) is the fraction of volume occupied by the solid skeleton.
The fundamental theory for thermal convection in bidisperse porous media can be found in [15,16,17].
The study of bidisperse convection has a large number of practical applications, such as industrial ones, for example in order to design heat pipes (as reported in [14], since the bidisperse wick structure significantly increases the area available for liquid film evaporation, it has been proposed for use in the evaporator of heat pipes), or medical ones, in fact brain and human bones may be modeled as bidisperse porous media (in particular, the analysis of the onset convection in a BDPM allows to understand and model interstitial fluid flow in bones or to develop tissue engineering strategy for bone defects [25, 26]). Since in bidisperse porous media the convection occurs at higher Rayleigh numbers, the heat transfer in BDPM due to the convective movement is delayed, and for this reason BDPM are significantly better used in thermal insulation problems and thermal management problem (such as cooling of data centers) than simple porous materials [8, 9, 17].
As reported in [27], bidisperse porous media are increasingly important in the chemical engineering field and regarding anisotropic materials, while anisotropic single porosity media have been widely studied by several authors (see for example [5, 12, 18]), anisotropic bidisperse porous materials may have much more potentials, since they offer many possibilities to design manmade materials for heat transfer or insulation problems, for oil recovery from underground reservoir, for nuclear waste recovery and so on (see [3, 10, 28, 29] and references therein). Therefore, in the present, we allow fully anisotropic permeabilities in both f-phase and p-phase.
The key role of rotation on the onset of thermal convection in porous materials has been pointed out by many authors in view of its practical applications in geophysics and in engineering (food process industry, chemical process industry, centrifugal filtration processes, rotating machinery) [30], hence the study of thermal convection in rotating BDPM may be necessary and useful as well, see for instance [2, 4], which deal with the onset of convection in a horizontal layer of rotating isotropic BDPM, according to Darcy’s law and taking into account the Vadasz term, respectively, or [3], which analyzes the onset of convection in a horizontally isotropic rotating BDPM.
Envisaging a rotating machinery constituted by an engineered fully anisotropic bidisperse porous material, the aim of this paper is to analyze the onset of thermal convection in an anisotropic bidisperse porous medium uniformly rotating about a vertical axis, through linear and nonlinear stability theory. The plan of the paper is as follows. The mathematical model and the associated perturbation equations are introduced in Sect. 2. In Sect. 3 the strong version of the principle of exchange of stabilities is proved and the linear instability analysis of the thermal conduction solution is performed, to determine the steady instability threshold. In Sect. 4, the nonlinear stability analysis of the thermal conduction solution is performed, proving the coincidence between the linear and the nonlinear stability thresholds with respect to the \(L^2\)-norm. In Sect. 5, in order to analyze the influence of rotation and of anisotropic permeability on the onset of convection, numerical simulations are presented. The paper ends with a conclusions section, in which all the results are collected.
2 The mathematical model
Let Oxyz be a reference frame with fundamental unit vectors \(\mathbf{i},\mathbf{j},\mathbf{k}\) (\(\mathbf{k}\) pointing vertically upward) and let L be a layer of an anisotropic bidisperse porous medium, saturated by an homogeneous incompressible fluid heated from below. Let us assume that the layer L—of thickness d—rotates about the vertical axis z, with constant angular velocity \({\varvec{\Omega }}=\Omega \mathbf{k}\) and that the temperature in the macropores \((T_f)\) and the temperature in the micropores \((T_p)\) are the same, i.e., \(T^f=T^p=T\).
Let us assume that the axes (x, y, z) are the principal axes of the permeability, so the permeability tensors in the macropores and in the micropores may be written as
where
In the Oberbeque–Boussinesq approximation and extending the Darcy’s Law in order to include the Coriolis term in the momentum equations for the micropores and the macropores, the governing equations for thermal convection are [2, 27]:
where
are the reduced pressures, \(\mathbf{x}=(x,y,z)\), \(\mathbf{v}^s\) = seepage velocity for \(s=\{f,p\}\), \(\zeta \) = interaction coefficient between the f-phase and the p-phase, \(\mathbf{g}=-g \mathbf{k}\) = gravity, \(\mu \) = fluid viscosity, \(\varrho _F\) = reference constant density, \(\alpha \) = thermal expansion coefficient, c = specific heat, \(c_p\) = specific heat at a constant pressure, \((\varrho c)_m=(1-\varphi )(1-\epsilon )(\varrho c)_{sol}+\varphi (\varrho c)_f+\epsilon (1-\varphi )(\varrho c)_p\), \(k_m=(1-\varphi )(1-\epsilon )k_{sol}+\varphi k_f+\epsilon (1-\varphi )k_p\) = thermal conductivity (the subscript sol is referred to the solid skeleton).
To (1), the following boundary conditions are appended
where \(\mathbf{n}\) is the unit outward normal to the impermeable horizontal planes delimiting the layer and \(T_L>T_U\).
The problem (1)-(2) admits the steady state (conduction solution):
Defining \(\{ \mathbf{u}^f, \mathbf{u}^p, \theta , \pi ^f, \pi ^p \}\) a perturbation to the steady solution, the evolution equations for the perturbation fields are
where \(\mathbf{u}^f=(u^f,v^f,w^f), \ \mathbf{u}^p=(u^p,v^p,w^p)\). Using the following non-dimensional parameters
where the scales are given by
and introducing the Taylor number \({\mathcal {T}}\) and the thermal Rayleigh number R, respectively, given by
the resulting non-dimensional perturbation equations, omitting all the asterisks, are
under the initial conditions
with \(\nabla \cdot \mathbf{u}^s_0=0\), for \(s=\{f,p\}\), and the boundary conditions
The above equations are defined in \(\{ (x,y,z,t) \in {\mathbb {R}}^4 | z \in (0,1), t>0 \}\).
In the sequel, we will suppose that the perturbation fields are periodic in the x and y directions of period \(\displaystyle {\frac{2 \pi }{l}}\) and \(\displaystyle {\frac{2 \pi }{m}}\), respectively, and we will denote by
the periodicity cell.
3 Instability analysis
In this section we will perform linear instability analysis of the basic solution, to this aim let us first linearise the perturbation Eq. (4), i.e.,
Since the system (6) is autonomous, we seek solutions which have time-dependence like \(e^{\sigma t}\), i.e., solutions of form
with \(\sigma \in {\mathbb {C}}\) and \(s=\{f,p\}\). By virtue of (7), (6) becomes
Let \(^*\) be the complex conjugate of a field. Multiplying \((8)_1\) by \(\mathbf{u}^{f*}\), \((8)_2\) by \(\mathbf{u}^{p*}\) and \((8)_3\) by \(\theta ^{*}\), integrating each equation over the periodic cell V and adding the resulting equations, one obtains
where \(\mathbf{M}^f=(\mathbf{K}^f)^{-1}\) and \(\mathbf{M}^p=(\mathbf{K}^p)^{-1}\), while \((\cdot , \cdot )\) and \(\Vert \cdot \Vert \) are inner product and norm on the Hilbert space \(L^2(V)\), respectively. Setting \(\sigma =\sigma _r+i \sigma _i\), the imaginary part of equation (9) is
Applying the same procedure to the complex conjugate of (8), multiplying by \(\mathbf{u}^f, \mathbf{u}^p, \theta \) one gets
Adding (10) and (11), one obtains
and hence the strong version of the principle of exchange of stabilities holds: if the convection sets in, it arises necessary via a stationary motion (steady convection).
To determine the instability threshold for the onset of stationary convection, let us consider system (8) with \(\sigma =0\), i.e.,
From system (1), one obtains
where A is the coefficients matrix of system \((12)_{1,2}\)–\((12)_{4,5}\) and
Hence, differentiating equations (13) with respect to z and equations \((12)_3\)–\((12)_6\) with respect to x and y, by virtue of the incompressible conditions \((12)_{7}\)–\((12)_{8}\), differentiating with respect to z, i.e.,
one obtains the following system
where \(\hat{\gamma _s}=\gamma _s+1\), for \(s=1,2\) and
By virtue of periodicity of perturbation fields in the horizontal directions x and y, taking into account the boundary conditions (5), since \(\{ \sin (n \pi z) \}_{n \in {\mathcal {N}}}\) is a complete orthogonal system for \(L^2([0,1])\), employing normal modes solutions [7]:
from (15) one obtains
where \(\Lambda _n=n^2 \pi ^2 + l^2 + m^2\) and
Finally, requiring a zero determinant for (17), the linear instability threshold for the onset of stationary convection is:
where both numerator and denominator of the right hand side of (18) are positive. The minimization (18) is numerically analyzed in Sect. 5.
Let us point out that
-
(i)
assuming \(h_1=h_2=h\), \(k_1=k_2=k\) (horizontally isotropic case) and for \({\mathcal {T}}\rightarrow 0\), i.e., in the absence of rotation, we get
$$\begin{aligned} R_L^2=\min _{n,a^2} \dfrac{{\hat{\Gamma }} \Lambda _n}{a^2} \dfrac{a^4 \Gamma {\hat{\Gamma }}^{-1} + n^4 \pi ^4 + a^2 n^2 \pi ^2 {\hat{K}} {\hat{\Gamma }}^{-1} }{a^2 (4+\gamma _1+\gamma _2) + n^2 \pi ^2 (\frac{\gamma _1}{k} + \frac{\gamma _2}{h} +4)} \end{aligned}$$where \(a^2=l^2+m^2\) and
$$\begin{aligned} \begin{aligned} {\hat{K}}&= \Bigl [ \gamma _1+\gamma _2+\frac{\gamma _1}{k}+\frac{\gamma _2}{h} + \gamma _1 \gamma _2 \Big ( \frac{1}{k} + \frac{1}{h} \Big ) \Bigr ], \\ \Gamma&= \gamma _1 \gamma _2 + \gamma _1 + \gamma _2, \\ {\hat{\Gamma }}&= \frac{\gamma _1}{k} + \frac{\gamma _2}{h} + \frac{\gamma _1}{k} \frac{\gamma _2}{h}, \end{aligned} \end{aligned}$$that coincides with the instability threshold found in [29];
-
(ii)
the case of a non-rotating layer of isotropic bidisperse porous medium (assuming \(h_s=k_s=1\) for \(s=1,2\) and as \({\mathcal {T}}\rightarrow 0\)) leads to
$$\begin{aligned} R^2_L= \min _{n,a^2} \dfrac{\Lambda ^2}{a^2} \dfrac{\gamma _1 \gamma _2 + \gamma _1 + \gamma _2}{\gamma _1 + \gamma _2 +4} \end{aligned}$$that is the same threshold found in [8].
4 Nonlinear stability
In order to study the influence of rotation on the nonlinear stability of the conduction solution, since the Coriolis terms in momentum equations are antisymmetric, instead of applying the standard energy method, let us apply the differential constraint approach (see [5, 11, 24]).
To this end, let us set
and by virtue of \((4)_5\), one obtains
Setting
with
the space of kinematically admissible solutions. The variational problem (21) is equivalent to the following variational problem:
where \(\lambda (\mathbf{x})\) and \(\psi (\mathbf{x})\) are Lagrange multipliers and
By virtue of Poincaré inequality, since
from (20) one obtains that condition \(R<R_E\) guarantees the global nonlinear stability of the conduction solution with respect to the \(L^2\)-norm, according to the following inequality
Remark 1
Multiplying \((8)_1\) by \(\mathbf{u}^f\), \((8)_2\) by \(\mathbf{u}^p\), integrating over the period cell V and adding the resulting equations, one finds
Setting \({\hat{k}}=\max (k_1,k_2,1)\) and \({\hat{h}}=\max (h_1,h_2,1)\) and using the generalized Cauchy inequality on the right-hand side of (24), one obtains
and hence condition \(R<R_E\) guarantees that \(\Vert \mathbf{u}^f \Vert ^2 \rightarrow 0\) and \(\Vert \mathbf{u}^p \Vert ^2 \rightarrow 0\) as \(t \rightarrow \infty \), too.
In order to solve the variational problem (22), let us consider the associated Euler–Lagrange equations:
Defining the operators
and taking \(2 \Delta \) of \((26)_{2,3,4,5}\), the Euler–Lagrange equations become
Eliminating variable \(\theta \) and setting
one obtains
By employing normal modes
from (28) one obtains
Requiring a zero determinant for (31) we find
and hence the global nonlinear stability threshold and the linear instability threshold coincide and subcritical instabilities do not exist.
5 Numerical simulations
We now present numerical results to solve (18), in order to analyze the asymptotic behavior of \(R_L^2\) with respect to \({\mathcal {T}}\), \(h_i\), \(k_i\), for \(i=1,2\), i.e., to study the influence of rotation and anisotropic permeability on the onset of convection. As regards the physical parameters, in all numerical simulations, we have chosen a set of values analogous to those ones fixed in [27], in order to compare our results with those ones obtained in [27], to stress the influence of rotation and anisotropy on the onset of convection.
In all the computations, we have performed, the minimum of \(R_L^2\) with respect to n is attained at \(n=1\). Each of the following tables and figures show the stabilizing effect of rotation on the onset of convection.
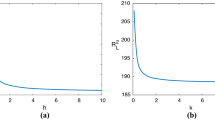
a Critical Rayleigh number \(R^2_L\) as function of the Taylor number \({\mathcal {T}}\) for \(h_1=10,h_2=1,k_1=0.1,k_2=1,\eta =0.2,\gamma _1=10,\gamma _2=50\). b Critical Rayleigh number \(R^2_L\) as function of the Taylor number \({\mathcal {T}}\) for \(h_1=0.1,h_2=1,k_1=10,k_2=1,\eta =0.2,\gamma _1=10,\gamma _2=50\)
Table 1 shows that for large values of the Taylor number \({\mathcal {T}}\) and when \(h_1>>k_1\), m becomes zero, this means that, as rotation increases, the convection cells become rolls with the axis in the y-direction. Table 2 shows a transition from convection patterns as rolls along y-axis (\(m=0\) for very small \({\mathcal {T}}\)) to convection patterns as rolls along x-axis (\(l=0\)), as the rotation increases and for \(h_1<<k_1\). For these physical values, the asymptotic behavior of \(R_L^2\) with respect to \({\mathcal {T}}\) is shown in Fig. 1. We can also observe that, as \({\mathcal {T}}\) increases, \(R_L^2\) increases more slowly when \(h_1<<k_1\) then \(h_1>>k_1\).
Let us point out that bi-dimensional convection cells (rolls along x-axis for \(l=0\) and rolls along y-axis for \(m=0\)) were already found in [27] as an effect of anisotropic macropermeability and micropermeability in absence of rotation.
From Table 3, we numerically find out that for parameters \(\{ h_1=1,h_2=0.1,k_1=1,k_2=10,\eta =0.2,\gamma _1=2,\gamma _2=0.2 \}\) the critical value of m is mainly zero, except for very small values of the Taylor number \({\mathcal {T}}\in [0,3)\), for which l and m are both nonzero, i.e., for very little rotation of the layer, three-dimensional convection cells are expected.
As a matter of fact, the wavelengths in the x and y directions are \({\hat{x}}=\frac{2 \pi }{l}\) and \({\hat{y}}=\frac{2 \pi }{m}\). The condition \({\hat{y}} / {\hat{x}}=0\) implies \(l=0\), this means that the convective fluid motion occurs in the y and z directions (the solution is a function of y and z), i.e., the convection cells are rolls in the x-direction. Instead, the condition \({\hat{y}} / {\hat{x}} \rightarrow \infty \) implies \(m=0\) and the convective fluid motion occurs in the x and z directions, so the cells are rolls in the y-direction [27].
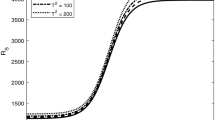
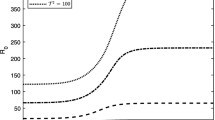
Tables 4 and 5 exhibit the influence of anisotropy parameters for both macropores and micropores on the onset of convection, and the values of \(h_1,h_2,k_1,k_2\) are fixed such that the permeability ratios in the macropores and micropores are different, in particular we set \(\{ h_1=3.3,h_2=0.9,k_1=0.2,k_2=1.1 \}\) (see [27]) and we vary \(h_s,k_s\) for \(s=1,2\) in turn to see how each parameter affects the Rayleigh number. As in [27], we numerically find out a very complex relationship between the macro and micro permeability parameters and the critical Rayleigh and wave numbers. For increasing \(h_1,h_2,k_1,k_2\), we can see a similar trend, i.e., \(R_L^2\) increases up to a maximum before decreasing. From 4(a) and from 5(a), we can see a first transition from rolls along x-axis to three-dimensional cells and then another transition to rolls along y-axis, while 4(b) and 5(b) displays a mirror behavior with respect to 4(a) and 5(a) , respectively.
In Fig. 2 the critical Rayleigh number \(R_L^2\) is represented as function of the Taylor number \({\mathcal {T}}\) for \(h_1=0.1,1,5,10\) and the others parameters are fixed as \(h_2=0.9,k_1=0.2,k_2=1.1,\eta =0.2,\gamma _1=0.9,\gamma _2=1.8\), with the aim to graphically analyze the values shown in Table 4a.
6 Conclusions
The onset of thermal convection in a horizontal layer of anisotropic BDPM, uniformly rotating about a vertical axis and uniformly heated from below, has been analyzed, according to Darcy’s law in both micropores and macropores. In particular, it has been proved that:
-
the strong version of the principle of exchange of stabilities holds, and hence, when the convection arises, it sets in through a stationary motion;
-
the linear instability threshold and the global nonlinear stability threshold in the \(L^2-\)norm coincide: this is an optimal result since the stability threshold furnishes a necessary and sufficient condition to guarantee the global (i.e., for all initial data) nonlinear stability.
Moreover, it has been numerically analyzed the influence of the rotation and the influence of the anisotropy on the onset of convection.
Availability of data and material
This article does not contain any additional data.
References
Bernardi, C., Girault, V., Rajagopal, K.R.: Discretization of an unsteady flow through a porous solid modeled by Darcy’s equations. Math. Models Methods Appl. Sci. 18(12), 2087–2123 (2008)
Capone, F., De Luca, R., Gentile, M.: Coriolis effect on thermal convection in a rotating bidisperive porous layer. Proc. R. Soc. A. 476, 20190875 (2020). https://doi.org/10.1098/rspa.2019.0875
Capone, F., De Luca, R., Gentile, M.: Thermal convection in rotating anisotropic bidispersive porous layers. Mech. Res. Commun. (2020). https://doi.org/10.1016/j.mechrescom.2020.103601
Capone, F., De Luca, R.: The effect of the Vadasz number on the onset of thermal convection in rotating bidispersive porous media. Fluids 5(4), 173 (2020). https://doi.org/10.3390/fluids5040173
Capone, F., Gentile, M.: Sharp stability results in LTNE rotating anisotropic porous layer. Int. J. Therm. Sci. 134, 661–664 (2018)
Capone, F., Gentile, M., Hill, A.A.: Double-diffusive penetrative convection simulated via internal heating in an anisotropic porous layer with throughflow. Int. J. Heat Mass Transf. 54(7–8), 1622–1626 (2011)
Chandrasekhar, S.: Hydrodynamic and Hydromagnetic Stability. Dover Publicationas, New York (1981)
Gentile, M., Straughan, B.: Bidispersive thermal convection. Int. J. Heat Mass Transf. 114, 837–840 (2017)
Gentile, M., Straughan, B.: Bidispersive vertical convection. Proc. R. Soc. A. 473, 20170481 (2017). https://doi.org/10.1098/rspa.2017.0481
Gentile, M., Straughan, B.: Bidispersive thermal convection with relatively large macropores. J. Fluid Mech. 898, A14 (2020). https://doi.org/10.1017/jfm.2020.411
Hill, A.A.: A differential constraint approach to obtain global stability for radiation-induced double-diffusive convection in a porous medium. Math. Meth. Appl. Sci. 32(8), 914–921 (2009)
Kvernvold, O., Tyvand, P.A.: Nonlinear thermal convection in anisotropic porous media. Mech. Appl. Math. 90(4), 609–624 (1977)
Malek, J., Rajagopal, K.R., Ruzicka, M.: Existence and regularity of solutions and the stability of the rest state for fluids with shear dependent viscosity. Math. Models Methods Appl. Sci. 05(06), 789–812 (1995)
Nield, D.A., Bejan, A.: Convection in Porous Media, 5th edn. Springer, New York (2017)
Nield, D.A., Kuznetsov, A.V.: Forced convection in a bi-disperse porous medium channel: a conjugate problem. Int. J. Heat Mass Transf. 47, 5375–5380 (2004)
Nield, D.A., Kuznetsov, A.V.: Heat transfer in bidisperse porous media. Transp. Phenom. Porous Media III, 34–59 (2005). https://doi.org/10.1016/B978-008044490-1/50006-5
Nield, D.A., Kuznetsov, A.V.: The onset of convection in a bidisperse porous medium. Int. J. Heat Mass Transf. 49(17–18), 3068–3074 (2006)
Nield, D.A., Kuznetsov, A.V.: The effects of combined horizontal and vertical heterogeneity on the onset of convection in a porous medium with vertical throughflow. Transp. Porous Media 90, 465 (2011)
Pires, G.E., Rajagopal, K.R., Videman, J.H.: On the derivation of Reynolds-type equation for flows through porous media due to pressure gradients. J. Porous Media 23, 1137–1151 (2020)
Rajagopal, K.R., Na, T.Y.: Natural convection flow of a non-Newtonian fluid between two vertical flat plates. Acta Mech. 54, 239–246 (1985)
Rajagopal, K.R.: On a hierarchy of approximate models for flows of incompressible fluids through porous solids. Math. Models Methods Appl. Sci. 17(02), 215–252 (2007)
Rajagopal, K.R., Srinivasan, S.: Flow of fluids through porous media due to high pressure: Part 2, unsteady flows. J. Porous Media 17, 751–762 (2014)
Srinivasan, S., Bonito, A., Rajagopal, K.R.: Flow of a fluid through a porous solid due to high pressure gradients. J. Porous Media 16, 193–203 (2013)
Straughan, B.: Global nonlinear stability in porous convection with a thermal non-equilibrium model. Proc. R. Soc. A. 462, 409–418 (2006)
Straughan, B.: Convection with Local Thermal Non-equilibrium and Microfluidic Effects. Adv Mechanics and Matematics, vol. 32. Springer, Cham (2015)
Straughan, B.: Bidispersive double diffusive convection. Int. J. Heat Mass Transf. 126, 504–508 (2018)
Straughan, B.: Anisotropic bidispersive convection. Proc. R. Soc. A. 475, 20190206 (2019)
Straughan, B.: Horizontally isotropic bidispersive thermal convection. Proc. R. Soc. A 474, 20180018 (2018). https://doi.org/10.1098/rspa.2018.0018
Straughan, B.: Horizontally isotropic double porosity convection. Proc. R. Soc. A. 475, 20180672 (2019)
Vadasz, P.: Flow and thermal convection in rotating porous media. In: Vafai, K. (ed.) Handbook of Porous Media. Marcel Dekker, New York (2000)
Vasudevaiah, M., Rajagopal, K.R.: On fully developed flows of fluids with a pressure dependent viscosity in a pipe. Appl. Math. 4, 341–353 (2005)
Acknowledgements
This paper has been performed under the auspices of the GNFM of INdAM. G. Massa would like to thank Progetto Giovani GNFM 2020: “Problemi di convezione in nanofluidi e in mezzi porosi bidispersivi”. The Authors would like to thank the anonymous referees for suggestions which have led to improvements in the manuscript.
Funding
Open access funding provided by Universitá degli Studi di Napoli Federico II within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests and that there are no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Capone, F., Gentile, M. & Massa, G. The onset of thermal convection in anisotropic and rotating bidisperse porous media. Z. Angew. Math. Phys. 72, 169 (2021). https://doi.org/10.1007/s00033-021-01592-w
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00033-021-01592-w