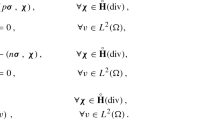Abstract
We consider an improved Nernst–Planck–Poisson model first proposed by Dreyer et al. in 2013 for compressible isothermal electrolytes in non-equilibrium. The elastic deformation of the medium, that induces an inherent coupling of mass and momentum transport, is taken into account. The model consists of convection–diffusion–reaction equations for the constituents of the mixture, of the Navier–Stokes equation for the barycentric velocity and of the Poisson equation for the electrical potential. Due to the principle of mass conservation, cross-diffusion phenomena must occur, and the mobility matrix (Onsager matrix) has a non-trivial kernel. In this paper, we establish the existence of a global-in-time weak solution, allowing for a general structure of the mobility tensor and for chemical reactions with fast nonlinear rates in the bulk and on the active boundary. We characterise the singular states of the system, showing that the chemical species can vanish only globally in space, and that this phenomenon must be concentrated in a compact set of measure zero in time.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Increasing the efficiency of actual high-performance energy storage systems requires an exact understanding of their fundamental physical principles. Of particular interest is ion transport in electrolytes, for instance in lithium-ion batteries. In the neighbourhood of interfaces, the classical description using the Nernst–Planck theory is failing for various reasons (see [11, 12]): first of all, the Nernst–Planck model neglects the high pressures induced by the Lorentz force that affect the charge transport. Secondly, it does not take into account the interaction between the solvent and the charged constituents. A third drawback of the Nernst–Planck theory is the widely used assumption of local charge neutrality. This assumption completely fails in the vicinity of the boundaries where electric charges accumulate. An improved model able to remedy these deficiencies was proposed in the paper [12]. In [11, 13], this model was further extended to include (i) finite volume effects of the constituents, (ii) the viscosity of the mixture and (iii) chemical reactions in the bulk and on electrochemical interfaces. The improved model rests on three supporting pillars:
-
The universal conservation principles for mass, electrical charge, momentum and energy;
-
The entropy principle for bulk and surfaces, which allows to choose thermodynamically consistent material models;
-
A special construction of the free energy-functional, designed in the papers [13, 26] for electrolytes.
Throughout the paper, we shall focus on the isothermal case and need to formulate universal balance equations only for mass, momentum and charge. If the considered electrolyte is a fluid mixture of N chemical substances, these equations assume the form
where the main variables are the mass densities \(\rho _1, \ldots ,\rho _N \) of the substances in the mixture, the components \(v_1, \, v_2, \, v_3\) of the velocity field and the electric potential \(\phi \). Notice that we overall denote by \(\varrho \) the total mass density \(\sum _{i=1}^N \rho _i\) of the electrolyte. In the right-hand side of the Navier–Stokes equations, the contribution \(-n^F \, \nabla \phi \) is the Lorentz or Coulomb force. The density of free charges is \(n^F:= \sum _{i=1}^N \bar{Z}_i \, \rho _i\) with constants \(\bar{Z}_1,\ldots ,\bar{Z}_N\). Assuming a linear description of dielectric displacement in the electrolyte, the evolution of \(\phi \) is driven by the Poisson equation with the universal Gauss constant \(\epsilon _0\) and the susceptibility \(\chi \) of the electrolyte, here likewise assumed constant.
The diffusion fluxes \(J^1, \ldots ,J^N\), the reaction densities \(r_1,\ldots ,r_N\) and the components \(\mathbb {S}\) (viscous stress) and p (thermodynamic pressure) of the stress tensor, represent physical phenomena that dissipate energy. In order to provide constitutive equations for these quantities, relating them to the main variables, our model uses the entropy principle as a guideline—after the universal conservation laws, this is the second pillar.
The chemical potentials, denoted by \(\mu _1,\ldots ,\mu _N\), are the essential pivot making the link between the densities and the thermodynamic consistent description of transport mechanisms. They are defined as derivatives of a free energy density \(\varrho \psi \) via \(\mu _i := \partial _{\rho _i} \varrho \psi \) for \(i=1,\ldots ,N\). In the paper, we restrict to free energy densities of the form \(\varrho \psi = h(\theta , \, \rho _1,\ldots ,\rho _N)\), where the function h encodes the energetic behaviour (volume extension and mixing entropy) of the electrolyte without the electromagnetic contribution. Recall that the absolute temperature \(\theta \), which is assumed fixed, is only a parameter (isothermal case).
For the diffusion fluxes, the gradients \(\nabla (\mu _j/\theta ) + (\bar{Z}_j/\theta ) \, \nabla \phi \) for \(j=1,\ldots ,N\) are identified as the driving forces for the diffusion process, and the thermodynamic consistent model postulates the proportionality
where the factor \(\{M_{i,j}(\rho )\}_{i,j=1,\ldots ,N}\) shall be called the mobility tensor. If \(M(\rho )\) is positive semi-definite for all states, this definition of the diffusion fluxes guarantees that the contribution of diffusion to the production of entropy is non-negative.
In order to model the reactions \(r_1, \ldots , r_N\) in a similar spirit, we shall make use of constitutive equations proposed first in [13] to obtain a closure equation of the form
where s is the number of active reactions, \(\{\gamma ^k_i\} \in \mathbb {R}^{s\times N}\) is a matrix of stoichiometric coefficients, and \(\Psi : \, \mathbb {R}^s \rightarrow \mathbb {R}\) a convex potential. Here, we denoted by \(\mu \) the vector \((\mu _1,\ldots ,\mu _N)\) of chemical potential.
The pressure shall obey the Gibbs–Duhem equation
Finally, the analysis of the entropy production shows that the viscous stress \(\mathbb {S}\) can be consistently chosen of standard Newtonian form with constant coefficients. We will restrict for convenience to this simplifying assumption. Together with the Poisson equation to determine the electric potential, the final PDE model assumes the form
where we omit for convenience every dependence on temperature, and write for simplicity \(\rho = (\rho _1,\ldots ,\rho _N)\) in the arguments of M and h. We see that, for a known free energy potential h, these equations form a closed system for the variables \(\rho \) and v. To close the PDE system, we choose the free energy
where \(c_i\), \(m_i >0\), \(\bar{V}_i > 0\) are certain constants, \(k_B\) is the Boltzmann constant, and F a nonlinear function describing the volume extension of the mixture. We refer to Sects. 2.1, 2.2, and 2.3 for in-depth discussions of the three steps of the model derivation after the papers [11,12,13] and the book [20]. We explain (3) in Sect. 2.3 in more details.
From the viewpoint of analysis we first remark that, up to the complex looking definition of the thermodynamic pressure imposed by the multicomponent character, Eqs. (2) are very similar to the single-component compressible Navier–Stokes equations. They shall indeed allow the same type of natural bounds.
However, in the new model, the diffusion fluxes in (1) cannot be brought into the standard diagonal form assumed by the Nernst–Planck theory, and this for at least two reasons. At first, the matrix M is subject to the zero column-sum constraint \(\sum _{i=1}^N M_{i,j} = 0\) due to the fact that we model diffusion fluxes. At second, the choice (3) of the free energy potential h leads, unlike the case of the standard Boltzmann entropy \(\rho \, \log \rho \), to a nondiagonal Hessian. Hence, the diffusion tensor is in general both nondiagonal and singular. As to this last point, the equations in (1) cannot constitute a parabolic system for the variables \(\rho _1,\ldots ,\rho _N\). Indeed, summing up over \(i=1,\ldots ,N\) and using the zero column-sup side-condition for M, we derive the continuity equation \(\partial _t \varrho + {{\,\mathrm{div}\,}}(\varrho \, v) = 0\). This shows that one component of the solution vector is driven by an hyperbolic equation. Thus, whereas classical models of electrochemistry yield diagonal drift–diffusion or diffusion–reaction systems, the new model for electrolytes exhibits a completely different structure and must be studied with techniques of mathematical fluid dynamics.
In the present paper, we establish the existence of a global-in-time weak solution. Our result is consistent with the physical definitions and restrictions concerning the objects h, M, \(\hat{R}\) and p. In particular, we allow for
-
1.
A general structure of the mobility tensor with a non-trivial kernel;
-
2.
Chemical reactions of arbitrary growth rate in the bulk and on the active part of the boundary;
-
3.
A pressure contribution to the diffusion flux, which is encoded in the choice of the free energy.
A feature worth to note separately is the original thermodynamic modelling for the reaction rates. The choice of \(\Psi \) discussed here does not lead to the structure of products of monomials in the concentrations. As a consequence, energy dissipation yields a control of the reaction terms in Orlicz classes associated with the dual potential \(\Psi ^*\), and global-in-time weak solutions can be defined without the help of the re-normalisation techniques (see [17]) necessary to handle models traditionally called ‘of mass action type’ (see, a. o., [4, 6, 17, 21,22,23, 30]).
In addition to the existence statements, we are able to characterise the singularities of the system associated with the vanishing of species. We show that, except for the occurrence of a complete vacuum—which is entirely non-physical in the range of validity of the model—the mass density of a species can vanish only globally in the spatial domain and that this phenomenon is concentrated in a compact set of measure zero in time.
Our method relies at first on a priori estimates that result from the thermodynamically consistent modelling, and from the conservation of total mass. The estimates are partly a consequence of known results for the Poisson equation or the Navier–Stokes equations, but we can regard the estimates on the chemical potentials of the mixture constituents, in particular in the presence of chemical reactions, as original (Theorem 11.3). The control on diffusion gradients and the chemical reactions is used to reveal a relationship between the blow-up of differences of chemical potentials and the entire vanishing of certain groups of species. In order to exclude the latter phenomenon, a restriction on the initial net masses of the involved constituents turns out sufficient.
Compactness techniques constitute the second fundament of our method. Note that the Aubin–Lions compactness Lemma and its generalisations, which are typically invoked in similar investigations (see for instance [8]), attain their limit in the context of the PDE system (1), (2), (3) due to the complexity of the relationship between time derivatives (transport) and diffusion gradients. We exploit the original ideas of [24] based on structural PDE arguments as an adequate substitute. Moreover, we invoke the compactness properties of the Navier–Stokes operator established first in [28] and extended in [15] to show compactness for the total mass density.
Since large parts of the modelling work in [12] are original and not yet well known in the mathematical literature devoted to the analysis of models for the electrolyte, we are not able to quote a direct precursor for our analysis in the context of electrochemistry. Similar models are known only in the context of multicomponent gas dynamics. We refer to the book [18] for an overview about models in this area and for first insights into their strong solution analysis. It is to note that the global weak solution analysis of multicomponent flow models is, up to few exceptions, widely unexplored. Let us here mention the papers [31] and [34] where models of compressible mixtures with energy balance, but without electric field, were studied. These models are not derived from exactly the same thermodynamic principles that are used in our study: Particularly, the constitutive equations for the pressure, for the diffusion fluxes and for the reaction terms, are different in [31] and in [12]. The compactness question occurs there like in our analysis but is solved assuming a special structure of the viscosity tensor, called Bresch–Desjardins condition. The latter allows to obtain estimates on the density gradient, a device which is not at our disposal here. A further difference between the two mixture models concerns cross-diffusion, which is described in [31] and [34] by a special choice of the mobility matrix, whereas we allow for general symmetric positive semi-definite matrices. Note that the mobility matrix must be symmetric at least in a binary mixture.
Among recent less directly related investigations let us mention: In the context of general diffusion, [2, 25]; for models with simplified diffusion and pressure laws [4, 16]; for the analysis of incompressible models of Nernst–Planck–Poisson type [5, 7, 22].
Due to the length of the investigation, let us point out at three main parts in the manuscript. The first part consists of Sects. 2–7. Here, we derive the model, we set up, for the functional analytic treatment, an equivalent formulation which exhibits more stability against extreme behaviour (species vanishing, vacuum), and we propose a survey of the main mathematical results. The second part (Sects. 8–11) is devoted to the construction of approximate solutions respecting the natural a priori estimates. The third part (Sects. 12, 13, 14) is concerned with the investigation of compactness properties, and with the proof of convergence of the approximation scheme.
2 Improved Nernst–Planck–Poisson model
The model will be introduced following [13]. It is formulated for the normal regime of the system, in particular it is assumed that the mass densities of the constituents do not vanish. Throughout the paper, the bounded domain \(\Omega \subset \mathbb {R}^3\) is representing an electrolytic mixture. The boundary of \(\Omega \) possesses a disjoint decomposition \(\partial \Omega = \Gamma \cup \Sigma \): The surface \(\Gamma \) represents an active interface between an electrode and the electrolyte, where chemical reactions and adsorption may occur. The other surface \(\Sigma \) represents an inert outer wall with no reactions and no adsorption.
The mixture consists of \(N \in \mathbb {N}\) species denoted by \(A_1, \ldots , A_N\). A molecule of \(A_i\) has the elementary mass \(m_i > 0\) and, as ions are involved, it carries a multiple \(z_i\in \mathbb {Z}\) of the elementary charge \(e_0\).
We assume that the system is isothermal so that the absolute temperature, denoted by \(\theta \), is a positive constant. Under the isothermal assumption, the thermodynamic state of the mixture at time \(t\in [0,T]\) is described by the mass densities \(\rho _1, \ldots , \rho _N\) of the species, the barycentric velocity v of the mixture and the electric field E. As usual in electrochemistry, a quasi-static approximation of the electric field is considered, i.e. the magnetic field is constant and the electric field satisfies \(E = - \nabla \phi \). The scalar function \(\phi \) is called electrical potential.
The active boundary \(\Gamma \) can be viewed as a mixture of \(N^\Gamma = N + N^\text {ext}\) constituents denoted by \(A_1, \ldots , A_{N^\Gamma } \), where the additional \(N^\text {ext}\) constituents take into account the species of the adjacent exterior matter, i.e. electrode species. Thus, we only consider surface chemical reactions with participating species that also exist in the adjacent bulk domains. The surface constituents have the surface mass densities \(\rho ^{\Gamma }_1, \ldots , \, \rho ^{\Gamma }_{N^\Gamma }\).
We consider \(s\in \mathbb {N}\) chemical reactions in the bulk and \(s^\Gamma \in \mathbb {N}\) surface reactions on the boundary \(\Gamma \), respectively. The \(k^{\mathrm{th}}\) chemical reaction in the bulk (\(k\in \{1,\ldots ,s\}\)) and on the boundary (\(k\in \{1,\ldots ,s^\Gamma \}\)) possesses the general structure

The constants \(a_i^k\), \(b_i^k\) and \(a_{\Gamma ,i}^k\), \(b_{\Gamma ,i}^k\) are positive integers called stoichiometric coefficients. For \(k = 1,\ldots ,s\), we define a vectorial coefficient associated with the \(k^{\mathrm{th}}\) bulk reaction via
Due to the inclusion of the masses, \(\gamma ^1, \ldots , \gamma ^s\) are not the usual stoichiometric vectors, but this will simplify the notation. The forward reaction rate of the \(k^{\mathrm{th}}\) reaction is \(R^f_k>0\), and the backward reaction rate is \(R^b_k>0\). The net reaction rate of the \(k^{\mathrm{th}}\) reaction is defined as
The same definitions hold for the surface reactions on \(\Gamma \). Here, the vectorial coefficients are defined via
and the surface reaction rates are \(R^\Gamma _k = R^{\Gamma ,f}_k -R^{\Gamma ,b}_k\) for \(k = 1,\ldots ,s^\Gamma \). Since charge and mass are conserved in every single reaction
2.1 Balance equations in the bulk
In the isothermal case, the evolution of the thermodynamic state is described by the equations of partial mass balances, of momentum balance, and by the Poisson equation.
In \(]0,T[ \times \Omega \) the mixture obeys for \(i = 1,\ldots ,N\) the partial mass balances
Here, v denotes the barycentric velocity of the mixture, while \(J^1, \ldots , J^N\) are called the diffusion fluxes. The total mass is defined as \(\varrho = \sum _{i=1}^N \rho _i\). Together with v it has to satisfy the continuity equation
Thus, the conservation of total mass yields additional constraints on the diffusion fluxes and the mass productions:
While the constraint (6)\(_2\) is a consequence of the conservation of mass in every chemical reaction (cf. (4)), the side condition on the diffusion fluxes has to be guaranteed by an appropriate constitutive modelling.
The principle momentum balance possesses the expression
Herein \(\sigma \) denotes the Cauchy stress tensor, \(\varrho \, b\) is the force density due to gravitation, and the symbol \(n^F \, E\) stands for the Lorentz force due to the electric field. The quantity \(n^F\) represents the free charge density that is defined via
Throughout the paper, we are going to neglect the gravitational force that plays no role in the analysis.
In the electrostatic setting the balance equation for the electric field reduces to the Poisson equation for the electrical potential,
Here, \(\chi > 0\) is the constant susceptibility of the electrolyte.
2.2 Constitutive equations
The constitutive equations for the mass fluxes, the reaction rates and the stress tensor can be derived from one single free energy density \(\varrho \psi \) of a general form
The derivatives
are called chemical potentials, In the isothermal setting, the balance equations and the free energy density yield a local entropy production \(\xi = \xi _D + \xi _R + \xi _V \ge 0\) with three contributions due to diffusion, \(\xi _D\), reaction, \(\xi _R\), and viscosity, \(\xi _V\) (see [3, 13, 29]). A constitutive model that relies on the free energy function of the form (9) implies explicit expressions for the three entropy productions as binary products. From these expressions, we may derive constitutive equations that yield three separate non-negative entropy productions. For more details regarding the derivation of the entropy production, we refer to [3, 9, 29]. In [3], it is shown how cross-effects revealing the Onsager symmetry can be introduced.
Diffusion fluxes The entropy production due to diffusion reads
Here, \(D^1,\ldots ,D^N\) are the thermodynamic driving forces for diffusion, The simplest constitutive ansatz for the diffusion fluxes \(J^1,\ldots ,J^N\) that implies \(\xi _D\ge 0\) is given by
The proportionality factor \(M \in \mathbb {R}^{N\times N}_{\text {sym}}\) is called the mobility matrix. It is positive semi-definite and may depend on \(\rho \). Moreover, the side condition \(\sum _{i=1}^N J^i =0\) is complied with if the mobility matrix satisfies
For instance, following the paper [12], one can construct M from an empirical mobility matrix \(M_{\text {emp}}(\rho )\) and a linear operator \(\mathcal {P}: \, \mathbb {R}^N \rightarrow \mathbb {R}^{N-1} \times \{0\}\) via
where \(d_1, \ldots , d_{N-1} >0\) are diffusion constants, and the lines of the matrix \(\mathcal {P}\) are given by the differences \(e^i-e^N\) of standard basis vectors for \(i = 1,\ldots ,N\). In fact, any operator \(\mathcal {P}\) that satisfies for \(i=1,\ldots ,N\) the condition \(\sum _{j=1}^N \mathcal {P}_{i,j} = 0\) can be chosen in (12) in order that (11) is valid. However our analytical results do not rely on the particular structure (12) of the matrix M.
Reaction rates The entropy production due to chemical reactions assumes the form
The driving forces \(D^{\text {R}}_1, \ldots , D^{\text {R}}_s\) are defined, for \(k =1,\ldots ,s\), via \(D^{\text {R}}_k = \sum _{i=1}^N \gamma ^k_i \, \mu _i\). To achieve \(\xi _{\text {R}}\ge 0\), we assume that the vector of production rates are derived from a convex, non-negative potential
This choice is in fact more general than in [13], where the following potential is employed,
with positive constants \(\alpha _1, \ldots , \alpha _s\) and constants \(\beta _1, \ldots \beta _s \in ]0, \, 1[\), \(C \in \mathbb {R}\) arbitrary. The latter corresponds to an ansatz of Arrhenius type, which is widely used in chemistry,
Stress tensor The entropy production due to viscosity is \(\xi _V = \tfrac{1}{2}(\sigma +p~\text {Id}):D(v)\), with the driving force \(D(v) = (\partial _i v_j + \partial _j v_i)_{i,j=1,\ldots ,3}\), and the identity matrix \(\text {Id}\). We split the Cauchy stress tensor into a viscous part \(\mathbb {S}^{\text {visc}}\) and the pressure p via \(\sigma = - p\, \text {Id} + \mathbb {S}^{\text {visc}}\). Then, the material pressure can be calculated from the free energy function (9). The resulting representation is called Gibbs–Duhem equation and reads
The simplest constitutive choice for the viscous stress tensor \(\mathbb {S}^{\text {visc}}\) satisfying \(\xi _V\ge 0\) describes a Newtonian fluid. It reads
where \(\eta > 0\) is the shear viscosity, and the coefficient \(\lambda \) of bulk viscosity satisfies \(\lambda +\frac{2}{3} \, \eta \ge 0\).
2.3 Choice of the free energy function
The constitutive model is derived from a free energy density of the general form (9). To describe an elastic mixture, the free energy density \(\varrho \psi \) is additively split into three contributions,
The constants \(\mu ^{\text {ref}}_i\) (\(i = 1,\ldots ,N\)) are related to the reference states of the pure constituents. The contribution \(h^{\text {mech}}\) is the mechanical part of the free energy that is neglected in the classical Nernst–Planck theory. The function \(h^{\text {mix}}\) represents the mixing entropy.
In the presentation of [11, 12], the contributions \(h^{\text {mech}}\) and \(h^{\text {mix}}\) are naturally given as functions of the number densities \(n_1 ,\ldots ,n_N\) of the constituents. These are defined via \(n_i := \rho _i/m_i\) (\(i = 1,\ldots ,N\)). The number fractions are defined via \(y_i := n_i/\sum _{j=1}^N n_j\) for \(i =1,\ldots ,N\).
The mechanical free energy is associated with the isotropic elastic deformation of the mixture. It takes into account different reference partial volumes \(V_1, \ldots , \, V_N \in \mathbb {R}_+\) of the constituents. Assuming a constant bulk compression modulus \(K > 0\), the mechanical free energy according to [11] is a function of the mixture volume \(\sum _{i=1}^N n_i \, V_i\):
Here, \(p_{\text {ref}}\) is a constant reference value of the pressure. Another possible choice, corresponding to a polynomial state-equation (Tait equation), is
For the sake of generality, we express \(h^{\text {mech}}\) in the form
Dreyer et al. use \(F(x) := x \, \ln x + C_1\) for an ideal mixture, whereas the Tait equation corresponds to \(F(x) =c_{\alpha } \, x^{\alpha } + C_2\). The contribution \(h^{\text {mix}}\) results from the entropy of mixing and is given by
where \(k_B\) is the Boltzmann constant.
2.4 The model for the boundary \(\Gamma \)
The active boundary \(\Gamma \) represents an interface between the electrolyte and an external material. In the most important application, the external material is an electrode which is likewise a mixture of \(N^{\text {ext}} \in \mathbb {N}\) constituents. Here, we have analogous quantities to those that occur in the electrolyte, namely the barycentric velocity, and diffusion fluxes and so on. To distinguish between the electrolyte and the external material, we make use of the suffix \({ }^\text {ext}\) in connection with external quantities.
In this paper, we assume for simplicity that the constituents occurring on \(\Gamma \) also exist in the bulk, either in the electrolyte or in the external material. Thus, the interface \(\Gamma \) is a mixture of \(N^\Gamma = N + N^{\text {ext}}\) constituents. The equations of an interface representing a surface mixture are derivable in the context of surface thermodynamics, and we refer the interested reader to [1, 13, 20]. As in the bulk, there are universal surface balance equations and material-depending surface constitutive equations. To simplify the surface equations, we assume on \(]0,T[ \times \Gamma \):
-
(a)
Time variations of the surface mass densities and tangential transport are negligible in comparison to mass transfer across the surface and to chemical surface reactions.
-
(b)
The interface is fixed in space, i.e. the interfacial normal speed is zero.
-
(c)
There is no velocity slip and the normal barycentric velocity is equal to the interfacial normal speed, i.e. we have \(v = 0\) on \(]0,T[ \times \Gamma \).
Surface mass balances and surface reaction rates In what follows the interfacial unit normal \(\nu \) points into the external material. Under the assumptions (a), (b), (c), the surface mass balance equations on \(]0,T[ \times \Gamma \) reduce to
Here, we make use of the convention that the N first species on \(\Gamma \) are the electrolyte constituents, while the constituents with indices \(N+1, \ldots , N+N^{\text {ext}}\) are the external ones.
It remains to specify the surface mass production \(r^{\Gamma }\) due to surface reactions. As in the bulk, the production \(r^{\Gamma }\) is related to the surface reaction rates \(R^{\Gamma }\) by
The interfacial entropy production \(\xi ^\Gamma _{\text {R}}\) due to chemical reaction is (see [13])
The entropy production of the surface has the same structure as the corresponding entropy production in the bulk (13). Thus, in order to satisfy the entropy inequality, an ansatz similar to (14), (15) may be used. We assume the existence of a potential \(\Psi ^\Gamma \) so that
Normal diffusion fluxes Under the assumptions (a), (b) and (c), the constitutive equations proposed in [13, 20] for the normal diffusion fluxes at \(]0,T[ \times \Gamma \) simplify to
Here, \(\mu ^\Gamma _1, \ldots , \mu ^{\Gamma }_{N}\) are the surface chemical potentials of the electrolytic species, whereas the quantities \(\mu ^{\Gamma }_{N+1}, \ldots , \mu ^{\Gamma }_{N+N^{\text {ext}}}\) are associated with the external species. These equations describe the adsorption of a constituent from the bulk to the surface. The kinetics of this process is controlled by positive semi-definite matrices
Simpler form of the transmission conditions In the general thermodynamic setting, the surface chemical potentials are derivatives of a surface free energy. Due to the assumption of stationary surface equations, and that the boundary is fixed, we are able to formulate all surface equations in terms of the bulk chemical potentials. From a mathematical viewpoint the equation system (21), (23) only serves to eliminate the surface chemical potentials \(\mu ^\Gamma \) in order to calculate the external fluxes of the electrolytic species (see the appendix, section C).
Denoting by \(\mathrm{R}( M^{\Gamma })\) the range of \(M^{\Gamma }\), we define \(\hat{s}^{\Gamma } := {{\,\mathrm{dim}\,}}\mathrm{R}( M^{\Gamma })\), and we choose basis vectors \(\hat{\gamma }^1,\ldots ,\hat{\gamma }^{\hat{s}^{\Gamma }}\) for \(\mathrm{R}( M^{\Gamma })\). The conditions (21), (23) allow to represent the flux of the electrolytic species via
Here, the external response \(J^0\) is a mapping from \([0,T] \times \Gamma \) into \({{\,\mathrm{span}\,}}\{\hat{\gamma }^1,\ldots ,\hat{\gamma }^{\hat{s}^{\Gamma }} \}\). The modified reaction term \(\hat{r}\) is a map on \([0,T] \times \Gamma \times \mathbb {R}^{\hat{s}^{\Gamma }}\), which possesses the structure
Moreover, there is a convex non-negative potential \(\hat{\Psi }^{\Gamma }: \, [0,T] \times \Gamma \times \mathbb {R}^{\hat{s}^{\Gamma }} \rightarrow \mathbb {R}\) such that \(\hat{R}^{\Gamma }(t, \, x, \, D) = - \nabla _D \hat{\Psi }^{\Gamma }(t, \, x, \, D)\) for all \((t,x,D) \in [0,T] \times \Gamma \times \mathbb {R}^{\hat{s}^{\Gamma }}\), and \(\nabla _D \hat{\Psi }^{\Gamma }(t, \, x, \, 0) = 0\) for all \((t,x) \in [0,T] \times \Gamma \). The data \(\mu ^{\text {ext}}\), \(M^{\Gamma }\) and \(M^{\Gamma ,\text {ext}}\) are included in the position dependence of \(J^0\) and \(\hat{\Psi }^{\Gamma }\). In the analysis we shall for simplicity assume that this \(J^0\) and this \(\hat{\Psi }^{\Gamma }\) are the boundary data. In applications the solution of a few additional nonlinear algebraic equations are necessary to compute them.
Electrical potential The boundary condition for the electrical potential can be derived from Maxwell’s equations for surfaces, which are satisfied in the quasi-static stetting by a continuous electrical potential (see [13]). On \(]0,T[ \times \Gamma \) we impose the condition \(\phi = \phi _0\), where \(\phi _0\) is the given electric potential at \(]0,T[ \times \Gamma \).
3 Summary of model equations
Domain \({\Omega }\) Summarising, the evolution of the state \((\rho ,v,\varphi )\) in \(]0,T[\times \Omega \) is described by the PDE-system
Here, the chemical potentials \(\mu _i\) are related to the densities via (10), the function h is chosen of the form (18) with (19) and (20), and \(\mathbb {S}^{\text {visc}}\) is subject to (17).
Boundary \({\Gamma }\) We have on \(]0,T[ \times \Gamma \) the boundary conditions
where the external chemical potentials \(\mu ^{\text {ext}}\), the external potential \(\phi _0\) and the kinetic matrices \(M^{\Gamma }\) and \(M^{\Gamma ,\text {ext}}\) are given. The reaction rates \(R^\Gamma \) are satisfying (22). Recall that the conditions (28) represent \(N^{\Gamma }\) equations and are a shorter form for (21). Alternatively to (28), (29) and (30),
Boundary \(\varvec{\Sigma }\) We choose as simple as possible a model on the surface \(]0,T[\times \Sigma \) where basically all effects can be neglected: No mass flux \((\rho _i \, v + J^i) \cdot \nu = 0\) for \(i = 1, \ldots , N\); Complete adherence of the fluid \(v = 0\); No surface charge \(\nabla \phi \cdot \nu = 0\).
Initial conditions Initial conditions are prescribed for the variables \(\rho _1, \ldots , \rho _N\). We denote them \(\rho ^0_{i}\), \(i = 1,\ldots ,N\). Moreover, an initial state \(v^0\) is also given for the velocity vector.
4 Notation
To get rid of overstressed indexing, we simplify the notation by making use of vectors. For instance, we denote \(\rho \) the vector of mass densities, n the vector of number densities, i.e.
Moreover, we define the vector \(\mathbb {1} := 1^N := (1, \, 1, \ldots , 1) \in \mathbb {R}^N\), and we introduce the quotients of charge over mass \(e^0 \, z_i/m_i =: \bar{Z}_i\), and of volume over mass \(V_i/m_i =: \bar{V}_i\) as vectors via
Using these conventions, we have a. o. the identities \(\varrho = \mathbb {1} \cdot \rho \), \(n^F = \bar{Z} \cdot \rho \), \(n \cdot V = \rho \cdot \bar{V}\), etc.
With \(\mathbb {R}_+ = ]0, \, +\infty [\) and \(\mathbb {R}_{0,+} := [0, \, +\infty [\), we define \(\mathbb {R}^N_+ := (\mathbb {R}_+)^N\) and \(\mathbb {R}^N_{0,+} = (\mathbb {R}_{0,+})^N\).
The diffusion fluxes \(J^1, \ldots , J^N\) span a rectangular matrix \( J = \{J^{i}_{j}\} \in \mathbb {R}^{N \times 3} \). The upper index corresponds to the lines of this matrix. Vectors of \(\mathbb {R}^N\) are multiplicated from the left, as for instance in \(\mathbb {1} \cdot J = \sum _{i=1}^N J^i\) which is an identity in \(\mathbb {R}^3\).
The vectors \(\gamma ^1, \ldots , \gamma ^s\) span a rectangular matrix \(\gamma = \{\gamma ^k_i\} \in \mathbb {R}^{s \times N}\). The upper index corresponds to the line of the matrix. Vectors of \(\mathbb {R}^s\) are multiplicated from the left, as for instance in the identity \(r = R \cdot \gamma = \sum _{k=1}^s R_k \, \gamma ^k\) in \(\mathbb {R}^N\). Analogously the vectors \(\gamma ^1_{\Gamma }, \ldots , \gamma ^{s^{\Gamma }}_{\Gamma }\) span a rectangular matrix \(\gamma _{\Gamma } = \{\gamma ^k_{\Gamma ,i}\} \in \mathbb {R}^{s^{\Gamma } \times N^{\Gamma }}\). In order to describe the reactions, we shall further make use of the abbreviations \(\bar{R}: \, \mathbb {R}^s \rightarrow \mathbb {R}^s\), \(\bar{R} := -\nabla _{D^{\mathrm{R}}} \Psi \) and \(\hat{R}^{\Gamma }: \, \mathbb {R}^{\hat{s}^{\Gamma }} \rightarrow \mathbb {R}^{\hat{s}^{\Gamma }}\), \(\hat{R}^{\Gamma } := -\nabla _{\hat{D}^{\mathrm{R}}} \hat{\Psi }^{\Gamma }\).
For notational simplicity, we introduce the positive constant
Moreover, since the constants K, \(k_{B}\) and \(\theta \) play no role in the analysis we shall, for the sake of simplicity, normalise them to one.
We denote with \(\lambda _1\) the Lebesgue measure on \(]0, \, T[\), with \(\lambda _3\) the Lebesgue measure on \(\Omega \), and with \(\lambda _4\) the Lebesgue measure on Q. If the context is clear enough, we also employ the abbreviation \(|\cdot |\) for the Lebesgue measure of a set indifferently of its dimension.
Functional classes We define \(Q_t = ]0,t[ \times \Omega \) and \(S_t := ]0,t[ \times \Gamma \). We set \(Q := Q_T\) and \(S := S_T\). For \(1\le p, \, q < + \infty \), we employ the notations \(L^{p,q}(Q) \cong L^p(0,T; \,L^q(\Omega ))\).
We make use of standard Sobolev spaces for spatial domains and space-time domains. In particular, recall that \(W^{1,0}_p(Q) \cong L^p(0,T; \, W^{1,p}(\Omega ))\). We define \(W^{1,0}_{p,S}(Q) := \{u \in W^{1,0}_p(Q) \, : \, \text {trace}(u) = 0 \text { in } L^p(S)\}\).
For a convex, non-negative potential \(\Psi \in C(\mathbb {R}^s)\), \(s \ge 1\) (and for its conjugate \(\Psi ^*\)), the vectorial Orlicz classes \( L_{\Psi }(Q; \, \mathbb {R}^{s})\) and \(L_{\Psi ^*}(Q; \, \mathbb {R}^{s})\) are well known. We make use of the notation
For \(\hat{\Psi }^{\Gamma } \in L^{\infty }(S;\, C^2(\mathbb {R}^{\hat{s}^{\Gamma }}))\), we define a vectorial Orlicz class \(L_{\hat{\Psi }^{\Gamma }}(S; \, \mathbb {R}^{\hat{s}^{\Gamma }})\) as the set of all measurable \(\hat{D}^{\Gamma ,\text {R}}: \, S \rightarrow \mathbb {R}^{\hat{s}^{\Gamma }}\) such that
5 Mathematical assumptions on the data
From the thermodynamic viewpoint, the free energy function h, the mobility matrix M and the potentials \(\Psi \), \(\Psi ^{\Gamma }\) are the essential objects determining the properties of the constitutive equations. Mathematical results can be obtained under suitable restrictions to these objects. In addition, restrictions are as usual necessary concerning the geometry and the quality of boundary and initial states. In this investigation, we are not concerned with pointing at optimal classes for the second type of data.
Assumptions on the free energy function Our estimates on the (relative) chemical potentials require the special form (18), where the mixing entropy obeys the precise representation (20). We allow for a certain generality only at the level of the function \(h^{\text {mech}}\) which we assume of the form (19).
Thereby, we assume that F belongs to \(C^2(\mathbb {R}_+) \cap C(\mathbb {R}_{0,+})\) and is a strictly convex function. Moreover, we assume that there are \(3/2< \alpha < + \infty \) and constants \(0 < c_0, \, c_1\) such that
and that there are positive constants \(k_0 < k_1\), \(k_2 < k_3\) and \(s_1> s_0 > 0\) such that
For the analysis, we further crucially need that \(F^{\prime }: \, \mathbb {R}_+ \rightarrow \mathbb {R}\) is surjective. This is not satisfied for instance by the pure polynomial ansatz according to Tait, but it always follows from (35) in connection with the strict convexity of F. The assumptions (34), (35) cover the typical choice \(F(s) = s \, \ln s\)—as for instance in [12]—in the range of finite densities, but require superlinear growth for large arguments. The restriction \(\alpha >3/2\) is imposed by the available methods for the weak solution analysis of (single-component) Navier–Stokes equations.
Assumptions on the mobility matrix M is symmetric and positive semi-definite. Throughout the paper, we assume that M is mass conservative, that is
Moreover, we assume that the entries of M are continuous functions of the vector \(\rho \) of the partial mass densities, with at most linear-growth in \(\rho \).
Except for these few points, the exact structure of the mobility matrix is a delicate topic (in particular, there are connections to the Maxwell–Stefan theory, see [3, 18]). In this paper we restrict ourselves to the assumption that M has rank \(N-1\) independently on \(\rho \). In other words, denoting \(0 = \lambda _1(M) \le \lambda _2(M) \le \ldots \le \lambda _N(M)\) the eigenvalues of the matrix M, we assume that there are positive constants \(0 < \underline{\lambda } \le \overline{\lambda }\) such that
Let us remark that due to this assumption, only regularisations of the original ansatz of the paper [12] are included in the analysis: In formula (12), we must, for example, apply a cut-off from below to the entries of the empirical matrix \(M_{\text {emp}}\).
Assumptions on the reaction rates The reaction rates are derived from a strictly convex, non-negative potentialFootnote 1\(\Psi \in C^2(\mathbb {R}^s)\). It is possible to consider general convex potentials with super linear growth but, for the sake of technical simplicity, we shall require at least linear growth of the rates via
As to the adsorption coefficients \(M^{\Gamma }\) and \(M^{\Gamma ,\text {ext}}\) occurring in the boundary conditions (29), (30) they play in the analysis a role comparable to linear reactions. We assume them to be symmetric and positive semi-definite constant matrices. Moreover, in connection to the no slip condition (31), it is no restriction to require that \(M^{\Gamma } \, 1^{N} = 0\) and \(M^{\Gamma ,\text {ext}} \, 1^{N^{\text {ext}}} = 0\). Under these conditions, the modified reaction potential \(\hat{\Psi }^{\Gamma }\) on the boundary fulfils (see appendix, section C for a proof)
Assumptions on the domain \(\Omega \)and the boundary \(\Gamma \). \(\Omega \subset \mathbb {R}^3\) is bounded and of class \(\mathcal {C}^{0,1}\). In connection with the optimal regularity of the solution to the Poisson equation with mixed-boundary conditions, we introduce the exponent \(r(\Omega , \, \Gamma )\) as the sup. of all numbers in the range \([2,+\infty [\) such that
It is well known that \(r(\Omega , \, \Gamma ) > 2\) in general (see [19] a. o.), but there are numerous situations where, depending on the boundary of the domain and the structure of the surface \(\Gamma \), the optimal exponent satisfies \(r(\Omega , \, \Gamma ) > 3\) (see [10] for results and discussions on this topic). We require that
with \(\alpha \) from (34). This of course might be a restriction only if \(\alpha < 2\).
Assumptions on the remaining boundary data We consider only non-degenerate initial and boundary data, whereby we mean that
Note that the last assumption in (42) guarantees that \(J^0 \in L^{\infty }(]0,T[ \times \Gamma ; \, \{\hat{\gamma }^1,\ldots \hat{\gamma }^{\hat{s}^{\Gamma }}\})\) (see the appendix, section C). Therefore, there are coefficients \(\jmath _1, \ldots , \jmath _{\hat{s}^{\Gamma }} \in L^{\infty }([]0,T[ \times \Gamma )\) such that
The reaction vectors: critical manifold For the analysis of our special model of chemical reactions, we need to introduce a technical notion. Denote \(W \subseteq \mathbb {1}^{\perp } \subset \mathbb {R}^N\) the linear subspace given by
Recall that \(\hat{\gamma }^1, \ldots , \hat{\gamma }^{\hat{s}^{\Gamma }}\) are the reduced reaction vectors associated with the matrix \(M^{\Gamma }\). They are elements from \(\mathbb {1}^{\perp }\). Call selection S of cardinality \(|S| \le N\) a subset \(\{i_1, \ldots , i_{|S|}\}\) of \(\{1, \ldots , N\}\) such that \(i_1< \ldots < i_{|S|}\). For every selection, we introduce the corresponding projector \(P_S: \, \mathbb {R}^N \rightarrow \mathbb {R}^{N}\) via \(P_S(\xi )_i = \xi _{i}\) for \(i \in S\), and \(P_S (\xi )_i = 0\) otherwise. We define a linear subspace \(W_S \subset \mathbb {R}^{N}\) via
The selection S will be called uncritical if \({{\,\mathrm{dim}\,}}(W_S) = |S|\) and critical otherwise.
For every selection S, we denote \(S^{\text {c}}\) the complementary index set \(\{1, \ldots ,N\} {\setminus } S\). It can easily be shown that the manifold
is the finite union of submanifolds of dimension at most \(N-1\). We say that the initial compatibility condition is satisfied if the vector of initial net masses \(\bar{\rho }_0 := \int \limits _{\Omega } \rho ^0 \, \mathrm{d}x \in \mathbb {R}^{N}_{+}\) satisfies \(\bar{\rho }_0 \not \in \mathcal {M}_{\text {crit}}\).
6 Identification of natural variables in the equations of mass transfer
The three following factors affect the solution concept and the analysis of Eq. (25):
-
State-constraints (\(\rho \ge 0\));
-
The mobility matrix has a non-trivial kernel (\(M \, \mathbb {1} = 0\)). The PDE system is not parabolic;
-
For weak solutions, the continuity equation \(\partial _t \varrho + {{\,\mathrm{div}\,}}(\varrho \, v) = 0\) might generate a local vacuum.
6.1 State-constraints
The pair of vector fields \((\rho , \, \mu ): \, [0,T]\times \Omega \rightarrow \mathbb {R}^N_+ \times \mathbb {R}^N\) is subject to the algebraic relation \(\mu = \nabla _{\rho } h(\rho )\) (cf. (10)). Obviously: The vector of mass densities \(\rho \) must belong to the domain of the free energy function, while the vector of chemical potentials belongs to its image.
Meaningful choices of the function h must in general guarantee that the domain of \(\nabla _{\rho } h\) is a subset of \(\mathbb {R}^N_+\). Indeed, the algebraic constraint on \(\rho \) must be comply with the physical non-negativity restriction on the mass densities. The vector of chemical potentials \(\mu \) must belong to the image of \(\nabla _{\rho } h\). There are models, for instance the special constitutive assumption (18) with Tait equation for F, for which this image is a true subset of \(\mathbb {R}^N\).
These algebraic state-constraints are a fundamental obstacle to the application of a functional analytic method to prove the solvability of the model. In order to overcome this difficulty, we exploit a particular observation: For the special constitutive assumption (18), we can show that \(\nabla _{\rho } h: \, \mathbb {R}^N_+ \rightarrow \mathbb {R}^N\) is a bijection if the first derivative of the function F is surjective onto \(\mathbb {R}\). At least for a relevant particular choice of h, the PDE system is unconstrained in \(\mu \), and the chemical potentials are a favourable set of variables to perform existence theory or numerical approximation. This was already noted in the context of multicomponent gas dynamics (see [18, 7, 25]).
6.2 A ‘hyperbolic’ component
Diffusion and chemical reactions are the dissipative structures that provide a control on the vector \(\mu \). But the fluxes \(J^1,\ldots ,J^N\) and the functions \(r_1, \ldots , r_N\) occurring in the system (25) in fact only depend on the projection of the vector \(\mu \) on the subspace \(\mathbb {1}^{\perp } := \{\xi \in \mathbb {R}^N \, : \, \xi \cdot \mathbb {1} = 0\}\) (see the side condition (11) for the diffusion fluxes, and the restriction (4) on the vectors \(\gamma ^1, \ldots , \gamma ^s\)).
Thus, natural estimates can be obtained only for a \((N-1)\)-dimensional projection of the vector \(\mu \). Due to this observation it was noted in [12] that a change of variables is advantageous in order to define the solution. It is to note that this tool is also known from precursor investigations under the concept of entropic variables: We refer to [18] for an overview. Following these ideas, we keep as main variables:
-
(a)
On the one hand, one coordinate of the vector field \(\rho \), namely the total mass density \(\varrho = \rho \cdot \mathbb {1}\). This is the ‘hyperbolic’ component subject to the continuity equation (5);
-
(b)
On the other hand, \(N-1\) coordinates of the vector of chemical potentials \(\mu \) defined via a projection onto the linear space \(\mathbb {1}^{\perp } \subset \mathbb {R}^N\).
The possibility of these choices relies on an algebraic result that we want to afore mention here (See Sect. 8, Corollary 8.3 for the proof).
Proposition 6.1
Assume that the free energy function h satisfies the ansatz (18), (19), (20), and that the function F occurring in (19) belongs to \(C^2(\mathbb {R}_+) \cap C(\mathbb {R}_{0,+})\), is strictly convex, and possesses a surjective first derivative \(F^{\prime }\). Let \(\xi ^1, \ldots , \xi ^N \in \mathbb {R}^N\) be a basis of \(\mathbb {R}^N\) such that \(\xi ^N = \mathbb {1}\), and let \(\eta ^1, \, \ldots , \eta ^N \in \mathbb {R}^N\) be the vectors such that \(\xi ^i \cdot \eta ^j = \delta _i^j\) for \(i,j = 1,\ldots ,N\). We define a projector \(\Pi : \, \mathbb {R}^N \rightarrow \mathbb {R}^{N-1}\) and an extension operator \(\mathcal {E}: \, \mathbb {R}^{N-1} \rightarrow \mathbb {R}^N\) associated with the basis \(\{\xi ^i\}_{i=1\ldots ,N}\) via
Then, there are mappings \(\mathscr {R} \in C^1(\mathbb {R}_+ \times \mathbb {R}^{N-1} ; \, \mathbb {R}^N_+)\) and \(\mathscr {M} \in C^1(\mathbb {R}_+ \times \mathbb {R}^{N-1} ; \, \mathbb {R})\) such that the nonlinear algebraic equations \(\mu = \nabla _{\rho } h(\rho )\) are valid for \(\mu \in \mathbb {R}^N\) and \(\rho \in \mathbb {R}^N_+\) if and only if there are \(\varrho \in \mathbb {R}_+\) and \(q \in \mathbb {R}^{N-1}\) such that
In view of Proposition 6.1, we equivalently define a solution to the system of Eq. (25) as a pair \((\varrho , \, q)\), with a function \(\varrho : \, ]0,T[ \times \Omega \rightarrow \mathbb {R}_+\) and a vector field \(q: \, ]0,T[ \times \Omega \rightarrow \mathbb {R}^{N-1}\) such that
For instance, one might choose \(\xi ^i = e^{i}\) (\(i=1,\ldots , N-1\)). In this case, \(\eta ^{k} = e^{k} - e^{N}\) for \(k = 1,\ldots ,N-1\) and \(\eta ^N = e^N\). Thus, \(\Pi \mu \) is the vector \((\mu _{1}-\mu _{N}, \ldots , \mu _{N-1}-\mu _{N})\). For this reason, we propose to call relative chemical potentials the components of the new variable q.
In order to reexpress also in (26) and (27), the other occurrences of the original variables \(\rho \), \(\mu \), we use the following equivalences relying on (46):
Remark 6.2
-
It might be of importance to allow for a general \(\Pi \), as its choice can be suited to the structure of the mobility matrix (e.g. (12)) in order to simplify the structure of the diffusion.
-
In [14], we relaxed the lower bound in the condition (37) and used another strategy to introduce relative chemical potentials: define \(\hat{q} \in \partial \mathbb {R}^N_{-}\) via \(\hat{q} := \mu - \max _{i=1, \ldots , N} \mu _i \, \mathbb {1}\).
6.3 Vacuum oscillations
Although the pre-suppositions of the free energy model (18) in fact completely fail if the total mass density is below a lower critical value, the mathematical analysis cannot exclude the occurrence of a complete vacuum.
For our analytical treatment, a vacuum is characterised by the fact that the variables \(\varrho \) and q are ‘decoupled’ because the mapping \(q \mapsto \mathscr {R}(\varrho = 0, \, q)\) is trivial on the entire \(\mathbb {R}^{N-1}\). A concrete technical difficulty is raised concerning the compactness. Estimates on time-derivative are available only for the \(\rho \)-variables and do not transfer one to one to the q variables, since a sequence of mass densities \(\rho ^n = \mathscr {R}(\varrho _n, \, q^n)\) (\(n \in \mathbb {N}\)) such that \(\varrho _n \rightarrow 0\) would converge strongly even if the corresponding \(q^{n}\) exhibit oscillatory behaviour.
Since the reaction densities are nonlinear expressions of \(q_1,\ldots ,q_{N-1}\), the vacuum-oscillations affect the concept of the solution at this level: The representation \(R = - \partial _{D^{\mathrm{R}}}\Psi (\gamma ^1 \cdot \mathcal {E} q, \ldots , \gamma ^s \cdot \mathcal {E} q )\) for the production rates is restricted to the set where \(\varrho \) is strictly positive. An analogous situation occurs at the boundary \(]0,T[ \times \Gamma \) whenever it is in contact with a vacuum.
In order to include the possibility of this extreme behaviour, we relax the concept of a solution to (25), (28), (29), (30). It now contains four entries: the scalar \(\varrho : \, ]0,T[ \times \Omega \rightarrow \mathbb {R}_+\) (total mass density) and the vector field \(q: \, ]0,T[ \times \Omega \rightarrow \mathbb {R}^{N-1}\) (relative chemical potentials) like in the natural definition, but also the production factors in the bulk \(R: \, ]0,T[ \times \Omega \rightarrow \mathbb {R}^s\) and on the interface \(R^{\Gamma }: \, ]0,T[ \times \Gamma \rightarrow \mathbb {R}^{\hat{s}^{\Gamma }}\). We define the vacuum-free set via
For the representation of the bulk reactions, we require \(r = \sum _{k=1}^s \gamma ^k \, R_k\) with the following weaker condition:
We introduce a set \(S^+(\varrho ) \subseteq ]0,T[ \times \Gamma \) as the subset of all \((t,x) \in ]0,T[ \times \Gamma \) such that there is an open neighbourhood \(U_{t,x}\) with the property
For the concept of the solution, we ask for the representation \(\hat{r} = \sum _{k=1}^{\hat{s}^{\Gamma }} \hat{\gamma }^k \, R^{\Gamma }_{k}\) together with
7 The mathematical results
7.1 The solution class
For \(t > 0\), we recall that \(Q_t = ]0,t[ \times \Omega \), \(Q = Q_T\) and that \(S_t = ]0,t[ \times \Gamma \), \(S = S_T\). Exploiting the preliminary considerations of Sect. 6, a solution vector to the entire system (25), (26), (27) with boundary conditions (28), (29), (30), (31), (32) and initial conditions (\(=:\) Problem \(\mathrm{(P)}\)) is composed of the scalars \(\varrho : \, Q \rightarrow \mathbb {R}_+\) (total mass density) and \(\phi : \, Q \rightarrow \mathbb {R}\) (electrical potential) and of the vector fields \(q: \, Q \rightarrow \mathbb {R}^{N-1}\) (relative chemical potentials), and \(v: \, Q \rightarrow \mathbb {R}^{3}\) (barycentric velocity field). If we want to account for the possibility of vacuum, the production factors are not everywhere functions of these components only. Thus, we also introduce \(R: \, Q \rightarrow \mathbb {R}^s\), \(R^{\Gamma }: \, S \rightarrow \mathbb {R}^{\hat{s}^{\Gamma }}\) as variables. For a given vector \((\varrho , \, q, \, v, \, \phi , \, R, \, R^{\Gamma })\), we introduce on the base of Proposition 6.1 the auxiliary variables
An essential property of solutions is the mass and energy conservation.
Definition 7.1
We say that \((\varrho , \, q, \, v, \, \phi , \, R, \, R^{\Gamma })\) satisfies the (global) energy (in)equality with free energy function h and mobility matrix M if and only if the associated fields and variables (50) satisfy, for almost all \(t \in ]0,T[\),
We say that \((\varrho , \, q, \, v, \, \phi ,\, R, \, R^{\Gamma })\) satisfies the balance of net masses if the vector field
is subject to
The conservation of energy provides the natural bounds that will allow to define the weak solution. We introduce what one could call a natural class \(\mathcal {B}\), because this class naturally arises from the global energy and mass conservation identities associated with the model. The class \(\mathcal {B}\) reflects the regularity of the weak solution and depends on several parameters
-
The final time \(T >0\), the domain \(\Omega \) and the partition \(\Gamma \cup \Sigma \) of its boundary (see (40));
-
The choice of the free energy function h and in particular the growth exponent of (34);
-
The mobility matrix M, in particular its rank denoted by \({{\,\mathrm{rk}\,}}M\);
-
The choice of the potentials \(\Psi \) and \(\Psi ^{\Gamma }\) for the reaction densities.
The variables \(\varrho \), \(\phi \) and v will satisfy the conditions
with the exponents \(\alpha > 3/2\) and \(r(\Omega ,\Gamma ) > 2\) of the conditions (34) and (40), and with
For the variables R and \(R^{\Gamma }\), we consider the conditions
For the variable q, a control is achieved on the spatial gradient thanks to the assumption (37). However, in the context of flux boundary conditions, the bound on the \(L^1\)-norm is a non-trivial problem. We shall nevertheless obtain, in Theorem 11.3, the integrability in time via complex estimates involving the diffusion gradient, the reactions and the conservation of total mass. Under the assumption (38) of at least quadratic potentials, a natural class for the variable q is then
Due to the dissipation of chemical reactions, the variable q also satisfies the additional conditions
The natural class \(\mathcal {B}\) also encodes an information concerning the conservation of global mass (integration of (25) over \(\Omega \), (53)). We additionally introduce a non-negative function \(\Phi ^* \in C([0,T]^2)\), \(\Phi ^*(t,\, t) = 0\) constructed from the functions \(\Psi \), \(\Psi ^{\Gamma }\) (and thus from R and \(R^{\Gamma }\)) via
for all \(0 \le t_1 \le t_2 \le T\). Here, \(C_0\) is an appropriate constant that we will choose later. For a function \(u \in C^1([0,T])\), we define a weighted modulus of uniform continuity via
Definition 7.2
If \((\varrho , \, q, \, v, \, \phi , \, R, \, R^{\Gamma })\) fulfils (54)–(57) and (59), (60), (61), we define
where \(D^{\mathrm{R}}\), J, p are defined in (50), and \(\bar{\rho }\) in (52). We say that \((\varrho , \, q, \, v, \, \phi , \, R, \, R^{\Gamma })\) belongs to the class \(\mathcal {B}(T, \, \Omega , \, \alpha , {{\,\mathrm{rk}\,}}M, \, \Psi , \, \Psi ^{\Gamma })\) if and only if the number \([(\varrho , \, q, \, v, \, \phi , \, R,\, R^{\Gamma })]_{\mathcal {B}(T, \, \Omega , \, \alpha , \, {{\,\mathrm{rk}\,}}M, \, \Psi , \, \Psi ^{\Gamma })}\) is finite.
Definition 7.3
We call a vector \((\varrho , \, q, \, v, \, \phi , \, R, \, R^{\Gamma }) \in \mathcal {B}(T, \, \Omega , \, \alpha , \, N-1, \, \Psi , \, \Psi ^{\Gamma })\) a weak solution to the Problem \(\mathrm{(P)}\) if the energy inequality and the balance of net masses of Definition 7.1 are valid, and if the quantities \(\rho \), J, r and \(\hat{r}\), p and \(n^F\) obeying the Definitions (50) satisfy the relations
and if the identities (48) and (49) relating \(\varrho \), q, R and \(R^{\Gamma }\) are valid.
This concept of weak solution is well defined owing to standard estimates.
7.2 Main theorems
Theorem 7.4
(Global-in-time existence) Let \(\Omega \in C^{0,1}\). Assume that the free energy function h satisfies (34) and (35) and that the mobility matrix M satisfies (36) and (37). Let \(\Psi \in C^2(\mathbb {R}^s)\) and \(\Psi ^{\Gamma } \in C^2(\mathbb {R}^{s^{\Gamma }})\) be strictly convex, non-negative and satisfy (38). Assume that the initial data \(\rho ^0\) and \(v^0\), and the boundary data \(\mu ^{\text {ext}}\), \(\phi _0\) are non-degenerate in the sense of (42), and that one of the following conditions is valid:
-
(1)
\(\alpha \ge 2\);
-
(2)
\(\tfrac{9}{5} \le \alpha < 2\) and \(r(\Omega , \, \Gamma ) > \alpha ^{\prime }\);
-
(3)
\(\tfrac{3}{2}< \alpha < \tfrac{9}{5}\), \(r(\Omega , \, \Gamma ) > \alpha ^{\prime }\) and the vectors \(m \in \mathbb {R}^{N}_+\) and \(V \in \mathbb {R}^{N}_+\) are parallel.
Assume moreover that the vector \(\bar{\rho }^0 := \int \limits _{\Omega } \rho ^0(x) \, \mathrm{d}x\) of the initial net masses of the constituents has positive distance to the manifold \(\mathcal {M}_{\text {crit}}\) of (45). Then, for \(T > 0\) arbitrary, the problem \(\mathrm{(P)}\) possesses a weak solution in the class \(\mathcal {B}(T, \, \Omega , \, \alpha , \, N-1, \, \Psi , \, \Psi ^{\Gamma })\) (sense of Definition 7.3).
We can characterise the singular states of the system associated with species vanishing.
Theorem 7.5
We adopt the same assumptions as in Theorem 7.4. For every weak solution to \(\mathrm{(P)}\), the compact set \(K_0 := \{ t \in [0,T] \, : \, \min _{i=1, \ldots ,N} \bar{\rho }_i(t) = 0\}\) satisfies \(\lambda _1(K_0) = 0\). For almost all \(t \in [0,T] {\setminus } K_0\), the domain \(\Omega \) possesses the disjoint decomposition \(\Omega = \mathcal {P}_t \cup \mathcal {V}_t \cup \mathcal {N}_t\) where
-
(1)
\(\mathcal {P}_t = \{ x \in \Omega \, : \, \min _{i=1,\ldots ,N} \rho _i(t,x) > 0\}\) is a set where all components of the mixture are available;
-
(2)
\(\mathcal {V}_t = \{x \in \Omega \, : \, \varrho (t,x) = 0 \}\) is a set occupied by a complete vacuum;
-
(3)
\(\lambda _3(\mathcal {N}_t) = 0\).
If the initial net masses of the constituents belongs to the critical manifold, then it is possible that certain groups of species are completely consumed after finite time, and the solution then exists only up to this time. Afterwards, it might be necessary to restart the system with a smaller number of species.
Theorem 7.6
(Local-in-time existence) We adopt the same assumptions as in Theorem 7.4, except that we require \(\bar{\rho }_0 \in \mathcal {M}_{\text {crit}}\). Then, there are a time \(T_0 > 0\) depending only on the data, and a maximal time \(T_0 \le T^* \le +\infty \) such that for all \(t < T^*\), there is a weak solution \((\varrho , \, q, \, v, \, \phi , \, R,\, R^{\Gamma }) \in \mathcal {B}(t, \, \Omega , \, \alpha , \, N-1,\,\Psi , \, \Psi ^{\Gamma })\) in the sense of Definition 7.3 to \((P_{t})\). Moreover, the following alternative concerning \(T^*\) is valid:
-
(1)
Either \(T^* =+\infty \),
-
(2)
Or there is \((\varrho , \, q, \, v, \, \phi , \, R,\, R^{\Gamma }) \in \bigcap _{t < T^*}\mathcal {B}(t, \, \Omega , \, \alpha , \, N-1,\,\Psi , \, \Psi ^{\Gamma })\) that weakly solves \((P_t)\) for all \(t < T^*\), such that \(\min _{i=1, \ldots ,N} \bar{\rho }_i(t) > 0\) for all \(t \in [0,T^*[\), and such that
$$\begin{aligned} \lim _{t \rightarrow T^*} \min _{i=1, \ldots ,N} \bar{\rho }_i(t) = 0, \quad \liminf _{t \rightarrow T^*} \Vert q(t)\Vert _{L^1(\Omega ; \, \mathbb {R}^{N-1})} = +\infty . \end{aligned}$$
7.3 Structure of the next sections
Our plan for the next sections is as follows. According to the preliminary Sect. 6, the algebraic properties of Eq. (10) determines the analysis of the model. Our next Sect. 8 is therefore devoted to the proof of Proposition 6.1. After that, we shall turn our attention to the PDEs. In Sect. 9, we introduce thermodynamically consistent regularisations of the problem \(\mathrm{(P)}\) for which it is easier to prove the solvability. For this larger class of problems, we then derive the energy and global mass balance identities (Sect. 9.3) and the resulting a priori estimates (Sect. 10). Section 11 deals in particular with a priori estimates for the variable q, one of the most demanding part of the analysis. In order to pass to the limit with the numerous nonlinearities of the system, it is necessary to obtain compactness statements for the principal variables (Sect. 12). With this apparatus at hand, we are able to complete the proof of the main theorems in Sect. 13 and 14 devoted to existence.
8 The natural variables: algebraic statements
As far as the mass transfer part of the problem \(\mathrm{(P)}\) is concerned, the natural estimates resulting from the energy identity arise for the total mass density \(\varrho \) and for a \(N-1\) dimensional reduction of the vector \(\mu \), its projection on \(\mathbb {1}^{\perp }\). In this section, we describe the solution mapping for the nonlinear algebraic equation (10) in these variables. In particular, this section provides the rigorous derivation of the statements announced in Sect. 6.
8.1 The case of a general free energy
The algebraic relation between partial mass densities \(\rho \) and chemical potentials \(\mu \) is given by
In the isothermal case we can forget about the temperature-dependence, so \(h = h(\rho )\). Using tools of convex analysis, we immediately obtain that the relation (66) is invertible if h is a function of Legendre type on \(\mathbb {R}^N_+\), meaning that (cf. [32], chapter 26)
-
\(\rho \mapsto h(\rho )\) is strictly convex and continuously differentiable in \(\mathbb {R}^N_+\);
-
\(|\nabla _{\rho } h(\rho ^m)| \rightarrow +\infty \) for all \(\{\rho ^m\}_{m\in \mathbb {N}}\) such that \({{\,\mathrm{dist}\,}}(\rho ^m, \, \partial \mathbb {R}^N_+) \rightarrow 0\) (h is essentially smooth).
Lemma 8.1
Let \(h \in C^2(\mathbb {R}^N_+) \cap C(\mathbb {R}^N_{0,+})\) be a function of Legendre type on \(\mathbb {R}^N_+\). Let \(D^*_h \subseteq \mathbb {R}^N\) be the image \(\nabla _{\rho } h( \, \mathbb {R}^N_+)\), that is \(D^*_h = \{ \mu \in \mathbb {R}^N \, : \, \exists \, \rho \in \mathbb {R}^N_+, \, \mu = \nabla _{\rho } h(\rho )\} \). Then, the convex conjugate of h, denoted by \(h^*\), is a well-defined strictly convex function on \(D^*_h\), and it satisfies \(h^* \in C^2(D^*_h)\). Moreover, the relation (66) is valid for \(\mu \in D^*_h\) and \(\rho \in \mathbb {R}^{N}_+\) if and only if \(\rho = \nabla _{\mu } h^*(\mu )\).
Proof
The claim follows from the Theorem 26.5 of [32]. \(\square \)
Next we investigate the possibility to introduce ‘mixed’ coordinates to describe the set of solutions to (66). Let \(\xi ^1, \ldots , \xi ^N \in \mathbb {R}^N\) be a basis of \(\mathbb {R}^N\) such that \(\xi ^N := \mathbb {1}\). Choose \(\eta ^1, \, \ldots , \eta ^N \in \mathbb {R}^N\) such that \(\xi ^i \cdot \eta ^j = \delta _i^j\), \(i,j = 1,\ldots ,N\). We define \(\Pi : \, \mathbb {R}^N \rightarrow \mathbb {R}^{N-1}\) and \(\mathcal {E}: \, \mathbb {R}^{N-1} \rightarrow \mathbb {R}^N\) as in Proposition 6.1.
Corollary 8.2
Under the assumptions of Lemma 8.1, we define a set \(\mathscr {D} \subseteq \mathbb {R}_+ \times \mathbb {R}^{N-1}\) via
Then, \(\mathscr {D}\) is open, and there is a function \(\mathscr {M} \in C^1(\mathscr {D})\), \((s, \, q) \mapsto \mathscr {M}(s, \, q)\), such that if (66) holds with \(\mu \in D^*_h\) and \(\rho \in \mathbb {R}_+^N\), then
The derivatives of \(\mathscr {M}\) satisfy the identities
Proof
Define an open set \(\mathcal {U} \subset \mathbb {R}^{N-1} \times \mathbb {R}\) via
We define a function \(G: \, \mathcal {U} \times \mathbb {R}_+ \rightarrow \mathbb {R}\) via \(G(q, \, t, \, s) := \mathbb {1} \cdot \nabla _{\mu } h^*(\mathcal {E} q + t \, \mathbb {1}) - s \). We compute the partial derivatives and we use the strict convexity of \(D^2h^*\) to show that
Consider now the solution manifold for \(G = 0\) in \(\mathcal {U} \times \mathbb {R}_+\). Since \(G_t > 0\), we obtain from the implicit function theorem that there is \(\mathscr {M} \in C^1(\mathscr {D})\)
In particular, \(\partial _s \mathscr {M} = G_t^{-1}(q, \, t, \, s)\) and \(\partial _{q} \mathscr {M} = - G_{q}/G_t\).
Assume now that (66) is valid for \(\mu \in D^*_h\) and \(\rho \in \mathbb {R}_+^N\). We express \(\mu = \sum _{i=1}^{N-1} (\mu \cdot \eta ^i) \, \xi ^i + (\mu \cdot \eta ^N) \, \mathbb {1}\). Then, \(G(\Pi \mu , \, \mu \cdot \eta ^N, \, \rho \cdot \mathbb {1}) = 0\) so that \(\mu \cdot \eta ^N = \mathscr {M}(\rho \cdot \mathbb {1}, \, \Pi \mu )\). \(\square \)
Corollary 8.3
Assumptions as in Corollary 8.2. Then, there is a bijection \(\mathscr {R}: \, C^1(\mathscr {D}; \, \mathbb {R}^N_+)\) such that (66) is valid for \(\mu \in D^*_h\) and \(\rho \in \mathbb {R}^N_+\) if and only if \(\mu \cdot \eta ^N = \mathscr {M}(\rho \cdot \mathbb {1}, \, \Pi \mu )\) and \(\rho = \mathscr {R}(\rho \cdot \mathbb {1}, \, \Pi \mu )\).
Proof
For \((s, \, q) \in \mathscr {D}\), we define \(\mathscr {R}(s, \, q) := \nabla _{\mu } h^*( \mathcal {E}\, q + \mathscr {M}(s, \, q) \, \, \mathbb {1})\). We may compute that
In these formula, \(D^2h^*\) is evaluated at \(\mu = \mathcal {E} q + \mathscr {M}(s,q) \, \mathbb {1}\). In order to prove that \(\mathscr {R}\) is a bijection, it is sufficient to show that \(d\mathscr {R}\) is invertible. Let \(X = (r, \, q) \in \mathbb {R} \times \mathbb {R}^{N-1}\) arbitrary. Then, \(d\mathscr {R} \, X = 0\) means that for \(i = 1,\ldots ,N\) one has
The uniform invertibility of \(D^2h^*\) yields \(\mathcal {E} q = \mathbb {1} \, \left( \frac{r + D^2h^* \mathbb {1} \cdot \mathcal {E} q}{D^2h^* \mathbb {1} \cdot \mathbb {1}} \right) \). We now multiply this identity with \(\eta ^1,\ldots ,\eta ^{N-1}\), and since \(\eta ^j \cdot \mathbb {1} =0\) for \(j =1,\ldots ,N-1\), it follows that \(q_1 ,\ldots ,q_{N-1} = 0\). Therefore, also \(r = 0\). This proves that \(\mathscr {R}\) is bijective.
To prove the claimed equivalence, suppose first that (66) is valid. Applying Corollary 8.2, we find that \(\mu = (\mathcal {E} \circ \Pi ) \mu + \mathscr {M}(\rho \cdot \mathbb {1}, \, \Pi \mu ) \, \, \mathbb {1}\). Thus, \(\mu \cdot \eta ^N = \mathscr {M}(\rho \cdot \mathbb {1}, \, \Pi \mu )\). The definition of \(\mathscr {R}\) then yields \(\nabla _{\rho } h(\rho ) = \mu =\nabla _{\rho } h (\mathscr {R}(\varrho , \, \Pi \mu ))\), showing that \(\rho = \mathscr {R}(\varrho , \, \Pi \mu )\).
Reversely, if \(\rho = \mathscr {R}(\varrho , \, \Pi \mu )\) and \(\mu \cdot \eta ^N = \mathscr {M}(\rho \cdot \mathbb {1}, \, \Pi \mu )\), then the definition of \(\mathscr {R}\) yields \(\rho = \nabla _{\mu }h^*(\mathcal {E} \Pi \mu + \mu \cdot \eta ^N \, \mathbb {1}) = \nabla _{\mu }h^*(\mu )\), proving that (66) is valid. \(\square \)
The pressure function The pressure is given by the formula \(p := - h + \sum _{i=1}^N \rho _i \, \mu _i\). We immediately see under (66) that \(p = h^*(\mu )\) where \(h^*\) is the convex conjugate of h. We define a function \(P: \, \mathscr {D} \rightarrow \mathbb {R}\) via \(P(s, \, q) := h^*(\mathcal {E}\, q + \mathscr {M}(s, \, q) \, \mathbb {1})\).
Lemma 8.4
Let \((s, \, q) \in \mathscr {D}\). Then, \(P \in C^1(\mathscr {D})\) satisfies
In these formula, \(D^2h^*\) is evaluated at \(\mu = \mathcal {E} q + \mathscr {M}(s,q) \, \mathbb {1}\).
Proof
Define \(\mu := \mathcal {E} \, q + \mathscr {M}(s,\, q) \, \mathbb {1}\) and \(\rho = \nabla _{\mu } h^*(\mu )\). Then,
and the claim follows from Corollary 8.2. \(\square \)
8.2 Special constitutive choice of the free energy
For special choices of the free energy, we can find more explicit formula than Lemma 8.1. Under the conditions (18), (19), (20) the relation (66) reads
where \(c_1 , \ldots , c_N \in \mathbb {R}\) are constants related to the reference states, and \(y_i = \rho _i/(m_i\, \sum _j (\rho _j/m_j))\) is the number fraction. Recall that \(\bar{V}_i = V_i/m_i\). Note that the free energy \(h = h^{\text {ref}}+h^{\text {mech}}+h^{\text {mix}}\) satisfies the assumptions of Lemma 8.1 if we assume that the function \(F \in C^2(\mathbb {R}_+) \cap C(\mathbb {R}_{0,+})\) is of Legendre type on \(\mathbb {R}_+\). At first we want to characterise the set \(D^*_h\) and we need a preliminary Lemma.
Lemma 8.5
There is a function \(f \in C^1(\mathbb {R}^N)\) such that, if (68) is valid for \(\mu \in \mathbb {R}^N\) and \(\rho \in \mathbb {R}^N_+\), then \( F^{\prime }(\bar{V} \cdot \rho ) = f(\mu )\). Moreover, the function f satisfies the following inequalities
where c, \(C_i\) (\(i=1,2\)) are positive constants depending on V and m.
Proof
Define a function \(G: \, \mathbb {R}^N \times \mathbb {R} \rightarrow \mathbb {R}\), \((\mu , \, t) \mapsto G(\mu , \, t)\) via
For \(\mu \in \mathbb {R}^N\), it is readily verified that \(\lim _{t\rightarrow - \infty } G(\mu , \, t) = + \infty \) and that \(\lim _{t\rightarrow + \infty } G(\mu , \, t) = - 1\). Since \(G_t(\mu , \, t) < 0\), the solution manifold to \(G(\mu , \, t) = 0\) is a hyper-surface \(\{(\mu , \, f(\mu )) \, : \, \mu \in \mathbb {R}^N\}\) where \(\partial _{i}f(\mu ) = - G_t^{-1}(\mu , \, f(\mu )) \, G_{\mu _i}(\mu , \, f(\mu ))\). Easy computations show that
In particular, \(|\nabla _{\mu } f| \le \max m /\min V\). Moreover, if \(G(\mu , \, t) = 0\), then setting
we see that \(\mu _i = c_i + (V_i/m_i) \, t + (1/m_i) \, \ln y_i\) for \(i = 1, \ldots , N\). Since \(y \in ]0,1[^N\) and \(y \cdot \mathbb {1} = 1\), the estimates (69) easily follow. \(\square \)
We are now ready to prove an inversion formula for the relation (68).
Corollary 8.6
Assume that the function \(F \in C^2(\mathbb {R}_+) \cap C(\mathbb {R}_{0,+})\) is of Legendre type on \(\mathbb {R}_+\). Define \(D^*_h := \nabla _{\rho } h(\mathbb {R}^N_+)\). Then, \(D^*_h = \{\mu \in \mathbb {R}^N \, : \, f(\mu ) \in F^{\prime }(\mathbb {R}_+)\}\). If \(\mu \in D^*_h\), then
where \(F^*\) is the Legendre transform of F.
Proof
If \(\mu \in D^*_h\), then there is \(\rho \in \mathbb {R}_+^N\) such that \(\mu = \nabla _{\rho } h(\rho )\). Thus, (68) is valid, and Lemma 8.5 shows that \(F^{\prime }(\bar{V} \cdot \rho ) = f(\mu )\). Thus, \(f(\mu ) \in F^{\prime }(\mathbb {R}_+)\) and this first yields the inclusion \(D^*_h \subseteq \{\mu \in \mathbb {R}^N \, : \, f(\mu ) \in F^{\prime }(\mathbb {R}_+)\}\). In order to prove the reverse inclusion, consider \(\mu \in \mathbb {R}^N\) such that \(f(\mu ) \in F^{\prime }(\mathbb {R}_+)\). Define
We easily show that \(\nabla _{\rho } h(\rho ) = \mu \). Use of (70) yields
\(\square \)
Lemma 8.7
Adopt the same assumptions as in Corollary 8.6, and moreover assume that F fulfils (35). Then, \(\nabla _{\mu } h^* \in C^1(D^*_h)\), and for \(i,j=1,\ldots ,N\) there holds
with \( n \cdot V^2 := \sum _{i=1}^N V_i^2 \, n_i\). There are further constants \(C_0, \, C_1\) independent on \(\rho \) such that
Proof
By direct computation starting from (71), we obtain (72). This entails
The function \(s \, F^{\prime \prime }(s)\) is asymptotically equivalent to \(s \, s^{-1} = \mathrm{const}\) near zero (cf. (35)) and to \(s \, s^{\alpha -2} = s^{\alpha -1}\) for s large. Thus, there is a constant \(c_0 > 0\) such that \(\inf _{ s \in \mathbb {R}_+} s \, F^{\prime \prime }(s) \ge c_0\), and (73) follows. Further
Hence,
The estimate (74) is a consequence of (75) and of the Cauchy–Schwarz inequality: we can express \( V_i \, \rho _i = (V_i \, \sqrt{n_i}) \, (m_i \, \sqrt{n_i})\). In (74), we further make use of \(F^{\prime \prime }(\rho \cdot \bar{V}) \ge F^{\prime \prime }(c \, \varrho ) \ge \tilde{c} \, F^{\prime \prime }(\varrho )\) (cf. (35)). \(\square \)
As corollaries of Lemma 8.7, note that the functions \(\mathscr {M}\) of Corollary 8.2, \(\mathscr {R}_i\) of Corollary 8.3, and P of Lemma 8.4 all belong to \( \in C^1(\mathscr {D})\) and satisfy, for all \((s, \, q) \in \mathscr {D}\), the following inequalities:
Remark 8.8
For the applicability of our approximation methods, we are restricted to the case that \(D^*_h = \mathbb {R}^N\). In view of Corollary 8.6 this is basically the case if \(F^{\prime }\) is surjective. In this case, \(\mathscr {D} = \mathbb {R}_+ \times \mathbb {R}^{N-1}\) and there is no state-constraint on \(\mu \). Due to the bounds (76), the functions \(\mathscr {M}\), \(\mathscr {R}_i\) and P are globally Lipschitz continuous on \([0, \, r] \times \mathbb {R}^{N-1}\) for all \(r < +\infty \).
Remark 8.9
In the case that the growth exponent of the function F is less than 9/5, we rely in the analysis of the PDE system on the convexity of the function \(s \mapsto P(s, \, q)\) at fixed q. We are able to establish this property only in the very special case that P is a function of the total mass density. We note the following trivial observation: Define P as in Lemma 8.4 and assume that the vectors \(V \in \mathbb {R}^N_+\) and \(m \in \mathbb {R}^N_+\) are parallel. Then, P depends only on the first variable.
9 Approximate solutions
9.1 The regularisation strategy
The regularisation strategy, though not mass conservative, will be chosen thermodynamically consistent, since it consists in two essential steps:
-
(1)
A positive definite regularisation of the mobility matrix M;
-
(2)
A convex regularisation of the free energy function h.
The method involves three levels associated with positive parameter, say \(\sigma \), \(\delta \) and \(\tau \). We first modify the mobility matrix M in order to ensure ellipticity and allow a control on \(\nabla \mu \)
The \(\delta \)-regularisation consists in increasing the growth of the (mechanical) free energy modifying the function F that occurs in the definition of \(h^{\text {mech}}\) via \(F(\rho \cdot \bar{V}) \leadsto F(\rho \cdot \bar{V}) + \delta \, (\rho \cdot \bar{V})^{\alpha _{\delta }}\), \(\alpha _{\delta } > 3\). If the original growth exponent of F is larger than 3, this step can be omitted. We denote \(h_{\delta }\) the corresponding free energy function, that is
The \(\tau \)-regularisation is a stabilisation for the vector of chemical potentials. It consists in modifying the function \(h^*\) (or \((h_{\delta })^*\)) via
where \(\omega \in C^{2}(\mathbb {R})\) is a convex and increasing function for which we impose the growth conditions
For example, we may choose the function
which satisfies these assumptions. The choice of the regularisation \(\omega \) is by no means unique, the constants in the latter relation are determined from simple interpolation conditions. Essential for our purposes is in fact only the sublinear growth for \(s \rightarrow -\infty \) that is compatible with global convexity. The function \(h^*_{\tau ,\delta }\) is twice differentiable and strictly convex. Making use of the strict convexity, we easily show that the mapping \(\nabla h^*_{\tau ,\delta }: \, \mathbb {R}^N \rightarrow \mathbb {R}^N_+\) is bijective. Interpreting (78) as Legendre transform, we introduce a regularised free energy function via
which is a twice differentiable convex function on \(\mathbb {R}^N_+\). The main motivation for this construction is that the new free energy function has improved coercivity properties over the variables \(\rho \) and \(\mu \) as exposed in the following statement.
Lemma 9.1
Let the original free energy function h satisfy
with constants \(3/2< \alpha _0 < + \infty \) and \(0< c_0, \, c_1, \, C_0, \, C_1 < + \infty \). Let \(\alpha = \alpha _{\delta } > 3\) be the regularisation exponent of (77), and \(\omega \) a function satisfying (79). Define
Then, there are \(\tilde{c}_0, \, \tilde{c}_1 >0\), \(C_2 > 0\), and \(\tau _0(\alpha , \, \alpha _0) > 0\) such that, if \(\tau \le \tau _0\),
-
(1)
\(h_{\tau ,\delta }( \rho ) \ge \tilde{c}_0 \, ( |\rho |^{\alpha _0} + \delta \, |\rho |^{\alpha } + \tau \, \Phi _{\omega }(\mu )) - \tilde{c}_1\);
-
(2)
\(|D^2 h^*_{\tau ,\delta }(\mu )|/\varrho \le C_2\),
for all \(\rho \in \mathbb {R}^N_+\) and \(\mu \in \mathbb {R}^N \) connected by the identity \( \rho = \nabla _{\mu } h_{\tau ,\delta }^*(\mu )\).
Proof
The definition (80) implies that \(h_{\tau ,\delta }( \nabla h^*_{\tau ,\delta }(X)) = h_{\delta }( \nabla (h_{\delta })^*(X)) + \tau \, \Phi _{\omega }(X)\). By assumption, \(\rho \) and \(\mu \) are related via \(\rho = \nabla _{\mu } h_{\tau ,\delta }^*(\mu ) = \nabla _{\mu } (h_{\delta })^*(\mu ) + \tau \, \omega ^{\prime }(\mu )\), and we obtain for the regularised free energy the identity
On the other hand, the condition (79) ensures that \(\omega ^{\prime }(\mu _i) \le c_2 \, (1 + \omega ^{\prime }(\mu _i) \, \mu _i - \omega (\mu _i))^{1/\alpha }\). For \(\alpha >1\), denote by \(\underline{c}(\alpha ), \, \bar{c}(\alpha )\) two constants such that \(|a-b|^{\alpha } \ge \underline{c}(\alpha ) \, a^{\alpha } - \bar{c}(\alpha ) \, b^{\alpha }\) for all \(a, \, b >0\). Then,
Hence, we find positive numbers \(\tilde{c}\), \(\hat{c}\) and C depending only on \(\alpha \), \(\bar{V}\) and N such that
If we assume that \(\hat{c} \, \delta \, \tau ^{\alpha -1} \le 1/4\), then
We next use \(h(\rho - \tau \, \omega ^{\prime }(\mu )) \ge c_0 \, (\varrho - \tau \, |\omega ^{\prime }(\mu )|_1)^{\alpha _0} - c_1\). By similar arguments, and since \(\alpha _0 < \alpha \), the claim (1) follows.
To prove (2), observe that \(\varrho = \sum _{i=1}^N \partial _{\mu _i} h^*_{\tau ,\delta }(\mu )\). For \(X \in \mathbb {R}^N\), recall moreover that \(\partial _{i} h^*_{\tau ,\delta }(X) = \partial _i (h_{\delta })^*(X) + \tau \, \omega ^{\prime }(X_i)\) (cp. (78)). Hence, \(D^2_{i,j} h^*_{\tau ,\delta }(X) = D^2_{i,j}(h_{\delta })^*(X) + \tau \, \omega ^{\prime \prime }(X_i) \, \delta _{i,j}\). Making use of (73) and of the definition of \(h^*_{\delta ,\tau }\)
Moreover, owing to the choice of \(\omega \), there is a positive constant \(c_3\) such that \(\omega ^{\prime \prime }(X_i) \le c_3 \, \omega ^{\prime }(X_i)\) for all \(X \in \mathbb {R}^N\) (cf. (79)), and therefore,
We define \(C_2 := C_1 + c_3\), proving (2). \(\square \)
9.2 Approximation scheme
For the existence proof, we embeds the problem \(\mathrm{(P)}\) into a larger class of (approximate) problems \((P_{\tau ,\sigma ,\delta })\) characterised by an elliptic diffusion matrix \(M_{\sigma }\) and a regularised free energy \(h_{\tau ,\delta }\). Since in this approach it is possible to control the entire vector \(\mu \), a solution vector consists of the entries \(\mu \), v and \(\phi \).
In order to define the concept of solution, we introduce also in this case a natural class \(\mathcal {B}\) for the approximate solutions. If \(\delta , \, \sigma , \, \tau >0\), we say that \((\mu , \, v, \, \phi )\) belongs to \( \mathcal {B}(T, \, \Omega , \, \alpha , \, N, \, \Psi , \, \Psi ^{\Gamma })\) if and only if
Replacing in \([(\varrho , \, q, \, v, \, \phi , \, R, \,R^{\Gamma })]_{\mathcal {B}(T, \, \Omega , \, \alpha , \, N-1, \, \Psi , \, \Psi ^{\Gamma })}\) the norm of q in \(W^{1,0}_2(Q; \, \mathbb {R}^{N-1})\) with the full norm \(\Vert \mu \Vert _{W^{1,0}_2(Q; \, \mathbb {R}^N)}\), we introduce the natural ‘norm’ \([(\mu , \, v, \, \phi )]_{\mathcal {B}(T, \, \Omega , \, \alpha , \, N, \, \Psi , \, \Psi ^{\Gamma })}\).
We say that \((\mu , \, v, \, \phi )\) satisfies the approximate energy (in)equality if and only if the corresponding vector \((\varrho , \, q, \, v, \, \phi , \,R, \, R^{\Gamma })\) satisfies the energy (in)equality of Definition 7.1, with free energy function \(h_{\tau ,\delta }\) and mobility matrix \(M_{\sigma }\). For \(\delta , \, \sigma , \, \tau >0\), we call weak solution to the problem \((P_{\tau , \, \sigma , \, \delta })\) a vector \((\mu , \, v, \, \phi )\) subject to the energy inequality and such that the quantities
fulfil the identities (63), (65) and, instead of (64),
Since the second definition in (83) in general implies that \(\sum _{i=1}^N J^i \ne 0\), it is necessary to add this contribution in the momentum equation (84) in order to preserve the energy identity.
The existence of approximate solutions for the regularised scheme is not a trivial problem, because there is no monotone or pseudo-monotone structure inherent to the diffusion. We carry over this technical step in Sect. 14 by means of a time-continuous Galerkin method. It turns out that for parameters \(\delta , \, \sigma > 0\) and \(\tau \ge 0\), weak solutions to \((P_{\tau ,\sigma ,\delta })\) exist and develop no vacuum.
9.3 Derivation of the global energy and mass balance identities
In this paragraph, we motivate the thermodynamically consistent approximations \((P_{\tau ,\sigma ,\delta })\) by deriving the natural energy identity. The derivation assumes here only formal character, meaning that the existence of a solution with increased regularity is assumed to perform the calculations. A rigorous proof of the existence claim for \((P_{\tau ,\sigma ,\delta })\) with energy inequality is, due to its technicality, postponed to Sect. 14.
Proposition 9.2
Assume that there are vector fields \(\mu \in C^{0,1}([0,T] \times \Omega ; \, \mathbb {R}^N)\), \(v \in C^{0,1}([0,T] \times \Omega ; \, \mathbb {R}^3)\) and \(\phi \in L^{\infty }([0,T]; \, C^{0,1}(\Omega ))\) that satisfy, together with their associate variables \(\rho \), J, r, \(\hat{r}\), p, \(n^F\) defined in (83), the relations (63), (65), (84) and the initial and boundary conditions
We define \(\rho ^0 = \nabla _{\mu } h^*_{\tau ,\delta }(\mu ^0)\). Then, for all \(t \in ]0,T[\), the vector \((\mu , \, v, \, \phi )\) satisfies the energy equality (51) with free energy function \(h_{\tau ,\delta }\) and mobility matrix \(M_{\sigma }\).
Proof
Due to the additional regularity assumed, it is fairly standard to show that (63), (65), (84) imply in every \(t \in ]0,T[\) that
for all \(\psi \in W^{1,1}(\Omega ; \, \mathbb {R}^N)\), all \(\eta \in W^{1,1}_0(\Omega ; \, \mathbb {R}^3)\) and for all \(\zeta \in W^{1,1}_{\Gamma }(\Omega )\).
We insert \(\psi = \mu (t)\) into (85). The definition of \(\rho \) implies that \(\sum _{i=1}^N \rho _i \, \nabla \mu _i = \nabla h^*_{\tau ,\delta }(\mu ) = \nabla p\). Moreover, it yields \(\mu = \nabla _{\rho } h_{\tau ,\delta }(\rho )\), and therefore \(\partial _t \rho \cdot \mu = \partial _t h_{\tau ,\delta }(\rho )\). It follows that
We choose \(\psi = \bar{Z} \, \phi (t)\) in (85). Recall that \(r \cdot \bar{Z} = 0\), because \(\gamma ^k \cdot \bar{Z} = 0\) for every reaction vector (elementary charge conservation, see (4)). Thus,
We differentiate (87) in time, and we choose \(\zeta = \phi (t) - \phi _0(t)\), This entails
If we now add (91) to (88), it follows that
Next we choose \(\eta = v(t)\) in (86), which shows that
For \(\psi = |v(t)|^2 \, \mathbb {1}\) in (85), observing that \( r \cdot \mathbb {1} = 0 =\hat{r}\cdot \mathbb {1}\) by definition, it follows that \(\int \limits _{\Omega } \partial _t \varrho \, v^2 - \int \limits _{\Omega } (\varrho \, v + \sum _{i=1}^N J^i) \cdot \nabla v^2 = 0\), which directly entails
Thus, (93) now yields
We add (94) to (92) and obtain that
We integrate over time and are done. \(\square \)
The proof of the global mass conservation identities (53) is comparatively simpler. It suffices to insert \(\psi = e^i\) for \(i = 1,\ldots ,N\) into (85).
Proposition 9.3
We adopt the assumptions of Proposition 9.2. Then, for all \(t \in [0,T]\)
10 A priori estimates directly resulting from the energy equality
In this section, we derive a priori estimates on solutions to the problem \(\mathrm{(P)}\) that result from the energy identity. In order to include in our considerations both approximation scheme and limit problem, we consider generic free energy functions for which there are \(c_1 >0\), \(c_2\ge 0\) and \(C_i \ge 0\), \(i = 1,2,3\) and \(\tau > 0\) such that for all \(\rho \in \mathbb {R}^N_+\)
In view of Lemma 9.1, the growth condition (95) are precisely the ones to expect from the chosen stabilisation. Moreover, we consider mobility matrices \(M_{\sigma } = M(\rho ) + \sigma \, \text {Id}\), \(\sigma \ge 0\), such that M satisfies (36) and (37). We commence with a few standard estimates.
Proposition 10.1
Let \((\varrho , \, q, \, v, \, \phi , \, R,\, R^{\Gamma })\) satisfy the energy inequality of Definition 7.1 with free energy function h and mobility matrix M fulfilling (95), (36), (37). Then, there is a number \(C_0 > 0\) depending only on \(\Omega \), T, on the constants \(c_i\), \(C_i\) in the conditions (95), and on the quantity
such that, with \(\rho \), J, etc. obeying Definitions (50) or (83),
Proof
Due to the property (95),
For general velocity fields \(v \in W^{1,2}(\Omega ; \, \mathbb {R}^3)\), we invoke (17) to see that
In the case that \(v = 0\) on \(\partial \Omega \), integration by parts directly yields
For estimating the right hand of the energy identity
Owing to similar standard considerations
The Young inequality further implies that
Since \((\hat{\Psi }^{\Gamma })^*(t,x, \, -\frac{1}{4} \, R^{\Gamma }) = (\hat{\Psi }^{\Gamma })^*(t,x, \, \frac{1}{4} \, (-R^{\Gamma }) + \frac{3}{4} \, 0)\), convexity implies that
Recall that \(J^0\) possesses the representation (43), and therefore
Due to convex duality
Thus, for all \(t \in ]0,T[\), the dissipation inequality implies that
Owing to the thermodynamical consistency, we (at least) obtain that \(\sum _{i=1}^N J^i \cdot D^i \le 0\). Moreover, \(\lambda +\frac{2}{3} \, \eta \ge 0\) implies \(\mathbb {S}(\nabla v) \, : \, \nabla v \ge 0\). Exploiting the Gronwall Lemma, we thus obtain bounds for the quantities \(\Vert \sqrt{\varrho } \, v\Vert _{L^{\infty ,2}(Q)}\), \(\Vert \nabla \phi \Vert _{L^{\infty ,2}(Q)}\) and \(\Vert \rho \Vert _{L^{\infty ,\alpha }(Q)}\) and \(\tau \, \Vert \Phi _{\omega }(\mu )\Vert _{L^{\infty ,1}(Q)}\). It next follows that
Since \(\lambda +\frac{2}{3} \, \eta \ge 0\) this in turn implies bounds for \(\Vert {{\,\mathrm{div}\,}}v\Vert _{L^2(Q)}\), and for \(\Vert \nabla v\Vert _{L^2(Q)}\). Moreover, the production factors R and \(R^{\Gamma }\) are bounded in Orlicz classes
whereas the reaction driving forces satisfy \([D^{\text {R}}]_{L_{\Psi }(Q; \, \mathbb {R}^s)} + [\hat{D}^{\Gamma ,\text {R}}]_{L_{\hat{\Psi }^{\Gamma }}(S_{T};\, \mathbb {R}^{\hat{s}^{\Gamma }})} \le C_0\). It remains to exploit the dissipation due to diffusion and the driving forces \(D^1, \ldots , D^N\). At first we note that \(- \sum _{i=1}^N J^i \cdot D^i = \sum _{i,j} M_{i,j} \, D^i \cdot D^j\). For \(i = 1,\ldots ,N\) the Cauchy–Schwarz inequality and the growth condition (37) on M (or \(M_{\sigma }\)) imply that
Therefore, we obtain for the diffusion fluxes that
It follows that \(\Vert J^i\Vert _{L^{2,2\alpha /(1+\alpha )}(Q)} \le c \, (\int \limits _{Q} M D \, : \, D)^{1/2} \le C_0 \).
We finally want to obtain estimates on the gradients of the (relative) chemical potentials. Here, we make use of the Assumption (37) that yields
where \(P_{\mathbb {1}^{\perp }}\) is the orthogonal projection on the space \(\mathbb {1}^{\perp }\). Due to additive splitting of the driving force \(D^i = \nabla \mu _i + \bar{Z}_i \, \nabla \phi \), we can obtain that
We make use of the identity \(P_{\mathbb {1}^{\perp }} \mu = \sum _{i=1}^{N-1} q_i \, P_{\mathbb {1}^{\perp }} \xi ^i\). Due to the choice of \(\xi ^1,\ldots ,\xi ^{N-1}\), the vectors \(P_{\mathbb {1}^{\perp }} \xi ^1,\ldots , P_{\mathbb {1}^{\perp }} \xi ^{N-1}\) are a basis of \(\mathbb {1}^{\perp }\). Thus, there is a constant depending only on the choice of the projector \(\Pi \) such that \(|P_{\mathbb {1}^{\perp }} \nabla \mu |^2 \ge c_{\Pi } \, |\nabla q|^2\). This entails \(|\nabla q|^2 \le c \, (- \sum _{i=1}^N J^i \cdot D^i + |\nabla \phi |^2)\), proving that \(\Vert \nabla q\Vert _{L^2(Q)} \le C_0\). Since \(M_{\sigma } D \cdot D \ge \sigma \, D^2\), we also see that
which yields the bound for \(\sqrt{\sigma } \, \Vert \nabla \mu \Vert _{L^2(Q)}\). Moreover,
Due to the conditions (79), we verify that \(|\omega ^{\prime }|^{\alpha } \le c\, (1+\Phi _{\omega })\) and this directly yields
At last we can verify that the function \(w = \sqrt{1+|\mu |}\) possesses a distributional gradient in \(L^2(Q)\) and, making use also of the growth property of \(\Phi _{\omega }\), we prove the bound
Hence, the Sobolev embedding theorems and its extensions yield \(\Vert w\Vert _{L^{2,6}(Q)} \le C_{\sigma ,\tau }\). \(\square \)
Lemma 10.2
We adopt the assumptions of Proposition 10.1. Assume moreover that for almost all \(t \in ]0,T[\), the electrical potential \(\phi \in L^{\infty }(0,T; \, W^{1,2}(\Omega ))\) satisfies
with \(\phi _0 \in L^{\infty }(Q) \cap L^{\infty }(0,T; \, W^{1,\beta }(\Omega ))\), \(\beta = \min \{r(\Omega , \, \Gamma ), \, \frac{3\alpha }{(3-\alpha )^+}\}\). Then,
Moreover, \(\Vert n^F \, \nabla \phi \Vert _{L^{\infty ,\frac{\beta \alpha }{\beta +\alpha }}(Q)} \le \Vert n^F\Vert _{L^{\infty ,\alpha }(Q)} \, \Vert \nabla \phi \Vert _{L^{\infty ,\beta }(Q)}\) whenever \(\beta \ge \alpha ^{\prime }\).
Proof
We only need to recall that \(\alpha > 3/2\) and the definition of the exponent \(r(\Omega ,\Gamma ) \ge 2\) (see (40)). The estimates for \(\phi \) are standard consequences of second order elliptic theory, whereas the bound for \(n^F \, \nabla \phi \) follows from the Hölder inequality. \(\square \)
Next we can derive the uniform continuity estimate that results from the mass balance equations.
Proposition 10.3
Assumptions of Proposition 10.1. If \(\bar{\rho }\) satisfies the identity of Definition (53), then \([\bar{\rho }]_{C_{\Phi ^*}([0,T])} \le C_0\).
Proof
Let \(0 \le t_1 < t_2 \le T\). Note that by assumption \(\bar{\rho }(t_2) - \bar{\rho }(t_1) = \int \limits _{t_1}^{t_2} \{ \int \limits _{\Omega } r + \int \limits _{\Gamma } (\hat{r}+ J^0)\}\). We note that
We argue similarly with the other right-hand side terms. Recall the definition of the natural class \(\mathcal {B}\) to show that \(|\bar{\rho }(t_2) - \bar{\rho }(t_1)| \le \bar{C}_0 \, \Phi ^*(t_1,\, t_2)\). \(\square \)
In the course of the proofs, we shall also need bounds of more technical nature obtained via Hölder and Sobolev inequalities. We denote \(\alpha \) the growth exponent of the function h at infinity and \(\beta := \min \{r(\Omega , \, \Gamma ), \, 3\alpha /(3-\alpha )^+\}\) the optimal regularity of the electric field.
Lemma 10.4
We assume that the bounds in Proposition 10.1 are valid. Then,
Further, we shall need an improved bound on the pressure. This is also fairly standard and, therefore, we postpone the proof to the appendix.
Lemma 10.5
Assume that the relation (84) is valid:
-
If \(\alpha > 3\), then \(\Vert p\Vert _{L^{1+1/\alpha }(Q)} \le C_0\);
-
If \(3/2 < \alpha \le 3\), \(r(\Omega , \, \Gamma ) > \alpha ^{\prime }\) and \(\mathbb {1} \cdot J \equiv 0\), then \(\Vert p\Vert _{L^{1+\frac{2}{3}-\frac{1}{\alpha }}(Q)} \le C_0\).
The only piece of information still missing in order to obtain a bound in the natural class is the estimate on the vector q. This is the object of the next section.
11 A priori estimates for the (relative) chemical potentials
In this section, we show that a combination between the estimates on the reaction driving forces \(D^{\text {R}}, \, D^{\Gamma ,\text {R}}\), the control on the gradient of the relative potentials \((q_1, \ldots , q_{N-1})= \Pi \mu \) (cf. Proposition 10.1) and the balance of total mass (Proposition 9.3) allows to control also the \(L^2\)-norm of these functions in the sense of the natural class \(\mathcal {B}\).
The starting point is a given pair \((\varrho , \, q) \in L^{\infty ,\alpha }(Q) \times L^1(Q; \, \mathbb {R}^{N-1})\). We define \(\rho := \mathscr {R}(\varrho , \, q)\), \(\bar{\rho } := \int \limits _{\Omega } \rho \, \mathrm{d}x\) and \(\mu := \mathcal {E} q \) (see Sect. 8). An essential ingredient of the proof is the balance of total mass valid for all \(t \in ]0,T[\) implying, with the linear space W of (44),
At every point where \(\varrho > 0\), we may resort to the representations
Here, \(y_i = (\rho _i/m_i)/\sum _j (\rho _j/m_j)\).
We commence stating an obvious estimate, that results from Proposition 10.1.
Lemma 11.1
Define \(P_W: \, \mathbb {R}^N \rightarrow W\) the orthogonal projection on the subspace W. There is C depending only on \(\Omega \) such that
Proof
Consider the vectors \(\gamma ^k \in \mathbb {R}^N\), \(k \in \{ 1,\ldots ,s\}\) associated with the bulk reactions. Since we assume (38), then obviously \(\Vert \mu \cdot \gamma \Vert _{L^2(\Omega )}\) is controlled by \([D^{\text {R}}]_{L_{\Psi }(\Omega ;\, \mathbb {R}^s)}\). Since \(\gamma ^k \cdot \mathbb {1} = 0\) for all k, there is a constant \(c_{W,\Pi }\) depending on W and the choice of the projector \(\Pi \) such that \(|\nabla (\gamma \cdot \mu )| \le c_{W,\Pi } \, |\nabla \Pi \mu |\). We also obtain (trace theorem) that \(\Vert \mu \cdot \gamma \Vert _{L^2(\Gamma )} \le C \, \Vert \mu \cdot \gamma \Vert _{W^{1,2}(\Omega )}\). Thus,
We analogously observe that \(|\mu \cdot \hat{\gamma }|\) is controlled by \(|\hat{D}^{\Gamma ,\text {R}}|\), which is bounded by the data in \(L_{\hat{\Psi }^{\Gamma }}\) and, due to (38), also in \(L^2(]0,T[ \times \Gamma )\). We make use of the fact that \(\Vert \mu \cdot \hat{\gamma }\Vert _{L^2(\Omega )} \le C \, (\Vert \nabla (\mu \cdot \hat{\gamma })\Vert _{L^2(\Omega )} + \Vert \mu \cdot \hat{\gamma }\Vert _{L^2(]0,T[\times \Gamma )})\), and the claim follows. \(\square \)
We next setup a preliminary tool for the main estimate of this section.
Lemma 11.2
Let \(\epsilon > 0\). For \(u \in L^1(\Omega )\), define
For all \(\delta > 0\), there is \(C^* = C^*(\delta )\) depending only on \(\Omega \) such that for all \(u \in W^{1,1}(\Omega )\)
Proof
We at first show that for all \(\delta > 0\), there is \(c = c(\delta )\) depending only on \(\Omega \) such that
Otherwise, there is \(\delta _0 >0\) such that for all \(j \in \mathbb {N}\), one finds \(u_j \in W^{1,1}(\Omega )\) and \(A_j, \, B_j \subset \Omega \), \(|A_j|, \, |B_j| \ge \delta _0\) and
Consider \(\bar{u}_j := u_j/\Vert u_j\Vert _{L^1(\Omega )}\). Then, \(\Vert \bar{u}_j\Vert _{W^{1,1}(\Omega )} \le \Vert \nabla \bar{u}_j\Vert _{L^{1}(\Omega )} + 1 \le j^{-1} + 1\). Consequently, there are a subsequence (no new labels) and a limiting element \(\bar{u} \in L^{1}(\Omega )\) such that \(\bar{u}_j \rightarrow \bar{u}\) strongly in \(L^1(\Omega )\). But since \(\nabla \bar{u}_j \rightarrow 0\) strongly in \(L^1(\Omega )\), \(\bar{u}\) must be a constant. Since also \(\bar{u}^+ \, |A_j| + |\bar{u}^-| \, |B_j| \rightarrow 0\), it obviously follows that \(\bar{u} \equiv 0\). Thus, \(1 = \Vert \bar{u}_j\Vert _{L^1(\Omega )} \rightarrow 0\), a contradiction.
For \(u \in L^1(\Omega )\), we apply (100) with the choices
It follows that either \(\min \{|A|, \, |B|\} < \delta \) or that
\(\square \)
We define \(\tilde{s} := {{\,\mathrm{dim}\,}}W\), and we choose \(b^1, \ldots , b^{\tilde{s}} \in W\) to be some basis of W. We call a selection \(S \subseteq \{1, \ldots , N\}\)critical if the span of the vectors \(P_S(b^1), \ldots , P_{S}(b^{\tilde{s}})\) is a true subspace of \(P_{S}(\mathbb {R}^N)\). For all critical selections, the manifold \(W_S := {{\,\mathrm{span}\,}}\{P_S(b^1), \ldots , P_{S}(b^{\tilde{s}})\} \oplus P_{S^{c}}(\mathbb {R}^N)\) has at most dimension \(N-1\).
The critical manifold is defined via (45).
Theorem 11.3
Assume that \(\bar{\rho }(t) \in \{\bar{\rho }_0\} \oplus W\) for all \(t \in [0,T]\). Let \(\tilde{s} = {{\,\mathrm{dim}\,}}W\) and \( b^1, \ldots , b^{\tilde{s}}\) be a basis of W. Then, if \({{\,\mathrm{dist}\,}}(\bar{\rho }_0, \,\mathcal {M}_{\text {crit}}) > 0\), the estimate
is valid. Here, \(c_0^*\) and \(k_0\) depend on \({{\,\mathrm{dist}\,}}(\bar{\rho }_0, \, \mathcal {M}_{\text {crit}})\).
Proof
For \(t \in ]0,T[\), we define \(r_0(t) := \sum _{k=1}^{\tilde{s}} \Vert b^k \cdot \mu (t)\Vert _{L^1(\Omega )}\), and \(d_0(t) := \Vert \nabla q(t)\Vert _{L^1(\Omega )}\).
Preliminary Consider the function \(\hat{q}_i:= \mu _i - \max _{j=1,\ldots ,N} \mu _j\) for \(i = 1,\ldots ,N\). Then, \(\hat{q} \le 0\) componentwise.
Moreover, \(\hat{q}_i\) possesses the generalised gradient \(\nabla \hat{q}_i = \sum _{i_0 = 1}^N \nabla (\mu _i - \mu _{i_0}) \, \chi _{B_{i_0}}\), where the set \(B_{i_0}\) obeys the definition \(B_{i_0} := \{ x \in \Omega \, : \, \mu _{i_0} = \max _{j=1,\ldots ,N} \mu _j\}\). Recall that, for all \(i \ne i_0\), the vector \(e^i - e^{i_0}\) belongs to \({{\,\mathrm{span}\,}}\{\eta ^1, \ldots , \eta ^{N-1}\}\). Therefore, we can show that
First step Now, exploiting Lemma 11.2 with \(u = \hat{q}_i\) (recall that \(\hat{q}_i^+ = 0\) for \(i =1,\ldots ,N\)), we obtain for \(\delta , \, \epsilon >0\) and \(t \in ]0,T[\) the alternative
Due to the definitions of \(\hat{q}\), \(i_0\) and to the Assumption (99), there holds, in \(B_{i_0} \subseteq \Omega \),
Hence,
We define \(\epsilon _0 := \tfrac{1}{8\, |c|_{\infty } }\), \(a_0 := \sup _{j,k=1,\ldots N} |\bar{V}_j - \bar{V}_{k} |\). For \(0 <\epsilon \le \epsilon _0\) and \(t \in ]0,T[\), we also define
Due to the inequality (102), the set inclusion
is valid. We next observe that the set \(\Omega {\setminus } A_{\epsilon }(t)\) can be decomposed via
Due to the asymptotic behaviour of the function \(F^{\prime }\) (see (35)), there are \(\epsilon _1 >0\) and \(\bar{k}_1, \, \bar{k}_2 >0\) depending only on F and \(a_0\) such that
In particular, it follows that
Thus, invoking (103) and (104), we obtain that
On the other hand, we readily see that
Thus, if \(\lambda _3(\{x \, : \, \hat{q}_i(t, \, x) \ge - \tfrac{1}{\epsilon }\}) \le \delta \), we can invoke (105) and (106) to see that
For all \(0< \epsilon < \min \{\epsilon _0, \, \epsilon _1\}\) and \(0 < \delta \), we therefore obtain from the latter and from (101) that
The second inequality would further imply that
For all \(0< \epsilon < \min \{\epsilon _0, \, \epsilon _1\}\) and \(0 < \delta \), we therefore can conclude that
where \(C_0, \, C_1\) are certain constants depending on the data, but independent on q and \(\rho \).
Second step Let \(t \in ]0,T[\). Consider \(i_1 \in \{1, \ldots ,N\}\). Then, we claim that there are constants \(c_0, \, c_1 > 0\), depending only on the vectors \(b^1, \ldots , b^{\tilde{s}}\), and a critical index set \(J \supset \{i_1\}\) such that
We prove this claim inductively. Let us at first describe the induction step. Suppose that \(K \subset \{1,\ldots ,N\}\) is any non-critical index set. Then, by the definition of such a set, there are for all \(k \in K\) coefficients \(\lambda ^k_1, \ldots , \lambda ^k_{\tilde{s}}\) such that
Hence, scalar multiplication with \(\hat{q}\) yields
Choosing \(k \in K\) such that \(\Vert \hat{q}_k\Vert _{L^1(\Omega )} = \max _{j \in K} \Vert \hat{q}_j\Vert _{L^1(\Omega )}\) and \(\ell \in K^{c}\) such that \(\max _{j \in K^{c}} \Vert \hat{q}_j\Vert _{L^1(\Omega )} = \Vert \hat{q}_{\ell }\Vert _{L^1(\Omega )}\), it follows that
Suppose now that for the non-critical selection \(K \supseteq \{i_1\}\) of cardinality \(m\ge 1\), we already know that there are positive constants \(c_0(m), \, c_1(m)\) such that
Then, invoking the two latter inequalities, the strictly larger selection \(K(m+1) = K \cup \{\ell \}\) satisfies
We apply this inductively starting from the selection \(K(1) =\{i_1\}\). If K(1) is critical, we are done already. Otherwise, since K consists of only the one element \(i_1\), it satisfies (109) with \(c_0(1) = 1\) and \(c_1(1) = 0\). Thus, we find some strictly larger selection K(2) satisfying (109) again. After a finite number of steps, we must reach some critical selection \(J \supseteq \{i_1\}\), proving the subclaim (108).
Now, assume that for parameters \(0< \epsilon < \min \{\epsilon _0,\epsilon _1\}\) and \(0 < \delta \) the inequality
is valid with the constants \(c_0, \, c_1\) from (108). Then, there is a critical selection \(J \supseteq \{i_1\}\) such that
Employing the first step of the proof (cf. (107)) then yields
Thus, we have proved the new alternative
Third step By assumption \({{\,\mathrm{dist}\,}}(\bar{\rho }_0, \,\mathcal {M}_{\text {crit}}) > 0\). As we assume that \(\bar{\rho }(t) \in \bar{\rho }^0 \oplus W\), there holds \(P_S(\bar{\rho }(t)) \in P_S(\bar{\rho }^0) \oplus W_S\) for every selection S. For every critical selection J, the definition (45) implies that \(|P_J(\bar{\rho }(t))| \ge {{\,\mathrm{dist}\,}}(\bar{\rho }_0, \, M_{\text {crit}}) > 0\). This in turn implies that
Thus, there are \(\delta _0 > 0\) and \(\bar{\epsilon }_0 > 0\) depending only on \( {{\,\mathrm{dist}\,}}(\bar{\rho }_0, \, M_{\text {crit}})\) such that the hypothesis in (110) yields a contradiction for all \(\delta \le \delta _0\) and \(0 < \epsilon \le \min \{\epsilon _0, \, \epsilon _1,\, \bar{\epsilon }_0\}\). With \(d_0 := {{\,\mathrm{dist}\,}}(\bar{\rho }_0, \, M_{\text {crit}})\), one indeed may choose
Conclusion We define \(k := C^*(\tfrac{\delta _0}{2}) \, \epsilon ^{-1} \, \lambda _3(\Omega )\). For \(k \ge k_0 =C^*(\tfrac{\delta _0}{2}) \, \lambda _3(\Omega )\, [\min \{\epsilon _0, \, \epsilon _1,\, \bar{\epsilon }_0\}]^{-1}\), the alternative (110) implies that the set
has measure zero. Hence,
Lemma 11.1 provides the bound for \(r_0\) and, since we control the gradients of q in \(L^{2,2}(Q)\), the claim now follows easily. \(\square \)
If the vector of initial net initial masses \(\bar{\rho }_0\) is on the critical manifold, then the argument of Theorem 11.3 does not apply, and can prove only a local-in-time version of the estimate.
Lemma 11.4
Assume that (97) is valid. Define
Then, there is a time \(T_0 > 0\) depending on \(\mathcal {B}_0\) (cf. (96)) and on \(\inf _{i = 1,\ldots ,N} \bar{\rho }^0_{i}\) such that \(T^* \ge T_0\), and \(\Vert q\Vert _{L^2(Q_{t}; \, \mathbb {R}^{N-1})} \le C_{0,t}\) for all \(t < T^*\).
Proof
We recall Proposition 10.3, and we see that \(|\bar{\rho }(t) - \bar{\rho }^0| \le \tilde{C}_0 \, \Phi ^*(t,0)\) for all \(t \in [0,T]\). Thus, if \(T_0\) is such that \(\inf _{i = 1,\ldots ,N} \bar{\rho }^0_{i} -\tilde{C}_0 \, \Phi ^*(T_0,0) \ge c_0 > 0\), we obtain that \(\inf _{i = 1,\ldots ,N} \bar{\rho }_{i}(t) > c_0\) for all \(t \in [0,T_0]\). Due to the first step of the proof of Theorem 11.3, relation (107), it then follows that
almost everywhere on \([0, \, T_0]\) for all \(i = 1,\ldots ,N\), \(\delta _0\) appropriate, and all \(\epsilon \le \min \{\epsilon _0, \, \epsilon _1\}\). \(\square \)
12 Compactness
Our aim in this section is to derive a general compactness tool in order to pass to the limit with approximate solutions to the problem \(\mathrm{(P)}\). We will discuss here the passage to the limit with the parameters \(\delta \) and \(\sigma \). The limit passage for \(\tau \rightarrow 0\) can be dealt with comparably simpler methods: see Sect. 14. Since we do not want to specify with which of the approximation parameters—\(\delta \) or \(\sigma \)—we pass to the limit, we will consider families indexed by a generic parameter \(\epsilon >0\).
We thus study compactness for a ‘solution family’ \(\{(\varrho _{\epsilon }, \, q^{\epsilon }, \, v^{\epsilon }, \, \phi _{\epsilon },\, R^{\epsilon }, \, R^{\Gamma ,\epsilon })\}_{\epsilon > 0}\) which might for example correspond to free energy functions \(\{h_{\epsilon }\}_{\epsilon >0}\) and mobility matrices \(\{M_{\epsilon }\}_{\epsilon > 0}\). In this section, our minimal assumptions are that \(h_{\epsilon }(\rho ) \ge c_0 \, |\rho |^{\alpha } - c_1\) for all \(\rho \in \mathbb {R}^N_+\), and that \(M_{\epsilon } \xi \cdot \xi \ge \underline{\lambda } \, |P_{\mathbb {1}^{\perp }} \xi |^2\) for all \(\xi \in \mathbb {R}^N\). These conditions are satisfied with constants \(\alpha > 3/2\), \(c_0, \, c_1\) and \(\underline{\lambda }\) independent of \(\epsilon \).
Moreover, for both limits of interest (\(\sigma ,\,\delta \rightarrow 0\)), we can assume the validity of a representation
where \(F_{\epsilon }(s) = F(s) + \epsilon \, s^{\alpha _{\epsilon }}\). Here, F is a function of Legendre type on \(\mathbb {R}_+\), with surjective derivative. The map \(\mathscr {R} = \mathscr {R}^{\epsilon } \in C^1(]0,+\infty [ \times \mathbb {R}^{N-1}; \, \mathbb {R}^N)\), introduced in Corollary 8.3 to reparametrise the densities, satisfies the estimates (76) with uniform constants. Remark 8.8 thus shows that the family \(\{\mathscr {R}^{\epsilon }\}_{\epsilon > 0}\) is bounded uniformly in \(C^{0,1}([0, \, r] \times \mathbb {R}^{N-1})\) for all \(r < +\infty \). Hence, as \(\epsilon \rightarrow 0\),
where \(\mathscr {R} \in C^1(\mathbb {R}_+ \times \mathbb {R}^{N-1}) \cap C(\mathbb {R}_{0,+} \times \mathbb {R}^{N-1})\) corresponds to the limit free energy (\(\epsilon = 0\) in (111)).
In order to obtain the compactness, we shall need the information on distributional time-derivatives contained in the system (63), (64) (or (84) instead). For technical reasons, it is convenient to express these information in an older (though elementary) fashion (see [24], Lemma 5.1 for the inspiring precursor of all Aubin–Lions-type techniques). For the sake of brevity, we introduce an auxiliary vector \(\mathcal {A}\) associated with the solution vector \((\varrho , \, q, \, v, \, \phi , \, R,\, R^{\Gamma })\) and the auxiliary quantities (50), (83) via
where \(a = 5N+34\) is the number of scalar components of the vector \(\mathcal {A}\). Due to the structure of the weak formulation, the identities
are valid. Here, \(\mathscr {L}^{i,j}(\mathcal {A})\), \(i,j=1,2\) are certain linear combinations with bounded coefficients of the entries of the vector \(\mathcal {A}\). The following observation is elementary.
Remark 12.1
Consider a family \(\{(\varrho _{\epsilon }, \, q^{\epsilon }, \, v^{\epsilon }, \, \phi _{\epsilon }, \, R^{\epsilon }, \, R^{\Gamma ,\epsilon })\}_{\epsilon > 0}\) which satisfies a uniform bound in the class \(\mathcal {B}(T, \, \Omega , \, \alpha , \, N-1, \, \Psi , \, \Psi ^{\Gamma })\). Define and auxiliary quantity \(\mathcal {A}^{\epsilon }\) in the fashion of (113). If the representation (114) is valid, then there is a subsequence \(\{\epsilon _n\}_{n\in \mathbb {N}}\) such that for almost all \(t \in [0,T]\) the sequences \(\{\rho _{\epsilon _n}(t)\}_{n\in \mathbb {N}}\) and \(\{\varrho _{\epsilon _n} \, v^{\epsilon _n}(t)\}_{n\in \mathbb {N}}\) converge as distribution in \(\Omega \).
Proof
Define \(w^{\epsilon } := (\rho ^{\epsilon }, \, \varrho _{\epsilon } \, v^{\epsilon })\), and let Y be the Banach space \(W^{1,\infty }_0(\Omega ; \, \mathbb {R}^{N}) \times W^{1,\infty }_0(\Omega ; \, \mathbb {R}^{3})\). Obviously, the identity (114) implies the bound \(\Vert \partial _t w^{\epsilon }\Vert _{L^1(0,T; \, Y^*)} \le C_0 \, \sup _{\epsilon \in [0,1]} \Vert \mathcal {A}^{\epsilon }\Vert _{[L^1(Q)]^a}\). Moreover, for arbitrary \(0< t_1< t_2 < T\), the family \(\{\int \limits _{t_1}^{t_2} w^{\epsilon }(t) \, \mathrm{d}t\}_{\epsilon > 0}\) is uniformly bounded in \(L^{2\alpha /(1+\alpha )}(\Omega )\) (second bound in Lemma 10.4), hence compact in \(Y^*\).
We invoke Lemma 4 and Theorem 1 of [33] to show that \(w^{\epsilon }\) is in a compact subset of \(L^p(0,T; \, Y^*)\) for all \(1\le p < +\infty \). Hence, we find \(w \in L^1(0,T; \, Y^*)\) and can extract a subsequence \(\{\epsilon _{n}\}_{n\in \mathbb {N}}\) such that \(w^{\epsilon _n} \rightarrow w \in L^1(0,T; \, Y^*)\) and \(w^{\epsilon _n}(t) \rightarrow w(t)\) in \(Y^*\) for almost all \(t \in ]0,T[\). \(\square \)
At first we need to extract weakly convergent sub-sequences.
Lemma 12.2
Consider a family \(\{(\varrho _{\epsilon }, \, q^{\epsilon }, \, v^{\epsilon }, \, \phi _{\epsilon }, \, R^{\epsilon }, \, R^{\Gamma ,\epsilon })\}_{\epsilon > 0}\) which satisfies a uniform bound in the class \(\mathcal {B}(T, \, \Omega , \, \alpha , \, N-1, \, \Psi , \, \Psi ^{\Gamma })\). Define auxiliary quantities \(\rho ^{\epsilon }\), \(J_{\epsilon }\), \(r^{\epsilon }\), \(\hat{r}^{\epsilon }\), \(p_{\epsilon }\), \(n^F_{\epsilon }\) and \(\mathcal {A}^{\epsilon }\) in the fashion of (50) (or (83)) and (113). Assume that (114) is valid. Assume that for almost all \(t \in ]0,T[\), \(\phi _{\epsilon }(t)\) satisfies in the weak sense \(-\bar{\chi } \, \triangle \phi _{\epsilon }(t) = \bar{Z} \cdot \rho ^{\epsilon }(t)\) in \(\Omega \) with the boundary conditions \(\nu \cdot \nabla \phi _{\epsilon }(t) = 0 \) on \(\Sigma \) and \(\phi _{\epsilon }(t) = \phi _0(t)\) on \(\Gamma \). Then, there are
and a subsequence \(\{\epsilon _n\}_{n \in \mathbb {N}}\) such that as \(n \rightarrow \infty \):
Proof
Using the bounds in the natural class \(\mathcal {B}\), we at first extract a subsequence such that
We now make use of the identity (114) via Remark 12.1. Thus, for all \(t \in [0,T]\), we realise that the entire sequence \(\{\rho ^{\epsilon _n}(t)\}\) converges as distributions. Since it is uniformly bounded in \(L^{\alpha }(\Omega )\), we obtain that \(\{\rho ^{\epsilon _n}(t)\}\) weakly converges in \(L^{\alpha }(\Omega )\). The limit must be identical with \(\rho (t)\) for almost all \(t \in [0,T]\). Thus, making use of Remark 12.3 hereafter, \(\rho ^{\epsilon _n} \rightarrow \rho \) strongly in \([W^{1,0}_2(Q)]^*\), and this allows to show that \(\varrho ^{\epsilon _n} \, v^{\epsilon _n} \rightarrow \varrho \, v\) as distributions in Q. Clearly \(\xi = \varrho \, v\).
Next we define \(\phi (t) \in W^{1,2}(\Omega )\) to be the unique weak solution to the problem \(-\bar{\chi } \, \triangle \phi (t) = \bar{Z} \cdot \rho (t)\) with the boundary conditions \(-\nu \cdot \nabla \phi (t) = 0\) on \(\Sigma \) and \(\phi (t) = \phi _0(t)\) on \(\Gamma \). Due to Remark 12.3 we can verify, for almost all \(t \in ]0,T[\), the strong convergence \(\phi _{\epsilon _n}(t) \rightarrow \phi (t)\) in \(W^{1,2}(\Omega )\). Thus, it also follows that \(\bar{Z} \cdot \rho ^{\epsilon _n} \, \nabla \phi _{\epsilon _n} \rightarrow \bar{Z} \cdot \rho \, \nabla \phi \) weakly in \(L^{1}(Q)\), implying that \(k_L = n^F \, \nabla \phi \). Remark 12.1 implies that \(\varrho _{\epsilon _n}(t) \, v^{\epsilon _n}(t)\) converges as distributions to \(\varrho (t) \, v(t)\) for almost all \(t \in ]0,T[\), and therefore also weakly in \(L^{2\alpha /(1+\alpha )}(\Omega )\). Since \(2\alpha /(1+\alpha ) > 6/5\), it also follows \(\varrho _{\epsilon _n} \, v^{\epsilon _n} \rightarrow \varrho \, v\) strongly in \([W^{1,0}_2(Q)]^*\). This in turn allows to show that \(\varrho _{\epsilon _n} \, v^{\epsilon _n} \otimes v^{\epsilon _n} \rightarrow \varrho \, v \otimes v\) as distributions, that means \(\tilde{\xi } = \varrho \, v \otimes v\). \(\square \)
Remark 12.3
-
Let \(1 \le p \le + \infty \). Let \(\mathcal {K} : \, L^p(\Omega ) \rightarrow W^{1,p}(\Omega )\) be a bounded, compact operator. Assume that \(\{u_n\}_{n\in \mathbb {N}} \subset L^p(Q)\) is a sequence such that \(u_n(t) \rightarrow u(t)\) weakly in \(L^p(\Omega )\) for almost all \(t \in ]0,T[\). Then, \(\mathcal {K}(u_n(t)) \rightarrow \mathcal {K}(u(t))\) strongly in \(W^{1,p}(\Omega )\) for almost all \(t \in ]0,T[\).
-
If \(v_n \rightarrow v\) weakly in \(W^{1,0}_2(Q)\) and \(u_n(t) \rightarrow u(t)\) strongly in \([W^{1,2}(\Omega )]^*\) for almost all \(t \in ]0,T[\), then \(u_n \, v_n \rightarrow u \, v\) weakly in \(L^1(Q)\).
We next can obtain the strong convergence of the velocity field. This result is in principle known (see [28], page 9).
Corollary 12.4
Assumptions of Lemma 12.2. Then, there is a subsequence such that \(\varrho _{\epsilon _n} \, |v^{\epsilon _n} -v|^2\) converges to zero strongly in \(L^1(Q)\) and pointwise almost everywhere in Q.
Proof
Consider a sequence \(\{v^m\}\) of smooth vector fields such that \(v^m \rightarrow v\) in \(W^{1,0}_2(Q;\, \mathbb {R}^3)\) for \(m \rightarrow \infty \). Due to Lemma 12.2, \(\varrho _{\epsilon _n} \, |v^{\epsilon _n} -v^m|^2\) is readily seen to converge to \(\varrho \, |v -v^m|^2\) weakly in \(L^1(Q)\) for \(n \rightarrow \infty \). On the other hand, using the continuity of the embedding \(W^{1,2}(\Omega ) \subset L^r(\Omega )\) for \(r \le 6\), we show for all \(\alpha \ge 3/2\) that
With similar arguments
Thus, \(\limsup _{n\rightarrow \infty } \Vert \varrho _{\epsilon _n}\, |v^{\epsilon _n} -v|^2\Vert _{L^1(Q)} \le C_0 \, \Vert v-v^m\Vert _{W^{1,0}_2(Q)}^2\). Letting \(m \rightarrow +\infty \), the claim follows. \(\square \)
12.1 Conditional compactness statements
We now can prove the conditional compactness of the family \(\{\rho ^{\epsilon }\}_{\epsilon > 0}\). We will need the following auxiliary statements.
Lemma 12.5
Consider a family \(\{\mathscr {R}^{\epsilon }\}_{\epsilon > 0} \subset C(\mathbb {R}_{0,+} \times \mathbb {R}^{N-1}; \, \mathbb {R}^N_+)\) fulfilling (112). For \(x \in \mathbb {R}_+ \times \mathbb {R}^{N-1}\), we denote \(x = (x_1, \, \bar{x})\). Let \(K \subset L^1(\Omega ; \, \mathbb {R}^N)\) be a weakly sequentially compact set, and \(K^* \subset L^{1}(\Omega )\) a sequentially compact set. Let \(\phi ^1, \, \phi ^2, \ldots \in C^{\infty }(\overline{\Omega })\) be a countable, dense subset of \(C(\overline{\Omega }; \, \mathbb {R}^N)\).
For all \(\delta > 0\), there are \(C(\delta ) > 0\), \(m(\delta ) \in \mathbb {N}\) such that, for all \(0 < \epsilon _1, \, \epsilon _2 \le 1/m(\delta )\)
for all \(w^1,\, w^2 \in L^1(\Omega ; \, \mathbb {R}_+ \times \mathbb {R}^{N-1})\) such that
Proof
Clearly, it is sufficient to prove the existence of \(C(\delta )\) and \(m(\delta )\) and, for all \(0 <\epsilon _1, \, \epsilon _2 \le 1/m(\delta )\), the inequality
for all \(w^1,\, w^2 \in L^{1}(\Omega ; \, \mathbb {R}_+ \times \mathbb {R}^{N-1})\) such that \(\mathscr {R}^{\epsilon _i}(w^i) \in K\), \(w^i_1 \in K^*\) and \(\bar{w}^i \in W^{1,1}(\Omega ; \, \mathbb {R}^{N-1})\) for \(i =1,2\) and such that \(\Vert \mathscr {R}^{\epsilon _1}(w^1) - \mathscr {R}^{\epsilon _2}(w^2)\Vert _{L^1(\Omega )} \ge \delta \). We argue by contradiction. If the latter claim is not true, there is \(\delta _0>0\) such that for all \(n \in \mathbb {N}\) and \(i=1,2\), we can find \(0< \epsilon _{i,n} < 1/n\), \(w^{i,n} \in L^{1}(\Omega ; \, \mathbb {R}_+ \times \mathbb {R}^{N-1})\) such that \(\mathscr {R}^{\epsilon _{i,n}}(w^{i,n}) \in K\), \(w^{i,n}_1 \in K^*\), \(\bar{w}^{i,n} \in W^{1,1}(\Omega ; \, \mathbb {R}^{N-1})\) (\(i=1,2\)) satisfying the properties
Since we assume that \(\mathscr {R}^{\epsilon _{i,n}}(w^{i,n}) \in K\) for \(i =1,2\) and since K is a bounded set of \(L^1(\Omega )\), we obtain first that \(\Vert \bar{w}^{i,n}\Vert _{W^{1,1}(\Omega )}\le C\) for all \(n \in \mathbb {N}\). Thus, we can extract a subsequence that we not relabel such that for almost all \(x \in \Omega \) there exists \(\bar{w}^{i}(x) := \lim _{n\rightarrow \infty } \bar{w}^{i,n}(x)\).
Moreover, as \(w^{i,n}_1 \in K^*\), we can extract a subsequence such that \(w^{i,n}_1 \rightarrow w^{i}_1\) strongly in \(L^1(\Omega )\) and almost everywhere in \(\Omega \). Consequently, we obtain for a subsequence and for \(i=1,2\) that
Now using that \(\mathscr {R}^{\epsilon _{i,n}}(w^{i,n}) \in K\), we can pass to a subsequence again to see that \(\mathscr {R}^{\epsilon _{i,n}}(w^{i,n}) \rightarrow u^i\) weakly in \(L^1(\Omega ; \, \mathbb {R}^N)\) for \(i = 1,2\). The property (112) and the pointwise convergence of \(w^{i,n}\) yield \(u^i = \mathscr {R}(w^i)\). We next use the second implication of (115), that is,
so that \(\mathscr {R}(w^1) = \mathscr {R}(w^2)\) almost everywhere in \(\Omega \). Hence, \(\mathscr {R}^{\epsilon _{1,n}}(w^{1,n}) - \mathscr {R}^{\epsilon _{2,n}}(w^{2,n}) \rightarrow 0\) weakly in \(L^1(\Omega )\) and pointwise. This implies that \(\mathscr {R}^{\epsilon _{1,n}}(w^{1,n}) - \mathscr {R}^{\epsilon _{2,n}}(w^{2,n}) \rightarrow 0\) strongly in \(L^1(\Omega )\) and that the condition (116) is violated. \(\square \)
We now state and prove our main compactness tool.
Corollary 12.6
Consider a sequence \(\{\mathscr {R}^{\epsilon _n}\}_{n \in \mathbb {N}} \subset C(\mathbb {R}_{0,+} \times \mathbb {R}^{N-1}; \, \mathbb {R}^N_+)\) fulfilling (112). For \(n \in \mathbb {N}\), let \(w^n: \, [0,T] \rightarrow L^1(\Omega ; \, \mathbb {R}_+ \times \mathbb {R}^{N-1})\) be continuous. Assume that \(\bigcup _{n \in \mathbb {N}} \bigcup _{t \in [0,T]} \{w^n_1(t)\}\) is compact in \(L^1(\Omega )\), and that there is \(C_1\) independent on n such that \(\Vert \bar{w}^n\Vert _{L^1(Q; \, \mathbb {R}^{N-1})} + \Vert \nabla \bar{w}^n\Vert _{L^1(Q; \, \mathbb {R}^{N-1})} \le C_1\). Assume moreover that \( \Vert \mathscr {R}^{\epsilon _n}(w^n)\Vert _{L^{\infty ,\alpha }(Q; \, \mathbb {R}^{N-1})} \le C_1\), and that the sequence \(\{\mathscr {R}^{\epsilon _n}(w^n(t))\}_{n\in \mathbb {N}}\) converges as distributions in \(\Omega \) for almost all t.
Then, there is a subsequence (no new labels) for which there exists \(\rho (t,\, x) := \lim _{n\rightarrow \infty } \mathscr {R}^{\epsilon _n}(w^n(t,\, x))\) for almost all \((t,x) \in Q\), and \( \mathscr {R}^{\epsilon _n}(w^n(t,x))\rightarrow \rho \) strongly in \(L^1(Q; \, \mathbb {R}^N)\).
Proof
For simplicity let \(\mathscr {R}^{n} := \mathscr {R}^{\epsilon _n}\). For \(n \in \mathbb {N}\), the assumptions imply that \(\mathscr {R}^{n}(w^n(t)) \in L^{\alpha }(\Omega ; \, \mathbb {R}^N)\) for all \(t \in [0,T]\). We define \(K \subset L^1(\Omega ; \, \mathbb {R}^N)\) via \(K := \bigcup _{n \in \mathbb {N}} \bigcup _{t \in [0,T]} \{\mathscr {R}^{n}(w^n(t))\}\) By assumption K is bounded in \(L^{\alpha }(\Omega )\) and thus also weakly sequentially compact in \(L^1(\Omega )\).
By assumption again, the set \(K^* := \bigcup _{n \in \mathbb {N}} \bigcup _{t \in [0,T]} \{w^n_1(t)\}\) is compact in \(L^1(\Omega )\). For \(\delta >0\), we find the constants \(C(\delta )\) and \(m(\delta ) \in \mathbb {N}\) according to Lemma 12.5. For all \(n \in \mathbb {N}\) such that \(\epsilon _n < 1/m(\delta )\), we apply the inequality of this Lemma with \(\epsilon _1 = \epsilon _n\), \(\epsilon _2 = \epsilon _{n+p}\), \(w^1 = w^n(t)\) and \(w^2 := w^{n+p}(t)\) (\(p \in \mathbb {N}\) arbitrary). For \(t \in [0,T]\) it follows that
We integrate the relation (117) over the set ]0, T[ and this yields
The vector fields \(\mathscr {R}^n(w^n)\) weakly converges in \(L^1(\Omega ; \, \mathbb {R}^N)\) for almost all t to some element \(\rho \in L^{\infty ,\alpha }(Q; \, \mathbb {R}^N)\). Invoking the triangle inequality,
It follows that
Due to the uniform bound in \(L^{\infty ,\alpha }\), the functions \(g_n(t) := \int \limits _{\Omega } (\mathscr {R}^n(w^n(t))-\rho (t)) \cdot \phi ^i\) are uniformly bounded in \(L^{\infty }(0,T)\) independently on n. Hence, invoking the Fatou Lemma
The vector fields \(\mathscr {R}^n(w^n(t))\) weakly converges in \(L^1(\Omega )\) for almost all t. Hence, the right-hand is zero in the latter inequality, and \(\limsup _{n\rightarrow \infty } \sup _{k\ge n} \int \limits _{0}^T \left| \int \limits _{\Omega } (\mathscr {R}^k(w^k(t))-\rho (t)) \cdot \phi ^i\right| = 0\). It next follows that
and, since \(\delta \) is arbitrary, \( \limsup _{n\rightarrow \infty } \sup _{p \ge 0} \Vert \mathscr {R}^n(w^n) - \mathscr {R}^{n+p}(w^{n+p})\Vert _{L^1(Q)} = 0\). This means that \(\{\mathscr {R}^n(w^n)\}\) is a Cauchy sequence in \(L^1(Q)\). In particular, we can extract a subsequence such that \(\lim _{n\rightarrow +\infty } \mathscr {R}^n(w^n)\) exists almost everywhere in Q. \(\square \)
Corollary 12.7
We adopt the same assumptions as in Lemma 12.2, and we assume moreover that the family of the total mass densities \(\{\varrho _{\epsilon }(t)\}_{\epsilon \ge 0, \, t\in ]0,T[}\) is compact in \(L^1(\Omega )\). Assume further that the family of transformations \(\{\mathscr {R}^{\epsilon }\}_{\epsilon > 0}\) fulfils (112). Then, \(\rho ^{\epsilon _n} \rightarrow \rho \) strongly in \(L^1(Q; \, \mathbb {R}^N)\). Moreover, for almost all \((t, \, x) \in Q\) such that \(\varrho (t, \,x) > 0\), there exists \(q(t, \, x) := \lim _{n \rightarrow \infty } q^{\epsilon _n}(t, \, x)\). The identity \(\rho = \mathscr {R}(\varrho , \, q)\) is valid at almost every point of the set \(Q^+(\varrho ) = \{(t, \, x) \, : \, \varrho (t, \,x) > 0\}\).
Proof
We consider a subsequence \(\{\epsilon _n\}_{n\in \mathbb {N}}\) fulfilling the convergence properties of Lemma 12.2. We define \(w^n = (\varrho _{\epsilon _n}, \, q^{\epsilon _n})\), and verify easily that all requirements of Corollary 12.6 are satisfied. We apply this Corollary to first show that \(\rho ^{\epsilon _n} = \mathscr {R}^{\epsilon _n}(\varrho _{\epsilon _n}, \, q^{\epsilon _n})\) converges strongly in \(L^1(Q)\) and pointwise almost everywhere.
In order to also show that \(\{q^{\epsilon _n}\}\) converges strongly, we resort to the representation (111) and to the definition of \(\mathscr {R}^{\epsilon _n}\). For \(k = 1,\ldots , N-1\), they yield
As \(\{\eta ^1, \ldots ,\eta ^{N-1}\}\) are chosen to form a basis of \(\{\mathbb {1}\}^{\perp }\), we can represent for \(i \ne j\) arbitrary the vector \(e^i-e^j\) with a linear combination of the \(\sum _{k=1}^{N-1} a^{i,j}_k\, \eta ^k\), hence
We now choose j as the indice associated with the largest number fraction, which implies that \(| (1/m_j) \, \ln y^{\epsilon _n}_j| \le \ln N/\min m\). For \(i=1,\ldots ,N\), we deduce the inequality
Recall that \(F_{\epsilon }(s) = F(s) + \epsilon \, s^{\alpha }\) with \(\alpha > 3\), while F is associated with a growth exponent \(\alpha _0 \le \alpha \). We multiply with \(\min \{\varrho _{\epsilon _n}, \, 1\}\) and, using the growth conditions (35) for F and the uniform bounds for \(\rho ^{\epsilon _n}\) in \(L^{\infty ,\alpha _0}\), for \(\epsilon _n \, \varrho _{\epsilon _n}^{\alpha }\) in \(L^{\infty ,1}\), and for \(q^{\epsilon _n}\) in \(L^2\), it follows that
Since \(y^{\epsilon _n}_i = \rho ^{\epsilon _n}_i/(m_i \, \sum _j (\rho ^{\epsilon _n}_j/m_j))\) converges pointwise, we can choose a subsequence such that \( \min \{\varrho _{\epsilon _n}, \, 1\} \, \ln y^{\epsilon _n}_i \rightarrow \min \{\varrho , \, 1\} \, \ln y_i\) strongly in \(L^1(Q)\) and pointwise almost everywhere in Q.
Making use of (118), we then verify that
It remains to observe that \(( \min \{\varrho _{\epsilon _n}, \, 1\} - \min \{\varrho , \, 1\}) \, |q^{\epsilon _n}|\) is uniformly bounded in \(L^2(Q)\) and tends to zero in \(L^1(Q)\), to show that \(\lim _{n\rightarrow \infty } q^{\epsilon _n}(t,x) \) exists for almost all (t, x) such that \(\varrho (t,x) >0\). \(\square \)
In order to pass to the limit in the boundary reaction terms, we also discuss the strong convergence of the relative chemical potentials on the boundary \(]0,T[ \times \Gamma \).
Lemma 12.8
Assumptions of Corollary 12.7. Then, for almost every \((t, \, x) \in S^+(\varrho )\), there exists \( q(t,\, x) := \lim _{n\rightarrow \infty } q^{\epsilon _n}(t, \, x)\).
Proof
By definition, the surface \(S^+(\varrho )\) is relatively open and possesses an open neighbourhood U in Q such that \(|U \cap \{(t,x) \, : \, \varrho (t, \, x) = 0\}| = 0\). Thus, for \((t_0, \, x^0) \in S^+(\varrho )\) arbitrary, there is \(R >0\) such that the cube \(Q_R(t_0,x^0)\) with radius \(R >0\) and centred at \((t_0, \, x^0)\) is contained in U. For all \(\epsilon > 0\), there is a constant \(c = c(\Omega , \, \epsilon )\) such that
Here, \(\Gamma _R\) and \(\Omega _R\) denote the intersection of \(\Gamma \) and \(\Omega \) with \(Q_R(x^0)\), the three-dimensional cube with radius R centred at \(x^0\). With the help of this inequality, we obtain for almost all \(t \in ]t_0-R, \, t_0+R[\) that
Integrating in time, it follows that
Now as \((]t_0-R, \, t_0+R[ \times \Omega ) \cap Q_R(x^0))\) is a subset of U, Corollary 12.7 implies that \(\int \limits _{t_0-R}^{t_0+R} \Vert q^{\epsilon _n}(t)-q(t) \Vert _{L^1(\Omega _R(x^0))} \,\mathrm{d}t \rightarrow 0\). Hence, \(\limsup _{n\rightarrow \infty } \int \limits _{t_0-R}^{t_0+R} \Vert q^{\epsilon _n}(t)-q(t)\Vert _{L^1(\Gamma _R(x^0))} \, \mathrm{d}t = 0\). \(\square \)
It remains to enlighten the global convergence property of the variables \(\{q^{\epsilon _n}\}\) inclusively of the set where vacuum possibly occurs. The following statement is a simple consequence of the a priori estimates, so we might spare the proof for the sake of being concise.
Lemma 12.9
Under the same assumptions as in Corollary 12.7, there is a subsequence such that \(q^{\epsilon _n} \rightarrow q\) weakly in \(W^{1,0}_2(Q)\).
With the help of the compactness statement, we can now identify all remaining weak limits.
Corollary 12.10
Assumptions as in Corollary 12.7. Let J, p, r and \(\hat{r}\) denote the weak limit of \(J^{\epsilon _n}\), \(p_{\epsilon _n}\), \(r^{\epsilon _n}\) and \(\hat{r}^{\epsilon _n}\) constructed in Lemma 12.2. Then, for almost all \(t \in ]0,T[\), the following identities are valid:
Proof
Exploiting the convergence properties stated in Corollary 12.7 and Lemma 12.2, we see that
weakly in \(L^{2,\frac{2\alpha }{1+\alpha }}(Q)\). Since \(P_{\epsilon _n} \rightarrow P\) on compact subsets of \([0, \, \infty [\times \mathbb {R}^{N-1}\), the pointwise convergence of \(\{\rho ^{\epsilon _n}\}\) and \(\{q^{\epsilon _n}\}\) yield \( P_{\epsilon _n}(\varrho _{\epsilon _n}, \, q^{\epsilon _n}) \rightarrow P(\varrho , \, q)\) pointwise in \(Q^+(\varrho )\), while \(|P_{\epsilon _n}(\varrho _{\epsilon _n}, \, q^{\epsilon _n})| \le c \, \varrho _{\epsilon _n}^{\alpha } \rightarrow 0\) pointwise in \(Q {\setminus } Q^+(\varrho )\). The other claims are proved similarly. \(\square \)
We now resume the results of the section formulating our main (conditional) convergence statement.
Proposition 12.11
Consider a family \(\{(\varrho _{\epsilon }, \, q^{\epsilon }, \, v^{\epsilon }, \, \phi _{\epsilon },\, R^{\epsilon }, \, R^{\Gamma ,\epsilon })\}_{\epsilon > 0}\) which satisfies a uniform bound in the class \(\mathcal {B}(T, \, \Omega , \, \alpha , \, N-1, \, \Psi , \, \Psi ^{\Gamma })\). Assume the condition (112) for the family \(\{\mathscr {R}^{\epsilon }\}_{\epsilon > 0}\), the condition (114) on the time derivatives, and that \(\{\varrho _{\epsilon }\} \subset C([0,T]; \, L^1(\Omega ))\) with \(\{\varrho _{\epsilon }(t)\}_{t\in [0,T], \, \epsilon > 0}\) compact in \(L^1(\Omega )\). Then, there are a limiting element \((\varrho , \, q, \, v, \, \phi , \, R,\, R^{\Gamma }) \in \mathcal {B}\) and a subsequence \(\{\epsilon _n\}_{n \in \mathbb {N}}\) such that all convergence properties stated in Lemma 12.2, Corollary 12.4, Corollary 12.7, Lemma 12.8, Lemma 12.9 and Corollary 12.10 are valid.
We finally note an important consequence of Proposition 12.11 concerning the lower semi-continuity of the energy identity.
Corollary 12.12
Assumptions of Proposition 12.11. Let \(\{(\varrho _{\epsilon }, \, q^{\epsilon }, \, v^{\epsilon }, \, \phi _{\epsilon }, \, R^{\epsilon }, \, R^{\Gamma ,\epsilon })\}_{\epsilon > 0}\) satisfy for \(\epsilon > 0\) the energy inequality with mobility matrix \(M_{\epsilon } \ge M\), and free energy functions \(h_{\epsilon }\) having the property
Then, the limiting element \((\varrho , \, q, \, v, \, \phi , \, R, \, R^{\Gamma })\) constructed in Proposition 12.11 satisfies the energy inequality with free energy function h and mobility matrix M.
The proof is rather obvious. For the limit passage \(\delta \rightarrow 0\), the free energies \(\{h_{\delta }\}_{\delta > 0}\) converge uniformly on compact subsets of \(\overline{\mathbb {R}}^N_+\) (see (77)). For the limit passage \(\tau \rightarrow 0\), we use that the family \(\{h_{\tau }\}_{\tau > 0}\) is constructed via convex duality (see (80)) and that the dual functions \(h_{\tau }^*\) converge uniformly on compact subsets of \(\mathbb {R}^N\) (see (78)).
12.2 Compactness of the total mass density
We showed that boundedness in the energy class together with the existence of weak time derivatives implies the compactness of the solution vector if the condition \(\{\varrho _{\epsilon }(t)\} \subseteq K^*\) for all t is satisfied, where \(K^*\) is a fixed compact of \(L^1(\Omega )\). Using an extension of the method of Lions for the compressible Navier–Stokes operator, we can show that this condition is satisfied for the approximation schemes of interest to us. We in fact show the compactness in \(C([0,T]; \, L^1(\Omega ))\), which is a stronger statement.
Proposition 12.13
Consider a family \(\{(\varrho _{\epsilon }, \, q^{\epsilon }, \, v^{\epsilon }, \, \phi _{\epsilon },\, R^{\epsilon }, \, R^{\Gamma ,\epsilon })\}_{\epsilon > 0} \subset \mathcal {B}\) which is uniformly bounded in the natural class \(\mathcal {B}(T, \, \Omega , \, \alpha , \, N-1, \, \Psi , \, \Psi ^{\Gamma })\) and satisfies the assumptions of Lemma 12.2. Let \(\{\bar{J}^{\epsilon }\}_{\epsilon >0} \subset L^2(Q; \, \mathbb {R}^3)\) be a family of perturbations such that \(\bar{J}^{\epsilon } \rightarrow 0\) strongly in \(L^2(Q)\) as \(\epsilon \rightarrow 0\) and such that
Suppose that the identities
are valid for all \(\psi \in C^1_c([0,T[; \, C^1(\overline{\Omega }))\) and all \(\eta \in C^1_c([0,T[; \, C^1_c(\Omega ; \, \mathbb {R}^3))\). Assume that either \(\alpha \ge 9/5\), or that \(3/2< \alpha < 9/5\) and the vectors \(\bar{V}\) and \(1^N\) are parallel. Then, for every sequence \(\{\epsilon _n\}_{n\in \mathbb {N}}\), the sequence \(\{\varrho _{\epsilon _n}\}_{n \in \mathbb {N}}\) is compact in \(C([0,T]; \, L^1(\Omega ))\).
Insiders in mathematical fluid dynamics will directly conclude from the representation of the pressure \(p = P(\varrho , \, q)\), with P increasing in \(\varrho \) and with \(\nabla q\) controlled, that the total mass density must be compact. For readers less familiar with the Lions theory, a sketch of the proofs allowing for independent reading is given in the appendix, section B.
13 Existence of solutions
Weak solutions to \(\mathrm{(P)}\) are defined in the spirit of viscosity solutions by passing to the limit \(\sigma \rightarrow 0\) and then \(\delta \rightarrow 0\) in the approximation scheme \((P_{\tau =0,\sigma ,\delta })\).
Proposition 13.1
We adopt the assumptions of Theorems 7.4, 7.6. For \(\sigma > 0\) and \(\delta > 0\) assume that there is \((\mu ^{\sigma ,\delta }, \, v^{\sigma ,\delta },\, \phi _{\sigma ,\delta }) \in \mathcal {B}(T, \, \Omega , \, \alpha , \, N,\, \Psi , \, \Psi ^{\Gamma })\), subject to the energy inequality and to the global conservation of partial masses, that weakly solves \((P_{\tau =0,\sigma ,\delta })\). Then, \(\mathrm{(P)}\) possesses a weak solution (as stated in Theorems 7.4, 7.6).
Proof
We first show the claim under the assumptions of Theorem 7.4 (Global existence).
The validity of the mass conservation identity (63) implies that the vector of net masses \(\bar{\rho }^{\sigma ,\delta } \in C_{\Phi ^*}([0,T]; \, \mathbb {R}^N)\) satisfies
We apply the bounds in Sects. 10 (statements 10.1–10.5) and 11 (Theorem 11.3), and we obtain that
Here, we distinguish the regularisation exponent \(\alpha _{\delta } > 3\) and the original growth exponent \(3/2< \alpha < + \infty \) of the free energy function.
Moreover, time integration in (63) and (84) means that (114) is valid.
We fix \(\delta >0\). By construction, the condition \(\alpha _{\delta } > 3\) is valid. With the help of Lemma A.2 in the appendix, we verify that
As the bounds (76) imply that (112) is valid, Proposition 12.13 applied with \(\bar{J}^{\sigma } := \mathbb {1} \cdot J^{\sigma }\) now guarantees that the family \(\{\varrho _{\sigma ,\delta }\}_{\sigma > 0}\) is compact in \(C([0,T]; \, L^1(\Omega ))\). It remains to apply Proposition 12.11 in order to obtain the convergence to a weak solution \((\varrho _{\delta }, \, q^{\delta }, \, v^{\delta }, \, \phi _{\delta },\, R^{\delta }, \, R^{\Gamma ,\delta }) \in \mathcal {B}(T, \, \Omega , \, \alpha _{\delta }, \, N-1,\, \Psi , \, \Psi ^{\Gamma }) \) to \((P_{\tau =0, \sigma = 0, \delta })\).
For the passage to the limit \(\delta \rightarrow 0\) the reasoning is the same. The second of the bounds (122) is available. Since there is no perturbation \(\bar{J}^{\delta }\) in the mass conservation equation, Proposition 12.13 guaranties at once the uniform in time compactness in \(C([0,T]; \, L^1(\Omega ))\) of \(\{\varrho _{\delta }\}_{\delta > 0}\), and Proposition 12.11 guarantees the convergence to a weak solution to \(\mathrm{(P)}\).
In order to prove the additional claims of Theorem 7.5 concerning the singularities, we recall the inequality \(\Vert \min \{\varrho _{\sigma ,\delta }, \, 1\} \, \ln y^{\sigma ,\delta }_i\Vert _{L^{\min \{\alpha ^{\prime },2\}}(Q)} \le C_0\) (derivation in (119)), where \(y^{\sigma ,\delta }_i\) are the associated number fractions. With the pointwise convergence of the densities and Fatou’s Lemma, this inequality always implies that the limiting number fractions are strictly positive almost everywhere outside of the vacuum set.
It remains to discuss the case of Theorem 7.6 about local-in-time existence. Due to Proposition 10.3, \([\bar{\rho }^{\sigma ,\delta }]_{C_{\Phi ^*}([0,T]; \, \mathbb {R}^N)} \le C_0\). We can extract sub-sequences such that \(\rho ^{\sigma ,\delta }\) converges weakly in \(L^{\alpha }(Q)\), and \(\bar{\rho }^{\sigma ,\delta }\) converges uniformly on [0, T]. We define a time \(T^*_{\sigma ,\delta }\) via
We know that \(T^*_{\sigma ,\delta } \ge T_0 > 0\) where \(T_0\) is fixed by the data (cf. Lemma 11.4). At first we can extract a subsequence such that \(T^*_{\sigma , \delta } \rightarrow T^*\). Due to the continuity of \(\bar{\rho }\), we see that \(0 = \inf \bar{\rho }^{\sigma ,\delta }(T^*_{\sigma ,\delta }) \rightarrow \inf \bar{\rho }(T^*) \).
Consider now \(T^{\prime } \in [0, \, T^*[\) arbitrary. Then, for all \(\sigma \le \sigma _0(T^* - T^{\prime })\), and \(\delta \le \delta _0(T^* - T^{\prime })\), we establish the estimates (122) with T replaced by \(T^{\prime }\). We then finish the proof as for Theorem 7.4 with T replaced by \(T^{\prime }\). By definition, we now have \(\lim _{T^{\prime } \rightarrow T^*} \min _{i=1,\ldots ,N} \bar{\rho }_i(T^{\prime }) = 0\). Hence, there must exist an index \(i_1\) such that \(\bar{\rho }_{i_1}(T^*) = 0\). For \(t < T^*\), we then consider the function \(\hat{q}_{i_1} = \mu _{i_1} - \max _{i=1,\ldots ,N} \mu _i \le 0\). We can introduce constants
and show that the set \(A_0(t) := \{x \in \Omega \, : \, \varrho (t,x) \ge \bar{a}_0\}\) satisfies \(\lambda _3(A_0(t))\ge \bar{b}_0\) for all \(t \in ]0,T[\). Since \(\lambda _3(\{x \in \Omega \, : \, \varrho (t,x) \ge k\}) \le C_0/k\), we easily construct a set \(A_1(t) := \{x \in \Omega \, : \, \bar{a}_1 \ge \varrho (t,x) \ge \bar{a}_0\}\) such that \(\lambda _3(A_1(t))\ge \bar{b}_0/2\) for all \(t \in ]0,T[\). Now observe that \(x \in A_1(t)\) implies \(|F^{\prime }(\bar{V} \cdot \rho (t,x))| \le C(F, \, \bar{a}_0, \, \bar{a}_1)\). Thus, for \(t \in ]0,T[\) and \(x \in A_1(t)\)
For \(t \in ]0,T[\) and \(x \in A_1(t)\) it follows that \(\hat{q}_{i_1}(t,x) \le \tfrac{1}{m_{i_1}} \, \ln \rho _{i_1}(t,x) + \tilde{C}(F, \, \bar{a}_0, \, \bar{a}_1)\). Due to the Jensen inequality
In this way, we easily see that \(\liminf _{t \rightarrow T^*} \Vert \hat{q}_{i_1}(t)\Vert _{L^1(\Omega )} = + \infty \). \(\square \)
Due to Proposition 13.1, it is sufficient to prove the solvability of the problem \((P_{\tau =0,\sigma ,\delta })\) in order to complete the proof of the existence theorems. We are going to carry over this last step by means of a Galerkin approximation described hereafter.
14 Galerkin approximation for \((P_{\tau =0,\sigma ,\delta })\)
We choose
-
(1)
A countable, linearly independent system \(\eta ^1, \, \eta ^2,\ldots \in W^{1,\infty }_0(\Omega ; \, \mathbb {R}^3)\) dense in \(W^{1,2}_0(\Omega ; \, \mathbb {R}^3)\), in order to approximate the variable v;
-
(2)
A countable, linearly independent system \(\zeta ^1, \, \zeta ^2,\ldots \in W^{1,\infty }_{\Gamma }(\Omega )\) dense in \(W^{1,2}_{\Gamma }(\Omega )\), in order to approximate the variable \(\phi \);
In order to approximate the variables \(\mu \), we need a countable system \(\psi ^1, \, \psi ^2,\ldots \) of \(W^{1,\infty }(\Omega ; \, \mathbb {R}^N)\) dense in \(W^{1,2}(\Omega ; \, \mathbb {R}^N)\). For technical reasons, we have to require additional properties of this set. For \(n \in \mathbb {N}\), and \(i,j \in \{1, \ldots ,n\}\) such that \(i \le j\), we introduce the products \(\tilde{\eta }^{i,j} = \eta ^i \cdot \eta ^j\) with \(\eta ^1, \ldots , \eta ^n\) from (1). By means of an obvious renumbering, we denote these functions \(\tilde{\eta }^{s}\) for \(s = 1,\ldots , n \, (n+1)/2\). For all \(n \in \mathbb {N}\), we assume that there is \(p = p(n) > n\) such that the following additional conditions are valid
Obvious corollaries of this property are
For \(n \in \mathbb {N}\), we are looking for approximate solutions
following the ansatz
where the vector fields \(a = a^{(n)} \in C^1([0,T]; \, \mathbb {R}^p)\), \(b = b^{(n)} \in C^1([0,T]; \, \mathbb {R}^n)\) and \(c = c^{(n)} \in C^1([0,T]; \, \mathbb {R}^n)\) are to determine.
Our approximation scheme is \((P_{\tau ,\sigma ,\delta })\) as described in Sect. 9. We choose \(\tau = 1/n\), and we project this scheme on the Galerkin space. In order to state approximate equations, we need to recall the definition (80) the free energy functions \(h_{\tau ,\delta }\). In this point, we introduce the abbreviation
In order to approximate Eq. (25), we consider for \(s \in \{1, \ldots ,p(n)\}\) the equations
Introduce a matrix-valued mapping \(\mu \mapsto A^1(\mu )= \{a_{i,j}(\mu )\}_{i,j=1,\ldots ,p(n)}\) via
Owing to the convexity of \(h^*_{\delta }\) and of the function \(\omega \), we see that \(A^1(\mu )\) is symmetric and positive semi-definite. Due to the ansatz (128) for \(\mu ^n\), we can now express (130) in the equivalent form
In order to approximate Eq. (84), we consider for \(s \in \{1, \ldots ,n\}\) the equations
Introduce \(\mu \mapsto A^2(\mu ) = \{a^{(2)}_{i,j}(\mu )\}_{i,j=1,\ldots ,n}\)
Owing to the non-negativity of \(\nabla _{\mu } h^*_{\delta }\) and of \(\omega ^{\prime }\), we see that \(A^2(\mu )\) is symmetric and positive semi definite. Due to the ansatz (128) for \(v^n\) and \(\mu ^n\), we can express (132) in the equivalent form
In order to determine \(\phi _n\), we use the ansatz \(\phi _n = \tilde{\phi }_n + \phi _0\) and we consider the projection onto \({{\,\mathrm{span}\,}}\{\zeta ^1, \ldots ,\zeta ^n\}^*\) of the Poisson equation, that is
We make use of the ansatz (128) for \(\phi _n\), and we see that the vector \(c_1, \ldots c_n\) can be determined via for a linear system \(A \, c = f\) where
Since the matrix A is by assumption invertible, we obtain that \(c = A^{-1} f =: \tilde{f}(a)\).
Overall, the Galerkin approximation (130), (132), (134) has the form
We consider the initial conditions
Here, we require for the reason of consistency that
We moreover assume that \(\Vert \mu ^{0,n}\Vert _{L^{\infty }(\Omega )} \le C_0\) which, by definition, implies for \(i = 1,\ldots ,N\) that
At first we can obtain local existence for the problem (135), (136).
Proposition 14.1
There is \(\epsilon = \epsilon (n, \, a^{0,n}, \, b^{0,n})\) such that the problem (135), (136) possesses a solution in \(C^1([0, \, \epsilon ]; \, \mathbb {R}^p \times \mathbb {R}^n)\).
Proof
Recall (137). Consider the matrix \(A^1(\mu ^0) = \int \limits _{\Omega } D_{\ell ,s}^2h_{\tau _n,\delta }^*(\mu ^0) \, \psi ^j_{\ell } \, \psi ^i_s \) (cf. (131)). Owing to the strict convexity of \(h_{\tau _n,\delta }^*\) on compact sets, \(A^1(\mu ^0)\) is positive definite and therefore invertible, and \(\Vert [A^1(\mu ^0)]^{-1}\Vert \le C(a^0, \, n)\). The matrix \(A^2(\mu ^0)\) (cf. (133)) is uniformly invertible because \(\nabla _{\mu } h^*_{\tau _n,\delta }\) is strictly positive on compact subsets of \(\mathbb {R}^N_+\), and \(\Vert [A^2(\mu ^0)]^{-1}\Vert \le C(a^0, \, n)\).
The block-diagonal matrix A in (135) satisfies \(\det A = \det A^1 \, \det A^2\). Thus, A is invertible at \(a^0, \, b^0\), and standard perturbation arguments yield the claim. \(\square \)
Next we want establish a continuation property for the solution, and we need a priori estimates.
Proposition 14.2
Assume that the approximate system (135), (136) possesses a solution \((a, \, b) \in C^1([0,T^*[; \, \mathbb {R}^p \times \mathbb {R}^n)\) for a \(T^* > 0\). Then, \(\mu ^n\), \(v^n\) and \(\phi _n\) satisfy the energy identity with free energy \(h_{\tau _n,\delta }\) and mobility matrix \(M_{\sigma }\).
Proof
We apply the ideas of Proposition 9.2. We can multiply (130) with \(\mu ^n\). Due to the additional property (125) and to (126) on the system \(\{\psi ^1, \ldots , \psi ^p\}\), we can also multiply (130) with \(\bar{Z} \, \phi _n\). Second, we multiply (132) with \(v^n\). Due again to the additional property (125) and to (126) we can also choose \(|v^n|^2 \, \mathbb {1}\) as a test function in (130). The claim follows. \(\square \)
Next we verify a continuation criterion.
Proposition 14.3
Under the assumptions of Proposition 14.2, there is a constant C(n) independent on time such that \(\Vert \mu ^n\Vert _{L^{\infty }([0,T^*]\times \Omega )} + \Vert v^n\Vert _{L^{\infty }([0,T^*]\times \Omega )} + \Vert \phi _n\Vert _{L^{\infty }([0,T^*]\times \Omega )}\le C(n)\).
Proof
We want to obtain a \(L^{\infty }\) bound for \(\mu ^n\). By construction, for \(t \in ]0,T^*[\) arbitrary,
Now we prove: There is \(c = c(n)\) such that \(|x|_{L^{\infty }}^{1/2} \le c \, \Vert |x \cdot \psi |^{1/2}\Vert _{L^1(\Omega )}\) for all \(x \in \mathbb {R}^p\). Otherwise there is for each \(j \in \mathbb {N}\) a \(x^j \in \mathbb {R}^p\) such that \(|x^j|_{{\infty }}^{1/2} \ge j \, \Vert |x^j \cdot \psi |^{1/2}\Vert _{L^1(\Omega )}\). Thus, \( \Vert |\bar{x}^j \cdot \psi |^{1/2}\Vert _{L^1(\Omega )} \le j^{-1}\) with \(\bar{x}^j = x^j / |x^j|_{L^{\infty }}\). For a subsequence, \(\bar{x}^j \rightarrow \bar{x}\) in \(\mathbb {R}^p\), \(|\bar{x}|_{\infty } = 1\). But since \(\Vert |\bar{x} \cdot \psi |^{1/2}\Vert _{L^1(\Omega )} = 0\), we obtain that \(\bar{x} \cdot \psi = 0\) in \(\Omega \), and due to the choice of the system \(\{\psi ^1, \ldots ,\psi ^p\}\), it follows that \(\bar{x} = 0\), a contradiction. Hence,
and this implies that \(\Vert \mu ^n \Vert _{L^{\infty }([0,T^*]\times \Omega )} \le C(n)\). The properties of \(\mathscr {R}^*\) entail
From the bound \(\int \limits _{\Omega } \mathscr {R}^*(\mu ^n(t)) \cdot \mathbb {1} \, |v^n(t)|^2 \le C_0\), we obtain that \(\Vert v^n\Vert _{L^{\infty }([0,T^*]\times \Omega )} \le C_0 \, c(n)^{-1}\). Analogously, \(\int \limits _{\Omega } |\nabla \phi _n(t)|^2 \le C_0\) implies that \(\Vert \nabla \phi _n\Vert _{L^{\infty }([0,T^*]\times \Omega )}\le C(n)\), and since \(\phi _n = \phi _0\) on \([0,T^*] \times \Gamma \), the claim follows. \(\square \)
Corollary 14.4
Let \(T > 0\). Then, the approximate system (135), (136) possesses a solution \((a, \, b) \in C^1([0,T]; \, \mathbb {R}^p \times \mathbb {R}^n)\).
Proof
Owing to Proposition 14.1, there is \(T^* > 0\) such that (135), (136) possesses a solution \((a, \, b) \in C^1([0, \, T^*]; \, \mathbb {R}^p \times \mathbb {R}^n)\). Since \(\Vert \mu ^n \Vert _{L^{\infty }([0,T^*]\times \Omega )} \le C(n)\), we have \(\inf _{i=1,\ldots ,N} \inf _{[0,T^*]\times \Omega } \mathscr {R}^*_i(\mu ^n) \ge c(n)\), hence the matrix \(A^1(\mu ^n(t))\) (cp. (131)) is invertible for all \(t \in [0, \, T^*]\) with \(\Vert [A^1(\mu ^n(t))]^{-1}\Vert \le C(n)\). The matrix \(A^2(\mu ^n(t))\) (cf. (133)) is likewise invertible, and the norm of the inverse satisfies a uniform bound \( \Vert [A^2(\mu ^n(t))]^{-1}\Vert \le C(n)\) on \([0,T^*]\). Due to Proposition 14.3, the functions \(\mu ^n(T^*)\), \(v^n(T^*)\) and \(\phi _n(T^*)\) belong to \(L^{\infty }(\Omega )\) and their norm in this space is bounded independently on t.
Thus, the problem (135), with initial data \((a(T^*), b(T^*))\) possesses solution in an interval \([T^*, \, T^*+\epsilon (n)]\), and the claim follows reiterating this argument. \(\square \)
Proposition 14.5
Let \(n \in \mathbb {N}\) and \(T >0\). The Galerkin approximation (130), (132), (134), possesses a solution with the regularity (127) such that the dissipation inequality is valid with free energy function \( h_{\tau _n,\delta }\) and mobility matrix \(M_{\sigma }\).
Uniform estimates
We define \(\tau _n := 1/n\) and
The family \(\{\mu ^n, \, v^n, \, \phi _n\}_{n\in \mathbb {N}}\) satisfies the bounds of Proposition 10.1 and Lemma 10.4 due to the energy identity. Since \(\mathbb {1} \in {{\,\mathrm{span}\,}}\{\psi ^1,\ldots ,\psi ^p\}\), the balance of net masses is also valid, hence also the bound of Proposition 10.3. In order to obtain a uniform bound for \(\{p_n\}\), we make use of the identity \(\nabla p_n = \sum _{i=1}^N \partial _{\mu _i} h_{\tau _n,\delta }^*(\mu ^n) \, \nabla \mu ^n_i = \sum _{i=1}^N \rho ^n_i \, \nabla \mu ^n_i\). It implies that
We combine with the bound for \(\{p_n\}\) in \(L^{\infty ,1}(Q)\) to obtain, via the Sobolev embedding, that \(\{p_n\}\) is bounded in \(L^{2,6\alpha /(3+\alpha )}(Q)\).
With the uniform estimate for \(\{\nabla \phi _n\}\) in \(L^{\infty ,2}(Q)\), we bound \(\{\bar{Z} \cdot \rho ^n \, \nabla \phi _n\}\) in \(L^{\infty ,2\alpha /(\alpha +2)}(Q)\).
In order to extract weakly convergent subsequences for all relevant quantities, it remains only to show that the norms \(\Vert \mu ^{n}\Vert _{L^2(Q)}\) are bounded independently on n. We next sketch the arguments to obtain this bound. We consider perturbed mass densities
Owing to Proposition 10.1, \(\Vert r^n - \rho ^n\Vert _{L^{\infty ,\alpha }(Q)} = \tau _n \, \Vert \omega ^{\prime }(\mu ^n)\Vert _{L^{\infty ,\alpha }(Q)} \le C_0 \, n^{-1/\alpha ^{\prime }}\). The approximate vector of net masses \(\bar{\rho }^n \in C^1([0,T]; \, \mathbb {R}^N)\) defined via \(\bar{\rho }^n(t) = \int \limits _{\Omega } \rho ^n(t) \, \mathrm{d}x\) satisfies by assumption \(\bar{\rho }^n(0) \rightarrow \rho ^0\) for \(n \rightarrow \infty \). Therefore, for every \(\epsilon >0\) we find \(n_0(\epsilon )\) such that for all \(n \ge n_0\)
Hence, the quantities \(\bar{r}^n(t) := \int \limits _{\Omega } r^n(t) \, \mathrm{d}x\) fulfil \(\bar{r}^n(t) \in B_{\epsilon +c \, n^{-\alpha ^{\prime }}} (\bar{\rho }^0) \oplus W \) for all \(n\ge n_0\). For all \(\epsilon > 0\) and \(n_0 \in \mathbb {N}\) such that \(\epsilon +c \, n_0^{-\alpha ^{\prime }} \le \frac{1}{2} \, {{\,\mathrm{dist}\,}}(\bar{\rho }^0, \, \mathcal {M}_{\text {crit}})\), the distance of \(\bar{r}^n(t)\) to the critical manifold remains strictly positive. The definition (129) implies that \(\mu ^n = \nabla _{\rho } h_{\delta }(r^n)\), which means that (cf. (98), (111))
where \(\tilde{y}_i^n = r^n_i/(m_i \, \sum _j (r^n_j/m_j))\) are the associated fractions. This is the structure required to apply Theorem 11.3 (cf. (98)). Hence, a uniform estimate is available in \(L^2(Q; \, \mathbb {R}^{N-1})\) for the relative chemical potentials \((\eta ^1\cdot \mu ^n, \ldots ,\eta ^{N-1}\cdot \mu ^n)\).
To obtain an estimate for the complete vector \(\mu \), we choose the index i associated with the largest fraction \(\tilde{y}_i^n \ge 1/N\). By means of (139), we see that \(\max _i \mu ^n_i \ge c_0 + F_{\delta }^{\prime }(r^n \cdot \bar{V}) \, \bar{V}_i\). Obviously, we also can state that \(\max _i \mu ^n_i \le c_1 \, (1+| F_{\delta }^{\prime }(r^n \cdot \bar{V})|)\). Thus, employing the growth conditions (34) and(35), there are sets \(A_n(t) \subseteq \Omega \) and constants \(a_0, \, b_0 >0\) such that \(\lambda _3(A_n(t)) \ge a_0\) and \(|\max _i \mu ^n_i(t, \, x)|\le b_0\) almost everywhere on \(A_n(t)\). We do not detail this construction here, referring to the relations (124) and the proof of Lemma A.1 for similar ideas. Applying Lemma 11.2, and using the fact that \(\Vert \nabla \mu ^{n}\Vert _{L^2(Q)} \le C_0 \, \sigma ^{-1/2}\), we obtain the bound \(\Vert \max \mu ^n\Vert _{L^2(Q)} \le C(a_0) \, (\sigma ^{-1/2} + b_0) \).
Passage to the limit \(n \rightarrow \infty \)
Due to the condition (125), we can multiply Eq. (130) with \(\psi = v^n \cdot \eta ^s \, \mathbb {1}\), \(s \in \{1, \ldots ,n\}\) arbitrary. We obtain that
Thus, it follows that
Rearranging terms
Making use of the latter identity and of (132)
Due to the identities (130) and (140) we obtain for all \(t \in [0,T]\) the representation
Here, \(\mathscr {L}_{i,j}(\mathcal {A}^n)\) are linear combinations in \(\mathcal {A}\) naturally defined by the right-hands of (130) and (132). Since the systems \({{\,\mathrm{span}\,}}\{\psi ^1, \ldots , \, \psi ^{p(n)} \}\) and \({{\,\mathrm{span}\,}}\{\eta ^1, \ldots , \eta ^n\}\) are dense in \(C^1\) for \(n \rightarrow \infty \), we easily show that there is a subsequence such that \(\rho ^{n}(t)\) and \(\varrho _{n}(t) \, v^{n}(t)\) converge as distributions for all \(t \in ]0,T[\). Thus, the conclusions of Lemma 12.2 are valid and we can produce a limit element \((\mu , \, v, \, \phi )\). In particular, the limit \(\phi \in L^{\infty }(0,T; \, W^{1,2}(\Omega ))\) is a weak solution to \(-\bar{\chi } \, \triangle \phi = \bar{Z}\cdot \rho \) in Q with \(\nu \cdot \nabla \phi = 0\) on \(]0,T[\times \Sigma \) and \(\phi =\phi _0\) on \(]0,T[\times \Gamma \). Hence, the estimates of Lemma 10.2 apply, with which it is proved that \((\mu , \, v, \, \phi ) \in \mathcal {B}(T, \, \Omega , \, \alpha , \, N, \, \Psi , \, \Psi ^{\Gamma })\).
In order to obtain the strong convergence of the sequence, we make use of the identity \(\nabla \rho ^n = D^2h_{\tau _n,\delta }^*(\mu ^n) \, \nabla \mu ^n\). We can show that \( |D^2h_{\tau _n,\delta }^*(\mu ^n)| \le C \, \varrho _n\) (cf. proof of Lemma A.2, relation (2)). Hence, as in (138), we see that \(\Vert \nabla \rho _n\Vert _{L^{2,2\alpha /(1+\alpha )}(Q)} \le C_0 \, \sigma ^{-1/2}\). With this uniform bound on the spatial gradient and the distributional convergence for all t, we conclude from standard arguments that \(\{\rho ^n\}\) converges strongly in \(L^1(Q; \, \mathbb {R}^N)\).
Then, owing to the uniform bound \(\Vert \mu ^n\Vert _{L^2(Q)} \le C_0\), we can show that \(\mu := \lim _{n\rightarrow \infty } \mu ^n\) exists almost everywhere in Q. Here, we start from the representation (139) and repeat the argument of Corollary 12.7. We obtain pointwise convergence in the whole of Q because the vacuum can be excluded for \(\sigma > 0\) (see the estimate in Lemma A.1).
It remains to identify \((\mu , \, v, \, \phi ) \in \mathcal {B}(T, \, \Omega , \, \alpha , \, N, \, \Psi , \, \Psi ^{\Gamma })\) as a weak solution to the problem \((P_{\tau =0,\sigma ,\delta })\). Passage to the limit in the energy identity is unproblematic if it is relaxed to an inequality (see Corollary 12.12).
Passage to the limit in the integral identities is also straightforward up to one instance: The sequence \(\mathbb {1} \cdot J^{n} \otimes v^n\) does not satisfy a better uniform bound than in \(L^{1,3/2}(Q; \mathbb {R}^{3\times 3})\). However, recall that \(\mathbb {1} \cdot J^{n} = \sigma \, (\nabla \sum _{i=1}^N \mu _i^n + \sum _{i=1}^N\bar{Z}_i \, \nabla \phi _n)\). Thus, for a test function \(\zeta \in C^2_c(Q)\), \(k\in \{1, \ldots , N\}\) and \(\ell = 1,2,3\)
Since \(\mu ^n \rightarrow \mu \) strongly in \(L^2(Q)\), we then can show that
Thus \(\mathbb {1} \cdot J^{n} \otimes v^n \rightarrow \mathbb {1} \cdot J \otimes v\) as distributions.
Notes
It is always possible to achieve the non-negativity, because the model only requires that \(\Psi \) has a global minimum in zero, but its value is not prescribed.
References
Albano, A.M., Bedeaux, D., Mazur, P.: Boundary conditions and non-equilibrium thermodynamics. Phys. A 82(3), 438–462 (1975)
Bothe, D.: On the Maxwell–Stefan approach to multicomponent diffusion. In: Progress in Nonlinear Differential Equations and Their Applications vol. 80, pp. 81–93. Springer, Berlin (2011)
Bothe, D., Dreyer, W.: Continuum thermodynamics of chemically reacting fluid mixtures. Acta Mech. 226, 1757–1805 (2015)
Bothe, D., Fischer, A., Pierre, M., Rolland, G.: Global wellposedness for a class of reaction–advection–anisotropic–diffusion systems. J. Evol. Equ. 17, 101–130 (2017)
Bothe, D., Fischer, A., Saal, J.: Global well-posedness and stability of electro-kinetic flows. SIAM J. Math. Anal. 46, 1263–1316 (2014)
Canizo, J.-A., Desvillettes, L., Fellner, K.: Improved duality estimates and applications to reaction–diffusion equations. Commun. Partial Differ. Equ. 39, 1185–1204 (2014)
Chen, X., Jüngel, A.: Analysis of an incompressible Navier–Stokes–Maxwell–Stefan system. Commun. Math. Phys. 340, 471–497 (2015)
Chen, X., Jüngel, A., Liu, J.G.: A note on Aubin–Lions–Dubinskiǐ lemmas. Acta Appl. Math. 133, 33–43 (2014)
deGroot, S.R., Mazur, P.: Non-Equilibrium Thermodynamics. North Holland, Amsterdam (1963)
Disser, K., Kaiser, H.-C., Rehberg, J.: Optimal Sobolev regularity for linear second-order divergence elliptic operators occurring in real-world problems. SIAM J. Math. Anal. 47, 1719–1746 (2015)
Dreyer, W., Guhlke, C., Landstorfer, M.: A mixture theory of electrolytes containing solvation effects. Electrochem. Commun. 43, 75–78 (2014)
Dreyer, W., Guhlke, C., Müller, R.: Overcoming the shortcomings of the Nernst–Planck model. Phys. Chem. Chem. Phys. 15, 7075–7086 (2013)
Dreyer, W., Guhlke, C., Müller, R.: Modeling of electrochemical double layers in thermodynamic non-equilibrium. Phys. Chem. Chem. Phys. 17, 27176–27194 (2015)
Druet, P.-E.: Analysis of improved Nernst–Planck–Poisson models of isothermal compressible electrolytes subject to chemical reactions: the case of a degenerate mobility matrix. Preprint 2321 of the Weierstrass Institute for Applied Analysis and Stochastics, Berlin, 2016. http://www.wias-berlin.de/preprint/2321/wias_preprints_2321.pdf
Feireisl, E., Novotnỳ, A., Petzeltovà, H.: On the existence of globally defined weak solutions to the Navier–Stokes equations. J. Math. Fluid Mech. 3, 358–392 (2001)
Feireisl, E., Petzeltovà, H., Trivisa, K.: Multicomponent reactive flows: global-in-time existence for large data. Commun. Pure Appl. Anal. 7, 1017–1047 (2008)
Fischer, J.: Global existence of renormalized solutions to entropy-dissipating reaction–diffusion systems. Arch. Ration. Mech. Anal. 218, 553–587 (2015)
Giovangigli, V.: Multicomponent Flow Modeling. Birkhäuser, Boston (1999)
Gröger, K.: A \(W^{1, p}\)-estimate for solutions to mixed boundary value problems for second order elliptic differential equations. Math. Ann. 283, 679–687 (1989)
Guhlke, C.: Theorie der elektrochemischen Grenzfläche. Ph.D. thesis, Technische-Universität Berlin, Germany. German (2014)
Haskovec, J., Hittmeir, S., Markowich, P.A., Mielke, A.: Decay to equilibrium for energy–reaction–diffusion systems. SIAM J. Math. Anal. 50, 1037–1075 (2016)
Herberg, M., Meyries, M., Prüss, J., Wilke, M.: Reaction–diffusion systems of Maxwell–Stefan type with reversible mass-action kinetics. Nonlinear Anal. Theory Methods Appl. 159, 264–284 (2017)
Herz, M., Knabner, P.: A thermodynamically consistent model for multicomponent electrolyte solutions. Preprint, arXiv:1605.07455 [math.AP], 2016. https://arxiv.org/pdf/1605.07455v1.pdf
Hopf, E.: Über die Anfangswertaufgabe für die hydrodynamischen Grundgleichungen. Math. Nach. 4, 213–231 (1951). German
Jüngel, A., Stelzer, I.: Existence analysis of Maxwell–Stefan systems for multicomponent mixtures. SIAM J. Math. Anal. 45, 2421–2440 (2013)
Landstorfer, M., Guhlke, C., Dreyer, W.: Theory and structure of the metal/electrolyte interface incorporating adsorption and solvation effects. Electrochim. Acta 201, 187–219 (2016)
Lions, P.-L.: Mathematical Topics in Fluid Dynamics, vol. 1. Incompressible Models. Oxford Science Publication, Oxford (1996)
Lions, P.-L.: Mathematical Topics in Fluid Dynamics, Vol. 2. Compressible Models. Oxford Science Publication, Oxford (1998)
Meixner, J., Reik, H.G.: Thermodynamik der irreversiblen Prozesse, vol. 3, pp. 413–523. Springer, Berlin (1959)
Mielke, A., Haskovec, J., Markowich, P.A.: On uniform decay of the entropy for reaction–diffusion systems. J. Dyn. Differ. Equ. 27, 897–928 (2015)
Mucha, P.B., Pokorny, M., Zatorska, E.: Heat-conducting, compressible mixtures with multicomponent diffusion: construction of a weak solution. SIAM J. Math. Anal. 47, 3747–3797 (2015)
Rockafellar, R.T.: Convex Analysis. Princeton University Press, Princeton (1970)
Simon, J.: Compact sets in the space \(L^p(0, T;B)\). Ann. Mat. Pura Appl. 146, 65–96 (1986)
Zatorska, E.: Mixtures: sequential stability of variational entropy solutions. J. Math. Fluid Mech. 17, 437–461 (2015)
Acknowledgements
Open Access funding provided by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A. Proofs of some auxiliary statements
1.1 Proof of Lemma 10.5
The proof relies on the availability of a solution operator to the problem
for all f having mean value zero over \(\Omega \), so that for all \(1< q < +\infty \) the estimates
are valid. For details about the solution operator, see among others [15], section 3.1.
Due to the natural estimates, the density satisfies a bound in \(L^{\infty ,\alpha }(Q)\). We begin with the case \(\alpha > 3\). For all \(\eta \in C^1_c([0,T[; \, C^1_c(\Omega ; \, \mathbb {R}^3))\) the function p obeys
We make use of the estimates
Let \(t \in ]0,T[\) and consider according to (141) a solution to the problem
Since \(\bar{\varrho }(t) =\Vert \varrho _0\Vert _{L^{1}(\Omega )}\) for all t as a consequence of (63), (142) yields
The identity (63) also implies that
and since we assume \(\alpha > 3\), this yields
The properties (142) hence imply that \(\Vert X_t\Vert _{L^{2}(Q)} \le c \, \Vert \varrho _t\Vert _{L^{2}(0,T; \, [W^{1,2}(\Omega )]^*)} \le C_0\). Owing to the inequalities \(6\alpha /(5\alpha -6) < 2\) and \(3\alpha /(2\alpha -3) < \alpha \), we see with the help of the bounds (143) that \(|\int \limits _{Q} p \, {{\,\mathrm{div}\,}}X| \le C_0\). Thus, \(\int \limits _{Q} p \, \varrho \le C_0\), and since \(\varrho \ge c\, p^{1/\alpha }\) the claim follows.
If \(\alpha \le 3\), then we assume that \(\mathbb {1} \cdot J = 0\) and, for all \(\eta \in C^1_c([0,T[; \, C^1_c(\Omega ; \mathbb {R}^3))\), p satisfies
We apply the estimates (143) for the right-hand except for the last one. The exponent \(\beta \) of (58) satisfies \(\beta \ge \min \{3, \, r(\Omega , \, \Gamma )\} > \alpha ^{\prime }\) by assumption. Hence, \(\beta \alpha /(\beta +\alpha ) > 1\). Since \(3\alpha /(2\alpha -3) \ge 3\), and since \(W^{1,3}(\Omega )\) is continuously embedding in \(L^q(\Omega )\) for all \(q < +\infty \),
It can be shown using (63) that \(\varrho \) is a solution to the continuity equation in the sense of renormalised solutions (see [28] or [15]) and that, for all \(s >0\) and \(\psi \in C^1_c(0,T; \, C^1(\overline{\Omega }))\)
Defining \(r := 2\alpha /(2s+\alpha )\)
Thus, \(\Vert \varrho ^s \, {{\,\mathrm{div}\,}}v\Vert _{L^{2,r}(Q)} \le C_0\). Moreover, defining \(\tilde{r} = 6\alpha /(6s+\alpha )\)
and this shows that \(\Vert \varrho ^s \, v\Vert _{L^{2,\tilde{r}}(Q)} \le C_0\), \(\tilde{r} = 6\alpha /(6s+\alpha )\). Making use of the Sobolev inequality
For the choice \(s = \frac{2}{3}\alpha - 1\), it follows that \(\Vert (\varrho ^{s})^{\prime }\Vert _{L^{2}(0,T; \, [W^{1,6\alpha /(6+\alpha )}(\Omega )]^*)} \le C_0\). Now we consider a solution to the problem \({{\,\mathrm{div}\,}}X = \varrho ^{s}(t) - \bar{\varrho }^{s}(t)\) in \(\Omega \) with \(X = 0\) on \( \partial \Omega \). Hence, \(\Vert X\Vert _{L^{\infty }(0,T; \, W^{1,3\alpha /(2\alpha -3)}(\Omega ))} \le C_0\) and \(\Vert X_t\Vert _{L^{2,6\alpha /(5\alpha -6)}(Q)} \le C_0\) due to the properties (142). We see again that \(\int \limits _{Q} p \, {{\,\mathrm{div}\,}}X\) is finite, and Lemma 10.5 is proved.
1.2 Special estimates for \(\sigma > 0\) and \(\tau > 0\)
In the case \(\sigma > 0\), the dissipation inequality provides \(\sqrt{\sigma } \, \Vert \nabla \mu \Vert _{L^2(Q)} \le C_0\), hence a gradient bound for all coordinates of the vector \(\mu \). We recall that we can always express \(\rho = \nabla _{\mu } h^*_{\tau ,\delta }(\mu )\). Hence, \(\nabla \rho = (\nabla \mu \cdot D^2h^*_{\tau ,\delta }(\mu ))\), and the inequalities (73) or Lemma 9.1, (2), imply that
where C is independent of all approximation parameters.
Lemma A.1
Assume \(\sigma >0\). Then, \(\Vert \ln \varrho \Vert _{W^{1,0}_2(Q)} \le C_0 \, \sigma ^{-1/2}\).
Proof
Due to the global mass conservation \(\Vert \varrho (t) \Vert _{L^1(\Omega )} = M_0\) for all \(t \in ]0,T[\), we find parameter \(\epsilon _0>0, \, \delta _0>0\) depending only on the data such that, for all \(t \in ]0,T[\),
Let \(1> \gamma > 0\). Due to (144), \(|\nabla \ln (\varrho +\gamma )| \le C \, |\nabla \mu |\). Thus, \(\sqrt{\sigma } \, \Vert \nabla \ln (\varrho +\gamma )\Vert _{L^2(Q)} \le C\). Applying (100) (see the proof of Lemma 11.2)
We integrate in time and obtain that \( \Vert \ln (\varrho +\gamma )\Vert _{L^{2,1}(Q)} \le C_0 \, (1+\sigma ^{-1/2})\). We let \(\gamma \rightarrow 0\), and obtain a control on \(\Vert \ln \varrho \Vert _{L^{2,1}(Q)}\). Due to (144) and the Sobolev embedding, the claim follows. \(\square \)
Lemma A.1 allows to show the following statement.
Lemma A.2
Assume \(\sigma > 0\). Then, \(\Vert ((\mathbb {1} \cdot J^{\sigma } )\cdot \nabla \ln \varrho _{\sigma })^+\Vert _{L^1(Q)} \le C_0 \, \sqrt{\sigma }\).
Proof
For a while we are now going to forget about the \(\delta \) indices. We compute that
where \(\xi ^1, \, \ldots , \, \xi ^{N-1}\) are chosen as to form an orthonormal basis of \(\mathbb {1}^{\perp }\). Thus, introducing for \(k =1,\ldots ,N\) the driving forces \(D_k := \nabla \mu ^{\sigma }_k + \bar{Z}_k \, \nabla \phi _{\sigma }\), we obtain that
Making use of the identity \(-\sum _{i=1}^N J^{i,\sigma } = \sigma \, (\mathbb {1} \cdot D)\)
Since \(| \xi ^{\ell } \cdot D| \le c \, |\Pi \, D| \le c \, \sqrt{M D \cdot D}\) for \(\ell = 1,\ldots ,N-1\), it follows that
We invoke Lemma 9.1, (2), and find a constant \(C_2\) such that \(|D^2 h^*_{\tau }(\mu ^{\sigma })|/\varrho _{\sigma } \le C_2\). Together with (145), this implies that \(\Vert ((\mathbb {1} \cdot J^{\sigma } )\cdot \nabla \ln \varrho _{\sigma })^+\Vert _{L^1(Q)} \le C_0 \, \tilde{C}_1 \, \sqrt{\sigma }\). \(\square \)
Appendix B. Compactness of the total mass density
In Sect. 12, we showed that boundedness in the energy class together with the existence of weak time derivatives implies the compactness of the solution vector if the condition \(\varrho _{\epsilon }(t) \in K^*\) is satisfied, where \(K^*\) is a fixed compact of \(L^1(\Omega )\). The aim of the present section is to give readers enough insights into the proof of Proposition 12.13 as to allow independent reading of the paper. We commence with a preliminary remark.
Remark B.1
Under the assumptions of Proposition 12.13, we apply Lemma 12.2 and we find a weakly convergent subsequence and limiting elements such that
for all \(\psi \in C^1_c([0,T[; \, C^1(\overline{\Omega }))\) and for all \(\eta \in C^1_c([0,T[; \, C^1_c(\Omega ; \, \mathbb {R}^3))\).
There is a branching in the proof: We consider separately the cases \(\alpha > 3\) and \(3/2 < \alpha \le 3\).
1.1 The case \(\alpha > 3\)
We are going to establish after Lions convergence properties associated with the effective viscous flux \(p_{\epsilon _n} - \eta ^{\prime } \, {{\,\mathrm{div}\,}}v^{\epsilon _n}\). Here, we abbreviate \(\eta ^{\prime } := \lambda + 2 \, \eta > 0\).
Lemma B.2
Let p, v and \(\varrho \) denote the same weak limits as in Remark B.1. Then,
Proof
Let \(\zeta \in C^1_c(0,T)\). Consider for \(t \in ]0,T[\) the weak solution \(\psi _{\epsilon } \in W^{1,2}(\Omega )\) to the auxiliary problem \(-\triangle \psi _{\epsilon } = \varrho _{\epsilon }(t) \, \zeta (t)\) in \(\Omega \) with \(\psi _{\epsilon } = 0\) on \(\partial \Omega \). Then, \(\Vert \psi _{\epsilon }\Vert _{L^{\infty }(0,T; \, W^{2,\alpha }_{\text {loc}}(\Omega ))} \le c_{\zeta } \, \Vert \varrho _{\epsilon }\Vert _{L^{\infty }(0,T; \, L^{\alpha }(\Omega ))}\). Moreover, due to (120), the time-derivative \(u = \partial _t\psi _{\epsilon }\) is a weak solution to
Hence, since \(6\alpha /(6+\alpha ) \ge 2\) for \(\alpha > 3\)
For \(\varphi \in C^1_c(\Omega )\) arbitrary, we consider the field \(X^{\epsilon } := -\varphi \, \nabla \psi _{\epsilon }\). Then,
Define \(\psi \in W^{1,2}(\Omega )\) to be the weak solution to the auxiliary Problem \(-\triangle \psi = \varrho _{\epsilon }(t) \, \zeta (t)\) in \([W^{1,2}_0(\Omega )]^*\). Then, it is readily proved (use Remark 12.3) for \(X =- \nabla \psi \, \varphi \) that
Since \(2 > 6\alpha /(5\alpha -6)\) and \(\alpha > 3\alpha /(2\alpha -3)\) (this is exactly the case for \(\alpha > 3\)), we can show that the assumptions of Lemma B.3 after this proof are satisfied. Thus,
Moreover,
Hence, in view of the choice of \(X^{\epsilon }\),
We also note that \(\int \limits _{Q} p_{\epsilon } \, {{\,\mathrm{div}\,}}X^{\epsilon } = \int \limits _{Q} p_{\epsilon } \, \varrho _{\epsilon } \, \varphi \, \zeta - \int \limits _{Q} p_{\epsilon } \, \nabla \psi _{\epsilon } \cdot \nabla \varphi \). Moreover,
Multiplying the Navier–Stokes equation with \(X^{\epsilon }\) and the limiting equation with X, we then easily obtain that \(\int \limits _{Q} \zeta \, \varphi \, (p_{\epsilon } - \eta ^{\prime } \, {{\,\mathrm{div}\,}}v^{\epsilon }) \, \varrho _{\epsilon } \rightarrow \int \limits _{Q} \zeta \, \varphi \, (p - \eta ^{\prime } \, {{\,\mathrm{div}\,}}v) \, \varrho \). \(\square \)
The following Lemma recalls the fundamental technical observations due to Lions ([28], page 17–21) about the compensated compactness of the acceleration terms (see also [15], section 3.4).
Lemma B.3
Assumptions of Proposition 12.13. Let \(a > 6\alpha /(5\alpha -6)\) and \(b > \max \{2, 3\alpha /(2\alpha -3)\}\). Consider \(\{X^{\epsilon }\}_{\epsilon > 0}, \, X \subset L^2(Q; \, \mathbb {R}^3)\) such that for \(\epsilon \rightarrow 0\)
Then, \(\varrho _{\epsilon } \, v^{\epsilon } \cdot \partial _t X^{\epsilon } + \varrho _{\epsilon } \, v^{\epsilon } \otimes v^{\epsilon } \, : \, \nabla X^{\epsilon } \rightarrow \varrho \, v \cdot \partial _t X + \varrho \, v \otimes v \, : \, \nabla X\) weakly in \(L^1(Q)\).
We next use an important property of our regularisation.
Lemma B.4
Let \(\varrho _{\epsilon }\) satisfy (120). Then, \(\varrho _{\epsilon } \in C([0,T]; \, L^1(\Omega ))\), and for all \(t \in [0,T]\)
Denote \(\varrho \) a weak limit of \(\{\varrho _{\epsilon _n}\}\). Then, \(\varrho \in C([0,T]; \, L^1(\Omega ))\) and for all \(t \in [0,T]\)
Proof
Owing to Lemma A.1, we can rely for \(\epsilon > 0\) on the fact that \(\ln \varrho _{\epsilon } \in W^{1,0}_2(Q)\). Making use of well-known smoothing techniques in time, of which we spare the details here, we can multiply Eq. (120) with the function \(1 + \ln \varrho _{\epsilon }\). If follows for almost all \(t \in ]0,T[\) that
The first claim (148) follows. The second claim (149) follows from the fact that \(\varrho \) is a renormalised solution to (146). This was shown in [28] (for instance on page 14, see also [27], Lemma 2.3) and [15], section 3.5. In order to state (148), (149) for all \(t \in [0,T]\), we need that \(\varrho ^{\epsilon }\) and \(\varrho \) belong to \(C([0,T]; \, L^1(\Omega ))\). This was proved in [28], page 23. \(\square \)
The compactness of the mass density will follow from a last observation. Comparable ideas are to find for instance in [28], section 8.5.
Lemma B.5
If p, v and \(\varrho \) denote the weak limits according to Remark B.1 then, for all \(\zeta \in C^1(\overline{Q})\) such that \(\zeta \ge 0\) in Q, there holds
Proof
We note that \(p_{\epsilon _n} = P_{\epsilon _n}(\varrho _{\epsilon _n}, \, q^{\epsilon _n})\) with the functions \(P_{\epsilon _n}\) of Lemma 8.4. Due to the estimates (76), we can rely on the property
Moreover, due to Lemma 8.4, \(\partial _{s}P_{\epsilon _n} \ge c_0\). For arbitrary non-negative \(u \in C^{1}(\overline{Q})\), we therefore obtain that \((P_{\epsilon _n}(\varrho _{\epsilon _n}, \, q^{\epsilon _n}) - P_{\epsilon _n}(u, \, q^{\epsilon _n})) \, (\varrho _{\epsilon _n}-u) \ge c_0 \, (\varrho _{\epsilon _n}-u)^2\). Hence,
Since \(\nabla P_{\epsilon _n}(u, \, q^{\epsilon _n}) = \partial _sP_{\epsilon _n}(u, \, q^{\epsilon _n}) \, \nabla u + \sum _{j=1}^{N-1} \partial _{q_j}P_{\epsilon _n}(u, \, q^{\epsilon _n}) \, \nabla q^{\epsilon _n}_j\), Lemma 8.4 and the estimates (76) imply that
It follows that \(\Vert \nabla P_{\epsilon _n}(u, \, q^{\epsilon _n})\Vert _{L^{2}(Q)} \le C_u \, C_0\). Since moreover \(|P_{\epsilon _n}(u, \, q^{\epsilon _n})| \le C \, |u|^{\alpha }\), there is \(a = a_u\in L^{\infty }(Q) \cap W^{1,0}_2(Q)\) and a subsequence such that
We easily show that \(\int \limits _{Q} P_{\epsilon _n}(u, \, q^{\epsilon _n}) \, (\varrho _{\epsilon _n}-u) \, \zeta \rightarrow \int \limits _{Q} a \, (\varrho - u) \, \zeta \). Note that the inequality \(P_{\epsilon _n}(u, \, q^{\epsilon _n}) \le c \, |u|^{\alpha }\) implies that \(|a| \le c \, |u|^{\alpha }\). We obtain that
It suffices now to approximate \(\varrho \) in \(L^{1+\alpha }(Q)\) with functions u of \(C^{1}(\overline{Q})\). \(\square \)
Lemma B.6
Assumptions of Proposition 12.13 for \(\alpha > 3\). Then, for every sequence \(\{\epsilon _n\}_{n \in \mathbb {N}} \) such that the convergence properties of Remark B.1 are valid:
-
1.
\(\varrho _{\epsilon _n}(t) \rightarrow \varrho (t)\) strongly in \(L^1(\Omega )\) for all \(t \in ]0,T[\).
-
2.
The family \(\bigcup _{n \in \mathbb {N}} \{\varrho _{\epsilon _n}\}\) is sequentially compact in \(C([0,T]; \, L^1(\Omega ))\).
Proof
We consider an arbitrary sequence of times \(\{t_{n}\}_{n \in \mathbb {N}} \subset ]0,T[\) such that \(t_{n} \rightarrow t^*\) for \(n \rightarrow \infty \). We choose for \(j \in \mathbb {N}\) a non-negative function \(f_j \in C^1(\mathbb {R})\) with the following properties
We define functions \(\zeta _{j,n} \in C^1_c(Q)\) via \( \zeta _{j,n}(t, \, x) := f_j(t_n-t) \, f_j({{\,\mathrm{dist}\,}}(x, \, \partial \Omega ))\). Note that \( \zeta _{j,n} \rightarrow \zeta _j:= f_j(t^*-t) \, f_j({{\,\mathrm{dist}\,}}(x, \, \partial \Omega ))\) uniformly in Q for \(n \rightarrow \infty \). Moreover, \(|\nabla _4 \zeta _{j,n}| \le c \, j\) and
We then rephrase
With \(o_n := \Vert (\bar{J}^{\epsilon _n} \cdot \nabla \ln \varrho _{\epsilon _n})^+\Vert _{L^1(Q)}\), the identity (148) yields
Moreover, owing to (149),
Thus, subtracting the two latter identities
Due to (151), we can bound
Moreover, we easily show that \(\Vert \zeta _{j,n}- \chi _{[0,t^*]} \, \chi _{\Omega }\Vert _{L^{2,\frac{2\alpha }{\alpha -2}}(Q)} \le c \, j^{-1+1/\alpha } + |t_n-t^*|^{1/2}\), and therefore
Since \(\zeta _{n,j} \rightarrow \zeta _j\) uniformly in Q, Lemma B.2 implies that
Further, Lemma B.5 implies that
For a certain \(r > 0\), it follows from (152) that
where we also use the assumption that \(\lim _{n\rightarrow \infty } o_n = 0\). Since \(\varrho _{\epsilon _n} \in C([0,T]; \, \mathcal {D}^{*}(\Omega ))\), we show easily that \(\varrho _{\epsilon _n}(t_{n}) \rightarrow \varrho (t^*)\) as distributions in \(\Omega \), and this added to (153) yields
We now deduce both claims of the Lemma.
In order to establish (1), we choose \(t_n = t \in [0,T]\) fixed. Then, due to (154), we see that \(\varrho _{\epsilon _n}(t) \rightarrow \varrho (t)\) strongly in \(L^1(\Omega )\). The claim (1) follows
In order to prove (2), we observe that \(\varrho _{\epsilon _n} \in C([0,T]; \, L^1(\Omega ))\) for all \(n \in \mathbb {N}\) and that also \(\varrho \in C([0,T]; \, L^1(\Omega ))\). This was observed in Lemma B.4. If \(\bigcup _{n \in \mathbb {N}} \{\varrho _{\epsilon _n}\}\) is not compact in \(C([0,T]; \, L^1(\Omega ))\), we find \(\delta _0 > 0\) and a subsequence \(\{n_k\}\) such that \(\max _{t \in [0,T]} \Vert \varrho _{\epsilon _{n_k}}(t) - \varrho (t)\Vert _{L^1(\Omega )} \ge \delta _0\), hence also a \(t_k \in [0,T]\) such that \(\Vert \varrho _{\epsilon _{n_k}}(t_k) - \varrho (t_k)\Vert _{L^1(\Omega )} \ge \delta _0\). We can always extract a subsequence such that \(t_k \rightarrow t^* \in [0,T]\), an applying the result (154), it follows that \(\varrho _{\epsilon _{n_k}}(t_{k}) \rightarrow \varrho (t^*)\) strongly in \(L^1(\Omega )\). \(\square \)
1.2 The case \(3/2 < \alpha \le 3\)
If we cannot rely on the condition \(\alpha >3\), additional technical problems occur. Nevertheless, the passage to the limit can be carried over using an extension of the method of Lions (\(\alpha \ge 9/5\), [28], Chapter 5) and Feireisl, Novotný and Petzeltová (\(3/2< \alpha < 9/5\), [15]) . Here, we have to assume that the approximate solutions satisfy global mass conservation exactly (the perturbation \( \bar{J}^{\epsilon }\) in (120), (121) vanishes). In particular, it holds that
Lemma B.2 and the further reasoning have to be modified. Here, we will stick to the approach of Feireisl, Novotný and Petzeltová in [15]. One introduces for \(k \in \mathbb {N}\) the cut-off function
It is possible to extract a subsequence (which might be a different one for all values of k), and to find \(a_k \in L^{\infty }(Q)\) such that \(T_k(\varrho _{\epsilon }) \rightarrow a_k\) weakly in \(L^p(Q)\) for all \(1<p<\infty \). Exploiting the a priori bounds, it follows that
so that \(\Vert a_k(t) - \varrho (t)\Vert _{L^1(\Omega )} \le C_0 \, \left( k\right) ^{-\alpha /\alpha ^{\prime }}\). Thus, \(a_k\) is an approximation of \(\varrho \). Now, the arguments of [15], Lemma 4.4 allow to prove that the limit \(\varrho \) is also a renormalised solution to (146), and to obtain the following statement.
Lemma B.7
Let \(\varrho _{\epsilon }\) satisfy (155). Define
Then, for all \(\epsilon > 0\), the function \(\varrho _{\epsilon }\) belongs to \(C([0,T]; \, L^1(\Omega ))\) and for all \(t \in [0,T]\)
Denote \(\varrho \) the weak limit of \(\{\varrho _{\epsilon _n}\}\). Then, \(\varrho \in C([0,T]; \, L^1(\Omega ))\) and for all \( t \in [0,T]\)
Proof
We can reproduce the proof [15], Lemma 4.4 (see also the section 4.6) one to one. \(\square \)
With the same method as in Lemma B.2, one moreover proves
Lemma B.8
Let p, v and \(\varrho \) denotes the weak limits according to Remark B.1. Then, for one subsequence possibly depending on k
We next can establish the essential property of Lemma B.5 also if \(\alpha \le 3\).
Lemma B.9
For all \(t \in [0,T]\) there holds:
If \(\{P_{\epsilon _n}\}\) is moreover a family of convex functions of \(\varrho \) (see Remark 8.9), then
Proof
For arbitrary non-negative \(u \in C^{1}(\overline{Q})\), we have
As in the proof of Lemma B.5, we use that the functions \(P_{\epsilon _n}(u, \, q^{\epsilon _n})\) have a bounded gradient in \(L^{2}(Q)\) for fixed u. Exploiting the weak convergence \(p_{\epsilon _n} \rightharpoonup p\) and \(T_k(\varrho _{\epsilon _n}) \rightharpoonup a_k\), we can show that
Here, \(\beta (u)\) denote a weak limit of \(P_{\epsilon _n}(u, \, q^{\epsilon _n})\). Since \(a_k \le k\) almost everywhere in Q, it is possible to represent \(a_k = T_k(a_k)\). Therefore, we can approximate \(a_k\) with functions \(T_k(u)\), \(u \in C^1(\overline{Q})\), and it follows that
If P is a convex function depending only on \(\varrho \), then we follow [15], Lemma 4.3. \(\square \)
At last we mention the equivalent of Lemma B.6.
Lemma B.10
-
1.
\(\varrho _{\epsilon _n}(t) \rightarrow \varrho (t)\) strongly in \(L^1(\Omega )\) for almost all \(t \in ]0,T[\).
-
2.
The family \(\bigcup _{n \in \mathbb {N}} \{\varrho _{\epsilon _n}\}\) is sequentially compact in \(C([0,T]; \, L^1(\Omega ))\).
Proof
We have
From Lemma B.9, we obtain the inequality
Now we distinguish two cases, according to whether the density satisfies a bound in \(L^2(Q)\). If \(\alpha \ge 9/5\), the density is bounded in \(L^2(Q)\), hence the right-hand of the latter relation converges to zero for \(k \rightarrow \infty \). If \(\alpha < 9/5\), but the function P is convex in the first argument, there is the stronger statement
Thus, using that both terms on the left-hand are non-negative
This shows that \(c_0 \, \Vert a_k - T_k(\varrho )\Vert _{L^2(Q_t)} \le |\eta ^{\prime }| \, \Vert {{\,\mathrm{div}\,}}v\Vert _{L^2(Q)}\). If \(3/2< \alpha < 9/5\) and if P depends only on \(\varrho \), we thus can prove that \(a_k - T_k(\varrho )\) is uniformly bounded in \(L^2(Q)\), and converges at least weakly to zero in this space. Thus, in both cases, it follows that
Now we introduce, for \(k > 2\) and \(n \in \mathbb {N}\), the variables \(u_{k,\epsilon }\) such that \(u_{k,\epsilon _n} \, \ln u_{k,\epsilon _n} = L_k(\varrho _{\epsilon _n})\). Denoting \(\psi \) the inverse of the function \(t \mapsto t \, \ln t\) in the range \([2,+\infty ]\), we have
Thus,
We make use of the latter to show that
It follows that \(\liminf _{k, \, n \rightarrow \infty } \int \limits _{\Omega } u_{k,\epsilon _n}(t_n) \, \ln u_{k,\epsilon _n}(t) \ge \int \limits _{\Omega } \varrho (t) \, \ln \varrho (t)\). Using the definition of \(u_{k,\epsilon _n}\) and (156), we conclude that the equality sign is valid, showing that \(u_{k,\epsilon }(t) \rightarrow \varrho (t)\) strongly in \(L^1(\Omega )\), and thus due to (157) also that \(\varrho _{\epsilon _n}(t_n) \rightarrow \varrho (t)\) strongly in \(L^1(\Omega )\). The claims follow using the same argument as in Lemma B.6. \(\square \)
Appendix C. The boundary reduction
We prove that the boundary conditions (28), (29), (30) allow to compute the flux of the electrolytic species as a function of a \((N-1)\)-dimensional reduction of the vector \(\mu \) from the bulk and of the data. We make use of the algebraic equations
which result from (28), (29), (30), in order to eliminate the occurrences of the surface potentials \(\mu ^{\Gamma }\). Note that (158) makes sense if we reinterpret, via trivial extension, the matrices \(M^{\Gamma }\) and \(M^{\Gamma ,\text {ext}}\) as positive semi-definite elements of \(\mathbb {R}^{N^{\Gamma } \times N^{\Gamma }}_{\text {sym}} \). The vectors \(\mu \) and \(\mu ^{\text {ext}}\) are trivially extended as well according to the scheme \(\mu \leadsto (\mu , \, 0) \in \mathbb {R}^N \times 0^{N^{\text {ext}}}\) and \(\mu ^{\text {ext}} \leadsto (0, \, \mu ^{\text {ext}}) \in 0^N \times \mathbb {R}^{N^{\text {ext}}}\). For the sake of simplicity, we do not introduce explicitly these operators by means of additional symbols.
For the solution to (158), a linear subspace \(\mathcal {V} := {{\,\mathrm{span}\,}}\{\gamma _{\Gamma }^1,\ldots ,\gamma _{\Gamma }^{s^{\Gamma }}\} \oplus \mathrm{R}(M^{\Gamma ,\text {ext}}) \oplus \mathrm{R}(M^{\Gamma }) \) is introduced. We introduce
-
The numbers \(d^{\Gamma } = {{\,\mathrm{dim}\,}}\mathcal {V}\) and \(\hat{s}^{\Gamma } := {{\,\mathrm{dim}\,}}\mathrm{R} (M^{\Gamma }) \le d^{\Gamma }\);
-
The positive eigenvalues \(\lambda _1,\ldots ,\lambda _{\hat{s}^{\Gamma }}\) with orthonormal eigenvectors \(b^1, \ldots , b^{\hat{s}^{\Gamma }}\) of \(M^{\Gamma }\);
-
Vectors \(b_{\hat{s}^{\Gamma }+1},\ldots , b_{d^{\Gamma }} \in \mathbb {R}^{N^{\Gamma }}\) such that \(\{b_1,\ldots , b_{d^{\Gamma }} \}\) is a basis for \(\mathcal {V}\);
-
The abbreviation \(d^{\text {ext}} = {{\,\mathrm{rk}\,}}M^{\text {ext}}\), the nonzero eigenvalues \(\lambda ^{\text {ext}}_1,\ldots , \lambda ^{\text {ext}}_{d^{\text {ext}}}\) with orthonormal eigenvectors \(e^{1}, \ldots , e^{d^{\text {ext}}} \in \mathbb {R}^{N^{\Gamma }}\) of \(M^{\Gamma ,\text {ext}}\).
The latter notations imply that \(M^{\Gamma ,\text {ext}}_{i,j} = \sum _{k=1}^{d^{\text {ext}}} \lambda ^{\text {ext}}_k\, e^{k}_i \, e^{k}_j\) for \(i,j=1,\ldots ,N^{\Gamma }\). Recalling now that \(\{b^1,\ldots , b^{d^{\Gamma }} \}\) is a basis of \(\mathcal {V}\), there are coefficients \(\{A_{j,\ell }\}_{j =1 \ldots , s^{\Gamma }, \,\, \ell = 1, \ldots ,d^{\Gamma }}\) and \(\{\tilde{A}_{j,\ell }\}_{j =1 \ldots , d^{\text {ext}}, \,\, \ell = 1, \ldots ,d^{\Gamma }}\) such that
Employing these notations and properties, we see that
Moreover, there is a representation
Due to the two latter relations, (158) is equivalent to
Choose \(\Psi ^{\Gamma }\) from (22). We introduce an auxiliary potential \(\tilde{\Psi } \in C^2(\mathbb {R}^{d^{\Gamma }})\) via
With \(X = (b^1 \cdot \mu ^{\Gamma }, \ldots , b^{d^{\Gamma }} \cdot \mu ^{\Gamma }) \in \mathbb {R}^{d^{\Gamma }}\) and \(Y := (b^1 \cdot \mu , \ldots , b^{\hat{s}^{\Gamma }} \cdot \mu ) \in \mathbb {R}^{\hat{s}^{\Gamma }}\) the identities (161) are valid if and only if
Here, \(\overline{\mathcal {D}} \in \mathbb {R}^{d^{\Gamma }\times \hat{s}^{\Gamma }}\) is the rectangular matrix
It can be verified that \(\tilde{\Psi }\) is strictly convex on \(\mathbb {R}^{d^{\Gamma }}\) and the following statement is then obvious.
Lemma C.1
The solution to Eq. (161) at the point \(X = (b^1 \cdot \mu ^{\Gamma }, \ldots , b^{d^{\Gamma }} \cdot \mu ^{\Gamma }) \in \mathbb {R}^{d^{\Gamma }}\) and \(Y := (b^1 \cdot \mu , \ldots , b^{\hat{s}^{\Gamma }} \cdot \mu ) \in \mathbb {R}^{\hat{s}^{\Gamma }}\) is given by \(X = \partial \tilde{\Psi }^*(\overline{\mathcal {D}} \, Y - w)\).
In view of Lemma C.1, the flux \(J_{\nu }\) in (28) possesses the equivalent representation
in which \(Y = (b^1 \cdot \mu , \ldots , b^{\hat{s}^{\Gamma }} \cdot \mu ) \in \mathbb {R}^{\hat{s}^{\Gamma }}\). We introduce a potential \(\hat{\Psi }^{\Gamma } \in C^2(\mathbb {R}^{\hat{s}^{\Gamma }} \times \mathbb {R}^{d^{\Gamma }})\) via
Then, at the point \(Y =(b^1 \cdot \mu , \ldots , b^{\hat{s}^{\Gamma }} \cdot \mu )\) we obtain the equivalence
We reinterpret the identity (165) by defining
-
A modified reaction rate vector field \(\hat{R}^{\Gamma } \in C^{1}(\mathbb {R}^{\hat{s}^{\Gamma }} \times \mathbb {R}^{d^{\Gamma }})\) via \(\hat{R}^{\Gamma }(Y, \, w) := - \partial _Y \hat{\Psi }^{\Gamma }(Y, \, w)\),
-
Modified reaction vectors \(\hat{\gamma }^k := b^k\) and driving forces \(\hat{D}^{\Gamma ,\text {R}}_k := \hat{\gamma }^k \cdot \mu \) for \(k =1,\ldots ,\hat{s}^{\Gamma }\).
Lemma C.2
Making use of the potential \(\hat{\Psi }^{\Gamma }\) from (164), we define
with \(w_k := \sum _{j=1}^{d^{\text {ext}}} \tilde{A}_{j,k} \, \lambda _j^{\text {ext}} \, e^j \cdot \mu ^{\text {ext}}\) for \(k = \ldots ,d^{\Gamma }\) and \(\jmath _i(w) := \lambda _i \, \partial _{i} \tilde{\Psi }^*(- w)\) for \(i = 1,\ldots ,\hat{s}^{\Gamma }\). Then, the conditions (28), (29), (30) imply that \(J_{\nu } = - \hat{r} - J^0\).
It remains to show that \(\hat{r}\) has the desired structure of a reaction term.
Proposition C.3
Assume that \(\Psi ^{\Gamma } \in C^2(\mathbb {R}^{s^{\Gamma }})\) is a strictly convex, non-negative potential satisfying (38). Assume that \(M^{\Gamma }\) and \(M^{\Gamma ,\text {ext}}\) are positive semi definite elements of \(\mathbb {R}^{N^{\Gamma } \times N^{\Gamma }}_{\text {sym}}\). Let \(\hat{s}^{\Gamma } := {{\,\mathrm{rk}\,}}M^{\Gamma }\). We define the reduced potential \(\hat{\Psi }^{\Gamma } \) via (164). Then, \(\hat{\Psi }^{\Gamma } \in C^{1}(\mathbb {R}^{\hat{s}^{\Gamma }} \times \mathbb {R}^{d^{\Gamma }})\) is non-negative, and the function \(Y \mapsto \hat{\Psi }^{\Gamma }(Y, \, w)\) is of class \(C^{2}(\mathbb {R}^{\hat{s}^{\Gamma }})\), strictly convex and coercive for all \(w \in \mathbb {R}^{d^{\Gamma }}\).
Proof
Due to the representation (164), \(\hat{\Psi }^{\Gamma }\) is of class \(C^1\) and even of class \(C^2\) in the first variable. The second derivative \(D^2\hat{\Psi }^{\Gamma }\) is given by
Due to convex conjugation, the identity \(D^2 \tilde{\Psi }^*(\mathcal {D} \, Y - w) = [D^2 \tilde{\Psi }(X)]^{-1}\) is valid at the point \(X = \partial \tilde{\Psi }^*( \overline{\mathcal {D}}\, Y - w)\). The definition of \(\tilde{\Psi }\) induces \(D^2 \tilde{\Psi }(X) = D^2 \tilde{\Psi }^1(X) + \widetilde{\mathcal {D}}\). Here, we denote by \(\widetilde{\mathcal {D}} \in \mathbb {R}^{d^{\Gamma }\times d^{\Gamma }}\) the matrix \( {{\,\mathrm{diag}\,}}(\lambda _1,\ldots ,\lambda _{\hat{s}^{\Gamma }}, 0, \ldots , 0) \), and \(\tilde{\Psi }^1 := \Psi ^{\Gamma }(A \, X) + \frac{1}{2} \, \sum _{k=1}^{d^{\text {ext}}} \lambda _k^{\text {ext}} (\tilde{A}_k \cdot X)^2\).
Therefore, \(D^2 \hat{\Psi }^{\Gamma }(Y, \, w) = \mathcal {D}- \overline{\mathcal {D}}^\mathsf{T} \, [D^2 \tilde{\Psi }^1(X) + \widetilde{\mathcal {D}} ]^{-1} \, \overline{\mathcal {D}} .\) By definition (recall also the definitions (159) of the matrices A and \(\tilde{A}\)), for \(\eta \in \mathbb {R}^{d^{\Gamma }}\) arbitrary
where we make use of the Assumption (38). The latter estimate and elementary arguments yield \(\lambda _{\min } (D^2 \hat{\Psi }^{\Gamma }) \ge c_0 \, \lambda _{\min }(\mathcal {D})/(c_0+\lambda _{\max }(\mathcal {D})) .\)\(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dreyer, W., Druet, PÉ., Gajewski, P. et al. Analysis of improved Nernst–Planck–Poisson models of compressible isothermal electrolytes. Z. Angew. Math. Phys. 71, 119 (2020). https://doi.org/10.1007/s00033-020-01341-5
Received:
Revised:
Published:
DOI: https://doi.org/10.1007/s00033-020-01341-5
Keywords
- Electrolyte
- Electrochemical interface
- Chemical reaction
- Compressible fluid
- Navier–Stokes equations
- Advection–diffusion–reaction equations
- PDE system of mixed type
- A priori estimates
- Weak solution