On an equation arising in natural convection boundary layer flow in a porous medium

Abstract

A generalization of a boundary value problem treated previously by Magyari et al. (ZAMP 53:782–793, 2002a; Transp Porous Medium 46:91–102, 2002b), Zhang (Math Anal Appl 417:361–375, 2014) and Paullet (Appl Math E Notes 14:123–126, 2014) for a prescribed wall temperature and by Zhang (Appl Math Comput 339:367–373, 2018) for a prescribed wall heat flux is considered. The problem involves a parameter $\lambda$ and an exponent p. Numerical solutions are obtained for representative values of $\lambda$ and p, a feature of which is the existence of critical values $\lambda _c$ of $\lambda$ with two solution branches in $\lambda >\lambda _c$, with $\lambda _c$ dependent on p. Asymptotic solutions for large $\lambda$ and large p are derived for both types of boundary condition. For large $\lambda$, the nature of the solution is essentially different on upper and on the lower branches with similar feature being seen in the behaviour for p large.

1 Introduction

The boundary value problem

$$\begin{aligned} \theta ''+\lambda \,\theta '+\theta ^2=0, \quad \theta (0)=1, \ \ \theta \rightarrow 0 \ \text{ as } \ y \rightarrow \infty , \end{aligned}$$

(1)

where primes denote differentiation with respect to the independent variable y has been treated by Magyari et al. [1, 2]. This problem arose in looking for similarity solutions in the free convection boundary layer flow on a vertical surface in a porous material. In particular, a wall temperature proportional to $x^m$ was assumed, where the coordinate x measures distance along the surface, with Eq. (1) appearing as the special case of $m=-1$. The analysis for this particular case was shown to be different to the other values of m and so is a limiting case for m. Equations of the type given in (1) have a relatively long history and have also arisen in flows on stretching surfaces, see for example the original work of Sakiadis [3], Crane [4] and Banks [5] with a full review being provided by Wang [6].

The problem described by Eq. (1) has also been considered in a more theoretical way by Zhang [7]. Several properties of the solution were established including the existence of a critical value $\lambda _c$ with two solution branches for $\lambda >\lambda _c$, seen also in the numerical integrations of [1, 2]. However, existence or nonexistence of solutions for $0<\lambda <\lambda _c$ remains an open question. Paullet [8] further proved that for some range less than $\lambda _c$, no solution to Eq. (1) exists. Bounds on the critical value $\lambda _c$ were derived consistent with that computed by [1, 2]. Zhang [9] also considered the ‘prescribed wall flux condition’, i.e. the same equation given in (1) but now subject to the boundary conditions

$$\begin{aligned} \theta '(0)=-1, \ \ \theta \rightarrow 0 \ \text{ as } \ y \rightarrow \infty . \end{aligned}$$

(2)

As for the ‘prescribed wall temperature condition’ in equation (1), properties of the solution were established theoretically again including bounds on the critical value leading to the existence of two solution branches.

Our aim here is to extend the problems considered by Zhang [7, 9] to the more general case

$$\begin{aligned} \theta ''+\lambda \,\theta '+\theta ^p=0, \end{aligned}$$

(3)

for an exponent $p > 1$ subject to prescribed wall temperature condition given in (1) or to the prescribed wall flux condition (2). We assume throughout that $\lambda \ge 0$ and, following Zhang [7, 9], we limit our attention to those solutions for which the integral $\displaystyle \mathop {\int }\limits _0^\infty \theta (y)\,\mathrm{d}y$ is bounded. As a consequence, here we consider only those solutions which are exponentially small, of $O(\text{ e }^{-\lambda \,y})$, for y large. We note that there are also other solutions which are algebraic, of $O(y^{-1/(p-1)})$ for y large.

Equations which involve a term of the type $\theta ^p$, as in (3), have arisen in the somewhat different context of convective flow in a porous medium with local heat generation being modelled by $\theta ^p$ ($p>1$), see [10,11,12,13,14] for example. We start with the case of a prescribed wall heat flux.

Fig. 1

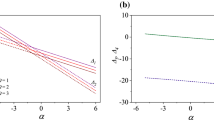
Plots of $\theta (0)$ against $\lambda$ for a $p=2$, b $p=5$ and c $p=10$ obtained from the numerical solution of Eq. (4)

Fig. 2

A plot of $\theta (0)$ against p for $\lambda =1.5$ obtained from the numerical solution of Eq. (4)

Fig. 3

The critical values: plots of a $\lambda _c$ and b $\theta _c(0)$, the value of $\theta (0)$ at $\lambda _c$, plotted against p

2 Prescribed wall heat flux

Here we examine the problem given by

$$\begin{aligned} \theta ''+\lambda \,\theta '+\theta ^p=0, \quad \theta '(0)=-1, \ \ \theta \rightarrow 0 \ \text{ as } \ y \rightarrow \infty , \end{aligned}$$

(4)

restricting our attention to those solutions which are exponentially small for y large. In Fig. 1a, we plot $\theta (0)$ against $\lambda$ for $p=2$, the case treated in [9], obtained from the numerical solution of Eq. (4). There is a critical value $\lambda _c$ of $\lambda$, where $\lambda _c \simeq 1.41$, with two solution branches for $\lambda >\lambda _c$. On the lower solution branch, $\theta (0)$ decreases slowly to zero as the value of $\lambda$ is increased, whereas on the upper branch $\theta (0)$ increases very rapidly as $\lambda$ is increased. In Fig. 1b, c, we plot $\theta (0)$ against $\lambda$ for $p=5$ and $p=10$. There are again a critical values $\lambda _c$ with now $\lambda _c \sim 1.182$ and $\lambda _c \simeq 1.095$ with values of $\theta (0)$ on the lower branch again approaching zero as $\lambda$ is increased. However, the upper branch continues to large values of $\lambda$ with $\theta (0)$ increasing relatively slowly for the larger values of p.

We can gain further information about the nature of the solution by plotting $\theta (0)$ against p for a given value of $\lambda$ which we do in Fig. 2, taking $\lambda =1.5$. There is a critical value $p_c$ of p, here $p_c \simeq 1.595$ with two solution branches in $p>p_c$. On the upper branch $\theta (0)$ reaches a maximum value of approximately 1.713 at $p \simeq 2.1$. Both solution branches continue to large p appearing to approach constant values for p large. Further calculations for much larger values of p suggest that $\theta (0) \rightarrow 1$ on the upper branch and that $\theta (0)$ approaches a nonzero positive value on the lower branch.

On integrating Eq. (4) and applying the boundary conditions, we obtain

$$\begin{aligned} \lambda \,\theta (0)=1+\mathop {\int }\limits _0^\infty \theta ^p\,\mathrm{d}y, \end{aligned}$$

(5)

so that $\theta (0)>\lambda ^{-1}$. This lower bound on $\theta (0)$ is seen for the lower branch in Fig. 2 and provides a reasonable estimate for the lower branch solutions seen in Fig. 1.

We can calculate the critical values numerically following the approach described in [15, 16], for example, and in Fig. 3a we plot the values of $\lambda _c$ and in Fig. 3b the values of $\theta _c(0)$, the value of $\theta (0)$ at $\lambda =\lambda _c$, against p. Our direct calculation of the critical values gives a better estimate of $\lambda _c \simeq 1.40920$ for $p=2$, with $\theta _c(0) \simeq 1.18710$, towards the higher end of the range $1.37824< \lambda _c<1.41665$ given [9]. Both the values of $\lambda _c$ and $\theta _c(0)$ decrease as p is increased, as perhaps could be expected from Fig. 1, with $\lambda _c \rightarrow 2$ as $p \rightarrow 1$.

We now consider the nature of the solution when $\lambda$ is large as seen in Fig. 1.

2.1 Solution for $\lambda$ large

We first consider the solution on the lower branch by writing

$$\begin{aligned} \theta =\lambda ^{-1}\,H, \quad \zeta =\lambda \,y. \end{aligned}$$

(6)

Equation (4) then becomes

$$\begin{aligned} H''+H'+\lambda ^{-(p+1)}\,H^p=0, \quad H'(0)=-1, \ \ H \rightarrow 0 \ \text{ as } \zeta \rightarrow \infty , \end{aligned}$$

(7)

where primes now denote differentiation with respect to $\zeta$. The leading-order solution is $H_0=\text{ e }^{-\zeta }$. For the term $H_1$ at $O(\lambda ^{-(p+1)})$, we obtain

$$\begin{aligned} H_1''+H_1'=-\text{ e }^{-p\,\zeta }, \ \ \ H_1'(0)=0, \ \ H_1 \rightarrow 0 \ \text{ as } \ \zeta \rightarrow \infty , \end{aligned}$$

(8)

giving

$$\begin{aligned} H_1=\frac{1}{p(p-1)}\,\biggl (p\,\text{ e }^{-\zeta }-\text{ e }^{-p\,\zeta }\biggr ), \end{aligned}$$

(9)

so that, on the lower branch

$$\begin{aligned} \theta (0) \sim \lambda ^{-1}(1+\lambda ^{-(p+1)}\, p^{-1}+\cdots ) \ \ \text{ as } \ \lambda \rightarrow \infty , \quad (p \ne 1), \end{aligned}$$

(10)

consistent with the results shown in Fig. 1 and expression (5). We note that this result is, to leading order, independent of the exponent p and that the asymptotic limit is approached more rapidly as the value of p is increased.

For the upper branch solution, we put

$$\begin{aligned} \theta =\lambda ^{2/(p-1)}\, h \quad (p>1), \end{aligned}$$

(11)

with $\zeta$ given in (6). Equation (4) becomes

$$\begin{aligned} h''+h'+h^p=0, \quad h'(0)=-\lambda ^{-(p+1)/(p-1)}, \ \ h \rightarrow 0 \ \ \text{ as } \ \zeta \rightarrow \infty . \end{aligned}$$

(12)

The leading-order problem is

$$\begin{aligned} h''+h'+h^p=0, \quad h'(0)=0, \ \ \ h \rightarrow 0 \ \ \text{ as } \ \zeta \rightarrow \infty . \end{aligned}$$

(13)

This is a homogeneous problem, and for a nontrivial solution, we suppose that $h(0)=a_0$ for some constant $a_0>0$ which we expect to depend on p. We then put

$$\begin{aligned} h=a_0\, \overline{h}, \ \ \ \overline{\zeta }=a_0^{(p-1)/2}\, \zeta , \end{aligned}$$

(14)

so that Eq. (13) is now

$$\begin{aligned} \overline{h}''+a_0^{(1-p)/2}\,\overline{h}'+\overline{h}^p=0, \quad \overline{h}(0)=1, \ \ \overline{h}'(0)=0 \ \ \overline{h} \rightarrow 0 \ \ \text{ as } \ \overline{\zeta } \rightarrow \infty . \end{aligned}$$

(15)

Equation (15) is, in effect, an eigenvalue problem for $a_0$. In Fig. 4, we plot $a_0$ against p obtained from the numerical solution of Eq. (15). We see that $a_0$ reaches a maximum value of approximately 1.2418 at $p \simeq 4.9$ with $a_0 \rightarrow 1$ slowly for large values of p and going almost to zero close to $p=1$. For $p=2$, $a_0\simeq 0.8587$ so that $\theta (0) \sim 0.8587\,\lambda ^2+\cdots$, for $p=5$, $a_0\simeq 1.1821$ giving $\theta (0) \sim 1.1821\,\lambda ^{1/2}$ and for $p=10$, $a_0\simeq 1.19265$ with $\theta (0) \sim 1.19265\,\lambda ^{2/9}+\cdots$ as $\lambda \rightarrow \infty$. The difference in the powers of $\lambda$ in these cases accounts for the way the upper branch solutions increase with $\lambda$, rapidly for $p=2$ (Fig. 1a) and much more slowly for $p=10$ (Fig. 1c).

2.2 Solution for p large

If $\theta <1$, then the term $\theta ^p$ in Eq. (4) is negligible for p large and hence has the solution, to leading order, of

$$\begin{aligned} \theta =\lambda ^{-1}\, \text{ e }^{-\lambda \,y}, \end{aligned}$$

(16)

so that $\theta (0) \sim \lambda ^{-1}+\cdots$ as $p \rightarrow \infty$ on the lower solution branch, as can be seen in Fig. 2 for $\lambda =1.5$.

Fig. 4

Large $\lambda$ solution: a plot of $a_0$ against p obtained from the numerical solution of Eq. (15)

Fig. 5

Profile plots of $\theta$ and $\theta '$ against y for the upper branch solution for $p=61.8$ and $\lambda =1.5$ obtained from the numerical solution of Eq. (4)

The nature of the solution on the upper branch for p large can be seen in Fig. 5 where we plot $\theta$ and $\theta '$ against y for $p=61.8$ and $\lambda =1.5$. For these parameter values, $\theta (0) \simeq 1.06346$. We see that $\theta$ decreases monotonically from its wall value. However, there is a thin region next to the wall where $\theta '$ decreases rapidly before increasing to its outer value. To describe this solution, we start in the outer region by putting $y=Y_0+\overline{y}$, where $Y_0$ depends on p. This leaves equation (4) unaltered and to the leading-order solution $\theta =\text{ e }^{-\lambda \,\overline{y}}$ in the outer region.

In the wall region, Eq. (4) becomes, at leading order,

$$\begin{aligned} \theta ''+\theta ^p=0, \end{aligned}$$

(17)

to be solved subject to

$$\begin{aligned} \theta =\theta _0, \ \ \theta '=-1 \ \ \text{ at } \ y=0, \ \ \ \theta =1, \ \ \theta '=-\lambda \ \ \text{ at } \ y=Y_0. \end{aligned}$$

(18)

Equation (17) can be integrated to obtain, on satisfying conditions (18),

$$\begin{aligned} \frac{\theta _0^{\, p+1}-1}{p+1}=\frac{\lambda ^2-1}{2}. \end{aligned}$$

(19)

From (19), to have $\theta _0>1$ requires having $\lambda >1$. From expression (19), we have

$$\begin{aligned} \theta _0 = \biggl (1+\frac{1}{2}\,(1+p)\,(\lambda ^2-1)\biggr )^{1/1+p}. \end{aligned}$$

(20)

Expression (20) gives $\theta _0 \simeq 1.0606$ for $p=61.8$ and $\lambda =1.5$, the case plotted in Fig. 5, showing good agreement with the value of 1.0635 determined by solving Eq. (17) numerically.

We can calculate $Y_0$ from

$$\begin{aligned} Y_0=\mathop {\int }\limits _1^{\theta _0}\,\frac{{\mathrm d}\theta }{\bigl (\lambda ^2+\frac{2}{p+1}\,(1-\theta ^{p+1})\bigr )^{\!\! 1/2}} \, \sim \left( \frac{\log p}{p}\right) \, \lambda ^{-1}+\cdots , \end{aligned}$$

(21)

showing that the thickness of the inner region decreases as the value of p is increased. The asymptotic expression given in (21) gives $Y_0\simeq 0.0445$ for $p=61.8$ and $p=1.5$ in good agreement with the value 0.0446 obtained from the numerical solution of (4). The above analysis indicates why $\lambda _c \rightarrow 1$ as $p\rightarrow \infty$, as indicated in Fig. 3a. Expression also (20) shows that $\theta _c(0) \rightarrow 1$ in this limit, as can seen in Fig. 3b.

3 Prescribed wall temperature

Here we consider the problem

$$\begin{aligned} \theta ''+\lambda \,\theta '+\theta ^p=0, \quad \theta (0)=1, \ \ \theta \rightarrow 0 \ \text{ as } \ y \rightarrow \infty , \end{aligned}$$

(22)

for $p > 1$, where primes again denote differentiation with respect to y and again limiting our attention to those solutions which are exponentially small for y large.

Fig. 6

Plots of $\theta '(0)$ against $\lambda$ for a $p=2$, b $p=5$ and c $p=10$ obtained from the numerical solution of Eq. (22)

Fig. 7

Plots of $\theta '(0)$ against p for $\lambda =1.5$ obtained from the numerical solution of Eq. (22)

In Fig. 6, we plot $\theta '(0)$ against $\lambda$ for $p=2$, Fig. 6a, $p=5$, Fig. 6b and for $p=10$, Fig. 6c, obtained from the numerical solution of Eq. (22). In each case, we see the existence of a critical value $\lambda _c$ of $\lambda$ with $\lambda _c \simeq 1.079$ for $p=2$, in agreement with the value given in [1], $\lambda _c \simeq 0.648$ for $p=5$ and $\lambda _c \simeq 0.404$ for $p=10$. The critical points appear to arise where $\theta '(0)=0$ and gives rise to two solution branches in $\lambda >\lambda _c$. On the lower branch, the values of $\theta '(0)$ are negative and appear to decrease linearly with $\lambda$. On the upper branch $\theta '(0)>0$ with the values of $\theta '(0)$ increasing with $\lambda$, much more rapidly for $p=2$ than for $p=5$ or for $p=10$. In Fig. 7, we plot $\theta '(0)$ against p for $\lambda =1.5$. Again we see the existence of a critical value $p_c$, here at $p_c \simeq 1.238$ with two solution branches in $p>p_c$. The lower solution branch has $\theta '(0)$ negative and approaches a constant value which appears to be $-\lambda$ as p is increased. The upper branch has $\theta '(0)>0$, reaches a maximum value of approximately 3.144 at $p \simeq 2.059$ before decreasing as p is increased and appears to approach the value of $\lambda$ very slowly for large p, seen in numerical solutions to much larger values of p than used to plot Fig. 7.

We can integrate Eq. (22) in this case to obtain

$$\begin{aligned} \theta '(0)=-\lambda +\mathop {\int }\limits _0^\infty \theta ^p\,\mathrm{d}y, \end{aligned}$$

(23)

giving a lower bound $\theta '(0)>-\lambda$ and providing a reasonable estimate for the lower branch solutions seen in Figs. 6 and 7.

Fig. 8

The critical values: plots of $\lambda _c$ against p

Fig. 9

Large $\lambda$ solution—upper branch: a plot of $b _0$ against p obtained from the numerical solution of equation (33)

Fig. 10

Profile plots of $\theta$ and $\theta '$ against y for the upper branch solution for $p=96.94$ and $\lambda =1.5$ obtained from the numerical solution of Eq. (22)

The critical values $\lambda _c$ are determined by making a linear perturbation $\theta _1$ to Eq. (22). This leads to

$$\begin{aligned} \theta _1''+\lambda _c\,\theta _1'+p\,\theta _c^{\, p-1}\,\theta _1=0, \ \ \ \theta _1(0)=0, \ \ \theta _1'(0)=1, \ \ \theta _1 \rightarrow 0 \ \text{ as } \ y \rightarrow \infty , \end{aligned}$$

(24)

where $\theta _c$ is the solution to (22) at $\lambda =\lambda _c$ and the additional boundary condition on $\theta _1'(0)$ is applied to force a nontrivial solution. Equations (22, 24) are then an eigenvalue problem for $\lambda _c$. Since $\theta _c'$ is a solution to Eq. (24), we can construct the full solution as

$$\begin{aligned} \theta _1=A_1\,\theta _c'\,\mathop {\int }\limits _0^y\frac{\text{ e }^{-\lambda _c\,x}}{\theta _c'(x)^2}\,\mathrm{d}x+B_1\,\theta '_c, \end{aligned}$$

(25)

for constants $A_1, B_1$. Since $\theta _c$ is of $O(\text{ e }^{-\lambda _c\,y})$ as $y \rightarrow \infty$, the integral in the first term on the right-hand side of (25) is of $O(\text{ e }^{\lambda _c\,y})$ and so this term tends to a nonzero constant value, so that $A_1=0$. Hence $\theta _1=B_1\,\theta _c'$. From which it follows that $B_1=0$ resulting in a trivial solution unless $\theta _c'(0)=0$, as suggested above, and then $B_1=-1$. So to determine the critical values we can solve Eq. (22) with the extra condition that $\theta _c'(0)=0$ and so giving an eigenvalue problem for $\lambda _c$. In Fig. 8, we plot the critical values $\lambda _c$ against p. The values of $\lambda _c$ decrease as p is increased and appear to approach 2 as $p \rightarrow 1$.

In passing we note that, for the prescribed wall heat flux case, the above analysis still gives $\theta _1=B_1\,\theta _c'$. For this case, we apply the boundary conditions $\theta _1(0)=1, \theta _1'(0)=0$; hence, $\theta _1=-\theta _c'$. Hence $\theta _1'(0)=-\theta _c''(0)=0$ and applying this in Eq. (3) gives the relation

$$\begin{aligned} \lambda _c=\theta _c(0)^p \quad \text{ or } \ \ \theta _c(0)=\lambda _c^{1/p}, \end{aligned}$$

(26)

which can be seen in Fig. 3b.

3.1 Solution for $\lambda$ large

For the lower branch, we put $\overline{y}=\lambda \,y$, leaving $\theta$ unscaled. Eq. (22) becomes

$$\begin{aligned} \theta ''+\theta '+\lambda ^{-2}\,\theta ^p=0, \end{aligned}$$

(27)

still satisfying the boundary conditions in (22). We expand

$$\begin{aligned} \theta (\overline{y};\lambda )=\theta _0(\overline{y})+\lambda ^{-2}\,\theta _1(\overline{y})+\cdots . \end{aligned}$$

(28)

Equation (27) gives

$$\begin{aligned} \theta _0=\text{ e }^{-\overline{y}}, \ \ \ \theta _1=\frac{1}{p(p-1)}\,\bigl (\text{ e }^{-\overline{y}}-\text{ e }^{-p\,\overline{y}}\bigr ). \end{aligned}$$

(29)

From (29), we have

$$\begin{aligned} \theta '(0) \sim -\lambda \,\biggl (1-\frac{\lambda ^{-2}}{p}+ \cdots \biggr ) \ \ \ \text{ as } \ \lambda \rightarrow \infty . \end{aligned}$$

(30)

Expression (30) agrees to leading order with (23) and shows why the linear form for $\theta '(0)$ seen in Fig. 6 is approached at relatively small values of $\lambda$.

For the upper branch, we write

$$\begin{aligned} \theta =\lambda ^{2/(p-1)}\,g , \ \ \ \xi =\lambda \,y \qquad \ (p>1). \end{aligned}$$

(31)

Equation (22) then gives

$$\begin{aligned} g''+g'+g^{\, p}=0, \ \quad g(0)=\lambda ^{-2/(p-1)}, \ \ g \rightarrow 0 \ \text{ as } \ \xi \rightarrow \infty . \end{aligned}$$

(32)

The leading-order problem satisfies homogeneous boundary conditions and, if we assume that $g'(0)=b_0$ ($b_0>0$) and write $g=b_0^{2/(p+1)}\,\overline{g}$, $\overline{\xi }=b_0^{(p-1)/(p+1)}\, \xi$, we obtain

$$\begin{aligned} \overline{g}''+b_0^{-(p-1)/(p+1)}\,\overline{g}'+\overline{g}^{\, p}=0, \ \ \overline{g}(0)=0, \ \ \overline{g}'(0)=1, \ \ \overline{g} \rightarrow 0 \ \text{ as } \ \overline{\xi } \rightarrow \infty . \end{aligned}$$

(33)

Equation (33) is then an eigenvalue problem for $b_0$. In Fig. 9, we plot $b_0$ against p obtained from the numerical solution of Eq. (33). The values of $b_0$ have a maximum of approximately 2.275 at $p \simeq 7.0$ before decreasing very slowly as p is increased. As p decreases towards 1, the values of $b_0$ become small, virtually zero at $p \simeq 1.2$, similar to the plot on Fig. 4.

From (31), for the upper branch,

$$\begin{aligned} \theta '(0) \sim b_0\,\lambda ^{(p+1)/(p-1)}+\cdots \ \ \text{ as } \ \lambda \rightarrow \infty . \end{aligned}$$

(34)

Expression (34) explains why the values for $\theta '(0)$ on the upper branch increase more rapidly with $\lambda$ for $p=2$, of $O(\lambda ^3)$, Fig. 6a, than for $p=5$ of $O(\lambda ^{3/2})$ and more noticeably for $p=10$, of $O(\lambda ^{11/9})$, Fig. 6b, c.

3.2 Solution for p large

For the lower branch solutions $\theta <1$ on $0<y<\infty$ and so the term $\theta ^p$ becomes negligible for p large. Solving the resulting equation gives $\theta =\text{ e }^{-\lambda \, y}$ so that

$$\begin{aligned} \theta '(0) \rightarrow -\lambda \ \ \text{ as } \ p\rightarrow \infty , \end{aligned}$$

(35)

as can be seen in Fig. 7.

The structure of the solution for p on the upper branch can be seen in Fig. 10 where we plot $\theta$ and $\theta '$ against y for $p=96.94$. There is an outer region $y \ge Y_1(p)$ where $\theta \le 1$ and the term $\theta ^p$ in Eq. (22) is negligible. If we put $y=Y_1+\overline{y}$, Eq. (22) becomes, to leading order,

$$\begin{aligned} \theta ''+\lambda \,\theta '=0, \quad \ \theta \rightarrow 0 \ \text{ as } \ \overline{y} \rightarrow \infty , \end{aligned}$$

(36)

where primes now denote differentiation with respect to $\overline{y}$. Equation (36) is solved subject to the condition that $\theta =1$ at $\overline{y}=0$, i.e. defining the position of $Y_1$ as where $\theta =1$. This gives $\theta =\text{ e }^{-\lambda \,\overline{y}}$.

For the inner region, $\theta \ge 1$ and the term $\lambda \,\theta '$ in Eq. (22) is negligible. Hence we again have equation (17) at leading order now to be solved subject to, on matching with the outer region,

$$\begin{aligned} \theta (0)=1, \ \ \theta (Y_1)=1, \ \ \theta '(Y_1)=-\lambda . \end{aligned}$$

(37)

This gives

$$\begin{aligned} \theta '^{\, 2}=\lambda ^2+\frac{2}{p+1}\,\biggl (1-\theta ^{\, p+1}\biggr ). \end{aligned}$$

(38)

From (38)

$$\begin{aligned} \theta '(0) \sim \lambda +\cdots \quad \text{ as } \ p \rightarrow \infty . \end{aligned}$$

(39)

Expression (38) gives a maximum value $\theta _\mathrm{max}$ for $\theta$ as

$$\begin{aligned} \theta _\mathrm{max}=\left( \frac{(p+1)\,\lambda ^2}{2}+1\right) ^{\!\! 1/{p+1}} \sim 1+\frac{1}{p+1}\,\log \left( \frac{\lambda ^2(p+1)}{2}+1\right) +\cdots , \end{aligned}$$

(40)

showing that the maximum value of $\theta$ decreases to 1 as p increases. Expression (40) gives a value $\theta _\mathrm{max} \simeq 1.0493$ for the results plotted in Fig. 10 as compared to a value of approximately 1.051 obtained from the numerical integration. From (38), we can get an approximation to $Y_1$ for p large as

$$\begin{aligned} Y_1 \sim \frac{2}{\lambda }\,(\theta _\mathrm{max}-1) \sim \frac{2}{\lambda (p+1)}\,\log \left( \frac{\lambda ^2(p+1)}{2}+1\right) , \end{aligned}$$

(41)

showing the thickness of the inner region decreases as p increases. From (41), we calculate $Y_1 \simeq 0.066$, rather smaller than the value of 0.090 seen in the numerical integration of Eq. (22). The above analysis places no restriction on $\lambda$ suggesting that $\lambda _c \rightarrow 0$ as $p \rightarrow \infty$ as appears to be borne out by the results plotted in Fig. 8 and in our numerical integrations to much larger values of p.

Additional comment

Besides the heat transfer application in natural convective flow, boundary value problem (3) can also be treated as the model of linear damping oscillator with nonlinear elastic or stiffness. The mechanical examples include pendulums and masses connected to a spring. For example, Eq. (3) can be described as a damped motion of a particle that is attached to a nonlinear spring of stiffness $|\theta |^{p-1}\,\theta$.

If we put $G=\theta '$, we can write Eq. (3) as

$$\begin{aligned} G\,\frac{{\mathrm d}G}{{\mathrm d}\theta }+\lambda \,G+\theta ^p=0, \end{aligned}$$

(42)

then being an Abel equation of the second kind [17]. As a consequence our numerical solutions, particularly those shown in Figs. 1, 2, 6 and 7, act as separatrices giving a range of initial values for either $\theta (0)$ for the prescribed heat flux case or $\theta '(0)$ for the prescribed temperature case between our solutions which will also satisfy the outer condition for given values of p and $\lambda$. However, these latter (intermediate) solutions are algebraic for y large, of $O(y^{-1/{p-1}})$, whereas our solutions are exponentially small, of $O(\text{ e }^{-\lambda \,y})$, for y large. This difference in the form of the solution for large y meant that the numerical programme D02AGF in the NAG library [18] we used for solving the two-point boundary value problems (4) or (22) found only the exponentially decaying and not the intermediate solutions. Further, Zhang [7, 9] introduced the constraint that the integral $\displaystyle \mathop {\int }\limits _0^\infty \theta (y)\,\mathrm{d}y$ should be bounded. Thus the intermediate solutions do not satisfy this integral constraint. Further, Zhang [7] also applied the additional constraint that $\theta '(0)\le 0$ for the prescribed temperature case so only the lower branch solutions seen in Fig. 6 will ‘normal solutions’ in the sense described in [7].

4 Conclusions

We have considered a generalization of a boundary value problem treated previously by Magyari et al. [1, 2], Zhang [7] and Paullet [8] for a prescribed wall temperature and by Zhang [9] for a prescribed wall heat flux. The problem involves a parameter $\lambda$ and an exponent p. Numerical solutions are obtained for representative values of $\lambda$ and p for both cases, Figs. 1, 2, 3, 7 and 8. A feature of these results is the existence of critical values $\lambda _c$ of $\lambda$ with two solution branches in $\lambda >\lambda _c$, the dependence $\lambda _c$ on p being shown in Figs. 4 and 9. Zhang [9] established that there are no bounded solutions for $\lambda <\lambda _c$ when $p=2$. We expect a similar result to hold for general values of p.

Asymptotic solutions for large $\lambda$ and large p are derived for both types of boundary condition. For large $\lambda$, the nature of the solution is essentially different on upper and on the lower branches, as seen expressions (30) for the lower branch and (34) for the upper branch. A similar feature is seen in the behaviour for p large. On the lower branches, $\theta <1$ for $y>0$ so that the term $\theta ^p$ in Eq. (4) or (22) is negligible giving a relatively simple form for large p. However, for the upper branches a double region structure is seen, Figs. 6 and 10, requiring matching the solution in these regions. This results in the asymptotic forms (20) for the prescribed wall heat flux and (39) for the prescribed wall temperature.