1 Introduction

This paper is devoted to the analysis of the limit shape, for \(\varepsilon \rightarrow 0^+\), of the critical front profile for the 1-dimensional reaction-convection-diffusion equation

$$\begin{aligned} u_t=\varepsilon \left( \frac{u_x}{\sqrt{1-u_x^2}}\right) _x - (h(u))_x + f(u), \quad u=u(x, t), \; x \in \mathbb {R}, \, t \in \mathbb {R}, \end{aligned}$$
(1)

under the following assumptions:

(F):

\(f \in C([0, 1])\) is such that \(f(0)=f(1)=0\), \(f(s) > 0\) for \(s \in (0, 1)\) and there exists \(k > 0\) for which \(f(s) \leqslant ks\), \( f(s) \leqslant k(1-s)\) for every \(s \in [0, 1]\);

(H):

\(h \in C^2([0, 1])\) is such that \(h(0)=h'(0)=0\).

The second-order operator appearing in Eq. (1), known as the relativistic or Born-Infeld operator, embodies a singular diffusion, constraining regular solutions to be subject to the a priori bound \(\vert u_x \vert < 1\). It models diffusion in the Lorentz-Minkowski space (see, e.g., the references in [2, 10]) and, at the same time, it appears in Born-Infeld electrodynamics [4], as mentioned in [10, 17]. In these contexts, the fact that the (normalized) constant 1 represents an unsurmountable threshold for \(\vert u_x \vert \) is in line with the physical assumption that the speed is bounded by the speed of light - in the former case - or the electric field is bounded by the so-called Born field strength parameter - in the latter one.

Problems with nonlinear diffusion have received growing attention in the recent years, dealing with a wide range of qualitatively different diffusion operators including saturating, anisotropic or fractional ones. They build upon the well known theory for the linear diffusion case, for which the pioneering works go back to the first half of the 20\({}^{\text {th}}\) century [8, 16, 18]. In [8], the unknown u was seen as the concentration of an advantageous gene inside a population in a 1-dimensional spatial framework, and it was observed that traveling fronts - i.e., strictly monotone regular solutions \(u(x, t)=v(x+ct)\) joining two equilibria - naturally emerge. Such solutions may be employed in comparison arguments in order to deduce the properties of the solutions of the initial-value problems associated with the considered reaction-diffusion equation, including their long-term behavior, cf. [1, 7, 13].

In this work, we are concerned with increasing traveling fronts for (1), which solve the second-order problem

$$\begin{aligned} \left\{ \begin{array}{l} \varepsilon \displaystyle \left( \frac{v'}{\sqrt{1-(v')^2}}\right) ' - (c+h'(v)) v' + f(v) = 0 \\ v(-\infty )=0, \, v(+\infty )=1, \, v' > 0. \end{array} \right. \end{aligned}$$
(2)

Since (2) is autonomous, it possesses an uncountable family of solutions obtained via z-translation (\(z=x+ct\)); hence, in order to be able to properly deal with the limit of profiles for \(\varepsilon \rightarrow 0^+\), we impose since the very beginning the condition \(v(0)=1/2\), allowing us to recover uniqueness of the solution of (2) for fixed \(\varepsilon \). Of course, the choice of the constant 1/2 is arbitrary, and replacing it with any constant belonging to (0, 1) would produce the same qualitative outcomes as the ones described in the forthcoming sections. Writing the differential equation in (2) as the equivalent first-order system in the phase plane

$$\begin{aligned} \left\{ \begin{array}{l} v'=\dfrac{w}{\sqrt{1+w^2}} \\ \varepsilon w'=(c+h'(v))\dfrac{w}{\sqrt{1+w^2}} - f(v), \end{array} \right. \end{aligned}$$

one has

$$\begin{aligned} \frac{dw}{dv} =\frac{c+h'(v)}{\varepsilon } - f(v) \frac{\sqrt{1+w^2}}{\varepsilon w}, \quad (w > 0), \end{aligned}$$

so that \(y(v)=\varepsilon (\sqrt{1+w(v)^2}-1)\) satisfies the first-order two-point problem

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle y'= (c+h'(v)) \frac{\sqrt{y(2\varepsilon +y)}}{\varepsilon +y} - f(v) \\ y(0)=0, \, y(1)= 0, \, y > 0 \text { on } (0, 1) \end{array} \right. \end{aligned}$$
(3)

(see also [7, 11, 20]). Explicitly, it holds

$$\begin{aligned} y(v)=\varepsilon \left( \frac{1}{\sqrt{1-v'(z(v))^2}}-1\right) \quad \text { and } \quad v'(z)=\frac{\sqrt{y(v(z))(2\varepsilon +y(v(z))}}{\varepsilon +y(v(z))}, \end{aligned}$$
(4)

while the two boundary conditions in (3) come from the fact that the monotone function v has to attain the two equilibria 0 and 1 with zero derivative. In presence of a monostable reaction, we will see that the admissible traveling speeds c for the wave profiles solving (2) form an unbounded interval \([c^*_\varepsilon , +\infty )\) (see Sect. 2), whose lower endpoint is known as critical speed; the solution \(v_\varepsilon \) of (2) for \(c=c_\varepsilon ^*\), unique up to translations in the variable \(z=x+ct\), is called critical profile. It is natural to wonder the behavior of \(c_\varepsilon ^*\) and \(v_\varepsilon \) as \(\varepsilon \rightarrow 0^+\), that is, for vanishing diffusion.

In the 0-convection case, namely for constant h, it was shown in [10] that, under a mild additional assumption on f, the limit speed \(\bar{c}=\lim _{\varepsilon \rightarrow 0^+} c_\varepsilon ^*\) is strictly positive and coincides with \(f(v_+)\), where \(v_+ \in (0, 1)\) is the largest solution of the equation \(\int _0^v f(s) \, ds=vf(v)\). Furthermore, if one denotes by \(\mathcal {V}_I^0(z; \underline{z}, \underline{v})\) the unique positive solution of \(\displaystyle \left\{ \begin{array}{l} \bar{c}v'=f(v) \\ v(\underline{z})=\underline{v} \end{array} \right. \) and defines

$$\begin{aligned} \mathcal {V}_L^0(z; \underline{z}, \underline{v})=\left\{ \begin{array}{ll} 0 &{}\quad z \in (-\infty , \underline{z}-\underline{v}) \\ z-\underline{z}+\underline{v} &{}\quad z \in [\underline{z}-\underline{v}, 1+\underline{z}-\underline{v}] \\ 1 &{}\quad z \in (1+\underline{z}-\underline{v}, +\infty ), \end{array} \right. \end{aligned}$$

for given \(\underline{v} \in (0, 1)\) and \(\underline{z} \in \mathbb {R}\), it turns out that the limit profile \(\bar{v}=\lim _{\varepsilon \rightarrow 0^+} v_\varepsilon \) (to be meant in uniform sense) is obtained by gluing \(\mathcal {V}_I^0\) and \(\mathcal {V}_L^0\) in a \(C^1\) way, for suitable values of \(\underline{z}\) and \(\underline{v}\). Explicitly, [10, Theorem 25] states that

$$\begin{aligned} \begin{array}{lll} \bar{v}(z) = \left\{ \begin{array}{l} \mathcal {V}_L^0(z; 0, 1/2) \\ \mathcal {V}_I^0(z; v_+-1/2, v_+) \end{array} \right. &{} \begin{array}{l} z\in (-\infty , v_+-1/2] \\ z \in (v_+-1/2, +\infty ) \end{array} &{} \text {if } v_+ \geqslant 1/2 \\ \bar{v}(z) = \left\{ \begin{array}{ll} \mathcal {V}_L^0(z; z_+, v_+)\\ \mathcal {V}_I^0(z; 0, 1/2) \end{array} \right. &{} \begin{array}{l} z\in (-\infty , z_+] \\ z \in (z_+, +\infty ) \end{array}&\text {if } v_+ < 1/2, \end{array} \end{aligned}$$

being \(z_+ < 0\) the unique real number for which \(\mathcal {V}_I^0(z_+; 0, 1/2)=v_+\). Summarizing, the limit speed is strictly positive and the limit profile becomes sharp on one side only, near the equilibrium 0. This represents a deep difference with respect to models with linear [15] or saturating [9] diffusion, for which \(c_\varepsilon ^* \rightarrow 0\) for \(\varepsilon \rightarrow 0^+\) and the limit profile \(\bar{v}\) coincides with the Heaviside function. The crucial point leading to the above outcome for the Born-Infeld operator consists in the possibility to provide a lower bound for the critical speed which is not compatible with a completely piecewise linear limit profile: roughly speaking, it was shown in [10] that \(\bar{c} \geqslant \sup _{v \in (0, 1]} \dfrac{F(v)}{v} > F(1)\), while if it were \(\bar{v}(z) =\mathcal {V}_L^0(z; 0, 1/2)\) for every \(z \in \mathbb {R}\) one would have \(\bar{c}=F(1)\) [10, Corollary 23].

It is natural to wonder if this scenario is preserved in presence of a convective term. As is well known, in the linear diffusion case with monostable reaction the convection leads to a shift of the critical speed, compared with the model which encompasses reaction and diffusion only (see, in a more general framework, [19, Theorem 1.4]). Moreover, in the nonlinear case, the convection may amplify some nonlinear effects such as, for instance, the singularities appearing for a saturating diffusion [14] (see also [12]). Hence, a quite specific shape of the limit profile as the one reported above may potentially be altered by the action of a convective term.

As a first difference with respect to [10, Theorem 25], in the case \(f \equiv 0\) the presence of the sole convection steers in fact the limit profile for (2) to have derivative everywhere equal to 1 when it takes values different from the equilibria, as can be easily seen looking at the equivalent first-order two-point problem

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle y'= (c+h'(v)) \frac{\sqrt{y(2\varepsilon +y)}}{\varepsilon +y} \\ y(0)=0, \, y(1)= 0, \, y > 0 \text { on } (0, 1). \end{array} \right. \end{aligned}$$
(5)

The differential equation herein is explicitly integrable; solving the associated Cauchy problem with initial condition \(y(0)=0\) by separating variables yields the positive solution

$$\begin{aligned} y_\varepsilon (v)=\displaystyle \sqrt{\varepsilon ^2+ (cv+h(v))^2}-\varepsilon , \end{aligned}$$

provided that \(cv+h(v) > 0\) for every \(v \in (0, 1)\). Imposing the latter boundary condition in (5), one then finds that \(c=-h(1)\), independently of \(\varepsilon \), and this implies that \(y_\varepsilon (v) \rightarrow h(v) - h(1) v\) for every \(v \in [0, 1]\) (actually, with uniform convergence). Due to (4), this means that the limit profile \(\bar{v}\) must necessarily have slope 1 whenever it takes a value different from 0 and 1; since \(v_\varepsilon (0)=1/2\) for every \(\varepsilon > 0\), it will be \(v_\varepsilon '(z) \rightarrow 1\) for any \(z \in (-1/2, 1/2)\) and \(\bar{v}\) constant elsewhere, namely \(\bar{v} \equiv \mathcal {V}_L(\cdot ; 0, 1/2)\). Notice that, in order for (5) to have a solution, here it has to be \(h(v) > h(1) v\) for every \(v \in (0, 1)\), that is, h cannot be convex on [0, 1]. Convex convections support indeed the existence of decreasing fronts, corresponding to problem (5) where we take the opposite sign in the right-hand side. In any case, the purely convective model thus leads to a fully piecewise linear limit profile.

In case of interplay between reaction and convection, the question is now whether the above one-sided sharpening effect can be fully accentuated or destroyed, according to the amplitude and to the concavity of the convective term. Thanks to a careful study of problem (3), we provide a possible answer in our main result (Theorem 3.1). Setting \(S(v):=\dfrac{F(v)-h(v)}{v}\), this may be summarized as follows:

if S is strictly increasing (resp., decreasing), then the critical profile for (1) converges, for \(\varepsilon \rightarrow 0^+\), to a fully piecewise linear (resp., to a fully regular, as long as it takes positive values) profile; on the contrary, if S reaches a strict positive maximum inside (0, 1), then the limit profile is obtained with a gluing procedure similar to the one in [10, Theorem 25], being sharp near 0 and rounded (regular) near 1.

To show the validity of such a statement, which represents the core of Sect. 3, it will be crucial to provide a suitable estimate of the critical speed associated with (2), see Sect. 2. Finally, Sect. 4 deals with an example where Theorem 3.1 applies, given by the Fisher-Burgers equation with Born-Infeld diffusion, for which it completely covers the possible records which may arise. Contextually, we also show some related numerical simulations illustrating the theoretical results (Figs. 1–4). We point out that it would be interesting to investigate the shape of the limit critical profile in fourth-order models governed by the biharmonic operator, as well (see, e.g., [3]); in particular, one could wonder if the one-sided sharpening of the limit critical profile [10], as well as the regularizing/sharpening effect of the convection in the present paper, could also arise in quasilinear versions of them.

2 Estimating the Critical Speed

In this section, we show some bounds for the critical speed associated with (2), thanks to the analysis of its equivalent first-order reduction (3). We start by formalizing the concept of admissible speed.

Definition 2.1

We say that \(c \in \mathbb {R}\) is an admissible speed if problem (3) has a solution.

Our first goal is to provide an estimate for the admissible speeds of increasing fronts. To this end, we first observe that, assuming (F) and (H), the condition

$$\begin{aligned} cv+h(v) > 0 \quad \text { for every } v \in (0, 1] \end{aligned}$$

has here to hold, as can be easily deduced by integrating Eq. (2) on \((-\infty , z)\), for any \(z \in \mathbb {R} \cup \{+\infty \}\). Consequently, it has in particular to be \(c+h(1) > 0\), in line with the discussion in the Introduction. Second, from \(c > -h(v)/v\), passing to the limit for \(v \rightarrow 0^+\) we infer

$$\begin{aligned} c \geqslant -h'(0) = 0, \end{aligned}$$

so that any admissible speed for (3) is nonnegative. Furthermore, since for every \(y \geqslant 0\) it is \(\sqrt{y(2\varepsilon +y)}\leqslant \varepsilon + y\), and \(f > 0\) on (0, 1), we deduce that any solution of (3) satisfies

$$\begin{aligned} y'(v) \leqslant (c+h'(v)-f(v)) \frac{\sqrt{y(v)(2\varepsilon +y(v))}}{\varepsilon +y(v)} \quad \text { for every } v \in [0, 1]; \end{aligned}$$
(6)

integrating such an inequality with the initial condition \(y(0)=0\) necessarily implies \(cv+h(v)-F(v) > 0\) and \(y(v) \leqslant \sqrt{\varepsilon ^2+(cv+h(v)-F(v))^2}-\varepsilon \) for every \(v \in (0, 1)\), where we have set \(F(v)=\int _0^v f(s) \, ds\). Consequently, it has to be

$$\begin{aligned} c \geqslant \sup _{v \in (0, 1]} \frac{F(v)-h(v)}{v}. \end{aligned}$$
(7)

The following lemma ensures the existence of an unbounded interval of admissible speeds.

Lemma 2.2

Assume (F) and (H). If

$$\begin{aligned} c \geqslant \max _{v \in [0, 1]} f(v) - \min _{v \in [0, 1]} h'(v) + 2\sqrt{\varepsilon \sup _{v \in (0, 1]}\frac{f(v)}{v}}, \end{aligned}$$
(8)

then c is admissible for (3).

Proof

Assuming (8), for fixed \(\varepsilon > 0\) we seek \(\beta > 0\) such that the positive solution \(y_\beta \) of \( \left\{ \begin{array}{l} y_\beta '= \displaystyle \beta \frac{\sqrt{y_\beta (2\varepsilon +y_\beta )}}{\varepsilon +y_\beta } \\ y_\beta (0)=0 \end{array} \right. \) satisfies

$$\begin{aligned} y_\beta '-(c+h'(v))\dfrac{\sqrt{y_\beta (2\varepsilon +y_\beta )}}{\varepsilon +y_\beta }+f(v) \leqslant 0 \quad \text { for every } v \in [0, 1]. \end{aligned}$$
(9)

This will provide a positive lower solution for the (forward) Cauchy problem associated with (3)\(_{1}\) with initial condition \(y(0)=0\), where (3)\(_{1}\) stands for the differential equation in (3). Since, on the other hand, the unique solution of (3)\(_{1}\) fulfilling \(y(1)=0\) cannot vanish in (0, 1) due to the sign of f, this will allow one to find a solution of (3) by a standard uniqueness argument.

Using the explicit expression of \(y_\beta \), (9) will be true if, for every \(v \in (0, 1]\), it holds

$$\begin{aligned} \beta ^2 -(c+h'(v)-f(v))\beta + \varepsilon \frac{f(v)}{v}\leqslant 0. \end{aligned}$$

This inequality is implied by the condition

$$\begin{aligned} \beta ^2 -\Big (c+\min _{v \in [0, 1]} h'(v)-\max _{v \in [0, 1]} f(v)\Big )\beta + \sup _{v \in (0, 1]} \varepsilon \frac{f(v)}{v} \leqslant 0; \end{aligned}$$

thanks to (8), there exists at least one positive \(\beta \) for which such an inequality holds. One can choose, for instance,

$$\begin{aligned} \beta =\frac{c+\min _{v \in [0, 1]} h'(v)-\max _{v \in [0, 1]} f(v)}{2} > 0, \end{aligned}$$

correspondingly finding the desired positive lower solution \(y_\beta \).

We point out that the value appearing in the right-hand side of (8) is strictly positive, coherently with the previous discussion, as \(\min _{v \in [0, 1]} h'(v) \leqslant h'(0) =0\). Now, the argument in the proof of Lemma 2.2 ensures that if c is admissible and \(c' > c\), then also \(c'\) is admissible; moreover, arguing as in the proof of [5, Proposition 3.2], the use of Arzelà-Ascoli Theorem ensures that also the infimum of admissible speeds is an admissible speed. For every fixed \(\varepsilon > 0\), the set of admissible speeds for (3) is then an interval, denoted by \([c_\varepsilon ^*, +\infty )\); its lower endpoint \(c_\varepsilon ^*\) is called critical speed and the associated front profile is called critical profile. Notice that Lemma 2.2 provides an upper bound for \(c_\varepsilon ^*\).

Remark 2.3

Assumption (F) ensures the existence of the considered profiles (since, together with (H), it makes the right-hand side in (8) finite), and guarantees that they are true heteroclinic connections between 0 and 1, being defined on the whole real line and reaching the equilibria only at infinity (cf. [5, Proposition 2.3]).

We are interested in the limit behavior of \(c_\varepsilon ^*\) and \(v_\varepsilon \) for \(\varepsilon \rightarrow 0^+\); to this end, we will examine the solution \(y_\varepsilon \) of the first-order reduction (3). We set

$$\begin{aligned} \bar{c}=\lim _{\varepsilon \rightarrow 0^+} c_\varepsilon ^*, \quad \bar{v}=\lim _{\varepsilon \rightarrow 0^+} v_\varepsilon , \quad \bar{y}=\lim _{\varepsilon \rightarrow 0^+} y_\varepsilon . \end{aligned}$$

In this respect, we underline that if we consider speeds c for which \(c+h'(v) \geqslant 0\) for every v (for sure such a condition has to hold in a right neighborhood of 0, due to the sign of y), then \(c_\varepsilon ^*\) is monotone increasing in \(\varepsilon \), thus it converges for \(\varepsilon \rightarrow 0^+\); this follows from comparison principles applied to the first-order backward problem for (3)\(_{1}\) with initial condition \(y(1)=0\), which enjoys uniqueness. In the general case, we are here assuming that \(c_\varepsilon ^*\) has a limit for \(\varepsilon \rightarrow 0^+\); if this is in principle not ensured, in what follows we can initially replace \(\lim _{\varepsilon \rightarrow 0^+} c_\varepsilon ^*\) with \(\limsup _{\varepsilon \rightarrow 0^+} c_\varepsilon ^*\), whenever necessary, with the very same proof (referring in particular to Proposition 2.4) thanks to the properties of inferior and superior limits. Observe moreover that such a superior limit is finite in view of (8). A posteriori, after Theorem 3.1, since from any \(\varepsilon _n \rightarrow 0^+\) we can extract a subsequence \(\varepsilon _{n_k}\) for which \(c_{\varepsilon _{n_k}}^*\), \(v_{\varepsilon _{n_k}}\) and \(y_{\varepsilon _{n_k}}\) always converge to the same limit, under our assumptions \(c_\varepsilon ^*\) will in fact converge. On the other hand, the front profiles \(v_\varepsilon \) are equi-Lipschitz continuous and bounded in \(C^1\) since \(0 \leqslant v_\varepsilon \leqslant 1\) and \(\Vert v_\varepsilon ' \Vert _{L^\infty (\mathbb {R})} \leqslant 1\), hence there exists a Lipschitz continuous function \(\bar{v}\) such that \(\bar{v}(z)=\lim _{\varepsilon \rightarrow 0^+} v_\varepsilon (z)\) for every \(z \in \mathbb {R}\) and \(v_\varepsilon \rightarrow \bar{v}\) uniformly on compact subsets of \(\mathbb {R}\) (actually, the convergence is uniform on the whole real line in view of [6, Lemma 2.4]). Finally, for what concerns \(y_\varepsilon \), due to the sign of \(c_\varepsilon ^*\) for sure it will be \(y_\varepsilon ' \geqslant -\max _{v \in [0, 1]} \vert h'(v) \vert - f(v)\), hence the backward solution of \(y'=-\max _{v \in [0, 1]} \vert h'(v) \vert -f(v)\) satisfying \(y(1)=0\) is a positive upper solution for \(y_\varepsilon \), for every \(\varepsilon \). Consequently, there exists \(Y_\infty > 0\) such that

$$\begin{aligned} \Vert y_\varepsilon \Vert _{L^\infty (0, 1)} \leqslant Y_\infty \end{aligned}$$
(10)

for every \(\varepsilon > 0\); since \(y \mapsto \dfrac{\sqrt{y(2\varepsilon +y)}}{\varepsilon + y}\) is increasing, (3)\(_{1}\) then yields the existence of \(Y_\infty ' >0\) for which

$$\begin{aligned} \Vert y_\varepsilon ' \Vert _{L^\infty (0, 1)} \leqslant Y_\infty ' \end{aligned}$$
(11)

for every \(\varepsilon > 0\). By the Arzelà-Ascoli Theorem, the bounds (10) and (11) imply that \(y_\varepsilon \) converges uniformly to its limit \(\bar{y}\) for \(\varepsilon \rightarrow 0^+\) and \(\bar{y}\) is a continuous function, nonnegative on [0, 1].

To begin with, we give an estimate of the limit critical speed \(\bar{c}\) for \(\varepsilon \rightarrow 0^+\) in case the limit profile contains a linear piece with slope 1.

Proposition 2.4

Assume that \(\bar{v}(z)=\mathcal {V}_L(z; z_0, v_0)\) on \([z_0, z_1]\), for some real numbers \(z_0 < z_1\), \(v_0 \in [0, 1)\). Let also \(\bar{v}(z_1)=v_1\in (0, 1]\) (so that \(\bar{v}(z)=z-z_0+v_0\) on \([z_0, z_1]\), being \(z_1-z_0=v_1-v_0\)). Then,

$$\begin{aligned} \bar{c}=\frac{F(v_1)-F(v_0)-h(v_1)+h(v_0)}{v_1-v_0}+\frac{\bar{y}(v_1)-\bar{y}(v_0)}{v_1-v_0}. \end{aligned}$$

Proof

Since \(\{v_\varepsilon \}_\varepsilon \) is bounded in \(C^1([z_0, z_1])\), the family \(\{v_\varepsilon '\}_\varepsilon \) is bounded in \(L^2(z_0, z_1)\) and hence there exists \(w \in L^2(z_0, z_1)\) for which, up to subsequences, \(v_\varepsilon ' \rightharpoonup w\) in \(L^2(z_0, z_1)\) for \(\varepsilon \rightarrow 0^+\). Passing to a further subsequence, if necessary, w has to coincide almost everywhere with \(\bar{v}'\) in the points where \(\bar{v}\) is differentiable, so that \(w(z)=1\) for almost every \(z \in [z_0, z_1]\). Multiplying the differential equation in (2) by \(v'_\varepsilon \) and integrating on \([z_0, z_1]\) one obtains, for every \(\varepsilon > 0\), that

$$\begin{aligned} c_\varepsilon ^* \Vert v_\varepsilon ' \Vert ^2_{L^2(z_0, z_1)}\!+ \!\!\int _{z_0}^{z_1} h'(v_\varepsilon (z)) v_\varepsilon '(z)^2 \, dz = \varepsilon \left( \frac{1}{\sqrt{1-v_\varepsilon '(z_1)^2}}\!-\!\frac{1}{\sqrt{1-v_\varepsilon '(z_0)^2}}\right) \\ +F(v_\varepsilon (z_1))\!-\!F(v_\varepsilon (z_0)) \!= \! y_\varepsilon (v_\varepsilon ^1)-y_\varepsilon (v_\varepsilon ^0) + F(v_\varepsilon ^1)-F(v_\varepsilon ^0), \end{aligned}$$

where \(v_\varepsilon ^0:=v_\varepsilon (z_0)\), \(v_\varepsilon ^1:=v_\varepsilon (z_1)\). Using the weak semicontinuity of the norm, the first summand in the left-hand side is bounded from below by \(\bar{c}(v_1-v_0)\) in the limit for \(\varepsilon \rightarrow 0^+\). As for the second one, we observe that \(h'(v_\varepsilon )v_\varepsilon ' \rightarrow h'(\bar{v})w\) strongly in \(L^2(z_0, z_1)\), in view of the uniform convergence of \(v_\varepsilon \) to \(\bar{v}\) and of the fact that \(h \in C^2\). Since \(v_\varepsilon ' \rightharpoonup w\) in \(L^2(z_0, z_1)\), we conclude that

$$\begin{aligned} \int _{z_0}^{z_1} h'(v_\varepsilon (z)) v_\varepsilon '(z)^2 \, dz \rightarrow \int _{z_0}^{z_1} h'(\bar{v}(z)) w(z)^2 \, dz = h(v_1)-h(v_0), \end{aligned}$$

where the last equality follows from the properties of absolutely continuous functions. Being \(\lim _{\varepsilon \rightarrow 0^+} v_\varepsilon ^0 = v_0\) and \(\lim _{\varepsilon \rightarrow 0^+ }v_\varepsilon ^1 = v_1\), using (10) and (11) one has that \(y_\varepsilon (v_\varepsilon ^0) \rightarrow \bar{y}(v_0)\) and \(y_\varepsilon (v_\varepsilon ^1) \rightarrow \bar{y}(v_1)\) for \(\varepsilon \rightarrow 0^+\). Therefore, we infer

$$\begin{aligned} \bar{c} \leqslant \frac{\bar{y}(v_1)-\bar{y}(v_0)}{v_1-v_0} + \frac{F(v_1)-F(v_0)-h(v_1)+h(v_0)}{v_1-v_0}. \end{aligned}$$

On the other hand, integrating the inequality (6) - with \(c=c_\varepsilon ^*\) - between \(v_0\) and \(v_1\) provides \(\displaystyle \sqrt{y_\varepsilon (v_1)(2\varepsilon +y_\varepsilon (v_1))}-\sqrt{y_\varepsilon (v_0)(2\varepsilon +y_\varepsilon (v_0))} \leqslant c_\varepsilon ^*(v_1-v_0)+h(v_1)-h(v_0)-F(v_1)+F(v_0)\), which passing to the limit for \(\varepsilon \rightarrow 0^+\) yields the reversed inequality for \(\bar{c}\). The conclusion follows.\(\square \)

Corollary 2.5

Let \(\bar{v}(z) = \mathcal {V}_L^0(z; 0, 1/2)\) for every \(z \in \mathbb {R}\). Then, \(\bar{c}=F(1)-h(1)\).

3 The Role of the Convective Term in the Shape of the Limit Profile

From the discussion in Sect. 2, we have understood that a key quantity in determining the asymptotic value of the critical speed and the asymptotic shape of the critical profile is

$$\begin{aligned} S(v):=\dfrac{F(v)-h(v)}{v}. \end{aligned}$$

In view of assumptions (F) and (H), S can be extended by continuity setting \(S(0)=0\), and for this reason \(\sup _{v \in (0, 1]} S(v) \geqslant 0\). In the next statement, we see how different assumptions on S produce different outcomes regarding \(\bar{c}\) and \(\bar{v}\); the exposition is maintained to a more readable level in order to avoid overloading the contents and the proofs, since we are mainly interested in highlighting the different phenomena which can arise, rather than in providing the corresponding optimal assumptions. In any case, our results fully cover the most natural case of Fisher-Burgers type Eqs. (see (14)), for which we are able to give a complete picture.

In the following, we set \(\mathcal {V}_L(z; \underline{z}, \underline{v})=\mathcal {V}_L^0(z; \underline{z}, \underline{v})\), and we denote by \(\mathcal {V}_I(\cdot ; \underline{z}, \underline{v})\) the unique \(C^1\)-solution of

$$\begin{aligned} \left\{ \begin{array}{l} (\bar{c}+h'(v))v'=f(v) \\ v(\underline{z})=\underline{v}; \end{array} \right. \end{aligned}$$
(12)

here we implicitly assume that \(\bar{c}+h'(\underline{v}) > 0\), in line with the monotonicity of the solutions we are interested in and in order to avoid degeneracy. Of course, the solution of (12) might possibly be defined only on a neighborhood of \(\underline{z}\) or might escape the interval [0, 1], depending on the expressions of f and \(h'\). We still comment about this after Theorem 3.1.

With these preliminaries, we now have the following.

Theorem 3.1

Let f and h fulfill assumptions (F) and (H). The following hold:

  1. 1)

    if \(S'(v) < 0\) for every \(v \in (0, 1]\), then \(\bar{c}=0\) and \(\bar{v}\equiv \mathcal {V}_I(\cdot ; 0, 1/2)\) as long as \(\bar{v} > 0\), while \(\bar{v}=0\) elsewhere;

  2. 2)

    if \(0 < \sup _{v \in (0, 1]} S(v) \ne S(1)\) and \(f-h'\) has a unique local maximum point in [0, 1], then \(\bar{c}=f(v_+)-h'(v_+)\), where \(v_+\) is the largest solution of the equation \(F(v)-h(v)=v(f(v)-h'(v))\), and the limit profile \(\bar{v}\) is given by

    $$\begin{aligned} \begin{array}{lll} \bar{v}(z) = \left\{ \begin{array}{l} \mathcal {V}_L(z; 0, 1/2) \\ \mathcal {V}_I(z; v_+-1/2, v_+) \end{array} \right. &{} \begin{array}{l} z\in (-\infty , v_+-1/2] \\ z \in (v_+-1/2, +\infty ) \end{array} &{} \text {if } v_+ \geqslant 1/2 \\ \bar{v}(z) = \left\{ \begin{array}{ll} \mathcal {V}_L(z; z_+, v_+)\\ \mathcal {V}_I(z; 0, 1/2) \end{array} \right. &{} \begin{array}{l} z\in (-\infty , z_+] \\ z \in (z_+, +\infty ) \end{array}&\text {if } v_+ < 1/2, \end{array} \end{aligned}$$

    where, in the latter case, \(z_+ < 0\) is the unique real number for which \(\mathcal {V}_I(z_+; 0, 1/2)=v_+\);

  3. 3)

    if \(S'(v) > 0\) for every \(v \in (0, 1)\), then \(\bar{c}=F(1)-h(1)\) and \(\bar{v}\equiv \mathcal {V}_L(\cdot ; 0, 1/2)\).

Proof

We first notice that if \(\bar{c} > 0\), then there exists \(v_1 \in (0, 1)\) such that \(\bar{y}(v) > 0\) for every \(v \in (0, v_1)\); indeed, if \(c < \bar{c}\) is sufficiently small, then the positive solution of (3)\(_{1}\) satisfying \(y(0)=0\) is greater or equal than the positive solution of

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle y'= c \frac{\sqrt{y(2\varepsilon +y)}}{\varepsilon +y} \\ y(0)=0, \end{array} \right. \end{aligned}$$

uniformly in \(\varepsilon \). This can be seen, for instance, performing an argument similar to the one in the proof of [10, Lemma 26], thanks to the fact that \(h'(0)=0\) and hence \(\bar{c}+h'(v) > 0\) in a right neighborhood of 0. Hence, it makes sense to define \(\widetilde{v}:=\sup \{v \in (0, 1] \mid \bar{y} > 0 \text { on } (0, v)\}\). One has that \(\bar{y}(\widetilde{v})=0\), by the continuity of \(\bar{y}\); moreover, for every \([\alpha , \beta ] \subset (0, v_1)\), it holds that \(y_\varepsilon \rightarrow \bar{y}\) in \(C^1([\alpha , \beta ])\), where \(\bar{y}(v)=\bar{c}v+h(v)-F(v)\) (as can be seen letting \(\alpha \rightarrow 0^+\)).

The proof then proceeds differently according to the considered case.

  1. 1)

    If by contradiction it were \(\bar{c} > 0\), by the previous observations one would have \(\bar{y}(\widetilde{v})=0\) and hence, by the expression of \(\bar{y}\),

    $$\begin{aligned} \bar{c}=\frac{F(\widetilde{v})-h(\widetilde{v})}{\widetilde{v}} \leqslant 0, \end{aligned}$$

    against the assumption. Hence, \(\bar{c}=0\). For fixed \(\xi \in (0, 1)\), let now \(M_\varepsilon =\max _{v \in [\xi , 1]} y_\varepsilon (v)\) and let \(v_{M, \varepsilon } \in [\xi , 1)\) be such that \(y_\varepsilon (v_{M,\varepsilon })=M_\varepsilon \) (we drop the dependences on \(\xi \) for the sake of readability); up to subsequences, one can assume that \(v_{M, \varepsilon } \rightarrow v^* \in [\xi , 1]\). If by contradiction it were \(\varepsilon /M_\varepsilon \rightarrow 0\), passing to the limit in

    $$\begin{aligned} 0 \geqslant y_\varepsilon '(v_{M, \varepsilon })=(c_\varepsilon ^*+h'(v_{M, \varepsilon })) \frac{\sqrt{M_\varepsilon (2\varepsilon +M_\varepsilon )}}{\varepsilon +M_\varepsilon }-f(v_{M, \varepsilon }) \end{aligned}$$

    one would obtain \(h'(v^*) \leqslant f(v^*)\), implying that \(S'(v^*) \geqslant 0\) against the assumption. It follows that \(y_\varepsilon \rightarrow 0\) uniformly and, for any fixed \(\xi > 0\), \(M_\varepsilon \rightarrow 0\) with order \(\varepsilon \) (if this occurred with a stronger order, one would easily find the contradiction \(y_\varepsilon ' \rightarrow -f < 0\)). For fixed \(\zeta \in \mathbb {R}\), using the expression of y provided by (4) then ensures the existence of \(0< K < 1\) such that \(\Vert v'_\varepsilon \Vert _{L^\infty (\zeta , +\infty )} \leqslant K\). For any \(\psi \in C_c^\infty ([\zeta , +\infty ))\), one can then pass to the limit for \(\varepsilon \rightarrow 0^+\) in

    $$\begin{aligned} -\int _{\zeta }^{+\infty } \!\!\frac{\varepsilon v_{\varepsilon }'(z)}{\sqrt{1-(v_{\varepsilon }'(z))^2}} \psi '(z) \, dz + \int _{\zeta }^{+\infty }\!\! (c_{\varepsilon }^*v_\varepsilon (z)+h(v_\varepsilon (z))) \psi '(z) \, dz \\ + \int _{\zeta }^{+\infty } \!\! f(v_{\varepsilon }(z)) \psi (z) \, dz = 0, \end{aligned}$$

    finally obtaining that \(\bar{v}\) satisfies \(h'(\bar{v})\bar{v}'-f(\bar{v})=0\) whenever \(\bar{v} > 0\). It follows that \(\bar{v}(z) = \mathcal {V}_I(z; 0, 1/2)\) for every \(z \in \mathbb {R}\) such that \(\bar{v}(z) > 0\).

  2. 2)

    In this second case, we have \(\bar{c} > 0\) in view of (7) and thus \(\widetilde{v} > 0\) is well defined. Moreover, we observe that necessarily \(\widetilde{v} < 1\), otherwise \(\bar{c}=F(1)-h(1)\) and hence \(\bar{y}(v)=(F(1)-h(1))v-F(v)+h(v) > 0\) for every \(v \in (0, 1)\), contradicting the assumption \(\sup _{v \in (0, 1]} S(v) \ne S(1)\). We now claim that

    $$\begin{aligned} \bar{c}=\frac{F(\widetilde{v})-h(\widetilde{v})}{\widetilde{v}}=f(v_m)-h'(v_m)=f(\widetilde{v})-h'(\widetilde{v}), \end{aligned}$$
    (13)

    where \(v_m \in (0, \widetilde{v})\) is such that \(\bar{y}(v_m)=M:=\max _{v \in [0, \widetilde{v}]} \bar{y}(v)\). The first equality in (13) is a straight consequence of the fact that \(\bar{y}(\widetilde{v})=0\), while the second one follows from the \(C^1\)-convergence of \(y_\varepsilon \) to \(\bar{y}\) on any interval \([\alpha , \beta ] \subset (0, \widetilde{v})\), since

    $$\begin{aligned} 0 \leftarrow \displaystyle y_\varepsilon '(v_m)= & {} (c_\varepsilon ^*+h'(v_m)) \frac{\sqrt{y_\varepsilon (v_m)(2\varepsilon +y_\varepsilon (v_m))}}{\varepsilon +y_\varepsilon (v_m)} - f(v_m) \\ {}\rightarrow & {} \bar{c}+h'(v_m) - f(v_m), \end{aligned}$$

    being \(y_\varepsilon (v_m) \rightarrow M > 0\). As for the last equality in (13), we first observe that, for fixed \(v^1 > \widetilde{v}\), integrating the inequality \(y_\varepsilon '(v) \leqslant (c_\varepsilon ^*+h'(v)-f(v)) \dfrac{\sqrt{y_\varepsilon (v) (2\varepsilon +y_\varepsilon (v))}}{\varepsilon +y_\varepsilon (v)}\) on \([\widetilde{v}, v^1]\) yields \( \sqrt{y_\varepsilon (v^1)(2\varepsilon +y_\varepsilon (v^1))}-\sqrt{y_\varepsilon (\widetilde{v})(2\varepsilon +y_\varepsilon (\widetilde{v}))} \leqslant c_\varepsilon ^*(v^1-\widetilde{v})+h(v^1)-h(\widetilde{v}) - F(v^1)+F(\widetilde{v}), \) which passing to the limit for \(\varepsilon \rightarrow 0^+\) produces (recalling that \(\bar{y}(\widetilde{v})=0\) and \(\bar{y}(v^1) \geqslant 0\))

    $$\begin{aligned} \bar{c} \geqslant \frac{F(v^1)-F(\widetilde{v})-h(v^1)+h(\widetilde{v})}{v^1-\widetilde{v}}; \end{aligned}$$

    passing now to the limit for \(v^1 \rightarrow \widetilde{v}^+\), we obtain \(\bar{c} \geqslant f(\widetilde{v})-h'(\widetilde{v})\). As for the reversed inequality, we observe that since \(\bar{y}(\widetilde{v}) = 0 < \bar{y}(v)\) for every \(v \in (0, \widetilde{v})\), there exists a sequence \(v_n \nearrow \widetilde{v}\) such that \(\bar{y}'(v_n) \leqslant 0\). Recalling the expression of \(\bar{y}\) in the interval \((0, \widetilde{v})\) and the \(C^1\)-convergence of \(y_\varepsilon \) to \(\bar{y}\), it then follows that

    $$\begin{aligned} 0 \geqslant \bar{y}'(v_n) = \bar{c}+h'(v_n) - f(v_n), \end{aligned}$$

    which yields the desired inequality passing to the limit for \(n \rightarrow +\infty \). We now proceed similarly as in case 1) and as in the proof of [10, Theorem 25]. For fixed \(\sigma > 0\), we define \(M_\varepsilon =\max _{v \in [\widetilde{v}+\sigma , 1]} y_\varepsilon (v)\) and we let \(v_{M, \varepsilon } \in [\widetilde{v}+\sigma , 1)\) be such that \(y_\varepsilon (v_{M, \varepsilon })=M_\varepsilon \). Up to subsequences, \(v_{M, \varepsilon } \rightarrow v^* \in [\widetilde{v}+\sigma , 1]\); if it were \(\varepsilon /M_\varepsilon \rightarrow 0\), arguing as in case 1) one would find \(\bar{c}+h'(v^*)-f(v^*) \leqslant 0\), which is impossible in view of the assumption on \(f-h'\) (since the equation \(\bar{c}+h'(v)-f(v)=0\) has the two distinct solutions \(v_m\) and \(\widetilde{v}\)). Hence \(M_\varepsilon \rightarrow 0\) with order \(\varepsilon \), \(y_\varepsilon \rightarrow 0\) uniformly in \([\widetilde{v}+\sigma , 1]\) for every \(\sigma > 0\), \(\widetilde{v}=v_+\) and \(\bar{v}\) is piecewise linear with slope 1 as long as it takes values in \((0, v_+)\); when taking values in \((v_+, 1)\), instead, \(\bar{v}\) coincides with the solution of (12) gluing with the previous branch in such a way that, overall, the solution is \(C^1\). This is equivalent to the statement in case 2).

  3. 3)

    The assumption \(S' > 0\) and (7) imply that

    $$\begin{aligned} \bar{c} \geqslant \sup _{v \in (0, 1]} S(v)=F(1)-h(1) > 0. \end{aligned}$$

    With the same notation as above, in this case we have that \(\widetilde{v}\) necessarily coincides with 1, for if by contradiction \(\widetilde{v} < 1\), one would deduce \(\bar{y}(\widetilde{v})=\bar{c}\widetilde{v}+h(\widetilde{v})-F(\widetilde{v})=0\), implying, in view of the fact that \(S' > 0\), the contradiction

    $$\begin{aligned} \bar{c}= \dfrac{F(\widetilde{v})-h(\widetilde{v})}{\widetilde{v}} < F(1)-h(1). \end{aligned}$$

    Hence, \(\bar{c}=F(1)-h(1)\) and \(\bar{y}(v)=\bar{c}v+h(v)-F(v) > 0\) for every \(v \in (0, 1)\). Using a similar argument as the one mentioned in the Introduction for the 0-convection case, this implies that \(\bar{v} \equiv \mathcal {V}_L(\cdot ; 0, 1/2)\), concluding the statement.

Some comments are in order, in particular about the above case 1). Setting \(z_0=\inf \{z \in (-\infty , 0) \mid \mathcal {V}_I(z; 0, 1/2) > 0\}\), it may be \(z_0=-\infty \) or \(z_0 \in (-\infty , 0)\), according to whether the improper integral \(\int _0^{1/2} h'(s)/f(s) \, ds\) diverges or not. In the former case, \(\mathcal {V}_I(\cdot ; 0, 1/2)\) (henceforth briefly denoted by \(\mathcal {V}_I\)) is positive and regular on the whole real line and \(v_\varepsilon \rightarrow \bar{v}\) with \(C^1\)-convergence, while in the latter one it holds \(\mathcal {V}_I(z_0)=0\) and the differential equation for \(\mathcal {V}_I\) degenerates at \(z_0\). If \(\mathcal {V}_I'(z_0) > 0\), \(\mathcal {V}_I\) may then be prolonged so as to escape the interval [0, 1], while if \(\mathcal {V}_I'(z_0)=0\) it may be prolonged in a \(C^1\)-way to 0 in the interval \((-\infty , z_0)\). Noticing that \(v_\varepsilon \rightarrow \mathcal {V}_I\) in \(C^1(z, +\infty )\) for every \(z > z_0\), similarly as in [10, Remark 29], it will be

$$\begin{aligned} \lim _{z \rightarrow z_0^+} \bar{v}'(z)=\lim _{z \rightarrow z_0^+} \mathcal {V}_I'(z)=\lim _{z \rightarrow z_0^+} \frac{f(\mathcal {V}_I(z))}{h'(\mathcal {V}_I(z))}; \end{aligned}$$

hence, a crucial role is here played by the limit \(\ell :=\lim _{s \rightarrow 0^+} f(s)/h'(s)\). If \(\ell =0\), then \(\bar{v}\) may be prolonged to a globally \(C^1\)-function, being \(\lim _{z \rightarrow z_0^+}\bar{v}'(z)=0=\lim _{z \rightarrow z_0^-} \bar{v}'(z)\) (this last equality holding since necessarily \(\bar{v} \equiv 0\) in \((-\infty , z_0)\)). Otherwise, if \(\ell > 0\) then \(\bar{v}\) is sharp near 0. This issue does not arise for the inviscid piece of limit profile in case 2), since the boundedness of the considered front profiles in \(C^1\), together with the fact that f is positive on (0, 1), prevents \(\bar{c}+h'(v)\) from vanishing in the interval \([v_+, 1)\), otherwise one would reach the contradiction \(0=f(v)\) for some \(v \in [v_+, 1)\).

We make some further remarks about the statement of Theorem 3.1. We notice that case 1) only occurs if \(h'(s) > 0\) for every \(s \in (0, 1]\), namely only for suitable strictly increasing convections. Indeed, the conditions \(S(0)=0\) and \(S'(v) < 0\) for every \(v \in (0, 1]\) imply that \(S(v) < 0\) for every \(v> 0\); since moreover

$$\begin{aligned} S'(v)=\frac{f(v)-h'(v)-S(v)}{v}, \end{aligned}$$

it has necessarily to be \(f(v)-h'(v)-S(v) < 0\), that is, \(f(v)+\vert S(v) \vert < h'(v)\) for \(v > 0\). Notice that this implies that the differential equation in (12) can degenerate only when \(v=0\).

Case 3) cannot instead occur if h is everywhere increasing, since from the fact that \(S'(v) > 0\) for every \(v \in (0, 1)\) it follows that \(f(1)-h'(1)-S(1)=-h'(1)-S(1) \geqslant 0\), hence \(h'(1)\) has to be strictly negative (being here \(S(1) > 0\)). However, the assumption \(S'(v) > 0\) for every \(v \in (0, 1)\) may be fulfilled for convections which are locally increasing near 0, like \(h(s)=s^2(\delta -s)\), for a sufficiently small \(\delta >0\), provided that \(f(v) >h'(v)+S(v)\) for every \(v \in (0, 1)\).

In particular, since \(h'(0)=0\), the conditions \(h''(v) < 0\) (implying strict concavity) and \(h''(v) > 0\) (implying strict convexity) for every v are ruled out, respectively, from cases 1) and 3). Case 2) depends instead on the quantitative interplay between f and \(h'\), rather than on the sign of \(h'\), hence in principle it can occur regardless of the monotonicity (and of the convexity) of h. One may wonder if the sign assumption \(S' < 0\) (resp., \(S' > 0\)) on the derivative of S could be replaced by a weaker condition like \(\sup _{v \in (0, 1]} S(v)=0\) (resp., \(\sup _{v \in (0, 1]} S(v)= F(1)-h(1)\)), but for the sake of brevity we have preferred a slightly stronger hypothesis, in order to proceed with a simpler and shorter proof.

4 An Example: A Quasilinear Fisher-Burgers Equation

We here illustrate the statement of Theorem 3.1 for the Fisher-Burgers type equation

$$\begin{aligned} u_t=\varepsilon \left( \frac{u_x}{\sqrt{1-u_x^2}}\right) _x - (\alpha u^2)_x + ku(1-u) =0, \end{aligned}$$
(14)

in dependence on two parameters \(\alpha \in \mathbb {R}\), \(k > 0\), showing some related numerical simulations performed with Wolfram Mathematica\(^{\copyright }\) software. To this end, we set

$$\begin{aligned} \begin{array}{ll} \varepsilon =2\cdot 10^{-3}, \, k=1 \text { and: } \\ \alpha =1, \; \alpha =0.5 (=k/2) \ \text {(top line)}, \\ \alpha =0.05, \; \alpha =-0.05 \ \text {(middle line)}, \\ \alpha =-1/6 (=-k/6), \; \alpha = -0.5 \ \text {(bottom line)}. \end{array} \end{aligned}$$
(15)
Fig. 1
figure 1

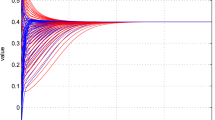
For \(\varepsilon , k, \alpha \) as in (15), we show the graph of the critical profile \(v_\varepsilon \) for (14). The values of \(\bar{c}\) predicted by Theorem 3.1 are, respectively, \(\bar{c}=0\) (top line), \(\bar{c}=0.152, 0.187\) (middle line), \(\bar{c}=1/3, 2/3\) (bottom line), while here we have found the approximations \(c_\varepsilon ^* \approx 0.07, 0.09\) (top line), \(c_\varepsilon ^* \approx 0.163, 0.234\) (middle line), \(c_\varepsilon ^* \approx 0.336, 0.667\) (bottom line)

Full size image

For Eq. (14) one has

$$\begin{aligned} S(v)=\displaystyle \left( \frac{k}{2}-\alpha \right) v-k\frac{v^2}{3} \end{aligned}$$

and it is immediately seen that if \(\alpha \geqslant k/2\), then the assumptions of case 1) in the statement of Theorem 3.1 are satisfied. However, since \(\lim _{s \rightarrow 0} f(s)/h'(s)=k/(2\alpha )\), the inviscid profile \(\mathcal {V}_I\) exits the interval [0, 1], while \(\bar{v}\) is constrained between 0 and 1 and hence \(\bar{v} \equiv 0\) on the left of the vanishing point for \(\mathcal {V}_I\). In particular, \(\bar{v}\) is not \(C^1\) and is sharp near the value 0, similarly to the case without convection. This outcome is reproduced in Fig. 1, top line. If instead \(\alpha \in (-k/6, k/2)\), then \(S'(1) < 0\) and case 2) of Theorem 3.1 occurs; moreover, it can be easily checked that \(f-h'\) has a unique maximum, so that the limit profile is again sharp on the “left” side only (Fig. 1, middle line). Finally, if \(\alpha \leqslant -k/6\), it is immediate to see that \(S'(v) > 0\) for every \(v \in (0, 1)\), so that the limit configuration for \(v_\varepsilon \) is fully piecewise linear, in accord with case 3) of Theorem 3.1 (Fig. 1, bottom line). Summarizing, Theorem 3.1 completely characterizes \(\bar{v}\) for Fisher-Burgers type equations: the limit profile is never regular, becoming fully sharp (near both the values 0 and 1) if the convection is sufficiently negative (in particular, concave). Of course, for fixed \(\varepsilon > 0\) the profiles are always smooth, anyway in the pictures we can spot quite neatly the asymptotic trend stated in the theorem.

Fig. 2
figure 2

For \(k=1\) and \(\alpha =1\), we depict the critical front solution \(v_\varepsilon \) of (14) (black) and the inviscid profile \(\mathcal {V}_I\) (gray) in the cases \(\varepsilon =0.002\) (left) and \(\varepsilon =0.0002\) (right). In the former case \(c_\varepsilon ^* \approx 0.07\), as in Fig. 1, while in the latter one we find \(c_\varepsilon ^* \approx 0.024\)

Full size image
Fig. 3
figure 3

For \(h(s)=s^{3/2}\) and \(f(s)=s(1-s)\), we depict the critical front profile \(v_\varepsilon \) for (1) (black) and the inviscid profile \(\mathcal {V}_I\) (gray) for \(\varepsilon =0.01\) (left) and \(\varepsilon =0.002\) (right). Here \(c_\varepsilon ^* \approx 0.143\) (left), \(c_\varepsilon ^* \approx 10^{-3}\) (right)

Full size image

In Fig. 2, we zoom into the above case 1), showing how the critical profile \(v_\varepsilon \) modifies its shape for smaller \(\varepsilon \); we explicitly plot the inviscid profile \(\mathcal {V}_I\) (gray) to highlight how much \(v_\varepsilon \) and \(\mathcal {V}_I\) become almost indistinguishable whenever strictly positive.

We finally corroborate our discussion about the importance of the value of \(\lim _{s \rightarrow 0^+} f(s)/h'(s)\) in the possible regularization of the limit profile in the above case 1). In Fig. 3, we show the critical profile \(v_\varepsilon \) for \(\varepsilon =0.01\) (left) and \(\varepsilon =0.002\) (right) in case \(f(s)=s(1-s)\) and \(h(s)=s^{3/2}\) (notice that, in this case, h is not \(C^2\) at \(s=0\)); here, \(\lim _{s \rightarrow 0^+} f(s)/h'(s)=0\), so that \(\bar{v}\) is everywhere \(C^1\) and reaches the equilibrium 0 in finite time. On the other hand, in Fig. 4 we show the shape of \(v_\varepsilon \) for \(\varepsilon =0.1\) (left) and \(\varepsilon =0.01\) (right) in case \(f(s)=s^2(1-s)\) and \(h(s)=s^2\), for which the inviscid profile \(\mathcal {V}_I\) is regular and reaches the equilibrium 0 only at \(-\infty \), since the integral \(\int _0^{1/2} h'(s)/f(s) \, ds\) diverges. Consequently, \(\bar{v}\) is everywhere \(C^1\) and \(\bar{v}(z) > 0\) for every \(z \in \mathbb {R}\). We notice again that \(\bar{v}\) and \(\mathcal {V}_I\) appear indistinguishable in the considered interval.

Fig. 4
figure 4

For \(h(s)=s^2\) and \(f(s)=s^2(1-s)\), we depict the critical front profile \(v_\varepsilon \) for (1) (black) and the inviscid profile \(\mathcal {V}_I\) (gray) for \(\varepsilon =0.1\) (left) and \(\varepsilon =0.01\) (right). Here \(c_\varepsilon ^* \approx 0.046\) (left), \(c_\varepsilon ^* \approx 10^{-4}\) (right)

Full size image