Abstract
In this work, we consider some evolutionary models for k-currents in \(\mathbb {R}^d\). We study a transport-type equation which can be seen as a generalisation of the transport/continuity equation and can be used to model the movement of singular structures in a medium, such as vortex points/lines/sheets in fluids or dislocation loops in crystals. We provide a detailed overview of recent results on this equation obtained mostly in (Bonicatto et al. Transport of currents and geometric Rademacher-type theorems. arXiv:2207.03922, 2022; Bonicatto et al. Existence and uniqueness for the transport of currents by Lipschitz vector fields. arXiv:2303.03218, 2023). We work within the setting of integral (sometimes merely normal) k-currents, covering in particular existence and uniqueness of solutions, structure theorems, rectifiability, and a number of Rademacher-type differentiability results. These differentiability results are sharp and can be formulated in terms of a novel condition we called “Negligible Criticality condition” (NC), which turns out to be related also to Sard’s Theorem. We finally provide a new stability result for integral currents satisfying (NC) in a uniform way.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Transport phenomena are widespread in physics and engineering. Given a bounded (time-dependent) vector field \( {\varvec{b}}_t = {\varvec{b}}(t,\cdot ): \mathbb {R}^d \rightarrow \mathbb {R}^d \), with \(t \in [0,1]\), the transport equation
describes the transport of scalar fields \(u :[0,1] \times \mathbb {R}^d \rightarrow \mathbb {R}\). On the other hand, the continuity equation
characterises the transport of densities or, more generally, measures \( \mu _t = \mu (t,\cdot ) \) representing (possibly singular) mass distributions. The initial data \(\overline{u}\) and \(\overline{\rho }\) are usually given and the goal is to investigate existence, uniqueness and structure of solutions.
Another instance of a transport phenomenon is the movement of dislocations, serving as the primary mechanism for plastic deformation in crystalline materials, such as metals [1, 16]. Dislocations represent topological defects within the crystal lattice, carrying both an orientation and a “topological charge” known as the Burgers vector. When examining fields \( \tau _t = \tau (t, \cdot ): \mathbb {R}^3 \rightarrow \mathbb {R}^3 \) describing continuously-distributed dislocations (with a fixed Burgers vector) being transported by a velocity field \( {\varvec{b}}_t \), the resulting equation is the dislocation-transport equation:
The three equations (CE), (TE) and (DT) can be cast into the single, unifying geometric transport equation
where \(({ T}_t)_{t>0}\) is a family of k-currents in \(\mathbb R^d\), \(k \in \{0, \ldots ,d\}\), and \(\mathcal L_{{\varvec{b}}_t} T_t\) is the Lie derivative of \(T_t\) in the direction of the field \({\varvec{b}}_t\), defined as
This formula is obtained by duality via Cartan’s formula for differential forms. We understand (GTE) in a weak sense, meaning that for every \( \psi \in \textrm{C}^{\infty }_c((0, 1)) \) and each smooth \( k \)-form \( \omega \in \mathscr {D}^k(\mathbb {R}^d) \) it holds
Written in coordinates for different values of k, the geometric transport equation (GTE) encompasses the classical transport equation (\(k = d\)), the continuity equation (\(k= 0\)), as well as the equations for the transport of dislocation lines in crystals (\(k=1\)) – and even the movement of membranes in liquids (\(k=d-1\)). Notice that in all these equations, the case of “singular” objects being transported is just as natural as the case of fields. Apart from dislocations, which were previously discussed, the movement of point masses, lines, or sheets is particularly relevant in fluid mechanics when considering concentrated vorticity. Intermediate-dimensional structures also emerge in the context of Ginzburg-Landau energies, even in static situations (e.g. [2, 13, 17]).
This work offers a broad overview of the state of the art around (GTE). We provide a general theory for the geometric transport equation in the case of transported integral (sometimes only normal) k-currents, including the case of intermediate dimensions (\(k \ne 0,d\)). We present in particular:
-
a comparison between the notions of weak solutions and of space-time solutions (see below for more details); this includes a detailed analysis of various possible definitions of variations, scattered in the literature and collected and compared here;
-
a structure theorem: For a space-time current, this theorem details the structure of its disintegration. We introduce the notion of “critical points” of a space-time current, which turn out to be crucial in the study of transport-type phenomena;
-
various rectifiability results: we study under which conditions a time-indexed collection of boundary-less integral k-currents can be seen as the slices of a space-time integral current;
-
the Advection Theorem: we show that a boundaryless space-time current satisfies the negligible criticality condition (meaning that critical points are negligible for the mass measure of the current) if and only if its slices are advected by some vector field in the sense of (GTE);
-
Existence & Uniqueness Theorem in the Lipschitz framework: In the case where the driving vector field is assumed Lipschitz, we show the existence and uniqueness of a path of integral currents solving (GTE);
-
various Rademacher-type Differentiability Theorems, showing that a time-indexed family of boundaryless integral currents, satisfying suitable Lipschitz assumptions, is a solution to (GTE) for some driving vector field;
-
a new stability result, giving some sufficient conditions for the “equi-integrability” of space-time currents. We show under which assumptions a family of integral space-time currents satisfying the negligible criticality condition in a uniform sense is pre-compact (in the topology of currents) and the limit points also satisfy the criticality condition.
We conclude this short introduction with a few words on one of the pivotal notions of this work, namely space-time solutions to (GTE). This concept builds on the theory introduced in [19] and can be explained, in the case of integral currents, as follows: Let S be a \((k+1)\)-integral current in \([0,1] \times \mathbb {R}^d\). Denote by \(S\vert _t\) the slice of S at time t (with respect to the time projection \(\textbf{t}(t, x):= t\)) and by \(S(t):= \textbf{p}_*(S\vert _t)\) its pushforward under the spatial projection \(\textbf{p}(t,x):= x\). Standard theory gives that S(t) is an integral k-current in \(\mathbb {R}^d\) and that the orienting map \(\vec {S} \in L^\infty (\Vert S\Vert ; {\textstyle \bigwedge }_k(\mathbb {R}\times \mathbb {R}^d))\) (with \(|\vec {S}| = 1\) \(\Vert S\Vert \)-a.e.) decomposes orthogonally as
where \(\vec {S}\vert _t\) is the orienting map of the slice \(S\vert _t\) (see Fig. 1) and
Here, \(\nabla ^S\textbf{t}\) is approximate gradient of \(\textbf{t}\) with respect to S, i.e., the projection of \(\nabla \textbf{t}\) onto the approximate tangent space to (the rectifiable carrier of) S. We can now define the geometric derivative of S as the (normal) change of position per time of a point travelling on the current being transported, that is,
for \(\Vert S\Vert \)-a.e. (t, x). Clearly, this quantity exists only outside the critical set \(\textrm{Crit}(S):=\{(t,x)\in [0,1]\times \mathbb {R}^d:\nabla ^S \textbf{t}(t,x)=0\}\), which is in turn related to Sard’s theorem and play a major role in this work.
We then say that a space-time current S as above is a space-time solution of (GTE) if
One can see without too much effort that space-time solutions give rise to weak solutions: The projected slices \(S(t) := \textbf{p}_*(S\vert _t)\) of an integral \((k+1)\)-current S satisfying (1.1) solve (GTE). The converse question, that is, when a collection of currents \(\{T_t\}_t\) solving (GTE) can be realised as the slices of a space-time current is more challenging and will be one of the recurring themes of the paper.
2 Notation and Preliminaries
This section fixes our notation and recalls some basic facts. We refer the reader to [15, 18] for notation and the main results we use about differential forms and currents.
2.1 Linear and Multilinear Algebra
Let \(d \in \mathbb {N}\) be the ambient dimension. We will often use the projection maps \(\textbf{t}:\mathbb {R}\times \mathbb {R}^d\rightarrow \mathbb {R}\), \(\textbf{p}:\mathbb {R}\times \mathbb {R}^d\rightarrow \mathbb {R}^d\) from the (Euclidean) space-time \(\mathbb {R}\times \mathbb {R}^d\) onto the time and space variables, respectively, which are given as
We also define, for every given \(t\in \mathbb {R}\), the immersion map \(\iota _t:\mathbb {R}^d \rightarrow \mathbb {R}\times \mathbb {R}^d\) by
If V is a (finite-dimensional, real) vector space, for every \(k \in \mathbb {N}\), we let \({\textstyle \bigwedge }^k V\) be the space of k-covectors on V, and \({\textstyle \bigwedge }_k(V)\) be the space of k-vectors on V. We denote the duality pairing between \(v\in {\textstyle \bigwedge }_k V\) and \(\alpha \in {\textstyle \bigwedge }^k V\) by \(\bigl \langle v,\alpha \bigr \rangle \). Referring to [4, Section 5.8], given a k-vector v in V, we denote by \({{\,\textrm{span}\,}}(v)\) the smallest linear subspace W of V such that \(v \in {\textstyle \bigwedge }_k(W)\). A similar definition is given for a k-covector \(\alpha \) in V.
Whenever V is an inner product space, we can endow \({\textstyle \bigwedge }_k V\) with an inner product (Euclidean) norm \(|\cdot |\) by declaring \(\textrm{e}_I:=\textrm{e}_{i_1}\wedge \ldots \wedge \textrm{e}_{i_k}\), as I varies in the k-multi-indices of \(\{1,\ldots , n\}\), as orthonormal whenever \(\textrm{e}_1,\ldots ,\textrm{e}_n\) are an orthonormal basis of V. A simple k-vector \(\eta \in {\textstyle \bigwedge }_k V\) is called a unit if there exists an orthonormal family \(v_1,\ldots ,v_k\) such that \(\eta =v_1\wedge \ldots \wedge v_k\), or equivalently if its Euclidean norm \(|\eta |\) equals 1. We define the comass of \(\alpha \in {\textstyle \bigwedge }^kV\) as
and the mass of \(\eta \in {\textstyle \bigwedge }_kV\) as
Given a linear map \(S:V\rightarrow W\), we define \({\textstyle \bigwedge }^k S :{\textstyle \bigwedge }_k V\rightarrow {\textstyle \bigwedge }_k W\) by
on simple vectors and then we extend this definition by linearity to all of \({\textstyle \bigwedge }_k V\). If there is no risk of confusion, we will often write simply S instead of \({\textstyle \bigwedge }^{k}S\) to denote the extension of the map S to \({\textstyle \bigwedge }^k V\).
We denote by \(\mathscr {D}^k(\mathbb {R}^d)\) the space of smooth k-forms on \(\mathbb {R}^d\) with compact support. The integer k will also be called the degree of \(\omega \in \mathscr {D}^k(\mathbb {R}^d)\) and the comass of a form \(\omega \in \mathscr {D}^k(\mathbb {R}^d)\) is
The pullback of a covector \(\alpha \in {\textstyle \bigwedge }^kV\) with respect to a linear map \(S:V\rightarrow W\) is given by
on simple k-vectors and then extended by linearity. Therefore,
If \(f:\mathbb {R}^d \rightarrow \mathbb {R}^d\) is differentiable and proper (meaning that preimages of compact sets are themselves compact) and \(\omega \in \mathscr {D}^k(\mathbb {R}^d)\), we define the pullback \(f^*\omega \in \mathscr {D}^k(\mathbb {R}^d)\) to be the differential form \(f^*\omega \) given by
The properness of the pullback map f can be omitted if the pullback form \(f^* \omega \) is always integrated against a current of compact support. Here, we usually use \(\textbf{t}\) and \(\textbf{p}\) as pullback maps, which are not proper, but in all instances the compound expressions in which they appear are compactly supported and no issue of well-definedness arises.
2.2 Currents
We refer to [15] for a comprehensive treatment of the theory of currents, summarising here only the main notions that we will need. The space of k-dimensional currents \(\mathscr {D}_k(\mathbb {R}^d)\) is defined as the dual of \(\mathscr {D}^k(\mathbb {R}^d)\), where the latter space is endowed with the locally convex topology induced by local uniform convergence of all derivatives. Then, the notion of (sequential weak*) convergence is the following:
The boundary of a current is defined as the adjoint of De Rham’s differential: if T is a k-current, then \(\partial T\) is the \((k-1)\)-current given by
We denote by \(\textrm{M}_k(\mathbb {R}^d)\) the space of k-currents with finite mass in \(\mathbb {R}^d\), where the mass of a current \(T \in \mathscr {D}_k(\mathbb {R}^d)\) is defined as
Let \(\mu \) be a finite measure on \(\mathbb {R}^d\) and let \({\tau } :\mathbb {R}^d \rightarrow {\textstyle \bigwedge }_k(\mathbb {R}^d)\) be a map in \(\textrm{L}^1(\mu )\). Then we define the current \(T:={\tau }\mu \) as
We recall that all currents with finite mass can be represented as \(T= \tau \mu \) for a suitable pair \(\tau , \mu \) as above. In the case when \(\Vert \tau \Vert =1\) \(\mu \)-a.e., we denote \(\mu \) by \(\Vert T\Vert \) and we call it the mass measure of T. As a consequence, we can write \(T=\vec {T}\Vert T\Vert \), where \(\Vert \vec {T}\Vert =1\) \(\Vert T\Vert \)-almost everywhere. One can check that, if \(T=\tau \mu \) with \(\tau \in \textrm{L}^1(\mu )\), then \(\Vert T\Vert =\Vert \tau \Vert \mu \), hence
Given a current \(T=\tau \mu \in \mathscr {D}_k(\mathbb {R}^d)\) with finite mass and a vector field \(v:\mathbb {R}^d \rightarrow \mathbb {R}^d\) defined \(\Vert T\Vert \)-a.e., we define the wedge product
The pushforward of \(T\) with respect to a proper \(\textrm{C}^1\)-map \(f:\mathbb {R}^d \rightarrow \mathbb {R}^d\) is defined by
In the case of measures, we employ instead the standard notation \(f_{\#} \mu \) for the pushforward of \(\mu \) under a map f, namely, the measure defined by \(f_{\#}\mu (A)=\mu (f^{-1}(A))\).
If T is simple, i.e., \(\vec {T}\) is a simple k-vector \(\Vert T\Vert \)-almost everywhere, then the same inequality holds with the mass norm \(\Vert \cdot \Vert \) replaced by the Euclidean norm \(|\cdot |\).
Given two currents \(T_1\in \mathscr {D}_{k_1}(\mathbb {R}^{d_1})\) and \(T_2\in \mathscr {D}_{k_2}(\mathbb {R}^{d_2})\), their product \(T_1\times T_2\) is a well-defined current in \(\mathscr {D}_{k_1+k_2}(\mathbb {R}^{d_1}\times \mathbb {R}^{d_2})\).
A k-current on \(\mathbb {R}^d\) is said to be normal if both T and \(\partial T\) have finite mass. The space of normal k-currents is denoted by \(\mathrm N_k(\mathbb {R}^d)\). The weak* topology on the space of (normal) currents has good properties of compactness and lower semicontinuity: if \((T_j)_j\) is a sequence of currents with \(\textbf{M}(T_j) + \textbf{M}(\partial T_j) \le C < +\infty \) for every \(j \in \mathbb {N}\), then there exists a normal current T such that, up to a subsequence, \(T_j \overset{*}{\rightharpoonup }T\). Furthermore,
An integer-multiplicity rectifiable k-current T is a k-current of the form

where:
-
(1)
\(R \subset \mathbb {R}^d\) is countably \(\mathscr {H}^k\)-rectifiable (that is, it can be covered up to a \(\mathscr {H}^k\)-null set by countably many images of Lipschitz functions from \(\mathbb {R}^k\) to \(\mathbb {R}^d\)) with \(\mathscr {H}^k(R \cap K) < \infty \) for all compact sets \(K \subset \mathbb {R}^d\);
-
(2)
\(\vec {T} :R \rightarrow {\textstyle \bigwedge }_k \mathbb {R}^d\) is \(\mathscr {H}^k\)-measurable and for \(\mathscr {H}^k\)-a.e. \(x \in R\) the k-vector \(\vec {T}(x)\) is simple, unit (\(|\vec {T}(x)| = 1\)), and its span coincides with the approximate tangent space \(\textrm{Tan}_x R\) to R at x;
-
(3)
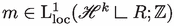 ;
;
The map \(\vec {T}\) is called the orientation map of T and m is the multiplicity. Let \(T = \vec {T} \Vert T\Vert \) be the Radon–Nikodým decomposition of T with the total variation measure  . Then we have
. Then we have
We then define the space of integral k-currents (\(k \in \mathbb {N}\cup \{0\}\)):
For \(F \subset \mathbb {R}^d\) closed, the subspaces \(\textrm{I}_k(F)\), \(\textrm{N}_k(F)\) are defined as the spaces of all \(T \in \textrm{I}_k(\mathbb {R}^d)\), or \(T \in \textrm{N}_k(\mathbb {R}^d)\), respectively, with support (in the sense of measures) in F. Since F is closed, these subspaces are weakly* closed.
An important property of integral currents is the Federer-Fleming compactness theorem [18, Theorems 7.5.2, 8.2.1]: Let \((T_j)_j \subset \mathrm I_k(\mathbb {R}^d)\) with
Then, there exists a (not relabeled) subsequence and a \(T \in \mathrm I_k(\mathbb {R}^d)\) such that \(T_j \overset{*}{\rightharpoonup }T\) in the sense of currents.
2.3 Flat Norms
For \(T \in \textrm{I}_k(\mathbb {R}^d)\), the (Whitney) flat norm is given by
and one can also consider the flat convergence \(\textbf{F}(T-T_j) \rightarrow 0\) as \(j \rightarrow \infty \). Under the mass bound \(\sup _{j\in \mathbb {N}} \, \big ( \textbf{M}(T_j) + \textbf{M}(\partial T_j) \big ) < \infty \), this flat convergence is equivalent to weak* convergence (see, for instance, [18, Theorem 8.2.1] for a proof). The flat norm admits also a dual representation (see [15, 4.1.12]) as
When \(\partial T=0\), one can also consider the homogeneous flat norm
which also admits a dual representation as
If T is integral, one can also consider the corresponding integral versions of (2.1) and (2.3), called integral flat norm and integral homogeneous flat norm respectively:
These, however, do not admit a dual representation as in (2.2) and (2.4). Notice that these are not proper norms because \(\textrm{I}_k(\mathbb {R}^d)\) is not a vector space. In the following, we will also consider the homogeneous flat norms \(\mathbb {F}, \mathbb {F}_{\textrm{I}}\) on the whole \(\textrm{N}_{k}(\mathbb {R}^d)\) or \(\textrm{I}_{k}(\mathbb {R}^d)\), in which case they are understood to be \(+\infty \) on currents that are not boundaryless.
2.4 Slicing and Coarea Formula for Integral Currents
Given a Lipschitz function \(f:\mathbb {R}^n\rightarrow \mathbb {R}\) and \(S\in \textrm{N}_{k+1}(\mathbb {R}^n)\), the slicing of S at level t is defined by the following, which will be referred to as the cylinder formula:

The slices with respect to f are also characterised by the following property:

see, e.g., [9] or also [15, 4.3.2]. For integral currents the following coarea formula holds [19, Section 2.4]: For every non-negative Borel function \(g :\mathbb {R}^n \rightarrow \mathbb {R}\) we have
where \(\nabla ^S f(z)\) denotes the tangential gradient of the map f on the approximate tangent space to S at z, that is, the projection of the vector \(\nabla f(z)\) onto the approximate tangent space to S at z (see [7, Theorem 2.90]). The equality (2.6) holds also whenever \(g \in \textrm{L}^1(|\nabla ^S f|\Vert S\Vert )\).
2.5 Disintegration of Measures
Given the product structure of the space-time \(\mathbb {R}\times \mathbb {R}^d\), we will often work with product measures or generalised product measures and we will consider the disintegration of measures on \(\mathbb {R}\times \mathbb {R}^d\) with respect to the map \(\textbf{t}\), for which we follow the approach of [3]. Let \(\{\mu _t\} = \{\mu _t: t \in \mathbb {R}\}\) be a family of finite (vector) measures on \(\mathbb {R}\times \mathbb {R}^d\). We say that such a family is Borel if
is Borel for every test function \(\phi \in \textrm{C}_c(\mathbb {R}\times \mathbb {R}^d)\). Given a measure \(\nu \) on \(\mathbb {R}\) and a family \(\{\rho _t: t \in \mathbb {R}\}\) of measures on \(\mathbb {R}^d\) such that
we define the generalised product \(\nu \otimes \rho _t\) as the measure on \(\mathbb {R}\times \mathbb {R}^d\) such that
for every \(\phi \in \textrm{C}_c(\mathbb {R}^d)\).
Let now \(\mu \) be a (possibly vector-valued) measure in \(\mathbb {R}\times \mathbb {R}^d\) and let \(\nu \) be a measure on \(\mathbb {R}\) such that \(\textbf{t}_{\#}\mu \ll \nu \). Then, there exists a Borel family \(\{\mu _t: t \in \mathbb {R}\}\) of (possibly vector-valued) measures on \(\mathbb {R}\times \mathbb {R}^d\) such that:
-
(i)
\(\mu _t\) is supported on \(\{t\} \times \mathbb {R}^d\) for \(\nu \)-a.e. \(t \in \mathbb {R}\);
-
(ii)
\(\mu \) can be decomposed as
$$\begin{aligned} \mu = \int _\mathbb {R}\mu _t \; \textrm{d}\nu (t), \end{aligned}$$which means
$$\begin{aligned} \mu (A) = \int _\mathbb {R}\mu _t(A) \; \textrm{d}\nu (t), \end{aligned}$$(2.7)for every Borel set \(A \subset \mathbb {R}\times \mathbb {R}^d\).
Any family \(\{\mu _t\}\) satisfying the conditions (i) and (ii) above will be called a disintegration of \(\mu \) with respect to \(\textbf{t}\) and \(\nu \). We remark that, from (2.7) we obtain
for every Borel function \(\phi :\mathbb {R}\times \mathbb {R}^d \rightarrow [0,+\infty ]\).
2.6 Decomposability Bundle
We recall from [4] the definition and a few basic facts about the decomposability bundle of a measure.
Given a measure \(\mu \) on \(\mathbb {R}^n\), the decomposability bundle is a \(\mu \)-measurable map \(x\mapsto V(\mu ,x)\) (defined up to \(\mu \)-negligible sets) which associates to \(\mu \)-a.e. x a subspace \(V(\mu ,x)\) of \(\mathbb {R}^n\). The map V satisfies the following property: Every Lipschitz function \(f :\mathbb {R}^n\rightarrow \mathbb {R}\) is differentiable at x along the subspace \(V(\mu ,x)\), for \(\mu \)-a.e. \(x\in \mathbb {R}^n\). Moreover, this map is \(\mu \)-maximal in a suitable sense, meaning that \(V(\mu ,x)\) is, for \(\mu \)-a.e. x, the biggest subspace with this property (see [4, Theorem 1.1]). The directional derivative of f at x in direction \(v \in V(\mu ,x)\) will be denoted by Df(x)[v]. Observe that this is a slight abuse of notation, as the full differential Df might not exist at x, even though the directional derivative exists.
A key fact about the decomposability bundle with regard to the theory of normal currents is the following [4, Theorem 5.10]: Given a normal k-current \(T=\vec {T}\Vert T\Vert \) in \(\mathbb {R}^n\), it holds that
In particular, given any Lipschitz function f, we can define \(D_T f\) at \(\Vert T\Vert \)-a.e. point as the restriction of the differential of f to \({{\,\textrm{span}\,}}(\vec T)\). We will usually just write Df instead of \(D_T f\) when this differential is evaluated in a direction in \({{\,\textrm{span}\,}}(\vec T)\).
For a normal current \(T\in \textrm{N}_k(\mathbb {R}^d)\), it is possible to define the pushforward \(f_*T\) when \(f:\mathbb {R}^d\rightarrow \mathbb {R}^d\) is merely Lipschitz [15, 4.1.14]. Classically, no explicit formula for this pushforward was available. However, it is shown in [4, Proposition 5.17] that the pushforward formula, in fact, remains true:
Lemma 2.1
Suppose that \(T=\tau \mu \) is a normal k-current in \(\mathbb {R}^n\), and \(f :\mathbb {R}^n\rightarrow \mathbb {R}^m\) is a proper, injective Lipschitz map. Then, the pushforward current \(f_*T\) satisfies
where \(\tilde{\mu }=f_\#\mu \), and \(\tilde{\tau }(y)=Df(x) [\tau (x)] = D_T f(x) [\tau (x)]\) with \(y=f(x)\).
3 Space-Time Currents: Variations and Disintegration
3.1 Notions of Variation and AC Integral Currents
Given a (locally compact) metric space \((X,\mathsf d)\) and a curve \(t \mapsto \gamma (t) \in X\), \(t \in [a,b]\) (\(a < b\)), we define the pointwise variation of \(\gamma \) as
We further define the essential variation of the curve \(\gamma \) as
We extend the same definition to curves \(\gamma \) which are only defined for \(\mathscr {L}^1\)-a.e. \(t \in [a,b]\). In this case, the supremum in (3.1) is taken over families of partitions such that \(\gamma \) is defined at \(t_i\) for every i. By [5, Remark 2.2], the infimum in the definition of essential variation is achieved and therefore, if \({\mathsf d}\text {-}\textrm{eV}(\gamma :[a,b]) < \infty \), then there exist two good representatives, the right-continuous representative \(\gamma _+\) and the left-continuous representative \(\gamma _-\) such that
If \({\mathsf d}\text {-}\textrm{eV}(\gamma ;[a,b])<\infty \), then \({\mathsf d}\text {-}\textrm{eV}(\gamma ; \varvec{\cdot })\) can be extended to a finite measure on the Borel subsets of [a, b].
In this vein, for for \(S\in \textrm{I}_{k+1}([0,1] \times \mathbb {R}^d)\) and \(U\in \textrm{N}_{k+1}([0,1] \times \mathbb {R}^d)\) with  we set, with a little abuse of notation,
we set, with a little abuse of notation,

for every closed interval \([a,b] \subset [0,1]\). Recall that we denote by \(S(t):=\textbf{p}_{*}(S|_t)\) the pushforward of the slice \(S|_t\) onto \(\mathbb {R}^d\). Likewise we define the slices \(U|_t\) and the pushforwards \(U(t):=\textbf{p}_{*}(U|_t)\) for \(\mathscr {L}^1\)-a.e. t.
On the other hand, in the work [19] the author introduced the (space-time) variation of an integral space-time current. Given a current S of finite mass, i.e., \(S \in \textrm{M}_{k+1}([0,1] \times \mathbb {R}^d)\), we define the (space-time) variation of S on the interval [a, b] to be
Here and in the following, we will often write \(\textbf{p}(\vec {S})\) instead of \({\textstyle \bigwedge }^{k+1} \textbf{p}(\vec {S})\) for ease of notation. We remark that, if S is integral, then \(\vec {S}\) is simple and so is \(\textbf{p}(\vec {S})\). Therefore, in this case, \( \Vert \textbf{p}(\vec {S})\Vert = |\textbf{p}(\vec {S})|\). One can further see that \({\textrm{Var}}(S; \varvec{\cdot })\) can be extended to all Borel sets (by the very same formula) to define a non-negative finite measure on \(\mathbb {R}\), which will still be denoted by \({\textrm{Var}}(S;\varvec{\cdot })\).
One might wonder which relation exists between these various notions of variation. It is fairly easy to see that the space-time variation bounds from above the pointwise variation; in general, however, the opposite inequality may not hold, due to the possible presence of jumps in the path \(t\mapsto S|_t\). Indeed, whenever a jump occurs at a certain time \(t_0\), \({\textrm{Var}}(S;\varvec{\cdot })\) depends on the particular current that connects \(S|_{t_0^-}\) and \(S|_{t_0^+}\), while \(\mathbb {F}_{\textrm{I}}\text {-}\textrm{eV}\) always measures the optimal connection. The next theorem entails that jumps are in fact the only obstructions to the equality between \({\textrm{Var}}\) and  .
.
Theorem 3.1
(Equality of variations) Let \(S\in \textrm{I}_{k+1}([0,1] \times \mathbb {R}^d)\) with  and such that \({\textrm{Var}}(S;\varvec{\cdot })\) is non-atomic. Then,
and such that \({\textrm{Var}}(S;\varvec{\cdot })\) is non-atomic. Then,

Theorem 3.1 plays a central place in this work and can be seen as a generalisation to any codimension of the following formula, valid for a function \(u :[0,1] \rightarrow \mathbb {R}\) that is continuous and of bounded variation:
where  and \(\tau \) is the forward-pointing unit tangent to \(\text {graph}(u)\).
and \(\tau \) is the forward-pointing unit tangent to \(\text {graph}(u)\).
We do not discuss here the proof of Theorem 3.1 and we refer the reader to [10, Theorem 5.3]. We simply remark that it is obtained as a consequence of the following space-time rectifiability result:
Theorem 3.2
(Rectifiability) Let \(t \mapsto T_t \in \textrm{I}_k(\mathbb {R}^d)\), \(t \in [0,1]\), with \(\partial T_t = 0\) for every \(t \in [0,1]\), and such that

Then, there exists \(S \in \textrm{I}_{k+1}(\mathbb {R}\times \mathbb {R}^d)\) with  such that:
such that:
-
(a)
\(S(t) = \textbf{p}_*(S\vert _t) = T_t\) for \(\mathscr {L}^1\)-a.e. \(t \in [0,1]\);
-
(b)
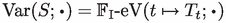 as measures on [0, 1].
as measures on [0, 1].
Theorem 3.2 is indeed a space-time rectifiability result for general integral currents: Under a \({{\,\textrm{BV}\,}}\) bound in time, we can “glue” the currents of a path \(t \mapsto T_t\) in a space-time integral current, whose space-time variation coincides with the pointwise one of the path. These gluing procedures play an important role in our analysis and we will be exploited several times throughout this work.
Remark 3.3
It is possible to show that, if we further assume that the variation is non-atomic, i.e. there are no jumps in the path \(t \mapsto T_t\), then the current S in Theorem 3.2 is unique. See, for more details, Corollary [10, Corollary 6.5].
We conclude this section introducing the class of absolutely continuous (\({{\,\textrm{AC}\,}}\)) integral space-time currents:

3.2 Disintegration of Space-Time Integral Currents
We now turn our attention to the disintegration structure of space-time integral currents. Let \(S \in \textrm{I}_{k+1}([0,1] \times \mathbb {R}^d)\) and let \(\Vert S\Vert \) denote its mass measure. We define the critical set of S as
Here, \(\nabla ^S\textbf{t}\) is approximate gradient of \(\textbf{t}\) with respect to S, i.e., the projection of \(\nabla \textbf{t}\) onto the approximate tangent space to the \(\mathscr {H}^{k+1}\)-rectifiable carrier of S.
Theorem 3.4
(Disintegration structure) Let \(S \in \textrm{I}_{k+1}([0,1] \times \mathbb {R}^d)\) and let \(\{\mu _t\}\) the disintegration of \(\Vert S\Vert \) with respect to the map \(\textbf{t}\) and the measure
where \((\textbf{t}_{\#}\Vert S\Vert )^s\) denotes the singular part (with respect to \(\mathscr {L}^1\)) of \(\textbf{t}_{\#}\Vert S\Vert \), i.e.
Then the following statements hold:
-
(i)
For \(\lambda ^s\)-a.e. \(t \in \mathbb {R}\) the measure \(\mu _t\) is concentrated on \(\textrm{Crit}(S)\).
-
(ii)
For \(\mathscr {L}^1\)-a.e. \(t \in \mathbb {R}\) the measure \(\mu _t\) can be decomposed as
$$\begin{aligned} \mu _t =|\nabla ^S\textbf{t}|^{-1} \Vert S\vert _t \Vert + \mu ^s_t, \end{aligned}$$where \(\mu ^s_t\) is a measure which is concentrated on \(\textrm{Crit}(S)\) and is singular with respect to \(|\nabla ^S\textbf{t}|^{-1} \Vert S\vert _t\Vert \) and also with respect to \(\mathscr {H}^k\).
The disintegration of the mass measure \(\Vert S \Vert \) with respect to the map \(\textbf{t}\) can therefore be written as
Observe that, by the Besicovitch differentiation theorem (see, e.g., [7, Thm. 2.22]), \(\mu _t^s\) can be identified (for \(\mathscr {L}^1\)-a.e. t) with the restriction of \(\mu _t\) to the set
This conveys the idea that \(\mu _t^s\) is more concentrated than \(\mathscr {H}^k\).
We remark that, in general, all terms in the disintegration (3.3) can be non-zero.
The measure \(\lambda ^s\) takes into account singular-in-time behaviour and one can surmise it vanishes if S is (absolutely) continuous in time. The next proposition confirms this intuition and contains a characterisation of \({{\,\textrm{AC}\,}}\) space-time current via time projections.
Proposition 3.5
Let \(S \in \textrm{I}_{k+1}([0,1] \times \mathbb {R}^d)\) with  . Then, \(S \in \textrm{I}^{{{\,\textrm{AC}\,}}}_{1+k}([0,1] \times \mathbb {R}^d)\) if and only if \(\lambda ^s = 0\), i.e.,
. Then, \(S \in \textrm{I}^{{{\,\textrm{AC}\,}}}_{1+k}([0,1] \times \mathbb {R}^d)\) if and only if \(\lambda ^s = 0\), i.e.,

On the other hand, the measures \(\mu _t^s\) in (3.3) account for a completely different type of singularity, measuring a sort of diffuse concentration that is “smeared out in time”. These aspects will be further investigated in the next section.
3.3 Negligible Criticality Condition and Sard-type Property
The considerations at the end of the previous section inspire the following definitions, which turn out to be central:
Definition 3.6
A space-time current \(S \in \textrm{I}_{1+k}([0,1] \times \mathbb {R}^d)\) is said to satisfy the negligible-criticality condition (with respect to the map \(\textbf{t}\)) if

where \(\textrm{Crit}(S)\) is the critical set of S defined in (3.2).
The condition (NC) means that for \(\Vert S\Vert \)-a.e. (t, x), \(\textrm{span}\,(\vec {S}(t,x))\not \subseteq \{0\}\times \mathbb {R}^d\) (i.e., the approximate tangent space to S has almost always a non-trivial time component).
We also consider the following (in general weaker) condition:
Definition 3.7
A current \(S \in \textrm{I}_{1+k}([0,1] \times \mathbb {R}^d)\) is said to have the Sard property (with respect to the map \(\textbf{t}\)) if
where \(\mu ^s_t\) is as in Theorem 3.4.
The following lemma clarifies the relationship between (NC) and the Sard property.
Lemma 3.8
Let \(S \in \textrm{I}_{1+k}([0,1] \times \mathbb {R}^d)\). Then, the following statements are equivalent:
-
(i)
S has the Sard property, i.e., \(\mu ^s_t = 0\) for \(\mathscr {L}^1\)-a.e. \(t \in \mathbb {R}\);
-
(ii)
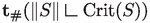 is singular with respect to \(\mathscr {L}^1\).
is singular with respect to \(\mathscr {L}^1\).
Furthermore, (NC) implies both of them.
Notice that this is indeed a Sard-type property: if \(f:\mathbb {R}^d\rightarrow \mathbb {R}\) is a \(\textrm{C}^1\) function and \(\Gamma {:=}\{(f(x),x): x \in \mathbb {R}^d\}\subset \mathbb {R}\times \mathbb {R}^d\) denotes its graph, then f has the classical Sard property (namely, \(\mathscr {L}^1(f(\{x:\nabla f(x)=0\}))=0\)) if and only if the natural integral d-current associated to \(\Gamma \) has the Sard property in the sense of Definition 3.7.
The following structure result offers some equivalent conditions to the negligible criticality property for \({{\,\textrm{AC}\,}}\) currents.
Proposition 3.9
Let \(S \in \textrm{I}^{{{\,\textrm{AC}\,}}}_{1+k}([0,1] \times \mathbb {R}^d)\). Then, the following are equivalent:
-
(i)
S has the (NC) property, i.e.,
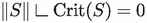 ;
; -
(ii)
it holds that
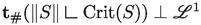 ;
; -
(iii)
S has the Sard property, i.e., \(\mu ^s_t = 0\) for \(\mathscr {L}^1\)-a.e. \(t \in \mathbb {R}\);
-
(iv)
\(\Vert S \Vert \ll \int _0^1 \Vert S\vert _t \Vert \; \textrm{d}t\), that is, for every Borel set \(A \subset [0,1] \times \mathbb {R}^d\)
$$\begin{aligned} \int _0^1 \Vert S\vert _t \Vert (A) \; \textrm{d}t = 0 \implies \Vert S\Vert (A) = 0. \end{aligned}$$
Furthermore, if any of the above conditions holds, then the disintegration of the mass measure \(\Vert S\Vert \) with respect to \(\textbf{t}\) and \(\mathscr {L}^1\) has the form
Observe that if \(k=0\), the Sard property is always satisfied, that is, for every \(S \in \textrm{I}_{1}(\mathbb {R}\times \mathbb {R}^d)\) it holds that  , since by the area formula \(\mathscr {H}^{1}(\textbf{t}(C)) = 0\). So, the effects related to the criticality are not present in all of the classical theory of BV- or AC-maps (which can be recovered as the \(k = 0\) endpoint of our theory).
, since by the area formula \(\mathscr {H}^{1}(\textbf{t}(C)) = 0\). So, the effects related to the criticality are not present in all of the classical theory of BV- or AC-maps (which can be recovered as the \(k = 0\) endpoint of our theory).
For \(k > 1\), instead, the Sard property is not always satisfied and it is possible to construct \({{\,\textrm{AC}\,}}\) (even Lipschitz) integral currents that do not have the Sard property. We refer the reader to [10, Section 9] for the details of the construction of such an example—see Fig. 2 for a visual depiction of some steps of the construction.
We conclude this section by observing that it is not clear how to extend the theory developed within these paragraphs to normal space-time currents. This extension, beside having a purely mathematical interest, would be extremely important in connection with applications, too. Indeed, the “diffuse” setting of normal currents is the natural one to consider, allowing one to deal with fields of singular objects, as it is often required in Materials Science.
4 Geometric Derivative and Advection Theorem
In this section, we show one of the main results, more precisely what we call the advection theorem. This result entails that for space-time currents satisfying the negligible criticality condition (NC), there exists an advecting vector field – namely their slices satisfy the transport equation (GTE). Furthermore, also the converse holds. These results should be compared with e.g. [8, Theorem 8.3.1], where a similar advection theorem is established within the class of probability measures.
Recall that, if \(S\in \textrm{I}^{{{\,\textrm{AC}\,}}}_{k+1}([0,1] \times \mathbb {R}^d)\) then, by Proposition 3.9, the condition (NC) is equivalent to S having the Sard property or also to
We define the geometric derivative of such an S as
where \(\xi = |\nabla ^S \textbf{t}|^{-1}\nabla ^S \textbf{t}\) on \(\textrm{Crit}(S)^c\). Observe that \({\varvec{b}}\) is well-defined \((\int _0^1 \Vert S\vert _t \Vert \; \textrm{d}t)\)-almost everywhere and under (NC), both \(\xi \) and \({\varvec{b}}\) are well-defined also \(\Vert S\Vert \)-almost everywhere.
The main result reads as follows:
Theorem 4.1
(Advection) Let \(S\in \textrm{I}^{{{\,\textrm{AC}\,}}}_{k+1}([0,1] \times \mathbb {R}^d)\) with  satisfy (NC). Then, the geometric derivative \({\varvec{b}}:= \frac{\textrm{D}}{\textrm{D}t} S\) defined in (4.1) belongs to \(\textrm{L}^1( \int _0^1 \Vert S\vert _t \Vert \; \textrm{d}t)\) and it holds that
satisfy (NC). Then, the geometric derivative \({\varvec{b}}:= \frac{\textrm{D}}{\textrm{D}t} S\) defined in (4.1) belongs to \(\textrm{L}^1( \int _0^1 \Vert S\vert _t \Vert \; \textrm{d}t)\) and it holds that
Conversely, if there exists a vector field \({\varvec{b}}\in \textrm{L}^1( \int _0^1 \Vert S\vert _t \Vert \; \textrm{d}t)\) such that (4.2) holds, then S satisfies (NC).
Proof
We here sketch only the proof of the sufficiency part, referring the interested reader to the original paper [10] for the complete proof (notice that the proof of the necessity part requires a suitable gluing techique that will be discussed later in this work). Suppose we are given \(S\in \textrm{I}^{{{\,\textrm{AC}\,}}}_{k+1}([0,1] \times \mathbb {R}^d)\) with  satisfying (NC). We therefore have the disintegration
satisfying (NC). We therefore have the disintegration

In particular, since S has (NC), then  and therefore
and therefore
It will be convenient to write this conclusion in the following form:
We now want to prove that for every \(\psi \in \textrm{C}^\infty _c((0,1))\) and for every \(\omega \in \mathscr {D}^k(\mathbb {R}^d)\) it holds that
Notice that
where in the second-to-last equality we used (4.3). Using also the commutativity between boundary and pushforward, we have thus shown
Observe now that for any k-current \(T\), for any \(f \in \textrm{C}_c^\infty (\mathbb {R})\), and any \(\omega \in \mathscr {D}^k(\mathbb {R}^d)\), the Leibniz rule holds in the form

Using this in (4.5) and also taking into account that \(d(\psi \circ \textbf{t})=(\psi '\circ \textbf{t})dt\) as well as (2.5),

Since \(\psi \in \textrm{C}^\infty _c((0,1))\) and  , the term \((\psi \circ \textbf{t})\partial S\) vanishes. Recalling that, by definition, \(S(t)=\textbf{p}_*(S|_t)\), we finally obtain (4.4). \(\square \)
, the term \((\psi \circ \textbf{t})\partial S\) vanishes. Recalling that, by definition, \(S(t)=\textbf{p}_*(S|_t)\), we finally obtain (4.4). \(\square \)
5 Well-Posedness for Lipschitz Velocity Fields
Relying on the space-time approach, we now present a well-posedness result for (GTE). We show that a Lipschitz condition on the vector field \({\varvec{b}}\) is sufficient to ensure existence and uniqueness of solutions to the initial-value problem for the geometric transport equation.
Theorem 5.1
Let \(b:\mathbb {R}^d \rightarrow \mathbb {R}^d\) be a globally bounded and Lipschitz vector field with flow \(\Phi _t = \Phi (t,\varvec{\cdot }) :\mathbb {R}^d \rightarrow \mathbb {R}^d\) and let \(\overline{T} \in \textrm{N}_k(\mathbb {R}^d)\) be a k-dimensional normal current on \(\mathbb {R}^d\). Then, the initial-value problem
admits a solution \((T_t)_{t \in (0,1)} \subset \textrm{N}_k(\mathbb {R}^d)\) of normal k-currents, which is unique in the class of normal k-currents. The solution is given by the pushforward of the initial current under the flow, namely, \(T_t=(\Phi _t)_*\overline{T}\). In particular, if \(\overline{T}\) is integral, then so is \(T_t\), \(t \in (0,1)\).
Notice that, at a technical level, it is not immediately clear why Theorem 5.1 should hold true. We know that solutions to (GTE) can be understood as the transport of the currents \(T_t\) along the flow lines of \({\varvec{b}}\). However, since the flow of \({\varvec{b}}\) is merely Lipschitz, it may well occur that it is not (fully) differentiable anywhere on the support of the transported currents, therefore questioning the possibility of performing pointwise computations.
In order to overcome these difficulties we combine the space-time approach developed in the sections above with a relatively recent tool from Geometric Measure Theory, namely the notion of decomposability bundle, introduced by Alberti and Marchese [4]. This tool ensures that, while full differentiability of the flow \(\Phi _t\) on the support of \(\overline{T}\) may fail, the derivative of \(\Phi _t\) still exists in a sufficiently good sense to define the pushforward \((\Phi _t)_*\overline{T}\) pointwise (and not via the homotopy formula) – see Lemma 2.1.
Additionally, we remark that the existence part of Theorem 5.1 can be proved by means of a simple approximation argument that does not necessitate the decomposability bundle (but assumes the existence of solutions when the drift is smooth). In this section we will therefore focus on the uniqueness part.
5.1 The Case \(k=0\): Uniqueness for the Continuity Equation
We present first a simple proof of uniqueness for the transport of 0-currents, i.e., signed measures advected via the continuity equation. Our proof differs from the classical one that can be found, e.g., in [8, Proposition 8.3.1] – see also [6, 12, 14].
In the case of 0-currents the geometric transport equation (GTE) reduces to the continuity equation
where \((\mu _t)_{t \in (0,1)}\), is a family of signed measures. We understand this equation in the usual distributional sense, i.e.
for all \(\psi \in \textrm{C}^1_c((0,1) \times \mathbb {R}^d)\).
We illustrate our proof idea by showing uniqueness under the additional regularity assumption that \({\varvec{b}}\) is of class \(\textrm{C}^1\). The key is to show directly that the solution is necessarily given by
or, equivalently, that given a solution \((\mu _t)_{t \in (0,1)}\), the map \(t\mapsto (\Phi _{-t})_\#\mu _t\) is constant. It is therefore natural to test the weak formulation (5.2) with a function of the form \(\psi (t,x)=\alpha (t)\beta (\Phi _{-t}(x))\). The field is \(\textrm{C}^1\), and so is its flow \(\Phi \), thus one can differentiate \(\psi \) classically. On the one hand we have that
where we used the defining property of \(\Phi \). On the other hand, by an elementary computation on the directional derivative of the flow (see [11, Lemma 2.3]) we have
Plugging the two terms in the weak formulation gives that
for all \(\alpha \in \textrm{C}^1((0,1))\) and all \(\beta \in \textrm{C}^1(\mathbb {R}^d)\). From this we deduce that \(t\mapsto (\Phi _{-t})_\#\mu _t\) is constant, as required.
5.2 The Lipschitz Case
We now consider the case when \({\varvec{b}}\) is Lipschitz. Notice that, setting \(\mu := \mathscr {L}^1(\textrm{d}t) \otimes \mu _t(\textrm{d}x)\), two equivalent ways of formulating the PDE are the following:
for all \(\psi \in \textrm{C}_c^1((0,1) \times \mathbb {R}^d)\), where \(\tilde{\nabla }\psi (t,x):=(\partial _t \psi (t,x),\nabla \psi (t,x))\). Equivalently,
for all \(\psi \in \textrm{C}_c^1((0,1) \times \mathbb {R}^d)\).
Having introduced this notation, we can present the following key result.
Lemma 5.2
In the setting above, \((1,{\varvec{b}}(x)) \in V(\mu ,(t,x))\) for \(\mu \)-a.e. (t, x). In particular, every Lipschitz function \(\psi :(0,1)\times \mathbb {R}^d\rightarrow \mathbb {R}\) is differentiable in direction \((1,{\varvec{b}}(x))\) for \(\mu \)-a.e. \((t,x)\in (0,1)\times \mathbb {R}^d\).
Proof
Let U be the 1-current in \((0,1)\times \mathbb {R}^d\) defined by \(U:=(1,{\varvec{b}}(x)) \mu \). Then (5.3) can be understood as
hence U is a normal 1-current without boundary in \((0,1)\times \mathbb {R}^d\). Thus, the assertion follows by (2.8). \(\square \)
One can easily show, as a consequence of Lemma 5.2, that one can use any Lipschitz test function in the distributional formulation of the continuity equation (5.1). This crucial ingredient allows us to get the desired uniqueness, as we are about to show.
Proof of the uniqueness statement of Theorem 5.1 in the case \(k=0\)
We choose as test function \(\psi (t,x) := \alpha (t) \beta (\Phi _{-t}(x))\), where \(\alpha \in \textrm{C}^1_c((0,1))\) and \(\beta \in \textrm{C}^1_c(\mathbb {R}^d)\). Recalling that \(\Phi _{-t}\) is Lipschitz, also \(\psi \) is a Lipschitz function and therefore, by Lemma 5.2,
At this point, one can easily compute (at every point) the integrand, showing that
Then, plugging (5.5) into (5.4), we have
This holds for every \(\alpha \in \textrm{C}^1_c((0,1))\), hence we obtain that the map \(t \mapsto \bigl \langle (\Phi _t)^{-1}_{\#}\mu _t, \beta \bigr \rangle \) is constant for every \(\beta \). Recalling the weak\(^*\) continuity of \(t\mapsto \mu _t\) it follows that
and since \(\beta \) is arbitrary we have \((\Phi _t)^{-1}_{\#}\mu _t = \mu _0\) as measures, i.e. \(\mu _t = (\Phi _t)_{\#} \mu _0\). \(\square \)
5.3 The Case \(k>0\): Gluing of Transported Currents
The strategy presented above for the continuity equation essentially carries over to the case \(k>0\) and can be adapted with minor modifications. We single out here a single technical difficulty: we need to find a replacement for Lemma 5.2 or, more precisely, for the space-time 1-current U, defined directly as \(U=(1,{\varvec{b}})\mu \) in the proof of Lemma 5.2. In order to do this, we need to resort once again to gluing techniques. The following proposition constitutes another approach (beside the one presented in Theorem 3.2) to turn a path of integral currents into a space-time current. It applies when we know a priori that our path of integral currents satisfies the geometric transport equation.
Lemma 5.3
Let \((T_t)_{t \in (0,1)} \subset \textrm{N}_k(\mathbb {R}^d)\) with \(\partial T_t=0\) be a weakly\(^*\)-continuous solution to (GTE). Write \(T_t=\vec {T}_t\Vert T_t\Vert \), with \(\vec {T}_t\) unit k-vectors and let \(\vec {T}:(0,1)\times \mathbb {R}^d\rightarrow {\textstyle \bigwedge }_k(\mathbb {R}\times \mathbb {R}^d)\) be the k-vector field defined \(\mathscr {L}^1_t \otimes \Vert T_t\Vert \)-almost everywhere by
where we recall that \(\iota _t(x):=(t,x)\). Define the current
Then U is a normal \((k+1)\)-current in \((0,1)\times \mathbb {R}^d\), and  .
.
The fact that U is normal allows one to use the Alberti-Marchese’s theory, and in particular we immediately obtain the following result:
Corollary 5.4
Define the measure \(\mu :=\mathscr {L}^1(\textrm{d}t) \otimes \Vert T_t\Vert \) in \(\mathbb {R}\times \mathbb {R}^d\). Then, we have \({{\,\textrm{span}\,}}((1,{\varvec{b}})\wedge \vec {T_t}(x))\subset V(\mu ,(t,x))\) for \(\mu \)-a.e. (t, x) in \((0,1)\times \mathbb {R}^d\).
We refer the reader to [11] for the complete proof.
6 Rademacher-type Differentiability Result
We collect in this section two Rademacher-type differentiability theorems for paths of currents. Given a path \(t\mapsto T_t\in \textrm{I}_k(\mathbb {R}^d)\), \(\partial T_t=0\), which is absolutely continuous in time with respect to the homogeneous integral flat norm \(\mathbb {F}_\textrm{I}\), we ask when we can find a vector field \({\varvec{b}}_t :\mathbb {R}^d\rightarrow \mathbb {R}^d\) that solves the geometric transport equation. The existence of such a vector field implies that the path \(t \mapsto T_t\) is differentiable in a geometric sense, hence the designation “Rademacher”.
Theorem 6.1
(Weak differentiability) Let \(t \mapsto T_t \in \textrm{I}_k(\mathbb {R}^d)\), \(t \in [0,1]\), with \(\partial T_t=0\) for every \(t \in [0,1]\), be a path that is absolutely continuous with respect to the homogeneous integral flat norm \(\mathbb {F}\) (which is implied by \(\mathbb {F}_\textrm{I}\)-absolute continuity), that is,
for some \(g\in \textrm{L}^1([0,1])\) and all \(s < t\). Then, there exists a finite-mass \((k+1)\)-current \(R_t\in \textrm{M}_{k+1}(\mathbb {R}^d)\) that solves the equation
We next ask when the currents \(R_t\) are actually of the form \(-{\varvec{b}}_t\wedge T_t\) for some vector field \({\varvec{b}}_t\), so that we can solve the geometric transport equation in the original formulation (GTE). This question is more subtle, and after the previous sections it is perhaps not surprising that a positive answer is strictly related to the property (NC) or, equivalently, the Sard property (S).
Theorem 6.2
(Strong differentiability) Let \(t \mapsto T_t \in \textrm{I}_k(\mathbb {R}^d)\), \(t \in [0,1]\), be a path that is absolutely continuous with respect to the homogeneous integral flat norm \(\mathbb {F}_\textrm{I}\) and such that
Let S be the unique current given by Theorem 3.2 (and Remark 3.3) in this setting. If S satisfies (NC), then there exists \({\varvec{b}}\in \textrm{L}^1(\mathscr {L}^1 \otimes \Vert T_t\Vert )\) such that (GTE) holds, that is,
In some special cases – namely when \(k\in \{0,d-2,d-1,d\}\) – it is known that \(\mathbb {F}_{\textrm{I}}\) coincides with \(\mathbb {F}\), and thus all the results can be stated using the latter norm.
Corollary 6.3
Let \(k \in \{0,d-2,d-1,d\}\) and let \(t \mapsto T_t \in \textrm{I}_k(\mathbb {R}^d)\), \(t \in [0,1]\), be a path that is absolutely continuous with respect to the homogeneous (non-integral) flat norm \(\mathbb {F}\) and such that
Let S be the unique current given by Theorem 3.2 (and Remark 3.3) in this setting. If S satisfies (NC), then there exists \({\varvec{b}}\in \textrm{L}^1(\mathscr {L}^1 \otimes \Vert T_t\Vert )\) such that (GTE) holds.
For general k it is not known whether, for \(T\in \textrm{I}_k(\mathbb {R}^d)\), the definitions of homogeneous flat norm and homogeneous integral flat norm give rise to equivalent norms.
7 Stability of \({{\,\textrm{AC}\,}}\) Integral Currents with (NC)
In this final section, we study the stability properties of absolutely continuous space-time integral currents and of the condition (NC).
Proposition 7.1
Let \((t \mapsto T^\varepsilon _t)_{\varepsilon >0} \subset {{\,\textrm{AC}\,}}((0,1); \textrm{I}_k(\mathbb {R}^d))\) be a family of curves of currents with \(\partial T^\varepsilon _t = 0\) for every \(\varepsilon >0\) and \(t \in (0,1)\). Assume that
For each \(\varepsilon >0\), denote by \(S^\varepsilon \in \textrm{I}_{1+k}^{{{\,\textrm{AC}\,}}}(\mathbb {R}\times \mathbb {R}^d)\) the (unique) current given by Theorem 3.2 (and Remark 3.3) in this setting. Then the following statements are true:
-
(i)
If \(\sup _{\varepsilon >0} \mathbb {F}\text {-}\textrm{pV}(t \mapsto T_t^\varepsilon ; \mathbb {R}) < \infty \) or, equivalently, \(\sup _{\varepsilon >0} {\textrm{Var}}(S^\varepsilon ; \mathbb {R}) < \infty \), then there exists \(S \in \textrm{I}_{1+k}(\mathbb {R}\times \mathbb {R}^d)\) such that \(S^\varepsilon \overset{*}{\rightharpoonup }S\) up to a (non-relabelled) subsequence, in the sense of \((1+k)\)-currents on \(\mathbb {R}\times \mathbb {R}^d\).
-
(ii)
Assume the currents \(S^\varepsilon \) satisfy the uniform negligible criticality condition, i.e. there exist vector fields \({\varvec{b}}_t^\varepsilon \in \textrm{L}^1(\mathscr {L}^1 \otimes \Vert T^\varepsilon _t\Vert )\) such that
$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t} T^\varepsilon _t + \mathcal {L}_{{\varvec{b}}_t^\varepsilon } T_t^e = 0, \end{aligned}$$and such that the maps \(B^\varepsilon :(0,1) \rightarrow \mathbb {R}\) defined by
$$\begin{aligned} t \mapsto \int _{\mathbb {R}^d} |{\varvec{b}}^\varepsilon (t,x)| \, \textrm{d}\Vert T_\varepsilon ^t\Vert (x) \end{aligned}$$are uniformly integrable on (0, 1). Then there exists \(S \in \textrm{I}^{{{\,\textrm{AC}\,}}}_{1+k}(\mathbb {R}\times \mathbb {R}^d)\) such that \(S^\varepsilon \overset{*}{\rightharpoonup }S\) up to a (non-relabelled) subsequence, in the sense of \((1+k)\)-currents on \(\mathbb {R}\times \mathbb {R}^d\).
-
(iii)
Suppose that the vector fields \({\varvec{b}}^\varepsilon _t\) defined in Point (ii) converge uniformly, as \(\varepsilon \rightarrow 0\), to a continuous vector field \({\varvec{b}}_t\). Then there exists \(S \in \textrm{I}^{{{\,\textrm{AC}\,}}}_{1+k}(\mathbb {R}\times \mathbb {R}^d)\) such that \(S^\varepsilon \overset{*}{\rightharpoonup }S\) up to a (non-relabelled) subsequence, in the sense of \((1+k)\)-currents on \(\mathbb {R}\times \mathbb {R}^d\) and the current S has (NC).
Proof
We split the proof in various parts.
-
(i)
It is enough to apply [19, Theorem 3.7].
-
(ii)
By the same arguments used in the proof of Lemma [10, Lemma 3.5], we have that for every measurable set \(I \subset \mathbb {R}\) it holds
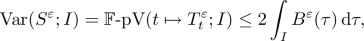
whence we deduce that the (absolutely continuous) measures \({\textrm{Var}}(S^\varepsilon , \varvec{\cdot })\) have uniform integrable densities. Applying Point (i) and Dunford-Pettis’ Theorem we therefore conclude that the family \(S^\varepsilon \) converges, up to a subsequence, to a current S whose variation is still absolutely continuous.
-
(iii)
It is clear that there exists a limit current \(S \in \textrm{I}^{{{\,\textrm{AC}\,}}}_{1+k}(\mathbb {R}\times \mathbb {R}^d)\) because the assumption of Point (ii) is automatically satisfied. We now show that any such limit S has (NC), because its slices solve the geometric transport equation with vector field \({\varvec{b}}\) (as we know, this is indeed equivalent to (NC) in view of Theorem 4.1). By assumption we have that for every \(\varepsilon >0\), for every \(\psi \in \textrm{C}^\infty _c((0,1))\) and every \(\omega \in \mathscr {D}^k(\mathbb {R}^d)\) it holds
$$\begin{aligned} 0 = \int _0^1 \left( \langle T^\varepsilon _t,\omega \rangle \psi '(t)+\langle {\varvec{b}}^\varepsilon _t \wedge T^\varepsilon _t, d\omega \rangle \psi (t) \right) \,\textrm{d}t. \end{aligned}$$(7.1)By the weak convergence of currents we have that \(\langle T^\varepsilon _t,\omega \rangle \rightarrow \langle T_t,\omega \rangle \), where \(T_t :=S(t)\) are the projected slices of S and thus, by the Dominated convergence theorem,
$$\begin{aligned} \int _0^1 \langle T^\varepsilon _t,\omega \rangle \psi '(t) \,\textrm{d}t \rightarrow \int _0^1 \langle T_t,\omega \rangle \psi '(t) \,\textrm{d}t. \end{aligned}$$(7.2)For the other term, instead, we have
$$\begin{aligned} {\varvec{b}}_t^\varepsilon \wedge T^\varepsilon _t -{\varvec{b}}_t \wedge T_t&= ({\varvec{b}}_t^\varepsilon - {\varvec{b}}_t)\wedge T^\varepsilon _t + {\varvec{b}}_t \wedge (T^\varepsilon _t - T_t). \end{aligned}$$For every fixed \(t \in (0,1)\), the mass of the first term can be estimated by
$$\begin{aligned} \textbf{M}( ({\varvec{b}}_t^\varepsilon - {\varvec{b}}_t)\wedge T^\varepsilon _t) \le \Vert {\varvec{b}}_t^\varepsilon -{\varvec{b}}_t \Vert _{C_{x}^0} \textbf{M}(T^\varepsilon _t) \rightarrow 0, \qquad \text {as } \varepsilon \rightarrow 0. \end{aligned}$$(7.3)Furthermore, since all currents \(T^\varepsilon _t\) and \(T_t\) have uniformly bounded mass, we can test them against continuous forms, not necessarily smooth and compactly supported. Therefore for every \(t \in (0,1)\) we have
$$\begin{aligned} \langle {\varvec{b}}_t \wedge (T^\varepsilon _t - T_t), \alpha \rangle = \langle T^\varepsilon _t - T_t, i_{{\varvec{b}}_t}\alpha \rangle \rightarrow 0 \qquad \text {as } \varepsilon \rightarrow 0 \end{aligned}$$(7.4)for every \(\alpha \in \mathscr {D}^{k+1}(\mathbb {R}^d)\) (it is fairly easy to check that the k-form \(i_{{\varvec{b}}_t}\alpha \) has continuous coefficients, since \({\varvec{b}}_t\) is continuous). Choosing in particular \(\alpha = d\omega \) in (7.4) and combining it with (7.3) and (7.2), we can pass to the limit in (7.1) obtaining
$$\begin{aligned} 0 = \int _0^1 \left( \langle T_t,\omega \rangle \psi '(t)+\langle {\varvec{b}}_t \wedge T_t, d\omega \rangle \psi (t) \right) \,\textrm{d}t, \end{aligned}$$which concludes the proof.
\(\square \)
References
Abbaschian, R., Abbaschian, L., Reed-Hill, R. E.: Physical Metallurgy Principles - SI Edition. Cengage Learning, (2009)
Alberti, G., Baldo, S., Orlandi, G.: Variational convergence for functionals of Ginzburg-Landau type. Indiana Univ. Math. J. 54(5), 1411–1472 (2005)
Alberti, G., Bianchini, S., Crippa, G.: A uniqueness result for the continuity equation in two dimensions. J. Eur. Math. Soc. (JEMS) 16(2), 201–234 (2014)
Alberti, G., Marchese, A.: On the differentiability of Lipschitz functions with respect to measures in the Euclidean space. Geom. Funct. Anal. 26(1), 1–66 (2016)
Ambrosio, L.: Metric space valued functions of bounded variation. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 17(3), 439–478 (1990)
Ambrosio, L., Bernard, P.: Uniqueness of signed measures solving the continuity equation for Osgood vector fields. Atti Accad. Naz. Lincei Rend. Lincei Mat. Appl. 19(3), 237–245 (2008)
Ambrosio, L., Fusco, N., Pallara, D.: Functions of bounded variation and free discontinuity problems. Oxford Mathematical Monographs. The Clarendon Press, Oxford University Press, New York (2000)
Ambrosio, L., Gigli, N., Savaré, G.: Gradient flows in metric spaces and in the space of probability measures. Lectures in Mathematics ETH Zürich, 2nd edn. Birkhäuser Verlag, Basel (2008)
Ambrosio, L., Kirchheim, B.: Currents in metric spaces. Acta Math. 185(1), 1–80 (2000)
Bonicatto, P., Del Nin, G., Rindler, F.: Transport of currents and geometric Rademacher-type theorems. (2022). arXiv:2207.03922
Bonicatto, P., Del Nin, G., Rindler, F.: Existence and uniqueness for the transport of currents by Lipschitz vector fields. J. Funct. Anal. p 110315 (2024). arXiv:2303.03218
Bonicatto, P., Gusev, N.A.: Non-uniqueness of signed measure-valued solutions to the continuity equation in presence of a unique flow. Atti Accad. Naz. Lincei Rend. Lincei Mat. Appl. 30(3), 511–531 (2019)
Brezis, H., Coron, J.-M., Lieb, E.H.: Harmonic maps with defects. Commun. Math. Phys. 107(4), 649–705 (1986)
Clop, A., Jylhä, H., Mateu, J., Orobitg, J.: Well-posedness for the continuity equation for vector fields with suitable modulus of continuity. J. Funct. Anal. 276(1), 45–77 (2019)
Federer, H.: Geometric measure theory, volume 153 of Die Grundlehren der mathematischen Wissenschaften. Springer, (1969)
Hull, D., Bacon, D. J.: Introduction to Dislocations. 5 edition, (2011)
Jerrard, R.L., Soner, H.M.: The Jacobian and the Ginzburg-Landau energy. Calc. Var. Part.Differ. Equ. 14(2), 151–191 (2002)
Krantz, S.G., Parks, H.R.: Geometric integration theory. Birkhäuser, Basel (2008)
Rindler, F.: Space-time integral currents of bounded variation. Calc. Var. Part. Differ. Equ. 62, 54 (2023)
Acknowledgements
The content of this note is an expanded version of a seminar the author gave at the VII RISM School, held in Varese within the Riemann Prize Week (10–14 July, 2023). He acknowledges the organisers of this event for their kind invitation. The author is also grateful to Giacomo Del Nin and Filip Rindler for useful discussions.
Funding
Open access funding provided by Università degli Studi di Trento within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bonicatto, P. On the Transport of Currents. Milan J. Math. (2024). https://doi.org/10.1007/s00032-024-00394-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00032-024-00394-9




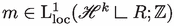 ;
;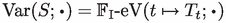 as measures on [0, 1].
as measures on [0, 1].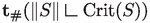 is singular with respect to
is singular with respect to 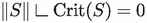 ;
;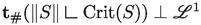 ;
;