Abstract
The aim of this introductory survey is to acquaint the reader with important objects in complex algebraic geometry: K3 surfaces and their higher-dimensional analogs, hyper-Kähler manifolds. These manifolds are interesting from several points of view: dynamical (some have interesting automorphism groups), arithmetical (although we will not say anything on this aspect of the theory), and geometric. It is also one of those rare cases where the Torelli theorem allows for a powerful link between the geometry of these manifolds and lattice theory. We do not prove all the results that we state. Our aim is more to provide, for specific families of hyper-Kähler manifolds (which are projective deformations of punctual Hilbert schemes of K3 surfaces), a panorama of results about projective embeddings, automorphisms, moduli spaces, period maps and domains, rather than a complete reference guide. These results are mostly not new, except perhaps those of Appendix B (written with E. Macrì), where we give in Theorem B.1 an explicit description of the image of the period map for these polarized manifolds.
Similar content being viewed by others
Notes
This strange name was coined by Weil in 1958: “ainsi nommées en l’honneur de Kummer, Kähler, Kodaira et de la belle montagne K2 au Cachemire.”
A theorem of Cantat [23] says that a smooth compact Kähler surface S with an automorphism of positive entropy is bimeromorphic to either \(\textbf{P}^2\), or to a 2-dimensional complex torus, or to an Enriques surface, or to a K3 surface. If the automorphism has no fixed points, S is birational to a projective K3 surface of Picard number greater than 1 and conversely, there is a projective K3 surface of Picard number 2 with a fixed-point-free automorphism of positive entropy (see [100] or Theorem 2.17).
Let X be a smooth compact real manifold of (real) dimension 4. Its second Wu class \(v_2(X)\in H^2(X,\textbf{Z}/2\textbf{Z})\) is characterized by the property (Wu’s formula)
$$\begin{aligned} \forall x\in H^2(X,\textbf{Z}/2\textbf{Z})\qquad v_2(X)\cup x=x\cup x. \end{aligned}$$The class \(v_2\) can be expressed as \(w_2+w_1^2\), where \(w_1\) and \(w_2\) are the first two Stiefel–Whitney classes. When X is a complex surface, one has \(w_1(X)=0\) and \(w_2(X)\) is the reduction modulo 2 of \(c_1(X)\) (which is 0 for a K3 surface).
As explained in the proof of [8, Lemma IV.2.6], there is an inclusion \(H^0(S,\Omega ^1_S)\subset H^1(S,\textbf{C}) \) for any compact complex surface S, so that \(H^0(S,\Omega ^1_S)=0\) for a K3 surface S. We then have \(H^2(S,\Omega ^1_S)=0\) by Serre duality and the remaining number \(h^1(S,\Omega ^1_S)\) can be computed using the Riemann–Roch theorem \(\chi (S,\Omega ^1_S)=\int _S{{\,\textrm{ch}\,}}(\Omega ^1_S){{\,\textrm{td}\,}}(S)=\frac{1}{2} c_1^2(\Omega ^1_S)-c_2(\Omega ^1_S)+2{{\,\textrm{rank}\,}}(\Omega ^1_S)=-20\) (because \(c_1(\Omega ^1_S)=0\) and \(c_2(\Omega ^1_S)=24\)).
It is known that all compact complex surfaces with even \(b_1\) (so that includes K3 surfaces) are in fact Kähler (a nontrivial result! See [8, Theorem IV.(3.1)]).
Let \(\zeta :=e^{i\pi /4}\). For each \(i\in \{1,3,5,7\}\) and each \(j\in \{0,1,2\}\), intersect S with the plane \(\Pi _{ij}\subset \textbf{P}^3\) with equation \(x_3=\zeta ^ix_j\). We get the quartic curve with equation \(x_{j'}^4+x_{j''}^4=0\), where \(\{0,1,2\}=\{j,j',j''\}\). This is the union of 4 lines passing through a point. That is a total of \(4\times 3\times 4=48\) lines.
This case does not occur when \(\rho (S)=1\).
It might be a bit premature to talk about “general polarized K3 surfaces” here but the statements below hold whenever \({{\,\textrm{Pic}\,}}(S)= \textbf{Z}L\), a condition that can be achieved by slightly perturbing (S, L); we will come back to that in Sect. 2.9.
This is one of the two components of the family of all 5-dimensional isotropic subspaces for a nondegenerate quadratic form on \(\textbf{C}^{10}\).
The group \({{\,\textrm{NS}\,}}(X)\) is the group of line bundles on X modulo numerical equivalence; it is a finitely generated abelian group. When \(H^1(X,{\mathscr {O}}_X)=0\) (for example, for K3 surfaces), it is the same as \({{\,\textrm{Pic}\,}}(X)\).
This presentation is correct but a bit misleading: \(\Omega _{2e}\) has in fact two irreducible components (interchanged by complex conjugation) and one usually chooses one component \(\Omega _{2e}^+\) and considers the subgroups of the various orthogonal groups that preserve this component (denoted by \(O^+\) in [37, 38, 72]), so that \({\mathscr {P}}_{2e} ={\widetilde{O}}^+({\Lambda }_{{{\,\mathrm{{K3}}\,}},2e})\backslash \Omega _{2e}^+\).
If (S, L) is very general, this follows from standard deformation theory; the general argument is clever and relies on Kronecker’s theorem and the fact that 21, the rank of \(L^\bot \), is odd [48, Corollary 3.3.5].
If \(\sigma \) is an automorphism of a metric space (X, d), we set, for all positive integers m and all \(x,y\in X\),
$$\begin{aligned} d_m(x,y):=\max _{0\le i<m}d(\sigma ^i(x),\sigma ^i(y)). \end{aligned}$$For \(\varepsilon >0\), let \(s_m(\varepsilon )\) be the maximal number of disjoint balls in X of radius \(\varepsilon /2\) for the distance \(d_m\). The topological entropy of \(\sigma \) is defined by
$$\begin{aligned} h(\sigma ):=\lim _{\varepsilon \rightarrow 0}\limsup _{m\rightarrow \infty }\frac{\log s_m(\varepsilon )}{m}\ge 0 . \end{aligned}$$Automorphisms with positive entropy are the most interesting from a dynamical point of view.
This can be deduced as in [40, Lemma 4.3.3] from the Torelli theorem and the surjectivity of the period map, because this lattice does not represent \(-2\); the square-4 class given by the first basis vector is even very ample on S since the lattice does not represent 0 either. Oguiso gives in [100] a geometric construction of the surface S as a quartic in \(\textbf{P}^3\). It was later realized in [34] that S is a determinantal Cayley surface (meaning that its equation can be written as the determinant of a \(4\times 4\)-matrix of linear forms) and that the automorphism \(\sigma \) had already been constructed by Cayley in 1870 (moreover, \({{\,\textrm{Aut}\,}}(S)\simeq \textbf{Z}\), generated by \(\sigma \)); that article gives very clear explanations about the various facets of these beautiful constructions.
The fact that X is simply connected implies \(H_1(X,\textbf{Z})=0\), hence the torsion of \(H^2(X,\textbf{Z})\) vanishes by the Universal Coefficient Theorem.
The integer k(m) was made explicit (but very large) by work of Demailly and Siu, but is still far from the value \(k(m)=2m+2\) conjectured by Fujita in general, or from the optimistic value \(k(m)=3\) conjectured (for hyper-Kähler manifolds) by Huybrechts [48, p. 34] and O’Grady. It was proved in [87, Theorem A] that one can take \(k(2)=15\).
Song checked in [105, Proposition 3.4] that this is the case if and only if the divisibility is either \(p^s\) or \(2p^s\), where p is a prime number and \(s\ge 0\).
One has \(h^\bot \simeq M\oplus \textbf{Z}\ell \oplus \textbf{Z}(u-nv)\), hence \(D(h^\bot )\simeq \textbf{Z}/(2m-2)\textbf{Z}\times \textbf{Z}/ 2n\textbf{Z}\), with generators \(\frac{1}{2m-2}\ell \) and \(\frac{1}{2n} (u-nv) \), and intersection matrix \(\left( {\begin{matrix} -\frac{ 1}{2m-2} &{} 0 \\ 0 &{}-\frac{ 1}{2n}\end{matrix}}\right) \).
We have \({\Lambda }^{(2)}_{{{\,\mathrm{{K3}}\,}}^{[m]},2n}\simeq M\oplus \langle e_1,e_2\rangle \), with \(e_1=(m-1)v+\ell \) and \(e_2:=-u+ \frac{n+m-1}{4}v\), with intersection matrix as desired. It contains \(M\oplus \textbf{Z}e_1\oplus \textbf{Z}(e_1-2e_2)\simeq {\Lambda }^{(1)}_{{{\,\mathrm{{K3}}\,}}^{[m]},2n}\) as a sublattice of index 2 and discriminant group \( \textbf{Z}/(2m-2)\textbf{Z}\times \textbf{Z}/2n\textbf{Z}\). This implies that \(D(h^\bot )\) is the quotient by an element of order 2 of a subgroup of index 2 of \( \textbf{Z}/(2m-2)\textbf{Z}\times \textbf{Z}/2n\textbf{Z}\). When n is odd, it is therefore isomorphic to \( \textbf{Z}/( m-1)\textbf{Z}\times \textbf{Z}/ n\textbf{Z}\). One can choose as generators of each factor \(\frac{1}{m-1}e_1\) and \(\frac{1}{n}(e_1-2e_2)\), with intersection matrix \(\left( {\begin{matrix} -\frac{ 2}{m-1} &{} 0 \\ 0 &{}-\frac{ 2}{n}\end{matrix}}\right) \). When \(n=m-1\) (which implies n even), the lattices \((\textbf{Z}^2, \left( {\begin{matrix} -2n &{} -n \\ -n &{} -n\end{matrix}}\right) )\) and \((\textbf{Z}^2, \left( {\begin{matrix} - n &{} 0 \\ 0 &{} -n\end{matrix}}\right) )\) are isomorphic, hence \(D(h^\bot )\simeq \textbf{Z}/n\textbf{Z}\times \textbf{Z}/ n\textbf{Z}\), with generators \(\frac{1}{n}(e_1-e_2)\) and \(\frac{1}{n} e_2 \), and intersection matrix \(\left( {\begin{matrix} -\frac{ 1}{n} &{} 0 \\ 0 &{}-\frac{ 1}{n}\end{matrix}}\right) \).
More generally, one checks that \(D(h^\bot )\simeq \textbf{Z}/ n\textbf{Z}\times \textbf{Z}/( m-1)\textbf{Z}\) if and only if \(v_2(n)=v_2(m-1)\). If \(v_2(n)>v_2(m-1)\), one has \(D(h^\bot )\simeq \textbf{Z}/ 2n\textbf{Z}\times \textbf{Z}/( (m-1)/2)\textbf{Z}\), and analogously if \(v_2(m-1)>v_2(n)\).
A line bundle L on S is m-very ample if, for every 0-dimensional scheme \(Z\subset S\) of length \(\le m+1\), the restriction map \(H^0(S,L)\rightarrow H^0(Z,L\vert _Z)\) is surjective (in particular, 1-very ample is just very ample).
This example was presented by Mukai in [80, Example 0.6] as one of the first examples of hyper-Kähler manifolds (in that article, the Mukai flop is called elementary transformation). The hyper-Kähler fourfold X is the neutral component of the compactified Picard scheme of the family of curves in |L|.
The line bundle \(L_2^{\otimes 2}(-\delta )\) is ample (Example 3.18 or Example 3.13) but it has base-points: the morphism \(\varphi _{L^{\otimes 2}}:S\rightarrow \textbf{P}^5\) is the composition of the double cover \(\varphi _{L}:S\rightarrow \textbf{P}^2\) with the Veronese embedding and the map \(\varphi _2:S^{[2]}\dashrightarrow {{\,\mathrm{\textsf{Gr}}\,}}(2,6)\) is not defined along the image of the embedding \(\textbf{P}^2\hookrightarrow S^{[2]}\) given by the double cover \(\varphi _L\). Therefore, \((S^{[2]},L_2^{\otimes 2}(-\delta ))\) cannot be the variety of lines of a smooth cubic fourfold (see [49, Remark 3.22] for another argument).
We need to compute \(h^0({{\,\mathrm{\textsf{Gr}}\,}}(6,10),{\mathscr {I}}_X(1))\). Only two terms from the Koszul complex contribute:
 , of dimension \(\left( {\begin{array}{c}10\\ 3\end{array}}\right) =120\), and
, of dimension \(\left( {\begin{array}{c}10\\ 3\end{array}}\right) =120\), and 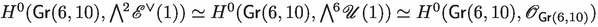 , of dimension 1. Hence \(H^0({{\,\mathrm{\textsf{Gr}}\,}}(6,10),{\mathscr {I}}_X(1))\) has dimension
, of dimension 1. Hence \(H^0({{\,\mathrm{\textsf{Gr}}\,}}(6,10),{\mathscr {I}}_X(1))\) has dimension  (thanks to L. Manivel for doing these computations).
(thanks to L. Manivel for doing these computations).More intrinsically, one sees that X is the linear section of \({{\,\mathrm{\textsf{Gr}}\,}}(6,10)\) by the projectivization of the kernel of the contraction map
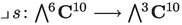 , whose image is the hyperplane defined by s (here s is the element of
, whose image is the hyperplane defined by s (here s is the element of 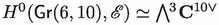 that defines X).
that defines X).The main result of [2] is that X(W) is a deformation of \(S^{[4]}\), where (S, L) is a very general polarized K3 surface of degree 14. One can therefore write the class of the polarization on X(W) as \(H=aL_4-b\delta \), with \(2=H^2=14a^2-6b^2\), hence \(a^2\equiv b^2 -1\pmod 4\). This implies that a is even, hence so is \(\gamma \). Since \(\gamma \mid H^2\), we get \(\gamma =2\) (note that the condition \(n+m\equiv 1\pmod 4\) of Theorem 3.5 holds).
One may follow the argument in the proof of [41, Theorem 7] and compute explicitly the Beauville–Fujiki form on a resolution of the rational map induced by the complete linear system of the movable divisor.
Since any compact Kähler manifold which is Moishezon is projective, X is projective if and only if \(X'\) is projective. The general statement here is that if \(\sigma ^*\) maps a Kähler class of \(X'\) to a Kähler class of X, the map \(\sigma \) is an isomorphism [46, Proposition 27.6].
If \(N:=\dim _\textbf{C}(X)\) and \(Y:=X\smallsetminus U\), this follows from example from the long exact sequence
$$\begin{aligned} H_{2N-2}(Y,\textbf{Z}) \rightarrow H_{2N-2}(X,\textbf{Z})\rightarrow H_{2N-2}(X,Y,\textbf{Z})\rightarrow H_{2N-3}(Y,\textbf{Z}), \end{aligned}$$the fact that \(H_j(Y,\textbf{Z})=0\) for \(j>2(N-2)\ge \dim _\textbf{R}(Y)\), and the duality isomorphisms \(H_{2N-i}(X,\textbf{Z}) \simeq H^i(X,\textbf{Z})\) and \(H_{2N-i}(X,Y,\textbf{Z}) \simeq H^i(X\smallsetminus Y,\textbf{Z})\).
This still requires some work, and reading [11, Sects. 12 and 13] might help.
The statement of item (c) of that proposition is clarified in the latest arXiv version.
If (a, b) is a solution to that equation, its “square” \((a^2+e(m-1)b^2,2ab) \) is also a solution and one has \(a^2+e(m-1)b^2\equiv a^2\equiv 1\pmod {m-1}\). So there always exist solutions with the required property.
Also, we always have the inequalities \( \frac{eb_1}{a_1(m-1)}\le \frac{eb'_1}{a'_1}<\sqrt{\frac{e}{m-1}}\) between slopes and the first inequality is strict when \(m\ge 3\) (when the equation \((m-1)a^2-eb^2=1\) has a minimal positive solution \((a_1,b_1)\) and \(m\ge 3\), the minimal solution of the equation \({\mathscr {P}}_{e(m-1)}(1)\) is \((2(m-1)a_1^2-1,2a_1b_1)\) by Lemma A.2 and this is \((a'_1,b'_1)\); hence \(\frac{eb'_1}{a'_1}>\frac{eb_1}{a_1(m-1)}\)).
If they are equal, we are in one of the following cases described in Example 3.20 (we set \(g:=\gcd ({m+e},2e)\))
-
either \((m+e)L_m-2e\delta \) has square 0 and \(2e(m+e)^2=4e^2(2m-2)\), which implies \( (m+e)^2=2e (2m-2)\), hence \( (m-e)^2=-4e\), absurd;
-
or \( m+e =g(m-1)a_1\) and \(2e=geb_1\), which implies \(b_1\le 2 \) and
$$\begin{aligned} a_1^2\, \frac{e+1}{2}\le a_1^2(m-1)=1+eb_1^2+1\le 1+4e+1 \end{aligned}$$hence either \(a_1=b_1=2\), absurd, or \(a_1=1\), and \(m+e=g(m-1)\) implies \(g=2\), \(b_1=1\), and \(m=e+2\), the only case when the cones are equal;
-
or \( m+e =g a'_1\) and \(2e=geb'_1\), which implies \(g\le 2\) and
$$\begin{aligned} (m+e)^2 =g^2a_1^{\prime 2}=g^2(e(m-1)b_1^{\prime 2}+1) =4e(m-1)+g^2 \end{aligned}$$hence \((m-e)^2 = -4e +g^2\le -4e+4\le 0\) and \(e=m=1\), absurd.
-
Since the equation \({\mathscr {P}}_{n, 4e'}(-5)\) is solvable, \(d:=\gcd (n,e')\in \{1,5\}\). If \(ne'\) is a perfect square, we can write \(n=du^2\) and \(e'=dv^2\). This is easily checked to be incompatible with the equality \( (ua+2vb)(ua-2vb)=-5/d\).
As in footnote 10, \(O^+(H^2(X,\textbf{Z}),q_X)\) is the index-2 subgroup of \(O (H^2(X,\textbf{Z}),q_X)\) of isometries that preserve the positive cone \({{\,\textrm{Pos}\,}}(X)\).
One has \(D(H^2(X,\textbf{Z}))\simeq \textbf{Z}/(2m-2)\textbf{Z}\) and \(O(D(H^2(X,\textbf{Z})),{\bar{q}}_X)\simeq \{x\pmod {2m-2}\mid x^2\equiv 1\pmod {4t} \}\simeq (\textbf{Z}/2\textbf{Z})^{\rho (m-1)}\) [37, Corollary 3.7]. One then uses the surjectivity of the canonical map \(O^+(H^2(X,\textbf{Z}),q_X)\rightarrow O(D(H^2(X,\textbf{Z})),{\bar{q}}_X) \) (see Sect. 2.7).
As in footnote 10, one usually chooses one component \(\Omega _{h_\tau }^+\) of \(\Omega _{h_\tau } \), so that \({\mathscr {P}}_\tau ={\widehat{O}}^+({\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}} ,h_\tau )\backslash \Omega _{h_\tau }^+\) (see [38, Theorem 3.14]).
This strange duality was already noticed in [7, Proposition 3.2].
Note that H is movable and nef on \({\mathscr {M}}(r,L,r)\) for all \(e>r^2\) (see footnotes 48 and 59).
Let G be the subgroup \({\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}} / (\textbf{Z}h_\tau \oplus h_\tau ^\bot )\) of \(D(\textbf{Z}h_\tau )\times D(h_\tau ^\bot )\). An element of \(O(h_\tau ^\bot )\) is in \(O({\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}} ,h_\tau )\) if and only if it induces the identity on \(p_2(G)\subset D(h_\tau ^\bot )\). This is certainly the case if it is in \({{\widetilde{O}}}(h_\tau ^\bot )\) and the lift is then in \(\widetilde{O}({\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}} ,h_\tau )\) since it induces the identity on \(D(\textbf{Z}h_\tau )\times D(h_\tau ^\bot )\), hence on its subquotient \(D({\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}})\).
The following holds:
-
the inclusion \(\iota _1\) is an equality if \(\gcd (\frac{2n}{\gamma },\frac{2m-2}{\gamma },\gamma )=1\) [37, Proposition 3.12(i)];
-
the inclusion \(\iota _2\) is an equality if \(m=2\);
-
the inclusion \(\iota _3\) defines a normal subgroup and is an equality if \(m-1\) is a prime power (Sect. 3.8);
-
the inclusion \(\iota _3\iota _2\) defines a normal subgroup and, if \(\gcd (\frac{2n}{\gamma },\frac{2m-2}{\gamma },\gamma )=1\), the corresponding quotient is the group \((\textbf{Z}/2\textbf{Z})^\alpha \), where \(\alpha = \rho \bigl ( \frac{m-1}{\gamma }\bigr )\) when \(\gamma \) is odd, and \(\alpha = \rho \bigl ( \frac{2m-2}{\gamma }\bigr )+\varepsilon \) when \(\gamma \) is even, with \(\varepsilon =1\) if \( \frac{2m-2}{\gamma }\equiv 0\pmod 8\), \(\varepsilon =-1\) if \( \frac{2m-2}{\gamma }\equiv 2\pmod 4\), and \(\varepsilon =0\) otherwise [37, Proposition 3.12(ii)].
-
By (6), we have \(D(h_\tau ^\bot )\simeq \textbf{Z}/2n\textbf{Z}\times \textbf{Z}/2\textbf{Z}\), with \(q(1,0)=-\frac{1}{2n}\) and \(q(0,1)=-\frac{1}{2}\) in \(\textbf{Q}/2\textbf{Z}\). When \(n\equiv -1\pmod 4\), one checks that any isometry must leave each factor of \(D(h_\tau ^\bot )\) invariant, so that \(O(D(h_\tau ^\bot ))\simeq O(\textbf{Z}/2n\textbf{Z})\). When \(n\equiv 1\pmod 4\), there are extra isometries \((0,1)\mapsto (n,0)\), \((1,0)\mapsto (a,1)\), where \(a^2+n\equiv 1\pmod {4n}\).
O’Grady’s hypersurfaces \({\mathbb {S}}'_2\cup {\mathbb {S}}''_2\), \({\mathbb {S}}^\star _2\), \({\mathbb {S}}_4\) are our \({\mathscr {D}}_{2,2}^{(1)} \), \({\mathscr {D}}_{2,4}^{(1)} \), \({\mathscr {D}}_{2,8}^{(1)} \).
The argument is classical: let X be a hyper-Kähler manifold, let \(\omega \) be a symplectic form on X, let \(\sigma \) be an automorphism of X, and write \(\sigma ^*\omega =\xi \omega \), where \(\xi \in \textbf{C}^\star \). Assume that \((X,\sigma )\) deforms along a subvariety of the moduli space; the image of this subvariety by the period map consists of period points which are eigenvectors for the action of \(\sigma ^*\) on \(H^2(X,\textbf{C})\) and the eigenvalue is necessarily \(\xi \). In our case, the span of the image by the period map is \(H^\bot \), which is therefore contained in the eigenspace \(H^2(X,\textbf{C})_\xi \).
If \(H^{\pm 1}\) is ample, the relation \(\sigma ^*H^{\pm 1}=H^{\pm 1}\) implies that \(\sigma \) is biregular. Conversely, if \(\sigma \) is biregular, consider an ample line bundle A on X. Then \(A\otimes \sigma ^*A\) is ample and is proportional to H, hence either H or \(H^{-1}\) is ample. This reasoning shows that either H or \(H^{-1}\) is always movable.
Given a twisted cubic C contained in the cubic fourfold W, with span \(\langle C\rangle \simeq \textbf{P}^3\), take any quadric \(Q\subset \langle C\rangle \) containing C; the intersection \(Q\cap W\) is a curve of degree 6 which is the union of C and another twisted cubic \(C'\). The curve \(C'\) depends on the choice of Q, but not its image in X (thanks to Ch. Lehn for this description). The map \([C]\mapsto [C']\) defines an involution \(\sigma \) on X; the fact that it is biregular is not at all clear from this description, but follows from the fact that \(\sigma ^*H=H\). The fixed locus of \(\sigma \) has two (Lagrangian) connected components and one is the image of the canonical embedding \(W\hookrightarrow X\) [64, Theorem B(2)].
This conjecture states that if (X, H) is a polarized hyper-Kähler manifold corresponding to a general point of a moduli space \({}^m\!\!{\mathscr {M}}^{(\gamma )}_{2}\) (with \(m\ge 2\) and \(\gamma \in \{1,2\}\)), the linear system |H| is base-point free and the morphism \(\varphi _H\) has degree 2 onto its image and factors through the quotient of X by its involution from Proposition 4.3.
When Mukai proved in 1984 in [80] the existence of a symplectic form on moduli spaces of sheaves on an abelian or K3 surface, it was expected that these moduli spaces would give many new examples of hyper-Kähler manifolds. Huybrechts quashed these hopes in 1997 with [44, Theorem 6.3] by proving that the deformation types of many of these moduli spaces were already known. Yoshioka then treated the general case (including the case of sheaves on an abelian surface) in [112].
Since \(e>1\), the morphism \({\overline{\Psi }}_{{S^{[m]}}}^B\) is injective and any nontrivial birational involution \(\sigma \) of \( {S^{[m]}} \) induces a nontrivial involution \(\sigma ^*\) of \({{\,\textrm{Pic}\,}}({S^{[m]}})\) that preserves the movable cone; in particular, primitive generators of its two extremal rays need to have the same lengths. Since \(m\ge 3\), this implies (Example 3.20) that items (a) and (c) hold. The other extremal ray of \({{\,\textrm{Mov}\,}}(S^{[m]})\) is then spanned by \(a_1L_m-eb_1\delta \), where \((a_1,b_1)\) is the minimal positive solution of the equation \(a^2-e(m-1)b^2=1\) that satisfies \(a_1\equiv \pm 1\pmod {m-1}\).
The lattice \({{\,\textrm{Pic}\,}}(S^{[m]})=\textbf{Z}L_m\oplus \textbf{Z}\delta \) has intersection matrix \(\left( {\begin{matrix} 2e&{} 0\\ 0&{}-(2m-2)\end{matrix}}\right) \) and its orthogonal group is
$$\begin{aligned} O({{\,\textrm{Pic}\,}}(S^{[m]}))=\left\{ \begin{pmatrix} a&{} \alpha m'b\\ e'b&{}\alpha a \end{pmatrix} \Big |\ a,b\in \textbf{Z}, \ a^2-e'm'b^2=1,\ \alpha =\pm 1 \right\} , \end{aligned}$$where \(g :=\gcd (e,m-1)\) and we write \(e=g e'\) and \(m-1=g m'\). Since \(\sigma ^*(L_m)=a_1L_m-eb_1\delta \), we must therefore have \(g=\gcd (e,m-1)=1\).
The transcendental lattice \({{\,\textrm{Pic}\,}}(S^{[2]} )^\bot \subset H^2( S^{[2]},\textbf{Z})\) carries a simple rational Hodge structure (this is a classical fact found for example in [48, Lemma 3.1]). Since the eigenspaces of the involution \(\sigma ^*\) of \( H^2( S^{[2]},\textbf{Z})\) are sub-Hodge structures, the restriction of \(\sigma ^*\) to \({{\,\textrm{Pic}\,}}(S^{[2]} )^\bot \) is \(\varepsilon {{\,\textrm{Id}\,}}\), with \(\varepsilon \in \{\pm 1\}\). As in the proof of Proposition 4.3 and with its notation, we write \(L_m=u+ev\); we have
$$\begin{aligned} \sigma ^* (u+ev)= & {} a_1(u+ev)-eb_1\delta \\ \sigma ^* (u-ev)= & {} \varepsilon (u-ev), \end{aligned}$$which implies \(2e\sigma ^*(v) = (a_1-\varepsilon )u+e(a_1+\varepsilon )v-eb_1\delta \), hence \(2e\mid a_1-\varepsilon \) and \(2\mid b_1\).
According to that reference, the extremal rays of the three fundamental chambers in the moving cones are the orthogonal complement of divisors \(D=b\mathop {\textrm{div}}\nolimits (D)L_3-a\delta \) such that
-
either \(D^2=-12\) and \(\mathop {\textrm{div}}\nolimits (D)=2\): it gives the equation \(a^2-10b^2=3\), which has no solutions (reduce modulo 5);
-
either \(D^2=-36\) and \(\mathop {\textrm{div}}\nolimits (D)=4\): it gives the equation \(a^2-40b^2=9\), which has solutions (7, 1) and (13, 2) (the corresponding rays appear in (28));
-
either \(D^2=-2\) and \(\mathop {\textrm{div}}\nolimits (D)=1\): it gives gives the equation \(2a^2-5b^2=1\), which has no solutions (reduce modulo 5);
-
either \(D^2=-4\) and \(\mathop {\textrm{div}}\nolimits (D)=4\): it gives gives the equation \(a^2-40b^2=1\), which has solution (19, 3) (the corresponding ray is the other ray of the moving cone);
-
either \(D^2=-4\) and \(\mathop {\textrm{div}}\nolimits (D)=2\): it gives gives the equation \(a^2-10b^2=1\) with b odd, which has no solutions.
-
This is the group \(\textbf{Z}\rtimes \textbf{Z}/2\textbf{Z}\), also isomorphic to the free product \( \textbf{Z}/2\textbf{Z}\star \textbf{Z}/2\textbf{Z}\).
Since \(x_1>1\), we have \(0<x_tx_1^{-1}<x_t\). Since \(x_t\) corresponds to a minimal solution, this implies \(x_tx_1^{-1}< \sqrt{t}\), hence \({\bar{x}}_tx_1>\sqrt{t}\). By minimality of \(x_t\) again, we get \({\bar{x}}_tx_1\ge x_t\).
If \(b_t\) is even, we have \(a'_t=a_t\), \(b'_t=b_t/2\), and \(x'_t=x_t\). If t is even, we have \(4\mid t\), \(a'_t=2a_{t/4}\), \(b'_t=b_{t/4}\), and \(x'_t=2x_{t/4}\). If \(b_t\) and t are odd,
-
either \(b_1\) is even (and \(a_1\) is odd) and the second argument of any solution of \({\mathscr {P}}_e(t)\) associated with \((a_t,b_t)\) or its conjugate remains odd, so that the solution \((a'_t,2b'_t)\) of \({\mathscr {P}}_e(t)\) is in neither of these two classes;
-
or \(b_1\) is odd, we have \(a_tb_1-a_1b_t\equiv a_t+a_1 \equiv t+e+1+e\equiv 0 \pmod 2\), hence \(x'_t={\bar{x}}_tx_1\).
-
Since \(a_1\) and \(b_1\) are relatively prime, the equality \(2a_1b'_t=b_1a'_t\) implies that there exists a positive integer c such that \(2b'_t=cb_1\) and \(a'_t=ca_1\); plugging these values into the equation \({\mathscr {P}}_{4e}(t)\), we get \(t=c^2\), which contradicts our hypothesis that t is not a perfect square.
If (a, b) is a solution to \({\mathscr {P}}_{e_1,e_2}(t)\) and \((a_1,b_1)\) is a solution to \({\mathscr {P}}_{e_1e_2}(1)\), and if we set \(x_1:=a_1+b_1\sqrt{e_1e_2}\), then \((e_1a+b\sqrt{e_1e_2})x_1=:e_1a'+b'\sqrt{e_1e_2}\), where \((a',b')\) is again a solution to \({\mathscr {P}}_{e_1,e_2}(t)\).
One checks that for all \(\alpha ^2 > 1/e\), all stable sheaves in X are stable for the Bridgeland stability condition \(\sigma _{\alpha ,0}\) (in Bridgeland’s notation). Therefore, by [10, Lemma 9.2], the class H is nef: it corresponds exactly to the (nonexistent) stability condition at \(\alpha ^2=1/e\).
We do not know in general whether these rays are rational.
When \(m-1\) is prime or equal to 1, there is a unique equivalence class; in general, the number of equivalence classes is the index of \( {\widehat{O}}({\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}} )\) in \( O^+({\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}})\), that is \(2^{\max \{\rho (m-1)-1,0\}}\) (Sect. 3.8 or [72, Lemma 9.4]).
If \(s=2\), we have \(d=n(m-1)/2\), so that both n and \(m-1\) are even, and we need to solve \(a(a+b)(m-1)+b^2 \bigl (\frac{n+m-1}{4}\bigr )\equiv 1\pmod 4\). The reader is welcome to determine the number of solutions of this equation and see how many different elements of order 2 in the group \(D(h_\tau ^\bot )\) (which was determined in footnote 19) are obtained in this way in each case. This will produce more hypersurfaces avoided by the image of the period map.
This follows from a more general “strange duality” statement as follows. Consider the Kuznetsov component \({\mathscr {K}}\!u(W)\) of the derived category \(\textrm{D}^\textrm{b}(W)\) [58]. As explained in [3, Sect. 2], one can associate with such a category a weight-2 Hodge structure on the lattice \({\widetilde{\Lambda }}_{{{\,\mathrm{{K3}}\,}}}\); we denote it by \({\widetilde{\Lambda }}_{W}\). Moreover, there is a natural primitive sublattice \(A_2\hookrightarrow {\widetilde{\Lambda }}_{\text {alg}, W}\); we denote its canonical basis by \((u_1,u_2)\): it satisfies \(u_1^2=u_2^2=2\) and \(u_1\cdot u_2=-1\).
Let \(\sigma _0=({\mathscr {A}}_0,Z_0)\) be the Bridgeland stability condition constructed in [13, Theorem 1.2]. Given a Mukai vector \({{\textbf{v}}}\in {\widetilde{\Lambda }}_{\text {alg}, W}\), we denote by \(M_{\sigma _0}({{\textbf{v}}})\) the moduli space of \(\sigma _0\)-semistable objects in \({\mathscr {A}}_0\) with Mukai vector \({{\textbf{v}}}\). If there are no properly \(\sigma _0\)-semistable objects, \( M_{\sigma _0}({{\textbf{v}}})\) is, by [12], a smooth projective hyper-Kähler manifold of dimension \({{\textbf{v}}}^2+2\) and there is a natural Hodge isometry \(H^2(M_{\sigma _0}({{\textbf{v}}}),\textbf{Z})\simeq {{\textbf{v}}}^\perp \) such that the embedding \(\theta _{M_{\sigma _0}({{\textbf{v}}})}\) can be identified with \(\theta _{{{\textbf{v}}}}:{{\textbf{v}}}^\perp \hookrightarrow {\widetilde{\Lambda }}_{{{\,\mathrm{{K3}}\,}}}\). Moreover, there is by [10] a natural ample class \(\ell _{\sigma _0}({{\textbf{v}}})\) on \(M_{\sigma _0}({{\textbf{v}}})\).
By [65], there are isomorphisms \(F(W)\simeq M_{\sigma _0}(u_1)\) and \(X(W)\simeq M_{\sigma _0}(u_1+2u_2)\). Moreover, possibly after multiplying by a positive constant, the class \(\ell _{\sigma _0}(u_1)\) on \(M_{\sigma _0}(u_1)\) (respectively, the class \(\ell _{\sigma _0}(u_1+2u_2)\) on \(M_{\sigma _0}(u_1+2u_2)\)) corresponds to the Plücker polarization on F(W) (respectively, to the degree-2 polarization on X(W)). Finally, an easy computation shows \(\ell _{\sigma _0}(u_1)=\theta _{u_1}(u_1+2u_2)\) and \(\ell _{\sigma _0}(u_1+2u_2)=\theta _{u_1+2u_2}(u_1)\). The strange duality statement follows directly from this: the periods of both polarized varieties are identified with the orthogonal complement of the \(A_2\) sublattice. We notice that, in this example, this gives a precise formulation of the strange duality between polarized hyper-Kähler manifolds in terms of Le Potier’s strange duality [63] between the two moduli spaces (on a noncommutative K3 surface).
References
Addington, N.: On two rationality conjectures for cubic fourfolds. Math. Res. Lett. 23, 1–13 (2016)
Addington, N., Lehn, M.: On the symplectic eightfold associated to a Pfaffian cubic fourfold. J. Reine Angew. Math. 731, 129–137 (2017)
Addington, N., Thomas, R.: Hodge theory and derived categories of cubic fourfolds. Duke Math. J. 163, 1885–1927 (2014)
Amerik, E., Verbitsky, M.: Teichmüller space for hyperkähler and symplectic structures. J. Geom. Phys. 97, 44–50 (2015)
Amerik, E., Verbitsky, M.: Morrison-Kawamata cone conjecture for hyperkähler manifolds. Ann. Sci. Éc. Norm. Supér. 50, 973–993 (2017)
Apostolov, A.: Moduli spaces of polarized irreducible symplectic manifolds are not necessarily connected. Ann. Inst. Fourier 64, 189–202 (2014)
Apostolov, A.: On irreducible symplectic varieties of \(\text{K3}^{[n]}\)-type, Ph.D. thesis, Universität Hannover (2014)
Barth, W., Hulek, K., Peters, C., van de Ven, A.: Compact Complex Surfaces, 2nd edn, Ergebnisse der Mathematik und ihrer Grenzgebiete 4. Springer, Berlin (2004)
Bayer, A., Hassett, B., Tschinkel, Y.: Mori cones of holomorphic symplectic varieties of K3 type. Ann. Sci. Éc. Norm. Supér. 48, 941–950 (2015)
Bayer, A., Macrì, E.: Projectivity and birational geometry of Bridgeland moduli spaces. J. Am. Math. Soc. 27, 707–752 (2014)
Bayer, A., Macrì, E.: MMP for moduli of sheaves on K3s via wall-crossing: nef and movable cones, Lagrangian fibrations. Invent. Math. 198, 505–590 (2014). Corrected version at arXiv:1704.01439
Bayer, A., Lahoz, M., Macrì, E., Nuer, H., Perry, A., Stellari, P.: Stability conditions in families. Publ. Math. Inst. Hautes Études Sci. 133, 157–325 (2021)
Bayer, A., Lahoz, M., Macrì, E., Stellari, P.: Stability conditions on Kuznetsov components. Ann. Sci. Éc. Norm. Supér. (eprint, to appear)arXiv:1703.10839
Beauville, A.: Variétés Kähleriennes dont la première classe de Chern est nulle. J. Differ. Geom. 18, 755–782 (1983)
Beauville, A.: Some remarks on Kähler manifolds with \(c_1= 0\). Classification of algebraic and analytic manifolds (Katata, 1982), 1–26, Progr. Math., vol. 39. Birkhaüser Boston, Boston (1983)
Beauville, A., Donagi, R.: La variété des droites d’une hypersurface cubique de dimension 4. C. R. Acad. Sci. Paris Sér. I Math. 301, 703–706 (1985)
Benedetti, V., Song, J.: Divisors in the moduli space of Debarre–Voisin varieties (eprint)arXiv:2106.06859
Beri, P., Cattaneo, A.: On birational transformations of Hilbert schemes of points on K3 surfaces. Math. Z. 301, 1537–1554 (2022)
Boissière, S., Camere, C., Mongardi, G., Sarti, A.: Isometries of ideal lattices and hyperkähler manifolds, Int. Math. Res. Not., 963–977 (2016)
Boissière, S., Camere, C., Sarti, A.: Complex ball quotients from manifolds of K3\(^{[n]}\)-type. J. Pure Appl. Algebra 223, 1123–1138 (2019)
Boissière, S., Cattaneo, A., Nieper-Wißkirchen, M., Sarti, A.: The automorphism group of the Hilbert scheme of two points on a generic projective K3 surface. In: Proceedings of the Schiermonnikoog Conference, K3 Surfaces and their Moduli, Progress in Mathematics, vol. 315. Birkhäuser, Basel (2015)
Boissière, S., Sarti, A.: A note on automorphisms and birational transformations of holomorphic symplectic manifolds. Proc. Am. Math. Soc. 140, 4053–4062 (2012)
Cantat, S.: Dynamique des automorphismes des surfaces projectives complexes. C. R. Acad. Sci. Paris Sér. I Math. 328, 901–906 (1999)
Catanese, F., Göttsche, L.: \(d\)-very-ample line bundles and embeddings of Hilbert schemes of 0-cycles. Manuscr. Math. 68, 337–341 (1990)
Cattaneo, A.: Automorphisms of Hilbert schemes of points on a generic projective K3 surface. Math. Nachr. 292, 2137–2152 (2019)
Cattaneo, A., Fu, L.: Finiteness of Klein actions and real structures on compact hyper-Kähler manifolds. Math. Ann. 375, 1783–1822 (2019)
Chen, X., Gounelas, F., Liedtke, Ch.: Rational curves on lattice-polarised K3 surfaces. Algebr. Geom. 9, 443–475 (2022)
Clozel, L., Ullmo, E.: Équidistribution de sous-variétés spéciales. Ann. Math. 161, 1571–1588 (2005)
Debarre, O., Han, F., O’Grady, K., Voisin, C.: Hilbert squares of K3 surfaces and Debarre–Voisin varieties. J. Éc. Polytech. Math. 7, 653–710 (2020)
Debarre, O., Iliev, A., Manivel, L.: Special prime Fano fourfolds of degree 10 and index 2. In: Hacon, C., Mustaţă, M., Popa, M. (eds.) Recent Advances in Algebraic Geometry, 123–155, London Mathematical Society Lecture Notes Series, vol. 417. Cambridge University Press, Cambridge (2014)
Debarre, O., Kuznetsov, A.: Gushel–Mukai varieties: classification and birationalities. Algebr. Geom. 5, 15–76 (2018)
Debarre, O., Macrì, E.: On the period map for polarized hyperkähler fourfolds. Int. Math. Res. Not. IMRN 22, 6887–6923 (2019). Corrected version at arXiv:1704.01439
Debarre, O., Voisin, C.: Hyper-Kähler fourfolds and Grassmann geometry. J. Reine Angew. Math. 649, 63–87 (2010)
Festi, D., Garbagnati, A., van Geemen, B., van Luijk, R.: The Cayley–Oguiso free automorphism of positive entropy on a K3 surface. J. Mod. Dyn. 7, 75–96 (2013)
Fujiki, A.: On automorphism groups of compact Kähler manifolds. Invent. Math. 44, 225–258 (1978)
Gritsenko, V., Hulek, K., Sankaran, G.K.: The Kodaira dimension of the moduli of K3 surfaces. Invent. Math. 169, 519–567 (2007)
Gritsenko, V., Hulek, K., Sankaran, G.K.: Moduli spaces of irreducible symplectic manifolds. Compos. Math. 146, 404–434 (2010)
Gritsenko, V., Hulek, K., Sankaran, G.K.: Moduli of K3 surfaces and irreducible symplectic manifolds, Handbook of moduli, vol. I, pp. 459–526, Adv. Lect. Math. (ALM), vol. 24. Int. Press, Somerville (2013)
Guan, D.: On the Betti numbers of irreducible compact hyperkähler manifolds of complex dimension four. Math. Res. Lett. 8, 663–669 (2001)
Hassett, B.: Special cubic fourfolds. Compos. Math. 120, 1–23 (2000)
Hassett, B., Tschinkel, Y.: Moving and ample cones of holomorphic symplectic fourfolds. Geom. Funct. Anal. 19, 1065–1080 (2009)
Hassett, B., Tschinkel, Y.: Flops on holomorphic symplectic fourfolds and determinantal cubic hypersurfaces. J. Inst. Math. Jussieu 9, 125–153 (2010)
Hassett, B., Tschinkel, Y.: Hodge theory and Lagrangian planes on generalized Kummer fourfolds. Mosc. Math. J. 13, 33–56 (2013)
Huybrechts, D.: Birational symplectic manifolds and their deformations. J. Differ. Geom. 45, 488–513 (1997)
Huybrechts, D.: Compact hyperkähler manifolds: basic results, Invent. Math. 135, 63–113 (1999). Erratum in Invent. Math. 152, 209–212 (2003)
Huybrechts, D.: Compact Hyperkähler Manifolds, in Calabi–Yau Manifolds and Related Geometries, Lectures from the Summer School held in Nordfjordeid, June 2001. Universitext, Springer, Berlin (2003)
Huybrechts, D.: A Global Torelli theorem for hyperkähler manifolds (after Verbitsky), Séminaire Bourbaki 2010/2011. Astérisque, Exp. no 1040 348, 375–403 (2012)
Huybrechts, D.: Lectures on K3 Surfaces. Cambridge Studies in Advanced Mathematics, vol. 158. Cambridge University Press, Cambridge (2016)
Huybrechts, D.: Hodge theory of cubic fourfolds, their Fano varieties, and associated K3 categories. In: Birational Geometry of Hypersurfaces, pp. 165–198. Unione Mat. Italiana LN, vol. 26. Springer (2019)
Iliev, A., Kapustka, G., Kapustka, M., Ranestad, K.: Hyper-Kähler fourfolds and Kummer surfaces. Proc. Lond. Math. Soc. 115, 1276–1316 (2017)
Iliev, A., Kapustka, G., Kapustka, M., Ranestad, K.: EPW cubes. J. Reine Angew. Math. 748, 241–268 (2019)
Iliev, A., Ranestad, K.: K3 surfaces of genus 8 and varieties of sums of powers of cubic fourfolds. Trans. Am. Math. Soc. 353, 1455–1468 (2001)
Iskovskikh, V., Prokhorov, Y.: Fano Varieties, V. Algebraic Geometry. Springer, Berlin (1999)
Kapustka, G., Kapustka, M., Mongardi, G.: EPW sextics vs EPW cubes, (eprint) arXiv:2202.00301
Kawamata, Y.: On Fujita’s freeness conjecture for 3-folds and 4-folds. Math. Ann. 308, 491–505 (1997)
Kim, Y.-J., Laza, R.: A conjectural bound on the second Betti number for hyper-Kähler manifolds. Bull. Soc. Math. Fr. 148, 467–480 (2020)
Knutsen, A.L.: On \(k\)th-order embeddings of K3 surfaces and Enriques surfaces. Manuscr. Math. 104, 211–237 (2001)
Kuznetsov, A.: Derived categories of cubic fourfolds. In: Cohomological and Geometric Approaches to Rationality Problems, pp. 219–243, Progr. Math., vol. 282. Birkhäuser, Boston (2010)
James, D.G.: On Witt’s theorem for unimodular quadratic forms. Pac. J. Math. 26, 303–316 (1968)
Laface, A.: Mini-course on K3 surfaces. http://halgebra.math.msu.su/Lie/2011-2012/corso-k3.pdf
Lai, K.-W.: New cubic fourfolds with odd degree unirational parametrizations. Algebra Number Theory 11, 1597–1626 (2017)
Laza, R.: The moduli space of cubic fourfolds via the period map. Ann. Math. 172, 673–711 (2010)
Le Potier, J.: Dualité étrange, sur les surfaces (2005). https://www.imj-prg.fr/tga/jlp/Brest.071105.pdf
Lehn, C., Lehn, M., Sorger, C., van Straten, D.: Twisted cubics on cubic fourfolds. J. Reine Angew. Math. 731, 87–128 (2017)
Li, C., Pertusi, L., Zhao, X.: Twisted cubics on cubic fourfolds and stability conditions (eprint)arXiv:1802.01134
Li, J., Liedtke, C.: Rational curves on K3 surfaces. Invent. Math. 188, 713–727 (2012)
Liedtke, C.: Lectures on supersingular K3 surfaces and the crystalline Torelli theorem. In: Proceedings of the Schiermonnikoog Conference, K3 Surfaces and their Moduli, Progress in Mathematics, vol. 315. Birkhäuser, Basel (2015)
Looijenga, E.: The period map for cubic fourfolds. Invent. Math. 177, 213–233 (2009)
Looijenga, E.: Teichmüller spaces and Torelli theorems for hyperkähler manifolds. Math. Z. 298, 261–279 (2021)
Marian, A., Oprea, D.: Generic strange duality for K3 surfaces, with an appendix by Yoshioka, K. Duke Math. J. 162, 1463–1501 (2013)
Markman, E.: Integral constraints on the monodromy group of the hyperKähler resolution of a symmetric product of a K3 surface. Int. J. Math. 21, 169–223 (2010)
Markman, E.: A survey of Torelli and monodromy results for holomorphic-symplectic varieties. In: Complex and Differential Geometry, pp. 257–322, Springer Proc. Math., vol. 8. Springer, Heidelberg (2011)
Markman, E.: Prime exceptional divisors on holomorphic symplectic varieties and monodromy-reflections. Kyoto J. Math. 53, 345–403 (2013)
Markman, E., Mehrotra, S.: Hilbert schemes of K3 surfaces are dense in moduli. Math. Nachr. 290, 876–884 (2017)
Markman, E., Yoshioka, K.: A proof of the Kawamata–Morrison Cone Conjecture for holomorphic symplectic varieties of K3\(^{[n]}\) or generalized Kummer deformation type. Int. Math. Res. Not. 24, 13563–13574 (2015)
Matsushita, D.: On almost holomorphic Lagrangian fibrations. Math. Ann. 358, 565–572 (2014)
Mongardi, G.: Automorphisms of Hyperkähler manifolds, Ph.D. thesis, Università Roma Tre (2013) (eprint). arXiv:1303.4670
Mongardi, G.: A note on the Kähler and Mori cones of hyperkähler manifolds. Asian J. Math. 19, 583–591 (2015)
Morrison, D.: The Geometry of K3 Surfaces, Lectures Delivered at the Scuola Matematica Interuniversitaria (SIM), Cortona (1988). http://web.math.ucsb.edu/~drm/manuscripts/cortona.pdf
Mukai, S.: Symplectic structure of the moduli space of sheaves on an abelian or K3 surface. Invent. Math. 77, 101–116 (1984)
Mukai, S.: Curves, K3 surfaces and Fano 3-folds of genus \(\le 10\). In: Algebraic Geometry and Commutative Algebra, vol. I, pp. 357–377. Kinokuniya, Tokyo (1988)
Mukai, S.: Biregular classification of Fano 3-folds and Fano manifolds of coindex 3. Proc. Natl. Acad. Sci. U.S.A. 86, 3000–3002 (1989)
Mukai, S.: Polarized K3 surfaces of genus 18 and 20. In: Complex Projective Geometry (Trieste, 1989/Bergen, 1989), pp. 264–276, London Math. Soc. Lecture Note Ser., vol. 179. Cambridge Univ. Press, Cambridge (1992)
Mukai, S.: Curves and K3 surfaces of genus eleven. In: Moduli of vector bundles (Sanda, 1994; Kyoto, 1994), pp. 189–197, Lecture Notes in Pure and Appl. Math., vol. 179. Dekker, New York (1996)
Mukai, S.: Polarized K3 surfaces of genus thirteen. In: Moduli Spaces and Arithmetic Geometry, pp. 315–326, Adv. Stud. Pure Math., vol. 45. Math. Soc. Japan, Tokyo (2006)
Mukai, S.: K3 surfaces of genus sixteen. In: Minimal Models and Extremal Rays (Kyoto, 2011), pp. 379–396, Adv. Stud. Pure Math., vol. 70. Math. Soc. Japan (2016)
Mukherjee, J., Raychaudhury, D.: Remarks on projective normality for certain Calabi–Yau and hyperkähler varieties. J. Pure Appl. Algebra 224, 106383 (2020)
Nagell, T.: Introduction to Number Theory, 2nd edn. Chelsea Publishing Co., New York (1964)
Nikulin, V.: Integral symmetric bilinear forms and some of their geometric applications. Izv. Akad. Nauk SSSR Ser. Mat. 43, 111–177 (1979). English transl.: Math. USSR Izv. 14, 103–167 (1980)
Nuer, H.: Unirationality of moduli spaces of special cubic fourfolds and K3 surfaces. In: Rationality Problems in Algebraic Geometry, Levico Terme, Italy, 2015, pp. 161–167, Lecture Notes in Math., vol. 2172. Springer International Publishing (2016)
O’Grady, K.: Desingularized moduli spaces of sheaves on a K3. J. Reine Angew. Math. 512, 49–117 (1999)
O’Grady, K.: A new six-dimensional irreducible symplectic variety. J. Algebr. Geom. 12, 435–505 (2003)
O’Grady, K.: Involutions and linear systems on holomorphic symplectic manifolds. Geom. Funct. Anal. 15, 1223–1274 (2005)
O’Grady, K.: Dual double EPW-sextics and their periods. Pure Appl. Math. Q. 4, 427–468 (2008)
O’Grady, K.: Periods of double EPW-sextics. Math. Z. 280, 485–524 (2015)
Oguiso, K.: K3 surfaces via almost-primes. Math. Res. Lett. 9, 47–63 (2002)
Oguiso, K.: Tits alternative in hyperkähler manifolds. Math. Res. Lett. 13, 307–316 (2006)
Oguiso, K.: Bimeromorphic automorphism groups of non-projective hyperkähler manifolds—a note inspired by C. T. McMullen. J. Differ. Geom. 78, 163–191 (2008)
Oguiso, K.: Automorphism groups of Calabi–Yau manifolds of Picard number two. J. Algebr. Geom. 23, 775–795 (2014)
Oguiso K.: Free Automorphisms of Positive Entropy on Smooth Kähler Surfaces. In: Algebraic Geometry in East Asia, Taipei 2011, pp. 187–199, Adv. Stud. Pure Math., vol. 65. Math. Soc. Japan, Tokyo (2015)
Ortiz, A.: Riemann–Roch polynomials of the known Hyperkähler manifolds (eprint)arXiv:2006.09307
Saint-Donat, B.: Projective models of K-3 surfaces. Am. J. Math. 96, 602–639 (1974)
Sawon, J.: A bound on the second Betti number of hyperkähler manifolds of complex dimension six. Eur. J. Math. 8, 1196–1212 (2022)
Serre, J.-P.: Cours d’arithmétique. P.U.F, Paris (1970)
Song, J.: On the image of the period map for polarized hyper Kähler manifolds of \(\text{ K3}^{[m]}\)-type. Int. Math. Res. Not. IMRN (eprint, to appear) arXiv:2101.04791
Tanimoto, S., Várilly-Alvarado, A.: Kodaira dimension of moduli of special cubic fourfolds. J. Reine Angew. Math. 752, 265–300 (2019)
van den Dries, B.: Degenerations of cubic fourfolds and holomorphic symplectic geometry, Ph.D. thesis, Universiteit Utrecht (2012). https://dspace.library.uu.nl/bitstream/handle/1874/233790/vandendries.pdf
Verbitsky, M.: Mapping class group and a global Torelli theorem for hyper Kähler manifolds. Appendix A by Eyal Markman. Duke Math. J. 162, 2929–2986 (2013)
Viehweg, E.: Weak positivity and the stability of certain Hilbert points. III. Invent. Math. 101, 521–543 (1990)
Voisin, C.: Théorème de Torelli pour les cubiques de \(\textbf{P}^5\). Invent. Math. 86, 577–601 (1986). Erratum: A Torelli theorem for cubics in \(\textbf{P}^5\). Invent. Math. 172, 455–458 (2008)
Voisin, C.: Remarks and questions on coisotropic subvarieties and 0-cycles of hyper-Kähler varieties, in K3 surfaces and their moduli, pp. 365–399, Progr. Math., vol. 315. Birkhäuser, Basel (2016)
Yoshioka, K.: Moduli spaces of stable sheaves on abelian surfaces. Math. Ann. 321, 817–884 (2001)
Author information
Authors and Affiliations
Corresponding author
Additional information
These notes were originally written (and later expanded) for two different mini-courses, one given for a summer school on Texel Island, The Netherlands, August 28–September 1, 2017, and the other for the CIMPA Research School organized at the Pontificia Universidad Católica del Perú in Lima, Peru, September 4–15, 2017. The author would like to thank both sets of organizers for their support: Bas Edixhoven (\(\dagger \)), Gavril Farkas, Gerard van der Geer, Jürg Kramer, and Lenny Taelman for the first school, Richard Gonzáles and Clementa Alonso for the CIMPA school.
Appendices
Pell-Type Equations
We state or prove a few elementary results on some diophantine equations.
Given nonzero integers e and t with \(e>0\), we denote by \({\mathscr {P}}_e(t)\) the Pell-type equation
where a and b are integers (the usual Pell equation is the case \(t=1\)). A solution (a, b) of this equation is called positive if \(a>0\) and \(b>0\). If e is not a perfect square, (a, b) is a solution if and only if the norm of \(a+b\sqrt{e}\) in the quadratic number field \(\textbf{Q}(\sqrt{e})\) is t.
A positive solution with minimal a is called the minimal solution; it is also the positive solution (a, b) for which the “slope” \(b/a=\sqrt{\frac{1}{e }-\frac{t}{ea^2}}\) is minimal when \(t>0\), maximal when \(t<0\). Since the function \(x\mapsto x+\frac{t}{x}\) is increasing on the interval \((\sqrt{|t|},+\infty )\), the minimal solution is also the one for which the real number \(a+b\sqrt{e}\) is \( >\sqrt{|t|}\) and minimal.
Assume that e is not a perfect square. There is always a minimal solution \((a_1,b_1)\) to the Pell equation \({\mathscr {P}}_e(1)\) and if \(x_1:=a_1+b_1\sqrt{e}\), all the solutions of the equation \({\mathscr {P}}_e(1)\) correspond to the “powers” \(\pm x_1^n\), for \(n\in \textbf{Z}\), in \( \textbf{Z}[\sqrt{e}]\).
If an equation \({\mathscr {P}}_e(t)\) has a solution (a, b), the elements \(\pm (a+b\sqrt{e})x_1^n\) of \(\textbf{Z}[\sqrt{e}]\), for \(n\in \textbf{Z}\), all give rise to solutions of \({\mathscr {P}}_e(t)\) which are said to be associated with (a, b). The set of all solutions of \({\mathscr {P}}_e(t)\) associated with each other form a class of solutions. A class and its conjugate (generated by \((a,-b)\)) may be distinct or equal.
Assume that t is positive but not a perfect square. Let (a, b) be a solution to the equation \({\mathscr {P}}_e(t)\) and set \(x:=a+b\sqrt{e}\). If \(x=\sqrt{t}\), we have \({\bar{x}}=t/x=x\), hence \(b=0\); this contradicts our hypothesis that t is not a perfect square, hence \(x\ne \sqrt{t}\).
A class of solutions to the equation \({\mathscr {P}}_e(t)\) and its conjugate give rise to real numbers which are ordered as followsFootnote 55
where \(x_t=a_t+b_t\sqrt{e}\) corresponds to a solution which is minimal in its class and \({\bar{x}}_t\) is its conjugate. We have \(x_t= {\bar{x}}_tx_1\) if and only if the class of the solution \((a_t,b_t)\) is associated with its conjugate. The inequality \(x_t\le {\bar{x}}_tx_1\) implies \(a_t\le a_ta_1-eb_tb_1\), hence
This inequality between slopes also holds for the solution \(\bar{x}_tx_1\) in the conjugate class (because \(({\bar{x}}_tx_1)x_1^{-1}=\bar{x}_t<\sqrt{t}\)) but for no other positive solutions in these two classes.
We will need the following variation on this theme. We still assume that t is positive and not a perfect square. Let \((a'_t,b'_t)\) be the minimal positive solution to the equation \({\mathscr {P}}_{4e}(t)\) (if it exists) and set \(x'_t:= a'_t+b'_t\sqrt{4e}\).Footnote 56
If \(b_1\) is even, \((a_1,b_1/2)\) is the minimal solution to the equation \({\mathscr {P}}_{4e}(1)\) and we obtain from (33) the inequality
As above, the only other solution (among the class of \((a'_t,b'_t)\) and its conjugate) for which this inequality between slopes also holds is the “next” solution, which corresponds to \({\bar{x}}'_tx_1\).
If \(b_1\) is odd, \((a'_1,b'_1)= (2eb_1^2+1,a_1b_1)\) is the minimal solution to the equation \({\mathscr {P}}_{4e}(1)\), so that \(x'_1=x_1^2\). The solutions associated with \((a'_t,b'_t)\) correspond to the \(\pm x'_tx_1^{2n}\), \(n\in \textbf{Z}\). We still get from (33) the inequality
which is in fact strict.Footnote 57 No other solution associated with \((a'_t,b'_t)\) or its conjugate satisfies this inequality between slopes.
The following criterion [88, Theorem 110] ensures that in some cases, any two classes of solutions are conjugate, so that the discussion above applies to all solutions.
Lemma A.1
Let u be a positive integer which is either prime or equal to 1, let e be a positive integer which is not a perfect square, and let \(\varepsilon \in \{-1,1\}\). If the equation \({\mathscr {P}}_e(\varepsilon u)\) is solvable, it has one or two classes of solutions according to whether u divides 2e or not; if there are two classes, they are conjugate.
We now extend slightly the class of equations that we are considering: if \(e_1\) and \(e_2\) are positive integers, we denote by \({\mathscr {P}}_{e_1,e_2}(t)\) the equation
Given an integral solution (a, b) to \({\mathscr {P}}_{e_1,e_2}(t)\), we obtain a solution \((e_1a,b)\) to \({\mathscr {P}}_{e_1e_2}(e_1t)\). If \(e_1\) is square free, all the solutions to \({\mathscr {P}}_{e_1e_2}(e_1t)\) arise in this way; in general, all the solutions whose first argument is divisible by \(e_1\) arise. A positive solution (a, b) to \({\mathscr {P}}_{e_1,e_2}(t)\) is called minimal if a is minimal. If \(e_1e_2\) is not a perfect square, we say that the solutions (a, b) and \((a',b')\) of \({\mathscr {P}}_{e_1,e_2}(t)\) are associated if \((e_1a,b)\) and \((e_1a',b')\) are associated solutions of \({\mathscr {P}}_{e_1e_2}(e_1t)\).Footnote 58
Let \(\varepsilon \in \{-1,1\}\); assume that the equation \({\mathscr {P}}_{e_1,e_2}(\varepsilon )\) has a solution \((a_\varepsilon ,b_\varepsilon )\) and set \(x_\varepsilon := e_1a_\varepsilon +b_\varepsilon \sqrt{e_1e_2}\). Let \((a,b)\in \textbf{Z}^2\) and set \(x:=e_1a+b\sqrt{e_1e_2}\). We have
where \(x{\bar{x}}=e_1\varepsilon y{\bar{y}}\). In particular, x is a solution to the equation \({\mathscr {P}}_{e_1 e_2}(e_1t)\) if and only if y is a solution to the equation \({\mathscr {P}}_{e_1 e_2}( \varepsilon t)\). This defines a bijection between the set of solutions to the equation \({\mathscr {P}}_{e_1, e_2}(t)\) and the set of solutions to the equation \({\mathscr {P}}_{e_1 e_2}(\varepsilon t)\) (the inverse bijection is given by \(y\mapsto x=\varepsilon {\bar{x}}_\varepsilon y\)).
The proof of the following lemma is left to the reader.
Lemma A.2
Let \(e_1\) and \(e_2\) be positive integers. Assume that for some \(\varepsilon \in \{-1,1\}\), the equation \({\mathscr {P}}_{e_1,e_2}(\varepsilon )\) is solvable and let \((a_\varepsilon ,b_\varepsilon )\) be its minimal solution. Then, \(e_1e_2\) is not a perfect square and the minimal solution of the equation \({\mathscr {P}}_{e_1e_2}(1)\) is \((e_1a_\varepsilon ^{2}+e_2b_\varepsilon ^2,2a_\varepsilon b_\varepsilon )\), unless \(e_1= \varepsilon = 1\) or \(e_2=-\varepsilon =1\),
We now assume \(t<0\) (the discussion is entirely analogous when \(t>0\) and leads to the reverse inequality in (38)) and \(-t\) is not a perfect square. Let \((a_t,b_t)\) be the minimal solution to the equation \({\mathscr {P}}_{e_1,e_2}(t )\) and set \(x_t:= e_1a_t+b_t\sqrt{e_1e_2}\), solution to the equation \({\mathscr {P}}_{e_1 e_2}(e_1t)\) which is minimal among all solutions whose first argument is divisible by \(e_1\). We have as in (33) the inequalities
with \(x_1:= \frac{1}{e_1}x_\varepsilon ^2\) by Lemma A.2. The increasing correspondence with the solutions to the equation \({\mathscr {P}}_{e_1 e_2}(\varepsilon t)\) that we described above maps \(x_tx_1^{-1}\) to \(\frac{1}{e_1}x_tx_1^{-1}x_\varepsilon =x_tx_\varepsilon ^{-1}\) and \(-{\bar{x}}_t\) to \(-\frac{1}{e_1}{\bar{x}}_tx_\varepsilon \). Since the product of these positive numbers is \(-t \), we have
In particular, \(-\frac{1}{e_1}{\bar{x}}_tx_\varepsilon \) corresponds to a positive solution, hence
Moreover, \((a_t,b_t)\) is the only positive solution to the equation \({\mathscr {P}}_{e_1,e_2}(t )\) among those appearing in (36) that satisfies this inequality. When |t| is prime, Lemma A.1 implies that any two classes of solutions are conjugate, hence all positive solutions appear in (36), and (38) holds for only one positive solution to the equation \({\mathscr {P}}_{e_1,e_2}(t )\).
Finally, one small variation: we assume that \((a_\varepsilon ,b_\varepsilon )\) is the minimal solution to the equation \({\mathscr {P}}_{e_1,e_2}(\varepsilon )\) but that \((a_t,b_t)\) is the minimal solution to the equation \({\mathscr {P}}_{e_1,4e_2}(t )\). Then we have
and, when |t| is prime, \((a_t,b_t)\) is the only solution that satisfies that inequality. The proof is exactly the same: since \(2a_\varepsilon b_\varepsilon \) is even, \(x_1\) still corresponds to the minimal solution to the equation \({\mathscr {P}}_{4e_1 e_2}(1)\); in (36), we have solutions to the equation \({\mathscr {P}}_{4e_1 e_2}(e_1t)\) and in (37), we have solutions to the equation \({\mathscr {P}}_{e_1 e_2}(\varepsilon t)\), but this does not change the reasoning.
The Image of the Period Map (with E. Macrì)
In this second appendix, we generalize Theorem 3.32 in all dimensions. Recall the set up: a polarization type \(\tau \) is the \(O(\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}})\)-orbit of a primitive element \(h_\tau \) of \( \Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}\) with positive square and \({}^m\!{\mathscr {M}}_\tau \) is the moduli space for hyper-Kähler manifolds of type \( {{\,\mathrm{{K3}}\,}}^{[m]}\) with a polarization of type \(\tau \). There is a period map
The goal of this appendix is to prove the following result.
Theorem B.1
(Bayer, Debarre–Macrì, Amerik–Verbitsky) Assume \(m\ge 2\). Let \(\tau \) be a polarization type. The image of the restriction of the period map \(\wp _{\tau }\) to any component of the moduli space \({}^m\!{\mathscr {M}}_\tau \) is the complement of a finite union of explicit Heegner divisors.
The procedure for listing these divisors will be explained in Remark B.6. The proof of the theorem is based on the description of the nef cone for hyper-Kähler manifolds of type \({{\,\mathrm{{K3}}\,}}^{[m]}\) in [9, 78] (another proof follows from [4]). We start by revisiting these results. Recall (see (12)) that the (unimodular) extended K3 lattice is
Let X be a projective hyper-Kähler manifold of type \(K3^{[m]}\). We defined in Sect. 3.7.1 its Markman–Mukai lattice \({{\widetilde{\Lambda }}}_X\), isometric to \( {\widetilde{\Lambda }}_{{{\,\mathrm{{K3}}\,}}}\) and endowed with a weight-2 Hodge structure. It comes with a canonical morphism of Hodge structures \(\theta _X:H^2(X,\textbf{Z}) \hookrightarrow {\widetilde{\Lambda }}_{X}\) and a generator \({{\textbf{v}}}_X\) (of type (1, 1)) of \(\theta _X(H^2(X,\textbf{Z}))^\bot \) that satisfies \( {{\textbf{v}}}_X^2=2m-2\). We set
so that \({{\,\textrm{NS}\,}}(X)=\theta _X^{-1}({\widetilde{\Lambda }}_{\text {alg},X})\). Finally, we set
The hyperplanes \(\theta _X^{-1}({{\textbf{s}}}^\perp )\subset {{\,\textrm{NS}\,}}(X)\otimes \textbf{R}\), for \({{\textbf{s}}}\in {\mathscr {S}}_X\), are locally finite in the positive cone \({{\,\textrm{Pos}\,}}(X)\). The dual statement of [9, Theorem 1] is then the following (see also [11, Theorem 12.1]).
Theorem B.2
Let X be a projective hyper-Kähler manifold of type \(K3^{[m]}\). The ample cone of X is the connected component of
that contains the class of an ample divisor.
Note that changing \({{\textbf{v}}}_X\) into \(-{{\textbf{v}}}_X\) changes \({\mathscr {S}}_X\) into \(-{\mathscr {S}}_X\), but the set in (40) remains the same.
Example B.3
Let (S, L) be a polarized K3 surface of degree 2e and let r be a positive integer. Recall from Remark 4.5 that the moduli space \(X:={\mathscr {M}}(r,L,r)\), when smooth, is a hyper-Kähler manifold of type \({{\,\mathrm{{K3}}\,}}^{[m]}\), where \(m:=1-r^2+e\), and carries a class H of square 2. In fact, the vector \({{\textbf{v}}}_X\) above is \((r,-r,L)\in U\oplus {\Lambda }_{{{\,\mathrm{{K3}}\,}}}={\widetilde{\Lambda }}_{{{\,\mathrm{{K3}}\,}}}\) and H is \(\theta _X^{-1}((1,1,0))\). Consider the vector \({{\textbf{s}}}:= (-1,1,0)\in {\widetilde{\Lambda }}_{\text {alg},X}\). We have \({{\textbf{s}}}^2=-2\), \({{\textbf{s}}}\cdot {{\textbf{v}}}_X=2r \), and \(H\in \theta _X^{-1}({{\textbf{s}}}^\perp )\). When \(2r\le {{\textbf{v}}}_X^2/2= m-1\), that is, when \( e\ge r^2+2r\), the class \({{\textbf{s}}}\) is in \({\mathscr {S}}_X\), hence, by the theorem, H is not ample on X.
Assume now \({{\,\textrm{Pic}\,}}(S)=\textbf{Z}L\), so that the Picard number of X is 2. When \(r^2<e\le r^2+2r-1\), the class H is ample on X ([93, Corollary 4.15] and Remark 4.5).
It can actually be shown that for all \(e>r^2\), the class H is nef on X.Footnote 59 However, we do not know the nef cone except when \(r=1\), where \(X=S^{[e]}\) and everything is described in Example 4.11 (see also Example 4.6 for the case \(e=r^2+1\)). One can only say that
-
when \(r^2<e\le r^2+2r-1\), the manifold X carries a biregular nontrivial involution (Remark 4.5) that interchanges the two extremal rays of \({{\,\textrm{Nef}\,}}(X)\);Footnote 60
-
when \( e\ge r^2+2r\), one ray is spanned by H, the other is rational by [99, Theorem 1.3(1)].
We rewrite Theorem B.2 in terms of the existence of certain rank-2 lattices in the Néron–Severi group as follows.
Proposition B.4
Let \(m\ge 2\). Let X be a projective hyper-Kähler manifold of type \(K3^{[m]}\) and let \(h_X\in {{\,\textrm{NS}\,}}(X)\) be a primitive class such that \(h_X^2>0\). The following conditions are equivalent:
-
(i)
there exist a projective hyper-Kähler manifold Y of type \(K3^{[m]}\), an ample primitive class \(h_Y\in {{\,\textrm{NS}\,}}(Y)\), and a Hodge isometry \(g:H^2(X,\textbf{Z}) {{\,\mathrm{{\mathop {\rightarrow }\limits ^{{}_{\scriptstyle \sim }}}}\,}}H^2(Y,\textbf{Z})\) such that \([\theta _X]=[\theta _Y\circ g]\) and \(g(h_X)=h_Y\);
-
(ii)
there are no rank-2 sublattices \(L_X\subset {{\,\textrm{NS}\,}}(X)\) such that
-
\(h_X\in L_X\), and
-
there exist integers \(0\le k \le m-1\) and \(a\ge -1\), and \(\kappa _X\in L_X\), such that
$$\begin{aligned} \kappa _X^2 = 2(m-1) ( 4 (m-1) a -k^2 ), \qquad \kappa _X\cdot h_X =0, \qquad \frac{\theta _X(\kappa _X) + k {{\textbf{v}}}_X}{2(m-1)} \in {\widetilde{\Lambda }}_{{{\,\mathrm{{K3}}\,}}}. \end{aligned}$$
-
Again, if one changes \({{\textbf{v}}}_X\) into \(-{{\textbf{v}}}_X\), one needs to take \(-\kappa _X\) instead of \( \kappa _X\).
Proof
Assume that a pair \((Y,h_Y)\) satisfies (i) but that there is a lattice \(L_X\) as in (ii). The rank-2 sublattice \(L_Y:=g(L_X)\subset H^2(Y,\textbf{Z})\) is contained in \( {{\,\textrm{NS}\,}}(Y)\). We also let \(\kappa _Y:=g(\kappa _X)\in L_Y\) and choose the generator \({{\textbf{v}}}_Y:={{\textbf{v}}}_X\in {\widetilde{\Lambda }}_{{{\,\mathrm{{K3}}\,}}}\) of \(H^2(Y,\textbf{Z})^\perp \). We then have
and
Moreover, we have \({{\textbf{s}}}_Y\in {\widetilde{\Lambda }}_{\text {alg},Y}\). By Theorem B.2, \(h_Y\) cannot be ample on Y, a contradiction.
Conversely, assume that there exist no lattices \(L_X\) as in (ii). By [72, Lemma 6.22], there exists a Hodge isometry \(g':H^2(X,\textbf{Z}){{\,\mathrm{{\mathop {\rightarrow }\limits ^{{}_{\scriptstyle \sim }}}}\,}}H^2(X,\textbf{Z})\) such that \([\theta _X\circ g']=[\theta _X]\) and \(g'(h_X)\in \overline{{{\,\textrm{Mov}\,}}}(X)\). Since \(g'(h_X)\in {{\,\textrm{NS}\,}}(X)\) and \(g'(h_X)^2>0\), by [72, Theorem 6.17 and Lemma 6.22] and [41, Theorem 7], there exist a projective hyper-Kähler manifold Y of type \(K3^{[m]}\), a nef divisor class \(h_Y\in {{\,\textrm{Nef}\,}}(Y)\), and a Hodge isometry \(g'':H^2(X,\textbf{Z}) {{\,\mathrm{{\mathop {\rightarrow }\limits ^{{}_{\scriptstyle \sim }}}}\,}}H^2(Y,\textbf{Z})\) such that \([\theta _X]=[\theta _Y\circ g'']\) and \(g''(g'(h_X))=h_Y\). Assume that \(h_Y\) is not ample. Since \(h_Y^2>0\) and \(h_Y\) is nef, there exists by Theorem B.2 a class \({{\textbf{s}}}_Y\in {\mathscr {S}}_Y\) such that \({{\textbf{s}}}_Y\cdot \theta _Y(h_Y)=0\). We set \(a:=\frac{1}{2}{{\textbf{s}}}_Y^2\), \(k:= {{\textbf{s}}}_Y\cdot {{\textbf{v}}}_Y\), and
Let \(L_Y\) be the sublattice of \(H^2(Y,\textbf{Z})\) generated by \(h_Y\) and \(\kappa _Y\). Then \(L_X:=g^{-1}(L_Y)\) satisfies the conditions in (ii), a contradiction. \(\square \)
When \(m-1\) is a prime number, this can be written only in terms of \(H^2(X,\textbf{Z})\).
Proposition B.5
Assume that \(p:=m-1 \) is either 1 or a prime number. Let X be a projective hyper-Kähler manifold of type \(K3^{[m]}\) and let \(h_X\in {{\,\textrm{NS}\,}}(X)\) be a primitive class such that \(h_X^2>0\). The following conditions are equivalent:
-
(i)
there exist a projective hyper-Kähler manifold Y of type \(K3^{[m]}\), an ample primitive class \(h_Y\in {{\,\textrm{NS}\,}}(Y)\), and a Hodge isometry \(g:H^2(X,\textbf{Z}) {{\,\mathrm{{\mathop {\rightarrow }\limits ^{{}_{\scriptstyle \sim }}}}\,}}H^2(Y,\textbf{Z})\) such that \(g(h_X)=h_Y\);
-
(ii)
there are no rank-2 sublattices \(L_X\subset {{\,\textrm{NS}\,}}(X)\) such that
-
\(h_X\in L_X\), and
-
there exist integers \(0\le k \le p\) and \(a\ge -1\), and \(\kappa _X\in L_X\), such that
$$\begin{aligned} \kappa _X^2 = 2p ( 4 p a -k^2 ), \qquad \kappa _X\cdot h_X =0, \qquad 2p \mid \mathop {\textrm{div}}\nolimits _{H^2(X,\textbf{Z})}(\kappa _X). \end{aligned}$$
-
Proof
As explained in [72, Sects. 9.1.1 and 9.1.2], under our assumption on m, there is a unique \(O({\widetilde{\Lambda }}_{{{\,\mathrm{{K3}}\,}}})\)-orbit of primitive isometric embeddings \( \Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}\hookrightarrow {\widetilde{\Lambda }}_{{{\,\mathrm{{K3}}\,}}}\). This implies that any Hodge isometry \( H^2(X,\textbf{Z}) {{\,\mathrm{{\mathop {\rightarrow }\limits ^{{}_{\scriptstyle \sim }}}}\,}}H^2(Y,\textbf{Z})\) commutes with the orbits \([\theta _X]\) and \([\theta _Y]\).
We can choose the embedding \(\theta :\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}\hookrightarrow {\widetilde{\Lambda }}_{{{\,\mathrm{{K3}}\,}}}\) as follows. Let us fix a canonical basis (u, v) of a hyperbolic plane U in \({\widetilde{\Lambda }}_{{{\,\mathrm{{K3}}\,}}}\). We define \(\theta \) by mapping the generator \(\ell \) of \(I_1(-2p)\) to \(u-pv\). We also choose \({{\textbf{v}}}:=u+pv\) as the generator of \(\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}^\perp \).
By Proposition B.4, we only have to show that given a class \(\kappa \in \Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}\) with divisibility 2p and such that \(\kappa ^2 = 2p ( 4p a -k^2 )\), either \( \theta (\kappa )+ k{{\textbf{v}}}\) or \(\theta (-\kappa )+ k{{\textbf{v}}}\) is divisible by 2p in \({\widetilde{\Lambda }}_{{{\,\mathrm{{K3}}\,}}}\). Since \(\mathop {\textrm{div}}\nolimits _{H^2(X,\textbf{Z})}(\kappa )\) is divisible by 2p, we can write \(\kappa =2pw+r\ell \), with \(w\in U^{\oplus 3}\oplus E_8(-1)^{\oplus 2}\) and \(r\in \textbf{Z}\). By computing \(\kappa ^2\), we obtain the equality
In particular, \(r^2-k^2\) is even, hence so are \( r + k \) and \( -r + k \). Moreover, p divides \(r^2-k^2\), hence also \( \varepsilon r + k \), for some \(\varepsilon \in \{-1,1\}\). Then
is divisible by 2p, as we wanted. \(\square \)
Before proving the theorem, we briefly review polarized marked hyper-Kähler manifolds of type \({{\,\mathrm{{K3}}\,}}^{[m]}\), their moduli spaces, and their periods, following the presentation in [72, Sect. 7] (see also [6, Sect. 1]).
Let \( {}^m{\mathfrak {M}}\) be the (smooth, nonHausdorff, 21-dimensional) coarse moduli space of marked hyper-Kähler manifolds of type \({{\,\mathrm{{K3}}\,}}^{[m]}\) (see [45, Sect. 6.3.3]), consisting of isomorphisms classes of pairs \((X,\eta )\) such that X is a compact complex (not necessarily projective) hyper-Kähler manifold of type \({{\,\mathrm{{K3}}\,}}^{[m]}\) and \(\eta :H^2(X,\textbf{Z}){{\,\mathrm{{\mathop {\rightarrow }\limits ^{{}_{\scriptstyle \sim }}}}\,}}\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}\) is an isometry. We let \(({}^m{\mathfrak {M}}^{\,t})_{t\in {\mathfrak {t}}}\) be the family of connected components of \({}^m{\mathfrak {M}}\). By [72, Lemma 7.5], the set \({\mathfrak {t}}\) is finite and is acted on transitively by the group \(O(\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}})\).
Let \(h\in \Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}\) be a class with \(h^2>0\) and let \(t\in {\mathfrak {t}}\). Let \({}^m{\mathfrak {M}}^{\,t,+}_{h^\perp }\subset {}^m{\mathfrak {M}}^{\,t}\) be the subset parametrizing the pairs \((X,\eta )\) for which the class \(\eta ^{-1}(h)\) is of Hodge type (1, 1) and belongs to the positive cone of X, and let \( {}^m{\mathfrak {M}}^{\,t,a}_{h^\perp }\subset {}^m{\mathfrak {M}}^{\,t,+}_{h^\perp }\) be the open subset where \(\eta ^{-1}(h)\) is ample on X. By [72, Corollary 7.3], \({}^m{\mathfrak {M}}^{\,t,a}_{h^\perp }\) is connected, Hausdorff, and 20-dimensional.
The relation with our moduli spaces \({}^m\!{\mathscr {M}}_\tau \) is as follows. Let \(\tau \) be a polarization type and let M be an irreducible component of \({}^m\!{\mathscr {M}}_\tau \). Pick a point \((X_0,H_0)\) of M and choose a marking \(\eta _0:H^2(X_0,\textbf{Z}){{\,\mathrm{{\mathop {\rightarrow }\limits ^{{}_{\scriptstyle \sim }}}}\,}}\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}\). If \(h_0:=\eta _0( H_0 )\), the \(O(\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}})\)-orbit of \(h_0\) is the polarization type \(\tau \), and the pair \((X_0,\eta _0)\) is in \({}^m{\mathfrak {M}}^{\,t_0,a}_{h_0^\perp }\), for some \(t_0\in {\mathfrak {t}}\). As in [72, (7.4)], we consider the disjoint union
It is acted on by \(O(\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}})\) and, by [72, Lemma 8.3], there is an analytic bijection
Proof of Theorem B.1
Let M be an irreducible component of \({}^m\!{\mathscr {M}}_\tau \). Pick a point \((X_0,H_0)\) of M and choose a marking \(\eta _0:H^2(X_0,\textbf{Z}){{\,\mathrm{{\mathop {\rightarrow }\limits ^{{}_{\scriptstyle \sim }}}}\,}}\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}\). As above, set \(h_0:=\eta _0( H_0 )\in \Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}\) and let \(t_0\in {\mathfrak {t}}\) be such that the pair \((X_0,\eta _0)\) is in \({}^m{\mathfrak {M}}^{\,t_0,a}_{h_0^\perp }\). Given another point (X, H) of M, by using the bijection (41), we can always find a marking \(\eta :H^2(X,\textbf{Z}){{\,\mathrm{{\mathop {\rightarrow }\limits ^{{}_{\scriptstyle \sim }}}}\,}}{\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}}\) for which \((X, \eta )\) is in \({}^m{\mathfrak {M}}^{\,t_0,a}_{h_0^\perp }\) and \(H =\eta ^{-1}(h_0)\).
By [72, Corollary 9.10], for all \((X,\eta )\in {}^m{\mathfrak {M}}^{\,t_0}\), the primitive embeddings
are all in the same \(O({\widetilde{\Lambda }}_{{{\,\mathrm{{K3}}\,}}})\)-orbit. We fix one such embedding \(\theta \) and a generator \({{\textbf{v}}}\in {\widetilde{\Lambda }}_{{{\,\mathrm{{K3}}\,}}}\) of \(\theta (\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}})^\perp \). As in Proposition B.4, we consider the Heegner divisors \( {\mathscr {D}}_{\tau ,K}\) in the quotient \( {\mathscr {P}}_\tau := {\widehat{O}}({\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}} ,h_0)\backslash \Omega _{\tau }\), where K is a primitive, rank-2, signature-(1, 1), sublattice of \({\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}}\) such that \(h_0\in K\) and there exist integers \(0\le k \le m-1\) and \(a\ge -1\), and \(\kappa \in K\) with
There are finitely many such divisors. Indeed, since the signature of K is (1, 1), we have \(\kappa ^2<0\). Moreover, we have \(\kappa ^2\ge 2(m-1) ( -4 (m-1) -(m-1)^2 )\), hence \(\kappa ^2\) may take only finitely many values. As explained in the proof of Lemma 3.28, this implies that there only finitely many Heegner divisors of the above form.
We claim that the image of the period map
coincides with the complement of the union of these Heegner divisors. We first show the image does not meet these divisors. Let \((X,H)\in M\) and, as explained above, choose a marking \(\eta \) such that \((X,\eta )\in {}^m{\mathfrak {M}}^{\,t_0,a}_{h_0^\perp }\), where \(h_0:=\eta (H)\). If \((X,H)\in {\mathscr {D}}_{\tau ,K}\), for K as above, the lattice \(K\subset {{\,\textrm{NS}\,}}(X)\) satisfies condition (ii) of Proposition B.4, which is impossible.
Conversely, take a point \(x\in {\mathscr {P}}_{\tau }\). The refined period map defined in [72, (7.3)] is surjective (this is a consequence of [45, Theorem 8.1]). Hence there exists \((X,\eta _X)\in {}^m{\mathfrak {M}}^{\,t_0,+}_{h_0^\perp }\) such that \(H_X:=\eta _X^{-1}(h_0)\) is an algebraic class in the positive cone of X and \((X,H_X)\) has period point x. By [45, Theorem 3.11], X is projective. We can now apply Proposition B.4: if x is outside the union of the Heegner divisors described above, there exist a projective hyper-Kähler manifold Y of type \(K3^{[m]}\), an ample primitive class \(H_Y\), and a Hodge isometry \(g:H^2(X,\textbf{Z}) {{\,\mathrm{{\mathop {\rightarrow }\limits ^{{}_{\scriptstyle \sim }}}}\,}}H^2(Y,\textbf{Z})\) such that \([\theta _X]=[\theta _Y\circ g]\) and \(g(H_X)=H_Y\). By [72, Theorem 9.8], g is a parallel transport operator; by [72, Definition 1.1(1)], this means that if \(\eta _Y:=\eta \circ g^{-1}\), the pair \((Y,\eta _Y)\) belongs to the same connected component \({}^m{\mathfrak {M}}^{\,t_0}\) of \({}^m{\mathfrak {M}}\). Moreover, \((Y,\eta _Y )\) is in \( {}^m{\mathfrak {M}}^{\,t_0,+}_{h_0^\perp }\) and since \(\eta _Y^{-1}(h_0)=H_Y\) is ample, it is even in \({}^m{\mathfrak {M}}^{\,t_0,a}_{h_0^\perp }\). By (41), it defines a point of M which still has period point x. This means that x is in the image of \({\mathscr {P}}_\tau \), which is what we wanted. \(\square \)
Remark B.6
Let us explain how to list the Heegner divisors referred to in the statement of Theorem B.1. Fix a representative \(h_\tau \in \Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}\) of the polarization \(\tau \). For each \(O({\widetilde{\Lambda }}_{{{\,\mathrm{{K3}}\,}}})\)-equivalence class of primitive embeddings \( \Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}\hookrightarrow {\widetilde{\Lambda }}_{{{\,\mathrm{{K3}}\,}}}\),Footnote 61 pick a representative \(\theta \) and a generator \({{\textbf{v}}}\) of \(\theta (\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}})^\perp \). Let T be the saturation in \({\widetilde{\Lambda }}_{{{\,\mathrm{{K3}}\,}}}\) of the sublattice generated by \(\theta (h_\tau )\) and \({{\textbf{v}}}\). By [6, Theorem 2.1], the abstract isometry class of the pair \((T,\theta (h_\tau ))\) determines a component M of \({}^m\!{\mathscr {M}}_\tau \) (and all the components are obtained in this fashion). Now list, for all integers \(0\le k \le m-1\) and \(a\ge -1\), all \( {\widehat{O}}({\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}},h_\tau )\)-orbits of primitive, rank-2, signature-(1, 1), sublattices K of \({\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}}\) such that \(h_\tau \in K\) and there exist \(\kappa \in K\) satisfying (42).
The image \(\wp _\tau (M)\) is then the complement in \({\mathscr {P}}_\tau \) of the union of the corresponding Heegner divisors \({\mathscr {D}}_{\tau ,K}\). The whole procedure is worked out in a particular case in Example B.7 below (there are more examples in Sect. 3.11 in the case \(m=2\)).
A priori, the image of \(\wp _{\tau }\) may be different when restricted to different components M of \({}^m\!{\mathscr {M}}_\tau \) (see [105] for more results in this direction).
Example B.7
The moduli space \({}^4\!{\mathscr {M}}_2^{(2)}\) for hyper-Kähler manifolds of type \({{\,\mathrm{{K3}}\,}}^{[4]}\) with a polarization of square 2 and divisibility 2 is irreducible (Theorem 3.5). Let us show that the image of the period map \({^4}\wp _{2}^{(2)}\) is the complement of the three irreducible Heegner divisors \({^4}{\mathscr {D}}_{2,2}^{(2)}\), \({^4}{\mathscr {D}}_{2,6}^{(2)}\), and \({^4}{\mathscr {D}}_{2,8}^{(2)}\).
We begin with the more general case where m is divisible by 4 and \(p:=m-1\) is an odd prime number. We follow the recipe given in Remark B.6. The irreducibility of \({}^m\!{\mathscr {M}}_2^{(2)}\) (Theorem 3.5) means that we can fix the embedding \(\theta :{\Lambda _{{{\,\mathrm{{K3}}\,}}^{[4]}}}\hookrightarrow {\widetilde{\Lambda }}_{{{\,\mathrm{{K3}}\,}}}\) and the class \(h=h_\tau \in {\Lambda _{{{\,\mathrm{{K3}}\,}}^{[4]}}}\) as we like. Let us fix bases \((u_i,v_i)\), for \(i\in \{1,\dots ,4\}\), for each of the four copies of U in \({\widetilde{\Lambda }}_{{{\,\mathrm{{K3}}\,}}}\). We choose the embedding
given by mapping the generator \(\ell \) of \(I_1(-2p)\) to \(u_1-pv_1\). We also set \({{\textbf{v}}}:=u_1+pv_1\) (so that \({{\textbf{v}}}^\perp =\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}\)) and \(h:= 2(u_2+\frac{m}{4}v_2) + \ell \).
As explained in Remark B.6 (and using Proposition B.5), the image of the period map is the complement of the Heegner divisors of the form \( {\mathscr {D}}_{\tau ,K}\), where K is a primitive, rank-2, sublattice of \( {\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}}\) such that \(h\in K\) and there exist integers \(0\le k \le p\) and \(a\ge -1\), and \(\kappa \in K\) with
Since we are interested in the lattices \(K^\bot \), this is equivalent, by strange duality, to looking at the lattices \(K^\bot \) in \(h^\bot ={\Lambda _{{{\,\mathrm{{K3}}\,}}^{[2]}}}\), where K now contains the primitive class \({{\textbf{v}}}\), of square 2p. This is a computation that was done during the proof of Proposition 3.29(2)(c): in the notation of that proof, if we write \(\kappa =b\kappa _\textrm{prim}\), with \(\kappa _\textrm{prim}\) primitive, and \({{\,\textrm{disc}\,}}(K^\bot )=:-2e\),
-
either \((\mathop {\textrm{div}}\nolimits _{{\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}}}(\kappa _\textrm{prim}),\kappa _\textrm{prim}^2)=(1,-2e/p)\) and \(p\mid e\);
-
or \((\mathop {\textrm{div}}\nolimits _{{\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}}}(\kappa _\textrm{prim}),\kappa _\textrm{prim}^2)=(p,-2pe)\) and \(p\not \mid e\).
In the first case, we have \( 2p\mid \mathop {\textrm{div}}\nolimits _{{\Lambda _{{{\,\mathrm{{K3}}\,}}^{[m]}}}}(\kappa ) =2b\) and, writing \(b=2pb'\) and \(e=pe'\), we obtain
This implies \(2p\mid k\), and since \(0\le k \le p\), we get \(k=0\), \(a=-1\), and \(e'=b'=1\). This corresponds to the irreducible divisor \({^m}{\mathscr {D}}_{2,2p}^{(2)}\).
In the second case, we write similarly \(b=2b'\) and we obtain
Writing \(k=2k'\), we get \( k^{\prime 2} -pa= eb^{\prime 2}\), with \(k'>0\).
Assume now \(p=3\). The only possible pairs (k, a) are then \((0,-1)\), (2, 0), and \((2,-1)\). When \((k,a)=(0,-1)\), the discussion above shows that we obtain the divisor \({^4}{\mathscr {D}}_{2,6}^{(2)}\).
When \((k,a)=(2,0)\), we obtain \(e=1\), hence the divisor \({^4}{\mathscr {D}}_{2,2}^{(2)}\). When \((k,a)=(2,-1)\), we obtain \(e\in \{1,4\}\), hence the extra divisor \({^4}{\mathscr {D}}_{2,8}^{(2)}\).
Example B.8
(a) The image of the period map \( {}^8\!{\mathscr {M}}_2^{(2)}\rightarrow {}^8\!{\mathscr {P}}_2^{(2)}\) is the complement of \({^8}{\mathscr {D}}_{2,2}^{(2)}\cup {^8}{\mathscr {D}}_{2,4}^{(2)}\cup {^8}{\mathscr {D}}_{2,8}^{(2)}\cup {^8}{\mathscr {D}}_{2,14}^{(2)}\cup {^8}{\mathscr {D}}_{2,16}^{(2)}\cup {^8}{\mathscr {D}}_{2,18}^{(2)}\cup {^8}{\mathscr {D}}_{2,22}^{(2)}\cup {^8}{\mathscr {D}}_{2,32}^{(2)}\).
(b) The image of the period map \( {}^{12}\!{\mathscr {M}}_2^{(2)}\rightarrow {}^{12}\!{\mathscr {P}}_2^{(2)}\) is the complement of \({^{12}}{\mathscr {D}}_{2,2}^{(2)}\cup {^{12}}{\mathscr {D}}_{2,6}^{(2)}\cup {^{12}}{\mathscr {D}}_{2,8}^{(2)}\cup {^{12}}{\mathscr {D}}_{2,10}^{(2)}\cup {^{12}}{\mathscr {D}}_{2,18}^{(2)}\cup {^{12}}{\mathscr {D}}_{2,22}^{(2)}\cup {^{12}}{\mathscr {D}}_{2,24}^{(2)}\cup {^{12}}{\mathscr {D}}_{2,28}^{(2)}\cup {^{12}}{\mathscr {D}}_{2,30}^{(2)}\cup {^{12}}{\mathscr {D}}_{2,32}^{(2)}\cup {^{12}}{\mathscr {D}}_{2,40}^{(2)}\cup {^{12}}{\mathscr {D}}_{2,50}^{(2)}\cup {^{12}}{\mathscr {D}}_{2,54}^{(2)}\cup {^{12}}{\mathscr {D}}_{2,72}^{(2)}\).
(c) Let p be a prime number such that \(p\equiv -1\pmod 4\). The complement of the image of the period map \( {}^{p+1}\!{\mathscr {M}}_2^{(2)}\rightarrow {}^{p+1}\!{\mathscr {P}}_2^{(2)}\) contains \({^{p+1}}{\mathscr {D}}_{2,2(l^2-pa)}^{(2)}\) for all \(0\le l\le \frac{p-1}{2}\) and \(-1\le a< l^2/p\), but none of the divisors \({^{p+1}}{\mathscr {D}}_{2,2e}^{(2)}\) for \(e> \frac{(p+1)^2}{4}\).
Remark B.9
The ample cone of a projective hyper-Kähler fourfold of type \(K3^{[2]}\) was already described in Theorem 3.16. This description involved only classes \({{\textbf{s}}}\in {\mathscr {S}}_X\) such that \({{\textbf{s}}}^2=-2\) and \({{\textbf{s}}}\cdot {{\textbf{v}}}_X\in \{0,1\}\). We still find these classes in higher dimensions [77, Corollary 2.9]:
-
classes \({{\textbf{s}}}\) with \({{\textbf{s}}}^2=-2\) and \({{\textbf{s}}}\cdot {{\textbf{v}}}_X=0\); in the notation of Proposition B.4, we have \(a=-1\), \(k=0\), and \(\theta _X(\kappa _X)=2(m-1){{\textbf{s}}}\), and the lattice \( \textbf{Z}h\oplus \textbf{Z}\frac{1}{2(m-1)}\kappa _X\) has intersection matrix \(\begin{pmatrix} h^2 &{}\quad 0 \\ 0 &{}\quad -2\end{pmatrix}\) but may or may not be primitive;
-
classes \({{\textbf{s}}}\) with \({{\textbf{s}}}^2=-2\) and \({{\textbf{s}}}\cdot {{\textbf{v}}}_X=1\); in the notation of Proposition B.4, we have \(a=-1\), \(k=1\), and \(\theta _X(\kappa _X)=2(m-1){{\textbf{s}}}-{{\textbf{v}}}_X\); the lattice \( \textbf{Z}h\oplus \textbf{Z}\kappa _X\) has intersection matrix \(\begin{pmatrix} h^2 &{} 0 \\ 0 &{} -2(m-1)(4m-3)\end{pmatrix}\) and may or may not be primitive.
When \(m\in \{3,4\}\), complete lists of possible pairs \((\kappa _{\text {prim}}^2,\mathop {\textrm{div}}\nolimits (\kappa _{\text {prim}}))\) are given in [77, Sects. 2.2 and 2.3]:
-
when \(m=3\), we have
$$\begin{aligned} (\kappa _{\text {prim}}^2,\mathop {\textrm{div}}\nolimits (\kappa _{\text {prim}}))\in \{(-2,1),(-4,2),(-4,4), (-12,2), (-36,4)\}; \end{aligned}$$ -
when \(m=4\), we have
$$\begin{aligned} (\kappa _{\text {prim}}^2,\mathop {\textrm{div}}\nolimits (\kappa _{\text {prim}}))\in \{(-2,1),(-6,2),(-6,3),(-6,6),(-14,2),(-24,3),(-78,6)\}. \end{aligned}$$
Depending on m and on the polarization, not all pairs in these lists occur: in Example B.7 (where \(m=4\)), only the pairs \((-6,3)\), \((-2,1)\), and \((-24,3)\) do occur.
Whenever \(m-1\) is a power of a prime number, the pair \((\kappa _{\text {prim}}^2,\mathop {\textrm{div}}\nolimits (\kappa _{\text {prim}}))=(-2m-6,2)\) is also in the list [77, Corollary 2.9]: in our notation, it corresponds to \({{\textbf{s}}}^2=2a=-2\) and \({{\textbf{s}}}\cdot {{\textbf{v}}}_X =k=m-1\).
When the divisibility \(\gamma \) of the polarization h is 1 or 2, we list some of the Heegner divisors that are avoided by the period map.
Proposition B.10
Consider the period map
When \(\gamma =1\), the image of \(\,{}^m\wp ^{(1)}_{2n}\) does not meet
-
\(\nu \) of the components of the hypersurface \({}^m{\mathscr {D}}_{2n,2n(m-1)}^{(1)}\), where \(\nu \in \{0,1,2\}\) is the number of the following congruences that hold: \(n+m\equiv 2\pmod 4\), \(m\equiv 2\pmod 4\), \(n\equiv 1\pmod 4\);
-
one of the components of the hypersurface \({}^m{\mathscr {D}}_{2n,8n(m-1)}^{(1)}\);
-
when \(m-1\) is a prime power, one component of the hypersurface \({}^m{\mathscr {D}}_{2n,2(m-1)(m+3)n}^{(1)}\).
When \(\gamma =2\) (so that \(n+m\equiv 1\pmod 4\)), the image of \(\, {}^m\wp ^{(2)}_{2n}\) does not meet
-
one of the components of the hypersurface \({}^m{\mathscr {D}}_{2n,2n(m-1)}^{(2)}\);
-
when \(m-1\) is a power of 2, one component of the hypersurface \({}^m{\mathscr {D}}_{2n,(m-1)(m+3)n/2}^{(2)}\).
Proof
No algebraic class with square \(-2\) can be orthogonal to \(h_\tau \) (see Remark B.9). As in the proof of Theorem 3.32, there is such a class \(\kappa \) if and only if the period point belongs to the hypersurface \({}^m{\mathscr {D}}^{(\gamma )}_{2n,K} \), where K is the rank-2 lattice with intersection matrix \(\bigl ({\begin{matrix}2n&{}0\\ 0&{}-2\end{matrix}}\bigr )\). This hypersurface is a component of \({}^m{\mathscr {D}}^{(\gamma )}_{2n,d} \), where \(d:=|{{\,\textrm{disc}\,}}(K^\bot )|\) can be computed using the formula
from [38, Lemma 7.5] (see (19)), where \(s:=\mathop {\textrm{div}}\nolimits _{h_\tau ^\bot }(\kappa )\in \{1,2\}\).
Assume \(\gamma =1\), so that \(D(h_\tau ^\bot )\simeq \textbf{Z}/(2m-2)\textbf{Z}\times \textbf{Z}/2n\textbf{Z}\) (see (6)). As in the proof of Proposition 3.29, we write \(\kappa =a(u-nv)+b\ell +cw\), so that \(1=-\frac{1}{2}\kappa ^2= na^2+(m-1)b^2+(\frac{1}{2} w^2)c^2\), and \(s =\gcd (2na,2(m-1)b,c) \) is 1 if c is odd, and 2 otherwise.
If \(s=1\), we have \(d=8n(m-1)\) and \(\kappa _*=0\), and, by Eichler’s criterion, this defines an irreducible component of \({}^2{\mathscr {D}}_{2n,8n(m-1)}^{(1)}\) (to prove that it is nonempty, just take \(a=b=0\), \(c=1\), and \(w^2=-2\)).
If \(s=2\), we have \(d=2n(m-1)\) and \(\kappa _*\) has order 2. More precisely,
Conversely, to obtain such a class \(\kappa \) with square \(-2\), one needs to solve the equation \(na^2+(m-1)b^2+rc^2=1\), with c even and r any integer. It is equivalent to solve \(na^2+(m-1)b^2\equiv 1\pmod 4\) and one checks that this gives the first item of the proposition.
Assume \(\gamma =2\), so that \({{\,\textrm{disc}\,}}(h_\tau ^\bot )=n(m-1)\) (see (7)) and \(d=\frac{2}{s^2}n(m-1)\in \{2n(m-1),\frac{n(m-1)}{2}\} \). As in the proof of Proposition 3.29, we may take \(h_\tau ^\bot =\textbf{Z}w_1\oplus \textbf{Z}w_2\oplus M\), with \(w_1:= (m-1)v+\ell \) and \(w_2:=-u+\frac{n+m-1}{4}v\) and write \(\kappa =aw_1+bw_2+cw\). The equality \(\kappa ^2=-2\) now reads \(1=a(a+b)(m-1)+b^2 \bigl (\frac{n+m-1}{4}\bigr )-c^2\bigl (\frac{1}{2} w^2\bigr )\), and again, \(s=1\) if c is odd, \(s=2\) if c is even.
Again, the case \(s=1\) gives rise to a single component of \({}^2{\mathscr {D}}_{2n,2n(m-1)}^{(1)}\), since it corresponds to \(\kappa _*=0\) (take \(a=b=0\) and \(c=1\)).Footnote 62
Assume now that \(m-1\) is a prime power. In that case, no algebraic class with square \(-2m-6\) and divisibility 2 can be orthogonal to \(h_\tau \) (see Remark B.9). Assume that there is such a class \(\kappa \).
When \(\gamma =1\), keeping the same notation as above, we need to solve \(na^2+(m-1)b^2+(\frac{1}{2} w^2)c^2=m+3\), with a and c even. Just taking \(c=2\), \(a=0\), and \(b=1\) works, with \(d=\frac{8(m+3)n(m-1) }{\gcd (2na,2(m-1)b,c)^2}=2(m-1)(m+3)n\). In the notation of Example B.7, we may take \({{\textbf{v}}}=u_1+(m-1)v_1\), \(\ell =u_1-(m-1)v_1\), \(h= u_2+nv_2 \), \(\kappa =(m-1)(2(u_3-v_3)+\ell )\), and \({{\textbf{s}}}=u_3-v_3+u_1\).
When \(\gamma =2\), we need to solve \(a(a+b)(m-1)+b^2 \bigl (\frac{n+m-1}{4}\bigr )-c^2\bigl (\frac{1}{2} w^2\bigr )=m+3\), with \(a(m-1)\) and c even, and \(d=\frac{2(m+3)n(m-1) }{\gcd (2na,2(m-1)b,c)^2}\mid (m-1)(m+3)n/2\), so that both n and \(m-1\) are even. In that case, take \(c=2\), \(b=0\), and \(a=1\). In the notation of Example B.7, we may take \({{\textbf{v}}}=u_1+(m-1)v_1\), \(\ell =u_1-(m-1)v_1\), \(h= 2(u_2+\frac{n+m-1}{4}v_2)+\ell \), \(\kappa =(m-1)((m-1)v_2+2(u_3-v_3)+\ell )\), and \({{\textbf{s}}}=\frac{m-1}{2}v_2+u_3-v_3+u_1\). \(\square \)
1.1 The Period Map for Cubic Fourfolds
Let \({\mathscr {M}}_{\text {cub}}\) be the moduli space of smooth cubic hypersurfaces in \(\textbf{P}^5\). With any cubic fourfold W, we can associate its period, given by the weight-2 Hodge structure on \(H^4_{\text {prim}}(W,\textbf{Z})\). The Torelli Theorem for cubic fourfolds [110] says that the period map is an open embedding. By [16, Proposition 6], there is a Hodge isometry \(H^4_{\text {prim}}(W,\textbf{Z})(-1) \simeq H^2_{\text {prim}}(F(W),\textbf{Z})\). Hence, we can equivalently consider the period map for (smooth) cubic fourfolds as the period map of their (smooth) Fano varieties of lines, which are hyper-Kähler fourfolds of type \({{\,\mathrm{{K3}}\,}}^{[2]}\) with a polarization of square 6 and divisibility 2. The latter form a dense open subset in the moduli space \({}^2\!{\mathscr {M}}_{6}^{(2)} \).
By [32, Theorem 8.1], the image of the corresponding period map \( {}^2\!{\mathscr {M}}_{6}^{(2)} \rightarrow {}^2{\mathscr {P}}_{6}^{(2)}\) is exactly the complement of the Heegner divisor \({}^2{\mathscr {D}}_{6,6}^{(2)}\). The description of the image of the period map for cubic fourfolds, which is smaller, is part of a celebrated result of Laza and Looijenga [62, 68].
Theorem B.11
(Laza, Looijenga) The image of the period map for cubic fourfolds is the complement of the divisor \({}^2{\mathscr {D}}_{6,2}^{(2)}\cup {}^2{\mathscr {D}}_{6,6}^{(2)}\).
It had been known for some time (see [40]) that the image of the period map for cubic fourfolds is contained in the complement of \({}^2{\mathscr {D}}_{6,2}^{(2)}\cup {}^2{\mathscr {D}}_{6,6}^{(2)}\).
Let W be a smooth cubic fourfold containing no planes (this is equivalent to saying that its period point is not on the Heegner divisor \({}^2{\mathscr {D}}_{6,8}^{(2)}\)). We explained in Sect. 3.6.3 the construction (taken from [64]) of a hyper-Kähler eightfold \(X(W)\in {}^4\!{\mathscr {M}}_2^{(2)}\). It follows from [65, Proposition 1.3] that the varieties F(W) and X(W) are “strange duals” in the sense of Remark 3.24.Footnote 63
It follows from Theorem B.11 that the image of the set of X(W) by the period map \( {}^4\!{\mathscr {M}}_{2}^{(2)} \rightarrow {}^4{\mathscr {P}}_{2}^{(2)}\) contains the complement of the Heegner divisors \({}^2{\mathscr {D}}_{6,2}^{(2)}\), \( {}^2{\mathscr {D}}_{6,6}^{(2)}\), and \( {}^2{\mathscr {D}}_{6,8}^{(2)}\). Since the image of this period map is exactly the complement of these Heegner divisors (Example B.7), we obtain that any element of \( {}^4\!{\mathscr {M}}_{2}^{(2)} \) is of the form X(W). We provide below a different proof (due to Bayer and Mongardi) of this statement and of a weaker form of Theorem B.11.
Proposition B.12
(Bayer, Mongardi) (a) Any element of \( {}^4\!{\mathscr {M}}_{2}^{(2)}\) is of the type X(W), for some smooth cubic fourfold \(W\subset \textbf{P}^5\) containing no planes.
(b) The image of the period map for cubic fourfolds contains the complement of \({}^2{\mathscr {D}}_{6,2}^{(2)}\cup {}^2{\mathscr {D}}_{6,6}^{(2)}\cup {}^2{\mathscr {D}}_{6,8}^{(2)}\).
Sketch of proof of Proposition B.12
Any eightfold X in the moduli space \(^{4}\!{\mathscr {M}}_{2}^{(2)}\) has, by Proposition 4.3, an anti-symplectic regular involution. Upon varying the eightfold in the moduli space, the fixed loci form a smooth family. In particular, since, when \(X=X(W)\), the fixed locus contains a copy of the cubic fourfold W, and any smooth deformation of a cubic fourfold is a cubic fourfold as well (this is due to Fujita; see [53, Theorem 3.2.5]), there exists for any \(X\in {^{4}\!{\mathscr {M}}_{2}^{(2)}}\) a smooth cubic fourfold \(W_X\subset X\) fixed by the involution, and the periods of \(W_X\) and X are compatible because they are strange duals, as explained above.
By Example B.7, the image of the period map for \(^{4}\!{\mathscr {M}}_{2}^{(2)}\) is exactly the complement of the union of the Heegner divisors \({^4}{\mathscr {D}}_{2,2}^{(2)}\), \({^4}{\mathscr {D}}_{2,6}^{(2)}\), and \({^4}{\mathscr {D}}_{2,8}^{(2)}\), and these divisors correspond by strange duality to the (irreducible) Heegner divisors \({}^2{\mathscr {D}}_{6,2}^{(2)}\), \({}^2{\mathscr {D}}_{6,6}^{(2)}\), and \({}^2{\mathscr {D}}_{6,8}^{(2)}\) in the period domain of cubic fourfolds. \(\square \)
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Debarre, O. Hyper-Kähler Manifolds. Milan J. Math. 90, 305–387 (2022). https://doi.org/10.1007/s00032-022-00366-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00032-022-00366-x
Keywords
- K3 surfaces
- Hyper-Kähler manifolds
- Birational isomorphisms
- Automorphisms
- Torelli theorem
- Period domains
- Noether–Lefschetz loci
- Cones of divisors
- Nef classes
- Ample classes
- Movable classes
- Moduli spaces




 , of dimension
, of dimension 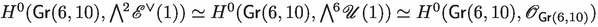 , of dimension 1. Hence
, of dimension 1. Hence  (thanks to L. Manivel for doing these computations).
(thanks to L. Manivel for doing these computations).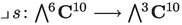 , whose image is the hyperplane defined by s (here s is the element of
, whose image is the hyperplane defined by s (here s is the element of 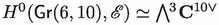 that defines X).
that defines X).