Skip to main content
SpringerLink
Log in

Variational Approach to the Orbital Stability of Standing Waves of the Gross-Pitaevskii Equation

  • Published:
Milan Journal of Mathematics Aims and scope Submit manuscript

Abstract

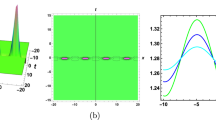
This paper is concerned with the mathematical analysis of a masssubcritical nonlinear Schrödinger equation arising from fiber optic applications. We show the existence and symmetry of minimizers of the associated constrained variational problem. We also prove the orbital stability of such solutions referred to as standing waves and characterize the associated orbit. In the last section, we illustrate our results with few numerical simulations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. G. P. Agrawal, Nonlinear Fiber Optics. Academic Press, 2007.

  2. W. Bao and Qiang Du, Computing the ground state solution of Bose-Einstein condensates by a normalized gradient flow. Siam J. Sci. Comput., 25(5) (2006), 1674-1697.

  3. Berestycki H., Cazenave T.: Instabilité des états stationnaires dans les équations de Schrödinger et de Klein-Gordon non linéaires. C. R. Acad. Sci. Paris. 293, 489–492 (1981)

    MATH  MathSciNet  Google Scholar 

  4. Bruneau C.H., Di Menza L., Lehner T.: Numerical resolution of some nonlinear Schröinger-like equations in plasmas. Numer. Methods for Partial Differential Equations, 15, 672–696 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  5. Carles R.: Critical nonlinear Schrödinger equation with and without harmonic potential. Math. Models Meth. Appl. Sci. 12, 1513–1523 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  6. Carles R.: Remarks on the nonlinear Schrödinger equation with harmonic potential. Ann. Henri Poincaré 3, 757–772 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  7. Cazenave T., Lions P.L.: Orbital stability of standing wave for some Schrödinger equations. Comm. Math. Phys. 85, 549–561 (1982)

    Article  MATH  MathSciNet  Google Scholar 

  8. T. Cazenave, Semilinear Schrödinger equations. Courant Lecture Notes Vol. 10, American Mathematical Society, Provi- dence, RI, (2003)

  9. Cipolatti R.: On the instability of ground states for a Davey-Stewartson system. Ann. Inst. H. Poincaré Phys. Théor. 58, 85–104 (1993)

    MATH  MathSciNet  Google Scholar 

  10. R. Fukuizumi, Stability of standing waves for nonlinear Schrödinger equations with critical power nonlinearity and potentials. Advances in Differential Equations. Vol. 10 No. 2 (2005), 259-276.

  11. R. Fukuizumi and M. Ohta, Instability of standing waves for the nonlinear Schrödinger equation with potentials. Differential and Integral Equations Vol. 6, No. 16 (2003) 691- 706.

  12. R. Fukuizumi and M. Ohta, Stability of standing waves for nonlinear Schrödinger equations with potentials. Differential and Integral Equations. Vol.16 No. 1 (2003), 111-128.

  13. R. Fukuizumi, Stability and instability of standing waves for the Schrödinger equation with harmonic potential. Discrete an continuous dynamical systems Vol. 7 No. 3 (2001), 525-544.

  14. Fukuizumi R., Hadj Selem F., Kikuchi H.: Stationary problem related to nonlinear Schrödinger equations on the unit ball. Nonlinearity 25, 2271–2301 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  15. Gonçcalves Rebeiro J.M.: Instability of symmetric stationary states for some nonlinear Schrödinger equations with an external magnetic field. Ann. Inst. H. Poincaré Phys. Théor. 54, 403–433 (1991)

    Google Scholar 

  16. Grandall M.G., Rabinowitz P.G.: Bifurcation from a simple eigenvalue, J. Functional Analysis 8, 321–340 (1991)

    Article  Google Scholar 

  17. Grillakis M., Shatah J., Strausz W.A.: Stability theory of solitary waves in presence of symmetry I, J. Funct. Anal. 74, 160–197 (1987)

    Article  MATH  MathSciNet  Google Scholar 

  18. Guo Y., Seiringer R.: On the Mass Concentration for BoseEinstein Condensates with Attractive Interactions. Lett. Math. Phys. 104, 141–156 (2014)

    Article  MATH  MathSciNet  Google Scholar 

  19. F. Hadj Selem, Etude théorique et numérique d’états stationnaires localisés pour l’équation de Schrödinger non linéaire avec potentiel quadratique, thèse d’Etat 2010.

  20. F. Hadj Selem, Radial solutions with prescribed numbers of zeros for the nonlinear Schrödinger equation with harmonic potential. Nonlinearity 24 (2011), 1795-1819.

  21. H. Hajaiej, Cases of equality and strict inequality in the extended HardyLittlewood inequalities. Proc. Royal Soc. Edin. A 05 (2005), 135(03), 643-662.

  22. H. Hajaiej, P.A. Markowich and S. Trabelsi, Minimizers of a class of constrained vectorial variational problems: Part I. Milan J. Math. Vol 82 (2014), 81-98.

  23. Z. Han-Lei and G. Qiang, Dynamics of Bose-Einstein condensates in a one-dimensiona l optical lattice with double-well potential. Frontiers of Physics, Vol. 8, Issue 4 (2013), 375-380.

  24. M. Hirose and M. Ohta, Structure of positive radial solution of scalar field equations with harmonic potential. J. Diff. eqt. bf(178)(2) (2002), 519-540.

  25. Hirose M., Ohta M.: Uniqueness of positive solutions to scalar field equation with harmonic potential. Funkcial Ekvac. 50, 67–100 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  26. Jackson R.K., Weinstein M.K: Geometric analysis of bifurcation and symmetry breaking in Gross-Pitaevskii equation. J. Stat. Phys. 116, 881–905 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  27. E.W.Kirr, P.G. Kevrekidis, E. Shlizerman, M.I. Weinstein, Symmetry-breaking bifurcation in nonlinear Schrödinger/GrossPitaevskii equations. SIAM J. Math. Anal. 40 (2008), 566-604.

  28. Kirr E.W., Kevrekidis P.G., Pelinovsky D.E.: Symmetry-breaking bifurcation in the nonlinear Schrödinger equation with symmetric potentials. Commun.Math. Phys. 308(3), 795–844 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  29. B. Noris, H. Tavares and G. Verzini, Existence and orbital stability of the ground states with prescribed mass for the L 2 -critical and supercritical NLS on bounded domains. arXiv:1307.3981.

  30. Oh Y.G.: Cauchy problem and Ehrenfest’s law of nonlinear Schrödinger equations with potentials. J. Differ. Equations 81, 255–274 (1989)

    Article  MATH  Google Scholar 

  31. Oh Y.G.: Stability of semiclassical bound states of nonlinear Schrödinger equations with potentials. Comm. Math. Phys. 121, 11–33 (1989)

    Article  MATH  MathSciNet  Google Scholar 

  32. Ohta M.: Instability of standing waves for the generalized Davey-Stewartson sysytem. Ann. Inst. H. Poincaré Phys. Théor. 62, 69–80 (1995)

    MATH  Google Scholar 

  33. Ohta M.: Stability of standing waves for the generalized Davey-Stewartson system. J. Dynam. Differential. Equations. 6, 325–334 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  34. Rabinowitz P.H.: Some global results for nonlinear eigenvalues problems. J. Functional Analysis 7, 487–513 (1971)

    Article  MATH  MathSciNet  Google Scholar 

  35. H.A. Rose, and M.I. Weinstein, On the bound states of the nonlinear Schrödinger equation with a linear potential. Phys. D. 30 (1988), 207-218.

  36. Shatah J., Strauss W.: Instability of nonlinear bound states. Commun. Math. Phys. 100, 173–190 (1985)

    Article  MATH  MathSciNet  Google Scholar 

  37. T. Tsurumi and M. Wadati, Collapses of wave functions in multidimensional nonlinear Schrödinger equations under harmonic potential. J. Phys. Soc. Jpn. 66 (1997), 3031- 3034.

  38. Weinstein M.I.: Lyapunov stability of ground states of nonlinear dispersive evolution equations. Comm. Pure Appl. Math. 39, 51–68 (1986)

    Article  MATH  MathSciNet  Google Scholar 

  39. Zhang J.: Stability of standing waves for nonlinear Schrödinger equations with unbounded potentials. Z. Angew. Math. Phys. 51, 498–503 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  40. Zhang J.: Stability of attractive Bose-Einstein condensates. J. Stat. Phys. 101, 731–746 (2000)

    Article  MATH  Google Scholar 

  41. Zhang J.: Sharp threshold for global existence and blowup in nonlinear Schrödinger equation with harmonic potential. Commun. Partial Differ. Equ. 30, 1429–1443 (2005)

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. French Atomic Energy Commission, Neurospin, Saclay, France

    Fouad Hadj Selem

  2. Department of Mathematics, College of Science, King Saud University, P.O. Box 2455, Riyadh, 11451, Saudi Arabia

    Hichem Hajaiej

  3. Division of Mathematics & Computer Science & Engineering, King Abdullah University of Science and Technology, Thuwal, 23955-6900, Saudi Arabia

    Peter A. Markowich & Saber Trabelsi

Authors
  1. Fouad Hadj Selem
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hichem Hajaiej
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Peter A. Markowich
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Saber Trabelsi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Peter A. Markowich.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hadj Selem, F., Hajaiej, H., Markowich, P.A. et al. Variational Approach to the Orbital Stability of Standing Waves of the Gross-Pitaevskii Equation. Milan J. Math. 82, 273–295 (2014). https://doi.org/10.1007/s00032-014-0227-5

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00032-014-0227-5

Mathematics Subject Classification

Keywords

Search

Navigation