Abstract
This paper provides a unified combinatorial framework to study orbits in certain affine flag varieties via the associated Bruhat–Tits buildings. We first formulate, for arbitrary affine buildings, the notion of a chimney retraction. This simultaneously generalizes the two well-known notions of retractions in affine buildings: retractions from chambers at infinity and retractions from alcoves. We then present a recursive formula for computing the images of certain minimal galleries in the building under chimney retractions, using purely combinatorial tools associated to the underlying affine Weyl group. Finally, for Bruhat–Tits buildings in the function field case, we relate these retractions and their effect on minimal galleries to double coset intersections in the corresponding affine flag variety.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Buildings enable the study of the groups which act on them via a combination of algebraic, combinatorial, and geometric methods. The current work exemplifies this combination of approaches, in the setting of affine buildings. An affine building X of type (W,S) is a union of subcomplexes called apartments. Each apartment is a copy of the Coxeter complex for (W,S); that is, the tessellation of Euclidean space whose maximal simplices, called alcoves, are in bijection with the elements of W. Simplicial maps, called retractions, from X to a fixed apartment allow us to study structures in the entire building by considering (their image in) just one apartment.
We begin by simultaneously generalizing the two well-known classical notions of retractions of an affine building, by formalizing retractions from chimneys (see Section 3). We then establish a combinatorial recursion which allows us to compute the images of certain galleries in X under chimney retractions; a special case of this recursion is stated as Theorem 1.1 later in this introduction. Many (but not all) affine buildings are of algebraic origin, in the sense that they are the Bruhat–Tits building for a reductive group G over a local field F with a discrete valuation (see [7, 37]). In this setting, a chimney corresponds to a choice of a (spherical) standard parabolic subgroup of G(F) and an element of the affine Weyl group W. In Theorems 1.2 and 1.3, for F a function field we relate intersections of certain double cosets in the affine flag variety and affine Grassmannian, respectively, to families of galleries obtained by applying the corresponding chimney retraction. The case of general partial flag varieties is treated in Section 5 (see Theorem 5.14). The later sections of this introduction are mostly dedicated to formally stating these results and giving some examples. We provide many more examples in Section 6.
Our approach to the proof of Theorems 1.2 and 1.3 is a generalization of that in [31], which relies on the root group structure of G(F), and the identification of the (points of the) varieties in question with certain simplicial substructures of the building. The various double cosets then become orbits of simplices which can be described as pre-images under certain retractions, or equivalently as certain sets of positively folded galleries. We note that this approach is independent of the characteristic of F. This fact suggests that one should think of the Bruhat–Tits building as a tool to simultaneously study affine Grassmannians and other (partial) affine flag varieties in a characteristic-free setting.
Part of the motivation for this work is the following application to affine Deligne–Lusztig varieties. Consider the case where \(F = \mathbbm {k}((t))\) is the field of Laurent series with \(\mathbbm {k}\) an algebraic closure of a finite field, and let G be a split connected reductive group over \(\mathbbm {k}\). In this setting, a special case of Theorem 1.2 was combined with Theorem 6.3.1 of [12] to relate positively folded galleries in the Bruhat–Tits building for G(F) to affine Deligne–Lusztig varieties in the affine flag variety parameterized by translations, in a manner which makes the corresponding nonemptiness and dimension calculations tractable (see Theorem 5.8 of [28]). An analogous statement relating more general affine Deligne–Lusztig varieties to positively folded galleries can likewise be obtained by combining Theorem 1.2 with Theorem 11.3.1 of [13].
1.1 Retractions and Gallery Combinatorics
Positively folded galleries were first introduced by Littelmann and Gaussent–Littelmann in [14, 23] in the context of understanding highest weight representations of complex semisimple algebraic groups. Ram then developed the machinery of positively folded alcove walks [32], which provides a slightly different approach to the same underlying combinatorics. In this paper, we develop the more general combinatorics of galleries which are positively folded with respect to a chimney in an arbitrary affine building X (see Sections 2 and 3 for notation and formal definitions). All of these positively folded galleries are the images in a single apartment A of certain galleries in the entire building X, under the application of certain retractions X → A.
A chimney in an apartment A is a point in the boundary of A which is represented by a region of A lying between pairs of adjacent α-hyperplanes for all positive roots α in some sub-root system, and which “goes off to infinity” in the other root directions. In the special case that the sub-root system equals the entire root system, an associated chimney is represented by an alcove in A, rather than a boundary point. An example of a region representing a chimney where (W,S) is of type \(\tilde A_{2}\) is the gray shaded strip in Fig. 1. The chimney here has associated sub-root system {±α}, with α the black (positive) root, and the other positive roots shown in gray. Chimneys were first introduced by Rousseau in [34] (although our definition is different), and they are related to the generalized sectors for affine buildings appearing in [8, 9], for instance.
A retraction from a chimney folds the entire building X away from the chimney down onto A. Retractions from chimneys were, so far as we know, first described in [13] (for certain Bruhat–Tits buildings), and the retractions from [13] were used in [19]. Neither the existence of chimney retractions nor our methods of proof will surprise experts. Chimney retractions specialize to both of the classical retractions of affine buildings onto an apartment, namely the retraction centered at an alcove inside the apartment, and the retraction centered at a chamber at infinity (see, for example, [1]).
A gallery in A is positively folded with respect to the chimney if all its folds occur on sides of hyperplanes facing away from the chimney. The corresponding orientation on hyperplanes induced by a chimney generalizes the periodic orientations considered in [28, 31] (see also [16] for a general treatment of orientations). The galleries in Fig. 1 are the smooth paths starting at the origin and ending in arrows, and all of these galleries are positively folded with respect to the chimney represented by the gray shaded region.
1.2 Recursive Description of Shadows
A shadow with respect to a chimney is the set of end-simplices of all positively folded galleries of a particular (fixed) type. In Fig. 1, the shadow of the coroot lattice element λ is the set of all end-vertices of the depicted galleries; that is, the set of (colored) dots in which an arrow ends. Shadows were first defined in [16]. Our first main result, Theorem 4.8, establishes a recursive formula for shadows with respect to general chimneys in the setting of an arbitrary affine building of type (W,S); a special case of Theorem 4.8 is stated as Theorem 1.1 below.
Let y ∈ W and write y for the corresponding alcove in a fixed apartment A of X. We denote by Shy(λ) the shadow of λ with respect to the chimney for y, i.e., the set of end-vertices of galleries in A of a fixed type \(\vec {\lambda }\) which are folded away from y. For s ∈ S, let H be the hyperplane separating the alcoves y and ys, and let rH be the reflection of A in H. This setup permits the following recursive description of the shadow Shys(λ).
Theorem 1.1
Let λ be any element of the coroot lattice. For any y ∈ W and s ∈ S such that ℓ(ys) > ℓ(y), we have
where Hys is the half-apartment which is bounded by H and contains ys.
The idea of the recursion is that rH folds across the hyperplane H all parts of those galleries from the previous step which protrude across H, and thus folds these galleries away from the alcove ys. For example, we used Theorem 4.8 repeatedly to compute the shadow appearing in Fig. 2. In this figure, a hyperplane H which is crossed as one moves from the base alcove cf along the shaded region representing the chimney is shown in the same color as those alcoves in the shadow which are (first) obtained by applying the reflection rH. See Theorem 4.8 for the general version of Theorem 1.1, and its proof. Figure 1 shows that the shadow of λ is a (proper) subset of the intersection of the coroot lattice with the λ-Weyl polytope, a classical result which we recover from our recursion in Corollary 4.11.
Recursions similar to Theorem 1.1 have appeared in [4, 11], by adapting an algebraic reduction method of Deligne and Lusztig [10] to affine flag varieties. Different algorithms for computing certain shadows using word combinatorics can be found in [16], and those algorithms could be generalized to the cases considered in this work.
As we explain further after the proof of Theorem 4.8, determining the multiplicities of elements of the shadow is a delicate question. This can already be seen from Fig. 1, where the origin and the element β = β∨ of the coroot lattice have multiplicity 2, since there are two distinct galleries of type \(\vec {\lambda }\) ending at these points, but all other vertices in the shadow of λ have multiplicity 1. We leave the determination of such multiplicities, and their algebraic interpretation, to future work.
1.3 Algebraic Interpretation of Shadows
Shadows of chimneys also relate sets of positively folded galleries to certain orbits in (partial) affine flag varieties over function fields. The special cases of the affine flag variety and the affine Grassmannian are highlighted below in Theorems 1.2 and 1.3, respectively, which represent the next main results in this paper. It is well-known that the nonemptiness patterns of such double coset intersections are quite delicate, at least in the case of the affine flag variety. Recursive formulas such as Theorem 1.1 can be used, however, to precisely determine the sets of folded galleries arising in Theorems 1.2 and 1.3.
We now let \(F = \mathbbm {k}((t))\), for any field \(\mathbbm {k}\), and let G be any split, connected, reductive group over F. Let \(\mathcal {O} = \mathbbm {k}[[t]]\) be the ring of integers of F. Let X be the Bruhat–Tits building for G(F), with standard apartment A. Write I for the Iwahori subgroup of G(F). Note that I is a subgroup of \(G(\mathcal {O})\), and that I is the stabilizer in G(F) of the base alcove of A. Put \(K = G(\mathcal {O})\), and note that K is the stabilizer in G(F) of the origin of A. Denote by P = P(F) any standard spherical parabolic subgroup of G(F), with Levi decomposition P = MN = M(F)N(F), where M is the Levi component and N is its unipotent radical. Following [13], define the subgroup IP of G(F) by
Given an element of the affine Weyl group y ∈ W, denote by (IP)y the conjugate yIPy− 1.
The P-chimney lies between the hyperplanes Hα and Hα,1 of A for all positive roots α in M, and is antidominant for all roots in N. The (P,y)-chimney is then the image of the P-chimney under the action of y. For example, in Figs. 1 and 2, if M has root system {±α}, then the shaded region represents the P-chimney. A labeled folded alcove walk is a folded gallery in which certain simplices have been labeled by elements of the residue field \(\mathbbm {k}\) of F (see Section 5 for precise definitions).
Theorem 1.2
For any x,y,z ∈ W, there is a bijection between the points of the intersection
and the set of labeled folded alcove walks of type \(\vec {x}\) from the base alcove to z which are positively folded with respect to the (P,y)-chimney.
In the next statement, we write W0 for the spherical Weyl group, tλ for the translation by the element λ of the coroot lattice, and xλ ∈ W for the minimal length representative of the coset tλW0 in W/W0. Note that any double coset KtλK has a dominant representative.
Theorem 1.3
Let λ and μ be in the coroot lattice, with λ dominant, and let y ∈ W. Then there is a bijection between the points of the intersection
and the union over w ∈ W0 of the set of labeled folded alcove walks of type \(\overrightarrow {wx_{\lambda }}\) from the base alcove to an alcove containing μ which are positively folded with respect to the (P,y)-chimney.
In Section 5, we prove Theorem 1.2 as Theorem 5.11, and then use this to prove a generalization of Theorems 1.2 and 1.3 in which I and K, respectively, are replaced by parahoric subgroups of G(F) which stabilize faces of the base alcove containing the origin (see Theorem 5.14). We also establish a general nonemptiness result for double coset intersections in Theorem 5.16.
In some special cases, (parts of the statements of) Theorems 1.2 and 1.3 are folklore or recover earlier results. For instance, if P = B, the Borel subgroup of G(F), then Theorem 7.1 of [31] is the corresponding case of Theorem 1.2. More generally, for any w in the spherical Weyl group, Corollary 5.5 of [28] is the case of Theorem 1.2 where the intersection under consideration is IxI ∩ UwzI. Inspired by Peterson’s work on affine Schubert calculus [29], in joint work with Ram, the first author proved a bijection similar to Theorem 1.2 on intersections of positive and negative Iwahori orbits in the affine flag variety [27]. Special cases of the orbit intersections appearing in Theorem 1.3 were studied in [25, Thm 2.6.11(3)-(4)], [6, Paragraph 4.4], and [14]. In [17], the third author used similar double cosets to prove an analog for Bruhat–Tits buildings of Kostant’s convexity theorem [22] for symmetric spaces, which itself is a variant of a classical result of Schur [36] and Horn [20]. A count similar to the statement of Theorem 5.14 appears in the work of Abramenko, Parkinson, and Van Maldeghem [2], where intersections of Weyl-distance spheres in arbitrary locally finite buildings are studied (see Remark 5.15 for further details).
Figures 1 and 2 illustrate the statements of Theorems 1.3 and 1.2, respectively, for y = 1. If μ is the end-vertex of a gallery in Fig. 1, equivalently μ is in the shadow of λ with respect to the P-chimney, then by Theorem 1.3 any labeling of a gallery in this figure which ends at μ corresponds bijectively with a point in the (nonempty) intersection KtλK ∩ IPtμK, and conversely. In Fig. 2, any labeling of a gallery with final alcove z in this shadow corresponds to a point in the (nonempty) intersection IxI ∩ IPzI, and conversely.
1.4 Examples and Code
We conclude this work with Section 6, which provides many examples of shadows in rank 2. We observe some features of these shadows and illustrate how to use the recursion from Theorem 4.8. We have written Maple code for computing shadows in types \(\tilde {A}_{2}\), \(\tilde {C}_{2}\), and \(\tilde {G}_{2}\), and this code is available from the authors upon request.
2 Preliminaries
We now recall the definitions we will need and fix notation. We assume knowledge of affine Coxeter systems and affine buildings at the level of the references [1, 21], or [33].
In order to avoid notational complexities, we will assume for the remainder of this work that the affine Coxeter system (W,S) is irreducible. Our results in Sections 3 and 4 can be extended to reducible affine Coxeter systems (W,S), for example where (W,S) is of type \(\tilde A_{1} \times \tilde A_{1}\) so that the associated building X can be realized as a product of trees. We leave this extension as an exercise for the reader.
2.1 Affine Coxeter Systems and Affine Buildings
Our approach in this section is very similar to that of [24], which provides a way to discuss the affine Coxeter system (W,S) without assuming that (W,S) is the affine Weyl group for any particular group G(F). We do this so that we can then discuss an arbitrary affine building X of type (W,S).
Let (W,S) be an irreducible affine Coxeter system of rank n + 1 and let V be the associated n-dimensional real vector space on which W acts, which we can identify with n-dimensional Euclidean space. Write v0 for the origin of V. Then (W,S) has associated spherical Coxeter system (W0,S0) such that W0 is the stabilizer in W of v0 and \(S_0 = \{ s_{1}, \dots , s_{n} \}\) is the set of elements of \(S = \{ s_{0},s_{1}, \dots , s_{n}\}\) which fix v0. We typically use the letters x, y, and z for elements of W and u, v, and w for elements of W0. For algebraic reasons to be found below, we denote the elements of the translation subgroup of W by {tλ∣λ ∈ R∨}, where R∨ is a certain lattice in V (which is preserved by the actions of W and W0). For all λ,μ ∈ R∨, we have tλtμ = tλ+μ = tμ+λ = tμtλ. Any element x of W can be expressed uniquely as x = tλw where λ ∈ R∨ and w ∈ W0, and given any u ∈ W0 and λ ∈ R∨, we have utλu− 1 = tuλ. We write \(\ell :W \to \mathbb {Z}\) for the length function of the Coxeter system (W,S).
Let Φ be a crystallographic root system such that (W0,S0) is the Weyl group of Φ and R∨⊂ V is the associated coroot lattice. Denote the positive roots in Φ by Φ+, and denote the positive simple roots in Φ by \({\varDelta } = \{ \alpha _{1},\dots ,\alpha _{n}\}\). Given \(J \subseteq \{1,\dots ,n\}\), we denote by WJ the standard (spherical) parabolic subgroup of W0 generated by {sj∣j ∈ J}. Recall that (WJ,{sj}j∈J) is a Coxeter system. We will write ΦJ for the sub-root system of Φ associated to WJ, with positive roots \({\varPhi }_{J}^{+} = {\varPhi }^{+} \cap {\varPhi }_{J}\) and basis of positive simple roots ΔJ = {αj∣j ∈ J}. In particular, if J = ∅ then WJ is trivial and ΦJ = ΔJ = ∅, while if \(J = \{ 1,\dots ,n\}\) then WJ = W0, ΦJ = Φ, and ΔJ = Δ.
For each α ∈Φ and \(k \in \mathbb {Z}\), we write Hα,k for the affine hyperplane or wall of V given by Hα,k = {v ∈ V ∣〈α,v〉 = k} where the brackets denote the standard inner product on V. Note that Hα,k = H−α,−k for all α ∈Φ and \(k \in \mathbb {Z}\). Write sα,k for the (affine) reflection fixing Hα,k pointwise. Then each sα,k is an element of W, and every reflection in W is of this form. We will sometimes put Hα = Hα,0 and sα = sα,0. We remark that \(s_{i} = s_{\alpha _{i}}\) for 1 ≤ i ≤ n, and \(s_{0} = s_{\widetilde \alpha ,1}\) where \(\widetilde \alpha \) is the (unique) highest root in Φ. Let \({\mathscr{H}} = \{ H_{\alpha ,k} \mid \alpha \in {\varPhi }, k \in \mathbb {Z}\}\). The group W acts on the set \({\mathscr{H}}\) as follows. For α ∈Φ, \(k \in \mathbb {Z}\), μ ∈ R∨, and u ∈ W0, we have tμu ⋅ Hα,k = Huα,k+〈uα,μ〉.
An alcove is the closure of a maximal connected component of \(V \setminus {\mathscr{H}}\). Since (W,S) is irreducible, each alcove is a simplex. We write cf for the alcove bounded by the hyperplanes \(\{ H_{\alpha _{1}},\dots ,H_{\alpha _{n}}, H_{\widetilde \alpha ,1} \}\), and call cf the base alcove or the fundamental alcove. The set of alcoves in V is in bijection with the elements of W, and for x ∈ W we write x or xcf for the alcove x ⋅cf. A panel is a codimension one face of an alcove, and the supporting hyperplane of a panel p is the unique element of \({\mathscr{H}}\) which contains p.
Let \({\mathscr{H}}_{0} = \{ H_{\alpha } \mid \alpha \in {\varPhi } \}\), that is, \({\mathscr{H}}_{0}\) is the set of all hyperplanes in \({\mathscr{H}}\) which pass through the origin. A Weyl chamber is the closure of a maximal connected component of \(V \setminus {\mathscr{H}}_{0}\). Each Weyl chamber is a simplicial cone, and we will also refer to Weyl chambers as sectors. We define the dominant Weyl chamber \(\mathcal {{C}}_{f}\) to be the unique Weyl chamber which contains the base alcove cf. Thus \(\mathcal {{C}}_{f}\) is the set of points v ∈ V such that 〈α,v〉≥ 0 for every α ∈Φ+. We denote by \(\mathcal {{C}}^{op}_f\) the antidominant Weyl chamber, which is the unique chamber opposite \(\mathcal {{C}}_{f}\) in V, consisting of all points v ∈ V such that 〈α,v〉≤ 0 for all α ∈Φ+. The set of Weyl chambers is in bijection with the elements of W0, and for w ∈ W0 we often write \(\mathcal {C}_{w}\) for the Weyl chamber \(w \cdot \mathcal {{C}}_{f}\). Thus  and \(\mathcal {{C}}^{op}_f = \mathcal {C}_{w_{0}}\), where
and \(\mathcal {{C}}^{op}_f = \mathcal {C}_{w_{0}}\), where  is the identity element of W0 and w0 is its longest element.
is the identity element of W0 and w0 is its longest element.
For any root α ∈Φ, any \(k \in \mathbb {Z}\), and any w ∈ W0, we denote by αk,w the closed half-space of V bounded by the hyperplane Hα,k that contains a subsector of the Weyl chamber \(\mathcal {C}_{w}\). In particular, for any \(k \in \mathbb {Z}\) the half-space  contains a subsector of the dominant Weyl chamber \(\mathcal {{C}}_{f}\), and \(\alpha ^{k,w_{0}}\) contains a subsector of the antidominant Weyl chamber \(\mathcal {{C}}^{op}_f\). The group W acts naturally on the set \(\{ \alpha ^{k,w} \mid k \in \mathbb {Z}, w \in W_0 \}\) via (tμu) ⋅ αk,w = (uα)k+〈uα,μ〉,uw, where μ ∈ R∨ and u ∈ W0.
contains a subsector of the dominant Weyl chamber \(\mathcal {{C}}_{f}\), and \(\alpha ^{k,w_{0}}\) contains a subsector of the antidominant Weyl chamber \(\mathcal {{C}}^{op}_f\). The group W acts naturally on the set \(\{ \alpha ^{k,w} \mid k \in \mathbb {Z}, w \in W_0 \}\) via (tμu) ⋅ αk,w = (uα)k+〈uα,μ〉,uw, where μ ∈ R∨ and u ∈ W0.
Now let X be an affine building of type (W,S). We regard X as a simplicial complex, and for any apartment A of X we may fix an identification of A with V such that we may talk about hyperplanes, alcoves, Weyl chambers and so on in A. We will usually refer to the closed half-spaces of A determined by hyperplanes as half-apartments.
2.2 Galleries
This section recalls definitions concerning combinatorial galleries that will be used in the sequel. In this section, X is any affine building of type (W,S) irreducible, and A is any apartment of X.
We start with the following definition, which gives a special case of the combinatorial galleries of Gaussent and Littelmann (see Definition 8 of [14]).
Definition 2.1
A (finite) combinatorial gallery is a sequence of alcoves ci and faces pi in the affine building X
where the first and last faces \(p_{0} \subseteq c_{0}\) and \(p_{l+1}\subseteq c_{l}\) are simplices, and for 1 ≤ i ≤ l the face pi is a panel of both alcoves ci− 1 and ci.
We will also need the (obvious) extension of this definition to infinite galleries.
Definition 2.2
An infinite combinatorial gallery is an (infinite) sequence of alcoves ci and faces pi in the affine building X
where the first face \(p_{0} \subseteq c_{0}\) is a simplex, and for all i ≥ 1 the face pi is a panel of both alcoves ci− 1 and ci.
We remark that if ci− 1≠ci in either of these definitions, then there is no choice for the panel pi. We will often omit the word “combinatorial” when referring to galleries. All of our galleries will contain at least one alcove, and we will mostly be restricting attention to galleries that lie in a single apartment.
A gallery γ as in Definition 2.1 has length l + 1, that is, its length is the number of alcoves counted with multiplicity. We say that such a γ is minimal if it has minimal length among all galleries with first face p0 and last face pl+ 1. An infinite gallery γ as in Definition 2.2 is minimal if each of its initial finite subgalleries \((p_{0}, c_{0}, p_{1} , c_{1} , p_{2} , {\dots } , p_{i})\) is minimal.
Recall that each simplex in X has a type which is a subset of S.
Definition 2.3
Given a gallery γ as in Definition 2.1, the type of γ is given by the (l + 2)-tuple
where for 1 ≤ i ≤ l the panel pi has type \(s_{j_{i}} \in S\). If p0 = c1 and pl+ 1 = cl then we will usually write instead \(\text {type}(\gamma ) = (s_{j_{1}}, s_{j_{2}}, \dots , s_{j_{l}})\), so that the type of γ is a word in S.
It will not always be necessary to record the details of a gallery’s type. In particular, for x ∈ W and a fixed minimal gallery from cf to x, we will sometimes describe any gallery of this same type with first face cf as having type\(\vec {x}\). Similarly, for λ ∈ R∨ and a fixed minimal gallery from the origin to λ, we will sometimes describe any gallery of this same type with first face the origin as having type \(\vec {\lambda }\).
We finally recall several general definitions concerning orientations and positively folded galleries. See the introduction and [16] for some history concerning these notions.
Definition 2.4 (Definition 3.1 of 16)
An orientation of the apartment A is a map ϕ that assigns to every pair (c,p) consisting of an alcove c of A and a panel p of c one of the symbols + or −. We say that an alcove c is on the positive side of p if ϕ(c,p) = +.
Definition 2.5
Let γ be a combinatorial gallery as in Definition 2.1. For 1 ≤ i ≤ l, the gallery γ is said to be folded at pi, or to have a fold at pi, if ci− 1 = ci.
Combinatorial galleries include not just the alcoves ci but also the panels pi precisely in order to record the panels in which folds (may) occur. If γ is folded at pi we may also say that γ is folded at H, where H is the hyperplane supporting pi.
Definition 2.6 (Definition 4.5 of 16)
Fix an orientation ϕ of A and suppose that a combinatorial gallery γ lies in A. We say that γ is positively folded with respect to ϕ if for all i such that γ is folded at pi, one has ϕ(ci,pi) = +.
3 Chimneys, Retractions, Orientations, and Shadows
Throughout this section, we use the notation of Section 2. Thus X is an arbitrary affine building of type (W,S), with (W,S) irreducible, and A is any apartment of X, with a fixed identification of A with the vector space V. We define chimneys for such X in Section 3.1. In Section 3.2 we formulate retractions from chimneys, and in Section 3.3 we define the orientation induced by a chimney. Section 3.4 then defines shadows in our setting, and relates shadows to retractions.
3.1 Chimneys
In this section we give our definition of chimneys, in Definition 3.1 and its generalization Definition 3.7. We discuss the relationship between our definitions and related notions in the literature, and provide examples.
Definition 3.1
Let J be a subset of \(\{ 1, \dots , n \}\), with corresponding root system ΦJ. The J-chimney (in A) is the following collection of half-apartments of A:

Moreover, for any collection of integers \(\{n_{\beta }\in \mathbb {Z} \mid \beta \in {\varPhi }^{+} \setminus {\varPhi }_{J}^{+}\}\), the corresponding J-sector is the subcomplex of A given by

Write SJ(0) for the J-sector defined by the all-zeros sequence, i.e., \(n_{\beta }=0, \forall \beta \in {\varPhi }^{+} \setminus {\varPhi }_{J}^{+}\).
Before we continue with some examples of chimneys and J-sectors, we make a couple of remarks on the origin and broader mathematical context of chimneys.
Remark 3.2 (Chimneys and bordifications)
It is important to note that in our definition, a chimney is a collection of subsets of the apartment A, so a chimney is not itself a subset of A. The intersection of all half-apartments in a chimney is in fact most often empty, and the union of all such half-apartments is most often A. One way to think of the J-chimney ξJ is to see it as a direction at infinity of the affine building X which is determined by the given filter of half-apartments. More formally, a J-chimney for nonempty J is an alcove in the affine building for the Levi factor associated with J. In the rank 1 case, that is, where |J| = 1, this building is a panel tree.
The J-sectors should be thought of as representatives within A of the J-chimney, much like Weyl chambers (or sectors) in A are representatives of chambers in the spherical building at infinity. In other words, for a fixed J the collection of all J-sectors can be thought of as the collection of subcomplexes of A which “point towards” the J-chimney ξJ, which lies at infinity.
These ideas can be made precise as follows. One can show that ξJ describes a point in the combinatorial bordification \({\mathscr{C}}_{sph}(X)\) introduced by Caprace and Lécureux in Section 2.1 of [9], and that J-sectors are a special case of the generalized sectors introduced in Section 2.3 of [9]. We remark that Caprace and Lécureux are considering an arbitrary building X, and are generalizing results obtained for certain Bruhat–Tits buildings by Guivarc’h and Rémy in [15]. Another related work is the (unpublished) PhD thesis of Charignon [8], who defines a compactification of an arbitrary locally finite affine building by a collection of affine buildings at infinity.
In order to keep this work self-contained and focused on the case at hand, we decided to introduce our own definitions of chimneys and the associated sectors. Although the work of Caprace and Lécureux [9] takes place in the setting of an arbitrary building X, we restrict our attention to affine cases. Our algebraic applications in Section 5 are for affine buildings, and for (W,S) affine, the associated spherical root system provides a convenient way to describe chimneys and J-sectors. In later proofs we will mostly work with J-sectors rather than the chimney itself, although we will need our definition of a chimney to formulate the definition of a chimney-induced orientation (see Definition 3.24 below).
Remark 3.3 (Historical origin of chimneys)
The notion of a chimney in an affine building is not new. Chimneys (in French, cheminées) were first introduced by Rousseau (see, for example, [34] or [35]). In these works, a chimney is defined as the closure in the building of the union of a geodesic segment and a geodesic half-line which have the same origin and lie in the same apartment. A formulation of chimneys equivalent to Rousseau’s, and which relates chimneys to compactifications of affine buildings, appears in Section 4.2 of [8]. Our J-sectors are in fact a special case of Rousseau’s chimneys.
We now discuss some examples of J-chimneys and J-sectors.
Example 3.4
If J = ∅ then we have ΦJ = ∅ and so the chimney ξ∅ is the collection of all half-apartments containing subsectors of the antidominant Weyl chamber \(\mathcal {C}_{w_{0}}\). The corresponding J-sectors are all of the translates of \(\mathcal {C}_{w_{0}}\), that is, the collection of all sectors in A whose intersection with \(\mathcal {C}_{w_{0}}\) contains a subsector of \(\mathcal {C}_{w_{0}}\). In particular, the sector S∅(0) is equal to the antidominant Weyl chamber \(\mathcal {C}_{w_{0}}\). Thus the chimney ξ∅ can be identified with the chamber at infinity represented by the antidominant Weyl chamber.
Example 3.5
If \(J = \{ 1,\dots ,n\}\) then ΦJ = Φ. The J-chimney is the collection of all half-apartments containing the base alcove cf, and the only J-sector is the base alcove cf itself.
Example 3.6
Consider Figs. 1 and 2 of the introduction. Letting α = α1 be the black root in these figures, the other two (gray) roots can be labeled as α2 and α1 + α2, so that the three depicted roots are the positive roots in type \(\tilde {A_{2}}\). Then if J = {1}, the shaded region is an example of a J-sector.
Recall that the affine Weyl group W acts naturally on the collection of half-apartments in A. We now use this action to generalize J-chimneys and J-sectors.
Definition 3.7
For any \(J \subseteq \{ 1,\dots ,n\}\) and any y ∈ W, the (J,y)-chimneyξJ,y is obtained by acting on the J-chimney on the left by y, that is,
Hence, letting y = tμu with μ ∈ R∨ and u ∈ W0,
Similarly we obtain a (J,y)-sectorSJ,y({nβ}) := y ⋅ SJ({nβ}) for all y = tμu ∈ W and any set \(\{n_{\beta }\in \mathbb {Z} \mid \beta \in {\varPhi }^{+} \setminus {\varPhi }_{J}^{+}\}\) by
Write SJ,y(0) for the (J,y)-sector defined by the all-zeros sequence, i.e., \(n_{\beta }=0, \forall \beta \in {\varPhi }^{+} \setminus {\varPhi }_{J}^{+}\).
The next two examples generalize Examples 3.4 and 3.5, respectively.
Example 3.8
If J = ∅ and w ∈ W0, then any (J,w)-sector is a translate of the Weyl chamber \(w\mathcal {C}_{w_{0}} = \mathcal {C}_{ww_{0}}\), and the sector S∅,w(0) = w ⋅ S∅(0) is equal to the Weyl chamber \(\mathcal {C}_{ww_{0}}\). Thus the (∅,w)-chimney can be identified with the chamber at infinity represented by the Weyl chamber \(\mathcal {C}_{ww_{0}}\), and the chambers at infinity (in the boundary of A) are in bijection with the (∅,w)-chimneys.
Example 3.9
If \(J = \{1,\dots ,n\}\) and y ∈ W then the only (J,y)-sector is the alcove ycf. Thus every alcove in A is an instance of a (J,y)-sector.
3.2 Retractions from Chimneys
In this section we give our formulation of chimney retractions (see Definition 3.18). In order to give this definition and show that chimney retractions are well-defined, we will need several preliminary results and definitions. Throughout this section, \(J \subseteq \{1,\dots ,n\}\) and y ∈ W.
Lemma 3.10
Every (J,y)-sector contains at least one alcove, and if it contains more than one alcove, it contains infinitely many.
Proof
It is enough to prove the statement for J-sectors.
Suppose first that J = ∅. Then by Example 3.4, any J-sector contains a subsector of the antidominant Weyl chamber \(\mathcal {C}_{w_{0}}\), hence contains infinitely many alcoves.
Now suppose \(J = \{ 1,\dots ,n\}\). Then by Example 3.5, the only J-sector is the base alcove cf, so the statement holds in this case.
In all other cases, the sets \({\varPhi }_{J}^{+}\) and \({\varPhi }^{+} \setminus {\varPhi }^{+}_{J}\) are both nonempty, and any J-sector is contained in the region of A lying between Hα and Hα,1 for all \(\alpha \in {\varPhi }_{J}^{+}\). The conditions provided by the (finite) collection of roots in \({\varPhi }^{+} \setminus {\varPhi }^{+}_{J}\) then determine a cone containing infinitely many alcoves of this region of A. Hence the assertion of the Lemma. □
Definition 3.11
Let y = tμu ∈ W, where μ ∈ R∨ and u ∈ W0. Let SJ,y({nβ}) be a (J,y)-sector. A minimal infinite gallery
is regular with respect to SJ,y({nβ}) if for all \(\beta \in {\varPhi }^{+} \setminus {\varPhi }_{J}^{+}\) and every \(k \in \mathbb {Z}\) such that the half-apartment \((u\beta )^{k, uw_{0}}\) is a subset of the half-apartment \(y \cdot \beta ^{n_{\beta },w_{0}} = (u\beta )^{n_{\beta }+\langle u\beta , \mu \rangle , uw_{0}}\), there exists an index ik such that the alcove \(c_{i_{k}}\) of γ is contained in \((u\beta )^{k, uw_{0}}\).
The previous definition essentially means that a regular infinite gallery eventually crosses every hyperplane that “cuts across” the (J,y)-sector, and can only be trapped in a “strip” of the (J,y)-sector lying between two parallel hyperplanes if they are of type uα with \(\alpha \in {\varPhi }_{J}^{+}\).
For the next lemma we use the metric approach to buildings, details of which can be found in Section 12 of [1]. Thus we view the affine building X as a CAT(0) space equipped with the usual CAT(0) metric, which restricts to a Euclidean metric on each apartment.
Lemma 3.12
For every pair of alcoves c and d in X, and any points x ∈ c and y ∈ d, there exists a minimal gallery containing the (unique) geodesic segment from x to y. Moreover, every geodesic ray starting at x is contained in a minimal infinite gallery.
Proof
The statement about pairs of alcoves is taken from [26, Lemma 3.1]. To see the statement about infinite geodesic rays argue as follows. Each geodesic ray is contained in an apartment. By the first part of the current lemma each finite length initial piece is contained in a minimal gallery. Local finiteness of the Coxeter complex then implies that we may choose these initial pieces in a consistent way such that the resulting infinite gallery covering the geodesic ray is minimal. □
Corollary 3.13
Every (J,y)-sector that is not a single alcove contains a regular minimal infinite gallery.
Proof
A (J,y)-sector is by definition an intersection of half-apartments, hence (J,y)-sectors are convex, meaning that any two alcoves in a (J,y)-sector can be connected by a minimal gallery which lies in that sector. Now by Lemma 3.10, a (J,y)-sector which is not a single alcove contains infinitely many alcoves. By the proof of Lemma 3.10 and the specific shape of the (J,y)-sector described there, a (J,y)-sector which is not a single alcove contains a regular geodesic ray starting at a point x contained in the interior of an alcove c. This ray is, by Lemma 3.12, contained in a minimal infinite gallery γ beginning at c. Moreover γ is regular since the geodesic was regular. By convexity of the intersection of half-apartments, γ must be contained in the (J,y)-sector. □
We will use the following result of [8], which holds for arbitrary affine buildings (in fact for arbitrary buildings). Recall that any building has a complete apartment system.
Lemma 3.14 (Corollary 4.3.2 in 8)
For every alcove c in the affine building X and any minimal infinite gallery γ in X, there exists an apartment A′ in the complete apartment system of X that contains both c and an infinite subgallery of γ.
The next result will be crucial for our definition of a chimney retraction.
Proposition 3.15
Let \(J \subseteq \{1,\dots ,n\}\) and let y ∈ W. Then for every alcove c in X there exists a collection of integers \(\{n_{\beta }\in \mathbb {Z} \mid \beta \in {\varPhi }^{+} \setminus {\varPhi }_{J}^{+}\}\) and an apartment Ac,(J,y) in the complete apartment system of X such that Ac,(J,y) contains both c and the (J,y)-sector SJ,y({nβ}).
Proof
In the case that the unique (J,y)-sector is the alcove ycf this follows directly from the buildings axioms. In all other cases the set \({\varPhi }^{+} \setminus {\varPhi }^{+}_{J}\) is nonempty, and so SJ,y(0) contains by Corollary 3.13 a regular minimal infinite gallery γ. Then Lemma 3.14 yields an apartment \(A^{\prime }\) which contains both c and an infinite subgallery of γ. Put \(A_{c,(J,y)} = A^{\prime }\). By the regularity of γ and the fact that apartments intersect in convex sets, one obtains that the intersection of Ac,(J,y) with the apartment A does contain a (J,y)-sector SJ,y({nβ}) for a collection of integers nβ large enough. □
Proposition 3.15 is the natural generalization of the axiomatic fact that any pair of alcoves is contained in a common apartment, and at the same time a natural generalization of the statement of part (1) of the Theorem in [5, Section 8] to chimneys. Corollary 3.16 below is a direct consequence of the aforementioned proposition.
Corollary 3.16
For any \(J \subseteq \{1,\dots ,n\}\), any y ∈ W, and any (J,y)-chimney, the building X is (as a set) the union of all apartments containing a (J,y)-sector representing this chimney.
We now combine Proposition 3.15 with Lemma 3.10 to obtain the following.
Corollary 3.17
For any choice of an apartment Ac,(J,y) as in the statement of Proposition 3.15, the intersection A ∩ Ac,(J,y) contains at least one alcove. Hence there is a unique isomorphism Ac,(J,y) → A which fixes Ac,(J,y) ∩ A pointwise.
Proposition 3.15 and Corollary 3.17 are the reasons why chimney retractions as formulated in the next definition are well-defined. We note that we are using an apartment Ac,(J,y) in the complete apartment system on X to define this retraction.
Definition 3.18
Let X be an affine building and A an apartment of X. Let \(J \subseteq \{1,\dots ,n\}\) and let y ∈ W. For any alcove c of X, let rJ,y(c) be the image of c under the unique isomorphism that maps an apartment Ac,(J,y) as in the statement of Proposition 3.15 onto A while fixing Ac,(J,y) ∩ A pointwise. The resulting induced simplicial map
is the (J,y)-chimney retraction or the retraction from the (J,y)-chimney.
A chimney retraction or a retraction from a chimney is a (J,y)-chimney retraction for some \(J \subseteq \{ 1,\dots ,n\}\) and some y ∈ W. If  is the trivial element of W, we may write
is the trivial element of W, we may write  , and call rJ the retraction from the J-chimney.
, and call rJ the retraction from the J-chimney.
Remark 3.19
If J = ∅ and y = w ∈ W0, so that the (J,w)-chimney can be identified with a chamber at infinity (see Example 3.8), then the retraction from the (J,w)-chimney is the retraction onto A centered at this chamber at infinity. If \(J = \{1,\dots ,n\}\), so that the unique (J,y)-sector is the alcove ycf (see Example 3.9), then the retraction from the (J,y)-chimney is the retraction onto A centered at the alcove ycf. Thus in these cases the chimney retraction specializes to the two well-known retractions of affine buildings onto an apartment.
Remark 3.20
For arbitrary J, our formulation of the retraction rJ,y is a generalization and formalization of the retraction ρP,w which is described in Section 11.2 of [13], and also considered in Section 6 of [19]. We explain this further at Remark 5.4.
Remark 3.21
A slightly different approach to chimney retractions, which was explained to us by Jean Lécureux, would be to use Proposition 2.30 of [9], or similar results from [8]. Since the definitions and results of [9] hold for arbitrary buildings X, chimney retractions could then be defined for non-affine buildings as well (see also Remark 3.2).
The next corollary is an immediate consequence of our formulation of chimney retractions, and generalizes the corresponding result for retractions centered at chambers at infinity. See the second paragraph after Exercise 11.65 of [1].
Corollary 3.22
Let X be an affine building and A an apartment of X. Let \(J \subseteq \{1,\dots ,n\}\) and let y ∈ W. Then for any alcove c of X, there is an alcove d in some (J,y)-sector of A such that the image of the alcove c under the retraction rJ,y : X → A is equal to the image of c under the retraction onto A centered at d.
The following generalizes Corollary 3.22, and extends to all chimney retractions the corresponding result for retractions centered at chambers at infinity (see Exercise 11.67 of [1]). As explained further at Remark 5.4, this result also generalizes Lemma 6.4 of [19].
Corollary 3.23
Let X be an affine building and A an apartment of X. Let \(J \subseteq \{1,\dots ,n\}\) and let y ∈ W. Then for any bounded subset B of X, there is an alcove d in some (J,y)-sector of A such that the image of B under the retraction rJ,y : X → A is equal to the image of B under the retraction onto A centered at d.
Proof
If \(J= \{1,\dots ,n\}\) then the unique (J,y)-sector is the alcove y = ycf, so taking d = y we are done. Now assume that \(J \subsetneq \{1,\dots ,n\}\) and fix a (J,y)-sector in A. Then by Corollary 3.13, this (J,y)-sector contains a regular infinite gallery \( \gamma =(p_{0}, c_{0}, p_{1}, {\dots } , p_{i} , c_{i} , p_{i+1} , {\dots } )\). By similar arguments to those used to prove Proposition 3.15, since B is bounded, for all i large enough (depending on B) the restriction to B of rJ,y : X → A is equal to the restriction to B of the retraction onto A centered at ci. This completes the proof. □
3.3 Chimney-Induced Orientations and Positively Folded Galleries
In this section we define the natural orientation induced by a (J,y)-chimney, and hence say what it means for a combinatorial gallery to be positively folded with respect to a given chimney. The general definitions of an orientation and a positively folded gallery are stated in Section 2.2.
The key definition for this section is as follows. Recall from Definition 3.7 that a (J,y)-chimney is a collection of half-apartments in A.
Definition 3.24
Let \(J \subseteq \{1,\dots ,n\}\) and let y ∈ W. Let c be an alcove of A, let p be a panel of c, and let H be the hyperplane supporting p. The orientation induced by the(J,y)-chimney, denoted ϕJ,y, is defined by ϕJ,y(c,p) = + if and only if the half-apartment determined by H which contains c is not an element of the (J,y)-chimney.
Thus an alcove c is on the positive side of p with respect to the orientation ϕJ,y if, roughly speaking, c is on the side of p which faces away from the (J,y)-chimney. We say that a gallery in A is positively folded with respect to the(J,y)-chimney if it is positively folded with respect to the orientation ϕJ,y (see Definition 2.6). Thus a gallery is positively folded with respect to a given chimney if, roughly speaking, it is always folded away from this chimney.
The next result is immediate from Definition 3.24.
Lemma 3.25
Let ϕ = ϕJ,y be the orientation induced by the (J,y)-chimney and let H be a hyperplane of A. If p and \(p^{\prime }\) are panels of H, and c and \(c^{\prime }\) are alcoves of A containing p and \(p^{\prime }\), respectively, then \(\phi (c,p) = \phi (c^{\prime },p^{\prime })\) if and only if c and \(c^{\prime }\) are on the same side of H in A.
We now use Lemma 3.25 to make the following definition for chimney orientations (for an arbitrary orientation, it does not make sense to talk about the positive or negative side of a hyperplane).
Definition 3.26
Let ϕ = ϕJ,y be the orientation induced by the (J,y)-chimney. Let H be a hyperplane of A, let p be a panel in H and let c be an alcove containing p. Then c is on the positive side of H (with respect toϕ) if ϕ(c,p) = +, and c is on the negative side of H (with respect toϕ) if ϕ(c,p) = −.
Remark 3.27
The orientation induced by a chimney generalizes several notions of orientation that already appeared in the literature.
If J = ∅ then using Example 3.4, one can check that the orientation induced by the J-chimney is the same as the periodic orientation on hyperplanes considered in [31]. More generally, for w ∈ W0, the orientation induced by the (J,w)-chimney is the same as the periodic orientation on hyperplanes induced by the labeling at infinity \(\phi ^{\partial }_{w}\) as in Definition 3.7 of [28] (see also Definitions 3.10 and 3.13 of [16]); such an orientation is often called an orientation at infinity in [28]. In particular, the opposite standard orientation at infinity in [28] is that induced by the ∅-chimney, and this orientation is what is used for the main constructions in [28].
If \(J = \{1,\dots ,n\}\) and y ∈ W then the orientation induced by the (J,y)-chimney is opposite to the alcove orientation towards ycf from Definition 3.6 of [16]. More precisely, recall from Example 3.5 that y = ycf is the unique (J,y)-sector, and write ϕy for the alcove orientation towards ycf. Then ϕJ,y(c,p) = + if and only if ϕy(c,p) = −.
We now discuss braid-invariance of orientations. This will be used in Section 3.4 below.
Definition 3.28 ([16, Definition 5.2])
An orientation ϕ of A is braid-invariant if for any braid-equivalent reduced words \((s_{j_{1}},\dots ,s_{j_{l}})\) and \((s'_{j_{1}},\dots ,s'_{j_{l}})\) in S and any x ∈ W, there is a combinatorial gallery of type \((\text {type}(p_{0}),s_{j_{1}},\dots ,s_{j_{l}},\text {type}(p_{l+1}))\) with final alcove x which is positively folded with respect to ϕ if and only if there is a combinatorial gallery of type \((\text {type}(p_{0}),s'_{j_{1}},\dots ,s'_{j_{l}},\text {type}(p_{l+1}))\) with final alcove x which is positively folded with respect to ϕ.
It is proved in Proposition 4.33 of [28] (see also Proposition 5.3 of [16]) that for J = ∅ and any w ∈ W0, the orientation induced by the (J,w)-chimney is braid-invariant. (Example 3.4 and Remark 3.27 explain the relationship between this language and the terminology used in [28] and [16].) We now establish braid-invariance for arbitrary chimneys. We will describe in Remarks 4.9 and 5.12 how our main results give two other approaches to the proof of the following.
Proposition 3.29
Chimney-induced orientations are braid-invariant.
Proof
Let ϕ = ϕJ,y be a chimney-induced orientation. As in the proofs of [28, Proposition 4.33] and [16, Proposition 5.3], it suffices to consider reduced words \((s,t,s,\dots )\) and \((t,s,t,\dots )\) of length m, where s,t ∈ S are such that st has order \(m = m_{st} < \infty \), and galleries of these types with first alcove cf. All panels of such galleries are panels of types s or t which contain the origin, and all alcoves of such galleries are of the form vcf where v ∈〈s,t〉. It is then straightforward to verify that the orientation induced by the (J,y)-chimney is “locally” the same as the orientation induced by the (∅,w)-chimney, for some w ∈ W0 (depending on s, t, J, and y). To be precise, one can check that there is a w ∈ W0 such that for every pair (c,p) where c = vcf with v ∈〈s,t〉, and p is a panel of c of type s or t, we have ϕ(c,p) = ϕ∅,w(c,p). The result then follows from [28, Proposition 4.33] or [16, Proposition 5.3]. □
In the rest of the paper we will only consider orientations ϕ = ϕJ,y which are induced by some (J,y)-chimney.
3.4 Shadows
In this section we recall and slightly generalize the notion of a shadow which was first introduced in [16]. A special case of Definition 3.30 below, namely that where σ = τ = cf, is the notion of a regular shadow as introduced in [16, Definition 6.3]. Proposition 3.29 implies that shadows are well-defined and independent of the choice of minimal gallery γ in the following definition.
Definition 3.30
Let \(J \subseteq \{1,\dots ,n\}\) and y ∈ W. Let x ∈ W and let σ and τ be faces of the fundamental alcove cf which contain the origin. Fix a minimal gallery γ with first face σ and last face xτ. The shadow of xτ starting at σ with respect to the (J,y)-orientation, denoted ShJ,y(xτ,σ), is the set of final simplices of all galleries of type(γ) which have first face σ and are positively folded with respect to the (J,y)-chimney.
We sometimes say that a shadow is taken with respect to the(J,y)-chimney instead of with respect to the (chimney-induced) (J,y)-orientation.
Notation 3.31
We simplify terminology and notation for the most commonly used cases.
If J = {1,…,n}, then the (J,y)-chimney is just the alcove y = ycf. In this case, we will denote the shadow by Shy(xτ,σ).
If both σ and τ are equal to the fundamental alcove cf, so that xτ = xcf = x, the shadow of x with respect to the (J,y)-chimney is defined to be the shadow of x starting at cf with respect to the (J,y)-orientation. That is, ShJ,y(x) is the set of final alcoves of galleries of type \(\vec {x}\) which have first face and first alcove cf and which are positively folded with respect to the (J,y)-chimney. We denote this shadow by ShJ,y(x). If in addition \(J = \{1,\dots ,n\}\), we denote this shadow by Shy(x).
If σ and τ are both the origin, then λ := xτ is an element of the coroot lattice. In this case, the shadow ofλ with respect to the (J,y)-chimney is the set of final vertices of galleries of type \(\vec {\lambda }\) which have first face the origin and which are positively folded with respect to the (J,y)-chimney. We denote this shadow by ShJ,y(λ). If in addition \(J = \{1,\dots ,n\}\), we denote this shadow by Shy(λ).
Examples of shadows are given in Figs. 1 and 2 of the introduction, and in Section 6.
The next result gives an interpretation of shadows in terms of retractions. We write r : X → A for the retraction onto A centered at the base alcove cf. Recall from Definition 3.18 that rJ,y : X → A denotes the retraction (onto A) from the (J,y)-chimney.
Proposition 3.32
Let \(J \subseteq \{1,\dots ,n\}\) and let y ∈ W.
Let x ∈ W and let σ and τ be faces of the fundamental alcove cf which contain the origin. Let Wσ be the subgroup of W0 which fixes σ. Then the shadow of xτ with respect to the (J,y)-orientation starting at σ is the set of simplices given by
In particular, the shadow of x = xcf with respect to the (J,y)-chimney is the set of alcoves given by
For λ ∈ R∨, the shadow of λ with respect to the (J,y)-chimney is the set of elements of R∨ given by
Proof
Fix a minimal gallery γ with first face σ and last face xτ. By definition the shadow ShJ,y(xτ,σ) is then the collection of end-simplices of all galleries of type(γ) and first face σ.
As described in Section 4.3 of [16], the affine Weyl group W acts naturally on the set of combinatorial galleries in A. This action is type-preserving and also preserves minimality of galleries. Thus the stabilizer Wσ of the first face σ inside W permutes the set of all minimal galleries of type(γ) in A which have first face σ, and Wσ ⋅ xτ is the collection of all end-simplices of minimal galleries in A which start in σ and are of type(γ). Hence by definition of the retraction r, the set r− 1(Wσ ⋅ xτ) is the collection of all end-simplices of minimal galleries in X which start in σ and are of type(γ).
We prove first that the image of every such minimal gallery under rJ,y is positively folded with respect to the (J,y)-chimney, and has type(γ). The proof is exactly the same as the proof of Lemma 2.9 in [17], where one replaces the sector \(\mathcal {C}_{f}^{op}\) by a (J,y)-sector. The main argument then makes use of Proposition 3.15 and Corollary 3.22.
It then remains to show that every gallery in A of type(γ) which starts at σ and is positively folded with respect to the (J,y)-chimney is an image of a minimal one under the retraction rJ,y. This is the analog of Proposition 3.3 in [17] for chimney retractions. The proof of this proposition also carries over to the chimney case if we prove the analog of [17, Lemma 2.4]. This is done in Lemma 3.33 below. □
The next lemma completes the last step in the proof of Proposition 3.32. Note that in the following statement, the (J,y)-sectors are each contained in our fixed apartment A, but that once any apartment Ai contains some (J,y)-sector, we can also define the retraction onto Ai from the (J,y)-chimney.
Lemma 3.33
Let \(J \subseteq \{1,\dots ,n\}\) and y ∈ W. Let \(A_{1},A_{2},\dots ,A_{k}\) be a collection of apartments in X such that each Ai contains some (J,y)-sector. Denote by ri the retraction onto Ai from the (J,y)-chimney. Then
Proof
For all i the retraction ri maps, by definition, any apartment containing a (J,y)-sector isomorphically onto Ai. Corollary 3.16 implies that X is the union of such apartments. Define ρ := r1 ∘⋯ ∘ rk. Then on the one hand each apartment that contains a (J,y)-sector is isomorphically mapped onto A1 by ρ. On the other hand ρ is (Weyl-)distance nonincreasing. These two properties, which also hold for r1, uniquely characterize this retraction. Therefore r1 = ρ. □
4 A Recursive Description of Shadows
The main result in this section is Theorem 4.8, which gives a recursive description of shadows. A special case of this theorem was stated as Theorem 1.1 in the introduction. The examples in Section 6 illustrate how to apply our recursion.
We continue all notation from Section 3. Let H be a hyperplane in A. For y ∈ W, we denote by Hy the (closed) half-apartment of A which is bounded by H and contains the alcove y = ycf. In particular,  is the closed half-apartment of A which is bounded by H and contains the base alcove
is the closed half-apartment of A which is bounded by H and contains the base alcove  . For example, in Fig. 3,
. For example, in Fig. 3,  is the half-apartment to the left of H. We write rH for the reflection of A in H, and note that rH is type-preserving.
is the half-apartment to the left of H. We write rH for the reflection of A in H, and note that rH is type-preserving.
We now define two operators on galleries, \(e^{\L }_{H}\) and \(f^{\L }_{H}\). We will use these together with Lemma 4.7 to prove Theorem 4.8. Some parts of the following definitions are illustrated by Fig. 3.
Definition 4.1
Fix a hyperplane H of A, and let γ = (p0,c0,p1,c1, p2,…,pl,cl,pl+ 1) be a combinatorial gallery in A.
-
(i)
For 0 ≤ j < k ≤ l + 1, call \({\L }=[j,k] \subset \mathbb {N}\) an H-protrusion (of γ) if pj,pk ⊂ H and
 for all j ≤ i < k (note that pi ⊂ H may occur for some j < i < k). Given an H-protrusionL = [j,k], the associated subgallery of γ is
$$\gamma_{{\L}} := (p_{j} , c_{j} , p_{j+1} , {\ldots} , p_{k-1} , c_{k-1} , p_{k}).$$
for all j ≤ i < k (note that pi ⊂ H may occur for some j < i < k). Given an H-protrusionL = [j,k], the associated subgallery of γ is
$$\gamma_{{\L}} := (p_{j} , c_{j} , p_{j+1} , {\ldots} , p_{k-1} , c_{k-1} , p_{k}).$$Similarly, if pj ⊂ H and
 for all i ≥ j, then \({\L }=[j,\infty )\) is an H-protrusion, and we define γL to be the subgallery
$$\gamma_{{\L}} := (p_{j} , c_{j} , p_{j+1} , {\ldots} , p_{l} , c_{l} , p_{l+1}).$$
for all i ≥ j, then \({\L }=[j,\infty )\) is an H-protrusion, and we define γL to be the subgallery
$$\gamma_{{\L}} := (p_{j} , c_{j} , p_{j+1} , {\ldots} , p_{l} , c_{l} , p_{l+1}).$$ -
(ii)
Call \({\L }={\L }_{1} \sqcup {\L }_{2} \sqcup {\dots } \sqcup {\L }_{r} \subset \mathbb {N}\) an H-outcrop (of γ) if each Li is an H-protrusion. If L contains every possible H-protrusion, then L is the (unique) maximal H-outcrop. If \([j,\infty )\) is an H-protrusion, where j ≤ l is the largest index such that pj ⊂ H, and L contains every possible H-protrusion except for \([j,\infty )\), then we call L the (unique) near-maximal H-outcrop. We take the maximal or near-maximal H-outcrop to be L = ∅ if there are no H-protrusions.
-
(iii)
For 1 ≤ j < k ≤ l + 1, call \({\L }=[j,k] \subset \mathbb {N}\) an H-indentation if pj,pk ⊂ H and
 for all j ≤ i < k; note that if j is the smallest index such that pj ⊂ H then the interval [0,j] is by definition not an H-indentation.
for all j ≤ i < k; note that if j is the smallest index such that pj ⊂ H then the interval [0,j] is by definition not an H-indentation. -
(iv)
Call \({\L }={\L }_{1} \sqcup {\L }_{2} \sqcup {\dots } \sqcup {\L }_{r}\) where each Li is an H-indentation an H-ingrowth. If L contains every possible H-indentation, then L is the (unique) maximal H-ingrowth. We take the maximal H-ingrowth to be L = ∅ if there are no H-indentations.
Note that every gallery has a maximal outcrop, but that a near-maximal outcrop does not exist if the final simplex of γ is contained in  .
.
Example 4.2
Figure 3 shows an example of a gallery \(\gamma = (p_{0},c_{1},\dots ,p_{29},c_{29},p_{30})\), where p0 = v0 is the origin and c0 = cf. This gallery is illustrated with a black line. The red hyperplane H contains the panels p5, p13, p18, and p26 of γ. The intervals [5,13], [18,26], [18,30], \([26, \infty ]\), and \([18,\infty )\) are the H-protrusions, the maximal H-outcrop is \([5,13] \sqcup [18,\infty )\), and the near-maximal H-outcrop is [5,13] ⊔ [18,26]. The H-indentation [13,18] is equal to the maximal H-ingrowth.
We will now define the first of the two operators in question.
Definition 4.3
Let H and γ be as in Definition 4.1. Fix an H-protrusion L = [j,k]. If L = ∅, define \(e^{\L }_{H}(\gamma ) = \gamma \). Otherwise, define \(e^{\L }_{H}\) to be the operator which folds the subgallery γL onto the half-apartment  , that is,
, that is,
Similarly, if \({\L }=[j,\infty )\), define \(e^{\L }_{H}\) by
For an H-outcrop L = L1 ⊔ L2 ⊔… ⊔ Lr, we define \(e^{{\L }}_{H}=e^{{\L }_{1}}_{H}\circ e^{{\L }_{2}}_{H} \circ {\dots } \circ e^{{\L }_{r}}_{H}\). Note that since the intervals Li are disjoint, the operators \(e^{{\L }_{i}}_{H}\) pairwise commute.
The second operator, \(f^{{\L }}_{H}\), is the inverse of \(e^{\L }_{H}\), that is, the operator that unfolds a gallery across H.
Definition 4.4
Let H and γ be as in Definition 4.1. For L = [j,k] an H-indentation, define
Similarly, if pj ⊂ H with j ≥ 1 and  for all i ≥ j, then \({\L }=[j,\infty )\) is an H-indentation, and we define
for all i ≥ j, then \({\L }=[j,\infty )\) is an H-indentation, and we define
Let now L = L1 ⊔ L2 ⊔… ⊔ Lr be an H-ingrowth. As with the \(e^{\L }_{H}\) operators, we define \(f^{\L }_{H}(\gamma ) = \gamma \) if L = ∅ and otherwise we define \(f^{\L }_{H} = f^{{\L }_{1}}_{H}\circ f^{{\L }_{2}}_{H} \circ {\dots } \circ f^{{\L }_{r}}_{H}\).
Note that by definition \(f^{\L }_{H}\) preserves the initial simplex of γ.
Remark 4.5
The operators \(e^{\L }_{H}\) and \(f_{H}^{\L }\) are inspired by the root operators defined in [14], and this motivates our notation. However, we allow folds in hyperplanes orthogonal to non-simple root directions, and \(e^{\L }_{H}\) and \(f_{H}^{\L }\) may reflect more than one subgallery of γ (in the case that L is an H-outcrop or H-ingrowth).
Remark 4.6
Given a gallery γ, the galleries \(e_{H}^{\L }(\gamma )\) and \(f_{H}^{\L }(\gamma )\) have the same type as γ. This is because both \(e_{H}^{\L }\) and \(f_{H}^{\L }\) fix the initial simplex of γ, and the reflection rH is type-preserving.
The next lemma, concerning the effect of certain \(e_{H}^{\L }\) and \(f_{H}^{\L }\) on orientations, is the key technical result for the proof of Theorem 4.8. Recall from Section 3 that for \(J = \{ 1,\dots , n\}\) and y ∈ W, the unique (J,y)-sector is the alcove y = ycf, and a gallery γ is positively folded with respect to the (J,y)-chimney if and only if for every panel p at which γ is folded, the hyperplane supporting p separates the (identical) alcoves of γ which occur before and after this fold from y.
Lemma 4.7
Let \(J = \{ 1,\dots ,n\}\), y ∈ W, and s ∈ S, and let H be the unique hyperplane separating the alcoves ycf and yscf. Assume that ℓ(ys) > ℓ(y).
-
(1)
If a gallery γ is positively folded with respect to the (J,y)-chimney, then for the maximal or near-maximal H-outcrop L, the gallery \(e^{\L }_{H}(\gamma )\) is positively folded with respect to the (J,ys)-chimney.
-
(2)
If a gallery γ is positively folded with respect to the (J,ys)-chimney, then for the maximal H-ingrowth L, the gallery \(f^{\L }_{H}(\gamma )\) is positively folded with respect to the (J,y)-chimney.
Proof
We will prove (1); the proof of (2) is similar. Since ℓ(ys) > ℓ(y), we observe that  . Let γ = (p0,c0,p1,c1,p2,…,pl,cl,pl+ 1) and let L be the maximal H-outcrop. Then
. Let γ = (p0,c0,p1,c1,p2,…,pl,cl,pl+ 1) and let L be the maximal H-outcrop. Then
where qi = { pi if pi ⊂ Hy rH(pi) if pi ⊂ Hys and di = { ci if ci ⊂ Hy rH(ci) if ci ⊂ Hys.
Suppose that \(e^{{\L }}_{H}(\gamma )\) has a fold at its panel qi, so that di− 1 = di. We wish to show that the hyperplane supporting the panel qi separates di− 1 = di from the alcove yscf.
-
Case 1:
Suppose ci− 1≠ci, that is, γ is not folded at pi. Then \(e^{\L }_{H}\) acts as the identity on one of the alcoves ci− 1 and ci and as rH on the other. Assume first that di− 1 = ci− 1 and di = rH(ci). Then since ci− 1 ⊂ Hy and ci ⊂ Hys, we have pi ⊂ H and qi = pi. Since di = di− 1 = ci− 1 ⊂ Hy, this implies that H is the hyperplane supporting qi, and that H separates the alcoves di and yscf, as required. The proof when di = ci and di− 1 = rH(ci− 1) is similar.
-
Case 2:
Suppose ci− 1 = ci, that is, the gallery γ has a fold at pi. Let Hi be the hyperplane supporting pi. Since γ is positively folded with respect to the (J,y)-chimney, we know that Hi separates the alcoves ci and ycf. We consider two subcases.
-
Case 2(a):
The alcove ci− 1 = ci is in Hys. Then as L is the maximal H-outcrop, we have di− 1 = di = rH(ci) and qi = rH(pi). Since the hyperplane Hi separates the alcoves ci and ycf, the hyperplane rH(Hi) separates the alcoves rH(ci) and rH(ycf). Hence the hyperplane supporting qi separates the alcoves di and yscf, as required.
-
Case 2(b):
The alcove ci− 1 = ci is in Hy. Then di− 1 = di = ci and qi = pi. Since Hi separates the alcoves ci and ycf, it follows that \(d_{i} \not \subset {H_{i}^{y}}\). Therefore Hi≠H, and so Hi does not separate the alcoves yscf and ycf (since H is the unique hyperplane to do so). Hence \(ys{\textbf {c}_f} \subset {H_{i}^{y}}\). Thus Hi, the hyperplane supporting qi, separates the alcoves di and yscf.
This completes the proof of (1) for L the maximal H-outcrop. Now let j ≤ l be the largest index such that pj ⊂ H and assume that \([j,\infty )\) is an H-protrusion, so that if \({\L }' = {\L } \setminus [j,\infty )\) then L′ is the near-maximal H-outcrop. Continuing notation from above, we have that
That is, the gallery \(e_{H}^{{\L }'}(\gamma )\) is the same as \(e_{H}^{\L }(\gamma )\) except that we do not apply the reflection rH to the tail \(\gamma _{[j,\infty )} = (p_{j} , c_{j} , {\ldots } , c_{l} , p_{l+1})\).
We have already proved that \(e_{H}^{\L }(\gamma )\) is positively folded with respect to the (J,ys)-chimney. Hence the initial subgallery
of \(e_{H}^{{\L }'}(\gamma )\) is positively folded with respect to the (J,ys)-chimney. Next, consider the consecutive alcoves dj− 1 and cj. Since pj is the last panel of γ to lie in H and \([j,\infty )\) is an H-protrusion, we have that cj ⊂ Hys. As L is the maximal H-outcrop, if cj− 1 ⊂ Hys then dj− 1 = rH(cj− 1) ⊂ Hy. Also if cj− 1 ⊂ Hy then dj− 1 = cj− 1 ⊂ Hy. Hence dj− 1≠cj and so the gallery \(e^{{\L }'}_{H}(\gamma )\) is not folded at pj. Since pj is the last panel of γ to be contained in H, any folds in the tail \(\gamma _{[j,\infty )}\) are in hyperplanes \(H^{\prime } \neq H\). Now as the alcoves yscf and ycf are not separated by any hyperplanes except for H, it follows that \(\gamma _{[j,\infty )}\) is positively folded with respect to the (J,ys)-chimney. We conclude that \(e_{H}^{{\L }^{\prime }}(\gamma )\) is positively folded with respect to the (J,ys)-chimney, as required. □
Note that in item (1) of Lemma 4.7 the gallery \(e^{\L }_{H}(\gamma )\) is positively folded with respect to both the maximal and near-maximal outcrop in case both are defined.
We are now ready to prove the main result of this section. Although Theorem 4.8 below is stated only for shadows with respect to (J,y)-chimneys where \(J = \{1,\dots ,n\}\) (see Notation 3.31), by combining Corollary 3.23 and Proposition 3.32 with Theorem 4.8 we obtain a recursive description of shadows for all chimneys, as the sets r− 1(Wσ ⋅ xτ), r− 1(x), and r− 1(W0 ⋅ λ) appearing in Proposition 3.32 are all bounded. The key point in the proof of Theorem 4.8 is that galleries which are positively folded with respect to the (J,y)-chimney may not be positively folded with respect to the (J,ys)-chimney, and so some careful manipulation of galleries is needed in order to calculate the shadow correctly.
Theorem 4.8
Let x ∈ W and let σ and τ be faces of the fundamental alcove cf which contain the origin. Let y ∈ W and s ∈ S. If ℓ(ys) > ℓ(y), then
where H is the unique hyperplane separating the alcoves yscf and ycf.
Proof
As in the proof of Lemma 4.7, the hypothesis ℓ(ys) > ℓ(y) implies that  . Fix a minimal gallery γx with first face σ and last face xτ. We will use \({\varGamma }^{+}_{\mathbf {y}}(\gamma _{x},\zeta )\) to denote the set of all galleries of the same type as γx which end at the simplex ζ and are positively folded with respect to the (J,y)-chimney, where \(J = \{1,\dots ,n\}\).
. Fix a minimal gallery γx with first face σ and last face xτ. We will use \({\varGamma }^{+}_{\mathbf {y}}(\gamma _{x},\zeta )\) to denote the set of all galleries of the same type as γx which end at the simplex ζ and are positively folded with respect to the (J,y)-chimney, where \(J = \{1,\dots ,n\}\).
Suppose first that we have ζ ∈ Shy(xτ,σ). Then by definition of the shadow, there is a gallery \(\gamma \in {\varGamma }^{+}_{\mathbf {y}}(\gamma _{x},\zeta )\). Let L be the maximal H-outcrop of γ if ζ ∈ Hy and the near-maximal H-outcrop of γ if ζ ∈ Hys (if ζ ∈ H, then either choice will be valid). Then by Lemma 4.7(1), the gallery \(e_{H}^{\L }(\gamma )\) is positively folded with respect to the (J,ys)-chimney. For L both maximal and near-maximal, by choice of L the final simplex of \(e_{H}^{\L }(\gamma )\) is ζ. Hence \(e_{H}^{\L }(\gamma ) \in {\varGamma }^{+}_{\mathbf {ys}}(\gamma _{x},\zeta )\), and so ζ ∈ Shys(xτ,σ).
Now suppose we have \(\eta \in r_{H}(H^{ys} \cap \operatorname {Sh}_{\mathbf {y}}(x\tau ,\sigma ))\). Then there exists \(\gamma \in {\varGamma }^{+}_{\mathbf {y}}(\gamma _{x},\zeta )\), where ζ = rH(η), equivalently η = rH(ζ), and ζ ∈ Hys. Since the first simplex of γ is σ ⊂cf (by definition of the shadow), it follows that there is at least one panel of γ contained in H. So letting γ have final simplex pn+ 1 = ζ, the maximal H-outcrop L includes the index n + 1. Thus \(e_{H}^{\L }(\gamma )\) has final simplex rH(ζ) = η. By Lemma 4.7(1), we have that \(e_{H}^{\L }(\gamma )\) is positively folded with respect to the (J,ys)-chimney. So \(e_{H}^{\L }(\gamma ) \in {\varGamma }^{+}_{\mathbf {ys}}(\gamma _{x},\eta )\). Hence η ∈ Shys(xτ,σ).
For the other inclusion, let ζ be in Shys(xτ,σ) but not in Shy(xτ,σ). Then there exists a gallery γ from σ to ζ that is positively folded with respect to the (J,ys)-chimney, but is not positively folded with respect to the (J,y)-chimney. Let L be the maximal H-ingrowth of γ. By Lemma 4.7(2), the gallery \(f_{H}^{\L }(\gamma )\) is positively folded with respect to the (J,y)-chimney. If \(f_{H}^{\L }(\gamma )\) ends in ζ, then we contradict the fact that ζ∉Shy(xτ,σ). So \(f_{H}^{\L }(\gamma )\) ends in rH(ζ), implying that ζ ∈ Hy, and hence \(r_{H}(\zeta ) \in H^{ys} \cap \operatorname {Sh}_{\mathbf {y}}(x\tau ,\sigma )\). Thus \(\zeta \in r_{H}(H^{ys} \cap \operatorname {Sh}_{\mathbf {ys}}(x\tau ,\sigma ))\), which completes the proof. □
Remark 4.9
We observe that the proof of Theorem 4.8 shows that for any choice of minimal gallery γx from cf to x, and for every alcove z in the shadow Shys(x), there exists a gallery in \({\varGamma }^{+}_{\mathbf {y}}(\gamma _{x},\mathbf {z})\). In particular, given two different braid-equivalent reduced words for x, we have distinct minimal galleries γx and \(\gamma ^{\prime }_{x}\) with types given by these reduced words. Thus, for any z ∈ W such that z ∈ Shys(x), we obtain galleries in both \({\varGamma }^{+}_{\mathbf {y}}(\gamma _{x},\mathbf {z})\) and \({\varGamma }^{+}_{\mathbf {y}}(\gamma ^{\prime }_{x},\mathbf {z})\). This gives us another proof that the orientation induced by the (J,y)-chimney for \(J=\{1,\dots ,n\}\) is braid-invariant. Then by applying Corollary 3.23, we obtain another proof of braid-invariance for general chimneys (see Proposition 3.29).
Remark 4.10
The proof of Theorem 4.8 calculates the shadow using sets of positively folded galleries of the form \({\varGamma }^{+}_{\mathbf {y}}(\gamma _{x},\zeta )\). It is reasonable to ask whether one can determine the number of distinct galleries in \({\Gamma }^{+}_{\mathbf {y}}(\gamma _{x},\zeta )\), that is, whether one can calculate a “shadow with multiplicities”. Determining such multiplicities is a delicate problem, essentially because the operators \({e_{H}^{L}}\) and \({f_{H}^{L}}\) used in the proof of Theorem 4.8 may reflect all or only some of the portions of a gallery lying on the appropriate side of H.
As a corollary of Theorem 4.8, we obtain the following restriction on where the shadow of a coroot lattice element λ can lie. In the case that X is the Bruhat–Tits building for G(F) with standard apartment A, and the retraction onto A centered at y has the same effect on r− 1(W0 ⋅ λ) as the retraction from the chamber at infinity corresponding to the negative unipotent subgroup U− of G(F), Corollary 4.11 recovers a well-known containment found in Bruhat–Tits [6]. The convex hull Conv in the following statement is the metric convex hull in the apartment A.
Corollary 4.11
Let λ ∈ R∨ and y ∈ W. Then
That is, for \(J = \{1,\dots ,n\}\) and y ∈ W, the shadow of λ with respect to the (J,y)-chimney is contained in the λ-Weyl polytope.
Proof
The proof is by induction on ℓ(y). If ℓ(y) = 0, that is,  , then Shy(λ) equals the orbit W0 ⋅ λ by Proposition 3.32, and we are done. Now let \(s_{i_{1}} {\dots } s_{i_{k}}\) be a reduced word for y. To simplify notation, let \(y^{\prime } = s_{i_{1}} {\dots } s_{i_{k-1}}\) and \(s = s_{i_{k}}\), and let H be the hyperplane separating the alcoves \(y^{\prime }{\textbf {c}_f}\) and \(y^{\prime }s{\textbf {c}_f} = y{\textbf {c}_f}\). By Theorem 4.8 and inductive assumption, it suffices to show that the set \(r_{H}(H^{y^{\prime }s} \cap \operatorname {Conv}(W_0 \cdot \lambda ))\) is contained in Conv(W0 ⋅ λ). If the intersection \(H^{y^{\prime }s} \cap \operatorname {Conv}(W_0 \cdot \lambda )\) is empty there is nothing to show, so we assume that there is some \(\mu \in H^{y^{\prime }s} \cap \operatorname {Conv}(W_0 \cdot \lambda )\).
, then Shy(λ) equals the orbit W0 ⋅ λ by Proposition 3.32, and we are done. Now let \(s_{i_{1}} {\dots } s_{i_{k}}\) be a reduced word for y. To simplify notation, let \(y^{\prime } = s_{i_{1}} {\dots } s_{i_{k-1}}\) and \(s = s_{i_{k}}\), and let H be the hyperplane separating the alcoves \(y^{\prime }{\textbf {c}_f}\) and \(y^{\prime }s{\textbf {c}_f} = y{\textbf {c}_f}\). By Theorem 4.8 and inductive assumption, it suffices to show that the set \(r_{H}(H^{y^{\prime }s} \cap \operatorname {Conv}(W_0 \cdot \lambda ))\) is contained in Conv(W0 ⋅ λ). If the intersection \(H^{y^{\prime }s} \cap \operatorname {Conv}(W_0 \cdot \lambda )\) is empty there is nothing to show, so we assume that there is some \(\mu \in H^{y^{\prime }s} \cap \operatorname {Conv}(W_0 \cdot \lambda )\).
As the reflection rH fixes the hyperplane H, by considering convex hulls it is now enough to show that for each \(\mu \in H^{y^{\prime }s} \cap (W_0 \cdot \lambda )\), we have rH(μ) ∈ Conv(W0 ⋅ λ). Moreover, by applying an appropriate element of W0, it suffices to take \(\mu = \lambda \in H^{y^{\prime }s}\). That is, we are in the situation that the hyperplane H separates the origin from λ, and we wish to show that rH(λ) lies in Conv(W0 ⋅ λ).
Now H = Hβ,i for some root β (not necessarily simple) and some index i, where without loss of generality i > 0. More precisely, letting kλ = 〈β,λ〉 we have without loss of generality that 0 < i < kλ, since the origin lies in Hβ = Hβ,0, the coroot lattice point λ lies in the hyperplane \(H_{\beta ,k_{\lambda }}\), and H = Hβ,i separates the origin from λ. The reflection sβ in the hyperplane Hβ takes λ to another extremal vertex of Conv(W0 ⋅ λ), namely the vertex sβ(λ) = λ − kλβ∨. The image of λ under the reflection sβ,i in Hβ,i then lies on the line interval connecting λ and sβ(λ), since sβ,i(λ) = λ − (kλ − i)β∨ and 0 < i < kλ. This line interval is contained in Conv(W0 ⋅ λ) and we have rH = sβ,i, so rH(λ) is contained in Conv(W0 ⋅ λ) as required. □
In the following lemma we prove a more general version of the assertion of Corollary 4.11. As we will not use it in its full generality we will not formally introduce some of the notions used in the proof, but refer the reader to [16] instead.
Lemma 4.12
Let λ ∈ R∨ and let ϕ be any orientation (not just one induced by a chimney). Then \( \operatorname {Sh}_{\phi }(\lambda ) \subseteq \operatorname {Conv}(W_0 \cdot \lambda )\). That is, the shadow of a coroot lattice element λ with respect to any orientation is contained in the λ-Weyl polytope.
Proof
The shadow with respect to the trivial positive orientation contains (by definition) the end-vertices of all folded galleries of a fixed type. One can show that these end-vertices are just those elements ν of the coroot lattice whose dominant image ν+ under the W0-action is smaller than λ+, i.e., all ν such that ν+ ≤ λ+ in dominance order. This follows from the fact that Bruhat order on group elements (corresponding to all the end-alcoves of folded galleries of a fixed type) restricts to dominance order on vertices. But the condition ν+ ≤ λ+ in dominance order is the same as taking the convex hull of W0 ⋅ λ as shown in, for instance, Lemma 3.5 of [18]. Any vertex shadow is a subset of the trivial positive shadow and hence a subset of the λ-Weyl polytope. □
5 Positively Folded Galleries and Double Cosets
In this section we establish the connection between the previous combinatorial results on folded galleries, and double coset intersections inside the underlying algebraic groups in the function field case. We first record some additional definitions and notation in Section 5.1, then in Section 5.2 adapt the key concepts from Section 3 to this setting. Section 5.3 proves the main result of this section, Theorem 5.14, which generalizes Theorems 1.2 and 1.3 of the introduction. This theorem establishes a bijection between the points of certain double coset intersections in partial affine flag varieties, and certain sets of positively folded galleries which have been further “decorated” by elements of the residue field. We then prove a nonemptiness statement in Theorem 5.16, and finally apply Theorems 5.14 and 5.16 to the case of the affine Grassmannian in Corollary 5.18
5.1 Conventions
We continue all terminology and notation from Section 2, and include here some further items needed to state and prove the theorems in this section. We are not redefining anything from the Coxeter-theoretic setup used in Section 2, but rather providing additional algebraic interpretations for many of these notions.
Let \(\mathbbm {k}\) be any field (not necessarily finite), let \(F = \mathbbm {k}((t))\), and let G be a split, connected, reductive group over F. Let \(\mathcal {O} = \mathbbm {k}[[t]]\) be the ring of integers of F. Choose a split maximal torus T of G and a Borel subgroup B = TU, where U is the unipotent radical. Denote the underlying root system by Φ, and further assume that Φ is irreducible. Throughout the remainder of the paper, we denote by Φ+ those (spherical) roots which are positive with respect to the opposite Borel subgroup B−. We will discuss this convention further below.
Let W0 be the (finite or spherical) Weyl group of T in G; that is, W0 = NG(T)/T. For λ ∈ X∗(T), write tλ for the element in T(F) that is the image of t under the homomorphism \(\lambda : \mathbb {G}_{m} \rightarrow T\). Let \({\varDelta } = \{\alpha _{i} \}_{i=1}^{n}\) be a basis of simple roots in X∗(T), chosen such that each \(\alpha _{i} \in {\varPhi }^{+}\) is positive with respect to B−. We denote by α∨ = 2α/〈α,α〉 the coroot associated to α ∈Φ with respect to the pairing \(\langle \ ,\ \rangle : X^{*}(T) \times X_{*}(T) \rightarrow \mathbb {Z}\). Let \(R^{\vee } = \oplus _{i=1}^{n} \mathbb {Z} \alpha _{i}^{\vee } \subset X_{*}(T)\) be the coroot lattice. Let \(W = R^{\vee } \rtimes W_0\) be the affine Weyl group, and \(\widetilde {W} = X_{*}(T) \rtimes W_0\) be the extended affine Weyl group. We view W0 and W as acting on the vector space \(V = \mathbb {R}^{n}\), which we can identify with \(X_{*}(T)\otimes _{\mathbb {Z}} \mathbb {R}\). By abuse of notation, we use the same symbol for an element of W0 or W and a lift of this element to G(F).
Let X be the Bruhat–Tits building for G(F). Then X is a (thick) affine building of type (W,S). Our choice of split maximal torus T determines the standard apartment A of X. Under the identification \(A = X_{*}(T) {\otimes }_{\mathbb {Z}} \mathbb {R} = V\), the interior of any alcove in A can be described as the set of all points v ∈ V satisfying the strict inequalities kα < 〈α,v〉 < kα + 1, where α runs through Φ+ and \(k_{\alpha } \in \mathbb {Z}\) is some fixed integer (depending upon the alcove and α). Recall that the dominant Weyl chamber \(\mathcal {{C}}_{f}\) is the set of points v ∈ V such that 〈α,v〉≥ 0 for all α ∈Φ+. We note that our convention of Φ+ being the (spherical) roots which are positive with respect to B− in fact ensures that the elements of Φ which lie in the half-apartment of A which is bounded by the hyperplane \(H_{\widetilde \alpha }\) and contains the dominant Weyl chamber are exactly the positive roots Φ+.
As in [13], we choose the Iwahori subgroup I of G(F) to be the inverse image of the opposite Borel subgroup \(B^{-}(\mathbbm {k})\) under the projection map \(G(\mathcal {O}) \rightarrow G(\mathbbm {k})\). This convention ensures that for all λ in the coroot lattice, the element tλ acts on A by translation by λ (rather than by − λ, had we chosen I to be the preimage of B). The base alcove cf of A is the (unique) alcove of X whose stabilizer in G(F) is equal to I.
Given any α ∈Φ and \(k \in \mathbb {Z}\), we write Uα,k for the subgroup of G(F) which fixes pointwise the half-apartment of A which is bounded by the hyperplane Hα,k and contains the points v ∈ A such that 〈α,v〉≥ k. (Thus if α ∈Φ+ then Uα,k fixes the half-apartment  defined in Section 2.1, while if α ∈Φ− then Uα,k fixes the half-apartment \(\alpha ^{k,w_{0}}\).) The pair (α,k) corresponds to a unique affine root β and vice versa, so we sometimes denote the subgroup Uα,k by Uβ, and the reflection in the hyperplane Hβ := Hα,k by sβ ∈ W. Recall that W acts on the set of affine roots. Given x ∈ W and an affine root β, we write x(β) for the image of β under x. We also write α0 for the affine root such that \(U_{\alpha _{0}} = U_{-\widetilde \alpha ,-1}\), so that \(U_{\alpha _{0}}\) fixes the half-apartment consisting of the points v ∈ A such that \(\langle -\widetilde \alpha ,v\rangle \geq -1\), or equivalently \(\langle \widetilde \alpha ,v\rangle \leq 1\). In particular, \(U_{\alpha _{0}}\) fixes the base alcove and thus \(U_{\alpha _{0}}\) is a subgroup of I. We write s0 for the affine reflection \(s_{\widetilde \alpha ,1}\).
defined in Section 2.1, while if α ∈Φ− then Uα,k fixes the half-apartment \(\alpha ^{k,w_{0}}\).) The pair (α,k) corresponds to a unique affine root β and vice versa, so we sometimes denote the subgroup Uα,k by Uβ, and the reflection in the hyperplane Hβ := Hα,k by sβ ∈ W. Recall that W acts on the set of affine roots. Given x ∈ W and an affine root β, we write x(β) for the image of β under x. We also write α0 for the affine root such that \(U_{\alpha _{0}} = U_{-\widetilde \alpha ,-1}\), so that \(U_{\alpha _{0}}\) fixes the half-apartment consisting of the points v ∈ A such that \(\langle -\widetilde \alpha ,v\rangle \geq -1\), or equivalently \(\langle \widetilde \alpha ,v\rangle \leq 1\). In particular, \(U_{\alpha _{0}}\) fixes the base alcove and thus \(U_{\alpha _{0}}\) is a subgroup of I. We write s0 for the affine reflection \(s_{\widetilde \alpha ,1}\).
5.2 P-Chimneys and the Associated Retractions
Let P = P(F) be a standard spherical parabolic subgroup of G(F), meaning a subgroup of G(F) which contains the fixed Borel subgroup B = B(F). Then P has Levi decomposition P = MN, where M is the Levi component and N is its unipotent radical, with both M and N groups over F. Define \({\varDelta }_{M} \subseteq {\varDelta }\) to be the set of positive simple roots αj such that the subgroup \(U_{\alpha _{j}}\) is contained in M. Recall that in our conventions, each αj is positive with respect to the opposite Borel subgroup B−; however, note that for any α ∈Φ, the subgroup Uα is contained in M if and only if U−α is contained in M. Let \({\varPhi }_{M} \subseteq {\varPhi }\) be the sub-root system generated by ΔM and define \({\varPhi }_{M}^{+} = {\varPhi }^{+} \cap {\varPhi }_{M}\). Then \({\varPhi }_{M}^{+}\) consists of the elements α ∈Φ which are positive with respect to B− and are such that Uα is contained in M. We remark that putting \(\alpha ^{\prime } = -\alpha \), this is equivalent to \(\alpha ^{\prime } \in {\varPhi }\) being positive with respect to B = B+ and \(U_{\alpha ^{\prime }}\) being contained in M.
Now let \(J \subseteq \{ 1,\dots ,n\}\) be such that ΔM = {αj∣j ∈ J}. Then
where WJ is the standard parabolic subgroup of W0 generated by {sj∣j ∈ J}. Finally, the subgroup IP of G(F) is defined to be
Note that since I is a subgroup of \(G(\mathcal {O})\), the intersection I ∩ M will be a subgroup of \(G(\mathcal {O})\) as well, while N is defined over F. Also, the spherical subgroups Uα,0 which are contained in N will be all those of the form U−α where α ∈Φ∖ΦM is positive with respect to B−. In other words, as one would expect, those subgroups which are contained in N will be all those of the form \(U_{\alpha ^{\prime }}\) where \(\alpha ^{\prime } \in {\varPhi } \setminus {\varPhi }_{M}\) is positive with respect to B. We denote by R(IP) the set of all affine roots β such that the subgroup Uβ is contained in IP. Note that β ∈ R(IP) if and only if − β∉R(IP).
The following Bruhat decomposition result is established in [13] in the case \(F = \overline {\mathbb {F}_{q}}((t))\), where \(\overline {\mathbb {F}_{q}}\) is an algebraic closure of the finite field \(\mathbb {F}_{q}\), but the proof given there extends immediately to our setting \(F = \mathbbm {k} ((t))\). Recall that we denote the extended affine Weyl group of G(F) by \(\widetilde {W}\).
Lemma 5.1 (Lemma 11.2.1 of [13])
Let P = P(F) be a standard spherical parabolic subgroup of G(F). Then
We will need the following corollary in our proofs in Section 5.3.
Corollary 5.2
Let P = P(F) be a standard spherical parabolic subgroup of G(F). If \(z \neq z^{\prime }\) are distinct elements of the affine Weyl group W, then the double cosets IPzI and \(I_{P} z^{\prime } I\) are disjoint.
Proof
This holds since W is a subgroup of \(\widetilde {W}\). □
We now adapt our main definitions from Section 3 to this setting.
Definition 5.3
Fix a standard spherical parabolic subgroup P = PJ and let y ∈ W. The P-chimney, denoted ξP, is the J-chimney ξJ in the standard apartment from Definition 3.1. For any collection \(\{n_{\beta }\in \mathbb {Z} \mid \beta \in {\varPhi }^{+}\setminus {\varPhi }_{M}^{+}\}\), the corresponding P-sector is SP({nβ}) = SJ({nβ}). Write SP(0) for the P-sector defined by the all-zeros sequence, i.e., nβ = 0 for all \(\beta \in {\varPhi }^{+}\setminus {\varPhi }_{M}^{+}\). The (P,y)-chimney is the (J,y)-chimney ξP,y = ξJ,y from Definition 3.7; that is, ξP,y = y ⋅ ξP. For any collection \(\{n_{\beta }\in \mathbb {Z} \mid \beta \in {\varPhi }^{+}\setminus {\varPhi }_{M}^{+}\}\), the (P,y)-sector SP,y({nβ}) is the (J,y)-sector SJ,y({nβ}).
The (P,y)-chimney retraction is the retraction rP,y = rJ,y from Definition 3.18. We may put rP = rJ for the P-chimney retraction. The orientation induced by the(P,y)-chimney, denoted ϕP,y, is the orientation ϕJ,y from Definition 3.24, and a gallery is positively folded with respect to the(P,y)-chimney if it is positively folded with respect to the orientation ϕP,y. If  , put ϕP,y = ϕP.
, put ϕP,y = ϕP.
Let x ∈ W and let σ and τ be faces of the fundamental alcove cf which contain the origin. The shadow of xτ starting at σ with respect to the (P,y)-orientation, denoted ShP,y(xτ,σ), is the shadow ShJ,y(xτ,σ) from Definition 3.30. For λ ∈ R∨, the shadow of λ with respect to the (P,y)-orientation, denoted ShP,y(λ), is the shadow ShJ,y(λ) from Notation 3.31.
Remark 5.4
The retraction rP,y generalizes the retraction ρP,w described in Section 11.2 of [13] in the case that \(F = \overline {\mathbb {F}_{q}}((t))\), where \(\overline {\mathbb {F}_{q}}\) is an algebraic closure of the finite field \(\mathbb {F}_{q}\). For P = MN, it is stated in [13] that the retraction  has the same effect as retracting from any alcove which lies between Hα and Hα,1 for all \(\alpha \in {\varPhi }_{M}^{+}\) and is “sufficiently antidominant” for all roots in N. We have formalized this idea using P-sectors. The subgroup IP of G(F) is defined exactly as above in [13].
has the same effect as retracting from any alcove which lies between Hα and Hα,1 for all \(\alpha \in {\varPhi }_{M}^{+}\) and is “sufficiently antidominant” for all roots in N. We have formalized this idea using P-sectors. The subgroup IP of G(F) is defined exactly as above in [13].
The retraction ρP from [13] was also considered by Haines, Kapovich, and Millson in Section 6.3 of [19], where this retraction is denoted \(\rho _{I_{P},\mathcal {A}}\). Here, for ΔM the M-dominant Weyl chamber, they composed ρP : X → A with a further retraction A →ΔM to obtain a retraction of the building X onto ΔM. Our P-sectors are essentially the same as the sets of alcoves satisfying (a) and (b) in the statement of Lemma 6.4 of [19], and Lemma 6.4 of [19] is thus essentially the case rJ,y = ρP of Corollary 3.23 above (although our proof is different, since in Section 3 we are in the setting of an arbitrary affine building).
Example 5.5
Two one-dimensional examples for chimney-induced orientations are provided in Fig. 4, where the root system Φ = {±α1} is of type A1. If P = B, equivalently J = ∅, then \(\alpha _{1} \in {\varPhi }^{+}\setminus {\varPhi }_{M}^{+}\) and the chimney-induced orientation is the periodic orientation on the α1-hyperplanes depicted on the left. The P-chimney can then be identified with the point at infinity at the left-hand (antidominant) end of the apartment shown. If P = G(F), equivalently J = {1}, then \(\alpha _{1} \in {\varPhi }_{M}^{+}\), and the orientation induced by the P-chimney is as shown on the right, so that the positive side of each panel in an α1-hyperplane faces away from the base alcove cf; in this case, the alcove cf is the unique P-sector.
More generally, we have the following examples of P-chimneys and the corresponding subgroups IP.
Example 5.6
If P = B = B(F) = T(F)U(F), then ΦM = ∅ and we have M = T(F) and N = U(F), so \(I_{P}=I_{B} = T(\mathcal {O})U(F)\). As explained in Example 3.4, the chimney ξB = ξ∅ can be identified with the chamber at infinity represented by the antidominant Weyl chamber.
Example 5.7
If P = G(F) then ΦM = Φ and IP = I. The P-chimney is the collection of all half-apartments containing the base alcove cf, and the only P-sector is the base alcove cf itself.
We mention that Section 11.2 of [13] includes, in effect, an argument that IP stabilizes the P-chimney. In general, IP will be a proper subgroup of the stabilizer in G(F) of the P-chimney. For example, the stabilizer of the B-chimney is B(F) = T(F)U(F), while \(I_{B} = T(\mathcal {O} )U(F)\).
5.3 Double Cosets
In this section, we establish several bijections between cosets in flag varieties and folded galleries, leading up to our main result, Theorem 5.14. Our proofs here rely on and substantially generalize the cases that were treated in [31] and [28]. We consider double cosets in the affine flag variety in Proposition 5.10 and Theorem 5.11, then use these results to prove Theorem 5.14. We next relate nonemptiness of double coset intersections to shadows, in Theorem 5.16, and finally establish Corollary 5.18, which applies the results of this section to the affine Grassmannian.
Throughout this section, P = P(F) is a fixed standard spherical parabolic subgroup of G(F), y ∈ W, and ϕ = ϕP,y is the orientation induced by the (P,y)-chimney. We now extend the definitions of a labeled folded alcove walk from [31] and [28] to all orientations induced by chimneys.
Definition 5.8
Let \(\gamma = (p_{0},c_{0},p_{1},\dots , c_{l},p_{\ell +1})\) be a combinatorial gallery in the standard apartment A. For 1 ≤ i ≤ ℓ write Hi for the hyperplane supporting the panel pi. We say that γ crossespi from the negative side to the positive side (with respect toϕ) if the alcove ci− 1 is on the negative side of Hi with respect to ϕ, while the alcove ci≠ci− 1 is on the positive side of Hi with respect to ϕ (see Definitions 3.24 and 3.26). The definition of γ crossing pi from the positive side to the negative side is similar.
Recall our definition of the type of a gallery (Definition 2.3).
Definition 5.9
Let x ∈ W and fix a reduced word for x. A labeled folded alcove walk of type \(\vec {x}\) which is positively folded with respect to the (P,y)-chimney is a gallery
with first face p0 = c0 and last face pℓ+ 1 = cl of type \(\vec {x}\) which is positively folded with respect to the (P,y)-chimney, together with the following labelings of the panels \(p_{1},\dots ,p_{l}\):
-
(1)
if γ crosses pi from the negative side to the positive side, then the panel pi is labeled by an element of \(\mathbbm {k}\);
-
(2)
if γ crosses pi from the positive side to the negative side, then the panel pi is labeled by 0; and
-
(3)
if γ has a (positive) fold at pi, then the panel pi is labeled by an element of \(\mathbbm {k}^{\times }\).
The type of a labeled folded alcove walk is the type of the underlying (unlabeled) positively folded gallery.
We note that the previous two definitions are combinatorial in nature. Our proofs will rely upon the relationships between these combinatorial data and the groups and group elements we now define. Recall that Uα,k denotes the subgroup of G(F) which fixes pointwise the half-apartment of A which is bounded by the hyperplane Hα,k and contains the points v ∈ A such that 〈α,v〉≥ k. Given α ∈Φ and \(k \in \mathbb {Z}\), we now define the quotient
For β the unique affine root corresponding to (α,k), we write \(\overline U_{\beta } = \overline U_{\alpha ,k}\). For any β, the group \(\overline U_{\beta }\) is naturally isomorphic to the additive group \((\mathbbm {k},+)\). Moreover, \(\overline U_{\beta }\) is naturally isomorphic to a subgroup of G(F); we shall use this isomorphism without comment henceforth. For example, since \(\overline U_{\alpha _{0}}\) fixes the base alcove, we view \(\overline U_{\alpha _{0}}\) as a subgroup of I. Note that throughout the literature, the distinct groups Uβ and \(\overline U_{\beta }\) are both frequently called root (sub)groups of G(F). To avoid confusion, we do not repeat this terminology here, and instead use these two separate notations.
We write uβ(c) for an element of \(\overline U_{\beta }\), where \(c \in \mathbbm {k}\), so that c↦uβ(c) is an isomorphism from the additive group \((\mathbbm {k},+)\) onto \(\overline U_{\beta }\). Finally, for any affine root β and any \(c \in \mathbbm {k}^{\times }\), we define
For further properties of the elements nβ(c) and hβ(c), we refer the reader to [31, Section 3] and the references therein.
In order to prove Proposition 5.10 below, we will make use of three important relations in G(F). We will see in the proof of Proposition 5.10 that these relations allow us to rewrite a point in IxI as a point in (IP)yzI for certain z ∈ W. The fact that these relations exist follows from [3], for instance.
-
(1)
For all affine roots β, all b ∈ I, and all \(c \in \mathbbm {k}\), there exists a unique \(b^{\prime } \in I\) and a unique \(\tilde {c} \in \mathbbm {k}\) such that
$$ b u_{\beta}(c)s_{\beta} = u_{\beta}(\tilde{c})s_{\beta} b^{\prime}. $$(5.3.2) -
(2)
For all affine roots \(\beta , \beta ^{\prime }\) and all \(c \in \mathbbm {k}\),
$$ s_{\beta} u_{\beta^{\prime}}(c)s_{\beta}= u_{s_{\beta}(\beta^{\prime})}(\pm c), $$(5.3.3)where the sign for ± c is uniquely determined by the pair \(\beta , \beta ^{\prime }\).
-
(3)
For all affine roots β and all \(c \in \mathbbm {k}^{\times }\),
$$ u_{\beta}(c)s_{\beta} = u_{-\beta}(c^{-1})u_{\beta}(-c)h_{\beta}(c). \quad\quad \text{(Main Folding Law)} $$(5.3.4)
We now use the above relations to connect certain double cosets in G(F) to labeled folded alcove walks which are positively folded with respect to a P-chimney. The structure of the induction and resulting cases in the proof of Proposition 5.1 below are modeled upon similar results in [27, 31].
Proposition 5.10
Let P = MN be a standard spherical parabolic subgroup of G(F). Then:
-
(1)
For all x ∈ W, every point of IxI is a point of IPzI for some z ∈ W.
-
(2)
For all x,z ∈ W, the points of IxI ∩ IPzI are in bijection with the set of labeled folded alcove walks of type \(\vec {x}\) from cf to z which are positively folded with respect to the P-chimney.
Proof
The proof is by induction on the length of x. We begin by considering the case ℓ(x) = 1. In this case, x = sj for some \(j \in \{0,1,\dots , n\}\). Recall that for \(j \in \{1,\dots ,n\}\), the spherical root αj ∈Δ is a positive simple root with respect to B−, while α0 is the affine root such that \(U_{\alpha _{0}} = U_{-\widetilde \alpha ,-1}\). Note also that the subgroup \(U_{\alpha _{j}}\) is contained in I for all \(j \in \{0,1,\dots ,n\}\). If \(j \in \{1,\dots ,n\}\), this follows from αj being positive with respect to B− and I being the preimage of \(B^{-}(\mathbbm {k})\). For j = 0 recall that by definition \(U_{\alpha _{0}}\) fixes the half-apartment bounded by \(H_{\widetilde \alpha ,1}\) which contains cf, hence is contained in I. Similarly, for all \(j \in \{0, 1, \dots , n\}\), we have that \(\overline U_{\alpha _{j}}\) is a subgroup of I.
Now by Theorem 6.15 in [33], for example, we can write the points of IxI = IsjI as
Observe also that there is a unique minimal gallery \(\gamma _{s_{j}} = (p_{0}, c_{0}, p_{1}, c_{1},p_{2})\) of type \(\vec {s}_{j}\) with first face p0 = c0 = cf. This gallery \(\gamma _{s_{j}}\) has final face c1 = p2 = sjcf, and the supporting hyperplane of its panel p1 is \(H_{\alpha _{j},0}\) if \(j \in \{1,\dots ,n\}\) and \(H_{\widetilde \alpha ,1}\) if j = 0.
We first suppose that \(j \in \{1,\dots ,n\}\) and that \(U_{\alpha _{j}}\) is contained in M. Equivalently, the positive simple root αj lies in \({\varPhi }^{+}_{M}\). In this case, the minimal gallery \(\gamma _{s_{j}}\) crosses \(p_{1} \subset H_{\alpha _{j},0}\) from the negative to the positive side. Thus there is no positive fold possible at p1, and so all positively folded galleries of type \(\vec {s}_{j}\) with first face cf are in fact equal to \(\gamma _{s_{j}}\). Hence all such galleries have final alcove sjcf. It follows that for z≠sj, there are no labeled folded alcove walks of type \(\vec {s}_{j}\) from cf to z which are positively folded with respect to the P-chimney. If z = sj, then by labeling p1 by any element of \(\mathbbm {k}\), we obtain a labeled folded alcove walk of type \(\vec {x} = \vec {s}_{j}\) from cf to z = sjcf, and each such labeling of p1 corresponds to a distinct labeled folded alcove walk.
We then observe that \(u_{\alpha _{j}}(c) \in I \cap M\) for any \(c \in \mathbbm {k}\), so \(u_{\alpha _{j}}(c) \in I_{P}\) and thus \(u_{\alpha _{j}}(c)s_{j} I \in I_{P} s_{j} I\). Combining this with (5.3.5) we obtain that every point of IsjI is a point of IPsjI, which establishes (1) in this case. Using Corollary 5.2, it follows that for all z≠sj, the intersection IsjI ∩ IPzI is empty. For z = sj, the map taking the element \(c \in \mathbbm {k}\) which labels the panel p1 of \(\gamma _{s_{j}}\) to \(u_{\alpha _{j}}(c)s_{j} I\) induces a bijection between the set of labeled folded alcove walks of type \(\vec {x} = \vec {s}_{j}\) from cf to z = sjcf which are positively folded with respect to the P-chimney, and the points of IsjI ∩ IPsjI. This completes the proof of (2) in this case.
Next we suppose that \(j \in \{1,\dots ,n\}\) and that \(U_{\alpha _{j}}\) is not contained in M (hence \(U_{-\alpha _{j}}\) will be contained in N). In other words, \(\alpha _{j} \in {\varPhi }^{+} \setminus {\varPhi }^{+}_{M}\). In this case, the gallery \(\gamma _{s_{j}}\) crosses \(p_{1} \subset H_{\alpha _{j},0}\) from the positive to the negative side. We thus have two possible positively folded galleries of type \(\vec {x}= \vec {s}_{j}\) with first face cf: one equal to \(\gamma _{s_{j}}\), and the other obtained by folding \(\gamma _{s_{j}}\) in the panel p1, so as to have final face cf. Thus for  , there are no labeled folded alcove walks of type \(\vec {s}_{j}\) from cf to z which are positively folded with respect to the P-chimney. If z = sj then the panel p1 can only be labeled by 0, while if
, there are no labeled folded alcove walks of type \(\vec {s}_{j}\) from cf to z which are positively folded with respect to the P-chimney. If z = sj then the panel p1 can only be labeled by 0, while if  then the panel p1 can be labeled by any element of \(\mathbbm {k}^{\times }\).
then the panel p1 can be labeled by any element of \(\mathbbm {k}^{\times }\).
Now consider the point \(u_{\alpha _{j}}(c) s_{j} I\) of IsjI. If c = 0, then \(u_{\alpha _{j}}(c)\) is trivial so obviously \(u_{\alpha _{j}}(c)s_{j} I \in I_{P} s_{j} I\). However, if c≠ 0, then \(u_{\alpha _{j}}(c)\in I\) but \(u_{\alpha _{j}}(c)\notin I_{P}\). By the Main Folding Law (Eq. (5.3.4)), for all c≠ 0
Since αj∉R(IP), we have − αj ∈ R(IP), and so \(u_{-\alpha _{j}}(c^{-1}) \in I_{P}\). Then since \(u_{\alpha _{j}}(-c)\) and \(h_{\alpha _{j}}(c)\) are both elements of I, we obtain that  for all c≠ 0. We have now proved (1) in this case. We also see, using Corollary 5.2, that for all
for all c≠ 0. We have now proved (1) in this case. We also see, using Corollary 5.2, that for all  , the intersection IsjI ∩ IPzI is empty.
, the intersection IsjI ∩ IPzI is empty.
For (2), the previous paragraph shows that the unique point of IsjI ∩ IPsjI is \(u_{\alpha _{j}}(0)s_{j} I = s_{j}I\). Letting z = sj, we map the (unique) labeled folded alcove walk of type \(\vec {x} = \vec {s}_{j}\) from cf to z = sjcf with panel p1 labeled by 0 to the (unique) point \(u_{\alpha _{j}}(0)s_{j} I\) of IsjI ∩ IPsjI. Now suppose c≠ 0. Then for  , the map which takes the label \(c \in \mathbbm {k}^{\times }\) of the panel p1 in the gallery from cf to cf obtained by folding \(\gamma _{s_{j}}\) in \(H_{\alpha _{j},0}\) to the coset \(u_{\alpha _{j}}(c)s_{j} I\) induces a bijection between the set of labeled folded alcove walks of type \(\vec {x} = \vec {s}_{j}\) from cf to z = cf which are positively folded with respect to the P-chimney, and the points of
, the map which takes the label \(c \in \mathbbm {k}^{\times }\) of the panel p1 in the gallery from cf to cf obtained by folding \(\gamma _{s_{j}}\) in \(H_{\alpha _{j},0}\) to the coset \(u_{\alpha _{j}}(c)s_{j} I\) induces a bijection between the set of labeled folded alcove walks of type \(\vec {x} = \vec {s}_{j}\) from cf to z = cf which are positively folded with respect to the P-chimney, and the points of  . This completes the proof of (2) in this case.
. This completes the proof of (2) in this case.
Finally, we consider j = 0; that is, \(u_{\alpha _{0}}(c)s_{0} I \in I s_{0} I\). In this case, \(\gamma _{s_{0}}\) crosses \(p_{1} \subset H_{\widetilde \alpha ,1}\) from the negative to the positive side, and \(u_{\alpha _{0}}(c) \in I \cap I_{P}\) for all \(c\in \mathbbm {k}\). The remainder of the proofs of (1) and (2) in this case are then similar to the first case above, in which \(j \in \{1,\dots ,n\}\) and \(\alpha _{j} \in {\varPhi }_{M}^{+}\). We have now established the base case of our induction.
For the inductive step, let \((s_{j_{1}}, s_{j_{2}}, \dots , s_{j_{l}})\) be a reduced word for x, and let sj ∈ S be such that ℓ(xsj) > ℓ(x). Using Theorem 6.15 and then Lemma 7.4 of [33], we consider the element \(u_{j_{1}}(c_{1})s_{j_{1}} {\dots } u_{j_{l}}(c_{l})s_{j_{l}} u_{\alpha _{j}}(c)s_{j}\) of IxsjI, where \(c_{i}, c \in \mathbbm {k}\), and we have put \(u_{j_{i}}(c)\) for \(u_{\alpha _{j_{i}}}(c)\). Noting that \(u_{j_{1}}(c_{1})s_{j_{1}} {\dots } u_{j_{l}}(c_{l})s_{j_{l}}\) is a point of IxI, we have by the inductive hypothesis for (1) that there exist \(\tilde {u} \in I_{P}\), z ∈ W, and b ∈ I such that
Now by Eq. (5.3.2) there exist unique \(b^{\prime } \in I\) and \(\tilde {c} \in \mathbbm {k}\) such that \(b u_{\alpha _{j}}(c)s_{j}=u_{\alpha _{j}}(\tilde {c})s_{j} b^{\prime }\), and so
We now finish the proof of (1) by considering two cases.
-
Case 1:
The affine root z(αj) is in R(IP).
In this case, we observe that we have the equality
$$\tilde{u}z u_{\alpha_{j}}(\tilde{c}) s_{j} b^{\prime}= \tilde{u}z u_{\alpha_{j}}(\tilde{c})z^{-1}z s_{j} b^{\prime},$$and then by Eq. (5.3.3), we have
$$\tilde{u}z u_{\alpha_{j}}(\tilde{c})z^{-1}z s_{j} b^{\prime}= \tilde{u}u_{z(\alpha_{j})}(\pm \tilde{c})z s_{j} b^{\prime}.$$Since z(αj) ∈ R(IP),
$$ \tilde{u}u_{z(\alpha_{j})}(\pm \tilde{c})z s_{j} b^{\prime} \in I_{P} zs_{j} I. $$(5.3.7)Combining this with Eq. (5.3.6) we obtain that for any \(c_{i}, c \in \mathbbm {k}\),
$$ u_{j_{1}}(c_{1})s_{j_{1}} {\dots} u_{j_{l}}(c_{l})s_{j_{l}} u_{\alpha_{j}}(c)s_{j} \in I_{P} zs_{j} I. $$(5.3.8)This proves (1) in this case.
-
Case 2:
The affine root z(αj) is not in R(IP).
We will consider two subcases.
-
Case 2(a):
z(αj)∉R(IP) and \(\tilde {c} \neq 0\).
By the Main Folding Law (Eq. (5.3.4)), we have
$$ \begin{array}{@{}rcl@{}} \tilde{u}z u_{\alpha_{j}}(\tilde{c}) s_{j} b^{\prime} &=& \tilde{u}z u_{-\alpha_{j}}(\tilde{c}^{-1})u_{\alpha_{j}}(-\tilde{c})h_{\alpha_{j}}(\tilde{c}) b^{\prime} \\ &=&\tilde{u}z u_{-\alpha_{j}}(\tilde{c}^{-1})b^{\prime\prime} \end{array} $$where \(b^{\prime \prime }=u_{\alpha _{j}}(-\tilde {c})h_{\alpha _{j}}(\tilde {c}) b^{\prime } \in I\). By Eq. (5.3.3), we have
$$ \begin{array}{@{}rcl@{}} \tilde{u}z u_{-\alpha_{j}}(\tilde{c}^{-1})b^{\prime\prime} &=&\tilde{u}z u_{-\alpha_{j}}(\tilde{c}^{-1})z^{-1}z b^{\prime\prime} \\ &= &\tilde{u}u_{z(-\alpha_{j})}(\pm \tilde{c}^{-1})z b^{\prime\prime}. \end{array} $$Since \(u_{z(-\alpha _{j})}(\pm \tilde {c}^{-1}) \in I_{P}\),
$$ \tilde{u}u_{z(-\alpha_{j})}(\pm \tilde{c}^{-1})z b^{\prime\prime} \in I_{P} z I. $$(5.3.9)Using Eq. (5.3.6) we get that
$$ u_{j_{1}}(c_{1})s_{j_{1}} {\dots} u_{j_{l}}(c_{l})s_{j_{l}} u_{\alpha_{j}}(c)s_{j} \in I_{P} z I. $$(5.3.10)This proves (1) in this case.
-
Case 2(b):
z(αj)∉R(IP) and \(\tilde {c} = 0\).
We observe that \(u_{\alpha _{j}}(0)=u_{-\alpha _{j}}(0)\), and so we have
$$ \begin{array}{@{}rcl@{}} \tilde{u}z u_{\alpha_{j}}(0)z^{-1}z s_{j} b^{\prime} &=& \tilde{u}z u_{-\alpha_{j}}(0)z^{-1}z s_{j} b^{\prime} \\ &=& \tilde{u}u_{z(-\alpha_{j})}(0) z s_{j} b^{\prime}. \end{array} $$Since \(u_{z(-\alpha _{j})}\in {I_{P}},\)
$$ \tilde{u}u_{z(-\alpha_{j})}(0) z s_{j} b^{\prime} \in I_{P} zs_{j} I. $$(5.3.11)Using Eq. (5.3.6) we get that
$$ u_{j_{1}}(c_{1})s_{j_{1}} {\dots} u_{j_{l}}(c_{l})s_{j_{l}} u_{\alpha_{j}}(c)s_{j} \in I_{P} zs_{j} I. $$(5.3.12)
This proves (1) in this case, and so completes the proof of the inductive step for (1).
In order to complete the proof of (2), we first observe that by combining Eqs. (5.3.6), (5.3.7), (5.3.9), and (5.3.11), we have that whenever ℓ(xsj) > ℓ(x), every point of IxsjI is contained in either IPzI or IPzsjI for some z ∈ W such that IxI ∩ IPzI is nonempty. Hence by Corollary 5.2, the only double coset intersections \(Ixs_{j} I \cap I_{P} z^{\prime } I\) which are nonempty are those where \(z^{\prime } \in \{ z, zs_{j}\}\) and IxI ∩ IPzI is nonempty.
Now suppose there exists a labeled folded alcove walk of type \(\overrightarrow {x s_{j}}\) from cf to some alcove \(z^{\prime }{\textbf {c}_f}\) which is positively folded with respect to the P-chimney. As ℓ(xsj) > ℓ(x), we may assume that the last panel of this alcove walk is of type sj. Since there may be either a fold or a crossing at this last panel, by truncation we obtain a labeled folded alcove walk of type \(\vec {x}\) from cf to either \(z^{\prime }{\textbf {c}_f}\) or \(z^{\prime } s_{j} {\textbf {c}_f}\), respectively, which is positively folded with respect to the P-chimney. If \(IxI \cap I_{P} z^{\prime } I\) (respectively, \(IxI \cap I_{P} z^{\prime } s_{j} I\)) is empty, this contradicts the inductive assumption for (2). It follows that all labeled folded alcove walks of type \(\overrightarrow {x s_{j}}\) with first alcove cf which are positively folded with respect to the P-chimney have final alcove either zcf or zsjcf, where z ∈ W is such that IxI ∩ IPzI is nonempty.
Therefore to complete the proof of (2), we just need to consider the points of \(Ixs_{j}I \cap I_{P} z^{\prime } I\) where \(z^{\prime } \in \{ z, zs_{j}\}\) and IxI ∩ IPzI is nonempty. By the inductive hypothesis for (2), each point of IxI ∩ IPzI corresponds to a labeled folded alcove walk of type \(\vec {x}\) from cf to z which is positively folded with respect to the P-chimney. Since ℓ(xsj) > ℓ(x), a gallery of type \(\overrightarrow {xs_{j}}\) starting at cf can be obtained from a gallery of type \(\vec {x}\) from cf to z by adding either a crossing or a fold at the panel of z supported by \(H_{z(\alpha _{j})}\).
We will use the same cases as above to complete the proof.
-
Case 1:
The affine root z(αj) is in R(IP).
A gallery of type \(\overrightarrow {xs_{j}}\) from cf to zsjcf can be obtained from a gallery of type \(\vec {x}\) from cf to z by adding a crossing from zcf to zsjcf. In this case, crossing \(H_{z(\alpha _{j})}\) from zcf to zsjcf goes from the negative to the positive side. Thus the panel of \(H_{z(\alpha _{j})}\) at which this crossing occurs can be labeled by any element of \(\mathbbm {k}\). Now use the element \(\pm \tilde {c} \in \mathbbm {k}\) from Eq. (5.3.7) as this label. By the inductive hypothesis for (2), this induces a bijection between the set of labeled folded alcove walks of type \(\overrightarrow {xs_{j}}\) from cf to zsjcf which are positively folded with respect to the P-chimney, and the points of IxsjI ∩ IPzsjI.
-
Case 2:
The affine root z(αj) is not in R(IP).
In this case, a gallery crossing the hyperplane \(H_{z(\alpha _{j})}\) from zcf to zsjcf goes from the positive to the negative side. Hence a gallery γ of type \(\overrightarrow {xs_{j}}\) with initial subgallery of type \(\vec {x}\) going from cf to zcf can either be positively folded in \(H_{z(\alpha _{j})}\) or cross \(H_{z(\alpha _{j})}\). Folding in \(H_{z(\alpha _{j})}\) implies that γ ends at zcf and the panel of \(H_{z(\alpha _{j})}\) at which this fold occurs can be labeled by any element of \(\mathbbm {k}^{\times }\). If γ has a crossing at \(H_{z(\alpha _{j})}\) it will end at zsjcf, with the panel of \(H_{z(\alpha _{j})}\) at which this crossing occurs labeled by 0. We will see that the subcases below correspond to these two possibilities, respectively.
-
Case 2(a):
z(αj)∉R(IP) and \(\tilde {c} \neq 0\).
Here, we can use the element \(\pm \tilde {c}^{-1} \in \mathbbm {k}^{\times }\) from Eq. (5.3.9) to label the panel of \(H_{z(\alpha _{j})}\) at which a gallery ending at zcf (as described in the first possibility above) has a positive fold. By the inductive hypothesis for (2), this induces a bijection between the set of labeled folded alcove walks of type \(\overrightarrow {xs_{j}}\) from cf to zcf which are positively folded with respect to the P-chimney, and the points of IxsjI ∩ IPzI.
-
Case 2(b):
z(αj)∉R(IP) and \(\tilde {c} = 0\).
Now we use 0 to label the panel of \(H_{z(\alpha _{j})}\) between zcf and zsjcf, as in the second possibility described above. By Eq. (5.3.11) and the inductive hypothesis for (2), this induces a bijection between the set of labeled folded alcove walks of type \(\overrightarrow {xs_{j}}\) from cf to zsjcf which are positively folded with respect to the P-chimney, and the points of IxsjI ∩ IzsjI.
This completes the proof of Proposition 5.10. □
The next result extends Proposition 5.10(2) to (P,y)-chimneys.
Theorem 5.11
Let x,y,z ∈ W and let P be a standard spherical parabolic subgroup of G(F). Then there is a bijection between the points of the intersection
and the set of labeled folded alcove walks of type \(\vec {x}\) from cf to z which are positively folded with respect to the (P,y)-chimney.
Proof
Suppose uβ(c) ∈ (IP)y for some affine root β and \(c \in \mathbbm {k}\). This means that y− 1uβ(c)y ∈ IP. By Eq. (5.3.3), \(y^{-1}u_{\beta }(c)y= u_{y^{-1}(\beta )}(\pm c)\). Therefore, the result follows from Proposition 5.10(2) after transforming the orientation via the left action of y as described in [16, Definition 3.4]. □
Remark 5.12
We note that Theorem 5.11 does not depend on a choice of minimal word for x. Given two different reduced words for x, we can form minimal galleries of distinct types \(\vec {x}\) and \(\vec {x}^{\prime }\) corresponding to these words. For any z ∈ W such that there exists a (P,y)-positively folded gallery of type \(\vec {x}\) from cf to z, we know by Theorem 5.11 that the intersection IxI ∩ (IP)yzI is nonempty. The theorem further implies that if IxI ∩ (IP)yzI is nonempty, there exists a (P,y)-positively folded gallery of type \(\vec {x}^{\prime }\) from cf to z, since \(\vec {x}^{\prime }\) corresponds to another reduced expression for x. Thus, we have yet another proof of the braid-invariance of (P,y)-chimney orientations (compare Proposition 3.29 and Remark 4.9).
We now use Theorem 5.11 to prove Theorems 5.14, the main result of this section. Here, for any face σ of cf which contains the origin v0, we denote by K(σ) the parahoric subgroup of G(F) which is the stabilizer in G(F) of σ. (To avoid confusion with the spherical parabolic subgroup P, we are using the letter K for parahorics.) Thus in particular, K = K(v0) and I = K(cf). We write Wσ for the stabilizer of σ in W0.
Definition 5.13
Let σ and τ be faces of cf which contain the origin. Then x ∈ W is:
-
(1)
left-Wσ-reduced if ℓ(wx) ≥ ℓ(x) for all w ∈ Wσ;
-
(2)
right-Wτ-reduced if ℓ(xv) ≥ ℓ(x) for all v ∈ Wτ; and
-
(3)
(Wσ,Wτ)-reduced if x is left-Wσ-reduced and right-Wτ-reduced, i.e., ℓ(wx) ≥ ℓ(x) for all w ∈ Wσ and ℓ(xv) ≥ ℓ(x) for all v ∈ Wτ.
Theorem 5.14
Let P be a standard spherical parabolic subgroup of G(F). For any faces σ and τ of cf which contain the origin and any x,y,z ∈ W such that x is (Wσ,Wτ)-reduced, there is a bijection between the points of the intersection
and the union over w ∈ Wσ of the set of labeled folded alcove walks of type \(\overrightarrow {wx}\) from cf to z which are positively folded with respect to the (P,y)-chimney.
Note that the hypothesis that x is (Wσ,Wτ)-reduced does not lead to a loss of generality, since we can always find a representative of the double coset K(σ)xK(τ) that is of this form. This hypothesis is included only so that we can more easily describe the type of labeled walks required. The proof of this theorem uses techniques inspired by the proof of the equivalence of Theorems G and C in [30].
Proof
We first consider the case in which τ = cf, so that K(τ) = I. Recall that \(K(\sigma )=\sqcup _{w \in W_{\sigma }} IwI\). Since x is left-Wσ-reduced, for any w ∈ Wσ we have (IwI)xI = IwxI. This implies that
Thus, by Theorem 5.11, the points of K(σ)xI ∩ (IP)yzI are in bijection with the (disjoint) union over w ∈ Wσ of the set of labeled folded alcove walks of type \(\overrightarrow {wx}\) from cf to z which are positively folded with respect to the (P,y)-chimney. This completes the proof in the case that τ = cf.
Now suppose σ = cf and let τ be any face of cf which contains the origin. We may assume without loss of generality that τ≠cf. Fix a minimal gallery γ in the standard apartment A from cf to xτ. The points of IxK(τ) are then in bijection with the set of minimal galleries in the building X which are of the same type as γ.
Denote by \(\gamma ^{\prime }\) the gallery in A which is obtained from γ by removing its final simplex xτ. We claim that there is a bijection between the set of minimal galleries in X of the same type as γ and the set of minimal galleries in X of the same type as \(\gamma ^{\prime }\). To see this, note that the set of alcoves in A which contain the face τ of cf is given by {vcf∣v ∈ Wτ}. Hence the set of alcoves in A which contain the face xτ of x = xcf is given by {xvcf∣v ∈ Wτ}. Since x is right-Wτ-reduced and γ is a minimal gallery from cf to xτ, it follows that γ must have final alcove x, and so the truncated gallery \(\gamma ^{\prime }\) is a minimal gallery from cf to x. A similar truncation process establishes the claimed bijection between sets of minimal galleries in X.
Since the points of IxI are in bijection with the set of minimal galleries in X which are of the same type as \(\gamma ^{\prime }\), we now have a bijection between the points of IxK(τ) and those of IxI. By Theorem 5.11, the points of the intersection IxI ∩ (IP)yzI are in bijection with the set of labeled folded alcove walks of type \(\vec {x}\) from cf to z which are positively folded with respect to the (P,y)-chimney. Projecting points of (IP)yzI back to the flag variety G/K(τ) gives us points in (IP)yzK(τ). Thus, points in IxK(τ) ∩ (IP)yzK(τ) are also in bijection with the set of labeled folded alcove walks of type \(\vec {x}\) from cf to z which are positively folded with respect to the (P,y)-chimney. This completes the proof in the case that σ = cf.
Finally, let σ and τ be any faces of cf which contain the origin. As before, we observe that since x is left-Wσ-reduced,
Also, since x is right-Wτ-reduced, the points of K(σ)xK(τ) ∩ (IP)yzK(τ) are in bijection with the points of K(σ)xI ∩ (IP)yzI. Thus in general, the points of K(σ)xK(τ) ∩ (IP)yzK(τ) are in bijection with the union over w ∈ Wσ of the set of labeled folded alcove walks of type \(\overrightarrow {wx}\) from cf to z which are positively folded with respect to the (P,y)-chimney. □
Remark 5.15
In [2], Abramenko, Parkinson, and Van Maldeghem study and count the number of points in intersections of spheres (for the Weyl-distance) in certain buildings. While we assume for all of Section 5 that the building in question is a Bruhat–Tits building, and is thus of affine type, Abramenko, Parkinson, and Van Maldeghem study buildings of arbitrary type, but assume in addition that they are locally finite and regular. There is, however, some similarity to our results. Theorem 4.7 in [2] for example may be translated into a statement about the cardinality of the double coset intersections appearing in the statement of Theorem 5.14.
The next result determines nonemptiness of the double coset intersections appearing in Theorem 5.14.
Theorem 5.16
Let P be a standard spherical parabolic subgroup of G(F). For any faces σ and τ of cf which contain the origin and any x,y,z ∈ W such that x is (Wσ,Wτ)-reduced, the intersection
is nonempty if and only if there exists a gallery of type \((\text {type}(\sigma ),\vec {x},\text {type}(\tau ))\) from σ to zτ which is positively folded with respect to the (P,y)-chimney. Equivalently,
if and only if the simplex zτ lies in the shadow ShP,y(xτ,σ).
As with Theorem 5.14, the hypothesis on x here does not lead to any loss of generality.
Proof
Suppose first that K(σ)xK(τ) ∩ (IP)yzK(τ)≠∅. Then by Theorem 5.14, for some w ∈ Wσ there is a labeled folded alcove walk γ of type \(\overrightarrow {wx}\) from cf to z which is positively folded with respect to the (P,y)-chimney. We now use γ to construct a gallery \(\gamma ^{\prime \prime }\) of type \((\text {type}(\sigma ),\vec {x},\text {type}(\tau ))\) from σ to zτ which is positively folded with respect to the (P,y)-chimney. Since x is Wσ-reduced, we may choose a reduced word \((s_{i_{1}}, \dots , s_{i_{r}})\) for wx such that \(s_{i_{1}}{\dots } s_{i_{t}} = w\) and \(s_{i_{t+1}}{\dots } s_{i_{r}}=x\), and assume that γ is of type this word. Letting \(\gamma = (p_{0}, c_{0}, p_{1}, c_{1}, \dots , p_{r}, c_{r},c_{r+1})\), so that p0 = c0 = cf and cr = pr+ 1 = z, we may thus assume that the panel pj of γ has type \(s_{i_{j}}\) for 1 ≤ j ≤ r. This means that the first t panels \(p_{1},\dots ,p_{t}\) of γ must each contain σ, and so the alcove ct of γ lies in the star of σ in A. Therefore \(c_{t}=w^{\prime }{\textbf {c}_f}\) for some \(w^{\prime } \in W_{\sigma }\).
Now define \(\gamma ^{\prime }\) to be the subgallery of γ which starts at ct and continues in the same way as γ to z. Then \(\gamma ^{\prime }\) is a gallery of type \(\vec {x}\) from \(\mathbf {w}^{\prime }\) to z. Finally let \(\gamma ^{\prime \prime }\) be the gallery obtained from \(\gamma ^{\prime }\) by changing its first simplex to σ and its final simplex to zτ. Then by our choice of word for wx and x being right-Wτ-reduced, the gallery \(\gamma ^{\prime \prime }\) from σ to zτ is of type \((\text {type}(\sigma ),\vec {x},\text {type}(\tau ))\). All folds in \(\gamma ^{\prime \prime }\) are folds of the original gallery γ, and so \(\gamma ^{\prime \prime }\) is a gallery of the desired type which is positively folded with respect to the (P,y)-chimney.
Conversely, suppose we have a gallery \(\gamma ^{\prime \prime }\) of type \((\text {type}(\sigma ),\vec {x},\text {type}(\tau ))\) from σ to zτ which is positively folded with respect to the (P,y)-chimney. Let w be the first alcove of \(\gamma ^{\prime \prime }\) and note that w contains σ. Since x is left-Wσ-reduced, the second alcove of \(\gamma ^{\prime \prime }\) cannot contain σ. Similarly, the final alcove of \(\gamma ^{\prime \prime }\) contains zτ, and since x is right-Wτ-reduced, the final alcove of \(\gamma ^{\prime \prime }\) must be z. Now define γ to be the gallery obtained from \(\gamma ^{\prime \prime }\) by replacing its initial simplex σ by a minimal gallery from cf to w, and replacing its final simplex zτ by z. Then γ is a gallery of type \(\overrightarrow {wx}\) from cf to z, for a suitable choice of reduced word for wx. By construction the initial subgallery of γ from cf to w is minimal hence has no folds, while any folds in the portion of γ from w to z are also folds of \(\gamma ^{\prime \prime }\), thus γ is positively folded with respect to the (P,y)-chimney.
We can then obtain a labeled folded alcove walk of type \(\overrightarrow {wx}\) from cf to z which is positively folded with respect to the (P,y)-chimney by choosing a labeling each of the panels of γ according to the scheme given by Definition 5.9. Any such labeled folded alcove walk corresponds to a point of the intersection K(σ)xK(τ) ∩ (IP)yzK(τ) by Theorem 5.14. Therefore, this intersection is nonempty. □
Remark 5.17
In light of the above results, it is tempting to try to formulate a bijection directly between the points of the intersection K(σ)xK(τ) ∩ (IP)yzK(τ) and suitably labeled galleries of type \((\text {type}(\sigma ),\vec {x},\text {type}(\tau ))\) from σ to zτ which are positively folded with respect to the (P,y)-chimney. However, the following example shows that this is not always a useful compression.
In type \(\tilde {A}_{2}\), let τ = cf, so that K(τ) = I, and let σ = v0, so that K(σ) = K. Let x = s0 ∈ S be the reflection in the (affine) hyperplane \(H_{\widetilde \alpha ,1}\) which bounds cf. Then
In particular, the cells Is0I, Is1s0I, and Is2s0I are mutually disjoint. Now let P = B and  , so that the (P,y)-chimney is the B-chimney, and let z = s0. We claim that each of these three cells has nonempty intersection with (IP)yzI = IPs0I.
, so that the (P,y)-chimney is the B-chimney, and let z = s0. We claim that each of these three cells has nonempty intersection with (IP)yzI = IPs0I.
By Theorem 5.11, the intersections of Is0I, Is1s0I, and Is2s0I with IPs0I are nonempty if and only if there exist labeled folded alcove walks from cf to s0cf of types \(\overrightarrow {s_{0}}\), \(\overrightarrow {s_{1}s_{0}}\), and \(\overrightarrow {s_{2}s_{0}}\), respectively. Consider the galleries (cf,p0,s0cf), (cf,p1,cf,p0,s0cf), and (cf,p2,cf,p0,s0cf) from cf to s0cf, where for simplicity we have omitted the first face cf and last face s0cf of each gallery, and for i ∈{0,1,2} we abuse notation and write pi for the panel of cf of type si. These galleries have types \(\overrightarrow {s_{0}}\), \(\overrightarrow {s_{1}s_{0}}\), and \(\overrightarrow {s_{2}s_{0}}\), respectively, and are positively folded with respect to the B-chimney. Thus any labeling of their panels corresponds to a point in the intersection of Is0I, Is1s0I, and Is2s0I with IPs0I, respectively. This proves the claim.
Hence if we wished to instead enumerate points in Ks0I ∩ IPs0I by labeling just a gallery of the form (v0,cf,p0,s0cf), that is, a gallery of type the unique minimal gallery from σ = v0 to s0cf, then we would need the label at σ = v0 to capture all three of the above distinct types, and their labels. This does not provide any advantage over the union over w ∈ W0 described in Theorems 5.14.
We conclude this section by applying the results above to \(K = G(\mathcal {O})\), the stabilizer of the origin in G(F). In the following, for λ ∈ R∨ we write star(λ) for the star of λ in the standard apartment A, that is, the union of the set of alcoves of A which contain the vertex λ. Recall that for any λ ∈ R∨, there is a unique alcove xλcf in star(λ) which is at minimal distance from the base alcove cf. Equivalently, xλ ∈ W is the unique minimal length representative of the coset tλW0 in W/W0.
Corollary 5.18
Let λ,μ ∈ R∨, let P be a standard spherical parabolic subgroup of G(F), and let y ∈ W. Assume λ is dominant and let xλcf be the alcove in star(λ) closest to cf. Then there is a bijection between the points of the intersection
and the union over w ∈ W0 of the set of labeled folded alcove walks of type \(\overrightarrow {wx_{\lambda }}\) from cf to some alcove in star(μ) which are positively folded with respect to the (P,y)-chimney. Moreover,
if and only if the vertex μ lies in the shadow ShP,y(λ).
Note that, as in Theorems 5.14 and 5.16, the assumption on λ here does not lead to any loss of generality. The proof below will show why we do not need to specify the final alcove within star(μ) of the alcove walks that we consider.
Proof
Since λ is dominant, the element xλ ∈ W is (W0,W0)-reduced, and a minimal gallery from the origin v0 to λ of type \(\vec {\lambda }\) has first alcove cf and final alcove xλcf. Now xλ = tλv for some v ∈ W0, so KtλK = KtλvK = KxλK. Similarly, for any alcove zcf in star(μ), we have (IP)ytμK = (IP)yzK. We now apply Theorems 5.14 and 5.16. □
6 Examples in Rank Two
In this final section, we explore, rather informally, some examples of shadows in affine Coxeter groups of types \(\tilde {A}_{2}\) and \(\tilde {C}_{2}\). These examples will also illustrate our main recursive result, Theorem 4.8. We did not observe any fundamentally new behavior in type \(\tilde {G}_{2}\) and so omit this case.
Throughout this section A is a copy of the Coxeter complex of the given affine type, and R∨ is the corresponding coroot lattice, seen as a subset of the vertices of A. Recall from Corollary 4.11 that the shadow of a coroot lattice element λ is always contained in the λ-Weyl polytope. In case the shadow is taken with respect to a chamber at infinity, then by the convexity theorem [17], the shadow of λ is equal to the intersection of R∨ with the λ-Weyl polytope. However we will see that for general chimney-induced orientations, shadows may be non-convex, with both “notches” and “holes”. We will also observe that some of what is contained in the shadow can be described using “strings” in root directions.
We will explain one example in detail in Section 6.1, then sketch several further examples.
6.1 Shadows of Vertices in Type \(\tilde {A}_{2}\)
Let us first have a closer look at the picture on the left in Fig. 5, which is the same as Fig. 1 of the introduction.
With α1 = α = α∨ and α2 = β = β∨ as given in the figure, let λ = 2α + 2β ∈ R∨ and define J = {1}, so that WJ = 〈sα〉. We determine the shadow  of λ with respect to the J-chimney, using the minimal gallery γλ from the origin to λ. A J-sector representing the J-chimney is shown as the gray shaded region in Fig. 5.
of λ with respect to the J-chimney, using the minimal gallery γλ from the origin to λ. A J-sector representing the J-chimney is shown as the gray shaded region in Fig. 5.
By definition the elements of ShJ(λ) are exactly the end-vertices of all positively folded galleries of the same type as γλ. We have drawn all those galleries on the left of Fig. 5.
We now explain the recursive algorithm given by Theorem 4.8.
The algorithm: For a given coroot lattice element λ we obtain from Corollary 3.23 that ShJ(λ) = Shy(λ) for some alcove y “deep enough” inside a J-sector. One can then compute Shy(λ) as follows:
-
(1)
Choose a minimal gallery γy from cf to y and denote by \({\mathscr{H}}_{y}=(H_{1}, H_{2}, {\dots } ,H_{\ell (y)})\) the sequence of hyperplanes crossed by this gallery (in the order in which they appear).
-
(2)
As the end-vertices of all galleries in Γ0 := W0 ⋅ γλ (the blue dots in Fig. 5) are in the shadow (each of these is trivially positively folded), put
$$ \operatorname{Sh}^{0}_{\mathbf{y}}(\lambda):= W_0\cdot\lambda \subset \operatorname{Sh}_{\mathbf{y}}(\lambda). $$That is, \(\operatorname {Sh}^{0}_{\mathbf {y}}(\lambda )\) is the set of end-vertices of galleries in Γ0.
-
(3)
For \(i=1,\dots , \ell (y)\) proceed as follows: Let Γi be the set of galleries obtained from Γi− 1 by introducing (additional) positive folds along the hyperplane Hi in the above sequence \({\mathscr{H}}_{y}\), as in the proof of Theorem 4.8. Define \(\operatorname {Sh}^{i}_{\mathbf {y}}(\lambda )\) to be the set of end-vertices of galleries in Γi. Finally we obtain \(\operatorname {Sh}_{\mathbf {y}}(\lambda )=\operatorname {Sh}^{\ell (y)}_{\mathbf {y}}(\lambda )\).
In the last (repeated) step of the recursive construction, the reflection \(r_{H_{i}}\) will take end-vertices on the far side of Hi (i.e., vertices that used to be separated from cf by Hi) to end-vertices on the near side (i.e., on the same side of Hi as cf). Note that a vertex μ ∈ R∨ is on the far side of Hξ,−k, with k a non-negative integer, if and only if 〈μ,ξ〉 < −k. This procedure (potentially) adds new elements to the shadow.
We now describe this recursive procedure in more detail for the case shown on the left of Fig. 5. Put s0 := sα+β,1. We can choose y to be of the form \((s_{\beta } s_{\alpha } s_{0})^{N}{\textbf {c}_f}\) for a suitably large N = N(λ). We compute the shadow ShJ(λ) = Shy(λ) as follows.
In Step (1), the collection \({\mathscr{H}}_{y}\) is an initial subsequence of the sequence of hyperplanes
Step (2) yields Γ0 := W0 ⋅ γλ and
By the recursive procedure in Step (3) we have to consider the successive hyperplanes in the sequence \({\mathscr{H}}_{J}\). The first two such hyperplanes are Hβ,0 and Hα+β,0. Applying the corresponding reflections to vertices in W0 ⋅ λ that are on the far side of these hyperplanes gives us elements once again in W0 ⋅ λ. Therefore adding folds along these two hyperplanes does not add vertices to the shadow. Hence Γ2 = Γ1 = Γ0 and \(\operatorname {Sh}^{2}_{\mathbf {y}}(\lambda )=\operatorname {Sh}^{1}_{\mathbf {y}}(\lambda )=\operatorname {Sh}^{0}_{\mathbf {y}}(\lambda )\).
The next hyperplane is H3 := Hβ,− 1. Of the elements of W0 ⋅ λ, only 2α, − 2β, and − 2α − 2β are on the far side of H3. Reflect the tails of the (blue) minimal galleries which have these end-vertices along H3 and add the resulting positively folded galleries to Γ2 to obtain Γ3. These new galleries end at 2α + β, β, and − 2α + β, respectively. Hence \(\operatorname {Sh}^{3}_{\mathbf {y}}(\lambda ) = \operatorname {Sh}^{2}_{\mathbf {y}}(\lambda )\cup \{2\alpha + \beta , \beta , -2\alpha +\beta \}\).
Continuing in this manner we successively consider end-vertices which lie on the far side of the hyperplanes in the sequence \({\mathscr{H}}_{J}\) above, and the algorithm terminates when there are no such vertices remaining.
The shadow consists of all of the coroot lattice points in the λ-Weyl polytope except for ± (α + 2β) and is hence a strict subset of the intersection of R∨ with the λ-Weyl polytope. These missing vertices on opposite sides of the λ-Weyl polytope are an example of what we call “notches”.
6.2 Shadows of Alcoves in Type \(\tilde {A}_{2}\)
We now consider the shadow of an alcove as on the right-hand side of Fig. 5 (which is the same as Fig. 2 of the introduction). Let x ∈ W correspond to the (pink) alcove x at the bottom of the figure and let \(\gamma _{x}:{\textbf {c}_f}\rightsquigarrow \mathbf {x}\) be the (blue) minimal gallery. A J-sector is shaded in gray.
The shadow ShJ(x) can again be obtained by the algorithm described in Section 6.1, using the same “deep enough” alcove y and sequence of successively crossed hyperplanes \({\mathscr{H}}_{J}\). However the sets \(\operatorname {Sh}^{i}_{\mathbf {y}}(\mathbf {x})\) now consist of end-alcoves of certain positively folded galleries. In particular, the “starting set” \(\operatorname {Sh}_{\mathbf {y}}^{0}(\mathbf {x})\) is the set of end-alcoves of all minimal galleries of type γx with first alcove cf, and as γx is the unique such gallery, we have \(\operatorname {Sh}_{\mathbf {y}}^{0}(\mathbf {x})=\{ \mathbf {x} \}\). We have used the same color for a hyperplane Hi in the sequence \({\mathscr{H}}_{J}\) and the alcoves in ShJ(x) which are (first) obtained by applying the reflection \(r_{H_{i}}\).
Note that the shadow ShJ(x) is not a convex set. More precisely, the shadow of x is not the intersection of some collection of alcoves with some convex polytope in A. The elements z ∈ W such that z is in the shadow of x are, however, always subsets of the Bruhat interval between x and  . See [16] for the connection between shadows and Bruhat order.
. See [16] for the connection between shadows and Bruhat order.
We also draw attention to the following pattern: for any given root direction, say ξ, for which a ξ-hyperplane appears in the sequence \({\mathscr{H}}_{J}\), there is a first and last index of a ξ-hyperplane that appears in \({\mathscr{H}}_{J}\) before the algorithm terminates, and all of the indices in between also appear. For example, \(H_{\beta ,0}\in {\mathscr{H}}_{J}\) and \(H_{\beta , -3}\in {\mathscr{H}}_{J}\), and all β-hyperplanes of indices strictly between 0 and − 3 are in \({\mathscr{H}}_{J}\) as well. Folding γx along this collection of hyperplanes yields a “string” of alcoves in the shadow, with these alcoves differing from each other just by translating tβ. There is similarly a “string” of alcoves in the direction of the root α + β. These alcoves can in fact only be obtained by reflecting x in (α + β)-hyperplanes, so it is essential to consider non-simple root directions when computing the shadow.
6.3 Vertex Shadows with Respect to J-Chimneys in Type \(\tilde {C}_{2}\)
Have a look at the left-hand side of Fig. 6. In this example, we depict ShJ(λ) with respect to the J-chimney corresponding to the short simple coroot α∨. The same recursive procedure as described in Section 6.1 can be used to compute this shadow.
We observe that ShJ,y(λ) consists of all the coroot lattice points in the λ-Weyl polytope except for k(α∨ + β∨) with k ∈{± 1 ± 3}. That is the set of end-vertices of the galleries depicted. In this case, in addition to “notches” on opposite sides of the polytope the shadow also has “holes”, consisting of a line of spaced-out coroot lattice points cutting through the polytope. The number of distinct colored-in circles appearing at a coroot lattice point is equal to the multiplicity of this vertex in the shadow.
On the right-hand side of Fig. 6, we depict the shadow of the same λ with respect to the J-chimney for the long simple coroot β∨. In this case there are “notches” but no “holes”, as the shadow consists of all of the coroot lattice points in the λ-Weyl polytope except for ± (4α∨ + 2β∨). As on the right of Fig. 5, we have not drawn all of the positively folded galleries, but instead illustrate the recursion using color. The examples in Fig. 6 can be seen to contain “strings” of shadow elements, in both simple and non-simple root directions.
6.4 Vertex Shadow with Respect to a Shifted Chimney in Type \(\tilde {C}_{2}\)
We conclude this examples section by considering the shadow of the same vertex λ = 4α∨ + 3β∨ with respect to the chimney that lies between the α-hyperplanes of index 1 and 2, as shown in Fig. 7.
To find the shadow in this case, we may initially cross the same sequence of hyperplanes as for the J-chimney lying between Hα,0 and Hα,1, as on the left of Fig. 6. Thus we initially obtain the same collection of vertices in the shadow as before. We then cross Hα,1 to reach an alcove which lies deep in the shaded region depicted in Fig. 7. At this last step, we obtain new folded galleries, by reflecting in Hα,1. These additional galleries (and their predecessors) are drawn in Fig. 7. Therefore the shadow in this case contains more vertices than before. And in fact, the shadow now equals the intersection of R∨ with the λ-Weyl polytope (shown with multiplicity).
References
Abramenko, P., Brown, K.S.: Buildings, Theory and applications, vol. 248 of Graduate Texts in Mathematics Springer New York (2008)
Abramenko, P., Parkinson, J., Van Maldeghem, H.: Distance regularity in buildings and structure constants in Hecke algebras. J. Algebra 481, 158–187 (2017)
Billig, Y., Dyer, M.: Decompositions of Bruhat type for the Kac-Moody groups. Nova J. Algebra Geom. 3(1), 11–39 (1994)
Beazley, E.: Affine Deligne-Lusztig varieties associated to additive affine Weyl group elements. J. Algebra 349, 63–79 (2012)
Brown, K.S.: Buildings. Springer-Verlag, New York (1989)
Bruhat, F., Tits, J.: Groupes réductifs sur un corps local. Inst. Hautes Études Sci. Publ. Math. 41, 5–251 (1972)
Bruhat, F., Tits, J.: Groupes réductifs sur un corps local. II. Schémas en groupes. Existence d’une donnée radicielle valuée. Inst. Hautes Études Sci. Publ. Math. 60, 197–376 (1984)
Charignon, C.: Compactifications polygonales d’un immeuble affine (2009)
Caprace, P.-E., Lécureux, J.: Combinatorial and group-theoretic compactifications of buildings. Ann. Inst. Fourier (Grenoble) 61(2), 619–672 (2011)
Deligne, P., Lusztig, G.: Representations of reductive groups over finite fields. Ann. of Math. (2) 103(1), 103–161 (1976)
Görtz, U., He, X.: Dimensions of affine Deligne-Lusztig varieties in affine flag varieties. Doc. Math. 15, 1009–1028 (2010)
Görtz, U., Haines, T.J., Kottwitz, R.E., Reuman, D.C.: Dimensions of some affine Deligne-Lusztig varieties. Ann. Sci. École Norm. Sup. (4) 39(3), 467–511 (2006)
Görtz, U., Haines, T.J., Kottwitz, R.E., Reuman, D.C.: Affine Deligne-Lusztig varieties in affine flag varieties. Compos. Math. 146(5), 1339–1382 (2010)
Gaussent, S., Littelmann, P.: LS galleries, the path model and MV cycles. Duke Math. J. 127(1), 35–88 (2005)
Guivarc’h, Y., Rémy, B.: Group-theoretic compactification of Bruhat-Tits buildings. Ann. Sci. École Norm. Sup. (4) 39(6), 871–920 (2006)
Graeber, M., Schwer, P.: Shadows in Coxeter groups. Ann. Comb. 24(1), 119–147 (2020)
Hitzelberger, P.: Kostant convexity for affine buildings. Forum Math. 22(5), 959–971 (2010)
Hitzelberger, P.: Generalized affine buildings. Doctoral thesis. arXiv:0902.1107 e-prints (2009)
Haines, T.J., Kapovich, M., Millson, J.J.: Ideal triangles in Euclidean buildings and branching to Levi subgroups. J. Algebra 361, 41–78 (2012)
Horn, A.: Doubly stochastic matrices and the diagonal of a rotation matrix. Am. J. Math. 76, 620–630 (1954)
Humphreys, J.E.: Introduction to Lie algebras and representation theory, vol. 9. Springer, New York (1972). Graduate Texts in Mathematics
Kostant, B.: On convexity, the Weyl group and the Iwasawa decomposition. Ann. Sci. É,cole Norm. Sup. (4) 6, 413–455 (1974, 1973)
Littelmann, P.: A Littlewood-Richardson rule for symmetrizable Kac-Moody algebras. Invent. Math. 116(1-3), 329–346 (1994)
Lewis, J.B., McCammond, J., Petersen, T.K., Schwer, P.: Computing reflection length in an affine Coxeter group. Trans. Amer. Math. Soc. 371(6), 4097–4127 (2019)
Macdonald, I.G.: Spherical functions on a group of p-adic type. Ramanujan Institute, Centre for Advanced Study in Mathematics, University of Madras, Madras. Publications of the Ramanujan Institute, No. 2 (1971)
Marquis, T.: Conjugacy classes and straight elements in Coxeter groups. J. Algebra 407, 68–80 (2014)
Milićević, E., Ram, A.: The Geometric Peterson isomorphism: moduli of curves and alcove walks. preprint in preparation. (2022)
Milićević, E., Schwer, P., Thomas, A.: Dimensions of affine Deligne–Lusztig Varieties: A new approach via labeled folded alcove walks and root operators. Mem. Amer. Math. Soc. 261(1260), 0 (2019)
Peterson, D.: Lectures on quantum cohomology of G/P MIT (1996)
Parkinson, J., Ram, A.: Alcove walks, buildings, symmetric functions and representations. arXiv:0807.3602v1 (2008)
Parkinson, J., Ram, A., Schwer, C.: Combinatorics in affine flag varieties. J. Algebra 321(11), 3469–3493 (2009)
Ram, A.: Alcove walks, Hecke algebras, spherical functions, crystals and column strict tableaux. Pure Appl. Math. Q. 2(4, part 2), 963–1013 (2006)
Ronan, M.: Lectures on buildings, volume 7 of Perspectives in Mathematics. Academic Press Inc, Boston (1989)
Rousseau, G.: Immeubles des groupes réductifs sur les corps locaux. U.E.R. Mathématique, Université Paris XI, Orsay. Thèse de doctorat, Publications Mathématiques d’Orsay, No. 221–77.68 (1977)
Rousseau, G.: Exercices métriques immobiliers. Indag. Math. (N.S.) 12(3), 383–405 (2001)
Schur, I.: Über eine Klasse von Mittelbildungen mit Anwendungen auf die Determinantentheorie. Sitzungsber. Berl. Math. Ges. 22, 9–20 (1923). (1923)
Weiss, R.M.: The structure of affine buildings, volume 168 of Annals of Mathematics Studies. NJ, Princeton University Press (2009)
Acknowledgements
We thank Ulrich Görtz, Tom Haines, Jean Lécureux, Peter Littelmann, James Parkinson, Arun Ram, and Geordie Williamson for helpful conversations and correspondence. We also thank the University of Sydney Mathematical Research Institute for hosting a visit by the third author. The authors are grateful to the anonymous referees for their careful reading which resulted in several key clarifications.
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions. The first author was partially supported by NSF Grant DMS #1600982. The second author and this research was supported in part by ARC Grant DP180102437. The third author was partially supported by the DFG Project SCHW 1550/4-1.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Milićević, E., Naqvi, Y., Schwer, P. et al. A Gallery Model for Affine Flag Varieties via Chimney Retractions. Transformation Groups 29, 773–821 (2024). https://doi.org/10.1007/s00031-022-09726-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00031-022-09726-8


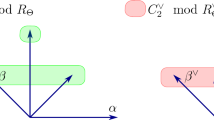




 for all j ≤ i < k (note that pi ⊂ H may occur for some j < i < k). Given an H-protrusionL = [j,k], the associated subgallery of γ is
for all j ≤ i < k (note that pi ⊂ H may occur for some j < i < k). Given an H-protrusionL = [j,k], the associated subgallery of γ is
 for all i ≥ j, then
for all i ≥ j, then  for all j ≤ i < k; note that if j is the smallest index such that pj ⊂ H then the interval [0,j] is by definition not an H-indentation.
for all j ≤ i < k; note that if j is the smallest index such that pj ⊂ H then the interval [0,j] is by definition not an H-indentation.


