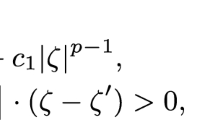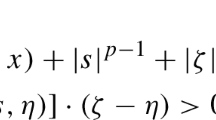Existence and regularity results for a class of singular parabolic problems with $L^1$ data

Abstract

In this paper we prove existence and regularity results for a class of parabolic problems with irregular initial data and lower order terms singular with respect to the solution. We prove that, even if the initial datum is not bounded but only in $L^1(\Omega )$, there exists a solution that “instantly” becomes bounded. Moreover we study the behavior in time of these solutions showing that this class of problems admits global solutions which all have the same behavior in time independently of the size of the initial data.

1 Introduction

In this paper we study the existence and the regularity of the solutions to the following boundary value parabolic problem

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t-\textrm{div}(a(x,t,\nabla u))=\frac{f}{u^{\gamma }}\,,&{} \quad \text{ in } \Omega _T\,,\\ u(x,t)=0\,, &{} \quad \text{ on } \Gamma \,,\\ u(x,0)=u_0(x)\,, &{} \quad \text{ in } \Omega \,, \end{array}\right. } \end{aligned}$$

(1.1)

where $\Omega$ is a bounded domain in ${\mathbb {R}}^N, N > 2$, $\Omega _T=\Omega \times (0,T)$, $0<T<+\infty$, and $\Gamma =\partial \Omega \times (0,T)$. Here, $\gamma >0$ is real parameter, the function $a:\Omega _T\times {\mathbb {R}}^N\rightarrow {\mathbb {R}}^N$ is a Carathéodory function¹ which satisfies the following structural assumptions for a.e. (x, t) in $\Omega _T$ and for every $\xi$ and $\eta$ in ${\mathbb {R}}^N$ with $\xi \ne \eta$

$$\begin{aligned}{} & {} a(x,t,\xi )\cdot \xi \ge \alpha |\xi |^p \,, \quad p\ge 2\,, \end{aligned}$$

(1.2)

$$\begin{aligned}{} & {} |a(x,t,\xi )|\le \Lambda \,|\xi |^{p-1} \,, \end{aligned}$$

(1.3)

$$\begin{aligned}{} & {} [a(x,t,\xi )-a(x,t,\eta )][\xi -\eta ]>\beta |\xi -\eta |^p \,, \end{aligned}$$

(1.4)

where $0< \alpha \le \Lambda$ and $\beta > 0$. On the data f and $u_0$ we assume

$$\begin{aligned}{} & {} f(x,t)\in L^r(0,T;L^m(\Omega ))\,, \,\, \textrm{with} \,\, \frac{1}{r}+\frac{N}{pm}<1, \,\, f(x,t)\ge 0\,\, \mathrm{a.e. in} \,\, \Omega _T\,, \nonumber \\ \end{aligned}$$

(1.5)

$$\begin{aligned}{} & {} u_0\in L^1(\Omega )\,, \quad u_0\ge 0\,. \end{aligned}$$

(1.6)

The difficulty of this kind of problems relies in the singularity in the right hand side, together with the nonlinearity of the principal part and the weak regularity of the initial datum which is only assumed in $L^1(\Omega )$.

We point out that the operator in divergence form in problem (1.1) includes as particular cases the Laplacian and the degenerate p-Laplacian (slow diffusion) which are widely studied in literature when $\gamma = 0$, i.e. when the singular reaction term is missing.

The presence of the singular term in the equation models many different physical problems. For example, problem (1.1) appears in the theory of heat conduction in electrically conducting materials, as described by Fulks and Maybee in 1960 in their pioneering paper [18]. Other useful applications of these singular parabolic problems appear in fluid mechanics, in the theory of non-Newtonian pseudoplastic flow and in the phenomena of signal trasmissions (see [1, 29, 35, 37] and the references therein).

The first result in literature on this parabolic problem seems to be the paper of Fulks and Maybee recalled above (see [18]) where the authors study the case of regular bounded data f and $u_0$ when the principal part is the Laplacian operator. After this interesting paper mostly of the studies were devoted to the stationary case, starting from the paper of Stuart (see [36]) published in 1976 and followed by that of Crandall, Rabinowitz and Tartar in 1977 (see [12]) and later (in 1991) by the nice paper of Lazer and McKenna (see [26]). The studies on the elliptic case continue also in the 2000s with many new interesting results like those by Boccardo and Orsina (see [8]) and by Boccardo and Casado-Diaz (see [5]) whose papers inspired many new investigations on this subject (see [17, 19,20,21,22,23] and the references therein). Further results can be found in [2, 4].

In the evolution case the results in literature are more fragmented and with the exception of the pioneering paper [18] the studies in the parabolic setting have all been essentially published in the last decade. We refer to the papers [1, 3, 6, 9, 10, 14, 15, 30].

In [3, 6, 9, 10] the special case when $f(x,t) \equiv \lambda$ in $\Omega _T$, with $\lambda$ a positive constant, is investigated assuming that the initial datum $u_0$ is bounded (with the only exception of [10] where the initial datum $u_0$ belongs to $L^r(\Omega )$ with $r \ge 2$ large enough) and when reaction terms (of different types) can appear in the equation.

In [14, 15] it is studied the regular case of bounded initial data too but with $f(x,t) \not \equiv \lambda$ . In particular, in [14] it is proved that the strong regularity assumption on $u_0$ together with the assumption (1.5) on f produces the boundedness of the solutions which allows to estimate the singular term and to construct a nonnegative solution u of (1.1).

It is worth to notice that the assumption (1.5) on f is a sharp assumption to have bounded solutions when $\gamma = 0$.

In [15], together with the boundedness of $u_0$, the following further assumption is retained:

$$\begin{aligned} \text{ for } \text{ every } \text{ compact } \,\, \omega \subset \Omega \,\, \text{ there } \text{ exists } \,\, c_{\omega }>0: \,\, u_0 \ge c_{\omega } \,\, \mathrm {a.e.}\,\text {in}\,\, \omega \end{aligned}$$

which is shown to produce the following property on the solutions:

$$\begin{aligned} \text{ there } \text{ exists } \,\, C_{\omega }>0: \,\, u \ge C_{\omega } \,\, \mathrm {a.e.} \, \text {in} \,\, \omega \times (0,T)\,. \end{aligned}$$

Notice that the previous estimate implies the following bound on the singular term

$$\begin{aligned} \frac{ f}{ u^{\gamma }} \le \frac{f}{C_{\omega }^{\gamma }} \,\, \mathrm{a.e.} \, \textrm{in}\,\, \omega \times (0,T)\,, \end{aligned}$$

which is crucial in order to prove the existence of a solution of (1.1).

Finally, in [30] and in [1] are studied the irregular cases when $u_0$ is a summable function and f is a summable function too (see [30]) or a bounded Radon measure (see [1]). In particular, in [30] the authors prove the existence of a “distributional solution” (see Definition 2.1 in [30]) which, in the case $\gamma \le 1$, belongs also to the energy space $L^p(0,T;W_0^{1,p}(\Omega ))$ if the initial datum belongs to $L^2(\Omega )$ and if f satisfies a further summability condition (see Lemma 3.5 in [30]).

Here, we want to complete the previous results studying the lacking case of initial datum $u_0$ in $L^1(\Omega )$ and f satisfying (1.5). In detail, we show here that even if $u_0$ belongs only to $L^1(\Omega )$, if f is suitably regular (i.e. if (1.5) holds true) then there exists a solution that “immediately” becomes bounded.

We point out that it is well known that if $f \equiv 0$, i.e. in absence of a reaction term, there exists (and is also unique see [32]) a solution of (1.1) that immediately becomes bounded (see for example [11, 31, 38] and the references therein). Moreover, even if $f \not \equiv 0$, this strong regularization phenomenon that produces “instantly” bounded solutions even if the initial datum is not bounded and very irregular (remember that here $u_0$ is only assumed in $L^1(\Omega )$) was already known if $\gamma =0$, i.e. in absence of a singularity in the lower order term (see [33]). What seems really surprising is that this phenomenon remains true even in presence of the singular term $f/u^{\gamma }$ which a priori can be “a very large term” since it results

$$\begin{aligned} \lim _{u \rightarrow 0^+} \frac{1}{u^{\gamma }} = +\infty \,. \end{aligned}$$

Indeed, also the gradient of this solution “instantly” regularizes; as a matter of fact u belongs to $L^p_{loc}((0,T];W^{1,p}_{loc}(\Omega ))$.

In this paper we study also the behavior in time of the solutions of (1.1). In particular we show that our problem admits global solutions. Moreover, we prove that all the global solutions belonging to a suitable class of solutions are unique. Finally, we prove that all these unique global solutions satisfy the same asymptotic behavior, independently from the value of the initial datum. In other words, for large value of t all the global solution of (1.1) exhibit the same behavior even if they assume different initial data.

We recall that other evolution problems involving singular lower order terms that, differently from our problem (1.1), depend also on the gradient of the solution, can be found in [13, 28]. Finally, existence results for a parabolic systems with singular sources can be found in [16].

The paper is organized as follows: in the next section we state our results in all the details, in Sect. 3 for the convenience of the reader we state some tools needed in the proof of the results which are given in the last Sect. 4.

2 Statement of results

Before stating our results we recall our notion of solution to problem (1.1) .

Definition 2.1

A weak solution to problem (1.1) is a function u satisfying

$$\begin{aligned}{} & {} u\in L^p_{loc}((0,T];W^{1,p}_{loc}(\Omega )) \end{aligned}$$

(2.1)

$$\begin{aligned}{} & {} u\ge 0 \quad \text{ a.e. } \text{ in }\,\, \Omega _T, \end{aligned}$$

(2.2)

$$\begin{aligned}{} & {} u^{\frac{p+\max \{0,\gamma -1\}}{p}}\in L^p_{loc}((0,T];W^{1,p}_{0}(\Omega )), \end{aligned}$$

(2.3)

$$\begin{aligned}{} & {} \frac{f}{u^{\gamma }}\in L^1_{loc}(\Omega _T)\,, \end{aligned}$$

(2.4)

and

$$\begin{aligned} -\iint _{\Omega _T}u\frac{\partial \phi }{\partial t}+\iint _{\Omega _T}a(x,t,\nabla u)\nabla \phi =\iint _{\Omega _T}\frac{f}{u^{\gamma }}\,\phi \end{aligned}$$

(2.5)

for any $\phi \in C^{\infty }_c(\Omega _T)$. Finally, u satisfies the initial condition in the following weak sense: u is the a.e. limit in $\Omega _T$ of a sequence $u_n \in C([0,T];L^2(\Omega )) \cap L^p(0,T;W^{1,p}_{loc}(\Omega ))\cap L^\infty (\Omega _T)$ satisfying

$$\begin{aligned} u_n(0)=u_{0n} \in C^{\infty }_c(\Omega ) \quad \textrm{with} \quad u_{0n} \rightarrow u_0 \,\, \textrm{in} \,\, L^1(\Omega )\,. \end{aligned}$$

(2.6)

Remark 2.1

We observe that the boundary condition $u(x,t)=0$ on $\Gamma$ in (1.1) is satisfied in the weak sense (2.3). Notice also that if $0 < \gamma \le 1$ then condition (2.3) becomes $u \in L^p_{loc}(0,T;W^{1,p}_{0}(\Omega ))$ that is the usual meaning of the null boundary condition.

The main result of the paper is the following.

Theorem 2.1

Assume (1.2)–(1.6). Then there exists a weak solution to problem (1.1) satisfying the following regularity property

$$\begin{aligned} u \in L^\infty (\varepsilon , T; L^{\infty }(\Omega ))\,\,\, \textrm{for every} \,\, \varepsilon >0\,. \end{aligned}$$

(2.7)

Moreover, the following estimates hold true for a.e. $t \in (0, T)$

$$\begin{aligned}{} & {} ||u(t)||_{L^{\infty }(\Omega )}\le M_0 + M_1 \frac{\Vert u_{0}\Vert _{L^1(\Omega )}}{e^{\sigma t}}\,, \quad \textrm{if } \,\, p = 2\,, \end{aligned}$$

(2.8)

$$\begin{aligned}{} & {} ||u(t)||_{L^{\infty }(\Omega )}\le M_0 + \min \left\{ \frac{M_2}{t^{\frac{1}{p-2}}}\,, M_3 \frac{\Vert u_0\Vert _{L^1(\Omega )}^{\frac{p}{N(p-2)+p}}}{t^{\frac{N}{N(p-2)+p}}} \right\} , \quad \textrm{if } \,\, p > 2 , \qquad \end{aligned}$$

(2.9)

where $\sigma =\sigma (|\Omega |)$, $M_0=M_0(\alpha ,p,N,|\Omega _T|,T,\Vert f\Vert _{r,m},r,m)$, $M_1 = M_1(N,\beta )$, $M_2 = M_2(N,\beta ,p,|\Omega |)$ and $M_3 = M_3(N,\beta )$ are all positive constants independent of $u_0$ and t.

Here and throughout the paper we denote C(s, v) and M(s, v) positive constants depending only on the variables in brackets, that can change from one line to the other.

Remark 2.2

We recall that the previous result was well known in absence of the singular term $\frac{f}{u^{\gamma }}$, i.e. when $f \equiv 0$, (see [31]) or when $\gamma = 0$ (see [33]). Theorem 2.1 shows that a strong regularization holds true being our solution u “immediately bounded” even in presence of the singular lower order term $\frac{f}{u^{\gamma }}$, and although the initial datum is not bounded and assumed to be only in $L^1(\Omega )$.

Remark 2.3

We notice that the $L^{\infty }$-estimates (2.8)–(2.9) allow to estimate the blow-up of the $L^{\infty }$-norm of u(t) when $t \rightarrow 0^+$ which occurs when the initial datum $u_0$ is unbounded. As a matter of fact, estimates (2.8)–(2.9) allow to affirm that if $p \ge 2$ the blow-up is controlled by the power $t^{-\frac{N}{N(p-2)+p}}$ (since when $p >2$ it results $\frac{1}{p-2} > \frac{N}{N(p-2)+p}$).

It is worth to notice that when $p >2$ it is also possible to give an universal $L^{\infty }$-bound on the solution u, i.e. an estimate that is independent of the initial datum $u_0$. As a matter of fact, by (2.9) it follows that the following universal bound holds true

$$\begin{aligned} \Vert u(t)\Vert _{L^{\infty }(\Omega )}\le M_0 + \frac{M_2}{t^{\frac{1}{p-2}}} = M, \end{aligned}$$

where $M=M(\alpha ,p,N,|\Omega _T|,T,\Vert f\Vert _{r,m},r,m,t,\beta )$ is a constant independent of $u_0$.

We notice that the solution u in Theorem 2.1 is obtained as the a.e. limit in $\Omega _T$ (indeed also other convergences will occur) of the sequence $u_n$ of the following problems

$$\begin{aligned} {\left\{ \begin{array}{ll} (u_n)_t-\textrm{div}(a(x,t,\nabla u_n))=\frac{f}{(u_n+\frac{1}{n})^{\gamma }}\,, &{} \quad \text{ in } \Omega _T\,,\\ u_n(x,t)=0\,, &{} \quad \text{ on } \Gamma \,,\\ u_n(x,0)=u_{0n}(x)\,, &{} \quad \text{ in } \Omega , \end{array}\right. } \end{aligned}$$

(2.10)

with $u_{0n}\in C^{\infty }_c(\Omega )$ satisfying

$$\begin{aligned} u_{0n}\rightarrow u_0\quad \quad \text{ in } \,\,L^1(\Omega )\,. \end{aligned}$$

(2.11)

It is possible to show that if in (2.10) we change the approximation of the initial datum, then we always get the same solution and hence we have a result of uniqueness for the solutions constructed by approximation. More in detail, this is established in the following uniqueness result.

Theorem 2.2

Assume (1.2)–(1.6). Let u be a weak solution of problem (1.1) obtained as the a.e. limit in $\Omega _T$ of the sequence $u_n \in L^p(0,T; W^{1,p}_0(\Omega ))\cap L^{\infty }(\Omega _T) \cap C([0,T];L^2(\Omega ))$ solutions of (2.10). Let ${\overline{u}}$ be a weak solution to problem (1.1) obtained as the a.e. limit in $\Omega _T$ of the sequence ${\overline{u}}_n \in L^p(0,T; W^{1,p}_0(\Omega ))\cap L^{\infty }(\Omega _T) \cap C([0,T];L^2(\Omega ))$ solutions of the following problems

$$\begin{aligned} {\left\{ \begin{array}{ll} ({\overline{u}}_n)_t-\textrm{div}(a(x,t,\nabla {\overline{u}}_n))=\frac{f}{({\overline{u}}_n+\frac{1}{n})^{\gamma }}\,, &{} \quad \text{ in } \Omega _T\,,\\ {\overline{u}}_n(x,t)=0\,, &{} \quad \text{ on } \Gamma \,,\\ {\overline{u}}_n(x,0)={\overline{u}}_{0n}(x)\,, &{} \quad \text{ in } \Omega , \end{array}\right. } \end{aligned}$$

(2.12)

with ${\overline{u}}_{0n}\in C^{\infty }_c(\Omega )$ satisfying

$$\begin{aligned} {\overline{u}}_{0n}\rightarrow u_0\quad \quad \text{ in } \,\,L^1(\Omega )\,. \end{aligned}$$

(2.13)

Then it results

$$\begin{aligned} u = {\overline{u}} \quad \mathrm{a.e. in } \quad \Omega _T\,. \end{aligned}$$

(2.14)

Remark 2.4

We point out that the previous result shows that in the notion of weak solution the choice of the approximation $u_{0n}$ of the initial datum $u_0$ doesn’t influence the weak solution u to problem (1.1), since a different choice of the approximation of the initial datum produces the same solution.

Finally, it is possible to show that if we change the initial datum all these “unique solutions” have the same asymptotic behavior. In details, we have the following result.

Theorem 2.3

Assume (1.2)–(1.6). Let u be a weak solution of problem (1.1) obtained as the a.e. limit in $\Omega _T$ of the sequence $u_n \in L^p(0,T; W^{1,p}_0(\Omega ))\cap L^{\infty }(\Omega _T) \cap C([0,T];L^2(\Omega ))$ solutions to (2.10). Assume $v_0 \in L^1(\Omega )$ and let v be a weak solution of the following problem

$$\begin{aligned} {\left\{ \begin{array}{ll} v_t-\textrm{div}(a(x,t,\nabla v))=\frac{f}{v^{\gamma }}\,,&{} \quad \text{ in } \Omega _T\,,\\ v(x,t)=0\,, &{} \quad \text{ on } \Gamma \,,\\ v(x,0)=v_0(x)\,, &{} \quad \text{ in } \Omega \,, \end{array}\right. } \end{aligned}$$

(2.15)

obtained as the a.e. limit in $\Omega _T$ of the sequence $v_n \in L^p(0,T; W^{1,p}_0(\Omega ))\cap L^{\infty }(\Omega _T) \cap C([0,T];L^2(\Omega ))$ solutions to the following problems

$$\begin{aligned} {\left\{ \begin{array}{ll} (v_n)_t-\textrm{div}(a(x,t,\nabla v_n))=\frac{f}{(v_n+\frac{1}{n})^{\gamma }}\,, &{} \quad \text{ in } \Omega _T\,,\\ v_n(x,t)=0\,, &{} \quad \text{ on } \Gamma \,,\\ v_n(x,0)=v_{0n}(x)\,, &{} \quad \text{ in } \Omega , \end{array}\right. } \end{aligned}$$

(2.16)

with $v_{0n}\in C^{\infty }_c(\Omega )$ satisfying

$$\begin{aligned} v_{0n}\rightarrow v_0\quad \quad \text{ in } \,\,L^1(\Omega )\,. \end{aligned}$$

(2.17)

Then there exist positive constants $M_1 = M_1(N,\beta )$, $M_3 = M_3(N,\beta )$ and $\sigma = \sigma (N)$ (which are exactly the same constants $M_1$, $M_3$ and $\sigma$ that appear in Theorem 2.1) such that the following estimates hold for almost every $t\in (0,T)$

$$\begin{aligned}{} & {} ||u(t)-v(t)||_{L^{\infty }(\Omega )}\le M_1 \frac{||u_{0}-v_{0}||_{L^1(\Omega )}}{t^{\frac{N}{2}}e^{\sigma t}}\,, \quad \textrm{if } \,\, p = 2 \,, \end{aligned}$$

(2.18)

$$\begin{aligned}{} & {} ||u(t)-v(t)||_{L^{\infty }(\Omega )}\le M_3 \frac{\Vert u_0-v_0\Vert _{L^1(\Omega )}^{\frac{p}{N(p-2)+p}}}{t^{\frac{N}{N(p-2)+p}}} \,, \quad \textrm{if } \,\, p > 2 \,. \end{aligned}$$

(2.19)

We show now that if the structure assumptions are verified for every $T>0$ then there exists a unique global solutions obtained by approximation. Before stating in details our results we recall what we mean here as global solution of (1.1).

Definition 2.2

We say that u is a global weak solution of (1.1), or equivalently, we say that u is a global weak solution of the following problem

$$\begin{aligned} {\left\{ \begin{array}{ll} {\begin{array}{ll} u_t-\text {div}(a(x,t,\nabla u))=\frac{f}{u^{\gamma }}\,,&{}{} \quad \text {in }\, \Omega \times (0,\infty )\,,\\ u(x,t)=0\,, &{}{} \quad \text {on }\, \partial \Omega \times (0,+\infty )\,,\\ u(x,0)=u_0(x)\,, &{}{} \quad \text {in }\, \Omega \,, \end{array}} \end{array}\right. } \end{aligned}$$

(2.20)

if u is a weak solution of (1.1) (according to Definition 2.1) for every $T>0$.

We have the following result.

Theorem 2.4

Assume that (1.2)–(1.5) hold true for every $T>0$ and let (1.6) be satisfied. Then, there exists a global weak solution u of (1.1) belonging to $L^{\infty }_{loc}((0,+\infty );L^{\infty }(\Omega ))$. Moreover, for every $T>0$, u is obtained as the a.e. limit in $\Omega _T$ of the sequence $u_n \in L^p(0,T; W^{1,p}_0(\Omega ))\cap L^{\infty }(\Omega _T) \cap C([0,T];L^2(\Omega ))$ solutions to (2.10).

Thus, if ${\overline{u}}$ is a global weak solution to problem (1.1) obtained for every $T>0$ as the a.e. limit in $\Omega _T$ of the sequence ${\overline{u}}_n \in L^p(0,T; W^{1,p}_0(\Omega ))\cap L^{\infty }(\Omega _T) \cap C([0,T];L^2(\Omega ))$ weak solutions of (2.12), then $u = {\overline{u}}$ a.e. in $\Omega \times (0,+\infty )$.

Finally, if $v_0 \in L^1(\Omega )$ and v is a global weak solution of problem (2.15) obtained as the a.e. limit in $\Omega _T$ (for every $T>0$) of the sequence $v_n \in L^p(0,T; W^{1,p}_0(\Omega ))\cap L^{\infty }(\Omega _T) \cap C([0,T];L^2(\Omega ))$ weak solutions to (2.16), then (2.18) and (2.19) hold true for every $t >0$. In particular, it results

$$\begin{aligned} \lim _{t \rightarrow + \infty }||u(t)-v(t)||_{L^{\infty }(\Omega )} = 0\,. \end{aligned}$$

(2.21)

3 Preliminary results

In this section we recall some known results that will be essential in the proofs of our results.

For $k>0$ and $s\in {\mathbb {R}}$ let us define the function $G_k(s)$ as follows

$$\begin{aligned} G_k(s)=(|s|-k)_+\hbox {sign}(s). \end{aligned}$$

Moreover for any measurable function v we will denote $v^+=\max (v,0)$ and $v^-=\max (-v,0)$.

Theorem 3.1

(Theorem 2.1 in [31]) Assume that

$$\begin{aligned} u \in C((0,T);L^{r}(\Omega )) \cap L^{b}(0,T;L^q(\Omega )) \cap C([0,T);L^{r_0}(\Omega )) \end{aligned}$$

(3.1)

where $\Omega$ is an open set of ${\mathbb {R}}^N$, (not necessary bounded), $N \ge 1$, $0<T\le +\infty$ and

$$\begin{aligned} 1 \le r_0< r<q \le + \infty , \quad b_0< b < q, \quad b_0 = \frac{(r-r_0)}{1-\frac{r_0}{q}}\,. \end{aligned}$$

(3.2)

Suppose that u satisfies the following integral estimates for every   $k>0$

$$\begin{aligned}{} & {} \int _\Omega |G_k(u)|^{r}(t_2) dx - \int _\Omega |G_k(u)|^{r}(t_1) dx \nonumber \\{} & {} \quad +\,c_1 \int _{t_1}^{t_2} \Vert G_k(u)(\tau )\Vert ^b_{L^q(\Omega )} d\tau \le 0, \quad \forall \,\,0< t_1< t_2 < T, \end{aligned}$$

(3.3)

$$\begin{aligned}{} & {} {} \Vert G_k(u)(t)\Vert _{L^{r_0}(\Omega )} \le c_2 \Vert G_k(u)(t_0)\Vert _{L^{r_0}(\Omega )}, \quad \text {for}\,\text {every} \,\,\, 0 \le t_0< t < T, \qquad \end{aligned}$$

(3.4)

where $c_1$ and $c_2$ are positive constants independent of k. Finally, let us define

$$\begin{aligned} u_0 \equiv u(x,0) \in L^{r_0}(\Omega ). \end{aligned}$$

(3.5)

Then there exists a positive constant $C_1$ (see formula (4.11) in [31]) depending only on N, $c_1$, $c_2$, r, $r_0$, q and b such that

$$\begin{aligned} \Vert u(t)\Vert _{L^\infty (\Omega )} \le C_1 \frac{\Vert u_0\Vert ^{h_0}_{L^{r_0}(\Omega )}}{t^{h_1}} \quad \text {for}\,\text {every} \,\,\, t \in (0,T), \end{aligned}$$

(3.6)

where

$$\begin{aligned} h_1 = \frac{1}{b - (r- r_0)- \frac{r_0b}{q}}, \quad \textrm{and} \quad h_0 = h_1 \left( 1-\frac{b}{q}\right) r_0\,. \end{aligned}$$

(3.7)

Moreover if $\Omega$ has finite measure we have an exponential decay if $b = r$ and universal bounds if $b > r$. More in detail we have the following result.

Theorem 3.2

(Theorem 2.2 in [31]) Let the assumptions of Theorem 3.1 hold true.

If $\Omega$ has finite measure and $b = r$ the following exponential decay occurs

$$\begin{aligned} \Vert u(t)\Vert _{L^\infty (\Omega )} \le C_2 \frac{\Vert u_0\Vert _{L^{r_0}(\Omega )}}{t^{h_1}e^{\sigma t}}, \quad \text {for}\,\text {every} \,\,\, t \in (0,T), \end{aligned}$$

(3.8)

where $C_2$ (see formula (4.17) in [31]) is a positive constant (depending only on N, $c_1$, $c_2$, r, $r_0$ and q), $u_0$ is as in (3.5), $h_1$ is as in (3.7), i.e. (recalling that here $r=b$)

$$\begin{aligned} h_1 = \frac{1}{ r_0 \left( 1 - \frac{r}{q}\right) }, \end{aligned}$$

(3.9)

and

$$\begin{aligned} \sigma = \frac{c_1 \kappa }{4(r-r_0)|\Omega |^{1-\frac{r}{q}}}, \quad \kappa \quad \textrm{arbitrarily} \; \textrm{fixed} \;\textrm{in} \quad \left( 0,1-\frac{r_0}{ r}\right) , \end{aligned}$$

(3.10)

where $|\Omega |$ denotes the measure of $\Omega$. If instead $\Omega$ has finite measure and $b > r$ we have the following universal bound

$$\begin{aligned} \Vert u(t)\Vert _{L^\infty (\Omega )} \le \frac{C_{\sharp }}{t^{h_2}} \quad \textrm{for}\; \textrm{every} \,\,\, t \in (0,T), \end{aligned}$$

(3.11)

where

$$\begin{aligned} h_2= h_1 + \frac{h_0}{b -r} = \frac{1}{b-r}, \end{aligned}$$

(3.12)

and $C_{\sharp }$, (see formula (4.19) in [31]), is a constant depending only on r, $r_0$, q, b, $c_1$, $c_2$ and the measure of $\Omega$.

4 Proof of the results

4.1 Proof of Theorem 2.1

The proof proceeds by steps.

Step 1: approximating problems.

In order to prove the existence of a solution to problem (1.1), we consider the following sequence of nonsingular approximating problems

$$\begin{aligned} {\left\{ \begin{array}{ll} (u_n)_t-\textrm{div}(a(x,t,\nabla u_n))=\frac{f}{(u_n+\frac{1}{n})^{\gamma }}\,, &{} \quad \text{ in } \Omega _T\,,\\ u_n(x,t)=0\,, &{} \quad \text{ on } \Gamma \,,\\ u_n(x,0)=u_{0n}(x)\,, &{} \quad \text{ in } \Omega , \end{array}\right. } \end{aligned}$$

(4.1)

with $n \in {\mathbb {N}}$ and $u_{0n}\in C^{\infty }_c(\Omega )$ satisfying

$$\begin{aligned} u_{0n}\ge 0, \quad u_{0n}\rightarrow u_0\quad \quad \text{ in } \,\,L^1(\Omega ) \end{aligned}$$

(4.2)

and

$$\begin{aligned} ||u_{0n}||_{L^1(\Omega )}\le ||u_0||_{L^1(\Omega )}. \end{aligned}$$

(4.3)

We point out that the approximating problem (4.1) has a nonnegative weak solution $u_n$, i.e. there exists $u_n \in L^p(0,T; W^{1,p}_0(\Omega ))\cap L^{\infty }(\Omega _T) \cap C([0,T];L^2(\Omega ))$ satisfying

$$\begin{aligned} - \int _{\Omega }u_{0n}\phi (0) -\iint _{\Omega _T} u_n\frac{\partial \phi }{\partial t}+\iint _{\Omega _T}a(x,t,\nabla u_n)\nabla \phi =\iint _{\Omega _T}\frac{f}{(u_n+\frac{1}{n})^{\gamma }}\phi \nonumber \\ \end{aligned}$$

(4.4)

for every $\phi \in C^{\infty }_c(\Omega \times [0,T))$ (see [27]).

In the following steps we prove some uniform estimates on the sequence $\{u_n\}_{n\in {\mathbb {N}}}$. To this aim, we introduce the following auxiliary sequence of approximating nonsingular problems

$$\begin{aligned} {\left\{ \begin{array}{ll} (v_n)_t-\textrm{div}(a(x,t,\nabla v_n))=\frac{f}{(v_n+\frac{1}{n})^{\gamma }},&{} \quad \text{ in } \,\Omega _T\,,\\ v_n(x,t)=0\,, &{} \quad \text{ on } \Gamma \,,\\ v_n(x,0)=0\,, &{} \quad \text{ in } \Omega . \end{array}\right. } \end{aligned}$$

(4.5)

As observed above, there exists a nonnegative weak solution $v_n$ belonging to $L^p(0,T; W^{1,p}_0(\Omega ))\cap L^{\infty }(\Omega _T) \cap C([0,T];L^2(\Omega ))$.

We recall that, being $v_n(x,0)=0$, it is possible to proceed exactly as in the proof of Proposition 2.13 of [14] getting the existence of a constant $M_0 = M_0(\alpha ,p,N,|\Omega _T|,T,\Vert f\Vert _{r,m},r,m)$ independent of n, such that for every n

$$\begin{aligned} ||v_n||_{L^{\infty }(\Omega _T)}\le M_0\,. \end{aligned}$$

(4.6)

Moreover, again thanks to the regularity of the initial datum $v_n(x,0)$, if $0 < \gamma \le 1$, it is possible to proceed as in the proof of Proposition 2.14 of [14], to derive that there exists a positive constant $C_1= C_1(\gamma ,\alpha ,p,N,|\Omega |,T,\Vert f\Vert _{r,m},r,m)$ independent of n, such that for every n

$$\begin{aligned} ||\nabla v_n||_{L^{p}(\Omega _T)} \le C_1 \,. \end{aligned}$$

(4.7)

Finally, if $\gamma > 1$, proceeding as in the proof of Proposition 2.16 of [14] (which again is possible thanks to regularity of the initial datum), we derive that there exists a positive constant $C_2= C_2(\gamma ,\alpha ,p,N,|\Omega |,T,\Vert f\Vert _{r,m},r,m,\Vert \varphi \Vert _{W_0^{1,p}})$ independent of n, such that for every n and for every non negative $\varphi \in C^{\infty }_0(\Omega )$

$$\begin{aligned} \int \!\!\int _{\Omega _T}|\nabla v_n|^p\varphi ^{p} \le C_2 \,. \end{aligned}$$

(4.8)

Step 2: $L^{\infty }$-estimates.

Using estimate (4.6) we prove now the following $L^{\infty }$-estimate on the sequence of solutions $\{u_n\}_{n\in {\mathbb {N}}}$ that will be crucial in the following in order to pass to the limit in (4.4).

In details, we have the following result.

Proposition 4.1

Assume (1.2)–(1.6). Then, for every $\varepsilon \in (0,T)$ there exists a constant $C_3$, independent of n, such that for every n

$$\begin{aligned} ||u_n||_{L^\infty (\Omega \times (\varepsilon ,T))}\le C_3 \,. \end{aligned}$$

(4.9)

The costant $C_3=C_3(\alpha ,\beta , N, p, |\Omega |, T, ||u_0||_{L^1},\varepsilon ,||f||_{r,m},r,m)$ is given in formula (4.21) and does not depend on $||u_0||_{L^1(\Omega )}$ if $p > 2$.

Proof

To prove estimate (4.9) we start showing that, for almost every $t\in (0,T)$, there exist positive constants $M_1 = M_1(N,\beta )$, $M_2 = M_2(N,\beta ,p,|\Omega |)$, $M_3 = M_3(N,\beta )$ and $\sigma = \sigma (N)$, independent of n, such that the following estimates hold

$$\begin{aligned}{} & {} ||u_n(t)-v_n(t)||_{L^{\infty }(\Omega )}\le M_1 \frac{||u_{0}||_{L^1(\Omega )}}{t^{\frac{N}{2}}e^{\sigma t}}\,, \quad \textrm{if } \,\, p = 2\,, \end{aligned}$$

(4.10)

$$\begin{aligned}{} & {} ||u_n(t)-v_n(t)||_{L^{\infty }(\Omega )}\le \min \left\{ \frac{M_2}{t^{\frac{1}{p-2}}}\,, M_3 \frac{\Vert u_0\Vert _{L^1(\Omega )}^{\frac{p}{N(p-2)+p}}}{t^{\frac{N}{N(p-2)+p}}}\, \right\} \,, \quad \textrm{if } \,\, p > 2 \,. \qquad \quad \end{aligned}$$

(4.11)

We point out explicitly that the constant $M_2$ is independent of $u_0$.

In order to prove the estimates above, we consider the difference of the problem solved respectively by $u_n$ and $v_n$ and we take $G_k(u_n-v_n)$ as test function. We have, for every $0<t_1<t_2<T$,

$$\begin{aligned}{} & {} \frac{1}{2}\int _{\Omega } |G_k(u_n-v_n)(t_2)|^2 -\frac{1}{2}\int _{\Omega } |G_k(u_n-v_n)(t_1)|^2 \\{} & {} \qquad +\int _{t_1}^{t_2}\!\!\!\int _{\Omega }\left( a(x,t,\nabla u_n)-a(x,t,\nabla v_n)\right) \nabla G_k(u_n-v_n) \\{} & {} \quad =\int _{t_1}^{t_2}\!\!\!\int _{\Omega }f\left( \frac{1}{(u_n+\frac{1}{n})^{\gamma }} -\frac{1}{(v_n+\frac{1}{n})^{\gamma }}\right) G_k(u_n-v_n)\,, \end{aligned}$$

and hence using assumption (1.4) we get

$$\begin{aligned}{} & {} \frac{1}{2}\int _{\Omega } |G_k(u_n-v_n)(t_2)|^2 -\frac{1}{2}\int _{\Omega } |G_k(u_n-v_n)(t_1)|^2\nonumber \\{} & {} \quad + \beta \int _{t_1}^{t_2}\!\!\!\int _{\Omega }|\nabla G_k(u_n-v_n)|^p \nonumber \\{} & {} \quad \le , \int _{t_1}^{t_2}\!\!\!\int _{\Omega }f\left( \frac{1}{(u_n+\frac{1}{n})^{\gamma }} -\frac{1}{(v_n+\frac{1}{n})^{\gamma }}\right) G_k(u_n-v_n)\,. \end{aligned}$$

(4.12)

Observing now that the function $G_k(u_n-v_n)$ has the same sign of the function $(u_n-v_n)$, the right hand side of (4.12) is negative and consequently we have

$$\begin{aligned}{} & {} \frac{1}{2}\int _{\Omega } |G_k(u_n-v_n)(t_2)|^2 -\frac{1}{2}\int _{\Omega } |G_k(u_n-v_n)(t_1)|^2\nonumber \\{} & {} \quad + \beta \int _{t_1}^{t_2}\!\!\!\int _{\Omega }|\nabla G_k(u_n-v_n)|^p \le 0\,. \end{aligned}$$

(4.13)

Thus, by Sobolev inequality we obtain

$$\begin{aligned}{} & {} \int _{\Omega } |G_k(u_n-v_n)(t_2)|^2 - \int _{\Omega } |G_k(u_n-v_n)(t_1)|^2 \nonumber \\{} & {} \quad + \quad 2\beta C_s \int _{t_1}^{t_2}\left( \int _{\Omega }| G_k(u_n-v_n)|^{p^*}\right) ^{p/p^*} \le 0\,, \end{aligned}$$

(4.14)

i.e. assumption (3.3) of Theorem 3.1 is satisfied by the function $u_n-v_n$ with $r=2$, $b=p, q=p^*$ and $c_1 = 2 \beta C_s$. Here we have denoted by $C_s= C(N,p)$ the Sobolev constant. Notice that it results $b = r$ if $p=2$ and $b >r$ if $p > 2$.

We show now that also the other integral estimate (3.4) of Theorem 3.1 is satisfied by the function $u_n-v_n$ with $r_0=c_2=1$. To this aim, take as test function in (4.1) and in (4.5) the function $\varphi = \left\{ 1- \frac{1}{[1+|G_k(u_n-v_n)|]^\delta }\right\} \textrm{sign}(u_n-v_n)$, $\delta >1$. Now subtracting the results we get for every $0 \le t_0 \le t < T$

$$\begin{aligned}{} & {} \int _{\Omega }|G_k(u_n-v_n)|(t) + \frac{1}{\delta - 1}\int _{\Omega }\left\{ 1- \frac{1}{[1+|G_k(u_n-v_n)|(t)]^{\delta -1}}\right\} \\{} & {} \quad + \quad \delta \int _{t_0}^{t}\!\!\!\int _{\Omega } [a(x,t,\nabla u_n) - a(x,t,\nabla v_n)] \frac{\nabla G_k(u_n-v_n)}{[1+|G_k(u_n-v_n)|(t)]^{\delta +1}} \\{} & {} \le \int _{\Omega }|G_k(u_n-v_n)|(t_0) + \frac{1}{\delta - 1}\int _{\Omega }\left\{ 1-\frac{1}{[1+|G_k(u_n-v_n)|(t_0)]^{\delta -1}}\right\} \\{} & {} + \quad \int _{t_1}^{t_2}\!\!\!\int _{\Omega }f\left( \frac{1}{(u_n+\frac{1}{n})^{\gamma }}-\frac{1}{(v_n+\frac{1}{n})^{\gamma }}\right) \left\{ 1- \frac{1}{[1+|G_k(u_n-v_n)|]^\delta }\right\} \textrm{sign}(u_n-v_n)\,. \end{aligned}$$

Observe that the last integral is negative (or null). Thus, thanks to assumption (1.4) by the previous inequality we deduce that

$$\begin{aligned} \int _{\Omega }|G_k(u_n-v_n)|(t) \le \int _{\Omega }|G_k(u_n-v_n)|(t_0) + \frac{|\Omega |}{\delta - 1} \,, \end{aligned}$$

from which, thanks to the arbitrary choice of $\delta >1$ we derive that for every $0 \le t_0 \le t < T$

$$\begin{aligned} \int _{\Omega }|G_k(u_n-v_n)|(t) \le \int _{\Omega }|G_k(u_n-v_n)|(t_0) \,, \end{aligned}$$

i.e. also (3.4) holds true. Hence, since we are assuming that the measure of $\Omega$ is finite, we can apply Theorem 3.2 obtaining the following estimates

$$\begin{aligned}{} & {} ||u_n(t)-v_n(t)||_{L^{\infty }(\Omega )}\le M_1 \frac{||u_{0n}||_{L^1(\Omega )}}{t^{\frac{N}{2}}e^{\sigma t}}\,, \quad \textrm{if } \,\, p = 2 \,, \end{aligned}$$

(4.15)

$$\begin{aligned}{} & {} ||u_n(t)-v_n(t)||_{L^{\infty }(\Omega )}\le \frac{M_2}{t^{\frac{1}{p-2}}}\,, \quad \textrm{if } \,\, p > 2 \,, \end{aligned}$$

(4.16)

where $M_1 = M_1(N,\beta )$ and $M_2 = M_2(N,\beta ,p,|\Omega |)$. By (4.15), thanks to (4.3), we deduce that (4.10) holds true. Notice that we can apply also Theorem 3.1 obtaining the following estimate when $p > 2$

$$\begin{aligned} ||u_n(t)-v_n(t)||_{L^{\infty }(\Omega )}\le M_3 \frac{\Vert u_{0n}\Vert _{L^1(\Omega )}^{\frac{p}{N(p-2)+p}}}{t^{\frac{N}{N(p-2)+p}}}\,, \end{aligned}$$

(4.17)

from which, using again (4.3) we get

$$\begin{aligned} ||u_n(t)-v_n(t)||_{L^{\infty }(\Omega )}\le M_3 \frac{\Vert u_{0}\Vert _{L^1(\Omega )}^{\frac{p}{N(p-2)+p}}}{t^{\frac{N}{N(p-2)+p}}}\,, \quad \textrm{if } \,\, p > 2\,, \end{aligned}$$

(4.18)

where $M_3=M_3(N,\beta )$. Now (4.11) follows by (4.18) and (4.16).

Thanks to the estimates (4.6) we have that

$$\begin{aligned}{} & {} ||u_n(t)||_{L^{\infty }(\Omega )} \le ||u_n(t)-v_n(t)||_{L^{\infty }(\Omega )} + ||v_n(t)||_{L^{\infty }(\Omega )} \\{} & {} \quad \le M_0 + ||u_n(t)-v_n(t)||_{L^{\infty }(\Omega )} \,. \end{aligned}$$

Thus, by the previous estimates and (4.10)–(4.11) we deduce

$$\begin{aligned}{} & {} ||u_n(t)||_{L^{\infty }(\Omega )}\le M_0 + M_1 \frac{||u_{0}||_{L^1(\Omega )}}{t^{\frac{N}{2}}e^{\sigma t}}\,, \quad \textrm{if } \,\, p = 2\,, \end{aligned}$$

(4.19)

$$\begin{aligned}{} & {} ||u_n(t)||_{L^{\infty }(\Omega )}\le M_0 + \min \left\{ \frac{M_2}{t^{\frac{1}{p-2}}}\,, M_3 \frac{\Vert u_0\Vert _{L^1(\Omega )}^{\frac{p}{N(p-2)+p}}}{t^{\frac{N}{N(p-2)+p}}} \right\} \,, \quad \textrm{if } \,\, p > 2 \,. \qquad \quad \end{aligned}$$

(4.20)

By (4.19)–(4.20) it follows (4.9) with

$$\begin{aligned} C_3 = \left\{ \begin{array}{ll} M_0 + M_1 \frac{||u_{0}||_{L^1(\Omega )}}{\varepsilon ^{\frac{N}{2}}e^{\sigma \varepsilon }}\,, &{} \quad \textrm{if} \,\, p=2\,, \\ M_0 + \min \left\{ \frac{M_2}{\varepsilon ^{\frac{1}{p-2}}}\,, M_3 \frac{\Vert u_0\Vert _{L^1(\Omega )}^{\frac{p}{N(p-2)+p}}}{\varepsilon ^{\frac{N}{N(p-2)+p}}} \right\} \,, &{} \textrm{if} \,\, p>2\,. \end{array} \right. \end{aligned}$$

(4.21)

$\square$

Step 3: gradient estimates.

We prove here some estimates on the gradients of the approximating solutions $u_n$.

Proposition 4.2

Assume (1.2)–(1.6). Then, for every $t\in (0,T)$ there exists a constant $C_4$, independent of n (see formula (4.23)) such that

$$\begin{aligned} \int _t^T\!\!\!\int _{\Omega } |\nabla (u_n-v_n)|^p\le C_4. \end{aligned}$$

(4.22)

Proof

Proceeding as in the proof of estimate (4.13) (the only difference is to choose $u_n-v_n$ as test function instead of $G_k(u_n-v_n)$) we get

$$\begin{aligned} \int _{t}^T\!\!\!\int _{\Omega } |\nabla (u_n-v_n)|^p \le \frac{1}{2\beta }\int _{\Omega } |(u_n(t)-v_n(t))|^2\,. \end{aligned}$$

By the previous estimate and the $L^{\infty }$-estimates (4.10)–(4.11) we deduce that

$$\begin{aligned} \int _{t}^T\!\!\!\int _{\Omega } |\nabla (u_n-v_n)|^p \le \frac{|\Omega |}{2\beta } \Vert u_n(t)-v_n(t)\Vert _{L^{\infty }(\Omega )}^2\le C_4\,, \end{aligned}$$

where

$$\begin{aligned} C_4 = \left\{ \begin{array}{ll} \frac{|\Omega |}{2\beta } \left( M_1 \frac{||u_{0}||_{L^1(\Omega )}}{t^{\frac{N}{2}}e^{\sigma t}}\right) ^2\,, &{} \quad \textrm{if} \,\, p=2\,,\\ &{} \\ \frac{|\Omega |}{2\beta } \left[ \min \left( \frac{M_2}{t^{\frac{1}{p-2}}}\,, M_3 \frac{\Vert u_0\Vert _{L^1(\Omega )}^{\frac{p}{N(p-2)+p}}}{t^{\frac{N}{N(p-2)+p}}} \right) \right] ^2\,, &{} \textrm{if} \,\, p>2\,. \end{array} \right. \end{aligned}$$

(4.23)

$\square$

To estimate now $\nabla u_n$ we need to distinguish between the two cases $0<\gamma \le 1$ and $\gamma >1$.

Step 3a: the case $0<\gamma \le 1$.

Proposition 4.3

Assume $0<\gamma \le 1$ and that (1.2)–(1.6) hold true. Then, for every $t\in (0,T)$ there exists a positive constant $C_5$, independent of n, see formula (4.25), such that for every $n\in {\mathbb {N}}$

$$\begin{aligned} \int _t^{T}\!\!\!\int _{\Omega }|\nabla u_n|^p \le C_5\,. \end{aligned}$$

(4.24)

Proof

In order to prove (4.24), we observe that, by (4.22) and (4.7) we obtain

$$\begin{aligned}{} & {} \int _t^{T}\!\!\!\int _{\Omega }|\nabla u_n|^p =\int _t^{T}\!\!\!\int _{\Omega }|\nabla (u_n-v_n)+\nabla v_n|^p \\{} & {} \quad \le 2^p\int _t^{T}\!\!\!\int _{\Omega }|\nabla (u_n-v_n)|^p +2^p\int _t^{T}\!\!\!\int _{\Omega }|\nabla v_n|^p \le C_5, \end{aligned}$$

where we have set

$$\begin{aligned} C_5 = 2^p (C_4 + C_1)\,. \end{aligned}$$

(4.25)

$\square$

Step 3b: the case $\gamma >1$.

Proposition 4.4

Assume $\gamma >1$ and that (1.2)–(1.6) hold true. Then, for every $t\in (0,T)$ there exists a positive constant $C_6$, independent of n, see formula (4.27), such that for every $n\in {\mathbb {N}}$

$$\begin{aligned} \int _t^T\!\!\!\int _{\Omega }|\nabla u_n|^p\varphi ^p \le C_6\,, \end{aligned}$$

(4.26)

for every non negative $\varphi \in C^\infty _0(\Omega )$.

Proof

We observe that for every non negative function $\varphi$ belonging to $C^\infty _0(\Omega )$, thanks to Proposition 4.2 and estimate (4.8)

$$\begin{aligned}{} & {} \int _t^{T}\!\!\!\int _{\Omega }|\nabla u_n|^p\varphi ^p=\int _t^{T}\!\!\!\int _{\Omega }|\nabla (u_n-v_n)+\nabla v_n|^p\varphi ^p \\{} & {} \quad \le 2^p\int _t^{T}\!\!\!\int _{\Omega }|\nabla (u_n-v_n)|^p\varphi ^p+2^p\int _t^{T}\!\!\!\int _{\Omega }|\nabla v_n|^p\varphi ^p\le C_6 \end{aligned}$$

where

$$\begin{aligned} C_6 = 2^p \left( C_4 \,||\varphi ||^p_{L^{\infty }(\Omega )}+ C_2 \right) \,, \end{aligned}$$

(4.27)

with $C_4$ the constant in estimate (4.22) and $C_2$ that in (4.8). $\square$

We conclude this step proving an estimate on the gradient of a suitable power of $u_n$.

Proposition 4.5

Assume $\gamma >1$ and that (1.2)–(1.6) hold true. Then, for every $\varepsilon \in (0,T)$ there exists a positive constant  $C_7$, independent of n, see formula (4.30), such that for every $n\in {\mathbb {N}}$

$$\begin{aligned} \int _\varepsilon ^{T}\!\!\!\int _{\Omega }\left| \nabla u_n^{\frac{\gamma +p-1}{p}}\right| ^p\le C_7 . \end{aligned}$$

(4.28)

Proof

Let $\varepsilon \in (0,T)$ arbitrarily fixed. Choosing $u_n^{\gamma }$ as test function in (4.1) we obtain, thanks to the $L^{\infty }$-estimate (4.9)

$$\begin{aligned}{} & {} \frac{1}{\gamma +1}\int _{\Omega }u_n^{\gamma +1}(T) +\alpha \gamma \int _{\varepsilon }^T\!\!\int _{\Omega } |\nabla u_n|^pu_n^{\gamma -1} \\{} & {} \quad \le \Vert f\Vert _{L^1(\Omega _T)}+\frac{1}{\gamma +1}\int _\Omega u_n(\varepsilon )^{\gamma +1} \le \Vert f\Vert _{L^1(\Omega _T)} + \frac{|\Omega |}{\gamma +1}C_3^{\gamma + 1}\,. \end{aligned}$$

Hence, it follows

$$\begin{aligned} \displaystyle \int _{t}^T\!\!\int _{\Omega } |\nabla u_n|^pu_n^{\gamma -1}\le C_8\,, \end{aligned}$$

(4.29)

where $C_8 = \left( \alpha \gamma \right) ^{-1}\left( \Vert f\Vert _{L^1(\Omega _T)} + \frac{|\Omega |}{\gamma +1}C_3^{\gamma + 1} \right) \,.$

Since it results

$$\begin{aligned} \int _{t}^T\!\!\int _{\Omega } |\nabla u_n|^p u_n^{\gamma -1}=\frac{p^p}{(\gamma +p-1)^p}\int _{t}^T\!\!\int _{\Omega } \left| \nabla u_n^{\frac{\gamma +p-1}{p}}\right| ^p\,, \end{aligned}$$

we deduce that

$$\begin{aligned} \int _{t}^T\!\!\int _{\Omega }\left| \nabla u_n^{\frac{\gamma +p-1}{p}}\right| ^p\le C_7, \end{aligned}$$

where

$$\begin{aligned} C_7 = C_8 \frac{(\gamma +p-1)^p}{p^p}\,. \end{aligned}$$

(4.30)

$\square$

Step 4: estimates on the singular lower order term.

We prove here some estimates on the singular lower order term.

Proposition 4.6

Assume (1.2)–(1.6). Then there exists a positive constant $C_9$, independent of n, with $C_9=C_9(C_3,\Lambda ,\varphi ,p)$ (where $C_3$ is defined in (4.9) with here $\varepsilon =t$), such that for every n

$$\begin{aligned} \int _t^T\!\!\int _\Omega \frac{f}{(u_n+\frac{1}{n})^\gamma }\varphi ^p(x)\le C_9\,, \end{aligned}$$

(4.31)

for every non negative $\varphi \in C^\infty _0(\Omega )$.

Proof

Choosing $\varphi ^p(x)$ as test function in (4.1), where $\varphi$ is a non negative function in $C^\infty _0(\Omega )$, we get

$$\begin{aligned} \int _t^T\langle (u_n)_t,\varphi ^p(x)\rangle +p\int _t^T\!\!\!\int _{\Omega } a(x,t,\nabla u_n)\varphi ^{p-1}\nabla \varphi =\int _t^T\!\!\!\int _{\Omega }\frac{f}{(u_n+\frac{1}{n})^\gamma }\varphi ^p, \end{aligned}$$

from which, using (1.3) and (4.9) we obtain

$$\begin{aligned}{} & {} \int _t^T\!\!\!\int _{\Omega }\frac{f}{(u_n+\frac{1}{n})^\gamma }\varphi ^p\le p \int _t^T\!\!\int _\Omega |a(x,t,\nabla u_n)|\varphi ^{p-1}|\nabla \varphi |+ C_{10}(C_3,\varphi )\\{} & {} \quad \le \Lambda p \int _t^T\!\!\int _\Omega |\nabla u_n|^{p-1}\varphi ^{p-1}|\nabla \varphi | + C_{10}\le C_9(C_3,\Lambda ,\varphi ,p), \end{aligned}$$

where we have used once again Young’s inequality with exponents $\frac{p}{p-1}$ and p and estimates (4.26) and (4.24). $\square$

Next estimate will be essential in the passage to the limit in the singular term.

Proposition 4.7

Assume (1.2)–(1.6). Then, for every $t\in (0,T)$ and $\mu >0$ there exists a positive constant $C_{11}$, independent of n and $\mu$, with $C_{11}=C_{11}(\Lambda ,\varphi )$ such that for every n and for every non negative $\varphi \in C^\infty _0(\Omega )$

$$\begin{aligned} \int \!\!\!\int _{\{\Omega \times (t,T)\}\cap \{0\le u_n < \mu \}}\frac{f}{(u_n+\frac{1}{n})^{\gamma }}\varphi ^p(x)\le C_{11}\mu \,. \end{aligned}$$

(4.32)

Proof

Thanks to estimate (4.9) proved above, the proof of this estimate can be obtained proceeding as in Proposition 2.20 of [14]. For the convenience of the reader we recall here the proof.

In order to prove (4.32), let $\mu >0$ and $t\in (0,T)$ arbitrarly fixed. Choosing $v_\delta = \frac{T_\delta (-(u_n-\mu )^-)}{\delta }\varphi ^p(x)$ as test function in problem (4.1), where $\varphi$ is a non negative function arbitrarily fixed in $C^\infty _0(\Omega )$, we get

$$\begin{aligned}{} & {} \int _t^T\langle (u_n)_t,\frac{T_\delta (-(u_n-\mu )^-)}{\delta }\varphi ^p(x)\rangle +\frac{1}{\delta }\int _t^T\!\!\!\int _{\Omega }a(x,t,\nabla u_n)\nabla (T_\delta (-(u_n-\mu )^-)\varphi ^p(x)\nonumber \\{} & {} \qquad +p\int _t^T\!\!\!\int _{\Omega }a(x,t,\nabla u_n)\frac{T_\delta (-(u_n-\mu )^-)}{\delta }\varphi ^{p-1}\nabla \varphi \nonumber \\{} & {} \quad =\int _t^T\!\!\!\int _{\Omega }\frac{f}{(u_n+\frac{1}{n})^{\gamma }}\cdot \frac{T_\delta (-(u_n-\mu )^-)}{\delta }\varphi ^p(x)\,. \end{aligned}$$

(4.33)

First we want to show that

$$\begin{aligned} \int _t^T\langle (u_n)_t,\frac{T_\delta (-(u_n-\mu )^-)}{\delta }\varphi ^p(x)\rangle \ge -\mu |\Omega |||\varphi ||^p_{L^\infty (\Omega )}. \end{aligned}$$

(4.34)

We introduce the function $v_{\delta ,\sigma }=\frac{T_\delta (-(u_{n,\sigma }-\mu )^-)}{\delta }$, where $u_{n,\sigma }$ is, for any fixed n and $\sigma \in {\mathbb {N}}$, the solution of the following o.d.e. problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{1}{\sigma }[u_{n,\sigma }]_t+ u_{n,\sigma }=u_n\\ u_{n,\sigma }(0)=u_{0,n}. \end{array}\right. } \end{aligned}$$

(4.35)

The function $u_{n,\sigma }$ satisfies the following properties (see [24, 25])

$$\begin{aligned}{} & {} u_{n,\sigma }\in L^p(0,T; W^{1,p}_0(\Omega )),\quad (u_{n,\sigma })_t\in L^{p}(0,T; W^{1,p}_0(\Omega )), \\{} & {} ||u_{n,\sigma }||_{L^\infty (Q_T)}\le ||u_n||_{L^\infty (Q_T)}, \\{} & {} u_{n,\sigma }\rightarrow u_n,\quad \text{ in } \, L^p(0,T; W^{1,p}_0(\Omega ))\,\, \text{ as } \sigma \rightarrow +\infty , \\{} & {} (u_{n,\sigma })_t\rightarrow (u_n)_t,\quad \text{ for } \sigma \rightarrow \infty \, \text{ in } \, L^{p'}(0,T; W^{-1,p'}(\Omega )). \end{aligned}$$

We get

$$\begin{aligned}{} & {} \int _t^T\langle (u_n)_t,\frac{T_\delta (-(u_n-\mu )^-)}{\delta }\varphi ^p(x)\rangle =\lim _{\sigma \rightarrow \infty }\int _t^T\!\!\!\int _{\Omega }(u_{n,\sigma }-\mu )^+_t\, \frac{T_\delta (-(u_n-\mu )^-)}{\delta }\varphi ^p(x) \\{} & {} \qquad -\lim _{\sigma \rightarrow \infty }\int _t^T\!\!\!\int _{\Omega }(u_{n,\sigma }-\mu )^-_t\, \frac{T_\delta (-(u_n-\mu )^-)}{\delta }\varphi ^p(x) \\{} & {} \quad = -\lim _{\sigma \rightarrow \infty }\int _t^T\!\!\!\int _{\Omega } (u_{n,\sigma }-\mu )^-_t\, \frac{T_\delta ((u_n-\mu )^-)}{\delta }\varphi ^p(x). \end{aligned}$$

Introducing now the function $\Phi _{\delta }(s)=\int _0^{(s-\mu )^-}\frac{T_\delta (\rho )}{\delta }d\rho$ we obtain from the previous equality

$$\begin{aligned}{} & {} \lim _{\sigma \rightarrow \infty }\int _t^T\!\!\!\int _{\Omega } (u_{n,\sigma }-\mu )^-_t \frac{T_\delta ((u_n-\mu )^-)}{\delta }\varphi ^p(x)=\lim _{\sigma \rightarrow \infty }\int _t^T\!\!\!\int _{\Omega } \frac{d}{dt}\Phi _{\delta }(u_{n,\sigma })\varphi ^p(x) \\{} & {} \quad =\lim _{\sigma \rightarrow \infty }\int _\Omega \Phi _{\delta }(u_{n,\sigma }-\mu )^-(T)\varphi ^p(x)-\lim _{\sigma \rightarrow \infty }\int _\Omega \Phi _{\delta }(u_{n,\sigma }-\mu )^-(t)\varphi ^p(x) \\{} & {} \quad \ge -\lim _{\sigma \rightarrow \infty }\int _\Omega \Phi _{\delta }(u_{n,\sigma }-\mu )^-(t)\varphi ^p(x)=-\int _\Omega \Phi _{\delta }(u_n-\mu )^-(t)\varphi ^p(x) \\{} & {} \quad \ge -\mu |\Omega |||\varphi ||^p_{L^\infty (\Omega )}, \end{aligned}$$

since $\displaystyle \int _\Omega \Phi _{\delta }(u_n-\mu )^-(t)\le \mu |\Omega |$. This proves (4.34).

By (4.34), observing that $\frac{T_\delta (-(u_n-\mu )^-)}{\delta }=0$ on the set $\{(x,t)\in Q_T : u_n(x,t)\ge \mu \}$, equality (4.33) implies

$$\begin{aligned}&{} \frac{1}{\delta }\int \!\!\!\int _{\{\Omega \times (t,T)\} \cap \{\mu -\delta \le u_n\le \mu \}}a(x,t,\nabla u_n)\nabla u_n\varphi ^p(x)\\{}&{} \qquad +\int _t^T\!\!\!\int _{\Omega }\frac{f}{(u_n+\frac{1}{n})^{\gamma }}\cdot \frac{T_\delta ((u_n-\mu )^-)}{\delta }\varphi ^p(x)\\{}&{} \quad \le p \int \!\!\!\int _{\{\Omega \times (t,T)\}\cap \{0\le u_n \le \mu \}} |a(x,t,\nabla u_n)|\varphi ^{p-1}|\nabla \varphi |+\mu |\Omega |||\varphi ||^p_{L^\infty (\Omega )}. \end{aligned}$$

Noting that, in view of (1.2), the first term in the left-hand side is nonnegative, by (1.3) and using Holder’s inequality, we get

$$\begin{aligned}{} & {} {} \int _t^T\!\!\!\int _{\Omega }\frac{f}{(u_n+\frac{1}{n})^{\gamma }}\cdot \frac{T_\delta ((u_n-\mu )^-)}{\delta }\varphi ^p(x)\nonumber \\{}{} & {} {} \quad \le p\Lambda \int \!\!\!\int _{\{\Omega \times (t,T)\}\cap \{0\le u_n \le \mu \}}|\nabla u_n|^{p-1}\varphi ^{p-1}|\nabla \varphi |+\mu |\Omega |||\varphi ||^p_{L^\infty (\Omega )}\nonumber \\{}{} & {} {} \quad \le p\Lambda \left( \int \!\!\!\int _{\{\Omega \times (t,T)\}\cap \{0\le u_n \le \mu \}}|\nabla u_n|^{p}\varphi ^{p}\right) ^{\frac{p-1}{p}} \left( \int _t^T\!\!\!\int _{\Omega } |\nabla \varphi |^p\right) ^{\frac{1}{p}}\nonumber \\{} & {} \quad \qquad +\mu |\Omega |||\varphi ||^p_{L^\infty (\Omega )}. \end{aligned}$$

(4.36)

Moreover, using the test function $-(u_n-\mu )^-\varphi ^p(x)$ in (4.1), where $\varphi$ is a non negative function belonging to $C^\infty _0(\Omega )$, we deduce that

$$\begin{aligned} \int \!\!\!\int _{\{\Omega \times (t,T)\}\cap \{0\le u_n \le \mu \}}|\nabla u_n|^p\varphi ^p(x)\le C_{12} \mu , \end{aligned}$$

(4.37)

where $C_{12}=C_{12}(\Lambda ,\varphi ,C_3)$ is a constant independent of n, $\mu$ and $\delta$.

Thus we can conclude that

$$\begin{aligned} \int _t^T\!\!\!\int _{\Omega }\frac{f}{(u_n+\frac{1}{n})^{\gamma }}\cdot \frac{T_\delta ((u_n-\mu )^-)}{\delta }\varphi ^p(x)\le C_{11}\mu , \end{aligned}$$

(4.38)

with $C_{11}=C_{11}(\Lambda ,\varphi ,C_3)$ a constant independent of n, $\mu$ and $\delta$.

Now we can pass to the limit for $\delta \rightarrow 0$ and n fixed in (4.38), using Lebesgue Theorem since $\frac{T_\delta ((u_n-\mu )^-)}{\delta }$ a.e. converges to 1 on the set $\{(x,t)\in Q_T : u_n(x,t)<\mu \}$. We get

$$\begin{aligned} \iint _{\{\Omega \times (t,T)\}\cap \{0\le u_n<\mu \}}\frac{f}{(u_n+\frac{1}{n})^{\gamma }}\varphi ^p(x)\le C_{11}\mu \end{aligned}$$

and (4.32) holds true. $\square$

Step 5: some convergences.

We prove here some convergences we need below to pass to the limit in the approximating problems (4.1).

Proposition 4.8

Assume (1.2)–(1.6). Then there exists a function u belonging to $L^p(t,T;W_{loc}^{1,p}(\Omega ))\cap L^\infty (t,T;L^{\infty }(\Omega ))$, for every $t\in (0,T)$, such that, up to a subsequence

$$\begin{aligned}{} & {} u_n\rightharpoonup u\quad \text{ weakly } \text{ in } \,L^p(t,T;W^{1,p}(\omega )),\,\,\textrm{for} \, \textrm{every} \,\, \omega \subset \subset \Omega , \end{aligned}$$

(4.39)

$$\begin{aligned}{} & {} u_n\rightarrow u\quad \text{ strongly } \text{ in } \,L^1(t,T;L^1_{loc}(\Omega ))\,, \end{aligned}$$

(4.40)

and

$$\begin{aligned} u_n\rightarrow u\quad \text{ a.e. } \text{ in } \,\Omega _T. \end{aligned}$$

(4.41)

Proof

The convergence (4.39) follows immediately by estimates (4.26) and (4.24).

By estimates (4.26) and (4.24), assumption (1.3) and (4.31) it follows that for every $\omega \subset \subset \Omega$ and $t \in (0,T)$

$$\begin{aligned} \frac{\partial u_n }{\partial t} \quad \text{ is } \text{ bounded } \text{ in } \,\, L^{p'}(t,T; W^{-1,p'}(\omega )) + L^1(\omega \times (t,T))\,. \end{aligned}$$

Hence it is possible to apply Corollary 4 in [34] to get that $u_n\rightarrow u$ in $L^1(\omega \times (t,T)$ and thus (4.40) follows. By (4.40) we deduce that also (4.41) holds true. $\square$

The following result will be essential to handle the singular term.

Proposition 4.9

Assume (1.2)–(1.6). Then, for every $t\in (0,T)$ and $\omega \subset \subset \Omega$ it results

$$\begin{aligned} \frac{f}{(u_n+\frac{1}{n})^{\gamma }}\rightharpoonup {\tilde{f}} \quad \quad \text{ in }\,\,L^1(\omega \times (t,T))\,. \end{aligned}$$

(4.42)

Proof

In order to prove (4.42) we have to show that, for every $\varepsilon >0$ arbitrarily fixed there exists $\delta >0$ such that, for all $A\subset \omega \times (t,T)$ with $|A|<\delta$, it results

$$\begin{aligned} \iint _{A} \frac{f}{(u_n+\frac{1}{n})^{\gamma }} \le \varepsilon \,. \end{aligned}$$

(4.43)

To this aim, we observe that by (4.32) we deduce that for every $t\in (0,T)$, $\mu >0$ and $\omega \subset \subset \Omega$ it results

$$\begin{aligned} \int \!\!\int _{\{\omega \times (t,T)\}\cap \{0\le u_n<\mu \}}\frac{f}{(u_n+\frac{1}{n})^{\gamma }}\le C_{11}\mu \,. \end{aligned}$$

(4.44)

By (4.44) we deduce that for all $A\subset \omega \times (t,T)$ it results

$$\begin{aligned}{} & {} \iint _{A} \frac{f}{(u_n+\frac{1}{n})^{\gamma }} = \iint _{A\cap \{0\le u_n< \mu \}} \frac{f}{(u_n+\frac{1}{n})^{\gamma }} + \iint _{A\cap \{u_n\ge \mu \}} \frac{f}{(u_n+\frac{1}{n})^{\gamma }} \nonumber \\{} & {} \quad \le C_{11}\mu +\iint _{A\cap \{u_n\ge \mu \}} \frac{f}{u_n^{\gamma }}\le C_{11}\mu +\iint _{A} \frac{f}{\mu ^{\gamma }} \,. \end{aligned}$$

(4.45)

Choosing $\mu = \frac{\varepsilon }{2C_{11}}$ and observing that since f is a summable function there exists $\delta >0$ such that, for all $A\subset \omega \times (t,T)$ with $|A|<\delta$, it results

$$\begin{aligned} \iint _{A} \frac{f}{\mu ^{\gamma }} \le \frac{\varepsilon }{2} \, \end{aligned}$$

i.e.

$$\begin{aligned} \iint _{A} f \le \left( \frac{\varepsilon }{2}\right) ^{\gamma +1}C_{11}^{-\gamma }\,, \end{aligned}$$

by (4.45) we get

$$\begin{aligned} \iint _{A} \frac{f}{(u_n+\frac{1}{n})^{\gamma }} \le \varepsilon \,, \end{aligned}$$

for all $A\subset \omega \times (t,T)$ with $|A|<\delta$ and hence (4.43) is proved.

Thanks to Dunford-Pettis’s Theorem, to conclude the proof it remains to show that there exists a positive constant $C_{13}$, independent of n, such that

$$\begin{aligned} \int _t^T\!\!\int _{\omega } \frac{f}{(u_n+\frac{1}{n})^{\gamma }} \le C_{13}\,. \end{aligned}$$

(4.46)

By (4.44) we deduce for every arbitrary fixed $\mu >0$ it results

$$\begin{aligned}{} & {} \int _t^T\!\!\int _{\omega } \frac{f}{(u_n+\frac{1}{n})^{\gamma }} = \int \!\!\int _{\{\omega \times (t,T)\}\cap \{0\le u_n<\mu \}}\frac{f}{(u_n+\frac{1}{n})^{\gamma }} \\{} & {} \quad +\int \!\!\int _{\{\omega \times (t,T)\} \cap \{ u_n\ge \mu \}}\frac{f}{(u_n+\frac{1}{n})^{\gamma }} \le C_{11}\mu + \frac{\Vert f\Vert _{L^1(\Omega _T)}}{\mu ^{\gamma }}\,. \end{aligned}$$

$\square$

Thanks to the previous result, we can prove now the a.e. convergence of the gradients of the sequence $\{u_n\}$.

Proposition 4.10

Assume (1.2)–(1.6). Then it results

$$\begin{aligned} \nabla u_n\rightarrow \nabla u \quad \text {a.e. in}\,\,\Omega _T. \end{aligned}$$

(4.47)

Proof

Let $t\in (0,T)$ and $\omega \subset \subset \Omega$ arbitrarily fixed. Thanks to (4.39) and Proposition 4.9 we can apply Theorem 4.1 of [7] in the set $\omega \times (t,T)$ and we obtain that

$$\begin{aligned} \nabla u_n\rightarrow \nabla u\quad \text { a.e. in}\,\,\omega \times (t,T)\,. \end{aligned}$$

Now the result follows thanks to the arbitrariness of t and $\omega$. $\square$

Step 6: existence of a solution.

We prove here that the limit function u constructed above is a weak solution of (1.1). By construction we have that (2.6) holds true. Moreover, since $u_n\ge 0$ a.e. in $\Omega _T$, by (4.41) it follows that $u\ge 0$ and hence (2.2) is satisfied. Finally, by (4.39) it follows that (2.1) is satisfied while (4.26), (4.24) together with (4.47), (4.41) and (4.9) imply that also (2.3) holds true.

Hence, it remains to prove that u satisfies (2.4) and (2.5).

Notice that, thanks to (4.46) and (4.41), for every $t\in (0,T)$ and $\omega \subset \subset \Omega$ arbitrarily fixed, it is possible to apply the Fatou’s Lemma obtaining

$$\begin{aligned} \int _t^T\!\!\int _{\omega } \frac{f}{u^{\gamma }} \le C_{13}\,. \end{aligned}$$

(4.48)

and hence (2.4) holds true. Notice that (4.48) means that it results

$$\begin{aligned} |\{ u = 0\} \cap \{ f \not = 0\}| = 0\,, \end{aligned}$$

or equivalently $\{ u = 0\} \subseteq \{ f = 0\}$ except for a set with zero measure and hence for any $\phi \in C^{\infty }_c(\Omega _T)$, it results

$$\begin{aligned} \iint _{\Omega _T \cap \{ u \not = 0\}} \frac{f}{u^{\gamma }} \,\phi = \iint _{\Omega _T } \frac{f}{u^{\gamma }} \,\phi \,. \end{aligned}$$

We conclude the proof proving (2.5) .

By (4.39), (4.47) and (1.3) it follows that

$$\begin{aligned} a(x,t,\nabla u_n) \,\, \rightharpoonup \,\, a(x,t,\nabla u)\quad \text{ in } \,\, L^{p'}_{loc}(\Omega _T). \end{aligned}$$

(4.49)

By (4.40), (4.49) and (4.42) it follows that we can pass to the limit in (4.4) obtaining that

$$\begin{aligned} -\iint _{\Omega _T}u\frac{\partial \phi }{\partial t}+\iint _{\Omega _T}a(x,t,\nabla u)\nabla \phi =\iint _{\Omega _T}{\tilde{f}} \,\phi \end{aligned}$$

(4.50)

for any $\phi \in C^{\infty }_c(\Omega _T).$ Hence thanks to (4.50) we can conclude that (2.5) holds true if we prove that for any $\phi \in C^{\infty }_c(\Omega _T)$, it results

$$\begin{aligned} \iint _{\Omega _T}{\tilde{f}} \,\phi = \iint _{\Omega _T \cap \{ u \not = 0\}} \frac{f}{u^{\gamma }} \,\phi \,. \end{aligned}$$

(4.51)

To this aim, we notice that, thanks to (4.41), we can apply the Dominated Convergence Theorem obtaining

$$\begin{aligned} \iint _{\Omega _T}\frac{f}{(u_n+\frac{1}{n})^{\gamma }}\chi _{\{u_n\ge \mu \}}\phi \,\, \rightarrow \,\, \iint _{\Omega _T}\frac{f}{u^{\gamma }}\chi _{\{u \ge \mu \}}\phi \,, \end{aligned}$$

(4.52)

for every $\phi \in C^\infty _c(\Omega _T)$ and $\mu >0$. By the following equality

$$\begin{aligned} \iint _{\Omega _T}\frac{f}{(u_n+\frac{1}{n})^{\gamma }}\phi - \iint _{\Omega _T}\frac{f}{(u_n+\frac{1}{n})^{\gamma }}\chi _{\{u_n\ge \mu \}}\phi = \iint _{\Omega _T}\frac{f}{(u_n+\frac{1}{n})^{\gamma }}\chi _{\{u_n< \mu \}}\phi \end{aligned}$$

thanks to and (4.52), (4.44) and (4.42) we deduce that for every $\phi \in C^\infty _c(\Omega _T)$ and $\mu >0$ it results

$$\begin{aligned} \left| \iint _{\Omega _T} {\tilde{f}}\phi - \iint _{\Omega _T}\frac{f}{u^{\gamma }}\chi _{\{u \ge \mu \}}\phi \right| \le C_{11} \mu \, ||\phi ||_{L^{\infty }(\Omega )}, \end{aligned}$$

where we recall that $C_{11}$ is a constant independent of $\mu$. By the previous inequality and the arbitrariness of $\mu$ we can conclude that (4.51) follows and hence (2.5) is satisfied. Thus, we can conclude that u is a weak solution of (1.1).

Step 7: $L^{\infty }$-estimates satisfied by u.

In this step we conclude the proof of Theorem 2.1 showing that the solution u constructed above satisfies (2.7)–(2.9).

By (4.9) and (4.41) it follows that u satisfies (2.7). By (4.19) and (4.41) we deduce (2.8). Finally (2.9) follows by (4.20) and (4.41). $\square$

4.2 Proof of Theorem 2.2

Proceeding as in the proof of inequalities (4.15) and (4.17) (the only change is to replace $v_n$ with ${\overline{u}}_n$) we deduce the following estimates

$$\begin{aligned}{} & {} ||u_n(t)-{\overline{u}}_n(t)||_{L^{\infty }(\Omega )}\le M_1 \frac{||u_{0n}-{\overline{u}}_{0n}||_{L^1(\Omega )}}{t^{\frac{N}{2}}e^{\sigma t}}\,, \quad \textrm{if } \,\, p = 2 \,, \end{aligned}$$

(4.53)

$$\begin{aligned}{} & {} ||u_n(t)-{\overline{u}}_n(t)||_{L^{\infty }(\Omega )}\le M_3 \frac{\Vert u_{0n}-{\overline{u}}_{0n}\Vert _{L^1(\Omega )}^{\frac{p}{N(p-2)+p}}}{t^{\frac{N}{N(p-2)+p}}}\,, \quad \textrm{if } \,\, p > 2 \,. \end{aligned}$$

(4.54)

Hence, passing to the limit on n and recalling that by assumption u and ${\overline{u}}$ are, the a.e. limit in $\Omega _T$ of (respectively) $u_n$ and ${\overline{u}}_n$, we deduce the assertion. $\square$

4.3 Proof of Theorem 2.3

Proceeding again as in the proof of inequalities (4.15) and (4.17) but with now $v_n$ solutions of (2.16) we deduce the following bounds

$$\begin{aligned}{} & {} ||u_n(t)-v_n(t)||_{L^{\infty }(\Omega )}\le M_1 \frac{||u_{0n}-v_{0n}||_{L^1(\Omega )}}{t^{\frac{N}{2}}e^{\sigma t}}\,, \quad \textrm{if } \,\, p = 2\,, \end{aligned}$$

(4.55)

$$\begin{aligned}{} & {} ||u_n(t)-v_n(t)||_{L^{\infty }(\Omega )}\le M_3 \frac{\Vert u_{0n}-v_{0n}\Vert _{L^1(\Omega )}^{\frac{p}{N(p-2)+p}}}{t^{\frac{N}{N(p-2)+p}}}\,, \quad \textrm{if } \,\, p > 2 \,. \end{aligned}$$

(4.56)

Hence, exactly as in the previous proof, passing to the limit on n and recalling that by assumption u and v are, the a.e. limit in $\Omega _T$ of (respectively) $u_n$ and $v_n$, we deduce the assertions. $\square$

4.4 Proof of Theorem 2.4

Let $u_{0,n} \in C_c^{\infty }(\Omega )$ satisfying (2.11) and let $T_0>0$ arbitrarily fixed. By Theorem 2.1 there exists a weak solution $u \in L^{\infty }_{loc}((0,T_0];L^{\infty }(\Omega ))$ of (1.1) in $\Omega _{T_0}$ obtained as the a.e. limit in $\Omega _{T_0}$ of $u_n \in L^p(0,T_0; W^{1,p}_0(\Omega ))\cap L^{\infty }(\Omega _{T_0}) \cap C([0,T_0];L^2(\Omega ))$ solutions to (2.10). We observe that by Theorem 2.2, if ${\overline{u}}$ is another weak solution to problem (1.1) obtained as the a.e. limit in $\Omega _{T_0}$ of the sequence ${\overline{u}}_n \in L^p(0,T_0; W^{1,p}_0(\Omega ))\cap L^{\infty }(\Omega _{T_0}) \cap C([0,T_0];L^2(\Omega ))$ weak solutions of (2.12), then $u = {\overline{u}}$ a.e. in $\Omega _{T_0}$.

Notice that, since the structure conditions are satisfied for every $T>0$, the approximating solutions $u_n$ are global solutions of (2.10). In particular, $u_n \in L^p(0,2T_0; W^{1,p}_0(\Omega ))\cap L^{\infty }(\Omega _{2T_0}) \cap C([0,2T_0];L^2(\Omega ))$ are solutions of our problem in $\Omega _{2T_0}$. Hence, it is possible to extract a subsequence of $u_n$, that we denote $u^{(1)}_n$, converging a.e. in $\Omega _{2T_0}$ to a weak solution $u^{(1)}$ of our problem in $\Omega _{2T_0}$. We notice that $u = u^{(1)}$ in $\Omega _{T_0}$. Iterating this procedure we get a global solution u which, by construction, satisfies the assertions. $\square$