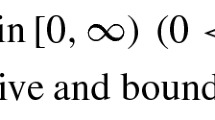Singular solutions of semilinear elliptic equations with supercritical growth on Riemannian manifolds

Abstract

In this paper, we shall discuss singular solutions of semilinear elliptic equations with general supercritical growth on spherically symmetric Riemannian manifolds. More precisely, we shall prove the existence, uniqueness and asymptotic behavior of the singular radial solution, and also show that regular radial solutions converges to the singular solution. In particular, we shall provide these properties on spherically symmetric Riemannian manifolds including the hyperbolic space as well as the sphere.

1 Introduction

We devote this paper to considering singular radial solutions to semilinear elliptic equations on the N-dimensional Riemannian model (M, g),

$$\begin{aligned} -\Delta _{g}u=f(u)\quad \text {in}\quad M\setminus \{0\}, \end{aligned}$$

(1.1)

where $N\ge 3$ and $f\in C^{2}[0,\infty )$. Here, M is a manifold admitting a pole o and whose metric g is denoted, in spherical coordinates around o, by

$$\begin{aligned} ds^{2} = dr^{2} + \psi (r)^{2} d\Theta ^{2},\ r\in (0,R),\ \Theta \in \mathbb {S}^{N-1}, \end{aligned}$$

where $d\Theta ^{2}$ denotes the canonical metric on the unit sphere $\mathbb {S}^{N-1}$, r is the geodesic distance between o and a point $(r, \Theta )$, and $\psi$ is a smooth positive function on (0, R) with some $R\in (0,+\infty ]$. We shall state the precise assumptions on $\psi$ later. Remark that the typical example of M in this paper is the N-dimensional hyperbolic space $\mathbb {H}^{N}$ ($\psi (r)=\sinh r$, $R=+\infty$), and the N-dimensional sphere $\mathbb {S}^{N}$ ($\psi (r)=\sin r$, $R=\pi$). Moreover, $\Delta _{g}$ denotes the Laplace–Beltrami operator on (M, g), and for a scalar function f, $\Delta _{g}$ is expressed by

$$\begin{aligned} \Delta _{g}f(r,\theta _{1},\ldots ,\theta _{N-1})=&\frac{1}{(\psi (r))^{N-1}}\frac{\partial }{\partial r}\left\{ (\psi (r))^{N-1}\frac{\partial f}{\partial r}(r,\theta _{1},\ldots ,\theta _{N-1})\right\} \\&+\frac{1}{(\psi (r))^{2}}\Delta _{\mathbb {S}^{N-1}}f(r,\theta _{1},\ldots ,\theta _{N-1}), \end{aligned}$$

where $\Delta _{\mathbb {S}^{N-1}}$ is the Laplace–Beltrami operator on $\mathbb {S}^{N-1}$.

There is an extensive literature on existence and properties of singular radial solutions of the following semilinear elliptic equations in $\mathbb {R}^{N}$:

$$\begin{aligned} -\Delta u=f(u)\quad \text {in}\quad \mathbb {R}^{N}\setminus \{0\}, \end{aligned}$$

(1.2)

where $N\ge 3$ and $f\in C^{2}[0,\infty )$. Indeed, for the case of $f(u)=u^{p}$ with $p>n/(N-2)$, (1.2) has the exact singular solution $u^{*}(r)=Ar^{-2/(p-1)}$, where

$$\begin{aligned} A=\left\{ \dfrac{2}{p-1}\left( N-2-\dfrac{2}{p-1}\right) \right\} ^{\frac{1}{p-1}}. \end{aligned}$$

If $p>p_{s}=(N+2)/(N-2)$, then the singular solution is unique (Proposition 3.1 in [39]). When $f(u)=e^{u}$, it was shown that (1.2) has the unique singular solution $u^{*}(r)=-2\log r+\log 2(N-2)$ [31]. Further cases of f(u) have also been researched. For $f(u)=u^{p}+g(u)$ with lower order term g, see [16, 17, 21, 25, 30, 33, 36, 37]. The case of $f(u)=e^{u}+g(u)$ was treated in [34, 37]. Moreover, [36] proved the existence and uniqueness of the singular solution for the both cases of $f(u)=u^{p}+o(u^{p})$ $(p>p_{S})$ and $f(u)=e^{u}+o(e^{u})$ as $u\rightarrow \infty$. Thereafter, for more general settings of f(u) (see $(f_{1})-(f_{2})$ below), the existence and uniqueness of the singular solution have been obtained in [37].

On the other hand, the structure of radial solutions to semilinear elliptic equations on Riemannian models has attracted a great interest. In the study, we consider solutions of the ordinary differential equation

$$\begin{aligned} u''(r)+(N-1)\dfrac{\psi '(r)}{\psi (r)}u'(r)+f(u)=0\quad \text {for}\quad r\in (0,R). \end{aligned}$$

(1.3)

Then, we denote by $\{u(r,\alpha )\}_{\alpha >0}$ the family of radial regular solutions of (1.1), i.e., $u(r,\alpha )$ is the solution of (1.3) satisfying $u(0)=\alpha$ and $u'(0)=0$. We shall state known results on the sphere and the hyperbolic space as typical models of Riemannian models. Firstly, we consider the case where $\psi (r)=\sin r$ and $R\le \pi$, i.e., M is the spherical cap or the sphere $\mathbb {S}^{N}$. For $f(u)=u^{p}$ with the Dirichlet condition $u(R)=0$, positive solutions to (1.3) were treated in [5] when $N=3$ and $p=5$. Then, they proved that (1.3) has no positive solutions for $R\in (0,\pi /2]$, and admits a positive solution for $R\in (\pi /2,\pi )$. Thereafter, under the same condition of f(u), [27] researches the properties of positive solutions precisely for $N\ge 3$ and $p>1$. Moreover, in [1], for $f(u)=u^{p}+\lambda u (\lambda \in \mathbb {R})$ with $u(R)=0$, the existence and non-existence of positive solutions to (1.3) were discussed when $N=3$ and $p=5$. Furthermore, for the case of $f(u)=-C_{N,p}u+u^{p}$ with $C_{N,p}=\frac{2}{p-1}\left( N-2-\frac{2}{p-1}\right)$, or $f(u)=2(N-2)(e^{u}-1)$, (1.3) arises in the research of the construction of non-radial solutions to corresponding semilinear elliptic equations in $\mathbb {R}^{N}$ ( [18, 35]). Other results were obtained in [2, 4, 7, 8, 12, 13, 15, 26, 32].

Next we consider the case where $\psi (r)=\sinh r$, $R=+\infty$, i.e., M is the hyperbolic space $\mathbb {H}^{N}$. For $f(u)=u^{p}$, [29] showed that there exists a unique $\bar{\alpha }>0$ such that $u(r,\bar{\alpha })$ is a positive entire solution in $H^{1}(\mathbb {H}^{N})$ for $p<p_{s}(N)$. In [14], they classified the positivity of radial solutions to (1.1) in $\mathbb {H}^{N}$ for $p>1$, and proved that the initial value $\bar{\alpha }$ is a threshold for the positivity of radial solutions for $p<p_{s}(N)$. Moreover, replacing $\mathbb {H}^{N}$ by M with appropriate conditions of $\psi$, [10] proved the similar structure of radial solutions of (1.1) in M as that of (1.1) in $\mathbb {H}^{N}$. In [10], they also studied the structure of radial solutions to (1.1) in M for the stability and separation phenomena. Concerning these properties, the existence of a critical exponent was also obtained in [24]. Furthermore, under the general setting of M, for the case of $f(u)=e^{u}$, the stability and separation phenomena of radial solutions were researched in [9]. Further situations and properties were studied in [3, 6, 9, 11, 22, 23, 38, 40].

Regarding singular solutions to (1.1), [27] obtained the existence and asymptotic behavior of a singular radial solution for the case of $f(u)=u^{p}$ with $p>p_{s}$ on the spherical cap, and showed that regular radial solutions converges to the singular solution. On the other hand, under the general setting of M including the case of $\mathbb {H}^{N}$, in [10], they listed an open problem on singular solutions. Indeed, for $f(u)=u^{p}$, they referred to the existence and the asymptotic behavior of singular solutions. Thereafter, considering the problem, [24] showed the existence and the asymptotic behavior of singular solutions on M including $\mathbb {H}^{N}$ for $N\ge 11$ and $p\ge p_{JL}$ (Theorem 1.3 of [24]), where the exponent $p_{JL}$ is the Joseph-Lundgren exponent, i.e., $p_{JL}=\tfrac{(N-2)^2-4N+8\sqrt{N-1}}{(N-2)(N-10)}$. We note that when $N\le 10$, the existence and the asymptotic behavior of singular solutions were not obtained. Moreover, for any $p>1$, the uniqueness of singular solutions was not investigated even in the cases of $\mathbb {S}^{N}$ and $\mathbb {H}^{N}$.

In this paper, motivated by the above results and the open problem, we shall research the existence, uniqueness and asymptotic behavior of radial singular solutions to (1.1). In order to introduce our main results, we shall firstly state precise assumptions of $\psi (r)$ and f(u). In the following, we shall suppose that for some $R>0$, $\psi$ satisfies

$(H_{1})$:

$\psi \in C^{2}([0,R))$, $\psi (0)=\psi ''(0)=0$, and $\psi '(0)=1$.

In [9, 10, 24], $(H_{1})$ with $R=\infty$ and additional assumptions were also supposed, such as the positivity of $\psi '(r)$ for $r\in (0,\infty )$ and the asymptotic behavior of $\psi '(r)/\psi (r)$ as $r\rightarrow \infty$. In those papers, the hyperbolic space $\mathbb {H}^{N}$ ($\psi (r)=\sinh r$, $R=+\infty$) is the typical model of M, and the assumption $(H_{1})$ was necessary for the geometric settings. In this paper, since we assume only $(H_{1})$, we can treat not only $\mathbb {H}^{N}$ but also the spherical cap or the sphere $\mathbb {S}^{N}$ ($\psi (r)=\sin r$, $R\le \pi$) as examples of M. This is the different situation as that of [9, 10, 24]. Moreover, f(u) satisfies the followings:

$(f_{1})$:

$f\in C^{2}[0,\infty )$, $f(u)>0$, and $F(u)<\infty$ for $u\ge u_{0}$ with some $u_{0}\ge 0$, where

$$\begin{aligned} F(u)=\int ^{\infty }_{u}\frac{ds}{f(s)}. \end{aligned}$$

$(f_{2})$:

There exists a finite limit

$$\begin{aligned} q=\lim _{u\rightarrow \infty }\frac{f'(u)^{2}}{f(u)f''(u)}(<\infty ). \end{aligned}$$

(1.4)

Remark that under $(f_{1})-(f_{2})$, the exponent q satisfies $q\ge 1$ and can be written by

$$\begin{aligned} q=\lim _{u\rightarrow \infty }F(u)f'(u). \end{aligned}$$

(1.5)

More precisely, see Lemma 2.1 below (also see Lemma 2.1 in [37]). Assumptions $(f_{1})-(f_{2})$ were posed in [37]. The exponent q in (1.4) was first considered in [19] to classify stable solutions. Moreover, concerning semilinear parabolic equations with $(f_{1})$ and (1.5), the solvability was also studied in [20]. Representative examples satisfying $(f_{1})-(f_{2})$ are $f(u)=u^{p}$ with $p>1$ $(q=p/(p-1))$ and $f(u)=e^{u}$ $(q=1)$. Further examples were given in [37]. Defining the growth rate of f by $p=\lim _{u\rightarrow \infty }uf'(u)/f(u)$, we observe form L’Hospital’s rule that

$$\begin{aligned} \frac{1}{p}=\lim _{u\rightarrow \infty }\frac{f(u)/f'(u)}{u} =\lim _{u\rightarrow \infty }\left( 1-\frac{f(u)f''(u)}{f'(u)^{2}}\right) =1-\frac{1}{q}. \end{aligned}$$

Hence, $1/p+1/q=1$. Then, we denote by $q_{s}$ the H$\ddot{\text {o}}$lder conjugate of the critical Sobolev exponent $p_{s}=(N+2)/(N-2)$, i.e.,

$$\begin{aligned} q_{s}=\frac{N+2}{4}. \end{aligned}$$

We note that the supercritical case $p>p_{s}$ corresponds to the case $q<q_{s}$. In this setting, we consider solutions of the ordinary differential equation to (1.3). We denote by $\{u(r,\alpha )\}_{\alpha >0}$ the family of radial regular solutions of (1.1), i.e., $u(r,\alpha )$ is the solution of (1.3) satisfying $u(0)=\alpha$ and $u'(0)=0$.

Then, we shall obtain the following main theorem:

Theorem 1.1

Let $\psi$ satisfy $(H_{1})$, and $N\ge 3$. Assume that $(f_{1})-(f_{2})$ with $q\in [1,q_{s})$ hold. Then, there exists a unique singular solution $u^{*}(r)$ of (1.3) for $0<r\le r_{0}$ with some $r_{0}\in (0,R]$, and the regular solution $u(r,\alpha )$ satisfies

$$\begin{aligned} u(r,\alpha )\rightarrow u^{*}(r)\quad \text {in}\quad C^{2}_{\text {loc}}(0,r_{0}]\quad \text {as}\quad \alpha \rightarrow \infty . \end{aligned}$$

(1.6)

Furthermore, the singular solution $u^{*}$ satisfies

$$\begin{aligned} u^{*}(r)=F^{-1}\left[ \frac{\psi (r)^{2}}{2N-4q}(1+o(1))\right] \quad \text {as}\quad r\rightarrow 0. \end{aligned}$$

(1.7)

In [10], they posed an open problem on the existence and the asymptotic behavior of singular solutions to (1.1) with $f(u)=u^{p}(p>1)$. When $p>p_{s}$, Theorem 1.1 gives an affirmative answer to that problem. Moreover, [24] showed the existence and the asymptotic behavior of singular solutions to (1.3) with $f(u)=u^{p}$, $p\ge p_{JL}$ and $N\ge 11$. Since $p_{s}<p_{JL}$ for $N\ge 11$, Theorem 1.1 extends the existence result to the case of $p>p_{s}$ with $N\ge 3$. Furthermore, when $\psi (r)=\sin r$ and $R<\pi$, in [27], the existence and asymptotic behavior of a singular solution to (1.3) for $f(u)=u^{p}$ with $p>p_{s}$ were proved. By Theorem 1.1, the uniqueness of the singular solution is also obtained.

In order to prove Theorem 1.1, we shall apply the methods in [36, 37]. In [36, 37], they changed the solution of (1.3) with $\psi (r)=r$ into a function. Furthermore, applying Pohozaev’s identity and comparison arguments, they obtained some a priori estimates of solutions near $r=0$ and showed the existence and properties of the singular solution. In this paper, we shall transform the solution to (1.3) under $(H_{1})$, construct modified Pohozaev type identity, and derive corresponding estimates of solutions.

This paper is organized as follows. In Sect. 2, we prove some preliminary results. In Sect. 3, we study the asymptotic behavior of a function, which was transformed from the solution to (1.3). We devote Sect. 4 to showing the uniqueness of the singular solution. In Sect. 5, we shall obtain the estimate of solutions. Then, finally, in Sect. 6, we give the proof of Theorem 1.1.

2 Preliminaries

First, we introduce the following lemmas.

Lemma 2.1

(Lemma 2.1 in [37]) Let $(f_{1})-(f_{2})$ hold. Then, $f'(u)\rightarrow \infty$ as $u\rightarrow \infty$. Furthermore, the exponent q in (1.4) satisfies $q\ge 1$ and q is also given by (1.5).

Lemma 2.2

(Lemma 2.4 in [37]) For any $\delta >0$, there exists a constant $C>0$ such that

$$\begin{aligned} f(u)\ge Cu^{\frac{q+\delta }{{q+\delta -1}}} \end{aligned}$$

for sufficiently large u.

In this paper, we assume that $(f_{1})-(f_{2})$ with $q\in [1,q_{s})$ hold. Thus, from Lemma 2.1, we may assume that

$$\begin{aligned} f'(u)>0\quad \text {for}\quad u\ge u_{0}, \end{aligned}$$

(2.1)

by replacing $u_{0}$ in $(f_{1})$.

From $(H_{1})$, there exists $R_{0}\in (0,R)$ such that

$$\begin{aligned} \psi '(r)>0\quad \text {for}\quad r\in [0,R_{0}). \end{aligned}$$

(2.2)

Hence, $\psi (r)$ is strictly increasing for $r\in [0,R_{0})$. Then, for a solution u of (1.3), we shall define a function $x=x(t)$ in $t\in (T_{0},\infty )$ by

$$\begin{aligned} \frac{F(u(r))}{\psi (r)^{2}}=\frac{e^{-x(t)}}{2N-4q},\quad t=-\log \psi (r), \end{aligned}$$

(2.3)

where $T_{0}=-\log \psi (R_{0})$. Since $N>2$, we shall remark that $2N-4q>0$ for $q\in [1,q_{s})$. Concerning x, the following holds:

Lemma 2.3

Let u be a solution to (1.3), and define x(t) by (2.3) with $q\in [1,q_{s})$. Then, for $t\in (T_{0},\infty )$, x(t) satisfies

$$\begin{aligned} x''(t)&-ax'(t)+b(Pe^{x(t)}-1)+(q-1)(x'(t))^{2}+(f'(u)F(u)-q)(x'(t)+2)^{2}\nonumber \\&-Q(x'(t)+2)=0, \end{aligned}$$

(2.4)

where

$$\begin{aligned} a=N+2-4q>0,\quad b=2N-4q>0, \end{aligned}$$

(2.5)

and

$$\begin{aligned} P=P(t)=\frac{1}{(\psi '(r))^{2}},\quad Q=Q(t)=\frac{\psi (r)\psi ''(r)}{(\psi '(r))^{2}}. \end{aligned}$$

Furthermore, in the case $q>1$, put $z(t)=e^{(q-1)x(t)}$. Then, for $t\in (T_{0},\infty )$, z(t) satisfies

$$\begin{aligned} \frac{F(u(r))}{\psi (r)^{2}}=\frac{z(t)^{-1/(q-1)}}{2N-4q}, \end{aligned}$$

and

$$\begin{aligned} z''&-az'+(q-1)b(Pz^{p}-z)+(q-1)(f'(u)F(u)-q)\left( \frac{z'}{(q-1)z}+2\right) ^{2}z\nonumber \\&-(q-1)Q\left( \frac{z'}{(q-1)z}+2\right) z=0, \end{aligned}$$

(2.6)

where $p=q/(q-1)$.

Proof

By (2.3), we have

$$\begin{aligned} F(u(r))=\frac{e^{-x(t)-2t}}{2N-4q}. \end{aligned}$$

(2.7)

Differentiating the above with respect to r, we derive

$$\begin{aligned} -\frac{u'(r)}{f(u)}=\psi '(r)\frac{x'(t)+2}{2N-4q}e^{-x(t)-t}. \end{aligned}$$

(2.8)

Differentiating again with respect to r, we have

$$\begin{aligned}&-\frac{u''(r)}{f(u)}+\frac{f'(u)}{f(u)^{2}}u'(r)^{2}\nonumber \\&\quad =\frac{e^{-x(t)-t}}{2N-4q}\left\{ \psi ''(r)(x'(t)+2)-\frac{\psi '(r)^{2}}{\psi (r)}(x''(t)-3x'(t)-2-x'(t)^{2})\right\} . \end{aligned}$$

(2.9)

From (2.7)–(2.8), it follows that

$$\begin{aligned} \frac{f'(u)}{f(u)^{2}}u'(r)^{2}&=f'(u)\frac{u'(r)^{2}}{f(u)^{2}}=f'(u)\psi '(r)^{2}\frac{e^{-x(t)}}{2N-4q}F(u)(x'(t)+2)^{2}. \end{aligned}$$

(2.10)

Then, by (2.9)–(2.10), we derive

$$\begin{aligned} \frac{u''(r)}{f(u)}=\frac{e^{-x(t)}}{2N-4q}\{&f'(u)\psi '(r)^{2}F(u)(x'(t)+2)^{2}-\psi (r)\psi ''(r)(x'(t)+2)\nonumber \\&+\psi '(r)^{2}(x''(t)-3x'(t)-2-x'(t)^{2})\}. \end{aligned}$$

(2.11)

Moreover, applying (2.8), we have

$$\begin{aligned} \frac{\psi '(r)}{\psi (r)}\frac{u'(r)}{f(u)}=-\psi '(r)^{2}\frac{x'(t)+2}{2N-4q}e^{-x(t)}. \end{aligned}$$

(2.12)

Then, we observe from (2.11)–(2.12) that

$$\begin{aligned} 0&=\frac{(2N-4q)e^{x(t)}}{\psi '(r)^{2}f(u)}\left( u''(r)+(N-1)\frac{\psi '(r)}{\psi (r)}u'(r)+f(u)\right) \\&=\frac{(2N-4q)e^{x(t)}}{\psi '(r)^{2}}\left( \frac{u''(r)}{f(u)}+(N-1)\frac{\psi '(r)}{\psi (r)}\frac{u'(r)}{f(u)}+1\right) \\&=f'(u)F(u)(x'(t)+2)^{2}-Q(t)(x'(t)+2)+(x''(t)-3x'(t)-2-x'(t)^{2})\\&\qquad -x'(t)(N-1)-2(N-1)+(2N-4q)P(t)e^{x(t)}. \end{aligned}$$

Thus, we obtain (2.4). Furthermore, for $q>1$, put $z(t)=e^{(q-1)x(t)}$. Then, by (2.3),

$$\begin{aligned} \frac{F(u(r))}{\psi (r)^{2}}=\frac{z^{-\frac{1}{q-1}}}{2N-4q}. \end{aligned}$$

Since $z(t)=e^{(q-1)x(t)}$, it follows from (2.4) that

$$\begin{aligned}&\{(q-1)e^{(q-1)x(t)}\}^{-1}(z''(t)-az'(t))=(q-1)x'(t)^{2}+x''(t)-ax'(t)\\&\quad =-b(P(t)e^{x(t)}-1)-(f'(u)F(u)-q)(x'(t)+2)^{2}+Q(t)(x'(t)+2). \end{aligned}$$

This implies that

$$\begin{aligned} z''(t)-az'(t)&=-b(q-1)(Pz^{\frac{q}{q-1}}-z)+(q-1)Q\left( \frac{1}{q-1}\frac{z'(t)}{z(t)}+2\right) z(t)\\&\qquad -(q-1)(f'(u)F(u)-q)\left( \frac{1}{q-1}\frac{z'(t)}{z(t)}+2\right) ^{2}z(t). \end{aligned}$$

Setting $p=q/(q-1)$, we obtain (2.6). $\square$

Lemma 2.4

Let u be a positive solution to (1.3). Assume that there exists $r_{0}\in (0,R_{0}]$ such that $u(r)\ge u_{0}$ for $0<r\le r_{0}$. Then, the followings hold :

• (i) $u'(r)\le 0$ for $0<r\le r_{0}$.

• (ii) $F(u(r))\ge \dfrac{\psi (r)^{2}}{2NC_{0}^{2}}$ for $0<r\le r_{0}$, where $C_{0}=\displaystyle \max _{r\in [0,r_{0}]}\psi '(r)\ge 1$.

Proof

(i) Assume to the contrary that there exists $r_{1}\in (0,r_{0}]$ such that $u'(r_{1})>0$. Since

$$\begin{aligned} (\psi (r)^{N-1}u'(r))'=-\psi (r)^{N-1}f(u)\le 0\quad \text {for}\quad 0<r\le r_{0}, \end{aligned}$$

the function $\psi (r)^{N-1}u'(r)$ is nonincreasing for $0<r\le r_{0}$. Then, it follows that

$$\begin{aligned} \psi (r)^{N-1}u'(r)\ge \psi (r_{1})^{N-1}u'(r_{1})>0\quad \text {for}\quad 0<r\le r_{1}. \end{aligned}$$

This implies that

$$\begin{aligned} u'(r)\ge C\psi (r)^{-(N-1)}\quad \text {for}\quad 0<r\le r_{1}, \end{aligned}$$

where $C=\psi (r_{1})^{N-1}u'(r_{1})>0$. Integrating the above on $(r,r_{1}]$, we obtain

$$\begin{aligned} u(r_{1})-u(r)\ge C\int ^{r_{1}}_{r}\psi (s)^{-(N-1)}ds. \end{aligned}$$

(2.13)

Applying $(H_{1})$, we see that $\displaystyle \lim _{r\rightarrow +0}\psi (r)/r=\psi '(0)=1$. Thus, there exists $\tilde{C}\ge 1$ such that $\psi (r)\le \tilde{C} r$ for $r\in (0,r_{1}]$. It follows from (2.13) that

$$\begin{aligned} u(r_{1})-u(r)&\ge C\tilde{C}^{-(N-1)}\int ^{r_{1}}_{r}\!\!\!s^{-(N-1)}ds =-\frac{C\tilde{C}^{-(N-1)}}{N-2}(r_{1}^{-(N-2)}-r^{-(N-2)})\\&\rightarrow \infty \quad \text {as}\quad r\rightarrow 0. \end{aligned}$$

Thus, letting $r\rightarrow 0$, we obtain $u(r)\rightarrow -\infty$. This contradicts $u\ge u_{0}$, and we see that $u'(r)\le 0$ for $0<r\le r_{0}$.

(ii) For $\rho \in (0,r)$, integrating $-(\psi (r)^{N-1}u'(r))'=\psi (r)^{N-1}f(u)$ on $[\rho ,r]$, we observe from (i) that

$$\begin{aligned} -\psi (r)^{N-1}u'(r)&=-\psi (\rho )^{N-1}u'(\rho )+\int ^{r}_{\rho }\psi (s)^{N-1}f(u(s))ds\\&\ge \int ^{r}_{\rho }\psi (s)^{N-1}f(u(s))ds. \end{aligned}$$

We recall from (2.1) that f(u) is strictly increasing for $u\ge u_{0}$. Thus, letting $\rho \rightarrow 0$ and applying (i), we have

$$\begin{aligned} -\psi (r)^{N-1}u'(r)\ge \int ^{r}_{0}\psi (s)^{N-1}f(u(s))ds\ge f(u(r))\int ^{r}_{0}\psi (s)^{N-1}ds. \end{aligned}$$

Then, it follows that

$$\begin{aligned} \frac{d}{dr}F(u(r))=-\frac{u'(r)}{f(u)}\ge \frac{1}{\psi (r)^{N-1}}\int ^{r}_{0}\psi (s)^{N-1}ds. \end{aligned}$$

Integrating the above on $[\rho ,r]$ with $0<\rho <r$, we have

$$\begin{aligned} F(u(r))&\ge F(u(\rho ))+\int ^{r}_{\rho }\frac{1}{\psi (z)^{N-1}}\int ^{z}_{0}\psi (s)^{N-1}dsdz\\&\ge \int ^{r}_{\rho }\frac{1}{\psi (z)^{N-1}}\int ^{z}_{0}\psi (s)^{N-1}dsdz. \end{aligned}$$

Setting $C_{0}=\displaystyle \max _{r\in [0,r_{0}]}\psi '(r)$, we observe from $(H_{1})$ that $C_{0}\ge 1$. Then, we have

$$\begin{aligned} F(u(r))&\ge \frac{1}{C_{0}}\int ^{r}_{\rho }\frac{1}{\psi (z)^{N-1}}\int ^{z}_{0}\psi (s)^{N-1}\psi '(s)dsdz =\frac{1}{NC_{0}}\int ^{r}_{\rho }\psi (z)dz\\&\ge \frac{1}{NC_{0}^{2}}\int ^{r}_{\rho }\psi (z)\psi '(z)dz =\frac{1}{2NC_{0}^{2}}(\psi (r)^{2}-\psi (\rho )^{2}). \end{aligned}$$

Letting $\rho \rightarrow 0$, we have $F(u(r))\ge \psi (r)^{2}/2NC_{0}^{2}$. $\square$

Lemma 2.5

Let u be a singular solution of (1.3) for $0<r\le r_{0}$. Then,

$$\begin{aligned} -\psi (r)^{N-1}u'(r)=\int ^{r}_{0}\psi (s)^{N-1}f(u(s))ds\quad \text {for}\quad 0<r\le r_{0}. \end{aligned}$$

(2.14)

Proof

Since $q<q_{s}=(N+2)/4$ and $N\ge 3$, we have $-N+2q<-N+2q_{s}<0$. Then, there exists $\delta >0$ such that

$$\begin{aligned} -N+2q+2\delta <0. \end{aligned}$$

(2.15)

Firstly, we claim that

$$\begin{aligned} f(u(r))=\mathcal {O}(\psi (r)^{-2q-2\delta })\quad \text {as}\quad r\rightarrow 0. \end{aligned}$$

(2.16)

Indeed, from (1.5), we find $u_{1}\ge u_{0}$ such that $F(u)f'(u)\le q+\delta$ for $u\ge u_{1}$. Then, we have

$$\begin{aligned} \frac{d}{du}(f(u)F(u)^{q+\delta })=F(u)^{q+\delta -1}\left\{ f'(u)F(u)-(q+\delta )\right\} \le 0\quad \text {for}\quad u\ge u_{1}. \end{aligned}$$

Since $f(u)F(u)^{q+\delta }$ is nonincreasing for $u\ge u_{1}$, we obtain

$$\begin{aligned} f(u)F(u)^{q+\delta }\le f(u_{1})F(u_{1})^{q+\delta }\quad \text {for}\quad u\ge u_{1}. \end{aligned}$$

Thus, it follows from Lemma 2.4 (ii) that for sufficiently small $r>0$,

$$\begin{aligned} f(u)\le f(u_{1})F(u_{1})^{q+\delta }F(u)^{-(q+\delta )}\le Cf(u_{1})F(u_{1})^{q+\delta }\psi (r)^{-2q-2\delta }. \end{aligned}$$

This implies that (2.16) holds. Moreover, it follows from Lemma 2.4 (i) that $-\psi (r)^{N-1}u'(r)\ge 0$ for $0<r\le r_{0}$. Then, we shall prove that

$$\begin{aligned} \liminf _{r\rightarrow 0}(-\psi (r)^{N-1}u'(r))=0. \end{aligned}$$

(2.17)

Assume to the contrary that $\displaystyle \liminf _{r\rightarrow 0}(-\psi (r)^{N-1}u'(r))>0$. Then, there exist $L>0$ and $r_{1}\le r_{0}$ such that $-\psi (r)^{N-1}u'(r)\ge L$ for $0<r\le r_{1}$, and thus,

$$\begin{aligned} u'(r)\le -L\psi (r)^{-(N-1)}\quad \text {for}\quad 0<r\le r_{1}. \end{aligned}$$

Setting $C_{0}=\displaystyle \max _{r\in [0,r_{0}]}\psi '(r)$ and integrating the above over $[r,r_{1}]$, we have

$$\begin{aligned} u(r_{1})-u(r)&\le -L\int ^{r_{1}}_{r}\frac{ds}{\psi (s)^{N-1}}\le -\frac{L}{C_{0}}\int ^{r_{1}}_{r}\frac{\psi '(s)}{\psi (s)^{N-1}}ds\\&=\frac{L}{C_{0}(N-2)}\left( \frac{1}{\psi (r_{1})^{N-2}}-\frac{1}{\psi (r)^{N-2}}\right) . \end{aligned}$$

Hence, there exists $C>0$ such that $u(r)\ge C\psi (r)^{-(N-2)}$ for sufficiently small $r>0$. Therefore, we observe from Lemma 2.2 that

$$\begin{aligned} f(u)\ge Cu(r)^{\frac{q+\delta }{{q+\delta -1}}}\ge C\psi (r)^{-(N-2)\frac{q+\delta }{{q+\delta -1}}} \end{aligned}$$

for sufficiently small $r>0$. Applying (2.16), we see that

$$\begin{aligned} 2q+2\delta -(N-2)\frac{q+\delta }{{q+\delta -1}}\ge 0. \end{aligned}$$

Then, we derive $2q+2\delta -N\ge 0$, and this contradicts (2.15). Thus, we obtain (2.17). Hence, there exists $r_{n}\rightarrow 0$ such that $-\psi (r_{n})^{N-1}u'(r_{n})\rightarrow 0$ as $n\rightarrow \infty$. From (1.3), we have

$$\begin{aligned} -(\psi (r)^{N-1}u'(r))'=\psi (r)^{N-1}f(u(r)). \end{aligned}$$

Integrating the above on $[r_{n},r]$, we derive

$$\begin{aligned} -\psi (r)^{N-1}u'(r)+\psi (r_{n})^{N-1}u'(r_{n})=\int ^{r}_{r_{n}}\psi (s)^{N-1}f(u(s))ds. \end{aligned}$$

Letting $n\rightarrow \infty$, we obtain (2.14). $\square$

Lemma 2.6

Let u be a singular solution of (1.3). Then,

$$\begin{aligned} \limsup _{r\rightarrow 0}\frac{\psi (r)^{2}}{F(u(r))}>0. \end{aligned}$$

Proof

Assume to the contrary that

$$\begin{aligned} \lim _{r\rightarrow 0}\frac{\psi (r)^{2}}{F(u(r))}=0. \end{aligned}$$

(2.18)

Take $q_{0}\in (q,q_{s})$, and define $z_{0}(t)$ by

$$\begin{aligned} \frac{F(u(r))}{\psi (r)^{2}}=\frac{z_{0}(t)^{-\frac{1}{q_{0}-1}}}{2N-4q_{0}}. \end{aligned}$$

(2.19)

Replacing q and z(t) with $q_{0}$ and $z_{0}(t)$ in Lemma 2.3, respectively, we obtain the following equation:

$$\begin{aligned} z_{0}''&-a_{0}z_{0}'+(q_{0}-1)b_{0}(Pz_{0}^{p}-z_{0})-(q_{0}-1)Q\left( \frac{z_{0}'}{(q-1)z_{0}}+2\right) z_{0}\nonumber \\&\qquad +(q_{0}-1)(f'(u)F(u)-q_{0})\left( \frac{z_{0}'}{(q_{0}-1)z_{0}}+2\right) ^{2}z_{0}=0, \end{aligned}$$

(2.20)

where $a_{0}=N+2-4q_{0}>0$, $b_{0}=2N-4q_{0}>0$, and $p_{0}=q_{0}/(q_{0}-1)>1$. Using (2.18)–(2.19), we have

$$\begin{aligned} z_{0}(t)=\left\{ \frac{1}{b_{0}}\frac{\psi (r)^{2}}{F(u(r))}\right\} ^{q_{0}-1}\rightarrow 0\quad \text {as}\quad t\rightarrow \infty . \end{aligned}$$

Moreover, since we observe from $(H_{1})$ that $P\rightarrow 1$ and $Q\rightarrow 0$ as $t\rightarrow \infty$, it follows from (1.5) that

$$\begin{aligned} -\frac{Q^{2}}{4(f'(u)F(u)-q_{0})}+b_{0}(Pz_{0}^{p-1}-1)\rightarrow -b_{0}<0\quad \text {as}\quad t\rightarrow \infty . \end{aligned}$$

Therefore, by $q_{0}>q$ and $(H_{1})$, there exists $t_{1}\in (T_{0},\infty )$ such that

$$\begin{aligned} 0<z_{0}<1,\ -\frac{Q^{2}}{4(f'(u)F(u)-q_{0})}+b_{0}(Pz_{0}^{p-1}-1)<0\quad \text {for}\quad t\ge t_{1}, \end{aligned}$$

(2.21)

and

$$\begin{aligned} f'(u)F(u)\le q_{0},\ u(r)\ge u_{0},\ \psi '(r)\ge \frac{1}{2}\quad \text {for}\quad 0<r\le r_{1}, \end{aligned}$$

(2.22)

where $r_{1}=e^{-t_{1}}$. Applying (2.20)–(2.22), we see that

$$\begin{aligned}&z_{0}''-a_{0}z_{0}'\\&\quad =-(q_{0}-1)z_{0}\left\{ (f'(u)F(u)-q_{0})\left( \frac{z_{0}'}{(q_{0}-1)z_{0}}+2-\frac{Q}{2(f'(u)F(u)-q_{0})}\right) ^{2}\right. \\&\qquad \left. -\frac{Q^{2}}{4(f'(u)F(u)-q_{0})}+b_{0}(Pz_{0}^{p-1}-1)\right\} >0\quad \text {for}\quad t\ge t_{1}. \end{aligned}$$

Hence, we derive $(e^{-a_{0}t}z_{0}')'>0$ for $t\ge t_{1}$, i.e., $e^{-a_{0}t}z_{0}'$ is increasing for $t\ge t_{1}$. Then, we shall prove that

$$\begin{aligned} z_{0}'(t)\le 0\quad \text {for}\quad t\ge t_{1}. \end{aligned}$$

(2.23)

Assume to the contrary that for some $t_{2}\ge t_{1}$, $z_{0}'(t_{2})>0$ holds. Since we have $e^{-a_{0}t}z_{0}'(t)\ge e^{-a_{0}t_{2}}z_{0}'(t_{2})$ for $t\ge t_{2}$, we derive

$$\begin{aligned} z_{0}'(t)\ge e^{a_{0}(t-t_{2})}z_{0}'(t_{2})\quad \text {for}\quad t\ge t_{2}. \end{aligned}$$

It follows from $z_{0}'(t_{2})>0$ that $z_{0}'(t)\rightarrow \infty$ as $t\rightarrow \infty$. Then, we see that $z_{0}(t)=\infty$ as $t\rightarrow \infty$, and this contradicts (2.21). Therefore, (2.23) holds. Thus, making use of (2.19), (2.21), and (2.23), we have for $0<r\le r_{1}$,

$$\begin{aligned} \frac{d}{dr}\left( \frac{\psi (r)^{2}}{F(u)}\right) =-\frac{2N-4q_{0}}{q_{0}-1} \psi '(r)e^{t}z_{0}(t)^{-\frac{q_{0}-2}{q_{0}-1}}z_{0}'(t)\ge 0. \end{aligned}$$

(2.24)

Moreover, it follows from (2.22) and Lemma 2.4 (i) that for $0<r\le r_{1}$,

$$\begin{aligned} \frac{d}{dr}\left( F(u)^{q_{0}}f(u(r))\right)&=-q_{0}F(u)^{q_{0}-1}u'(r)+F(u)^{q_{0}}f'(u(r))u'(r)\\&=F(u)^{q_{0}-1}\{(-q_{0})+F(u)f'(u(r))\}u'(r)\ge 0.\nonumber \end{aligned}$$

(2.25)

On the other hand, take $\varepsilon >0$ satisfying $4\varepsilon q_{0}<1$. From (2.18), we find $r_{2}\le r_{1}$ such that

$$\begin{aligned} \frac{\psi (r)^{2}f(u)}{F(u)f(u)}=\frac{\psi (r)^{2}}{F(u)}\le (N-2q_{0})\varepsilon \quad \text {for}\quad 0<r\le r_{2}. \end{aligned}$$

Hence, we obtain

$$\begin{aligned} \psi (r)^{2}f(u)\le (N-2q_{0})\varepsilon F(u)f(u)\quad \text {for}\quad 0<r\le r_{2}. \end{aligned}$$

(2.26)

Using Lemma 2.5, (2.22), (2.24)–(2.26), we have

$$\begin{aligned}&-\psi (r)^{N-1}u'(r)=\int ^{r}_{0}\psi (s)^{N-1}f(u)ds\le (N-2q_{0})\varepsilon \int ^{r}_{0} F(u)f(u)\psi (s)^{N-3}ds\\&\quad =2(N-2q_{0})\varepsilon \int ^{r}_{0} \left( \frac{\psi (s)^{2}}{F(u(s))}\right) ^{q_{0}-1}F(u(s))^{q_{0}}f(u(s))\psi (s)^{N-2q_{0}-1}\frac{1}{2}ds\\&\quad \le 2(N-2q_{0})\varepsilon \left( \frac{\psi (r)^{2}}{F(u(r))}\right) ^{q_{0}-1}F(u(r))^{q_{0}}f(u(r)) \int ^{r}_{0}\psi (s)^{N-2q_{0}-1}\psi '(s)ds\\&\quad =2\varepsilon \psi (r)^{N-2}F(u(r))f(u(r))\quad \text {for}\quad 0<r\le r_{2}. \end{aligned}$$

Hence, we derive $\psi (r)u'(r)+2\varepsilon F(u(r))f(u(r))\ge 0$ for $0<r\le r_{2}$. Then, it follows from (2.22) that for $0<r\le r_{2}$,

$$\begin{aligned} \frac{d}{dr}\left( \frac{\psi (r)^{4\varepsilon }}{F(u(r))}\right)&=\frac{\psi (r)^{4\varepsilon -1}}{F(u(r))^{2}f(u(r))}(4\varepsilon \psi '(r)F(u(r))f(u(r))+\psi (r)u'(r))\\&\ge \frac{\psi (r)^{4\varepsilon -1}}{F(u(r))^{2}f(u(r))}(2\varepsilon F(u(r))f(u(r))+\psi (r)u'(r))\ge 0. \end{aligned}$$

Thus, $\psi (r)^{4\varepsilon }/F(u(r))$ is non-decreasing and bounded for $0<r\le r_{2}$. Moreover, using (2.25), we see that $F(u)^{q_{0}}f(u)$ is also bounded for $0<r\le r_{2}$. Thus, we observe from Lemma 2.5 and (2.22) that for $0<r\le r_{2}$,

$$\begin{aligned} -\psi (r)^{N-1}u'(r)&=\int ^{r}_{0}F(u(s))^{q_{0}}f(u(s)) \left( \frac{\psi ^{4\varepsilon }(s)}{F(u(s))}\right) ^{q_{0}}\psi (s)^{N-1-4\varepsilon q_{0}}2\frac{1}{2}ds\\&\le 2C\int ^{r}_{0}\psi (s)^{N-1-4\varepsilon q_{0}}\psi '(s)ds=\frac{2C\psi (r)^{N-4\varepsilon q_{0}}}{N-4\varepsilon q_{0}}. \end{aligned}$$

By Lemma 2.4 (i), this implies that $u'(r)=\mathcal {O}(\psi (r)^{1-4\varepsilon q_{0}})$ as $r\rightarrow 0$. Since $4\varepsilon q_{0}<1$, we have $\displaystyle \lim _{r\rightarrow 0}u'(r)=0$. Hence, we obtain $\displaystyle \lim _{r\rightarrow 0}u(r)<\infty$. This contradicts the assumption that u is a singular solution of (1.3). $\square$

3 Asymptotic behavior

In this section, we assume that u is a singular solution of (1.3) and $u(r)\ge u_{0}$ for $0<r\le r_{0}$. Furthermore, we define x(t) by (2.3). Then, we shall prove the following proposition:

Proposition 3.1

$\displaystyle \lim _{t\rightarrow \infty }x(t)=0$, and $\displaystyle \lim _{t\rightarrow \infty }x'(t)=0$.

To the aim of the proof of Proposition 3.1, we prepare the next lemma.

Lemma 3.2

Let u be a positive solution to (1.3). Assume that there exists $r_{0}\in (0,R_{0})$ such that $u(r)\ge u_{0}$ for $0<r\le r_{0}$. Then, the followings hold :

• (i) $x(t)\le \log \dfrac{NC_{0}^{2}}{N-2q}$ for $t\ge t_{0}$, where $C_{0}=\displaystyle \max _{r\in [0,r_{0}]}\psi '(r)\ge 1$, and $t_{0}=-\log r_{0}$.

• (ii) $x'(t)\ge -2$ for $t\ge t_{0}$.

Proof

(i) It follows from (2.3) and Lemma 2.4 (ii) that

$$\begin{aligned} \frac{\psi (r)^{2}e^{-x(t)}}{2N-4q}=F(u(r))\ge \dfrac{\psi (r)^{2}}{2NC_{0}^{2}}\quad \text {for}\quad 0<r\le r_{0}. \end{aligned}$$

Thus, we have

$$\begin{aligned} e^{x(t)}\le \frac{NC_{0}^{2}}{N-2q}\quad \text {for}\quad t\ge t_{0}. \end{aligned}$$

This implies that $x(t)\le \log (NC_{0}^{2}/N-2q)$ for $t\ge t_{0}$.

(ii) We observe from (2.7) that $x(t)=-2t-\log (2N-4q)-\log F(u(r))$. Then, we obtain

$$\begin{aligned} x'(t)=-2+\frac{\psi (r)}{\psi '(r)}\frac{1}{F(u(r))}\left( -\frac{u'(r)}{f(u(r))}\right) . \end{aligned}$$

Applying (2.2) and Lemma 2.4 (i), we obtain $x'(t)\ge -2$ for $t\ge t_{0}$. $\square$

In order to prove Proposition 3.1, we consider the following two cases:

• (i) $x'(t)$ is nonoscillatory at $t=\infty$, that is, $x'(t)\ge 0$ or $x'(t)\le 0$ for sufficiently large t.

• (ii) $x'(t)$ is oscillatory at $t=\infty$, that is, the sign of $x'(t)$ changes infinitely many times as $t\rightarrow \infty$.

To begin with, we treat the case (i).

Lemma 3.3

Assume that $x'(t)$ is nonoscillatory at $t=\infty$. Then, $x(t)\rightarrow 0$ as $t\rightarrow \infty$.

Proof

Since u is a singular solution of (1.3), it follows from Lemma 2.6 and (2.3) that

$$\begin{aligned} \limsup _{t\rightarrow \infty }e^{x(t)}=\limsup _{r\rightarrow 0}\frac{\psi (r)^{2}}{(2N-4q)F(u(r))}>0. \end{aligned}$$

Hence, we obtain $\displaystyle \limsup _{t\rightarrow \infty }x(t)>-\infty$. When $x'(t)$ is nonoscillatory at $t=\infty$, x(t) is monotone increasing or decreasing for sufficiently large t. Thus, we have $\displaystyle \lim _{t\rightarrow \infty }x(t)>-\infty$. Moreover, it follows from Lemma 3.2 (i) that x(t) is bounded for $t\ge t_{0}$, and there exists $c\in \mathbb {R}$ such that

$$\begin{aligned} x(t)\rightarrow c\quad \text {as}\quad t\rightarrow \infty . \end{aligned}$$

(3.1)

We shall prove that $c=0$. Assume to the contrary that $c\not =0$. Then, we claim that

$$\begin{aligned} \lim _{t\rightarrow \infty }x'(t)=0. \end{aligned}$$

(3.2)

Indeed, first we consider the case where $x'(t)\ge 0$ for all t large enough. Since x(t) is bounded for $t\ge t_{0}$, we derive

$$\begin{aligned} \liminf _{t\rightarrow \infty }x'(t)=0. \end{aligned}$$

(3.3)

Assume to the contrary that $\displaystyle \limsup _{t\rightarrow \infty }x'(t)>0$. Then, let $t_{n}\rightarrow \infty$ be a sequence of local minimum points of $x'(t)$. It follows from (3.3) that

$$\begin{aligned} x''(t_{n})=0,\quad \text {and}\quad x'(t_{n})\rightarrow 0\quad \text {as}\quad n\rightarrow \infty . \end{aligned}$$

Applying (2.4), $(H_{1})$, and $\displaystyle \lim _{t\rightarrow \infty }f'(u)F(u)=q$, we see that

$$\begin{aligned}&b(P(t_{n})e^{x(t_{n})}-1)\\&\quad =ax'(t_{n})-(q-1)x'(t_{n})^{2}-(f'(u)F(u)-q)(x'(t_{n})+2)^{2}+Q(t_{n})(x'(t_{n})+2)\nonumber \\&\quad \rightarrow 0\quad \text {as}\quad n\rightarrow \infty .\nonumber \end{aligned}$$

(3.4)

On the other hand, we observe from (3.1) and $(H_{1})$ that

$$\begin{aligned} b(P(t_{n})e^{x(t_{n})}-1)\rightarrow b(e^{c}-1)\quad \text {as}\quad n\rightarrow \infty . \end{aligned}$$

From the assumption that $c\not =0$, it follows that $b(e^{c}-1)\not =0$. This contradicts (3.4), and we obtain (3.2) when $x'(t)\ge 0$ for all t large enough. Furthermore, for the case where $x'(t)\le 0$ for all sufficiently large t, we lead a contradiction by the similar argument as in the above. Then, we derive (3.2).

By (2.4), we have

$$\begin{aligned} x''(t)&=ax'(t)-b(P(t)e^{x(t)}-1)-(q-1)x'(t)^{2}-(f'(u)F(u)-q)(x'(t)+2)^{2}\\&\quad +Q(t)(x'(t)+2). \end{aligned}$$

Letting $t\rightarrow \infty$ and using (3.1)–(3.2), $(H_{1})$, and $\displaystyle \lim _{t\rightarrow \infty }f'(u)F(u)=q$, we obtain

$$\begin{aligned} x''(t)\rightarrow -b(e^{c}-1)\not =0\quad \text {as}\quad t\rightarrow \infty . \end{aligned}$$

Thus, we see that $|x'(t)|\rightarrow \infty$ as $t\rightarrow \infty$. This contradicts (3.2). Then, we have $c=0$, i.e., $x(t)\rightarrow 0$ as $t\rightarrow \infty$. $\square$

Next, we consider the case (ii).

Lemma 3.4

Assume that the sign of $x'(t)$ changes infinitely many times as $t\rightarrow \infty$. Then, $x'(t)$ is bounded for $t\ge t_{0}$.

Proof

Assume to the contrary that $\displaystyle \limsup _{t\rightarrow \infty }|x'(t)|=\infty$. It follows from Lemma 3.2 (ii) and the oscillation of $x'(t)$ that

$$\begin{aligned} -2\le \liminf _{t\rightarrow \infty }x'(t)\le 0<\limsup _{t\rightarrow \infty }x'(t)=\infty . \end{aligned}$$

(3.5)

First we consider the case where $q>1$. By (3.5), we find a sequence $\{t_{n}\}$ such that

$$\begin{aligned} t_{n}\rightarrow \infty ,\quad x'(t_{n})\rightarrow \infty \quad \text {as}\quad n\rightarrow \infty ,\quad \text {and}\quad x''(t_{n})=0. \end{aligned}$$

(3.6)

We observe from Lemma 3.2 (i) that $e^{x(t)}$ is bounded for $t\ge t_{0}$. Thus, using (2.4), (3.6), $(H_{1})$ and (1.5), we have

$$\begin{aligned} 0&=-ax'(t_{n})+b(P(t_{n})e^{x(t_{n})}-1)+(q-1)x'(t_{n})^{2}-Q(t_{n})(x'(t_{n})+2)\\&\quad +(f'(u)F(u)-q)(x'(t_{n})+2)^{2}\rightarrow \infty \quad \text {as}\quad n\rightarrow \infty . \end{aligned}$$

This is a contradiction.

Next, we consider the case where $q=1$. By (3.5), $x'(t)$ oscillates between 0 and an arbitrary fixed constant. Thus, for any $M>0$, there exists a sequence $\{t_{n}\}$ such that

$$\begin{aligned} t_{n}\rightarrow \infty \quad \text {as}\quad n\rightarrow \infty ,\quad x'(t_{n})=M,\quad \text {and}\quad x''(t_{n})\le 0. \end{aligned}$$

(3.7)

Then, making use of (3.7) and (2.4) with $q=1$, we have

$$\begin{aligned} 0&\le -x''(t_{n})\\&=-aM+b(P(t_{n})e^{x(t_{n})}-1)+(f'(u)F(u)-1)(M+2)^{2}-Q(t_{n})(M+2). \end{aligned}$$

This implies that

$$\begin{aligned} e^{x(t_{n})}\ge \frac{1}{bP(t_{n})}\{aM-(f'(u)F(u)-1)(M+2)^{2}+Q(t_{n})(M+2)\}+\frac{1}{P(t_{n})}. \end{aligned}$$

It follows from $(H_{1})$ and (1.5) that

$$\begin{aligned} \liminf _{n\rightarrow \infty }e^{x(t_{n})}\ge \frac{aM}{b}+1. \end{aligned}$$

Since $M>0$ is arbitrary, we can take sufficiently large $M>0$. This contradicts Lemma 3.2 (i).

Therefore, we obtain $\displaystyle \limsup _{t\rightarrow \infty }|x'(t)|<\infty$, and this implies that $x'(t)$ is bounded for $t\ge t_{0}$ when $q\ge 1$. $\square$

For the case of (ii), in order to show $\displaystyle \lim _{t\rightarrow \infty }x(t)=0$, we shall introduce another lemma. To this aim, we consider the ordinary differential equation

$$\begin{aligned} w''(t)-c(t)w'(t)+\gamma (w(t)^{p}-w(t))+G(t)=0\quad \text {for}\quad t\ge t_{0}, \end{aligned}$$

(3.8)

where $\gamma >0$ and $p>1$ are constants, $c\in C[t_{0},\infty )$ and $G\in C[t_{0},\infty )$. In addition, we assume that

$$\begin{aligned} c(t)\ge c_{*}>0\quad \text {for}\quad t\ge t_{0}, \end{aligned}$$

with some constant $c_{*}>0$, and

$$\begin{aligned} G(t)\rightarrow 0\quad \text {as}\quad t\rightarrow \infty . \end{aligned}$$

Then, the following lemma has been proved in [37].

Lemma 3.5

(Lemma 3.4 in [37]) Let $w\in C^{2}[t_{0},\infty )$ be a bounded positive solution of (3.8). Assume that the sign of $w'(t)$ changes infinitely many times as $t\rightarrow \infty$. Then, $w(t)\rightarrow 1$ as $t\rightarrow \infty$.

Applying Lemma 3.5, we shall obtain $\displaystyle \lim _{t\rightarrow \infty }x(t)=0$.

Lemma 3.6

Assume that the sign of $x'(t)$ changes infinitely many times as $t\rightarrow \infty$. Then, $x(t)\rightarrow 0$ as $t\rightarrow \infty$.

Proof

Firstly, we treat the case where $q=1$. It follows from Lemma 3.4 that $x'(t)$ is bounded for $t\ge t_{0}$. Since $Q(t)\rightarrow 0$ as $t\rightarrow \infty$ by $(H_{1})$, there exist $q_{0}>1$ and $t_{1}\ge t_{0}$ such that

$$\begin{aligned} a-(q_{0}-1)|x'(t)|+Q(t)>0\quad \text {for}\quad t\ge t_{1}, \end{aligned}$$

(3.9)

where a is the constant in (2.5) with $q=1$, i.e., $a=N-2>0$. Define $z(t)=e^{(q_{0}-1)x(t)}$. We observe from (2.4) with $q=1$ that z(t) satisfies

$$\begin{aligned} z''(t)-\alpha (t)z'(t)+b(q_{0}-1)(z(t)^{p_{0}}-z(t))+(q_{0}-1)H(t)=0, \end{aligned}$$

where $\alpha (t)=a+(q_{0}-1)x'(t)+Q(t)$, $p_{0}=q_{0}/(q_{0}-1)$, and

$$\begin{aligned} H(t)&=-b(1-P(t))z(t)^{p_{0}}+z(t)(f'(u)F(u)-1)(x'(t)+2)^{2}-2Q(t)z(t)\\&=e^{(q_{0}-1)x}\{-b(1-P)e^{(p_{0}-1)(q_{0}-1)x}+(f'(u)F(u)-1)(x'+2)^{2}-2Q\}. \end{aligned}$$

Then, it follows from (3.9) that

$$\begin{aligned} \alpha _{*}=\inf _{t\ge t_{1}}\alpha (t)>0. \end{aligned}$$

(3.10)

Moreover, we claim that

$$\begin{aligned} H(t)\rightarrow 0\quad \text {as}\quad t\rightarrow \infty . \end{aligned}$$

(3.11)

Indeed, Lemma 3.2 (i) implies that x(t) is bounded above for $t\ge t_{0}$, and Lemma 3.4 implies that $x'(t)$ is bounded for $t\ge t_{0}$. Furthermore, we have $f'(u)F(u)\rightarrow 1$ as $t\rightarrow \infty$ and it follows from $(H_{1})$ that $P(t)\rightarrow 1$ and $Q(t)\rightarrow 0$ as $t\rightarrow \infty$. Hence, (3.11) holds. Then, applying Lemma 3.5 with (3.10)–(3.11), we obtain $z(t)\rightarrow 1$ as $t\rightarrow \infty$. This implies that $x(t)\rightarrow 0$ as $t\rightarrow \infty$ in the case of $q=1$.

Next, we consider the case where $q>1$. Since $Q(t)\rightarrow 0$ as $t\rightarrow \infty$ by $(H_{1})$, there exists $t_{1}\ge t_{0}$ such that

$$\begin{aligned} a+Q(t)>0\quad \text {for}\quad t\ge t_{1}, \end{aligned}$$

(3.12)

where a is the constant in (2.5), i.e., $a=N+2-4q>0$. Define $z(t)=e^{(q-1)x(t)}$. It follows from (2.6) that z(t) satisfies

$$\begin{aligned}&z''(t)-az'(t)-Q(t)z'(t)+b(q-1)(z(t)^{p}-z(t))-b(q-1)(1-P(t))z(t)^{p}\\&+(q-1)(f'(u)F(u)-q)\left( \frac{z'(t)}{(q-1)z(t)}+2\right) ^{2}z(t)-2(q-1)Q(t)z(t)=0. \end{aligned}$$

Setting $\tilde{\alpha }(t)=a+Q(t)$, and

$$\begin{aligned} \tilde{H}(t)=-b(1-P)z^{p}+(f'(u)F(u)-q)\left( \frac{z'}{(q-1)z}+2\right) ^{2}z-2Qz, \end{aligned}$$

we derive

$$\begin{aligned} z''(t)-\tilde{\alpha }(t)z'(t)+b(q-1)(z(t)^{p}-z(t))+(q-1)H(t)=0. \end{aligned}$$

By (3.12), we have

$$\begin{aligned} \tilde{\alpha }_{*}=\inf _{t\ge t_{1}}\tilde{\alpha }(t)>0. \end{aligned}$$

(3.13)

Furthermore, applying $f'(u)F(u)\rightarrow q$ as $t\rightarrow \infty$ and the same way as in the case of $q=1$, we obtain

$$\begin{aligned} \tilde{H}&=e^{(q-1)x}\{-b(1-P)e^{(p-1)(q-1)x}+(f'(u)F(u)-q)(x'+2)^{2}-2Q\}\nonumber \\&\rightarrow 0\quad \text {as}\quad t\rightarrow \infty . \end{aligned}$$

(3.14)

Therefore, it follows from Lemma 3.5 with (3.13)–(3.14) that $z(t)\rightarrow 1$ as $t\rightarrow \infty$. Hence, $x(t)\rightarrow 0$ as $t\rightarrow \infty$ for $q>1$. $\square$

Now we are in a position to prove Proposition 3.1.

Proof

(Proof of Proposition 3.1) Combining Lemma 3.3 and Lemma 3.6, we derive $\displaystyle \lim _{t\rightarrow \infty }x(t)=0$.

We shall prove that $\displaystyle \lim _{t\rightarrow \infty }x'(t)=0$. Define $\alpha$ and $\beta$ by

$$\begin{aligned} \alpha =\limsup _{t\rightarrow \infty }x'(t),\quad \beta =\liminf _{t\rightarrow \infty }x'(t). \end{aligned}$$

To begin with, we show that

$$\begin{aligned} \alpha =\beta . \end{aligned}$$

(3.15)

Assume to the contrary that $\alpha \not =\beta$. Then, either $\alpha \not =0$ or $\beta \not =0$ holds. We may assume here that $\alpha \not =0$. First we consider the case where $q=1$. By $\alpha \not =\beta$, there exists a sequence $\{t_{n}\}$ with $\displaystyle \lim _{n\rightarrow \infty }t_{n}=\infty$ such that

$$\begin{aligned} x''(t_{n})=0,\quad \text {and}\quad x'(t_{n})\rightarrow \alpha \not =0\quad \text {as}\quad n\rightarrow \infty . \end{aligned}$$

We observe from (2.4) with $q=1$ that

$$\begin{aligned} ax'(t_{n})&=b(P(t_{n})e^{x(t_{n})}-1)+(f'(u)F(u)-1)(x'(t_{n})+2)^{2}\\&\quad -Q(t_{n})(x'(t_{n})+2). \end{aligned}$$

Letting $n\rightarrow \infty$ and applying $(H_{1})$, (1.5) with $q=1$, and $\displaystyle \lim _{t\rightarrow \infty }x(t)=0$, we derive $a\alpha =0$. This contradicts $\alpha \not =0$.

For $q>1$, let $z(t)=e^{(q-1)x(t)}$. Using $\displaystyle \lim _{t\rightarrow \infty }x(t)=0$, we have

$$\begin{aligned} \lim _{t\rightarrow \infty }z(t)=1,\quad \limsup _{t\rightarrow \infty }z'(t)=(q-1)\alpha ,\quad \liminf _{t\rightarrow \infty }z'(t)=(q-1)\beta . \end{aligned}$$

By $\alpha \not =\beta$, there exists a sequence $\{t_{n}\}$ with $\displaystyle \lim _{n\rightarrow \infty }t_{n}=\infty$ such that

$$\begin{aligned} z''(t_{n})=0,\quad \text {and}\quad z'(t_{n})\rightarrow (q-1)\alpha \not =0\quad \text {as}\quad n\rightarrow \infty . \end{aligned}$$

Then, we have

$$\begin{aligned} x'(t_{n})=\frac{z'(t_{n})}{q-1}e^{-(q-1)x(t_{n})}\rightarrow \alpha \quad \text {as}\quad n\rightarrow \infty , \end{aligned}$$

and thus,

$$\begin{aligned} \frac{z'(t_{n})}{z(t_{n})}=(q-1)x'(t_{n})\rightarrow (q-1)\alpha \quad \text {as}\quad n\rightarrow \infty . \end{aligned}$$

From (2.6), it follows that

$$\begin{aligned} az'(t_{n})&=(q-1)b(P(t_{n})z(t_{n})^{p}-z(t_{n}))-(q-1)Q(t_{n})\left( \frac{z'(t_{n})}{(q-1)z(t_{n})}+2\right) z(t_{n})\\&\quad +(q-1)(f'(u)F(u)-q)\left( \frac{z'(t_{n})}{(q-1)z(t_{n})}+2\right) ^{2}z(t_{n}). \end{aligned}$$

Letting $n\rightarrow \infty$ and applying $(H_{1})$, (1.5), we obtain

$$\begin{aligned} a(q-1)\alpha =0, \end{aligned}$$

which contradicts $\alpha \not =0$.

If we assume that $\beta \not =0$, then by the similar methods as in the above, we can lead a contradiction. Therefore, (3.15) holds in both cases where $q=1$ and $q>1$, and then, $x'(t)\rightarrow \alpha$ as $t\rightarrow \infty$. Moreover, since $x(t)\rightarrow 0$ as $t\rightarrow \infty$, we have $\alpha =0$. Hence, we obtain $x'(t)\rightarrow 0$ as $t\rightarrow \infty$. $\square$

4 Uniqueness of the singular solution

We shall prove the following theorem:

Theorem 4.1

There exists at most one singular solution of (1.3).

In order to prove Theorem 4.1, we shall apply the next lemma:

Lemma 4.2

(Lemma 4.2 in [28]) Let y(t) be a solution of

$$\begin{aligned} y''(t)-A(t)y'(t)+B(t)y(t)=0, \end{aligned}$$

(4.1)

where A(t) and B(t) are continuous functions satisfying

$$\begin{aligned} \lim _{t\rightarrow \infty }A(t)=\alpha>0,\quad \lim _{t\rightarrow \infty }B(t)=\beta >0. \end{aligned}$$

(4.2)

If y(t) is bounded as $t\rightarrow \infty$, then $y(t)\equiv 0$.

Proof

(Proof of Theorem 4.1) Let $u_{j}(r) (j=1, 2)$ be singular solutions of (1.3) for $0<r<r_{0}$. For $j=1, 2$, define $x_{j}(t)$ by

$$\begin{aligned} \frac{F(u_{j}(r))}{\psi (r)^{2}}=\frac{e^{-x_{j}(t)}}{2N-4q},\quad t=-\log \psi (r). \end{aligned}$$

It follows from Proposition 3.1 that $x_{j}(t)\rightarrow 0$ as $t\rightarrow \infty$ for $j=1, 2$. Define $y(t)=x_{1}(t)-x_{2}(t)$, and then y(t) is bounded as $t\rightarrow \infty$. Using Lemma 4.2, we shall show that $y(t)\equiv 0$.

By (2.4), $x_{j}(t)$ $(j=1, 2)$ satisfies

$$\begin{aligned} x_{j}''(t)&-ax_{j}'(t)+b(P(t)e^{x_{j}(t)}-1)+(q-1)x'_{j}(t)^{2}-Q(t)(x'_{j}(t)+2)\\&+(f'(u_{j})F(u_{j})-q)(x'_{j}(t)+2)^{2}=0. \end{aligned}$$

Setting

$$\begin{aligned} E(x_{1},x_{2})={\left\{ \begin{array}{ll} P(t)\dfrac{e^{x_{1}}-e^{x_{2}}}{x_{1}-x_{2}}&{}\quad \text {if}\quad x_{1}\not =x_{2},\\ P(t)e^{x_{1}}&{}\quad \text {if}\quad x_{1}=x_{2}, \end{array}\right. } \end{aligned}$$

we see that y(t) satisfies (4.1), where

$$\begin{aligned} A(t)&=a-(q-1)(x'_{1}+x'_{2})-(f'(u_{1})F(u_{1})-q)(x'_{1}+x'_{2}+4)+Q,\\ B(t)&=bE(x_{1},x_{2})+(x'_{2}(t)+2)^{2}(f'(u_{1})F(u_{1})-f'(u_{2})F(u_{2})). \end{aligned}$$

Let $w_{j}=F(u_{j})$ for $j=1, 2$. Then, we have

$$\begin{aligned} f'(u_{1})F(u_{1})-f'(u_{2})F(u_{2})=w_{1}f'(F^{-1}(w_{1}))-w_{2}f'(F^{-1}(w_{2})). \end{aligned}$$

By the mean value theorem, we derive

$$\begin{aligned} \frac{d}{dw}(wf'(F^{-1}(w)))=f'(F^{-1}(w))-wf''(F^{-1}(w))f(F^{-1}(w)). \end{aligned}$$

Hence, we find $\bar{w}$ between $w_{1}$ and $w_{2}$ such that

$$\begin{aligned} w_{1}&f'(F^{-1}(w_{1}))-w_{2}f'(F^{-1}(w_{2}))\\&=\{f'(F^{-1}(\bar{w}))-\bar{w}f''(F^{-1}(\bar{w}))f(F^{-1}(\bar{w}))\}(w_{1}-w_{2}). \end{aligned}$$

Recalling that $F'(u)=-1/f(u)$, we see that F is monotone. Thus, there exists $\bar{u}$ between $u_{1}$ and $u_{2}$ such that $F(\bar{u})=\bar{w}$. Then, we derive

$$\begin{aligned}&f'(u_{1})F(u_{1})-f'(u_{2})F(u_{2})\nonumber \\&=\{f'(F^{-1}(\bar{w}))-\bar{w}f''(F^{-1}(\bar{w}))f(F^{-1}(\bar{w}))\}(w_{1}-w_{2})\nonumber \\&=\left\{ 1-f'(\bar{u})F(\bar{u})\frac{f''(\bar{u})f(\bar{u})}{f'(\bar{u})^{2}}\right\} f'(\bar{u})(F(u_{1})-F(u_{2})). \end{aligned}$$

(4.3)

Defining $\bar{x}$ by

$$\begin{aligned} F(\bar{u}(t))=\frac{\psi (r)^{2}e^{-\bar{x}(t)}}{2N-4q}, \end{aligned}$$

(4.4)

we have

$$\begin{aligned} F(u_{1})-F(u_{2})=\frac{\psi (r)^{2}}{2N-4q}(e^{-x_{1}}-e^{-x_{2}})=-F(\bar{u})e^{\bar{x}}\frac{E(-x_{1},-x_{2})}{P}y. \end{aligned}$$

(4.5)

We observe from (4.3) and (4.5) that

$$\begin{aligned} B&(t)=bE(x_{1},x_{2})\\&-(x'_{2}+2)^{2}\left\{ 1-f'(\bar{u})F(\bar{u})\frac{f''(\bar{u})f(\bar{u})}{f'(\bar{u})^{2}} \right\} f'(\bar{u})F(\bar{u})e^{\bar{x}}\frac{E(-x_{1},-x_{2})}{P}. \end{aligned}$$

Then, we claim that A(t) and B(t) satisfies (4.2). Indeed, applying Proposition 3.1, (1.5), and $(H_{1})$, we derive

$$\begin{aligned} A(t)\rightarrow a>0\quad \text {as}\quad t\rightarrow \infty . \end{aligned}$$

Since $\bar{u}$ lies between $u_{1}$ and $u_{2}$, it follows from (4.4) that $\bar{x}$ lies between $x_{1}$ and $x_{2}$. Thus, by Proposition 3.1, we have $\bar{x}\rightarrow 0$ as $t\rightarrow \infty$. Moreover, since $E(x_{1},x_{2})$ are continuous at $x_{1}=x_{2}=0$, it follows from the mean-value theorem that

$$\begin{aligned} \lim _{t\rightarrow \infty }E(x_{1},x_{2})=1. \end{aligned}$$

Then, making use of (1.4)–(1.5), $(H_{1})$, and Proposition 3.1, we obtain

$$\begin{aligned} B(t)\rightarrow b>0\quad \text {as}\quad t\rightarrow \infty . \end{aligned}$$

Hence, A(t) and B(t) satisfies (4.2), and we observe from Lemma 4.2 that $y(t)\equiv 0$, i.e., $x_{1}(t)=x_{2}(t)$. Thus, (1.3) has at most one singular solution. $\square$

5 Estimate of solutions

We devote this section to obtaining an estimate for regular solutions to (1.3). To the aim, setting

$$\begin{aligned} G(u)=\int ^{u}_{0}f(s)ds, \end{aligned}$$

(5.1)

we construct a Pohozaev type identity.

Lemma 5.1

Let u(r) be a solution of (1.3) in $(r_{1},r_{2})\subset (0,\infty )$, and let $\mu$ be an arbitrary constant. Then, for each $r\in (r_{1},r_{2})$, we have

$$\begin{aligned} \frac{d}{dr}&\left\{ \psi (r)^{N}\left( \frac{1}{2}u'(r)^{2}+G(u)+\frac{\mu }{\psi }u(r)u'(r)\right) \right\} \nonumber \\ =&\psi (r)^{N-1}\left\{ \left( \mu +\left( 1-\frac{N}{2}\right) \psi '(r)\right) u'(r)^{2}+N\psi '(r)G(u)-\mu u(r)f(u(r))\right\} . \end{aligned}$$

(5.2)

Proof

We observe from (1.3) that

$$\begin{aligned} -(\psi ^{N-1}u')'&=\psi ^{N-1}f(u),\\ \left( \frac{|u'|^{2}}{2}\right) '&=u'u''=-\frac{\psi '}{\psi }(N-1)(u')^{2}-f(u)u'. \end{aligned}$$

Then, we have

$$\begin{aligned}&\frac{d}{dr}\left\{ \psi ^{N}\left( \frac{|u'|^{2}}{2}+G(u)+\frac{\mu }{\psi }uu'\right) \right\} \\&=\frac{N}{2}\psi ^{N-1}\psi '|u'|^{2}+\psi ^{N}\left( \frac{|u'|^{2}}{2}\right) '+N\psi ^{N-1}\psi 'G(u)+\psi ^{N}fu'\\&\qquad +\mu (\psi ^{N-1}u')'u+\mu \psi ^{N-1}(u')^{2}\\&=\psi ^{N-1}\left\{ \left( \mu +\left( \frac{N}{2}-(N-1)\right) \psi '\right) (u')^{2}+N\psi 'G(u)-\mu uf(u)\right\} . \end{aligned}$$

Thus, we obtain (5.2). $\square$

We define regular solutions to (1.3). For $\alpha >0$, we denote by $u(r, \alpha )$ a solution of (1.3) satisfying $u(0)=\alpha$ and $u'(0)=0$. Then, we show the following lemma:

Lemma 5.2

Assume that there exists $p_{0}>2N/(N-2)$ and $\hat{u_{0}}>0$ such that

$$\begin{aligned} 0<p_{0}G(u)<uf(u)\quad \text {for}\quad u>\hat{u_{0}}. \end{aligned}$$

(5.3)

(i) Let $\alpha >\hat{u_{0}}$. Assume that there exists $\hat{r_{0}}\in (0,R_{0})$ such that

$$\begin{aligned} u(r,\alpha )>\hat{u_{0}},\quad \frac{2N}{p_{0}(N-2)}<\psi '(r)\le \min _{u>\hat{u_{0}}}\frac{uf(u)}{p_{0}G(u)}\quad \text {for}\quad r\in (0,\hat{r_{0}}]. \end{aligned}$$

(5.4)

Then,

$$\begin{aligned} 0<-\psi (r) u'(r,\alpha )<\frac{2N}{p_{0}}u(r,\alpha )\quad \text {for}\quad r\in (0,\hat{r_{0}}]. \end{aligned}$$

(ii) Put

$$\begin{aligned} \delta =\frac{1}{2}+\frac{N}{p_{0}(N-2)},\quad \eta =\frac{1}{2}\left\{ 1-\frac{2N}{\delta (N-2)p_{0}}\right\} . \end{aligned}$$

(5.5)

Assume that there exists $r_{1}\in (0,R_{0})$ such that

$$\begin{aligned} \delta \le \psi '(r)\le \min _{u>\hat{u_{0}}}\frac{uf(u)}{p_{0}G(u)}\quad \text {for}\quad r\in (0,r_{1}]. \end{aligned}$$

(5.6)

Take any $\beta >\hat{u_{0}}$, and define $r_{\beta }$ by

$$\begin{aligned} r_{\beta }=\min \left[ r_{1},\left\{ \frac{2\beta }{f_{M}(\beta /\eta )}\right\} ^{\frac{1}{2}}\right] , \end{aligned}$$

(5.7)

where $f_{M}(r)=\displaystyle \max _{0\le s\le r}f(s)$. If $\alpha >\beta /\eta$, then $u(r,\alpha )>\beta$ for $r\in [0,r_{\beta }]$.

Proof

(i) Setting $\mu =N/p_{0}$ in (5.2), we have

$$\begin{aligned}&\frac{d}{dr}\left\{ \psi ^{N}\left( \frac{1}{2}(u')^{2}+G(u)+\frac{N}{p_{0}}\frac{uu'}{\psi }\right) \right\} \\&\quad =\psi ^{N-1}\left\{ \left( \frac{N}{p_{0}}+\left( 1-\frac{N}{2}\right) \psi '\right) (u')^{2}+N\psi 'G(u) -\frac{N}{p_{0}}uf(u)\right\} .\nonumber \end{aligned}$$

(5.8)

We observe from (5.4) that

$$\begin{aligned} \frac{N}{p_{0}}+\left( 1-\frac{N}{2}\right) \psi '<\frac{N}{p_{0}}-\frac{N-2}{2}\frac{2N}{p_{0}(N-2)} =0\quad \text {for}\quad r\in (0,\hat{r_{0}}]. \end{aligned}$$

(5.9)

Moreover, applying (5.4) again, we have

$$\begin{aligned} N\psi 'G(u)-\frac{N}{p_{0}}uf(u)=NG(u)\left( \psi '-\frac{uf(u)}{p_{0}G(u)}\right) \le 0\ \text {for}\ r\in (0,\hat{r_{0}}]. \end{aligned}$$

(5.10)

Combining (5.9)–(5.10) with (5.8), we derive

$$\begin{aligned} \frac{d}{dr}\left\{ \psi ^{N}\left( \frac{1}{2}(u')^{2}+G(u)+\frac{N}{p_{0}}\frac{uu'}{\psi }\right) \right\} <0\quad \text {for}\quad r\in (0,\hat{r_{0}}]. \end{aligned}$$

Integrating the above on (0, r] with $0<r\le \hat{r_{0}}$ and applying $(H_{1})$, we obtain

$$\begin{aligned} \psi ^{N}\left( \frac{1}{2}(u')^{2}+G(u)+\frac{N}{p_{0}}\frac{uu'}{\psi }\right) <0\quad \text {for}\quad r\in (0,\hat{r_{0}}]. \end{aligned}$$

Thus, we have

$$\begin{aligned} \frac{1}{2}(u')^{2}+G(u)+\frac{N}{p_{0}}\frac{uu'}{\psi }<0\quad \text {for}\quad r\in (0,\hat{r_{0}}]. \end{aligned}$$

(5.11)

It follows from (5.3)–(5.4) that $u(r,\alpha )>\hat{u_{0}}>0$ and $G(u)>0$ for $r\in (0,\hat{r_{0}}]$. Applying (5.11), we have

$$\begin{aligned} u'(r,\alpha )<0\quad \text {for}\quad r\in (0,\hat{r_{0}}]. \end{aligned}$$

(5.12)

Furthermore, by (5.11), we derive for $r\in (0,\hat{r_{0}}]$,

$$\begin{aligned} 0>\frac{1}{2}(u')^{2}+G(u)+\frac{N}{p_{0}}\frac{uu'}{\psi }>\frac{1}{2}(u')^{2}+\frac{N}{p_{0}} \frac{uu'}{\psi }=u'\left\{ \frac{u'}{2}+\frac{N}{p_{0}}\frac{u}{\psi }\right\} . \end{aligned}$$

Using (5.12), we obtain

$$\begin{aligned} 0<\frac{u'}{2}+\frac{N}{p_{0}}\frac{u}{\psi }\quad \text {for}\quad r\in (0,\hat{r_{0}}]. \end{aligned}$$

Therefore, we see that

$$\begin{aligned} -\psi u'<\frac{2N}{p_{0}}u\quad \text {for}\quad r\in (0,\hat{r_{0}}]. \end{aligned}$$

Combining (5.12) with the above, we obtain

$$\begin{aligned} 0<-\psi (r) u'(r,\alpha )<\frac{2N}{p_{0}}u(r,\alpha )\quad \text {for}\quad r\in (0,\hat{r_{0}}]. \end{aligned}$$

(ii) By $\alpha >\beta /\eta$ and $\eta <1/2$, we have

$$\begin{aligned} \alpha>\frac{\beta }{\eta }>2\beta>\beta >\hat{u_{0}}. \end{aligned}$$

Assume to the contrary that there exists $r_{*}\in (0,r_{\beta }]$ such that

$$\begin{aligned} u(r,\alpha )>\beta \quad \text {for}\quad r\in [0,r_{*}),\quad \text {and}\quad u(r_{*},\alpha )=\beta . \end{aligned}$$

(5.13)

Since $\alpha>\beta >\hat{u_{0}}$, $\delta >\frac{N}{p_{0}(N-2)}$ and $r_{*}\le r_{\beta }\le r_{1}$, we observe from Lemma 5.2 (i) with $\hat{r}_{0}=r_{\beta }$ that

$$\begin{aligned} u'(r,\alpha )<0\quad \text {for}\quad r\in (0,r_{*}]. \end{aligned}$$

(5.14)

Put $B=\beta /\eta$. Since $\alpha>B>\beta$, there exists $R_{B}\in (0,r_{*})$ such that

$$\begin{aligned} u(R_{B},\alpha )=B\quad \text {and}\quad u(r,\alpha )\le B\quad \text {for}\quad r\in [R_{B},r_{*}]. \end{aligned}$$

(5.15)

Let v be a solution of the initial value problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -(\psi ^{N-1}v')'=\psi ^{N-1}f_{M}(B)\quad \text {for}\quad r\in (R_{B},r_{*}),\\ v(R_{B})=u(R_{B},\alpha ),\quad v'(R_{B})=u'(R_{B},\alpha ). \end{array}\right. } \end{aligned}$$

(5.16)

First, we will show that

$$\begin{aligned} v(r)\le u(r,\alpha )\quad \text {for}\quad r\in [R_{B},r_{*}]. \end{aligned}$$

(5.17)

Put $w(r)=v(r)-u(r,\alpha )$. Then, w satisfies

$$\begin{aligned}&-(\psi ^{N-1}w')'=\psi ^{N-1}(f_{M}(B)-f(u(r,\alpha ))\quad \text {for}\quad r\in (R_{B},r_{*}),\\&w(R_{B})=v(R_{B})-u(R_{B},\alpha )=0,\quad w'(R_{B})=v'(R_{B})-u'(R_{B},\alpha )=0.\nonumber \end{aligned}$$

(5.18)

It follows from (5.15) that

$$\begin{aligned} f_{M}(B)\ge f(u(r,\alpha ))\quad \text {for}\quad r\in [R_{B},r_{*}]. \end{aligned}$$

Then, integrating (5.18) on $[R_{B},r]$ with $r\le r_{*}$, we obtain for $r\in [R_{B},r_{*}]$,

$$\begin{aligned} -\psi (r)^{N-1}w'(r)&=-\psi (R_{B})^{N-1}w'(R_{B})+\!\!\int ^{r}_{R_{B}}\!\!\!\psi (s)^{N-1}(f_{M}(B)-f(u(s,\alpha ))ds\\&=\int ^{r}_{R_{B}}\psi (s)^{N-1}(f_{M}(B)-f(u(s,\alpha )))ds\ge 0. \end{aligned}$$

Thus, we have $w'(r)\le 0$ for $r\in [R_{B},r_{*}]$. Since $w(R_{B})=0$ and w is non-increasing for $r\in [R_{B},r_{*}]$, we derive $w(r)\le 0$ for $r\in [R_{B},r_{*}]$. Therefore, (5.17) holds.

Secondly, integrating the equation in (5.16) on $[R_{B},r]$ with $r\le r_{*}$, we have

$$\begin{aligned} -\psi (r)^{N-1}v'(r)&=-\psi (R_{B})^{N-1}v'(R_{B}) +f_{M}(B)\int ^{r}_{R_{B}}\psi (s)^{N-1}ds\\&\le -\psi (R_{B})^{N-1}v'(R_{B})+f_{M}(B)\int ^{r}_{0}\psi (s)^{N-1}ds. \end{aligned}$$

From $r_{1}<R_{0}$ and (2.2), it follows that $\psi$ is strictly increasing on $[0,r_{1}]$. Hence, we derive

$$\begin{aligned} -v'(r)\le -\frac{\psi (R_{B})^{N-1}v'(R_{B})}{\psi (r)^{N-1}}+f_{M}(B)r. \end{aligned}$$

Integrating the above on $[R_{B},r_{*}]$, we obtain

$$\begin{aligned} -v(r_{*})+v(R_{B})&\le -\psi (R_{B})^{N-1}v'(R_{B})\int ^{r_{*}}_{R_{B}} \frac{ds}{\psi (s)^{N-1}}+f_{M}(B)\frac{r^{2}_{*}}{2}\\&=-\frac{\psi (R_{B})^{N-1}v'(R_{B})}{\delta }\int ^{r_{*}}_{R_{B}} \frac{\delta }{\psi (s)^{N-1}}ds+f_{M}(B)\frac{r^{2}_{*}}{2}. \end{aligned}$$

Since $v'(R_{B})=u'(R_{B},\alpha )<0$ by (5.14), $r_{*}\le r_{\beta }$, and $\delta \le \psi '(r)$ for $r\in (0,r_{\beta }]$ by (5.6)–(5.7), we have

$$\begin{aligned} -v(r_{*})&+v(R_{B})\le -\frac{\psi (R_{B})^{N-1}v'(R_{B})}{\delta }\int ^{r_{*}}_{R_{B}} \frac{\psi '(s)}{\psi (s)^{N-1}}ds+f_{M}(B)\frac{r^{2}_{\beta }}{2}\\&=\frac{\psi (R_{B})^{N-1}v'(R_{B})}{\delta (N-2)}\left( \frac{1}{\psi (r_{*})^{N-2}} -\frac{1}{\psi (R_{B})^{N-2}}\right) +f_{M}(B)\frac{r^{2}_{\beta }}{2}\\&\le \frac{\psi (R_{B})^{N-1}v'(R_{B})}{\delta (N-2)}\left( -\frac{1}{\psi (R_{B})^{N-2}}\right) +\beta \\&=-\frac{\psi (R_{B})v'(R_{B})}{\delta (N-2)}+\beta . \end{aligned}$$

Thus, by $v(R_{B})=u(R_{B},\alpha )$, $v'(R_{B})=u'(R_{B},\alpha )$ and Lemma 5.2 (i) with $\hat{r}_{0}=r_{\beta }$, we obtain

$$\begin{aligned} v(r_{*})&\ge v(R_{B})+\frac{\psi (R_{B})v'(R_{B})}{\delta (N-2)}-\beta =u(R_{B},\alpha ) +\frac{\psi (R_{B})u'(R_{B},\alpha )}{\delta (N-2)}-\beta \\&>u(R_{B},\alpha )+\frac{1}{\delta (N-2)}\left( -\frac{2N}{p_{0}}u(R_{B},\alpha )\right) -\beta \\&=u(R_{B},\alpha )\left\{ 1-\frac{2N}{\delta (N-2)p_{0}}\right\} -\beta . \end{aligned}$$

Using (5.5) and (5.15), we see that

$$\begin{aligned} v(r_{*})>2u(R_{B},\alpha )\eta -\beta =2B\eta -\beta =2\frac{\beta }{\eta }\eta -\beta =\beta . \end{aligned}$$

Then, it follows from (5.13) and (5.17) that

$$\begin{aligned} \beta <v(r_{*})\le u(r_{*},\alpha )=\beta . \end{aligned}$$

This leads a contradiction. Thus, $u(r,\alpha )>\beta$ for $r\in [0,r_{\beta }]$. $\square$

6 Proof of Theorem 1.1

Proof

(Proof of Theorem 1.1) Applying (1.4) and L’Hospital’s rule, we have

$$\begin{aligned} \lim _{u\rightarrow \infty }\frac{f(u)}{uf'(u)}=\lim _{u\rightarrow \infty }\frac{f(u)/f'(u)}{u} =\lim _{u\rightarrow \infty }\left( 1-\frac{f(u)f''(u)}{f'(u)^{2}}\right) =\frac{q-1}{q}. \end{aligned}$$

Then, since $f'(u)>0$ for sufficiently large u by Lemma 2.1, we see that $\displaystyle \lim _{t\rightarrow \infty }uf'(u)/f(u)=\infty$ for $q=1$. Defining G(u) by (5.1) and making use of L’Hospital’s rule again, we have

$$\begin{aligned} \lim _{u\rightarrow \infty }\frac{uf(u)}{G(u)}=\lim _{u\rightarrow \infty }\left( 1+\frac{uf'(u)}{f(u)}\right) ={\left\{ \begin{array}{ll} \dfrac{2q-1}{q-1}\quad &{}\text {if}\quad q>1,\\ \infty \quad &{}\text {if}\quad q=1. \end{array}\right. } \end{aligned}$$

(6.1)

Moreover, for $q\in (1,q_{s})$, we derive

$$\begin{aligned} \frac{2q-1}{q-1}>\frac{2N}{N-2}. \end{aligned}$$

Then, we take

$$\begin{aligned} p_{0}\in {\left\{ \begin{array}{ll} \left( \dfrac{2N}{N-2}, \dfrac{2q-1}{q-1}\right) \quad &{}\text {if}\quad q>1,\\ \left( \dfrac{2N}{N-2}, \infty \right) \quad &{}\text {if}\quad q=1. \end{array}\right. } \end{aligned}$$

From (6.1), we find $\hat{u_{0}}\ge u_{0}$ such that (5.3) holds. Furthermore, by $(H_{1})$, there exists $r_{1}\in (0,R_{0})$ such that (5.6) holds. Take $\beta >\hat{u_{0}}$, and define $\eta$ and $r_{\beta }$ by (5.5) and (5.7), respectively. Let $\alpha >\beta /\eta$. It follows from Lemma 5.2 (ii) that

$$\begin{aligned} u(r,\alpha )>\beta >\hat{u_{0}}\ge u_{0}\quad \text {for}\quad r\in [0,r_{\beta }]. \end{aligned}$$

Hence, using Lemma 2.4 (ii), we have

$$\begin{aligned} F(u(r,\alpha ))\ge \frac{\psi (r)^{2}}{2NC_{0}^{2}}\quad \text {for}\quad r\in (0,r_{\beta }], \end{aligned}$$

where $C_{0}=\displaystyle \max _{r\in [0,r_{\beta }]}\psi '(r)\ge 1$. Since $F'(u)=-1/f(u)<0$ for $u\ge u_{0}$, F is monotone decreasing for $u\ge u_{0}$, and

$$\begin{aligned} u(r,\alpha )\le F^{-1}\left[ \frac{\psi (r)^{2}}{2NC_{0}^{2}}\right] \quad \text {for}\quad r\in (0,r_{\beta }]. \end{aligned}$$

(6.2)

By Lemma 5.2 (i) and (6.2), we derive for $r\in (0,r_{\beta }]$,

$$\begin{aligned} 0<-\psi (r) u'(r,\alpha )<\frac{2N}{p_{0}}u(r,\alpha )\le \frac{2N}{p_{0}}F^{-1}\left[ \frac{\psi (r)^{2}}{2NC_{0}^{2}}\right] . \end{aligned}$$

(6.3)

Let $\{\alpha _{k}\}$ be a sequence satisfying $\alpha _{k}\rightarrow \infty$ as $k\rightarrow \infty$. We observe from (6.2)–(6.3) that $u(r,\alpha _{k})$ and $u_{r}(r,\alpha _{k})$ are uniformly bounded in $k\in \mathbb {N}$ on any compact subset of $(0,r_{\beta }]$. Since $f\in C^{2}[0,\infty )$ in (1.3), $u_{rr}(r,\alpha _{k})$ and $u_{rrr}(r,\alpha _{k})$ are also uniformly bounded on the subset. Then, by the Ascoli-Arzelá theorem with the diagonal argument, there exist $u^{*}\in C^{2}(0,r_{\beta }]$ and a subsequence, which is denoted by $\{u(r,\alpha _{k})\}$, such that

$$\begin{aligned} u(r,\alpha _{k})\rightarrow u^{*}(r)\quad \text {in}\quad C^{2}_{loc}(0,r_{\beta }]\quad \text {as}\quad k\rightarrow \infty . \end{aligned}$$

(6.4)

Then, $u^{*}$ satisfies (1.3) for $(0,r_{\beta }]$. Take any $\tilde{\beta }>\beta$. From Lemma 5.2 (ii), it follows that

$$\begin{aligned} u(r_{\tilde{\beta }},\alpha _{k})>\tilde{\beta }\quad \text {if}\quad \alpha _{k}>\frac{\tilde{\beta }}{\eta }. \end{aligned}$$

Thus, letting $k\rightarrow \infty$, we obtain $u^{*}(r_{\tilde{\beta }})\ge \tilde{\beta }$. We observe from that Lemma 2.1 and (5.7) that $f'(u)$, $f(u)\rightarrow \infty$ as $u\rightarrow \infty$ and $r_{\beta }\rightarrow 0$ as $\beta \rightarrow \infty$. Then, since $\tilde{\beta }>\beta$ is arbitrary and $u^{*}(r)$ is non-increasing for $(0,r_{\beta }]$ by Lemma 2.4 (i), we derive

$$\begin{aligned} u^{*}(r)\rightarrow \infty \quad \text {as}\quad r\rightarrow 0. \end{aligned}$$

This implies that $u^{*}$ is a singular solution. Therefore, we can define $u^{*}(r)$ on $(0,r_{0}]$ as a positive singular solution of (1.3) for some $r_{0}\in (0,R_{0})$.

Moreover, Theorem 4.1 implies that the singular solution $u^{*}$ of (1.3) is unique. Thus, for any sequence $\alpha _{k}\rightarrow \infty$, there exists a subsequence such that (6.4) holds. Therefore,

$$\begin{aligned} u(r,\alpha )\rightarrow u^{*}(r)\quad \text {in}\quad C^{2}_{loc}(0,r_{0}]\quad \text {as}\quad \alpha \rightarrow \infty , \end{aligned}$$

and, (1.6) holds. Applying Proposition 3.1 and (2.3), we obtain

$$\begin{aligned} F(u^{*}(r))=\frac{\psi (r)^{2}}{2N-4q}e^{-x(t)}=\frac{\psi (r)^{2}}{2N-4q}(o(1)+1)\quad \text {as}\quad r\rightarrow 0. \end{aligned}$$

Hence, we derive (1.7), and the proof is complete. $\square$